Mechanical Study on Leading Ductule and Pipe Roof Pre-Support Technologies in Tunnel Excavation
Abstract
1. Introduction
2. Numerical Simulations
2.1. Engineering Background
2.2. The Modeling Parameters
2.3. Finite Element Modeling
3. Results
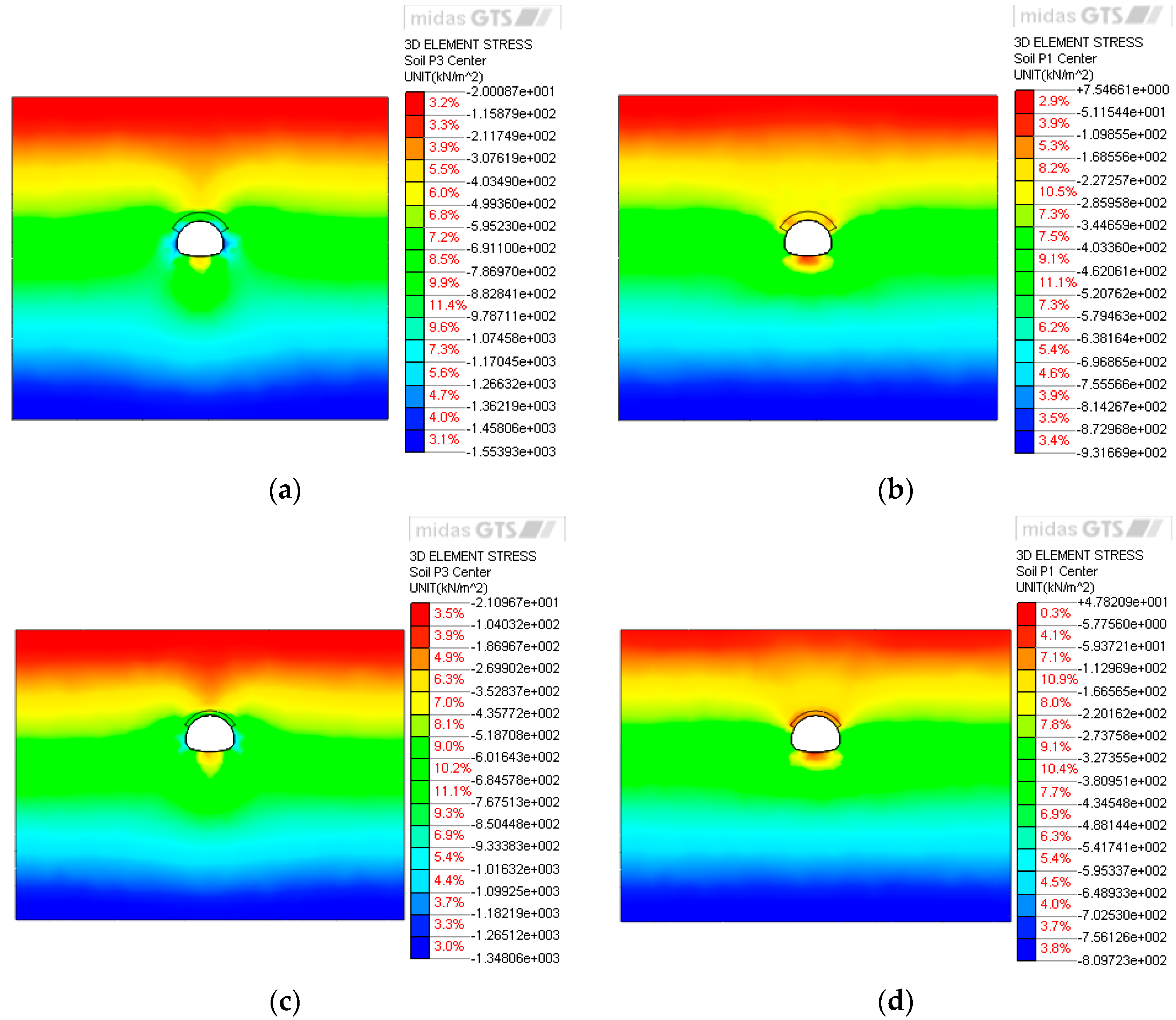
3.1. Stress Analysis of the Surrounding Rock
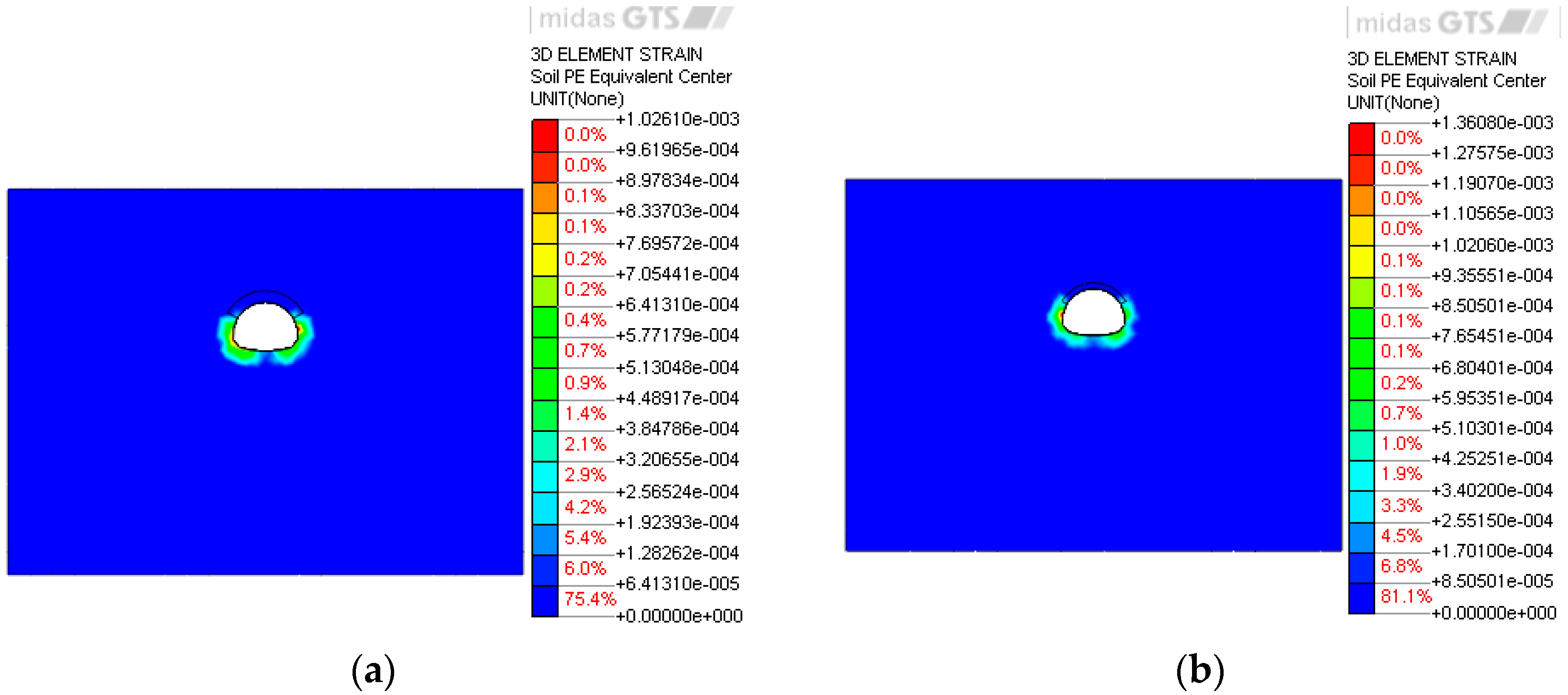
3.2. Plastic Zone Analysis of the Surrounding Rock
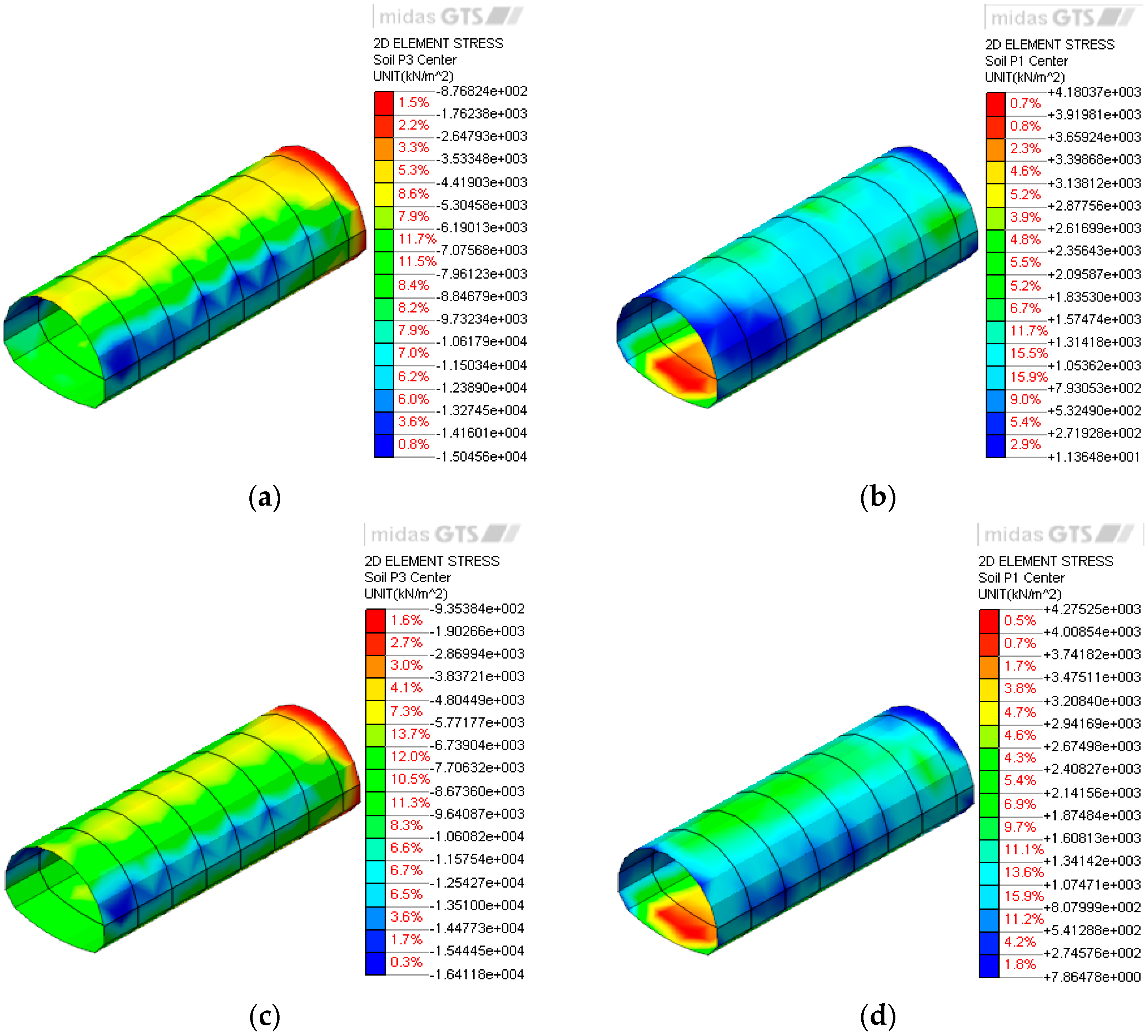
3.3. Stress Analysis of the Initial Support
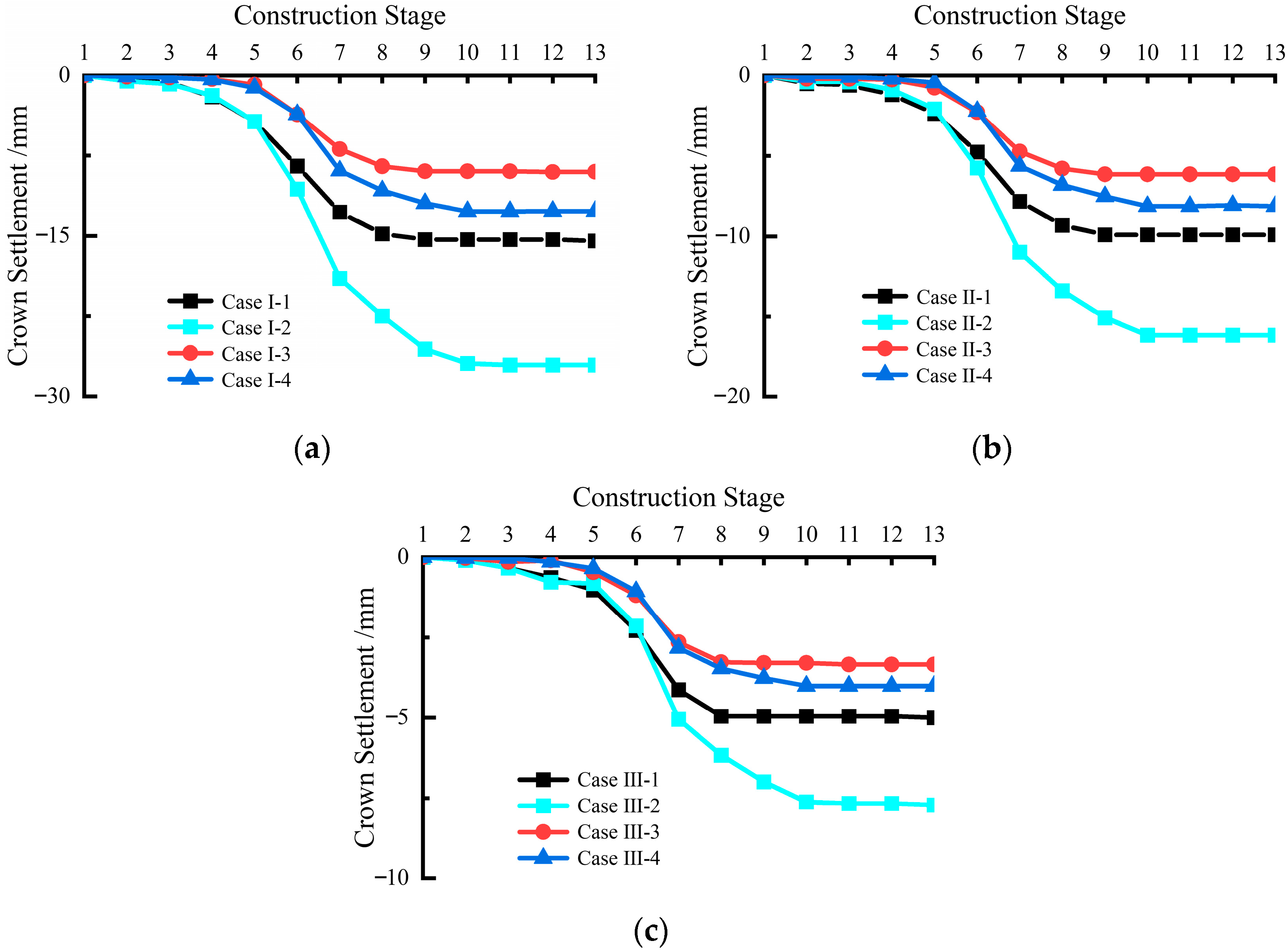
3.4. Analysis of Vault Settlement Displacement
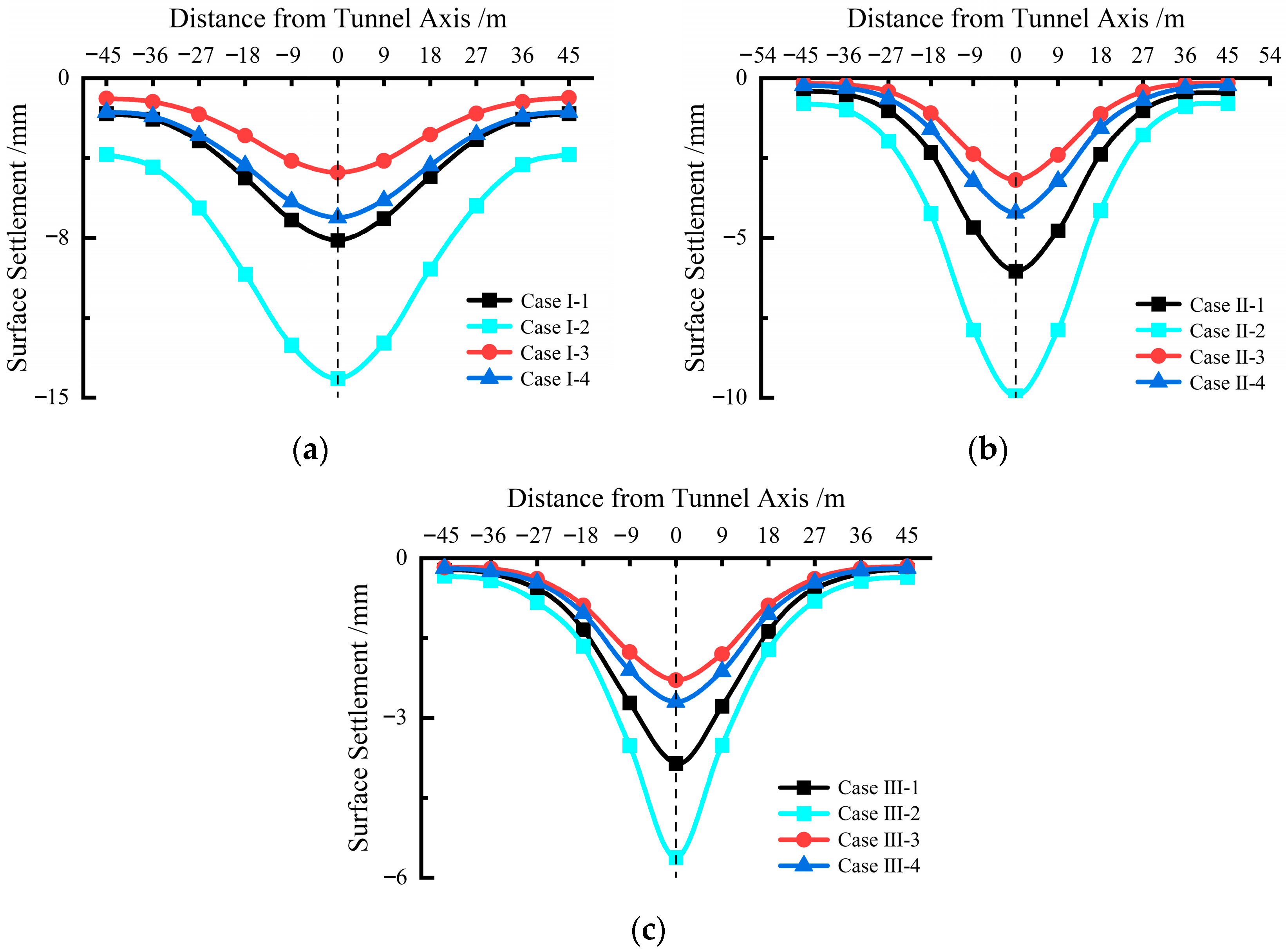
3.5. The Ground Settlement Analysis
4. Engineering Applications
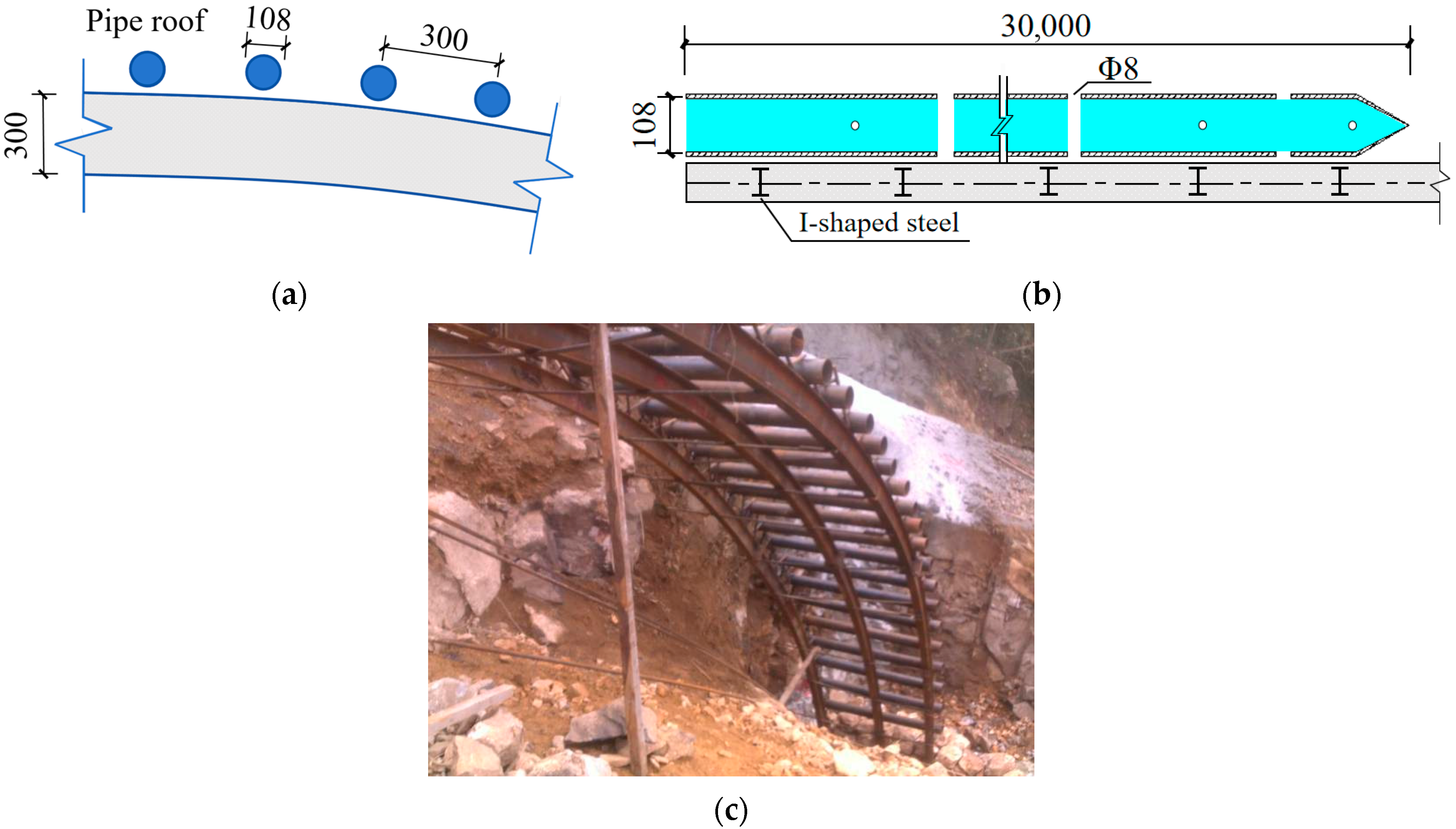
4.1. Pre-Support Arrangements
4.2. Field Monitoring and Result Analysis
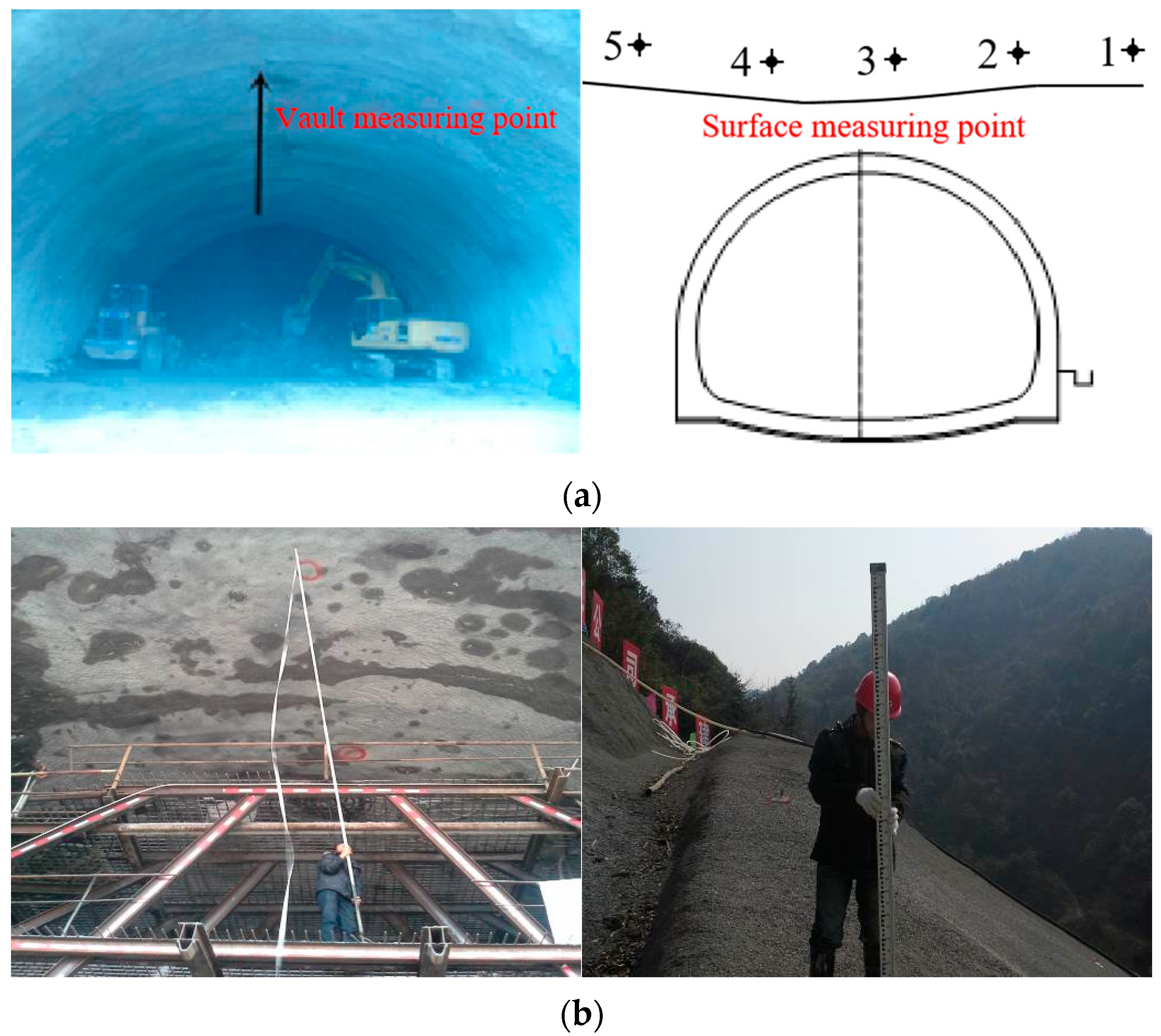
4.2.1. Monitoring Point Layout
4.2.2. Result Analysis
- (1)
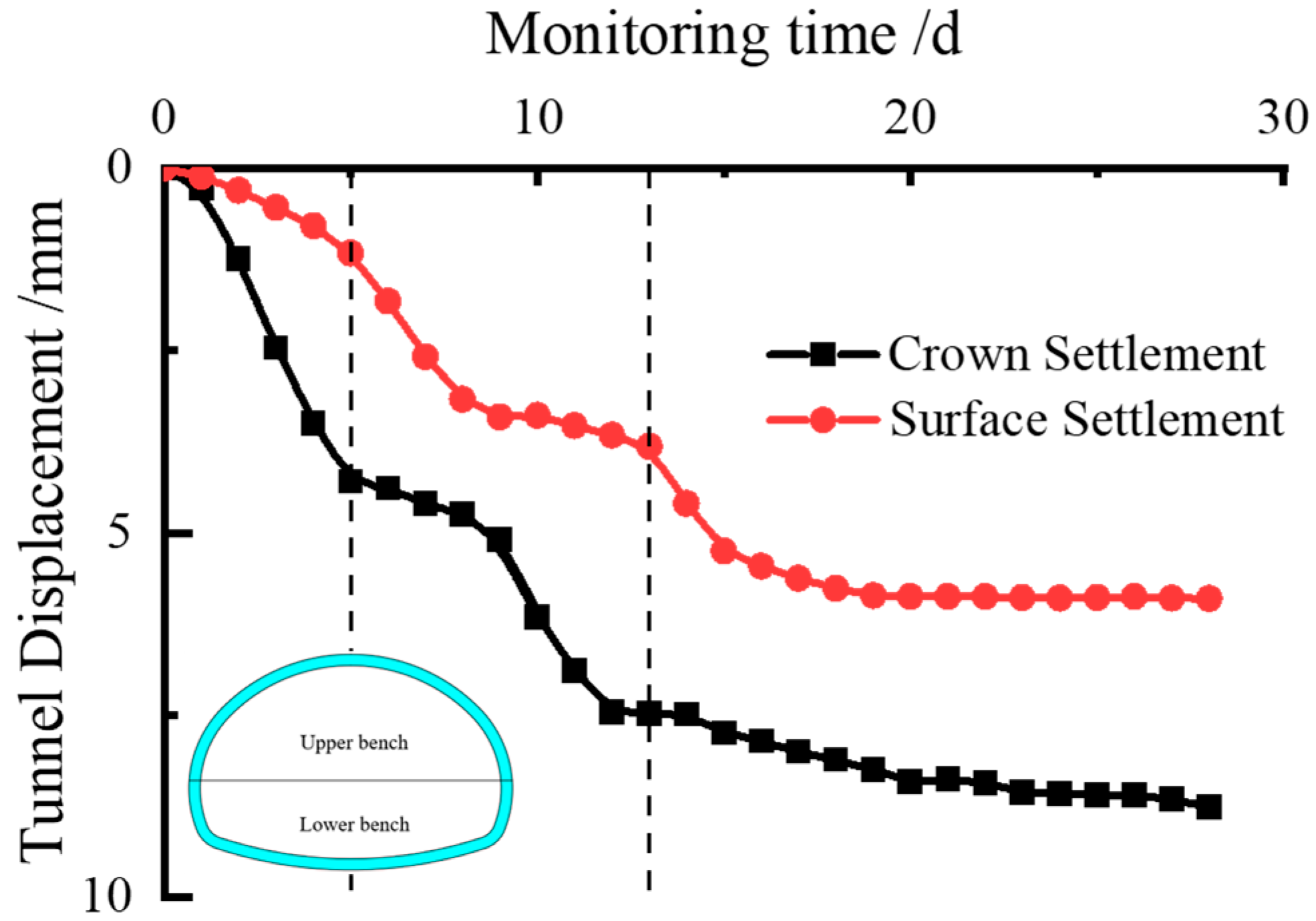
- During tunnel excavation, the crown settlement rate is closely related to the face position. When the upper bench face reached the monitoring section, the crown settlement rate increased significantly. As the face advanced further, the rate gradually decreased. The settlement rate peaked again when the lower bench face passed through, accompanied by a minor increase in settlement, before eventually stabilizing. The final crown settlement at this section was 8.76 mm. The numerical simulation results were slightly higher than the measured values, primarily due to the simplified assumption of horizontally homogeneous material for the surrounding rock in the numerical model, which did not fully account for the actual stratified ground and topographic variations.
- (2)
- The surface settlement trend was generally consistent with the crown settlement. The monitoring section YK10+280, located 10 m from the tunnel portal, exhibited minor settlement during the initial excavation phase due to construction disturbance. The settlement rate increased as the upper bench face approached the section, and a significant abrupt change occurred when the lower bench passed through. The final stabilized settlement value was 5.902 mm. As this point was directly above the tunnel, it experienced the maximum settlement. The numerical simulation results were slightly higher than the field measurements for the same reason mentioned above. Although blasting and construction activities caused some interference, the overall development of the settlement remained controllable under the effect of pipe roof pre-support, and the trend aligned well with the simulation results.
- (3)
- The pipe roof pre-support method significantly suppressed both crown and surface settlements. No major abrupt changes occurred throughout the excavation process, demonstrating that this technique effectively controls tunnel deformation and ensures subsequent construction safety.
5. Conclusions
- (1)
- Under greater burial depths, the maximum principal stress in the surrounding rock within the pipe roof reinforced zone is significantly higher than that observed with the leading ductule reinforcement. In contrast, under shallow burial conditions, the stress levels between the two methods are comparable. The plastic zone is primarily distributed in areas including the vault, arch waist, interface between the reinforced zone and the tunnel, sidewalls, and floor, exhibiting non-uniform thickness characteristics. Under shallow burial conditions, both pre-support methods effectively suppress the development of the plastic zone. These structures contribute to the stress redistribution of the surrounding rock and bear part of the external load, thereby reducing the compressive stress on the initial support and improving its mechanical state.
- (2)
- Despite its higher cost and more complex construction process, the pipe roof pre-support method demonstrates significant advantages in controlling the stress release and deformation of the surrounding rock due to its superior stiffness and larger reinforcement zone. It is particularly effective in preventing instability or structural failure under conditions of deep burial and weak surrounding rock. This method outperforms leading ductule pre-support in constraining the plastic zone and sharing the surrounding rock pressure, exhibiting a greater capacity to withstand high stress and demonstrating stronger adaptability and reliability in complex geological conditions.
- (3)
- Field monitoring demonstrated that the pipe roof pre-support effectively controlled the crown settlement within a safe range until it eventually stabilized. During construction, blasting and excavation activities induced certain surface settlements in the shallowly buried section; however, under the support of the pipe roof structure, surface deformation remained within acceptable limits and ultimately stabilized. The numerical simulation results showed good agreement with field measurements. Affected by the assumptions of the computational model, the simulated values were slightly higher than the measured data, indicating that the numerical method can effectively predict the deformation behavior of the surrounding rock induced by tunnel excavation. The simulation approach offers practical guidance for construction, and the conclusions of the study are considered reliable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hisatake, M.; Ohno, S. Effects of pipe roof supports and the excavation method on the displacements above a tunnel face. Tunn. Undergr. Space Technol. 2008, 23, 120–127. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Li, H.Y.; Liu, H.Y.; Li, G.; Shi, X. Load transferring mechanism of pipe umbrella support in shallow-buried tunnels. Tunn. Undergr. Space Technol. 2014, 43, 213–221. [Google Scholar] [CrossRef]
- Yang, S.; Wang, M.; Du, J.; Guo, Y.; Geng, Y.; Li, T. Research of jacking force of densely arranged pipe jacks process in pipe-roof pre-construction method. Tunn. Undergr. Space Technol. 2020, 97, 103277. [Google Scholar] [CrossRef]
- Zarei, H.; Moarefvand, P.; Salmi, E.F. Numerical modeling of umbrella arch technique to reduce tunnelling induced ground movements. Environ. Earth Sci. 2019, 78, 291. [Google Scholar] [CrossRef]
- Gong, L.; Feng, J.; Zhou, P.; Sun, D.; Zhou, F.; Hu, H.; Wang, L. Study on bearing failure characteristics and parameters of pipe roof support in super shallow buried tunnel in soft surrounding rock. Tunn. Undergr. Space Technol. 2023, 140, 105283. [Google Scholar] [CrossRef]
- Yang, C.; Chen, Y.; Huang, D.; Wang, L. Arching effect between the pipes of a pipe umbrella support system in a shallow-buried tunnel. KSCE J. Civ. Eng. 2019, 23, 5215–5225. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Rehman, H.; Yoo, H. Ground Stability Analysis in Non-Open-Cut Tunneling Method Using Small-Diameter Steel Pipe Piles. Appl. Sci. 2020, 10, 6906. [Google Scholar] [CrossRef]
- Oke, J.; Vlachopoulos, N.; Diederichs, M.S. Improved input parameters and numerical analysis techniques for temporary support of underground excavations in weak rock. In Proceedings of the RockEng12, 21st Canadian Rock Mechanics Symposium, Edmonton, AB, Canada, 5–9 May 2012. [Google Scholar]
- Xiao, J.Z.; Dai, F.C.; Wei, Y.Q.; Xing, Y.C.; Cai, H.; Xu, C. Analysis of mechanical behavior in a pipe roof during excavation of a shallow bias tunnel in loose deposits. Environ. Earth Sci. 2016, 75, 293. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Yan, S.; Du, J. Theoretical Analysis on the Effectiveness of Pipe Roofs in Shallow Tunnels. Appl. Sci. 2022, 12, 9106. [Google Scholar] [CrossRef]
- Xiao, H.; Zhou, S.; Sun, Y. Stability Analysis and Case Study of Shallow Tunnel Using Pipe Roof Support. Geotech. Geol. Eng. 2019, 37, 1249–1260. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, D.; Fang, Q.; Sun, Z.; Cao, L.; Li, A. Displacement Characteristics of Shallow-Buried Large-Section Loess Tunnel with Different Types of Pre-Supports: A Case Study of New Badaling Tunnel. Appl. Sci. 2019, 10, 195. [Google Scholar] [CrossRef]
- Huang, F.; Wu, C.; Jang, B.A.; Hong, Y.; Guo, N.; Guo, W. Instability mechanism of shallow tunnel in soft rock subjected to surcharge loads. Tunn. Undergr. Space Technol. 2020, 99, 103350. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, D.; Liu, D.; Tai, Q.; Hou, Y. Insights into the ground response characteristics of shallow tunnels with large cross-section using different pre-supports. Int. J. Rock Mech. Min. Sci. 2024, 175, 105663. [Google Scholar] [CrossRef]
- Bai, C.; Xue, Y.; Qiu, D.; Su, M.; Ma, X.; Liu, H. Analysis of factors affecting the deformation of soft rock tunnels by data envelopment analysis and a risk assessment model. Tunn. Undergr. Space Technol. 2021, 116, 104111. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, Y.; Xu, W.; Wang, H.; Wang, R.; Yang, X.; Ma, J.; Huang, W. Large Deformations and Numerical Analysis of a Typical Soft Rock Tunnel in the Chuxiong Section of the Yunnan Central Water Diversion Project. Int. J. Geomech. 2024, 24, 05024002. [Google Scholar] [CrossRef]
- Liu, K.; Li, S.; Ding, W.; Hou, M.; Gong, Y.; Li, H. Pre-supporting mechanism and supporting scheme design for advanced small pipes in the silty clay layer. Tunn. Undergr. Space Technol. 2020, 98, 103259. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Q.; Pei, Z.; Song, Z.; Wang, J. Construction sequence optimization and settlement control countermeasures of metro tunnels underpassing expressway. Adv. Civ. Eng. 2021, 2021, 8834368. [Google Scholar] [CrossRef]
- An, Y.L.; Zhou, J.; Ouyang, P.B.; Li, J.H. Analysis of tunnel face stability with advanced pipes support. J. Cent. South Univ. 2021, 28, 604–617. [Google Scholar] [CrossRef]
- Ma, P.; Shimada, H.; Sasaoka, T.; Hamanaka, A.; Dintwe, T.K.M.; Pan, D. Investigation on the Performance of Pipe Roof Method Adjacent to the Underground Construction. Geotech. Geol. Eng. 2021, 39, 4677–4687. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, X.; Guo, F.; Tao, L.; Liu, J.; Liao, W.; Tan, L.; Yang, X. Influence of the Advance Jacked Pipe on the Jacking Force of the Subsequent Pipe Based on Pipe–Soil Full Contact Model. Lithosphere 2024, 2024, lithosphere_2023_216. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, D.; Rong, Y.; Ma, Y.; Yao, C.; Sun, Y. Study on the stability of tunnel in weak surrounding rock considering initial support parameters and excavation method. KSCE J. Civ. Eng. 2024, 28, 2427–2439. [Google Scholar] [CrossRef]
- Liu, X.J.; Zhang, Y.X.; Gao, S.J.; Huang, D.; Yang, C. Mechanism analysis and treatment technique of surrounding rock instability for tunnel portal section in weak surrounding rock. Rock. Soil. Mech. 2012, 33, 2229–2234. [Google Scholar]
- Qiu, W.; Kong, C.; Liu, K. Three-Dimensional Numerical Analysis of the Tunnel for Polyaxial State of Stress. Math. Probl. Eng. 2015, 2015, 301241. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. 2D numerical investigation of segmental tunnel lining behavior. Tunn. Undergr. Space Technol. 2013, 37, 115–127. [Google Scholar] [CrossRef]
- Zaid, M.; Mishra, S. Numerical analysis of shallow tunnels under static loading: A finite element approach. Geotech. Geol. Eng. 2021, 39, 2581–2607. [Google Scholar] [CrossRef]
- Yen, J.; Shou, K. Numerical simulation for the estimation the jacking force of pipe jacking. Tunn. Undergr. Space Technol. 2015, 49, 218–229. [Google Scholar] [CrossRef]
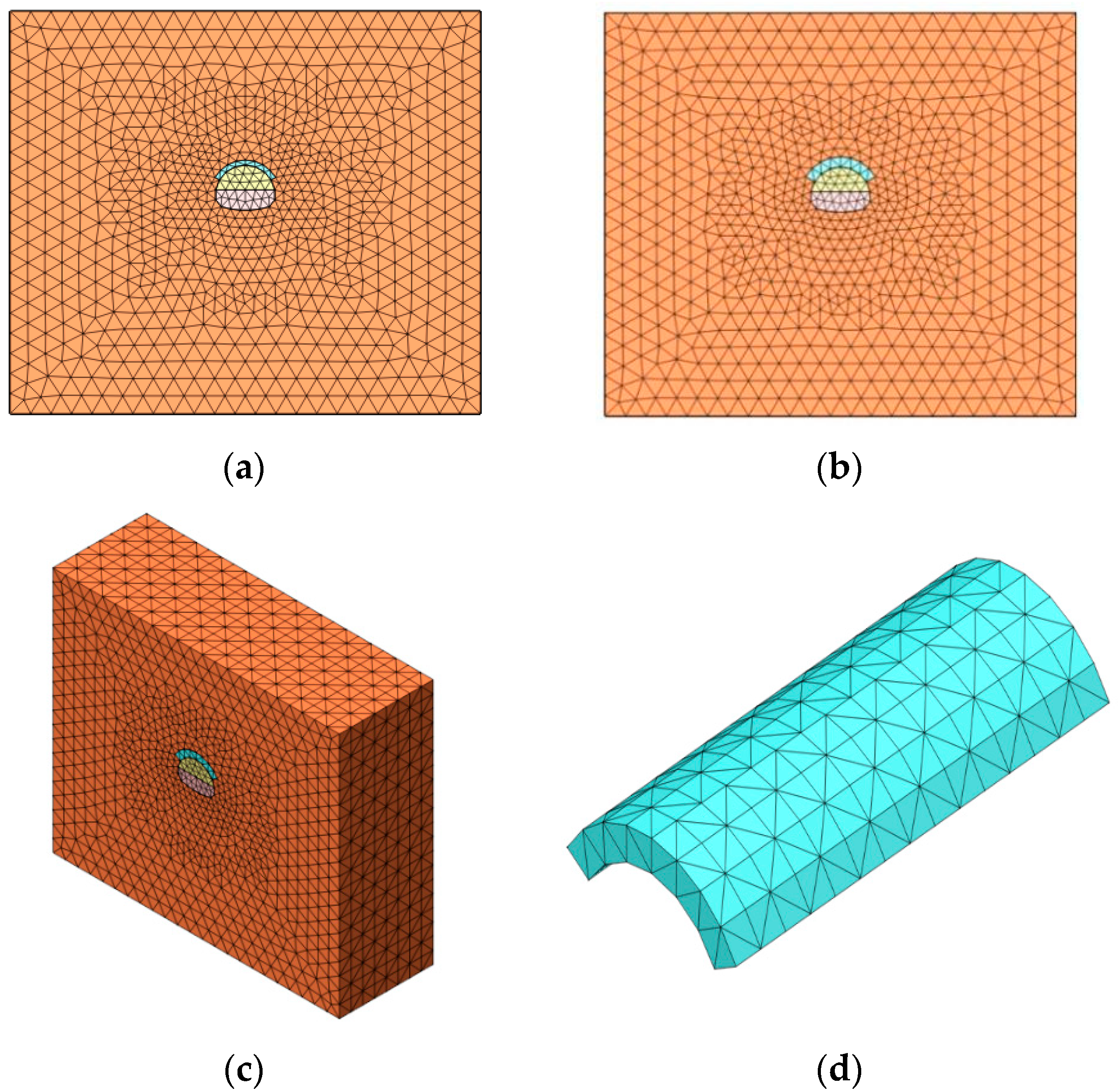

| Component | Elastic Modulus (kN/m2) | Poisson’s Ratio μ | Unit Weight γ (kN/m3) | Diameter D (m) |
|---|---|---|---|---|
| rock bolt | 2.1 × 107 | 0.2 | 78 | 0.025 |
| Item | IV Surrounding Rock | V Surrounding Rock | Reinforcement Area | Soft Shotcrete | Hard Shotcrete |
|---|---|---|---|---|---|
| Type | Solid | Solid | Solid | Plane | Plane |
| Elastic modulus (kN/m2) | 1 × 106 | 5 × 105 | 3 × 106 | 1.5 × 107 | 2.3 × 107 |
| Poisson’s ratio μ | 0.35 | 0.38 | 0.28 | 0.2 | 0.2 |
| Unit weight γ (kN/m3) | 22 | 20 | 24 | 23 | 23 |
| Cohesion C (kN/m2) | 150 | 50 | 300 | - | - |
| Internal friction angle φ (°) | 28 | 25 | 35 | - | - |
| Item | Burial Depths | Surrounding Rock Grade | Reinforcement Method | |
|---|---|---|---|---|
| Case I | Case I-1 | 30 m | V | P-S |
| Case I-2 | 30 m | V | STGI | |
| Case I-3 | 30 m | IV | P-S | |
| Case I-4 | 30 m | IV | STGI | |
| Case II | Case II-1 | 20 m | V | P-S |
| Case II-2 | 20 m | V | STGI | |
| Case II-3 | 20 m | IV | P-S | |
| Case II-4 | 20 m | IV | STGI | |
| Case III | Case III-1 | 10 m | V | P-S |
| Case III-2 | 10 m | V | STGI | |
| Case III-3 | 10 m | IV | P-S | |
| Case III-4 | 10 m | IV | STGI | |
| Procedure | Construction Description | Procedure | Construction Description |
|---|---|---|---|
| 1 | The initial stress definition | 8 | To excavate upper step 6 and bottom step 5 |
| 2 | The advanced reinforcement area hardening | 9 | To excavate upper step 7 and bottom step 6 |
| 3 | To excavate upper step 1 | 10 | To excavate upper step 8 and bottom step 7 |
| 4 | To excavate upper step 2 and bottom step 1 | 11 | To excavate bottom step 8 |
| 5 | To excavate upper step 3 and bottom step 2 | 12 | Spraying the concrete on step 8 |
| 6 | To excavate upper step 4 and bottom step 3 | 13 | Hardening the sprayed concrete |
| 7 | To excavate upper step 5 and bottom step 4 | ||
| Case | Maximum Principal Stress (MPa) | Minimum Principal Stress (MPa) | Case | Maximum Principal Stress (MPa) | Minimum Principal Stress (MPa) |
|---|---|---|---|---|---|
| Case I-1 | −1.434 | −0.328 | Case II-3 | −1.078 | −0.158 |
| Case I-2 | −1.165 | −0.338 | Case II-4 | −1.022 | −0.143 |
| Case I-3 | −1.553 | −0.311 | Case II-1 | −0.628 | −0.068 |
| Case I-4 | −1.49 | −0.186 | Case III-2 | −0.595 | −0.082 |
| Case II-1 | −1.017 | −0.229 | Case III-3 | −0.644 | −0.058 |
| Case II-2 | −0.977 | −0.147 | Case III-4 | −0.608 | −0.078 |
| Case | Settlement Displacement (mm) | Case | Settlement Displacement (mm) |
|---|---|---|---|
| Case I-1 | 15.9 | Case II-3 | 5.8 |
| Case I-2 | 27.1 | Case II-4 | 8.1 |
| Case I-3 | 8.8 | Case III-1 | 4.6 |
| Case I-4 | 12.3 | Case III-2 | 7.9 |
| Case II-1 | 9.8 | Case III-3 | 3 |
| Case II-2 | 16.2 | Case III-4 | 4.2 |
| Case | Settlement Displacement (mm) | Case | Settlement Displacement (mm) |
|---|---|---|---|
| Case I-1 | 7.6 | Case II-3 | 3.2 |
| Case I-2 | 14.1 | Case II-4 | 4.2 |
| Case I-3 | 4.4 | Case III-1 | 3.9 |
| Case I-4 | 6.5 | Case III-2 | 5.6 |
| Case II-1 | 6 | Case III-3 | 2.3 |
| Case II-2 | 9.9 | Case III-4 | 2.7 |
| Monitoring Section | Crown Settlement Displacement (mm) | Monitoring Section | Surface Settlement Displacement (mm) |
|---|---|---|---|
| YK10+274 | 8.76 | YK10+280 | 5.902 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Luo, H.; Liu, H.; Gu, J. Mechanical Study on Leading Ductule and Pipe Roof Pre-Support Technologies in Tunnel Excavation. Buildings 2025, 15, 3791. https://doi.org/10.3390/buildings15203791
Jiang Y, Luo H, Liu H, Gu J. Mechanical Study on Leading Ductule and Pipe Roof Pre-Support Technologies in Tunnel Excavation. Buildings. 2025; 15(20):3791. https://doi.org/10.3390/buildings15203791
Chicago/Turabian StyleJiang, Yunpeng, Hao Luo, Hui Liu, and Jianfeng Gu. 2025. "Mechanical Study on Leading Ductule and Pipe Roof Pre-Support Technologies in Tunnel Excavation" Buildings 15, no. 20: 3791. https://doi.org/10.3390/buildings15203791
APA StyleJiang, Y., Luo, H., Liu, H., & Gu, J. (2025). Mechanical Study on Leading Ductule and Pipe Roof Pre-Support Technologies in Tunnel Excavation. Buildings, 15(20), 3791. https://doi.org/10.3390/buildings15203791






