Experimental and Numerical Study on Ultra-High Performance Concrete Repair of Uniformly Corroded Reinforced Concrete Pipes

Abstract

This study investigates the deterioration of corroded reinforced concrete pipes and their restoration using ultra-high performance concrete (UHPC), utilizing Three-Edge Bearing Tests and 3D finite element analysis under uniform corrosion-induced wall thinning. Unrepaired pipes exhibit elastic behavior, crack propagation, and yield stages, with failure driven by concrete cracking and rebar yielding. UHPC repair mitigates load drop during crack propagation, extends the yield phase, and enhances plastic deformation capacity. Pipe load-bearing capacity is negatively correlated with corrosion thickness and positively correlated with repair thickness (R² > 0.979) and repair compensation ratio. Interfacial performance analysis indicates natural bond degradation under sustained loading, transitioning the pipe to a unitized structure. Embedding steel nails significantly improves interfacial bond strength, increasing failure bearing capacity by 2.91 and 3.56 times compared to natural and PE film interfaces, respectively. Numerical simulations reveal that interface shear strength is five times more influential on bearing capacity decay than interface fracture energy, underscoring its critical role in durability design. An optimization strategy is proposed: reinforce stress-concentrated areas with nails to enhance shear strength and prioritize monitoring interfacial slip to ensure service safety.

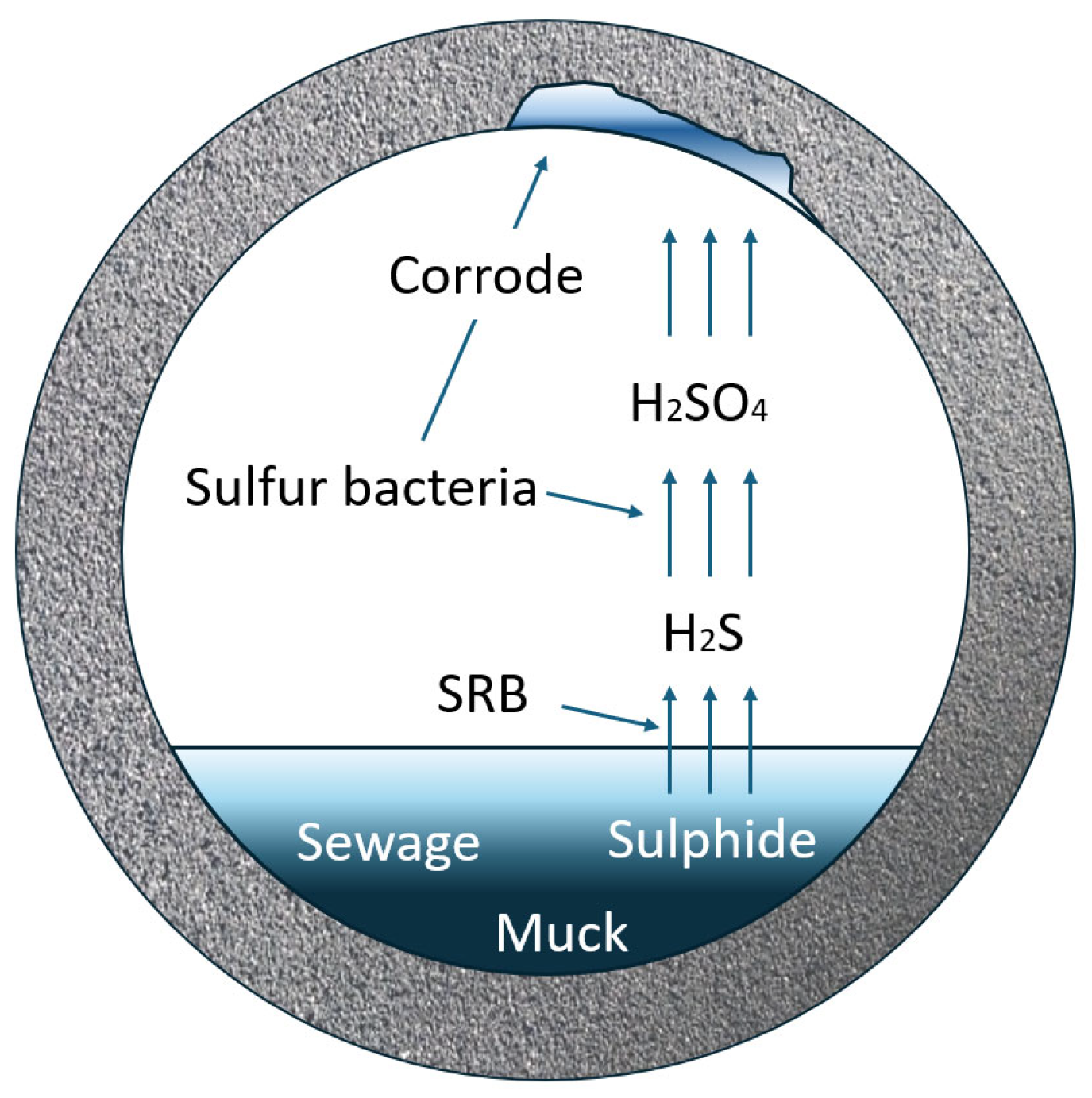
1. Introduction

Urban underground pipe networks are critical components of city infrastructure, serving as lifelines to ensure normal urban functionality [1]. Most drainage pipes are constructed using reinforced concrete pipes (RCPs), particularly susceptible to corrosion in groundwater environments [2]. Sulfides in groundwater are reduced to H₂S by sulfate-reducing bacteria (SRB) and subsequently oxidized by sulfur-oxidizing bacteria, forming biogenic sulfuric acid that corrodes the inner surface of RCPs. This leads to the thinning of the pipe’s inner wall, compromising the load-bearing capacity of the concrete and resulting in severe structural failure, as illustrated in Figure 1.

Sprayed lining, a common trenchless rehabilitation method, applies mortar to pipe interiors to form a structural layer [3]. Traditional mortar linings primarily act as protective barriers, contributing little to structural capacity [4]. In contrast, ultra-high performance concrete (UHPC), with its exceptional compressive strength, crack resistance, high stiffness, durability, and low creep, enables thinner, lighter structures with superior load-bearing and crack-control capabilities, making it increasingly vital for structural repairs [5,6,7]. These attributes position UHPC as a transformative material for structural repairs in demanding environments.

Scholars have approached UHPC’s application from diverse perspectives. Bolina et al. [8,9] highlight UHPC’s thermal stability, noting minimal compressive strength loss compared to normal-strength concrete (NSC), high-strength concrete (HSC), and ultra-high-strength concrete (UHSC) at elevated temperatures (degradation onset at 400 °C), with UHPC structures exhibiting significantly higher average cross-sectional temperatures under extreme conditions. In terms of mechanical behavior, Yang et al. [10] underscore the role of fiber reinforcement—straight, deformed, non-steel, or hybrid fibers—in enhancing UHPC’s tensile and impact properties, proposing fiber factor-based predictions to classify performance. Similarly, Shi et al. [11] emphasize that UHPC’s superior tensile strength and toughness, driven by fiber reinforcement, result in a fourfold increase in impact fracture energy compared to NSC, a finding that aligns with its structural repair potential.

The durability of UHPC in harsh environments is another focal point of research, with studies converging on its low permeability and resistance to corrosive agents. Yuan et al. [12] attribute UHPC’s reduced permeability to its low water-cement ratio and dense microstructure, which limit chloride and carbon dioxide ingress. Wu [13] and Yang et al. [14] further demonstrate UHPC’s resilience in corrosive settings, such as seawater dry-wet cycles and simulated wastewater environments (e.g., industrial wastewater, inorganic, and organic acids), where it outperforms conventional concrete, significantly extending the service life of drainage pipes. However, Cheng [15] notes that UHPC’s macroscopic performance degrades in sulfuric acid, with tensile strength most affected, followed by flexural strength, and compressive strength least impacted, highlighting a time-dependent corrosion pattern.

Interface behavior and structural interactions also attract significant attention, with some controversy regarding failure mechanisms. Liu et al. [16] analyze UHPC-based composites (e.g., mesh-reinforced UHPC, UHPC-filled steel tubes, and UHPC-strengthened NSC structures) under blast loading, noting that steel rebar in UHPC members causes strain concentration, leading to larger mid-span cracks and reduced ductility compared to NSC. Zhang et al. [17] and Liao [18] focus on UHPC-NC interface performance, observing that failures typically involve NC shear or mixed interface-NC failure rather than full delamination, with bond strength reaching 95% within 7 days and wet conditions enhancing strength by 28–59%. In contrast, studies on pipe failure by Buda-Ozog et al. [19] and Silva et al. [20] identify crown compression and longitudinal crack growth as dominant failure modes in reinforced concrete pipes, influenced by reinforcement ratio, section height, and wall thickness. For trenchless repairs, Shi et al. [21] and Zhang [22] highlight challenges with liner-host interactions, noting that grout detachment under high external loads and insufficient interface resistance can compromise the composite system, limiting the liner’s structural contribution.

Although UHPC is well-established for improving planar structural elements, its use in repairing corrosion-damaged pipes remains underexplored. This study fills this gap by systematically examining UHPC as a repair material for corrosion-thinned pipes. By assuming uniform wall thinning to simplify corrosion variability, we facilitate a controlled assessment of structural impacts. Using TEBT and nonlinear finite element modeling, we analyze the mechanics of UHPC-lined pipes across varying corrosion severities. This work provides innovative practical insights for enhancing the load-carrying capacity of urban pipeline infrastructure, advancing UHPC applications in pipe rehabilitation.

2. Experiments

2.1. Experimental Scheme

Tests were conducted on two pipe diameters, with the larger diameter chosen to facilitate interfacial pretreatment. Detailed specifications are provided in

Table 1. Pipe design parameters.

Design Indicators		Value
		DN200	DN400
Size	Wall thickness/mm	30	40
	Cover thickness/mm	10
	Length/mm	300
Circumferential reinforcement	Diameter/mm	3	5
	Inner diameter of the ring/mm	221	427
	Number of rings	18.5	20.6
	Pitch/mm	54.1	48.5
Longitudinal tendon	Diameter/mm	5
	Number	6

. The pipes were constructed using P.O. 42.5 cement (Jiuqi Building Materials Co., Ltd., Huaifang, China), with a mix ratio of cement/sand/water = 2.27:2.73:1. The test scheme is outlined in

Table 2. Test scheme of DN200.

Diameter	Group	Corrosion Thickness/mm	Repair Thickness/mm
DN200	FS0	0	0
	FS1 FS2 FS3	2	0 10 20
	FS4 FS5 FS6	5	0 10 20
	FS7 FS8 FS9	10	0 10 20

and

Table 3. Test scheme of DN400.

Diameter	Group	Structure Type	Processing Method	Repair Thickness/mm
DN400	JM0	Composite	Natural bonding	0
	JM1		Natural bonding	25
	JM2		Steel nail embedding	25
	JM3	Unitized	PE film adhesion	25

. For the repair thickness study, DN200 reinforced concrete pipes were evaluated under different corrosion and repair thickness conditions. To explore interfacial pretreatment, DN400 pipes were tested with three different interface types.

2.2. Material Properties

The UHPC (JiaGu Building Materials Co., Ltd., Zhengzhou, China) repair material was composed of P.O. 52.5 Portland cement, Class I fly ash, silica fume, quartz sand, 9 mm PVA fibers, VAE polymer powder, and polycarboxylate superplasticizer. Specimens were prepared according to Chinese Standards GB/T 50080-2016 [23] and GB/T 17671-2021 [24]. Mechanical properties were assessed based on standard protocols, with the results presented in

Table 4. Performance test results of UHPC.

Group	Fluidity/mm	Curing Time/d	Flexural Strength/MPa	Compressive Strength/MPa
1	184	1	6.0	55.7
2	181	7	10.4	64.3
3	185	28	17.9	84.7

. After curing for 1 and 7 days, the UHPC specimens exhibited superior compressive and flexural strengths, meeting the requirements for spray-applied repair materials. As depicted in Figure 2, the specimens remained intact following flexural strength testing. Fiber pull-out effects caused micro-cracking on the surface without complete fiber failure, contributing to ductility. This behavior facilitated sustained or enhanced strength after testing, confirming UHPC’s effectiveness as a repair material for improving the residual load-bearing capacity of existing pipes.

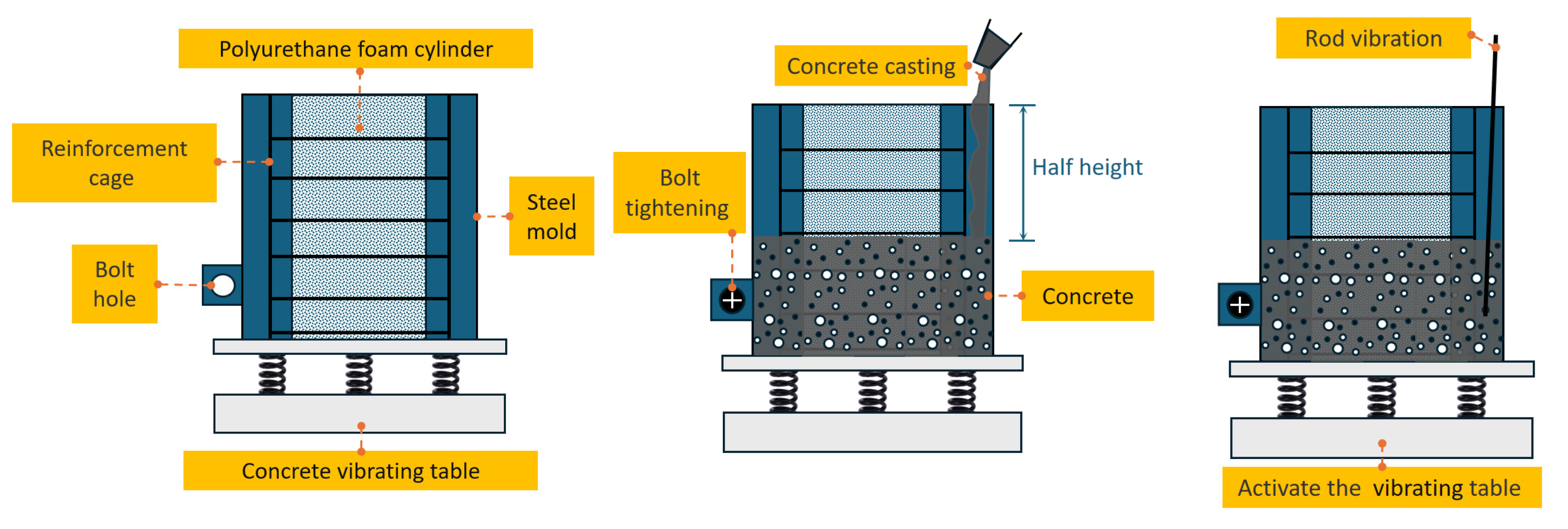
2.3. Specimen Preparation

The pipe fabrication process is illustrated in Figure 3. A uniform layer of lubricating oil was applied to the inner surface of the steel mold and the outer surface of the polyurethane (PU) foam cylinder. Subsequently, the reinforcement cage was positioned to ensure proper alignment of all components. The mold was then securely bolted and placed on a vibrating table. Concrete, prepared according to the designed mix ratio, was cast in two successive stages. Following casting, the mold was subjected to natural curing for 1 day before demolding. Thereafter, all pipes were cured indoors for 28 days.

Steel molds for DN200 pipes, uniformly with a diameter of 260 mm, were used, and the dimensions of the PU foam cylinders, corresponding to varying corrosion levels and repair thicknesses, are listed in

Table 5. PU foam mold size for DN200 pipes.

Corrosion	Diameter/mm	Repair/mm	Diameter/mm
2	204	10	184
		20	164
5	210	10	190
		20	170
10	220	10	200
		20	180

.

For DN400 pipes, steel molds had an outer diameter of 480 mm. Three types of interface treatments were applied: (1) Natural Bonding: A 350 mm diameter PU foam cylinder was used, followed by secondary casting with UHPC. (2) Steel nail embedding: The arrangement of the steel nails is depicted in Figure 4, with an axial spacing of 50 mm and a vertical spacing of 15 mm. The nails were secured in the holes using epoxy resin, followed by secondary casting after the resin had cured. (3) PE film adhesion: The inner wall was cleaned and polished, then covered with a PE film bonded using adhesive. The film was tightly clamped and left to cure for 1 day before secondary casting.

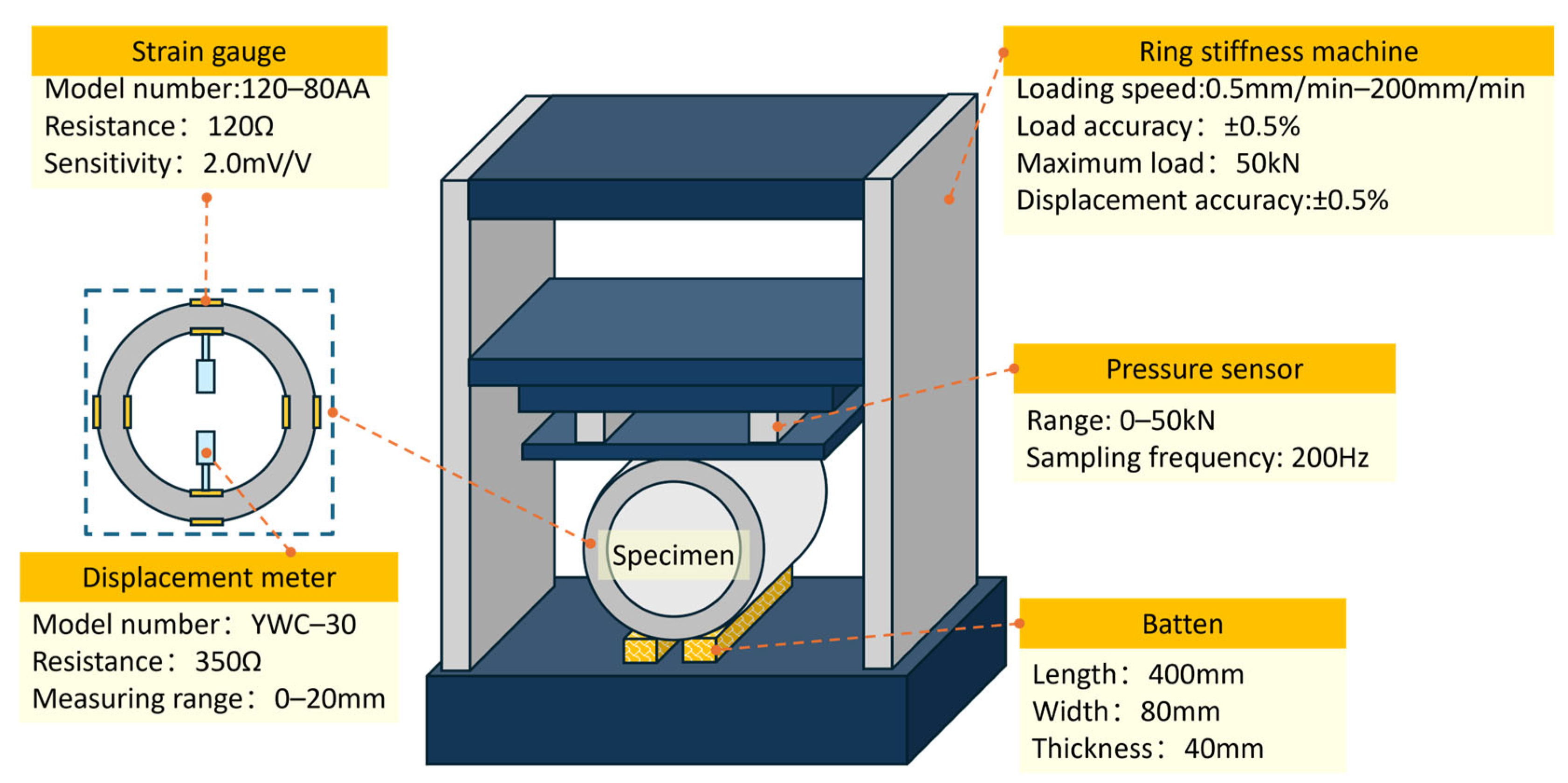
2.4. Three-Edge Bearing Test

The test followed the load method outlined in GB/T 16752-2017 [25]. As shown in Figure 5, a flat-plate loading test was conducted using a ring stiffness testing machine (Jin Jian Testing Instrument Co., Ltd., Chengde, China), equipped with an integrated system for controlling displacement and recording load–displacement data. Batten spacing was set at 25 mm for DN 200 pipes and 40 mm for DN 400 pipes. The loading rate was fixed at 5 mm/min, with a displacement limit of 10% of the pipe diameter. Strain gauges were installed at the crown, invert, and springlines on both the inner and outer pipe surfaces to measure strain at critical points. To account for spacer deformation during loading, YWC-30 displacement sensors (Jincheng Testing Instrument Factory, Liyang, China) were employed to monitor vertical displacement, thereby minimizing measurement errors.

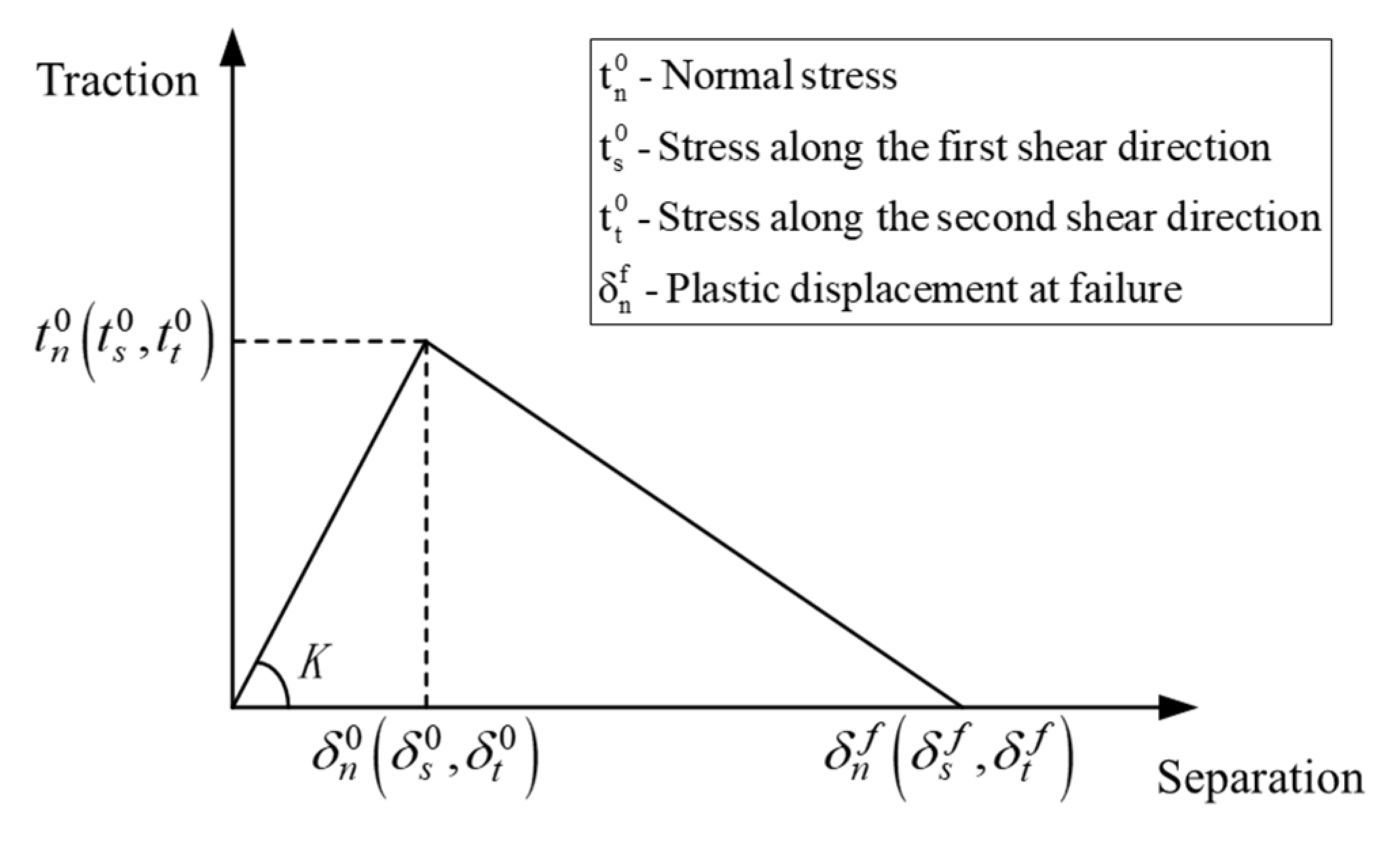
3. Numerical Simulations

Three-dimensional reinforced concrete pipe models, comprising the pipe body (meshed with C3D8R solid elements, as shown in Figure 6, feature a mesh division of 2° circumferentially, 10 mm radially, and 30 mm axially) and reinforcement (modeled with T3D2 truss elements, consists of circumferential ribs meshed at 2° intervals and longitudinal ribs divided into eight segments), were developed in ABAQUS 2024 using the concrete damage plasticity (CDP) model, with hinged constraints applied at the timber-pipe interface to simulate fixed support boundaries, as detailed in Section 2.1 [26].

Per the Chinese standard GB 50010-2010 [27], plastic damage factors for tension and compression are defined. The constitutive model in this study is established using Equations (1) and (2), and the plastic parameters of concrete and steel bars are shown in

Table 6. Plastic parameters [28,29,30,31,32].

Element	Parameter	Value
C30 concrete	Dilation angle, Ψ *	36°
	Elastic modulus, Ec	30,000 MPa
	Poisson’s ratio, ν	0.2
	Eccentricity, e	0.1
	Ratio of biaxial to uniaxial compressive strength, fb0/fc0	1.16
	Ratio of second stress invariants, kc	0.667
	Viscosity parameter, μ	0.0001
Reinforcing steel	Elastic modulus, Ecr	200,000 MPa
	Poisson’s ratio, νr	0.3

* The dilatation angle (Ψ) controls shear dilatancy, which is the material’s tendency to expand in volume under plastic deformation.

:

$${\sigma }_c=\left(1-d_c\right)E_c\left({\epsilon }_c-{\epsilon }_c^{pl}\right)$$

(1)

$${\sigma }_t=\left(1-d_t\right)E_c\left({\epsilon }_t-{\epsilon }_t^{pl}\right)$$

(2)

where σ_c, σ_t are axial compressive and tensile stresses of concrete; d_c, d_t are axial compressive and tensile damage factors of concrete; ε_c, ε_t are axial compressive and tensile strains of concrete; ε_c^pl, ε_t^pl are Axial plastic compressive and tensile strains of concrete; E_c is the elastic modulus of concrete (MPa).

The interface between the UHPC repair layer and the original pipe is modeled using a bilinear traction-separation cohesive model, which effectively captures material cracking and interfacial debonding. The cohesive interface model (Figure 7) relies on two key parameters: fracture energy (G_c), defined by the area under the traction-separation curve, and stiffness, characterized by normal and tangential components (K_nn, K_ss, and K_tt), with specific values presented in

Table 7. Cohesive interface model parameters [33].

Knn	Kss/Ktt	${\mathit{t}}_{\mathit{n}}^0$	${\mathit{t}}_{\mathit{s}}^0$$/{\mathit{t}}_{\mathit{t}}^0$	Gc
2887	73	9.3	16.1	0.9

.

The compressive stress–strain curve model proposed by Yang and Fang [34] is presented as follows:

$${\sigma }_c=\left\{\begin{array}{l}{f}_c{\displaystyle \frac{n\xi -{\xi }^2}{1+(n-2)\xi } }\epsilon \le {\epsilon }_0\\ f_c{\displaystyle \frac{\xi }{2{(\xi -1)}^2+\xi }} \epsilon >{\epsilon }_0\end{array}\right.$$

(3)

where f_c is peak stress; n is the ratio of initial elastic modulus to peak secant modulus, taken as 1.2; ξ is ε/ε₀, ε₀ is peak strain, taken as 3500 με.

The ductility of ultra-high-performance cement-based materials is relatively high. The bilinear stress–strain curve model proposed by Zhang et al. [35] is presented as follows:

$$\sigma (\epsilon )=\left\{\begin{array}{l}{\displaystyle \frac{f_{ct}}{{\epsilon }_{ca}} }0<\epsilon \le {\epsilon }_{ca}\\ f_{ct} {\epsilon }_{ca}<\epsilon \le {\epsilon }_{pc}\end{array}\right.$$

(4)

where f_ct is the Average stress during the strain-hardening stage; ε_ca is the initial cracking strain; ε_pc is the failure strain.

4. Results and Analysis

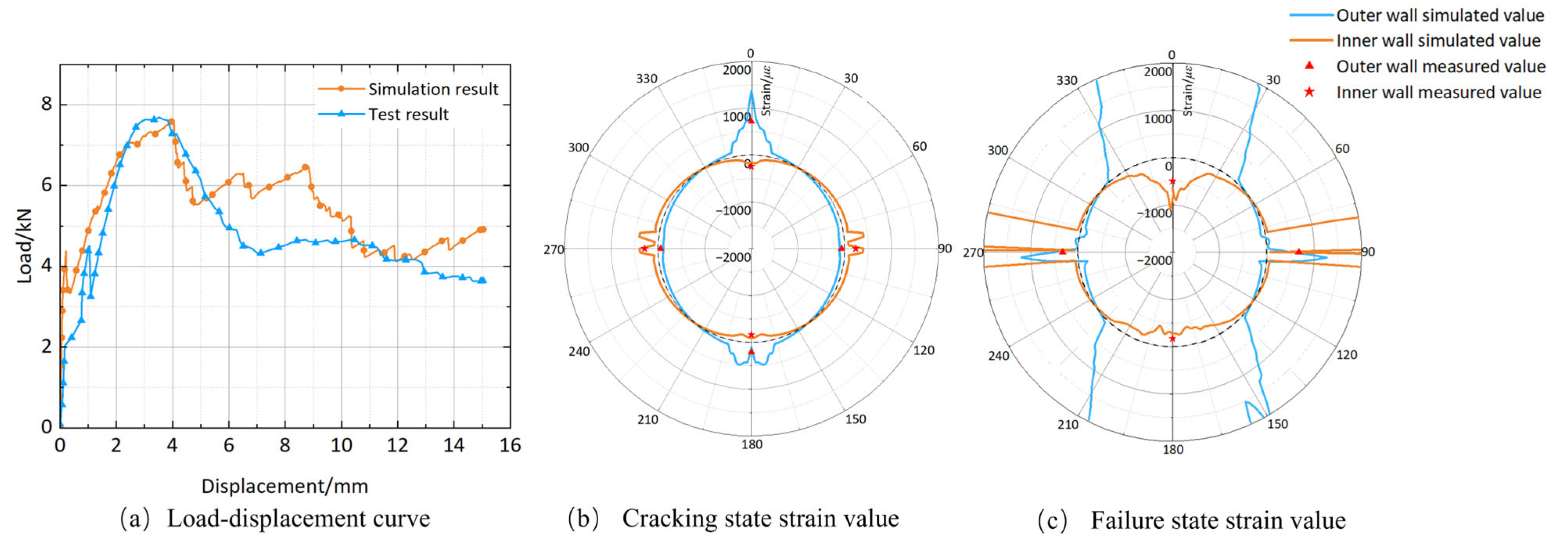
4.1. Model Validation

A finite element model of a DN200 pipe with a corrosion depth of 10 mm was validated against laboratory tests (Figure 8). The load–displacement responses exhibited strong agreement, with failure loads of 7.61 kN (numerical) and 7.69 kN (experimental), corresponding to a discrepancy of only 1%. Circumferential strains at critical locations also aligned with experimental measurements. In the cracked state, the model accurately reproduced stress distributions, showing compressive stresses on the outer wall and tensile stresses on the inner wall at the crown and invert, with reversed patterns and reduced strain magnitudes at the springlines. At failure, however, the simulated bearing capacity and crack-tip strains exceeded experimental results, attributable to the residual stiffness retained in damaged zones by the CDP model. Overall, the realistic reproduction of strain evolution lends confidence to the model’s reliability and applicability for engineering analysis.

4.2. Effect of Corrosion Thickness on Load-Bearing Capacity

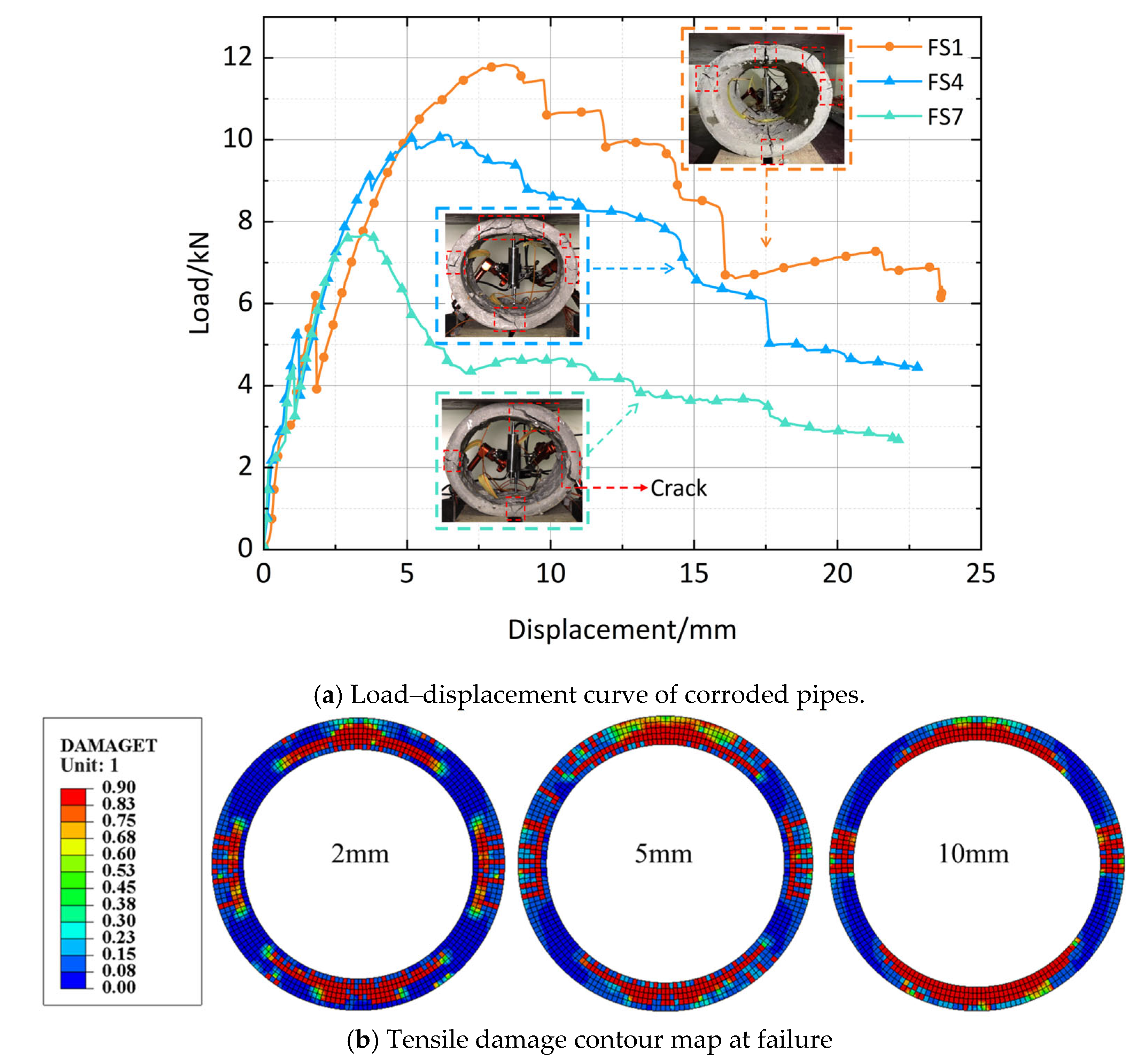
4.2.1. Effect on Unrepaired Pipes

Load capacities of pipe models FS0, FS1, FS4, and FS7 are presented in

Table 8. Load values for DN200 pipes.

Group	Corrosion Thickness/mm	TEBT		Numerical Simulations
		Crack Load/kN	Failure Load/kN	Crack Load/kN	Failure Load/kN
FS0	0	7.50	12.57	5.65	12.52
FS1	2	6.19	11.83	6.29	11.39
FS4	5	5.36	10.12	5.17	10.02
FS7	10	4.51	7.69	4.38	7.61

. Given the engineering relevance of failure load (F_max), this study investigates its correlation with corrosion thickness (x). Linear regression analysis of the data provides the following relationship:

Measured failure load (F_max):

$$F_{\max }=12.849-0.612x,R^2=0.979$$

(5)

Simulated failure load (F_max’):

$$F_{\max }\prime =12.631-0.599x,R^2=0.984$$

(6)

A robust negative linear relationship exists between failure load and corrosion thickness. Thus, regular wall thickness measurements of corroded reinforced concrete pipes, such as through ultrasonic techniques, allow for straightforward estimation of remaining load-carrying capacity, offering a dependable foundation for structural integrity evaluations.

The test results for corroded pipes, shown in Figure 9, highlight the evolution of tensile damage, with damage distribution varying spatially based on corrosion thickness. As the corrosion thickness increases from 2 mm to 5 mm, the tensile damage zone at the pipe crown expands by 46.15%, while damage on the lateral sides decreases by 28.57%. As shown in Figure 9b, when corrosion thickness increases from 5 mm to 10 mm, the damage area stabilizes, but the fraction of severely damaged units rises from 67.50% to 84.38%. Critical points show near-total deterioration, consistent with experimental findings. This results from rapid crack initiation and propagation at critical points under external loads once corrosion reaches the effective thickness. Although the damage area ceases to grow, severe concrete degradation at these points causes pipeline failure.

This behavior occurs because external loading causes rapid crack initiation and propagation at vulnerable points once a critical corrosion threshold is reached. Beyond this point, the further expansion of the damage zone is halted, but the damage at critical areas intensifies, leading to severe degradation of the concrete and eventual pipe failure. This pattern underscores the influence of corrosion on the pipe’s structural integrity, particularly when the corrosion reaches a critical level where localized damage dominates.

As depicted in Figure 8, the load-crack propagation relationship of a corroded pipe prior to repair is characterized across three distinct stages:

• Elastic Stage: a linear correlation between load and displacement is observed from the onset of loading until crack initiation. During this phase, short vertical cracks are formed in high-stress regions, specifically at the crown, invert, and springlines.
• Crack growth Stage: From crack initiation to failure load, cracks propagate to critical widths, causing concrete failure and a sharp load drop due to brittle capacity loss. Re-inforcing bars remain unyielding, supporting the load increase. Vertical cracks at the crown and invert develop into bending-shear diagonal fractures, tapering from wider bases to narrower tips at a 45° inclination toward the load point.
• Yield Stage: Post-reinforcement yield, the pipe fails with gradual load decline and ac-celerated deformation, marked by widespread structural degradation.

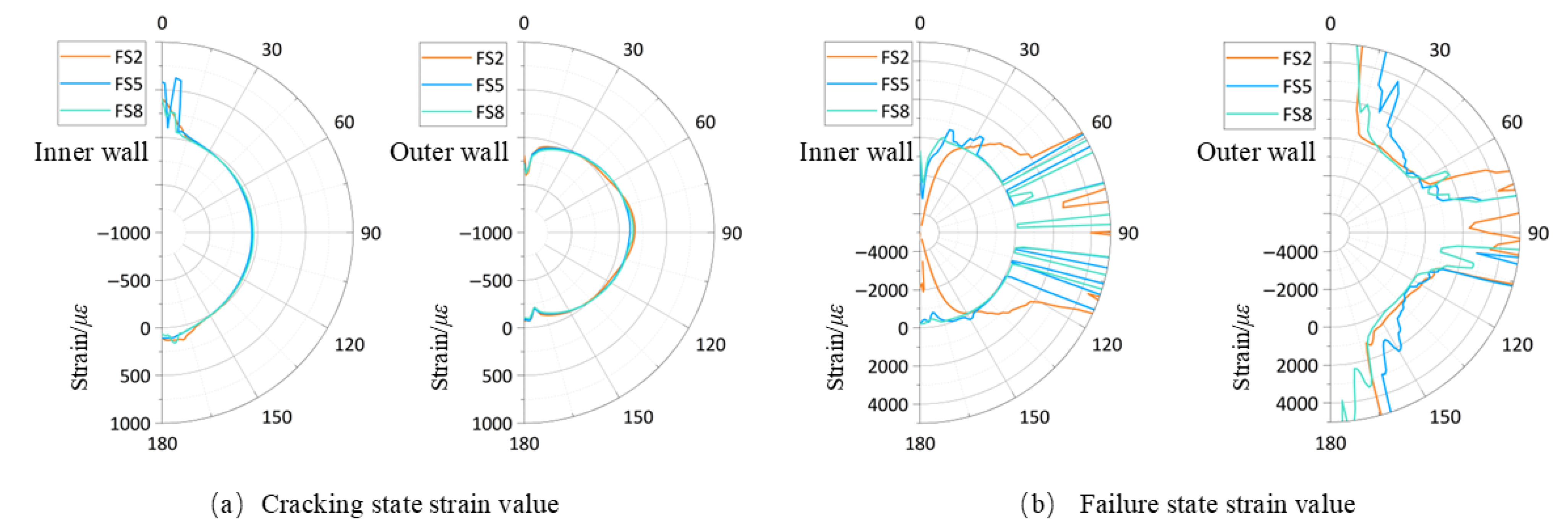
4.2.2. Effect on the Repaired Pipes

The above research highlights that corrosion thickness critically affects the evolution of structural damage in pipes. To quantitatively assess its sensitivity, this study establishes a model with a fixed repair layer thickness of 25 mm to investigate the load-bearing capacity of repaired pipes across different corrosion thicknesses. Results in

Table 9. Failure load for repaired pipes.

Group	Corrosion Thickness/mm	Failure Load/kN		Error
		TEBT	Numerical Simulation
FS2	2	24.87	25.24	1.49%
FS5	5	21.73	20.79	−4.33%
FS8	10	14.96	14.21	−5.01%

show that the numerical model closely replicates the observed load response, with a mean error of 3.61%. Linear regression is conducted to correlate corrosion thickness (x) with failure load (F_max).

Measured failure load (F_max):

$$F_{\max }=28.778-1.652x,R^2=0.957$$

(7)

Simulated failure load (F_max’):

$$F{\prime }_{\max }=29.272-1.838x,R^2=0.988$$

(8)

Equations (7) and (8) demonstrate a pronounced linear inverse relationship between the failure load of repaired pipes and initial corrosion thickness.

Figure 10 and Figure 11 presents the test results for repaired pipes, highlighting key failure mechanisms and load–displacement behavior:

• Before crack initiation, repaired pipes exhibit a near-linear load–displacement response, reflecting strong elastic compatibility between the UHPC lining and host pipe, with a consistent equivalent elastic modulus
• At crack onset, repaired pipes experience less load reduction than unrepaired ones, with the reduction decreasing as UHPC lining thickness increases, owing to the lining’s sustained post-cracking strength and enhanced flexural capacity.
• During yielding, repaired pipes show an extended yield plateau, indicating improved ductility. The UHPC lining’s high stiffness limits localized deformation, while fiber pullout restricts crack growth, allowing greater plastic strain and delaying buckling, shifting failure from brittle to ductile.
• With progressive loading and crack propagation, the equivalent elastic modulus gradually declines, especially in pipes with a corrosion thickness of 10 mm. Increased corrosion reduces the host pipe’s load-bearing capacity, transitioning the structure to a UHPC-dominated load-carrying system, with reduced interfacial friction accelerating modulus decline.

As illustrated in Figure 12, the circumferential strain profiles of repaired pipes with varying corrosion depths are presented under both cracking and ultimate failure states. In the cracking state, minimal variation in circumferential strain is observed across pipes with different corrosion thicknesses. Notably, strains at critical locations in repaired sections are significantly reduced compared to their pre-repair condition. This reduction is primarily attributed to the increased stiffness imparted by the repair layer, which effectively mitigates early crack propagation. In contrast, at the ultimate limit state, strains at critical points are observed to increase with greater corrosion depth, indicating that diminished wall thickness substantially impairs the pipe’s ability to withstand deformation.

The analysis reveals that the pipe corrosion thickness exhibits a strong linear negative correlation with load-bearing capacity in the natural bonding state, regardless of the repair status. However, greater corrosion thickness diminishes the pipe’s deformation resistance, reducing interface strength and consequently impacting the composite performance of the repaired system.

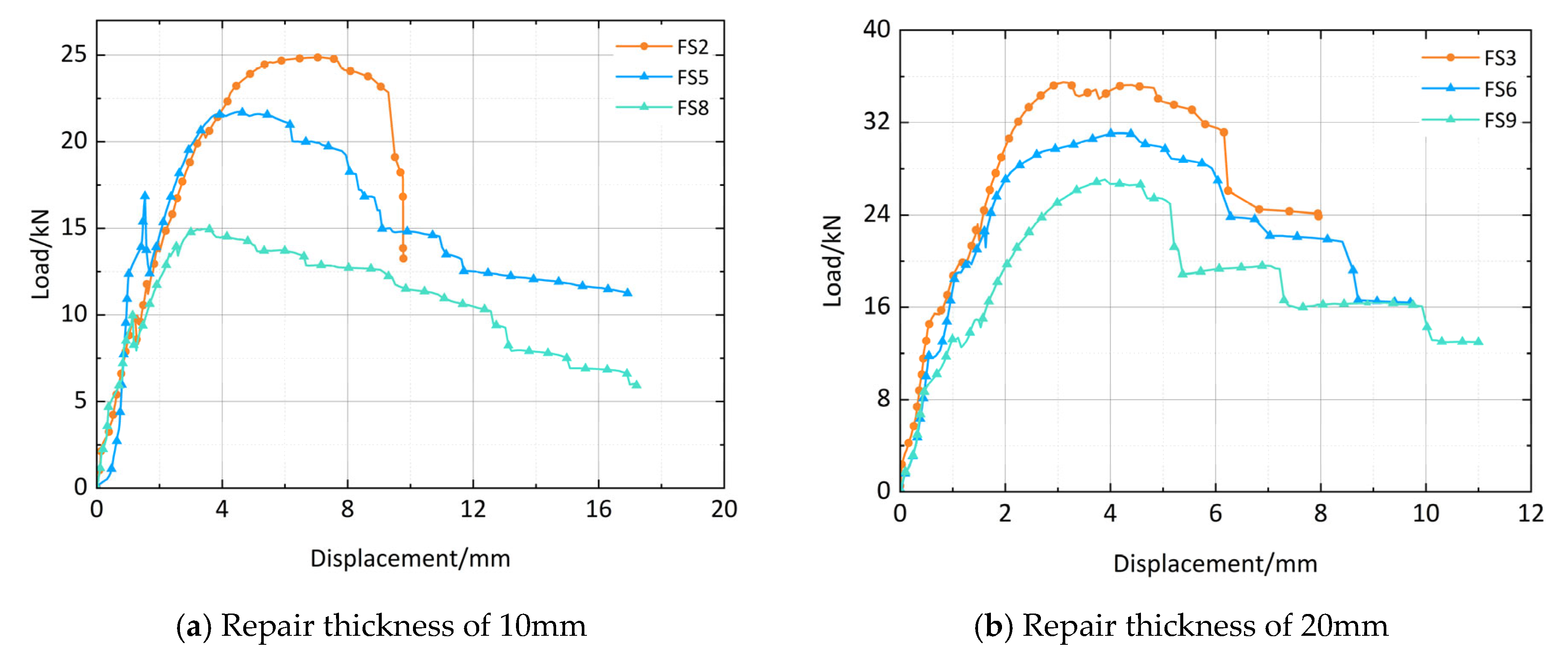
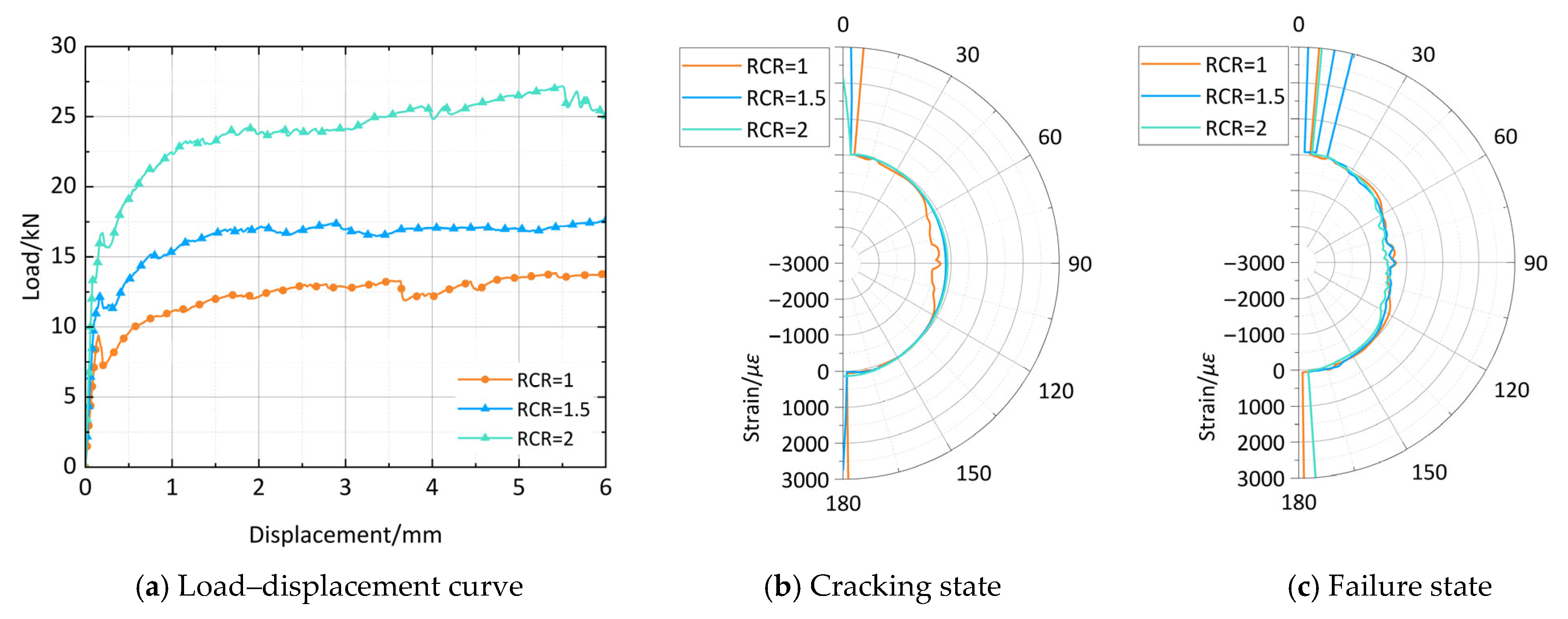
4.3. Effect of Repair Thickness on Load-Bearing Capacity

Table 10. Results of TEBT.

Group	Crack Load/kN	Failure Load/kN
FS1	6.19	11.83
FS2	9.80	24.87
FS3	15.41	35.64
FS4	5.36	10.12
FS5	16.85	21.73
FS6	22.83	31.08
FS7	4.51	7.69
FS8	9.97	14.96
FS9	13.37	27.09

presents the results of the indoor test. Linear regression was performed on pipe data with consistent corrosion thickness to examine the relationship between repair thickness (y) and failure load (F_max).

Corrosion thickness of 2 mm:

$$F_{\max 1}=1.191y+12.208,R^2=0.997$$

(9)

Corrosion thickness of 5 mm:

$$F_{\max 2}=1.048y+10.497,R^2=0.996$$

(10)

Corrosion thickness of 10 mm:

$$F_{\max 3}=0.970y+6.880,R^2=0.979$$

(11)

UHPC repair markedly enhanced the load-carrying capacity of reinforced concrete pipes. A strong linear positive correlation (R² > 0.979) was observed between repair thickness and performance improvement. For each 5 mm increment in repair thickness, the load capacity of pipes with 2 mm, 5 mm, and 10 mm corrosion increased by 48.78%, 49.92%, and 70.49%, respectively. Increased repair layer thickness augments the cross-sectional moment of inertia, effectively mitigating crack propagation.

A Repair Compensation Ratio (RCR), defined as the ratio of repair thickness to corrosion loss, was introduced to evaluate the combined influence of repair and corrosion on load-carrying capacity. As depicted in Figure 13b,c, during the cracking phase, repair thickness exhibits a negative correlation with circumferential strain at critical points; however, at the failure load state, a positive correlation emerges. This indicates that thicker repair layers effectively bolster initial crack resistance and long-term deformation resistance in repaired pipes.

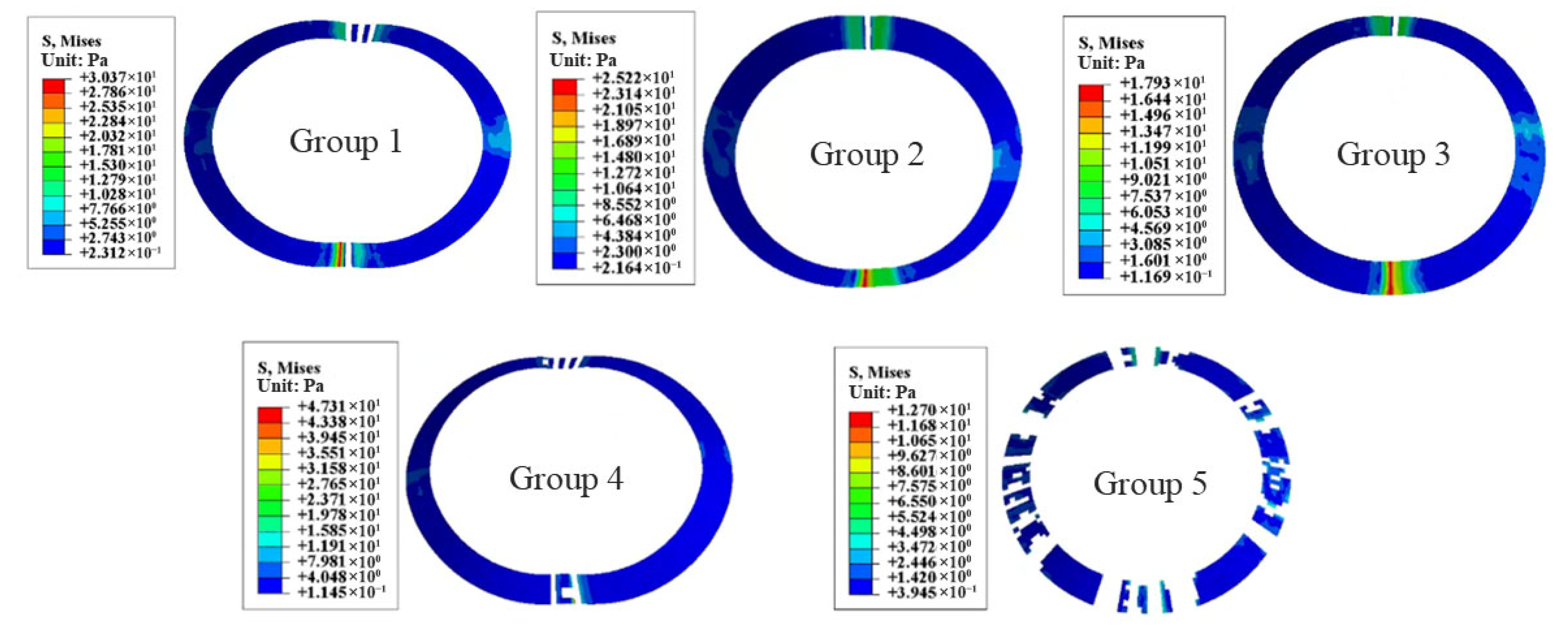
4.4. Effect of Interface Type on Load-Bearing Capacity

Experimental results indicate failure loads of 6.32 kN, 11.70 kN, 21.96 kN, and 10.71 kN for pipe groups JM0, JM1, JM2, and JM3, respectively. Post-repair, load capacities increased by 69.46%, 85.13%, and 247.47%, with JM2 (nail-embedded interface) showing the highest enhancement, 3.56 and 2.91 times greater than other groups.

The loading process diagrams of each group of specimens are shown in Figure 14. JM1 and JM2 developed cracks at the pipe’s top and bottom at displacements of 2.30 mm and 2.60 mm, respectively, while JM3 cracked at 1.32 mm, indicating lower crack resistance. JM1 and JM3 exhibited interfacial debonding; in JM1, debonding occurred post-failure load, enabling a slight load capacity increase post-cracking, whereas JM3’s debonding aligned with failure load, causing rapid lining failure and load stagnation. JM2 showed no debonding, retained partial load capacity post-cracking, and failed only due to excessive crack widening. These results highlight that nail embedding effectively prevents debonding, enhances bond strength, maintains composite integrity, and optimizes the lining’s supportive role.

Table 11. Failure load of DN400 models.

Group	${\mathit{t}}_{\mathit{n}}^0$/MPa	${\mathit{t}}_{\mathit{s}}^0/{\mathit{t}}_{\mathit{t}}^0$	Gc/(N/mm)	Failure Load/kN
1	9.3	16.1	0.1	17.77
2	9.3	16.1	0.5	17.42
3	9.3	16.1	0.9	17.57
4	3.3	4.5	0.9	16.46
5	0.33	0.45	0.9	15.78

presents failure load values for varying interface parameters, highlighting the combined influence of interface fracture energy and shear strength on the composite system’s load-bearing capacity. When interfacial shear strength is fixed at 16.1 MPa, increasing fracture energy from 0.1 N/mm to 0.9 N/mm results in a failure load variation of 1.9%. Conversely, with fracture energy held at 0.9 N/mm, reducing shear strength from 4.5 MPa to 0.45 MPa leads to a 9.5% decrease in failure load, five times the impact of fracture energy. This underscores the dominant role of interfacial shear strength in load-carrying capacity, as it governs resistance to interlayer slip under internal pressure, bending, and other loads. Slip triggers rapid structural instability, whereas fracture energy primarily mitigates delamination propagation more slowly, with less direct influence on failure load.

Figure 15 illustrates the Mises stress distribution, elucidating the mechanical response of interface parameters. Comparisons across conditions 1 to 3 show that increasing fracture energy markedly reduces the interfacial debonding area. Conversely, comparisons from conditions 3 to 5 reveal that decreasing interfacial shear strength significantly exacerbates interfacial slip, with a substantially greater impact than that of fracture energy.

TEBT results show that a smooth interface between the inner lining and existing pipe forms a unitized structure with a failure load 15.67% lower than a naturally bonded interface. A surface-to-surface contact model (friction coefficient μ = 0.1, normal hard contact) was developed to analyze load-bearing behavior, with results shown in Figure 16. At 93% of the failure load, tensile damage initiated at the crown of the existing pipeline, causing an abrupt load drop. The load then gradually recovered, supported by the inner lining until its failure triggered a second sudden load drop, aligning with experimental observations. Damage primarily affected the existing pipeline, with a noticeable gap between it and the inner lining. This suggests independent bending deformation of the pipeline and lining during loading, with no significant interface bonding. The existing pipeline reached its strength limit before the inner lining could contribute substantially, and interface slip limited the lining’s capacity, resulting in minimal enhancement of the repaired structure’s overall load-bearing capacity.

The results indicate that interfacial bonding depends on the combined effects of fracture energy and shear strength, with shear strength exerting a fivefold greater influence than fracture energy. Enhanced fracture energy can suppress debonding propagation, provided no interfacial sliding occurs. However, when sliding dominates failure, the benefits of increased fracture energy are diminished. Therefore, to enhance pipeline repair, locally reinforce shear strength at stress concentration zones (e.g., pipeline top, bottom, and spring line) using interface bolt fixation. During service, prioritize monitoring the interface sliding in these zones. Effective monitoring techniques include linear variable differential transformers (LVDTs), fiber Bragg grating (FBG) sensors, and inclinometers/inertial measurement units (IMUs).

5. Conclusions

This study investigates the load-bearing capacity of corroded reinforced concrete pipes through experimental and numerical methods, focusing on corrosion depth, repair thickness, and interface properties. Strain, load–displacement behavior, and damage progression were analyzed. Key findings are:

• Load–displacement response includes elastic, crack propagation, and yield phases. UHPC linings reduce crack-induced load drops, delay buckling, enhance yield capacity, and shift failure from brittle to ductile.
• The residual load-bearing capacity of corroded pipes exhibits a linear decrease with increasing corrosion depth, while it improves with greater repair thickness, enhancing both crack resistance and deformation capacity. Specifically, for each 5 mm increase in UHPC lining thickness, the load-bearing capacity of pipes with 2 mm, 5 mm, and 10 mm corrosion depths rises by 48.78%, 49.92%, and 70.49%, respectively.
• Interface shear strength and fracture energy significantly affect repaired pipe capacity. Higher fracture energy minimizes debonding, while lower shear strength increases sliding, impacting capacity fivefold more than debonding. Independent damage in composite systems reduces capacity compared to fully bonded structures. Interface design should optimize shear strength.
• Nail embedding enhances shear strength, increasing capacity by 2.91 times over natural bonding and preventing debonding. Unitized systems with polyethylene films reduce load-sharing due to sliding, lowering failure load by 15.67%. Localized shear reinforcement, such as nail embedding, is recommended for high-stress zones, with continuous monitoring of interfacial sliding for durability. Future research is advisable to optimize UHPC composition and investigate diverse interface treatments, including roughening and varied steel nail configurations, to further elucidate their impact on pipeline load capacity.