Optimized Gradient Boosting Framework for Data-Driven Prediction of Concrete Compressive Strength
Abstract
1. Introduction
Research Significance and Objectives
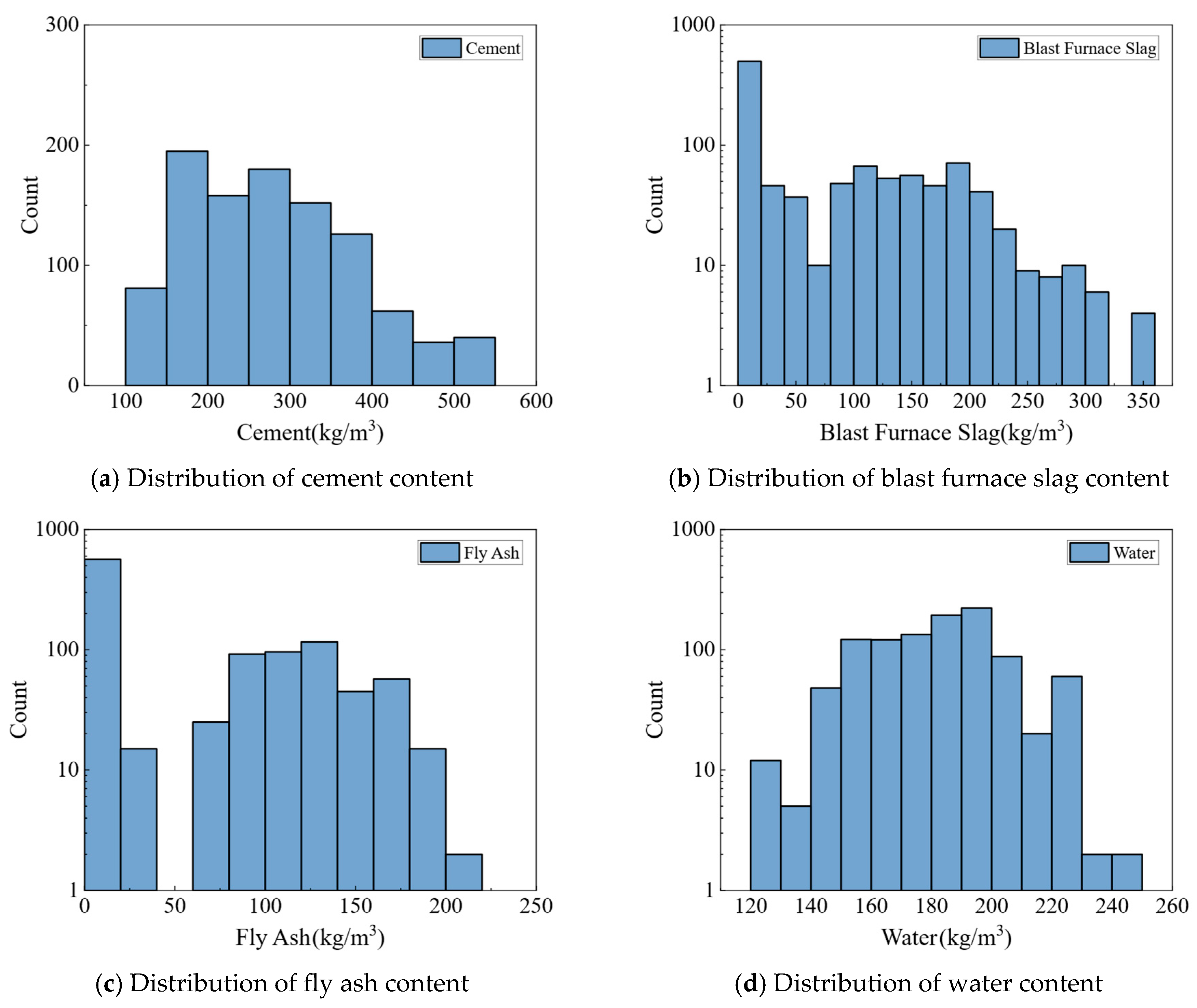
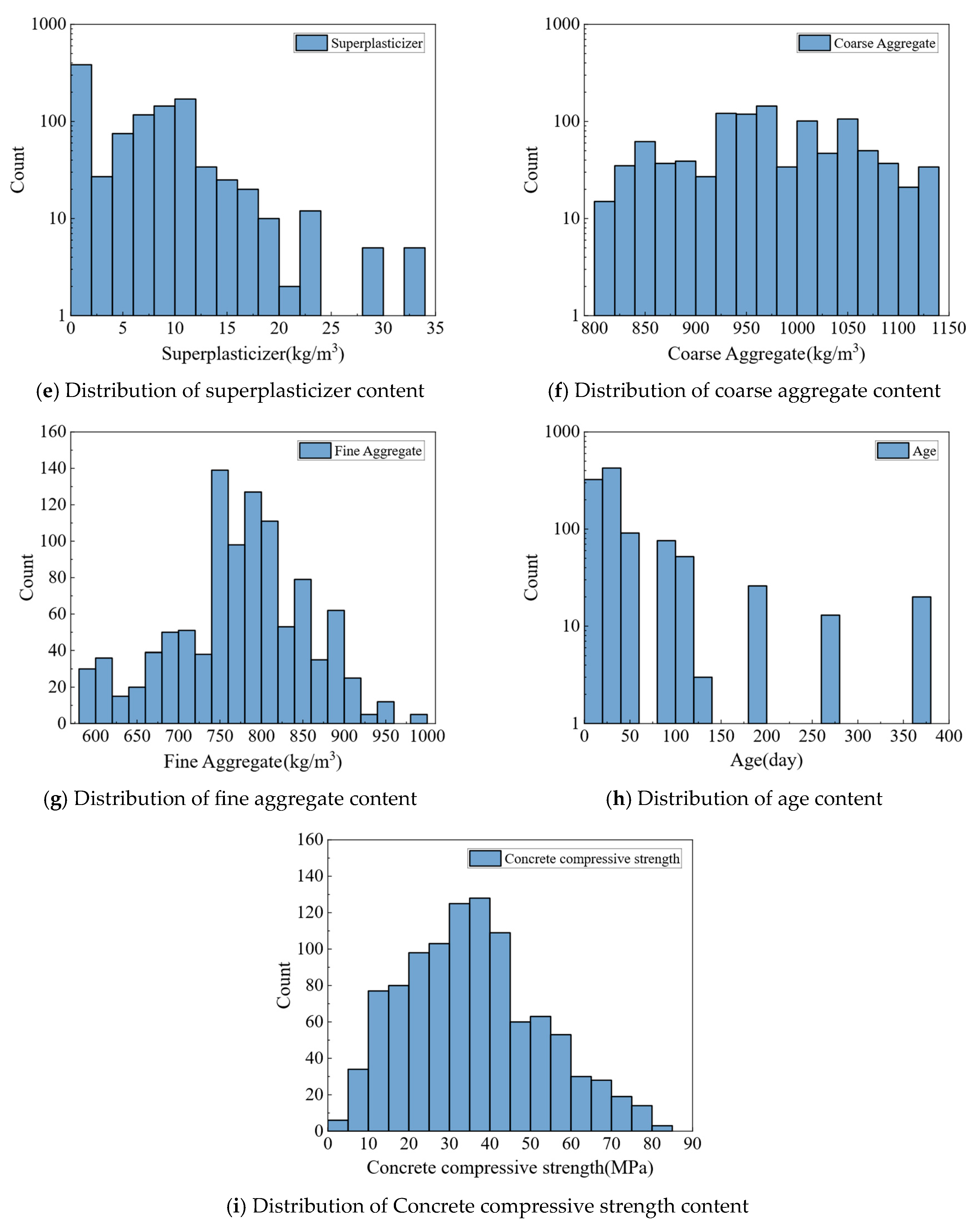
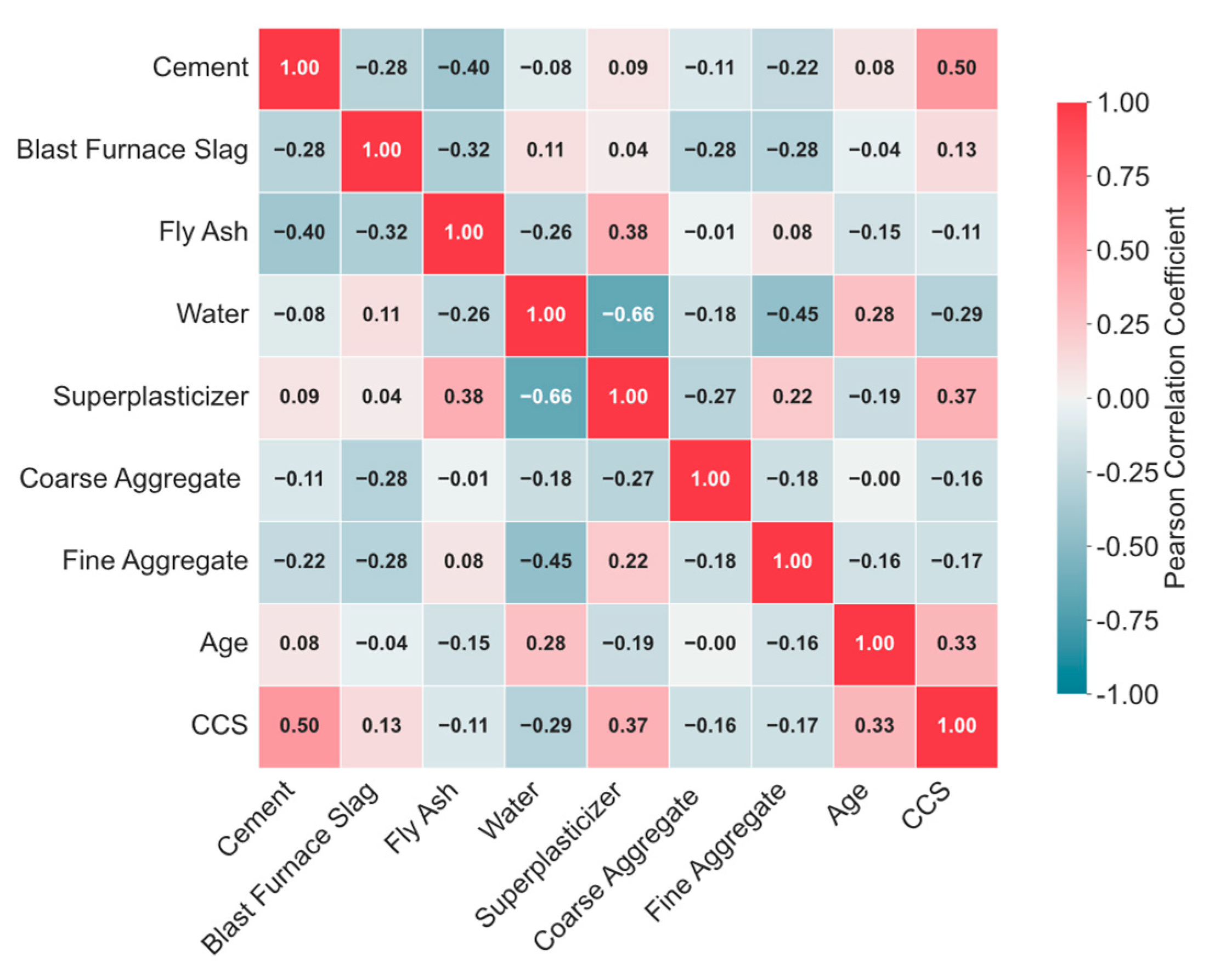
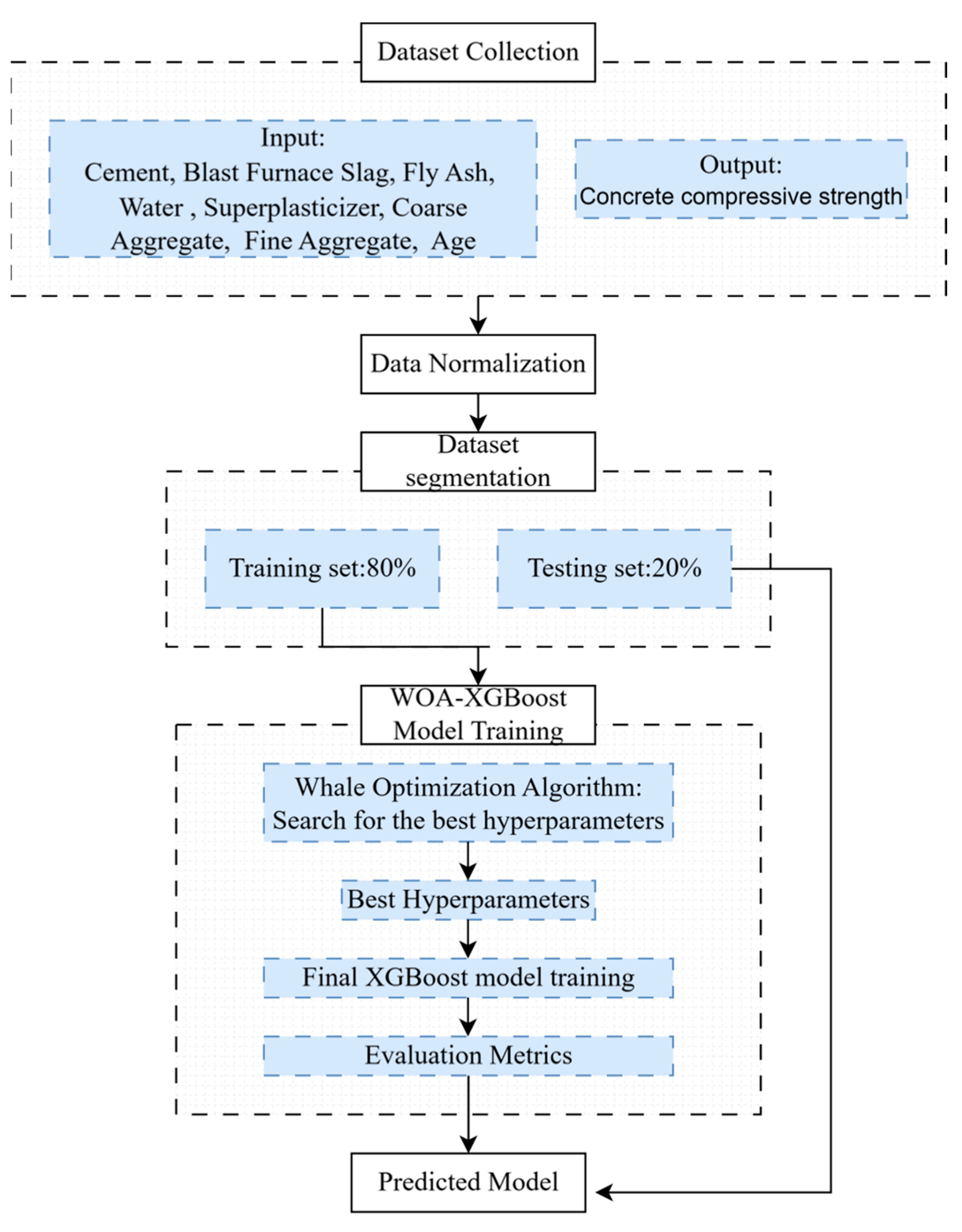
2. Database of Concrete Compressive Strength
3. Machine Learning Predictive Models
3.1. Model Introduction
3.1.1. Linear Regression
3.1.2. Random Forest
3.1.3. XGBoost
3.1.4. Whale Optimization Algorithm-Optimized XGBoostoost
3.1.5. LightBoost
3.1.6. CatBoost
3.1.7. Neural Networks
3.2. Training of Machine Learning Models
3.2.1. Grid Search for Training Machine Learning
3.2.2. Whale Optimization Algorithm XGBoostXGBoost
4. Result and Discussion
4.1. Model Comparison and Proposed Model
4.2. Data Variability Analysis
4.2.1. Feature Importance Analysis
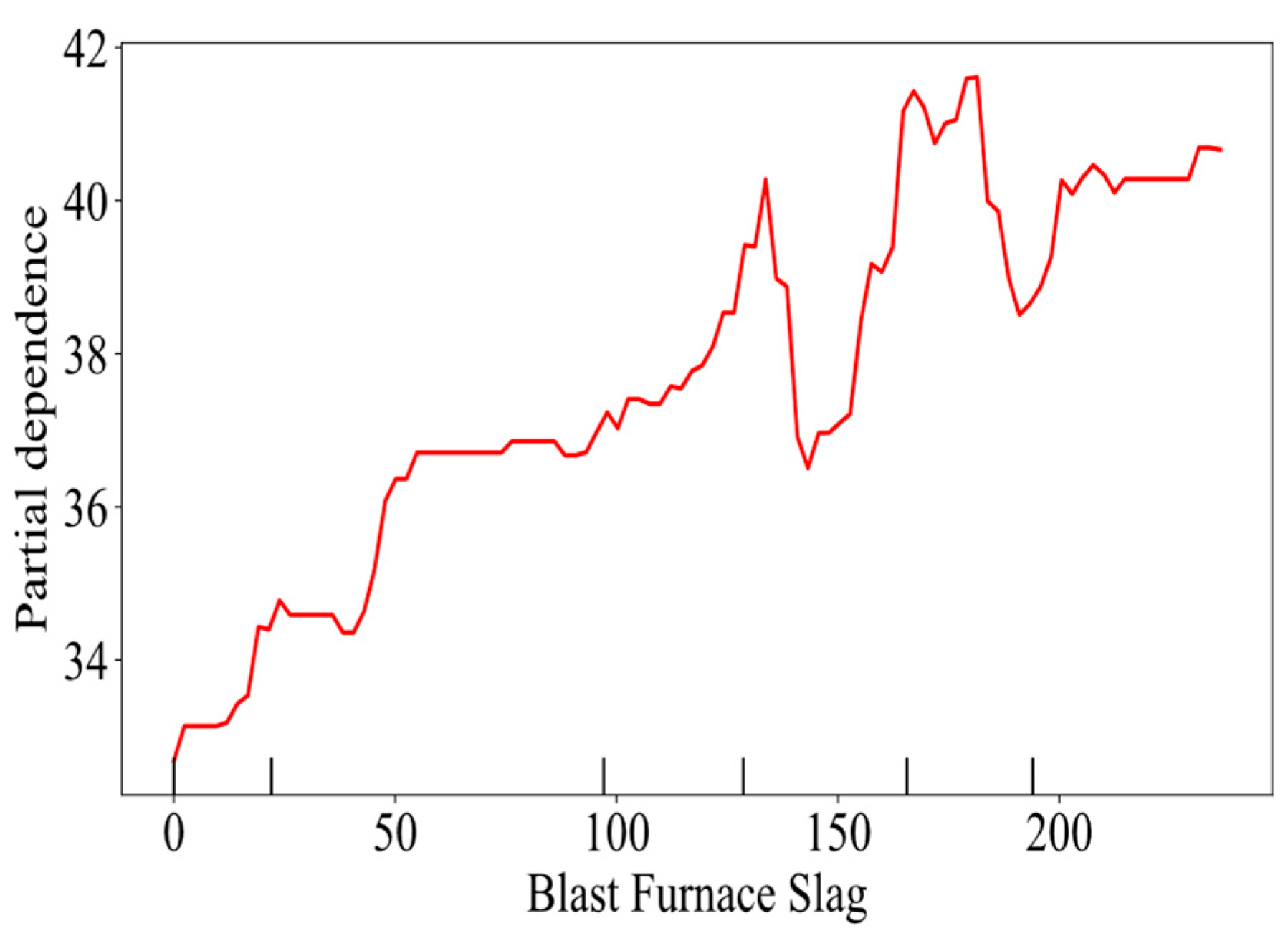
4.2.2. Feature Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, G.; Sun, B. Concrete compressive strength prediction using an explainable boosting machine mode. Case Stud. Constr. Mater. 2023, 18, e01845. [Google Scholar]
- Asteris, P.G.; Mokos, V.G. Concrete compressive strength using artificial neural networks. Neural Comput. Appl. 2020, 32, 11807–11826. [Google Scholar] [CrossRef]
- Moccia, F.; Yu, Q.; Fernández Ruiz, M.; Muttoni, A. Concrete compressive strength: From material characterization to a structural value. Struct. Concr. 2021, 22, E634–E654. [Google Scholar] [CrossRef]
- Güçlüer, K.; Özbeyaz, A.; Göymen, S.; Günaydın, O. A comparative investigation using machine learning methods for concrete compressive strength estimation. Mater. Today Commun. 2021, 27, 102278. [Google Scholar] [CrossRef]
- Paudel, S.; Pudasaini, A.; Shrestha, R.K.; Kharel, E. Compressive strength of concrete material using machine learning techniques. Clean. Eng. Technol. 2023, 15, 100661. [Google Scholar] [CrossRef]
- Amar, M. Comparative use of different AI methods for the prediction of concrete compressive strength. Clean. Mater. 2025, 15, 100299. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Vasiliadis, L.K. Interpretable machine learning for assessing the cumulative damage of a reinforced concrete frame induced by seismic sequences. Sustainability 2023, 15, 12768. [Google Scholar] [CrossRef]
- Izadifar, M.; Ukrainczyk, N.; Schönfeld, K.; Koenders, E. Activation energy of aluminate dissolution in metakaolin: MLFF-accelerated DFT study of vdW and hydration shell effects. Nanoscale Adv. 2025, 7, 4325–4335. [Google Scholar] [CrossRef]
- Dinesh, A.; Prasad, B.R. Predictive models in machine learning for strength and life cycle assessment of concrete structures. Autom. Constr. 2024, 162, 105412. [Google Scholar] [CrossRef]
- Hu, H.; Jiang, M.; Tang, M.; Liang, H.; Cui, H.; Liu, C.; Ji, C.; Wang, Y.; Jian, S.; Wei, C.; et al. Prediction of compressive strength of fly ash-based geopolymers concrete based on machine learning. Results Eng. 2025, 27, 106492. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.; Liang, W.; Liu, J.; Zhou, Y.; Lei, K.; Gao, Y.; Ou, W. Predictive Modeling of Compressive Strength in Tailings Concrete Using Explainable Machine Learning Approaches. Results Eng. 2025, 27, 105516. [Google Scholar] [CrossRef]
- Pazouki, G.; Tao, Z.; Saeed, N.; Kang, W.-H. Using artificial intelligence methods to predict the compressive strength of concrete containing sugarcane bagasse ash. Constr. Build. Mater. 2023, 409, 134047. [Google Scholar] [CrossRef]
- Al-Jamimi, H.A.; Al-Kutti, W.A.; Alwahaishi, S.; Alotaibi, K.S. Prediction of compressive strength in plain and blended cement concretes using a hybrid artificial intelligence model. Case Stud. Constr. Mater. 2022, 17, e01238. [Google Scholar] [CrossRef]
- Tayeh, B.A.; Akeed, M.H.; Qaidi, S.; Abu Bakar, B.H. Influence of sand grain size distribution and supplementary cementitious materials on the compressive strength of ultrahigh-performance concrete. Case Stud. Constr. Mater. 2022, 17, e01495. [Google Scholar] [CrossRef]
- Ma, Q.; Xiao, J.; Ding, T.; Duan, Z.; Song, M.; Cao, X. The prediction of compressive strength for recycled coarse aggregate concrete in cold region. Case Stud. Constr. Mater. 2023, 19, e02546. [Google Scholar] [CrossRef]
- Sánchez-Mendieta, C.; Galán-Díaz, J.J.; Martinez-Lage, I. Relationships between density, porosity, compressive strength and permeability in porous concretes: Optimization of properties through control of the water-cement ratio and aggregate type. J. Build. Eng. 2024, 97, 110858. [Google Scholar] [CrossRef]
- Mengistu, G.M.; Nemes, R. Predicting the compressive strength of sustainable recycled aggregate concrete using multi-NDT methods. Results Eng. 2025, 26, 105650. [Google Scholar] [CrossRef]
- Li, Y.; Zhong, R.; Yu, J.; Song, J.; Wang, Q.; Chen, C.; Li, X.; Liu, E. Uniaxial Compressive Strength of Concrete Inversion using Machine Learning and Computational Intelligence Approach. Results Eng. 2025, 26, 105627. [Google Scholar] [CrossRef]
- Sathiparan, N.; Jeyananthan, P.; Subramaniam, D.N. A comparative study of machine learning techniques and data processing for predicting the compressive strength of pervious concrete with supplementary cementitious materials and chemical composition influence. Next Mater. 2025, 9, 100947. [Google Scholar] [CrossRef]
- Heidari, S.I.G.; Safehian, M.; Moodi, F.; Shadroo, S. Predictive modeling of the long-term effects of combined chemical admixtures on concrete compressive strength using machine learning algorithms. Case Stud. Chem. Environ. Eng. 2024, 10, 101008. [Google Scholar] [CrossRef]
- Khan, A.Q.; Awan, H.A.; Rasul, M.; Siddiqi, Z.A.; Pimanmas, A. Optimized artificial neural network model for accurate prediction of compressive strength of normal and high strength concrete. Clean. Mater. 2023, 10, 100211. [Google Scholar] [CrossRef]
- Wang, Q.; Yao, G.; Kong, G.; Wei, L.; Yu, X.; Jianchuan, Z.; Ran, C.; Luo, L. A data-driven model for predicting fatigue performance of high-strength steel wires based on optimized XGBoost. Eng. Fail. Anal. 2024, 164, 108710. [Google Scholar] [CrossRef]
- Yu, X.; Hu, T.; Khodadadi, N.; Liu, Q.; Nanni, A. Modeling chloride ion diffusion in recycled aggregate concrete: A fuzzy neural network approach integrating material and environmental factors. Structures 2025, 73, 108372. [Google Scholar] [CrossRef]
- Elshaarawy, M.K.; Alsaadawi, M.M.; Hamed, A.K. Machine learning and interactive GUI for concrete compressive strength prediction. Sci. Rep. 2024, 14, 16694. [Google Scholar] [CrossRef] [PubMed]
- Concrete Compressive Strength. Available online: http://dx.doi.org/10.24432/C5PK67 (accessed on 22 May 2025).
- Monteiro, D.K.; Miguel, L.F.F.; Zeni, G.; Becker, T.; de Andrade, G.S.; de Barros, R.R. Whale Optimization Algorithm for structural damage detection, localization, and quantification. Discov. Civ. Eng. 2024, 1, 98. [Google Scholar] [CrossRef]
- Nguyen, H.; Cao, M.T.; Tran, X.L.; Tran, T.H.; Hoang, N.D. A novel whale optimization algorithm optimized XGBoost regression for estimating bearing capacity of concrete piles. Neural Comput. Appl. 2023, 35, 3825–3852. [Google Scholar] [CrossRef]
- Wei, J.; Gu, Y.; Lu, B.; Cheong, N. RWOA: A novel enhanced whale optimization algorithm with multi-strategy for numerical optimization and engineering design problems. PLoS ONE 2025, 20, e0320913. [Google Scholar] [CrossRef]
- Rahimnejad, A.; Akbari, E.; Mirjalili, S.; Gadsden, S.A.; Trojovský, P.; Trojovská, E. An improved hybrid whale optimization algorithm for global optimization and engineering design problems. PeerJ Comput. Sci. 2023, 9, e1557. [Google Scholar] [CrossRef]


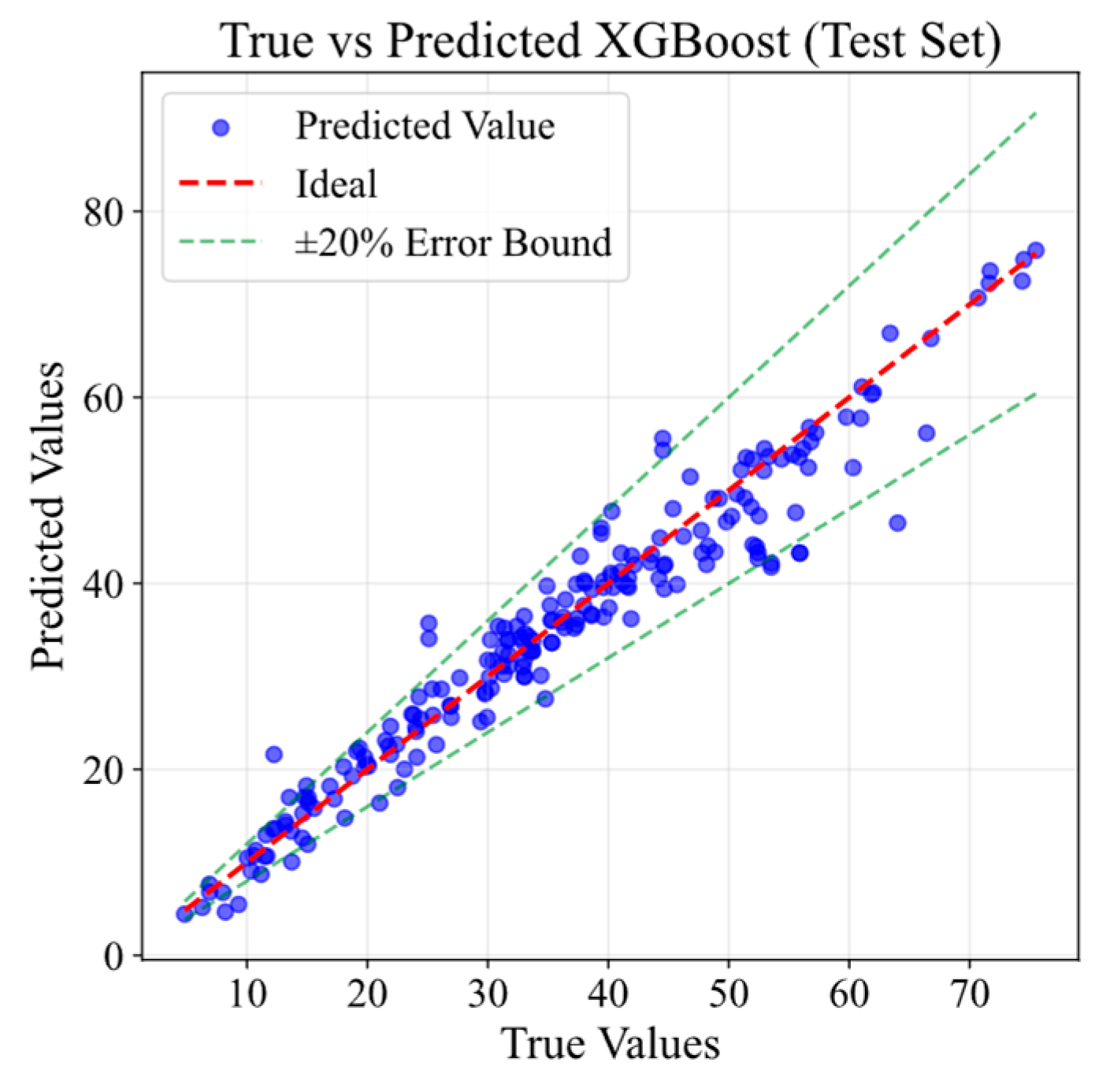
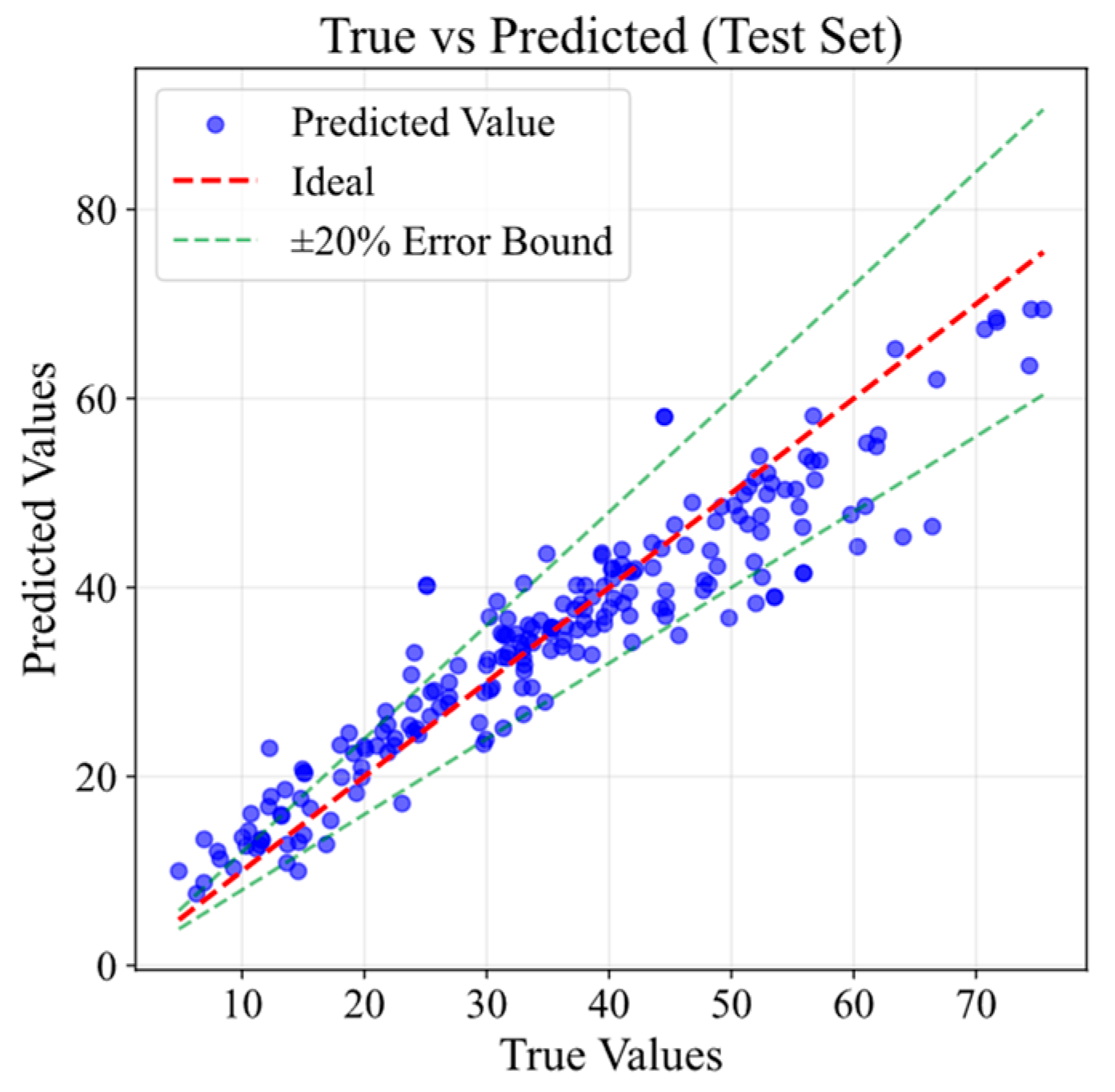
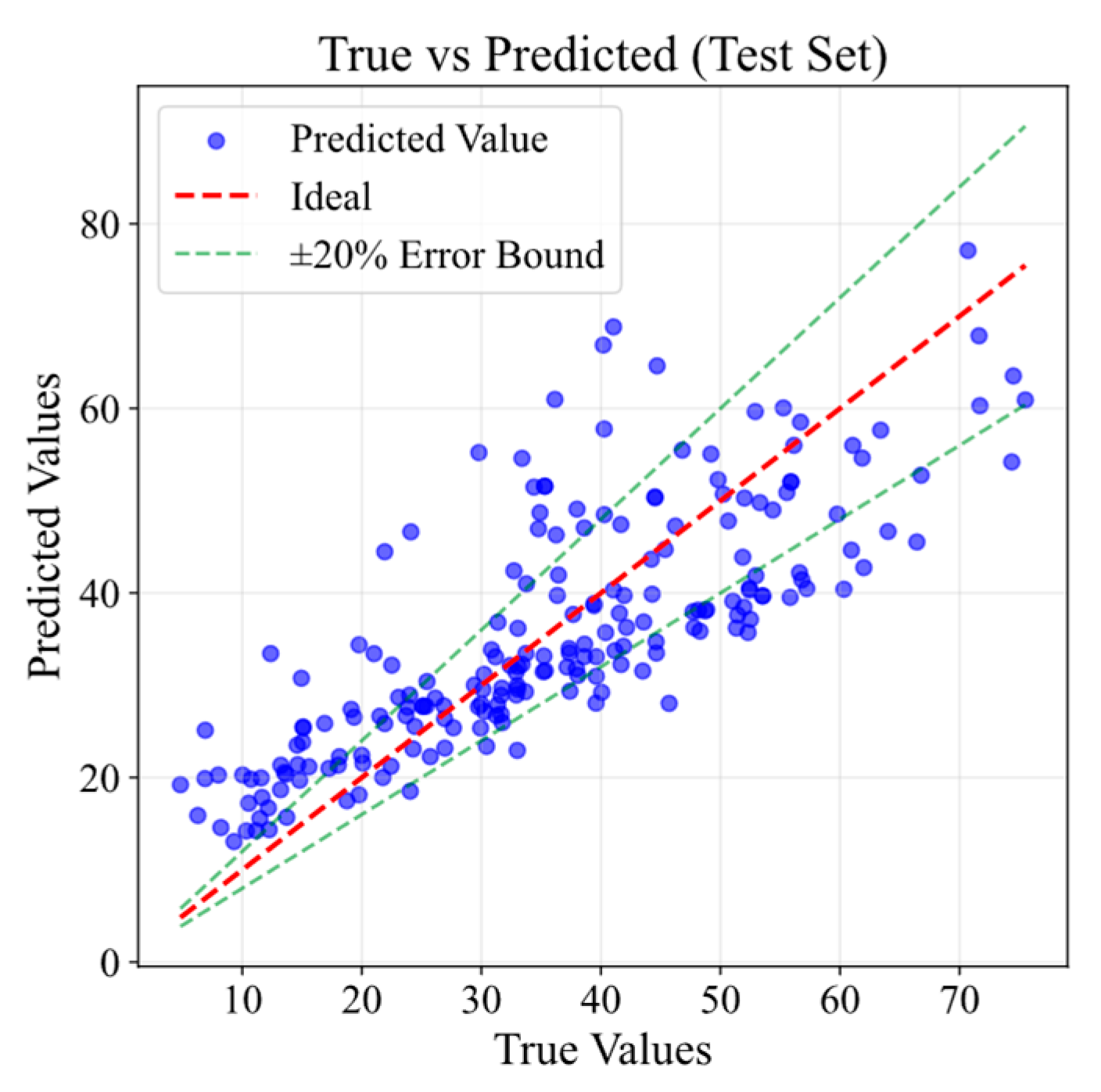
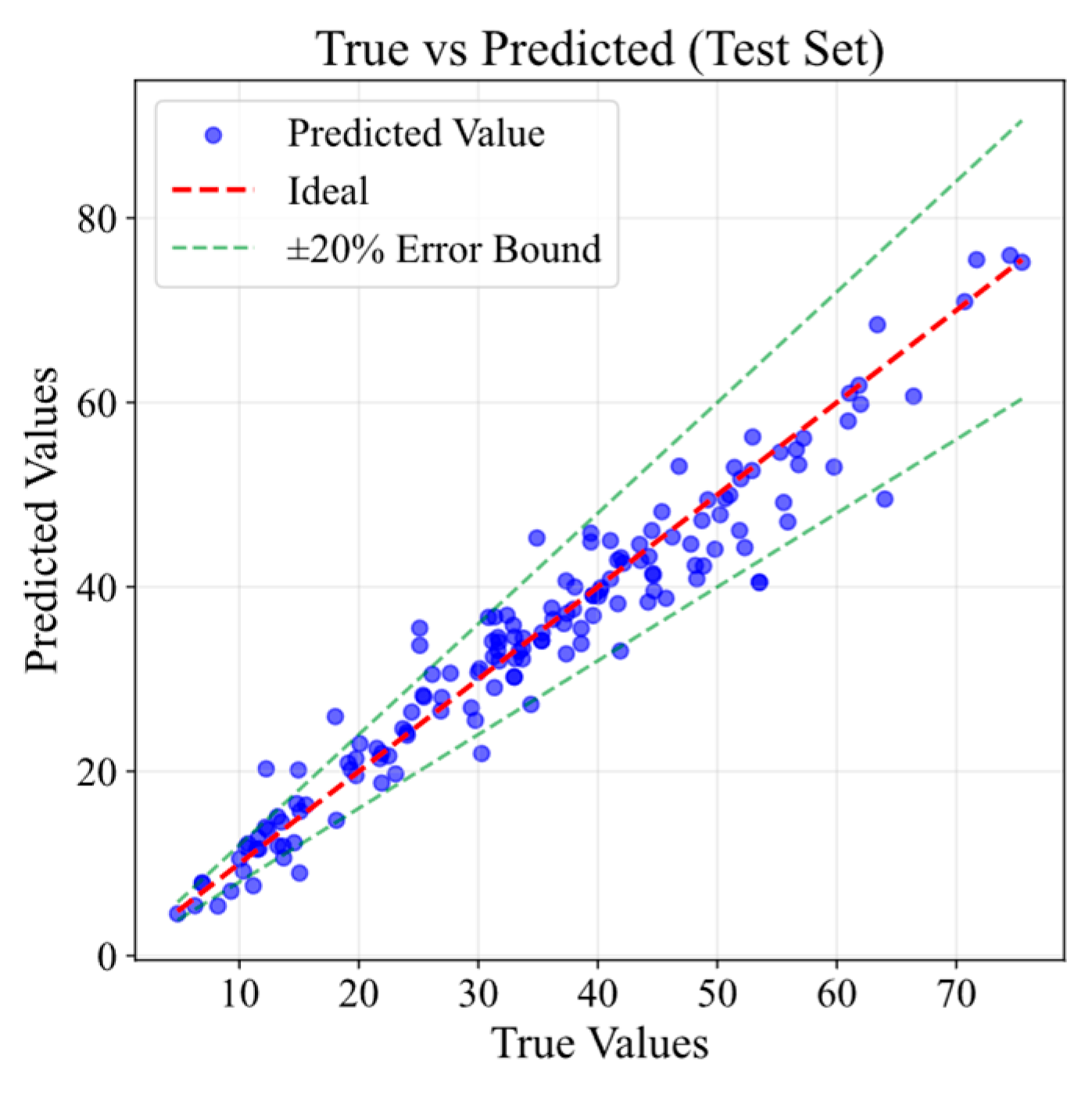
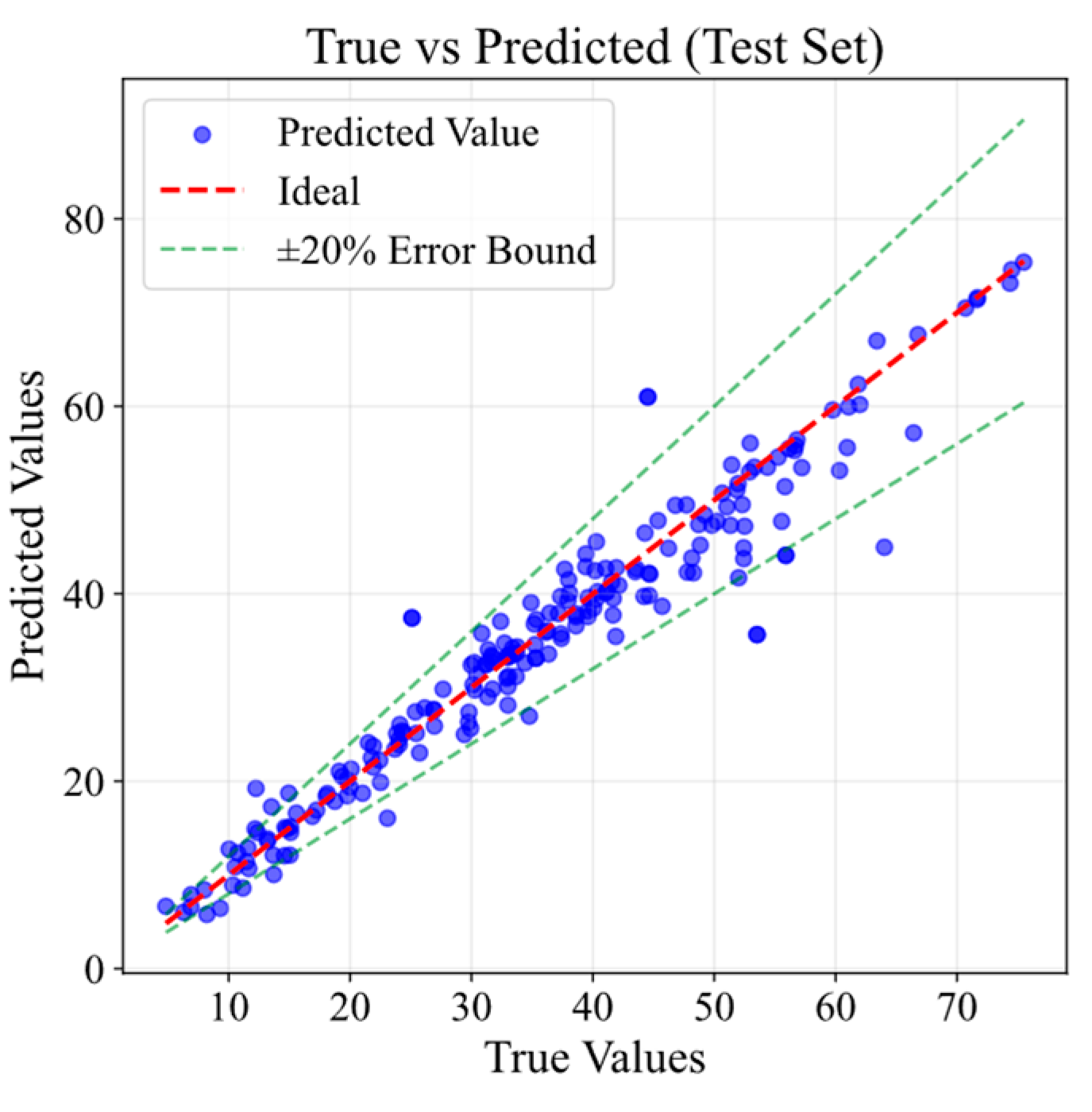
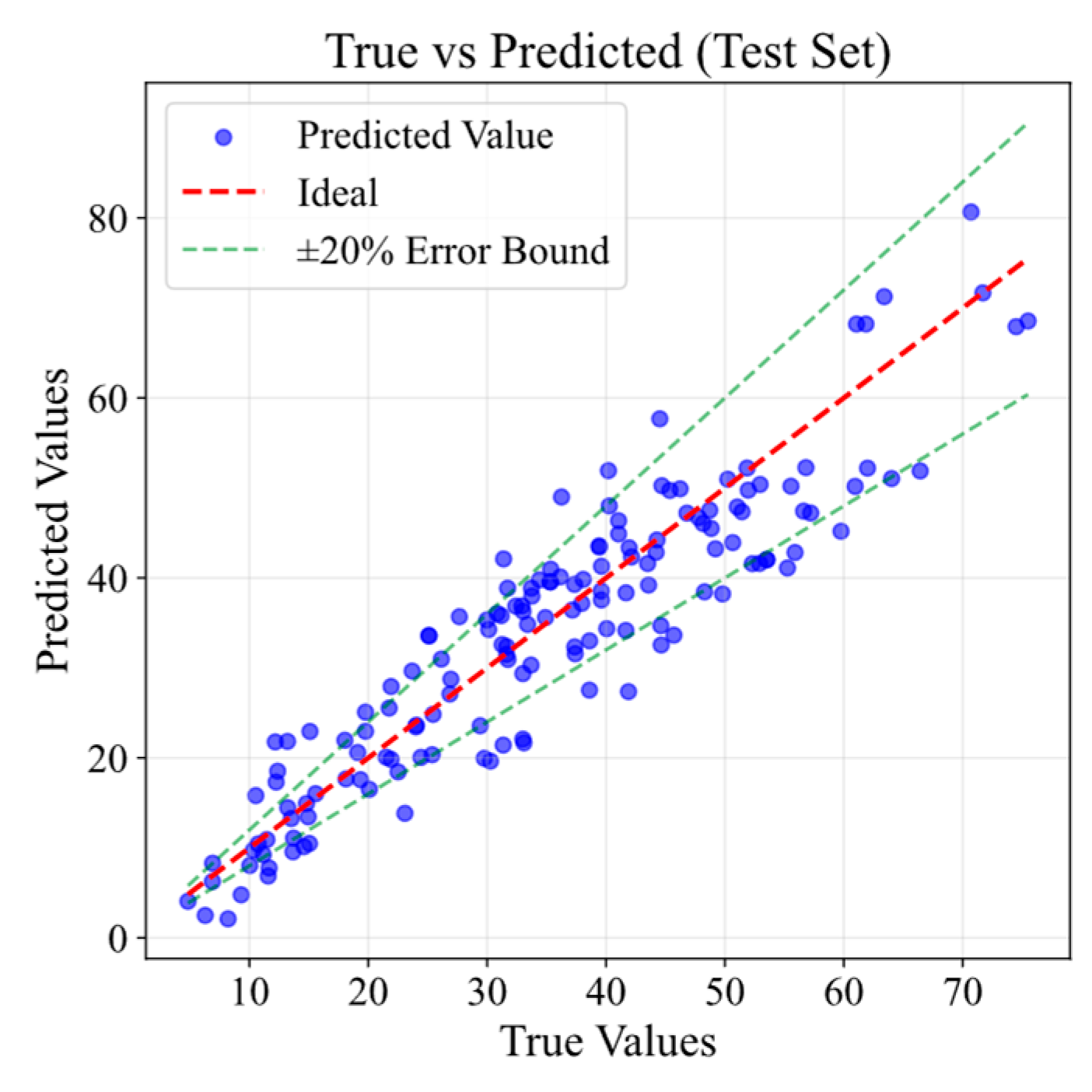
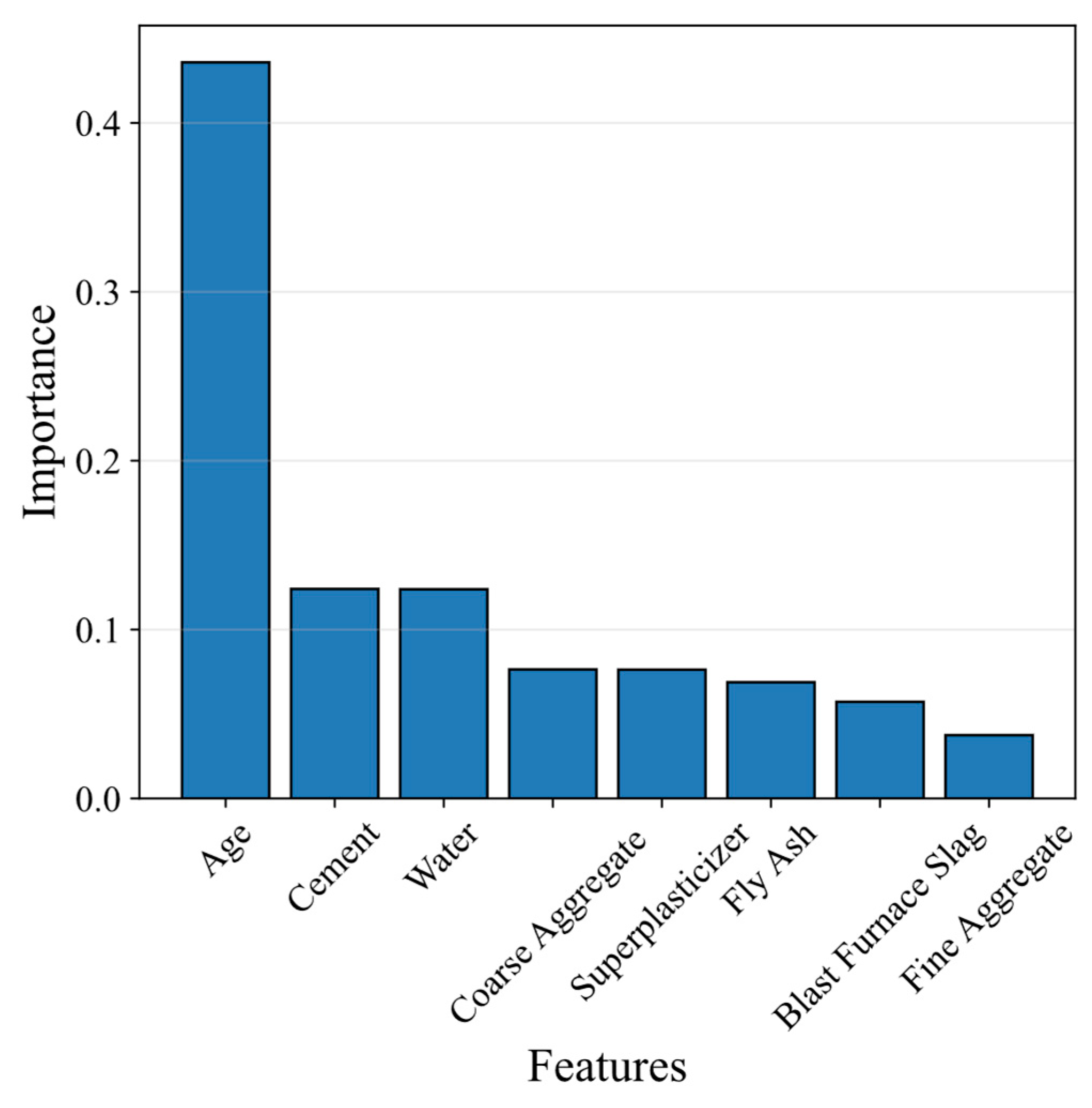

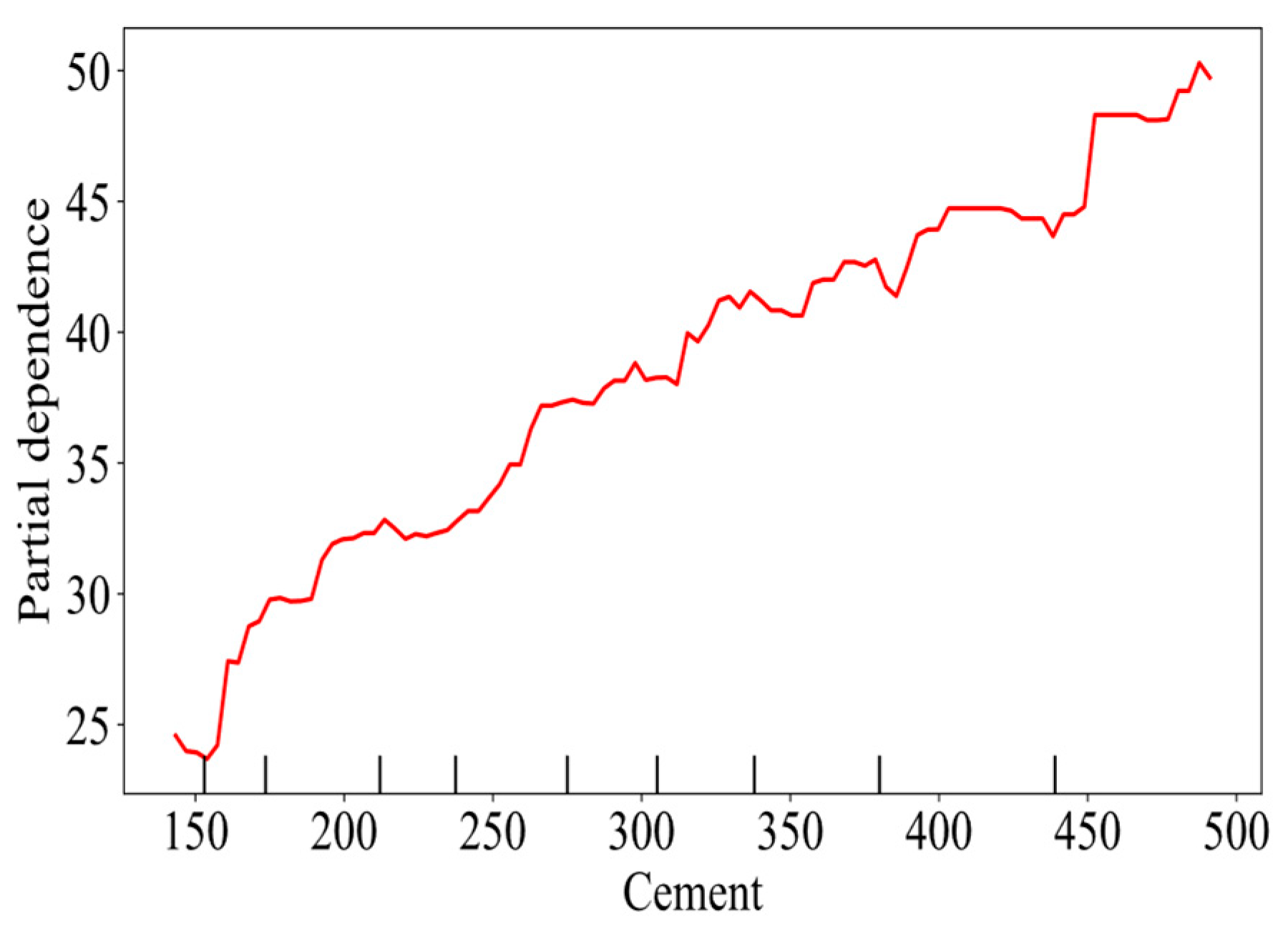
| WOXGBoost Training | WOXGBoost Test | XGBoost | Random Forest | Ridge Regression | |
|---|---|---|---|---|---|
| R2 | 0.9808 | 0.9412 | 0.9051 | 0.8762 | 0.6275 |
| MSE | 2.3277 | 3.8920 | 4.9440 | 8.9183 | 9.7967 |
| Continuation | |||||
| R2 | 0.9808 | 0.9412 | 0.9383 | 0.9294 | 0.8424 |
| MSE | 2.3277 | 3.8920 | 4.0181 | 4.2640 | 6.4248 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Zheng, P.; Zhang, J.; Cheng, L. Optimized Gradient Boosting Framework for Data-Driven Prediction of Concrete Compressive Strength. Buildings 2025, 15, 3761. https://doi.org/10.3390/buildings15203761
Sun D, Zheng P, Zhang J, Cheng L. Optimized Gradient Boosting Framework for Data-Driven Prediction of Concrete Compressive Strength. Buildings. 2025; 15(20):3761. https://doi.org/10.3390/buildings15203761
Chicago/Turabian StyleSun, Dawei, Ping Zheng, Jun Zhang, and Liming Cheng. 2025. "Optimized Gradient Boosting Framework for Data-Driven Prediction of Concrete Compressive Strength" Buildings 15, no. 20: 3761. https://doi.org/10.3390/buildings15203761
APA StyleSun, D., Zheng, P., Zhang, J., & Cheng, L. (2025). Optimized Gradient Boosting Framework for Data-Driven Prediction of Concrete Compressive Strength. Buildings, 15(20), 3761. https://doi.org/10.3390/buildings15203761





