Numerical Investigation of Seismic Soil–Structure–Excavation Interaction in Sand
Abstract
1. Introduction
2. Numerical Modeling
2.1. Meshing Considerations
2.2. Boundary Conditions
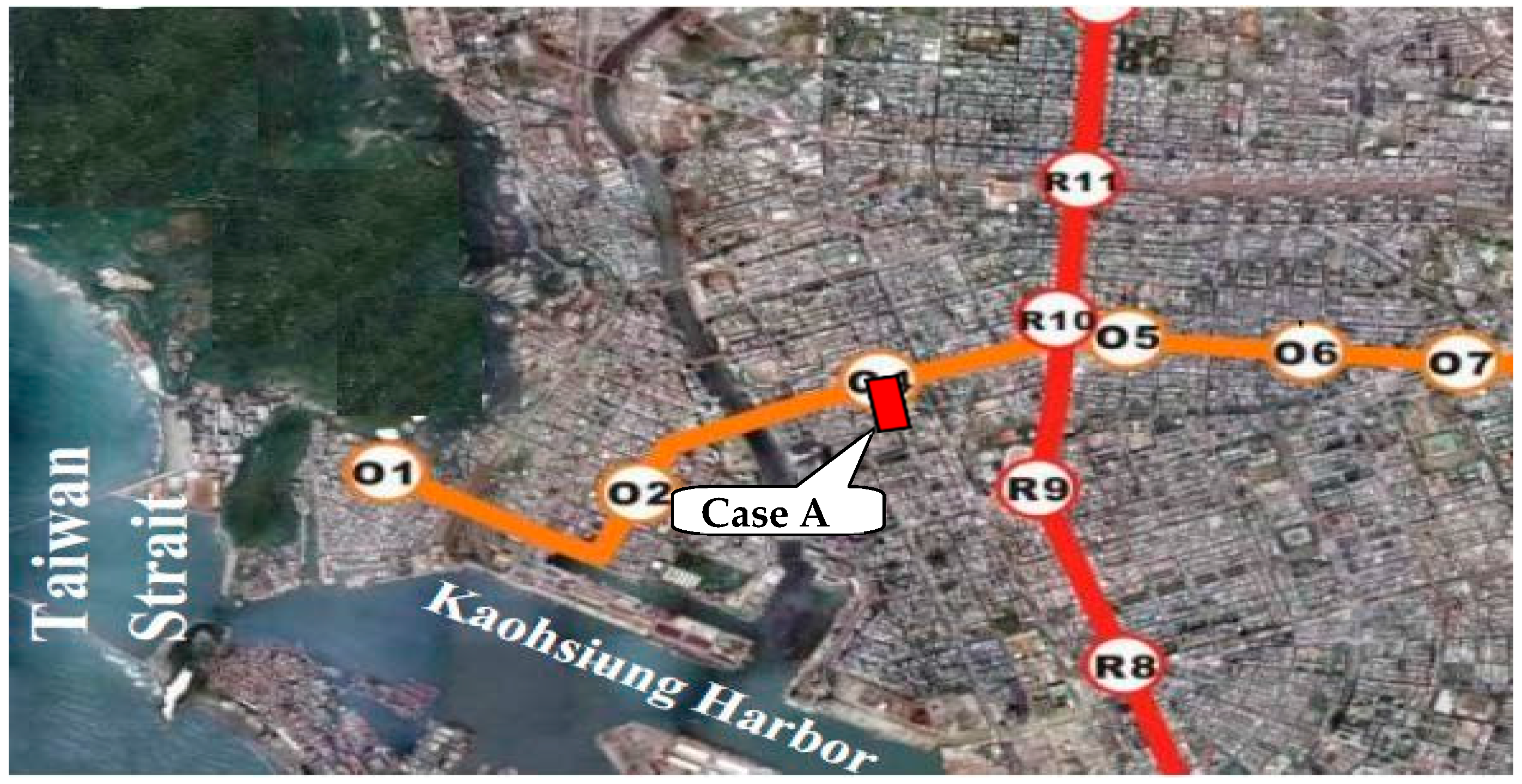
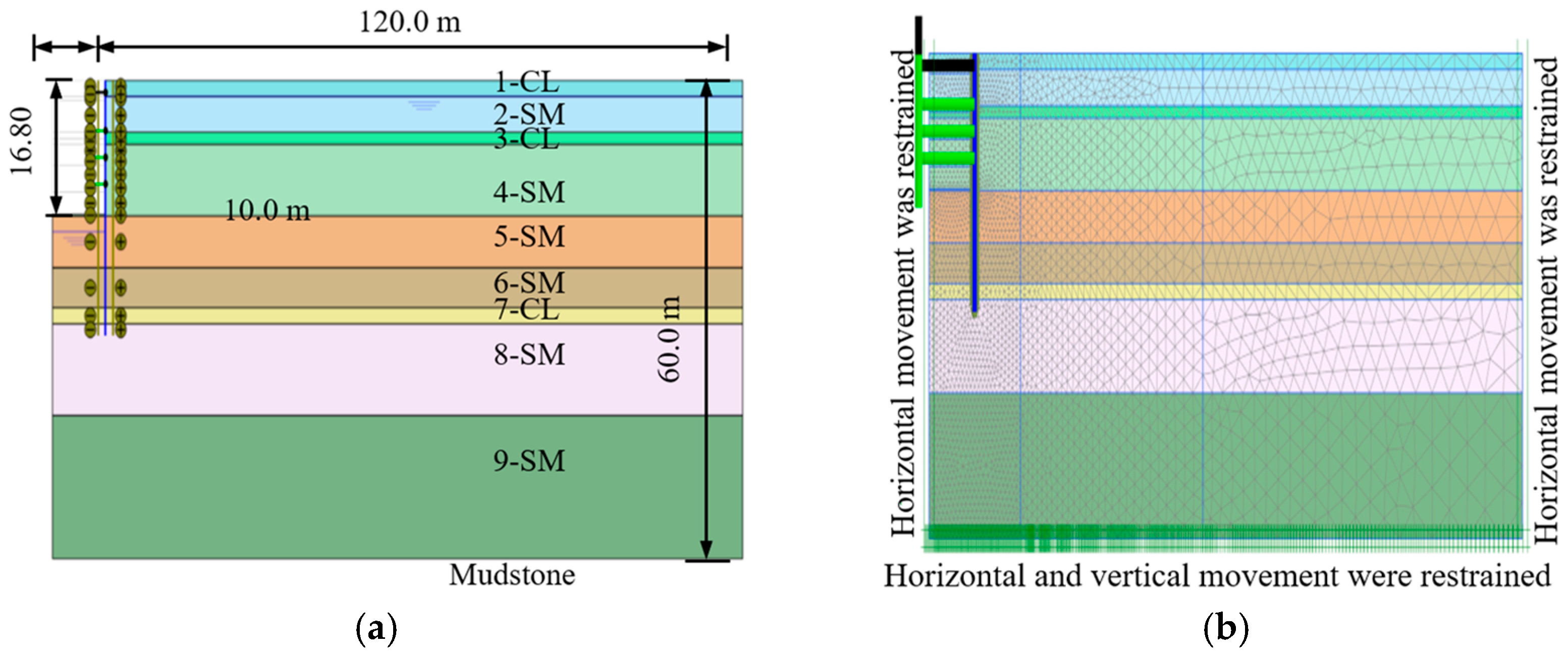
3. Verification of a Case Study on Deep Excavation in Sand [45]
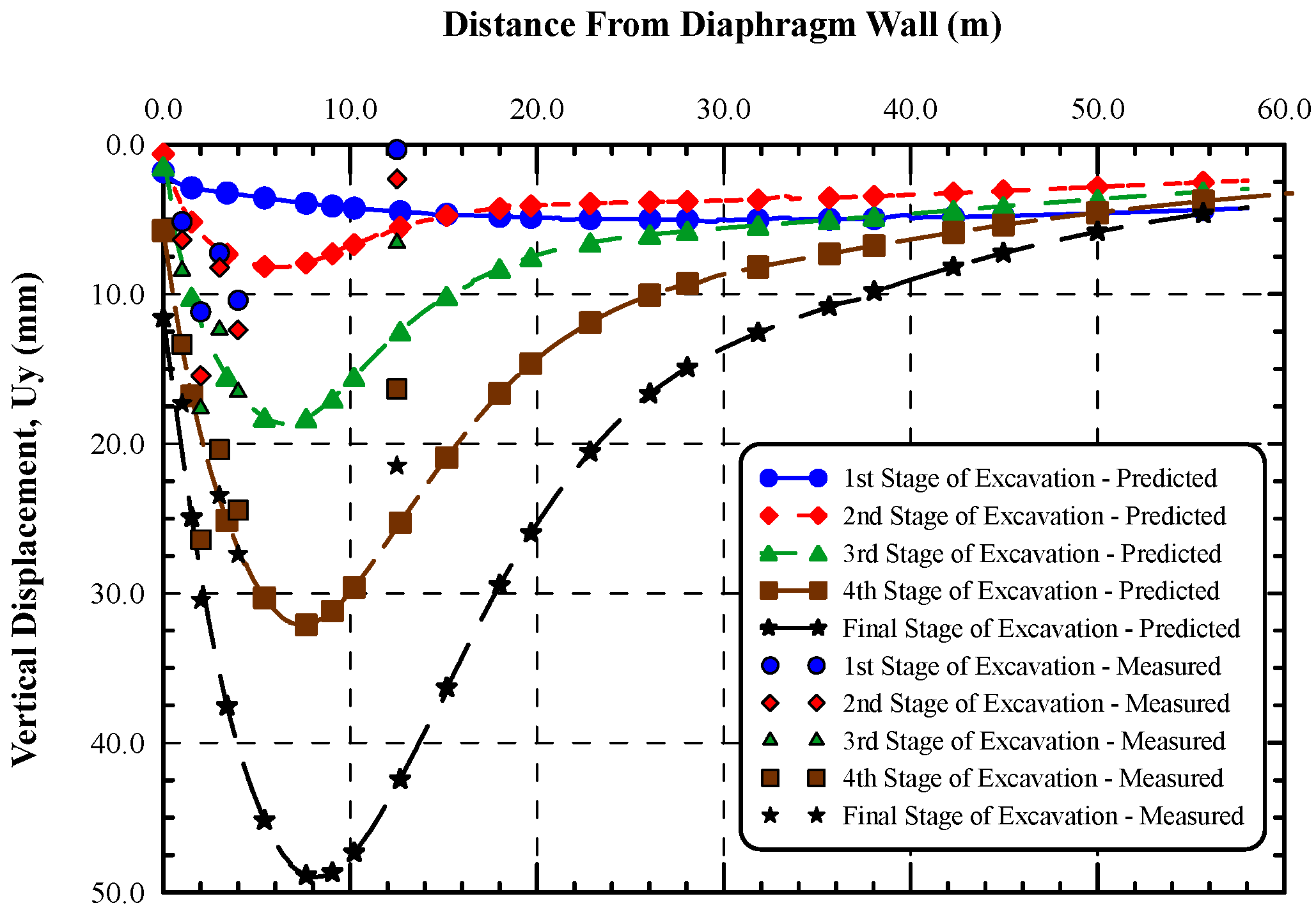
Verification Results of the FEM Model
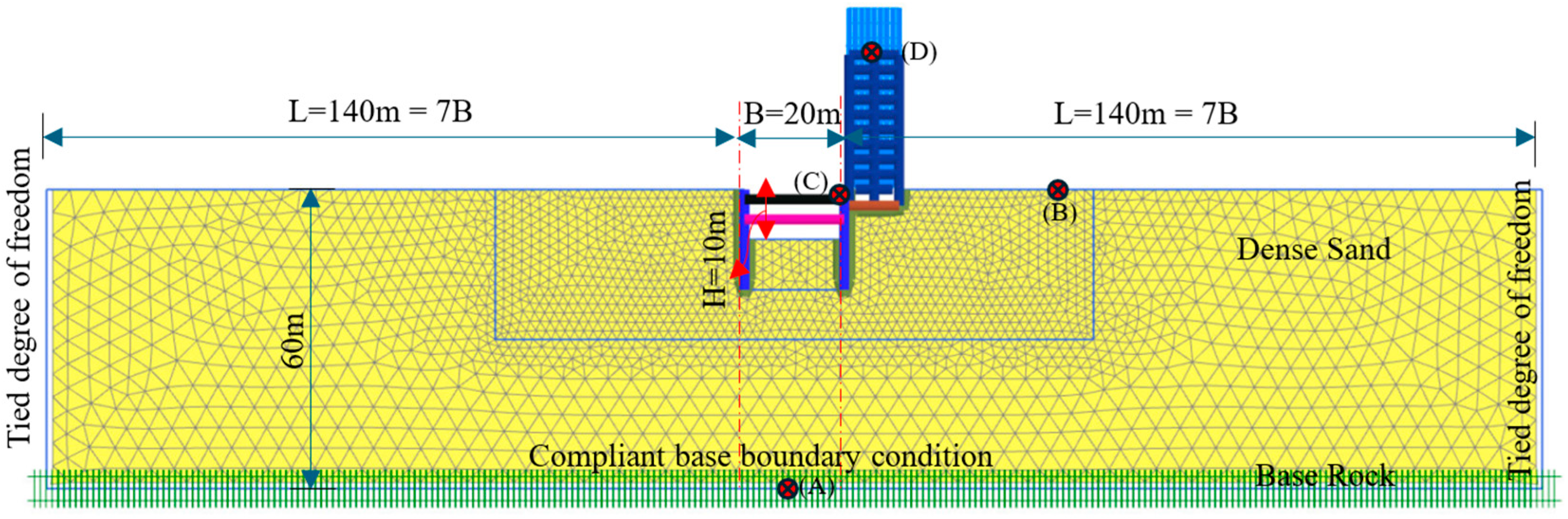
4. Dynamic Modeling of the Shoring System and Adjacent Structure
5. Parametric Study
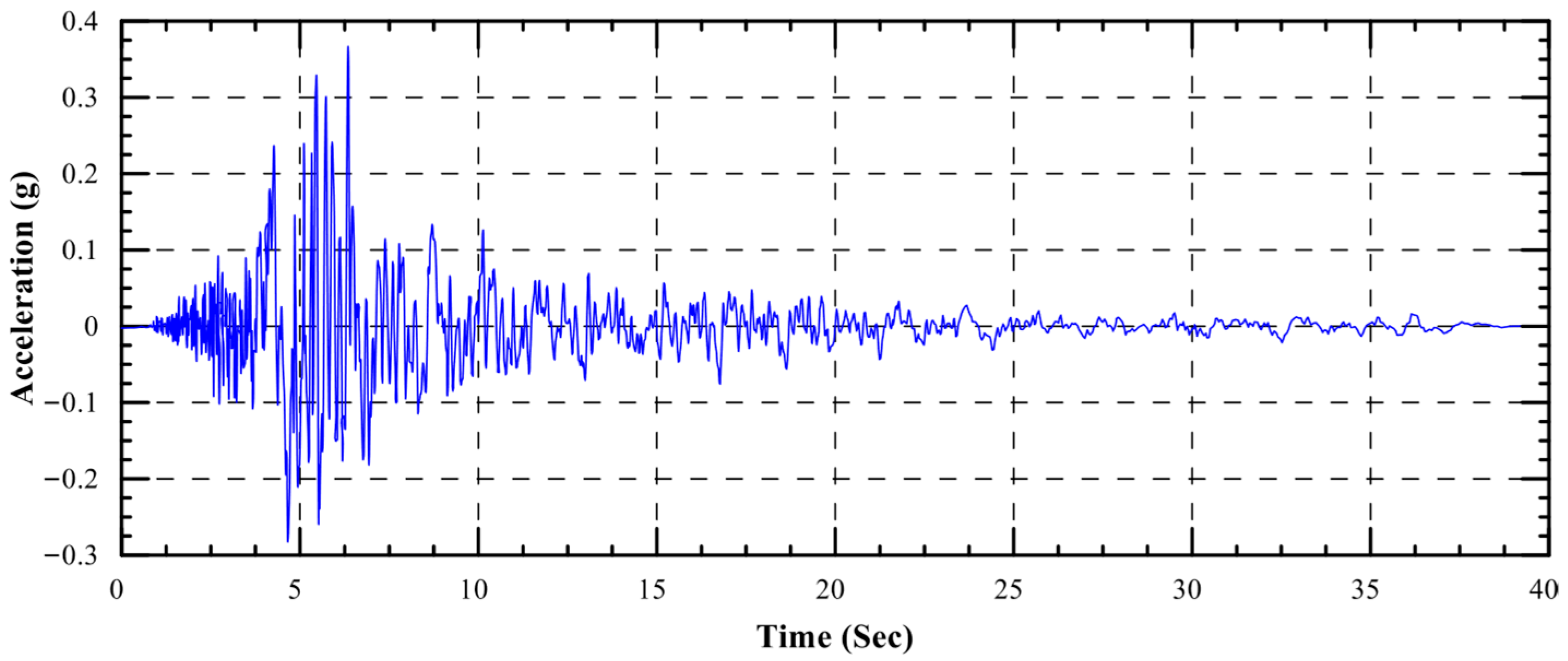
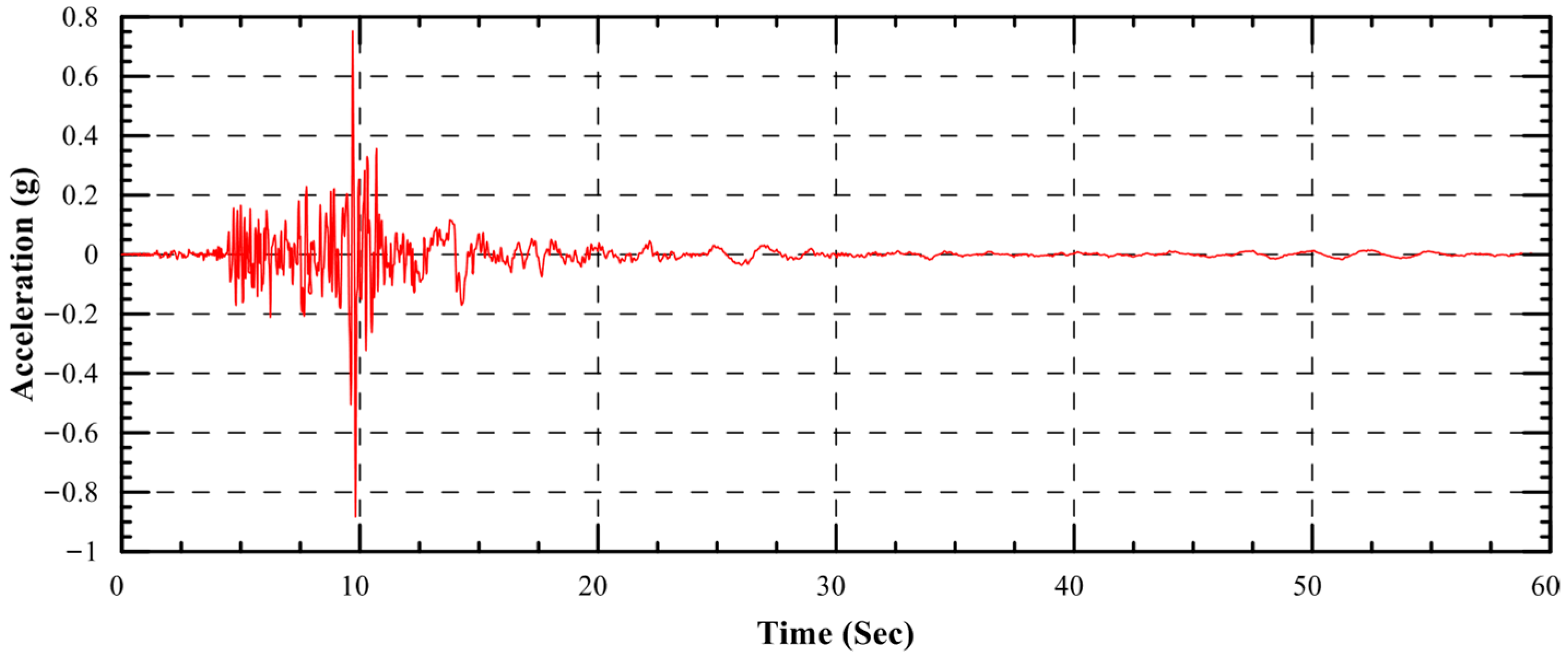
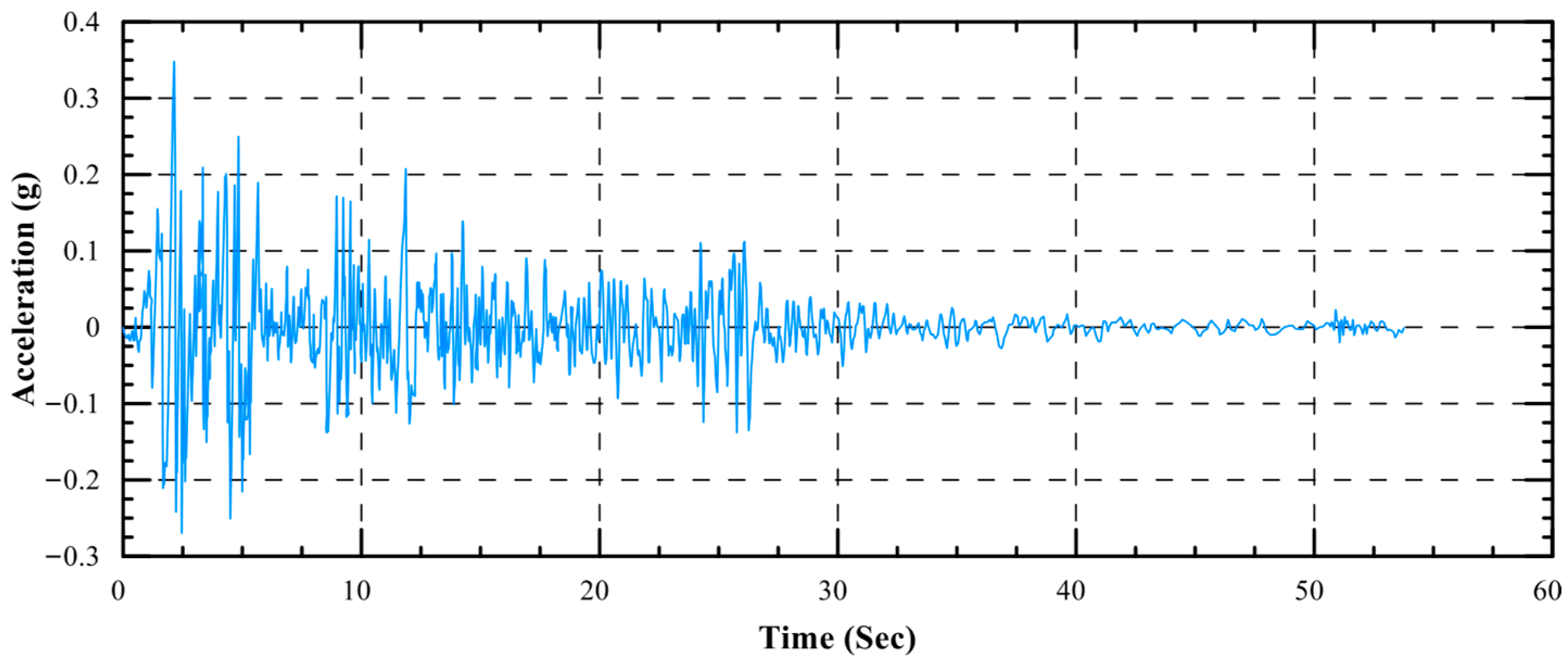
Characteristics of the Input Ground Motions
6. Analysis Results and Discussion
6.1. Effect of the Adjacent Structure’s Foundation Level on the Shoring System–Structure Interaction
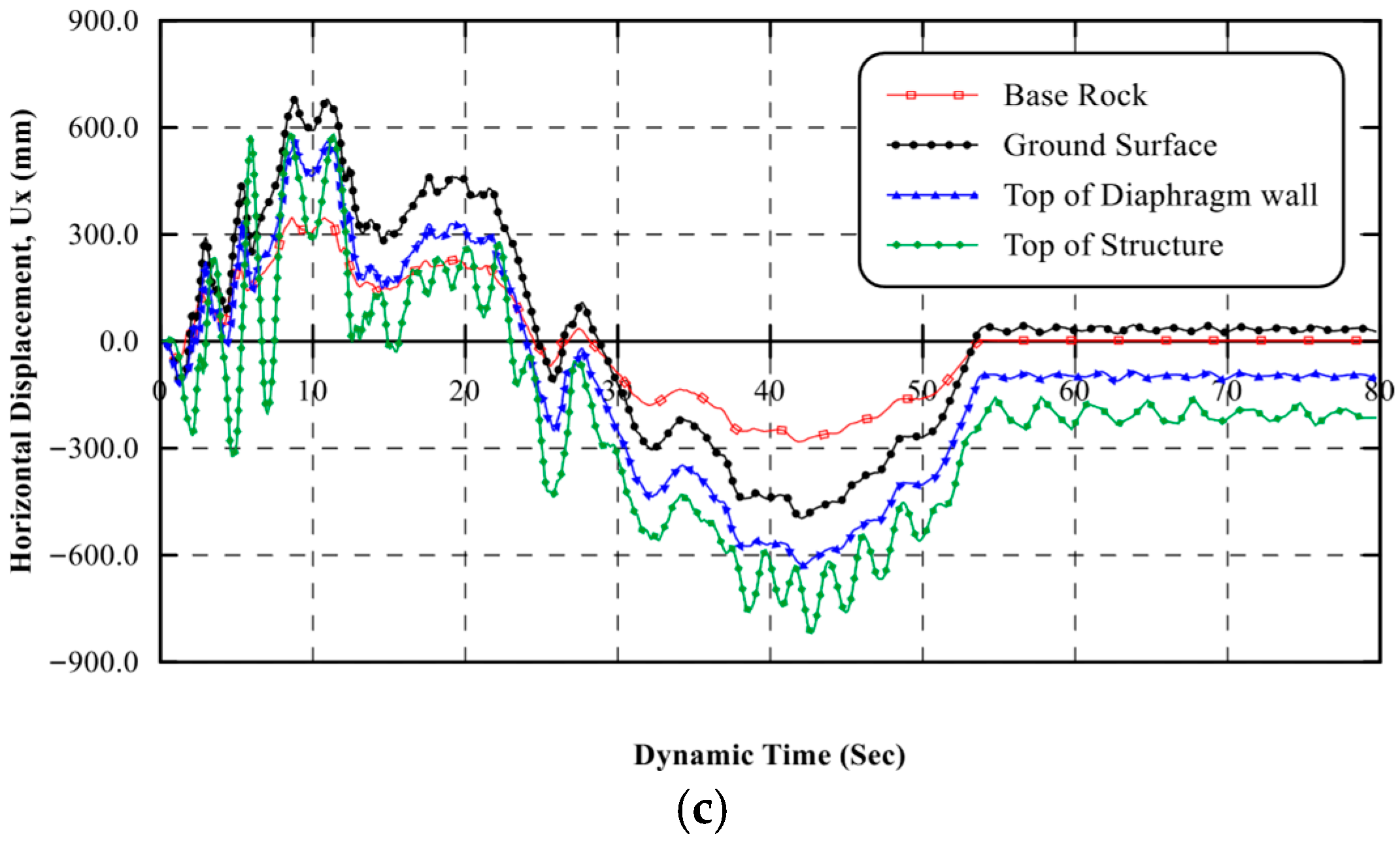
6.1.1. Displacement–Time History (DTH)
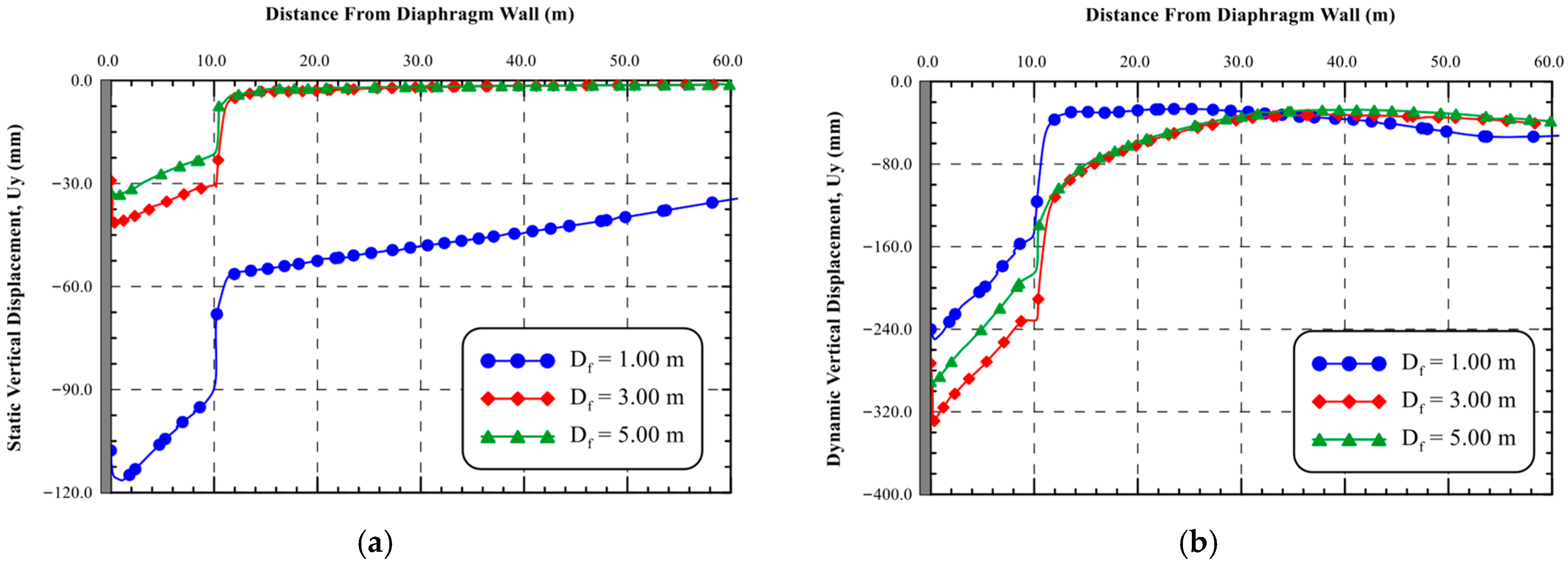
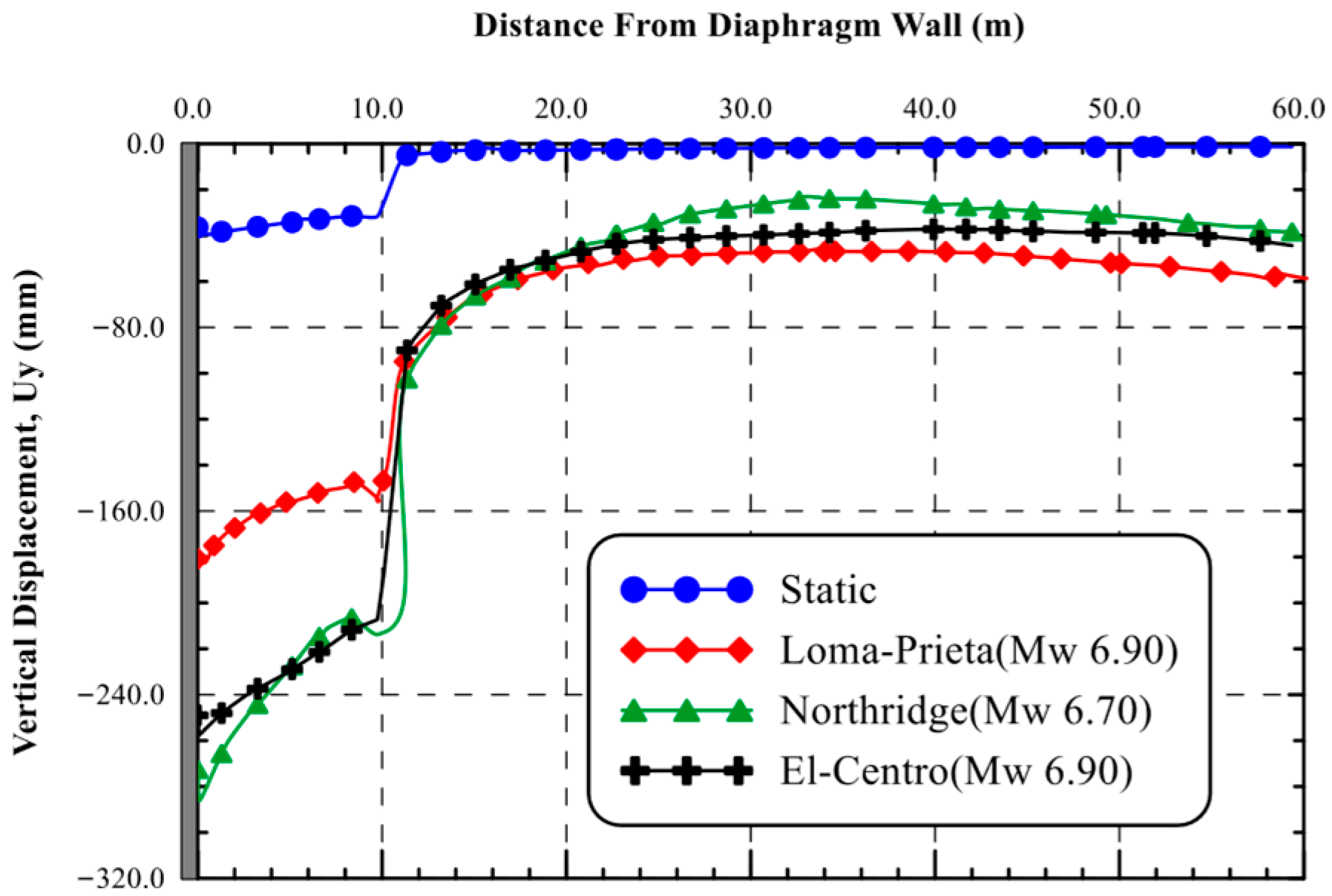
6.1.2. Settlement Trough Beside the Shoring System
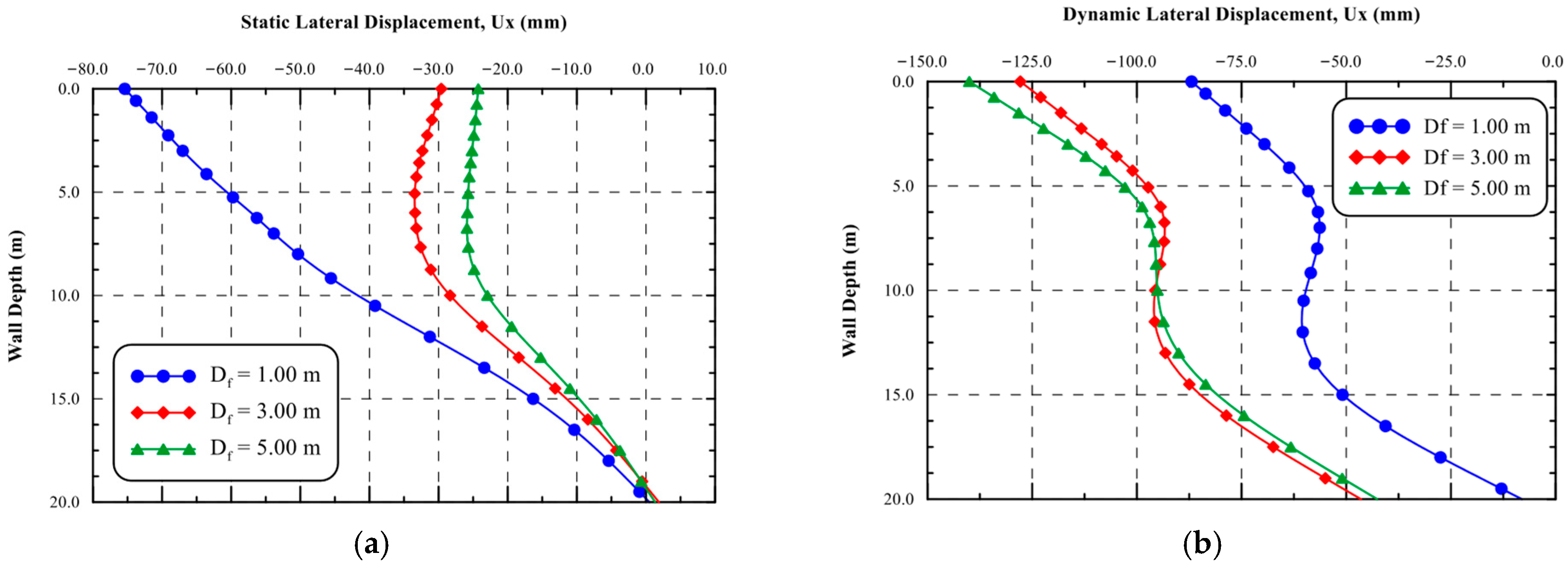
6.1.3. Lateral Displacement of the Shoring System
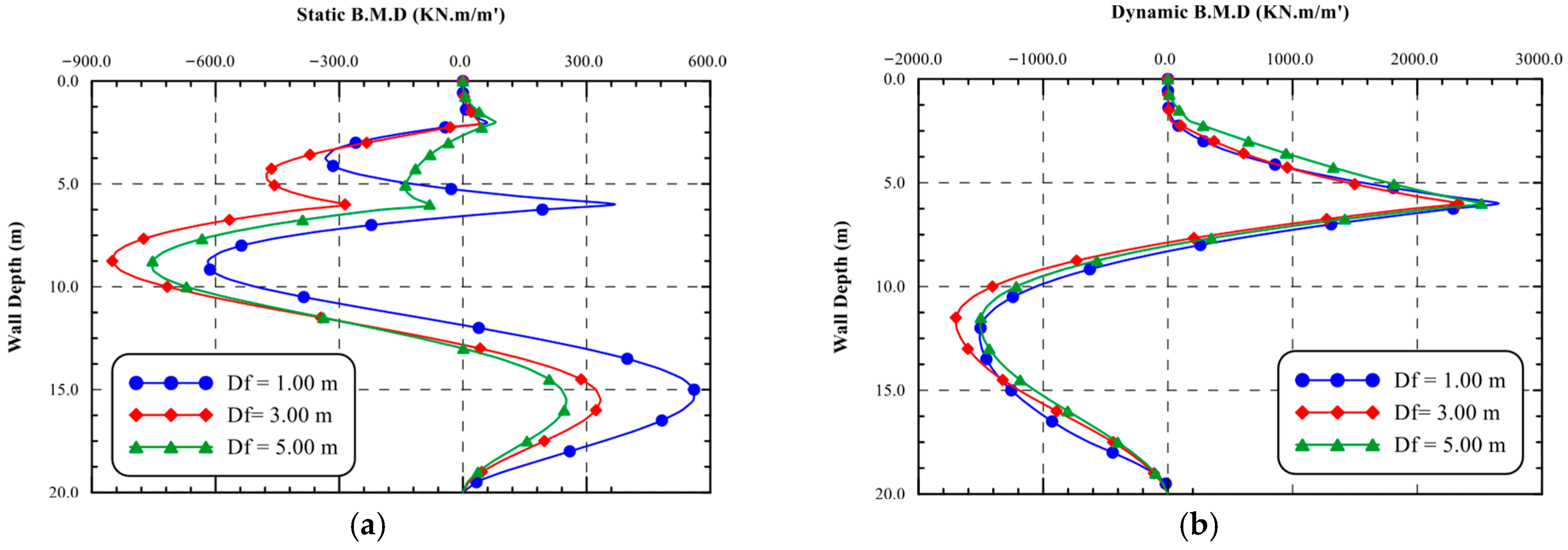
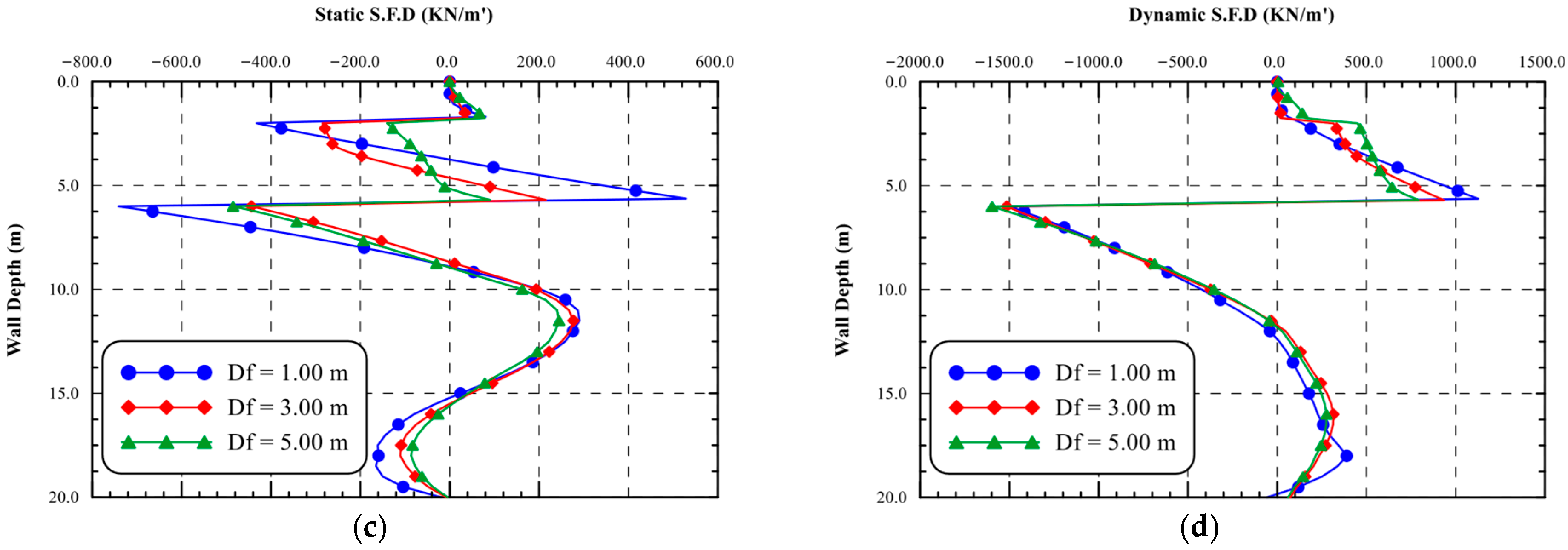
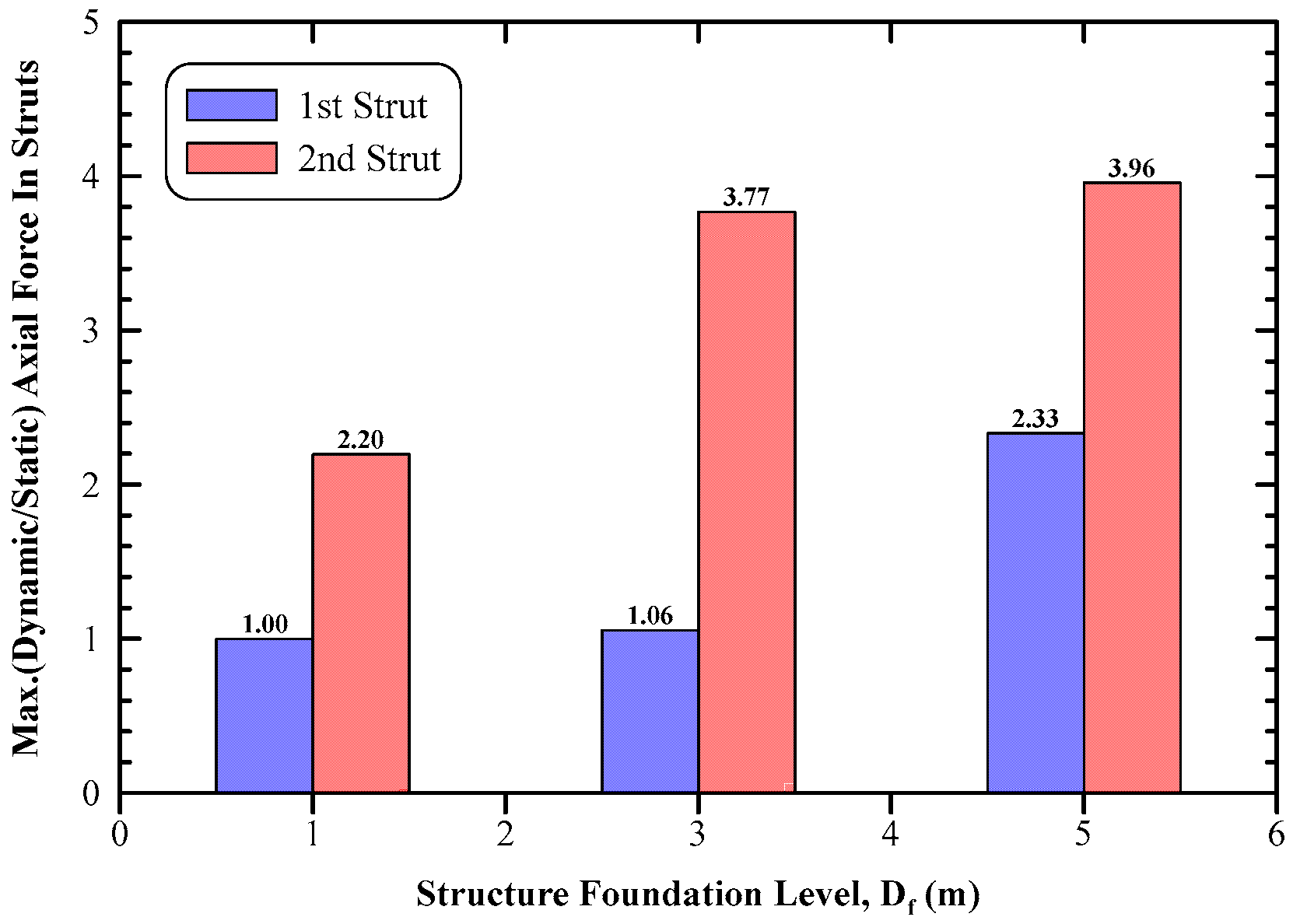
6.1.4. Straining Actions of the Diaphragm Wall and Its Supporting Struts
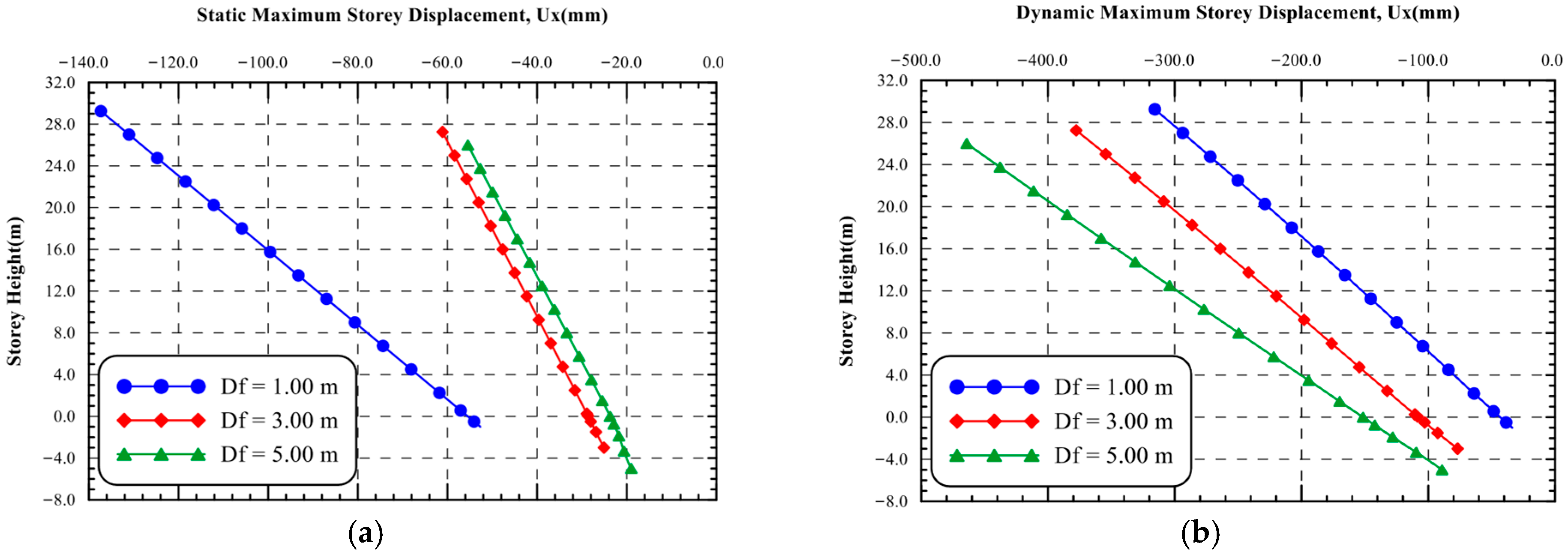
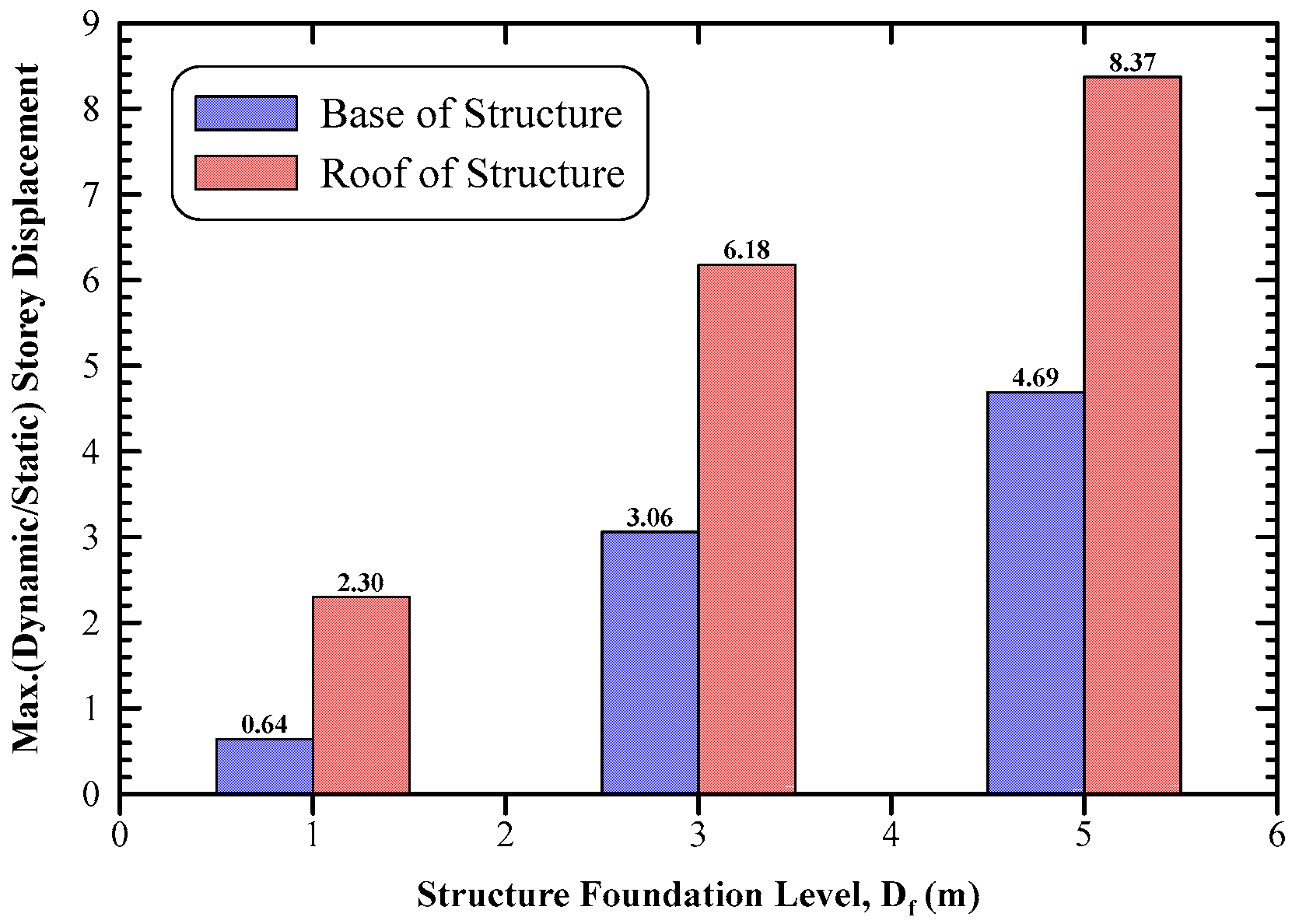
6.1.5. Response of the Structure Adjacent to the Shoring System
6.2. Effect of Earthquake Records on Shoring System–Structure Interaction
6.2.1. Displacement–Time History (DTH)
6.2.2. Lateral Displacement of the Shoring System
6.2.3. Settlement Trough Beside the Shoring System
6.2.4. Straining Actions of the Diaphragm Wall and Its Supporting Struts
6.2.5. Response of the Structure Adjacent to the Shoring System
7. Conclusions
- (a)
- Seismic performance of the entire system:
- As the building’s foundation level adjacent to the excavation increases, the permanent ground surface displacement decreased significantly, while the displacement at the top of the diaphragm wall and top of the structure increased significantly.
- The Loma-Prieta earthquake had a minimal effect on the soil at the ground surface, while the Northridge earthquake had a greater effect on the ground surface. However, the El-Centro and Northridge earthquakes had a great effect on the diaphragm wall and the adjacent structure.
- Settlements under dynamic analysis were 5.10, 7.0, and 7.50 times the maximum static ones under the Loma-Prieta, Northridge, and El-Centro records, respectively.
- (b)
- Seismic performance of the shoring system and its supporting elements:
- The dynamic moment increased by an average of 3.32 times the static one, while the average increase in shear force under dynamic conditions was 2.85 times that under static conditions.
- The average increases in the axial force of the two strut levels because of dynamic forces were 1.38 and 3.17 for the first and second struts, respectively, compared to static ones.
- The maximum bending moments under the Loma-Prieta, Northridge, and El-Centro records were 1.90, 3.04, and 2.93 times the static ones, while the maximum wall shear forces under the Loma-Prieta, Northridge, and El-Centro records were 2.34, 3.24, and 3.56 times the static ones, respectively.
- The axial forces in the first level of struts were 1.52, 1.94, and 1.64 times the static ones under the Loma-Prieta, Northridge, and El-Centro earthquakes, respectively. However, the axial force in the second level of struts was 4.39, 7.04, and 6.55 times the static one, respectively.
- (c)
- Seismic performance of the structure adjacent to the shoring system:
- The dynamic lateral displacement at the top roof was 2.30, 6.18, and 8.37 times the static ones as the foundation level increased from 1.00 m to 5.00 m depth, respectively.
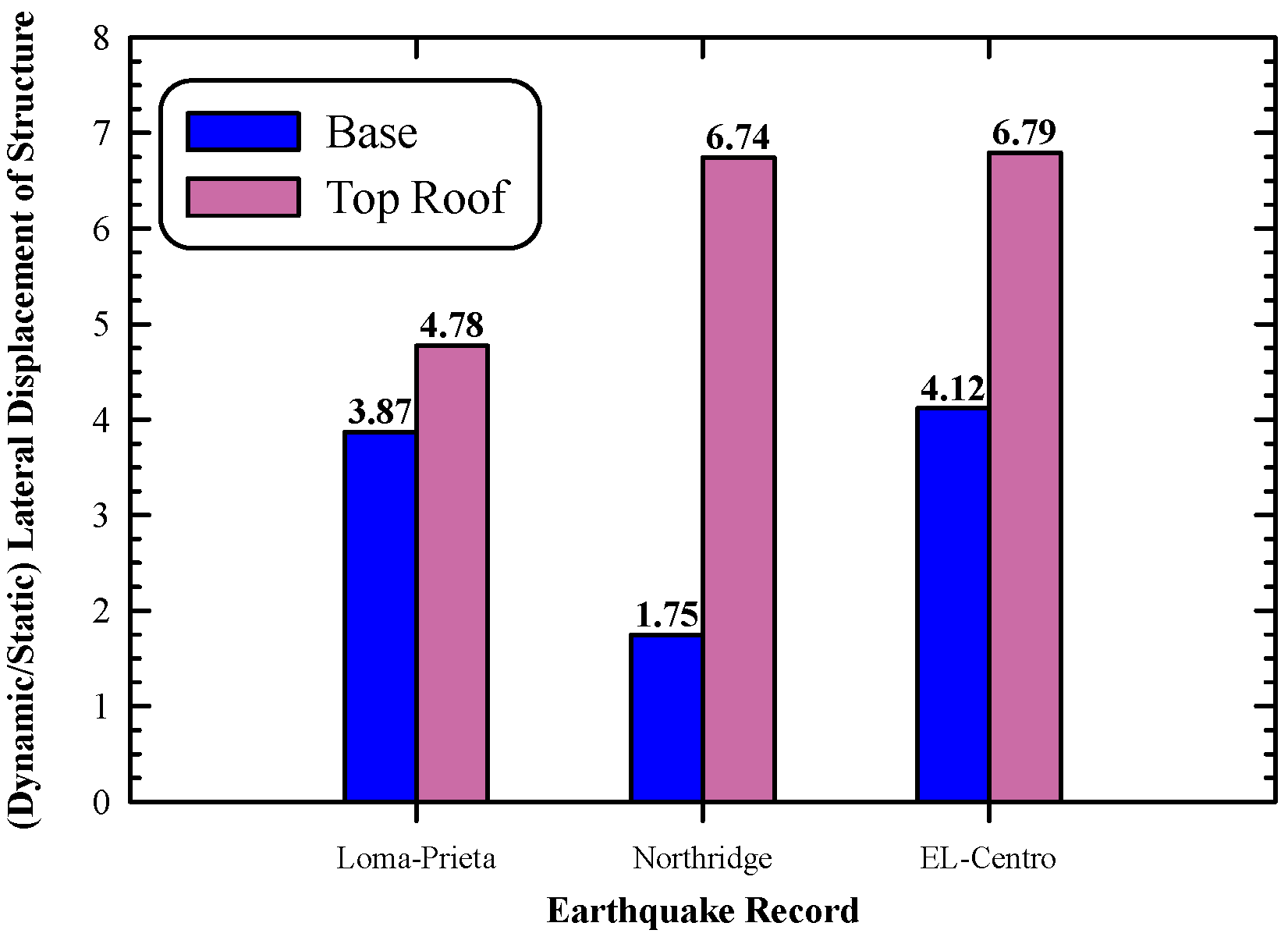
- The lateral displacements of the base of the structure were 3.87, 1.75, and 4.12 times the static ones under the Loma-Prieta, Northridge, and El-Centro earthquakes, respectively. On the other hand, the lateral displacements at the top roof in the dynamic analysis were 4.78, 6.74, and 6.79 times the static ones, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moormann, C. Analysis of wall and ground movements due to deep excavations in soft soil based on a new worldwide database. Soils Found. 2004, 44, 87–98. [Google Scholar] [CrossRef]
- Long, M. Database for retaining wall and ground movements due to deep excavations. J. Geotech. Geoenviron. Eng. 2001, 127, 203–224. [Google Scholar] [CrossRef]
- El Sawwaf, M.; Nazir, A.K. The effect of deep excavation-induced lateral soil movements on the behavior of strip footing supported on reinforced sand. J. Adv. Res. 2012, 3, 337–344. [Google Scholar] [CrossRef]
- Lam, S.Y.; Haigh, S.K.; Bolton, M.D. Understanding ground deformation mechanisms for multi-propped excavation in soft clay. Soils Found. 2014, 54, 296–312. [Google Scholar] [CrossRef]
- Ou, C.-Y.; Hsieh, P.-G.; Chiou, D.-C. Characteristics of ground surface settlement during excavation. Can. Geotech. J. 1993, 30, 758–767. [Google Scholar] [CrossRef]
- Huynh, Q.T.; Lai, V.Q.; Boonyatee, T.; Keawsawasvong, S. Behavior of a Deep Excavation and Damages on Adjacent Buildings: A Case Study in Vietnam. Transp. Infrastruct. Geotechnol. 2021, 8, 361–389. [Google Scholar] [CrossRef]
- Boscardin, M.D.; Cording, E.J. Building response to excavation-induced settlement. J. Geotech. Eng. 1989, 115, 1–21. [Google Scholar] [CrossRef]
- Hsieh, P.-G.; Ou, C.-Y. Shape of ground surface settlement profiles caused by excavation. Can. Geotech. J. 1998, 35, 1004–1017. [Google Scholar] [CrossRef]
- Liu, G.B.; Ng, C.W.; Wang, Z.W. Observed performance of a deep multistrutted excavation in Shanghai soft clays. J. Geotech. Geoenviron. Eng. 2005, 131, 1004–1013. [Google Scholar] [CrossRef]
- Kung, G.T.; Juang, C.H.; Hsiao, E.C.; Hashash, Y.M. Simplified Model for Wall Deflection and Ground-Surface Settlement Caused by Braced Excavation in Clays. J. Geotech. Geoenviron. Eng. 2007, 133, 731–747. [Google Scholar] [CrossRef]
- Wang, J.H.; Xu, Z.H.; Wang, W.D. Wall and Ground Movements due to Deep Excavations in Shanghai Soft Soils. J. Geotech. Geoenviron. Eng. 2010, 136, 985–994. [Google Scholar] [CrossRef]
- Bahrami, M.; Khodakarami, M.I.; Haddad, A. 3D numerical investigation of the effect of wall penetration depth on excavations behavior in sand. Comput. Geotech. 2018, 98, 82–92. [Google Scholar] [CrossRef]
- Ou, C.Y.; Hsieh, P.G.; Lin, Y.L. A parametric study of wall deflections in deep excavations with the installation of cross walls. Comput. Geotech. 2013, 50, 55–65. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Deb, K.; Sengupta, A. Estimation of Design Parameters for Braced Excavation in Clays. Geotech. Geol. Eng. 2017, 35, 857–870. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Deb, K.; Sengupta, A. Estimation of Design Parameters for Braced Excavation: Numerical Study. Int. J. Geomech. 2013, 13, 234–247. [Google Scholar] [CrossRef]
- Ou, C.Y.; Hsieh, P.G. A simplified method for predicting ground settlement profiles induced by excavation in soft clay. Comput. Geotech. 2011, 38, 987–997. [Google Scholar] [CrossRef]
- Hsiung, B.C.B. A case study on the behaviour of a deep excavation in sand. Comput. Geotech. 2009, 36, 665–675. [Google Scholar] [CrossRef]
- Yoo, C.; Lee, D. Deep excavation-induced ground surface movement characteristics—A numerical investigation. Comput. Geotech. 2008, 35, 231–252. [Google Scholar] [CrossRef]
- Arai, Y.; Kusakabe, O.; Murata, O.; Konishi, S. A numerical study on ground displacement and stress during and after the installation of deep circular diaphragm walls and soil excavation. Comput. Geotech. 2008, 35, 791–807. [Google Scholar] [CrossRef]
- Orazalin, Z.Y.; Whittle, A.J.; Olsen, M.B. Three-Dimensional Analyses of Excavation Support System for the Stata Center Basement on the MIT Campus. J. Geotech. Geoenviron. Eng. 2015, 141, 1–14. [Google Scholar] [CrossRef]
- Faheem, H.; Cai, F.; Ugai, K. Three-dimensional base stability of rectangular excavations in soft soils using FEM. Comput. Geotech. 2004, 31, 67–74. [Google Scholar] [CrossRef]
- Bose, S.K.; Som, N.N. Parametric study of a braced cut by finite element method. Comput. Geotech. 1998, 22, 91–107. [Google Scholar] [CrossRef]
- Ou, C.-Y.; Chiou, D.-C.; Wu, T.-S. Three-dimensional finite element analysis of deep excavations. J. Geotech. Eng. 1996, 122, 337–345. [Google Scholar] [CrossRef]
- Zdravkovic, L.; Potts, D.M.; John, H.D.S. Modelling of a 3D excavation in finite element analysis. In Stiff Sedimentary Clays: Genesis and Engineering Behaviour: Géotechnique Symposium in Print 2007; Emerald Publishing Limited: Leeds, UK, 2011; pp. 319–335. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Deb, K.; Sengupta, A. Effect of Fines on Behavior of Braced Excavation in Sand: Experimental and Numerical Study. Int. J. Geomech. 2016, 16, 04015018. [Google Scholar] [CrossRef]
- Callisto, L.; Soccodato, F.M.; Conti, R. Analysis of the Seismic Behaviour of Propped Retaining Structures. In Geotechnical Earthquake Engineering and Soil Dynamics IV; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Callisto, L.; Soccodato, F.M. Seismic design of flexible cantilevered retaining walls. J. Geotech. Geoenviron. Eng. 2010, 136, 344–354. [Google Scholar] [CrossRef]
- Konai, S.; Sengupta, A.; Deb, K. Behavior of braced excavation in sand under a seismic condition: Experimental and numerical studies. Earthq. Eng. Eng. Vib. 2018, 17, 311–324. [Google Scholar] [CrossRef]
- Ling, H.I.; Leshchinsky, D.; Wang, J.-P.; Mohri, Y.; Rosen, A. Seismic Response of Geocell Retaining Walls: Experimental Studies. J. Geotech. Geoenviron. Eng. 2009, 135, 515–524. [Google Scholar] [CrossRef]
- Ling, H.I.; Mohri, Y.; Leshchinsky, D.; Burke, C.; Matsushima, K.; Liu, H. Large-Scale Shaking Table Tests on Modular-Block Reinforced Soil Retaining Walls. J. Geotech. Geoenviron. Eng. 2005, 131, 465–476. [Google Scholar] [CrossRef]
- Ling, H.I.; Liu, H.; Mohri, Y. Parametric Studies on the Behavior of Reinforced Soil Retaining Walls under Earthquake Loading. J. Eng. Mech. 2005, 131, 1056–1065. [Google Scholar] [CrossRef]
- Mikola, R.G.; Sitar, N. Seismic Earth Pressures on Retaining Structures in Cohesionless Soils By Roozbeh Geraili Mikola and Nicholas Sitar Report Submitted to the California Department of Transportation (Caltrans) under Contract No. 65A0367 and NSF-NEES-CR Grant No. CMMI-093; California Department of Transportation, Division of Research and Innovation: Sacramento, CA, USA, 2013; p. 170. [Google Scholar] [CrossRef]
- Tufenkjian, M.R.; Vucetic, M. Dynamic Failure Mechanism of Soil-Nailed Excavation Models in Centrifuge. J. Geotech. Geoenviron. Eng. 2000, 126, 227–235. [Google Scholar] [CrossRef]
- Madabhushi, S.P.G.; Zeng, X. Simulating Seismic Response of Cantilever Retaining Walls. J. Geotech. Geoenviron. Eng. 2007, 133, 539–549. [Google Scholar] [CrossRef]
- Conti, R.; Madabhushi, G.S.P.; Viggiani, G.M.B. On the behaviour of flexible retaining walls under seismic actions. Geotechnique 2012, 62, 1081–1094. [Google Scholar] [CrossRef]
- Bahrami, M.; Khodakarami, M.I.; Haddad, A. Seismic behavior and design of strutted diaphragm walls in sand. Comput. Geotech. 2019, 108, 75–87. [Google Scholar] [CrossRef]
- 318 ACI Committee. Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- AISC. Steel Construction Manual 15th Edition; AISC: Chicago, IL, USA, 2017; Volume 53, pp. 21–25. [Google Scholar]
- Castaldo, P.; De Iuliis, M. Effects of deep excavation on seismic vulnerability of existing reinforced concrete framed structures. Soil Dyn. Earthq. Eng. 2014, 64, 102–112. [Google Scholar] [CrossRef]
- Khademalrasoul, A.; Shirmohammadi, A.; Pakbaz, M.S.; Labibzadeh, M. Seismic Soft Soil-Structure Interaction Using RLBRB-Equipped Strut in Deep Excavations. J. Earthq. Eng. 2022, 26, 3572–3600. [Google Scholar] [CrossRef]
- Ibrahim, K.M.H.I.; Ibrahim, T.E. Effect of historical earthquakes on pre-stressed anchor tie back diaphragm wall and on near-by building. HBRC J. 2013, 9, 60–67. [Google Scholar] [CrossRef]
- Mo, Y.L.; Hwang, J.M. Seismic response of reinforced concrete buildings close to deep excavation. Comput. Methods Appl. Mech. Eng. 1997, 145, 117–134. [Google Scholar] [CrossRef]
- Chowdhury, S.S.; Deb, K.; Sengupta, A. Behavior of underground strutted retaining structure under seismic condition. Earthq. Struct. 2015, 8, 1147–1170. [Google Scholar] [CrossRef]
- Yeganeh, N.; Bazaz, J.B.; Akhtarpour, A. Seismic analysis of the soil-structure interaction for a high rise building adjacent to deep excavation. Soil Dyn. Earthq. Eng. 2015, 79, 149–170. [Google Scholar] [CrossRef]
- Hsiung, B.C.B.; Dao, S.D. Evaluation of constitutive soil models for predicting movements caused by a deep excavation in sands. Electron. J. Geotech. Eng. 2014, 19, 17325–17344. [Google Scholar]
- Benz, T. Small-Strain Stiffness of Soils and its Numerical Consequences; University of Stuttgart—Institute of Geotechnical Engineering: Stuttgart, Germany, 2007. [Google Scholar]
- Hardin, B.O.; Drnevich, V.P. Shear Modulus and Damping in Soils: Design Equations and Curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Santos, J.; Correia, A. Reference threshold shear strain of soil. Its application to obtain an unique strain-dependent shear modulus curve for soil. In Proceedings of the XV International Conference on Soil Mechanics and Geotechnical Engineering, Istanbul, Turkey, 27–31 August 2001; pp. 267–270. [Google Scholar]
- Obrzud, R. The Hardening Soil Model: A Practical Guidebook; Zace Services: Lausanne, Switzerland, 2010. [Google Scholar]
- Brinkgreve, R.B.J.; Bakker, K.J.; Bonnier, P.G. The relevance of small-strain soil stiffness in numerical simulation of excavation and tunnelling projects. In Numerical Methods in Geotechnical Engineering; Taylor & Francis Group: London, UK, 2006; pp. 133–139. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method. Vol. 2: Solid and Fluid Mechanics, Dynamics and Non-Linearity, 4th ed.; McGraw-Hill: Columbus, OH, USA, 1991. [Google Scholar]
- Chopra, A.K. Dynamics of Structures 5th Edition SI Units Anul K Chopra; Pearson: London, UK, 2020; Volume 5. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Courier Corporation: Mineola, NY, USA, 2003. [Google Scholar]
- Kramer, S.L. Geotechnical Eartquake Engineering, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Hudson, M.; Idriss, I.M.; Beirkae, M. Quad4m User’s Manual; University of California: Davis, CA, USA, 1994. [Google Scholar]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Lysmer, J.; Udaka, T.; Tsai, C.; Seed, H.B. FLUSH-A Computer Program for Approximate 3-D Analysis of Soil-Structure Interaction Problems; California Univ., Richmond (USA). Earthquake Engineering Research Center: Berkeley, CA, USA, 1975. [Google Scholar]
- Zienkiewicz, O.C.; Bicanic, N.; Shen, F.Q. Earthquake Input Definition and the Trasmitting Boundary Conditions. In Advances in Computational Nonlinear Mechanics; Springer: Vienna, Austria, 1989; pp. 109–138. [Google Scholar] [CrossRef]
- Joyner, W.B.; Chen, A.T.F. Calculation of nonlinear ground response in earthquakes. Bull. Seismol. Soc. Am. 1975, 65, 1315–1336. [Google Scholar]
- PLAXIS 2D Reference Manual. In PLAXIS 2D 2024.2 Reference Manual 2D; Bentley Systems: Exton, PA, USA, 2024.
- Ou, C.-Y. Deep Excavation: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Khoiri, M.; Ou, C.Y. Evaluation of deformation parameter for deep excavation in sand through case histories. Comput. Geotech. 2013, 47, 57–67. [Google Scholar] [CrossRef]
- Likitlersuang, S.; Surarak, C.; Wanatowski, D.; Oh, E.; Balasubramaniam, A. Finite element analysis of a deep excavation: A case study from the Bangkok MRT. Soils Found. 2013, 53, 756–773. [Google Scholar] [CrossRef]
- ASCE Standard ASCE/SEI 7-16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2017. [CrossRef]
- Hokmabadi, A.S.; Fatahi, B.; Samali, B. Recording inter-storey drifts of structures in time-history approach for seismic design of building frames. Aust. J. Struct. Eng. 2012, 13, 175–179. [Google Scholar] [CrossRef]
- Ebadi-Jamkhaneh, M. Pounding Risk Assessment through Soil–Structure Interaction Analysis in Adjacent High-Rise RC Structures. Buildings 2024, 14, 2779. [Google Scholar] [CrossRef]
- Katsimpini, P.S. Seismic Response of Vertical Hybrid Concrete/Steel Frames Considering Soil–Structure Interaction. Buildings 2024, 14, 972. [Google Scholar] [CrossRef]
- Ekraminia, S.; Bonab, M.H.; Ghassemi, S.; Derakhshani, R. Experimental study on seismic response of underground tunnel–soil–piled structure interaction using shaking table in loose sand. Buildings 2023, 13, 2482. [Google Scholar] [CrossRef]
- Bian, X.; Wang, G. Study of structural seismic damage considering seasonal frozen soil–structure interaction. Buildings 2024, 14, 1493. [Google Scholar] [CrossRef]
- Alnmr, A.; Sheble, A.; Ray, R.; Ahmad, H. Parametric investigation of interaction between soil-surface structure and twin tunnel excavation: A comprehensive 2D numerical study. Infrastructures 2023, 8, 124. [Google Scholar] [CrossRef]
- PLAXIS 2D Scientific Manual. In PLAXIS PLAXIS 2D 2024.1 Scientific Manual 2D; Bentley Systems: Exton, PA, USA, 2023.
- PEER. PEER Ground Motion Database—PEER Center. NGA-West2. [Online]. Available online: https://ngawest2.berkeley.edu/ (accessed on 18 August 2024).
- Rankin, W.J. Ground movements resulting from urban tunnelling: Predictions and effects. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 1988, 5, 79–92. [Google Scholar] [CrossRef]
- Gazetas, G. Empirical seismic design method for waterfront anchored sheetpile walls. In Design and Performance of Earth Retaining Structures; The International Society for Soil Mechanics and Geotechnical Engineering (ISSMGE): Christchurch, New Zealand, 1990. [Google Scholar]













| Depth of Layer (m) | 60 |
|---|---|
| Soil type | Dense sand |
| SPT (N-Value) | 37 |
| Soil model | Hardening soil model with small strain (HS-small) |
| Unsaturated unit weight, γunsat (kN/m3) | 19 |
| Saturated unit weight, γsat (kN/m3) | 21 |
| Rayleigh damping (α) | 0.1634 |
| Rayleigh damping (β) | 1.662 × 10−3 |
| Damping ratio | 2% |
| Internal friction angle, | 36 |
| Cohesion, | 1 |
| Dilatancy angle, Ψ | 6 |
| Secant stiffness from drained triaxial test, | 50,000 |
| Reference tangent stiffness for oedometer primary loading, | 50,000 |
| Reference unloading/reloading stiffness, | 150,000 |
| Unloading/reloading Poisson’s ratio, ν’ur | 0.20 |
| Exponent of stress-level dependency of stiffness, m | 0.50 |
| Failure ratio, Rf | 0.90 |
| At-rest earth pressure coefficient, K0 | 0.4122 |
| Reference small-strain shear modulus, G0ref (kPa) | 180,000 |
| Shear strain magnitude at 0.722 G0, γ0.7 | 1 × 10−4 |
| Analysis type | Drained |
| Rinter | 0.67 |
| Studied Parameter | Parameter Variables | Chosen Parameters |
|---|---|---|
| Foundation level of the structure adjacent to the shoring system | Df = 1.0 m | H = 10 m B = 20 m, Tw = 80 cm D = H = 10 m Loma-Prieta EQ |
| Df = 3.0 m | ||
| Df = 5.0 m | ||
| Earthquake records | Loma-Prieta (1989), Mw = 6.90 | H = D = 10 m Tw = 80 cm B = 20 m |
| Northridge (1994), Mw = 6.70 | ||
| El-Centro (1940), Mw = 6.90 |
| Earthquake Record | Moment Magnitude (Mw) | PGA (g) | Duration (s) | Predominant Period, Tp (s) | Arias Intensity, Ia (m/s) | Significant Duration, Ds 5–95 (s) |
|---|---|---|---|---|---|---|
| Loma-Prieta (1989) | 6.90 | 0.37 | 39.90 | 0.22 | 1.35 | 11.37 |
| Northridge (1994) | 6.70 | 0.88 | 60.00 | 0.22 | 2.72 | 8.75 |
| El-Centro (1940) | 6.90 | 0.34 | 53.76 | 0.56 | 1.76 | 24.46 |
| Earthquake Record | Loma-Prieta, Mw = 6.9 | Northridge, Mw = 6.7 | El-Centro, Mw = 6.9 | |
|---|---|---|---|---|
| Ground surface | A,max (%) | 210 | 170 | 197 |
| Ux,per (mm) | 18.37 | 112.31 | 33.71 | |
| Top of the diaphragm wall | A,max (%) | 294 | 228 | 223 |
| Ux,per (mm) | −60.73 | −47.95 | −93.8 | |
| Top of the structure | A,max (%) | 297 | 558 | 289 |
| Ux,per (mm) | −148.39 | −215.48 | −230.45 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salem, T.N.; Elmahdy, M.S.; Katunský, D.; Dolníková, E.; El Ela, A.A. Numerical Investigation of Seismic Soil–Structure–Excavation Interaction in Sand. Buildings 2025, 15, 3732. https://doi.org/10.3390/buildings15203732
Salem TN, Elmahdy MS, Katunský D, Dolníková E, El Ela AA. Numerical Investigation of Seismic Soil–Structure–Excavation Interaction in Sand. Buildings. 2025; 15(20):3732. https://doi.org/10.3390/buildings15203732
Chicago/Turabian StyleSalem, Tarek N., Mahmoud S. Elmahdy, Dušan Katunský, Erika Dolníková, and Ahmed Abu El Ela. 2025. "Numerical Investigation of Seismic Soil–Structure–Excavation Interaction in Sand" Buildings 15, no. 20: 3732. https://doi.org/10.3390/buildings15203732
APA StyleSalem, T. N., Elmahdy, M. S., Katunský, D., Dolníková, E., & El Ela, A. A. (2025). Numerical Investigation of Seismic Soil–Structure–Excavation Interaction in Sand. Buildings, 15(20), 3732. https://doi.org/10.3390/buildings15203732










