A Study of a Noncontact Identification Method of Debonding Damage in External Thermal Insulation Composite Systems Based on Nonlinear Vibration
Abstract
1. Introduction
2. Materials and Methods
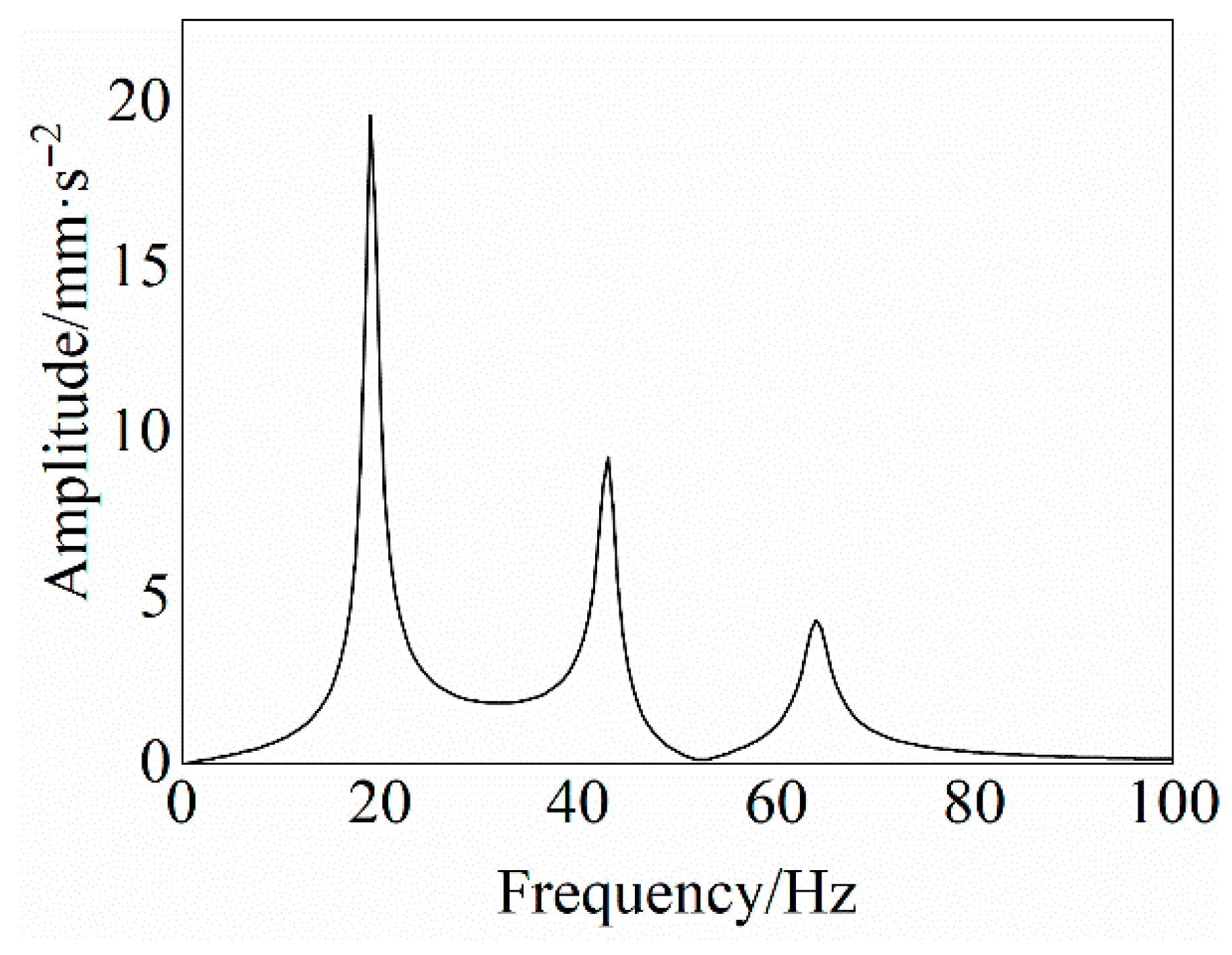
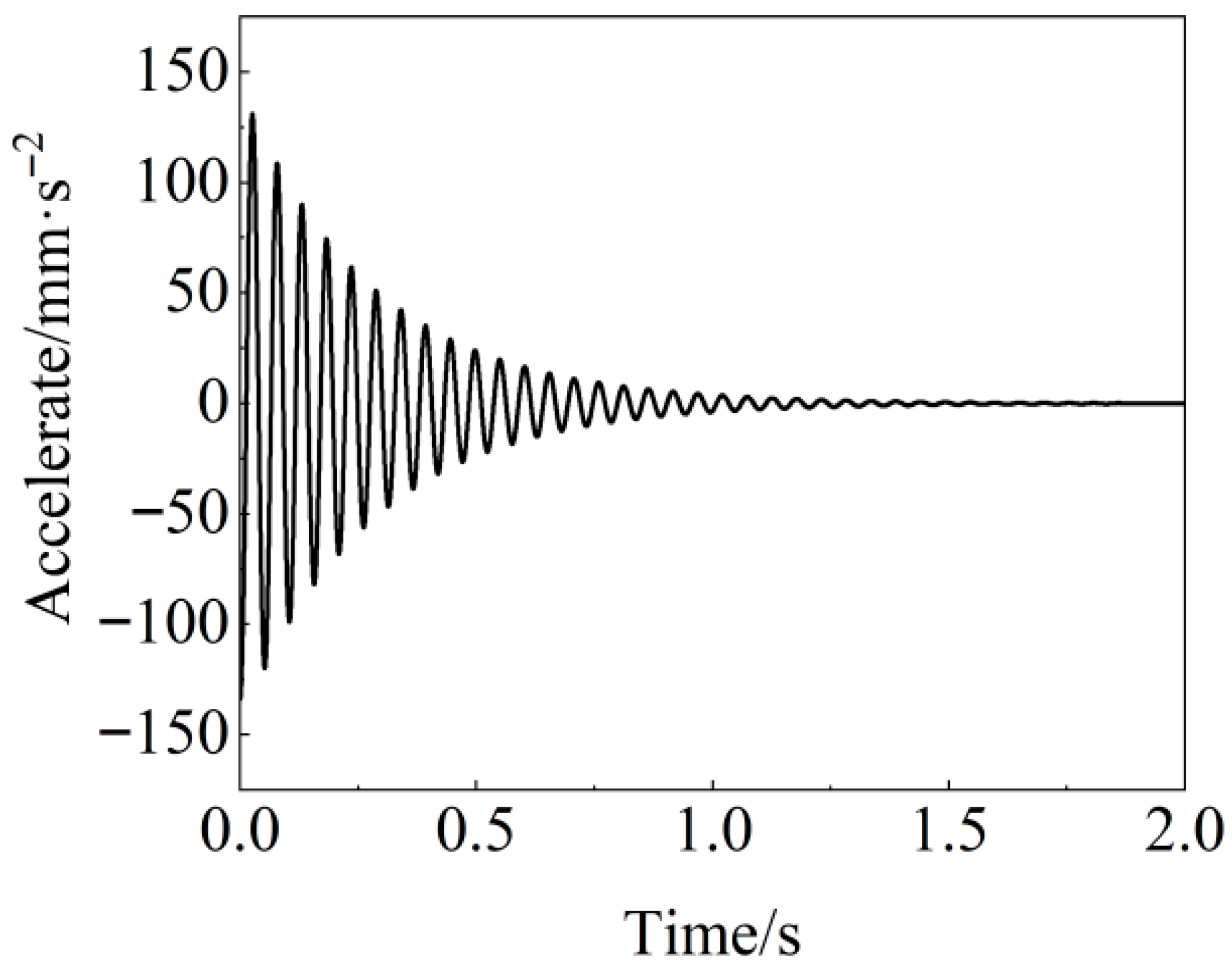
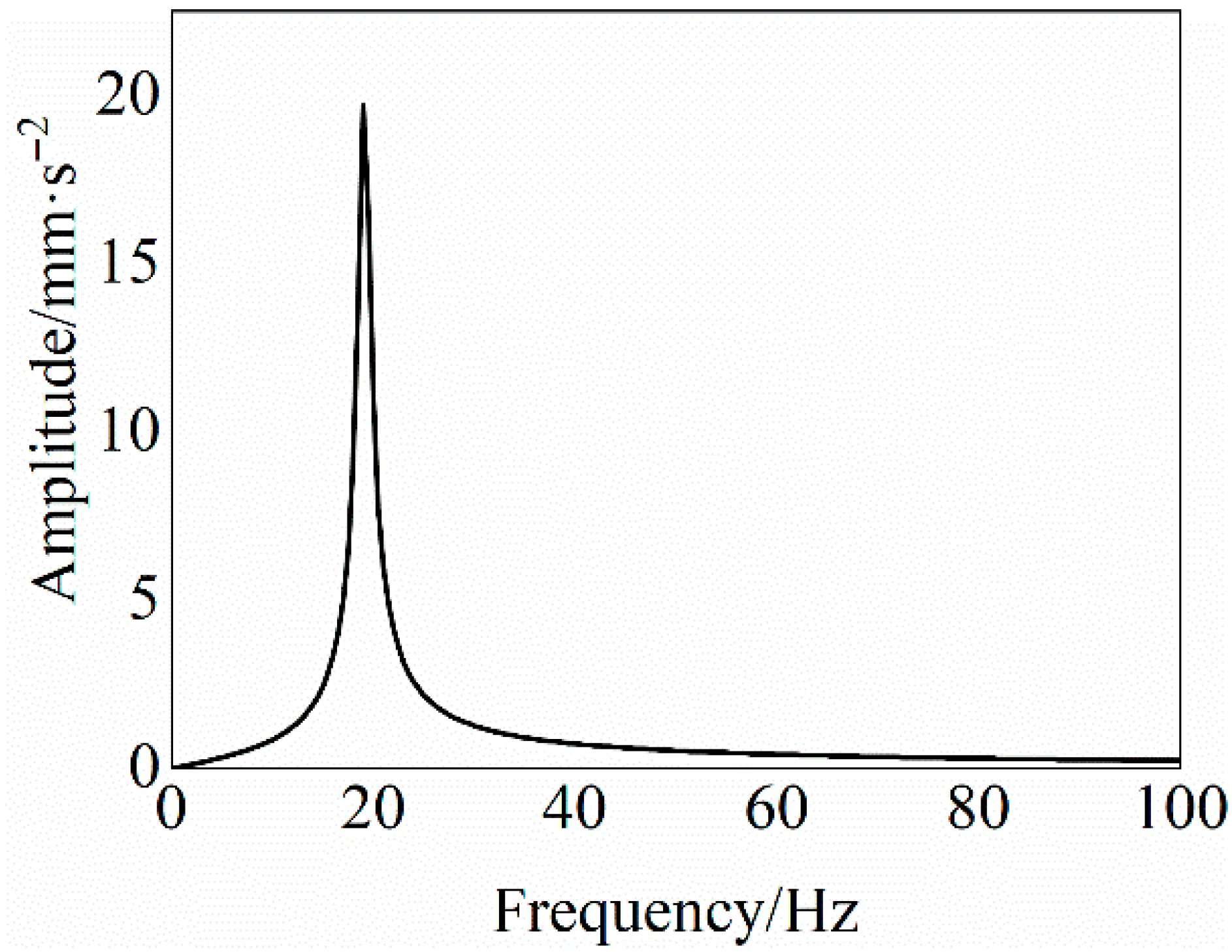
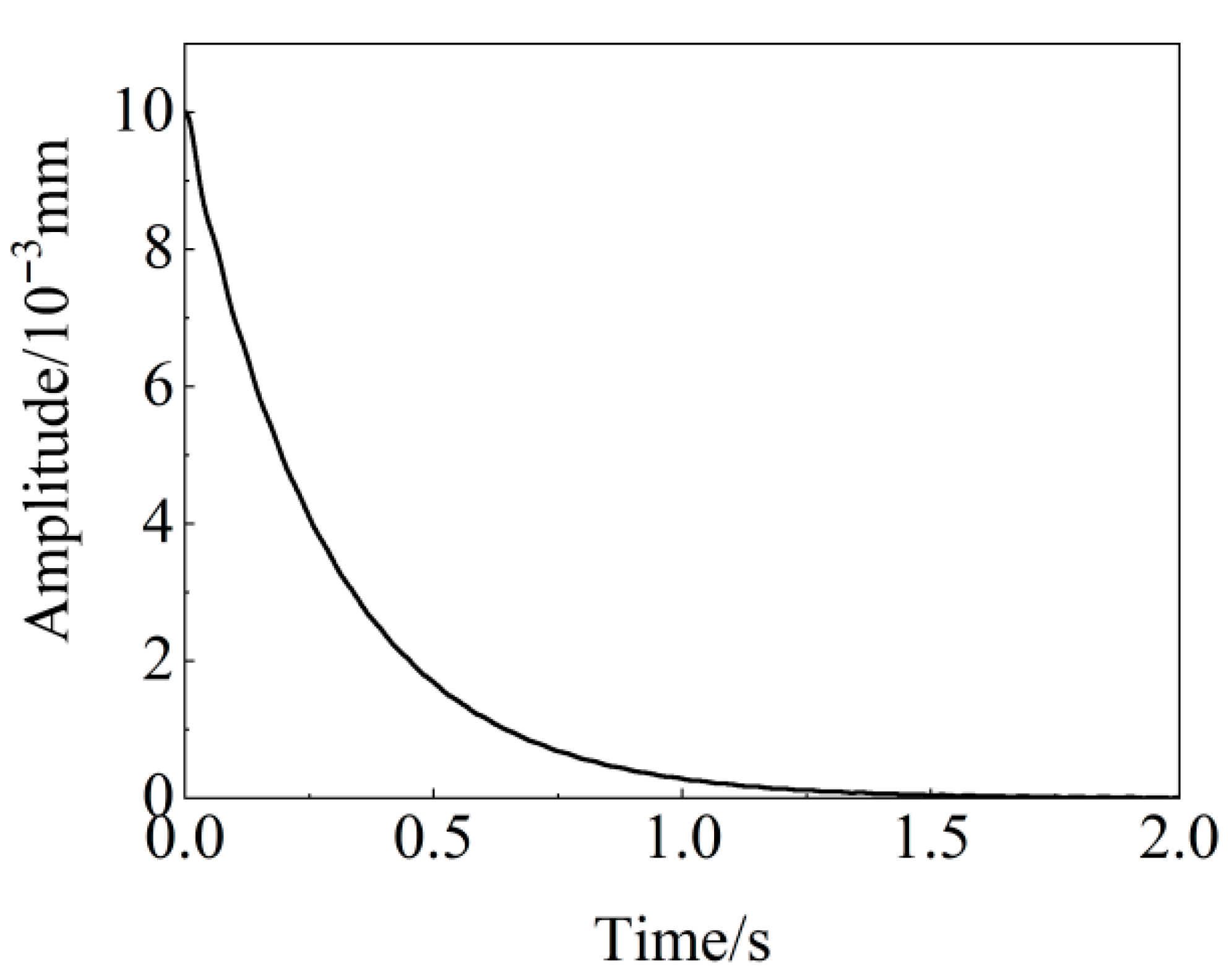
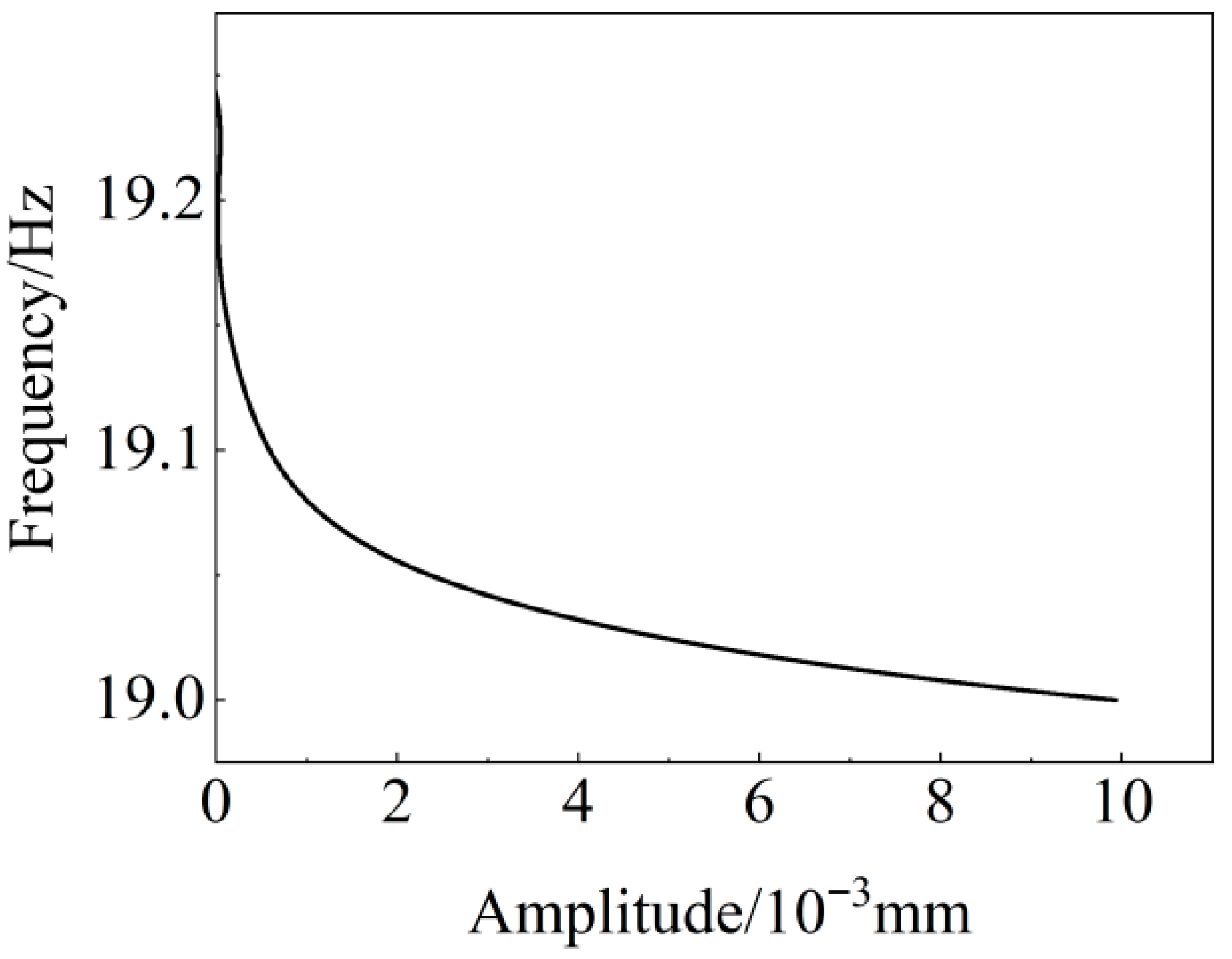
2.1. Nonlinear Vibration Theory
2.2. Variational Mode Decomposition
2.3. Hilbert Transform
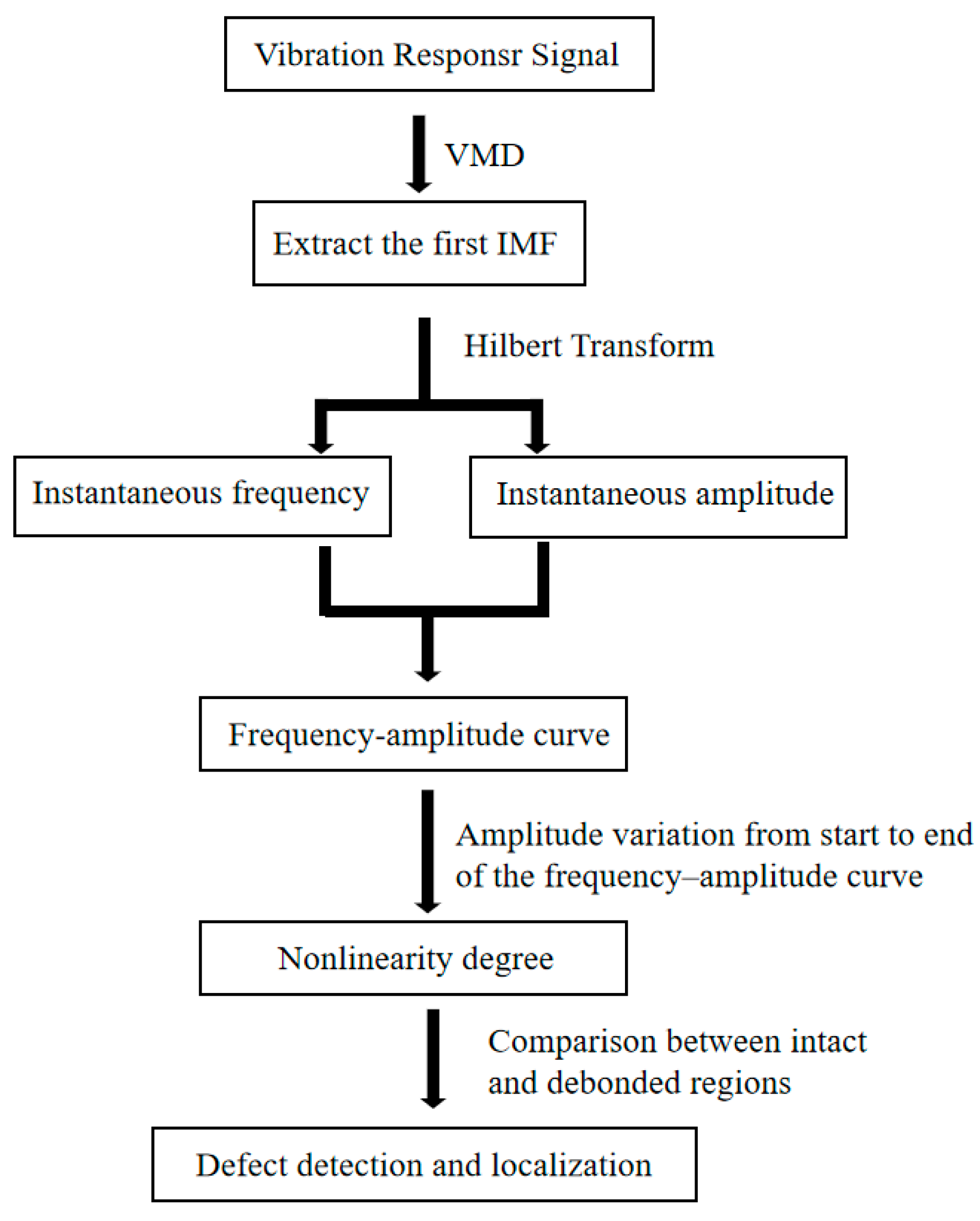
2.4. Defect Identification Procedure
3. Experimental Design for Debonding Defect Detection in ETICS
Specimen Fabrication
4. Results
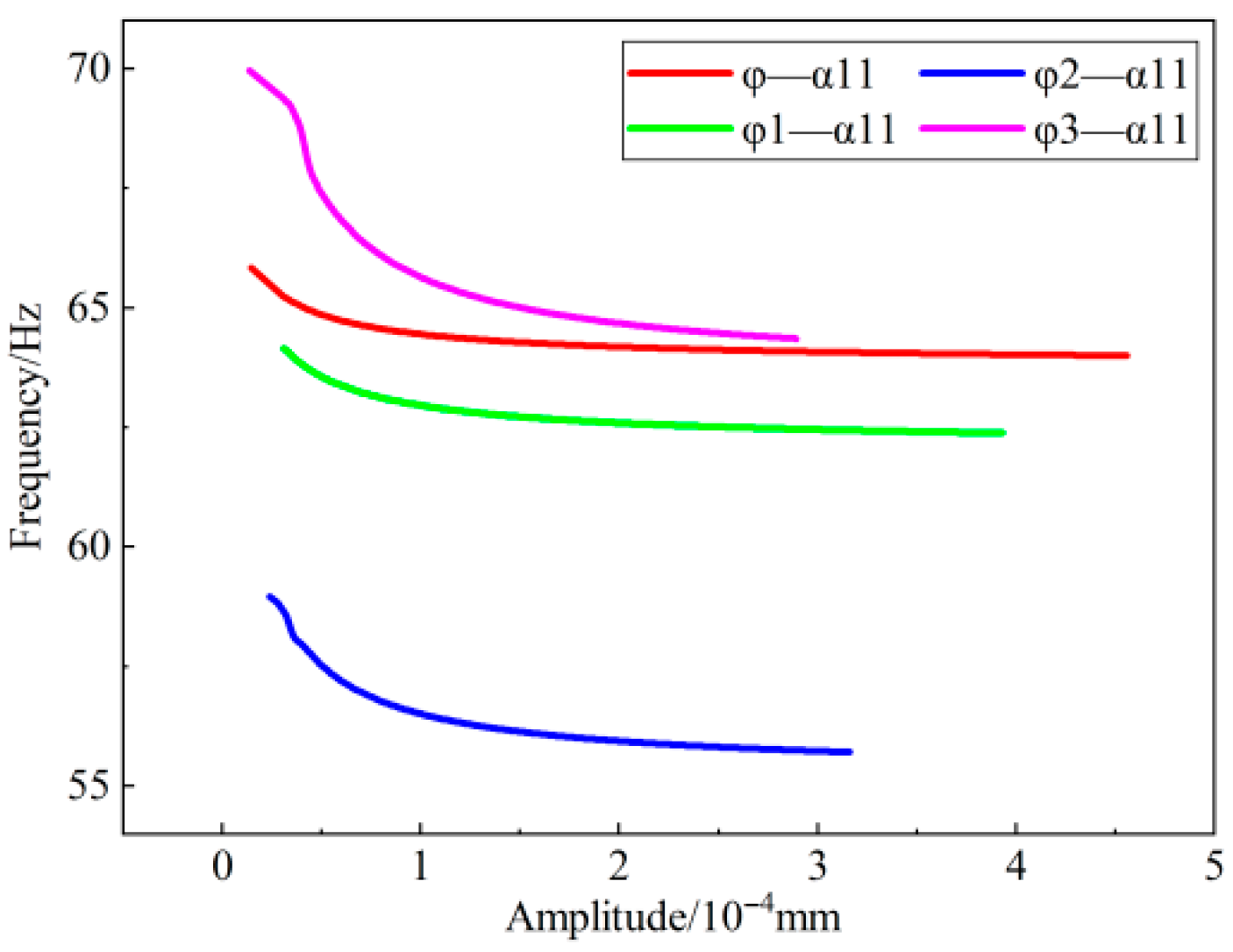
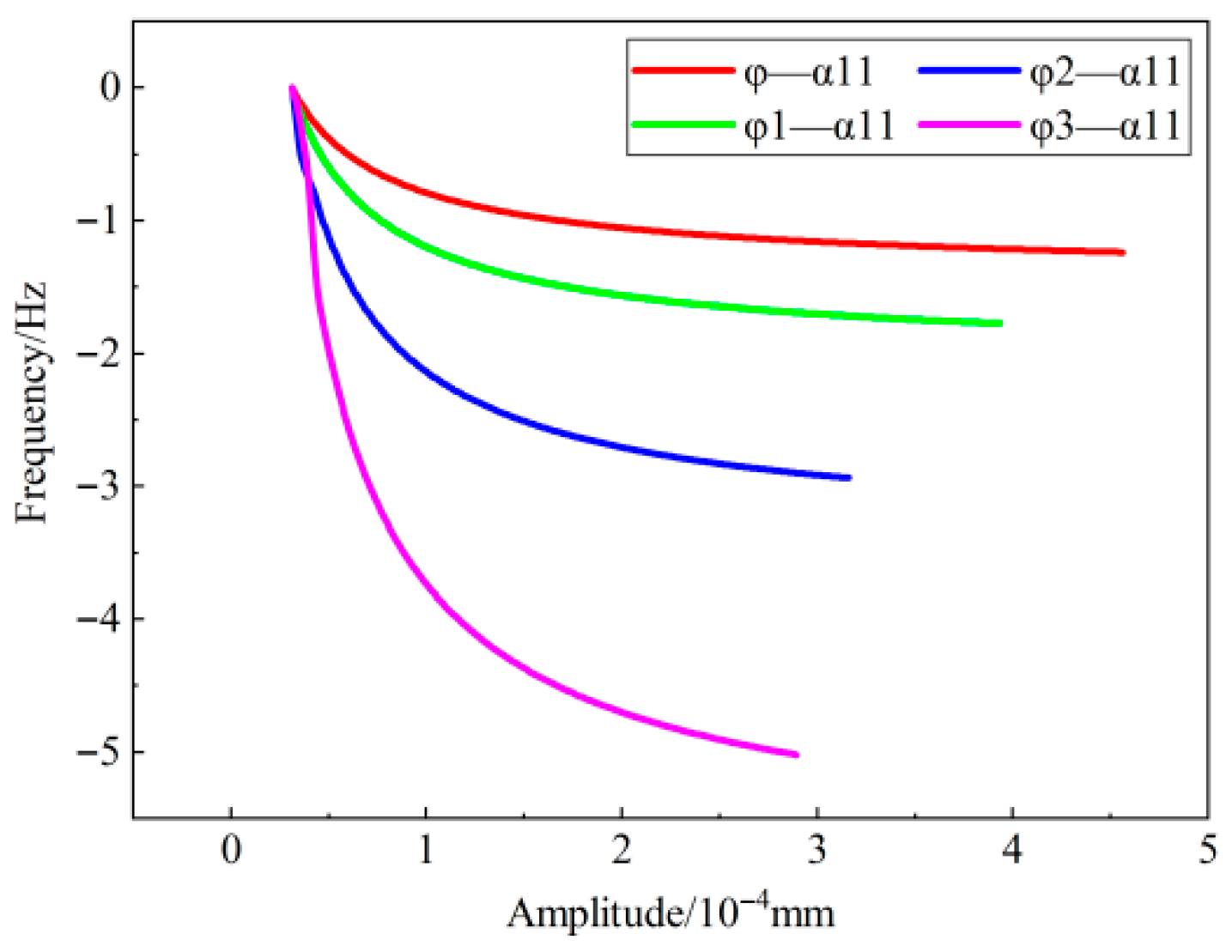
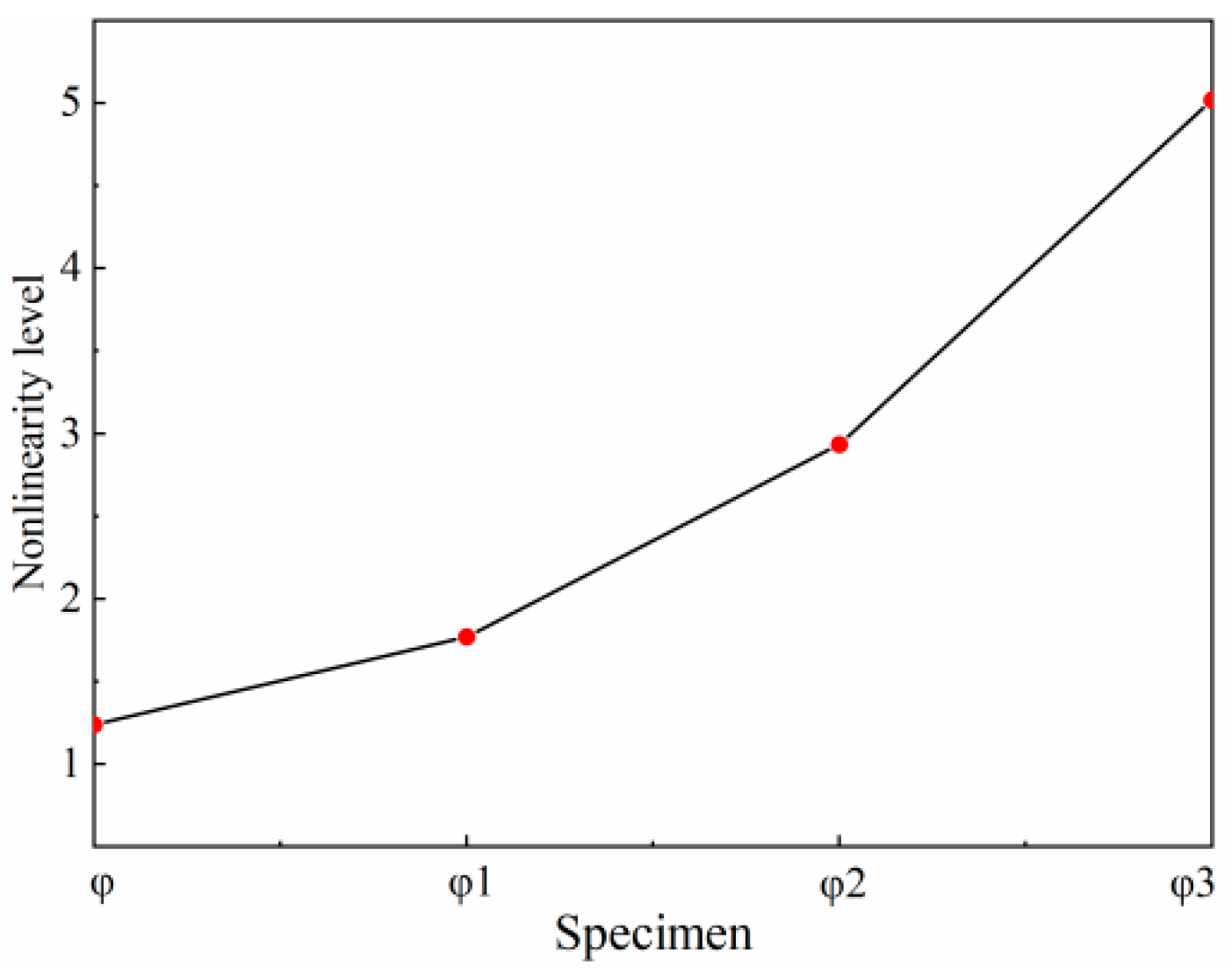
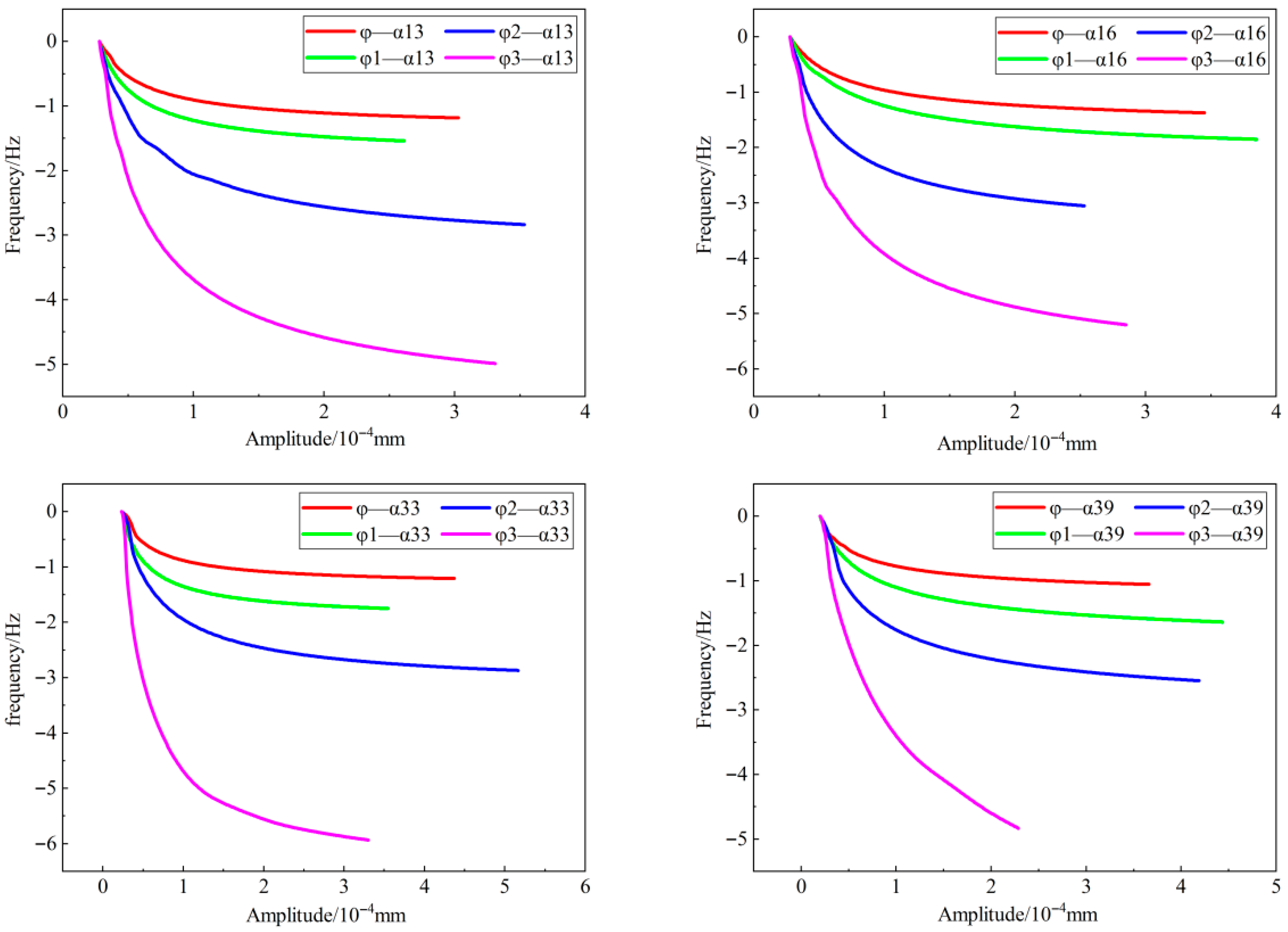
4.1. Identification of the Degree of Debonding Between the Adhesive Layer and the Insulation Layer
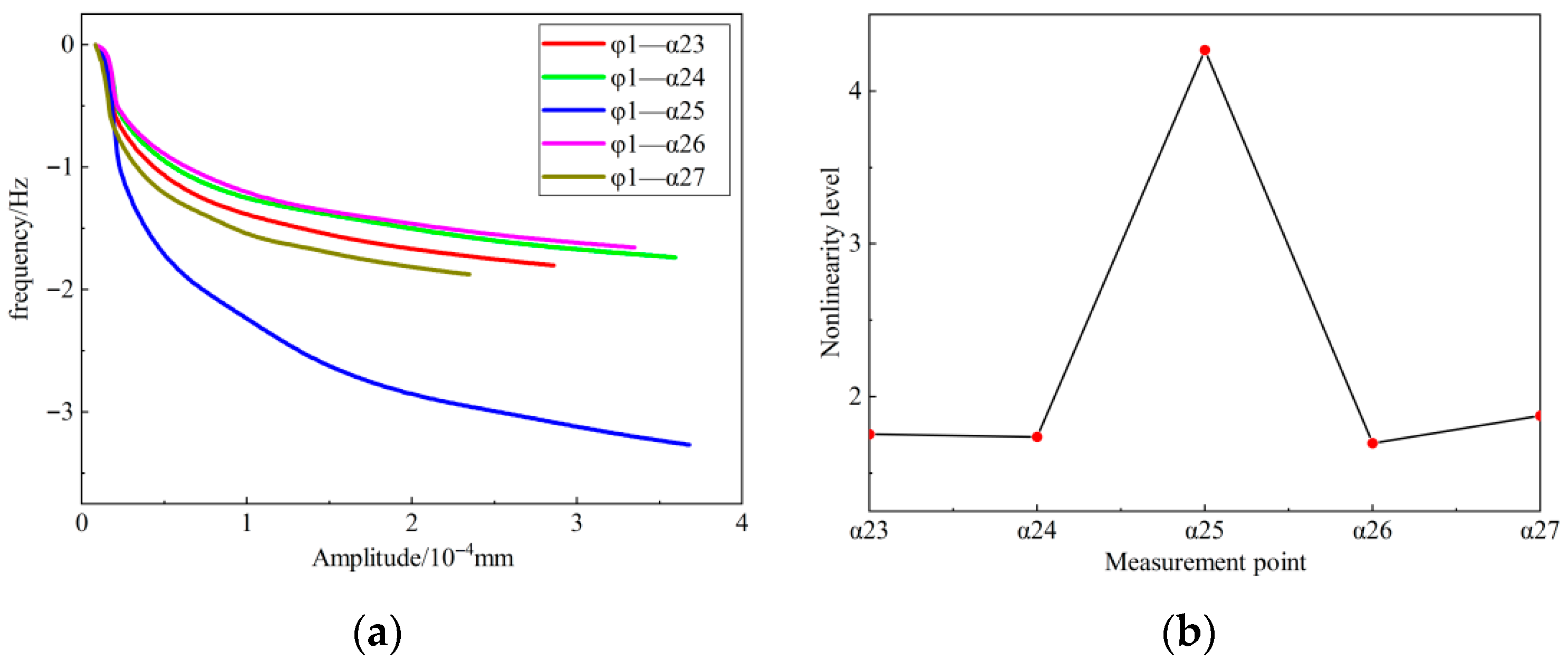
4.2. Influence of Measurement Point Location
4.3. Debonding Location Identification
5. Conclusions
- (1)
- The nonlinear vibration method can effectively identify debonding defects in external thermal insulation specimens.
- (2)
- There is a clear correlation between the nonlinearity index and the severity of debonding damage: as the extent of debonding increases, the degree of nonlinearity also rises.
- (3)
- The spatial distribution of nonlinearity indices at different measurement points can be used to locate debonding defects within the external thermal insulation specimens.
- (4)
- The relative position between the signal acquisition point and the debonding area does not affect the accuracy of defect detection.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huo, H.; Shao, J.; Huo, H. Contributions of energy-saving technologies to building energy saving in different climatic regions of China. Appl. Therm. Eng. 2017, 124, 1159–1168. [Google Scholar] [CrossRef]
- Yuan, K.; Xiong, H.; Wen, M.; Xu, J. Visualization of localized deformation of external thermal insulation composite systems during aging. Appl. Therm. Eng. 2022, 206, 118108. [Google Scholar] [CrossRef]
- Lourenço, T.; Matias, L.; Faria, P. Anomalies detection in adhesive wall tiling systems by infrared thermography. Constr. Build. Mater. 2017, 148, 419–428. [Google Scholar] [CrossRef]
- Li, Y.; Yang, X.; Gong, J.; Wang, J.; Jiang, Z.; Lan, T. Intelligent detection of bonding status in external building insulation layers using ground-penetrating radar. Autom. Constr. 2025, 173, 106100. [Google Scholar] [CrossRef]
- Zhang, D.; Zhan, C.; Chen, L.; Wang, Y.; Li, G. An in-situ detection method for assessing the thermal transmittance of building exterior walls using unmanned aerial vehicle–infrared thermography (UAV-IRT). J. Build. Eng. 2024, 91, 109724. [Google Scholar] [CrossRef]
- Fox, M.; Goodhew, S.; De Wilde, P. Building defect detection: External versus internal thermography. Build. Environ. 2016, 105, 317–331. [Google Scholar] [CrossRef]
- Lai, W.W.L.; Lee, K.K.; Poon, C.S. Validation of size estimation of debonds in external wall’s composite finishes via passive Infrared thermography and a gradient algorithm. Constr. Build. Mater. 2015, 87, 113–124. [Google Scholar] [CrossRef]
- Zar, A.; Hussain, Z.; Akbar, M.; Rabczuk, T.; Lin, Z.; Li, S.; Ahmed, B. Towards vibration-based damage detection of civil engineering structures: Overview, challenges, and future prospects. Int. J. Mech. Mater. Des. 2024, 20, 591–662. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, X.; Cao, D.; Wan, D.; Wei, S. Detection and safety assessment of bonding defects in architectural decorative surface layer based on the variation of vibration acceleration amplitude. Case Stud. Constr. Mater. 2025, 22, e04278. [Google Scholar] [CrossRef]
- Abdulkareem, M.; Bakhary, N.; Vafaei, M.; Noor, N.M.; Mohamed, R.N. Application of two-dimensional wavelet transform to detect damage in steel plate structures. Measurement 2019, 146, 912–923. [Google Scholar] [CrossRef]
- Pan, D.; Jiang, K.; Zhang, X.; Huang, Y. Sealant Delamination Detection of Structural Sealant Glazing Systems Based on Driving-Point Accelerance. Shock. Vib. 2020, 2020, 7260438. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, Y.; Huang, X.; Wang, J.; Fan, B.; Zhao, Z.; Zhu, J. Dynamic modeling of rotary blade crack with regard to three-dimensional tip clearance. J. Sound Vib. 2023, 544, 117414. [Google Scholar] [CrossRef]
- Castellini, P.; Martarelli, M.; Tomasini, E.P. Laser Doppler Vibrometry: Development of advanced solutions answering to technology’s needs. Mech. Syst. Signal Process. 2006, 20, 1265–1285. [Google Scholar] [CrossRef]
- Vegas, S.T.; Lafdi, K. A literature review of non-contact tools and methods in structural health monitoring. Ultrasound 2021, 49, 9–50. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Z.; Chen, J. Application of two dimensional Morlet wavelet transform in damage detection for composite laminates. Compos. Struct. 2023, 318, 117091. [Google Scholar] [CrossRef]
- Sugimoto, T.; Sugimoto, K.; Kosuge, N.; Utagawa, N.; Katakura, K. High-speed noncontact acoustic inspection method for civil engineering structure using multitone burst wave. Jpn. J. Appl. Phys. 2017, 56, 07JC10. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Y.; Ye, L. A non-contact inspection method of tile debonding using tuned acoustic wave and laser doppler vibrometer. J. Sound Vib. 2023, 564, 117875. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B.; Jiang, Y.; Wu, F.; Gao, Y. Ambient vibration-based quantitative assessment on tunnel lining defect using laser Doppler vibrometer. Measurement 2025, 239, 115481. [Google Scholar] [CrossRef]
- Chen, H.; Xue, J.; Gan, S.; Wang, J.; Li, Y.; Nie, X. Interfacial debonding detection for steel-concrete composite structures Part II: Scanning Doppler laser-based MASW and microphone combination-based impact-acoustic vibration. Structures 2024, 61, 106124. [Google Scholar] [CrossRef]
- Seresini, T.; Sunetchiieva, S.; Pfeiffer, H.; Wevers, M.; Glorieux, C. Defect Detection in Carbon Fiber-Reinforced Plate by Imaging of Mechanical Nonlinearity-Induced Sideband Vibrations. Vibration 2023, 6, 796–819. [Google Scholar] [CrossRef]
- Wang, B.; Shi, W.; Zhao, B.; Tian, X.; Tan, J. Detecting delamination defects in CFRP plates using nonlinear defect index of air-coupled Lamb waves and adaptively weighted imaging algorithm. Mech. Syst. Signal Process. 2024, 208, 111023. [Google Scholar] [CrossRef]
- Hafiz, A.; Schumacher, T.; Raad, A. A self-referencing non-destructive test method to detect damage in reinforced concrete bridge decks using nonlinear vibration response characteristics. Constr. Build. Mater. 2022, 318, 125924. [Google Scholar] [CrossRef]
- Lan, Z.; Saito, O.; Okabe, Y.; Deng, M.; Li, W. Baseline-free defects localization in CFRP laminates by acoustic nonlinear response of broadband guided waves. Appl. Acoust. 2025, 240, 110916. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, X.; Dai, H.; Shi, Z.; Song, J.; Xu, Y.; Wan, H.; Huan, R.; Wei, X. Phase evolution and control in a synchronized Duffing-type nonlinear micro-oscillator. Mech. Syst. Signal Process. 2024, 219, 111598. [Google Scholar] [CrossRef]
- Alam, M.Z.; Hosen, M.A.; Alam, M.S. A new modified Lindstedt–Poincare method for nonlinear damped forced oscillations. Results Phys. 2023, 51, 106673. [Google Scholar] [CrossRef]
- von Wagner, U.; Lentz, L.; Dänschel, H.; Gräbner, N. On Large Amplitude Vibrations of the Softening Duffing Oscillator at Low Excitation Frequencies—Some Fundamental Considerations. Appl. Sci. 2024, 14, 11411. [Google Scholar] [CrossRef]
- Rao, D.; Huang, M.; Shi, X.; Yu, Z.; He, Z. A Microseismic Signal Denoising Algorithm Combining VMD and Wavelet Threshold Denoising Optimized by BWOA. Comput. Model. Eng. Sci. 2024, 141, 187–217. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- JGJ 144–2019; Technical Standard for External Thermal Insulation on Walls. China Architecture & Building Press: Beijing, China, 2019. (In Chinese)
- Chen, H.; Ren, Y.; Gan, S.; Li, Y.; Wang, J.; Nie, X. Interfacial debonding detection for steel-concrete composite structures part I: Benchmark test and signal calibration of contact and non-contact measurement. Structures 2024, 62, 106123. [Google Scholar] [CrossRef]
- Aburakhia, S.; Hamieh, I.; Shami, A. Joint Instantaneous Amplitude-Frequency Analysis of Vibration Signals for Vibration-Based Condition Monitoring of Rolling Bearings. arXiv 2024, arXiv:2405.08919. [Google Scholar]
- Xiong, Q.; Guan, H.; Ma, H.; Wu, Z.; Guo, X.; Wang, W. Dynamic characteristic analysis of rotating blade with breathing crack. Mech. Syst. Signal Process. 2023, 196, 110325. [Google Scholar] [CrossRef]







| No. | Scenarios | Scheme | No. | Scenarios | Scheme |
|---|---|---|---|---|---|
| φ | No defection |  | 200 mm rectangular defect at the center of the panel |  | |
| 400 mm rectangular defect at the center of the panel |  | 600 mm rectangular defect at the center of the panel | 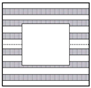 |
| Parameter | Value |
|---|---|
| Sampling Frequency | 78.125 kHz |
| Velocity Range | 4.5 m/s |
| Displacement Accuracy | 0.03 nm @ 20 kHz |
| Displacement Resolution | 0.1 nm |
| Velocity Resolution | 0.1 μm/s |
| Acceleration Resolution | 0.1 mg |
| Measurement Distance | 0.2~5 m |
| Displacement Range | ±10% of measurement distance |
| Frequency Range | 600 kHz |
| Laser Wavelength | 1550 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Yao, B.; Gao, C.; Zhou, H.; Shi, Y. A Study of a Noncontact Identification Method of Debonding Damage in External Thermal Insulation Composite Systems Based on Nonlinear Vibration. Buildings 2025, 15, 3728. https://doi.org/10.3390/buildings15203728
Hou X, Yao B, Gao C, Zhou H, Shi Y. A Study of a Noncontact Identification Method of Debonding Damage in External Thermal Insulation Composite Systems Based on Nonlinear Vibration. Buildings. 2025; 15(20):3728. https://doi.org/10.3390/buildings15203728
Chicago/Turabian StyleHou, Xuejun, Bin Yao, Chao Gao, Hui Zhou, and Yanwen Shi. 2025. "A Study of a Noncontact Identification Method of Debonding Damage in External Thermal Insulation Composite Systems Based on Nonlinear Vibration" Buildings 15, no. 20: 3728. https://doi.org/10.3390/buildings15203728
APA StyleHou, X., Yao, B., Gao, C., Zhou, H., & Shi, Y. (2025). A Study of a Noncontact Identification Method of Debonding Damage in External Thermal Insulation Composite Systems Based on Nonlinear Vibration. Buildings, 15(20), 3728. https://doi.org/10.3390/buildings15203728





