Probabilistic Model Optimization and Safety Assessment Methods for Existing Masonry Structures
Abstract
1. Introduction
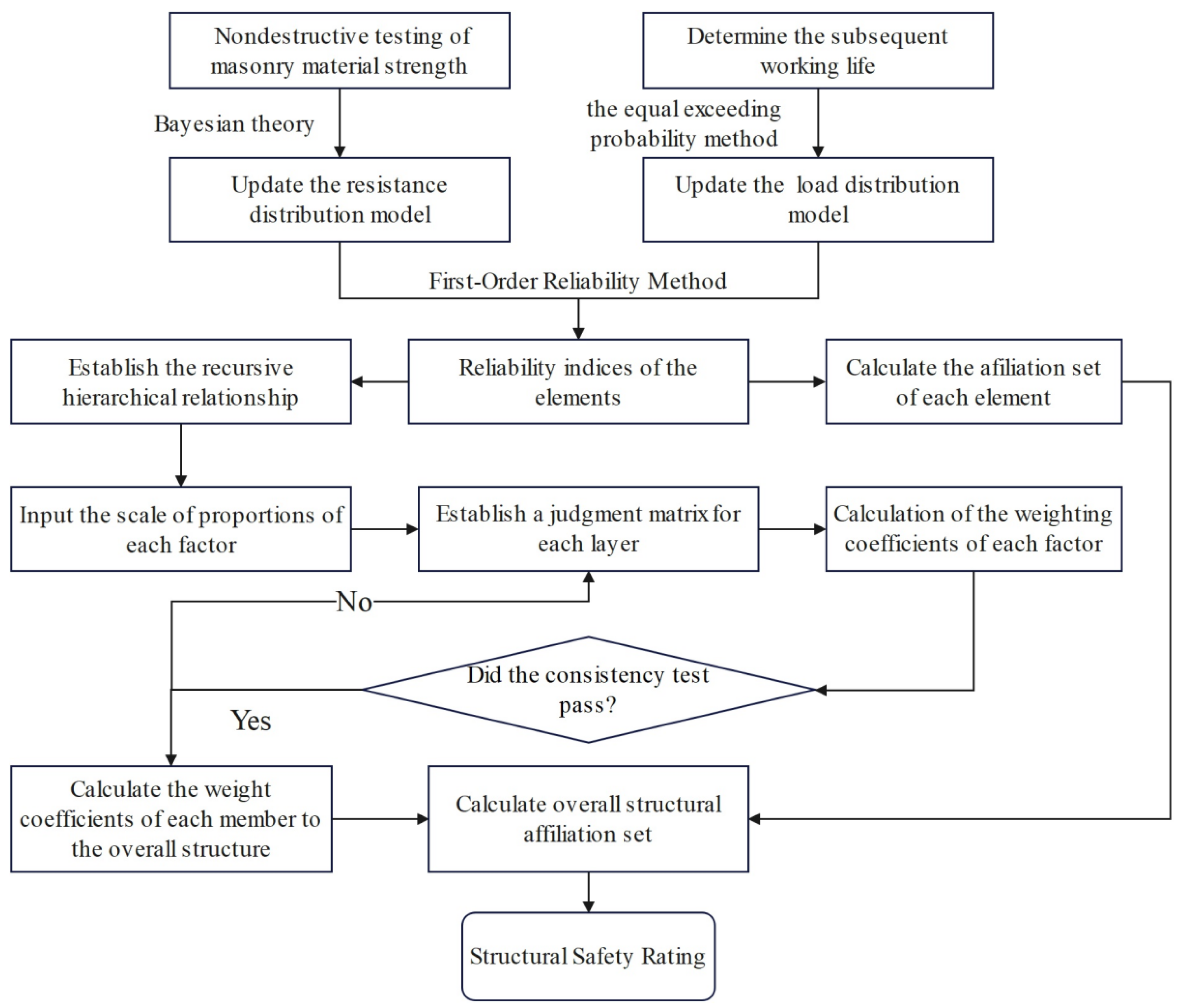
2. Update of the Member-Resistance Model for Existing Masonry Structures
2.1. On-Site Measured Material Strength Models
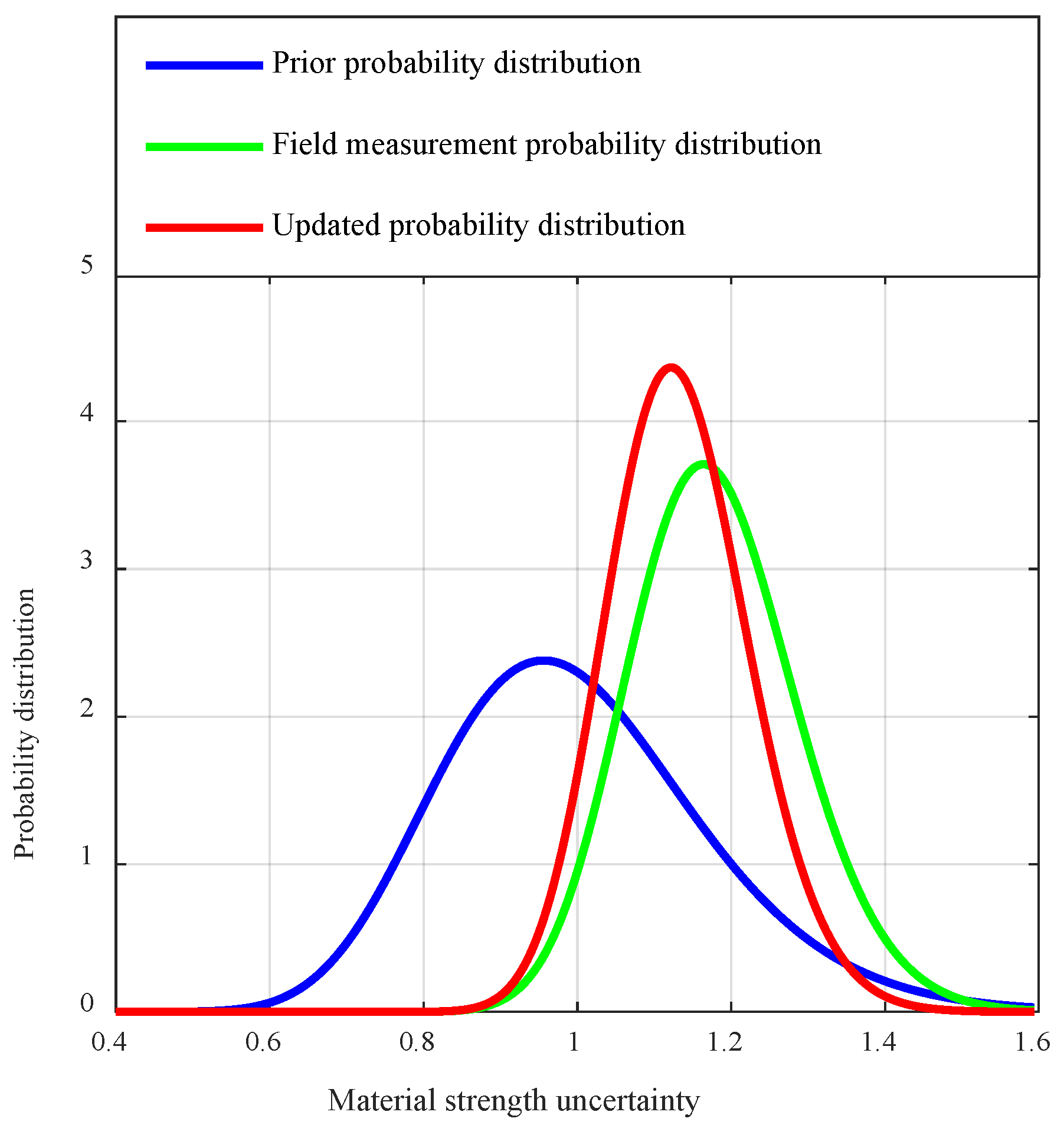
2.2. Resistance Model Update
2.3. Load Model Update
3. Reliability Assessments of Existing Masonry Structural Systems
3.1. Affiliation Set
3.2. Analytic Hierarchy Process (AHP)
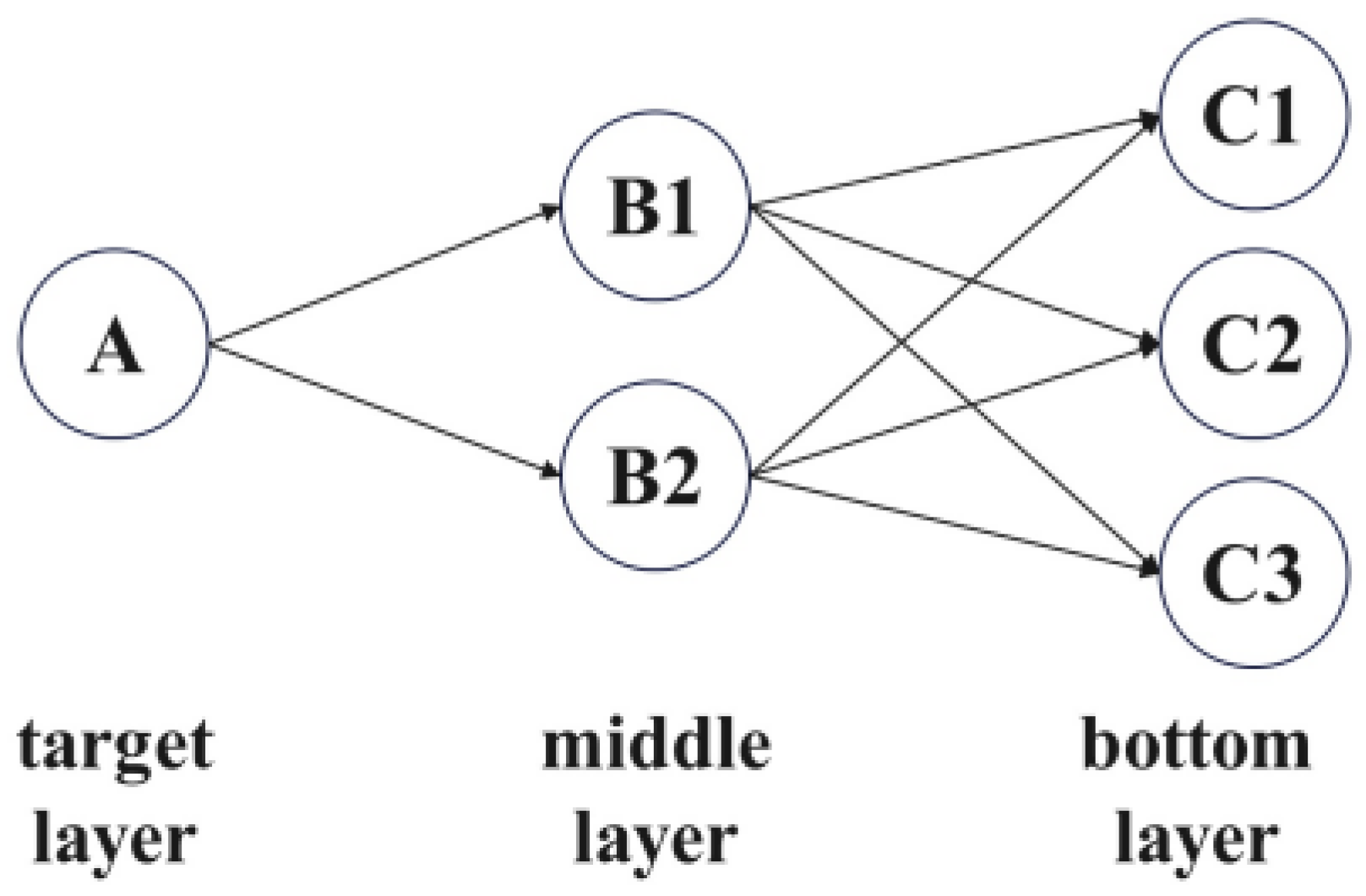
3.2.1. Hierarchical Recursive
3.2.2. Judgment Matrix
3.2.3. Hierarchical Ordering
3.2.4. Judgment Matrix Consistency Test
3.2.5. Assessment of Structural Systems
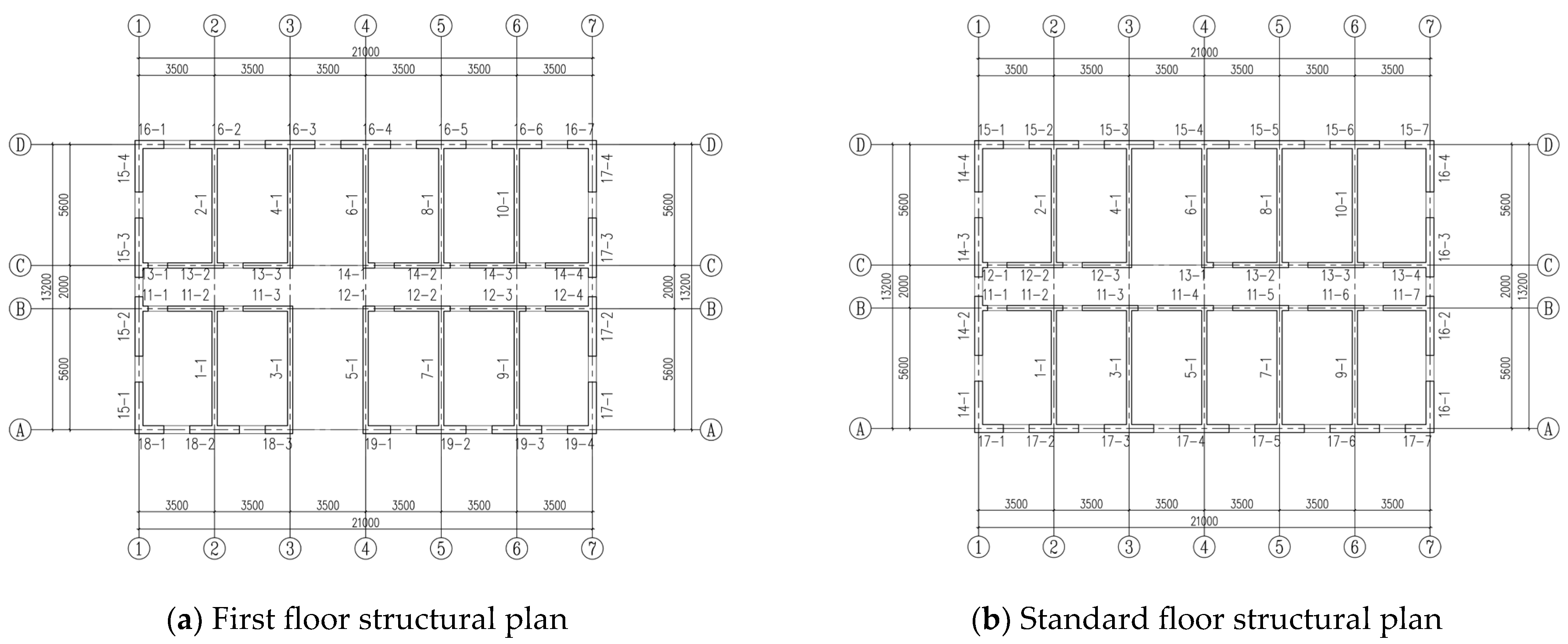
4. Assessment Case
4.1. Structural Safety Grade as Determined by GB 50292-2015
4.2. Safety Assessment Based on Model Updating and Affiliations
5. Results and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- GB 50292-2015; Standard for Appraisal of Reliability of Civil Buildings. 2015 ed. China Building Industry Press: Beijing, China, 2015; pp. 34–35.
- Wu, L.L.; Tang, C.M.; Luo, K.H.; Huang, S.M.; Lu, D.G. Discussion on the determination method of target reliability index for existing building assessment and retrofitting. China Civ. Eng. J. 2022, 55, 196–202. [Google Scholar] [CrossRef]
- Gu, X.L.; Chen, S.J.; Zhang, W.P. A practical method for reliability assessment of existing building structural systems. Struct. Eng. 2007, 23, 12–17. [Google Scholar]
- Freudenthal, A.M.; Garrelts, J.M.; Shinozuka, M. The analysis of structural safety. J. Struct. Div. ASCE 1966, 92, 267–325. [Google Scholar] [CrossRef]
- Ang, A.H.S.; Ma, H.F. On the reliability of structural systems. In Proceedings of the 3rd International Conference on Structural Safety and Reliability, Trondheim, Norway, 23–25 June 1981. [Google Scholar]
- Ditlevsen, O. Narrow reliability bounds for structural systems. J. Struct. Mech. 1979, 7, 453–472. [Google Scholar] [CrossRef]
- Thoft-Christensen, P.; Sorensen, J.D. Reliability of structural systems with correlated elements. Appl. Math. Model. 1982, 6, 171–178. [Google Scholar] [CrossRef]
- Murotsu, Y.; Okada, H.; Taguchi, K.; Grimmelt, M.; Yonezawa, M. Automatic generation of stochastically dominant failure modes of frame structures. Struct. Saf. 1984, 2, 17–25. [Google Scholar] [CrossRef]
- Thoft-Christensen, P.; Murotsu, Y. Application of Structural Systems Reliability Theory, 1st ed.; Springer: Berlin, Germany, 1986; pp. 37–46. [Google Scholar]
- Dong, C. Modern Structural System Reliability Theory and Applications; Science Press: Beijing, China, 2001. [Google Scholar]
- Lee, Y.; Song, J. Risk analysis of fatigue-induced sequential failures by branch-and-bound method employing system reliability bounds. J. Eng. Mech. 2011, 137, 807–821. [Google Scholar] [CrossRef]
- Hu, Y.C.; Guo, Z.B. Structural System Reliability Analysis: Theory and Applications; Tianjin University Press: Tianjin, China, 1992. [Google Scholar]
- Brown, C.B. A fuzzy safety measure. J. Eng. Mech. Div. ASCE 1980, 105, 855–872. [Google Scholar] [CrossRef]
- Blockley, D.I. The role of fuzzy sets in civil engineering. Fuzzy Sets Syst. 1979, 2, 267–278. [Google Scholar] [CrossRef]
- Yao, J.T.P. Safety and Reliability of Existing Structures; Pitman Advanced Publishing Program: Vancouver, BC, Canada, 1985. [Google Scholar]
- Wang, X.M.; Li, G.Q. Analysis and Evaluation for Exesting Housing Reliability. J. Wuhan Univ. Technol. 1999, 21, 43–46. [Google Scholar]
- Xia, C.C.; Liu, X.L. Damage evaluation expert system for one-storey reinforced concrete building (RACODE-I). Comput. Struct. Mech. Appl. 1989, 6, 64–71. [Google Scholar]
- Chen, S.J.; Gu, X.L.; Zhang, W.P. Application of analytic hierarchy process in reliability assessment of existing building structural systems. Struct. Eng. 2005, 21, 31–35. [Google Scholar]
- DG/TJ08-804-2005; Standard for Inspection and Assessment of Existing Building Structures. 1st ed. Shanghai Construction Engineering Standards Management Station: Shanghai, China, 2005.
- Andreolli, F.; Bragolusi, P.; D’ALpaos, C.; Faleschini, F.; Zanini, M.A. An AHP model for multiple-criteria prioritization of seismic retrofit solutions in gravity-designed industrial buildings. J. Build. Eng. 2022, 45, 103493. [Google Scholar] [CrossRef]
- Alkubaisi, A.; Alnsour, M.A. Using AHP method for development of existing building green assessment system in Jordan. Asian J. Civ. Eng. 2022, 23, 1231–1250. [Google Scholar] [CrossRef]
- Shen, P.; Chen, Y.; Ma, S.; Yan, Y. Safety assessment method of concrete-filled steel tubular arch bridge by fuzzy analytic hierarchy process. Buildings 2023, 14, 67. [Google Scholar] [CrossRef]
- Moon, H.; Mirmotalebi, S.; Jang, Y.; Ahn, Y.; Kwon, N. Risk evaluation of radioactive concrete structure decommissioning in nuclear power plants using fuzzy-AHP. Buildings 2024, 14, 1536. [Google Scholar] [CrossRef]
- Gashaw, D.Y.; Suryabhagavan, K.V.; Nedaw, D.; Gummadi, S. Rainwater harvesting in Modjo watershed, upper Awash River Basin, Ethiopia through remote sensing and fuzzy AHP. Geocarto Int. 2022, 37, 14785–14810. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, G.; Zhai, Y. Integrating AHP-Entropy and IPA Models for Strategic Rural Revitalization: A Case Study of Traditional Villages in Northeast China. Buildings 2025, 15, 2475. [Google Scholar] [CrossRef]
- Zheng, H.B. Appraisal and Reinforcement Research on Existing Reinforced Concrete Structure Based on Target Service Life and Overall Reliability. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2010. [Google Scholar]
- Li, J.; Chen, J.B. The number theoretical method in response analysis of nonlinear stochastic structures. Comput. Mech. 2007, 39, 693–708. [Google Scholar] [CrossRef]
- Chen, J.B.; Ghanem, R.; Li, J. Partition of the probability-assigned space in probability density evolution analysis of nonlinear stochastic structures. Probabilistic Eng. Mech. 2009, 24, 27–42. [Google Scholar] [CrossRef]
- Xu, J.; Chen, J.B.; Li, J. Probability density evolution analysis of engineering structures via cubature points. Comput. Mech. 2012, 50, 135–156. [Google Scholar] [CrossRef]
- Chen, J.B.; Yang, J.; Li, J. A GF-discrepancy for point selection in stochastic seismic response analysis of structures with uncertain parameters. Struct. Saf. 2016, 59, 20–31. [Google Scholar] [CrossRef]
- Chen, J.B.; Song, P.Y. A generalized L2-discrepancy for cubature and uncertainty quantification of nonlinear structures. Sci. China Technol. Sci. 2016, 59, 941–952. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.B.; Fan, W.L. The equivalent extreme-value event and evaluation of the structural system reliability. Struct. Saf. 2007, 29, 112–131. [Google Scholar] [CrossRef]
- Chen, J.B.; Li, J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters. Struct. Saf. 2007, 29, 77–93. [Google Scholar] [CrossRef]
- Chen, J.B.; Li, J. Dynamic response and reliability analysis of nonlinear stochastic structures. Probabilistic Eng. Mech. 2005, 20, 33–44. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.B. Stochastic Dynamics of Structures; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- John, S.K.; Cascardi, A.; Verre, S.; Nadir, Y. RC-columns subjected to lateral cyclic force with different FRCM-strengthening schemes: Experimental and numerical investigation. Bull. Earthq. Eng. 2025, 23, 1561–1590. [Google Scholar] [CrossRef]
- GB/T 50315-2011; Technical Standard for On-Site Inspection of Masonry Engineering. 2001 ed. China Building Industry Press: Beijing, China, 2011.
- GB 50003-2011; Code for Design of Masonry Structures. 2011 ed. China Building Industry Press: Beijing, China, 2011.
- GBJ 68-84; Unified Standard for Reliability Design of Building Structures. China Building Industry Press: Beijing, China, 1984.
- Wu, L.; Yang, T.; Guan, H.; Tang, C.; Zhao, Y. Study on safety assessment method considering the deterministic characteristics of existing masonry structures. Struct. Monit. Maint. 2025, 12, 121–135. [Google Scholar]
- GB 50068-2018; Unified Standard for Reliability Design of Building Structures. 2018 ed. China Building Industry Press: Beijing, China, 2018.
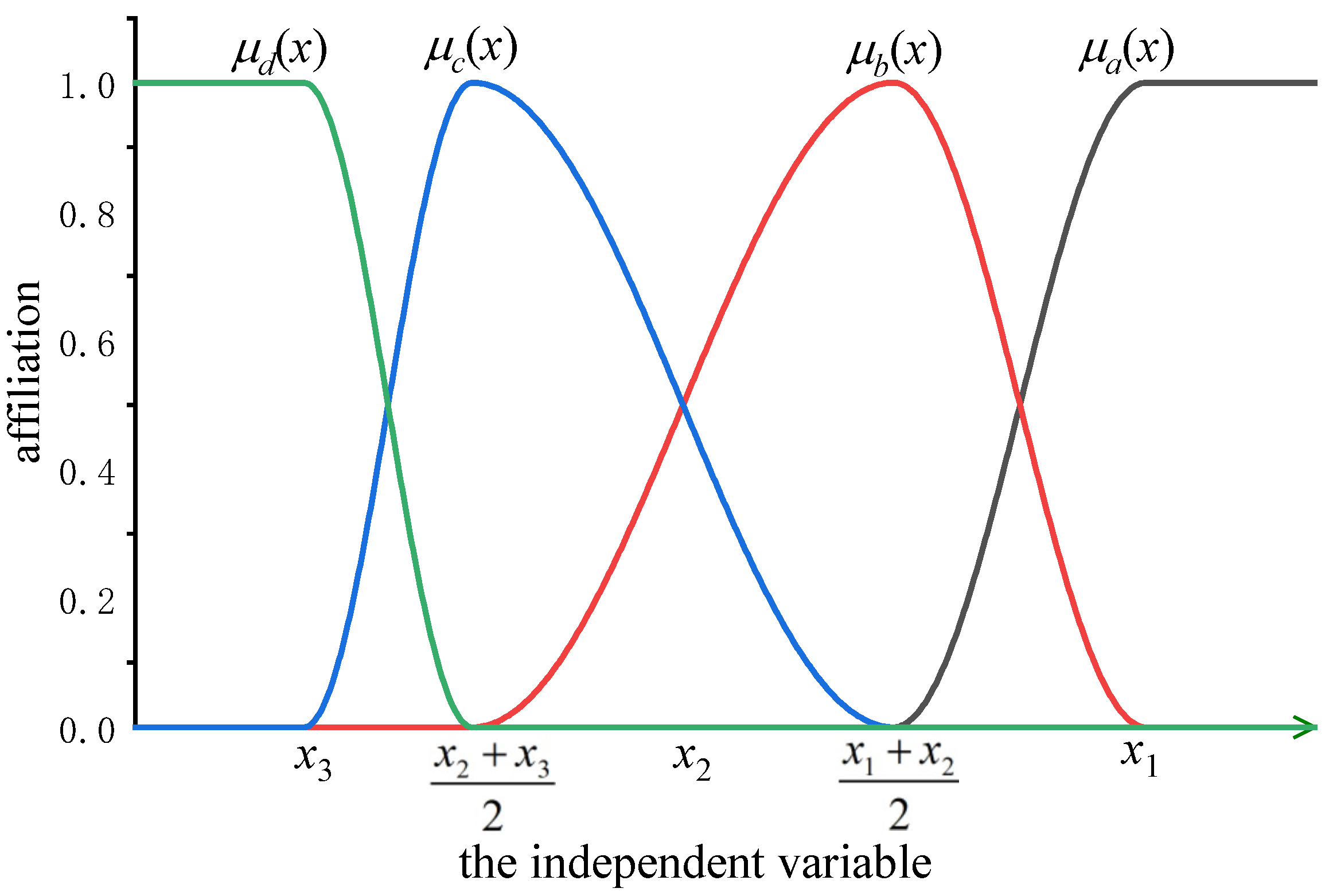
| Types | κ | δ | Types | κ | δ | ||
|---|---|---|---|---|---|---|---|
| Ωf | Axial compression | 1.00 | 0.174 | ΩP | Axial compression | 1.0922 | 0.2059 |
| Eccentric compression | 1.00 | 0.174 | Eccentric compression | 1.1814 | 0.2159 | ||
| Shear | 1.00 | 0.240 | Shear | 1.017 | 0.1260 | ||
| Ωa | Axial compression | 1.00 | 0.023 | R | Axial compression | 1.0922 | 0.2705 |
| Eccentric compression | 1.00 | 0.023 | Eccentric compression | 1.1814 | 0.2811 | ||
| Shear | 1.00 | 0.036 | Shear | 1.0170 | 0.2734 |
| Subsequent Working Years | SG | SQ | ||||||
|---|---|---|---|---|---|---|---|---|
| Dead Loads | Residential Live Loads | Office Live Loads | Wind | |||||
| κ | δ | κ | δ | κ | δ | κ | δ | |
| 10a | 1.06 | 0.07 | 0.486 | 0.308 | 0.371 | 0.407 | 0.455 | 0.256 |
| 20a | 0.554 | 0.270 | 0.437 | 0.346 | 0.673 | 0.225 | ||
| 30a | 0.594 | 0.252 | 0.475 | 0.318 | 0.822 | 0.210 | ||
| 40a | 0.622 | 0.241 | 0.502 | 0.300 | 0.928 | 0.201 | ||
| 50a | 0.644 | 0.233 | 0.524 | 0.288 | 1.000 | 0.194 | ||
| au | bu | cu | du |
|---|---|---|---|
| Scale eij | Meaning | Example |
|---|---|---|
| 1 | Elements i and j are of equal importance | Beams and columns have a comparable impact on the overall reliability of the structure. |
| 3 | Element i is slightly more important than element j | Main beams are slightly more important than secondary beams. |
| 5 | Element i is significantly more important than element j | Framing columns have a significantly higher risk of failure than infill walls. |
| 7 | To a strong degree, element i is more important than element j | Foundation elements are much more important than decorative elements. |
| 9 | Element i is extremely more important than element j | Bearing wall failures can lead to a direct collapse of the structure. |
| 2,4,6,8 | Indicates the intermediate values for the adjacent judgments above | It is difficult to clearly distinguish between “slightly important” and “obviously important”. |
| 1/(1~9) | The degree of unimportance of element i over element j | The importance of secondary beams is 1/3 of the importance of the main beams. |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RI | 0.00 | 0.00 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| Overall Reliability Rating | Residential Building | Industrial Building |
|---|---|---|
| Au | and | and |
| Bu | and | and |
| Cu | and | and |
| Du | or | and |
| First Floor | Second Floor | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | Rd/kN | SGk/kN | SQk/kN | Rd/(γ0S) | Grade | Number | Rd/kN | SGk/kN | SQk/kN | Rd/(γ0S) | Grade |
| 1-1 | 1161.21 | 795.98 | 166.6 | 0.9 | cu | 1-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 2-1 | 1161.21 | 795.98 | 166.6 | 0.9 | cu | 2-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 3-1 | 1161.21 | 946.34 | 176.52 | 0.78 | du | 3-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 4-1 | 1161.21 | 912.4 | 235.32 | 0.75 | du | 4-1 | 1220.54 | 709.71 | 179.06 | 1.02 | au |
| 5-1 | 1161.21 | 976.46 | 181.91 | 0.75 | du | 5-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 6-1 | 1161.21 | 928.96 | 240.71 | 0.74 | du | 6-1 | 1220.54 | 724.6 | 183.17 | 1.00 | au |
| 7-1 | 1161.21 | 795.98 | 166.6 | 0.9 | cu | 7-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 8-1 | 1161.21 | 795.98 | 166.6 | 0.9 | cu | 8-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 9-1 | 1161.21 | 795.98 | 166.6 | 0.9 | cu | 9-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 10-1 | 1161.21 | 795.98 | 166.6 | 0.9 | cu | 10-1 | 1220.54 | 623.5 | 127.40 | 1.22 | au |
| 11-1 | 118.59 | 66.71 | 9.13 | 1.18 | au | 11-1 | 121.92 | 50.87 | 6.96 | 1.59 | au |
| 11-2 | 602.96 | 268.38 | 36.75 | 1.49 | au | 11-2 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 11-3 | 533.39 | 247.10 | 36.07 | 1.43 | au | 11-3 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 12-1 | 103.98 | 82.47 | 12.2 | 0.84 | du | 11-4 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 12-2 | 602.96 | 268.38 | 36.75 | 1.49 | au | 11-5 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 12-3 | 602.96 | 268.38 | 36.75 | 1.49 | au | 11-6 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 12-4 | 548.47 | 210.67 | 27.61 | 1.81 | au | 11-7 | 563.9 | 153.78 | 21.00 | 2.44 | au |
| 13-1 | 118.59 | 66.71 | 9.13 | 1.18 | au | 12-1 | 121.92 | 50.87 | 6.96 | 1.59 | au |
| 13-2 | 602.96 | 268.38 | 36.75 | 1.49 | au | 12-2 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 13-3 | 533.39 | 226.65 | 36.75 | 1.54 | au | 12-3 | 548.41 | 177.13 | 27.48 | 2.02 | au |
| 14-1 | 103.98 | 75.13 | 12.2 | 0.9 | cu | 13-1 | 106.82 | 59.33 | 9.29 | 1.17 | au |
| 14-2 | 602.96 | 268.38 | 36.75 | 1.49 | au | 13-2 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 14-3 | 602.96 | 268.38 | 36.75 | 1.49 | au | 13-3 | 619.94 | 204.65 | 28.00 | 2.01 | au |
| 14-4 | 548.47 | 210.67 | 27.61 | 1.81 | au | 13-4 | 563.9 | 153.78 | 21.00 | 2.44 | au |
| 15-1 | 881.57 | 372.42 | 41.64 | 1.61 | au | 14-1 | 904.12 | 285.66 | 31.84 | 2.16 | au |
| 15-2 | 1057.09 | 443.54 | 41.66 | 1.65 | au | 14-2 | 1073.42 | 337.81 | 31.86 | 2.20 | au |
| 15-3 | 1057.09 | 443.54 | 41.66 | 1.65 | au | 14-3 | 1073.42 | 337.81 | 31.86 | 2.21 | au |
| 15-4 | 881.57 | 372.42 | 41.64 | 1.61 | au | 14-4 | 904.42 | 285.66 | 31.84 | 2.16 | au |
| 16-1 | 535.21 | 158.54 | 0.00 | 2.6 | au | 15-1 | 542.21 | 118.55 | 0.00 | 3.52 | au |
| 16-2 | 922.08 | 317.09 | 0.00 | 2.24 | au | 15-2 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 16-3 | 922.08 | 317.09 | 0.00 | 2.24 | au | 15-3 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 16-4 | 922.08 | 317.09 | 0.00 | 2.24 | au | 15-4 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 16-5 | 922.08 | 317.09 | 0.00 | 2.24 | au | 15-5 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 16-6 | 922.08 | 317.09 | 0.00 | 2.24 | au | 15-6 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 16-7 | 535.21 | 158.54 | 0.00 | 2.6 | au | 15-7 | 542.21 | 118.55 | 0.00 | 3.52 | au |
| 17-1 | 881.57 | 372.42 | 41.64 | 1.61 | au | 16-1 | 904.12 | 285.66 | 31.84 | 2.16 | au |
| 17-2 | 1057.09 | 443.54 | 41.66 | 1.65 | au | 16-2 | 1073.42 | 337.81 | 31.86 | 2.21 | au |
| 17-3 | 1057.09 | 443.54 | 41.66 | 1.66 | au | 16-3 | 1073.42 | 337.81 | 31.86 | 2.21 | au |
| 17-4 | 881.57 | 372.42 | 41.64 | 1.61 | au | 16-4 | 904.42 | 285.66 | 31.84 | 2.16 | au |
| 18-1 | 535.21 | 158.54 | 0.00 | 2.6 | au | 17-1 | 542.21 | 118.55 | 0.00 | 3.52 | au |
| 18-2 | 922.08 | 317.09 | 0.00 | 2.24 | au | 17-2 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 18-3 | 509.15 | 203.98 | 0.00 | 1.92 | au | 17-3 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 19-1 | 509.15 | 203.98 | 0.00 | 1.92 | au | 17-4 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 19-2 | 922.08 | 317.09 | 0.00 | 2.24 | au | 17-5 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 19-3 | 922.08 | 317.09 | 0.00 | 2.24 | au | 17-6 | 934.14 | 237.1 | 0.00 | 3.03 | au |
| 19-4 | 535.21 | 158.54 | 0.00 | 2.6 | au | 17-7 | 542.21 | 118.55 | 0.00 | 3.52 | au |
| First Floor | Second Floor | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Number | Β | Element Type | Affiliation Set | Weights | Number | Β | Element Type | Affiliation Set | Weights |
| 1-1 | 3.59 | Bearing wall | [0.0402,0.9598,0,0] | 0.0136 | 1-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 2-1 | 3.59 | Bearing wall | [0.0402,0.9598,0,0] | 0.0136 | 2-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 3-1 | 2.96 | Bearing wall | [0,0,0,1] | 0.0136 | 3-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 4-1 | 2.86 | Bearing wall | [0,0,0,1] | 0.0136 | 4-1 | 4.11 | Bearing wall | [1,0,0,0] | 0.0069 |
| 5-1 | 2.83 | Bearing wall | [0,0,0,1] | 0.0136 | 5-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 6-1 | 2.78 | Bearing wall | [0,0,0,1] | 0.0136 | 6-1 | 4.02 | Bearing wall | [1,0,0,0] | 0.0069 |
| 7-1 | 3.59 | Bearing wall | [0.0402,0.9598,0,0] | 0.0136 | 7-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 8-1 | 3.59 | Bearing wall | [0.0402,0.9598,0,0] | 0.0136 | 8-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 9-1 | 3.59 | Bearing wall | [0.0402,0.9598,0,0] | 0.0136 | 9-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 10-1 | 3.59 | Bearing wall | [0.0402,0.9598,0,0] | 0.0136 | 10-1 | 4.82 | Bearing wall | [1,0,0,0] | 0.0069 |
| 11-1 | 4.68 | Bearing wall | [1,0,0,0] | 0.0136 | 11-1 | 5.92 | Bearing wall | [1,0,0,0] | 0.0069 |
| 11-2 | 5.65 | Bearing wall | [1,0,0,0] | 0.0136 | 11-2 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 11-3 | 5.45 | Bearing wall | [1,0,0,0] | 0.0136 | 11-3 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 12-1 | 3.21 | Bearing wall | [0,0,0.0186,0.9814] | 0.0136 | 11-4 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 12-2 | 5.65 | Bearing wall | [1,0,0,0] | 0.0136 | 11-5 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 12-3 | 5.65 | Bearing wall | [1,0,0,0] | 0.0136 | 11-6 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 12-4 | 6.28 | Bearing wall | [1,0,0,0] | 0.0136 | 11-7 | 7.68 | Bearing wall | [1,0,0,0] | 0.0069 |
| 13-1 | 4.68 | Bearing wall | [1,0,0,0] | 0.0136 | 12-1 | 5.92 | Bearing wall | [1,0,0,0] | 0.0069 |
| 13-2 | 5.65 | Bearing wall | [1,0,0,0] | 0.0136 | 12-2 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 13-3 | 5.74 | Bearing wall | [1,0,0,0] | 0.0136 | 12-3 | 6.90 | Bearing wall | [1,0,0,0] | 0.0069 |
| 14-1 | 3.54 | Bearing wall | [0,0.8644,0.1356,0] | 0.0136 | 13-1 | 4.65 | Bearing wall | [1,0,0,0] | 0.0069 |
| 14-2 | 5.65 | Bearing wall | [1,0,0,0] | 0.0136 | 13-2 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 14-3 | 5.65 | Bearing wall | [1,0,0,0] | 0.0136 | 13-3 | 6.89 | Bearing wall | [1,0,0,0] | 0.0069 |
| 14-4 | 6.28 | Bearing wall | [1,0,0,0] | 0.0136 | 13-4 | 7.68 | Bearing wall | [1,0,0,0] | 0.0069 |
| 15-1 | 5.96 | Mountain wall | [1,0,0,0] | 0.0166 | 14-1 | 7.17 | Mountain wall | [1,0,0,0] | 0.0084 |
| 15-2 | 6.06 | Mountain wall | [1,0,0,0] | 0.0166 | 14-2 | 7.25 | Mountain wall | [1,0,0,0] | 0.0084 |
| 15-3 | 6.06 | Mountain wall | [1,0,0,0] | 0.0166 | 14-3 | 7.25 | Mountain wall | [1,0,0,0] | 0.0084 |
| 15-4 | 5.96 | Mountain wall | [1,0,0,0] | 0.0166 | 14-4 | 7.17 | Mountain wall | [1,0,0,0] | 0.0084 |
| 16-1 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 15-1 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 16-2 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 15-2 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 16-3 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 15-3 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 16-4 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 15-4 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 16-5 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 15-5 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 16-6 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 15-6 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 16-7 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 15-7 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 17-1 | 5.96 | Mountain wall | [1,0,0,0] | 0.0166 | 16-1 | 7.17 | Mountain wall | [1,0,0,0] | 0.0084 |
| 17-2 | 6.06 | Mountain wall | [1,0,0,0] | 0.0166 | 16-2 | 7.25 | Mountain wall | [1,0,0,0] | 0.0084 |
| 17-3 | 6.06 | Mountain wall | [1,0,0,0] | 0.0166 | 16-3 | 7.25 | Mountain wall | [1,0,0,0] | 0.0084 |
| 17-4 | 5.96 | Mountain wall | [1,0,0,0] | 0.0166 | 16-4 | 7.17 | Mountain wall | [1,0,0,0] | 0.0084 |
| 18-1 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 17-1 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 18-2 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 17-2 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 18-3 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 17-3 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 19-1 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 17-4 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 19-2 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 17-5 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 19-3 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 17-6 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| 19-4 | ≥10.00 | Window wall | [1,0,0,0] | 0.0038 | 17-7 | ≥10.00 | Window wall | [1,0,0,0] | 0.0020 |
| First Floor | Second Floor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | Grade1 | Grade2 | Grade3 | Number | Grade1 | Grade2 | Number | Grade1 | Grade2 | Number | Grade1 | Grade2 |
| 1-1 | cu | cu | bu | 14-4 | au | au | 1-1 | au | au | 13-4 | au | au |
| 2-1 | cu | cu | bu | 15-1 | au | au | 2-1 | au | au | 14-1 | au | au |
| 3-1 | du | du | cu | 15-2 | au | au | 3-1 | au | au | 14-2 | au | au |
| 4-1 | du | du | cu | 15-3 | au | au | 4-1 | au | au | 14-3 | au | au |
| 5-1 | du | du | cu | 15-4 | au | au | 5-1 | au | au | 14-4 | au | au |
| 6-1 | du | du | cu | 16-1 | au | au | 6-1 | au | au | 15-1 | au | au |
| 7-1 | cu | cu | bu | 16-2 | au | au | 7-1 | au | au | 15-2 | au | au |
| 8-1 | cu | cu | bu | 16-3 | au | au | 8-1 | au | au | 15-3 | au | au |
| 9-1 | cu | cu | bu | 16-4 | au | au | 9-1 | au | au | 15-4 | au | au |
| 10-1 | cu | cu | bu | 16-5 | au | au | 10-1 | au | au | 15-5 | au | au |
| 11-1 | au | au | au | 16-6 | au | au | 11-1 | au | au | 15-6 | au | au |
| 11-2 | au | au | au | 16-7 | au | au | 11-2 | au | au | 15-7 | au | au |
| 11-3 | au | au | au | 17-1 | au | au | 11-3 | au | au | 16-1 | au | au |
| 12-1 | du | cu | bu | 17-2 | au | au | 11-4 | au | au | 16-2 | au | au |
| 12-2 | au | au | au | 17-3 | au | au | 11-5 | au | au | 16-3 | au | au |
| 12-3 | au | au | au | 17-4 | au | au | 11-6 | au | au | 16-4 | au | au |
| 12-4 | au | au | au | 18-1 | au | au | 11-7 | au | au | 17-1 | au | au |
| 13-1 | au | au | au | 18-2 | au | au | 12-1 | au | au | 17-2 | au | au |
| 13-2 | au | au | au | 18-3 | au | au | 12-2 | au | au | 17-3 | au | au |
| 13-3 | au | au | au | 19-1 | au | au | 12-3 | au | au | 17-4 | au | au |
| 14-1 | cu | cu | bu | 19-2 | au | au | 13-1 | au | au | 17-5 | au | au |
| 14-2 | au | au | au | 19-3 | au | au | 13-2 | au | au | 17-6 | au | au |
| 14-3 | au | au | au | 19-4 | au | au | 13-3 | au | au | 17-7 | au | au |
| The proportions of the different grades of components | Structural safety rating | |||||||||||
| Current method | cu-grade: 15%, du-grade: 11% | The proportion of du-grade exceeds 5%, the structure is Du-grade. | ||||||||||
| New method | cu-grade: 17%, du-grade: 9% | , based on Table 6, the structure is Du-grade. | ||||||||||
| Live load is 1.5 kN/m2 | New method | bu-grade: 17%, cu-grade: 9% | , based on Table 6, the structure is Bu-grade. | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zhang, J.; Huang, S.; Yin, B.; Wu, L. Probabilistic Model Optimization and Safety Assessment Methods for Existing Masonry Structures. Buildings 2025, 15, 3716. https://doi.org/10.3390/buildings15203716
Wang F, Zhang J, Huang S, Yin B, Wu L. Probabilistic Model Optimization and Safety Assessment Methods for Existing Masonry Structures. Buildings. 2025; 15(20):3716. https://doi.org/10.3390/buildings15203716
Chicago/Turabian StyleWang, Fenglai, Jing Zhang, Shimin Huang, Baojiang Yin, and Lele Wu. 2025. "Probabilistic Model Optimization and Safety Assessment Methods for Existing Masonry Structures" Buildings 15, no. 20: 3716. https://doi.org/10.3390/buildings15203716
APA StyleWang, F., Zhang, J., Huang, S., Yin, B., & Wu, L. (2025). Probabilistic Model Optimization and Safety Assessment Methods for Existing Masonry Structures. Buildings, 15(20), 3716. https://doi.org/10.3390/buildings15203716






