Engineering Evaluation of the Buffeting Response of a Variable-Depth Continuous Rigid-Frame Bridge: Time-Domain Analysis with Three-Component Aerodynamic Coefficients and Comparison Against Six-Component Wind Tunnel Tests
Abstract
1. Introduction
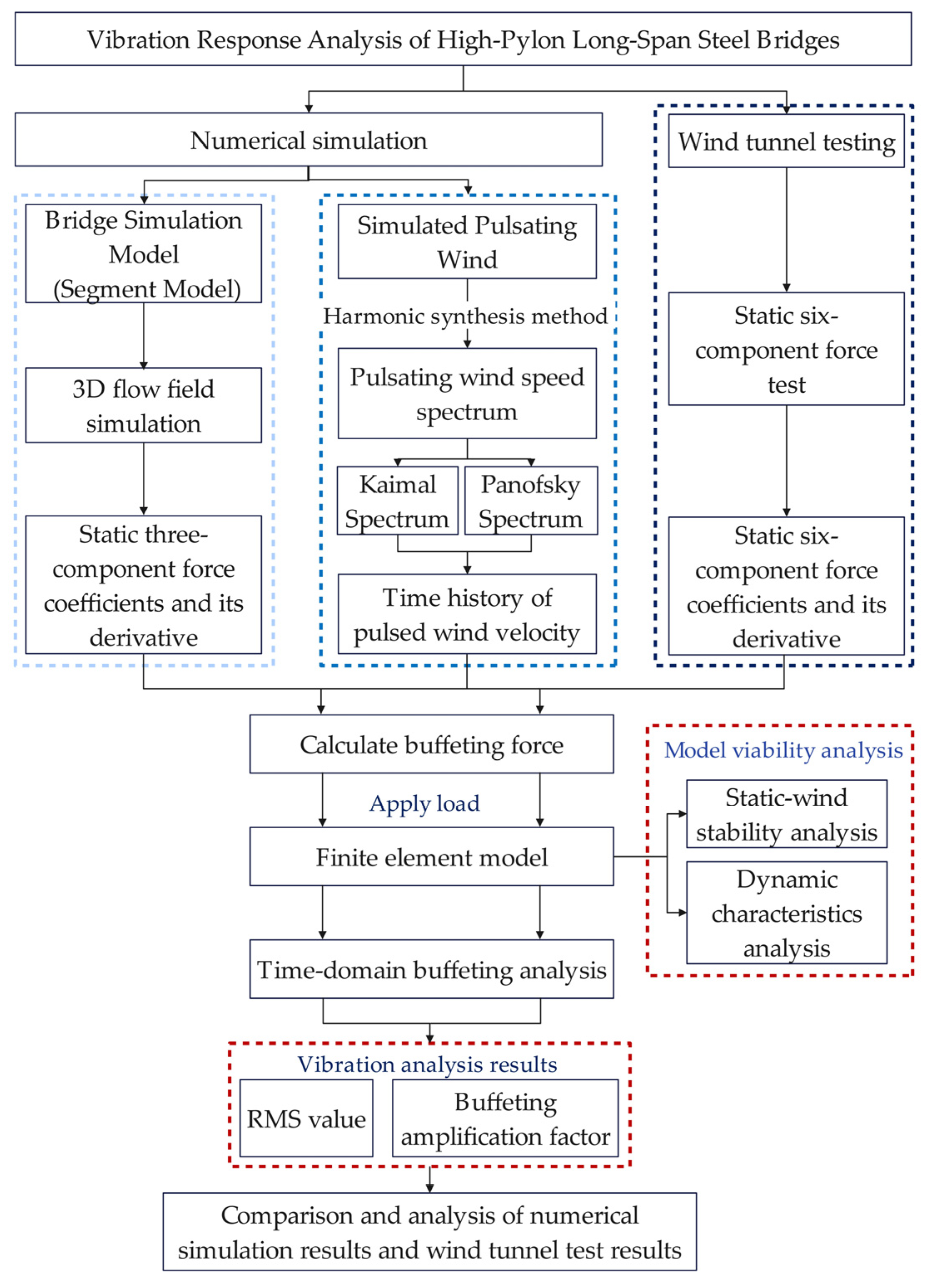
2. Case Study and Numerical Framework
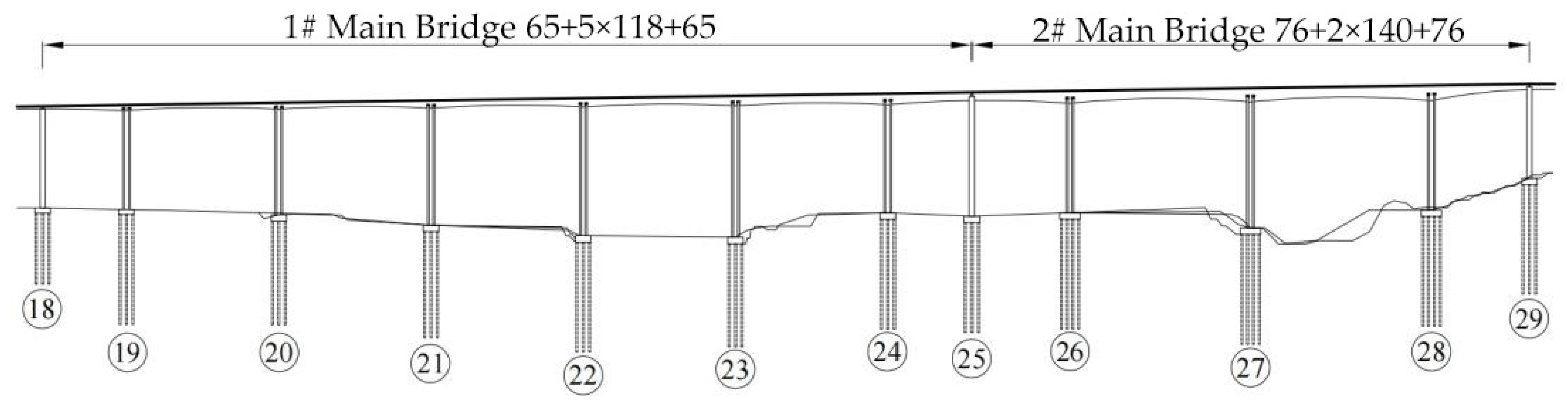
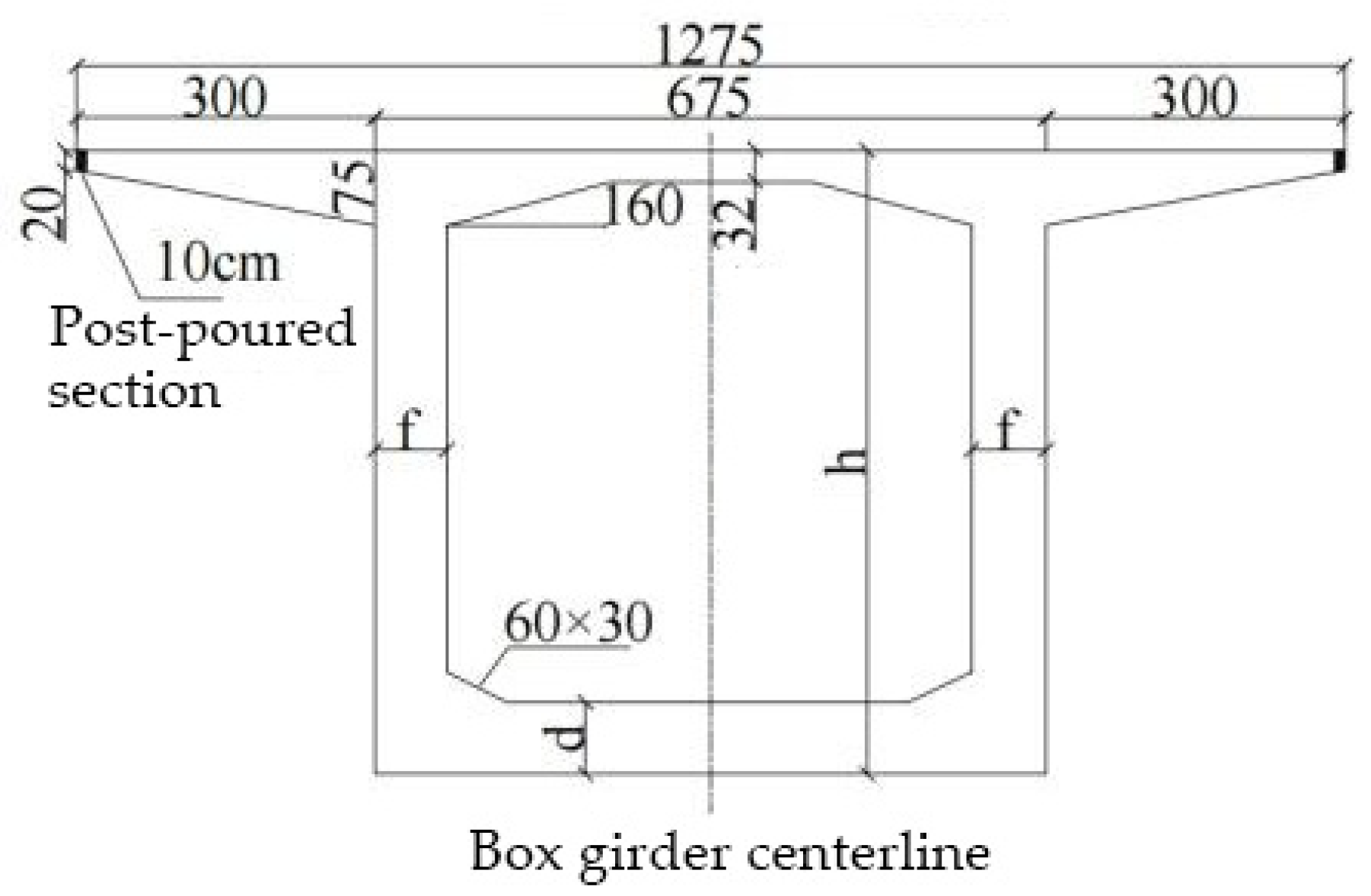
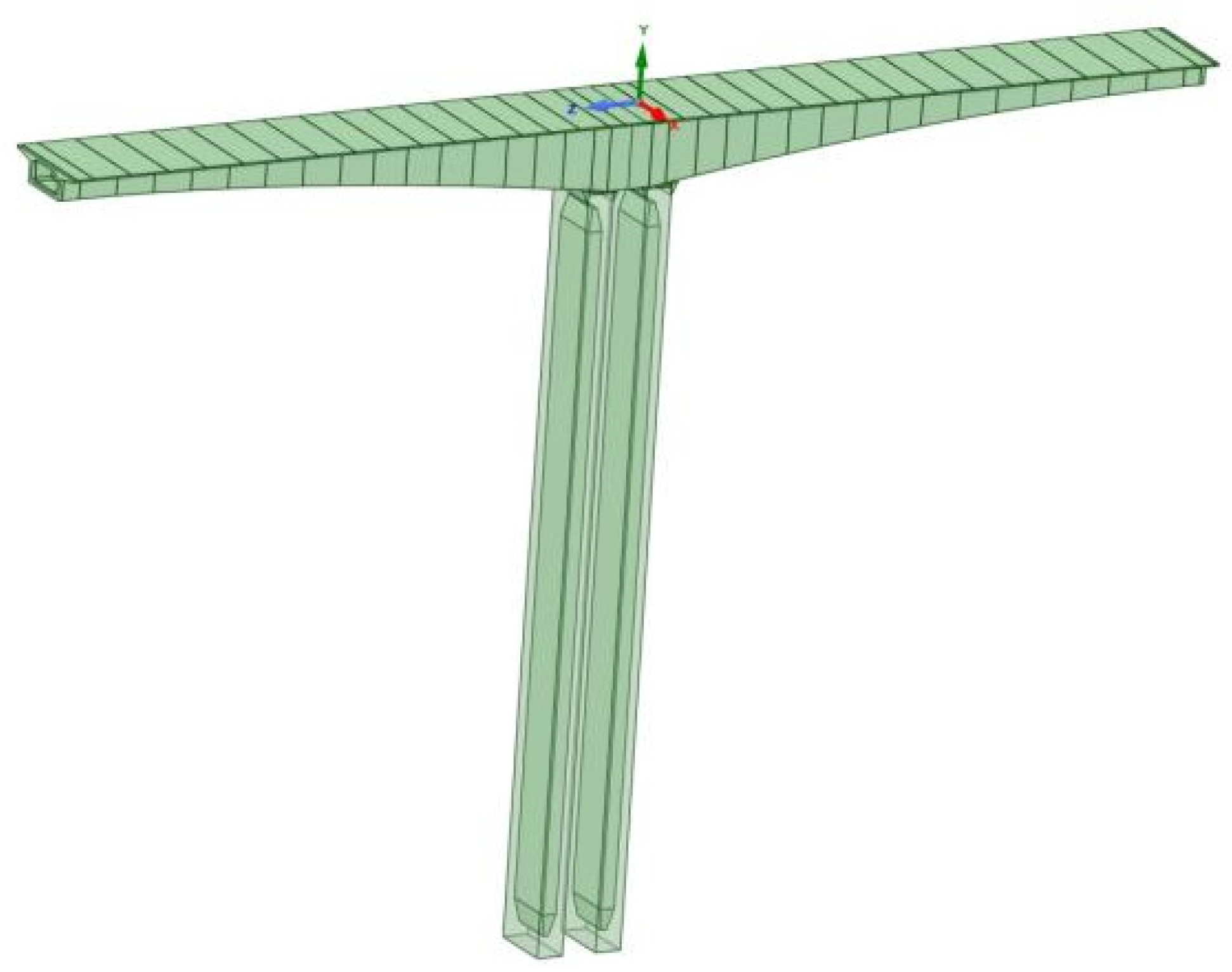
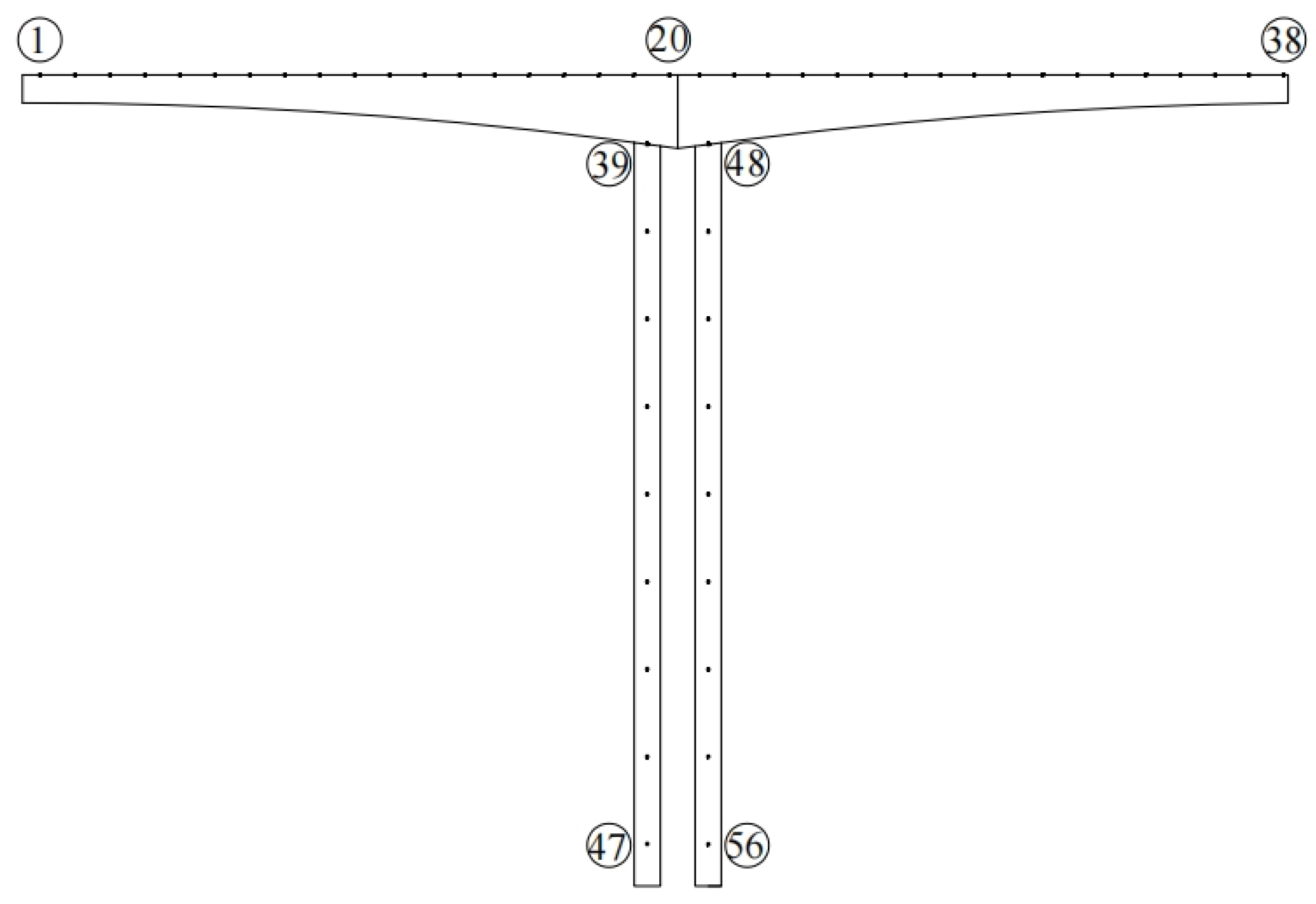
2.1. Bridge Description and 3D Simulation Model
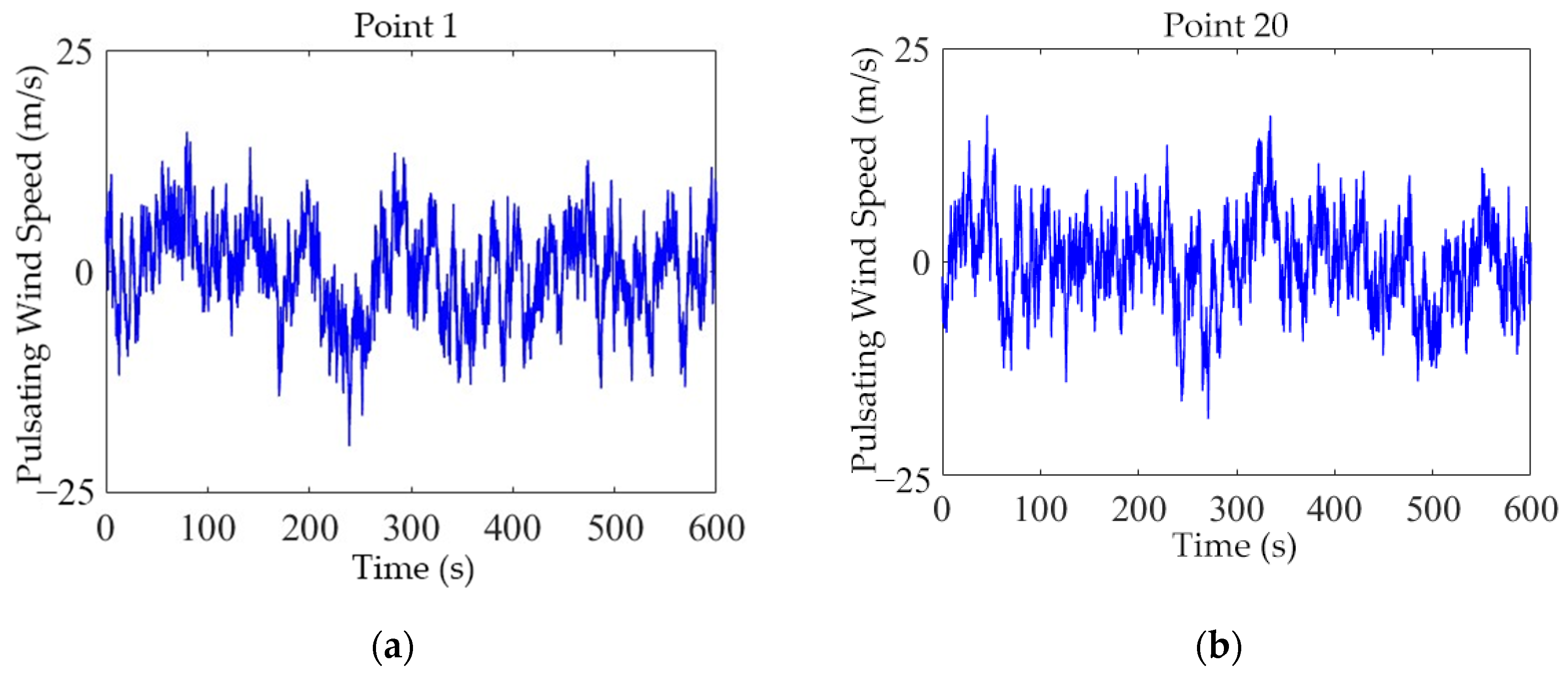
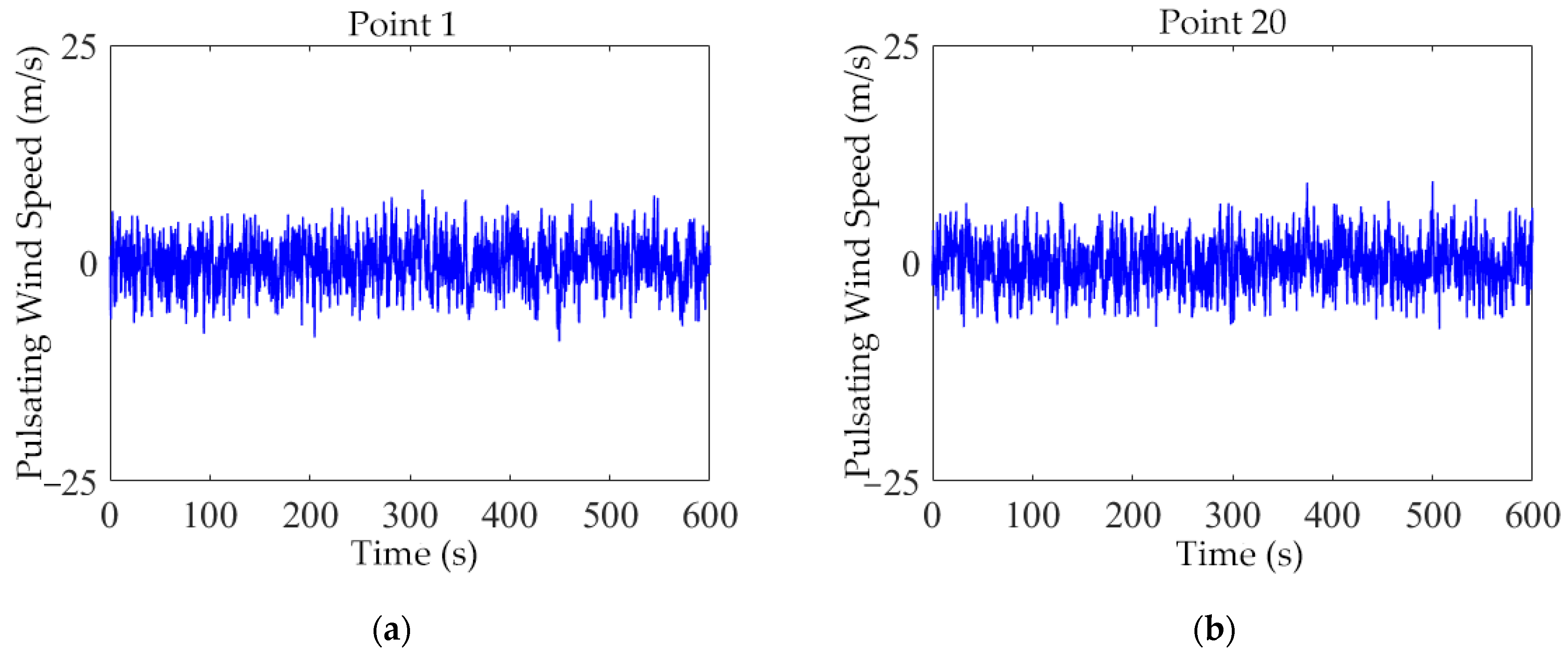
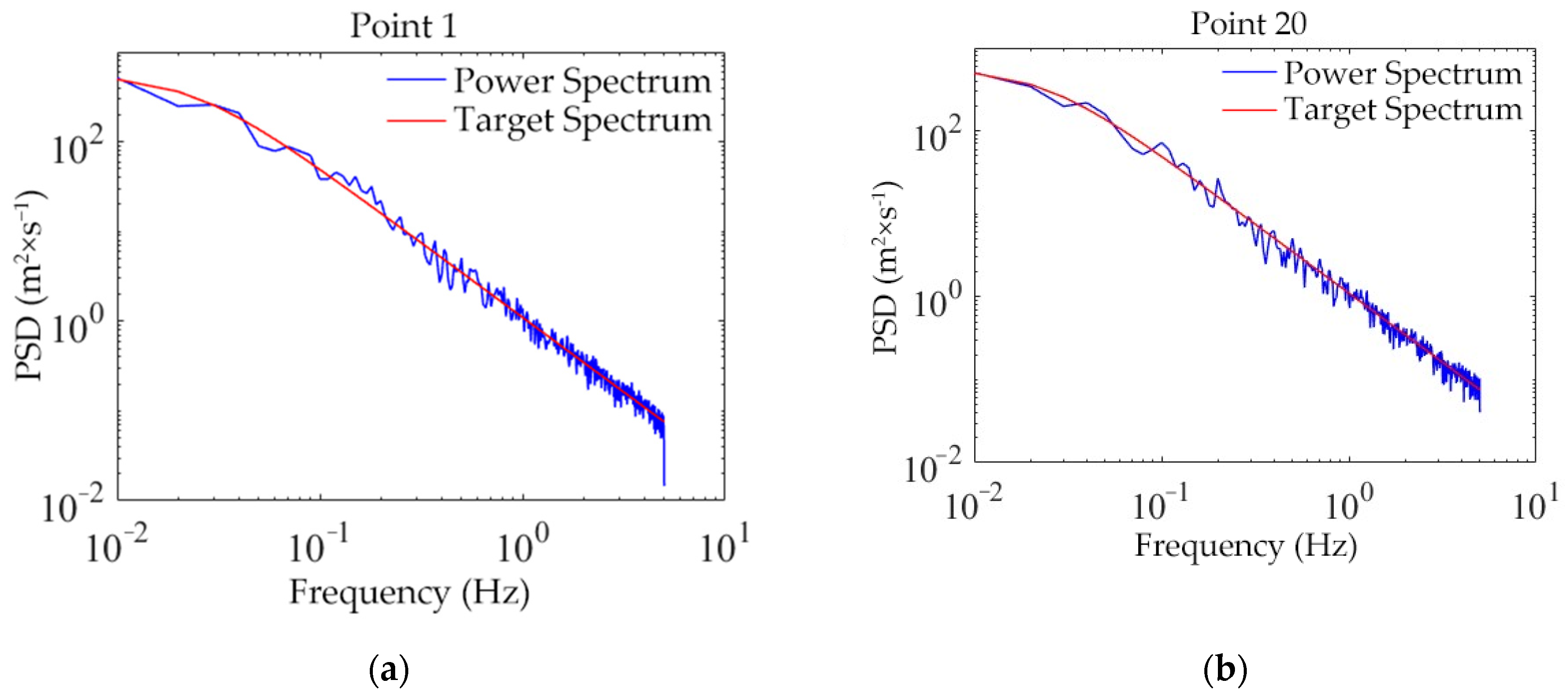
2.2. Simulation of the Fluctuating Wind Field
- (1)
- Target Spectra and Parameters
- (2)
- Multi-Point Harmonic Superposition
- (3)
- Consistency Check
2.3. Acquisition and Processing of Three-Component Coefficients
- (1)
- Computational Domain and Meshing
- (2)
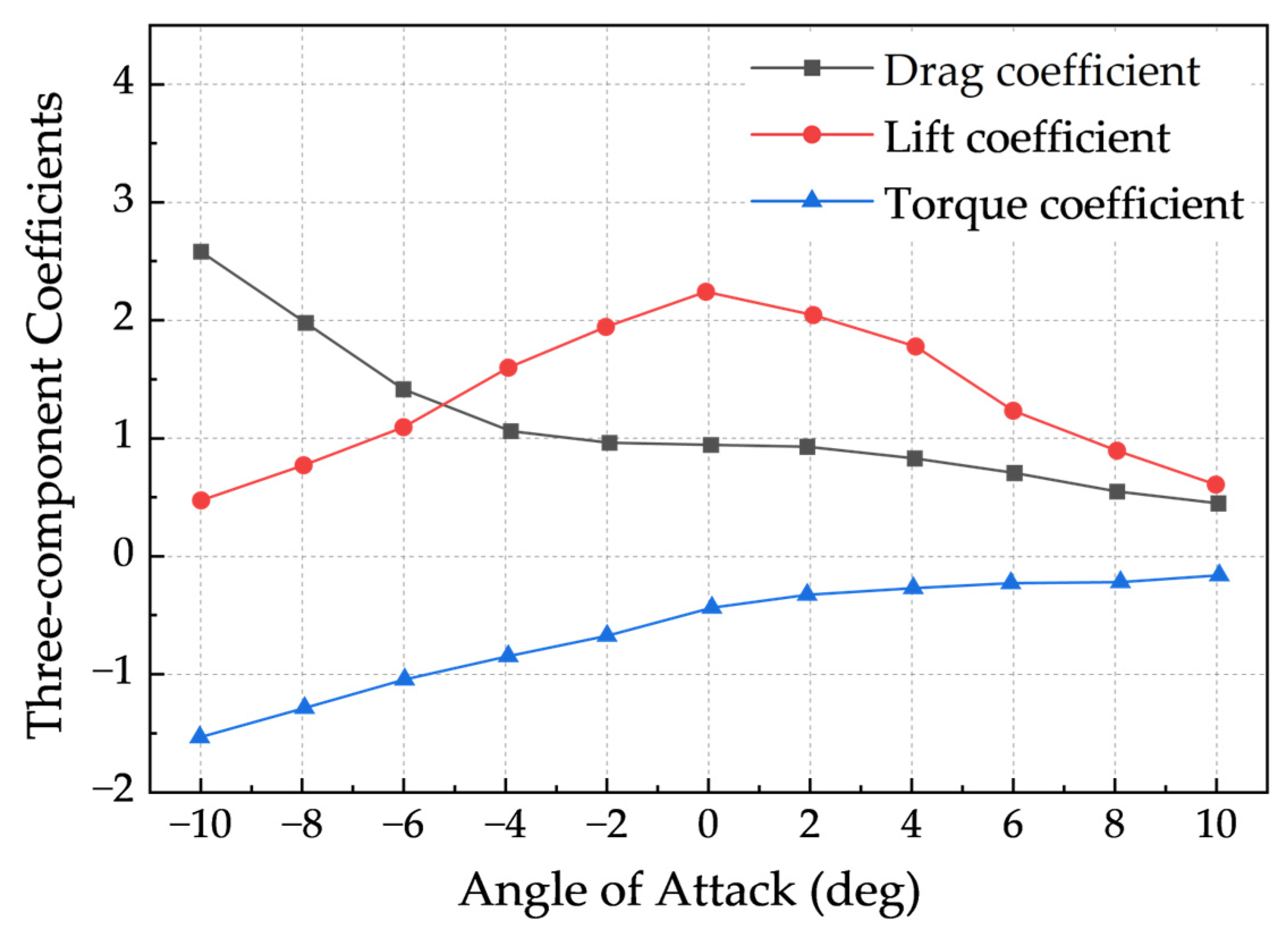
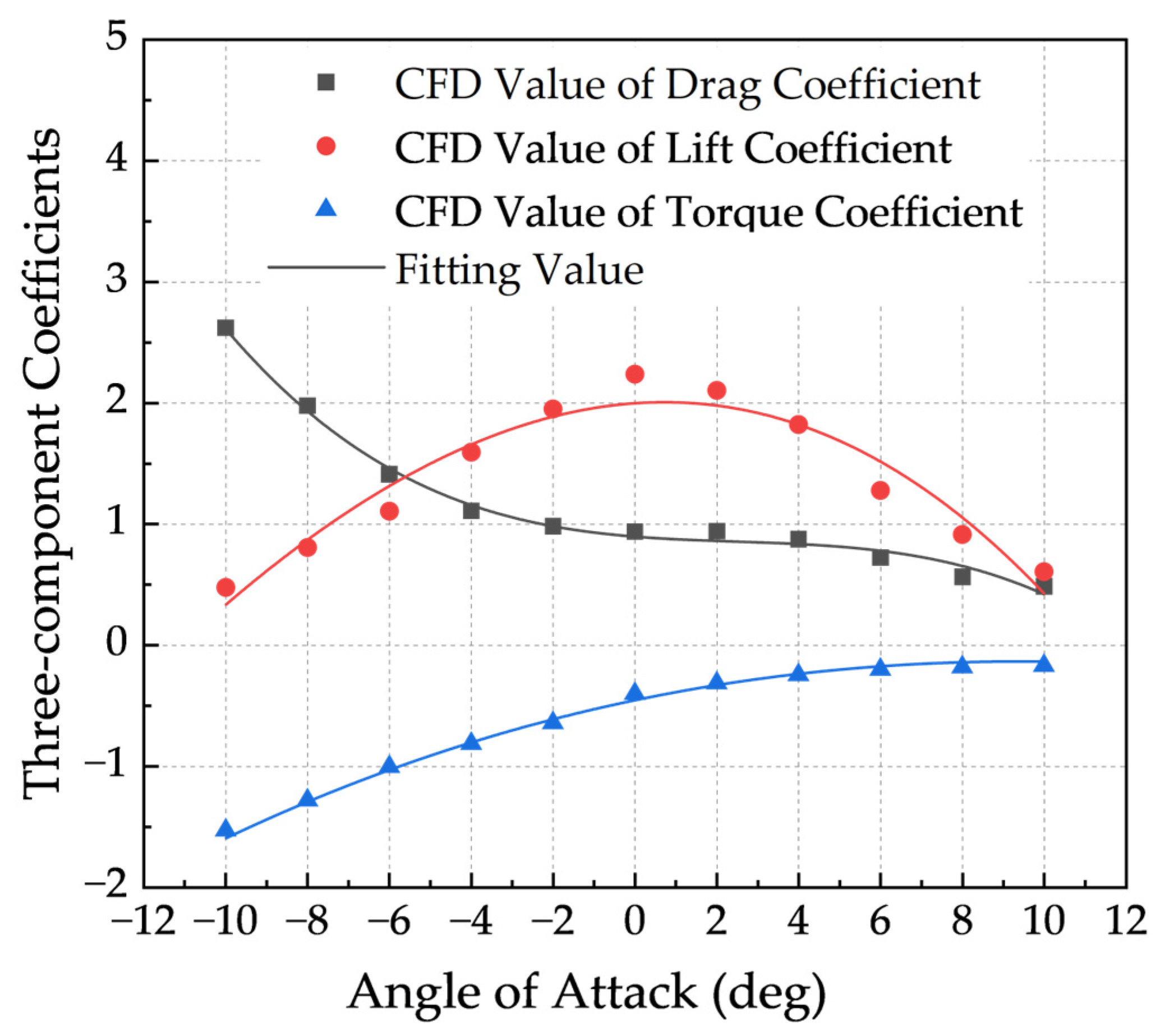
- Three-Component Coefficients for the Main Girder (Construction Stage)
2.4. Time-Domain Buffeting Analysis
2.4.1. Finite-Element Model Setup
2.4.2. Aerostatic (Static Wind) Stability Analysis
- (1)
- Calculation of Aerostatic (Static Wind) Loads
- (2)
- Aerostatic Stability Analysis
- (1)
- Perform a nonlinear solution under self-weight (stepi−1 = step0).
- (2)
- Extract the torsional angle vector of the main girder {θ}i−1, and compute the corresponding three-component coefficients; at this stage the effective angle of attack equals the initial value α0.
- (3)
- Prescribe an initial wind speed U0 and an increment ΔU; set the current wind speed Ui = U0(stepi).
- (4)
- At Ui, solve the geometric and material nonlinearity using the Newton–Raphson method to obtain a converged solution (inner iteration).
- (5)
- Extract the updated torsional angle vector of the (stiffened) main girder {θ}i, and recompute the three-component coefficients for this deformed state.
- (6)
- Check whether the Euclidean norm of the change in three-component coefficients is below the tolerance:where Na is the total number of nodes;Ck denotes the drag, lift, or torsional moment coefficient;i is the current load step index;epsk is the tolerance for the drag, lift, and torsional moment coefficients, taken as 5 × 10−7.
- (7)
- If the norm exceeds the tolerance, repeat steps (4)–(6) (outer iteration). If the number of iterations exceeds the preset limit, the current wind speed level is deemed difficult to converge; halve the wind speed increment and return to step (4) to recompute. If the increment falls below the preset minimum, terminate the analysis.
- (8)
- If the norm is within the tolerance, the solution at the current wind speed is converged; output the results and increase the wind speed by the specified increment to proceed to the next level.
- (9)
- Plot the deformation–wind speed curves and determine the critical wind speed for aerostatic instability.
2.4.3. Dynamic Characteristics
2.4.4. Buffeting Response Analysis
2.5. Six-Component Wind Tunnel Tests (Benchmark)
- (1)
- Similarity Criteria and Inflow Conditions
- (2)
- Test Model and Measurement System
- (3)
- Test Conditions and Procedure
3. Results and Discussion
3.1. Three-Dimensional Numerical Simulation: Results and Analysis
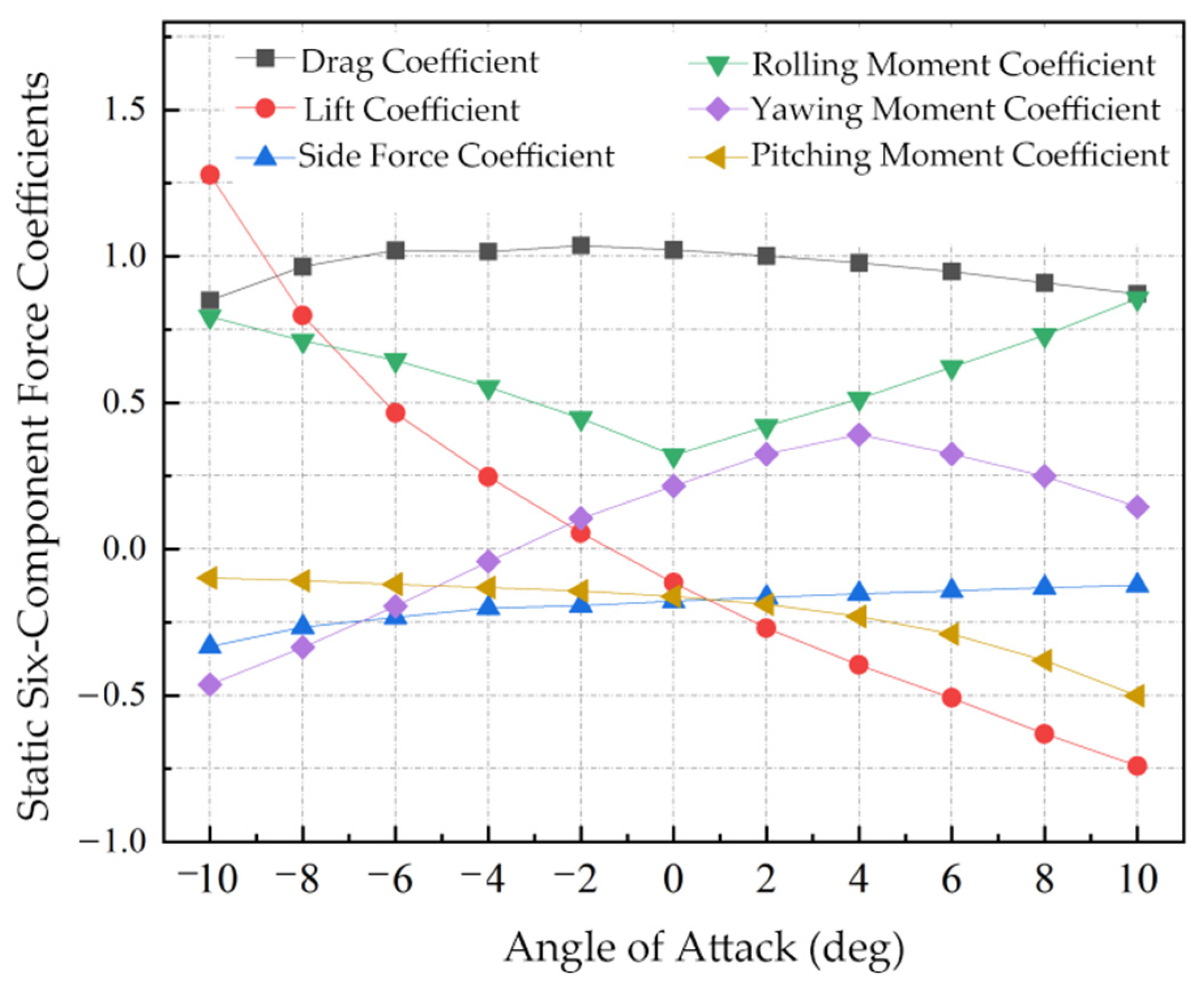
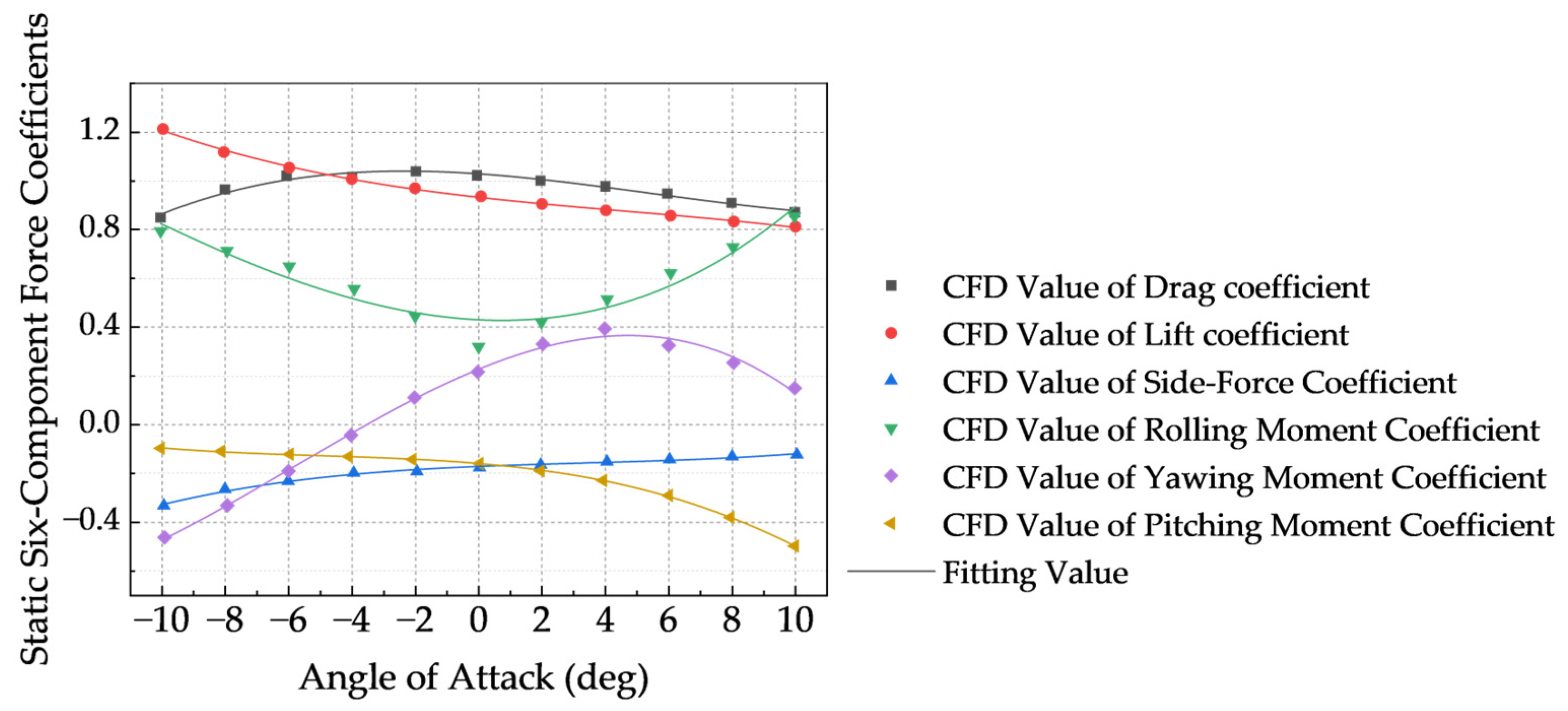
3.1.1. Static Three-Component Coefficients
3.1.2. Buffeting Response
- (1)
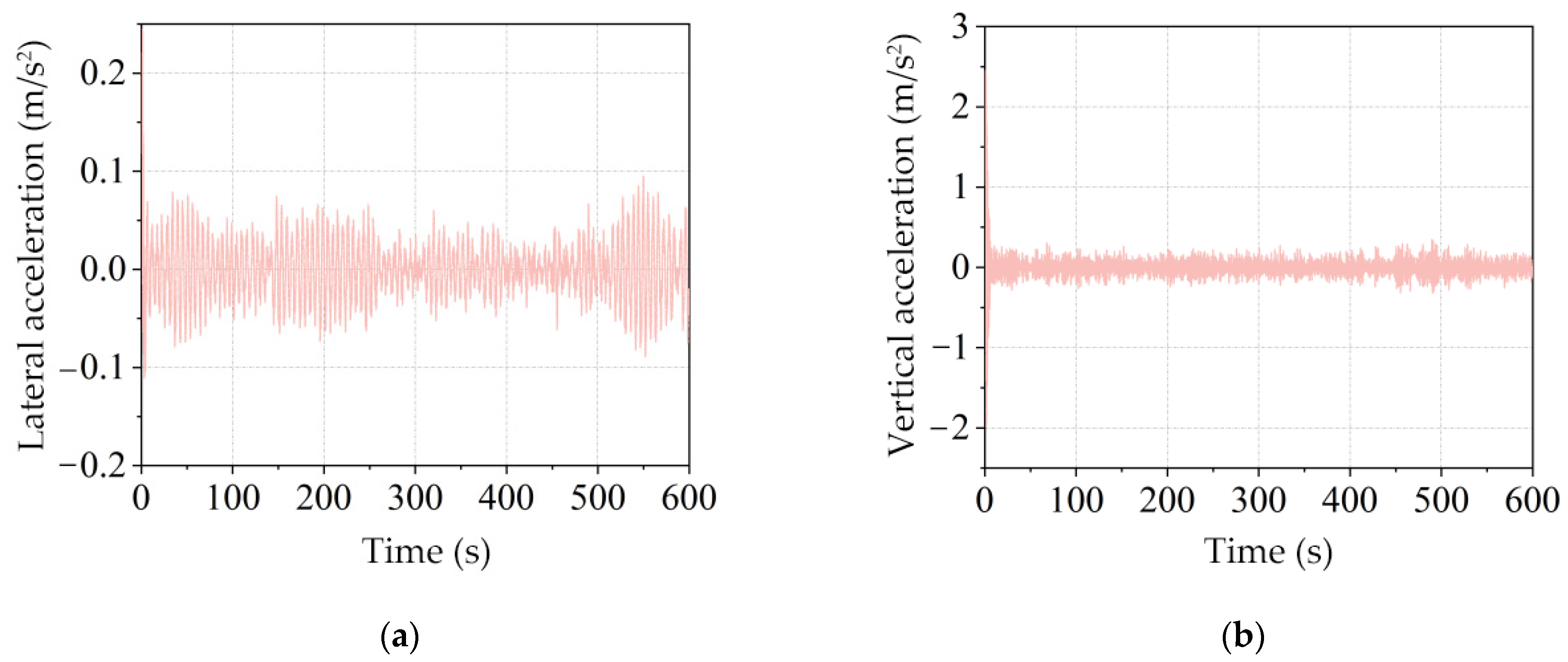
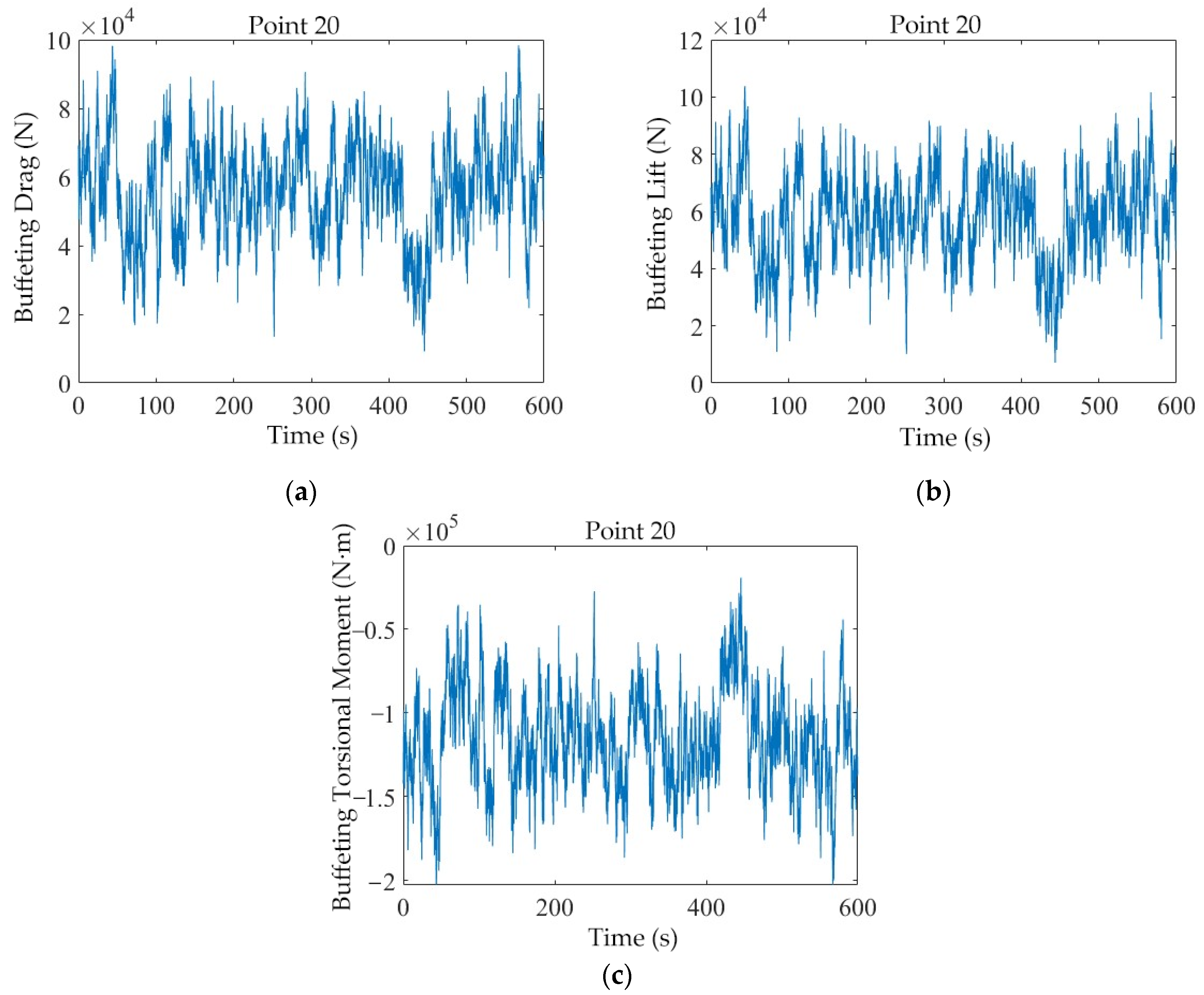
- Buffeting Force Time Histories
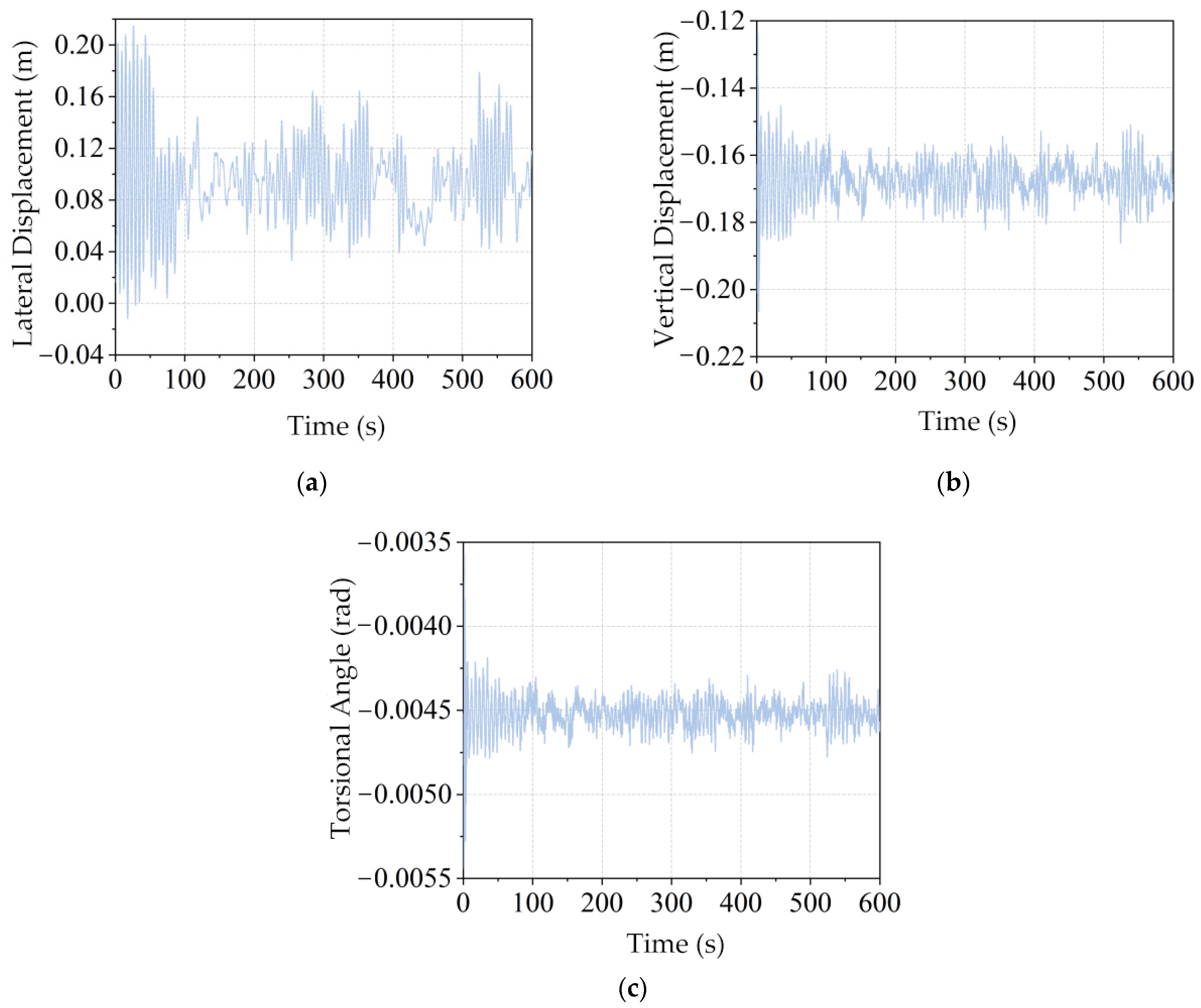
- (2)
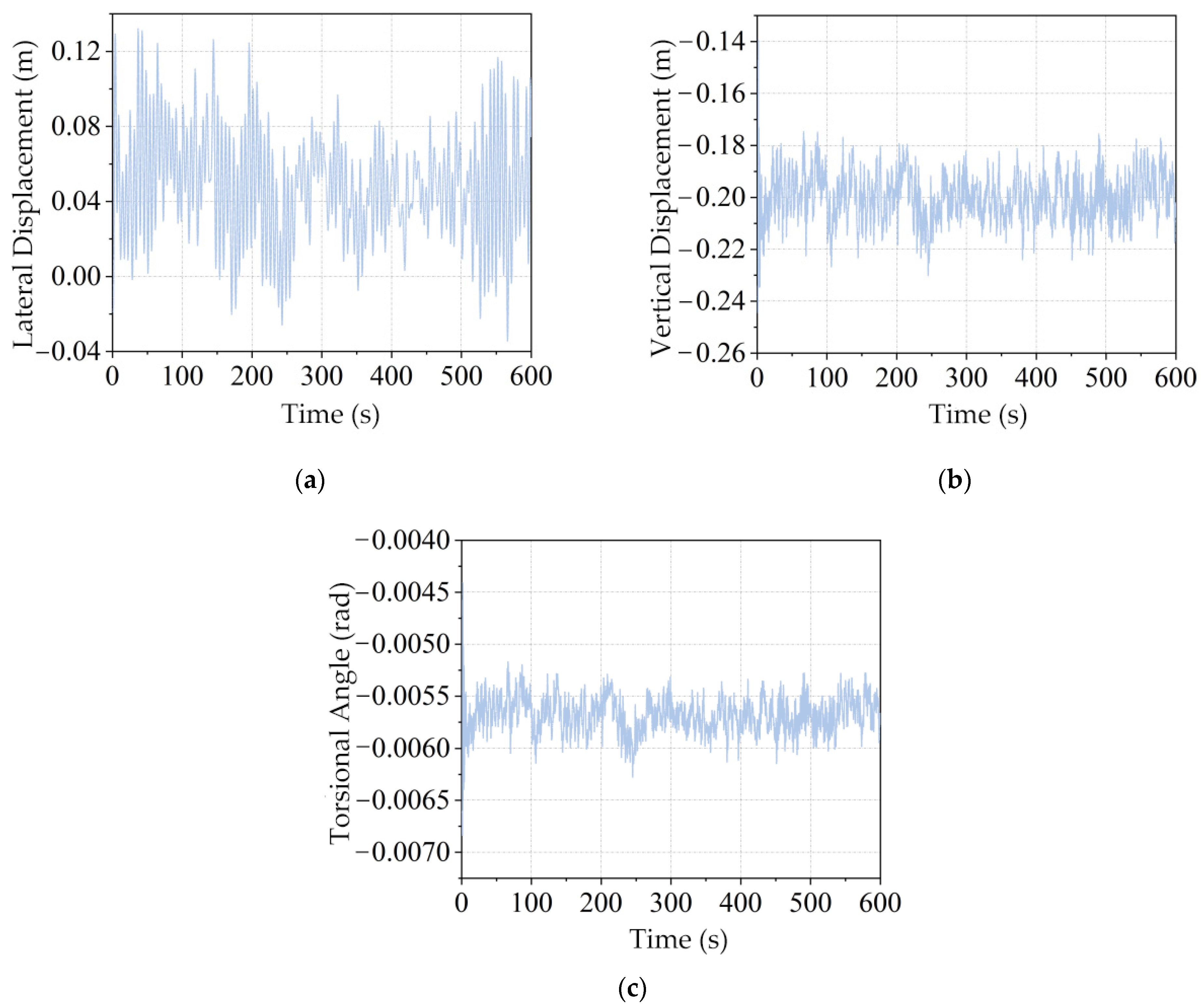
- Time-Domain Buffeting Analysis
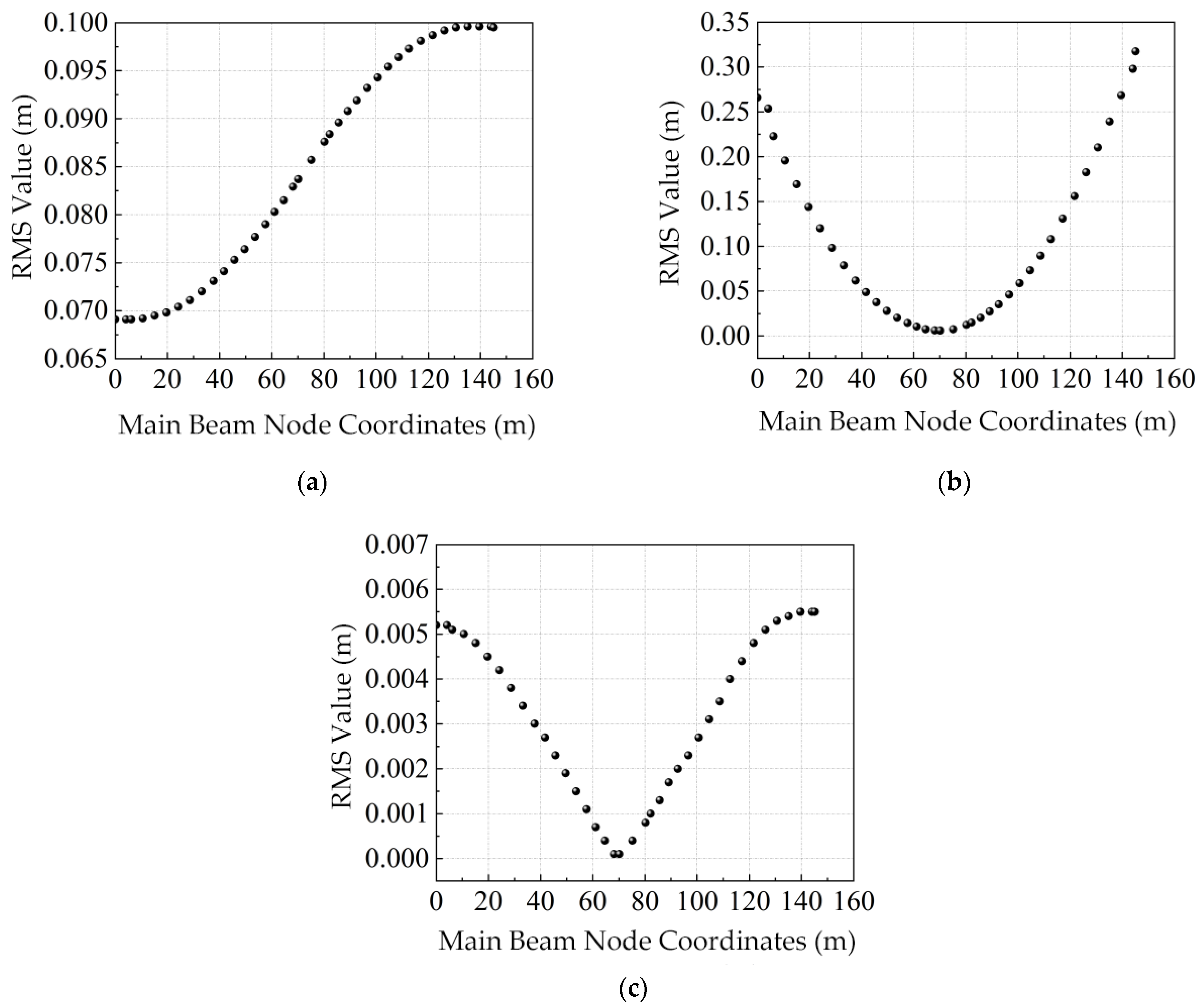
3.2. Wind Tunnel Results and Analysis
3.2.1. Static Six-Component Coefficients
3.2.2. Buffeting Response Based on Six-Component Data
- (1)
- Buffeting Force Time Histories
- (2)
- Time-Domain Buffeting Analysis
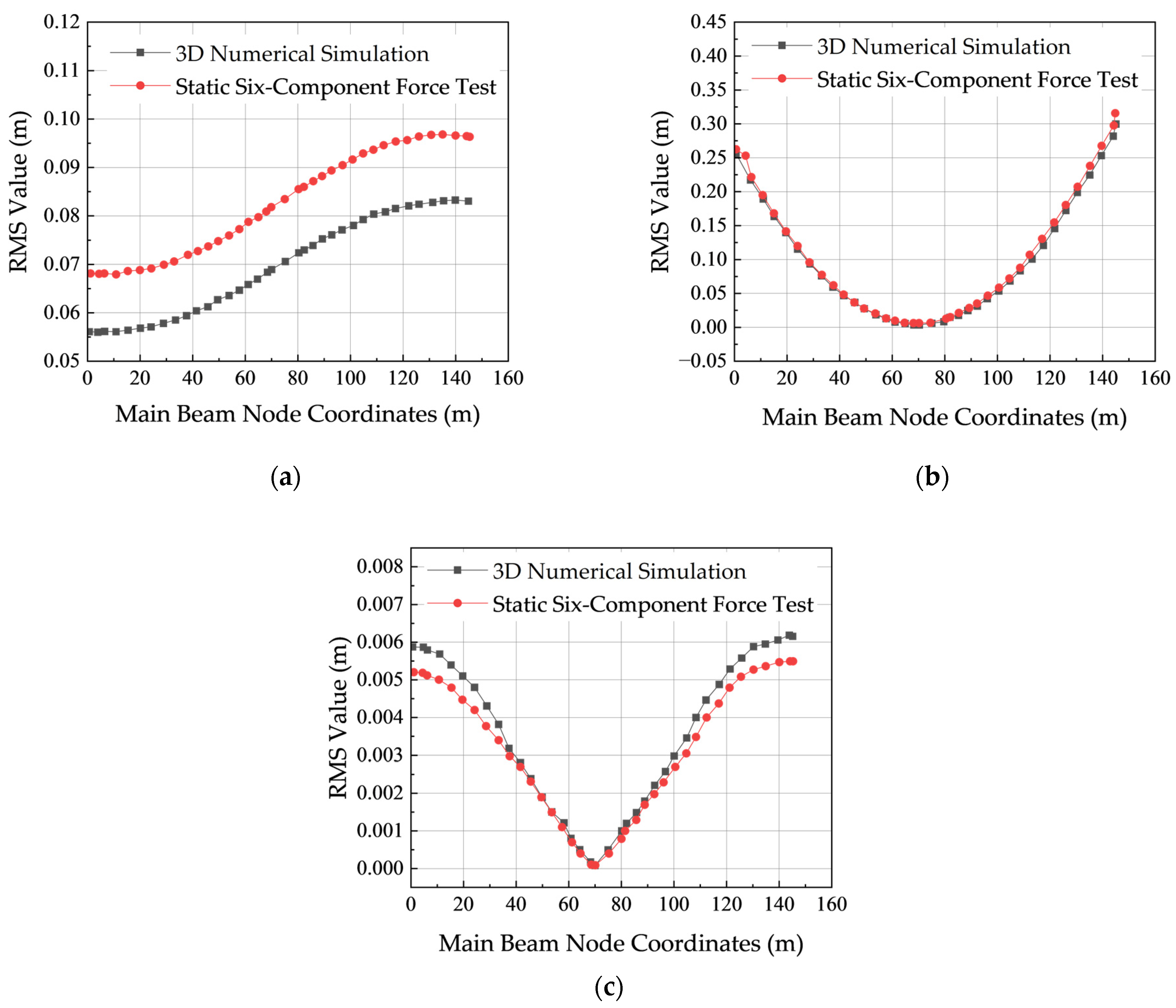
3.3. Numerical–Experimental Comparison
- (1)
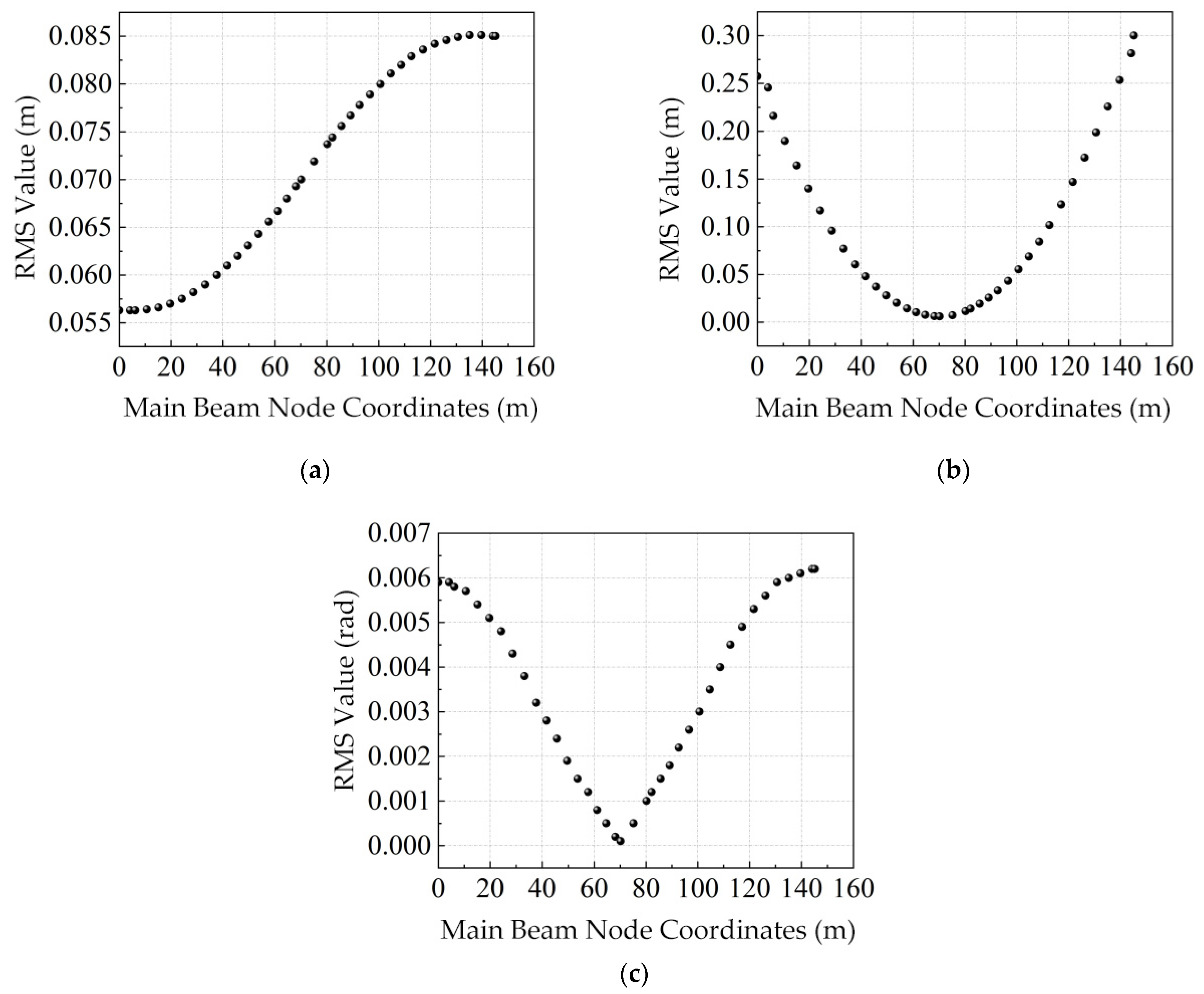
- RMS distribution comparison
- (2)
- Comparison of buffeting amplification factors
4. Conclusions
- (1)
- Applicability and limitations.
- (2)
- Engineering notes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z. Wind-Induced Vibration Stability and Control of Engineering Structures; Science Press: Beijing, China, 2013. [Google Scholar]
- Wang, Q.; Zhang, W.; Chen, R. Review of research methods on wind-induced vibration of mountain bridges. Highway 2024, 69, 149–153. [Google Scholar]
- Diana, G.; Fiammenghi, G.; Belloli, M.; Rocchi, D. Wind tunnel tests and numerical approach for long span bridges: The Messina Bridge. J. Wind Eng. Ind. Aerodyn. 2013, 122, 38–49. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, J.; Li, S.; Liu, Z.; Wu, Y. Combining active and passive wind tunnel tests to determine the aerodynamic admittances of a bridge girder. J. Wind Eng. Ind. Aerodyn. 2022, 231, 105180. [Google Scholar] [CrossRef]
- Diana, G.; Omarini, S. A non-linear method to compute the buffeting response of a bridge—Validation of the model through wind tunnel tests. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104163. [Google Scholar] [CrossRef]
- Yi, S.; Jin, D.; Li, S.; Jian, B.; Liu, J. Buffeting response prediction of long-span bridges based on different wind tunnel test techniques. Appl. Sci. 2022, 12, 3171. [Google Scholar] [CrossRef]
- Taylor, I.; Vezza, M. A numerical investigation into the aerodynamic characteristics and aeroelastic stability of a footbridge. J. Fluids Struct. 2008, 25, 155–177. [Google Scholar] [CrossRef]
- Hallak, H.P.; Pfeil, S.M.; Oliveira, D.R.S.; Battista, R.C.; de Sampaio, P.A.; Bezerra, C.M. Aerodynamic behavior analysis of Rio–Niterói Bridge by means of computational fluid dynamics. Eng. Struct. 2013, 56, 935–944. [Google Scholar] [CrossRef]
- Liu, L. Application of CFD in Aerodynamic Control Measures for Long-Span Bridges. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2007. [Google Scholar]
- Gao, Y.; Wang, H.; Xu, Z.; Tao, T.; Wang, F.; Xie, Y. Numerical simulation of aerostatic three-component coefficients of box-girder sections for long-span high-speed railway continuous bridges. J. Nanjing Univ. Technol. (Nat. Sci. Ed.) 2020, 42, 358–365. [Google Scholar]
- Davenport, A.G.; Agnew, R.; Harris, R.I. The application of statistical concepts to the wind loading of structures. Proc. Inst. Civ. Eng. 1961, 19, 449–472. [Google Scholar] [CrossRef]
- Jain, A.; Jones, N.P.; Scanlan, R.H. Coupled flutter and buffeting analysis of long-span bridges. J. Struct. Eng. 1996, 122, 716–725. [Google Scholar] [CrossRef]
- Caracoglia, L. Influence of uncertainty in selected aerodynamic and structural parameters on the buffeting response of long-span bridges. J. Wind Eng. Ind. Aerodyn. 2007, 96, 327–344. [Google Scholar] [CrossRef]
- Zhao, L.; Ge, Y. Sensitivity of buffeting response considering multi-component aerodynamic admittance. J. Vib. Shock 2010, 29, 84–88. [Google Scholar]
- Yang, Y.; Liao, H.; Li, Y. A practical time-domain method for buffeting analysis of cable-stayed bridges based on ANSYS. Acta Aerodyn. Sin. 2004, 22, 457–460. [Google Scholar]
- Zeng, X.; Han, D. Time-domain analysis of wind-induced buffeting of long-span bridges and its implementation in ANSYS. Bridge Constr. 2004, 1, 9–12. [Google Scholar]
- Calamelli, F.; Rossi, R.; Argentini, T.; Rocchi, D.; Diana, G. A nonlinear approach for the simulation of the buffeting response of long-span bridges under non-synoptic storm winds. J. Wind Eng. Ind. Aerodyn. 2024, 247, 105681. [Google Scholar] [CrossRef]
- Fenerci, A.; Øiseth, O. Measured buffeting response of a long-span suspension bridge compared with numerical predictions based on design wind spectra. J. Struct. Eng. 2017, 143, 04017131. [Google Scholar] [CrossRef]
- JTG/T 3360-01-2018; Research Institute of Highway, Ministry of Transport (Tongji University). Wind-Resistant Design Code for Highway Bridges. People’s Transportation Press: Beijing, China, 2019.
- Xu, Y.L.; Sun, D.K.; Ko, J.M.; Lin, J.H. Buffeting analysis of long span bridges: A new algorithm. Comput. Struct. 1998, 68, 303–313. [Google Scholar] [CrossRef]
- Morgenthal, K. Modelling Techniques for Buffeting Analysis of Long-span Bridges. In Proceedings of the IABSE Conference—Bridges and Structures Sustainability—Seeking Intelligent Solutions, Guangzhou, China, 8–11 May 2016; pp. 221–228. [Google Scholar]
- Shen, Z.; Li, J.; Gao, G.; Xue, X.F. Buffeting response of a composite cable-stayed bridge in a trumpet-shaped mountain pass. Adv. Struct. Eng. 2019, 23, 510–522. [Google Scholar] [CrossRef]
- da Costa, B.M.; Wang, J.; Jakobsen, J.B.; Øiseth, O.A.; þór Snæbjörnsson, J. Bridge buffeting by skew winds: A revised theory. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104806. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, Q.; Ding, Q.; Xu, Z. Identification and application of six-component aerodynamic admittance functions of a closed-box bridge deck. J. Wind Eng. Ind. Aerodyn. 2018, 172, 268–279. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, Y.; Geng, W.; Xu, X.; Lai, Y. A frequency-dependent uniform discretization scheme for simulating fluctuating wind field based on a frequency–wavenumber spectrum. J. Wind Eng. Ind. Aerodyn. 2024, 244, 105628. [Google Scholar] [CrossRef]
- Bekele, S.; Hangan, H. A comparative investigation of the TTU pressure envelope: Numerical versus laboratory and full-scale results. Wind Struct. 2002, 5, 337–346. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, Q. Study on three-component coefficients of a double-box composite-girder cable-stayed bridge. Eng. Constr. 2024, 38, 762–765. [Google Scholar]
- Gao, H.; Wang, F.; Guan, Q.; Hou, H.; Li, J. Research on the flutter stability of bridge sections based on an empirical formula of an aerostatic three-component coefficient. Buildings 2022, 12, 1212. [Google Scholar] [CrossRef]
- Wu, X. Numerical Study on Three-Component Coefficients of the Main Girder of High-Pier Long-Span Continuous Rigid-Frame Bridges. Master’s Thesis, Central South University, Changsha, China, 2010. [Google Scholar]
- Zhang, W.; Ge, Y. An iterative optimization method for nonlinear aerostatic stability of long-span bridges. In Proceedings of the 14th National Conference on Structural Wind Engineering, Nanjing, China, 27–30 August 2009. [Google Scholar]
- Guang, Z. Nonlinear Aerostatic Stability Analysis of Long-Span Suspension Bridges. Master’s Thesis, Chang’an University, Xi’an, China, 2022. [Google Scholar]
- Wang, L.; Shi, F.; Wang, Z.; Liang, S. Blockage effects in wind tunnel tests for tall buildings with surrounding buildings. Appl. Sci. 2022, 12, 7087. [Google Scholar] [CrossRef]
- Wei, G. Study on Six-Component Force Coefficients in Bridge Wind Tunnel Tests. Master’s Thesis, Chang’an University, Xi’an, China, 2009. [Google Scholar]
- GB 50009-2012; Ministry of Housing and Urban–Rural Development of the PRC. Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- Xie, W. Analysis of Wind-Induced Buffeting Response of High-Pier Long-Span Continuous Rigid-Frame Bridges in Mountainous Areas. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2019. [Google Scholar]


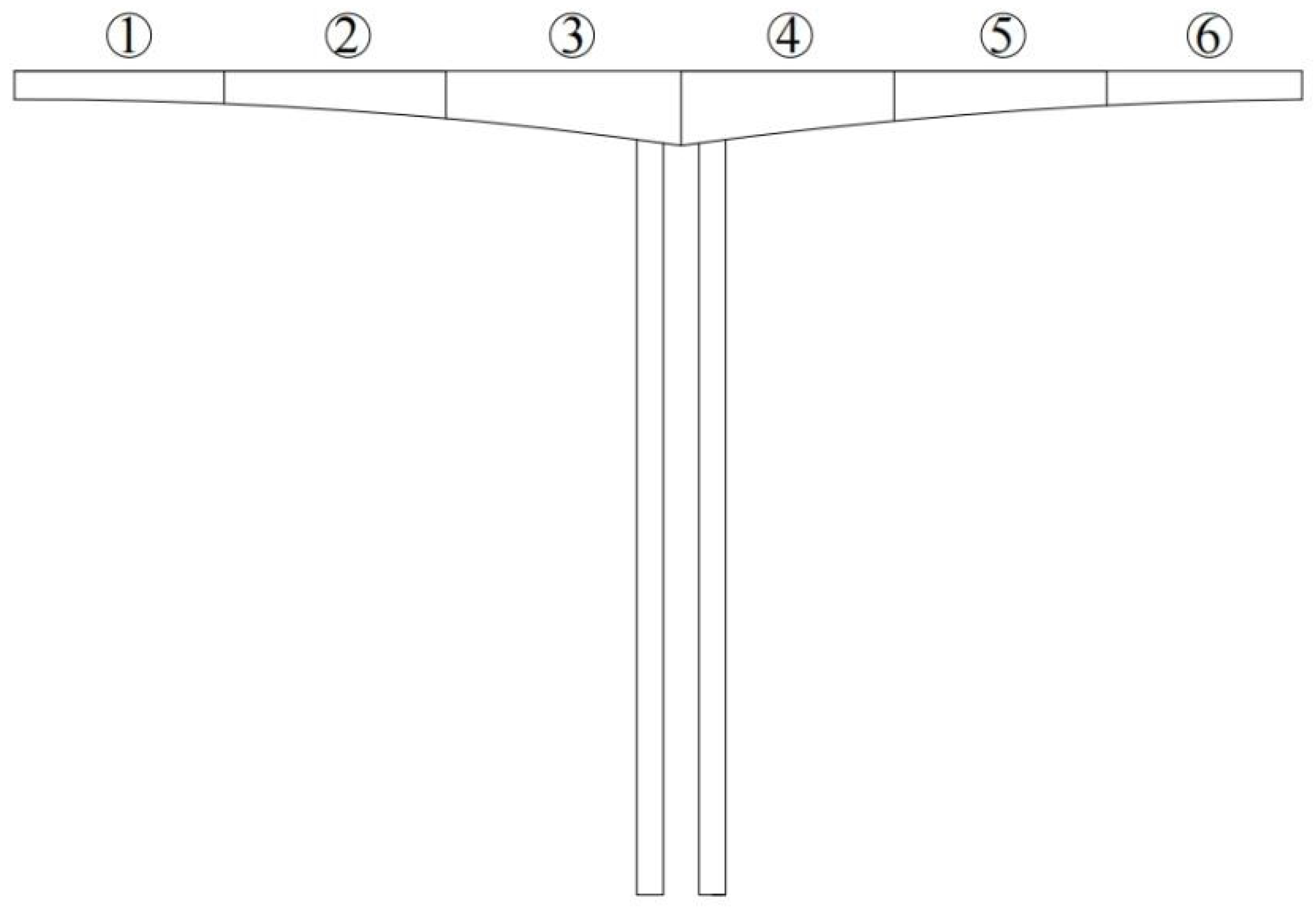

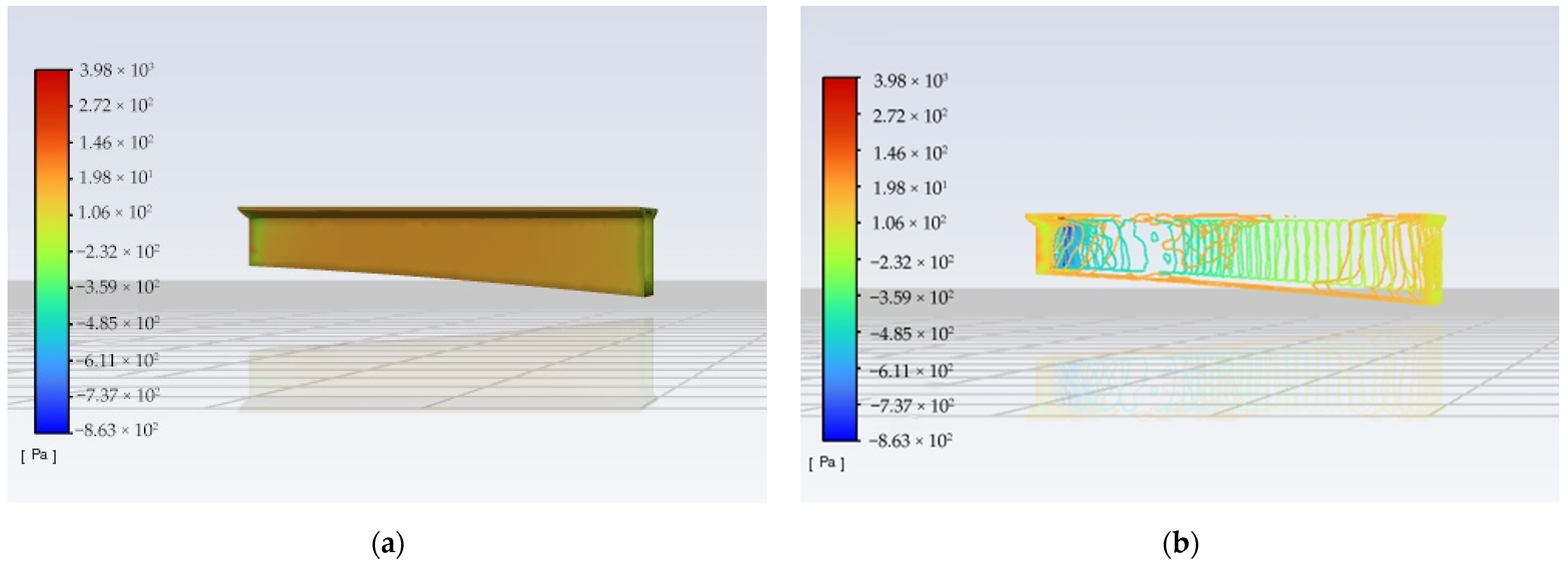
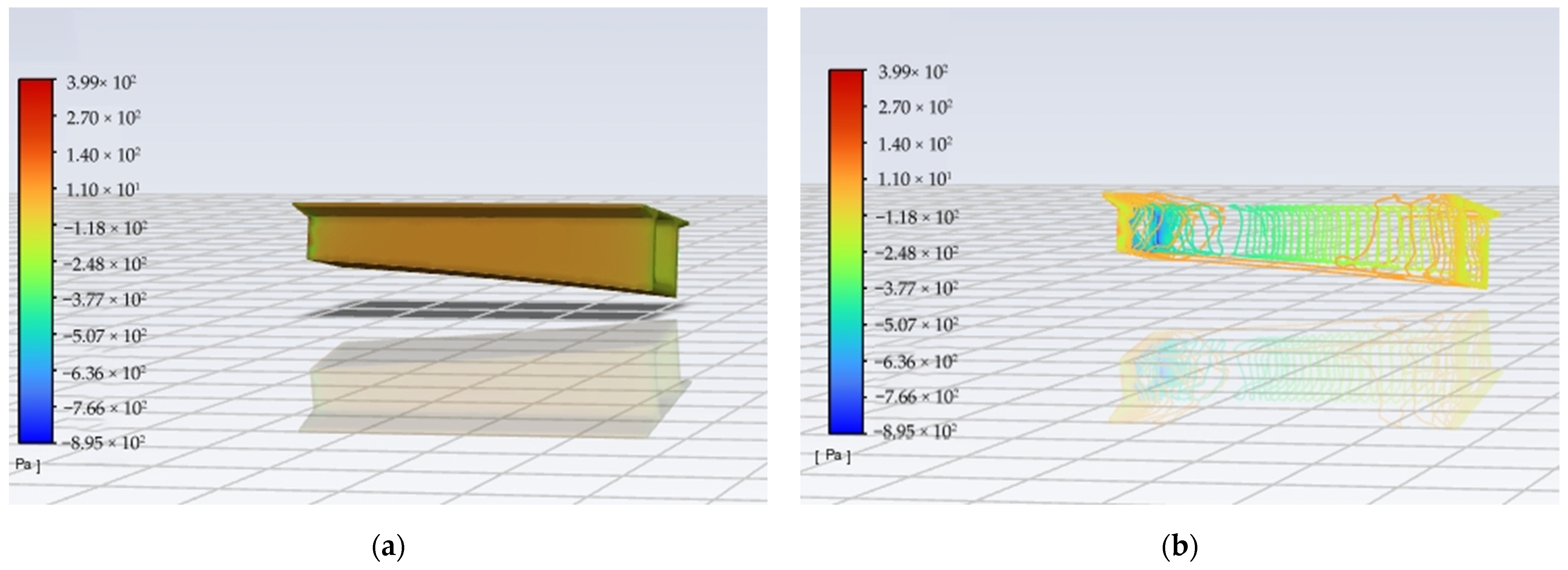


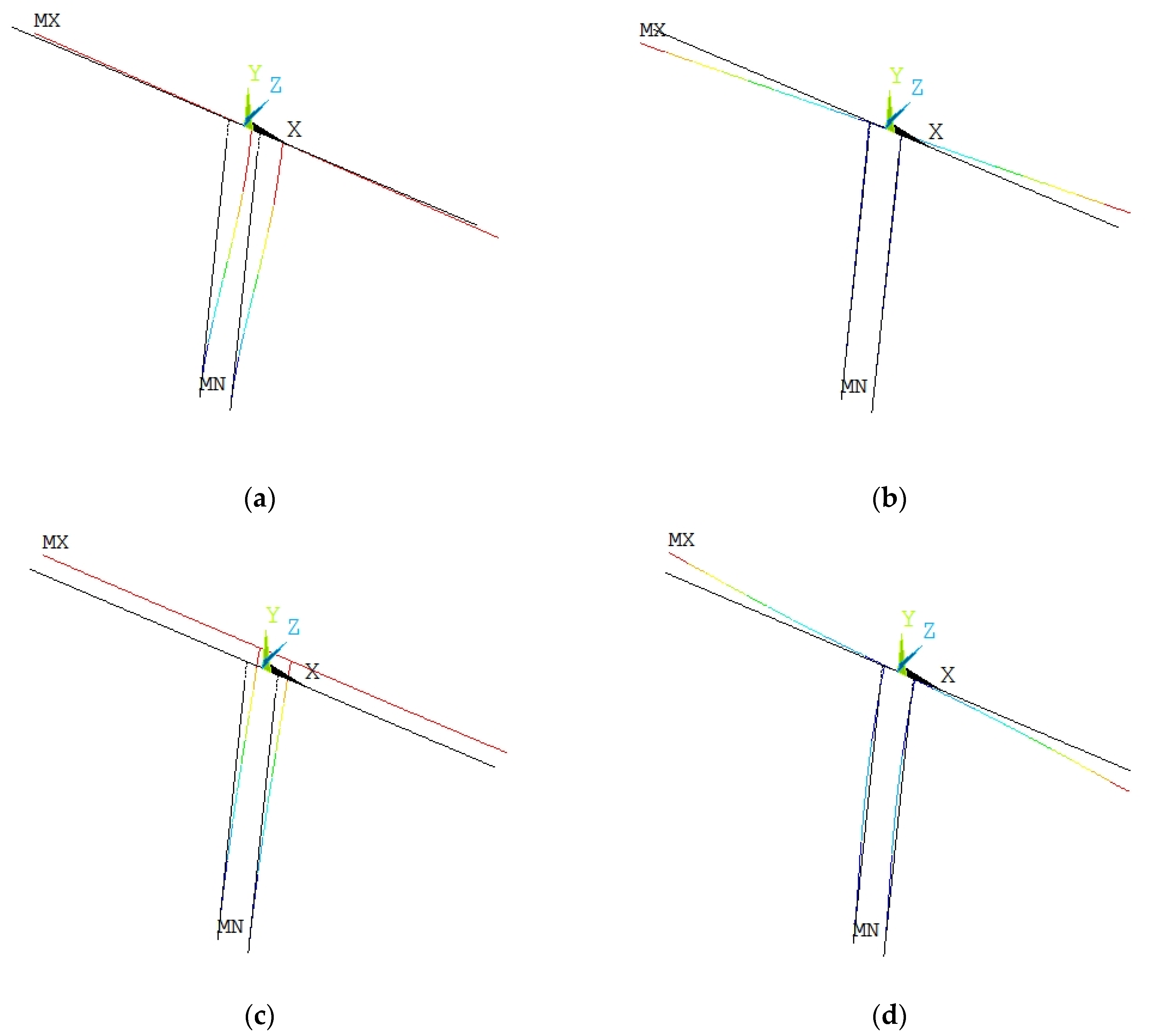







| Parameter | Value |
|---|---|
| Ground roughness z0 | 0.16 |
| Number of frequency samples N | 6000 |
| Cutoff frequency ω (Hz) | 3π |
| Simulation duration t (s) | 600 |
| Time step (s) | t/N |
| Sampling interval Δt (s) | 0.25 |
| Frequency increment (Hz) | ω/N |
| Main bridge span (m) | 145.16 |
| Design wind speed (m/s) | 28 |
| Computational Parameters | Value |
|---|---|
| Turbulence intensity | 5% |
| Turbulence viscosity ratio | 10 |
| Air density (kg/m3) | 1.225 |
| Air dynamic viscosity [kg/(m·s)] | 1.7894 × 10−5 |
| Inflow wind speed (m/s) | 28 |
| Location | Material | Elastic Modulus (MPa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|---|---|
| Main girder | C55 reinforced concrete | 3.55 × 104 | 0.2 | 2500 |
| Main pier | C50 reinforced concrete | 3.45 × 104 | 0.2 | 2500 |
| Block | Segment-Center Height Above Ground (m) | Reference Wind Speed (m/s) | Equivalent Static Gust Wind Speed (m/s) |
|---|---|---|---|
| 1#Block | 91.583 | 39.106 | 50.838 |
| 2#Block | 91.604 | 39.107 | 50.840 |
| 3#Block | 91.564 | 39.105 | 50.836 |
| 4#Block | 91.556 | 39.104 | 50.835 |
| 5#Block | 91.519 | 39.102 | 50.832 |
| 6#Block | 91.455 | 39.097 | 50.826 |
| 7#Block | 91.366 | 39.091 | 50.818 |
| 8#Block | 91.254 | 39.083 | 50.808 |
| 9#Block | 91.120 | 39.074 | 50.797 |
| 10#Block | 90.975 | 39.064 | 50.784 |
| 11#Block | 90.811 | 39.053 | 50.769 |
| 12#Block | 90.631 | 39.041 | 50.753 |
| 13#Block | 90.435 | 39.027 | 50.735 |
| 14#Block | 90.223 | 39.012 | 50.716 |
| 15#Block | 90.012 | 38.998 | 50.697 |
| 16#Block | 89.792 | 38.983 | 50.677 |
| 17#Block | 89.560 | 38.966 | 50.656 |
| 18#Block | 89.372 | 38.953 | 50.639 |
| 19#Block | 89.271 | 38.946 | 50.630 |
| 20#Block | 89.312 | 38.949 | 50.634 |
| 21#Block | 89.583 | 38.968 | 50.658 |
| 22#Block | 89.903 | 38.99 | 50.687 |
| 23#Block | 90.302 | 39.018 | 50.723 |
| 24#Block | 90.690 | 39.045 | 50.758 |
| 25#Block | 91.081 | 39.072 | 50.793 |
| 26#Block | 91.485 | 39.099 | 50.829 |
| 27#Block | 91.874 | 39.126 | 50.864 |
| 28#Block | 92.246 | 39.151 | 50.896 |
| 29#Block | 92.602 | 39.175 | 50.928 |
| 30#Block | 92.950 | 39.199 | 50.958 |
| 31#Block | 93.301 | 39.222 | 50.989 |
| 32#Block | 93.629 | 39.244 | 51.018 |
| 33#Block | 93.933 | 39.265 | 51.044 |
| 34#Block | 94.213 | 39.284 | 51.069 |
| 35#Block | 94.467 | 39.300 | 51.091 |
| 36#Block | 94.690 | 39.315 | 51.110 |
| 37#Block | 94.887 | 39.328 | 51.127 |
| Piers | 42.500 | 34.586 | 44.961 |
| Mode | Frequency (Hz) | Mode Description |
|---|---|---|
| 1 | 0.18882 | Pier bending (longitudinal) |
| 2 | 0.21200 | Pier torsion |
| 3 | 0.26118 | Pier bending (lateral) |
| 4 | 0.76390 | Girder vertical bending, antisymmetric |
| 5 | 1.15250 | Girder vertical bending, symmetric |
| 6 | 1.24830 | Girder vertical bending, symmetric; pier bending (longitudinal), symmetric |
| 7 | 1.36810 | Girder vertical bending, antisymmetric; pier bending (longitudinal) |
| 8 | 1.60110 | Girder lateral bending, symmetric; pier bending (lateral) |
| 9 | 2.37140 | Girder and pier lateral bending, second order, symmetric |
| 10 | 2.72060 | Girder lateral bending, second order, symmetric; pier lateral bending, second order, antisymmetric |
| Segment | Angle of Attack (Deg) | Drag Coefficient CD | Lift Coefficient CL | Torque Coefficient CM |
|---|---|---|---|---|
| 1 | −2 | 0.9745 | 1.9512 | −0.6351 |
| 0 | 0.9412 | 2.2459 | −0.4013 | |
| 2 | 0.9397 | 2.1027 | −0.3126 | |
| 2 | −2 | 0.8045 | 2.4146 | −0.3464 |
| 0 | 0.8273 | 2.2185 | −0.3006 | |
| 2 | 0.7942 | 1.8846 | −0.2840 | |
| 3 | −2 | 1.4136 | 1.2461 | −0.1946 |
| 0 | 1.4554 | 1.0189 | −0.1742 | |
| 2 | 1.4399 | 0.9449 | −0.1678 | |
| 4 | −2 | 1.3874 | 1.3154 | −0.1615 |
| 0 | 1.5001 | 1.1717 | −0.1426 | |
| 2 | 1.4754 | 1.0346 | −0.1310 | |
| 5 | −2 | 0.7156 | 2.4501 | −0.3045 |
| 0 | 0.7663 | 2.3302 | −0.2821 | |
| 2 | 0.6455 | 2.1031 | −0.2644 | |
| 6 | −2 | 0.9841 | 2.3594 | −0.4133 |
| 0 | 0.7778 | 2.3295 | −0.3913 | |
| 2 | 0.6951 | 1.9422 | −0.3712 |
| Segment | Angle of Attack (Deg) | Derivative of Drag Coefficient CD″ | Derivative of Lift Coefficient CL″ | Derivative of Torque Coefficient CM″ |
|---|---|---|---|---|
| 1 | −2 | 0.03461 | −0.06234 | −0.01573 |
| 0 | 0.02472 | −0.06460 | −0.01612 | |
| 2 | 0.01483 | −0.06686 | −0.01651 | |
| 2 | −2 | 0.01349 | −0.03745 | −0.01387 |
| 0 | 0.00696 | −0.02748 | −0.01068 | |
| 2 | 0.00043 | −0.01751 | −0.00749 | |
| 3 | −2 | −0.01849 | 0.01672 | −0.00671 |
| 0 | −0.01864 | 0.01432 | −0.00520 | |
| 2 | −0.01879 | 0.01192 | −0.00369 | |
| 4 | −2 | −0.01609 | 0.01896 | −0.00259 |
| 0 | −0.01620 | 0.01792 | −0.00312 | |
| 2 | −0.01631 | 0.01688 | −0.00364 | |
| 5 | −2 | 0.02140 | −0.04836 | −0.00683 |
| 0 | 0.01284 | −0.04136 | −0.00468 | |
| 2 | 0.00428 | −0.03436 | −0.00253 | |
| 6 | −2 | 0.03668 | −0.06962 | −0.00351 |
| 0 | 0.03432 | −0.06256 | −0.00180 | |
| 2 | 0.03196 | −0.05550 | −0.00010 |
| Response Type | Aerostatic Response | Buffeting Peak | Total Wind-Induced Response | Buffeting Amplification Factor |
|---|---|---|---|---|
| Lateral displacement (m) | 0.1851 | 0.1628 | 0.3479 | 1.88 |
| Vertical displacement (m) | −0.1343 | −0.2345 | 0.3688 | 2.746 |
| Torsional rotation (rad) | −0.0030 | −0.0063 | −0.0093 | 3.1 |
| Angle of Attack (Deg) | Drag Coefficient CD | Lift Coefficient CL | Side Force Coefficient CO | Rolling Moment Coefficient CMD | Yawing Moment Coefficient CML | Pitching Moment Coefficient CMO |
|---|---|---|---|---|---|---|
| −10 | 0.8504 | 1.2783 | −0.3332 | 0.7946 | −0.4626 | −0.0981 |
| −8 | 0.9649 | 0.7975 | −0.2666 | 0.7115 | −0.3351 | −0.1081 |
| −6 | 1.0205 | 0.4650 | −0.2329 | 0.6449 | −0.1946 | −0.1199 |
| −4 | 1.0168 | 0.2467 | −0.2009 | 0.5541 | −0.0419 | −0.1311 |
| −2 | 1.0371 | 0.0557 | −0.1929 | 0.4478 | 0.1050 | −0.1424 |
| 0 | 1.0221 | −0.1149 | −0.1778 | 0.3211 | 0.2164 | −0.1612 |
| 2 | 1.0010 | −0.2692 | −0.1641 | 0.4197 | 0.3249 | −0.1883 |
| 4 | 0.9776 | −0.3955 | −0.1520 | 0.5141 | 0.3915 | −0.2299 |
| 6 | 0.9479 | −0.5081 | −0.1419 | 0.6215 | 0.3256 | −0.2903 |
| 8 | 0.9098 | −0.6309 | −0.1317 | 0.7301 | 0.2494 | −0.3803 |
| 10 | 0.8721 | −0.7402 | −0.1235 | 0.8554 | 0.1440 | −0.5012 |
| Angle of Attack (Deg) | Drag Coefficient CD″ | Lift Coefficient CL″ | Side Force Coefficient CO″ | Rolling Moment Coefficient CMD″ | Yawing Moment Coefficient CML″ | Pitching Moment Coefficient CMO″ |
|---|---|---|---|---|---|---|
| −10 | −89.6682 | 240.2358 | −38.6734 | 34.0178 | 63.7766 | 27.5030 |
| −8 | −78.0545 | 207.4286 | −32.9866 | 44.3343 | 35.2213 | 16.4424 |
| −6 | −66.4409 | 174.6215 | −27.2999 | 54.6507 | 6.6660 | 5.3818 |
| −4 | −54.8273 | 141.8143 | −21.6131 | 64.9671 | −21.8894 | −5.6788 |
| −2 | −43.2136 | 109.0072 | −15.9263 | 75.2836 | −50.4447 | −16.7394 |
| 0 | −31.6000 | 76.2000 | −10.2395 | 85.6000 | −79.0000 | −27.8000 |
| 2 | −19.9864 | 43.3928 | −4.5527 | 95.9164 | −107.5553 | −38.8606 |
| 4 | −8.3727 | 10.5857 | 1.1340 | 106.2329 | −136.1106 | −49.9212 |
| 6 | 3.2409 | −22.2215 | 6.8208 | 116.5493 | −164.6660 | −60.9818 |
| 8 | 14.8545 | −55.0286 | 12.5076 | 126.8657 | −193.2213 | −72.0424 |
| 10 | 26.4682 | −87.8358 | 18.1944 | 137.1822 | −221.7766 | −83.1030 |
| Response Type | Aerostatic Response | Buffeting Peak | Total Wind-Induced Response | Buffeting Amplification Factor |
|---|---|---|---|---|
| Lateral displacement (m) | 0.1851 | 0.2146 | 0.3997 | 2.159 |
| Vertical displacement (m) | −0.1343 | −0.2066 | −0.3409 | 2.538 |
| Torsional rotation (rad) | −0.0030 | −0.0053 | −0.0083 | 2.767 |
| Response Type | Lateral Displacement | Vertical Displacement | Torsional Angle |
|---|---|---|---|
| RMSE | 0.0129 | 0.0064 | 0.0004 |
| nRMSE (range-normalized) | 0.4455 | 0.0208 | 0.0976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Tao, C.; Jia, J. Engineering Evaluation of the Buffeting Response of a Variable-Depth Continuous Rigid-Frame Bridge: Time-Domain Analysis with Three-Component Aerodynamic Coefficients and Comparison Against Six-Component Wind Tunnel Tests. Buildings 2025, 15, 3715. https://doi.org/10.3390/buildings15203715
Dong L, Tao C, Jia J. Engineering Evaluation of the Buffeting Response of a Variable-Depth Continuous Rigid-Frame Bridge: Time-Domain Analysis with Three-Component Aerodynamic Coefficients and Comparison Against Six-Component Wind Tunnel Tests. Buildings. 2025; 15(20):3715. https://doi.org/10.3390/buildings15203715
Chicago/Turabian StyleDong, Lin, Chengyun Tao, and Jie Jia. 2025. "Engineering Evaluation of the Buffeting Response of a Variable-Depth Continuous Rigid-Frame Bridge: Time-Domain Analysis with Three-Component Aerodynamic Coefficients and Comparison Against Six-Component Wind Tunnel Tests" Buildings 15, no. 20: 3715. https://doi.org/10.3390/buildings15203715
APA StyleDong, L., Tao, C., & Jia, J. (2025). Engineering Evaluation of the Buffeting Response of a Variable-Depth Continuous Rigid-Frame Bridge: Time-Domain Analysis with Three-Component Aerodynamic Coefficients and Comparison Against Six-Component Wind Tunnel Tests. Buildings, 15(20), 3715. https://doi.org/10.3390/buildings15203715






