Research on Dynamic Simulation and Optimization of Building Energy Consumption of Substations in Cold Regions Based on DeST: A Case Study of an Indoor Substation in Shijiazhuang

Abstract

Against the backdrop of the global energy crisis and the “dual carbon” goals (carbon peaking and carbon neutrality), the passive energy-saving design of substation buildings in cold regions faces severe challenges. This study systematically conducts a decomposed analysis of the shape coefficient, thermal performance of the building envelope (including external walls, internal walls, roofs, and external windows), and window-to-wall ratio of substation buildings in cold regions, quantifies the degree of influence of each factor, and proposes corresponding energy-saving design strategies. This study took a 110 kV substation in Yuhua District, Shijiazhuang City, Hebei Province, as the research object. A building energy consumption model was established based on DeST (2023) software, and the influence of the building shape coefficient, U-values of the envelope structure (external walls, internal walls, roofs, external windows), and window-to-wall ratio on the building’s cooling and heating loads was analyzed using the numerical simulation and control variable methods. Leveraging a rigorously validated, high-resolution simulation framework, we quantitatively dissect the marginal energy penalties and payoffs of every passive design variable governing fully indoor substations in cold-climate zones. The resultant multidimensional response surfaces are distilled into a deterministic, climate-specific passive energy-saving protocol that secures heating-energy savings of up to 43% without compromising electrical safety or operational accessibility. (1) Reducing the shape coefficient can significantly lower the heat load, and it is recommended to control it at 0.35–0.40; (2) The thermal performance of the envelope structure has a differential effect: the energy-saving effect is optimal when the U-value of external walls is 0.20–0.30 W/(m²·K) and the U-value of roofs is ≤0.25 W/(m²·K). A U-value of 2.4 W/(m²·K) is recommended for external windows, while the internal wall exerts a weak influence; (3) The window-to-wall ratio should be controlled by orientation: east-facing/north-facing ≤ 0.20, south-facing ≤ 0.35, and west-facing ≤ 0.30. Based on the above results, a comprehensive energy-saving strategy of “compact form–high-efficiency envelope–limited window-to-wall ratio” is proposed, which provides theoretical support and technical pathways for the energy-saving design of substation buildings in cold areas. Compared with existing substation buildings, the recommended parameters yield a significant reduction in total life-cycle carbon emissions and hold important practical significance for realizing the “dual carbon” goals (carbon peaking and carbon neutrality) of the power system.

1. Introduction

Against the backdrop of the global energy crisis and the “dual carbon” goals (carbon peaking and carbon neutrality), the energy-saving design of substations in cold regions faces significant challenges. As the core hub for energy conversion and distribution in power systems, the energy efficiency of substations directly impacts the overall operational efficiency of power grids. Substation buildings, as a type of industrial architecture, particularly in cold regions, account for a substantial proportion of total substation energy consumption. Furthermore, electrical equipment imposes stringent requirements on the thermal environment, which exacerbates the complexity of energy-saving design [1]. Therefore, reducing the energy consumption of substation buildings through diverse energy-saving measures is pivotal to research and design efforts focused on substation energy efficiency [2]. However, the substantial and continuous internal heat gain from equipment within substations fundamentally alters the composition and characteristics of heating and cooling loads. Consequently, some best practices applied in civil buildings (e.g., striving to minimize the U-values of external windows) may yield different or even opposite effects in substations. Hence, this study systematically investigates the impacts of shape coefficient, thermal performance of the building envelope (external walls, internal walls, roofs, external windows), and window-to-wall ratio on the energy consumption of substations in cold regions, quantifies the degree of influence of each factor, and proposes corresponding energy-saving design strategies.

Scholars both domestically and internationally have achieved a series of research accomplishments in the field of substation energy conservation. Internationally, existing studies primarily focus on technical pathways other than building energy consumption to reduce the comprehensive energy consumption of substations. For instance, Europe has leveraged the Energy Performance of Buildings Directive (EPBD) to drive the improvement of energy efficiency standards, with smart building technologies and the application of phase change materials emerging as research hotspots [3,4]. Tian, Zhongbei proposed an energy-efficient speed trajectory that uses only one gliding point and designed a statistical method-based energy optimization scheme for metro systems to reduce substation energy consumption [5]. Wei-Chen Lin investigated distribution network reconfiguration and adopted a swarm optimization algorithm to reduce line losses, thereby lowering substation losses [6]. Firmin, J. and Vagapov, Y. analyzed methods for reducing electrical energy losses in parallel transmission/distribution transformers and put forward approaches to cut down substation energy consumption [7]. Takeshi Sugimoto mentioned that capturing regenerative braking energy via energy storage systems (e.g., batteries, hybrid energy storage) can reduce reliance on substations, thereby decreasing substation energy consumption [8]. Lisha Shang et al. explored the key technologies of integrated energy-saving systems for substations in the context of smart grids, including energy consumption monitoring, data analysis, and energy-saving assessment methods [9].

Domestically, scholars have also conducted extensive research focusing on substation energy consumption. Shao-Jian Li’s group framed substation-building efficiency as an envelope-centric problem, advocating next-generation wall materials and augmented insulation layers to suppress conductive heat gains and losses [10]. Jicheng Wang et al., through a Heilongjiang prefabricated substation case study, demonstrated that industrialized off-site fabrication eradicates on-site wet trades, concomitantly reducing material waste and construction-phase energy demand [11]. Bin Ding’s field survey of indoor substations identified HVAC plants as the dominant energy end-use, proposing hybrid inverter-driven air conditioning coupled with buoyancy-driven natural ventilation to curtail operating consumption [12]. Zhen Zhang, working within Inner Mongolia’s climatic context, quantified the marginal energy penalties of window-to-wall ratio and envelope U-values for 110 kV substations and advanced envelope refinements tuned to severe cold conditions [1]. Yonghang Fan extended the analytical boundary to the whole life cycle, tracing carbon flows through construction and operation stages and formulating cross-stage mitigation packages for lifetime CO₂ abatement [13]. Ying Wang proposed the application of rooftop photovoltaic (PV) systems and air-source heat pumps in cold regions, achieving substantial reductions in both energy consumption and carbon emissions of substations [14]. Shuizhong Zhao developed an optimization model that minimizes life-cycle carbon emissions by simultaneously optimizing the thermal performance of the building envelope and on-site renewable energy utilization [15]. Yashan Hu demonstrated that optimizing the U-value of external walls can directly reduce the building’s energy demand and associated carbon emissions [16]. Wang Yifei analyzed the impacts of various influencing factors on the energy consumption of substation buildings in severe cold regions, thereby providing guidance for the early-stage energy-efficient design of substations under such climatic conditions [17].

Nevertheless, the following gaps remain:

• Existing studies lack a systematic, parametric analysis of the building-skin energy signature;
• The particular combination of cold-climate conditions and substations’ character as high internal-gain industrial buildings has not been adequately addressed.

To this end, this paper establishes a model based on a substation in Shijiazhuang City, Hebei Province, and uses numerical simulation methods to focus on solving the following key problems: (1) establish a building energy consumption model of a substation in cold areas; (2) quantitatively analyze the influence of thermal performance of the envelope structure on building energy consumption. The energy-saving optimization strategy of substation buildings based on climate adaptability is proposed.

The research results will provide theoretical support and technical paths for improving the energy efficiency level of substations in cold areas and have important practical significance for realizing the “double carbon” goal of the power system.

2. Research Object and Model Establishment

2.1. Determination of Energy-Consumption-Influencing Factors

2.1.1. Building Shape Factor

In cold regions, the building shape coefficient is one of the core factors affecting the energy consumption of substation buildings. The larger the shape coefficient, the greater the external surface area per unit building volume; consequently, more heat is lost through the building envelope in winter, leading to a significant increase in heating energy consumption [14,18,19]. In addition, building shape also indirectly affects indoor air distribution, as well as daylighting and ventilation performance, thereby influencing the energy consumption of substation buildings [20,21]. Therefore, controlling the shape coefficient within a reasonable range and optimizing building shape design is of great significance for energy conservation in substations in cold regions.

2.1.2. Building Envelope

In cold regions, the building envelope of substations is a core factor influencing their energy consumption levels. This study focuses on the substation building envelope, covering multiple components including external walls, internal walls, roofs, doors, windows, and window-to-wall ratios. It systematically adjusts the performance parameters of each envelope component and conducts an in-depth analysis of the energy consumption variation patterns of substation buildings. During this study, the total cooling and heating loads of the substation were adopted as the key indicators for analyzing building energy consumption. If the envelope system of substations in cold regions fails to meet energy-saving requirements, their energy consumption will significantly increase. In terms of external walls, some substations use traditional materials such as solid clay bricks, which exhibit poor thermal insulation performance and high thermal conductivity, making it difficult to effectively prevent heat loss [20,22]. Poor sealing of doors and windows, along with gaps, leads to cold air infiltration and heat loss from heating systems, forcing the heating system to operate under high load [23]. Roof insulation is often overlooked: insufficient insulation, inadequate thickness of the insulation layer, or poor material performance of the roof will result in substantial heat loss [15,24]. In summary, it is essential to enhance the energy-saving performance of the building envelope by adopting high-performance thermal insulation materials, optimizing the sealing design of doors and windows, and improving the roof insulation structure.

2.1.3. Equipment Heat Dissipation Has a Significant Impact on Building Energy Consumption

In cold regions, substation equipment is densely arranged, and electrical equipment generates substantial heat during operation; thus, heat dissipation is a critical factor affecting building energy consumption. If the heat produced by main transformers and GIS equipment fails to be dissipated in a timely manner, indoor temperatures will rise, elevating the load on air conditioning systems and consequently increasing energy consumption [14,25,26]. The heat dissipation mode and arrangement of equipment also influence heat dissipation efficiency: transformers primarily rely on radiative heat dissipation (accounting for over 55% of total heat dissipation), while convective heat dissipation accounts for a smaller proportion but is highly susceptible to ventilation conditions [27,28]. In addition, equipment heat dissipation is closely related to the operational safety and service life of equipment. Therefore, optimizing heat dissipation design and adopting advanced energy-saving technologies are of great significance for reducing substation energy consumption and ensuring stable equipment operation.

2.2. Model Building

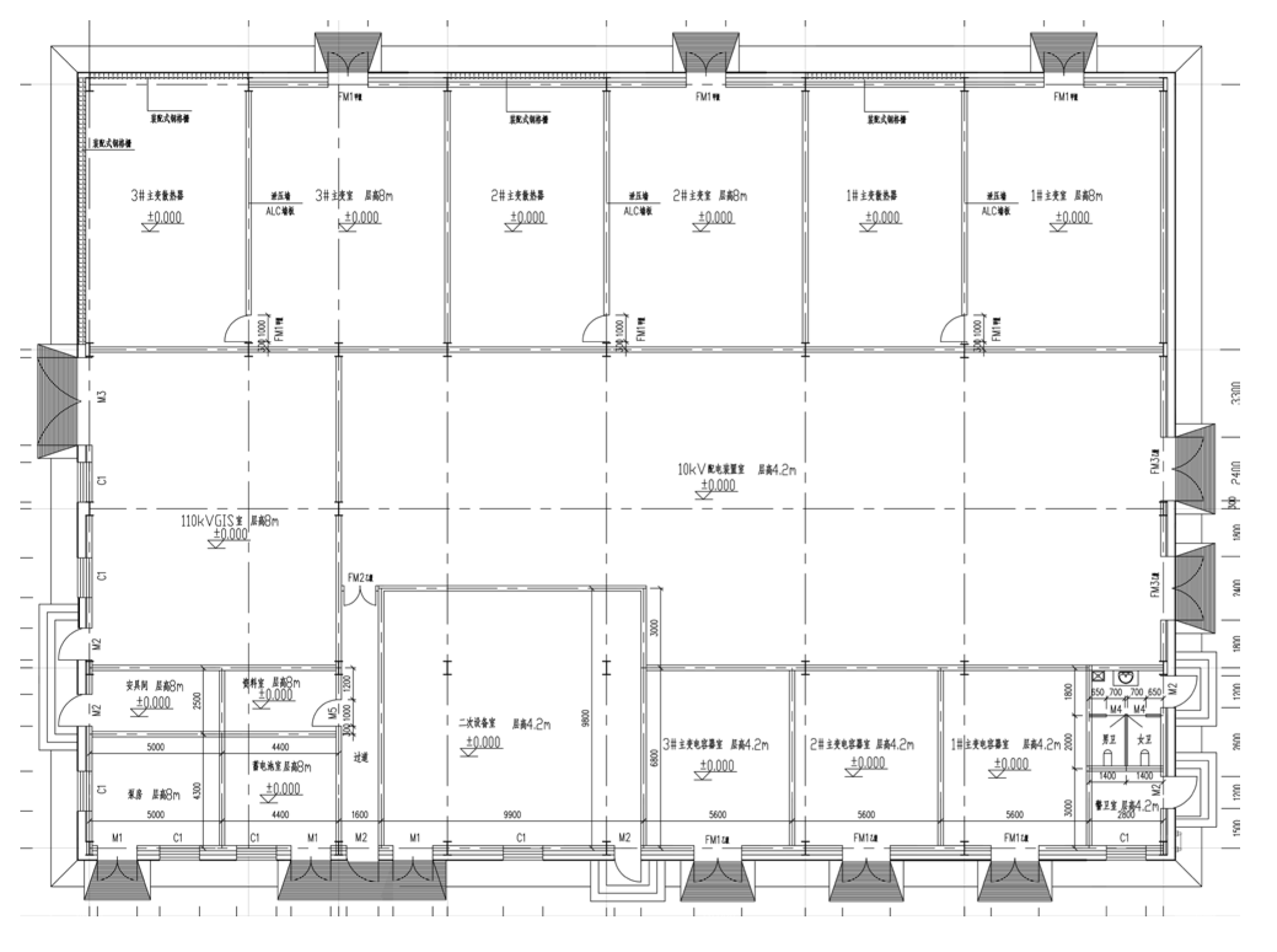
The building is located in Shijiazhuang Yuhua District, Jia Village, and is a 110 KV indoor manned–unmanned-type substation. Based on the establishment of the model, the substation construction area is about 1100 m², the indoor net height is basically 3.8 m, and the main function room includes the main transformer room, the main transformer capacitor room, the main transformer heat dissipation room, the 110 KV power distribution device room, the 110 KV GIS room, the secondary equipment room, the battery room, the pump room, the safety room, the data room, the duty room, the sanitary room, etc. Its floor plan is shown in Figure 1. It is of great significance to ensure the stable operation of the equipment.

This paper selects the above-mentioned typical substation building as the energy consumption simulation object, and through the analysis of the substation plane construction drawing, it can be seen that the design scheme is basically similar to the shape of the new indoor substation in the cold area in recent years and has typicality in the spatial layout and functional partitioning, which can better represent the architectural characteristics of the whole indoor substation in the cold area and provide a reliable reference for the relevant energy-saving design research. In the modeling process, the DeST-c (2023) energy consumption simulation software was used to establish an energy consumption calculation model (as shown in Figure 2) in strict accordance with the architectural drawings to ensure that the model can accurately reflect the thermal performance of the building.

2.3. Parameters of the Object of Study

The parameters required for this substation energy consumption simulation mainly include the following three parameters.

2.3.1. Basic Parameters for Calculating Energy Consumption of Substation

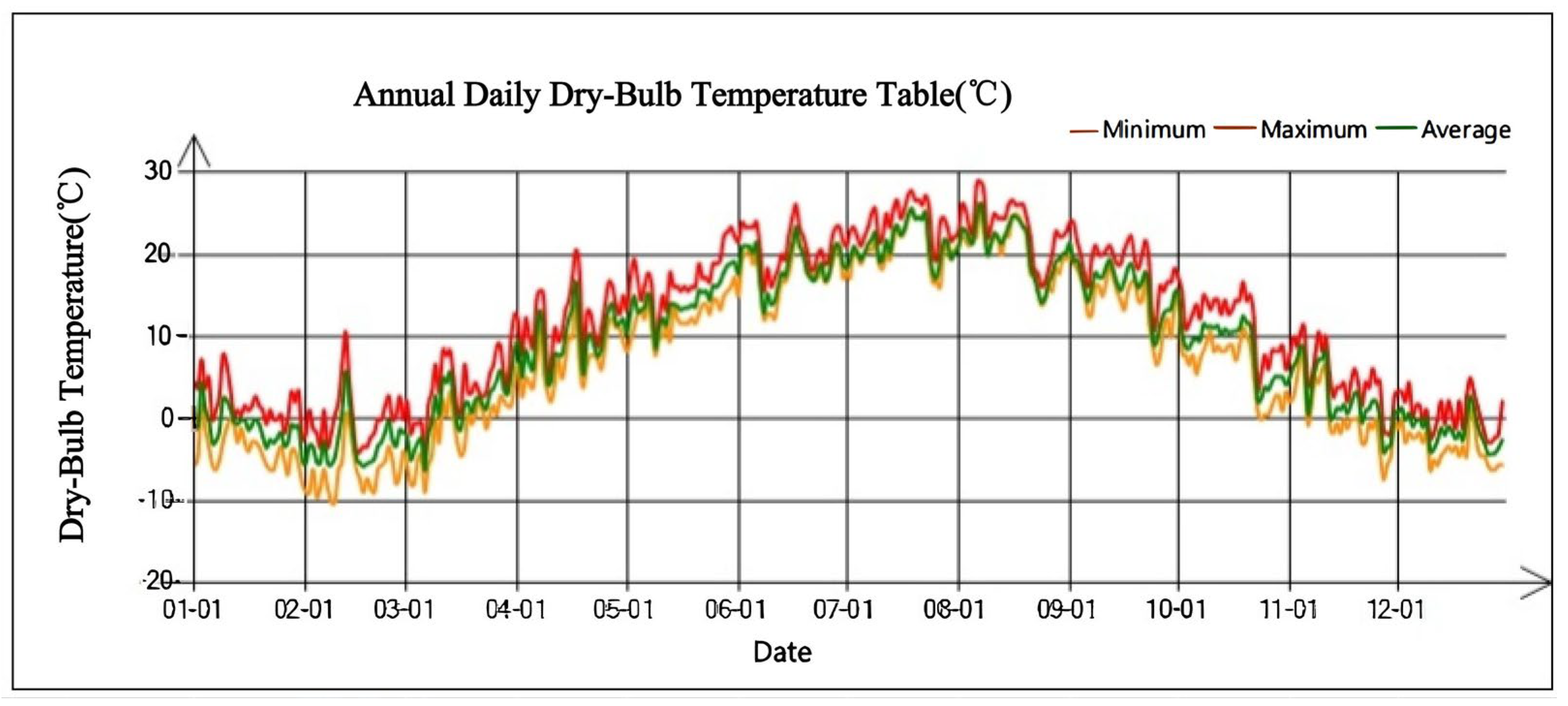
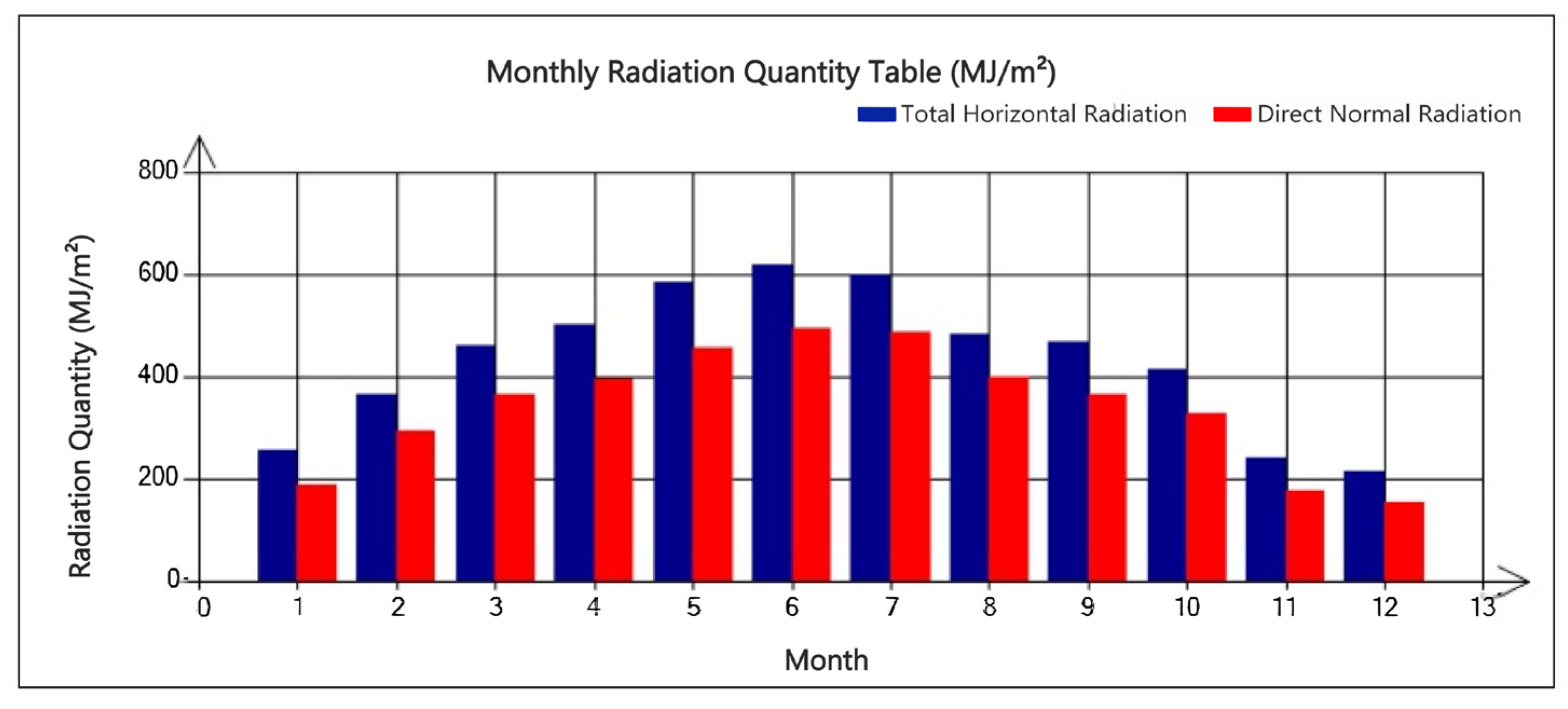
As a typical city in the cold region (IIB climate zone), Shijiazhuang’s thermal design strictly follows the requirements of the Code for Design of Heating, Ventilation and Air Conditioning of Civil Buildings (GB 50736-2012) [29,30]. The annual dry-bulb temperature and solar radiation are shown in Figure 3 and Figure 4, respectively. In summer, the calculated dry-bulb temperature outside the air-conditioned room is 34.1 °C, and the wet-bulb temperature is 26.4 °C; the outdoor temperature is calculated at 31 °C. In winter, the calculated temperature outside the heating room is −7.6 °C, the calculated temperature for ventilation and air conditioning is −10.5 °C, and the heating period is 119 days (15 November–15 March). In accordance with the relevant design codes, the indoor temperature of the substation building shall be set differently according to room function, with both summer air conditioning and winter heating design temperatures maintained within 20–28 °C. In addition, according to the design code, the design temperature of indoor air conditioning in summer and indoor heating in winter of this substation building is set between 20 °C and 28 °C, respectively, according to the function of the room.

In addition, based on the construction practices of the building envelope and its corresponding heat transfer system parameters specified in the construction drawings, the corresponding construction models were established in the building component library of the DeST (2023) software, and these construction methods were completely assigned to the simulation objects. The specific construction parameters of the building envelope are detailed in

Table 1. Structural hierarchy of the building envelope.

	Facades	Interior Walls	Roofing	Exterior Windows
Construct hierarchies	20 mm cement mortar 370 mm heavy mortar clay 90 mm expanded vermiculite 20 mm cement-free fiber board	20 mm cement mortar 157 mm heavy mortar clay 20 mm cement mortar 60 mm asphalt mineral wool board	2 mm aluminum 100 mm glass wool 2 mm aluminum	/
Heat transfer coefficient W/m2·K	0.458	0.90	0.531	1.8

.

2.3.2. Internal Disturbance Parameters of Substation Buildings

It will definitely become an important part of the energy consumption simulation research of substations. Through field investigation, the parameters of the functional rooms of the substation were sorted out in detail, as shown in Table 1 and

Table 2. Functional parameters of the substation.

Electrical Distribution Unit Building Room	The Name of the Device	Quantity	Rated Power (kW)	Operating Power (kW)	Set Air Conditioner Temperature (°C)	Running Time Period
Main transformer room	Intelligent control cabinet AC	2	3	1	/	All day
	Main transformer protection	2	0.08	0.096	20	All day
	Main transformer measurement and control	4	0.08	0.256	20	All day
10 KV power distribution room	10 KV power distribution unit AC	1	9.6	4.8	28	All day
	Heating power supply	1	20	20	/	All day (Seasonal)
	Lights	1	1.2	1.2	/	Short-term
	Protection of measurement and control devices	1	0.05	0.04	/	All day
	Segmented standby self-investment	1	0.05	0.03	/	All day
110 KV GIS power distribution room	110 KV power distribution unit AC	1	8	3	/	All day
	Heating power supply	1	16.5	16.5	/	All day (Seasonal)
	Lights	1	0.6	0.6	/	Short-term
	Protection of measurement and control devices	1	0.05	0.04	/	All day
	Segmented standby self-investment	1	0.05	0.03	/	All day
Capacitor room	Lights	1	0.3	0.3	/	Short-term
Secondary equipment room	UPS load	10	1	7.5	/	All day
	Protect measurement and control equipment	300	0.08	23.1	20	All day
Pumping station	Pump room power supply box	1	1.5	1.5	/	All day
	Lights	1	0.3	0.3	/	Short-term
Guardhouse	Lights	1	0.3	0.3	/	Short-term
Safety tool room	Lights	1	0.2	0.2	/	Short-term
Toilet	Lights	1	0.2	0.2	/	Short-term
	Electric heaters	1	2.5	2.5	/	Short-term
Aisle	Lights	1	0.5	0.5	/	Short-term

below.

2.3.3. Thermal Disturbance by Substation Construction Personnel

In the field investigation of typical unattended and manned substations, it was found that one person often stays in this type of substation, and it is permanent 24 h a day. The duty room is physically detached from the main substation volume and is therefore excluded from the thermal model.

Intermittent occupancy arises solely during inspection rounds: a duty operator sequentially enters each equipment compartment, introducing a transient load of 66 W sensible heat and 0.102 kg h⁻¹ moisture per individual, with a corresponding outdoor-air requirement of 30 m³ h⁻¹ person⁻¹, as stipulated in GB 50019-2015 [31].

Owing to the “unmanned-on-duty/manned-on-call” protocol, only one to two tours are executed per week, and doors remain sealed between visits; door-opening infiltration is accordingly disregarded in the energy balance.

A site audit of the Jiacun substation (Shijiazhuang) confirms that space conditioning is presently delivered by split-type units; an identical system topology is adopted in all subsequent simulations.

During inspection rounds the duty operator enters each equipment room; the resulting thermal disturbance is defined as max 1 person, min 0 persons, sensible heat 66 W/person, moisture release 0.102 kg h⁻¹ person⁻¹, and minimum outdoor-air rate 30 m³ h⁻¹ person⁻¹, in accordance with GB 50019-2015.

Because the substation is of the “unmanned-on-duty/manned-on-call” type, operators perform only 1–2 inspection tours per week, and doors remain closed at all other times. Consequently, door-opening effects are neglected in the energy analysis.

According to the survey of the Shijiazhuang Jiacun substation, the current air conditioner in the substation is a single air conditioner, and the subsequent simulation of this paper adopts this form of air conditioning.

The above is the design of the core parameters of a typical substation. Set the above parameters into the building energy model. Based on this, using the control variable method, a series of values for a single energy-consumption-influencing factor are assigned to the simulation model, allowing the direct generation of a corresponding list of building energy consumption values. The DeST software can derive the hourly energy consumption value of the building, select the desired part from the list of simulated values, combine it with data-processing tools, form a direct graph for energy consumption analysis, and use a linear regression model to analyze the sensitivity of energy consumption factors.

3. Theoretical Analysis

3.1. Calculation of Cooling and Heating Loads

3.1.1. Calculation of Dynamic Heat Transfer Load (Based on the Continuous-Time-Domain Transfer Function Method)

The method captures the envelope’s transient thermal behavior through a continuous-time transfer function that maps input disturbances—outdoor-temperature swings and internal heat-source variations—onto the resultant dynamic load in the time domain. Impulse-response coefficients embody the attenuation and time lag imposed by conduction, convection, and thermal mass, yielding a compact, single-zone model suited to high-fidelity transient load prediction. The governing expressions defined in the applicable standard are recapitulated below.

$$\mathrm{Q}\left(t\right)={\displaystyle \sum _{i=1}^n{a}_i}•T_{out}\left(t-{\tau }_i\right)+{\displaystyle \sum _{j=1}^m{b}_j}•Q_{\mathrm{int}}\left(t-{\tau }_j\right)$$

(1)

where:

• Q_(t) represents building load at time t (w);
• a_i: Outdoor-temperature disturbance transfer function coefficient (W·°C⁻¹);
• b_i: Internal-heat-source disturbance transfer function coefficient (dimensionless);
• T_out (t − i∆τ): Outdoor dry-bulb temperature at time t (°C);
• Q_int (t − j∆τ): Total internal heat-source intensity of the building at time t (W);
• ∆τ: Time step of the transfer function (h);
• n, m: Order of the transfer function (dimensionless).

3.1.2. Partition Dynamic Load Calculation (Based on Z-Transfer Function)

Tailored to multi-zone configurations, the technique discretizes the continuous heat-balance statement for every control volume. A Z-transfer function formalizes inter-zone thermal coupling—conductive exchange across partitions and air-flow-driven enthalpy transport—through a discrete delay operator that advances the solution sequentially at each time step. The canonical equation prescribed in the governing standard is given below.

$$Q_{\mathrm{k}}\left(\mathrm{z}\right)=\left({\displaystyle \frac{C_{\mathrm{k}}}{\Delta \mathrm{t}}}•{\displaystyle \frac{1-{\mathrm{z}}^{-1}}{1}}+{\displaystyle \sum _{\begin{array}{l}i=1\\ i\ne k\end{array}}^N\frac{1}{R_{\mathrm{ki}}}}\right){\mathrm{T}}_{\mathrm{k}}\left(\mathrm{z}\right)-{\displaystyle \sum _{\begin{array}{l}i=1\\ i\ne k\end{array}}^N\frac{1}{R_{ki}}}{z}^{-1}{T}_i\left(z\right)+Q_{\mathrm{int},k}\left(z\right)$$

(2)

where:

• Q_k(z): Z-transform of the cooling/heating load of zone i (W);
• T_k(z): Z-transform of the temperature of zone k (°C);
• C_k: Total thermal capacitance of zone k (J·°C⁻¹);
• R_ki: Coupling thermal resistance between zone k and zone i (°C·W⁻¹);
• z⁻¹: Delay operator in Z-transform (dimensionless);
• ∆t: Discrete sampling period (h);
• Z-transform of internal heat gains in zone k (W·Z⁰);
• Total number of building zones (dimensionless).

3.1.3. Dynamic Effects of Device Heat Dissipation (Unsteady-State Model)

Consider transient heat dissipation when the device is started or stopped or under variable load:

$$Q_{\mathrm{equip}}\left(\mathrm{t}\right)=P_{base}+\Delta P•\sin \left(\omega t+\varphi \right)+{\displaystyle \sum \delta \left(t-t_i\right)}•P_i$$

(3)

where P_base represents base power (W); ∆P,ω,ϕ denote amplitude, frequency, and phase of fluctuations, respectively; δ(t − t_i) presents the Dirac function; t_i indicates the time when the device starts and stops; and P_i denotes the power of device i (W).

3.1.4. Dynamic Model of Human Heat Dissipation (Based on Changes in Activity Level)

$$Q_{occupancy}\left(t\right)=N\left(\mathrm{t}\right)•\left[M•\left(1+\alpha •\Delta T\right)\right.\left.+W\right]$$

(4)

where N_t represents the number of people at time t (person); M denotes basal metabolic rate (W/person, typically 58–116 W/person); α presents the temperature sensitivity coefficient (e.g., 0.005/°C); ∆T indicates indoor and comfortable temperature difference (°C); and W denotes additional active heat dissipation (e.g., 40 W/person for office, 200 W/person for exercise).

3.1.5. Dynamic Calculation of Solar Radiation (Based on Azimuth and Hour Angles)

$${\mathrm{q}}_{\mathrm{solar}}\left(\mathrm{t}\right)=I\left(\mathrm{t}\right)•{\tau }_{\mathrm{glazing}}•{\rho }_{shading}•{\displaystyle \sum _{\mathrm{f}=1}^F{A}_f}•\cos \left({\theta }_f\left(t\right)\right)$$

(5)

where I(t) denotes solar irradiation at time t (W/m²); τ_glazing represents glass transmittance; ρ_shading  denotes shading factor; A_f indicates the fth exterior window area (m²) and θ_f(t) presents the angle (°) between the sun’s rays and the normal of the exterior window, calculated by the formula for the position of the sun.

$$\theta \left(\mathrm{t}\right)=\arccos \left[\sin \varphi •\sin \delta +\cos \varphi •\cos \delta •\cos \left(\omega \left(t\right)\right)\right.$$

(6)

where δ represents sun declination, ϕ denotes local geographic latitude, and ω indicates hour angle.

3.2. Regression Model Determination Coefficient

Coefficient of determination (R², R-squared) is determined as follows:

$${{\displaystyle R}}^2=1-{\displaystyle \frac{S{S}_{res}}{S{S}_{\mathrm{tot}}}}$$

(7)

where SS_res denotes the residual sum of squares, which is the difference between the predicted value of the model and the actual value.

$$S{S}_{\mathrm{res}}={\displaystyle {\sum }_{i=1}^n(y_i}-{\widehat{y}}_i{)}^2$$

(8)

where SS_tot represents the total sum of squares, which is the difference between the actual value and the mean value.

$$S{S}_{\mathrm{tot}}={\displaystyle {\sum }_{i=1}^n(y_i}-{\widehat{y}}_i{)}^2$$

(9)

Interpretation: R² indicates the proportion of the independent variable to the difference in the dependent variable, the range [0, 1]. If it is closer to 1, the better the fit.

4. Passive Energy-Saving Parameter Impact Analysis

4.1. The Influence of Body Shape Coefficient on the Energy Consumption of Substation Buildings

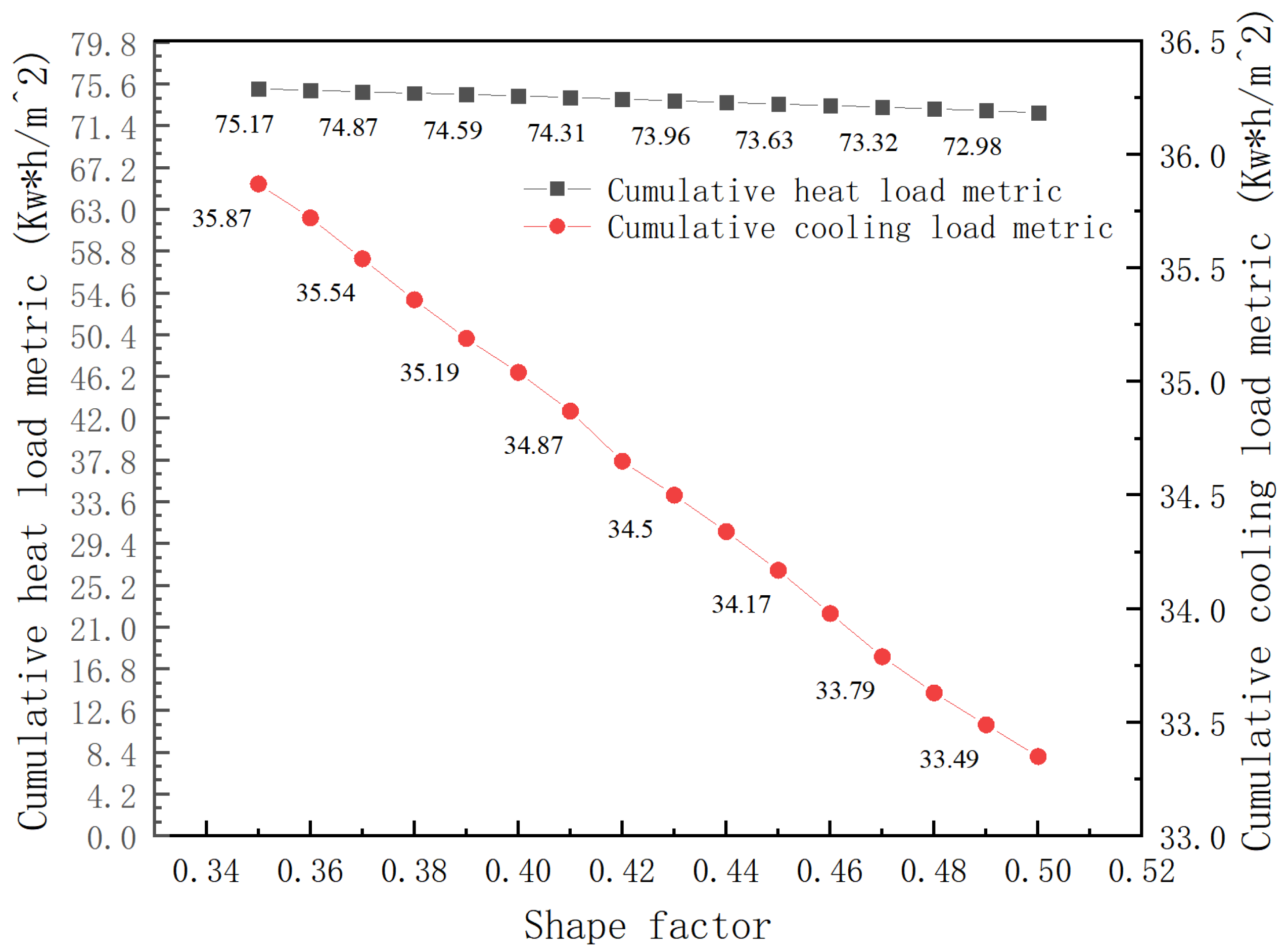
As the ratio of building dimensions to projection area, the shape coefficient is a key parameter affecting the energy consumption of substations in cold areas. The results show that the reduction in the shape coefficient can significantly reduce the heat loss and overall energy consumption of the building envelope, and the energy consumption of regular shapes (such as rectangles) is generally lower than that of irregular shapes [32]. In this study, a typical indoor substation (rectangular plan, single-story structure) in cold areas was taken as the object, and the heat transfer coefficient of each enclosure structure was selected according to Table 1, and a simulated sample with a body shape coefficient of 0.35–0.50 was established by the control variable method, and the relationship between building energy consumption (according to the climatic characteristics of Shijiazhuang and the requirements of relevant standards, the cooling load is calculated based on the period from 1 June to 31 August, while the heating load is considered from 15 November to 15 March of the following year, the same below) and the building shape coefficient (as shown in Figure 5).

The results of the numerical simulation study indicate that the shape coefficient exhibits a certain nonlinear influence on the energy consumption characteristics of substations in cold regions within the range of 0.35–0.50. When the shape coefficient increases from 0.35 to 0.50, the building’s cumulative heat load index decreases from 75.17 kW·h/m² to 72.75 kW·h/m², with a decrease of only 3.22%; the cooling load index decreases from 35.87 kW·h/m² to 33.35 kW·h/m², with a decrease of 7.03%, showing a simultaneous downward trend (p < 0.05). Notably, the increase in the shape coefficient leads to a rise in the building’s surface area-to-volume ratio (r = 0.89), but the heat loss effect is mitigated due to the optimization of the thermal performance of the envelope structure or internal heat sources. Under actual operating conditions, to maintain the required equipment temperature control, it is necessary to appropriately increase the load adjustment frequency of the heating system (Δf ≥ 10%) or the output power (Pmax increased by 5–8%), but the hidden energy consumption growth phenomenon is significantly alleviated compared with the original working condition. Numerical simulations show that under the current working condition, the influence of the shape coefficient on the heat load is weakened, while its optimization effect on the cooling load is more obvious. Based on the multi-objective optimization model, it is recommended that the optimal control range of the shape coefficient for substations in cold regions be 0.35–0.40. This range can ensure the basic stability of the theoretical heat load while controlling the increase in actual operating energy consumption within 3%, thereby achieving the optimization of the comprehensive energy efficiency ratio (EER), and its effect has been verified to have statistical significance through sensitivity analysis (p < 0.01).

4.2. The Influence of the Heat Transfer Coefficient of the Envelope Structure on the Energy Consumption of the Substation Building

The simulation platform, under the condition of keeping other parameters constant, quantifies the independent action law of the heat transfer coefficient of each enclosure component, respectively. Some studies have found that although reducing the heat transfer coefficient can effectively reduce the heat load of buildings, there is a significant economic inflection point: when the heat transfer coefficient falls to the critical threshold, the marginal gain of energy-saving benefits sharply decreases, and the cost input nonlinearly increases. Therefore, the purpose of this study is to analyze the quantitative relationship between the change in heat transfer coefficient of each part of the envelope structure (see

Table 3. List of design values for the change in heat transfer coefficient of each part of the envelope.

Envelope Structure	Heat Transfer Coefficient (W/(m2·K))
Facades	0.20	0.25	0.30	0.35	0.40	0.45	0.50
Interior walls	0.60	0.70	0.80	0.90	1.00	1.10	1.20
Roofing	0.20	0.25	0.30	0.35	0.40
Exterior windows	1.8	2.0	2.2	2.4	2.6	2.8	3.0
Window-to-wall ratio	0.05	0.10	0.15	0.20	0.25	0.30	0.35
	0.40	0.45	0.50	0.55	0.60	0.65	0.70

for details) and the energy consumption of the building through simulation so as to determine the optimal thermal parameters of each envelope under the premise of ensuring economic rationality so as to provide a design basis for engineering practice that takes into account thermal performance and economic feasibility.

4.2.1. Effect of Heat Transfer Coefficient of Exterior Wall on Energy Consumption

The control variable method is adopted, the heat transfer coefficient of other envelope structures is kept unchanged (see Table 1), the heat transfer coefficient of the exterior wall is varied (see

Table 4. Material parameters and corresponding heat transfer coefficients of exterior walls for each simulated working condition.

	Facade Materials 1 Thickness (mm)	Facade Materials 2 Thickness (mm)	Facade Materials 3 Thickness (mm)	Facade Materials 4 Thickness (mm)	Overall Exterior Wall Thickness (mm)	Exterior Wall U-Value (W/(m2·K))
Case 1	cement mortar20	clay-based heavy mortar110	expanded perlite270	cement mortar20	420	0.20
Case 2	cement mortar20	clay-based heavy mortar80	expanded perlite215	cement mortar20	335	0.25
Case 3	cement mortar20	clay-based heavy mortar90	expanded perlite175	cement mortar20	305	0.30
Case 4	cement mortar20	clay-based heavy mortar85	expanded perlite120	cement mortar20	245	0.35
Case 5	cement mortar20	clay-based heavy mortar140	expanded perlite100	cement mortar20	280	0.40
Case 6	cement mortar20	clay-based heavy mortar100	expanded perlite110	cement mortar20	250	0.45
Case 7	cement mortar20	clay-based heavy mortar60	expanded perlite100	cement mortar20	200	0.50

for the parameters of the exterior wall under different working conditions), and energy consumption simulations are conducted for scenarios with different heat transfer coefficients. The relationship between the heat transfer coefficient of the exterior wall and the building energy consumption is shown in Figure 6.

The numerical analysis of the above figure shows that when the heat transfer coefficient of the exterior wall is from 0.2 W/(m²·K) to 0.5 W/(m²·K), the cumulative heat load index significantly increased from 9.49 kW·h/m² to 14.81 kW·h/m² (an increase of 56.1%). This trend shows that the increase in the heat transfer coefficient in the exterior wall will significantly exacerbate the heat conduction loss of the envelope, resulting in the heating system needing to supplement the heat to maintain the thermal environment demand inside the substation under cold climate conditions, thereby increasing the energy consumption of building operation.

Although the cumulative cooling load index also changes with the increase in the heat transfer coefficient of the exterior wall, its absolute value is higher and the change range is relatively small. Given that the energy consumption of substations in cold regions is mainly dominated by heat loads, optimizing the thermal performance of the exterior wall plays a key role in reducing the overall energy consumption. Therefore, it is suggested that the exterior wall structure with a low heat transfer coefficient should be preferred in the design of substations in cold areas to effectively suppress heat loss and improve building energy efficiency. Therefore, the heat transfer coefficient of the exterior wall should be 0.20–0.30 (W/(m²·K)).

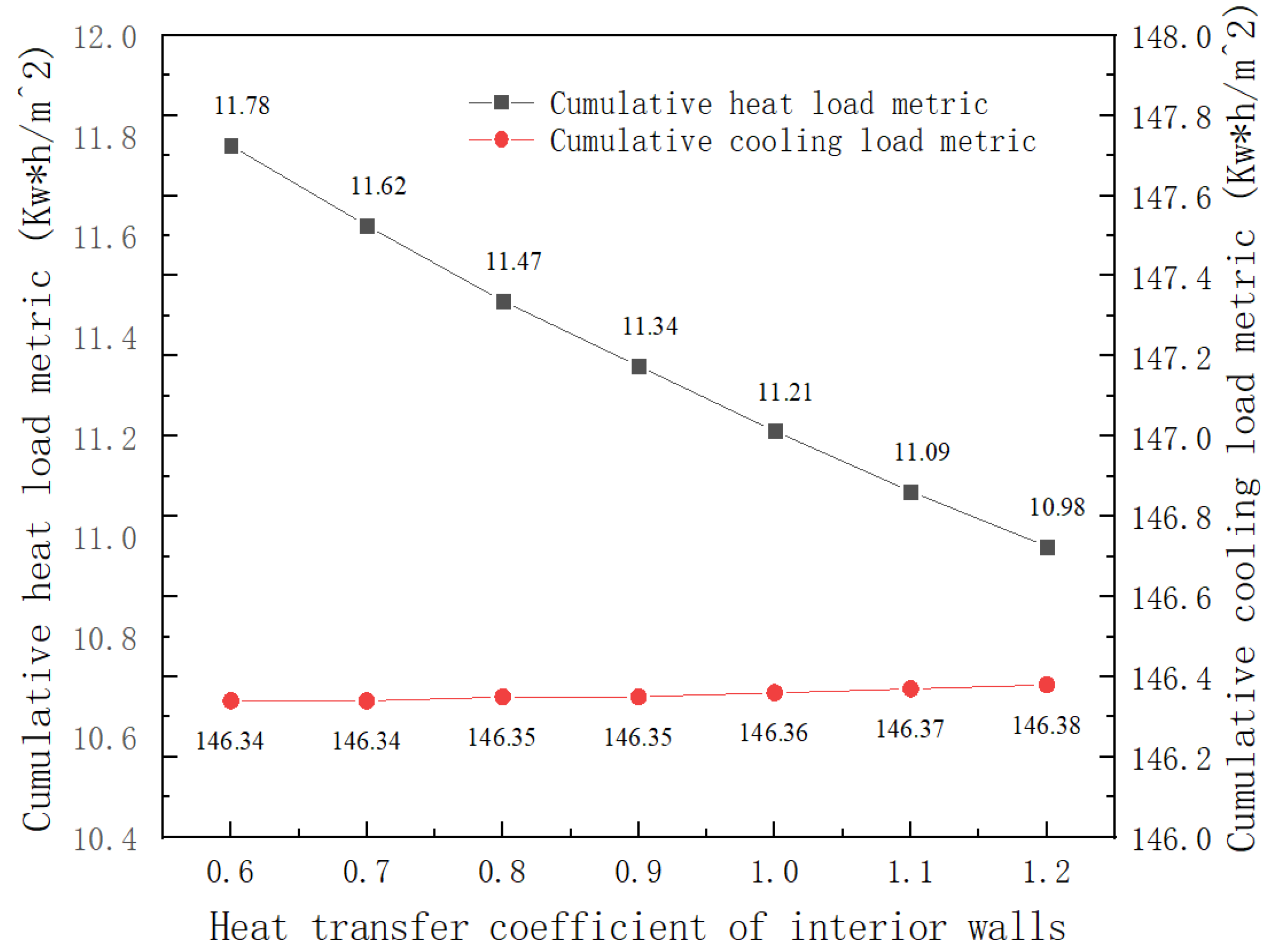
4.2.2. Effect of Heat Transfer Coefficient of Interior Wall on Energy Consumption

Under the premise of keeping the heat transfer coefficient of other enclosure structures unchanged (see Table 1), by varying the heat transfer coefficient of the interior wall (the wall parameters for each case are listed in

Table 5. Material parameters and heat transfer coefficients of interior walls for each simulation case.

	Interior Wall Materials 1 Thickness (mm)	Interior Wall Materials 2 Thickness (mm)	Interior Wall Materials 3 Thickness (mm)	Interior Wall Materials 4 Thickness (mm)	Total Thickness of the Interior Wall (mm)	Interior Wall U-Value (W/(m2·K))
Case 1	cement mortar20	clay-based heavy mortar85	cement mortar20	asphalt-impregnated120	245	0.6
Case 2	cement mortar20	clay-based heavy mortar110	cement mortar20	asphalt-impregnated95	245	0.7
Case 3	cement mortar20	clay-based heavy mortar95	cement mortar20	asphalt-impregnated80	215	0.8
Case 4	cement mortar20	clay-based heavy mortar110	cement mortar20	asphalt-impregnated65	215	0.9
Case 5	cement mortar20	clay-based heavy mortar110	cement mortar20	asphalt-impregnated55	205	1.0
Case 6	cement mortar20	clay-based heavy mortar120	cement mortar20	asphalt-impregnated45	205	1.1
Case 7	cement mortar20	clay-based heavy mortar105	cement mortar20	asphalt-impregnated40	185	1.2

), energy-use simulations are carried out for all interior-wall conditions; the resulting relationship between substation building energy consumption and interior-wall heat transfer coefficient is presented in Figure 7.

Numerical studies show that the change in heat transfer coefficient of the interior wall has a certain impact on the thermal performance of the substation in cold areas. When the heat transfer coefficient of the interior wall is increased from 0.6W/(m²·K) to 1.2 W/(m²·K), the cumulative heat load index showed a monotonic decreasing trend, from 11.78 kW·h/m² to 10.98 kW·h/m² (a decrease of about 6.8%). In contrast, although there are local fluctuations in the cumulative cooling load index and the total cooling load, the overall change range is small, indicating that the cooling load energy consumption is limited by the heat transfer coefficient of the interior wall.

This phenomenon can be attributed to the change in the heat conduction mechanism; the increase in the heat transfer coefficient of the interior wall improves the heat transfer efficiency of the interior wall and makes the indoor heat more easily diffuse to the adjacent low-temperature space through the interior wall. In cold regions, this type of heat transfer process can partially replace the active heating demand, thereby reducing the energy consumption of the heat load, so the cooling load index does not show significant changes. Therefore, the influence of the internal wall coefficient on the energy consumption of substation buildings in cold areas is almost negligible.

4.2.3. Effect of Roof Heat Transfer Coefficient on Energy Consumption

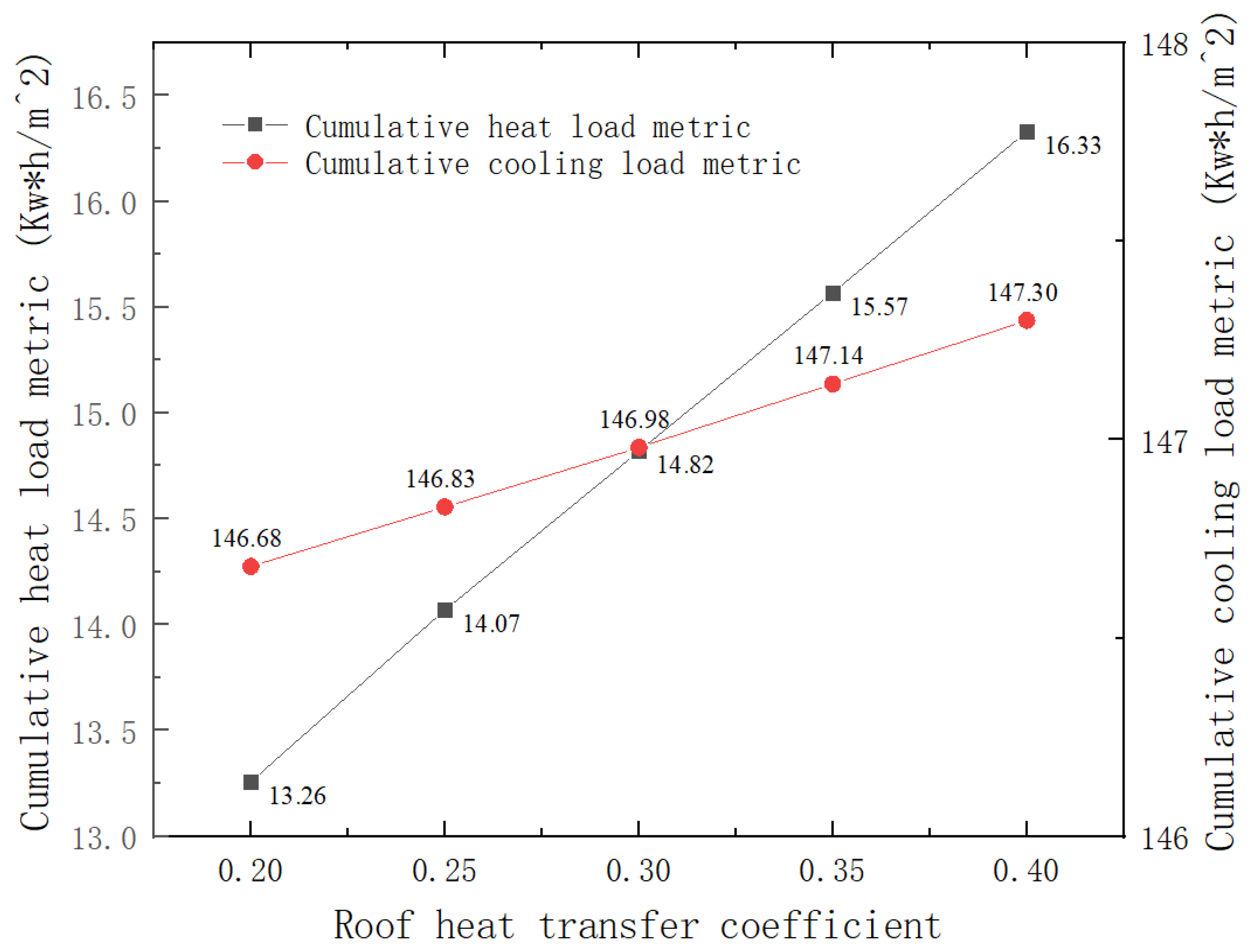
Under the premise of keeping the heat transfer coefficient of other enclosure structures unchanged (see Table 1), by altering the roof heat transfer coefficient (roof parameters for each case are given in

Table 6. Roof material parameters and corresponding heat transfer coefficients for each case.

	Roofing Material 1 Thickness (mm)	Roofing Material 2 Thickness (mm)	Roofing Material 3 Thickness (mm)	Roofing Material 4 Thickness (mm)	Total roof Thickness Millimeter (mm)	Roof Heat Transfer Coefficient (W/(m2·K))
Case 1	cement mortar20	expanded perlite270	reinforced concrete90	cement mortar20	400	0.20
Case 2	cement mortar20	heavy mortar clay215	reinforced concrete80	cement mortar20	335	0.25
Case 3	aluminum2	polystyrene foam150	aluminum2	none	154	0.30
Case 4	aluminum2	polystyrene foam125	aluminum2	none	129	0.35
Case 5	aluminum2	polystyrene foam110	aluminum2	none	114	0.40

), energy-use simulations are performed for all roof conditions; the resulting relationship between substation building energy consumption and roof heat transfer coefficient is shown in Figure 8.

According to the analysis of numerical simulation results, the change in roof heat transfer coefficient has a significant impact on the energy consumption characteristics of the substation. The research data shows that when the heat transfer coefficient of the roof is increased from 0.20 W/(m²·K) to 0.40 W/(m²·K), the cumulative heat load index shows an obvious monotonic increasing trend, from 13.26 kW·h/m² to 16.33 kW·h/m², an increase of 23.1%. In contrast, the cumulative cooling load index (Qc) increased simultaneously, but the change was relatively small (ΔQc < 12%).

This phenomenon can be explained from the perspective of building thermal engineering: the roof is an important part of the building envelope, and the increase in its heat transfer coefficient directly leads to a significant increase in the heat conduction loss (q = Ur × ΔT) of the roof. In cold climates, in order to maintain the stability of the indoor thermal environment of the substation, the heating system needs to additionally replenish the heat lost due to the increase in roof heat loss, resulting in a significant increase in heat load energy consumption. It can be seen that the increase in the roof heat transfer coefficient significantly improves the heat load energy consumption of the substation in the cold area, which means that in order to maintain indoor temperature, more energy needs to be consumed for heating, so in the construction and renovation of substations in cold areas, reducing the roof heat transfer coefficient is of great significance for reducing energy consumption. In summary, the heat transfer coefficient of the roof should be controlled within 0.25.

4.2.4. Influence of Heat Transfer Coefficient of Exterior Windows on Energy Consumption

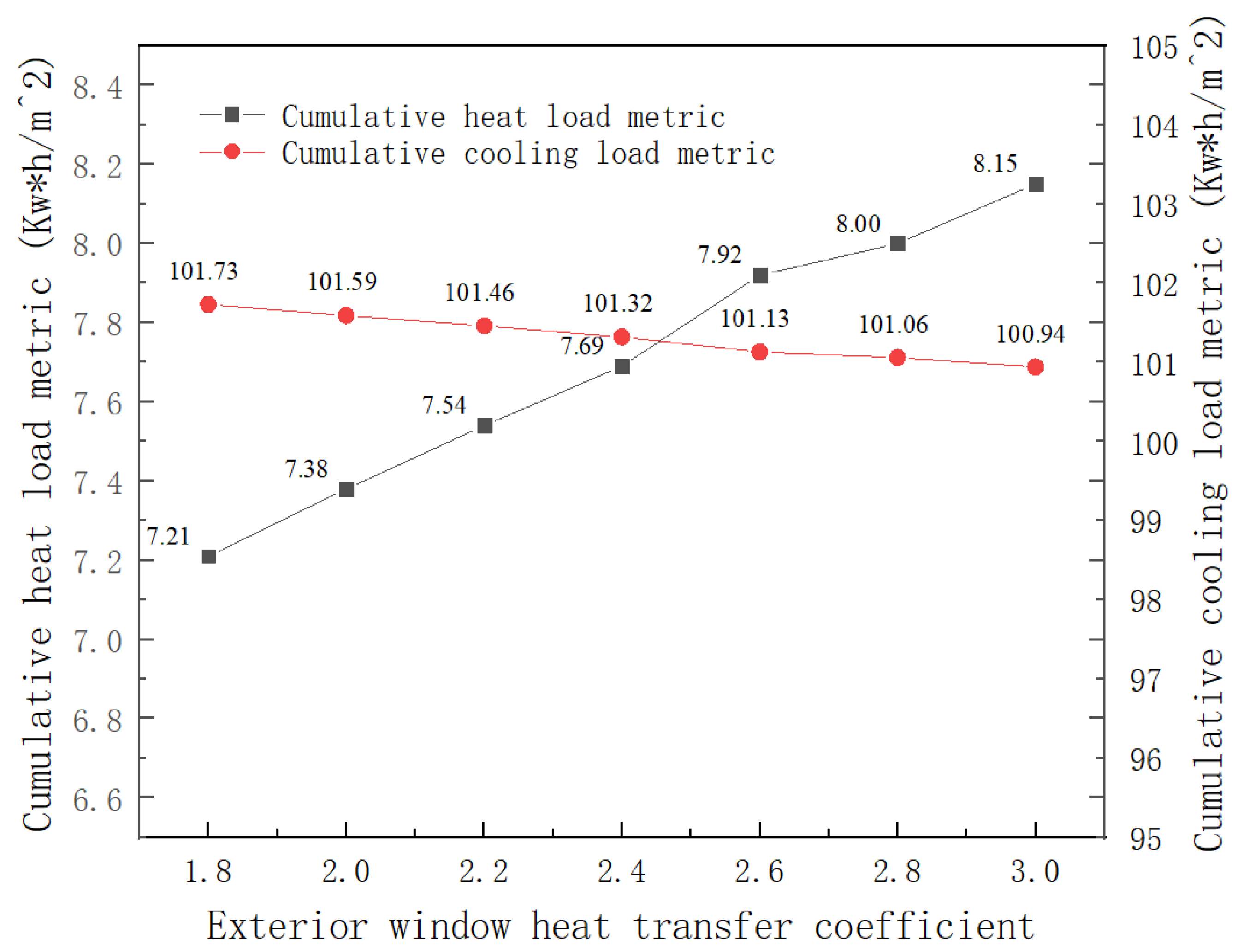
Under the premise of keeping the heat transfer coefficient of other enclosure structures unchanged (see Table 1), by varying the heat transfer coefficient of the external windows (window types for each case are listed in

Table 7. Parameters and corresponding heat transfer coefficients of external windows for each case.

	External Window Type	Shading Coefficient (SC) of External Windows	External Window Heat Transfer Coefficient (W/(m2·K))
Case 1	standard external1.8–0.5	0.5	1.8
Case 2	standard external window2.0–0.5	0.5	2.0
Case 3	standard external window2.2–0.5	0.5	2.2
Case 4	standard external window2.4–0.5	0.5	2.4
Case 5	standard external window2.6–0.5	0.5	2.6
Case 6	standard external window2.8–0.5	0.5	2.8
Case 7	standard external window3.0–0.5	0.5	3.0

), energy-use simulations are carried out for all window conditions; the resulting relationship between substation building energy consumption and external-window heat transfer coefficient is presented in Figure 9.

According to the results of numerical simulation, when the heat transfer coefficient of the exterior window increases, the cooling and heating load characteristics show an opposite trend. The heat transfer coefficient in the exterior window is increased from 1.8 W/(m²·K) to 3.0 W/(m²·K); the cumulative heat load index showed a linear growth trend with the increase in the heat transfer coefficient of the external window, from 7.21 kW·h/m² to 8.15 kW·h/m² (an increase of 13.0%). However, the cumulative cooling load index showed a linear decreasing trend with the increase in the heat transfer coefficient of the external window, from 101.73 kW·h/m² to 100.94 kW·h/m² (an increase of −0.78%). This phenomenon can be attributed to the fact that the indoor equipment of the substation building has a large amount of heat dissipation, and the increase in the heat transfer coefficient of the external window improves the heat transfer efficiency of the external window so that the indoor heat is easier to diffuse to the outer space through the external window, thereby reducing the cooling load. By establishing the energy–heat transfer coefficient response surface model, it is found that when the heat transfer coefficient of the exterior window is about 2.4 W/(m²·K), the co-optimization of heating load and cooling load can be realized, and a heat transfer coefficient of 3.0 W/(m²·K) can reduce the comprehensive energy consumption by about 3.00%; therefore, the heat transfer coefficient of the exterior window should be controlled at 2.4 W/(m²·K) or so.

4.3. Window-to-Wall Ratio and Orientation Optimization

Using the control variable method, the heat transfer coefficient of each envelope of the building remained unchanged (selected according to Table 1), and the energy consumption was simulated for the working conditions of different window-to-wall ratios of the four exterior windows facing the east, west, south, and north, and the simulation results are shown in

Table 8. Simulation results of heat load under different east window-to-wall ratios.

Window-To-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)	Window-to-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)
0.05	133.29	10.38	0.4	135.67	11.66
0.1	133.64	10.61	0.45	136	11.8
0.15	133.99	10.81	0.5	136.32	11.93
0.2	134.33	11.01	0.55	136.64	12.06
0.25	134.67	11.19	0.6	136.95	12.17
0.3	135.01	11.36	0.65	137.26	12.28
0.35	135.34	11.51	0.7	137.57	12.39

,

Table 9. Simulation results of heat load under different south window-to-wall ratios.

Window-To-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)	Window-To-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)
0.05	131.83	9.32	0.4	133.96	11.07
0.1	132.17	9.50	0.45	134.23	11.36
0.15	132.50	9.72	0.5	134.49	11.64
0.2	132.81	9.97	0.55	134.74	11.91
0.25	133.12	10.23	0.6	134.98	12.18
0.3	133.41	10.51	0.65	135.22	12.45
0.35	133.69	10.79	0.7	135.45	12.72

,

Table 10. Simulation results of heat load under different west window-to-wall ratios.

Window-To-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)	Window-To-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)
0.05	135.90	9.94	0.4	134.90	11.04
0.1	135.74	10.13	0.45	134.78	11.17
0.15	135.74	10.30	0.5	134.67	11.29
0.2	135.44	10.47	0.55	134.56	11.40
0.25	135.29	10.62	0.6	134.46	11.51
0.3	135.16	10.77	0.65	137.36	11.61
0.35	135.03	10.91	0.7	134.27	11.71

and

Table 11. Simulation results of heat load under different north window-to-wall ratios.

Window-To-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)	Window-To-Wall Ratio (W/(m2·K))	Cumulative Cooling Load Metric (kW·h/m2)	Cumulative Heat Load Metric (kW·h/m2)
0.05	132.87	10.47	0.4	134.21	12.49
0.1	133.09	10.79	0.45	134.38	12.74
0.15	133.29	11.10	0.5	134.54	12.98
0.2	133.49	11.40	0.55	134.69	13.21
0.25	133.68	11.69	0.6	134.84	13.43
0.3	133.86	11.97	0.65	134.99	13.64
0.35	134.04	12.23	0.7	135.13	13.85

.

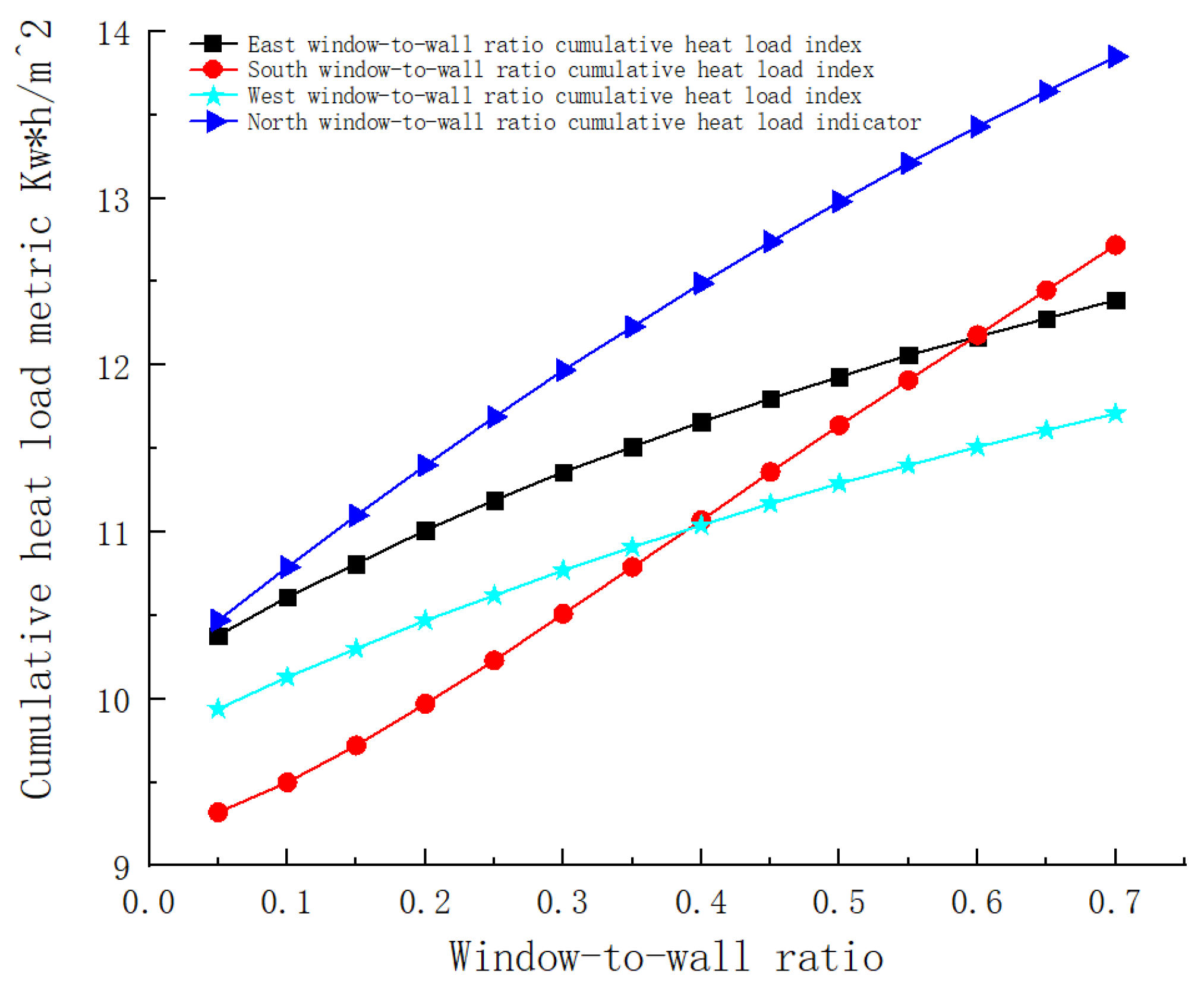
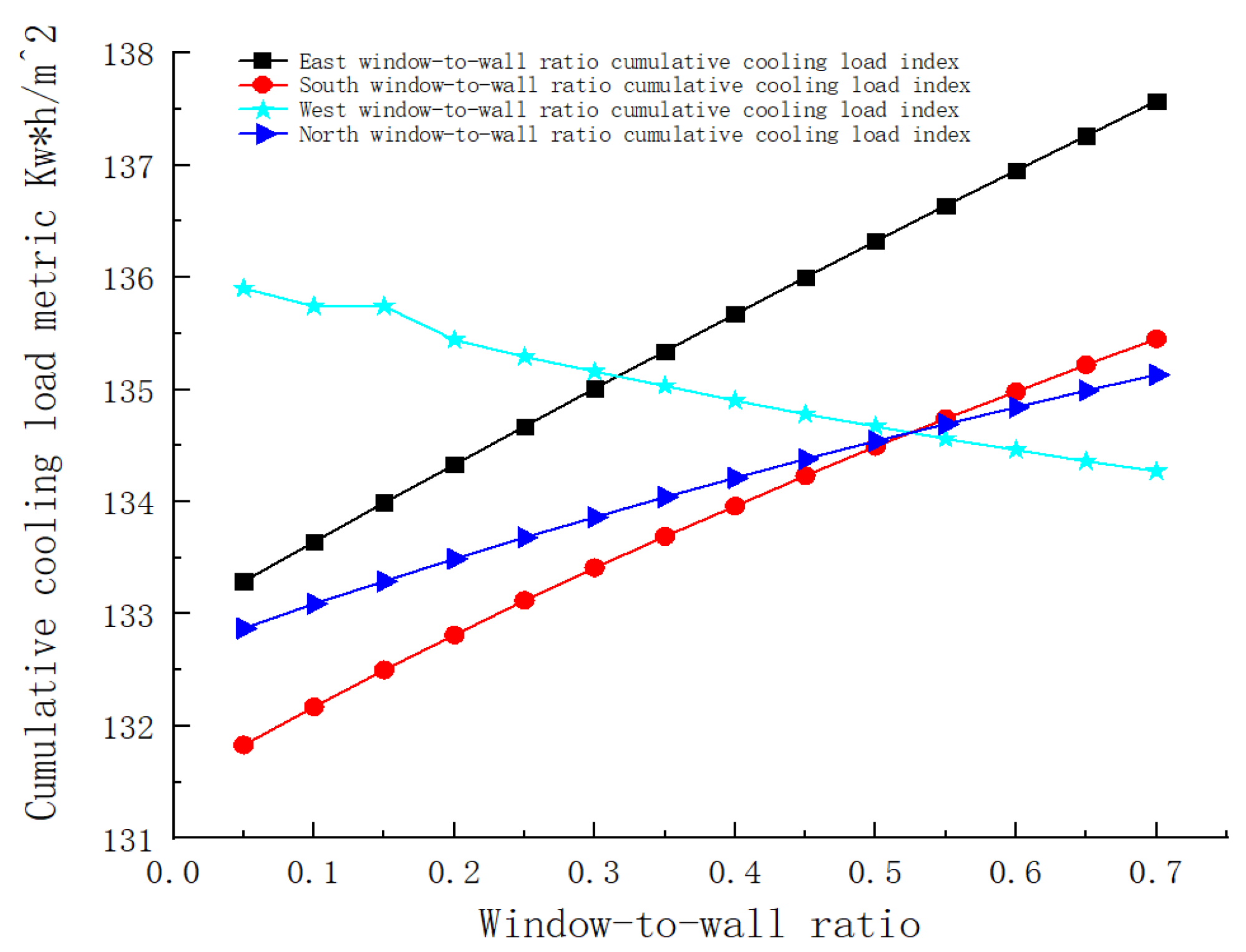
With the east-facing window-to-wall ratio increasing from 0.05 to 0.70, the annual cooling load per unit area increased from 133.29 kW·h/m² to 137.57 kW·h/m². The annual heat load per unit area increased from 10.38 kW·h/m² to 12.39 kW·h/m².

With the increase in the south-facing window-to-wall ratio from 0.05 to 0.70, the annual cooling load per unit area increased from 131.83 kW·h/m² to 135.45 kW·h/m², and the annual heat load per unit area increased from 9.32 kW·h/m² to 12.72 kW·h/m².

With the increase in the west-facing window-to-wall ratio from 0.05 to 0.70, the annual cooling load per unit area decreased from 135.90 kW·h/m² to 134.27² kW·h/m², and the annual heat load per unit area increased from 9.94 kW·h/m² to 11.71 kW·h/m².

With the increase in the north-facing window-to-wall ratio from 0.05 to 0.70, the annual cooling load per unit area increased from 132.87 kW·h/m² to 135.13 kW·h/m², and the annual heat load per unit area increased from 10.47 kW·h/m² to 13.85 kW·h/m².

Figure 10 and Figure 11 show the curves of the substation building energy consumption with different window-to-wall ratios when the envelope remains unchanged in the cold region model.

It can be seen that the window-to-wall ratio of substation buildings in cold regions has a significant impact on their energy consumption. In terms of cooling load, with the increase in the window-to-wall ratio, the cooling load of the substation generally shows an upward trend (except for the west orientation). It is worth noting that the cooling load changes in all directions show a linear growth trend, and there is no obvious turning point. Although the cooling demand in cold regions is relatively small, the higher cooling load can still lead to a significant increase in energy consumption during the transition season or when the equipment dissipates heat more. In terms of heat load, due to the long winter and low temperature in cold regions, the influence of window-to-wall ratio is more prominent, and the analysis shows that the increase in window-to-wall ratio will significantly increase the heat load, which is mainly due to the aggravation of heat loss caused by the reduction in thermal insulation performance of the building envelope. Looking at the average heat load in all directions, a larger window-to-wall ratio significantly increases the operating time of the heating equipment, which in turn significantly increases energy consumption. Therefore, in the design of substations in cold regions, special attention needs to be paid to the optimal selection of window-to-wall ratios.

All things considered, in the design of substations in cold areas, the window-to-wall ratio should be reasonably controlled. It is necessary not only to meet certain needs such as lighting and ventilation but also to reduce the window-to-wall ratio as much as possible to reduce energy consumption; the overall control window-to-wall ratio is below 0.30, the eastern and northern are ≤ 0.20, the southbound is ≤0.35, and the west-facing window-to-wall ratio should be controlled around 0.30. Through the scientific control of the window-to-wall ratio, the dual goals of energy saving, consumption reduction, and economic operation can be achieved under the premise of ensuring the functional requirements of the substation.

5. Differences in Contribution Rates of Energy-Consumption-Influencing Factors and Energy-Saving Design Recommendations

Based on the results of data analysis, this study adopted the linear regression method to establish a quantitative relationship model between the energy consumption of substation buildings and various factors influencing energy consumption. As shown in

Table 12. Functional relationship between the annual cumulative heating load index and the investigated building-energy factors.

Impact Factor	Linear Relation	R2
Number of shapes	y = −15.89x + 80.78	0.998
Facades	y = 17.75x + 5.929	1
Interior walls	y = −1.329x + 12.551	0.996
Roofing	y = 15.28x + 10.226	1
Exterior windows	y = 0.793x + 5.796	0.993
East window-to-wall ratio	y = 3.004x + 10.37	0.987
South window-to-wall ratio	y = 5.185x + 10.341	0.996
West window wall ratio	y = 5.374x + 8.94	0.999
North window wall ratio	y = 2.698x + 9.908	0.991

and

Table 13. Functional relationship between the annual cumulative cooling load index and the studied building energy consumption factor.

Impact Factor	Linear Relation	R2
Number of shapes	y = −17.13x + 41.87	0.999
Facades	y = 3.136x + 145.427	1
Interior walls	y = 0.068x + 146.295	0.94
Roofing	y = 3.1x + 146.056	1
Exterior windows	y = −0.671x + 102.93	0.993
East window-to-wall ratio	y = 6.585x + 133.088	1
South window-to-wall ratio	y = 3.458x + 132.782	0.996
West window wall ratio	y = 5.539x + 131.68	0.997
North window wall ratio	y = −2.568x + 135.984	0.987

, the linear regression equations between the annual cumulative heating load index, cooling load index, and key building energy consumption factors are presented, respectively. Furthermore, based on the regression coefficients of the linear regression model, visualized analysis charts of the influencing factors on energy consumption were plotted (as shown in Figure 12 and Figure 13). These mathematical models can quantitatively describe the influence patterns of building envelope parameters on energy consumption, providing a theoretical basis for the energy-saving optimization design of substation buildings.

Table 12 presents the simulation data regarding the impact of variations in various influencing factors (as analyzed previously) on the annual cumulative heating load index, along with the fitted linear regression equations between these influencing factors and heating load energy consumption. This provides mathematical model support for the subsequent quantitative evaluation of the contribution degree of each factor to the heating load.

Figure 12 employs a dual vertical axis coordinate system to conduct a visualized analysis of the effect of each influencing factor. The horizontal axis represents the parameters of influencing factors related to substation building energy consumption, including the building shape coefficient, U-values of the building envelope (including those of roofs, external walls, external windows, and internal walls), and window-to-wall ratios (for the east, west, south, and north orientations). The left vertical axis corresponds to the slope values of the linear regression equations for each influencing factor in Table 12, which reflect the marginal impact intensity of a unit change in a factor on the heating load index. The right vertical axis represents the contribution rate of each influencing factor to the annual cumulative heating load index, intuitively reflecting the overall impact weight of each factor. The curves in the figure illustrate the changing trend of the cumulative contribution rate of each influencing factor to heating load energy consumption, providing a visualized basis for key factor screening.

From the quantitative results, it can be observed that the influencing factors exhibit significant differences in their degrees of impact on the heating load: the shape coefficient, U-value of external walls, and U-value of roofs rank the highest in contribution rates, at 26.4%, 23.6%, and 22.7%, respectively. Their total cumulative contribution rate reaches 72.7%, making them key parameters requiring priority control in the energy-saving design of substations in cold regions. The window-to-wall ratio exerts a secondary impact, with variations across different orientations (7.7% for the west, 4.4% for the south, 4% for the east, and 2% for the north), and targeted optimization can be conducted in energy-saving design based on actual project requirements. The U-value of internal walls has a contribution rate of less than 1%, which exerts a negligible overall impact on the heating load; thus, it can be considered as appropriate or even omitted in optimization design according to specific project needs.

Table 13 presents the simulation data regarding the impact of variations in various influencing factors (as analyzed previously) on the annual cumulative cooling load index, along with the linear regression equations fitted between these influencing factors and cooling load energy consumption. This provides mathematical model support for the subsequent quantitative evaluation of the contribution degree of each factor to cooling load energy consumption.

Figure 13 employs a dual vertical axis coordinate system to conduct a visualized analysis of the effect of each influencing factor on cooling load energy consumption. The horizontal axis represents the parameters of influencing factors related to substation building energy consumption, including the building shape coefficient, U-values of the building envelope (including those of roofs, external walls, external windows, and internal walls), and window-to-wall ratios (for the east, west, south, and north orientations). The left vertical axis corresponds to the slope values of the linear regression equations for each influencing factor in Table 13, which reflect the marginal impact intensity of a unit change in a factor on the cooling load index. The right vertical axis represents the contribution rate of each influencing factor to the annual cumulative cooling load index, intuitively reflecting the overall impact weight of each factor. The curves in the figure illustrate the changing trend of the cumulative contribution rate of each influencing factor to cooling load energy consumption, providing a visualized basis for key factor screening.

Similarly, the quantitative results indicate that the influencing factors are ranked by their contribution degree in descending order as follows: building shape coefficient (17.13), east-facing window-to-wall ratio (6.585), west-facing window-to-wall ratio (5.539), south-facing window-to-wall ratio (3.458), external wall U-value (3.136), roof U-value (3.1), north-facing window-to-wall ratio (2.568), external window U-value (0.671), and internal wall U-value (0.068). Among these, the key influencing factors are the building shape coefficient, east-facing window-to-wall ratio, and west-facing window-to-wall ratio—their cumulative contribution ratio constitutes the “vital few”, while the remaining factors such as external wall U-value, roof U-value, and north-facing window-to-wall ratio fall into the category of the “trivial many”. This result exhibits a significant difference from the key influencing factors of the heating load, highlighting that due to the substantial heat generation from internal equipment in substation buildings, the composition of their cooling loads is distinctly different from that of ordinary civil buildings. The cooling demand relies more on the rational control of building form and the scale of window openings in the east and west orientations, rather than merely optimizing the thermal insulation performance of the building envelope.

6. Comparison of Carbon Emissions

Using YJK-Green software (V2025_r1.0), this study calculated the cradle-to-grave carbon emissions of both the as-built scheme and the scheme redesigned according to the proposed rules so as to verify the effectiveness of the new design strategy.

The accounting results show that the total carbon emissions under the existing working condition are 64.418 tCO₂/a, and the carbon emissions per unit area are 36.273 tCO₂/(a·m²); among which, the carbon emissions during the operation phase are 20.153 tCO₂/a, and the operational carbon emissions per unit area are 11.348 tCO₂/(a·m²). However, under the working condition after applying the design rules in this paper, the total carbon emissions decrease to 60.425 tCO₂/a, and the total carbon emissions per unit area are 34.025 tCO₂/(a·m²); the carbon emissions during the operation phase drop significantly to 14.904 tCO₂/a, and the operational carbon emissions per unit area are only 8.392 tCO₂/(a·m²).

It can be seen from this that the design rules and strategies proposed in this paper can effectively achieve carbon emission reduction: compared with the existing working condition, the total carbon emissions of the new working condition have decreased by 3.993 tCO₂/a, with a reduction rate of 6.19%; the reduction rate of total carbon emissions per unit area was 6.20%. More importantly, as the core link of carbon emissions, the carbon emissions during the operation phase have decreased by 5.249 tCO₂/a, with a substantial reduction rate of 26.04%, and the reduction rate of operational carbon emissions per unit area also reached 26.04%. This result fully confirms the scientific validity and practicality of the design rules and strategies in this paper for optimizing building energy efficiency, especially in reducing carbon emissions during the operation phase, and can provide strong support for the green and low-carbon design of substations in cold regions.

7. Conclusions

This study systematically analyzed the impacts of the building shape coefficient, U-values of the building envelope (including roofs, external walls, external windows, and internal walls), and window-to-wall ratios (for the east, west, south, and north orientations) on the energy consumption of fully indoor substation buildings in cold regions. By comparing the whole-life-cycle carbon emissions of buildings under current conditions and recommended operating conditions, a synergistic optimization strategy of “compact form-high-efficiency envelope-window-to-wall ratio restriction” was proposed to reduce building energy consumption and carbon emissions. Additionally, the degree of influence of each factor was quantified, and corresponding energy-saving design strategies were put forward.

(1)

Substation buildings should adopt a rectangular or near-cubic planar layout, with the building shape coefficient controlled within the range of 0.35–0.40, while maintaining the ratio of external wall length to depth between 1.2 and 1.5. In terms of functional layout, core functional rooms such as the main control room and relay room should be centrally arranged to form a compact building cluster, thereby reducing building energy consumption.

(2)

Regarding the U-values of the substation building envelope, it is recommended that the U-value of external walls be controlled between 0.20 and 0.30 W/ (m²·K), the U-value of roofs be limited to within 0.25 W/ (m²·K), and the U-value of external windows be around 2.4 W/(m²·K), so as to form a high-efficiency energy-saving building envelope.

(3)

The window-to-wall ratios of substation buildings require differentiated control based on building orientation: the west-facing window-to-wall ratio should be controlled at approximately 0.30, the east-facing and north-facing ratios should not exceed 0.20, and the south-facing ratio should not exceed 0.35. Rooms requiring air conditioning should be prioritized for location on the northern side of the building with external windows, while minimizing the window area on the western side as much as possible.