Multi-Level Loess Slope Displacement Calculation Based on Lumped Mass Method
Abstract
1. Introduction
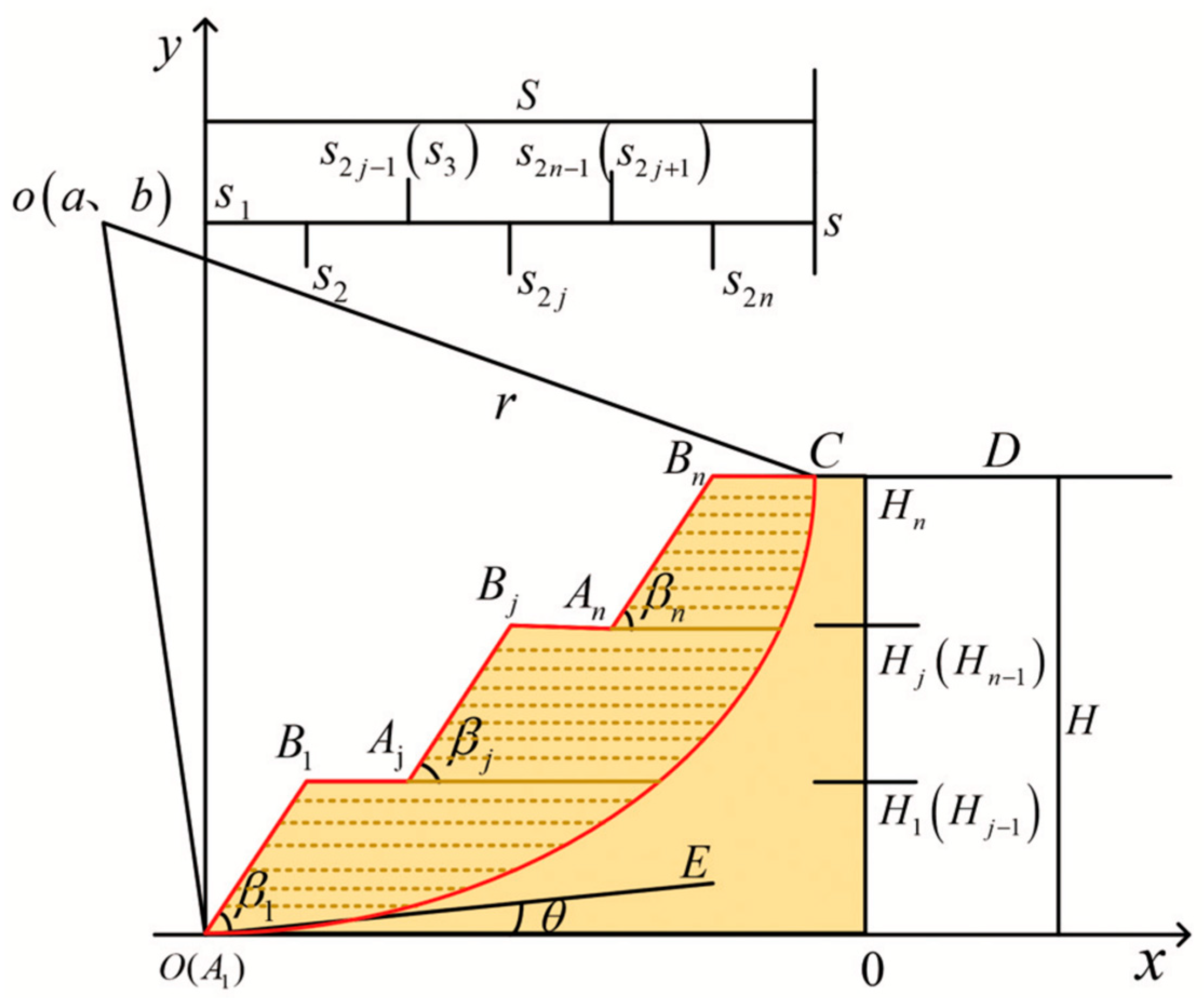
2. Theoretical Framework
3. Newmark-β Numerical Solution
4. Numerical Examples Verification and Comparative Analysis
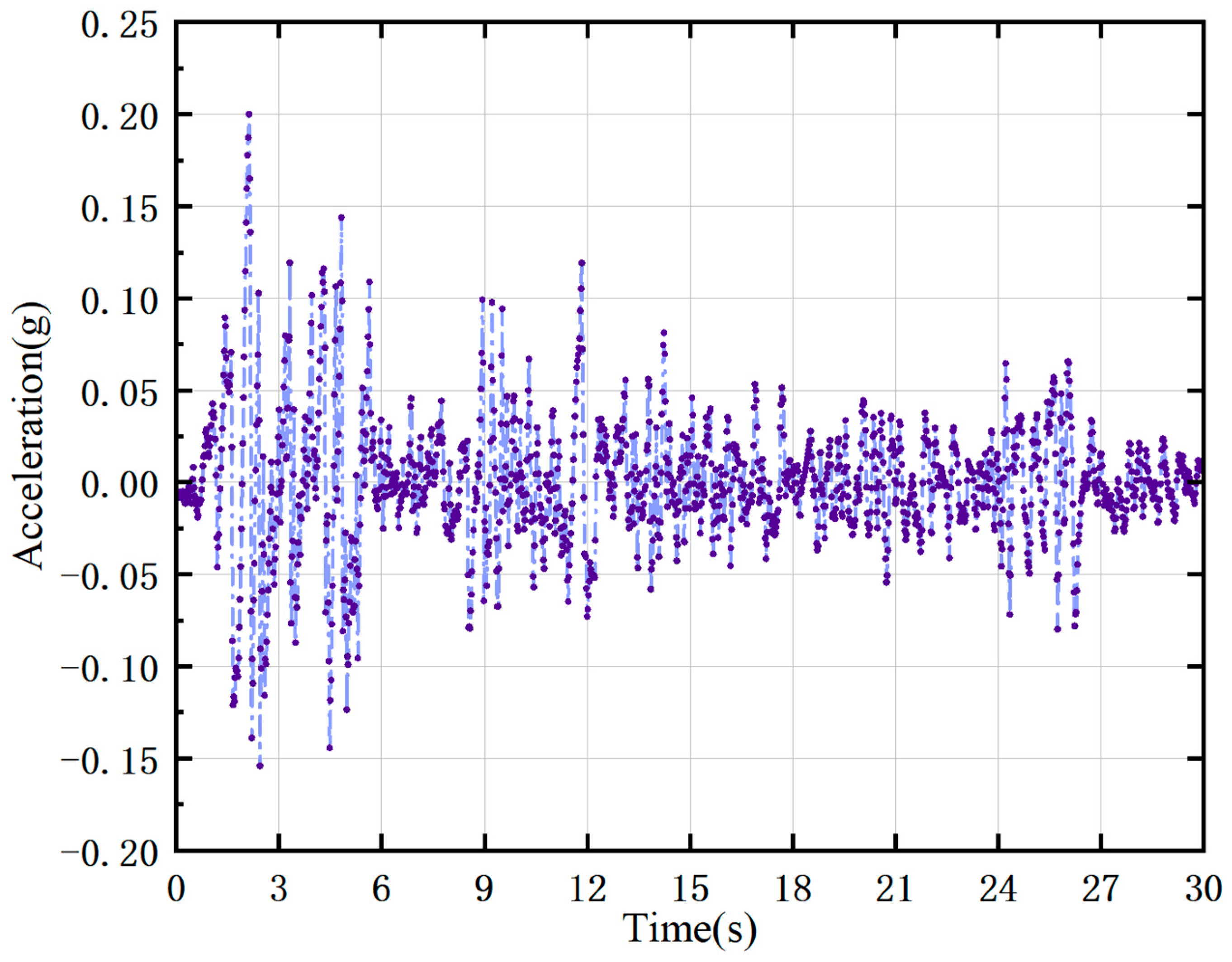
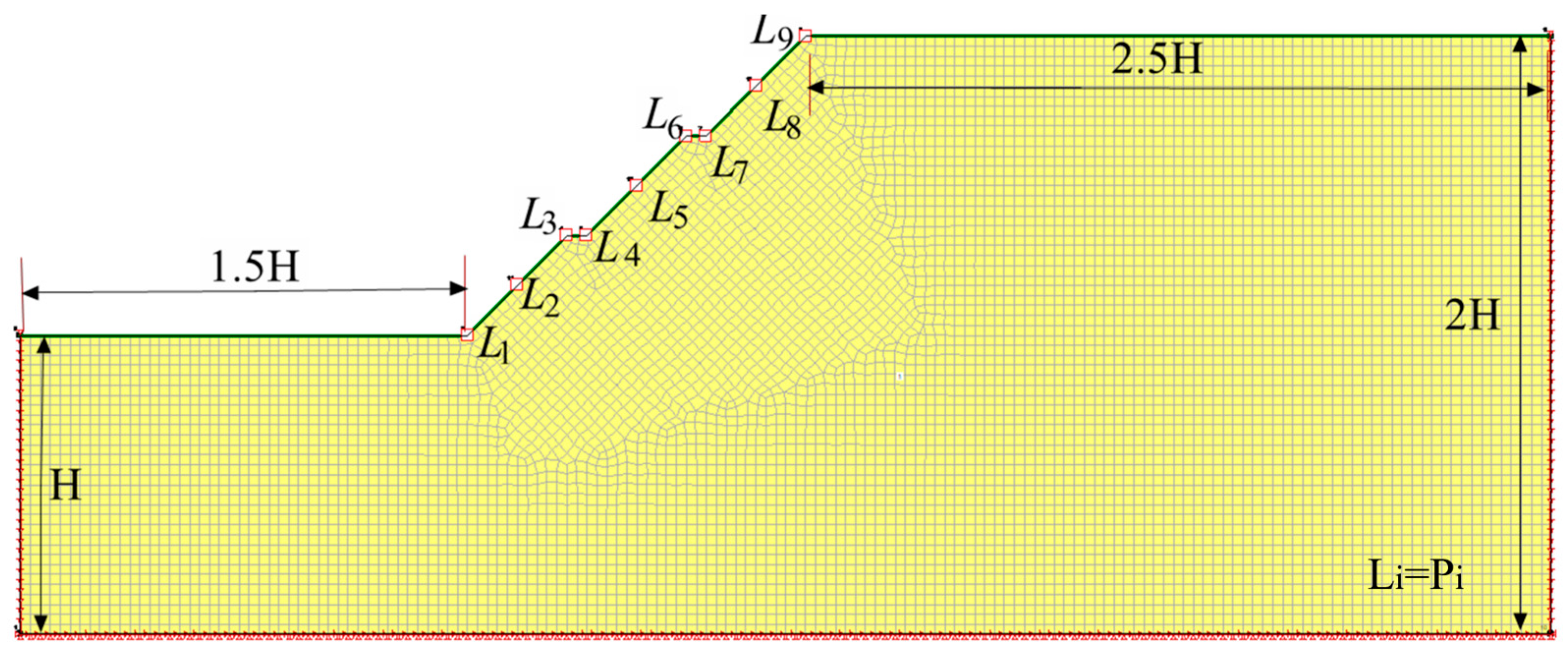
4.1. Model Establishment
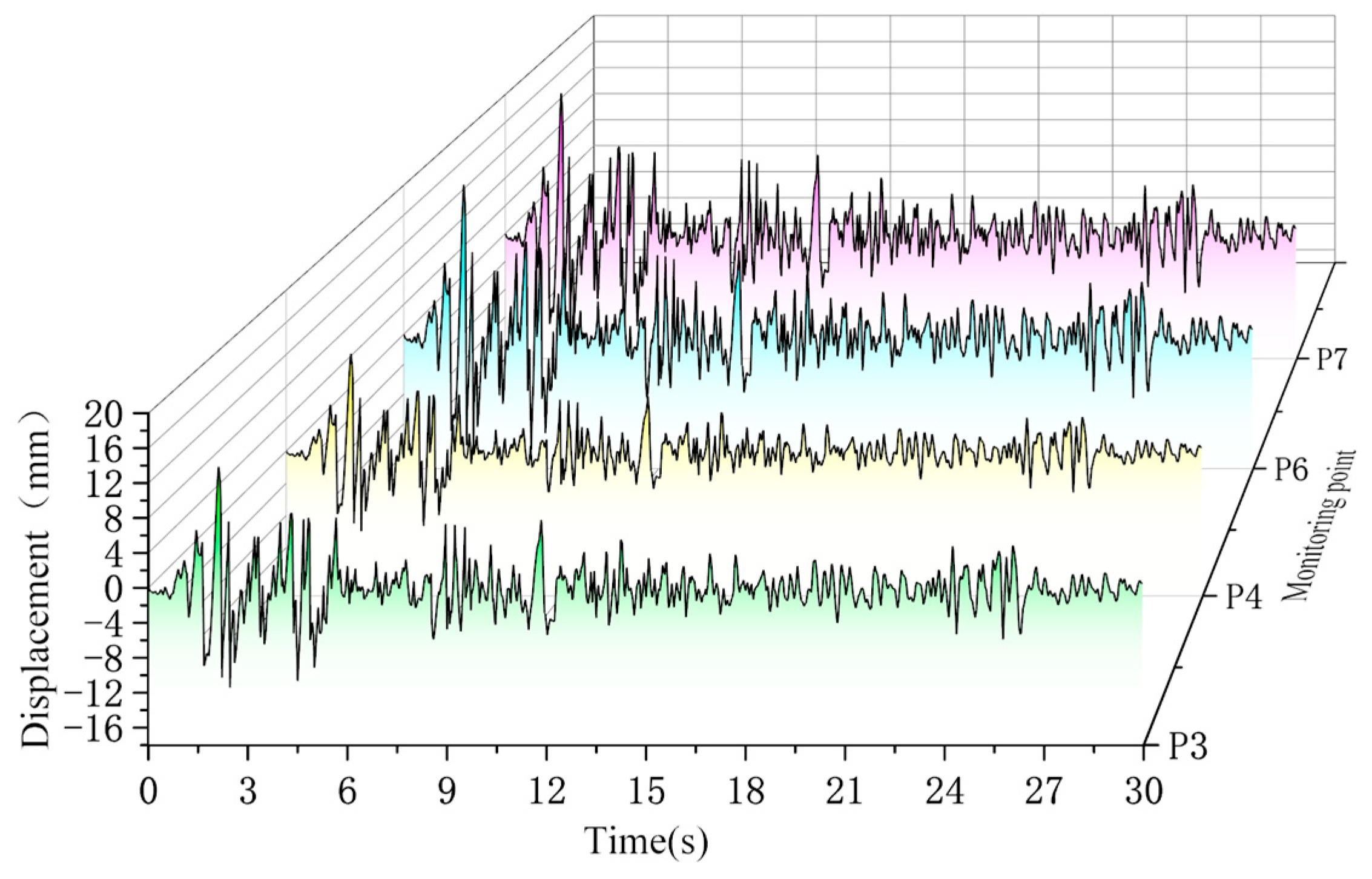
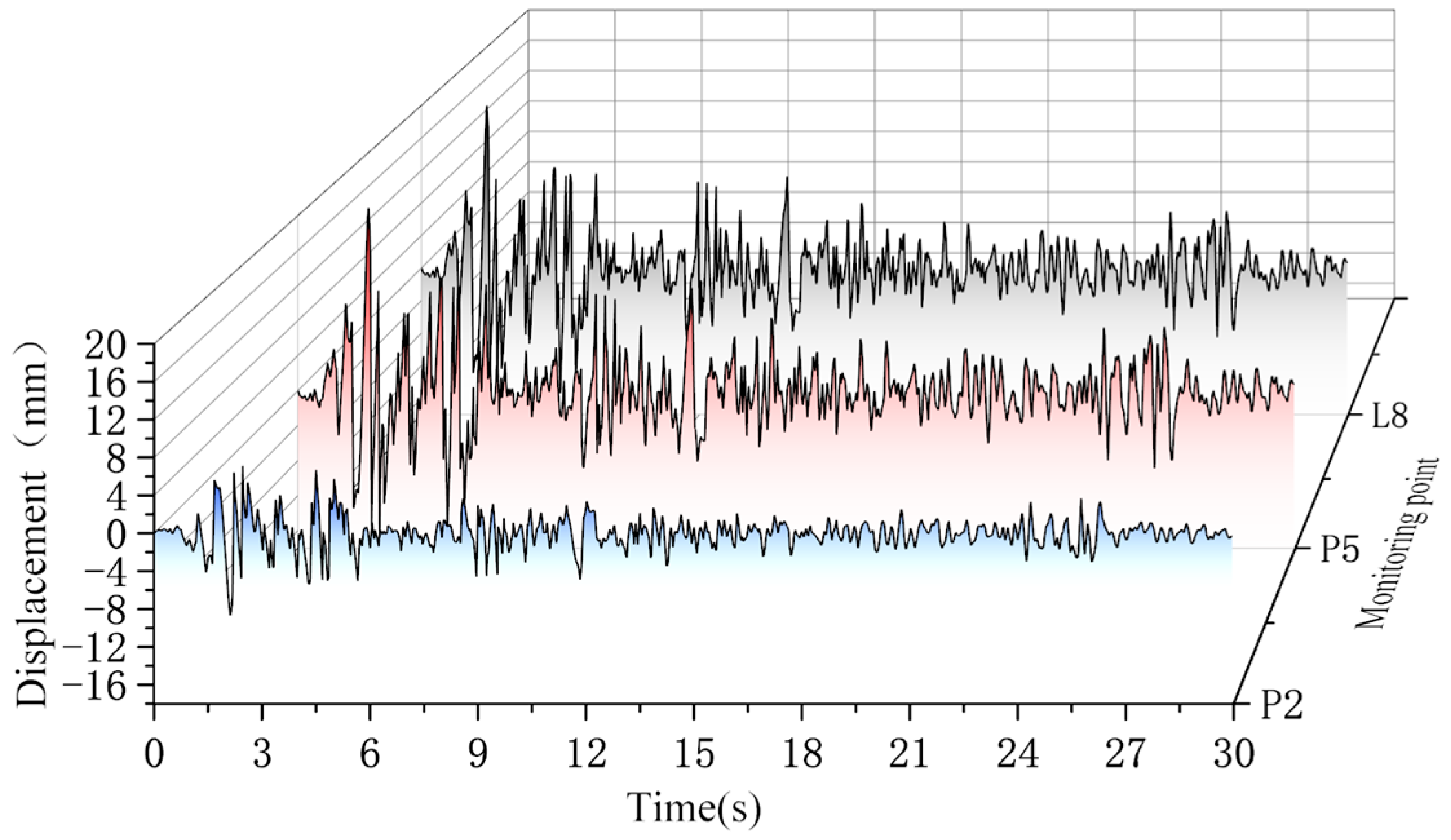
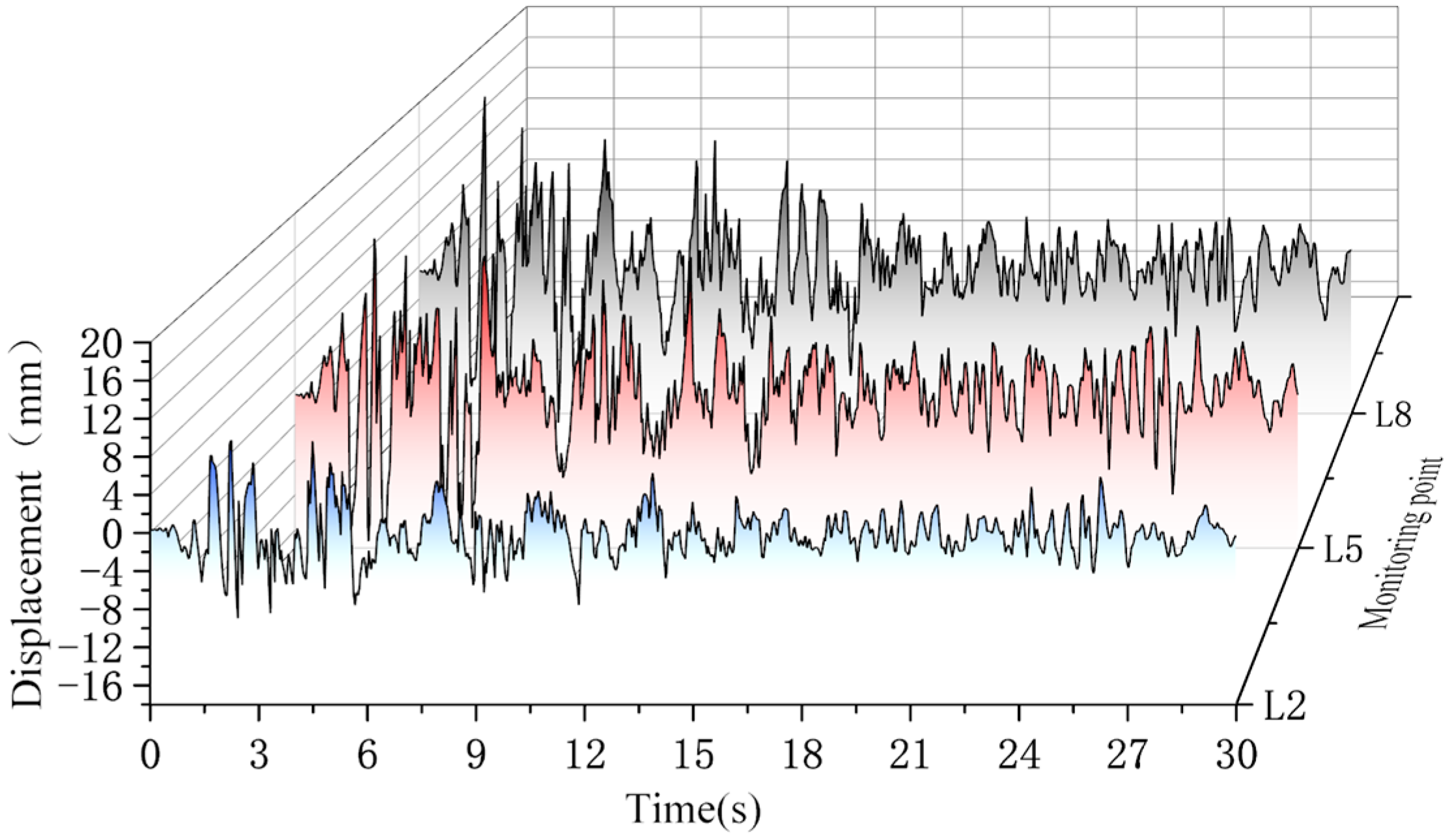
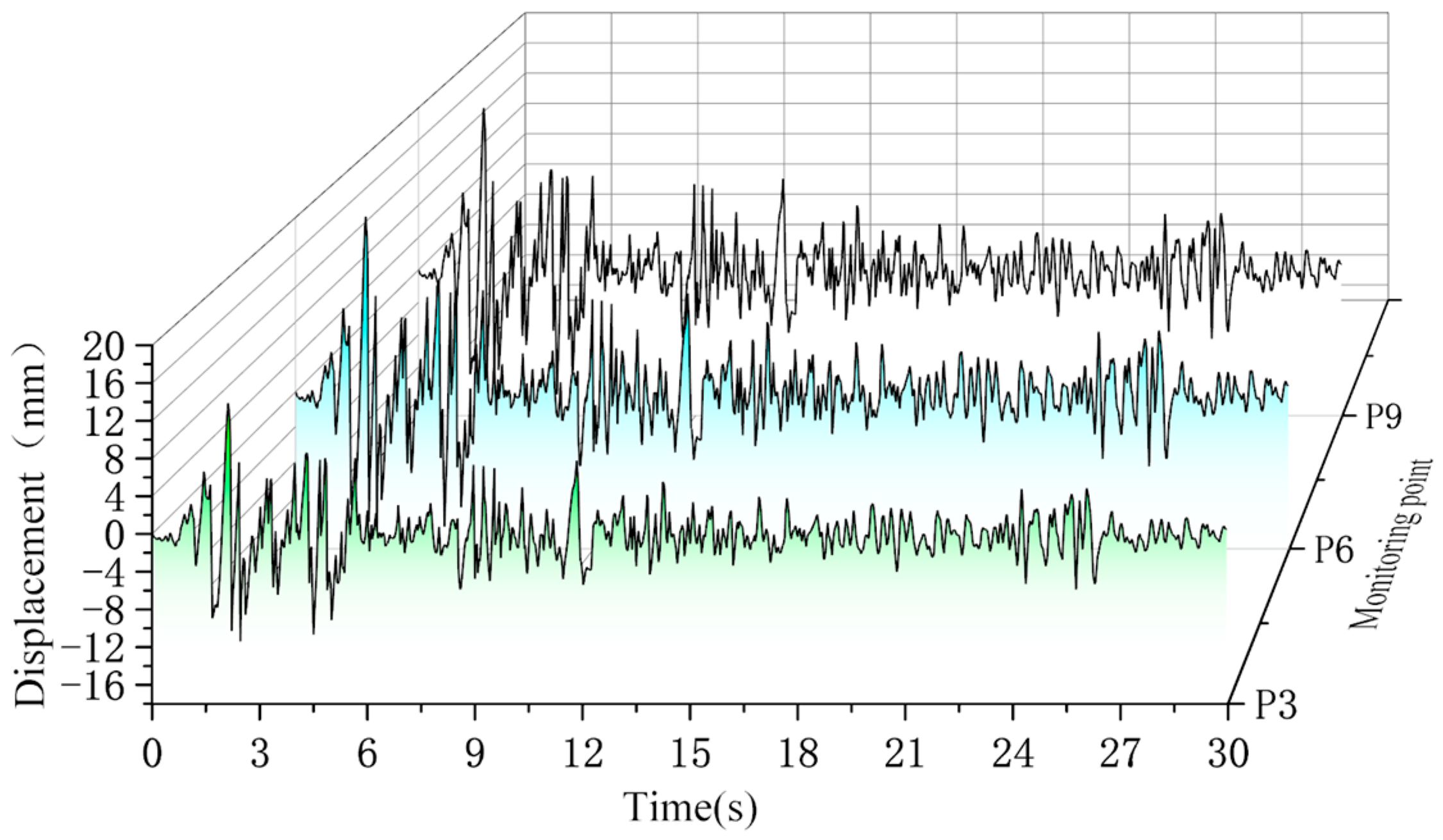
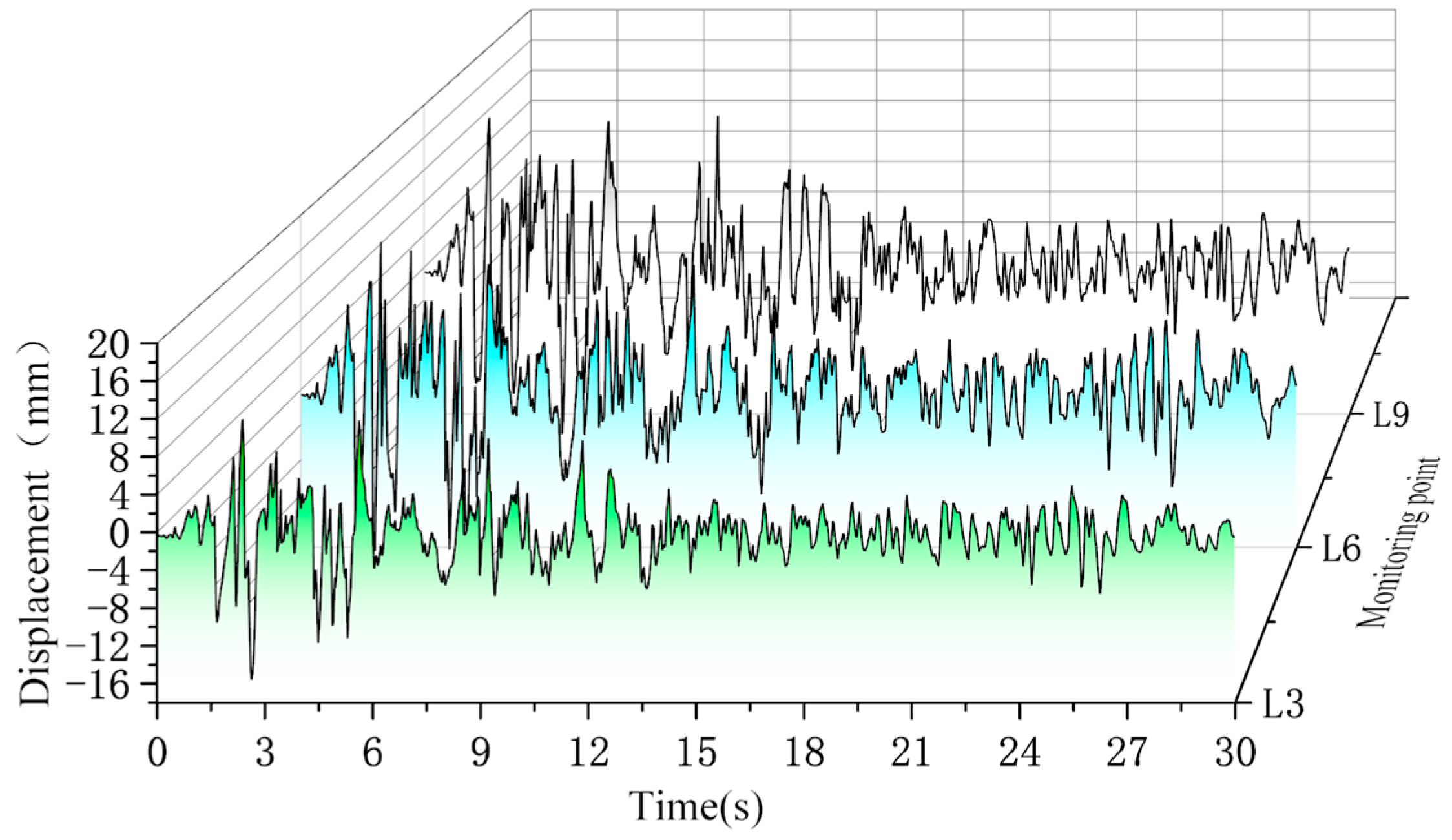
4.2. Model Validation and Comparative Analysis
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Relevant Formulas
References
- Huang, R.; Li, W. Research on development and distribution rules of geohazards induced by wenchuan earthquake on 12th may. Chin. J. Rock Mech. Eng. 2008, 27, 2585–2592. [Google Scholar]
- Huang, R. Mechanism and geomechanical modes of landslide hazards triggered by wenchuan 8.0 earthquake. Chin. J. Rock Mech. Eng. 2009, 28, 1239–1249. [Google Scholar]
- Xu, Q.; Peng, D.; Fan, X.M.; Dong, X.; Zhang, X.; Wang, X. Preliminary study on the characteristics and initiation mechanism of zhongchuan town flow slide triggered by jishishan ms 6. 2 earthquake in gansu province. Geomat. Inf. Sci. Wuhan Univ. 2025, 50, 207–222. [Google Scholar]
- Zhong, X.; Wang, Q.; Wang, Y. Characteristics of Damage to Rural Houses in the High-Intensity Area of the Jishishan Mw 6.2 Earthquake. Buildings 2024, 14, 3762. [Google Scholar] [CrossRef]
- Li, Z. The state of the art of the research on seismic landslide hazard at home and abroad. J. Catastrophology 2003, 18, 65–71. [Google Scholar]
- Li, Z.; Zhu, Y. Search model of slip surface and stability analysis of multi-step slope. Chin. J. Rock Mech. Eng. 2006, 25, 2841–2847. [Google Scholar]
- Guo, Z.; Huang, Q.; Liu, Y.; Jiang, Z.; Xie, Q.; Yu, D. Stability analysis and design optimization of multi-stage slope in gully land consolidation projects on the loess plateau. Bull. Eng. Geol. Environ. 2023, 82, 431. [Google Scholar] [CrossRef]
- Zheng, Y.; Ye, H.; Huang, R. Analysis and discussion of failure mechanism and fracture surface of slope under earthquake. Chin. J. Rock Mech. Eng. 2009, 28, 1714–1723. [Google Scholar]
- Jiang, Q.; Deng, Y.; Yang, N. Pseudo-dynamic seismic slope stability analysis based on rigorous slice method. China Earthq. Eng. J. 2023, 45, 716–723. [Google Scholar]
- Mostafaei, H.; Gilani, M.; Ghaemian, M. A comparative study between pseudo-static and dynamic analyses on rock wedge stability of an arch dam. Civ. Eng. J. 2018, 4, 179–187. [Google Scholar] [CrossRef]
- Yang, C.-W.; Zhang, J.-J.; Fu, X.; Zhu, C.-B.; Bi, J.-W. Improvement of pseudo-static method for slope stability analysis. J. Mt. Sci. 2014, 11, 625–633. [Google Scholar] [CrossRef]
- Karray, M.; Hussien, M.; Delisle, M. Framework to assess pseudo-static approach for seismic stability of clayey slopes. Can. Geotech. J. 2018, 55, 1860–1876. [Google Scholar] [CrossRef]
- Steedman, R.; Zeng, X. The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall. Geotechnique 1990, 40, 103–112. [Google Scholar] [CrossRef]
- Zeng, X.; Steedman, R. On the behaviour of quay walls in earthquakes. Geotechnique 1993, 43, 417–431. [Google Scholar] [CrossRef]
- Choudhury, D.; Nimbalkar, S. Seismic passive resistance by pseudo-dynamic method. Geotechnique 2005, 55, 699–702. [Google Scholar] [CrossRef]
- Choudhury, D.; Nimbalkar, S. Pseudo-dynamic approach of seismic active earth pressure behind retaining wall. Geotech. Geol. Eng. 2006, 24, 1103–1113. [Google Scholar] [CrossRef]
- Choudhury, D.; Nimbalkar, S. Seismic rotational displacement of gravity walls by pseudo-dynamic method: Passive case. Soil Dyn. Earthq. Eng. 2007, 27, 242–249. [Google Scholar] [CrossRef]
- Baziar, M.; Shahnazari, H.; Rabeti Moghadam, M. Sliding stability analysis of gravity retaining walls using the pseudo-dynamic method. Proc. Inst. Civ. Eng.-Geotech. Eng. 2013, 166, 389–398. [Google Scholar] [CrossRef]
- Yan, Z.; Deng, Y.; He, J.; Xuan, Y.; Wu, W. A pseudo-dynamic approach of seismic active pressure on retaining walls based on a curved rupture surface. Math. Probl. Eng. 2020, 2020, 6462034. [Google Scholar] [CrossRef]
- Deng, Y.; Xu, Z.; Sun, K. Pseudo dynamic seismic slope stability analysis method considering wave propagation effects. J. Earth Sci. Environ. 2019, 41, 623–630. [Google Scholar]
- Yan, M.; Xia, Y.; Liu, T. Limit analysis under seismic conditions of a slope reinforced with prestressed anchor cables. Comput. Geotech. 2019, 108, 226–233. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, A.; Xu, C.; Zheng, J. A modified newmark method for calculating permanent displacement of seismic slope considering dynamic critical acceleration. Adv. Civ. Eng. 2019, 2019, 9782515. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Ye, S. Calculation for permanent displacement of single slip surface of multi-stage loess slope based on energy method. Appl. Sci. 2022, 12, 8426. [Google Scholar] [CrossRef]
- Ye, S.; Xue, T.; Zhang, W. Multi-stage slope displacement analysis based on real-time dynamic newmark slider method. Soil Dyn. Earthq. Eng. 2023, 174, 108209. [Google Scholar] [CrossRef]
- Wang, D.; Li, X.; Guo, P. Analysis of the influence of step-by-step construction and prestress loss on the reinforcement of multi-stage slope by frame prestressed anchor. J. Ground Improv. 2023, 5, 383–390. [Google Scholar]
- Xue, T.; Ye, S.; Cao, C. Permanent displacement analysis of multistage loess slopes with multiple slip surfaces based on energy methods. Int. J. Geomech. 2023, 23, 04023192. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, Z.; Zhu, Y. Experimental study of the shaking table test and dynamic response of the loess slope reinforced by frame anchors. Soil Mech. Found. Eng. 2022, 59, 272–280. [Google Scholar] [CrossRef]
- Ye, S.; Huang, A. Sensitivity analysis of factors affecting stability of cut and fill multistage slope based on improved grey incidence model. Soil Mech. Found. Eng. 2020, 57, 8–17. [Google Scholar] [CrossRef]
- Wu, H.; Shao, S.; Shao, S. Variations in dynamic shear modulus of loess exposed to dry-wet cycles from xi’an area, China. Soil Dyn. Earthq. Eng. 2023, 173, 108126. [Google Scholar] [CrossRef]
- Li, J.; Ye, S.; Cui, X.; Liu, B.; Li, N. Displacement Calculation of a Multi-Stage Homogeneous Loess Slope Under Seismic Action. Buildings 2025, 15, 1484. [Google Scholar] [CrossRef]
- Ye, S.; Huang, A.; Fang, G. Dynamic response law and stability analysis of loess multi-stage high fill slope under horizontal seismic action. Technol. Earthq. Disaster Prev. 2020, 15, 1–10. [Google Scholar]
- Ye, S.; Fang, G.; Zhu, Y. Model establishment and response analysis of slope reinforced by frame with prestressed anchors under seismic considering the prestress. Soil Dyn. Earthq. Eng. 2019, 122, 228–234. [Google Scholar] [CrossRef]
- Bray, J.D.; Macedo, J. Performance-based seismic assessment of slope systems. Soil Dyn. Earthq. Eng. 2023, 168, 107–835. [Google Scholar] [CrossRef]
- Huang, B.; Ni, H.; Jin, Y.; Lu, Y. The integrated drill string dynamic model based on the lumped mass method and discrete element method. Mech. Syst. Signal Process. 2024, 221, 111723. [Google Scholar] [CrossRef]
- Makdisi, F.; Seed, H. Simplified procedure for estimating dam and embankment earthquake-induced deformations. J. Geotech. Eng. Div. 1978, 104, 849–867. [Google Scholar] [CrossRef]
- Kramer, S.; Smith, M. Modified newmark model for seismic displacements of compliant slopes. J. Geotech. Geoenvironmental Eng. 1997, 123, 635–644. [Google Scholar] [CrossRef]
- Acheampong, L.; Bryson, S. Estimation of unsaturated small-strain shear modulus in a laboratory test box and field site from a soil-water characteristic curve. Transp. Geotech. 2025, 52, 101599. [Google Scholar] [CrossRef]
- Zhang, W.; Han, L.; Feng, L.; Ding, X.; Wang, L.; Chen, Z.; Liu, H.; Aljarmouzi, A.; Sun, W. Study on seismic behaviors of a double box utility tunnel with joint connections using shaking table model tests. Soil Dyn. Earthq. Eng. 2020, 136, 106118. [Google Scholar] [CrossRef]
- Patil, M.; Choudhury, D.; Ranjith, P.; Zhao, J. Behavior of shallow tunnel in soft soil under seismic conditions. Tunn. Undergr. Space Technol. 2018, 82, 30–38. [Google Scholar] [CrossRef]
- Ma, C.; Lu, D.; Du, X.; Qi, C. Effect of buried depth on seismic response of rectangular underground structures considering the influence of ground loss. Soil Dyn. Earthq. Eng. 2018, 106, 278–297. [Google Scholar] [CrossRef]


| Soil Parameters | Numerical Value |
|---|---|
| Weight density of soil, γ (kN/m3) | 16.8 |
| Internal friction angle, φ (◦) | 24 |
| Cohesion, c (kPa) | 16 |
| Dynamic shear modulus, G (MPa) | 220 |
| Poisson’s ratio | 0.3 |
| Damping ratio | 0.1 |
| - | Monitoring Point | P3/L3 | P4/L4 | P6/L6 | P7/L7 |
|---|---|---|---|---|---|
| Peak Displacement /mm | Theoretical results | 15.43 | 14.87 | 21.48 | 21.59 |
| Simulation results | 15.54 | 15.38 | 20.02 | 20.07 |
| - | Monitoring Point | P2/L2 | P5/L5 | P8/L8 |
|---|---|---|---|---|
| Peak Displacement /mm | Theoretical results | 9.28 | 21.30 | 20.38 |
| Simulation results | 10.04 | 20.41 | 20.76 |
| - | Monitoring Point | P3/L3 | P6/L6 | P9/L9 |
|---|---|---|---|---|
| Peak Displacement /mm | Theoretical results | 15.43 | 21.48 | 20.47 |
| Simulation results | 15.54 | 20.02 | 19.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Ye, S.; Li, J.; Ye, W. Multi-Level Loess Slope Displacement Calculation Based on Lumped Mass Method. Buildings 2025, 15, 3695. https://doi.org/10.3390/buildings15203695
Liu B, Ye S, Li J, Ye W. Multi-Level Loess Slope Displacement Calculation Based on Lumped Mass Method. Buildings. 2025; 15(20):3695. https://doi.org/10.3390/buildings15203695
Chicago/Turabian StyleLiu, Bo, Shuaihua Ye, Jingbang Li, and Weina Ye. 2025. "Multi-Level Loess Slope Displacement Calculation Based on Lumped Mass Method" Buildings 15, no. 20: 3695. https://doi.org/10.3390/buildings15203695
APA StyleLiu, B., Ye, S., Li, J., & Ye, W. (2025). Multi-Level Loess Slope Displacement Calculation Based on Lumped Mass Method. Buildings, 15(20), 3695. https://doi.org/10.3390/buildings15203695





