Settlement Relevant Load Combinations and Force Redistribution in Structural Design
Abstract
1. Introduction
2. Materials and Methods
- A relatively flexible frame-type system,
- A relatively stiff wall-type system.
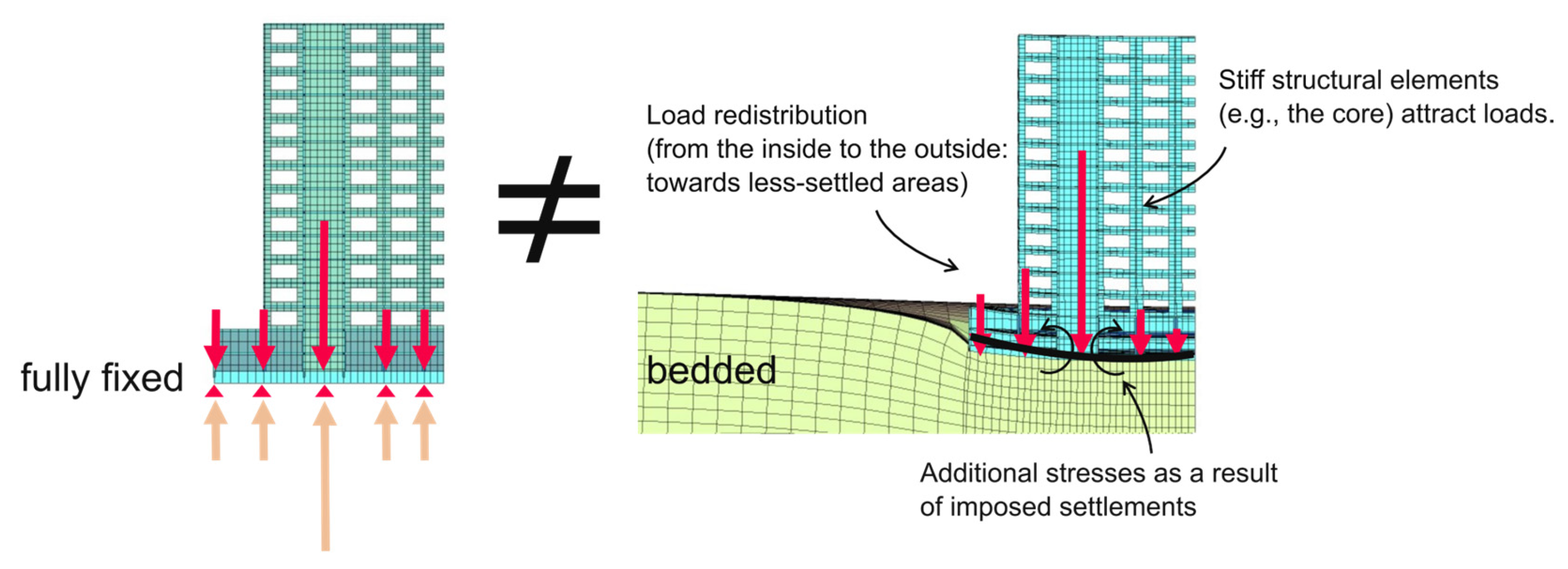
- Fixed horizontal displacements along the model boundaries and symmetry planes,
- A fully fixed base, and
- No-flow conditions at the bottom and along symmetry planes for consolidation analyses.
- Initial phase: Generation of initial in situ soil stresses.
- Excavation phase: Deactivation of the building pit; pit walls supported by prescribed displacements, which are fixed to zero; reset small-strain and displacements to zero.
- Foundation phase: Activation of the foundation slab including self-weight; reset displacements to zero.
- Superstructure phase: Activation of the “as-built” structure represented by linear-elastic plate and beam elements; surface loads corresponding to the selected load combinations applied; reset displacements to zero.
- Consolidation analysis (optional): Time-dependent analysis over a period of 30 years.
- Sequenced loading (optional): Final increase in variable loads after consolidation.
- Methodological constraints:
- ○
- Deterministic modeling without a full probabilistic framework.
- ○
- No validation against large-scale experimental data due to lack of suitable datasets.
- ○
- Use of the HSS model only, without comparison to other advanced constitutive models.
- Structural limitations:
- ○
- Only two idealized, symmetric structural systems (flexible frame-type and stiff wall-type).
- ○
- No consideration of asymmetric layouts, eccentric loading, or adjacent structures.
- ○
- Linear-elastic modeling of the foundation slab, without cracking or concrete creep.
- Geotechnical simplifications:
- ○
- Primary consolidation only, without soil creep.
- ○
- No anisotropy in stiffness or permeability.
- ○
- Fixed groundwater table, neglecting seasonal fluctuations.
- ○
- No coupled thermal–hydro-mechanical effects.
3. Settlement Relevant Load Combination
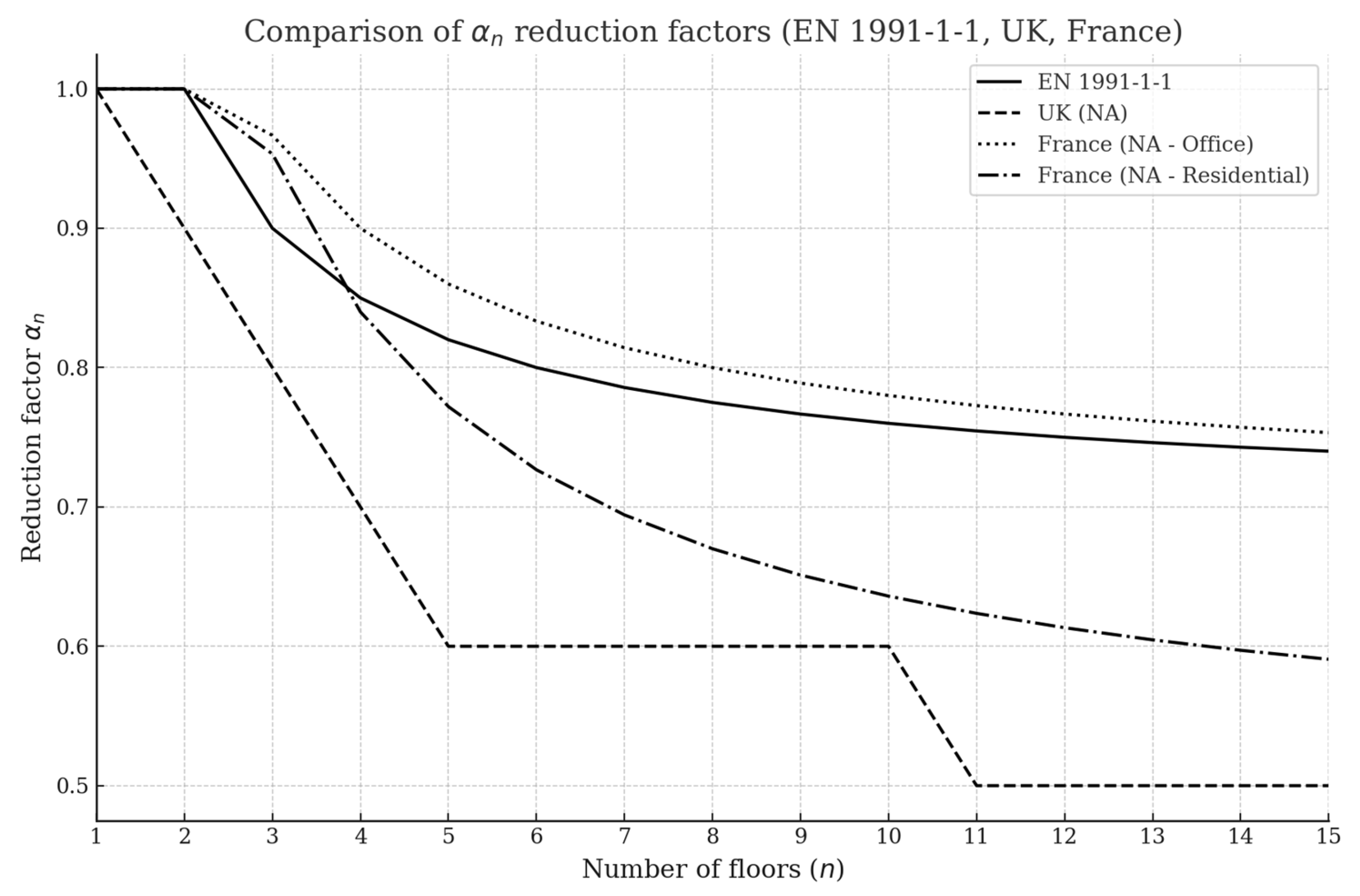
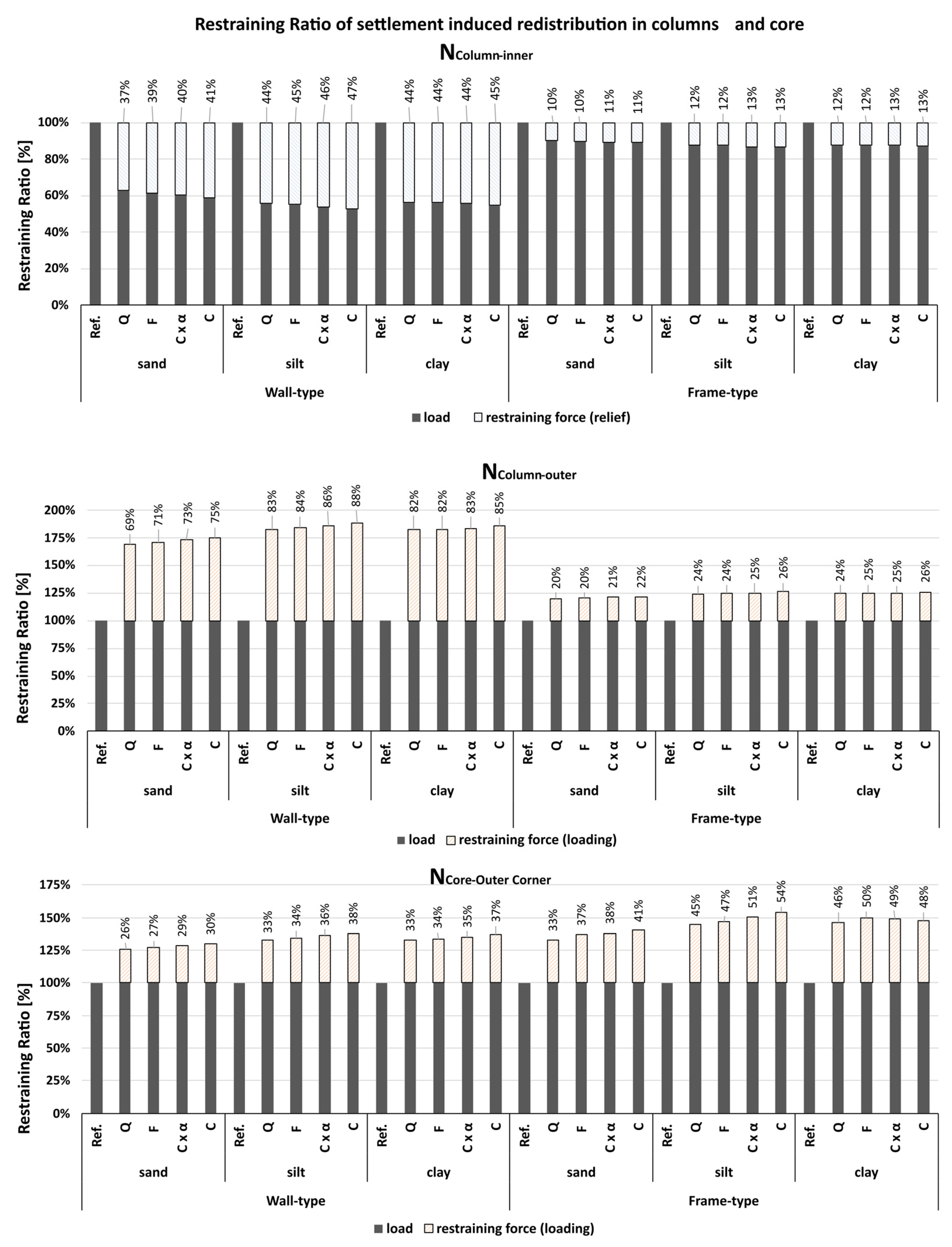
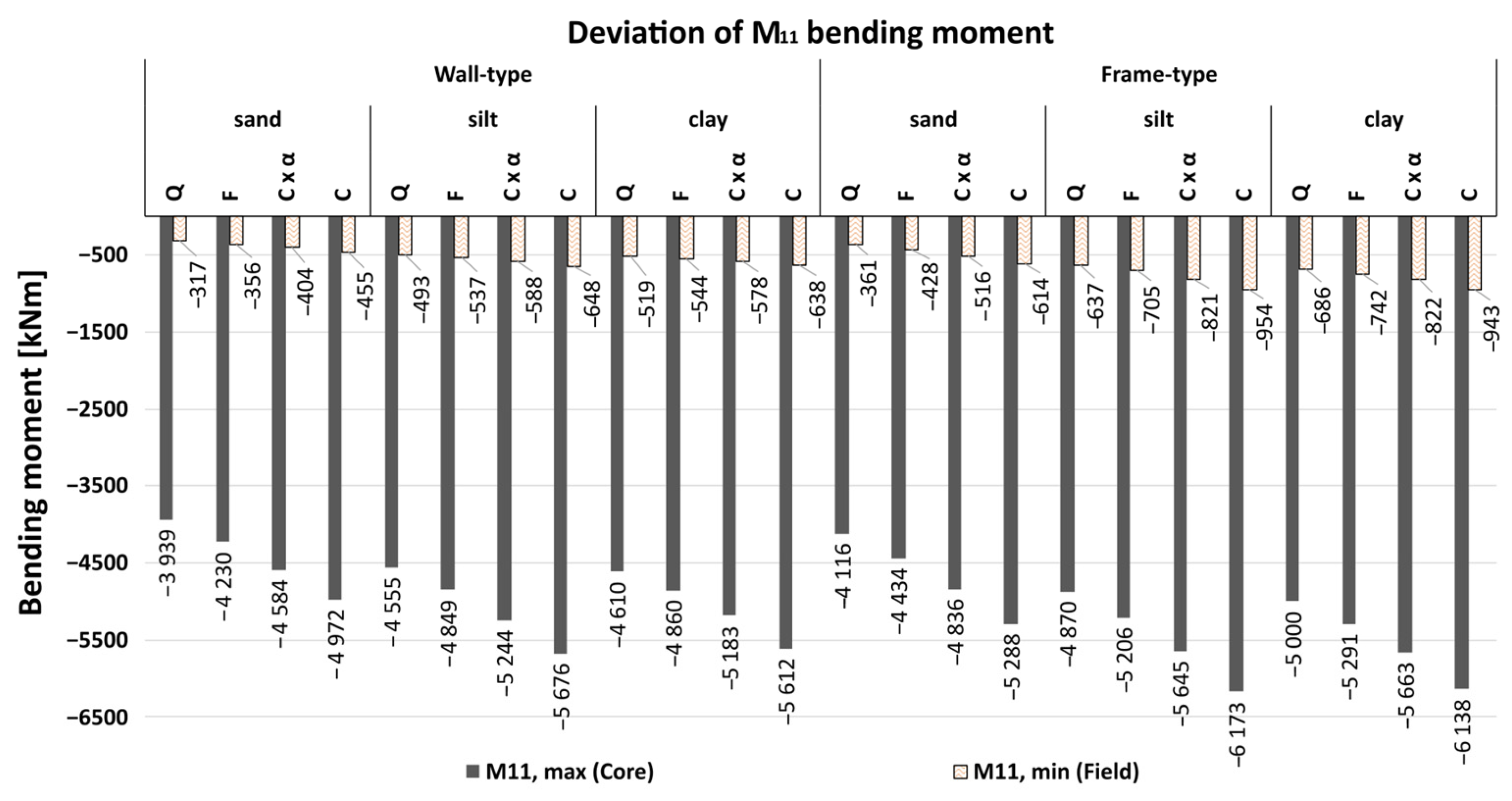
3.1. Load Redistribution Depending on Load Combination
- the quasi-permanent combination,
- the frequent combination,
- the characteristic combination with partial reduction factor αa,
- the characteristic combination.
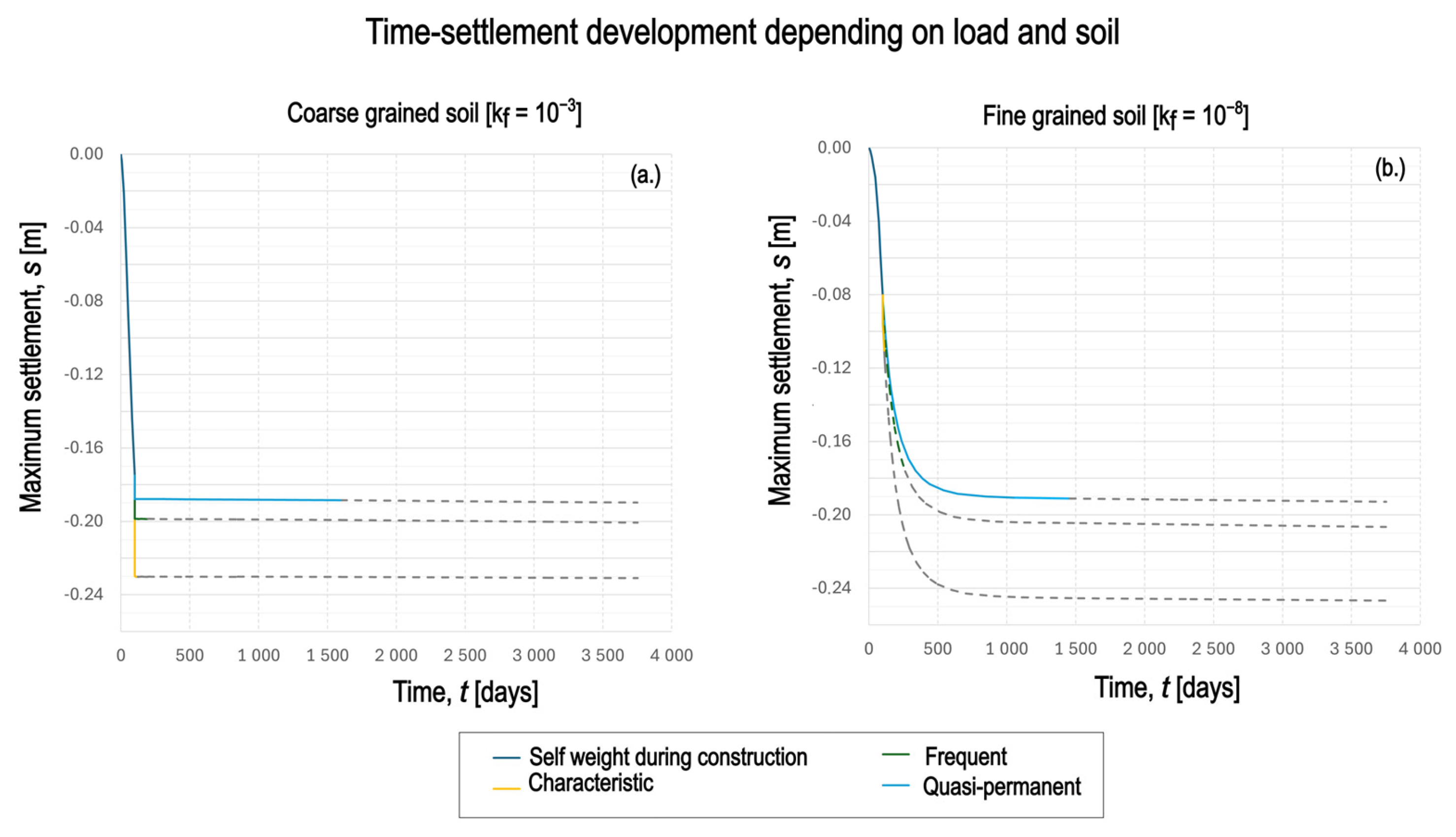
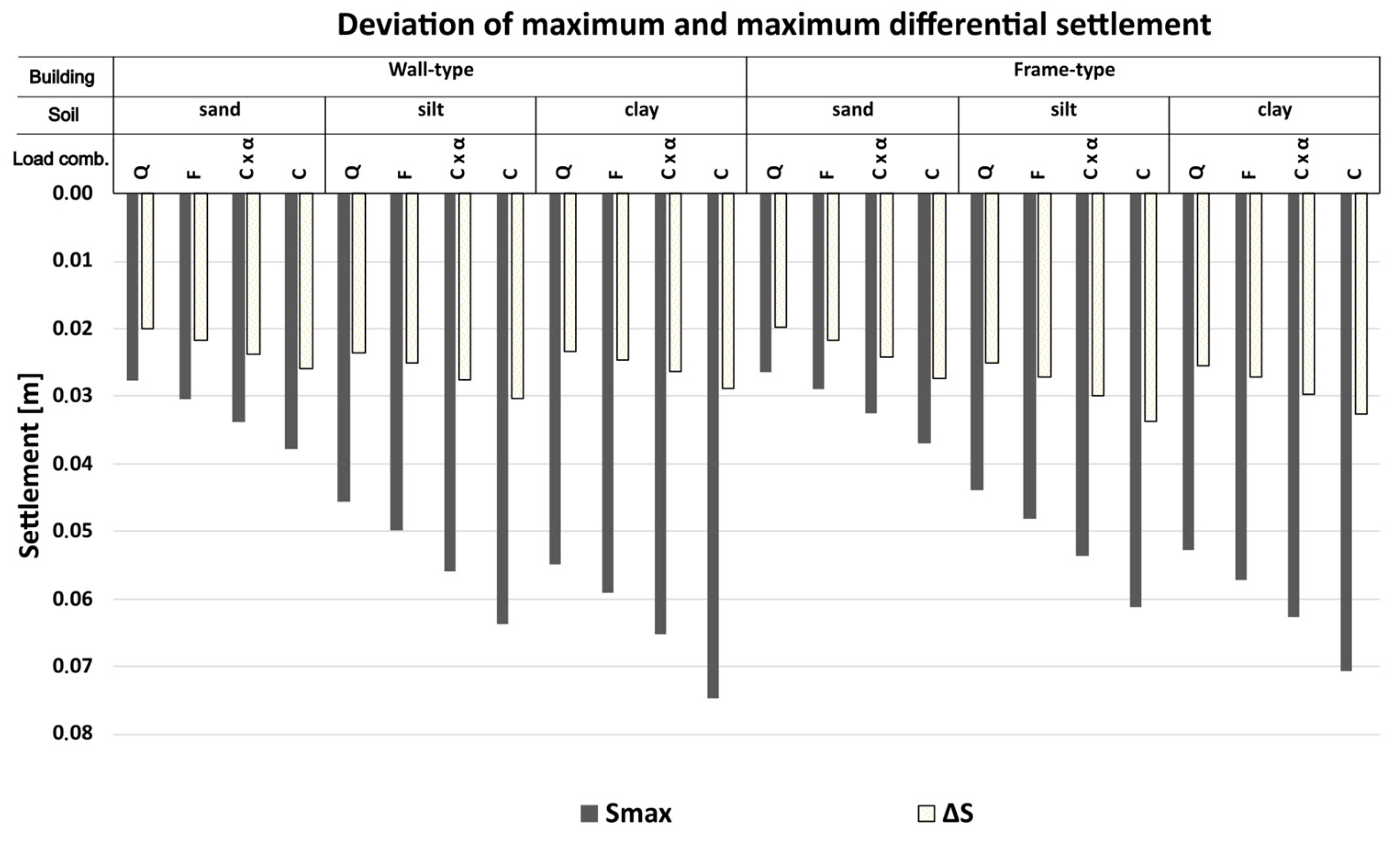
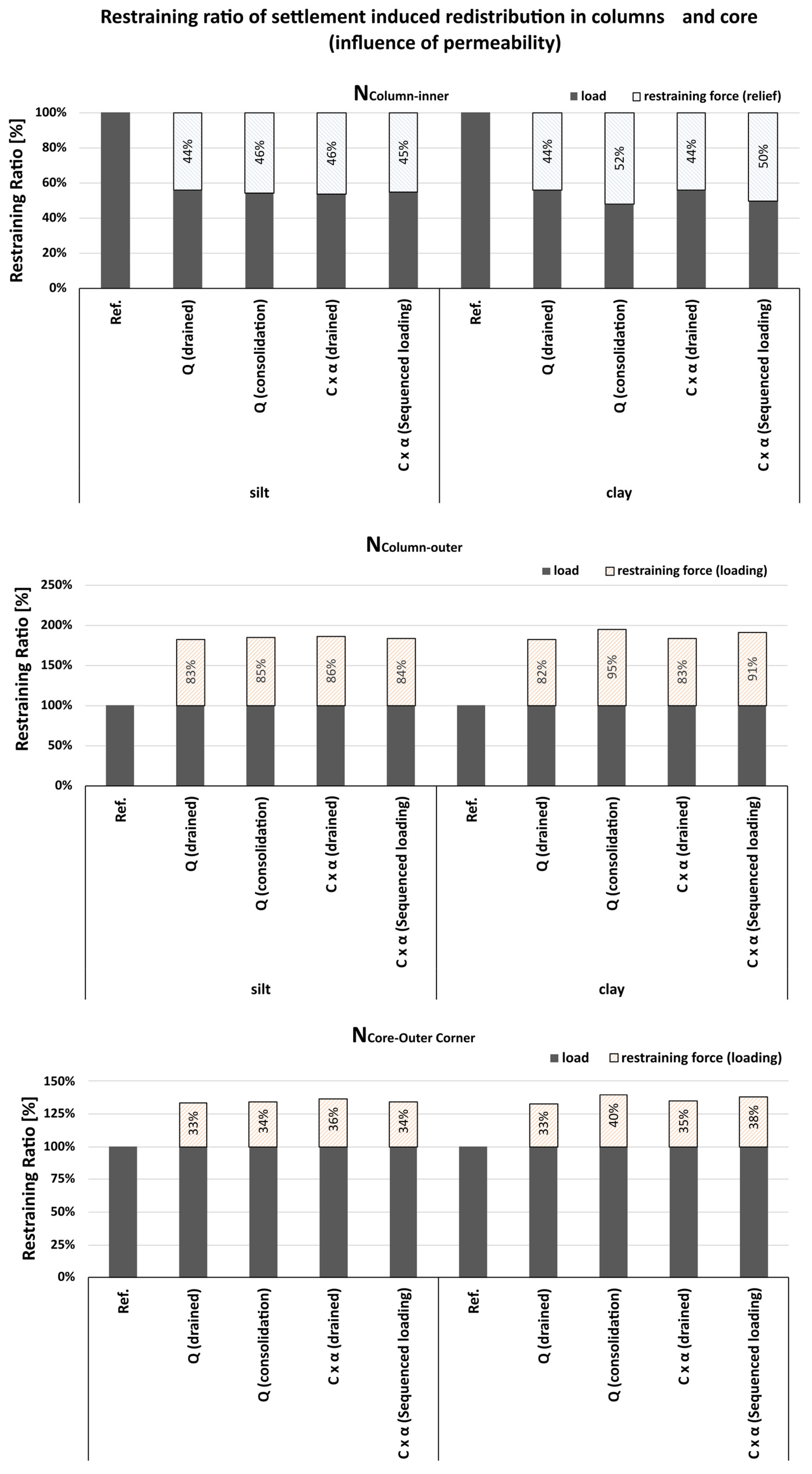
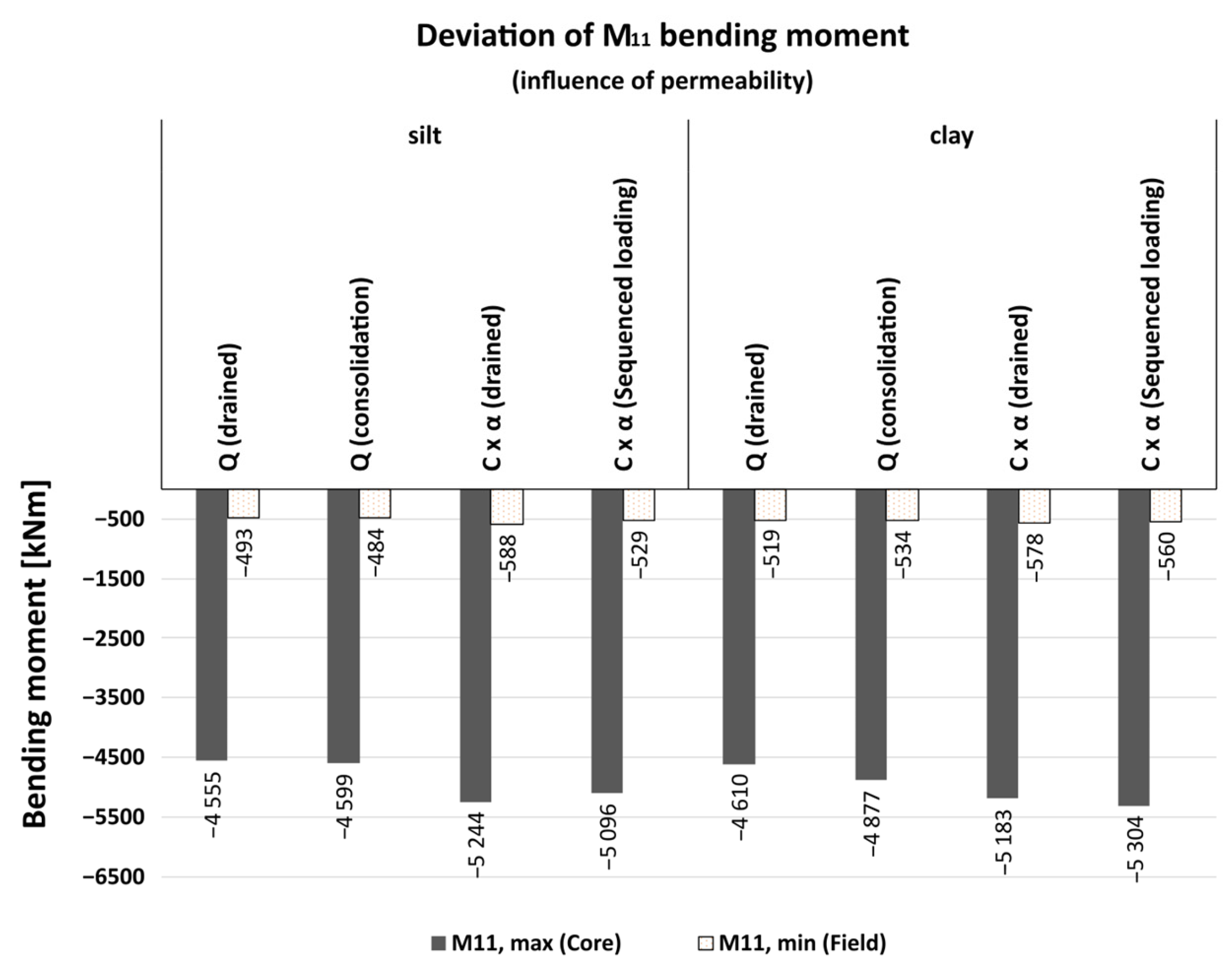
3.2. Influence of Permeability on Settlement Relevant Load Combination
- Time-consolidated settlement case: Continuous quasi-permanent loading over 30 years, representing the long-term settlement trough in cohesive soils.
- Sequenced loading case: A sudden application of the reduced characteristic load combination (including α) for one day after 30 years of consolidation.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EN1990:2002; CEN Eurocode—Basis of Structural Design. European Committee for Standardization: Brussels, Belgium, 2002.
- Witt, K.J. Grundbau-Taschenbuch, Part 3: Foundations and Geotechnical Structures, 8th ed.; Wilhelm Ernst & Sohn: Berlin, Germany, 2018; ISBN 978-3-433-03153-7. [Google Scholar]
- Wendehorst. Bautechnische Zahlentafeln, 35th ed.; Springer Vieweg: Wiesbaden, Germany, 2021; ISBN 978-3-658-32792-7. [Google Scholar]
- Boley, C.; Schmidt, H.-H.; Buchmaier, R.F. Handbook of Geotechnics: Fundamentals—Applications—Practical Experience, 2nd ed.; Springer Vieweg: Wiesbaden, Germany, 2019; ISBN 978-3-658-03054-4. [Google Scholar]
- Vogt-Breyer, C.; Schmidt, H.-H.; Buchmaier, R.F. Fundamentals of Geotechnics; Springer Vieweg: Wiesbaden, Germany, 2014. [Google Scholar]
- Krapfenbauer, T.J. Construction Tables: Textbook and Handbook for Civil Engineering, 19th ed.; Austrian Standards Institute: Vienna, Austria, 2013; ISBN 978-3-7100-2872-4. [Google Scholar]
- Schlicke, D.; Tschuchnigg, F.; Fischnaller, H.; Pfaff, K. Structural analysis and design of buildings using 3D global models. In BetonKalender 2024; Ch. VIII; Ernst & Sohn: Berlin, Germany, 2023; pp. 505–571. [Google Scholar]
- Fischer, D. Interaction between soil and structure—Permissible differential settlements and stresses of structures and foundations. In Mitteilungen des Instituts für Bodenmechanik und Felsmechanik der Universität Karlsruhe; Heft 21: Karlsruhe, Germany, 2009. [Google Scholar]
- Resch, J. Concept for Settlement-Relevant Load Combinations Considering Construction Stages and Soil–Structure Interaction. Master’s Thesis, Institute of Concrete Structures, Graz University of Technology, Graz, Austria, 2025. [Google Scholar]
- Rackwitz, R. Actions on structures. In Der Ingenieurbau; Structural Reliability, Actions; Ernst & Sohn: Berlin, Germany, 1998; Volume 8, pp. 73–408. [Google Scholar]
- EN 1990:2013; Eurocode—Basis of Structural Design. Austrian Standards Institute: Vienna, Austria, 2013.
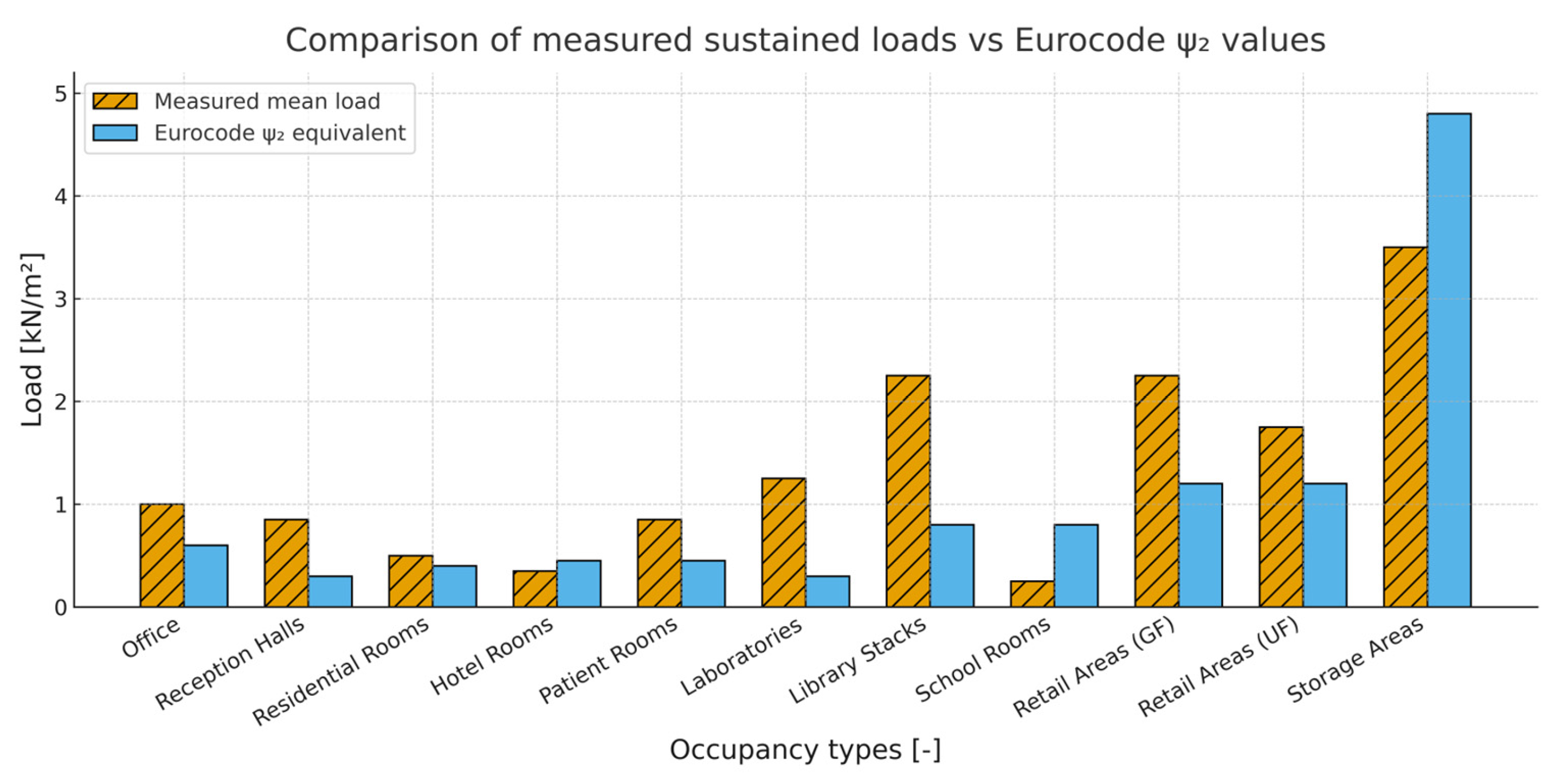
- Kumar, S. Live loads in office buildings: Point-in-time load intensity. Build. Environ. 2002, 37, 79–89. [Google Scholar] [CrossRef]
- Ruiz, S.E.; Soriano, A. Design live loads for office buildings in Mexico and the United States. J. Struct. Eng. 1997, 123, 816–822. [Google Scholar] [CrossRef]
- Choi, E.C.C. Live load in office buildings: Point-in-time load intensity of rooms. Proc. ICE—Struct. Build. 1992, 94, 299–306. [Google Scholar] [CrossRef]
- Culver, C.G. Survey Results for Fire Loads and Live Loads in Office Buildings; National Bureau of Standards Report; National Bureau of Standards: Washington, DC, USA, 1976.
- Mitchell, G.R.; Woodgate, R.W. Floor Loadings in Office Buildings: The Results of a Survey; Building Research Station: Watford, UK, 1971. [Google Scholar]
- Smit, G.; Clayton, C. The behaviour of modern flexible framed structures undergoing differential settlements. In Proceedings of the 5th International Young Geotechnical Engineers’ Conference, Paris, France, 31 August–1 September 2013; IOS Press: Amsterdam, Netherlands, 2013; pp. 285–288. [Google Scholar]
- Müller, D.; Tran, N.L.; Graubner, C.-A. Stochastic simulation of imposed loads in buildings. In Proceedings of the 12th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP12), Vancouver, BC, Canada, 12–15 July 2018. [Google Scholar]
- Honfi, D. Serviceability floor loads. Struct. Saf. 2014, 50, 27–38. [Google Scholar] [CrossRef]
- EN 1991-1-1:2011; Eurocode 1—Actions on Structures, Part 1-1: Densities, Self-Weight, Imposed Loads for Buildings. Austrian Standards Institute: Vienna, Austria, 2011.
- BSI. UK National Annex to Eurocode 1: Actions on Structures—Part 1-1 (BS EN 1991-1-1:2002); British Standards Institution: London, UK, 2002. [Google Scholar]
- AFNOR. NF P 06-111-2: National Annex to NF EN 1991-1-1—Eurocode 1: Actions on Structures; AFNOR: Paris, France, 2004. [Google Scholar]
- Schlicke, D. Resource-responsible construction with concrete through agile structural design. In Agile Digitalisierung im Baubetrieb: Innovative Wege zur Transformation und Best Practices; Springer: Wiesbaden, Germany, 2023; pp. 683–699. [Google Scholar]
- Stummer, S. Influence of Structural Stiffness on Settlement Behavior and Practical Advices. Master’s Thesis, Institute of Concrete Structures, Graz University of Technology, Graz, Austria, 2025. [Google Scholar]
- Stopp, K. Load-Bearing and Deformation Behaviour of Large-Area Founded Reinforced Concrete Structures Considering Soil–Structure Interaction. Ph.D. Thesis, Bergische Universität Wuppertal, Wuppertal, Germany, 2010. [Google Scholar]
- Sofistik, A.G. SOFiSTiK Structural Analysis Software, Version 2023; SOFiSTiK: Bavaria, Germany, 2023. [Google Scholar]
- Brinkgreve, R.; Engin, E.; Swolfs, W. PLAXIS 3D Reference Manual, Version 2024.3; Bentley Systems: Delft, The Netherlands, 2024. [Google Scholar]
- AK 2.4 “Excavations”. Recommendations of the Working Group ‘Numerics in Geotechnics’—EANG, 1st ed.; Ernst & Sohn: Berlin, Germany, 2014. [Google Scholar]
- Tschuchnigg, F. 3D Finite Element Modelling of Deep Foundations Employing an Embedded Pile Formulation. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2012. [Google Scholar]
- Von Soos, P.; Engel, J. Soil and rock properties—Their determination. In Grundbau-Taschenbuch, Part 1, 8th ed.; Witt, K.J., Ed.; Ernst & Sohn: Berlin, Germany, 2017; pp. 142–143. [Google Scholar]
- Benz, T. Small-Strain Stiffness of Soils and its Numerical Consequences. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2007. [Google Scholar]
- EN1997-1:2004; CEN Eurocode 7—Geotechnical Design, Part 1: General Rules. European Committee for Standardization: Brussels, Belgium, 2004.
- EN1992-1-1:2004; CEN Eurocode 2—Design of concrete structures, Part 1-1: General rules and rules for buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- fib. fib Model Code for Concrete Structures 2010; Ernst & Sohn: Berlin, Germany, 2013; ISBN 978-3-433-03061-5. [Google Scholar]
- Wallner, C.; Tschuchnigg, F.; Schlicke, D. Limits of linear-elastic soil in soil–structure interaction. Beton- Und Stahlbetonbau 2025, 120, 484–493. [Google Scholar] [CrossRef]

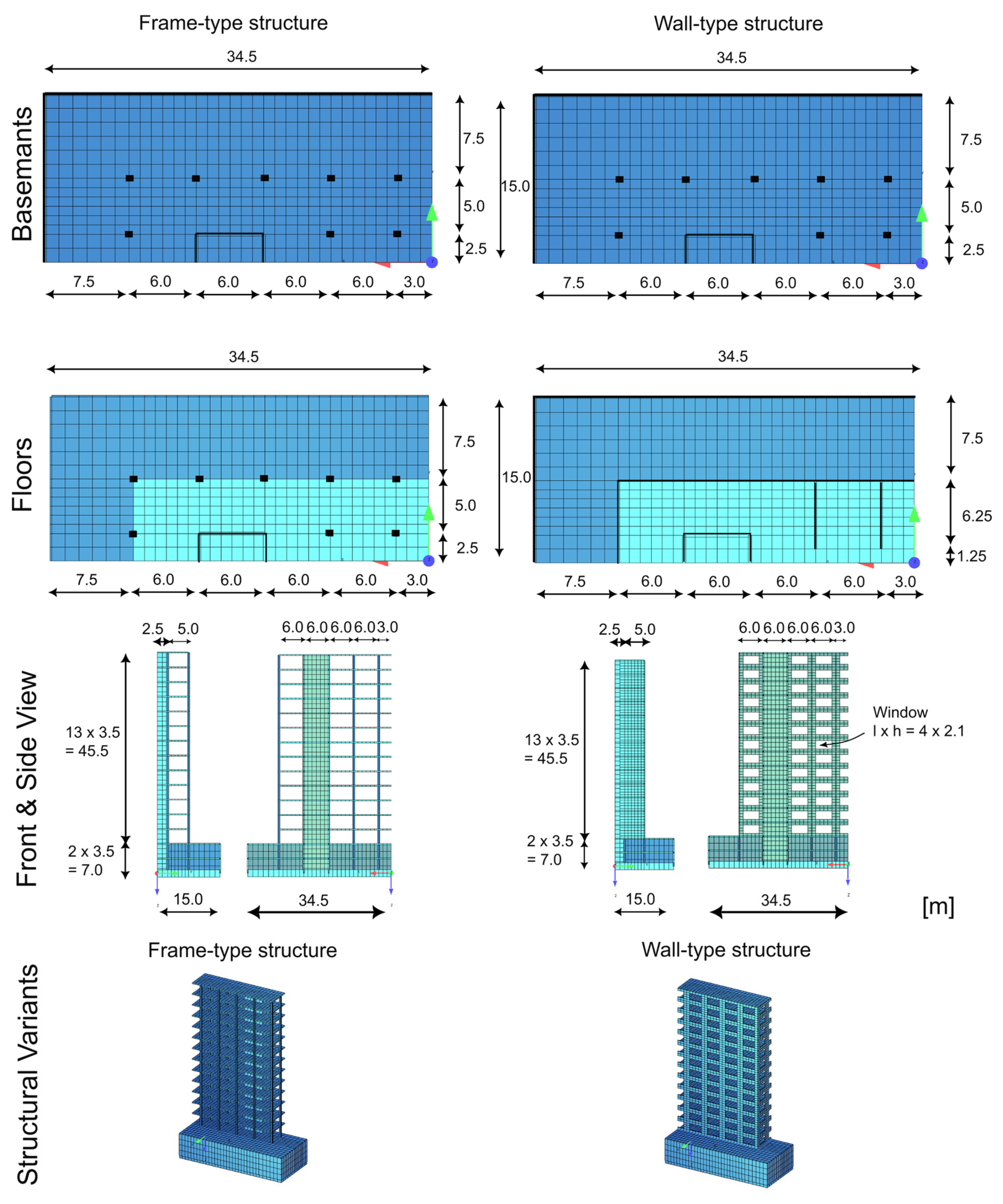
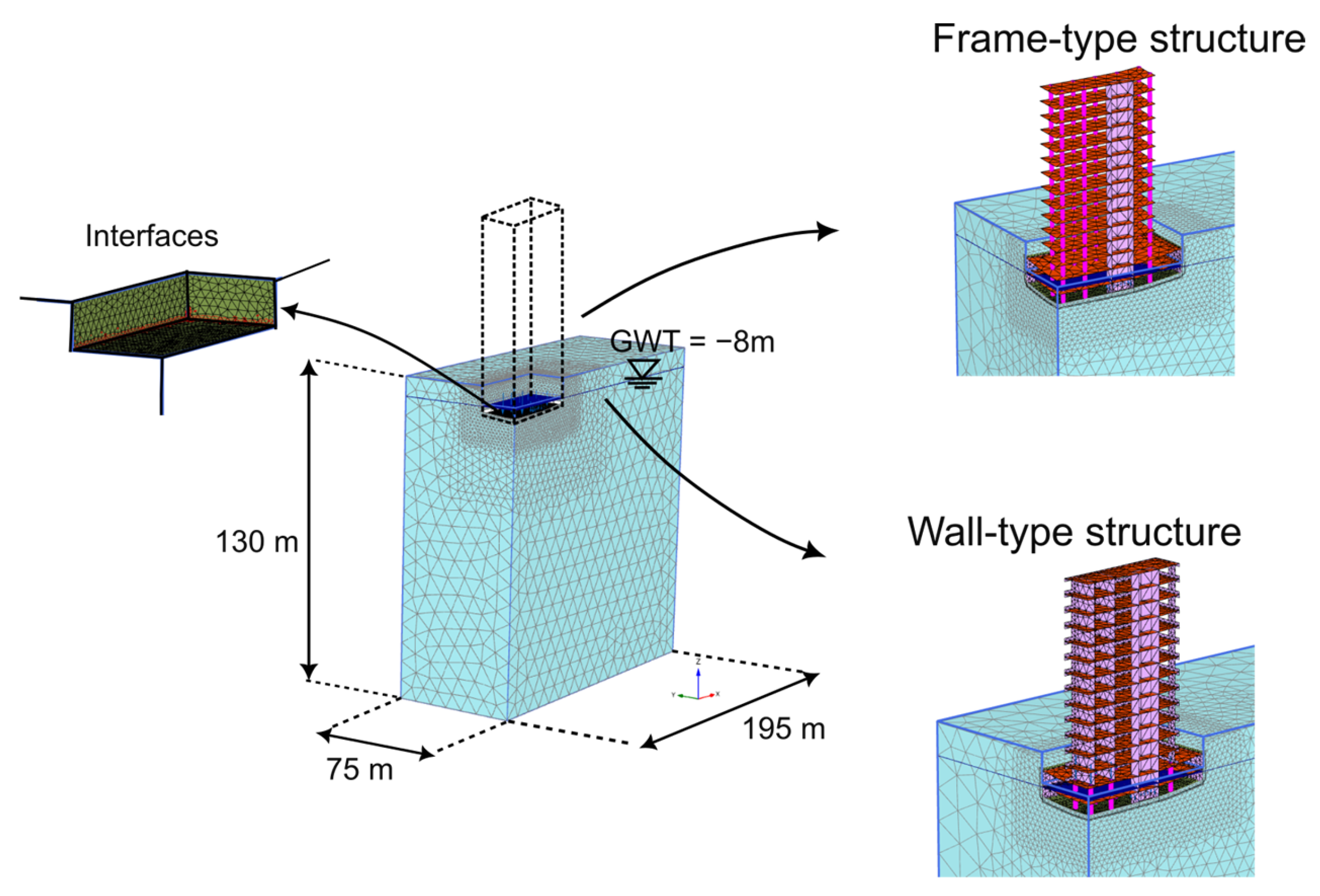


| Structural Component | Thickness | Material Property | Value |
|---|---|---|---|
| Foundation slab [m] | 1.75 | Poisson’s ratio ν [-] | 0.2 |
| Floor slab [m] | 0.28 | Elastic modulus E [MPa] | 30,000 |
| Columns [m] | 0.50 | Concrete unit weight [kN/m3] | 25 |
| Exterior & interior walls [m] | 0.20 | Flooring load [kN/m2] | 2 |
| Basement & core walls [m] | 0.30 | Facade load [kN/m2] | 3.5 |
| Soiltype | [kN/m3] | [kN/m3] | [m/s] | [°] | [kN/m2] | [°] | [-] | [kN/m2] | [kN/m2] | [kN/m2] | [-] | [kN/m2] | [-] | [-] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Clay | 20.5 | 21 | 10−10 | 28 | 2 | 0 | 0.2 | 4000 | 7000 | 30,000 | 1.0 | 50,000 | 2 × 10−4 | 0.53 |
| Silt | 19.0 | 20 | 10−8 | 29 | 2 | 0 | 0.2 | 12,000 | 16,000 | 47,000 | 0.7 | 78,300 | 1 × 10−4 | 0.51 |
| Sand | 17.5 | 20 | 10−4 | 36 | 0 | 6 | 0.2 | 30,000 | 30,000 | 90,000 | 0.5 | 150,000 | 1 × 10−4 | 0.41 |
| Load Combination | Formula | Result |
|---|---|---|
| Characteristic | ||
| Characteristic reduced by | ⋅ | |
| Frequent | ||
| Quasi-permanent |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wallner, C.; Resch, J.; Schlicke, D. Settlement Relevant Load Combinations and Force Redistribution in Structural Design. Buildings 2025, 15, 3596. https://doi.org/10.3390/buildings15193596
Wallner C, Resch J, Schlicke D. Settlement Relevant Load Combinations and Force Redistribution in Structural Design. Buildings. 2025; 15(19):3596. https://doi.org/10.3390/buildings15193596
Chicago/Turabian StyleWallner, Christian, Jakob Resch, and Dirk Schlicke. 2025. "Settlement Relevant Load Combinations and Force Redistribution in Structural Design" Buildings 15, no. 19: 3596. https://doi.org/10.3390/buildings15193596
APA StyleWallner, C., Resch, J., & Schlicke, D. (2025). Settlement Relevant Load Combinations and Force Redistribution in Structural Design. Buildings, 15(19), 3596. https://doi.org/10.3390/buildings15193596







