Mechanical Response of Composite Wood–Concrete Bonded Facade Under Thermal Loading
Abstract
1. Introduction
2. Analytical Method Development
- The structural behavior is limited to elasticity and small deformations, and the constitutive relationship is assumed to be linear.
- Displacements and rotations are limited, the displacement at the center of the panel is assumed to be zero, and the supports are placed at the ends of the panel.
- The temperature on the walls is constant so that the thermal gradient is assumed to act on a single layer, with the thermal load applied to the exterior face of the concrete while the wood is exposed to the ambient temperature of the environment.
- The method does not consider the shrinkage of the concrete.
3. Thermomechanical Modeling of Panels
- The first part of the model is thermal and transient, used to calculate the temperature distribution within the panel in response to applied thermal gradients.
- The second part is structural, allowing the evaluation of the panel’s mechanical response based on the applied nodal temperatures. The transient approach was chosen for the following reasons:
3.1. Basic Equations
3.2. Numerical Calculation Assumptions


4. Materials and Structures
4.1. Experimental Program and Test Conditions
4.2. Instrumentation
4.2.1. Temperature Sensors
4.2.2. LVDT and Strain Gauges
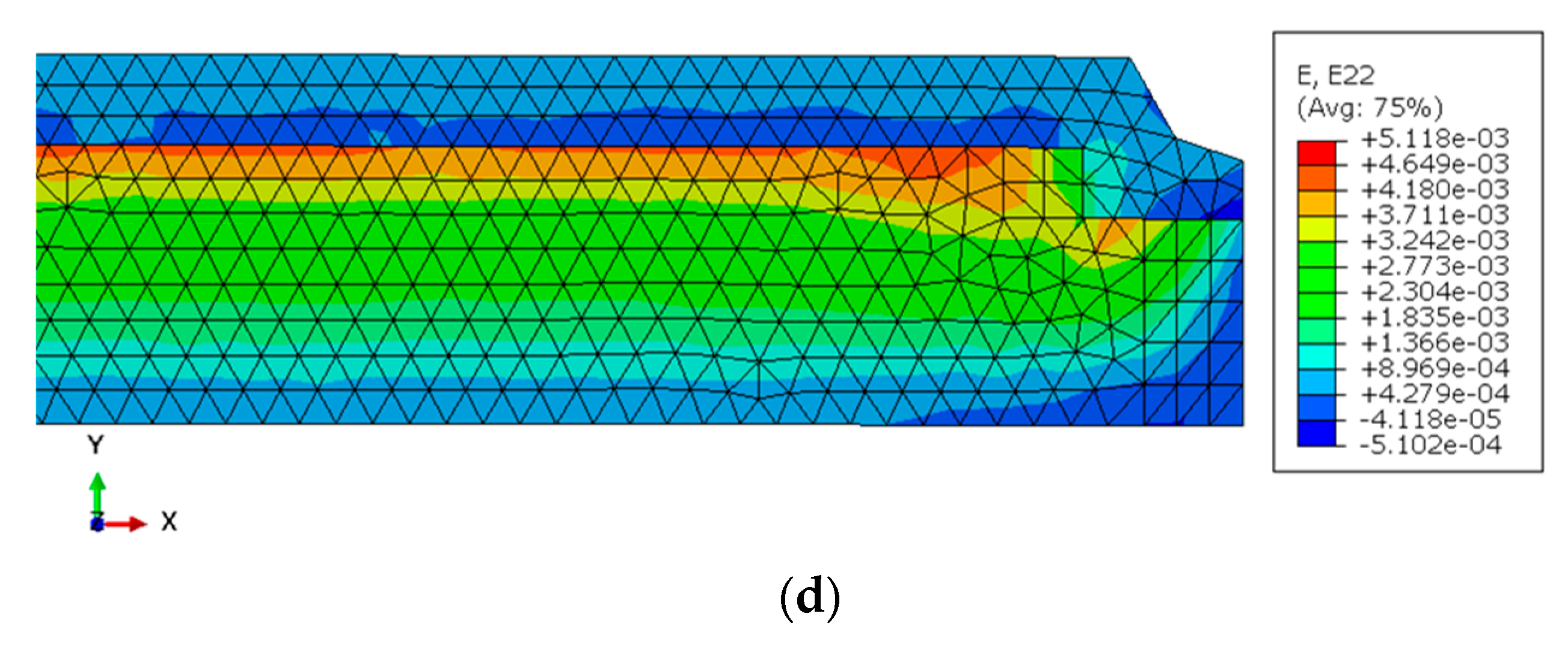
5. Results and Discussion
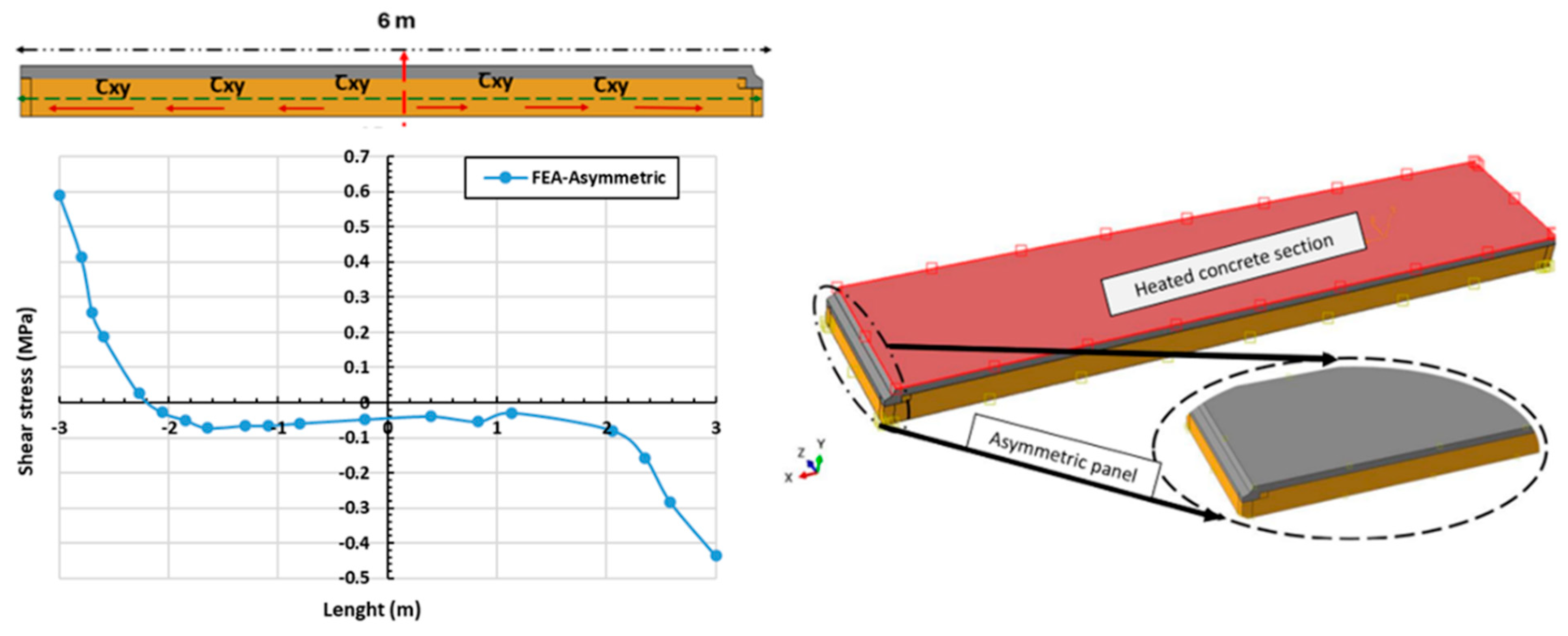
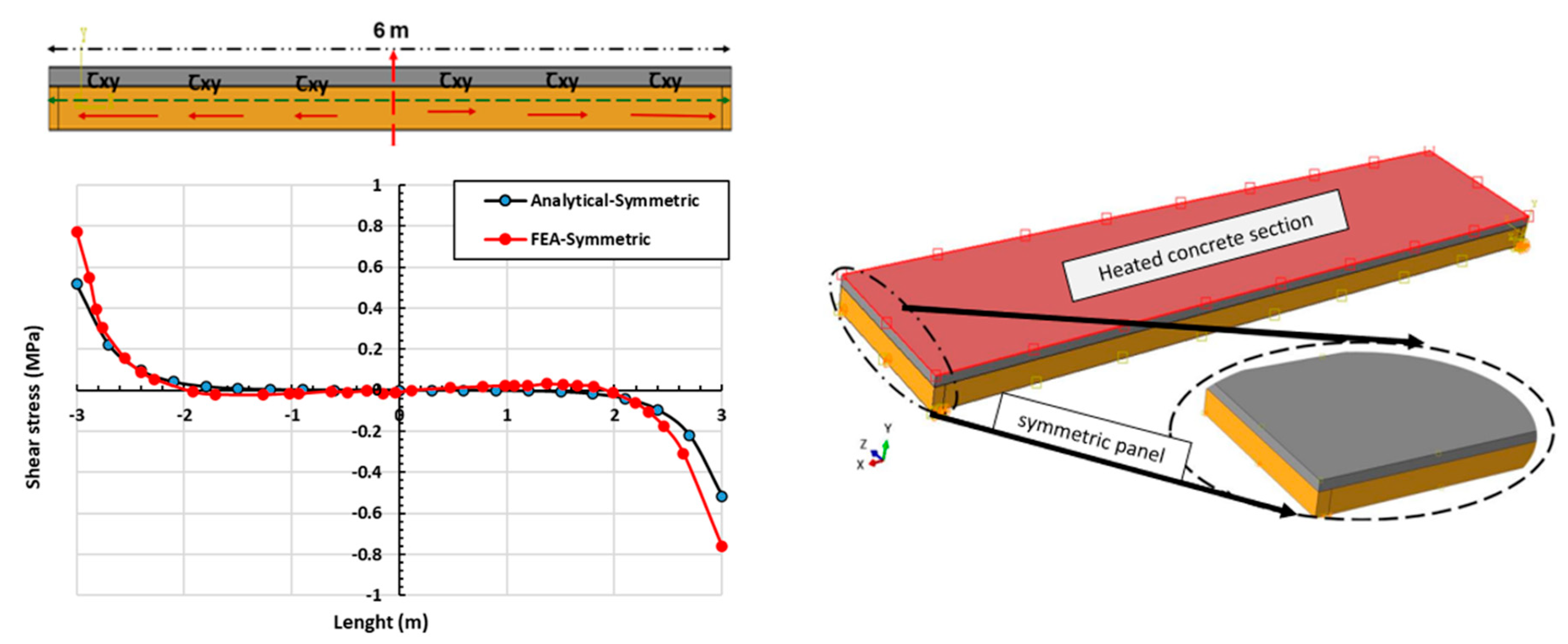
5.1. Analysis of Theoretical Results
5.2. Validation of the Numerical Model
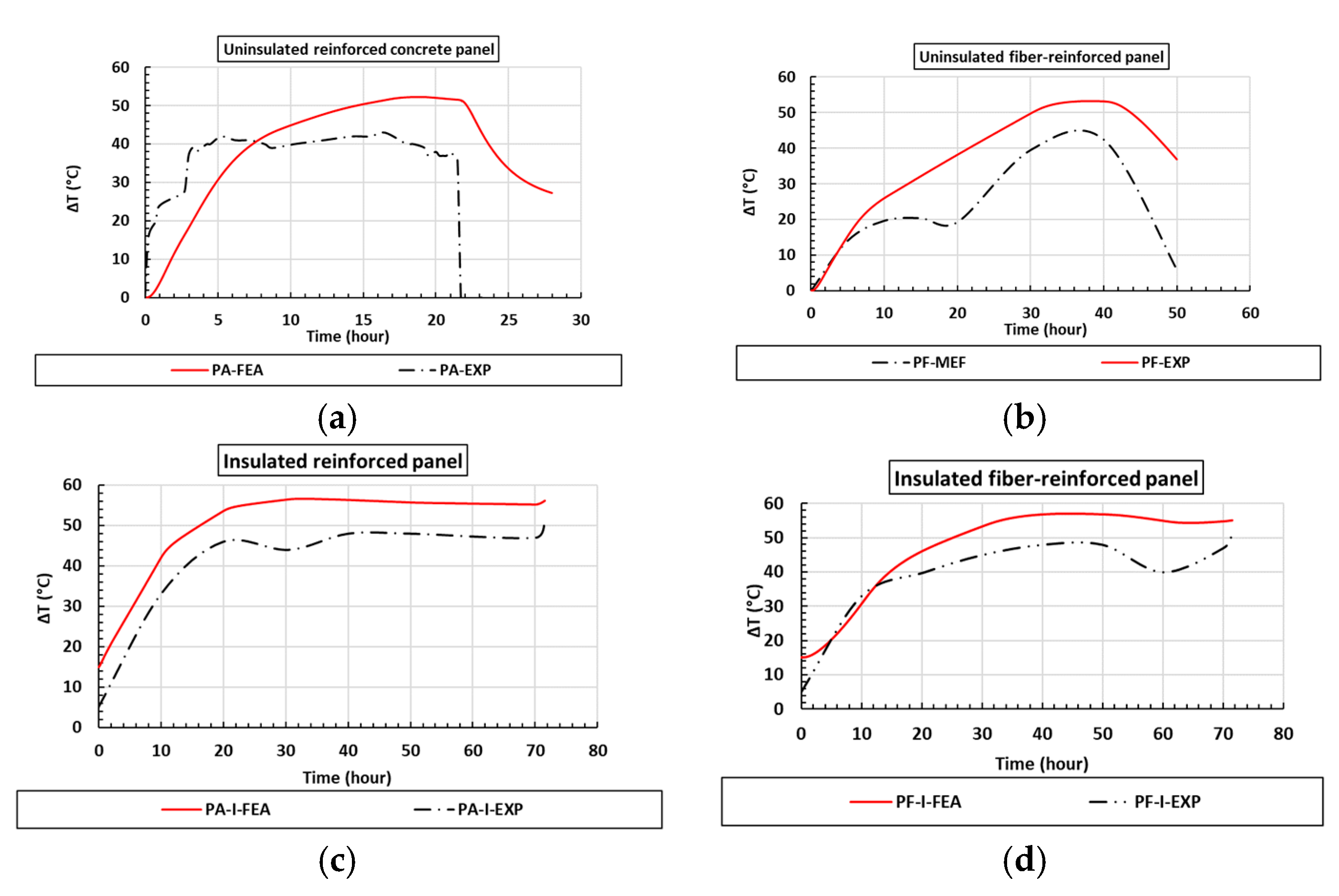
5.2.1. Temperature Gradient (∆T) Results
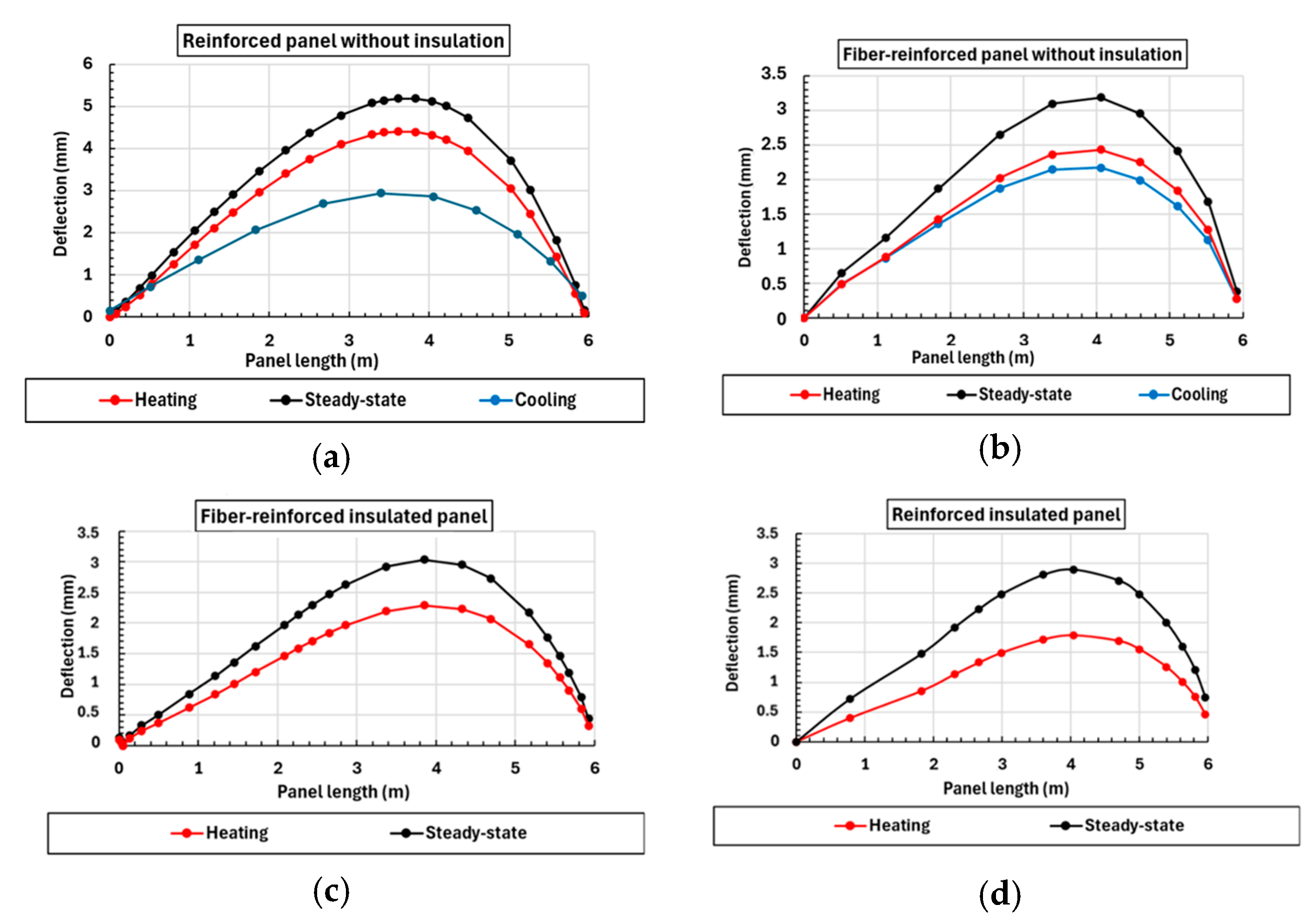
5.2.2. Thermal Bending
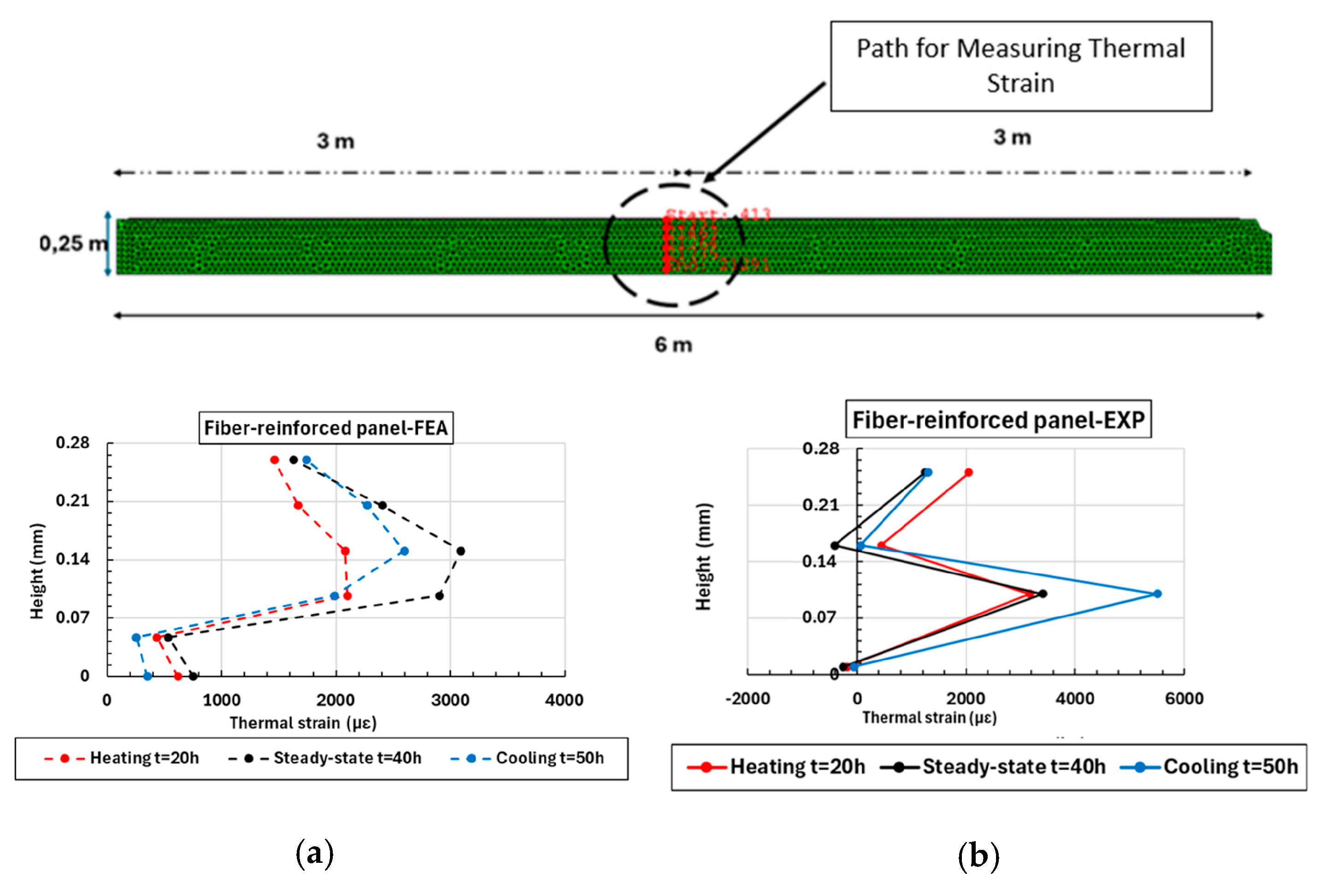
5.2.3. Thermal Strains
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| symbol | description | units |
| ratio of the composite to the non-composite moment of inertia | ||
| equal to 1 − α2. | ||
| ΔT | the temperature differential in the sandwich panel (T2–T1). | °C |
| ϕflexion | slip due to bending | mm/mm |
| slip due to axial deformation in the top layer. | mm | |
| τ | the shear stress in the middle layer of the intermediate layer | MPa |
| x | abscissa measured from mid-span. | mm |
| υ | bowing due to temperature differential | mm |
| area of the top layer | mm2 | |
| modulus of elasticity of the wood | MPa | |
| modulus of elasticity of the concrete | MPa | |
| moment of inertia. Indices 1 and 2 represent the top and bottom walls, respectively | mm4 | |
| sum of the moments in the two walls | N.mm | |
| sum of the moments in the two walls due to the panel’s curvature | N.mm | |
| bending moment due to temperature change. | N.mm | |
| thickness of the heated wythe | mm | |
| thickness of the unheated wythe | mm | |
| K | stiffness per unit area | N/mm |
| r1 | distances from the centroids of the heated and unheated wythes | mm |
| r2 | distances from the centroids of the unheated and unheated wythes | mm |
| r | distance between the axis of the walls and the centroid of the cross-sectional area | mm |
References
- Richart, F.E.; Williams, C.B. Tests of Composite Timber and Concrete Beams; Bulletin, no. 343; University of Illinois at Urbana Champaign, College of Engineering. Engineering Experiment Station: Champaign, IL, USA, 2007; Available online: https://hdl.handle.net/2142/4444 (accessed on 10 September 2025).
- Yeoh, D.; Fragiacomo, M.; De Franceschi, M.; Heng Boon, K. State of the art on timber-concrete composite structures: Literature review. J. Struct. Eng. 2011, 137, 1085–1095. [Google Scholar] [CrossRef]
- Rodrigues, J.N.; Dias, A.M.P.G.; Providência, P. Timber-concrete composite bridges: State-of-the-art review. BioResource 2013, 8, 6630–6649. Available online: https://bioresources.cnr.ncsu.edu/resources/timber-concrete-composite-bridges-state-of-the-art-review/ (accessed on 10 September 2025). [CrossRef]
- Weaver, C.A.; Davids, W.G.; Dagher, H.J. Testing and analysis of partially composite fiber-reinforced polymer-glulam-concrete bridge girders. J. Bridge Eng. 2004, 9, 316–325. [Google Scholar] [CrossRef]
- Parisi, M.A.; Piazza, M. Restoration and Strengthening of Timber Structures: Principles, Criteria, and Examples. Pract. Period. Struct. Des. Constr. 2007, 12, 177–185. [Google Scholar] [CrossRef]
- Naito, C.J.; Hoeman, J.M.; Shull, J.S.; Saucier, A.; Salim, H.A.; Bewick, B.T.; Hammons, M.I. Precast/Prestressed Concrete Experiments Performance on Non-Load Bearing Sandwich Wall Panels; Air Force Research Laboratory, Materials and Manufacturing Directorate, Tyndall Air Force Base: Bay County, FL, USA, 2011. [Google Scholar] [CrossRef]
- Pozza, L.; Scotta, R.; Polastri, A.; Ceccotti, A. Seismic behaviour of wood-concrete frame shear-wall system and comparison with code provisions. In Proceedings of the Meeting 45 of the Working Commission W18-Timber Structures, Växjö, Sweden, 27–30 August 2012; Available online: https://hdl.handle.net/11577/2525153 (accessed on 10 September 2025).
- Pham, H.S. Optimisation et Comportement en Fatigue de la Connexion Dois-BFUP pour de Nouveaux Ponts Mixtes. Ph.D. Thesis, Ecole Nationale des Ponts et Chaussées, Marne-la-Vallée, France, 2007. [Google Scholar]
- Gutkowski, R.; Brown, K.; Shigidi, A.; Natterer, J. Laboratory tests of composite wood–concrete beams. Constr. Build. Mater. 2008, 22, 1059–1066. [Google Scholar] [CrossRef]
- Augeard, E.; Michel, L.; Ferrier, E. Experimental and analytical study of the mechanical behavior of heterogeneous glulam–concrete beams and panels assembled by a specific treatment of wood. Constr. Build. Mater. 2018, 191, 812–825. [Google Scholar] [CrossRef]
- Glass, S.V.; Zelinka, S.L. Moisture relations and physical properties of wood. In Wood Handbook: Wood as an Engineering Material: Chapter 4, Centennial ed.; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010; pp. 1–4. Available online: https://research.fs.usda.gov/treesearch/37428 (accessed on 10 September 2025).
- Ge, H.; Tariku, F. Evaluation of the thermal performance of innovative pre-fabricated wall systems through field testing. In Proceedings of the Building Enclosure Science & Technology (BEST3) Conference, Atlanta, GA, USA, 2–4 April 2012. [Google Scholar]
- Sorensen, T.J.; Thomas, R.J.; Dorafshan, S.; Maguire, M. Thermal bridging in concrete sandwich walls. ACI Concr. Int. 2018, 40, 45–49. Available online: https://scholarsarchive.byu.edu/facpub/5519 (accessed on 10 September 2025).
- Keena, N.; Raugei, M.; Lokko, M.; Aly Etman, M.; Achnani, V.; Reck, B.K.; Dyson, A. A Life-cycle approach to investigate the potential of novel biobased construction materials toward a circular built environment. Energies 2022, 15, 7239. [Google Scholar] [CrossRef]
- Frenette, C.D.; Bulle, C.; Beauregard, R.; Salenikovich, A.; Derome, D. Using life cycle assessment to derive an environmental index for light-frame wood wall assemblies. Build. Environ. 2010, 45, 2111–2122. [Google Scholar] [CrossRef]
- Pérez-García, A.; Víllora, A.G.; Pérez, G.G. Building’s eco-efficiency improvements based on reinforced concrete multilayer structural panels. Energy Build. 2014, 85, 1–11. [Google Scholar] [CrossRef]
- Martins, C.; Dias, A.M.P.G.; Costa, R.; Santos, P. Environmentally friendly high performance timber–concrete panel. Constr. Build. Mater. 2016, 102, 1060–1069. [Google Scholar] [CrossRef]
- Du, H.; Hu, X.; Xie, Z.; Wang, H. Study on shear behavior of inclined cross lag screws for glulam-concrete composite beams. Constr. Build. Mater. 2019, 224, 132–143. [Google Scholar] [CrossRef]
- Clouston, P.; Schreyer, A. Design and use of wood–concrete composites. Pract. Period. Struct. Des. Constr. 2008, 13, 167–174. [Google Scholar] [CrossRef]
- Branco, J.M.; Cruz, P.J.S.; Piazza, M. Experimental analysis of laterally loaded nailed timber-to-concrete connections. Constr. Build. Mater. 2009, 23, 400–410. [Google Scholar] [CrossRef]
- Ferrier, E.; Labossière, P.; Neale, K.W. Mechanical behavior of an innovative hybrid beam made of glulam and ultrahigh-performance concrete reinforced with frp or steel. J. Compos. Constr. 2010, 14, 217–223. [Google Scholar] [CrossRef]
- Ferrier, E.; Labossière, P.; Neale, K.W. Modelling the bending behaviour of a new hybrid glulam beam reinforced with frp and ultra-high-performance concrete. Appl. Math. Model. 2012, 36, 3883–3902. [Google Scholar] [CrossRef]
- Leabu, V.F. Problems and performance of precast concrete wall panels. J. Proc. 1959, 56, 287–298. Available online: http://www.ijret.org (accessed on 10 September 2025).
- Mai, Y. Performance Evaluation of Sandwich Panels Subjected to Bending Compression and Thermal Bowing; Materials and Structures; Springer: Berlin/Heidelberg, Germany, 1980; Volume 13, pp. 159–168. [Google Scholar] [CrossRef]
- Losch, E.; Hynes, P.W.; Andrews, R.; Browning, R.; Cardone, P.; Devalapura, R.K.; Donahey, R.C.; Freedman, S.; Gleich, H.A.; Goettsche, G.E.; et al. State of the Art of Precast/Prestressed Concrete Sandwich Wall Panels; PCI Journal: Chicago, IL, USA, 2011; pp. 131–176. [Google Scholar]
- Sorensen, T.; Dorafshan, S.; Maguire, M. Thermal Evaluation of Common Locations of Heat Loss in Sandwich Wall Panels. In Proceedings of the Congress on Technical Advancement 2017, Duluth, MN, USA, 10–13 September 2017; pp. 173–184. [Google Scholar]
- Ghali, A.; Favre, R. Concrete Structures: Stresses and Deformations, 3rd ed.; First Published 2002, eBook Published 8 October 2018; CRC Press: London, UK, 2002; 608p, ISBN 9781315273389. [Google Scholar] [CrossRef]
- Maguire, M.; Roberts-Wollmann, C.; Cousins, T. Live-Load Testing and Long-Term Monitoring of the Varina-Enon Bridge: Investigating Thermal Distress. J. Bridge Eng. 2018, 23, 04018003. [Google Scholar] [CrossRef]
- Losch, E. Bowing of Insulated Precast Concrete Wall Panels. PCI J. 2003, 126–129. [Google Scholar]
- Hoffmeister, B.; Di Biase, P.; Richter, C.; Feldmann, M. Innovative steel-glass components for high-performance building skins: Testing of full-scale prototypes. Glass Struct. Eng. 2017, 2, 57–78. [Google Scholar] [CrossRef]
- Guitard, D.; El Amri, F. Modèles Prévisionnels de Comportement Élastique Tridimensionnel Pour Les Bois Feuillus et Les Bois Résineux. Ann. For. Sci. 1987, 44, 335–358. [Google Scholar] [CrossRef]
- Hassan, T.K.; Rizkalla, S.H. Analysis and design guidelines of precast, prestressed concrete, composite load-bearing sandwich wall panels reinforced with CFRP grid. PCI J. 2010, 55, 147–162. [Google Scholar] [CrossRef]
- Naito, C.; Hoemann, J.; Beacraft, M.; Bewick, B. Performance and Characterization of Shear Ties for Use in Insulated Precast Concrete Sandwich Wall Panels. J. Struct. Eng. 2012, 138, 52–61. [Google Scholar] [CrossRef]
- Ojalvo, I.U. Departures from Classical Beam Theory in Laminated, Sandwich, and Short Beams. AIAA J. 1977, 15, 1518–1521. [Google Scholar] [CrossRef]
- Pessik, S.; Mlynarczyk, A. Experimental evaluation of the composite behavior of precast concrete sandwich wall panels. PCI J. 2003, 48, 54–71. [Google Scholar] [CrossRef]
- Bush, T.D.; Wu, Z. Flexural Analysis of Prestressed Concrete Sandwich Panels with Truss Connectors. PCI J. 1998, 43, 76–86. [Google Scholar] [CrossRef]
- Tadros, M.K.; Ghali, A.; Dilger, W.H. Time-dependent analysis of composite frames. J. Struct. Div. 1977, 103, 871–884. [Google Scholar] [CrossRef]
- Foraboschi, P. Three-Layered Plate: Elasticity Solution. Compos. Part B Eng. 2014, 60, 764–776. [Google Scholar] [CrossRef]
- Foraboschi, P. Analytical Solution of Two-Layer Beam Taking into Account Nonlinear Interlayer Slip. J. Eng. Mech. 2009, 135, 1129–1146. [Google Scholar] [CrossRef]
- Granholm, H. Om Sammansatta Balkar och Pelare med Särskild Hänsyn till Spikade Träkonstruktioner: On Composite Beams and Columns with Particular Regard to Nailed Rimber Structures; Gumpert: Ingolstadt, Germany, 1949; Volume 17. [Google Scholar]
- Holmberg, A.; Plem, E. Behaviour of Load-Bearing Sandwich-Type Structures; Byggforskningen: Oslo, Norway, 1965. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011; Available online: https://ndl.ethernet.edu.et/handle/123456789/89731 (accessed on 10 September 2025).
- Dassault Systèmes. Abaqus Analysis User’s Guide, Version 2023; Dassault Systèmes: Providence, RI, USA. Available online: http://130.149.89.49:2080/v2016/pdf_books/CAE.pdf (accessed on 10 September 2025).
- EN 1995-1-1:2004; Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- Ferrara, G.; Michel, L.; Ferrier, E. Flexural behaviour of timber-concrete composite floor systems linearly supported at two edges. Eng. Struct. 2023, 281, 115782. [Google Scholar] [CrossRef]
- Dunlap, F. The Specific Heat of Wood; US Department of Agriculture, Forest Service: Washington, DC, USA, 1912; Volume 110. [Google Scholar]
- TenWolde, A.; McNatt, J.D.; Krahn, L. Thermal Properties of Wood and Wood Panel Products for Use in Buildings; Forest Products Lab: Madison, WI, USA, 1988. [Google Scholar]
- EN 1992-1-2:2004; Eurocode 2: Calcul des Structures en Béton—Partie 1-2: Règles générales—Calcul du Comportement au Feu. European Committee for Standardization: Brussels, Belgium, 2004.
- Khan, M.I.; Karahan, M. Testing of Natural Fiber Composites. In Natural Fibers to Composites; Nawab, Y., Saouab, A., Imad, A., Shaker, K., Eds.; Engineering Materials; Springer: Berlin/Heidelberg, Germany, 2022; pp. 131–148. [Google Scholar]

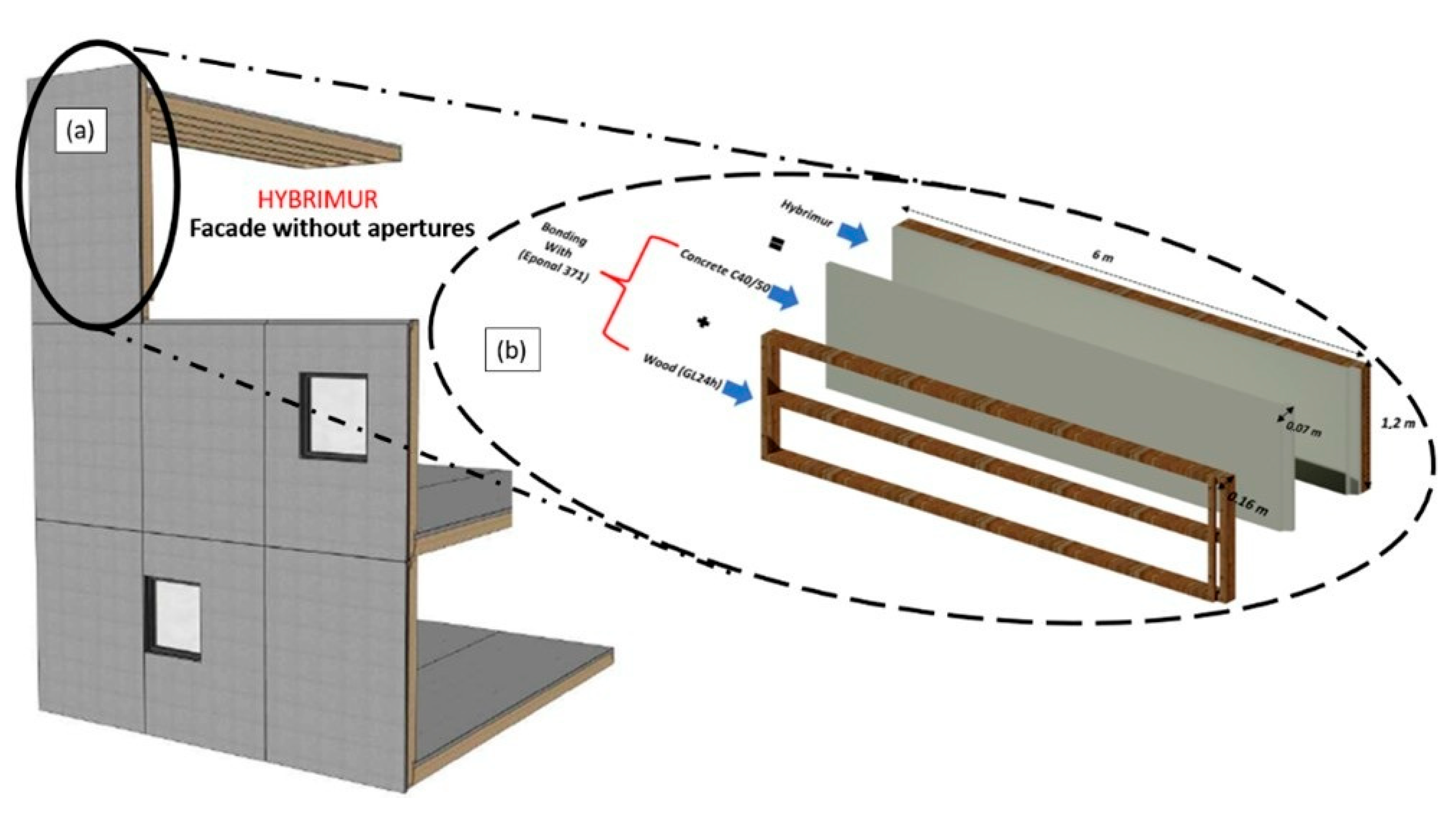



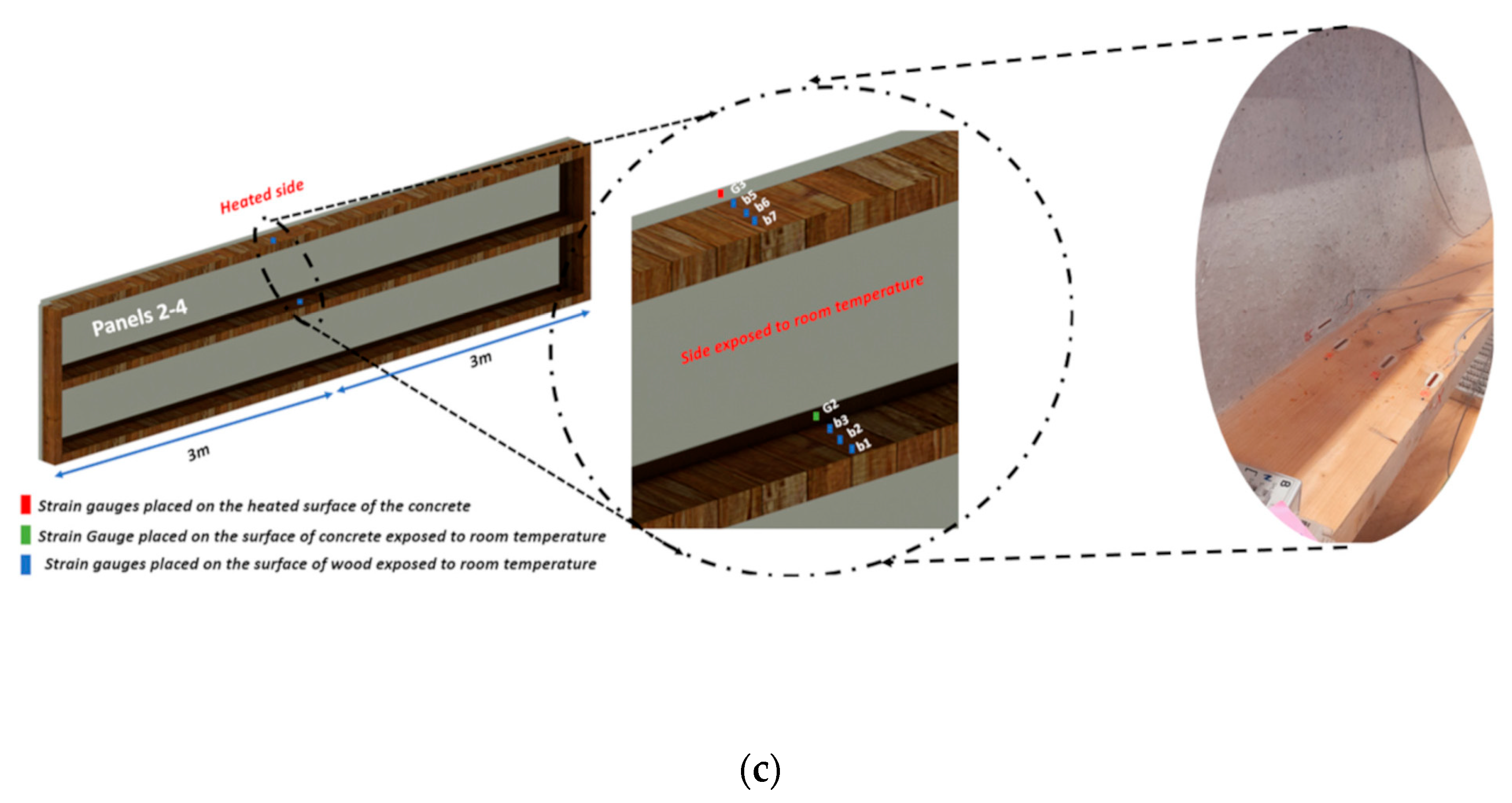






| Material | Parameter | Value |
|---|---|---|
| Concrete | [MPa] [%] [MPa] Poisson’s ratio (µ) Specific heat capacity (C) [KJ/kg K] Thermal conductivity (λ) [W/m K] Coefficient of thermal expansion (α) [] | 40.8 0.38 33 546 0.2 840 1.15 |
| Timber (GL24h) | [MPa] [MPa] [MPa] [MPa] [MPa] [MPa] Poisson’s ratio (µ) Specific heat capacity (C) [KJ/kg K] Thermal conductivity (λ) [W/m K] Coefficient of thermal expansion (α) [] | 24 (h = 12%) 16.5 24 2.7 11 600 9400 0.3 1600 0.15 |
| Resin | [MPa] [MPa] [%] [MPa] | 83 ± 4 32 ± 3 1.2 ± 0.2 3500 ± 500 |
| Tests | Panels | Conditioning | Applied Temperature (°C) | Loading Process | Loading Duration (Hours) | |
|---|---|---|---|---|---|---|
| Test 1 | FG-P1 | Without insulation | 65 | 24 | Heating Cooling | 50 |
| Test 2 | FG-P2-I | Insulated | 70 | 24 | Heating | 70 |
| Test 3 | R-P3 | Without insulation | 63 | 22 | Heating Cooling | 28 |
| Test 4 | R-P4-I | Insulated | 70 | 26 | Heating | 70 |
| Test 5 | R-P5 | Insulated | 67 | 22 | Heating | 62 |
| Specimens | Strain Gauges Positioned at Mid-Height | Strain Gauges Positioned at the Edges |
|---|---|---|
C2-Concrete B3-Wood B2-Wood B1-Wood G2-Concrete b3-Wood b2-Wood b1-Wood | ||
| Panel 1 Panel 3 Panel 5 | C3-Concrete B5-Wood B6-Wood B7-Wood | |
| Panel 2 Panel 4 | G3-Concrete b5-Wood b6-Wood b7-Wood |
| Position (m) | Shear Stress (MPa) | Difference | |
|---|---|---|---|
| Analytical | FEA | Analy/FEA (%) | |
| 1 | 0.52 | 0.77 | 32 |
| 2 | 0.04 | 0.05 | 20 |
| 3 | 0 | 0 | 0 |
| 4 | 0.04 | 0.05 | 20 |
| 6 | 0.52 | 0.77 | 32 |
| Panel | Condition | ∆T-FEA (°C) | ∆T-Exp (°C) | Difference (EXP/FEA) (%) |
|---|---|---|---|---|
| Reinforced panel | Uninsulated | 52 | 42 | −19 |
| Reinforced panel | Insulated | 56 | 46 | −17 |
| Fiberglass-reinforced panel | Uninsulated | 51 | 43 | −16 |
| Fiberglass-reinforced panel | Insulated | 56 | 51 | −8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Assal, R.; Michel, L.; Ferrier, E. Mechanical Response of Composite Wood–Concrete Bonded Facade Under Thermal Loading. Buildings 2025, 15, 3664. https://doi.org/10.3390/buildings15203664
Assal R, Michel L, Ferrier E. Mechanical Response of Composite Wood–Concrete Bonded Facade Under Thermal Loading. Buildings. 2025; 15(20):3664. https://doi.org/10.3390/buildings15203664
Chicago/Turabian StyleAssal, Roufaida, Laurent Michel, and Emmanuel Ferrier. 2025. "Mechanical Response of Composite Wood–Concrete Bonded Facade Under Thermal Loading" Buildings 15, no. 20: 3664. https://doi.org/10.3390/buildings15203664
APA StyleAssal, R., Michel, L., & Ferrier, E. (2025). Mechanical Response of Composite Wood–Concrete Bonded Facade Under Thermal Loading. Buildings, 15(20), 3664. https://doi.org/10.3390/buildings15203664









