Analysis of the Geometrical Size Effect on the Fatigue Performance of Welded T-Joints
Abstract
1. Introduction
2. Fatigue Tests
2.1. Mechanical Properties of the Material
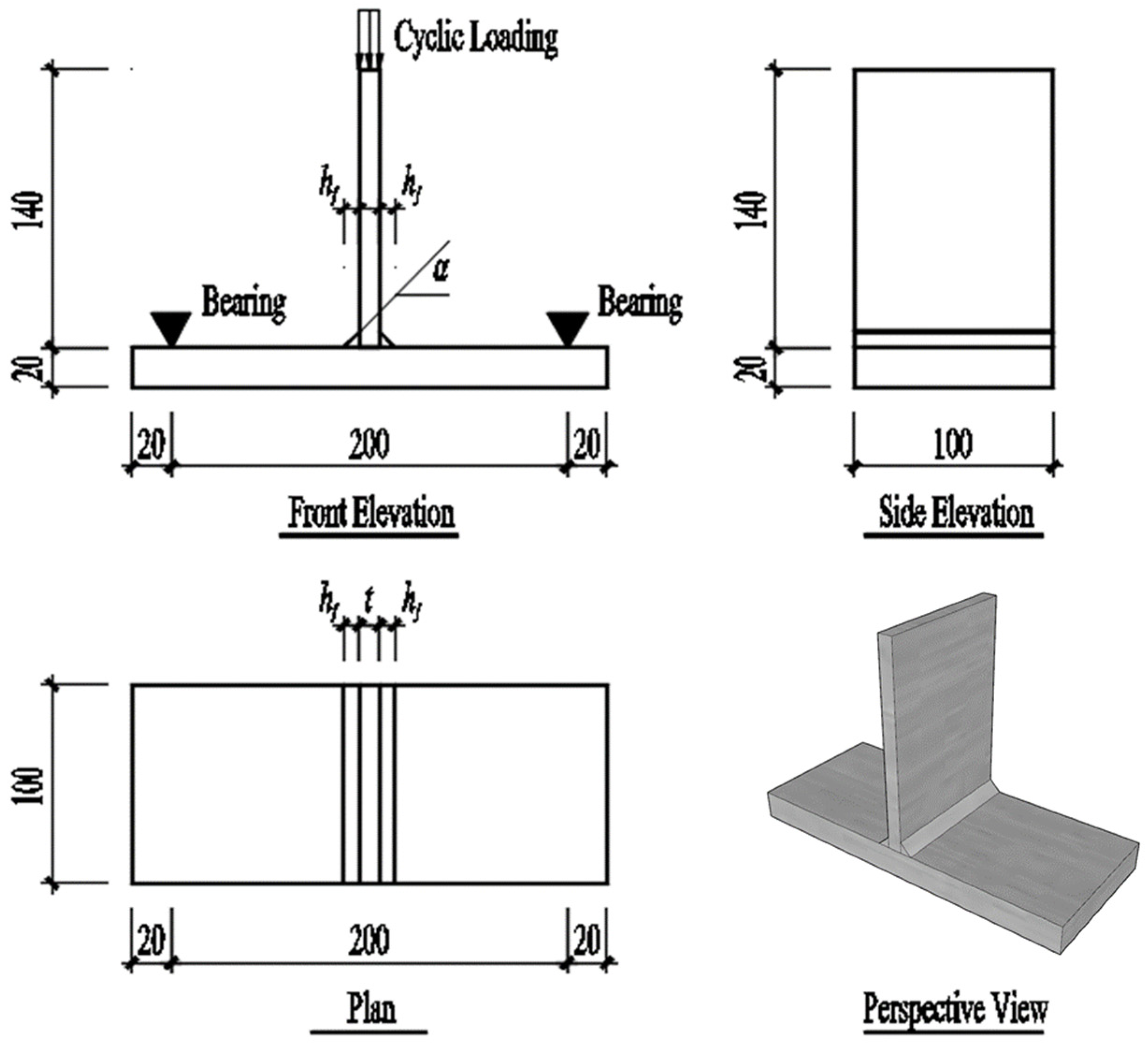
2.2. Specimen Design
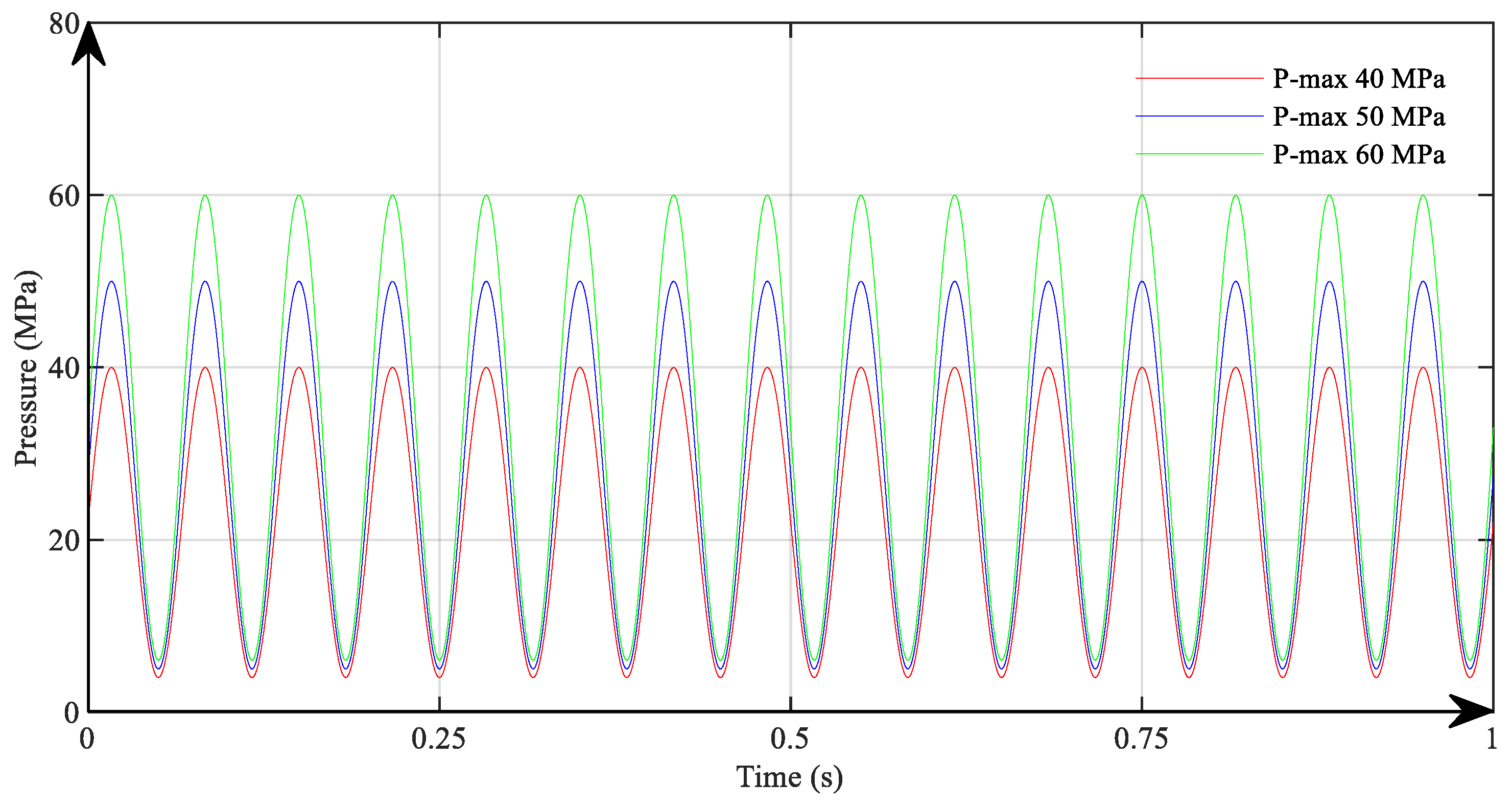
2.3. Test Setup and Loading Protocol
2.4. Measurement Scheme
3. Test Results
3.1. Test Phenomenon
3.2. Fatigue Life
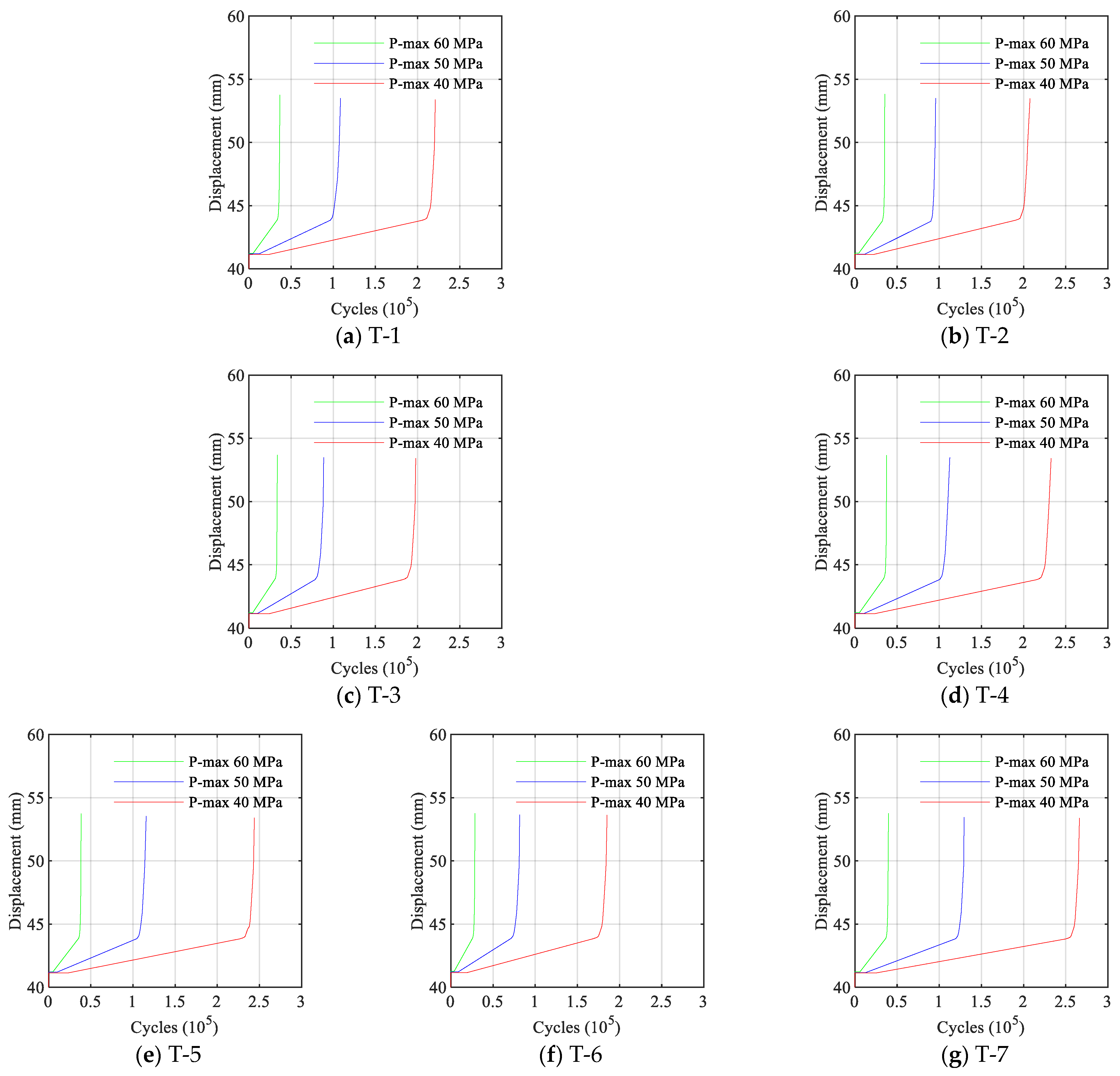
3.3. Displacement Curve
4. Test Analysis
4.1. Impact of Web Plate Thickness on Fatigue Life
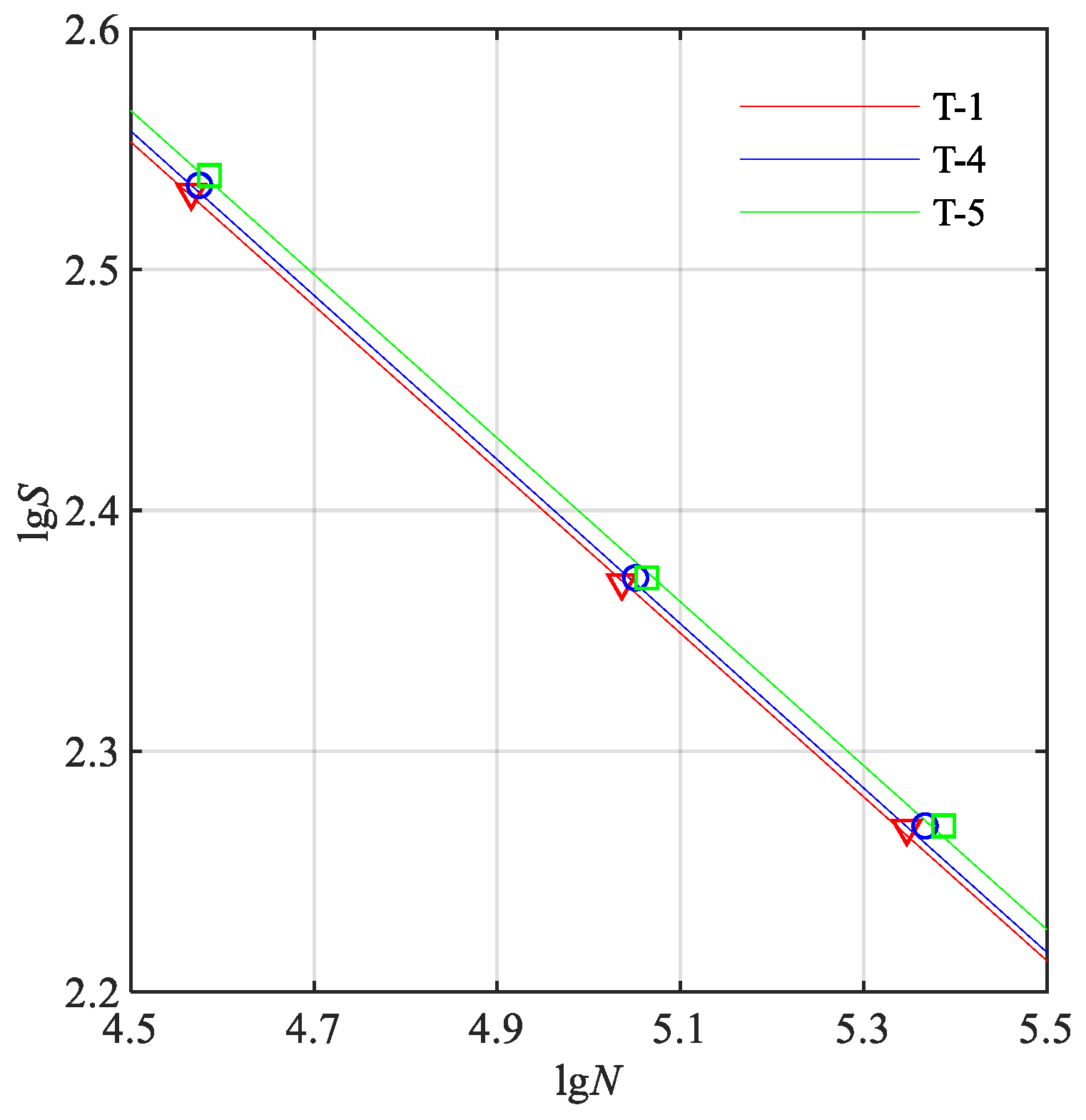
4.2. Impact of Weld Toe Size on Fatigue Life
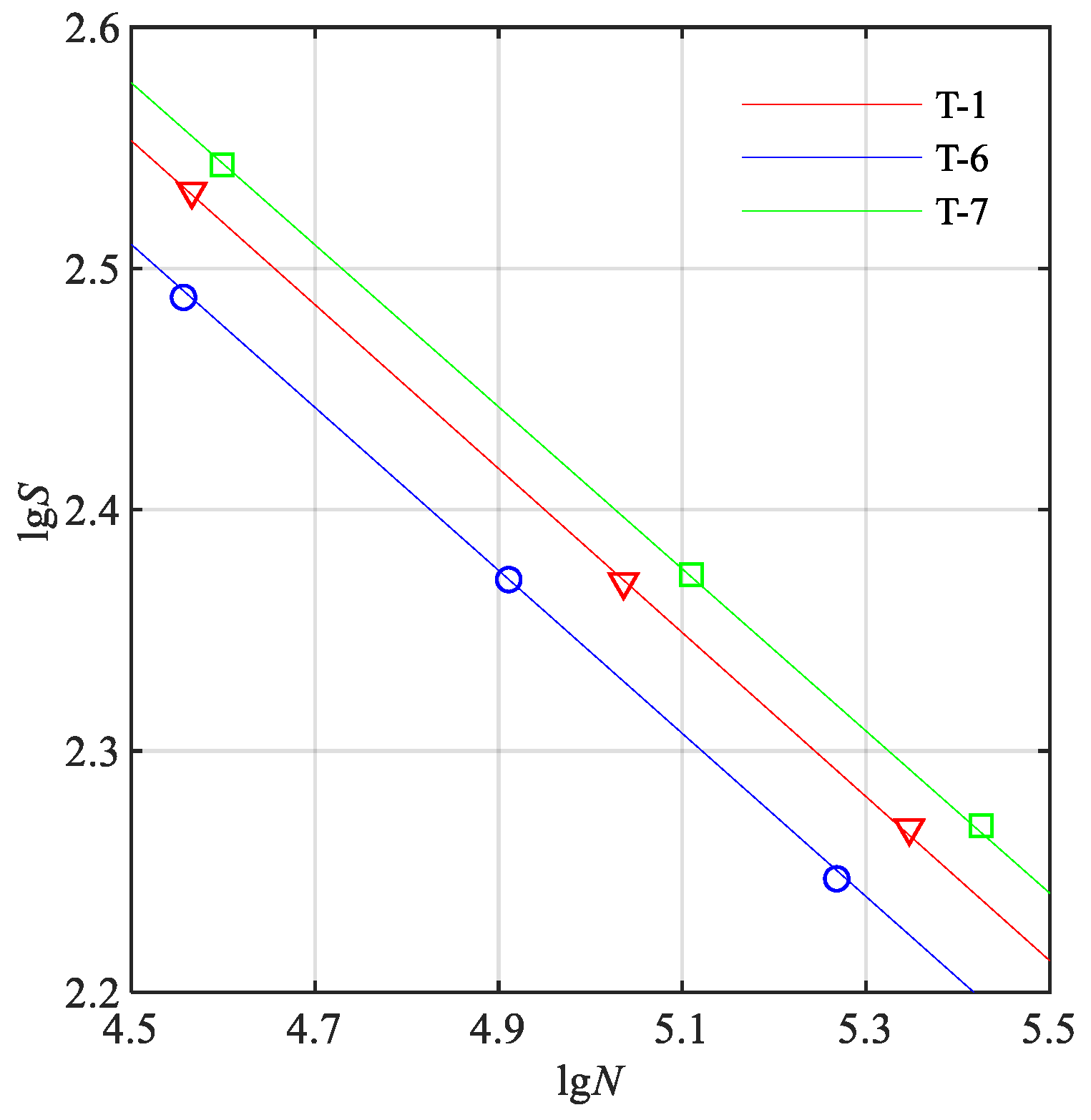
4.3. Impact of Welding Angle on Fatigue Life
4.4. Comparison of Experimental Data with Standards
5. Correlation Analysis of Factors Affecting Fatigue Life
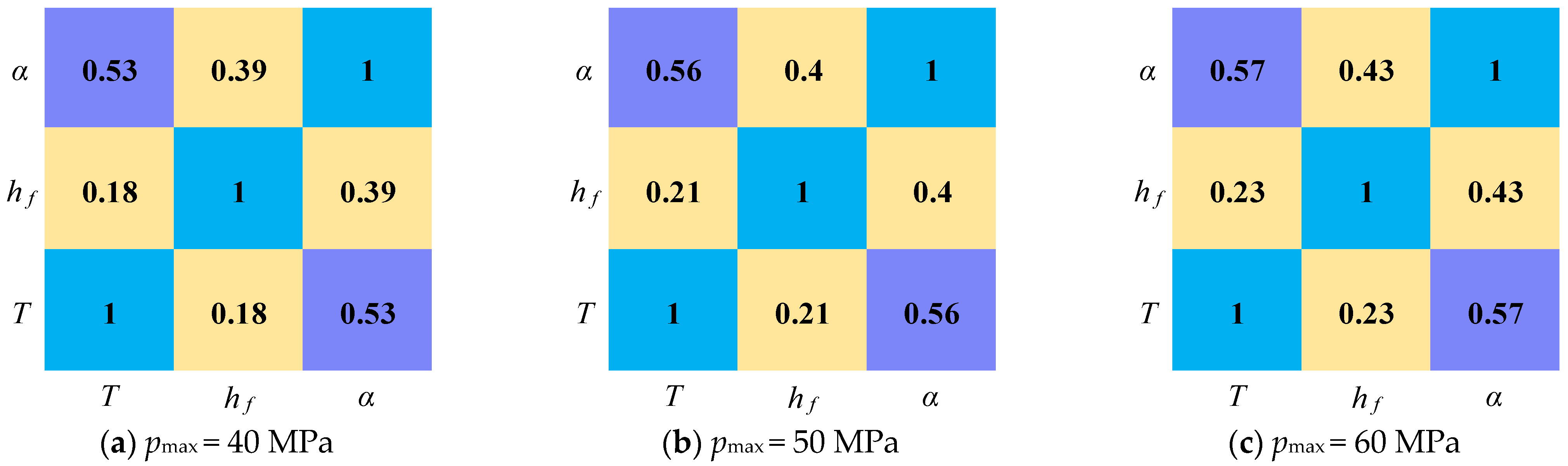
5.1. Correlation Among Geometrical Dimension Parameters
5.2. Correlation Between Geometrical Dimension Parameters and Stress Concentration Factor
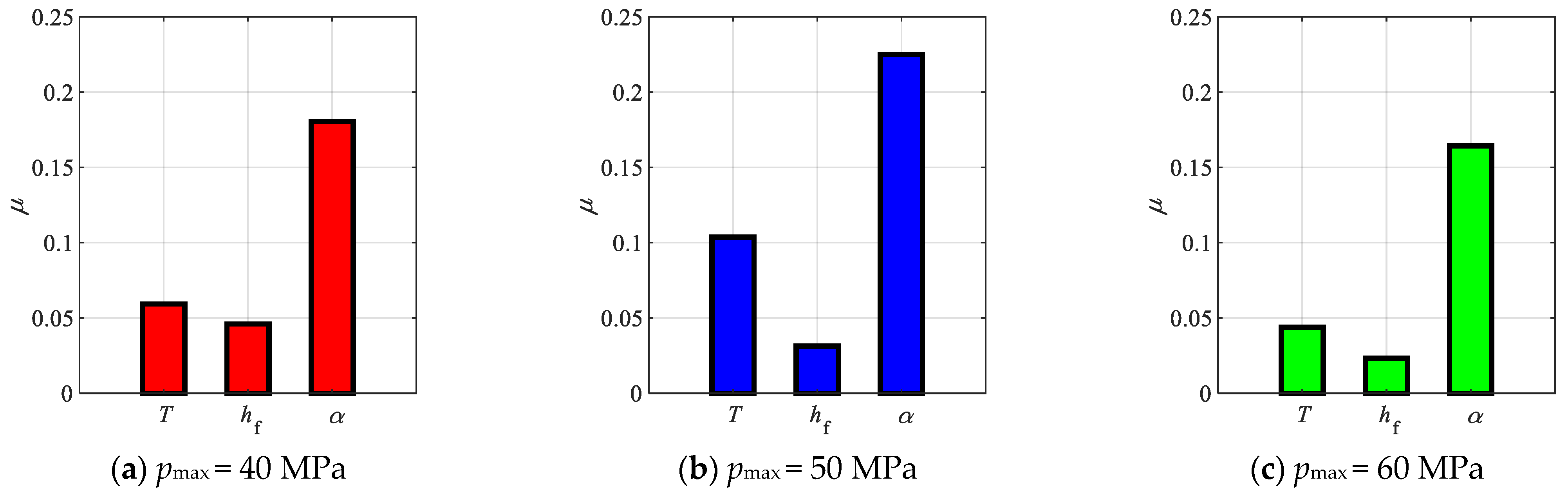
5.3. Impact of Geometrical Dimension Parameters on Fatigue Life
6. Conclusions
- (1)
- The maximum displacement evolution curve of welded T-joints under cyclic tensile loading exhibits three distinct stages-crack initiation, propagation, and final fracture-confirming the typical fatigue damage process. The real-time maximum displacement of T-joints can thus serve as an effective indicator for studying fatigue failure mechanisms and monitoring fatigue damage.
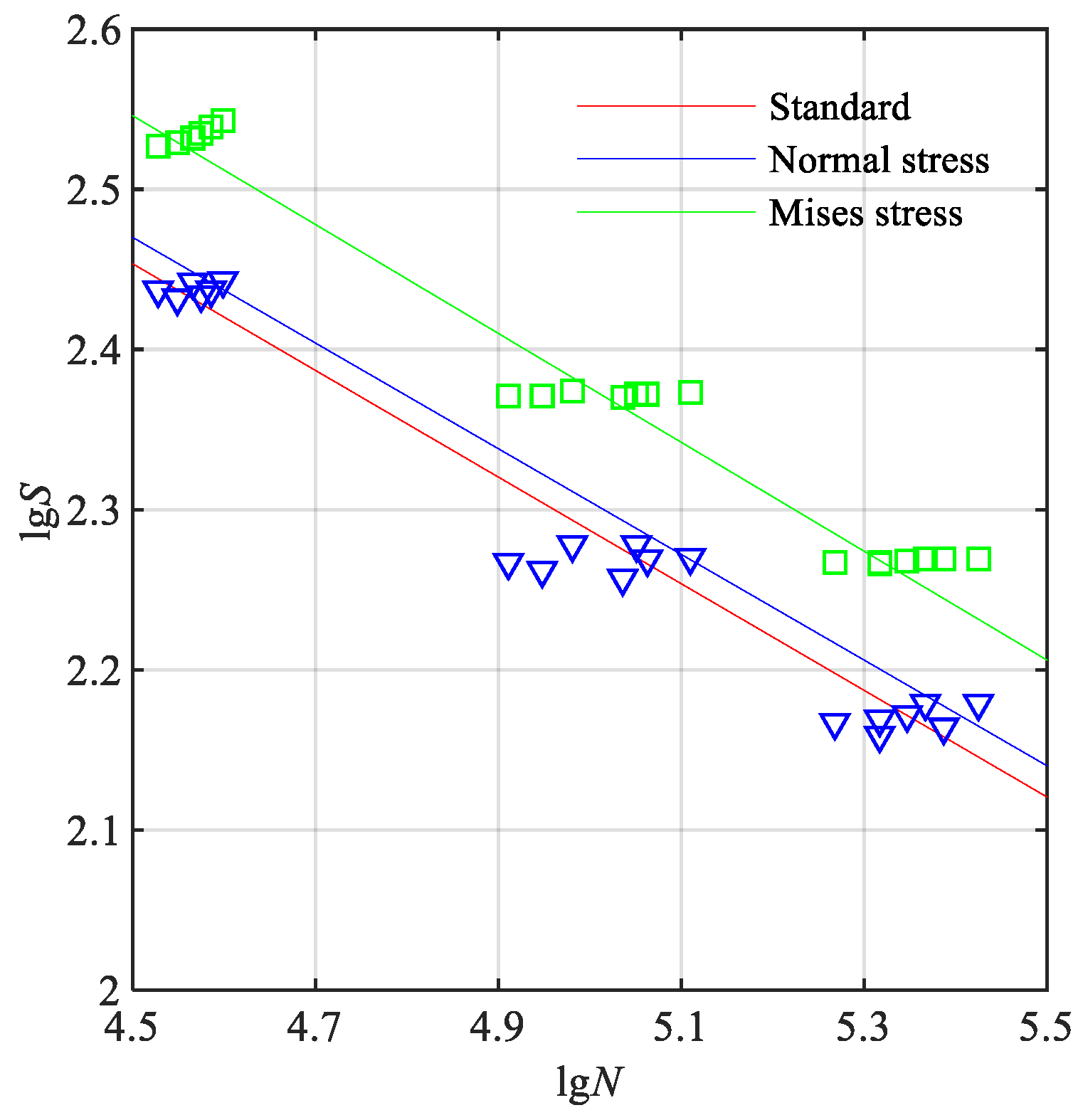
- (2)
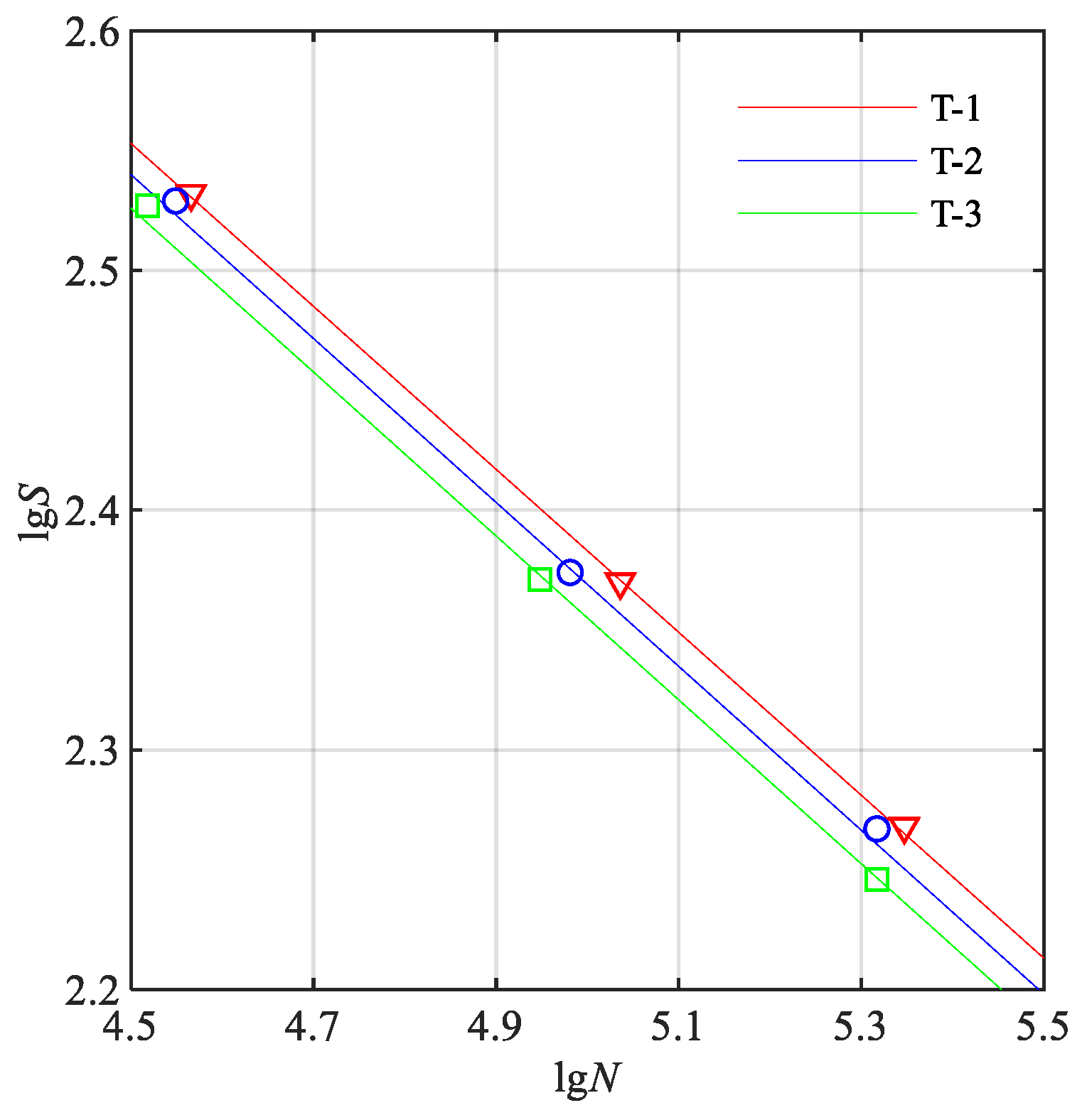
- Compared with fatigue life curves fitted using normal stress amplitude, those based on Mises stress amplitude show a higher degree of fit, indicating that Mises stress amplitude provides a more accurate representation of the fatigue performance of T-joints.
- (3)
- Web plate thickness, weld toe size, and welding angle are critical geometrical design parameters that significantly affect the fatigue life of T-joints. The web plate thickness shows an inverse relationship with fatigue life, while both weld toe size and welding angle are directly proportional to fatigue life.
- (4)
- Pearson correlation analysis revealed weak correlations among the geometrical parameters, indicating that the dimensional effects and stress concentration influencing fatigue life can be considered approximately independent.
- (5)
- Analysis based on the coefficient of variation shows that variations in weld toe size exert the smallest effect on fatigue life, whereas web plate thickness and welding angle have more pronounced effects, with welding angle being the most influential factor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fricke, W. Fatigue analysis of welded joints: State of development. Mar. Struct. 2003, 16, 185–200. [Google Scholar] [CrossRef]
- Hobbacher, A.F. Recommendations for Fatigue Design of Welded Joints and Components; Springer Nature Switzerland AG: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Milella, P.P. Fatigue and Corrosion in Metals; Springer Nature Switzerland AG: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Tong, L.; Huang, X.; Zhou, F.; Chen, Y. Experimental and numerical investigations on extremely-low-cycle fatigue fracture behavior of steel welded joints. J. Constr. Steel Res. 2016, 119, 98–112. [Google Scholar] [CrossRef]
- Liu, J.; Guo, T.; Feng, D.; Liu, Z. Fatigue performance of rib-to-deck joints strengthened with FRP angles. J. Bridge Eng. 2018, 23, 04018060. [Google Scholar] [CrossRef]
- Guo, T.; Liu, J.; Deng, Y.; Zhang, Z. Fatigue performance of orthotropic steel decks with FRP angles: Field measurement and numerical analysis. J. Perform. Constr. Facil. 2019, 33, 04019042. [Google Scholar] [CrossRef]
- Alencar, G.; de Jesus, A.; da Silva, J.G.S.; Calçada, R. Fatigue cracking of welded railway bridges: A review. Eng. Fail. Anal. 2019, 104, 154–176. [Google Scholar] [CrossRef]
- Manai, A.; Polach, R.U.F.B.; Al-Emrani, M. A probabilistic study of welding residual stresses distribution and their contribution to the fatigue life. Eng. Fail. Anal. 2020, 118, 104787. [Google Scholar] [CrossRef]
- Weng, S.; Meng, C.; Deng, J.; Zhao, L.; Pei, X.; Zhu, M. Fatigue life assessment of Q345 steel fillet welded joints with competitive failure modes. Eng. Fract. Mech. 2024, 298, 109913. [Google Scholar] [CrossRef]
- Zong, L.; Liu, H.; Ding, Y.; Cui, Y. Experimental and numerical study on fatigue damage evolution of Q690D welding details. J. Constr. Steel Res. 2024, 212, 108264. [Google Scholar] [CrossRef]
- Lai, B.-L.; Li, Y.-R.; Guo, T.; Vasdravellis, G.; Liew, J.Y.R. Overview of material constitutive law for additive manufacturing metal structures. Urban Lifeline 2025, 3, 11. [Google Scholar] [CrossRef]
- Connor, R.J.; Fisher, J.W. Consistent approach to calculating stresses for fatigue design of welded rib-to-web connections in steel orthotropic bridge decks. J. Bridge Eng. 2006, 11, 517–525. [Google Scholar] [CrossRef]
- Metrovich, B.; Fisher, J.W.; Yen, B.T. Theoretical development of lower bound S-N fatigue curves. J. Bridge Eng. 2012, 17, 517–525. [Google Scholar] [CrossRef]
- Frank, K.H.; Fisher, J.W. Fatigue strength of fillet welded cruciform joints. J. Struct. Div. 2021, 105, 1727–1740. [Google Scholar] [CrossRef]
- Demo, D.A.; Fisher, J.W. Analysis of fatigue of welded crane runway girders. J. Struct. Div. 2021, 120, 919–933. [Google Scholar] [CrossRef]
- Hirt, M.A.; Yen, B.T.; Fisher, J.W. Fatigue strength of rolled and welded steel beams. J. Struct. Div. 2021, 97, 1897–1911. [Google Scholar] [CrossRef]
- Horas, C.S.; Alencar, G.; De Jesus, A.M.; Calçada, R. Development of an efficient approach for fatigue crack initiation and propagation analysis of bridge critical details using the modal superposition technique. Eng. Fail. Anal. 2018, 89, 118–137. [Google Scholar] [CrossRef]
- Alencar, G.; de Jesus, A.; da Silva, J.G.S.; Calçada, R. A finite element post-processor for fatigue assessment of welded structures based on the Master S-N curve method. Int. J. Fatigue 2021, 153, 106482. [Google Scholar] [CrossRef]
- Alencar, G.; Hong, J.K.; de Jesus, A.; da Silva, J.G.S.; Calçada, R. The Master S-N curve approach for fatigue assessment of welded bridge structural details. Int. J. Fatigue 2021, 152, 106432. [Google Scholar] [CrossRef]
- Ban, H.; Zhu, J.; Shi, G. Cyclic loading tests on welded connections of stainless-clad bimetallic steel and modelling. J. Constr. Steel Res. 2020, 171, 106140. [Google Scholar] [CrossRef]
- Yang, X.; Ban, H.; Shi, Y.; Chung, K.F.; Hu, Y.F. Low-cycle fatigue behaviour of stainless-clad bimetallic steel welded connections. Thin-Walled Struct. 2024, 202, 112104. [Google Scholar] [CrossRef]
- Hai, L.; Ban, H.; Huang, C.; Shi, Y. Fatigue properties of titanium-clad bimetallic steel butt-welded joints. Thin-Walled Struct. 2024, 202, 112149. [Google Scholar] [CrossRef]
- Samadi, F.; Mourya, J.; Wheatley, G.; Khan, M.N.; Nejad, R.M.; Branco, R.; Macek, W. An investigation on residual stress and fatigue life assessment of T-shape welded joints. Eng. Fail. Anal. 2022, 141, 106685. [Google Scholar] [CrossRef]
- Zhao, Y.; Rao, G.; Wei, G. Experimental investigation of bending fatigue behaviors for T-shaped welded joint. Eng. Sci. Technol. 2024, 55, 101742. [Google Scholar] [CrossRef]
- Malschaert, D.; Veljkovic, M.; Maljaars, J. Numerical simulations of residual stress formation and its effect on fatigue crack propagation in a fillet welded T-joint. Eng. Fract. Mech. 2024, 306, 110236. [Google Scholar] [CrossRef]
- Xu, Y. Fatigue reliability evaluation using probability density evolution method. Probabilistic Eng. Mech. 2015, 42, 1–6. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Y. Probabilistic load flow calculation by using probability density evolution method. Electr. Power Energy Syst. 2018, 99, 447–453. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Y. A Chebyshev collocation based sequential matrix exponential method for the generalized density evolution equation. Probabilistic Eng. Mech. 2021, 63, 103118. [Google Scholar] [CrossRef]
- Tian, R.; Xu, Y. A modified Chebyshev collocation method for the generalized probability density evolution equation. Eng. Struct. 2024, 305, 117676. [Google Scholar] [CrossRef]
- Cheng, B.; Cao, X.; Ye, X.; Cao, Y. Fatigue tests of welded connections between longitudinal stringer and deck plate in railway bridge orthotropic steel decks. Eng. Struct. 2017, 153, 32–42. [Google Scholar] [CrossRef]
- Akyel, A.; Kolstein, M.; Bijlaard, F. Fatigue strength of repaired welded connections made of very high strength steels. Eng. Struct. 2018, 161, 28–40. [Google Scholar] [CrossRef]
- Martínez, J.; Adriano, V.; Araújo, J.; Ferreira, J.; da Silva, C. Geometrical size effect in the fatigue life predictions of aluminum wires with micro holes using methods of the critical distance. Eng. Fract. Mech. 2019, 209, 147–161. [Google Scholar] [CrossRef]
- Bai, S.; Li, Y.-F.; Huang, H.-Z.; Ma, Q.; Lu, N. A probabilistic combined high and low cycle fatigue life prediction framework for the turbine shaft with random geometric parameters. Int. J. Fatigue 2022, 165, 107218. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhan, M.; Fu, M. Microstructural and geometrical size effects on the fatigue of metallic materials. Int. J. Mech. Sci. 2022, 218, 107058. [Google Scholar] [CrossRef]
- Yang, W.K.; Hu, B.L.; Luo, Y.W.; Song, Z.M.; Zhang, G.P. Understanding geometrical size effect on fatigue life of A588 steel using a machine learning approach. Int. J. Fatigue 2023, 172, 107671. [Google Scholar] [CrossRef]
- Wang, C.S.; Wang, Y.Z.; De Corte, W.; Shu, C. Digital simulation of distortion-induced fatigue in steel bridges with different geometrical configurations. J. Constr. Steel Res. 2024, 216, 108613. [Google Scholar] [CrossRef]
- Tao, Z.Q.; Wang, Z.; Pan, X.; Su, T.; Long, X.; Liu, B.; Tang, Q.; Ren, X.; Sun, C.; Qian, G.; et al. A new probabilistic control volume scheme to interpret specimen size effect on fatigue life of additively manufactured titanium alloys. Int. J. Fatigue 2024, 183, 108262. [Google Scholar] [CrossRef]
- Ghanadi, M.; Hultgren, G.; Narström, T.; Clarin, M.; Barsoum, Z. Fatigue assessment of welded joints—Size effect and probabilistic approach. J. Constr. Steel Res. 2024, 221, 108884. [Google Scholar] [CrossRef]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture and Building Press: Beijing, China, 2017. (In Chinese)
- Chen, Y.; Pan, X.; Deng, L. Study on the localization of defects in typical steel butt welds considering the effect of residual stress. Appl. Sci. 2023, 13, 2648. [Google Scholar] [CrossRef]
- Shen, P.; Yang, P.; Chen, Y.; Yang, Y.; Zhou, J. Seismic performance of self-centering steel column base with buckling-restrained bars. J. Build. Eng. 2024, 91, 109474. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, B.; Wang, Y.; Xiao, S. A hybrid distribution characteristics of equivalent structural stress method for fatigue evaluation of welded structures. Int. J. Fatigue 2024, 179, 108057. [Google Scholar] [CrossRef]
- Quessy, J.; Lemaire-Paquette, S. The weighted characteristic function of the multivariate PIT: Independence and goodness-of-fit tests. J. Multivar. Anal. 2024, 201, 105272. [Google Scholar] [CrossRef]
- Shen, P.; Chen, Y.; Ma, S.; Yan, Y. Safety assessment method of concrete-filled steel tubular arch bridge by fuzzy Analytic Hierarchy Process. Buildings 2024, 14, 67. [Google Scholar] [CrossRef]
- Wilcox, R.R. Applying Contemporary Statistical Techniques; Elsevier Incorporation: Amsterdam, The Netherlands, 2003. [Google Scholar] [CrossRef]
- Han, S.; Li, D.; Li, K.; Wu, H.; Gao, Y.; Zhang, Y.; Yuan, R. Analysis and study of transmission line icing based on grey correlation pearson combinatorial optimization support vector machine. Measurement 2024, 236, 115086. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Shi, Z.; Wang, M.; Tan, H. Fatigue characteristics and energy evolution analysis of red sandstone under the coupling of freeze–thaw and cyclic loading. Int. J. Fatigue 2024, 185, 108331. [Google Scholar] [CrossRef]
- Liu, M.; Miranda, A.C.d.O.; Antunes, M.A.; Meggiolaro, M.A.; de Castro, J.T.P. Plastic stress concentration effects in fatigue strength. Int. J. Fatigue 2023, 168, 107394. [Google Scholar] [CrossRef]
- Kozakov, K.; Klusak, J. Fatigue lifetime predictions of notched specimens based on the critical distance and stress concentration factors. Theor. Appl. Fract. Mech. 2024, 133, 104579. [Google Scholar] [CrossRef]
- Oyegbile, A.D.; Muskulus, M. Enhancing fatigue reliability prediction of offshore wind turbine jacket joints through individual uncertainties for each degree of freedom of stress concentration factor. Mar. Struct. 2024, 96, 103634. [Google Scholar] [CrossRef]
- Chen, Y.; Pan, X.; Shen, P.; Li, Q.H.; Zhang, Y. Review of the influential weld details on fatigue failure of OSD in RD joints. Gradevinar 2025, 77, 471–484. [Google Scholar] [CrossRef]
- Hultgren, G.; Mansour, R.; Barsoum, Z. Fatigue strength assessment of welded joints incorporating the variability in local weld geometry using a probabilistic framework. Int. J. Fatigue 2023, 167, 107364. [Google Scholar] [CrossRef]
- Dong, L.; Feng, P.; Lu, C.; Zhang, P.; Ding, G. Rapid design for large-scale parallel CFRP cable with multi-source experimental data. Eng. Struct. 2024, 305, 117771. [Google Scholar] [CrossRef]




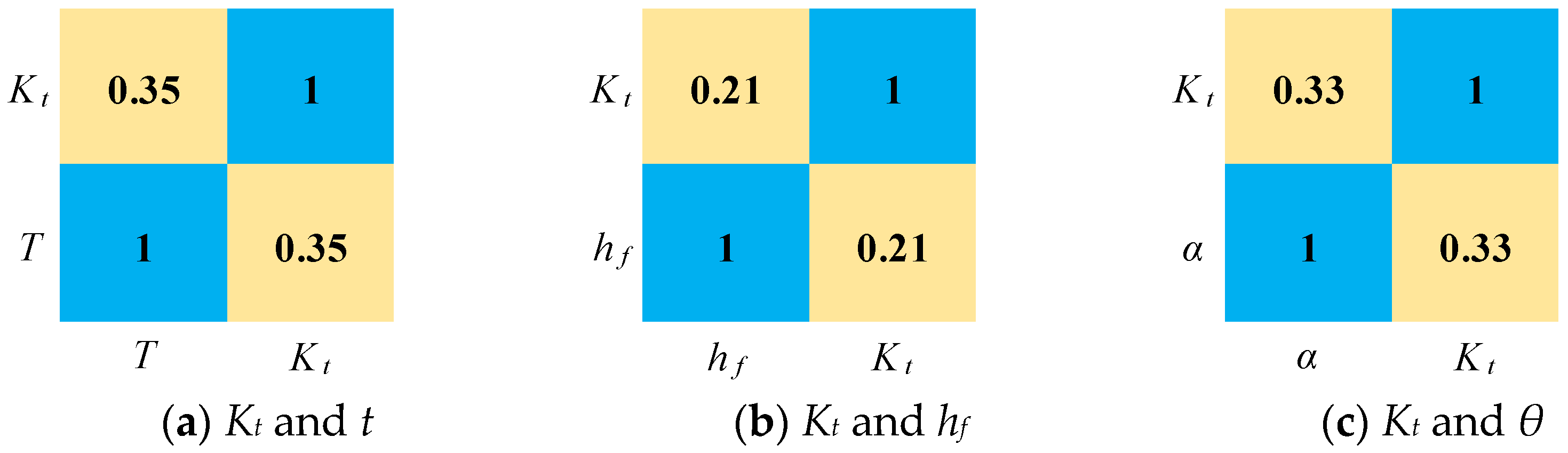
| Specification | t (mm) | fy (MPa) | fu (MPa) | Es (MPa) |
|---|---|---|---|---|
| Q355B | 10 | 375 | 515 | 2.11 × 105 |
| Q355B | 14 | 373 | 511 | 2.10 × 105 |
| Q355B | 18 | 380 | 520 | 2.14 × 105 |
| Q355B | 20 | 380 | 520 | 2.12 × 105 |
| Group | Base Plate Dimensions (mm) | Web Plate Dimensions (mm) | Weld Toe Size (mm) | Welding Angle (°) |
|---|---|---|---|---|
| T-1 | 240 × 100 × 20 | 140 × 100 × 10 | 8 | 45 |
| T-2 | 240 × 100 × 20 | 140 × 100 × 14 | 8 | 45 |
| T-3 | 240 × 100 × 20 | 140 × 100 × 18 | 8 | 45 |
| T-4 | 240 × 100 × 20 | 140 × 100 × 10 | 10 | 45 |
| T-5 | 240 × 100 × 20 | 140 × 100 × 10 | 12 | 45 |
| T-6 | 240 × 100 × 20 | 140 × 100 × 10 | 8 | 10 |
| T-7 | 240 × 100 × 20 | 140 × 100 × 10 | 8 | 60 |
| pmax (MPa) | T-1 | T-2 | T-3 | T-4 | T-5 | T-6 | T-7 |
|---|---|---|---|---|---|---|---|
| 60 | 36,785 | 35,362 | 33,692 | 37,608 | 38,532 | 28,622 | 39,748 |
| 50 | 108,653 | 95,702 | 88,685 | 112,496 | 115,682 | 81,561 | 129,406 |
| 40 | 222,493 | 207,635 | 197,812 | 232,642 | 243,951 | 185,237 | 266,234 |
| pmax | T-1 | T-2 | T-3 | T-4 | T-5 | T-6 | T-7 |
|---|---|---|---|---|---|---|---|
| 60 | 340.43 | 338.06 | 336.49 | 342.77 | 345.93 | 345.14 | 349.08 |
| 50 | 234.41 | 236.59 | 233.57 | 235.50 | 235.53 | 234.96 | 236.06 |
| 40 | 185.39 | 186.32 | 184.38 | 185.79 | 182.76 | 184.94 | 185.77 |
| Group | Web Plate Thickness (mm) | k | m |
|---|---|---|---|
| T-1 | 10 | 4.083 | 0.340 |
| T-2 | 14 | 4.079 | 0.342 |
| T-3 | 18 | 4.065 | 0.342 |
| Group | Weld Toe Size (mm) | k | m |
|---|---|---|---|
| T-1 | 8 | 4.083 | 0.340 |
| T-4 | 10 | 4.092 | 0.341 |
| T-5 | 12 | 4.096 | 0.340 |
| Group | Weld Toe Size (mm) | k | m |
|---|---|---|---|
| T-1 | 45 | 4.083 | 0.340 |
| T-6 | 10 | 4.031 | 0.338 |
| T-7 | 60 | 4.089 | 0.336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Shen, P.; Li, C.; Zhou, J. Analysis of the Geometrical Size Effect on the Fatigue Performance of Welded T-Joints. Buildings 2025, 15, 3627. https://doi.org/10.3390/buildings15193627
Chen Y, Shen P, Li C, Zhou J. Analysis of the Geometrical Size Effect on the Fatigue Performance of Welded T-Joints. Buildings. 2025; 15(19):3627. https://doi.org/10.3390/buildings15193627
Chicago/Turabian StyleChen, Yue, Peiwen Shen, Chang Li, and Jianting Zhou. 2025. "Analysis of the Geometrical Size Effect on the Fatigue Performance of Welded T-Joints" Buildings 15, no. 19: 3627. https://doi.org/10.3390/buildings15193627
APA StyleChen, Y., Shen, P., Li, C., & Zhou, J. (2025). Analysis of the Geometrical Size Effect on the Fatigue Performance of Welded T-Joints. Buildings, 15(19), 3627. https://doi.org/10.3390/buildings15193627






