Seismic Collapse of Frictionally Isolated Timber Buildings in Subduction Zones: An Assessment Considering Slider Impact
Abstract
1. Introduction
2. Archetype Buildings
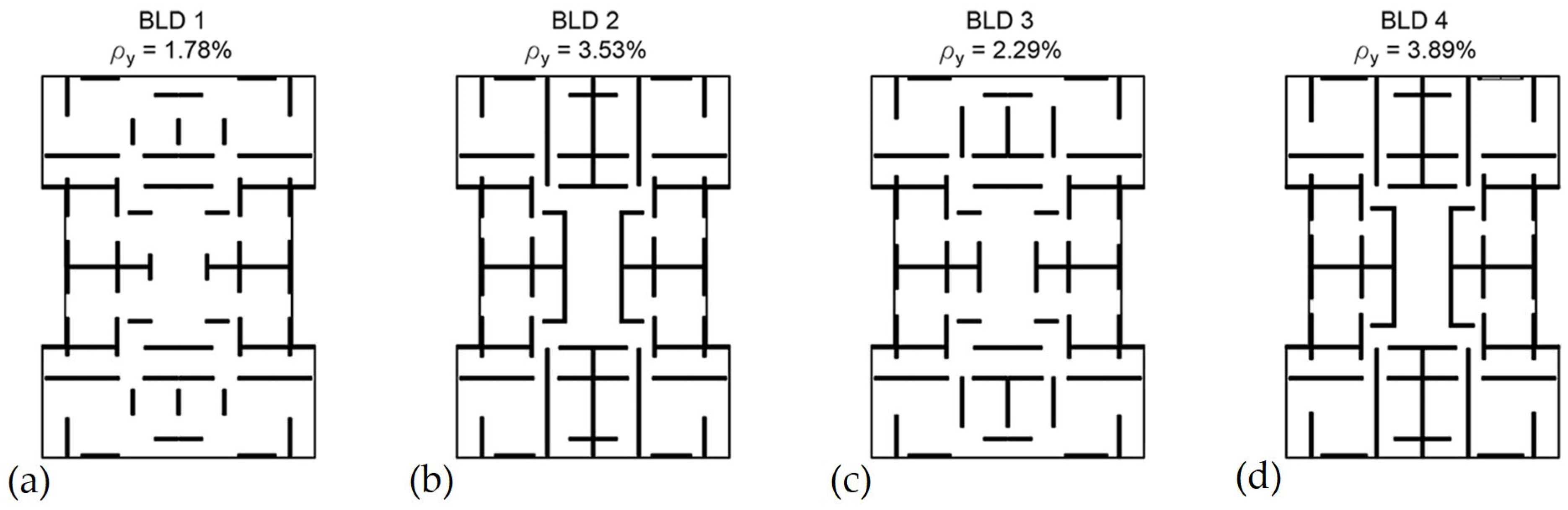
2.1. Architectural Configuration and Structural Layout
2.2. Structural Design
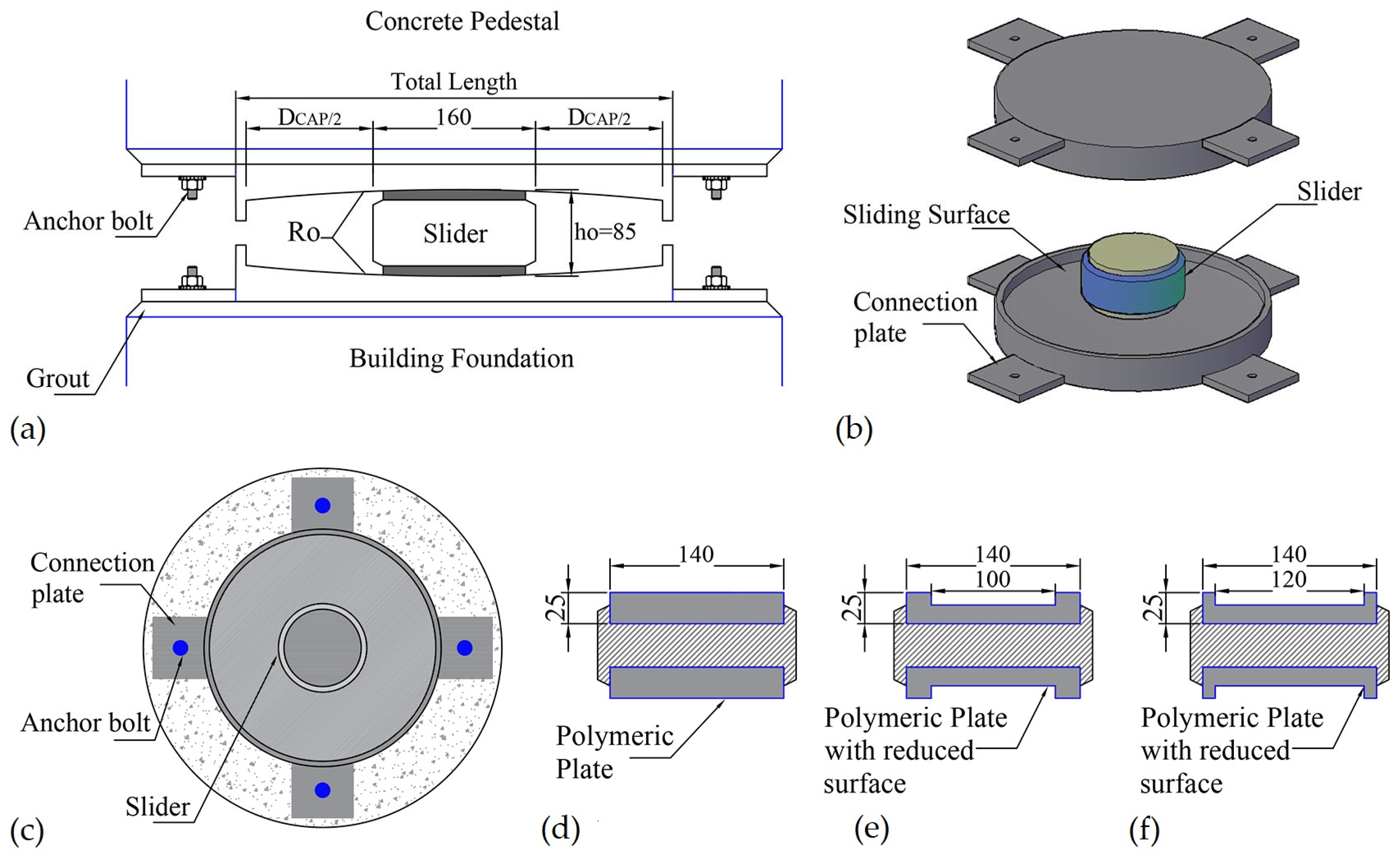
2.3. Isolation System Design
2.4. Superstructure Design
2.5. Modal Properties
3. Numerical Models for Evaluating Collapse
3.1. Overall Archetype Model Description
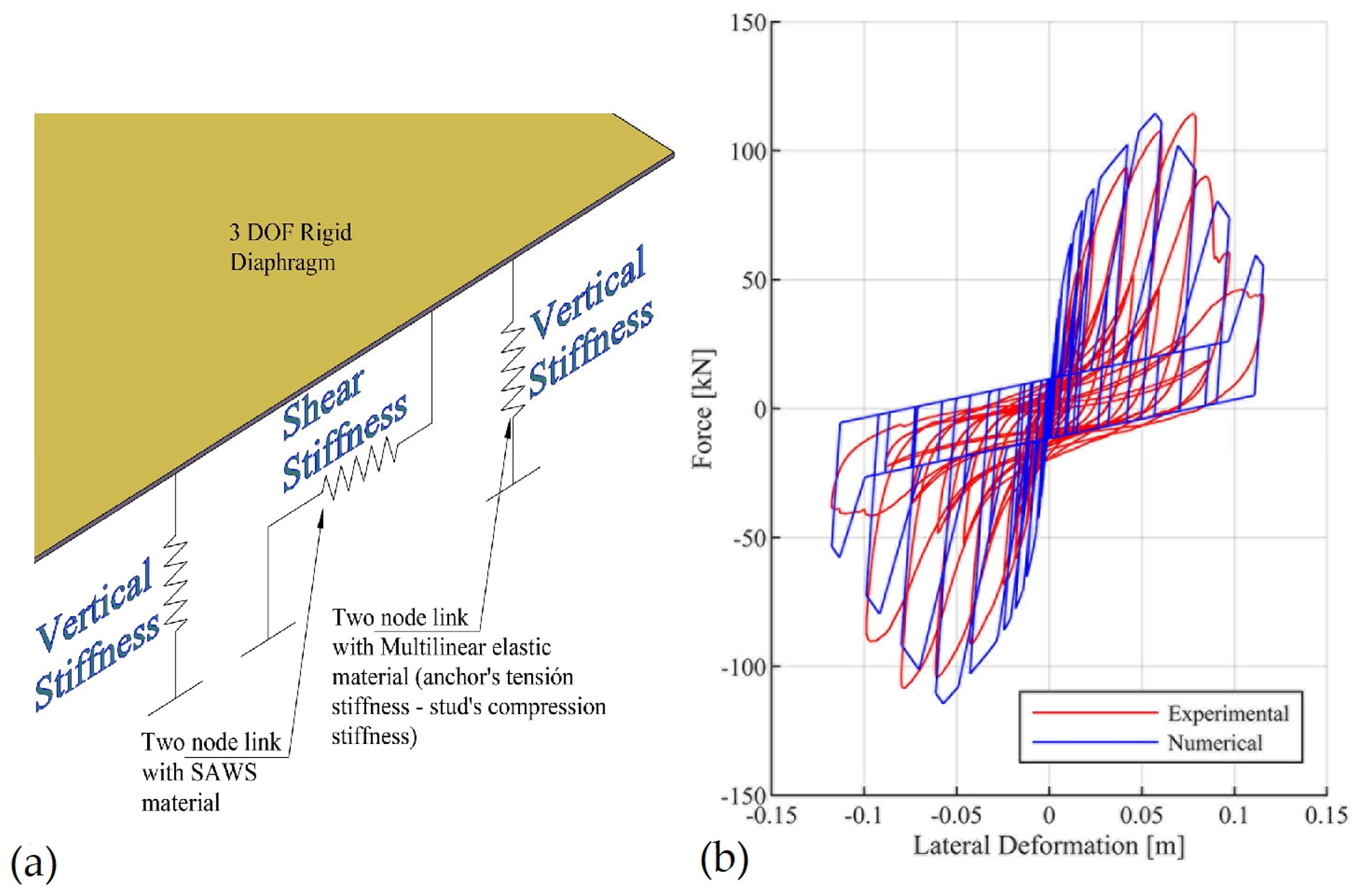
3.2. Superstructure Model
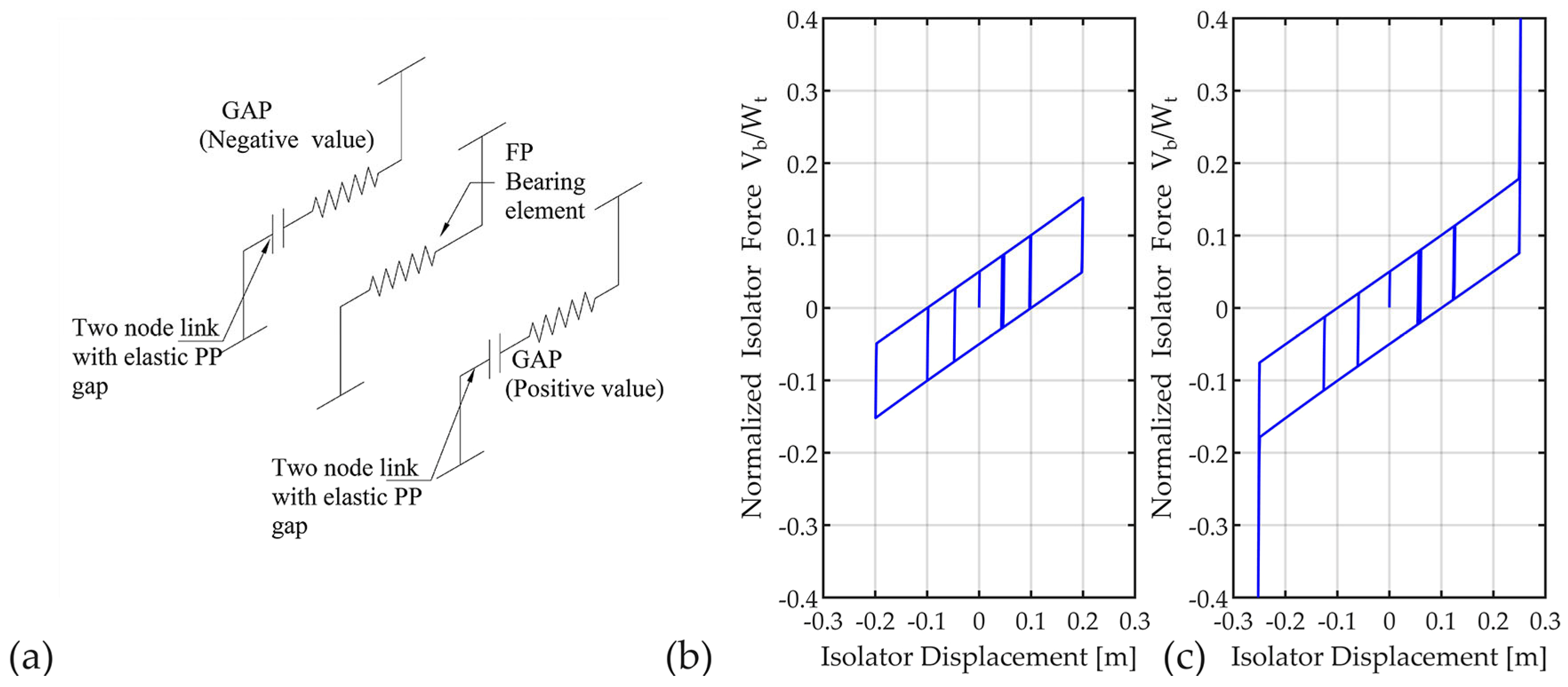
3.3. Isolation System Model
4. Collapse Assessment
4.1. Collapse Definition
4.2. Ground Motion Selection
4.3. Incremental Dynamic Analysis
4.4. Collapse Margin Ratio and Fragility Curves
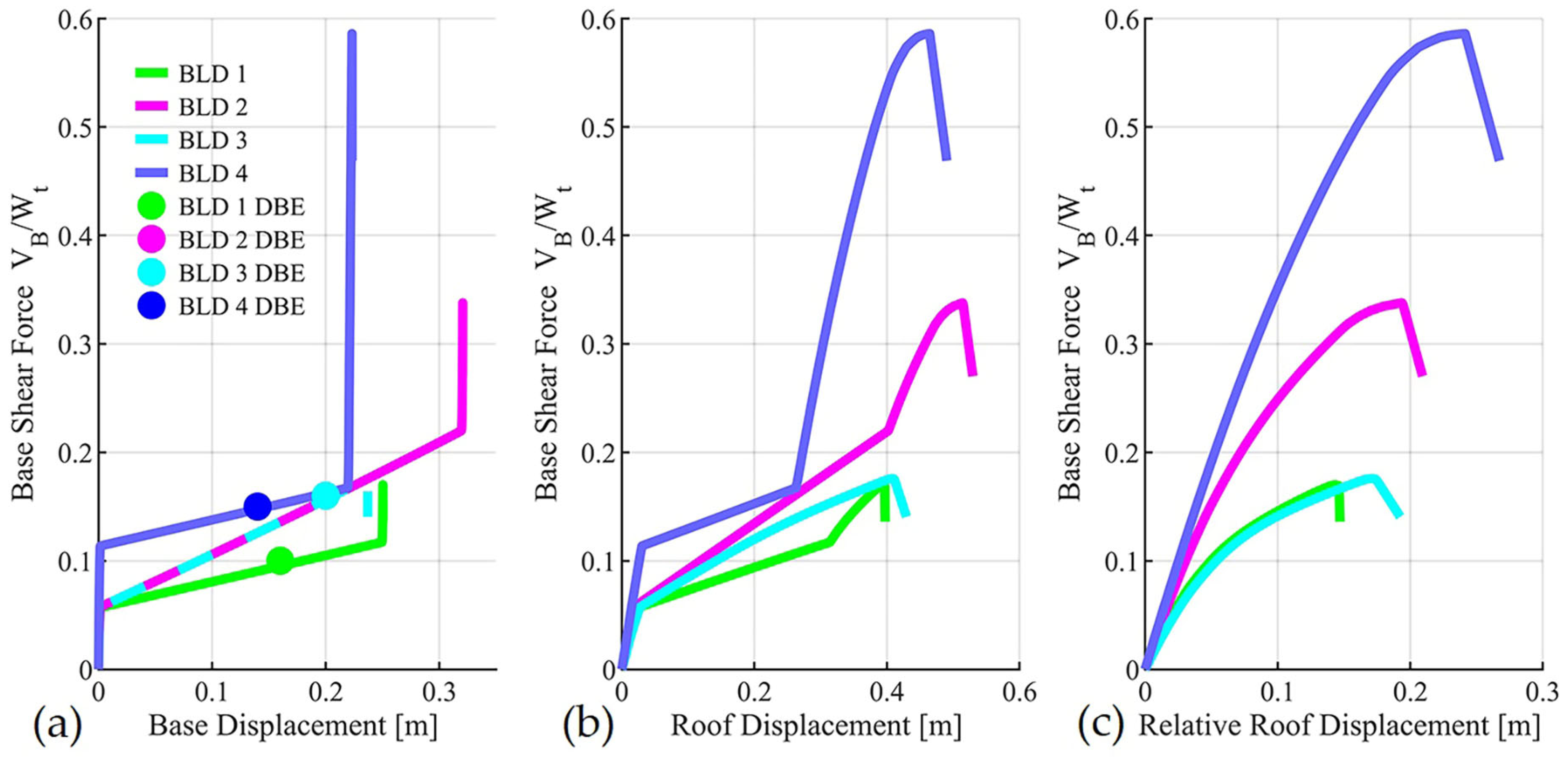
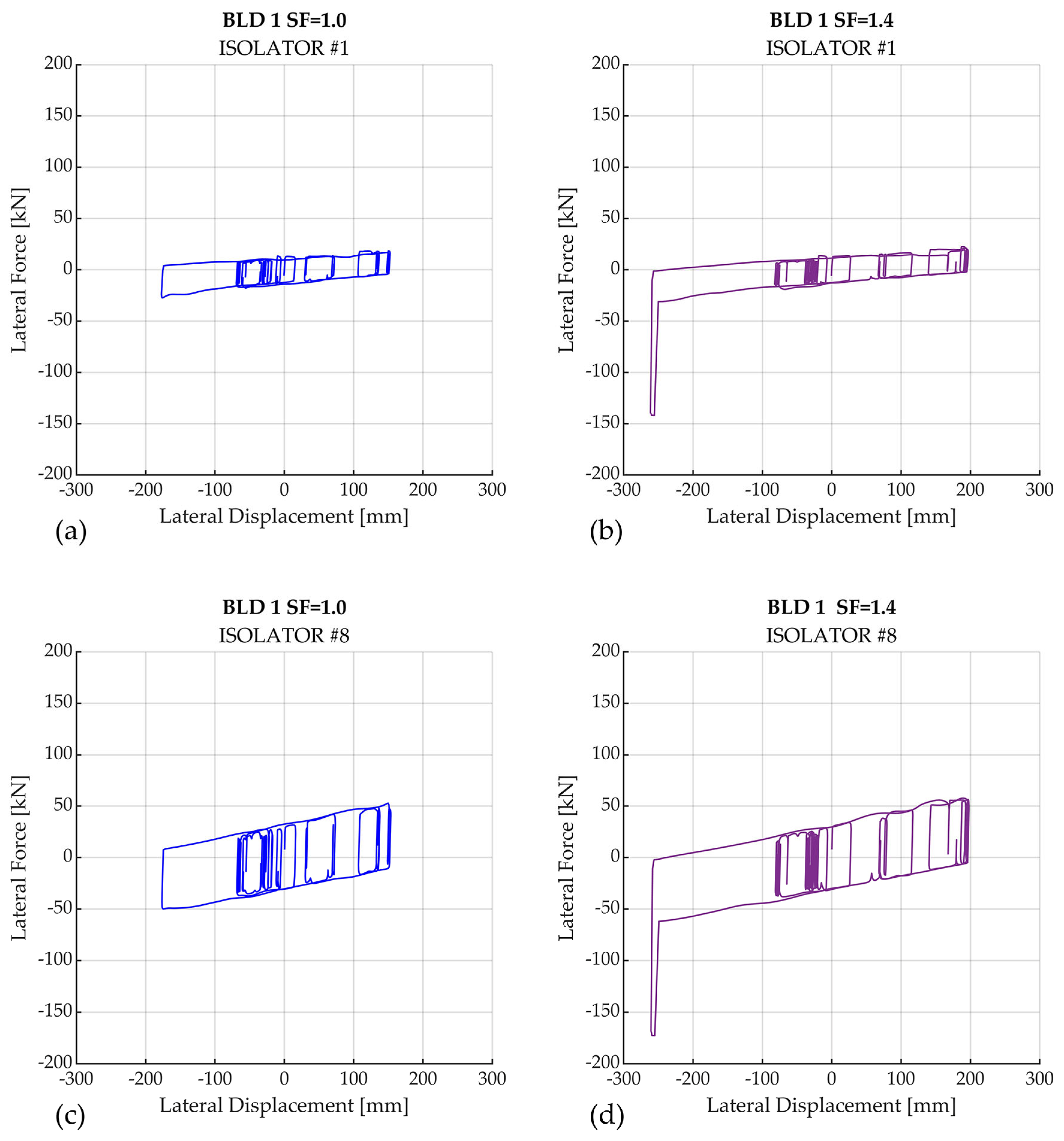
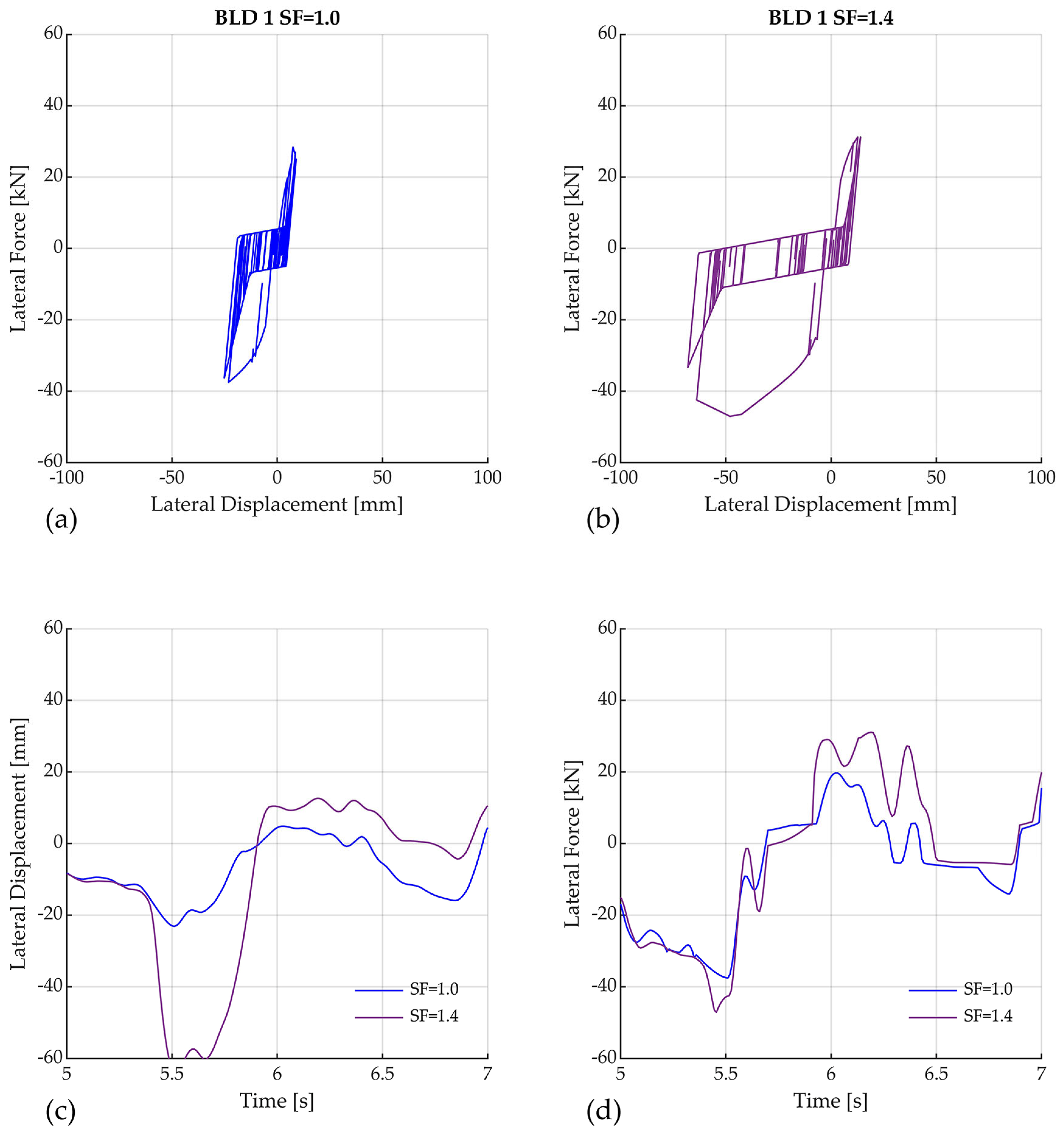
5. Results and Discussion
- The impact model does not include potential energy dissipation through perimeter ring plasticity;
- The fragility curves do not include the FEMA-specified 1.2 amplification factor for 3D models;
- The SSW model does not consider beneficial 3D coupling or gravity load effects.
6. Conclusions
- Code-conforming isolated LFTBs (R = 1, PDR ≤ 0.4%) can achieve acceptable collapse performance with reduced shear wall density and without continuous anchor tie systems (ATS), providing potential for substantial cost savings;
- Non-code-conforming designs, such as BLD-3 with a 0.7% PDR, showed marginal performance (CMR ≈ 1.0), highlighting that drift limits in NCh2745 should not be exceeded without proper compensation in wall strength or redundancy;
- The equivalent lateral force procedure, as prescribed by NCh2745, resulted in safe design outcomes for frictionally isolated regular LFTBs, even though nonlinear time history analysis is formally required;
- Archetypes with a period ratio close to 3.0, such as BLD-2 and BLD-4, displayed the best seismic performance. BLD-4, despite having the highest friction coefficient (μ = 0.12), achieved the highest CMR (1.55) and required compact isolators (40 cm length);
- The isolation system’s friction coefficient had a limited effect on global performance, provided that the stiffness of the isolation system and the superstructure were well balanced. High-friction systems, when properly designed, can yield compact and cost-effective isolators;
- Discrete hold-down anchors were sufficient to achieve good seismic performance in the archetypes, eliminating the need for costly continuous ATS and simplifying construction;
- Even in the presence of slider impact, acceptable collapse probabilities were achieved in BLD-2 and BLD-4, and performance could be further improved by increasing the gap distance between the slider and perimeter ring.
- The vertical component of seismic ground motion was not considered. Although consistent with prior FEMA P695 applications, future studies should assess its potential to amplify peak floor accelerations and drift demands. To the best of the author’s knowledge, the only studies that evaluated the seismic performance of isolated buildings using the FEMA P695 methodology, considering 3D models and the impact effect, are the study of isolated steel buildings by Masroor et al. [16] and the study of hybrid timber buildings by Quizanga et al. [33]. However, even in these studies, the effect of the vertical component was neglected, too. Thus, the effect of a record’s vertical component warrants further investigation, as incorporating this vertical component could potentially increase PFAs and PDRs.
- Axial load and 3D coupling effects in shear walls were not modeled. Including these effects is likely to enhance system stiffness and collapse resistance, as suggested by previous studies (e.g., [40]).
- Impact was modeled via a linear-elastic approach that simplified the impact effect simulation by using easily calculable stiffnesses, as in previous studies by Kitayama and Constantinou [19]. More advanced impact models, capable of simulating energy dissipation, could improve the realism of the analysis, albeit at a high computational cost. Moreover, experimental data on small-scale DCFP bearings in timber applications are currently lacking. For these reasons, the authors adopted this simplified modeling assumption, looking for a balance between simplicity and accuracy.
- This paper considers a limited number of archetype frames, all of which share the same plan and story number. This may limit the generality of these findings, as varying the number of stories would affect mass distribution and potentially the collapse fragility curves. Lower-rise buildings would likely exhibit reduced drift demands, whereas taller archetypes could experience increased instability. It should be noted that the results presented herein correspond to archetypes representative of five-story timber buildings on Site Class C soils with shallow foundations. Different structural and geotechnical parameters could influence the seismic response. For example, softer soils (e.g., Site D/E) may amplify isolation displacements and increase the likelihood of ring impact, while deeper foundation embedment could reduce lateral flexibility and modify isolator demands. While these aspects were outside the scope of the present study, they represent important directions for future research to extend the applicability of the findings.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACMR | Adjusted Collapse Margin Ratio |
| ASCE | American Society of Civil Engineers |
| ATS | Anchor tie system |
| Standard deviation | |
| Effective damping at the DBE level | |
| Effective damping at the MCE level | |
| BLD | Building |
| C | Seismic coefficient |
| CMR | Collapse margin ratio |
| Displacement capacity | |
| Displacement at the DBE level | |
| Displacement at the MCE level | |
| Total maximum displacement at MCE level | |
| DBE | Design Basis Earthquake |
| DCFP | Double concave friction pendulum |
| Maximum lateral displacement of the SSW | |
| EDP | Engineering demand parameter |
| FEMA | Federal Emergency Management Agency |
| FP | Single Friction Pendulum |
| ho | Slider height |
| IM | Intensity measure |
| Effective stiffness at the DBE level | |
| Effective stiffness at the MCE level | |
| LFTB | Light-frame timber building |
| Friction coefficient at high sliding speed | |
| MCE | Maximum considered earthquake |
| Normalization factor | |
| NSP | Nonlinear static pushover |
| OSB | Oriented strand board |
| Wall density | |
| PDR | Inter-story peak drift ratio |
| PFA | Peak floor acceleration |
| PET-P | Polyethylene terephthalate |
| PGA | Peak ground acceleration |
| PGV | Peak ground velocity |
| R | Response modification factor |
| Effective radius | |
| Radius of curvature of the sliding surfaces | |
| SAWS | Seismic Analysis of Woodframe Structures |
| SDPWS | Special Design Provisions for Wind and Seismic |
| SF | Scale factor |
| SSF | Spectral shape factor |
| SSW | Strong wood-frame shear wall |
| Median collapse capacity | |
| Spectral acceleration at the fundamental period at the MCE level | |
| Fundamental period | |
| Effective period at the DBE level | |
| Effective period at the MCE level | |
| Base shear force | |
| Total seismic weight | |
| Mean |
References
- Skullestad, J.L.; Bohne, R.A.; Lohne, J. High-rise Timber Buildings as a Climate Change Mitigation Measure—A Comparative LCA of Structural System Alternatives. Energy Procedia 2016, 96, 112–123. [Google Scholar] [CrossRef]
- Guindos, P. Fundamentos del diseño y la Construcción con Madera; Ediciones UC: Santiago, Chile, 2019. [Google Scholar]
- Ellingwood, B.R.; Rosowsky, D.V.; Pang, W. Performance of Light-Frame Wood Residential Construction Subjected to Earthquakes in Regions of Moderate Seismicity. J. Struct. Eng. 2008, 134, 1353–1363. [Google Scholar] [CrossRef]
- Kircher, C.A.; Reitherman, R.K.; Whitman, R.V.; Arnold, C. Estimation of Earthquake Losses to Buildings. Earthq. Spectra 1997, 13, 703–720. [Google Scholar] [CrossRef]
- Symans, M.D.; Cofer, W.F.; Fridley, K.J. Base Isolation and Supplemental Damping Systems for Seismic Protection of Wood Structures: Literature Review. Earthq. Spectra 2002, 18, 549–572. [Google Scholar] [CrossRef]
- Yang, T.Y.; Etebarian, H. Enhancing the seismic performance of mid-rise wood-frame buildings with rigid spine columns. Struct. Des. Tall Spec. Build. 2019, 28, e1556. [Google Scholar] [CrossRef]
- FEMA. FEMA P807. Seismic Evaluation and Retrofit of Multi-Unit Wood-Frame Buildings with Weak First Stories; Homeland Security: Washington, DC, USA, 2012.
- Wang, B.; Chen, P.; Zhu, S.; Dai, K. Seismic performance of buildings with novel self-centering base isolation system for earthquake resilience. Earthq. Eng. Struct. Dyn. 2023, 52, 1360–1380. [Google Scholar] [CrossRef]
- Liu, Q.; Guo, Z.; Zhu, S.; Wang, C.; Ren, X.; Wu, X. Performance-Based Seismic Design of Hybrid Isolation Systems with Gap-Tunable BRBs for Bearing-Supported Bridges. Symmetry 2022, 14, 1373. [Google Scholar] [CrossRef]
- Sakamoto, I.; Ohashi, Y.; Fujii, Y. Seismic Behavior of Base Isolated Two-storied Wooden Buildings. In Proceedings of the International Timber Engineering Conference, Tokyo, Japan, 23–25 October 1990; pp. 938–945. [Google Scholar]
- Van De Lindt, J.W.; Liu, H.; Symans, M.D.; Shinde, J.K. Seismic Performance and Modeling of a Half-Scale Base-Isolated Wood Frame Building. J. Earthq. Eng. 2011, 15, 469–490. [Google Scholar] [CrossRef]
- Jampole, E.; Deierlein, G.; Miranda, E.; Fell, B.; Swensen, S.; Acevedo, C. Full-Scale Dynamic Testing of a Sliding Seismically Isolated Unibody House. Earthq. Spectra 2016, 32, 2245–2270. [Google Scholar] [CrossRef]
- Quizanga, D.; Almazán, J.L.; Valdivieso, D.; López-García, D.; Guindos, P. Shaking table test of a timber building equipped with a novel cost-effective, impact-resilient seismic isolation system. J. Build. Eng. 2024, 82, 108402. [Google Scholar] [CrossRef]
- Pall, A.S.; Pall, R. Seismic response of a friction-base-isolated house in Montreal. In Proceedings of the 6th Canadian Conference on Earthquake Engineering, Toronto, ON, Canada, 12–14 June 1991; University of Toronto Press: Toronto, ON, Canada, 1991; pp. 375–382. [Google Scholar] [CrossRef]
- Zayas, V.; Low, S. Seismic Isolation of a Four-Story Wood Building. Earthquake Performance and Safety of Timber Structures; Forest Products Society Proc. No. 7289; Forest Products Society: Ruston, LA, USA, 1997; pp. 83–91. [Google Scholar]
- Masroor, A.; Mosqueda, G. Assessing the Collapse Probability of Base-Isolated Buildings considering Pounding to Moat Walls using the FEMA P695 Methodology. Earthq. Spectra 2015, 31, 2069–2086. [Google Scholar] [CrossRef]
- Bao, Y.; Becker, T.C. Inelastic response of base-isolated structures subjected to impact. Eng. Struct. 2018, 171, 86–93. [Google Scholar] [CrossRef]
- Bao, Y.; Becker, T.C.; Sone, T.; Hamaguchi, H. To limit forces or displacements: Collapse study of steel frames isolated by sliding bearings with and without restraining rims. Soil Dyn. Earthq. Eng. 2018, 112, 203–214. [Google Scholar] [CrossRef]
- Kitayama, S.; Constantinou, M.C. Seismic Performance Assessment of Seismically Isolated Buildings Designed by the Procedures of ASCE/SEI 7. Technical Report MCEER-18-004. University at Bufalo, State University of New York: New York, NY, USA, 2018; ISSN 1520-295X. [Google Scholar]
- Jampole, E.; Deierlein, G.; Miranda, E.; Fell, B.; Swensen, S.; Acevedo, C. An economic sliding isolation system for light frame residential structures. In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Sancin, L.; Rinaldin, G.; Fragiacomo, M.; Amadio, C. Seismic analysis of an isolated and a non-isolated light-frame timber building using artificial and natural accelerograms. Boll. Geofis. Teor. Ed. Appl. 2014, 55, 103. [Google Scholar] [CrossRef]
- NCh 2745-13; Análisis y Diseño Sísmico de Edificios con Aislación Sísmica. Instituto Nacional de Normalización: Santiago, Chile, 2013.
- FEMA. FEMA P695. Quantification of Building Seismic Performance Factors; Homeland Security: Washington, DC, USA, 2009.
- Mckenna, F.; Fenves, G.; Scott, M. Open system for earthquake engineering simulation; University of California: Berkeley, CA, USA, 2000; Available online: https://opensees.berkeley.edu (accessed on 16 September 2025).
- Vamvatsikos, D.; Allin Cornell, C. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Estrella, X.; Guindos, P.; Almazán, J.L.; Malek, S.; María, H.S.; Montaño, J.; Berwart, S. Seismic performance factors for timber buildings with woodframe shear walls. Eng. Struct. 2021, 248, 113185. [Google Scholar] [CrossRef]
- Guíñez, F.; María, H.S.; Almazán, J.L. Monotonic and cyclic behaviour of wood frame shear walls for mid-height timber buildings. Eng. Struct. 2019, 189, 100–110. [Google Scholar] [CrossRef]
- Estrella, X.; Guindos, P.; Almazán, J.L.; Malek, S. Efficient nonlinear modeling of strong wood frame shear walls for mid-rise buildings. Eng. Struct. 2020, 215, 110670. [Google Scholar] [CrossRef]
- American Society of Civil Engineers. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2022. [Google Scholar]
- Nch 433-of 1996 Mod 2012 Mod; Diseño sísmico de Edificios. Instituto Nacional de Normalización: Santiago, Chile, 2012.
- Computers and Structures Inc. SAP2000: Integrated Solution for Structural Analysis and Design, Structural Analysis Program; Computers and Structures Inc.: Berkeley, CA, USA, 2019. [Google Scholar]
- American Wood Council. Special Design Provisions for Wind and Seismic. 2015. Available online: https://awc.org/publications/2015-sdpws/ (accessed on 5 February 2025).
- Quizanga, D.; Almazán, J.L.; Torres-Rodas, P.; Guindos, P. Seismic performance of timber buildings retrofitted with hybrid walls and impact-resilient isolators. Soil Dyn. Earthq. Eng. 2025, 198, 109586. [Google Scholar] [CrossRef]
- Pei, S.; van de Lindt, J.W. Coupled shear-bending formulation for seismic analysis of stacked wood shear wall systems. Earthq. Eng. Struct. Dyn. 2009, 38, 1631–1647. [Google Scholar] [CrossRef]
- Folz, B.; Filiatrault, A. Cyclic Analysis of Wood Shear Walls. J. Struct. Eng. 2001, 127, 433–441. [Google Scholar] [CrossRef]
- Constantinou, M.; Mokha, A.; Reinhorn, A. Teflon Bearings in Base Isolation II: Modeling. J. Struct. Eng. 1990, 116, 455–474. [Google Scholar] [CrossRef]
- Gallegos, M.F.; Araya-Letelier, G.; Lopez-Garcia, D.; Parra, P.F. Seismic collapse performance of high-rise RC dual system buildings in subduction zones. Case Stud. Constr. Mater. 2023, 18, e02042. [Google Scholar] [CrossRef]
- Cando, M.A.; Hube, M.A.; Parra, P.F.; Arteta, C.A. Effect of stiffness on the seismic performance of code-conforming reinforced concrete shear wall buildings. Eng. Struct. 2020, 219, 110724. [Google Scholar] [CrossRef]
- Estrella, X.; Guindos, P.; Almazán, J.L. Ground motions for FEMA P-695 application in subduction zones. Lat. Am. J. Solids Struct. 2019, 16, e237. [Google Scholar] [CrossRef]
- Benedetti, F.; Jara-Cisterna, A.; Grandón, J.C.; Astroza, N.; Opazo-Vega, A. Numerical Analysis of the Seismic Performance of Light-Frame Timber Buildings Using a Detailed Model. Buildings 2022, 12, 981. [Google Scholar] [CrossRef]
- Takahashi, Y.; Masaki, N.; Anahara, K.; Isoda, H. Life-Cycle Cost Effectiveness of Base-Isolated Wooden House in Seismically Active Region. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]

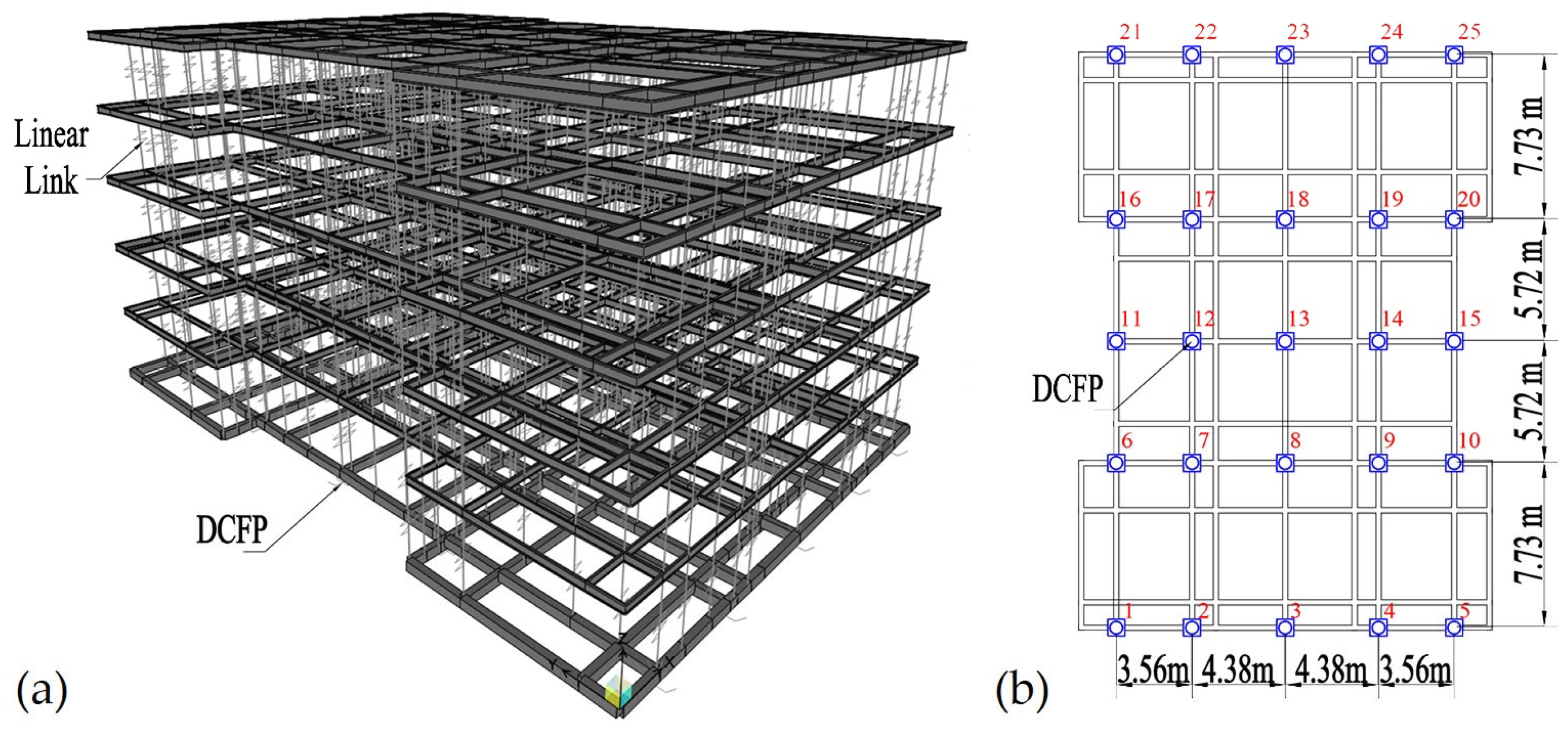

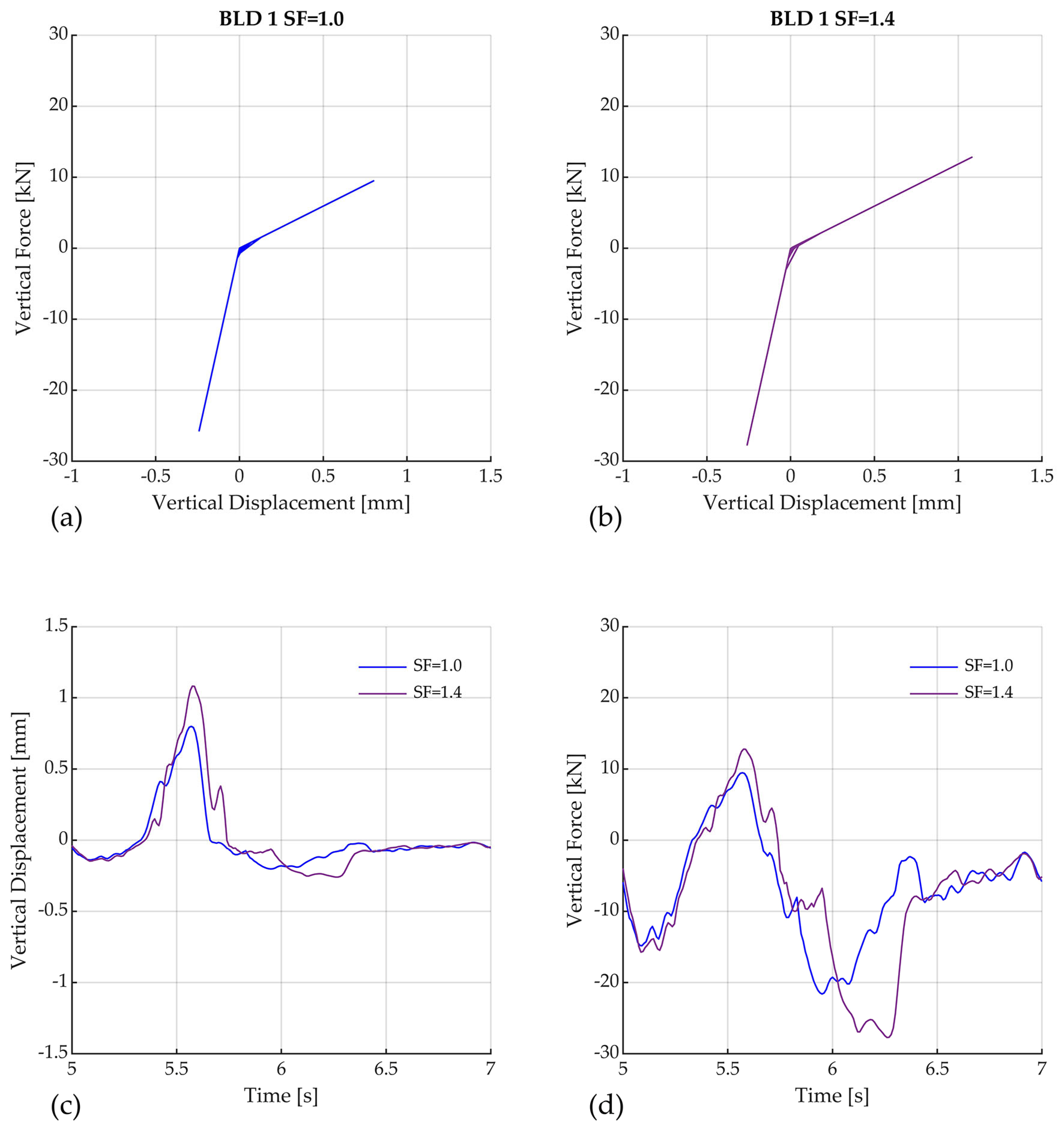
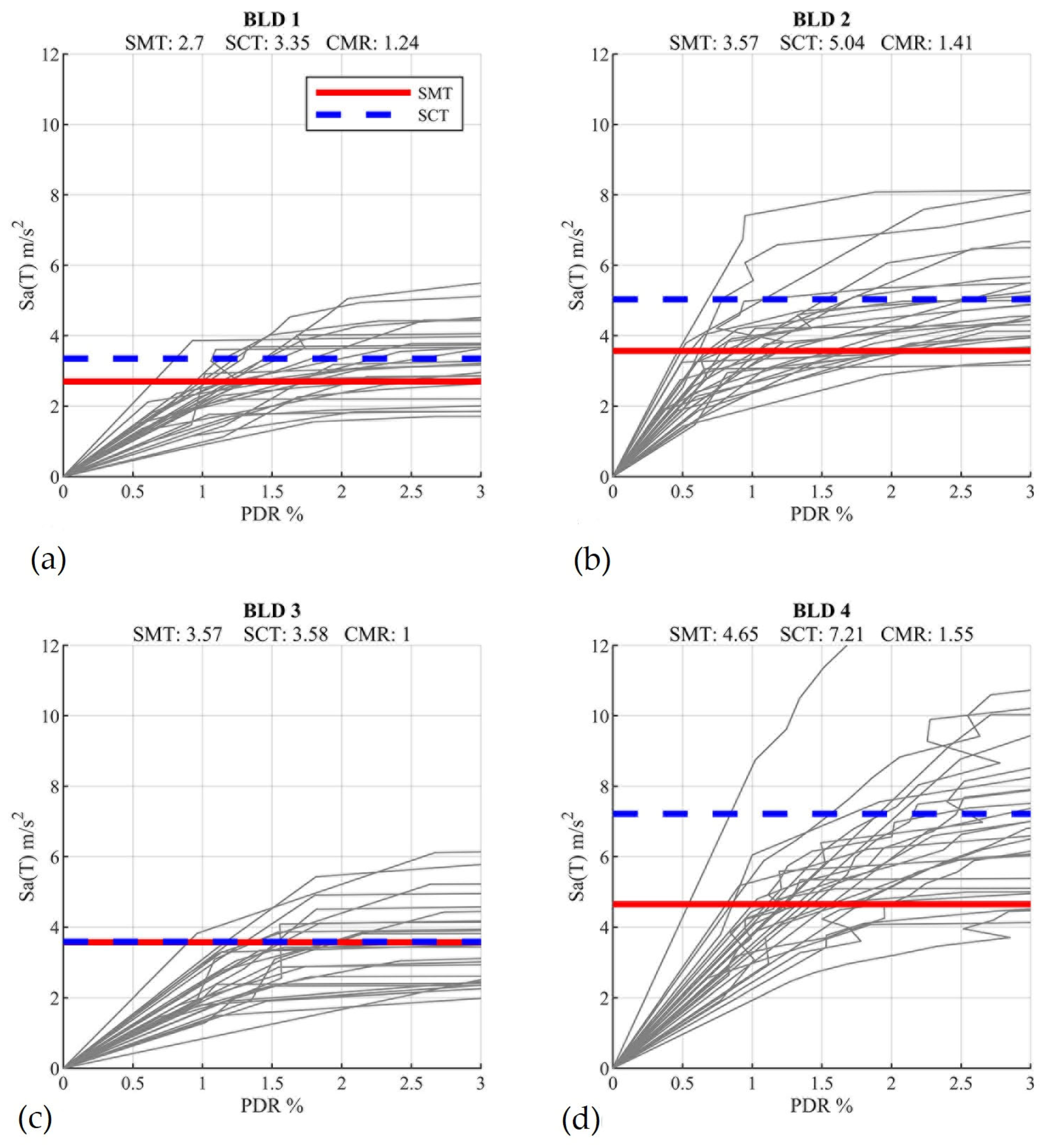
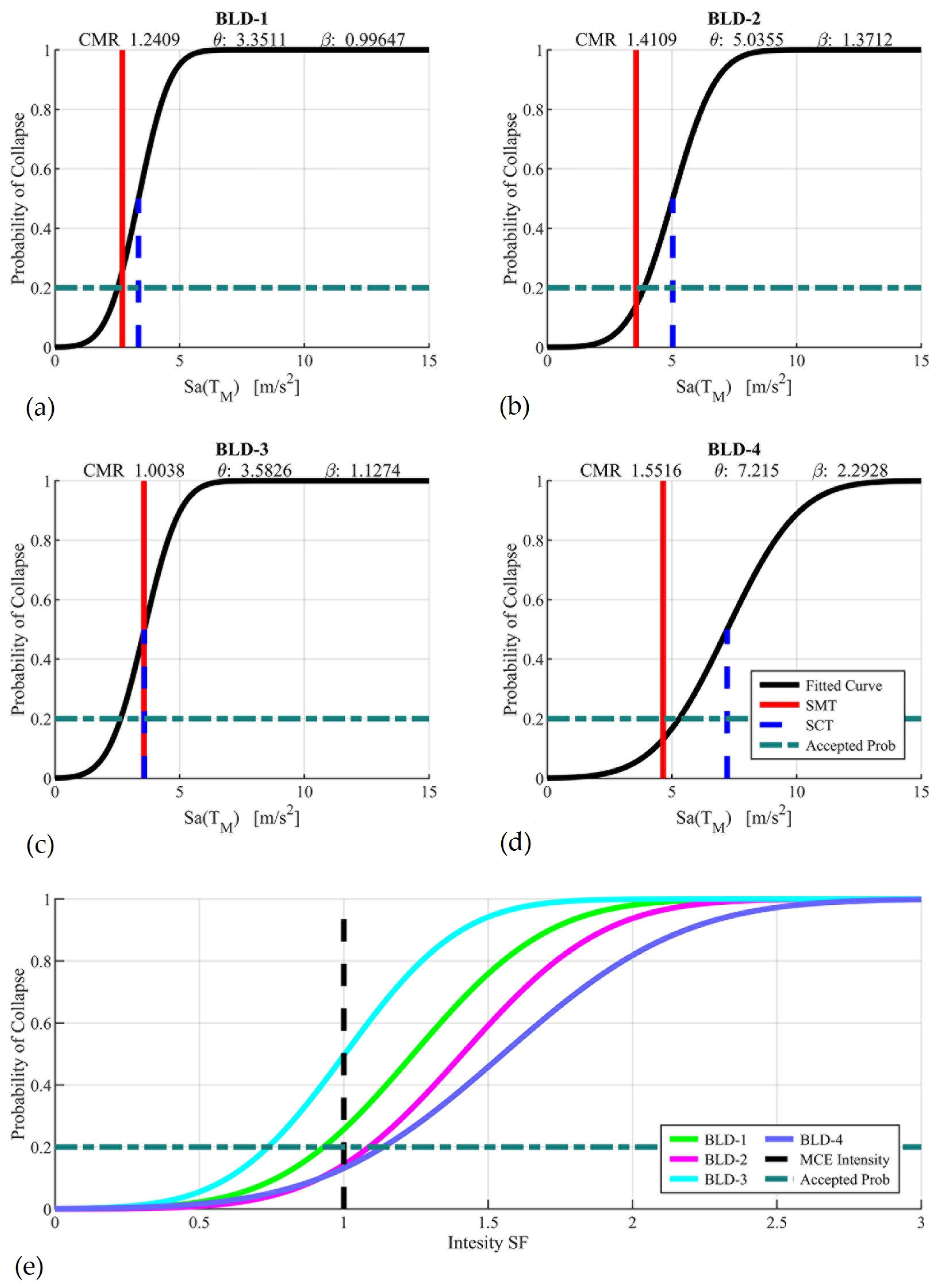
| Archetype ID | PDR Target [%] | [m] | |
|---|---|---|---|
| BLD-1 | 0.40 | 0.06 | 2.0 |
| BLD-2 | 0.40 | 0.06 | 1.0 |
| BLD-3 | 0.70 | 0.06 | 1.0 |
| BLD-4 | 0.40 | 0.12 | 2.0 |
| Isolator # | Axial Load [kN] | Isolator # | Axial Load [kN] | Isolator # | Axial Load [kN] | Isolator # | Axial Load [kN] | Isolator # | Axial Load [kN] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 219.17 | 6 | 313.77 | 11 | 128.60 | 16 | 313.77 | 21 | 219.17 |
| 2 | 225.18 | 7 | 422.30 | 12 | 320.89 | 17 | 422.30 | 22 | 225.18 |
| 3 | 138.59 | 8 | 518.88 | 13 | 147.32 | 18 | 518.88 | 23 | 138.59 |
| 4 | 225.18 | 9 | 422.30 | 14 | 320.89 | 19 | 422.30 | 24 | 225.18 |
| 5 | 219.17 | 10 | 313.77 | 15 | 128.60 | 20 | 313.77 | 25 | 219.17 |
| DBE Level | ||||
|---|---|---|---|---|
| Archetype ID | [mm] | [s] | [%] | [kN/mm] |
| BLD-1 | 157.00 | 2.51 | 37.92 | 4.52 |
| BLD-2 | 197.00 | 2.21 | 23.33 | 5.86 |
| BLD-3 | 197.00 | 2.21 | 23.33 | 5.86 |
| BLD-4 | 139.00 | 1.90 | 48.77 | 7.92 |
| MCE Level | ||||
| Archetype ID | [mm] | [s] | [%] | [kN/mm] |
| BLD-1 | 196.00 | 2.68 | 34.53 | 3.98 |
| BLD-2 | 259.00 | 2.31 | 19.49 | 5.34 |
| BLD-3 | 259.00 | 2.31 | 19.49 | 5.34 |
| BLD-4 | 171.00 | 2.05 | 46.40 | 6.78 |
| Archetype ID | [m] | [mm] | Total Length [mm] |
|---|---|---|---|
| BLD-1 | 3.92 | 250.00 | 430.00 |
| BLD-2 | 1.92 | 320.00 | 500.00 |
| BLD-3 | 1.92 | 320.00 | 500.00 |
| BLD-4 | 3.92 | 220.00 | 400.00 |
| Archetype ID | Seismic Coefficient C | Nail Spacing * | ||||||
|---|---|---|---|---|---|---|---|---|
| Story 1 | Story 2 | Story 3 | Story 4 | Story 5 | ||||
| BLD-1 | 10.01% | 2.84% | 1.78% | S50 | S100 | S100 | S100 | S150 |
| BLD-2 | 16.29% | 3.07% | 3.53% | D100 | S50 | S50 | S100 | S150 |
| BLD-3 | 16.29% | 2.88% | 2.29% | S100 | S150 | S150 | S150 | S150 |
| BLD-4 | 15.55% | 3.24% | 3.89% | D50 | D50 | D50 | D100 | D100 |
| Archetype ID |
Isolated LFTB [s] |
Fix LFTB [s] |
Ratio |
|---|---|---|---|
| BLD-1 | 2.84 | 1.01 | 2.81 |
| BLD-2 | 2.45 | 0.76 | 3.22 |
| BLD-3 | 2.49 | 1.05 | 2.37 |
| BLD-4 | 2.17 | 0.73 | 2.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quizanga, D.; Almazán, J.L.; Torres-Rodas, P. Seismic Collapse of Frictionally Isolated Timber Buildings in Subduction Zones: An Assessment Considering Slider Impact. Buildings 2025, 15, 3593. https://doi.org/10.3390/buildings15193593
Quizanga D, Almazán JL, Torres-Rodas P. Seismic Collapse of Frictionally Isolated Timber Buildings in Subduction Zones: An Assessment Considering Slider Impact. Buildings. 2025; 15(19):3593. https://doi.org/10.3390/buildings15193593
Chicago/Turabian StyleQuizanga, Diego, José Luis Almazán, and Pablo Torres-Rodas. 2025. "Seismic Collapse of Frictionally Isolated Timber Buildings in Subduction Zones: An Assessment Considering Slider Impact" Buildings 15, no. 19: 3593. https://doi.org/10.3390/buildings15193593
APA StyleQuizanga, D., Almazán, J. L., & Torres-Rodas, P. (2025). Seismic Collapse of Frictionally Isolated Timber Buildings in Subduction Zones: An Assessment Considering Slider Impact. Buildings, 15(19), 3593. https://doi.org/10.3390/buildings15193593






