A Markerless Photogrammetric Framework with Spatio-Temporal Refinement for Structural Deformation and Strain Monitoring
Abstract
1. Introduction
1.1. Motivation
1.2. Previous Studies
1.3. Need for Further Study and Research Purpose
1.4. Objectives
1.5. Contributions
- 1.
- Development and validation of filtering techniques: This study presents a spatio-temporal filtering framework that is specifically designed for markerless photogrammetric data. Instead of considering only spatial smoothing at a single time step, the proposed method also integrates temporal information, which effectively reduces random noise, enhances the precision of 3D deformation measurements and strain field estimations.
- 2.
- Experimental demonstration of method effectiveness: The study experimentally demonstrates the feasibility, accuracy, and improved computational efficiency of the proposed markerless approach through full-scale testing on a masonry wall under controlled loading, providing a reliable and efficient non-contact alternative for monitoring structural deformation in civil engineering applications.
- 3.
- Methodological advancement in non-contact monitoring: By integrating advanced image-based tracking with spatio-temporal refinement, the study contributes to the ongoing development of photogrammetry-based structural monitoring techniques, supporting the broader adoption of scalable, high-resolution, and target-free measurement systems in real-world practice.
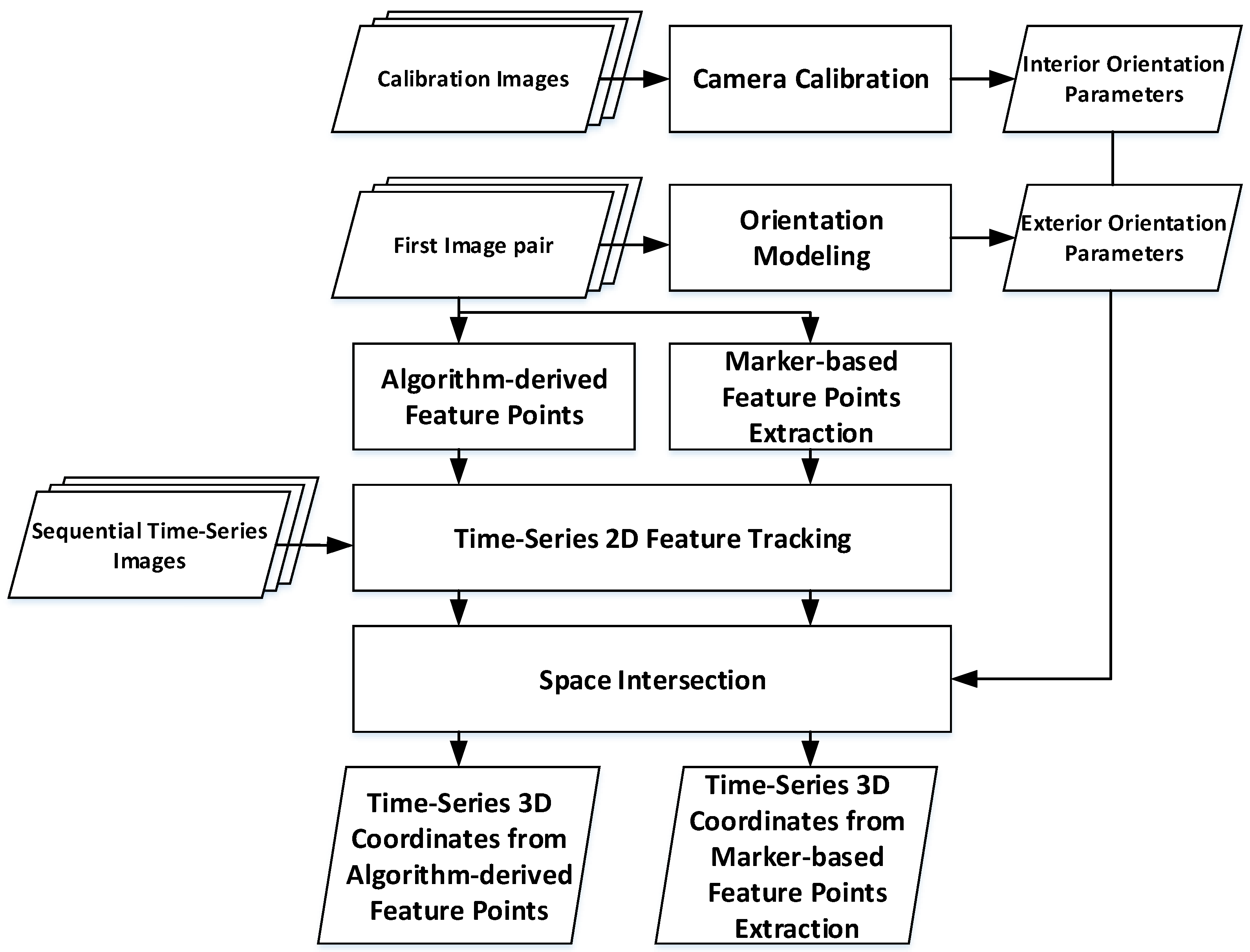
2. Methodology
2.1. Time-Series 3D Points Generation
- (1)
- Marker-based feature points: Artificial targets in the form of black circular markers were manually applied to the wall surface. The centroids of these circles were extracted as precise feature point locations. This approach offers the advantages of uniform distribution and well-defined, easily identifiable points.
- (2)
- Algorithm-derived feature points: The Speeded-Up Robust Features (SURF) [20] algorithm was used to detect keypoint descriptors directly from the images. This method does not require physical markers on the wall and can generate a much higher density of feature points compared to the artificial targets.
2.1.1. Camera Calibration to Determine IOPs
2.1.2. Orientation Modeling to Determine EOPs
2.1.3. Marker-Based Feature Points Extraction: Artificially Placed Feature Points
2.1.4. Algorithm-Derived Feature Points: Natural Image Feature Points
2.1.5. Time-Series 2D Feature Tracking
2.1.6. Three-Dimensional Points Generation Using Space Intersection
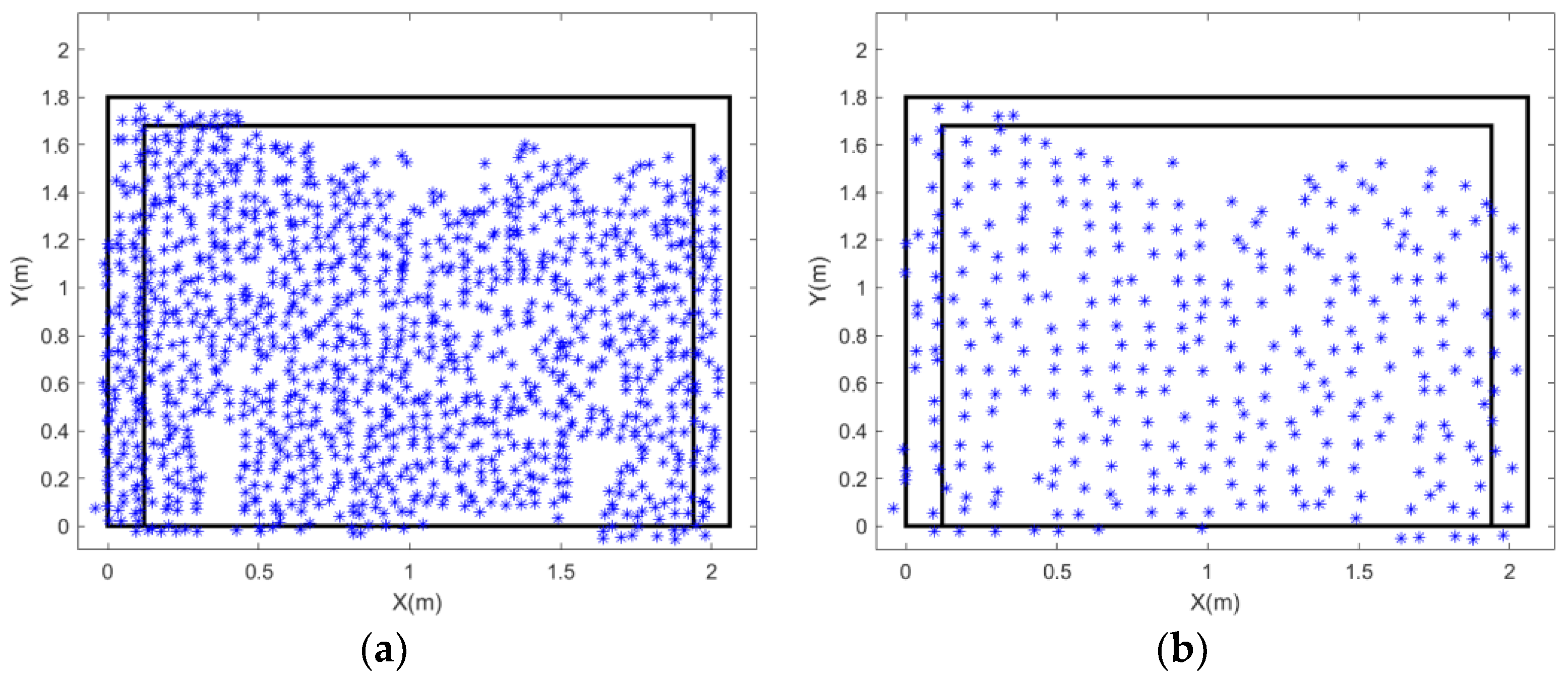
2.2. Spatio-Temporal Filtering of 3D Coordinates for the Algorithm-Derived Feature Points
2.2.1. Median Absolute Deviation (MAD) Filtering
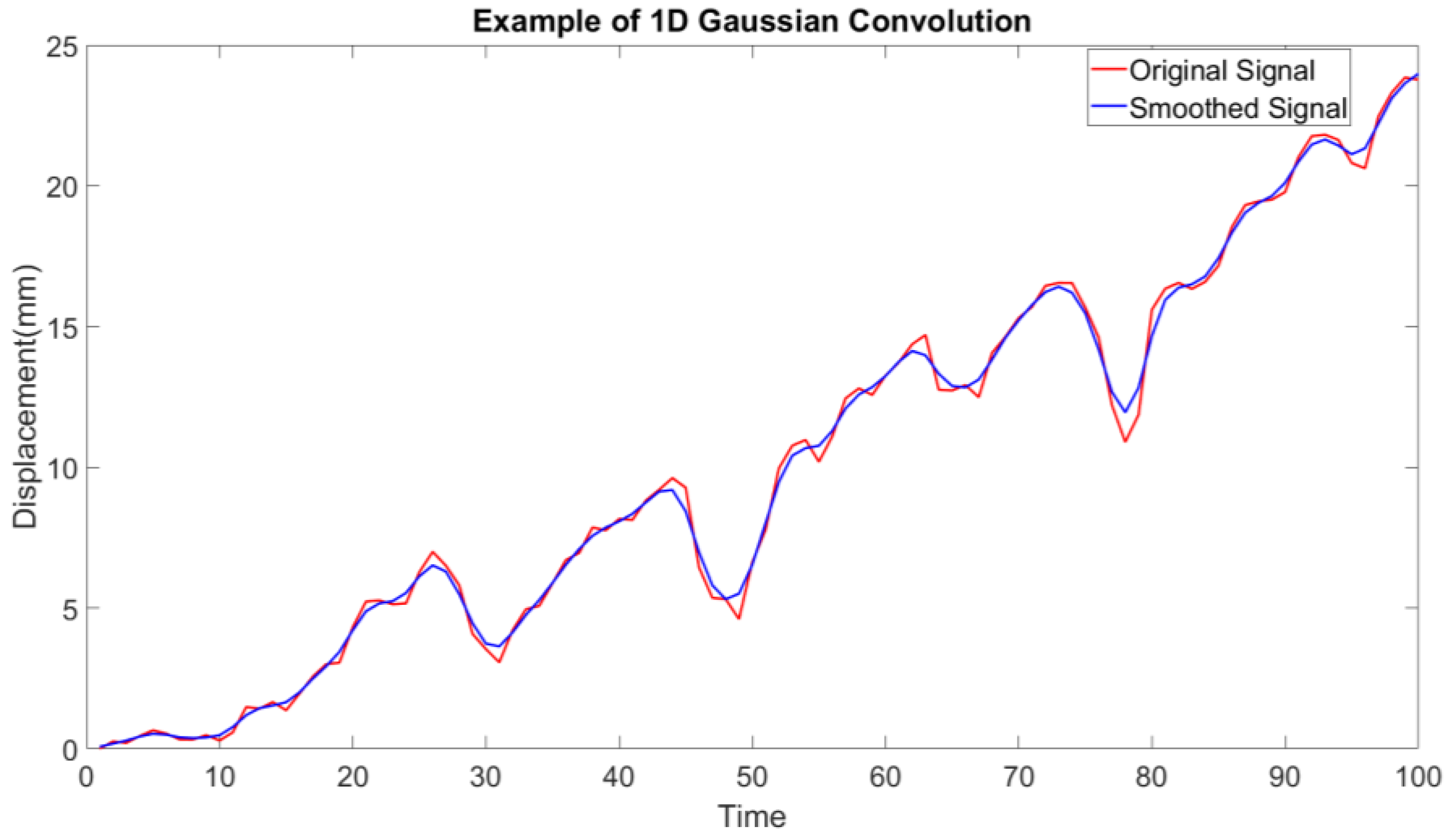
2.2.2. One-Dimensional Convolution Smoothing
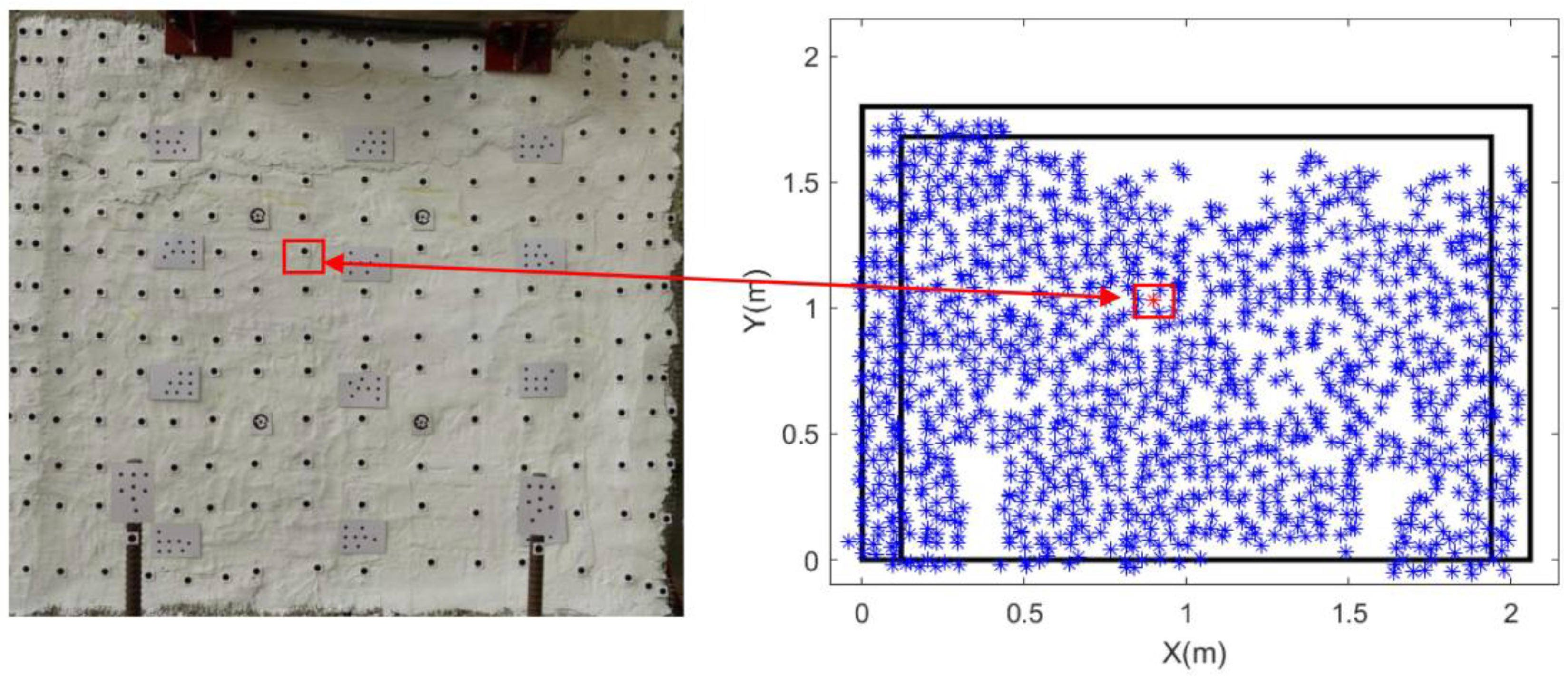
2.2.3. Selection of Representative Wall Surface Points Within Predefined Grids
2.3. Strain Calculation and Refinement
2.3.1. Strain Calculation
2.3.2. Strain Refinement
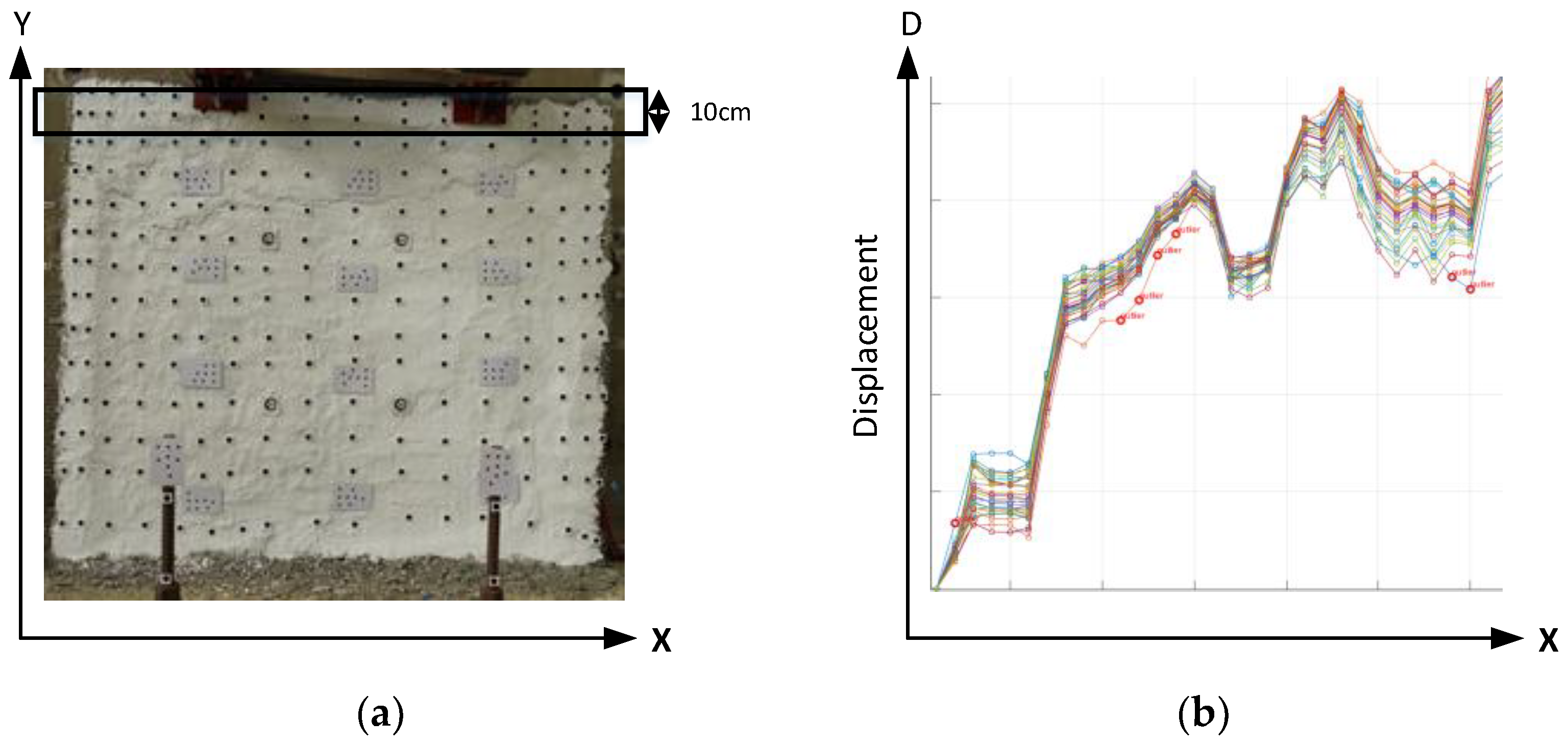
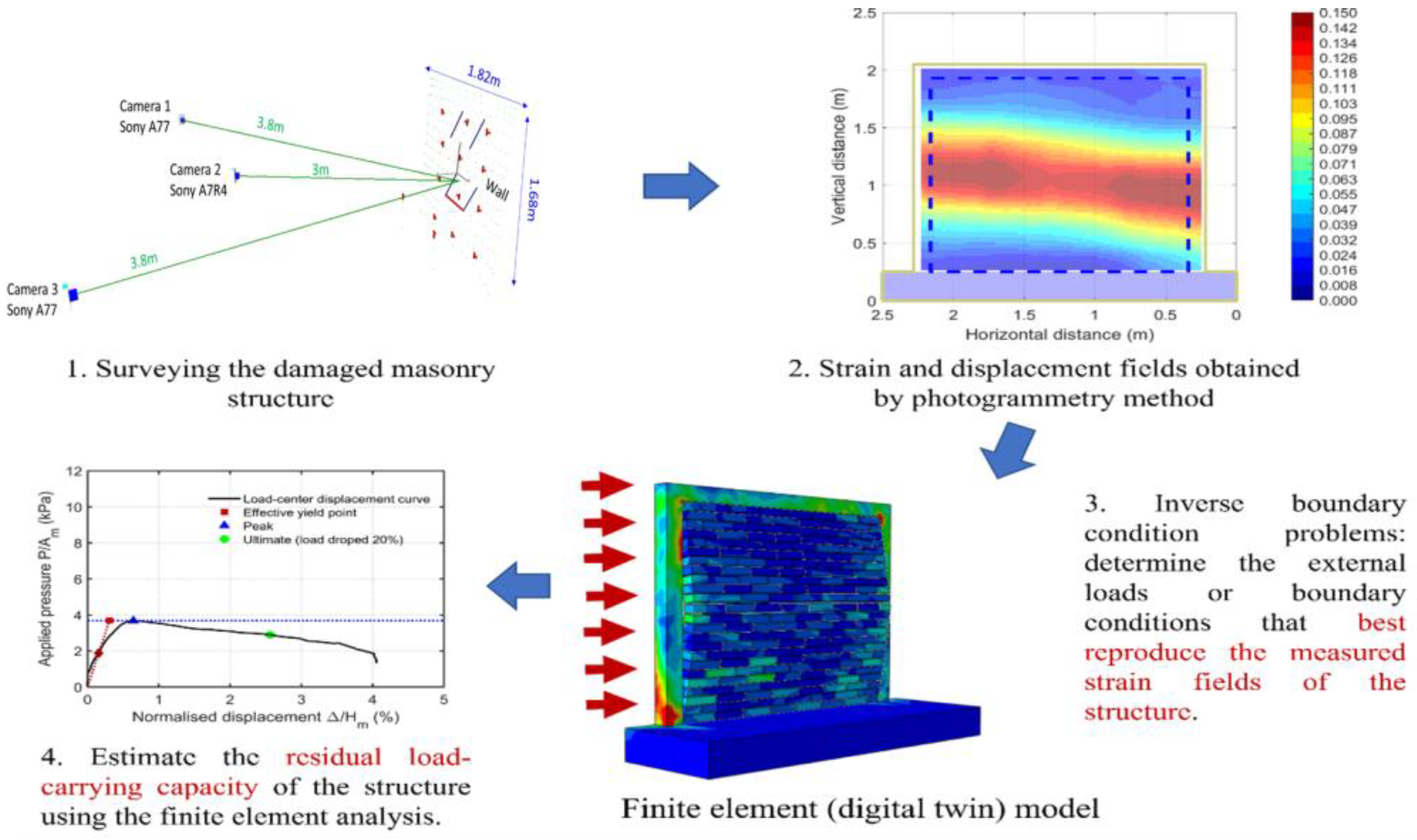
3. Experimental Data
4. Experimental Results
4.1. Precision of 3D Points from Space Intersection
4.2. Accuracy Evaluation of a 3D Point Using a Laser Ranger
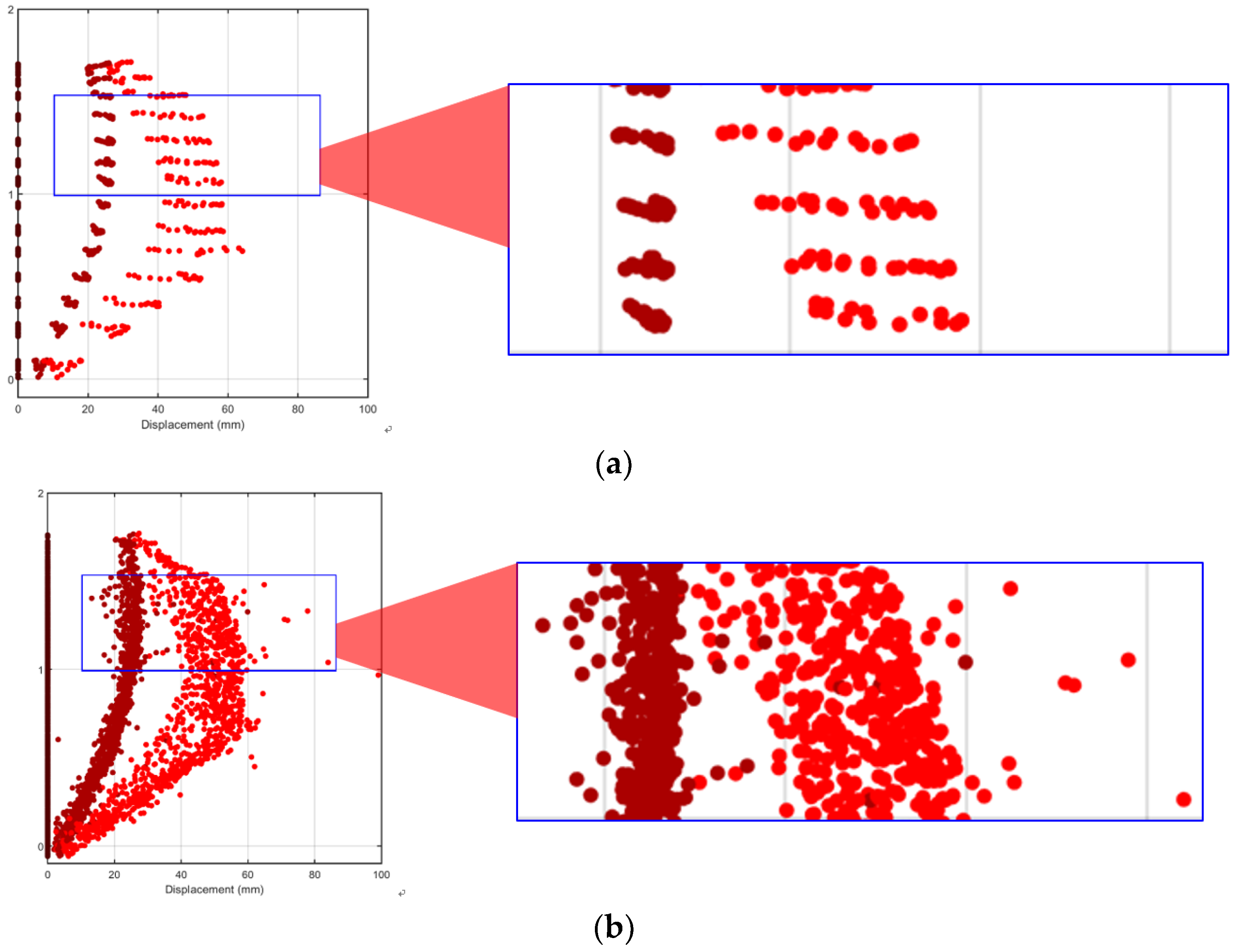
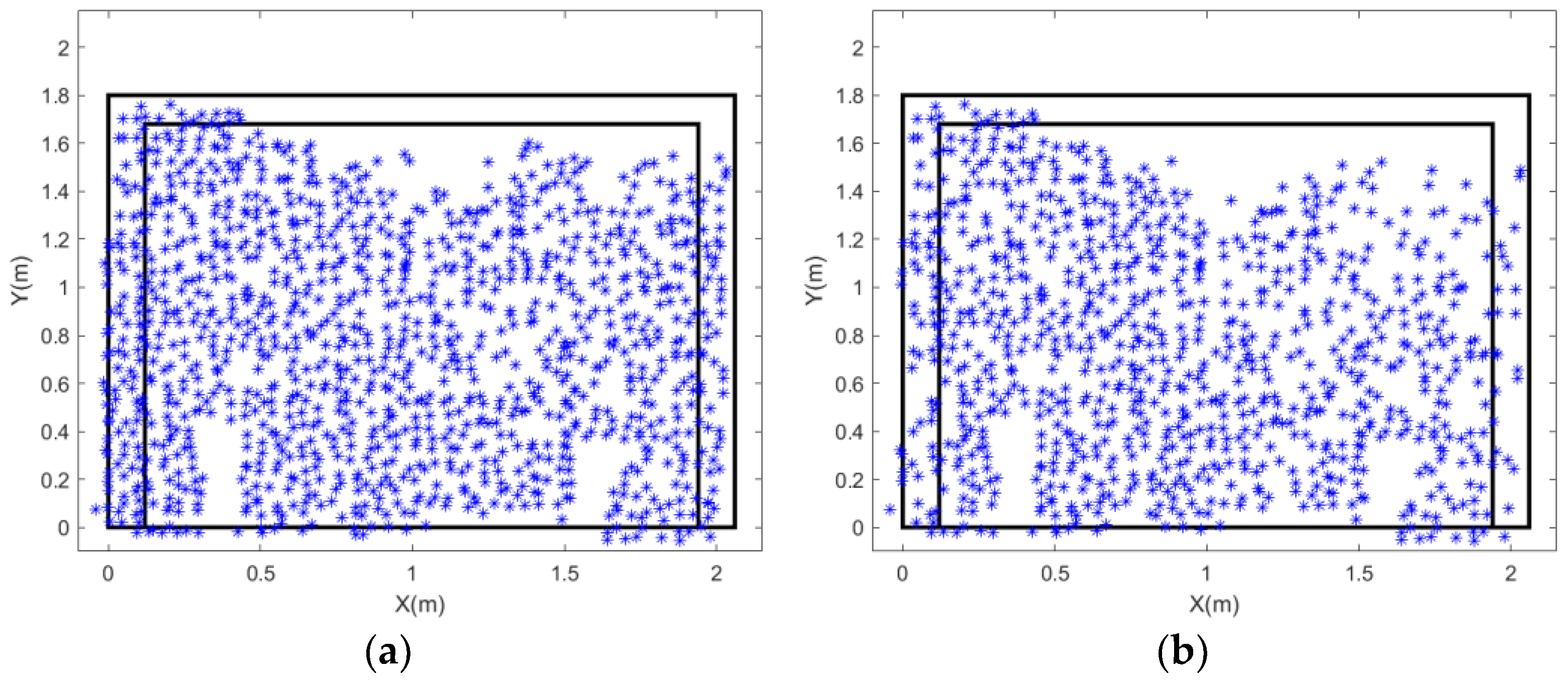
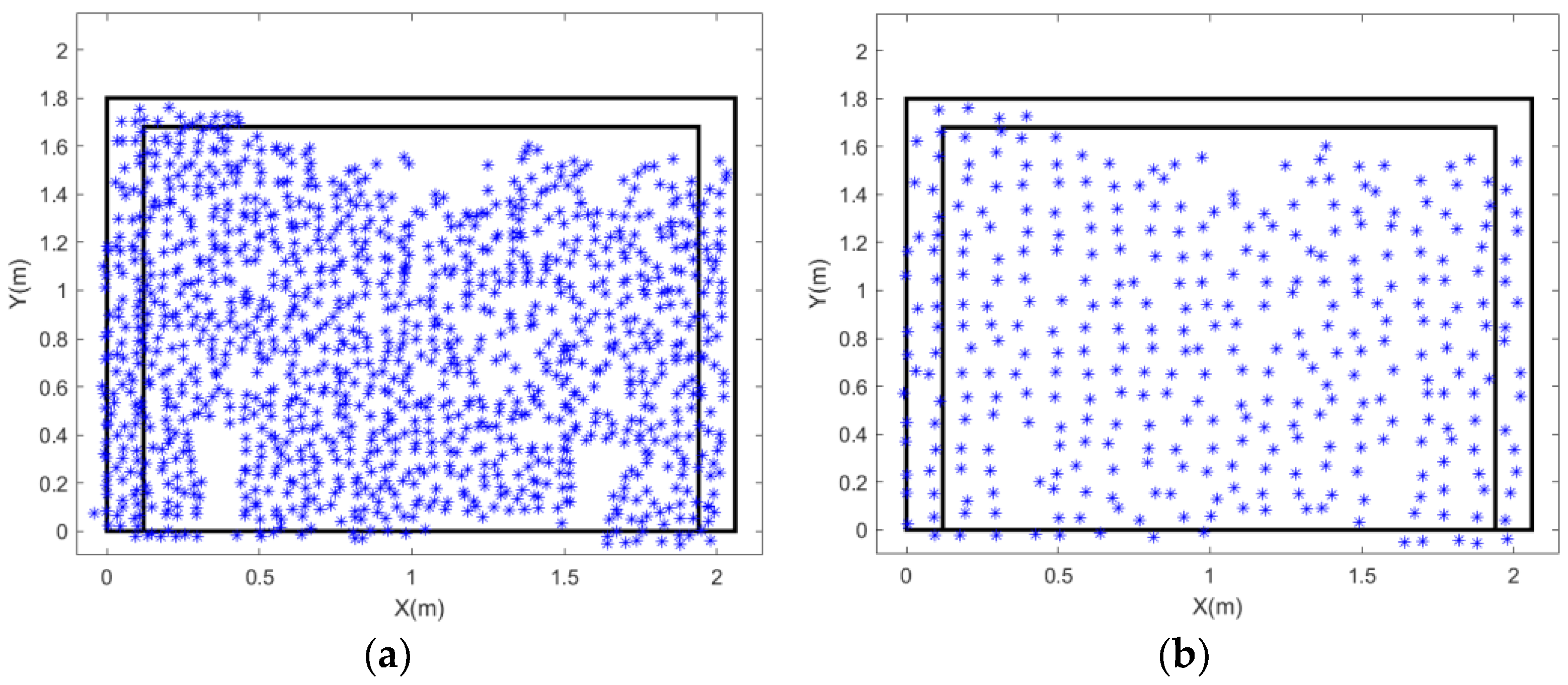
4.3. Spatio-Temporal Filtering for Targetless-Based 3D Displacement Analysis
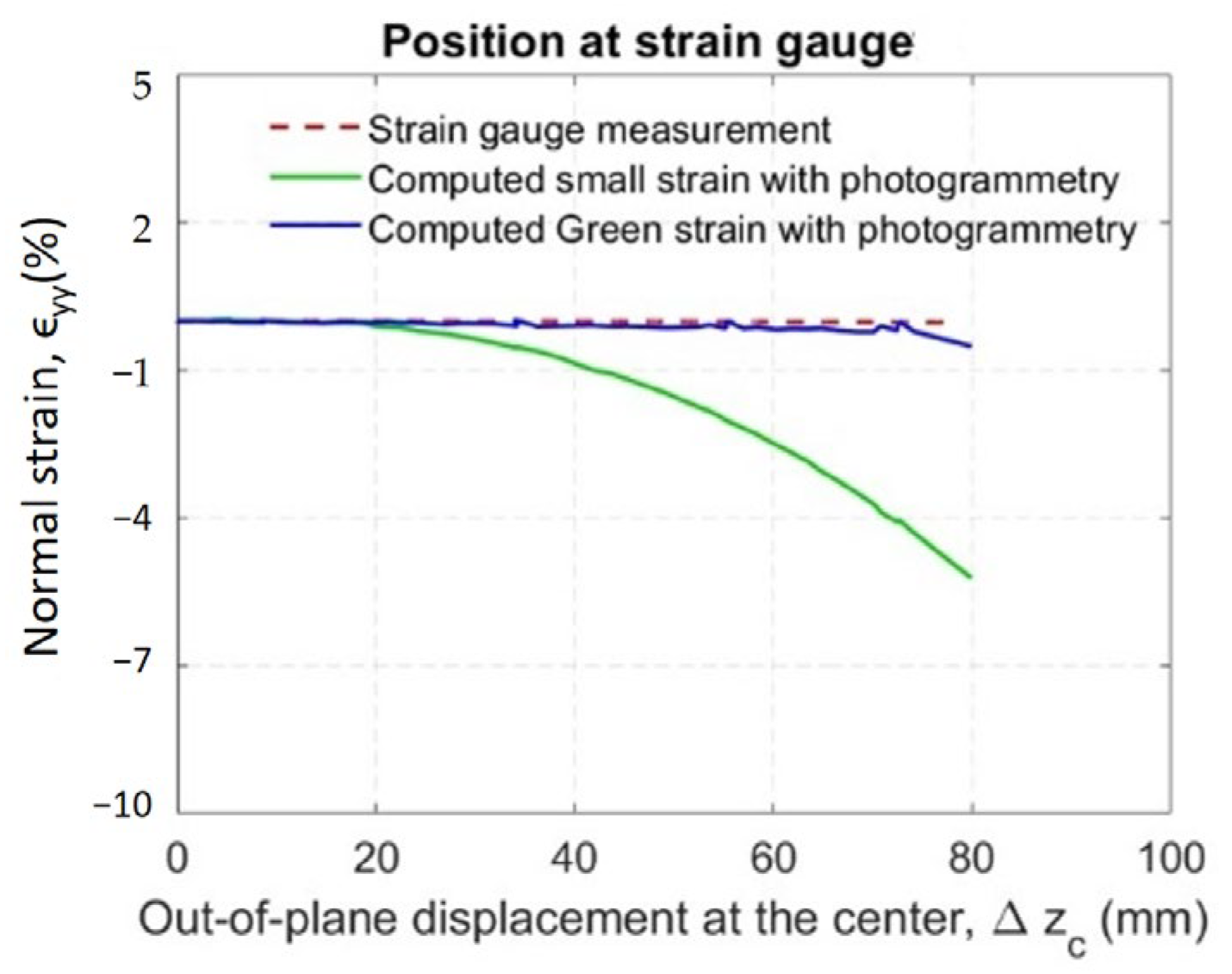
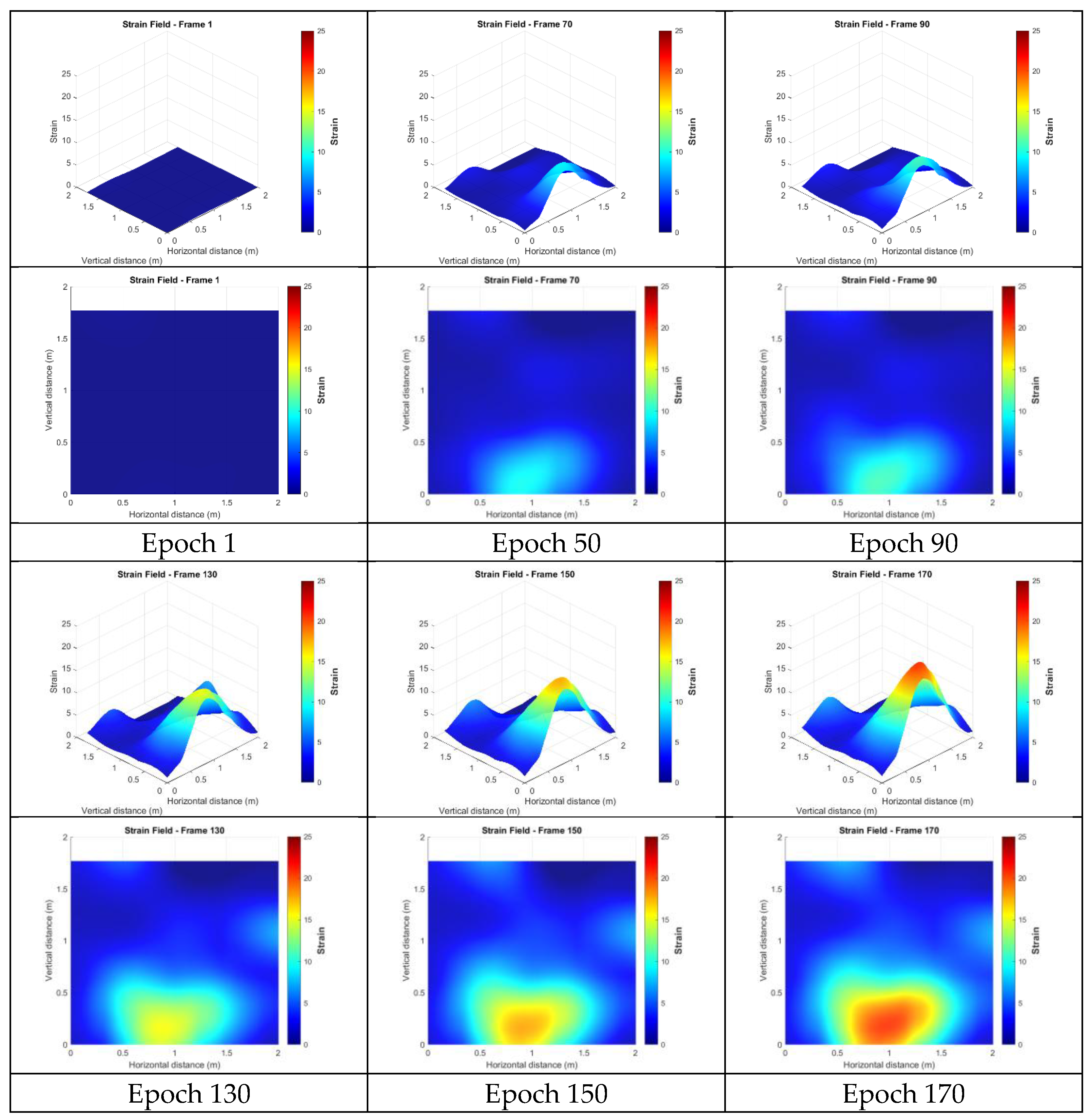
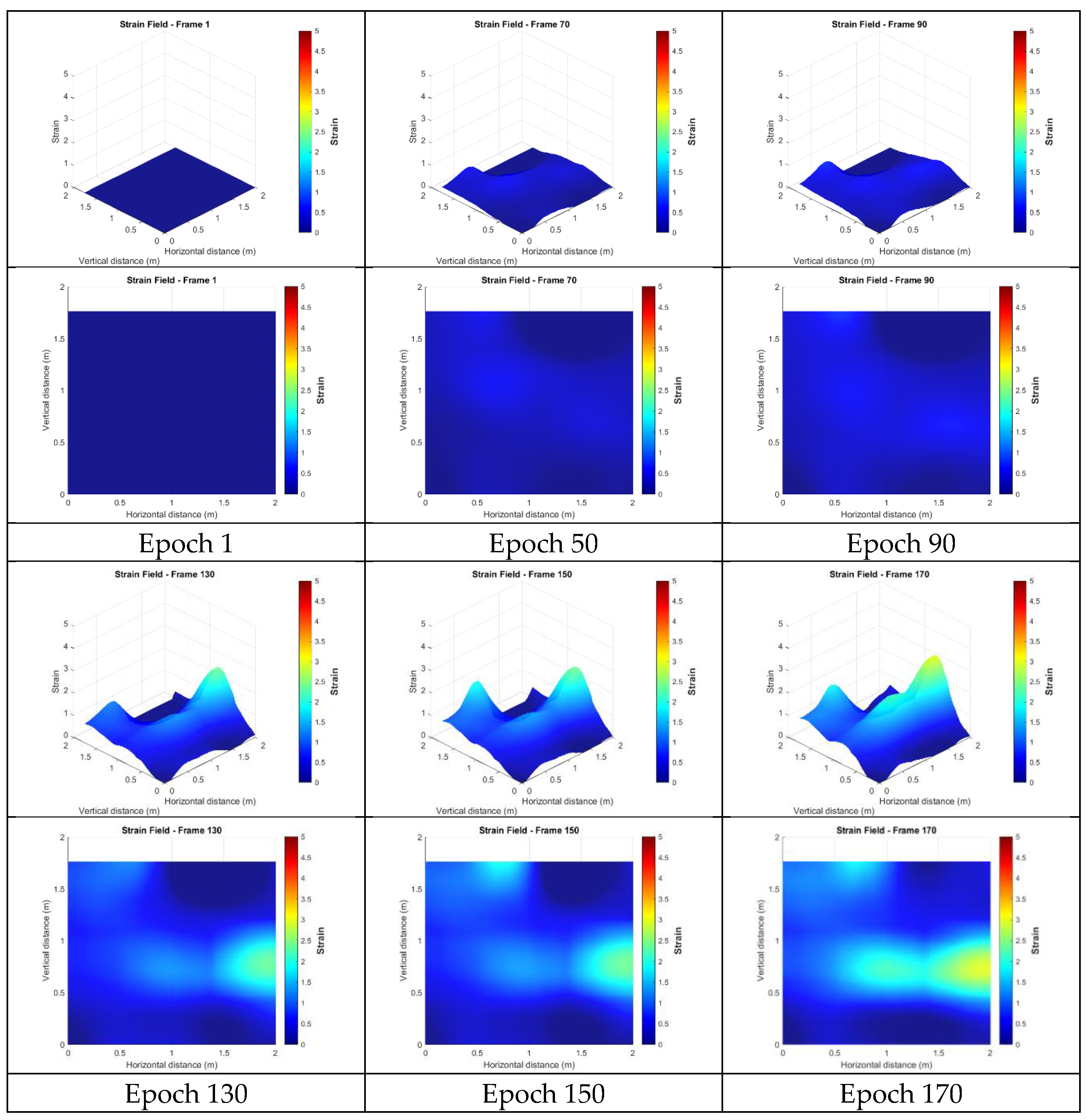
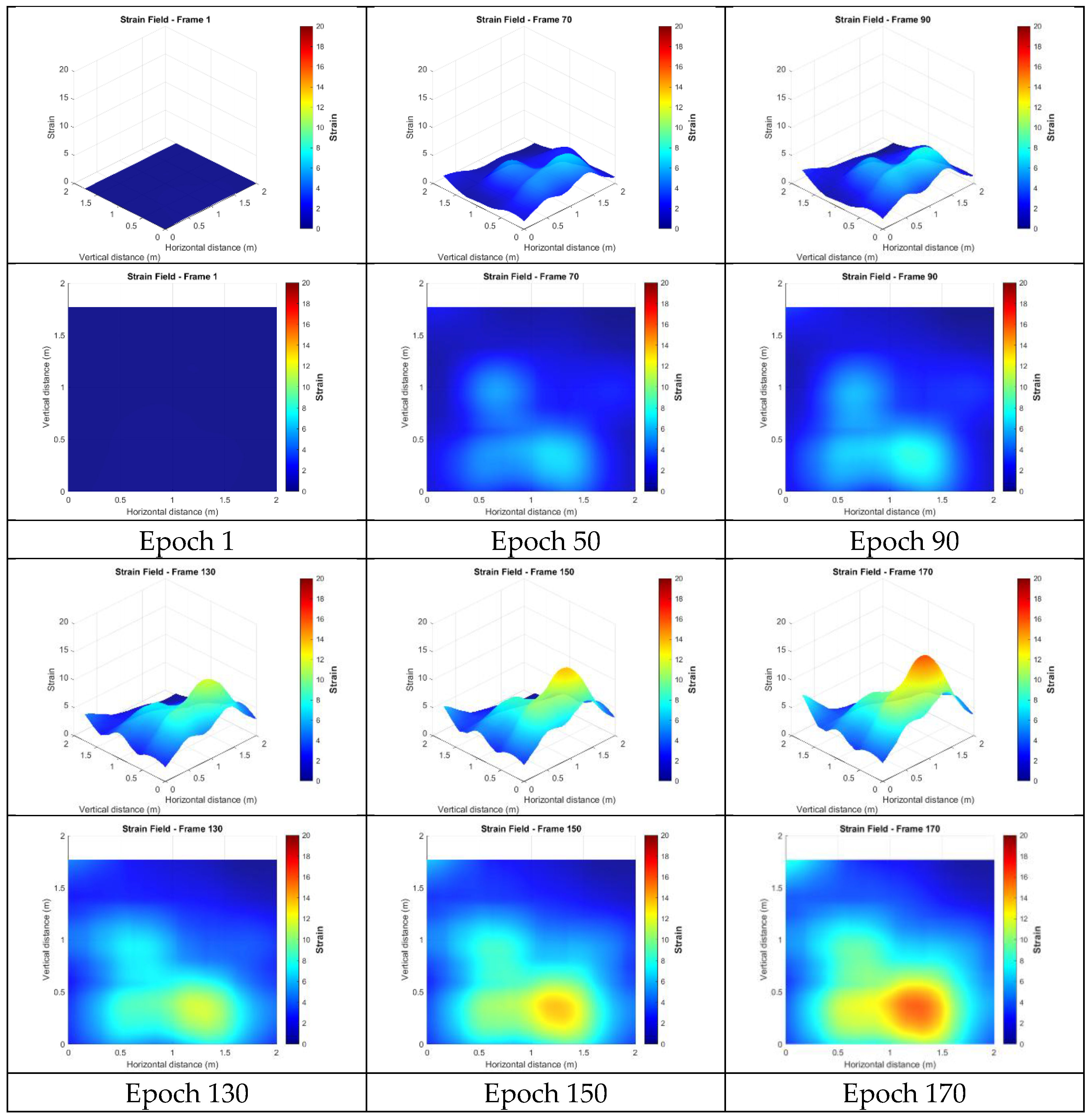
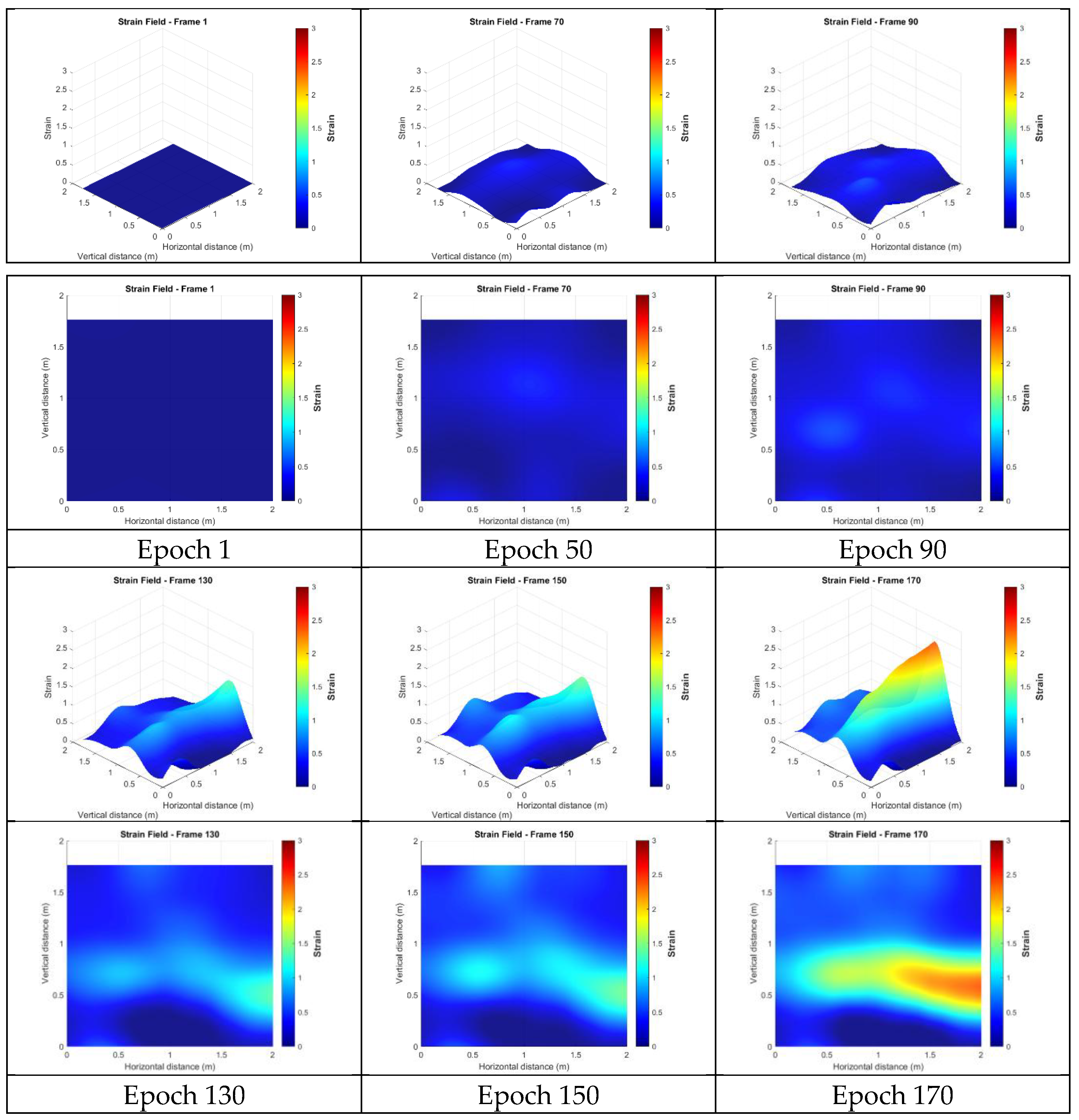
4.4. Strain Analysis
4.4.1. Strains from the Target Method
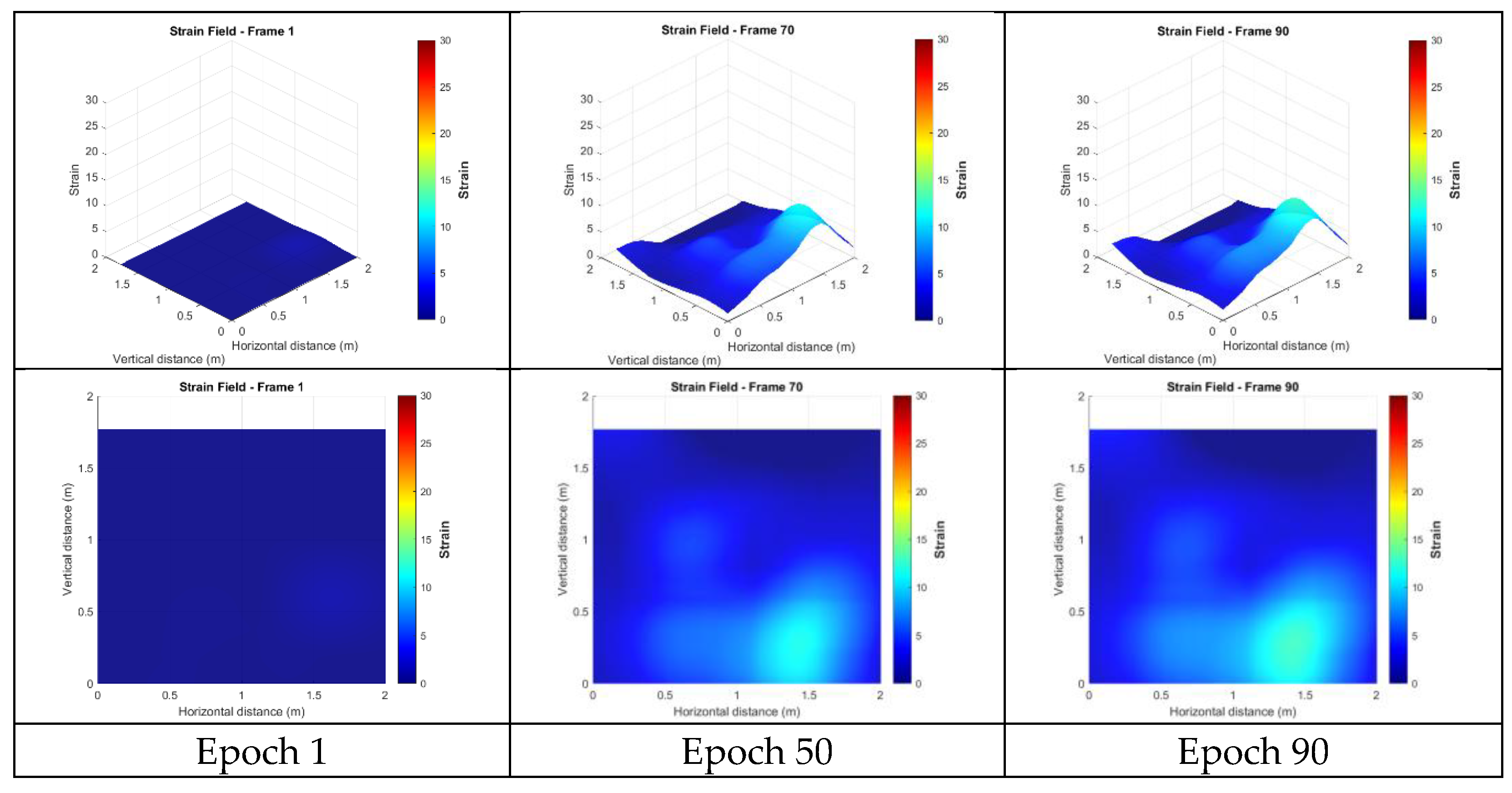
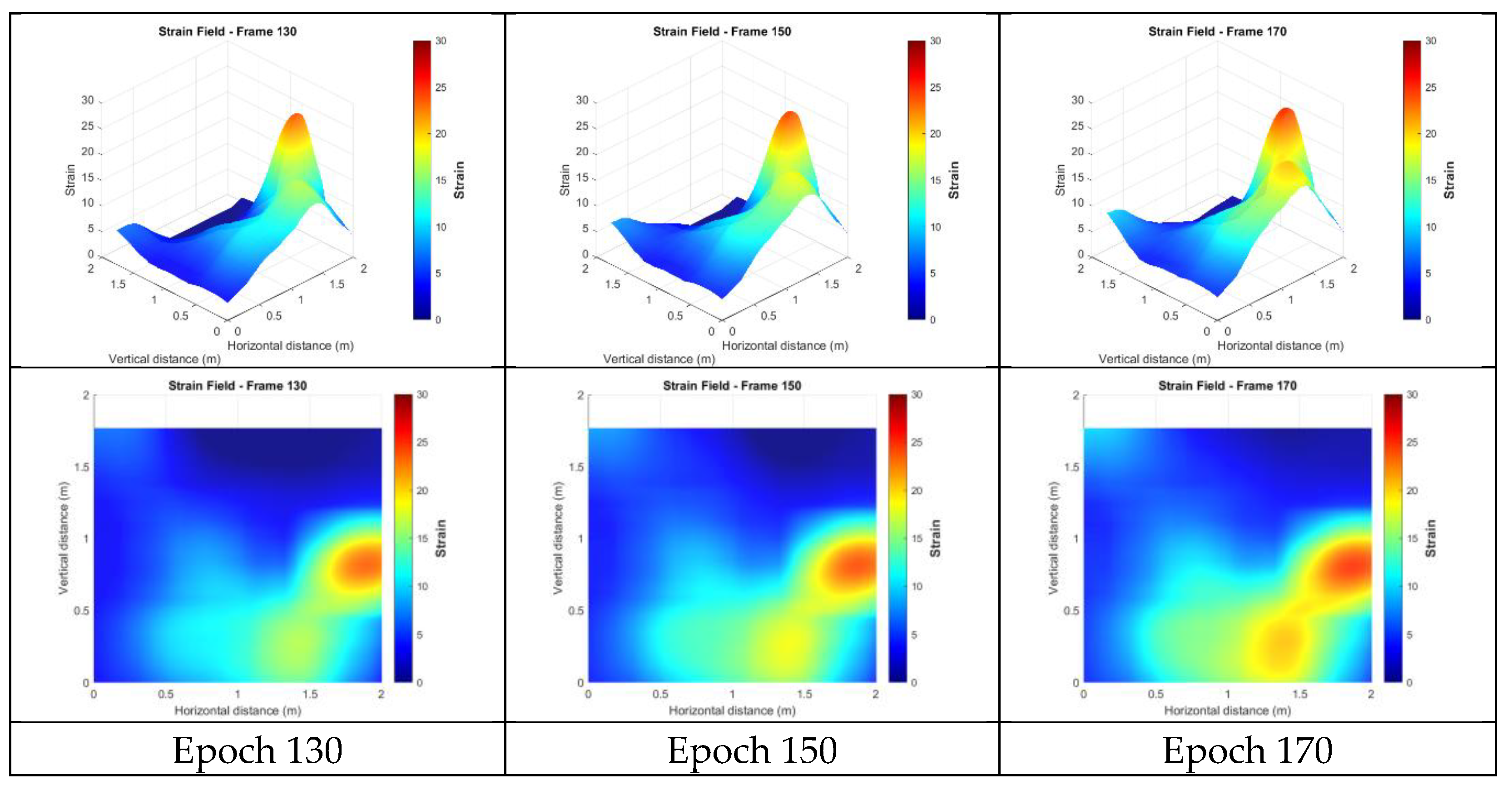
4.4.2. Strains from the Unfiltered Targetless Data
4.4.3. Strains from the Targetless Data After MAD Filtering in the Spatial Domain
4.4.4. Strains from the Targetless Data After 1D Convolution Smoothing in the Temporal Domain
4.4.5. Strains from the Targetless Data After Representative Point Selection
4.4.6. Strains from the Targetless Data After Spatio-Temporal Filtering
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Al-Ruzouq, R.; Dabous, S.A.; Junaid, M.T.; Hosny, F. Nondestructive deformation measurements and crack assessment of concrete structure using close-range photogrammetry. Results Eng. 2023, 18, 101058. [Google Scholar] [CrossRef]
- Mojsilović, N.; Salmanpour, A.H. Masonry walls subjected to in-plane cyclic loading: Application of digital image correlation for deformation field measurement. Int. J. Mason. Res. Innov. 2016, 1, 165–187. [Google Scholar] [CrossRef]
- Whiteman, T.; Lichti, D.D.; Chandler, I. Measurement of deflections in concrete beams by close-range digital photogrammetry. Geospatial Theory Process. Appl. 2002, 34, 40–48. [Google Scholar]
- Valença, J.; Júlio, E.N.B.S.; Araújo, H.J. Applications of photogrammetry to structural assessment. Exp. Tech. 2012, 36, 71–81. [Google Scholar] [CrossRef]
- González-Aguilera, D.; Gómez-Lahoz, J.; Sánchez, J. A new approach for structural monitoring of large dams with a three-dimensional laser scanner. Sensors 2008, 8, 5866–5883. [Google Scholar] [CrossRef]
- Liebold, F.; Maas, H.G. Advanced spatio-temporal filtering techniques for photogrammetric image sequence analysis in civil engineering material testing. ISPRS J. Photogramm. Remote Sens. 2016, 111, 13–21. [Google Scholar] [CrossRef]
- Liebold, F.; Maas, H.G.; Deutsch, J. Photogrammetric determination of 3D crack opening vectors from 3D displacement fields. ISPRS J. Photogramm. Remote Sens. 2020, 164, 1–10. [Google Scholar] [CrossRef]
- Liebold, F.; Bergmann, S.; Bosbach, S.; Adam, V.; Marx, S.; Claßen, M.; Hegger, J.; Maas, H.G. Photogrammetric image sequence analysis for deformation measurement and crack detection applied to a shear test on a carbon reinforced concrete member. In Proceedings of the International Symposium of the International Federation for Structural Concrete, Istanbul, Turkey, 5–7 June 2023; pp. 1273–1282. [Google Scholar]
- Wang, Y.; Qin, L. Progress of Application of Digital Image Correlation Method (DIC) in Civil Engineering. In Proceedings of the 2023 International Seminar on Computer Science and Engineering Technology (SCSET), New York, NY, USA, 29–30 April 2023; pp. 1–5. [Google Scholar]
- Bolhassani, M.; Rajaram, S.; Hamid, A.A.; Kontsos, A.; Bartoli, I. Damage detection of concrete masonry structures by enhancing deformation measurement using DIC. In Proceedings of the Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure 2016, Las Vegas, NV, USA, 22 April 2016; Volume 9804, pp. 227–240. [Google Scholar]
- Shih, M.H.; Sung, W.P.; Tung, S.H. Using the digital image correlation technique to measure the mode shape of a cantilever beam. In Proceedings of the 10th International Conference on Computational Structures Technology, Valencia, Spain, 4–17 September 2010; Volume 65. [Google Scholar]
- Shih, M.H.; Sung, W.P. Application of digital image correlation method for analysing crack variation of reinforced concrete beams. Sadhana 2013, 38, 723–741. [Google Scholar] [CrossRef]
- Tung, S.H.; Weng, M.C.; Shih, M.H. Measuring the in situ deformation of retaining walls by the digital image correlation method. Eng. Geol. 2013, 166, 116–126. [Google Scholar] [CrossRef]
- Zaya, M.A.; Adam, S.M.; Abdulrahman, F.H. Application of digital image correlation method in materials-testing and measurements: A review. J. Duhok Univ. 2023, 26, 145–167. [Google Scholar]
- Shih, M.H.; Tung, S.H.; Sung, W.P. Applying the integrated digital image correlation method to detect stress measurements in precision drilling. J. Test. Eval. 2024, 52, 25–41. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, Y.; Zhang, G.; Wang, Q.; Li, S.; Wang, Z.; Dong, M. Speckle noise suppression of a reconstructed image in digital holography based on the BM3D improved convolutional neural network. Appl. Opt. 2024, 63, 6000–6011. [Google Scholar] [CrossRef]
- Zhou, Y.; Zuo, Q.; Chen, N.; Zhou, L.; Yang, B.; Liu, Z.; Liu, Y.; Tang, L.; Dong, S.; Jiang, Z. Transformer based deep learning for digital image correlation. Opt. Lasers Eng. 2025, 184, 108568. [Google Scholar] [CrossRef]
- Wang, L.; Lei, Z. Deep learning based speckle image super-resolution for digital image correlation measurement. Opt. Laser Technol. 2025, 181, 111746. [Google Scholar]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Computer Vision–ECCV 2006: 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006: Proceedings, Part I 9; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Brown, D.C. Close-range camera calibration. Photogramm. Eng. Remote Sens. 1971, 37, 855–866. [Google Scholar]
- Fraser, C.S.; Hanley, H.B. Developments in close-range photogrammetry for 3D modelling: The iWitness example. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 5, 1682–1777. [Google Scholar]
- Teo, T. Video-based point cloud generation using multiple action cameras. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 55. [Google Scholar] [CrossRef]
- Wolf, P.R.; Dewitt, B.A. Elements of Photogrammetry with Applications in GIS, 3rd ed.; McGraw-Hill Higher Education: Columbus, OH, USA, 2000. [Google Scholar]
- Debella-Gilo, M.; Kääb, A. Sub-pixel precision image matching for measuring surface displacements on mass movements using normalized cross-correlation. Remote Sens. Environ. 2011, 115, 130–142. [Google Scholar]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J.P. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef]
- Fung, Y.C.; Tong, P. Classical and Computational Solid Mechanics; World Scientific: Hackensack, NJ, USA, 2001; pp. 525–529. [Google Scholar]
- Abdullah, Q.A. Mapping Matters. Photogramm. Eng. Remote Sens. 2009, 75, 1260–1261. [Google Scholar]














| Mean (STD_Intersection) | Std (STD_Intersection) | |||||||
|---|---|---|---|---|---|---|---|---|
| Unit: mm | ||||||||
| Targetless | 0.533 | 0.503 | 0.733 | 1.373 | 0.586 | 0.521 | 0.784 | 1.466 |
| Target | 0.251 | 0.238 | 0.346 | 0.601 | 0.141 | 0.135 | 0.195 | 0.430 |
| Number of Observation | Mean Error | RMSE | Max. Error | R2 | |
|---|---|---|---|---|---|
| Targetless | 186 | 0.7196 mm | 0.843 mm | 1.962 mm | 0.9992 |
| Target | 186 | 0.4440 mm | 0.527 mm | 1.403 mm | 0.9996 |
| Process Level | Max Strain |
|---|---|
| Target data | 3.873 |
| Targetless data without post-processing | 25.220 |
| Targetless data with MAD filtering | 17.042 |
| Targetless data with 1D Convolution smoothing | 3.9305 |
| Targetless data with representative point selection | 22.035 |
| Targetless with spatio-temporal filtering | 2.712 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teo, T.-A.; Mei, K.-H.; Yuen, T.Y.P. A Markerless Photogrammetric Framework with Spatio-Temporal Refinement for Structural Deformation and Strain Monitoring. Buildings 2025, 15, 3584. https://doi.org/10.3390/buildings15193584
Teo T-A, Mei K-H, Yuen TYP. A Markerless Photogrammetric Framework with Spatio-Temporal Refinement for Structural Deformation and Strain Monitoring. Buildings. 2025; 15(19):3584. https://doi.org/10.3390/buildings15193584
Chicago/Turabian StyleTeo, Tee-Ann, Ko-Hsin Mei, and Terry Y. P. Yuen. 2025. "A Markerless Photogrammetric Framework with Spatio-Temporal Refinement for Structural Deformation and Strain Monitoring" Buildings 15, no. 19: 3584. https://doi.org/10.3390/buildings15193584
APA StyleTeo, T.-A., Mei, K.-H., & Yuen, T. Y. P. (2025). A Markerless Photogrammetric Framework with Spatio-Temporal Refinement for Structural Deformation and Strain Monitoring. Buildings, 15(19), 3584. https://doi.org/10.3390/buildings15193584






