Research on Feature Variable Set Optimization Method for Data-Driven Building Cooling Load Prediction Model
Abstract
1. Introduction
2. Methodology
2.1. Construction of Candidate Feature Variable Set
2.2. Optimal Feature Subset Selection Method
2.2.1. Forward Search-Based Subset Selection Method
2.2.2. MRMR-MIC-Based Subset Evaluation Method
- (1)
- Correlation Evaluation Criterion
- (2)
- Redundancy evaluation criterion
2.3. Validation of Method Effectiveness
2.3.1. Performance Analysis of Feature Subset Optimization Method
2.3.2. Comparative Analysis of Different Feature Selection Methods
2.4. Case Study Description
3. Results
3.1. Feature Subset Selection Results
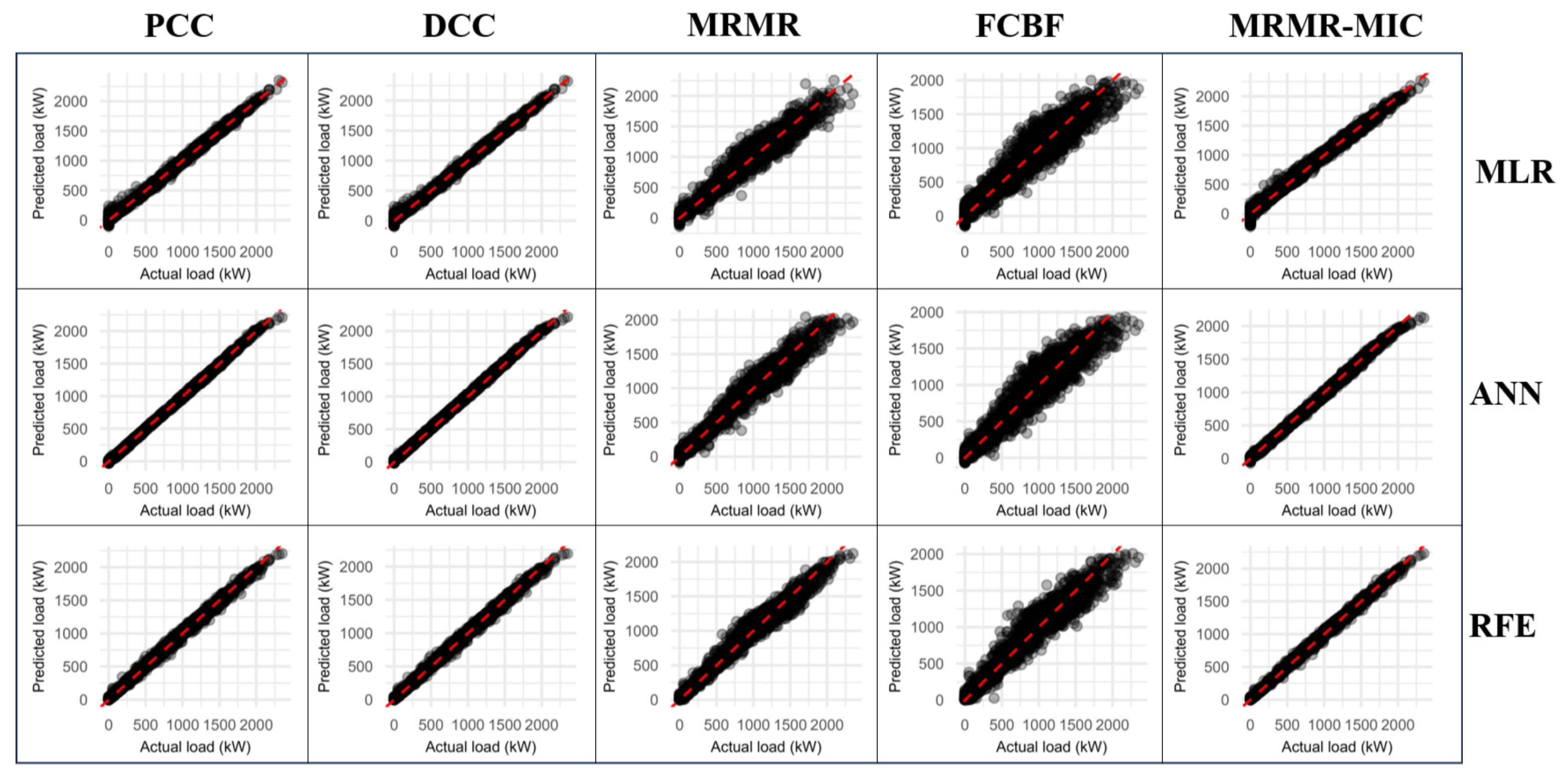
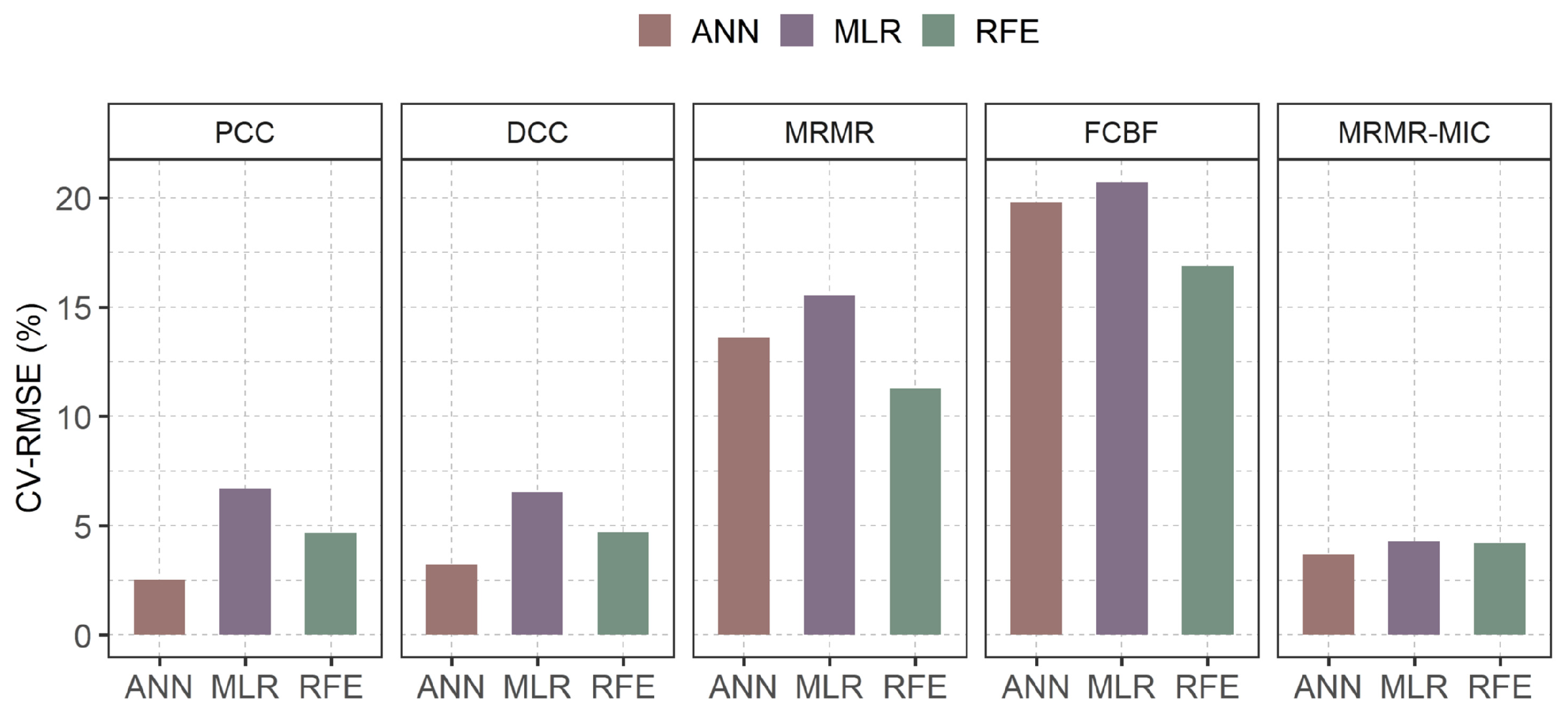
3.2. Evaluation Results of Feature Subset Selection Methods
4. Discussion
4.1. Interpretation of Key Findings and Methodological Advantages
4.2. Novelty and Accuracy of the Proposed MRMR-MIC Framework
4.3. Analysis of Influential Parameters on Cooling Load
4.4. Practical Implications for Building Energy Management
4.5. Limitations and Study Scope
4.6. Future Research Directions
5. Conclusions
- (1)
- Development of a Superior Feature Selection Methodology: The integration of the Maximal Information Coefficient (MIC) within the Maximum Relevance Minimum Redundancy (MRMR) principle proved to be a robust solution. This hybrid approach successfully overcomes the key limitations of conventional methods: it captures both linear and complex non-linear relationships (a weakness of PCC/DCC) while explicitly and effectively controlling for feature redundancy (a weakness of MRMR and FCBF, which use less suitable metrics for continuous data).
- (2)
- Quantifiable Performance Excellence: The case study results provide compelling evidence for the effectiveness of the proposed method. The MRMR-MIC framework achieved a 76% reduction in feature dimensionality, successfully identifying a concise yet highly predictive subset of only 40 variables from an initial set of over 170. Most importantly, this dramatic simplification was accomplished without sacrificing predictive accuracy, maintaining a low prediction error (CV-RMSE) below 5% across three different machine learning models (MLR, ANN, RFR).
- (3)
- Comprehensive and Physically Meaningful Feature Selection: Unlike other redundancy-control methods (especially FCBF), which omitted critical variables, the MRMR-MIC selected subset retained a physically interpretable combination of features spanning 8 attribute dimensions, including key meteorological parameters and internal loads. This underscores the method’s ability to preserve essential information while eliminating noise and redundancy.
- (4)
- Provision of a Generalizable Framework: The primary output of this research is not a universal feature list, but a powerful and generalizable methodology. The MRMR-MIC framework provides a systematic, data-driven approach to determining the necessary and sufficient sensing and data collection requirements for any specific building, thereby offering practical guidance for the development of cost-effective and efficient building energy management systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, R.; Lei, L. A hybrid model for real-time cooling load prediction and terminal control optimization in multi-zone buildings. J. Build. Eng. 2025, 104, 112120. [Google Scholar] [CrossRef]
- Abdel-Jaber, F.; Dirks, K.N. A review of cooling and heating loads predictions of residential buildings using data-driven techniques. Buildings 2024, 14, 752. [Google Scholar] [CrossRef]
- Zhong, F.; Yu, H.; Xie, X.; Wang, Y.; Huang, S.; Zhang, X. Short-term building cooling load prediction based on AKNN and RNN models. J. Build. Perform. Simul. 2024, 17, 742–755. [Google Scholar] [CrossRef]
- Huang, X.; Han, Y.; Yan, J.; Zhou, X. Hybrid forecasting model of building cooling load based on EMD-LSTM-Markov algorithm. Energy Build. 2024, 321, 114670. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Aydın, Y.; Bekdaş, G.; Isikdag, U.; Sadeghifam, A.N.; Abualigah, L. Cooling load prediction of a double-story terrace house using ensemble learning techniques and genetic programming with SHAP approach. Energy Build. 2024, 313, 114254. [Google Scholar] [CrossRef]
- Havaeji, S.; Anganeh, P.G.; Esfahani, M.T.; Rezaeihezaveh, R.; Moghadam, A.R. A comparative analysis of machine learning techniques for building cooling load prediction. J. Build. Pathol. Rehabil. 2024, 9, 119. [Google Scholar] [CrossRef]
- Myat, A.; Kondath, N.; Soh, Y.L.; Hui, A. A hybrid model based on multivariate fast iterative filtering and long short-term memory for ultra-short-term cooling load prediction. Energy Build. 2024, 307, 113977. [Google Scholar] [CrossRef]
- Da, T.N.; Cho, M.Y.; Thanh, P.N. Hourly load prediction based feature selection scheme and hybrid CNN-LSTM method for building’s smart solar microgrid. Expert Syst. 2024, 41, e13539. [Google Scholar] [CrossRef]
- Lu, Y.; Peng, X.; Li, C.; Tian, Z.; Kong, X.; Niu, J. Few-sample model training assistant: A meta-learning technique for building heating load forecasting based on simulation data. Energy 2025, 317, 134509. [Google Scholar] [CrossRef]
- Xue, P.; Jiang, Y.; Zhou, Z.; Chen, X.; Fang, X.; Liu, J. Multi-step ahead forecasting of heat load in district heating systems using machine learning algorithms. Energy 2019, 188, 116085. [Google Scholar] [CrossRef]
- Ardakanian, O.; Bhattacharya, A.; Culler, D. Non-intrusive occupancy monitoring for energy conservation in commercial buildings. Energy Build. 2018, 179, 311–323. [Google Scholar] [CrossRef]
- Powell, K.M.; Sriprasad, A.; Cole, W.J.; Edgar, T.F. Heating, cooling, and electrical load forecasting for a large-scale district energy system. Energy 2014, 74, 877–885. [Google Scholar] [CrossRef]
- Wong, S.L.; Wan, K.; Lam, T. Artificial neural networks for energy analysis of office buildings with daylighting. Appl. Energy 2010, 87, 551–557. [Google Scholar] [CrossRef]
- Kwok, S.; Lee, E. A study of the importance of occupancy to building cooling load in prediction by intelligent approach. Energy Convers. Manag. 2011, 52, 2555–2564. [Google Scholar] [CrossRef]
- Oliveira-Lima, J.A.; Morais, R.; Martins, J.F.; Florea, A.; Lima, C. Load forecast on intelligent buildings based on temporary occupancy monitoring. Energy Build. 2016, 116, 512–521. [Google Scholar] [CrossRef]
- Pang, Z.; Xu, P.; O’Neill, Z.; Gu, J.; Qiu, S.; Lu, X.; Li, X. Application of mobile positioning occupancy data for building energy simulation: An engineering case study. Build. Environ. 2018, 141, 1–15. [Google Scholar] [CrossRef]
- Tekler, Z.D.; Chong, A. Occupancy prediction using deep learning approaches across multiple space types: A minimum sensing strategy. Build. Environ. 2022, 226, 109689. [Google Scholar] [CrossRef]
- Sarwar, R.; Cho, H.; Cox, S.J.; Mago, P.J.; Luck, R. Field validation study of a time and temperature indexed autoregressive with exogenous (ARX) model for building thermal load prediction. Energy 2017, 119, 483–496. [Google Scholar] [CrossRef]
- Yang, J.; Ning, C.; Deb, C.; Zhang, F.; Cheong, D.; Lee, S.E.; Sekhar, C.; Tham, K.W. K-Shape clustering algorithm for building energy usage patterns analysis and forecasting model accuracy improvement. Energy Build. 2017, 146, 235–247. [Google Scholar] [CrossRef]
- Kapetanakis, D.S.; Mangina, E.; Finn, D.P. Input variable selection for thermal load predictive models of commercial buildings. Energy Build. 2017, 137, 13–26. [Google Scholar] [CrossRef]
- Ling, J.; Dai, N.; Xing, J.; Tong, H. An improved input variable selection method of the data-driven model for building heating load prediction. J. Build. Eng. 2021, 44, 103255. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Q.; Yuan, T.; Yang, F. Effect of input variables on cooling load prediction accuracy of an office building. Appl. Therm. Eng. 2018, 128, 225–234. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, S.; Yu, J.; Zhao, A. Hybrid forecasting model of building cooling load based on combined neural network. Energy 2024, 297, 131317. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81 Pt 1, 1192–1205. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Liu, H.; Liang, J.; Liu, Y.; Wu, H. A Review of Data-Driven Building Energy Prediction. Buildings 2023, 13, 532. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Bhattacharjee, A. Distance correlation coefficient: An application with bayesian approach in clinical data analysis. J. Mod. Appl. Stat. Methods 2014, 13, 23. [Google Scholar] [CrossRef]
- Senliol, B.; Gulgezen, G.; Yu, L.; Cataltepe, Z. Fast Correlation Based Filter (FCBF) with a different search strategy. In Proceedings of the 2008 23rd International Symposium on Computer and Information Sciences, Istanbul, Turkey, 27–29 October 2008; pp. 1–4. [Google Scholar]
- Spielvogel, L.G. A Standard of Care for Energy. Consult.-Specif. Eng. 2004, 36, 15–23. [Google Scholar]

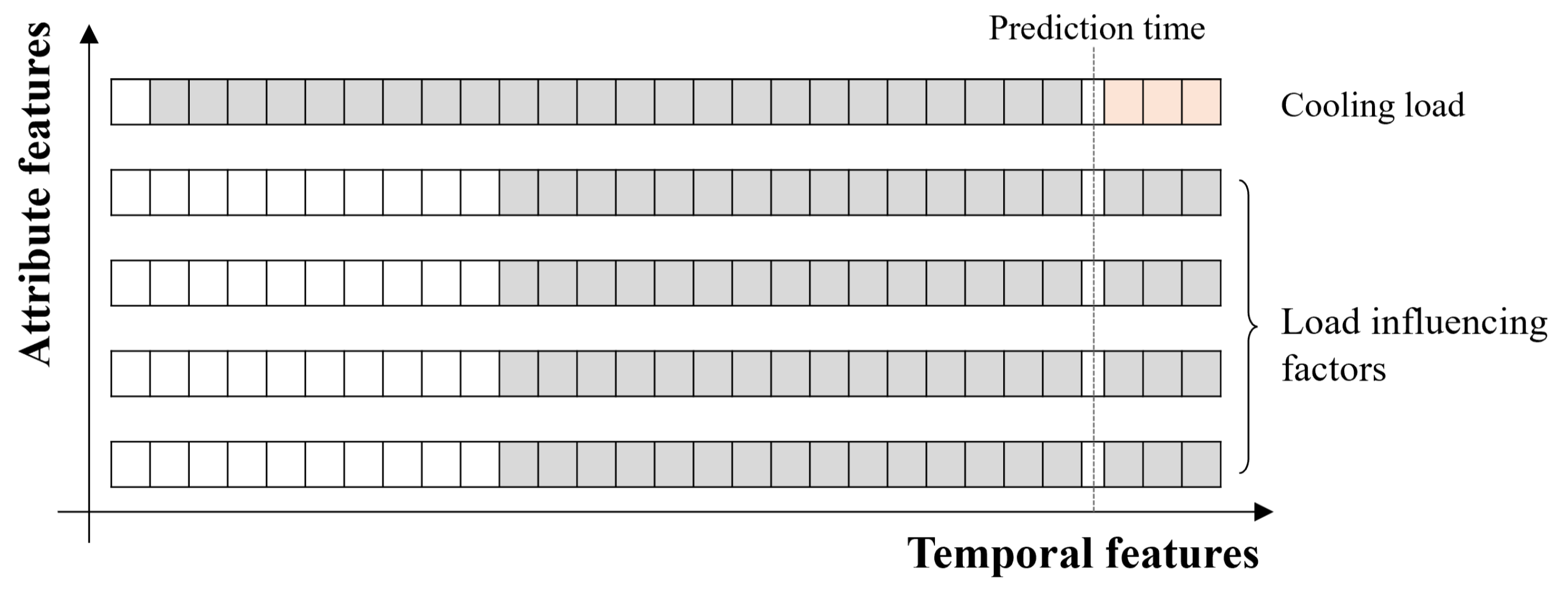


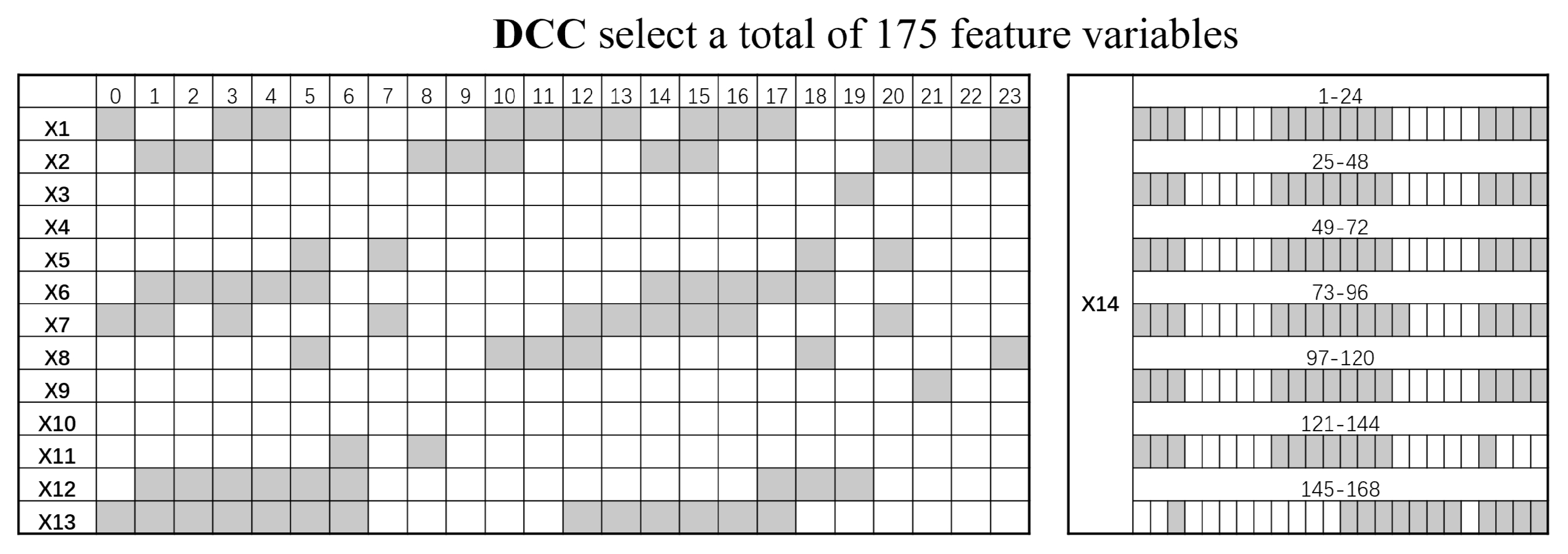



| NO. | Attribute | Time Lag Duration |
|---|---|---|
| X1 | Outdoor air dry-bulb temperature (°C) | 24 |
| X2 | Outdoor air dew-point temperature (°C) | 24 |
| X3 | Outdoor air wet-bulb temperature (°C) | 24 |
| X4 | Outdoor air humidity ratio (kg/kg) | 24 |
| X5 | Outdoor relative humidity (%) | 24 |
| X6 | Wind speed (m/s) | 24 |
| X7 | Sky temperature (°C) | 24 |
| X8 | Horizontal infrared radiation intensity (W/m2) | 24 |
| X9 | Diffuse solar radiation intensity (W/m2) | 24 |
| X10 | Direct solar radiation intensity (W/m2) | 24 |
| X11 | Occupant count (persons) | 24 |
| X12 | Lighting power (W) | 24 |
| X13 | Equipment power (W) | 24 |
| X14 | Historical cooling load (kW) | 24 × 7 |
| Parameters | Values | Units |
|---|---|---|
| Geographic location | Tianjin, 39.12° N, 117.20° E | -- |
| Building area | 27,400 | m2 |
| Window-to-wall ratio | South: 0.4; North: 0.3; East: 0.3; West: 0.3 | -- |
| Indoor design temperature | Summer: 26; Winter: 20 | °C |
| Indoor design humidity | 60 | % |
| External wall heat transfer coefficient | 0.41 | |
| Window heat transfer coefficient | 1.5 | |
| Roof heat transfer coefficient | 0.48 | |
| Floor heat transfer coefficient | 0.59 | |
| Air infiltration rate | 0.5 | h−1 |
| Fresh air volume | 30 | m3/person |
| Occupant density | 4 | m2/person |
| Lighting power density | 11 | |
| Equipment power density | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, D.; Ma, S.; Wu, L.; Wang, K.; Zhou, Z. Research on Feature Variable Set Optimization Method for Data-Driven Building Cooling Load Prediction Model. Buildings 2025, 15, 3583. https://doi.org/10.3390/buildings15193583
Bai D, Ma S, Wu L, Wang K, Zhou Z. Research on Feature Variable Set Optimization Method for Data-Driven Building Cooling Load Prediction Model. Buildings. 2025; 15(19):3583. https://doi.org/10.3390/buildings15193583
Chicago/Turabian StyleBai, Di, Shuo Ma, Liwen Wu, Kexun Wang, and Zhipeng Zhou. 2025. "Research on Feature Variable Set Optimization Method for Data-Driven Building Cooling Load Prediction Model" Buildings 15, no. 19: 3583. https://doi.org/10.3390/buildings15193583
APA StyleBai, D., Ma, S., Wu, L., Wang, K., & Zhou, Z. (2025). Research on Feature Variable Set Optimization Method for Data-Driven Building Cooling Load Prediction Model. Buildings, 15(19), 3583. https://doi.org/10.3390/buildings15193583






