Prediction of Plate End Debonding of FRP-Strengthened RC Beams Based on Explainable Machine Learning
Abstract
1. Introduction
2. Database Construction
2.1. Parameter Selection
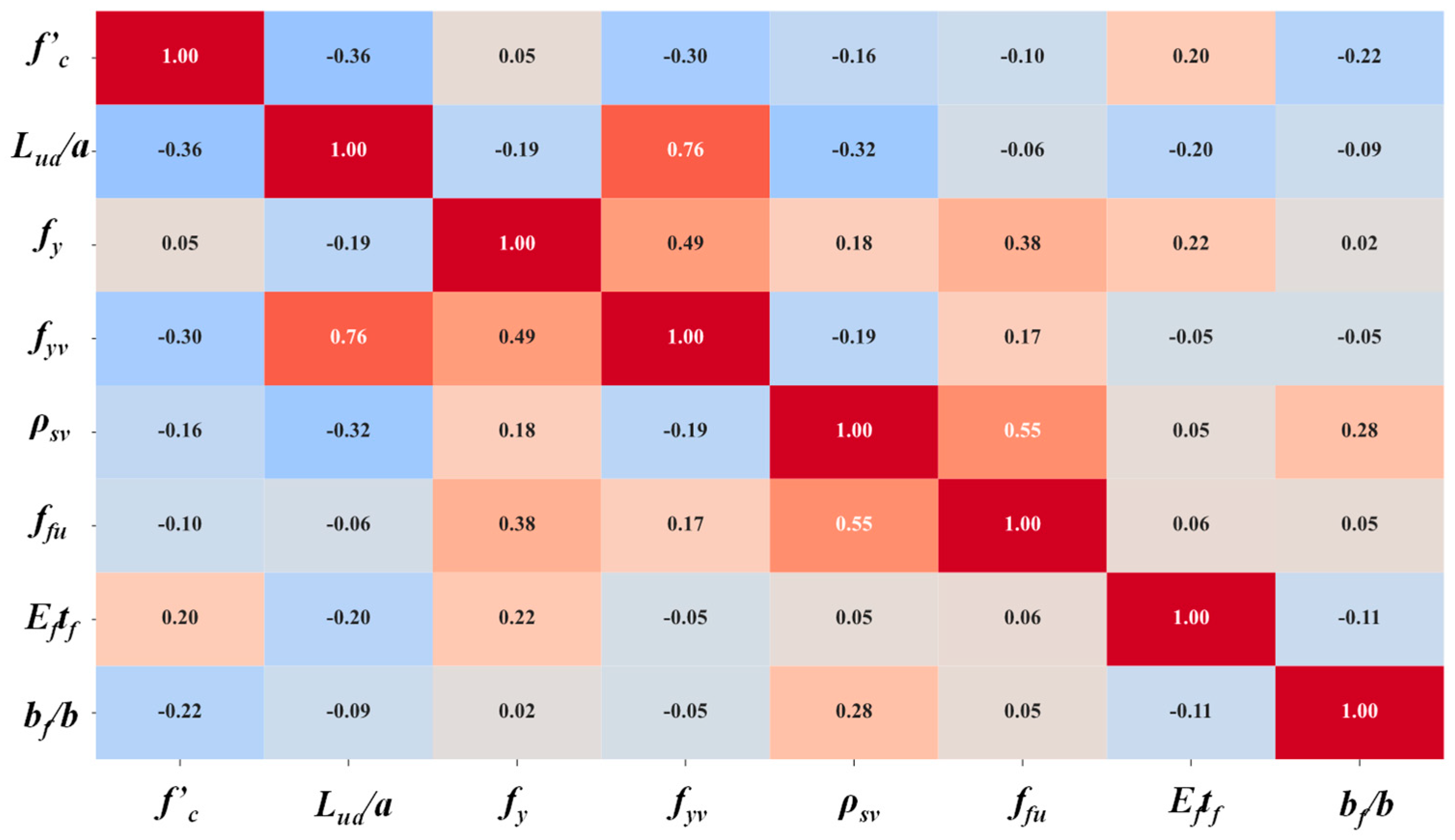
2.2. Parameter Analysis
3. Model Construction and Evaluation
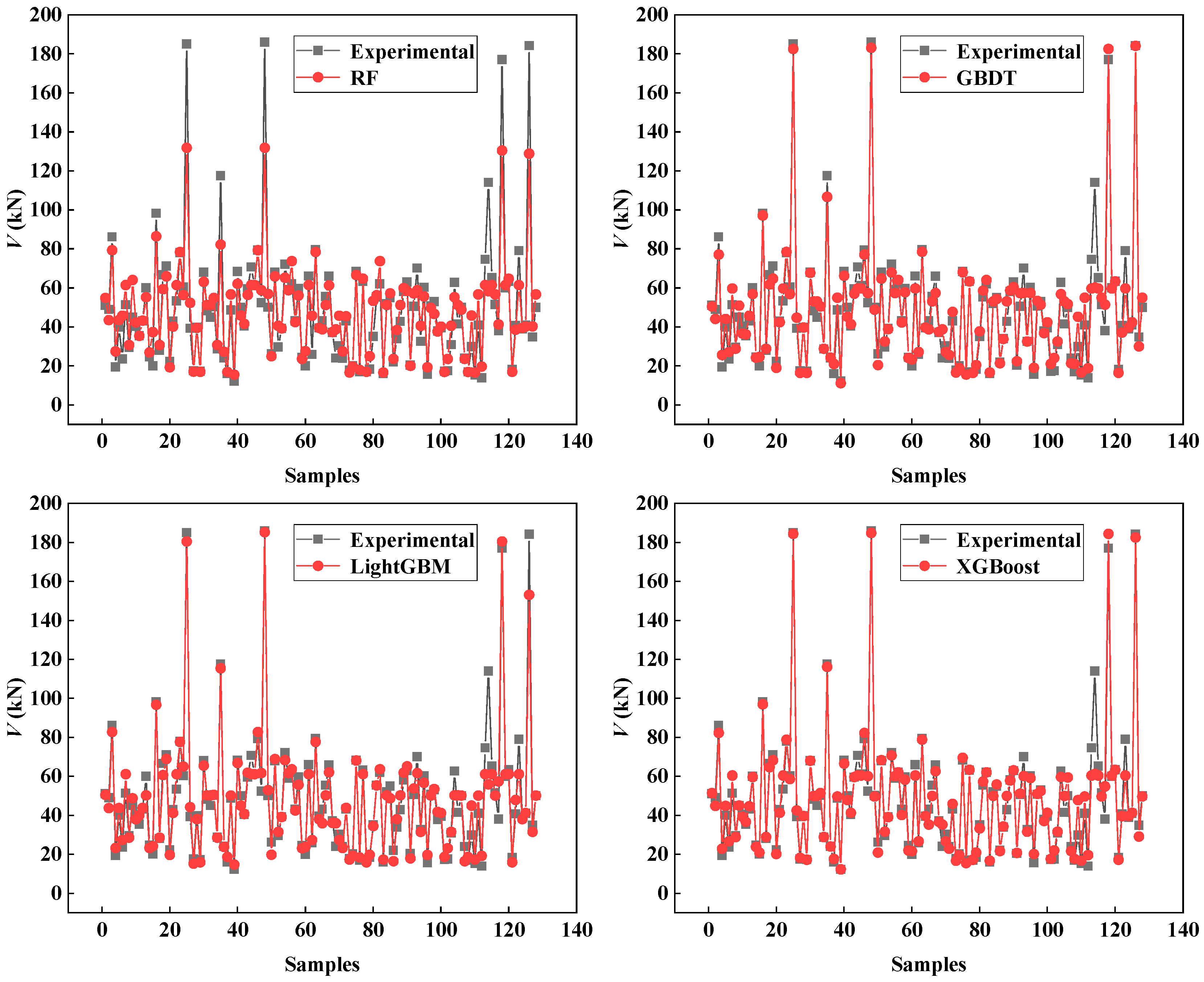
3.1. Ensemble Learning Models
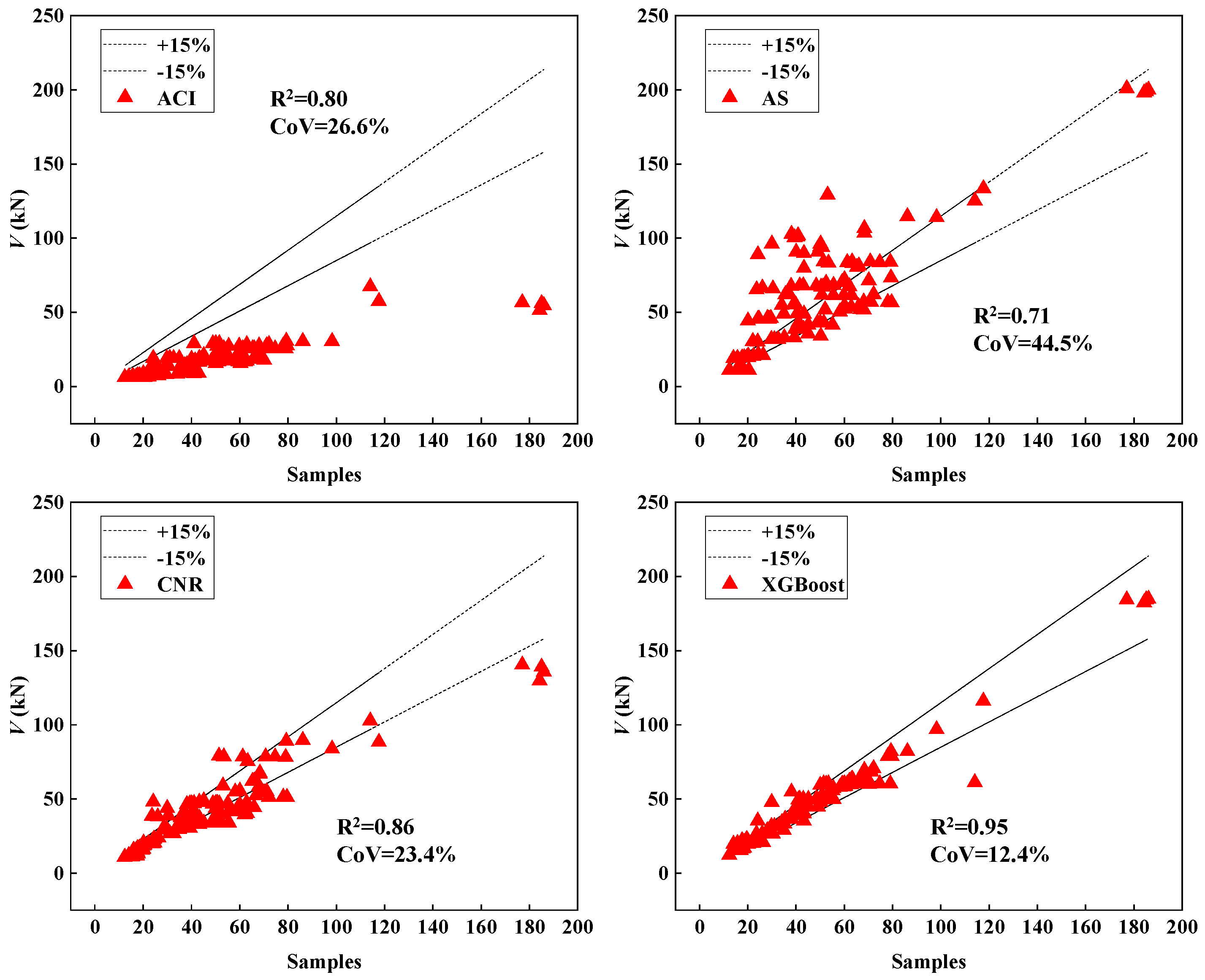
3.2. Model Recommended by Codes
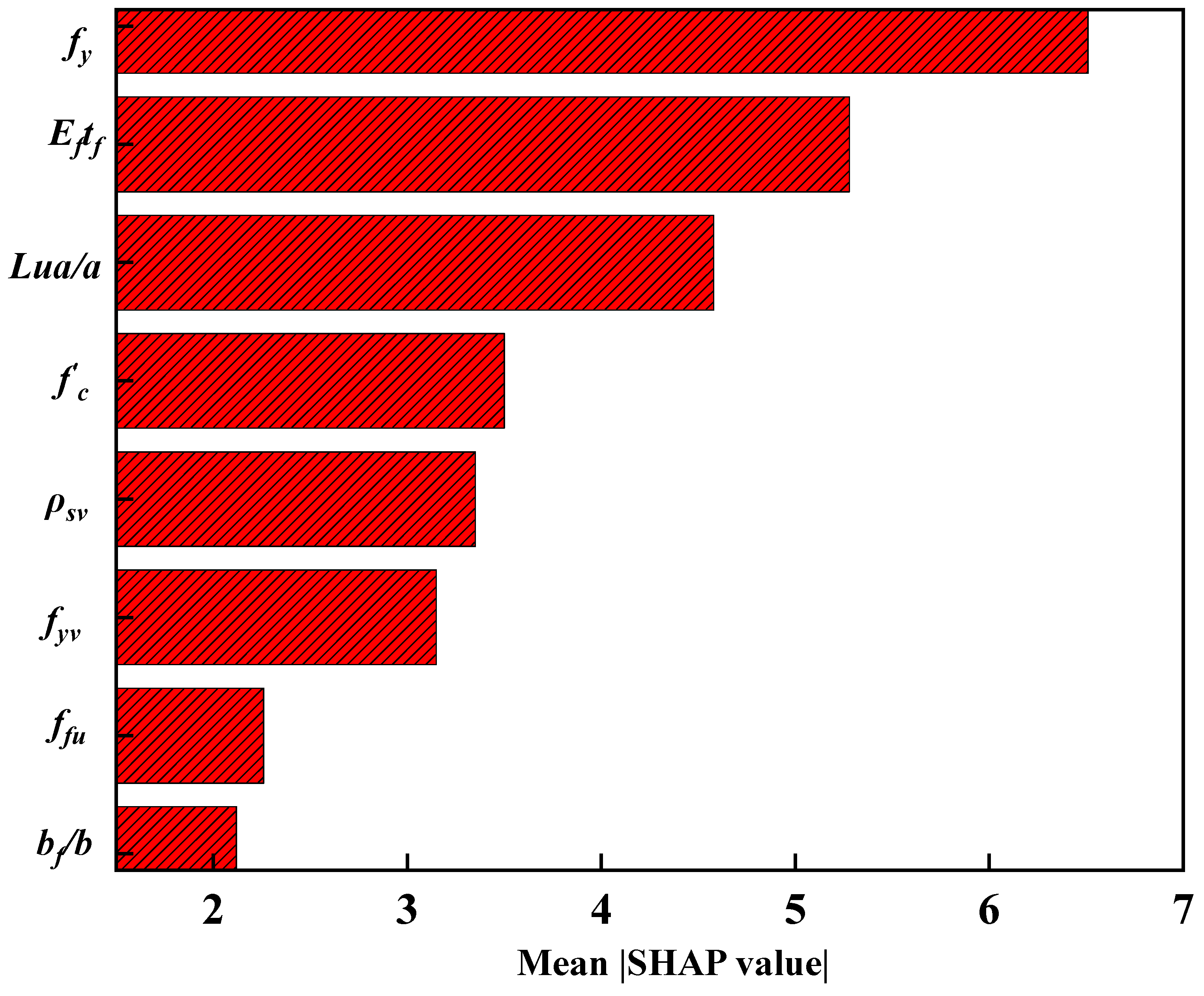
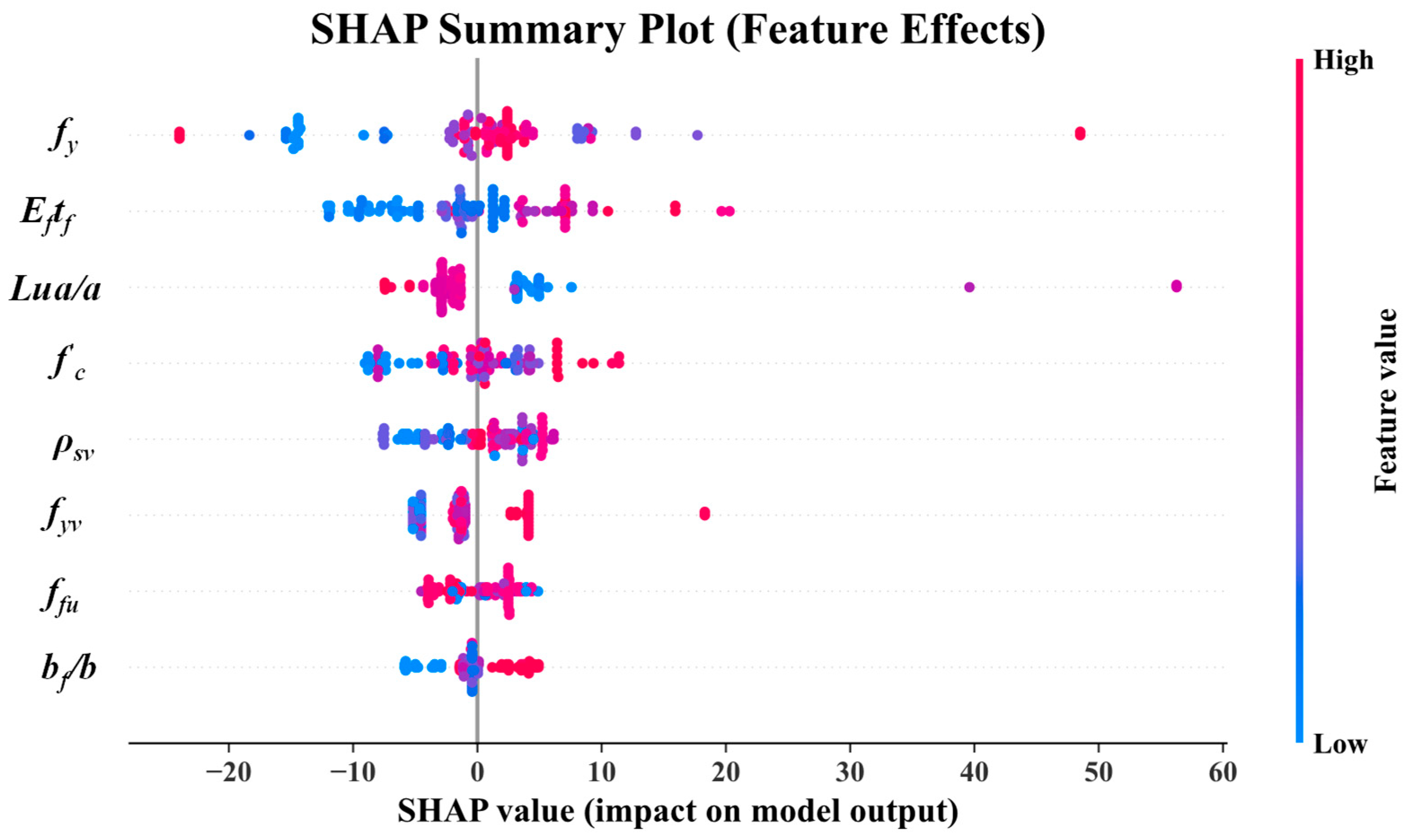
3.3. Parameter Study
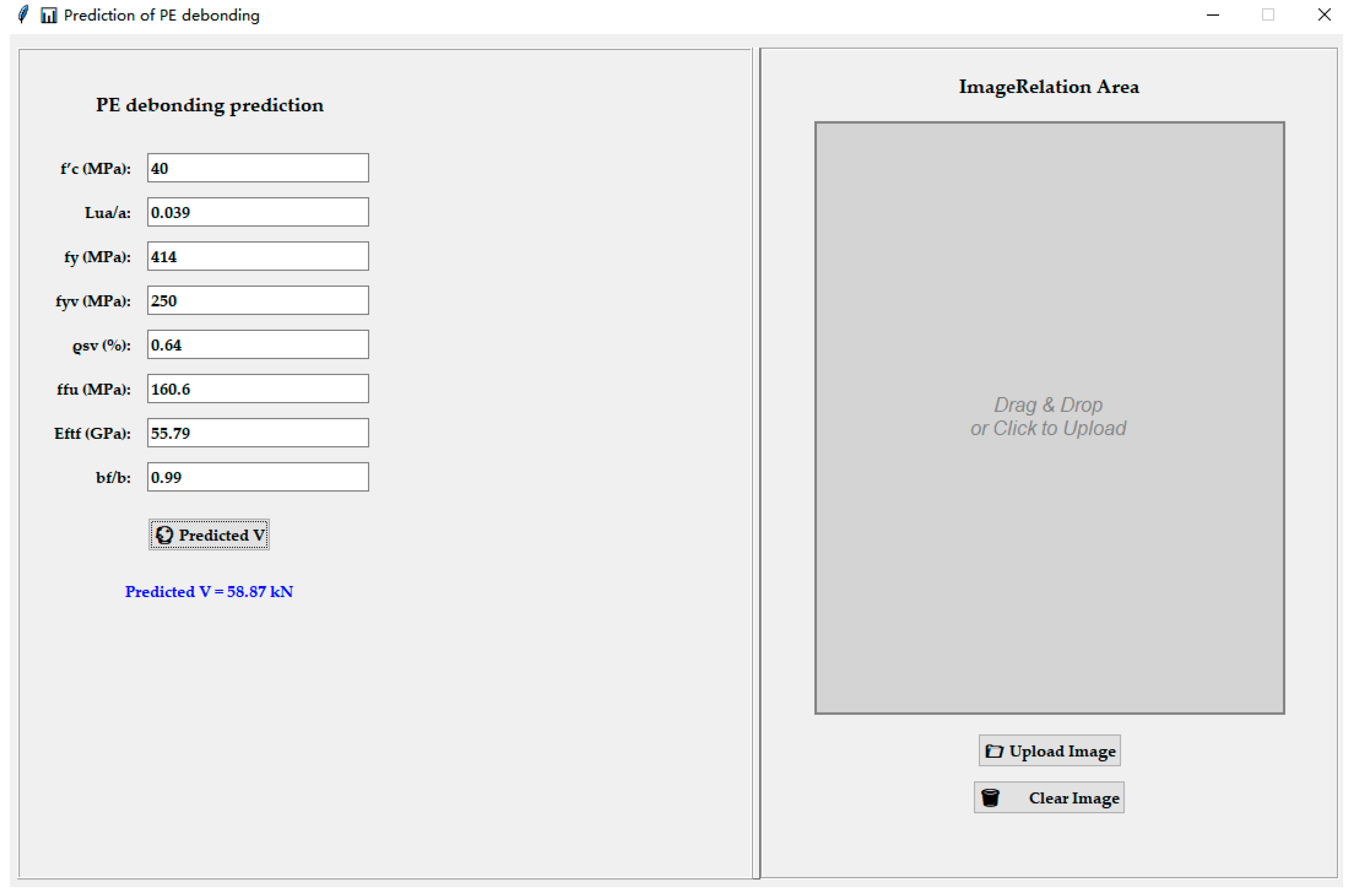
3.4. Graphical User Interface
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, C.; Taffese, W.Z.; Hu, T. Accurate prediction of punching shear strength of steel fiber-reinforced concrete slabs: A machine learning approach with data augmentation and explainability. Buildings 2024, 14, 1223. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, H.; Cheng, C.; Li, H.; Zhou, J. Explainable machine learning: Compressive strength prediction of FRP-confined concrete column. Mater. Today Commun. 2024, 39, 108883. [Google Scholar] [CrossRef]
- Sabzi, J.; Shamsabadi, E.A.; Esfahani, M.R.; Ozbakkaloglu, T. A study on reinforced concrete beams strengthened with FRP and FRCM. Eng. Struct. 2025, 329, 119687. [Google Scholar] [CrossRef]
- Hu, T.; Zhang, H.; Zhou, J. Prediction of the debonding failure of beams strengthened with FRP through machine learning models. Buildings 2023, 13, 608. [Google Scholar] [CrossRef]
- Li, G.; Hu, T.; Shao, Y.; Bai, D. Data-driven model for predicting intermediate crack induced debonding of FRP-strengthened RC beams in flexure. Structures 2022, 41, 1178–1189. [Google Scholar] [CrossRef]
- Al-Saawani, M.A.; El-Sayed, A.K.; Al-Negheimish, A.I. Assessment of plate-end debonding design provisions for RC beams strengthened with FRP. Lat. Am. J. Solids Struct. 2020, 17, e255. [Google Scholar] [CrossRef]
- Zhang, S.S.; Teng, J.G. End cover separation in RC beams strengthened in flexure with bonded FRP reinforcement: Simplified finite element approach. Mater. Struct. 2016, 49, 2223–2236. [Google Scholar] [CrossRef]
- ACI-440.2R; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures, Reported by ACI Committee 440. American Concrete Institute: Farmington Hills, MI, USA, 2017.
- Japan Society of Civil Engineers (JSCE). Recommendations for Upgrading of Concrete Structures with Use of Continuous Fiber Sheets; Concrete Engineering Series; Japan Society of Civil Engineers: Nagaoka, Japan, 2001. [Google Scholar]
- AS5100.8; Bridge Design, Part 8: Rehabilitation and Strengthening of Existing Bridges. Standards Australia: Sydney, Australia; SA1 Global Limited: Sydney, Australia, 2017.
- National Research Council. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures (CNR-DT 200 R1); CNR: Rome, Italy, 2013. [Google Scholar]
- Yao, J.; Teng, J.G. Plate end debonding in FRP-plated RC beams—I: Experiments. Eng. Struct. 2007, 29, 2457–2471. [Google Scholar] [CrossRef]
- Al-Saawani, M. Empirical shear based model for predicting plate end debonding in FRP strengthened RC beams. J. Civ. Eng. Manag. 2021, 27, 117–138. [Google Scholar] [CrossRef]
- El-Mir, A.; El-Zahab, S.; Nasr, D.; Semaan, N.; Assaad, J.; El-Hassan, H. Use of machine learning models to predict the water penetration depth in concrete. J. Build. Eng. 2024, 95, 110107. [Google Scholar] [CrossRef]
- Gharagoz, M.M.; Noureldin, M.; Kim, J. Explainable machine learning (XML) framework for seismic assessment of structures using Extreme Gradient Boosting (XGBoost). Eng. Struct. 2025, 327, 119621. [Google Scholar] [CrossRef]
- Zhu, Y.; Taffese, W.Z.; Chen, G. Enhancing FRP-concrete interface bearing capacity prediction with explainable machine learning: A feature engineering approach and SHAP analysis. Eng. Struct. 2024, 319, 118831. [Google Scholar] [CrossRef]
- Liu, X.; Sun, G.; Ju, R.; Li, J.; Li, Z.; Jiang, Y.; Zhao, K.; Zhang, Y.; Jing, Y.; Yang, G. Prediction of load-bearing capacity of FRP-steel composite tubed concrete columns: Using explainable machine learning model with limited data. Structures 2025, 71, 107890. [Google Scholar] [CrossRef]
- Chu, J.; Guo, B.; Zhong, T.; Guan, Q.; Wang, Y.; Niu, D. Explainable machine learning model for predicting compressive strength of CO2-cured concrete. Case Stud. Constr. Mater. 2025, 22, e04589. [Google Scholar] [CrossRef]
- Yan, J.; Su, J.; Xu, J.; Hua, K.; Lin, L.; Yu, Y. Explainable machine learning models for punching shear capacity of FRP bar reinforced concrete flat slab without shear reinforcement. Case Stud. Constr. Mater. 2024, 20, e03162. [Google Scholar] [CrossRef]
- Ritchie, P.A.; Thomas, D.A.; Lu, L.W.; Connelly, G.M. External Reinforcement of Concrete Beams Using Fiber Reinforced Plastic. Master’s Thesis, Lehigh University, Bethlehem, PA, USA, 1988. [Google Scholar]
- Quantrill, R.J.; Hollaway, L.C.; Thorne, A.M. Experimental and analytical investigation of FRP strengthened beam response: Part I. Mag. Concr. Res. 1996, 48, 331–342. [Google Scholar] [CrossRef]
- Arduini, M.; Di Tommaso, A.; Nanni, A. Brittle failure in FRP plate and sheet bonded beams. Struct. J. 1997, 94, 363–370. [Google Scholar]
- Beber, A.J.; Campos Filho, A.; Campagnolo, J.L. Flexural strengthening of R/C beams with CFRP sheets. Struct. Faults Repair 1999, 99, 39. [Google Scholar]
- David, E.; Djelal, C.; Ragneau, E.; Bodin, F.B. Use of FRP to strengthen and repair RC beams: Experimental study and numerical simulations. In Proceedings of the 8th Internet Conference on Advanced Composites for Concrete Repair, London, UK, 13–15 July 1999. [Google Scholar]
- Valcuende, M.; Benlloch, J.; Parra, C.J. Ductility of reinforced concrete beams strengthened with CFRP strips and fabric. Fibre-Reinf. Polym. Reinf. Concr. Struct. 2003, 2, 337–346. [Google Scholar]
- Hasnat, A.; Islam, M.M.; Amin, A.F.M.S. Enhancing the debonding strain limit for CFRP-strengthened RC beams using U-clamps: Identification of design parameters. J. Compos. Constr. 2016, 20, 04015039. [Google Scholar] [CrossRef]
- Gao, B.; Kim, J.K.; Leung, C.K. Experimental study on RC beams with FRP strips bonded with rubber modified resins. Compos. Sci. Technol. 2004, 64, 2557–2564. [Google Scholar] [CrossRef]
- Shi, Z.; Li, Q.; Li, L.; Shao, Y.; Hao, H. Data-Driven BLEVE Overpressure Prediction Using Explainable Machine Learning. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Limassol, Cyprus, 26–29 June 2025; Springer: Cham, Switzerland, 2025. [Google Scholar]

| Min | Max | Mean | 25% | 50% | 75% | Standard Deviation | |
|---|---|---|---|---|---|---|---|
| f’c | 19.2 | 66.4 | 41.5 | 33.6 | 41.8 | 49.2 | 10.53 |
| Lua/a | 0.47 | 1.31 | 0.89 | 0.68 | 0.97 | 1 | 0.20 |
| fy | 350 | 611 | 490 | 427 | 506 | 562 | 79.06 |
| fyv | 235 | 738 | 435 | 350 | 420 | 537 | 113.50 |
| ρsv | 0.11 | 1.68 | 0.65 | 0.43 | 0.64 | 0.9 | 0.30 |
| ffu | 160 | 4519 | 3005 | 2400 | 3425 | 3792.5 | 1077.77 |
| Eftf | 25.4 | 434.2 | 128.1 | 77.5 | 96.11 | 187.2 | 82.81 |
| bf/b | 0.3 | 1 | 0.77 | 0.6 | 0.71 | 1 | 0.20 |
| Training | Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Models | R2 | MAE | RMSE | MAPE | Models | R2 | MAE | RMSE | MAPE |
| RF | 0.85 | 6.05 | 10.7 | 13.80% | RF | 0.79 | 11.05 | 19.35 | 16.60% |
| GBDT | 0.97 | 3.12 | 4.31 | 8.10% | GBDT | 0.903 | 7.55 | 13.11 | 15.50% |
| LightGBM | 0.9811 | 2.96 | 3.88 | 7.90% | LightGBM | 0.87 | 8.79 | 15.13 | 16.40% |
| XGBoost | 0.9873 | 2.05 | 3.1764 | 5.50% | XGBoost | 0.906 | 7.15 | 12.93 | 14.10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Taffese, W.Z. Prediction of Plate End Debonding of FRP-Strengthened RC Beams Based on Explainable Machine Learning. Buildings 2025, 15, 3576. https://doi.org/10.3390/buildings15193576
Zheng S, Taffese WZ. Prediction of Plate End Debonding of FRP-Strengthened RC Beams Based on Explainable Machine Learning. Buildings. 2025; 15(19):3576. https://doi.org/10.3390/buildings15193576
Chicago/Turabian StyleZheng, Sheng, and Woubishet Zewdu Taffese. 2025. "Prediction of Plate End Debonding of FRP-Strengthened RC Beams Based on Explainable Machine Learning" Buildings 15, no. 19: 3576. https://doi.org/10.3390/buildings15193576
APA StyleZheng, S., & Taffese, W. Z. (2025). Prediction of Plate End Debonding of FRP-Strengthened RC Beams Based on Explainable Machine Learning. Buildings, 15(19), 3576. https://doi.org/10.3390/buildings15193576







