Structural Robustness Analysis of Reverse Arch Beam String-Inclined Column Structure
Abstract
1. Introduction
2. Field Measurements
2.1. Brief Introduction of Structure
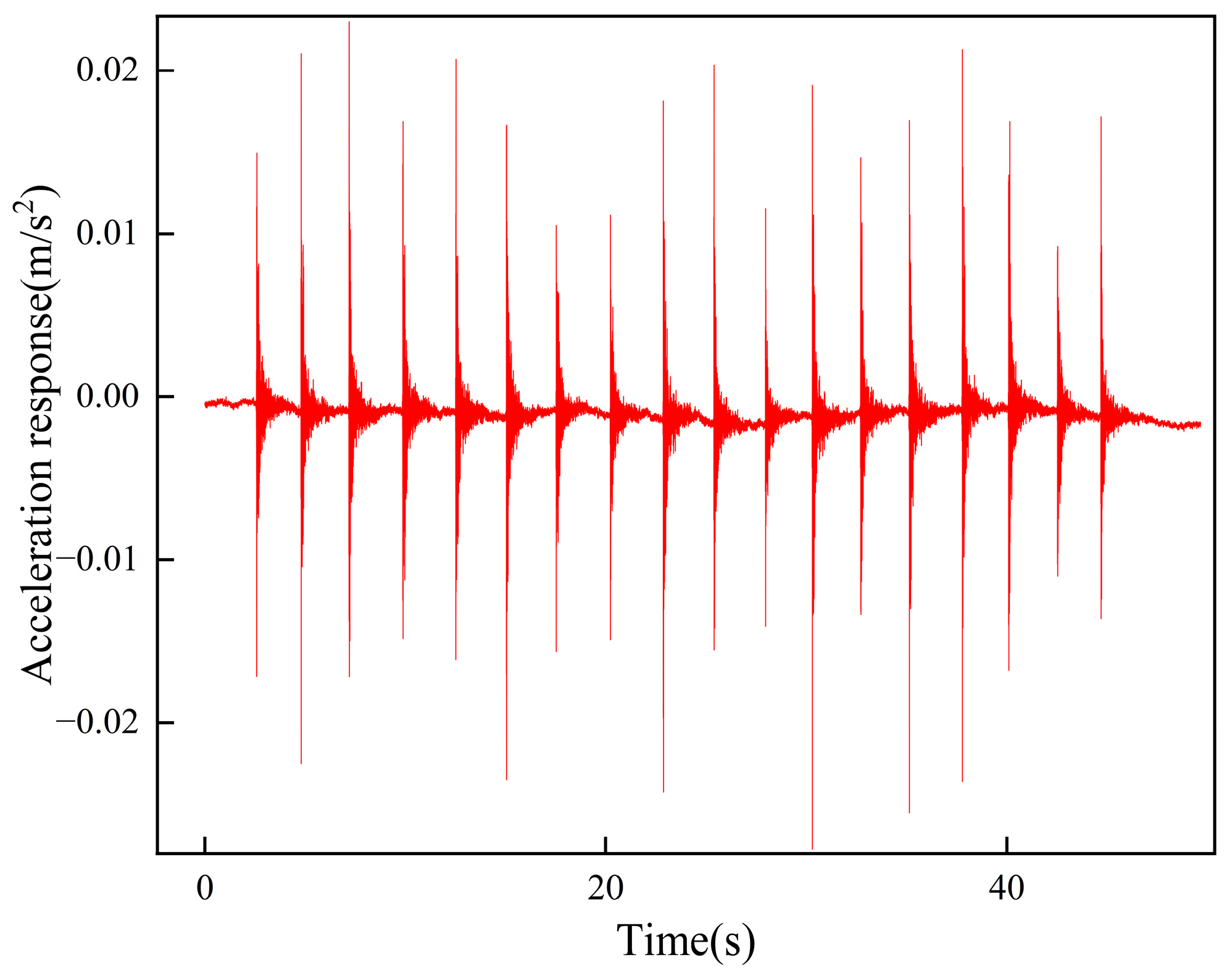
2.2. Test Methods
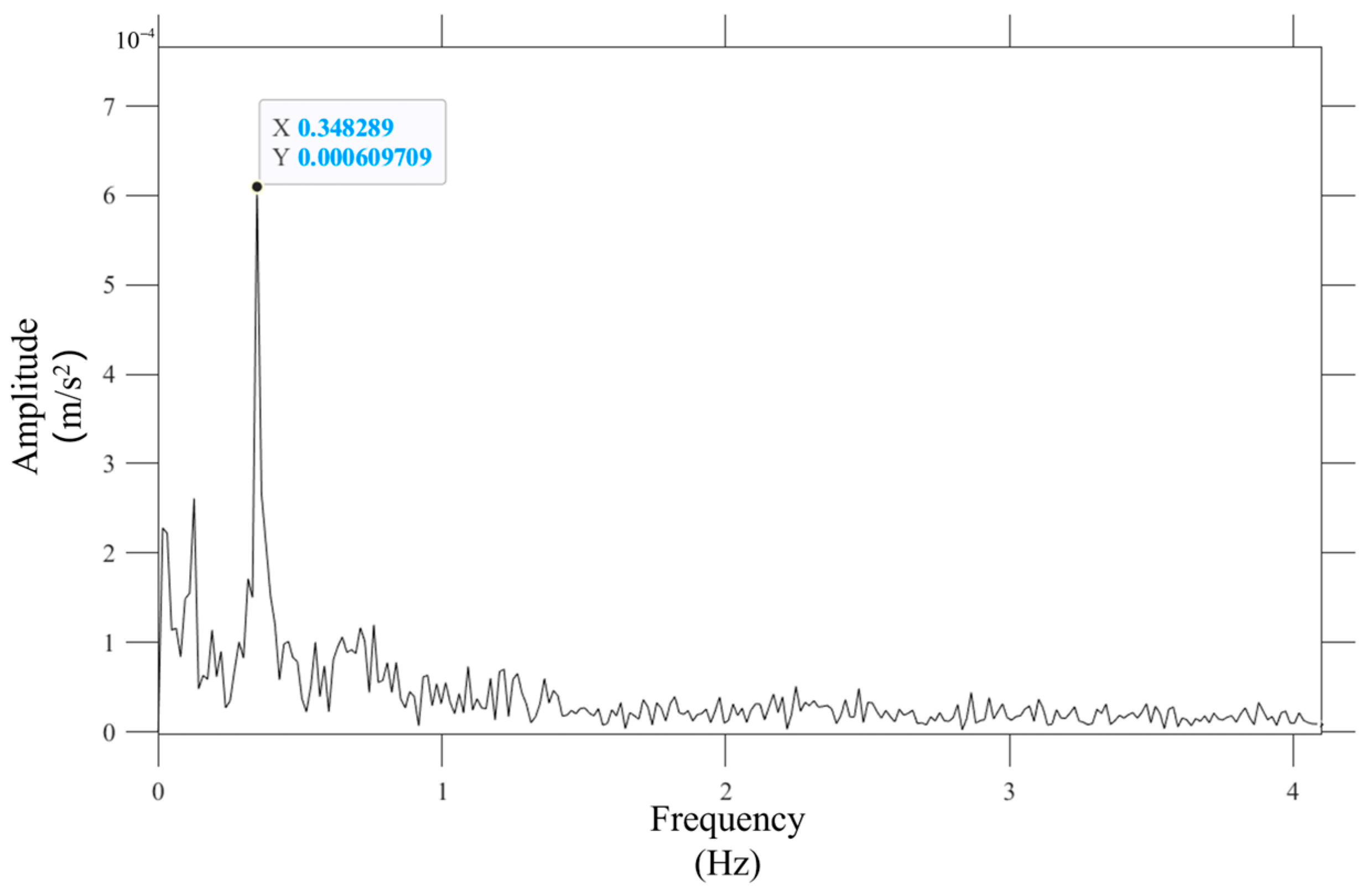
2.3. Analysis of Test Results
3. Finite Element Analysis
3.1. Finite Element Modeling Methods
3.2. Model Verification
3.3. Initial State
4. Structural Robustness Analysis
4.1. Methods for Analyzing Resistance to Progressive Collapse
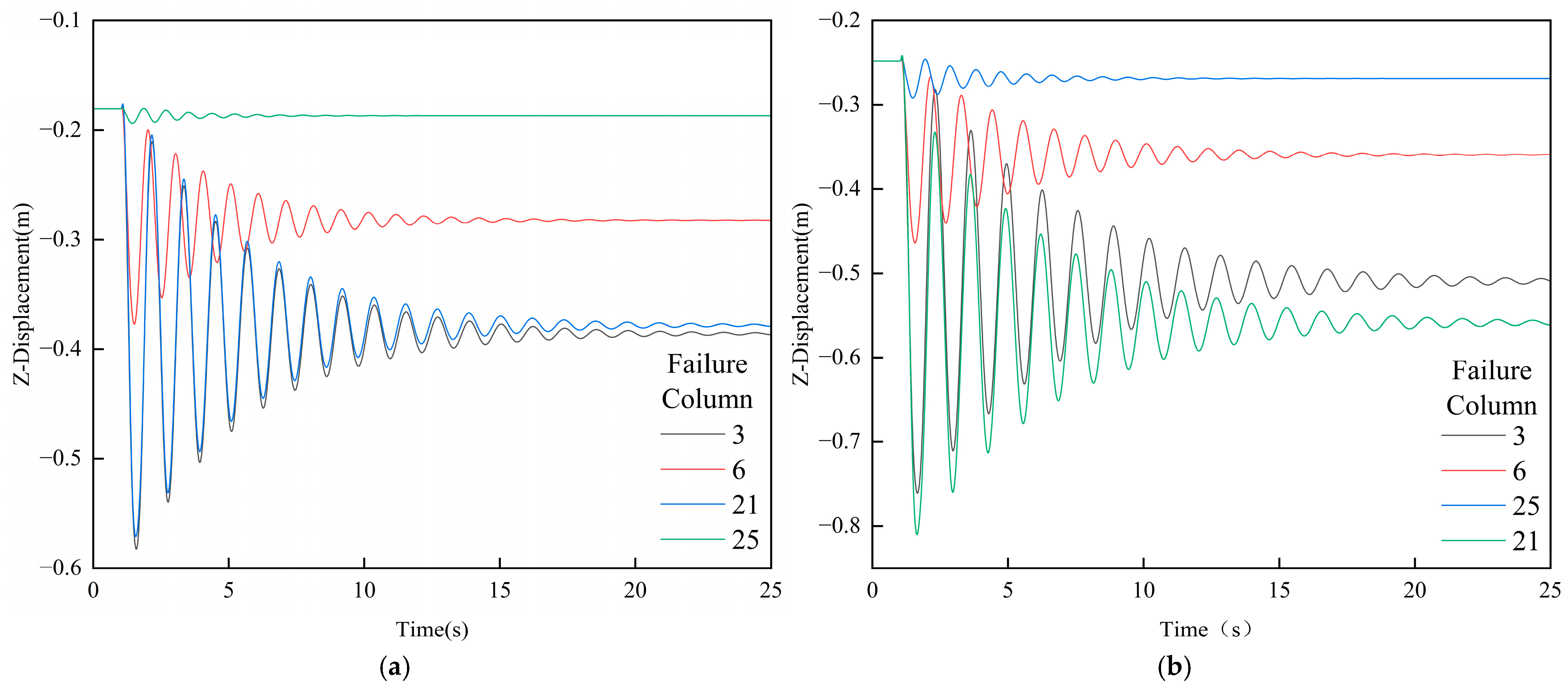
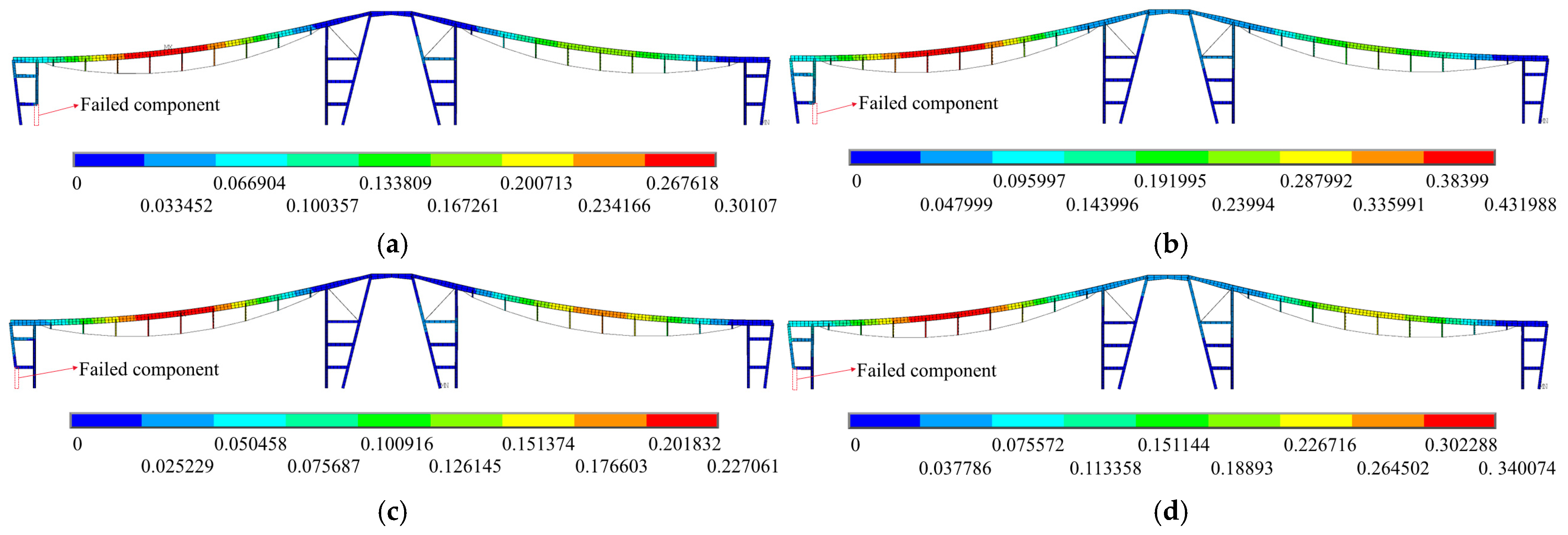
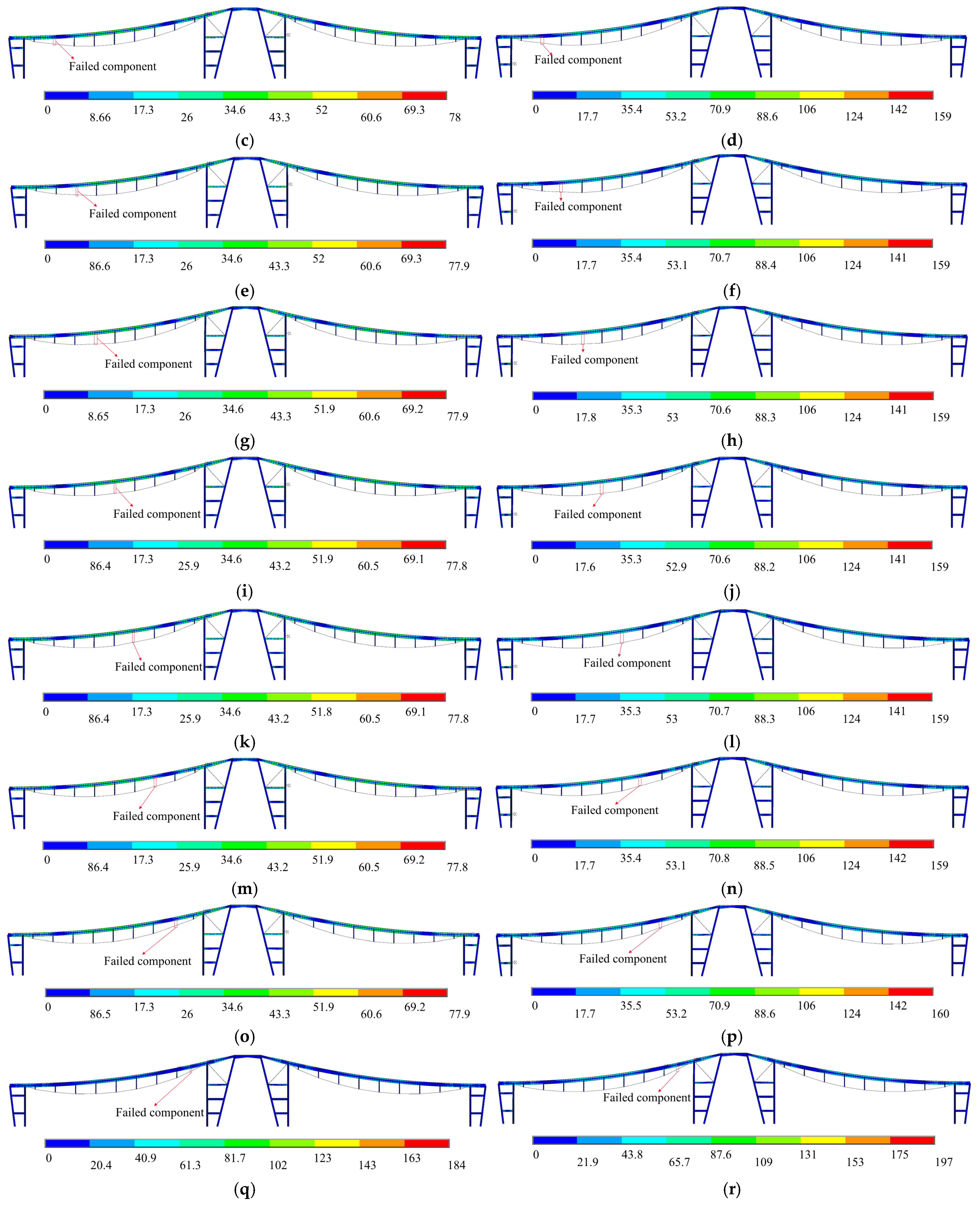
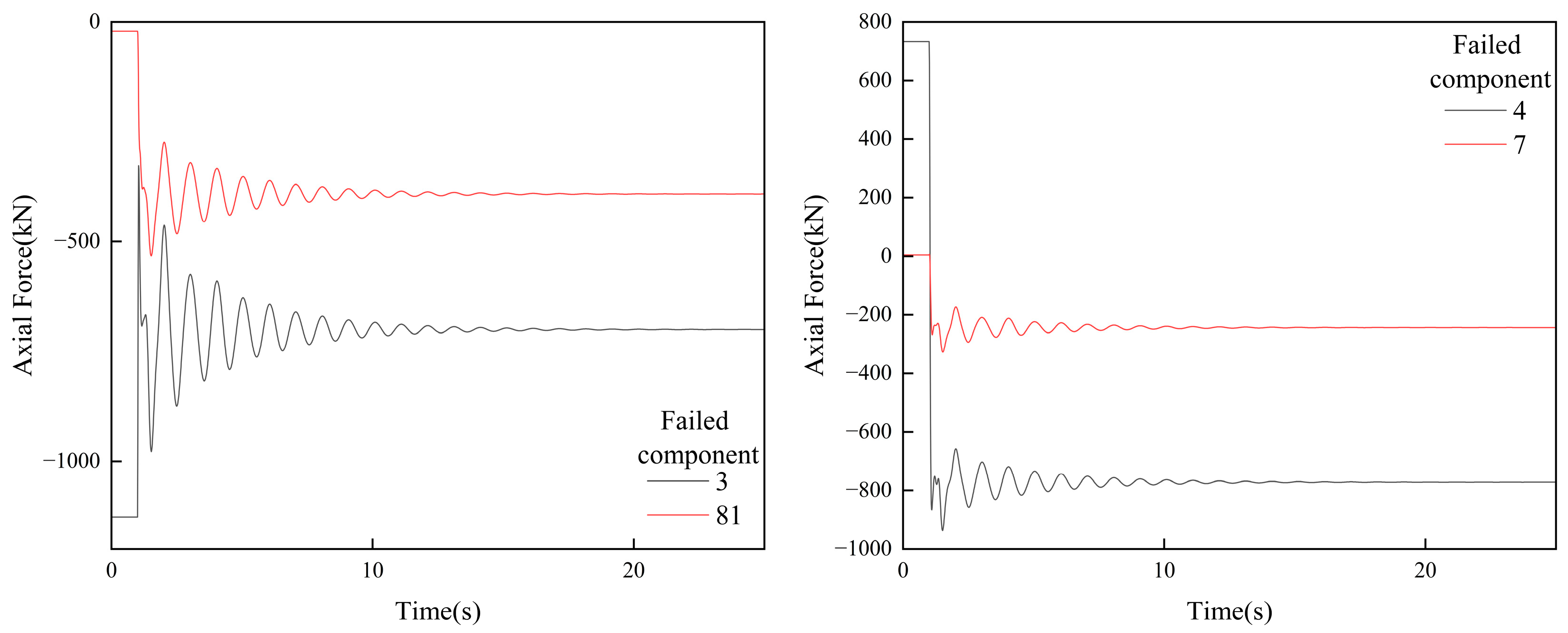
4.2. Column End Failure
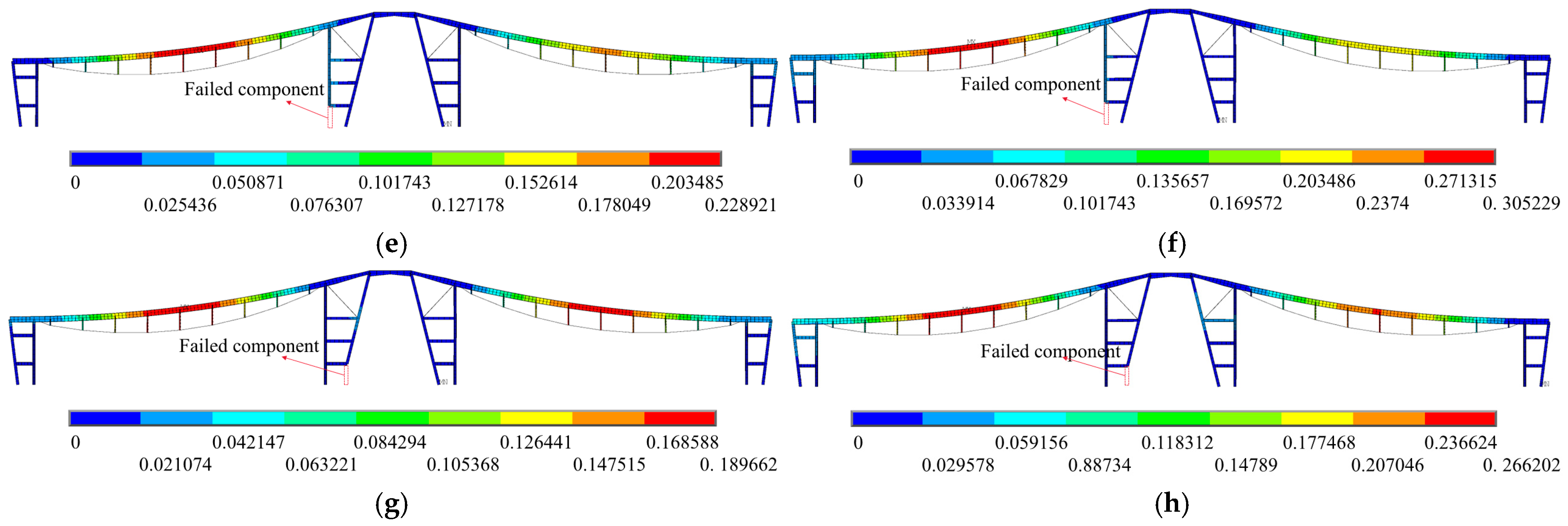
4.3. Column Base Failure
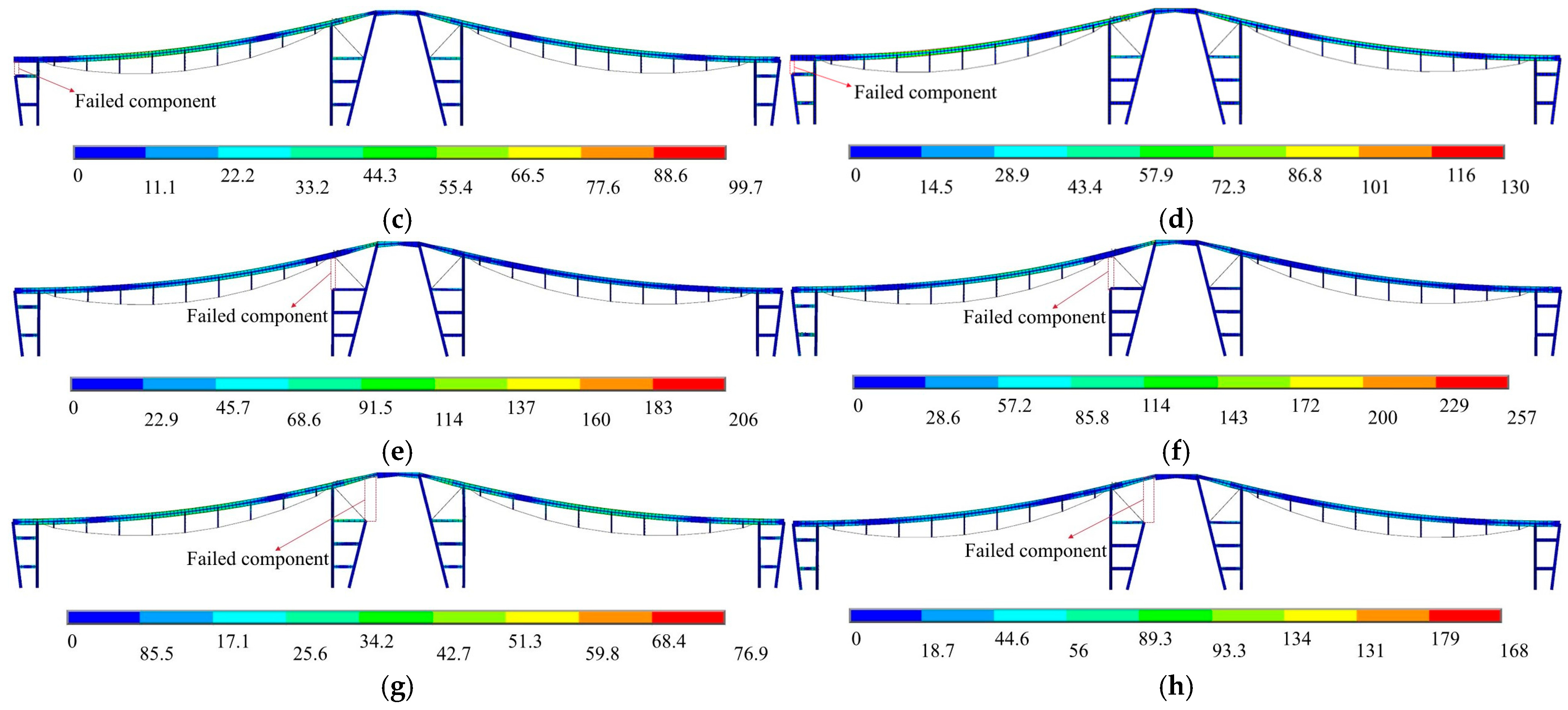
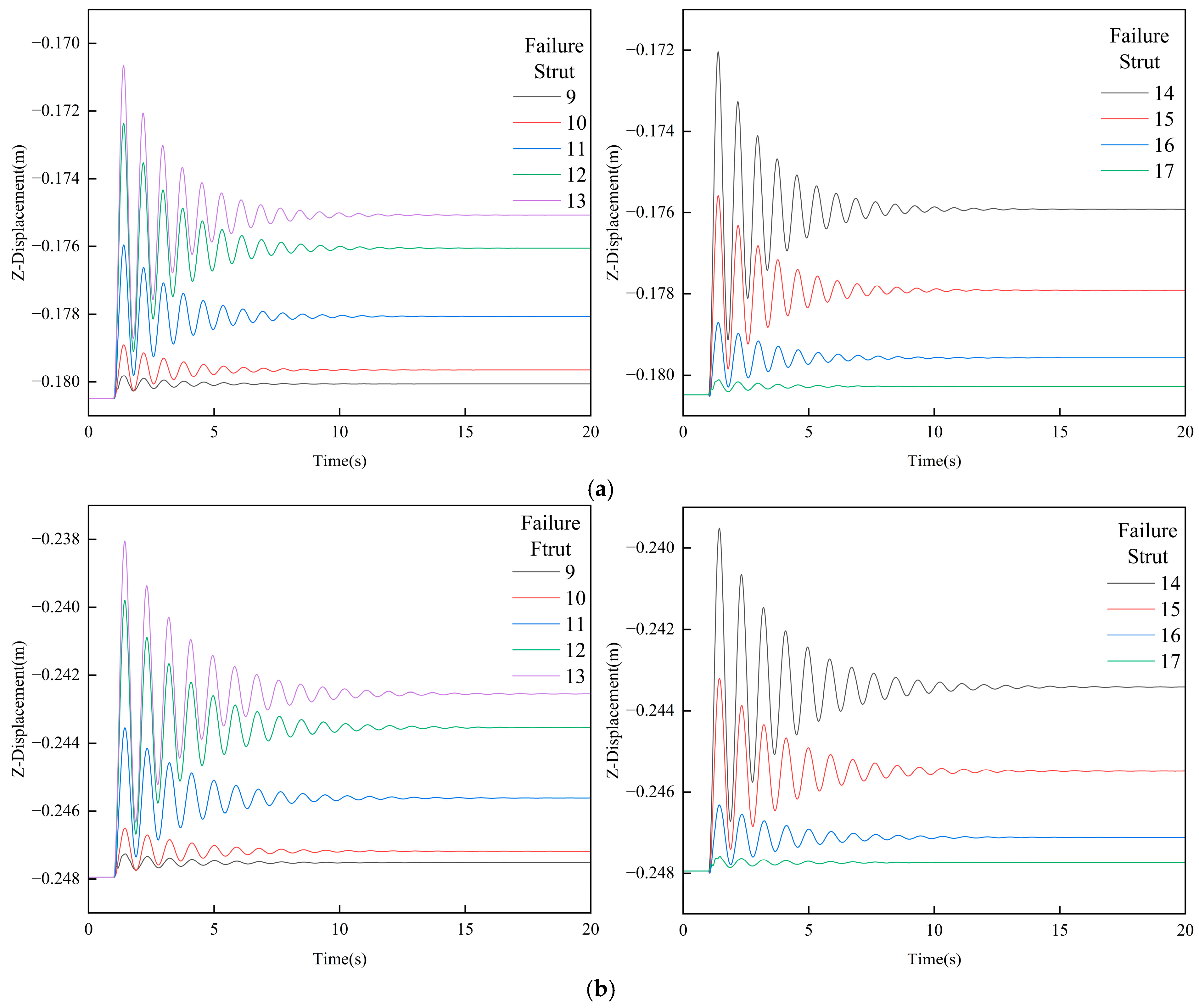
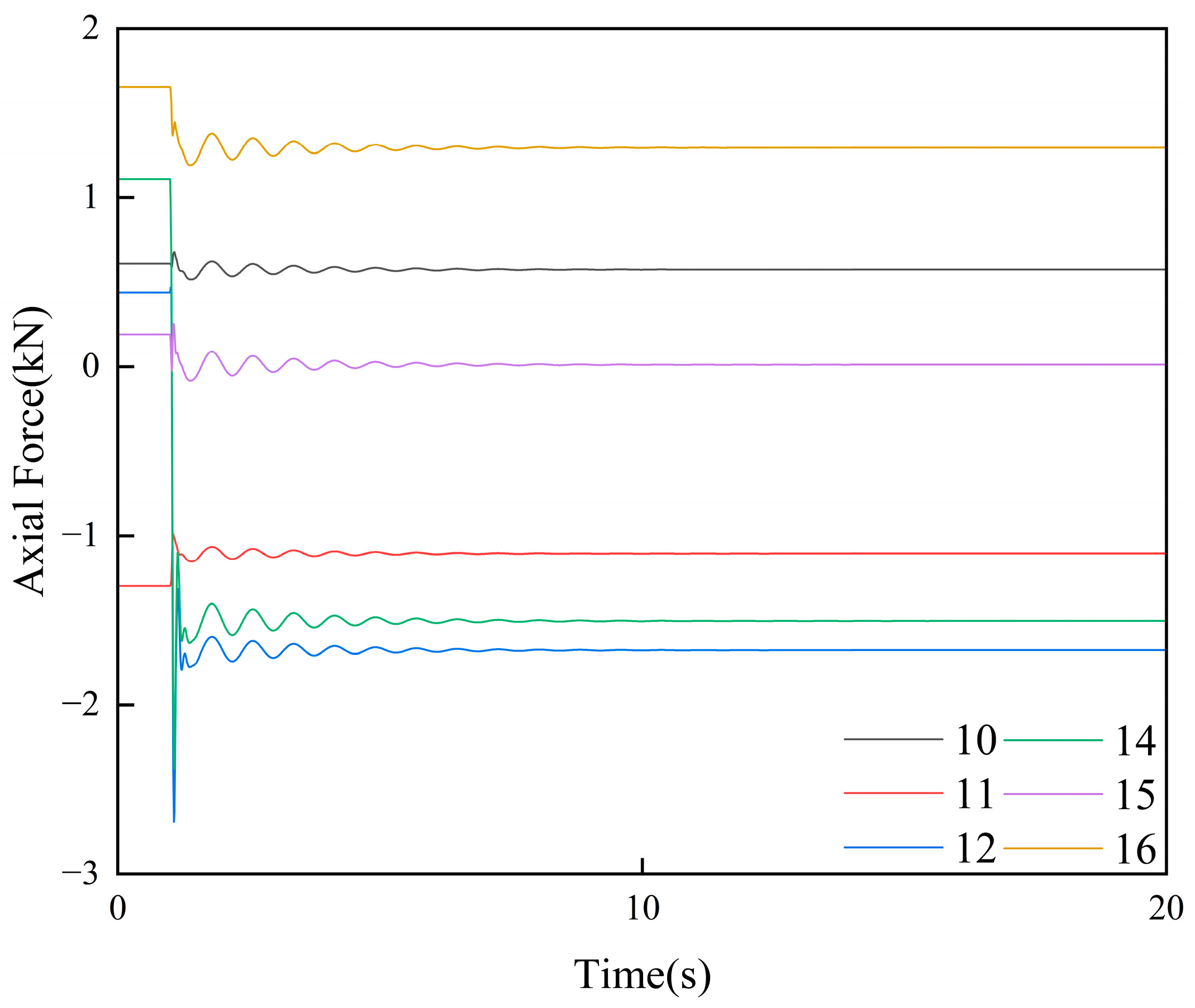
4.4. Strut Failure
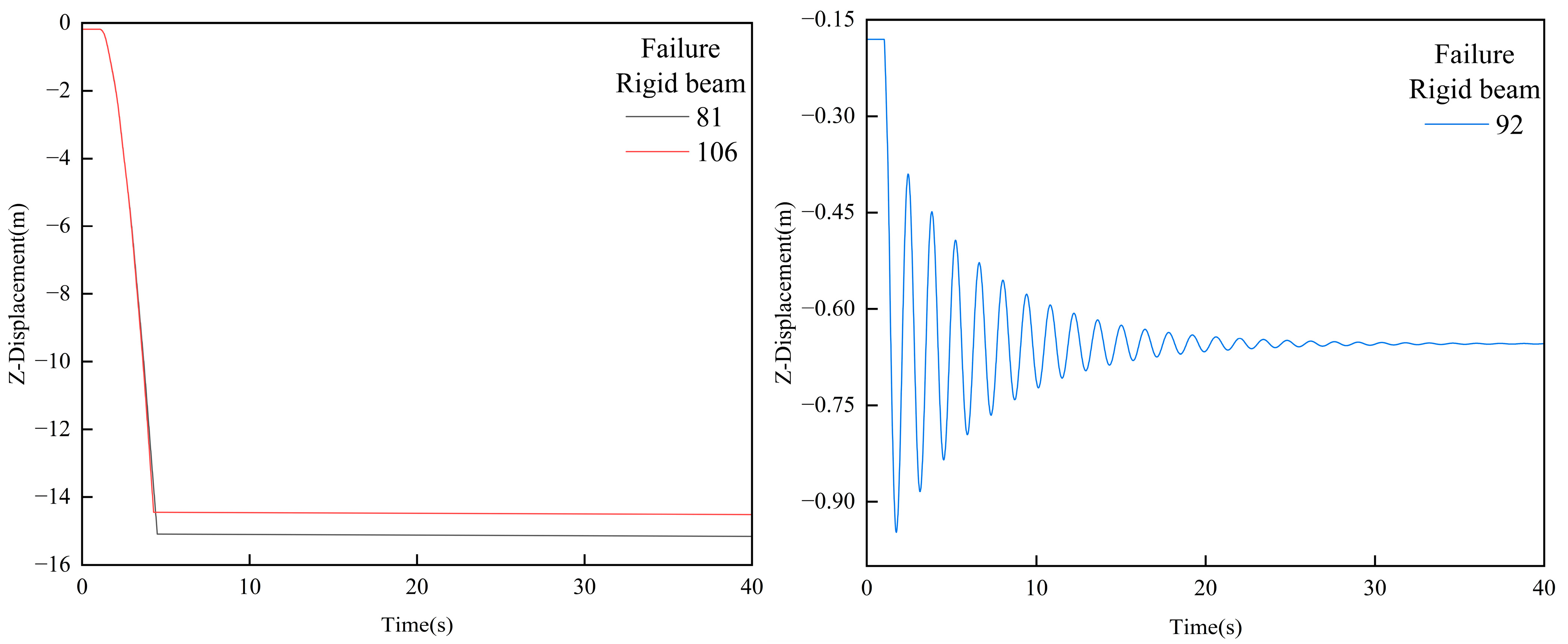
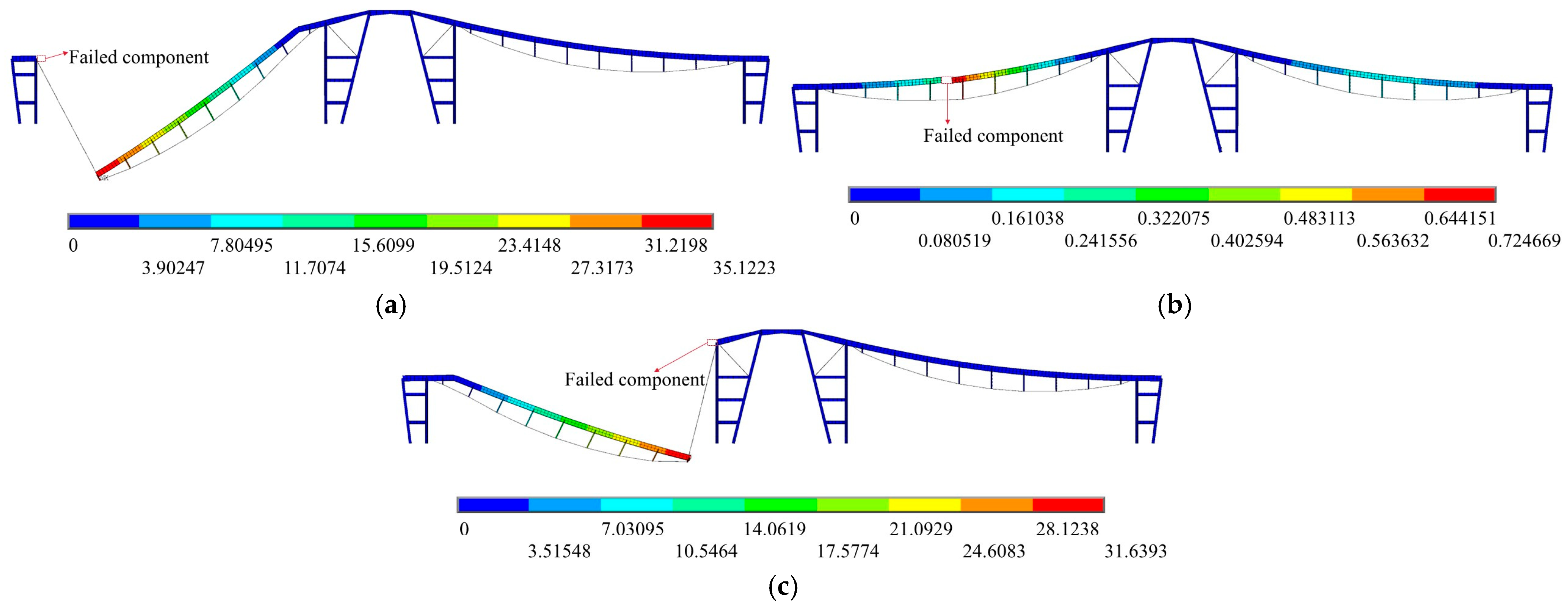
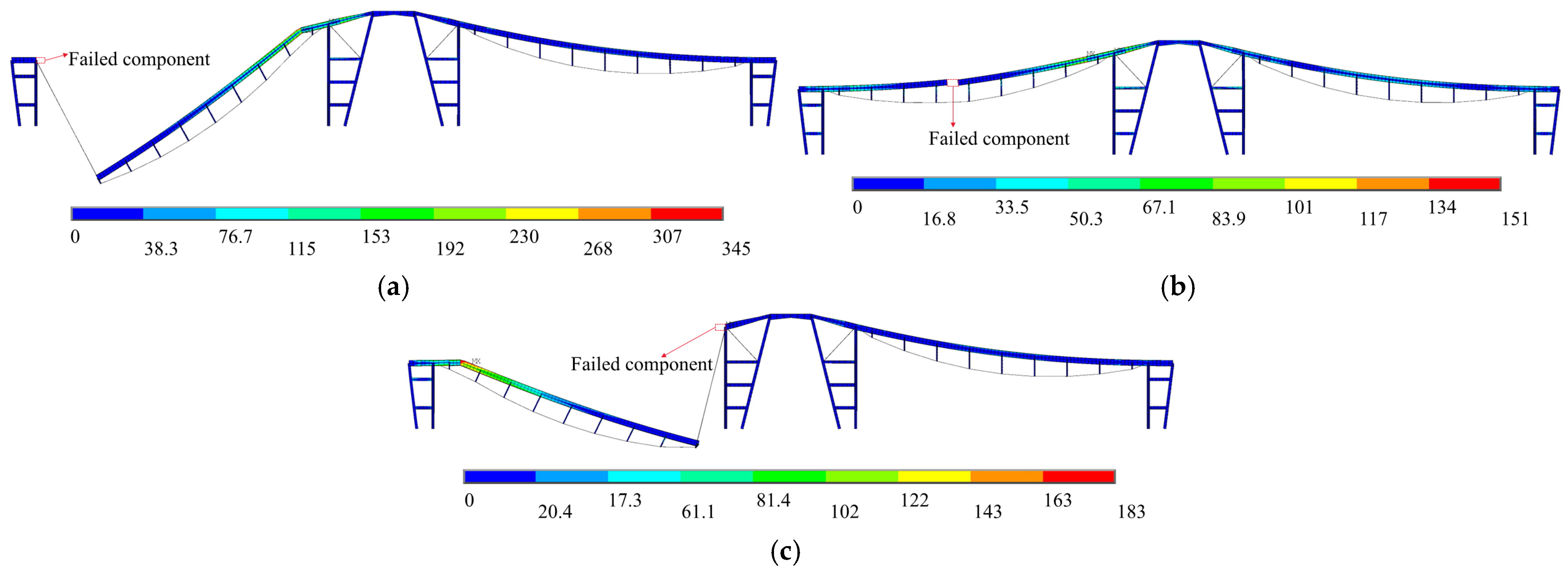
4.5. Upper Beam Failure
4.6. Internal Force Redistribution
4.6.1. Column End Failure
4.6.2. Column Base Failure
4.6.3. Strut Failure
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nair, R.S. Progressive collapse basics. In Proceedings of the Steel Building Symposium: Blast and Progressive Collapse Resistance, New York, NY, USA, 4–5 December 2003; American Institute of Steel Construction: Chicago, IL, USA, 2003; pp. 1–11. [Google Scholar]
- Kiakojouri, F.; De Biagi, V.; Chiaia, B.; Sheidaii, M.R. Progressive collapse of framed building structures: Current knowledge and future prospects. Eng. Struct. 2020, 206, 110061. [Google Scholar] [CrossRef]
- Adam, J.M.; Parisi, F.; Sagaseta, J.; Lu, X. Research and practice on progressive collapse and robustness of building structures in the 21st century. Eng. Struct. 2018, 173, 122–149. [Google Scholar] [CrossRef]
- Zhao, X.; Yan, S.; Xu, Z.; Wu, A. Research and application of beam string structures. Struct. Eng. Int. 2015, 25, 26–33. [Google Scholar] [CrossRef]
- Adam, J.M.; Buitrago, M.; Bertolesi, E.; Sagaseta, J.; Moragues, J.J. Dynamic performance of a real-scale reinforced concrete building test under a corner-column failure scenario. Eng. Struct. 2020, 210, 110414. [Google Scholar] [CrossRef]
- Buitrago, M.; Sagaseta, J.; Adam, M.J. Effects of sudden failure of shoring elements in concrete building structures under construction. Eng. Struct. 2018, 172, 508–522. [Google Scholar] [CrossRef]
- Buitrago, M.; Setiawan, A.; Makoond, N.; Gerbaudo, M.L.; Marin, L.; Cetina, D.; Caredda, G.; Sempertegui, G.; Oliver, M.; Adam, J.M. Failure analysis after the progressive collapse of a precast building. Eng. Struct. 2024, 321, 118893. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, X.; Li, Y.; Guan, H.; Diao, M.; Gilbert, B.P.; Sun, H. Real collapse responses of an RC flat plate structure under extreme overloading condition: Reversing load redistribution. Eng. Struct. 2025, 322, 119120. [Google Scholar] [CrossRef]
- Jin, Y.; Yu, X.; Li, B. Probabilistic assessment of progressive collapse resistance in RC slab-incorporated frame structures: Accounting for slab effects. J. Build. Eng. 2025, 103, 112119. [Google Scholar] [CrossRef]
- Zhao, Z.; Guan, H.; Li, Y.; Xue, H.; Gilbert, B.P. Collapse-resistant mechanisms induced by various perimeter column damage scenarios in RC flat plate structures. Structures 2024, 59, 105716. [Google Scholar] [CrossRef]
- Pang, B.; Wang, F.; Yang, J.; Nyunn, S.; Azim, I. Performance of slabs in reinforced concrete structures to resist progressive collapse. Structures 2021, 33, 4843–4856. [Google Scholar] [CrossRef]
- Agarwal, A.; Varma, H.A. Fire induced progressive collapse of steel building structures: The role of interior gravity columns. Eng. Struct. 2014, 58, 129–140. [Google Scholar] [CrossRef]
- Lan, D.; Jin, L.; Yang, Y.; Qian, K.; Zhang, R.; Li, J. Progressive collapse behavior of geometrically similar RC frames at ambient and elevated temperatures. Fire Saf. J. 2025, 152, 104325. [Google Scholar] [CrossRef]
- Zhu, Y.F.; Chen, C.H.; Huang, Y.; Huang, Z.H.; Yao, Y.; Keer, L.M. Dynamic progressive collapse of steel moment frames under different fire scenarios. J. Constr. Steel Res. 2020, 173, 106256. [Google Scholar] [CrossRef]
- Nan, Z.; Dai, X.; Chen, H.; Welch, S.; Usmani, A. A numerical investigation of 3D structural behaviour for steel-composite structures under various travelling fire scenarios. Eng. Struct. 2022, 267, 114587. [Google Scholar] [CrossRef]
- Lan, D.Q.; Jin, L.; Qian, K.; Zhang, R.B.; Li, J. Progressive collapse resistance of RC frames subjected to localized fire. J. Build. Eng. 2023, 79, 107746. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, M.; Zhou, M.; Chen, J. Dynamic Reliability Analysis of Nonlinear Structures Using a Duffing-System-Based Equivalent Nonlinear System Method. Int. J. Approx. Reason. 2020, 126, 84–97. [Google Scholar] [CrossRef]
- Kabando, E.K.; Gong, J. An overview of long-span spatial grid structures failure case studies. Asian J. Civ. Eng. 2019, 20, 1137–1152. [Google Scholar] [CrossRef]
- Pellecchia, C.; Cardoni, A.; Cimellaro, G.P.; Domaneschi, M.; Ansari, F.; Khalil, A.A. Progressive collapse analysis of the Champlain Towers South in Surfside, Florida. J. Struct. Eng. 2024, 150, 04023211. [Google Scholar] [CrossRef]
- Park, W.T. Inspection of collapse cause of Sampoong Department Store. Forensic Sci. Int. 2012, 217, 119–126. [Google Scholar] [CrossRef]
- Ahmadi, M.T.; Aghakouchak, A.A.; Mirghaderi, R.; Tahouni, S.; Garivani, S.; Shahmari, A.; Epackachi, S. Collapse of the 16-Story Plasco Building in Tehran due to Fire. Fire Technol. 2020, 56, 769–799. [Google Scholar] [CrossRef]
- Zhang, N.; Luo, B.; Liu, H.; Zhang, M. Prestress self-equilibrium force-finding method for cable-supported grid structures considering zero-stress state form-finding and the construction process. Buildings 2022, 12, 749. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, J.; Wu, X.; Li, N. Progressive collapse behavior of large-span truss string structures subjected to cable failure. KSCE J. Civ. Eng. 2024, 28, 1379–1391. [Google Scholar] [CrossRef]
- Shekastehband, B.; Abedi, K. Collapse behavior of tensegrity systems due to cable rupture. Int. J. Struct. Stab. Dyn. 2013, 13, 1250079. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Wang, X. Experimental study on collapse behaviour of truss string structures under cable rupture. J. Constr. Steel Res. 2021, 185, 106864. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, B.; Zhou, Z.; Zheng, Y. Theoretical Study on Progressive Collapse of Truss String Structures under Cable Rupture. J. Constr. Steel Res. 2022, 199, 107609. [Google Scholar] [CrossRef]
- Xu, Z.; Zhu, D. Impact of Continuous Cable-Strut Joints on the Anti-Progressive-Collapse Performance of Suspended-Dome Structures. Buildings 2023, 13, 2225. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, H.; Chen, Z.; Zhao, S.; Yang, S.; He, F. Investigation on the mechanical behavior of two-way glulam beam string. J. Build. Eng. 2024, 87, 108931. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, Y.; Adhikari, S.; Yin, Q.; Cai, J. Comparisons of design methods for beam string structure based on reliability and progressive collapse analysis. Structures 2021, 33, 2166–2176. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, P.; Guan, C.; Liu, T.; Kang, W.H.; Feng, P.; Gao, S. An ultra-lightweight CFRP beam-string structure. Compos. Struct. 2020, 257, 113149. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y. Key component capture and safety intelligent analysis of beam string structure based on digital twins. Symmetry 2022, 14, 1152. [Google Scholar] [CrossRef]
- Madan, K.S.; Dutta, S. Free vibration analysis of a laminated composite plate using experimental modal testing. Mater. Today Proc. 2023, 72 Pt 3, 1573–1583. [Google Scholar]
- Liu, G.; Cong, J.; Wang, P.; Du, S.; Wang, L.; Chen, R. Study on vertical vibration and transmission characteristics of railway ballast using impact hammer test. Constr. Build. Mater. 2022, 316, 125898. [Google Scholar] [CrossRef]
- Grosel, J.; Sawicki, W.; Pakos, W. Application of classical and operational modal analysis for examination of engineering structures. Procedia Eng. 2014, 91, 136–141. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, J.; Hu, J.; Xu, J.; Bai, T.; Lai, J.; Wang, P. Nonlinear vibration characteristics of turnout rails: Simulation and advanced nonlinear modal testing. Mech. Syst. Signal Process. 2025, 230, 112623. [Google Scholar] [CrossRef]
- Ahiwale, D.; Madake, H.; Phadtare, N.; Jarande, A.; Jambhale, D. Modal analysis of cracked cantilever beam using ANSYS software. Mater. Today Proc. 2022, 56, 165–170. [Google Scholar] [CrossRef]
- National Research Council Canada. National Building Code of Canada 2020; Canadian Commission on Building and Fire Codes: Ottawa, ON, Canada, 2020. [Google Scholar]
- General Services Administration. PBS-P100: Facilities Standards for the Public Buildings Service; Office of the Chief Architect: Washington, DC, USA, 2023.
- GB 50068-2018; Unified Standard for Reliability Design of Building, Structures; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China. China Architecture & Building Press: Beijing, China, 2018.
- Weng, J.; Tan, K.H.; Lee, C.K. Modeling progressive collapse of 2D reinforced concrete frames subject to column removal scenario. Eng. Struct. 2017, 141, 126–143. [Google Scholar] [CrossRef]
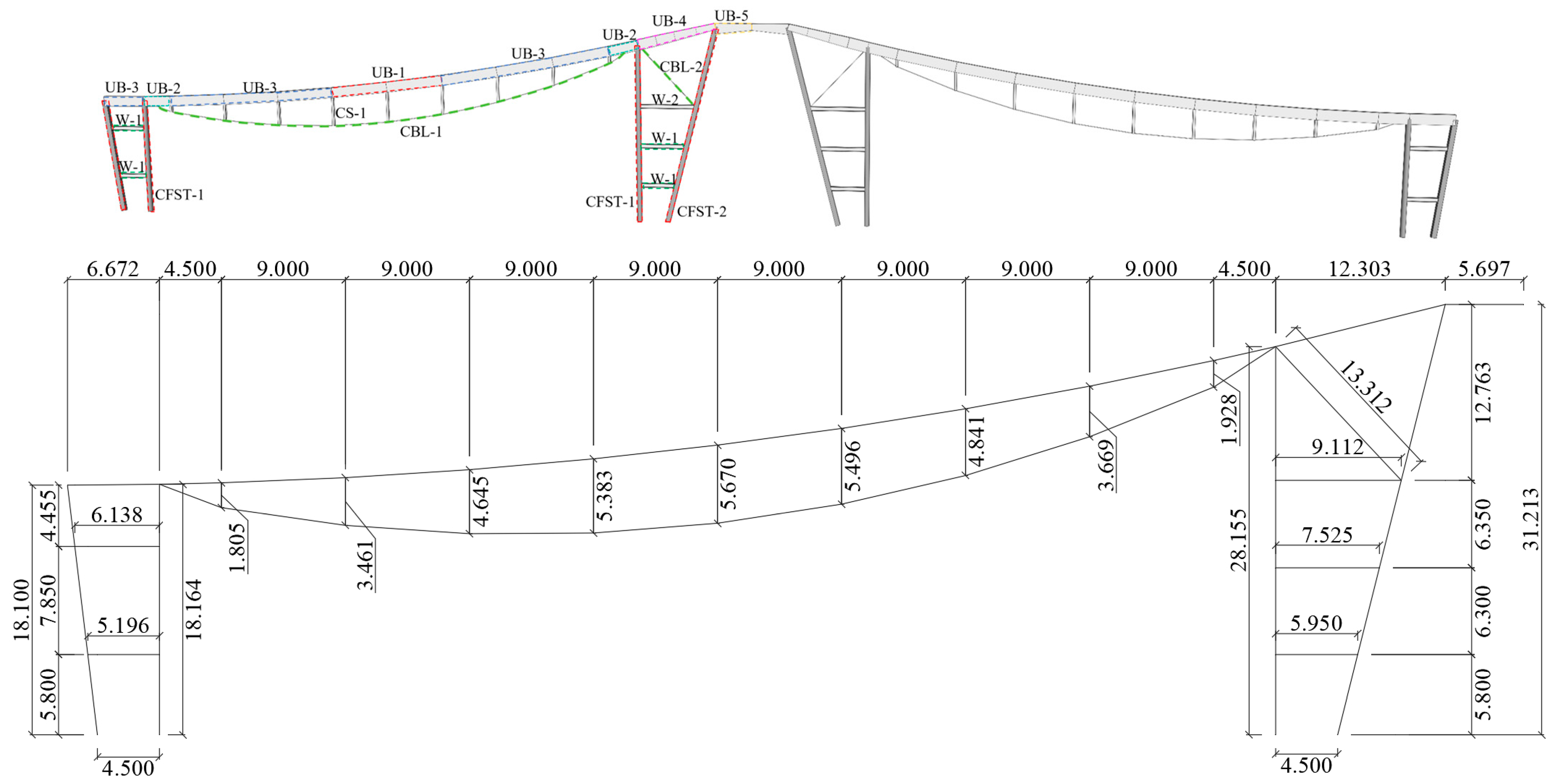















| Serial Number | Section Size (mm) | Serial Number | Section Size (mm) |
|---|---|---|---|
| UB-1 | 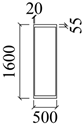 | CS-1 | 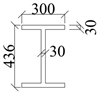 |
| UB-2 | 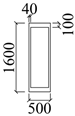 | CFST-1 | 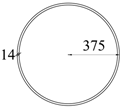 |
| UB-3 | 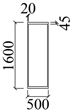 | CFST-2 |  |
| W-1 | 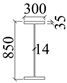 | UB-4 |  |
| W-2 | 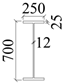 | UB-5 | 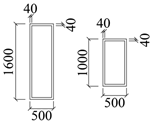 |
| CBL-1 | 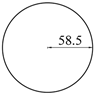 | CBL-2 | 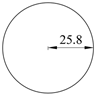 |
| Member | Modulus of Elasticity (Pa) | Poisson’s Ratio | Mass Density (kg/m3) | Yield Strength (MPa) |
|---|---|---|---|---|
| Upper beam | 2.06 × 1011 | 0.3 | 7850 | 345 |
| Cable strut | 2.06 × 1011 | 0.3 | 7850 | 345 |
| Cable | 1.6 × 1011 | 0.3 | 8050 | 1570 |
| Concrete-filled steel tubular column (circular) | 4.3 × 1010 | 0.21 | 3100 | 93 |
| Concrete-filled steel tubular column (square) | 4.3 × 1010 | 0.21 | 3100 | 108 |
| Name | Failure Component Number |
|---|---|
| End column | 3, 6, 21, 25 |
| Column base | 1, 4, 18, 22 |
| Upper beam | 81, 92, 106 |
| Strut | 9, 10, 11, 12, 13, 14, 15, 16, 17 |
| Column End Number | Before Failure (mm) | Maximum Displacement After Failure (mm) | After Failure to Balance (mm) | Maximum Displacement Variation (mm) | Maximum Stress (MPa) | Location of Maximum Stress |
|---|---|---|---|---|---|---|
| 3 | 180.49 | −582.45 | −386.64 | 401.96 | 137 | Beam 8 |
| 6 | 180.49 | −377.21 | −282.29 | 196.73 | 100 | Beam 8 |
| 21 | 180.49 | −571.01 | −378.94 | 390.52 | 206 | Beam 107 |
| 25 | 180.49 | −193.85 | −186.87 | 13.36 | 75 | Beam 107 |
| Column End Number | Before Failure (mm) | Maximum Displacement After Failure (mm) | After Failure to Balance (mm) | Maximum Displacement Variation (mm) | Maximum Stress (MPa) | Location of Maximum Stress |
|---|---|---|---|---|---|---|
| 3 | 247.92 | −760.70 | −509.22 | 512.78 | 168 | Beam 8 |
| 6 | 247.92 | −463.95 | −358.94 | 216.03 | 130 | Beam 107 |
| 21 | 247.92 | −809.89 | −561.21 | 561.97 | 257 | Beam 7 |
| 25 | 247.92 | −292.08 | −268.56 | 44.15 | 201 | Beam 7 |
| Serial Number | γi | γi′ |
|---|---|---|
| 3 | 1.142 | 1.054 |
| 6 | 0.564 | 0.448 |
| 21 | 1.100 | 1.264 |
| 25 | 0.035 | 0.083 |
| Column Base Number | Before Failure (mm) | Maximum Displacement After Failure (mm) | After Failure to Balance (mm) | Maximum Displacement Variation (mm) | Maximum Stress (MPa) | Location of Maximum Stress |
|---|---|---|---|---|---|---|
| 1 | 180.49 | −393.31 | −285.79 | 212.82 | 216 | Beam 7 |
| 4 | 180.49 | −259.44 | −220.02 | 78.95 | 92 | Beam 28 |
| 18 | 180.49 | −271.73 | −224.39 | 91.24 | 183 | Beam 26 |
| 22 | 180.49 | −192.18 | −186.32 | 11.69 | 106 | Beam 28 |
| Column Base Number | Before Failure (mm) | Maximum Displacement After Failure (mm) | After Failure to Balance (mm) | Maximum Displacement Variation (mm) | Maximum Stress (MPa) | Location of Maximum Stress |
|---|---|---|---|---|---|---|
| 1 | 247.92 | −565.25 | −400.84 | 317.33 | 183 | Beam 7 |
| 4 | 247.92 | −396.11 | −320.50 | 148.18 | 139 | Beam 107 |
| 18 | 247.92 | −347.19 | −295.49 | 99.26 | 237 | Beam 26 |
| 22 | 247.92 | −263.51 | −255.67 | 15.59 | 163 | Beam 7 |
| Serial Number | γi | γi′ |
|---|---|---|
| 1 | 0.583 | 0.617 |
| 4 | 0.219 | 0.293 |
| 18 | 0.243 | 0.192 |
| 22 | 0.032 | 0.031 |
| Number of Struts | Before Failure (mm) | Maximum Displacement After Failure (mm) | After Failure to Balance (mm) | Maximum Displacement Variation (mm) | Maximum Stress (MPa) | Location of Maximum Stress |
|---|---|---|---|---|---|---|
| 9 | 180.49 | −179.82 | −180.06 | 0.67 | 183 | Strut 10 |
| 10 | 180.49 | −178.91 | −179.65 | 1.58 | 78 | Beam 28 |
| 11 | 180.49 | −175.96 | −178.06 | 4.53 | 73 | Beam 28 |
| 12 | 180.49 | −172.36 | −176.05 | 8.13 | 78 | Beam 28 |
| 13 | 180.49 | −170.66 | −175.08 | 9.83 | 73 | Beam 28 |
| 14 | 180.49 | −172.04 | −175.92 | 8.45 | 73 | Beam 28 |
| 15 | 180.49 | −175.58 | −177.91 | 4.91 | 73 | Beam 28 |
| 16 | 180.49 | −178.70 | −179.57 | 1.78 | 78 | Beam 28 |
| 17 | 180.49 | −180.12 | −180.28 | 0.37 | 184 | Strut 16 |
| Number of Struts | Before Failure (mm) | Maximum Displacement After Failure (mm) | After Failure to Balance (mm) | Maximum Displacement Variation (mm) | Maximum Stress (MPa) | Location of Maximum Stress |
|---|---|---|---|---|---|---|
| 9 | 247.92 | −247.26 | −247.52 | 0.66 | 199 | Strut 10 |
| 10 | 247.92 | −246.51 | −247.18 | 1.42 | 159 | Beam 7 |
| 11 | 247.92 | −243.54 | −245.61 | 4.38 | 159 | Beam 7 |
| 12 | 247.92 | −239.80 | −243.54 | 8.13 | 159 | Beam 7 |
| 13 | 247.92 | −238.05 | −242.54 | 9.88 | 159 | Beam 7 |
| 14 | 247.92 | −239.51 | −243.42 | 8.42 | 159 | Beam 7 |
| 15 | 247.92 | −243.21 | −245.48 | 4.72 | 160 | Beam 7 |
| 16 | 247.92 | −246.32 | −247.12 | 1.61 | 160 | Beam 7 |
| 17 | 247.92 | −247.59 | −247.74 | 0.34 | 197 | Strut 16 |
| Serial Number | γi | γi′ |
|---|---|---|
| 9 | 0.002 | 0.002 |
| 10 | 0.005 | 0.003 |
| 11 | 0.013 | 0.009 |
| 12 | 0.025 | 0.018 |
| 13 | 0.030 | 0.022 |
| 14 | 0.025 | 0.018 |
| 15 | 0.014 | 0.010 |
| 16 | 0.005 | 0.003 |
| 17 | 0.001 | 0.001 |
| Upper Beam Number | Before Failure (mm) | Maximum Displacement After failure (mm) | After Failure to Balance (mm) | Maximum Displacement Variation (mm) | Maximum Stress (MPa) | Location of Maximum Stress | γi |
|---|---|---|---|---|---|---|---|
| 81 | 180.49 | 345 | Beam 104 | ||||
| 92 | 180.49 | −947.48 | −653.99 | 766.99 | 151 | Beam 104 | 2.623 |
| 106 | 180.49 | 349 | Beam 83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, M.; Zhou, Z.; Xu, X.; Wang, F. Structural Robustness Analysis of Reverse Arch Beam String-Inclined Column Structure. Buildings 2025, 15, 3556. https://doi.org/10.3390/buildings15193556
Wang S, Wang M, Zhou Z, Xu X, Wang F. Structural Robustness Analysis of Reverse Arch Beam String-Inclined Column Structure. Buildings. 2025; 15(19):3556. https://doi.org/10.3390/buildings15193556
Chicago/Turabian StyleWang, Sheng, Ming Wang, Zhixuan Zhou, Xiaotong Xu, and Fuming Wang. 2025. "Structural Robustness Analysis of Reverse Arch Beam String-Inclined Column Structure" Buildings 15, no. 19: 3556. https://doi.org/10.3390/buildings15193556
APA StyleWang, S., Wang, M., Zhou, Z., Xu, X., & Wang, F. (2025). Structural Robustness Analysis of Reverse Arch Beam String-Inclined Column Structure. Buildings, 15(19), 3556. https://doi.org/10.3390/buildings15193556







