1. Introduction
The relationship between the physical form of cities and the social dynamics that develop within them constitutes a central intention that spans centuries of urban design practices. Throughout history, architects and urbanists have sought to facilitate or even determine behaviors and social interactions through the design of urban space. When proposing an urban intervention, what is desired? To improve the performance of a specific activity? To make it more comfortable? To affect traffic? To make a space more beautiful, more distinctive, more universal? Are these architectural adaptations of urban space, modifications of activities that compose the city, or interventions in urban dynamics? And what is the urban-society relation?
In Readings in Planning Theory, Fainstein and Campbell [
1] remark on the difficulty of defining, delimiting, and even identifying a proper and consistent theoretical framework for urbanism. The discipline, due to its complex and multidisciplinary nature, touches, borrows, and adopts theories or fragments of theories and methodologies from various related and neighboring disciplines, such as economics, politics, social sciences, and geography. However, an urban theory with clear and proper axioms remains elusive. Authors relatively distant in time, such as Bailly [
2] and Rashid [
3], also discuss this, pointing to an insufficiency of commonly used epistemologies and suggesting the need for a theoretical body able to encompass the myriad of information and phenomena that are contributing to and occurring in the city [
4].
This paper reports on a work where we tried to address a particular dimension of this complex relationship: how the geometry of urban space, understood as the spatial distribution of places and the configuration of urban fabric, interferes with the topology of networks formed by daily encounters between inhabitants. We also had to address the inherent difficulties of building knowledge about urban phenomena, due to questions of scale in time and sheer number of information involved, besides the costs that could come from any sort of experiment in real life. Understanding these dynamics becomes essential for developing more effective urban policies and for planning cities that effectively promote social cohesion and quality of life.
Starting from complexity theory as our epistemological foundation, we understand that the city is an organism that functions at a level of complexity different from ours, operating at various scales and with a diversity of variables. We, as people, are to the city what organs and cells are to the human body. From this perspective, all systems form and are formed by networks of information exchange, whether this information is material, knowledge, culture, products, or energy. The city, therefore, is formed by networks of exchanges between people, companies, institutions, and other organizations that compose social complexity. These interactions are described through Complex Adaptive Systems (CASs) and have been approached this way by groups such as those led by Karakiewicz [
5], West [
6], Weinstock [
7], and Batty [
8], for example [
9,
10].
Within this CAS framework, an initial fundamental distinction was adopted between two interrelated but analytically separable dimensions: the geometry–city, characterized by the geometric configuration of built space, its streets, blocks, squares, and buildings, and the network–city, constituted by social interactions, encounter networks, information exchanges, and relationships established between people, institutions, and organizations in the urban fabric. We considered the network–city as the subsystem that encompasses urban dynamics—it is the social phenomenon, the interaction between people and their organizations, with all cultural, economic, religious, political, and material aspects. And the geometry–city is the materialization of the city, the adaptation of physical space, built to facilitate and enhance these activities and social interactions, a response to the need for spatiality to take place.
This distinction does not imply an absolute ontological separation between these dimensions, but rather an analytical resource that allows investigating how one dimension may influence the other. The following rationale is about this relationship of mutual influence: physical space is obviously constructed by society, but in what way does it interfere back with it, more specifically: does the geometry–city interfere with the network–city that shapes it? We then came up with a hypothesis postulating that the geometry of urban space does not significantly alter the topology of the social encounter network formed in inhabitants’ daily lives. We found this counterintuitive proposition more prone to help build an experiment able to stretch concepts and find a point of rupture.
To test this hypothesis and respond to the practical difficulties of conducting controlled experiments in real urban contexts, computer simulations appear as a quite advantageous option, changing the perspective from observation to proposition. A computational simulation would allow modeling the problem, i.e., defining the environment and characteristics of the experiment. This methodological approach allows us to simplify the multiplicity of variables at play and the temporal scales involved, building only the characteristics desired to be observed and bringing the events to an observable time scale. Also, as modeling is at its core, it is a propositional experiment, in the sense that modeling is a description of how one thinks something works, not exactly of how something actually works. As a proposed theoretical phenomenon, it must later be validated or discarded after real-world observations.
The developed simulator generates a map, the geometry–city, based on arbitrary geometry. Then it operates a population of agents that commute between daily activities, developing into the network–city. Here, a first reformulation of the model was needed. Just population and geometry are not enough to minimally describe our simplified city model, as well as a tier of activities. A resulting three-fold model was formulated, with network–city, geometry–city, and activity–city. The activity–city describes the activities the population commutes between and is mapped into the geometry–city. Several simulations of the population commutes were run with systematic variation of the geometry of maps and of the spatial distribution method of activities. This gave us enough diversity of scenarios to differentiate the resulting topologies of the network–city.
1.1. Theoretical Foundation
1.1.1. City as Complex System
Understanding cities as a complex system represents a paradigm shift in relation to traditional approaches to urbanism, which frequently treated the urban phenomena in a linear or mechanistic way. Complexity theory, developed from the work of researchers such as Ilya Prigogine [
11] and others, offers conceptual tools to understand systems as emergent properties arising from interactions between a set of elements, a result of behaviors generated by the collective that are not present in isolated components.
Considering the city as a CAS implies understanding that it emerges from the various levels of organization and interaction of the subsystems of which it is composed [
12]. This means a continuous interaction of the system (the city) with the dynamics of the environment and other systems, eventually internalizing these relationships in reorganizations of the subsystems that comprise it. In this process, subsystems emerge and disappear, and the connections and hierarchies between them, their quantity, and balance change. This same system causes modifications in the environment in an attempt to better maintain its homeostasis, sometimes through the allopoietic production of systems.
More concretely, it is understanding cities as emerging from their organizations, businesses, neighborhood associations, political groups, and families, aspects addressed by studies of social movements, decision-making strategies, and participatory projects. All are adapting to political, cultural, and economic changes. All these organizations, the society, and the city, ultimately emerge from individual behaviors and interactions, each at its level of complexity.
The systemic composition of a set of systems, or subsystems, is very helpful in our cause. A realistic approach would have to describe each present subsystem; however, they can also be combined in sets in a way that can be described by functions. A simplified description is helpful to understand specific relations in an isolated manner, not losing sight, however, of the bigger and more complex picture. Also, it is implied that one can describe the behavior of the systems on the set and then observe the result from their interaction. Such as to, for example, describe the systems you know about, and then observe the systems that emerge from their resulting behavior that you do not know about.
Our description of the system city resulting from the subsystems geometry–city, activity–city, and network–city, central to our investigation, finds its conceptual foundation in this theoretical framework. The geometry–city pair can be understood as the material substrate where interactions occur, providing possibilities and constraints for movements and encounters. The activity–city pair contains the activities that take place in the city and are exercised by the population, and is distributed, mapped into the geometry–city. The network–city, in turn, emerges as the population fulfills their daily routines executing their functions (jobs…) in the interaction with the other two subsystems, geometry–city and activity–city.
1.1.2. Network Theory and Topological Analysis
Network theory provides the fundamental methodological framework for analyzing relational structures that emerge from urban social interactions. Its foundations go back to Leonhard Euler’s pioneering work on the Königsberg bridge problem in 1736, which established the basic principles of graph theory by mathematically demonstrating the impossibility of traversing all the bridges of the Prussian city only once and returning to the starting point.
This seminal work established the crucial difference between geometric properties and topological properties of a system. While geometry deals with measures such as distances, angles, and areas in a Euclidean manner, topology focuses on relationships, connectivity, and flows. In our approach to the urban context, this distinction is fundamental: it could be possible for two cities to have completely different geometries and present similar topologies.
Later developments in network theory, particularly from the 1950s, established typologies and metrics that allow characterizing different types of relational structures. The work of Paul Erdős and Alfréd Rényi, developed throughout the 1950s and consolidated in 1959 [
13], provided the first rigorous mathematical model for random networks, where connections between nodes are established according to uniform probabilities. This model serves as a reference for comparison with networks that present specific structures.
The concept of “small worlds”, theorized by Stanley Milgram in his experiments of the 1960s and mathematically formalized by Duncan Watts and Steven Strogatz [
14] in the 1990s, revealed that many real networks combine apparently contradictory characteristics: high local clustering, where nodes tend to form densely connected groups, simultaneously with short paths between any two nodes of the network. This property is particularly relevant for urban social networks, where people tend to form close social groups while maintaining connections that cross different social circles.
Mark Granovetter’s contribution on “weak ties” [
15] provides crucial insights for urban social networks and lasted well into the 1990s as a milestone. Granovetter demonstrated that less intense connections are fundamental for information transmission between distinct social groups, functioning as bridges between clusters that would otherwise remain isolated. In the urban context, casual encounters may have a more important role in general social cohesion than intense but restricted relationships.
In the late 1990s, studying the internet and other databases, Albert-László Barabási and Réka Albert [
16] identified that these networks exhibited this characteristic of scale-free distribution and followed a power law function. The model became known as the Barabási–Albert model and describes networks whose growth occurs through preferential connection, which typically exhibit this scale-free distribution. It is so named because at any interval of the power function, it presents the same probability distribution of connections, as evident by the sloping line of the logarithmic scale.
For our analysis of urban encounter networks, some metrics can capture structural properties relevant to information diffusion and social cohesion. The average degree indicates basic relational density of the network; it shows the average of how many connections each knot has. The clustering coefficient measures the tendency for densely connected group formation. Network diameter indicates how many steps are necessary for information to traverse the entire network.
The number of connected components reveals whether the network forms a single integrated system or fragments into isolated subsets, a crucial aspect for evaluating social cohesion. Degree distribution characterizes the heterogeneity of connections, indicating whether the network has an egalitarian or hierarchical structure. Finally, the number of triangles or cliques in the network indicates the degree of local interconnection, providing a measure of connection robustness.
1.1.3. Spatial Networks and Urban Dynamics
Applying network theory to the urban context requires specific considerations about the spatial dimension of interactions. Unlike purely abstract networks, urban social networks are embedded in physical space, where geographic distances influence both the probability and cost of encounters and interactions [
17].
Marc Barthélémy, in his work on spatial networks [
18], developed specific theoretical frameworks for networks where the geometry of underlying space influences the formation and evolution of connections. In the urban context, this means recognizing that physical distance may translate into a cost and play a significant role. As such, the probability of encountering between two people is influenced not only by their social characteristics or individual preferences, but also by the physical distance between their places of residence, work, and daily activities.
This spatial dimension of urban networks introduces additional complexities in analysis. The overlap between the geometry of physical space and the topology of social networks can generate non-linear effects, where small changes in spatial configuration result in significant alterations in social connectivity patterns [
19,
20,
21].
Michael Batty, in “The New Science of Cities” [
8], argues that cities can be understood as networks at multiple scales, from physical infrastructure networks to networks of economic and social flows. This multi-scalar perspective is fundamental for our investigation, as it suggests that the relationship between geometry–city and network–city may manifest differently at different scales of analysis.
2. Materials and Methods
2.1. Limitations of Empirical Observation and Justification for Simulations
Empirical investigation of the relationship between urban spatial configuration and social network formation faces significant methodological challenges that motivated our choice for computational simulations. The first challenge refers to the temporal scale of urban phenomena. Changes in the physical configuration of cities occur on scales of decades, while effects on social networks may manifest over a few years. Direct observation of these phenomena would require long-term studies with control of multiple variables, which is very overwhelming and time-demanding, probably demanding coordination across generations.
The second challenge relates to the near impossibility of controlled experiments in real urban contexts. Ethical and practical reasons, like costs, tend to make it impossible to experimentally alter the configuration of existing cities to observe their effects. Comparative studies between different cities, although valuable, face the herculean problem of multiplicity of variables that make it difficult to observe one city, let alone cities enough to build a proper corpus to analyze. The third challenge refers to the complexity of observing urban social networks themselves. Systematically mapping daily encounters of a significant urban population would be logistically complex and invasive of individuals’ privacy.
Computational simulations offer a methodological alternative that allows circumventing these limitations. Through computational models, it is possible to precisely control variables of interest, systematically manipulate spatial configurations, and observe resulting effects on compressed temporal scales. Although they introduce the question of representation validity, simulations allow a systematic exploration of the logical implications of different theoretical assumptions about the relationship between space and society.
In various disciplines, computational simulations have been used as alternatives to experimentation. Using simulations, Wolfram [
22] presents the capacity of cellular automata to represent an infinity of agent behaviors based on neighborhood states, and Holland [
23] shows how spatial segregation of groups is expected when elements possess some degree of similarity preference and their distribution in space is not homogeneous.
2.2. Development of the Redinha Simulator
Our simulator, nicknamed Redinha (small net in Portuguese), was developed on the Unity platform, using C# programming language in the Visual Studio development environment. The choice of Unity platform was based on its capacity to integrate 2D/3D visual representations with agent-based simulations, offering flexibility for future developments that incorporate gamification [
24] elements or interactive interfaces for educational purposes.
The simulator architecture is based on object-oriented programming, a structure that naturally adapts to agent-based modeling (ABM). The system operates with four object classes: agents (representing people), activities (distributed in houses and jobs), places (spatial locations), and the encounter network (represented by an adjacency matrix).
Agent-based modeling was chosen for its adequacy to represent complex systems and because it is easy to model the known agents while observing the collective behaviors emerge from them. Each agent in the simulator possesses specific properties (house location, job location, displacement routine) and defined behaviors (movement toward destinations, recording encounters with other agents).
2.3. Model Axioms and Representations
Before coding the simulator, it is necessary to model, or describe, the operating principle of the phenomena to observe: the network formation from the encounter of a population of a “city” in their daily routine. Thus, the geometry–city is represented by the geometry of places distribution on a map. The activity–city describes the different activities people have to perform, or attend to, as well as processes of place designation to activities. Finally, the network–city, which is the registering of encounters within a population on their daily routines and agents that circulate on a map, commuting between assigned activities in the simulation.
The modeling of the mechanism that leads to these encounters constitutes the basic axioms of the simulation. It is from exploring the consequences of these axioms that we seek to answer our hypothesis, elaborating a succinct theorem. The starting principles are as follows:
hypothesis: the geometry of the space where people’s routines take place does not change the topology of the encounter network formed between them in their daily lives.
phenomenon: people’s encounters in their daily displacement routine.
For the modeling in the simulator, the following axioms and representations are used:
axioms:
representation:
each person is a node pn in the network;
the network is represented by an adjacency matrix E(pn,pn);
each encounter that happens between pi and pj adds 1 to the edge E(pi,pj);
people’s routine is defined by the displacement cycle between activities, the pair home and work;
activities occupy places on a map;
a map is constituted by places, which are points distributed in space following a determined geometry;
a scenario is composed of a map with objects attributed to places and people attributed to a home–work pair.
It is important to reinforce that this is a conceptual examination, where the mathematical limits are being explored. What is being investigated is the consequence of varying a specific parameter, the geometry of the map, and the question is not statistical, but qualitative in the difference between configurations. Encounters can happen anywhere people are within a specific distance from each other, be on the route to somewhere, or while at some activity. In order to capture just the geometry–city influence, a one-to-one base was established, assigning one activity to one person alone. The scenarios were also designed with this objective, aiming at stretching limits between geometries. In this way, it would be able to point out eventual differences in the resulting network. Our results are consequences of abstract “cities” that nonetheless can point out characteristics and phenomena to be searched for in real-world situations.
2.4. Experimental Configurations
To test the interferences from spatial geometry to social network topology, we developed a systematic set of experimental configurations that allow independently varying two dimensions: the geometry of place distribution and the pattern of activity assignment to these places.
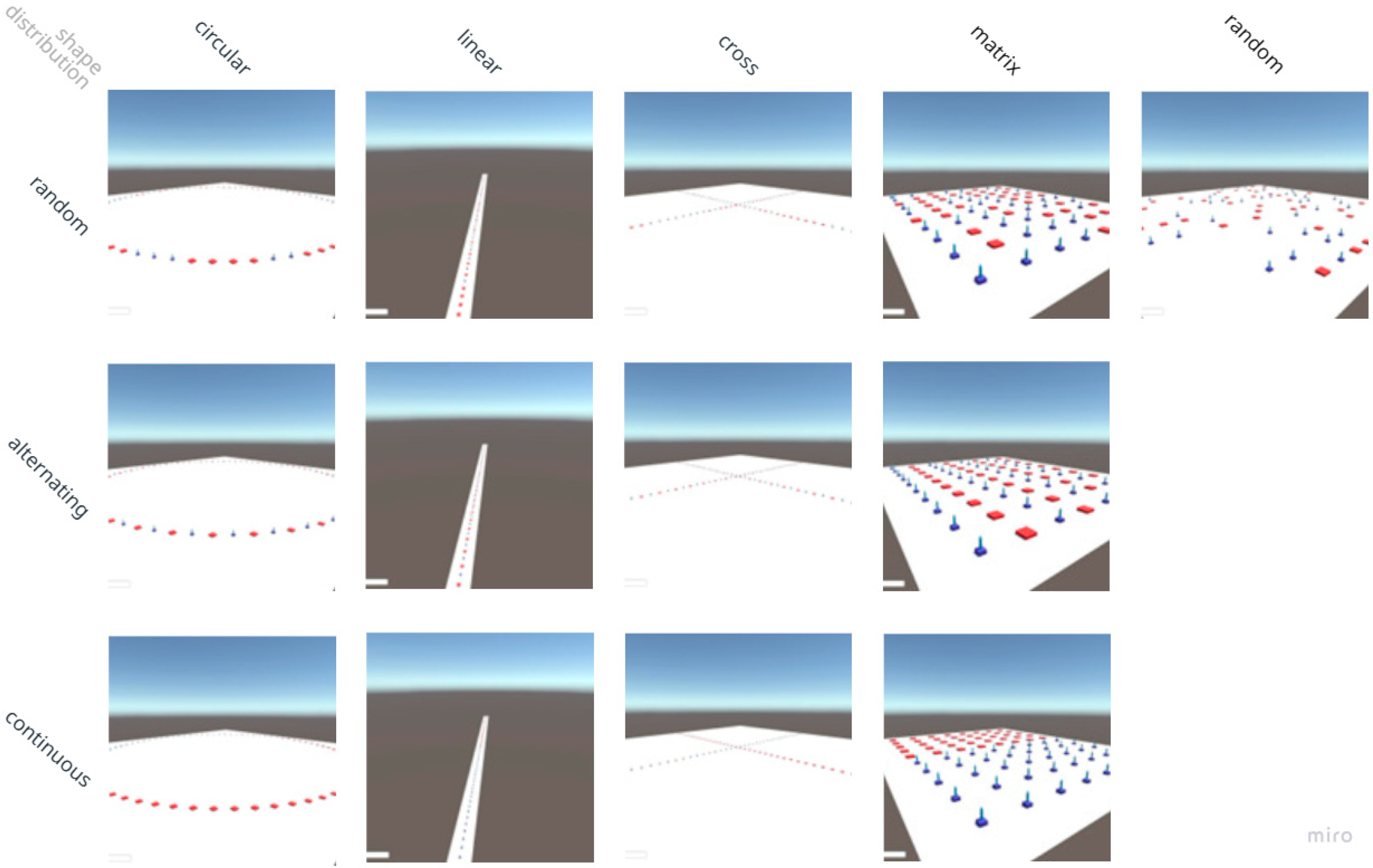
The tested geometries were chosen to maximize topological differences: line (one-dimensional geometry), cross (two-dimensional geometry with axial symmetry), circle (geometry with radial symmetry), matrix (regular two-dimensional geometry), and random point distribution (absence of defined geometric structure) (
Figure 1). These configurations represent everything from highly ordered structures to completely random arrangements, allowing observation of how the degree of spatial structuring affects social network formation.
Activity distribution patterns were conceived to represent different logics of urban organization (
Figure 2). Continuous distribution groups all homes in one region and all jobs in another, creating an analogy with modernist functional zoning that spatially separates different types of urban activities. Alternating distribution positions each person’s house and job as close neighbors, representing the neighborhood unit ideal, where all daily needs are met locally. Random distribution eliminates any specific spatial logic, serving as a control to evaluate the effects of structured patterns.
The combination of these two dimensions generated thirteen distinct experimental configurations. The redundancy of distribution variation over random points (where the placement position is already random) resulted in only one configuration for this geometry, and thus a total of thirteen unique scenarios for analysis (
Figure 3).
Each simulation used forty agents during ten daily cycles; a longer duration would not bring significant variation. The number of agents was limited by available computational capacities, and yet it was enough to show different structural patterns in the resulting networks. During experimental trials, the ten-day period proved enough to enhance any special topological differentiation. Any time longer would be unnecessary.
2.5. Data Collection and Analysis
The collected data consist of adjacency matrices generated by each simulation, recording all encounters occurring between agent pairs. These matrices were exported in CSV format and analyzed in Gephi software, a program specialized in complex network analysis and visualization.
Gephi automatically calculates various topological metrics and generates visualizations that facilitate qualitative interpretation of resulting structures. Calculated metrics include basic properties such as number of nodes and edges, average degree and network density, as well as clustering coefficient, network diameter, number of connected components, and degree distribution.
3. Results
3.1. General Network Formation Patterns
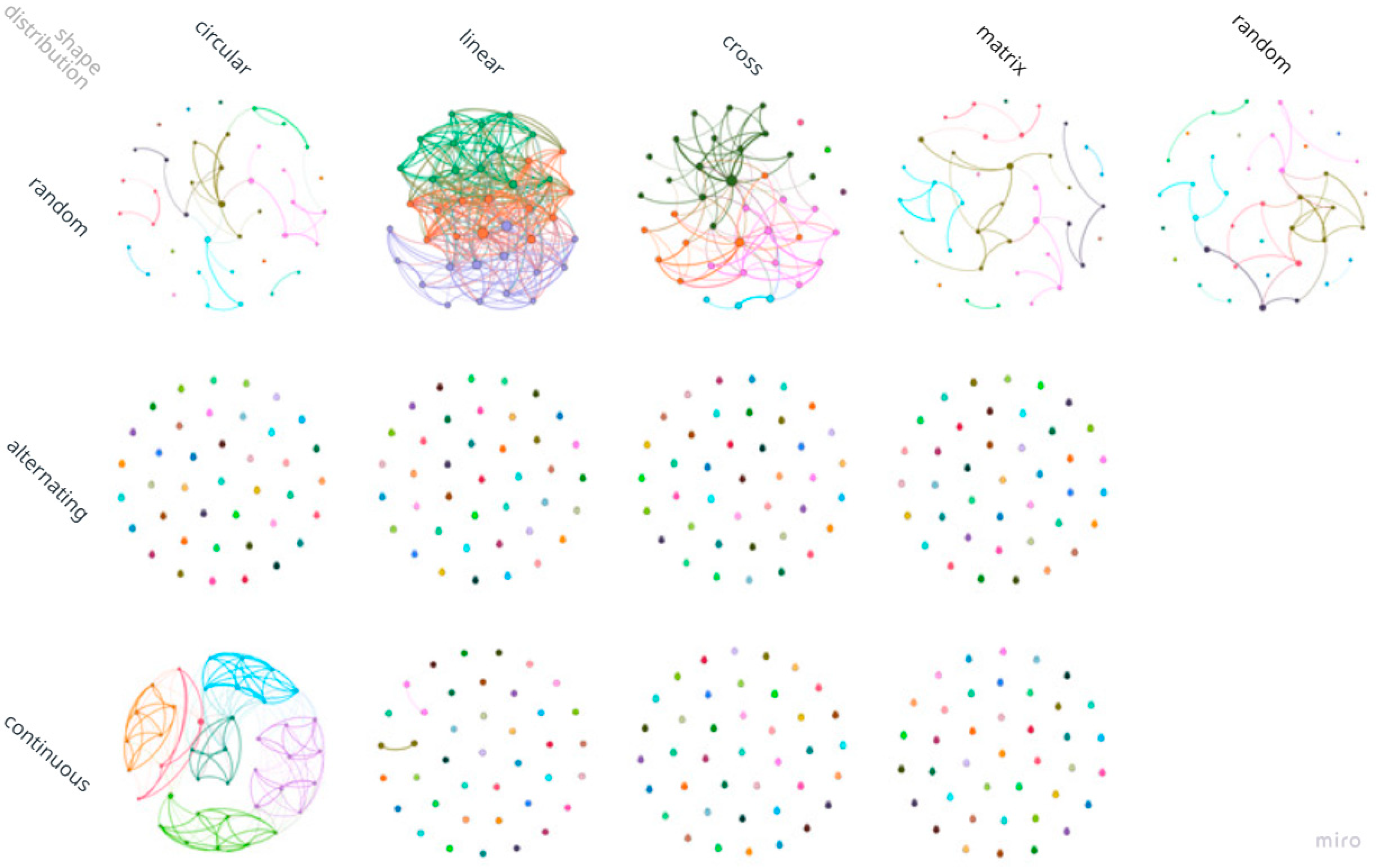
Analysis of the thirteen experimental scenarios revealed surprisingly clear patterns that partially contradict our initial hypothesis. Of the thirteen tested scenarios, only six generated networks with connections between agents. Even more revealing was discovering that network formation or non-formation followed patterns related not to base map geometry, but to activity distribution patterns.
All scenarios that used random activity distribution generated connected networks, regardless of the underlying geometry. This consistency crossed all five tested geometries—line, cross, circle, matrix, and random place distribution—suggesting that random activity distribution creates favorable conditions for encounter network formation independently of underlying spatial structure.
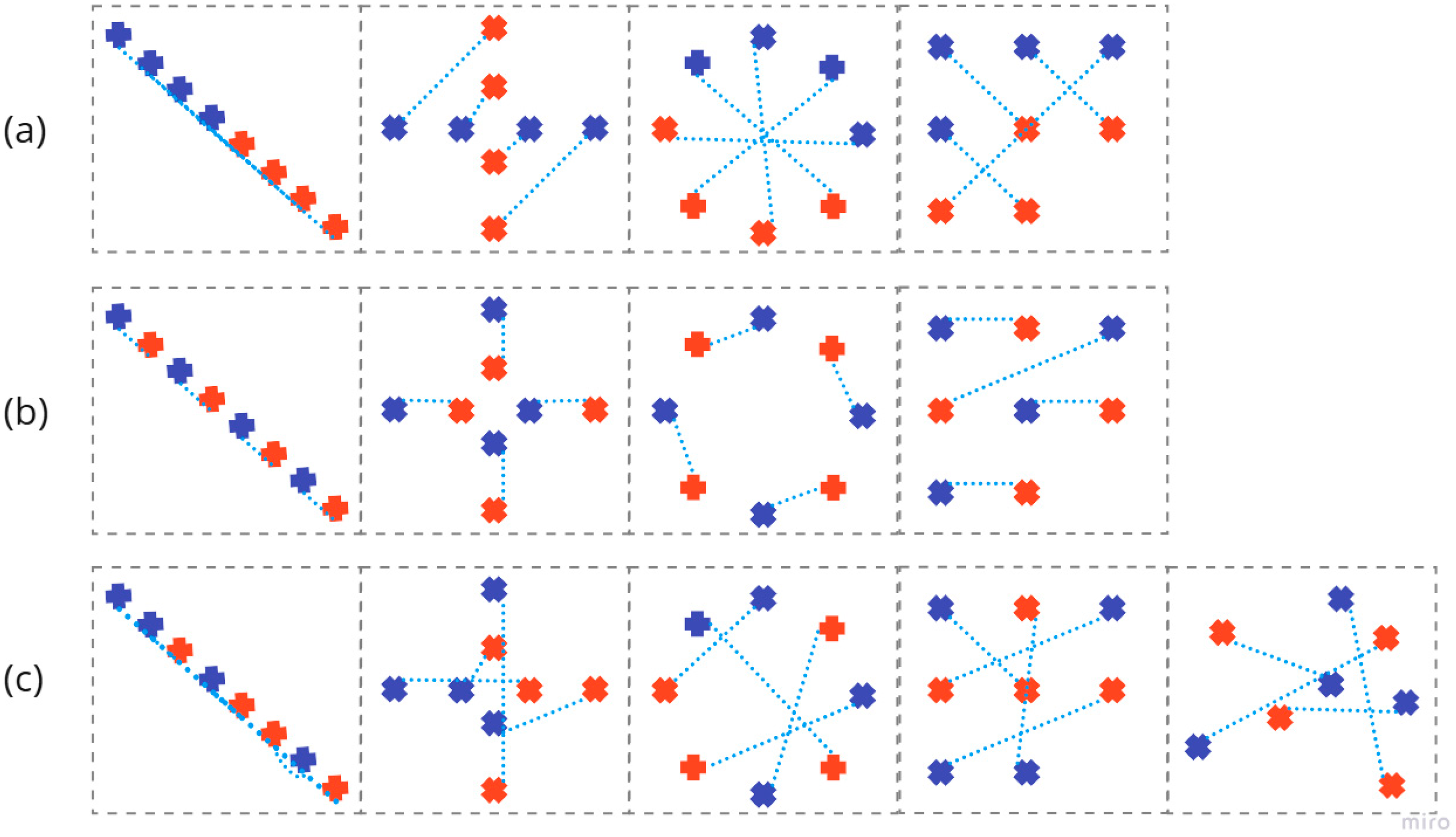
Conversely, the great majority of scenarios with continuous or alternating distributions did not generate significant connections between agents. This absence of connections reflected the fact that these configurations produced movement patterns that practically did not lead to encounters between different agents. Analysis of movement patterns revealed that these distributions tend to generate parallel or very short routes that do not spatially overlap (
Figure 4).
A notable exception to this pattern was the scenario that combined circular geometry with continuous distribution, which generated a densely connected network. This exception proved particularly instructive for understanding the underlying mechanisms of network formation. Its analysis demonstrated how specific characteristics of the combination between geometry and distribution can create special conditions for encounters (
Figure 5).
Configurations that resulted in lower-density networks, with an average degree of around 4, were those where agent routes were distributed over larger spatial areas. This included scenarios of circular, matrix, and random geometry, all with random activity distribution. In these configurations, although sufficient encounters occurred to connect the network, the spatial dispersion of movements limited encounter frequency between specific agent pairs.
Configurations that generated medium-density networks, with an average degree of around 7, were those where the underlying geometry partially channeled routes without forcing complete convergence. The main example was cross geometry with random distribution, where geometric structure created preferential movement corridors that increased encounter probability without completely eliminating spatial dispersion.
High-density networks, with average degrees between 11 and 19, resulted from configurations that forced route convergence in very restricted spatial areas. This included linear geometry with random distribution, where all routes overlapped in the line’s restricted area, and the special case of circular geometry with continuous distribution, where all agents were forced to pass through the circumference center.
3.2. Topological Characteristics of Formed Networks
Topological analysis of formed networks revealed that all presented characteristics were typical of random networks, with degree distributions that tended toward normal form and absence of pronounced hierarchical structures or evidence of preferential connection. This topological similarity between networks generated by very different spatial configurations suggests that, once basic conditions for network formation are established (route overlap), the resulting topology is determined more by the random nature of encounters than by specific geometry.
All networks presented the presence of local clusters, which could suggest that groups of agents with similar movement patterns tend to meet more frequently among themselves. However, pronounced clustering structures that divided networks into clearly separated communities were not observed, suggesting that movement patterns generated by the tested configurations were not sufficient to create significant social segregation.
The absence of scale-free [
16] or preferential connection structures in observed networks reflects specific characteristics of the implemented model, where all agents possess similar behaviors and where no mechanisms exist that systematically favor some agents over others in connection formation. An analysis of the degree distributions of networks formed in simulations reveals patterns consistent with random networks, as expected given the implemented model.
3.3. Network Formation and Non-Formation Mechanisms
Detailed analysis of movement patterns generated by each configuration revealed specific mechanisms through which different spatial arrangements facilitate or prevent network formation (
Figure 3).
Continuous distributions, when applied to line, cross, and matrix geometries, tend to produce parallel or non-overlapping routes. In these configurations, spatial separation between residential zone and work zone results in routes that, although they may be long, are relatively parallel to each other. In alternating distribution scenarios, proximity between each agent’s house and job results in very short routes that rarely extend enough to overlap with other agents’ routes.
Meanwhile, random distributions, regardless of underlying geometry, tend to produce multiple routes overlapping. Randomness in activity location results in routes with varied orientations and extensions, creating multiple overlap opportunities at different points in space. This dispersion of encounter opportunities results in networks with normal distribution connectivity.
We also observed configurations that force route convergence at specific areas. The clearest case is circular geometry with continuous distribution, where activity separation on opposite sides of the circumference forces all agents to pass through the geometric center of the figure. This forced convergence creates an area of extreme encounter density, resulting in highly connected networks where practically all agents meet all others.
4. Discussion
4.1. Hypothesis Reinterpretation in Light of Results
Results obtained through simulations require a reinterpretation of our initial hypothesis. The proposition that urban space geometry does not significantly alter social encounter network topology proves to be simultaneously confirmed and refuted, depending on how “geometry” is interpreted in this context.
If, using geometry, we understand the specific form of place distribution in space—whether linear, circular, matrix, or other—then the hypothesis is largely confirmed. Simulations demonstrated that networks with similar topological characteristics can emerge from completely different underlying geometries, provided basic conditions for route overlap are met. Random networks with similar statistical properties were formed in both linear and circular maps, in both matrix and random distributions.
However, if we expand the geometry concept to include route geometry generated by spatial activity distribution, then the hypothesis is decisively refuted. The set of the routes’ geometry rises as the determining factor for network formation, surpassing in importance the form of the spatial substrate where these routes develop.
This distinction reveals a previously unconsidered dimension in our initial formulation: the difference between a static geometry–city and the dynamic geometry of movement related to activity–city. Results suggest that it is dynamic geometry, determined using activity distribution logic, that effectively governs urban social network formation.
4.2. Implications for Urban Theory
Findings have significant implications for contemporary urban theory, particularly for debates about spatial determinism and social autonomy. The urbanistic thought tradition frequently assumed that interventions in cities’ physical form could generate predictable social transformations. Our results suggest a more complex and mediated relationship.
Urban physical form is not irrelevant for network formation; however, its influence is indirect and conditioned. Physical space acts primarily as a constraint system that delimits the set of possibilities for movement and encounter patterns, without univocally determining social results.
The finding of activity distribution primacy over geometric form also dialogues with contemporary debates about compact city versus dispersed city. Traditionally, these debates focus on the advantages and disadvantages of different urban morphologies. Our results suggest that it may be more important to consider how different urban functions are distributed within these morphologies than the specific density they assume.
4.3. Specific Network Formation Mechanisms
Detailed analysis of mechanisms through which different spatial configurations facilitate or prevent network formation reveals principles that may have broader applicability. The fundamental mechanism seems to be creating opportunities for daily route overlap. This overlap can occur in three main ways, each with different implications for resulting network characteristics.
Distributed overlap, characteristic of configurations with random activity distribution, creates multiple encounter opportunities spread throughout urban space. This pattern results in relatively egalitarian networks, where extreme connectivity concentration points do not emerge. From a social perspective, this type of configuration may favor diffuse social cohesion, where weak but numerous connections permeate the urban social fabric.
Channeled overlap, exemplified by cross geometry with random distribution, concentrates encounter opportunities in specific corridors while maintaining some general dispersion. This pattern may generate networks with moderate hierarchical structure, where certain movement axes become more important for general connectivity. Urbanistically, this suggests the importance of structuring axes that function as backbones of urban social life.
Concentrated overlap, observed in the case of circular geometry with continuous distribution, forces encounters at specific space points. This pattern results in highly dense but potentially vulnerable networks to central node removal. Socially, it may represent configurations where large urban centers function as obligatory passage points for most inhabitants.
4.4. Geometry’s Role as Constraint System
Result reinterpretation suggests that urban geometry acts primarily as a constraint system that defines the space of possibilities for social network formation, without univocally determining specific results. This constraint function operates in multiple dimensions.
The most obvious dimension refers to physical limits imposed by spatial configuration. More restrictive geometries, such as linear, limit route dispersion possibilities, forcing greater overlap. More open geometries, such as circular or matrix, offer greater flexibility for dispersion, allowing other factors (such as activity distribution) to determine effective movement patterns.
A less obvious dimension refers to the relative costs of different movement types. Although our model drastically simplifies this question by only considering straight-line movement, in urban reality, street geometry, topography, and other infrastructure elements create accessibility hierarchies that influence route choices. These hierarchies may reinforce or counterbalance activity distribution effects.
A third dimension refers to scale effects. Our analysis operated on a small spatial scale with a limited number of agents. It is possible that, at larger scales, with a greater number of agents and greater activity complexity, urban geometry effects manifest differently. The investigation of this scale question remains an important direction for future research.
Result interpretation must consider specific limitations of the implemented model. Urban routine simplification to the house–cycle eliminates real urban activity complexity, where people move between multiple destinations and where activities can generate distinct encounter patterns within them. This simplification was necessary to isolate specific spatial configuration effects, but obviously reduces correspondence with real urban situations.
Encounter criteria representation, as simple physical proximity, ignores the complexity of real social processes of relationship formation. People may be physically close without interacting socially significantly, while others may develop intense relationships based on brief but frequent encounters, and the spread of fashion or some contagious diseases occurs with different levels of proximity. The model captures only the spatial opportunity dimension for encounters, not the conversion of these opportunities into effective social relationships.
Despite these limitations, we understand that the model captures fundamental aspects of the relationship between spatial configuration and social network formation. The consistency of observed patterns across different geometries and the clarity of identified mechanisms suggest that revealed principles have validity that transcend the model simplifications.
4.5. Connections Implications for Urban Planning
Results connect with various currents of contemporary urban literature in ways that both confirm and challenge established perspectives. The discovery of activity distribution importance aligns with work in the urban economics tradition that emphasizes the role of relative activity location in determining social and economic interaction patterns.
Work on urban form and social capital [
25] frequently attributes social cohesion changes to urban morphology alterations, particularly low-density suburb growth. Our results suggest that it may be more important to consider how different activity types are distributed in suburbs than simply their density or form.
Literature on urban mobility and spatial justice, which investigates how different social groups have differentiated access to urban space, finds an echo in our results about how activity distribution patterns affect encounter opportunities. Configurations that generate parallel routes may inadvertently create social segregation even in the absence of explicit physical barriers.
Results have direct implications for urban design and planning strategies. The finding that activity–city is more determining than geometry–city suggests that urban planners should focus more attention on land use policies than on specific morphological configuration of urban fabrics.
This perspective does not imply that urban form is irrelevant, but rather that its relevance is mediated by activity distribution. Zoning that rigorously separates different activity types may inadvertently inhibit social network formation by creating parallel movement patterns or isolated areas. Conversely, policies that promote mixed use may facilitate networks even in less “ideal” morphological configurations.
Evidence that random activity distribution consistently generates networks suggests that urban policies promoting functional diversity may have social benefits beyond traditional economic or environmental justifications. Mixed use not only reduces displacement distances but also creates favorable conditions for network formation.
This perspective offers a new foundation for arguments against monofunctional zoning. Beyond traditionally identified problems—excessive dependence on motorized transport and socioeconomic segregation—monofunctional zoning may also inhibit social cohesion by reducing casual encounter opportunities between different social groups.
5. Limitations and Future Directions
This research presents important methodological limitations that must be recognized and that guide directions for future investigations. Principal limitations refer to the degree of simplification necessary to make simulation viable and isolate specific variables.
Model limitations: Urban routine reduction to the house–work cycle eliminates real urban activity complexity, where people move between multiple destinations and different activity types can generate distinct encounter patterns. Encounter representation as simple physical proximity ignores the complexity of real social processes of relationships. Straight-line movement permission eliminates constraints imposed by real urban infrastructure, where streets and blocks direct and limit possible routes. The exclusion of activity as a place of encounter is an obvious deviation from real-world mechanisms, though aimed to isolate the effects of urban form.
Scale limitations: A limited number of agents (40) and an invariant routine simulation period (10 days) may not capture dynamics that emerge only in larger populations or longer periods. The simple invariant routine certainly cuts out the effects of more real routines, which change over time, like weekend and vacation periods. Threshold effects, where certain network properties emerge only above critical sizes, may not have been observed due to these limitations.
As West [
6] suggests, criticality refers to the limit moment when the structure reaches its apex on the eve of collapse and destruction, leading to system reorganization over the debris of the previous one. This has been observed as a CAS characteristic, whether in ecological systems or business environments with company emergence and decline, in innovation processes, and technological substitution.
The empirical validation of findings represents a fundamental priority for future research. Emerging technologies for urban mobility data collection offer opportunities to map real movement patterns and verify whether identified principles manifest in effective urban contexts.
Conceptual expansions include incorporating multiple activities, social heterogeneity among agents, more sophisticated temporal dynamics, and realistic urban infrastructure. Applying principles to developing practical tools for urban planning offers opportunities for knowledge transfer from academic research to professional practice. The Redinha simulator, nonetheless, offers a platform for future investigations and can be expanded for different urban contexts and research questions.
6. Conclusions
This investigation’s central finding partially contradicts our initial hypothesis: although specific geometry–city does not determine particular structures in social networks, activity–city, especially its spatial distribution—and consequently resulting route geometry—is the determining factor for urban encounter network formation.
This result reorients our understanding of the relationship between physical space and social dynamics. Urban morphology acts as a constraint system that delimits possibilities for social interactions, but it is social practices—represented by activity distribution—that effectively determine encounter patterns. The discovery suggests that land use policies may be more effective for promoting social cohesion than interventions focused on urban morphology.
Computational simulation-based methodology so far corroborates its potential for exploring complex relationships within urban systems, offering systematic variable control that would be impractical in empirical studies. The developed simulator demonstrates the potential of computational tools for investigating emergent urban phenomena and the potential of propositional theoretical research so far.
For urban planning, if validated in real-world conditions, results offer a strong argument for mixed-use policies and against strict monofunctional zoning. Beyond traditionally recognized benefits, functional diversity facilitates social network formation by creating opportunities for daily route overlap.
Important limitations include urban routine simplification, simplified social encounter representation, and reduced simulation scale. Empirical validation through studies that correlate real urban configurations with effective social network measures represents a priority for future research.