Quantifying the Impact of Energy Storage Capacity on Building Energy Flexibility: A Case Study of the PV-ESS-GSHP System
Abstract
1. Introduction
2. Related Studies
3. Method
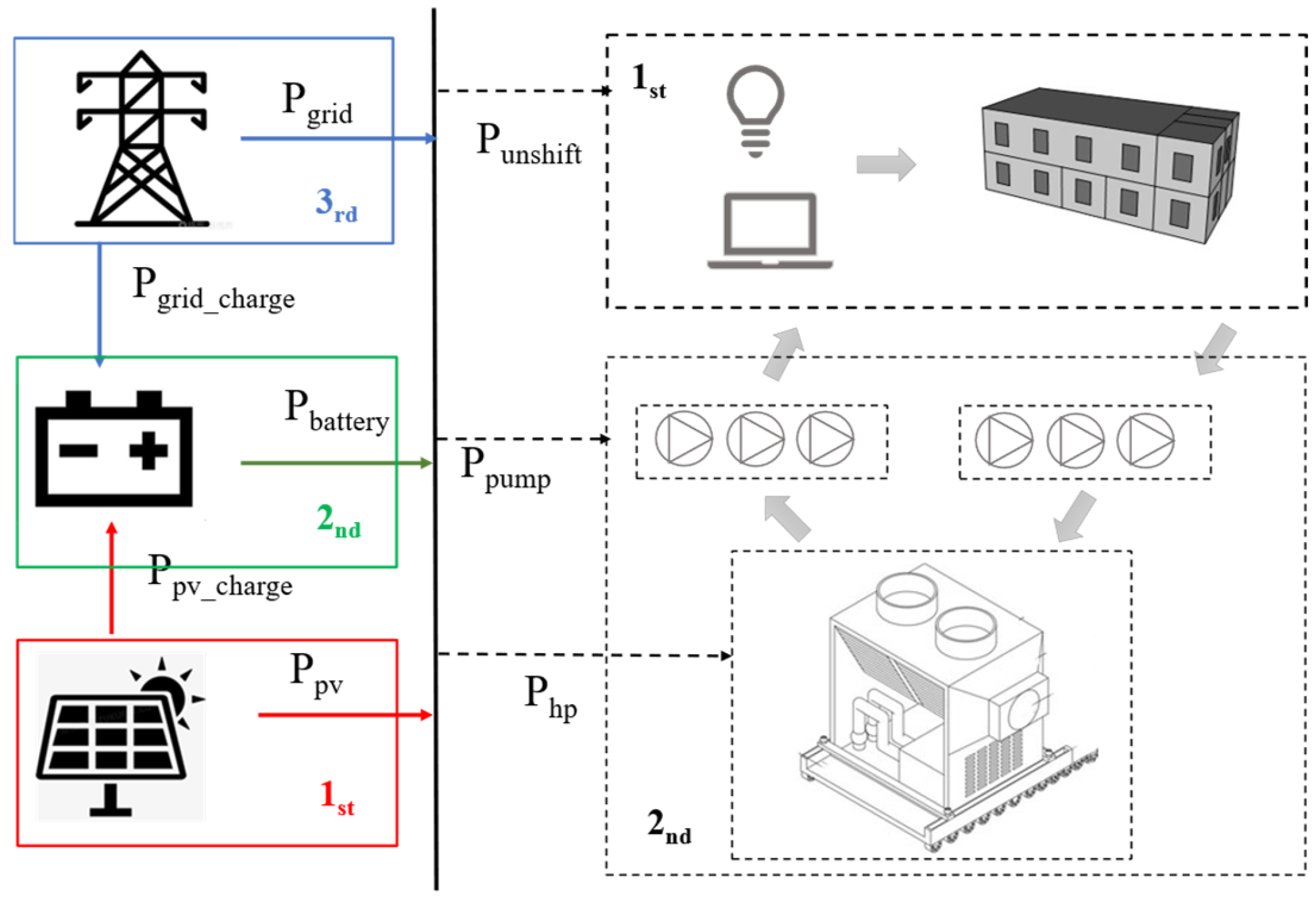
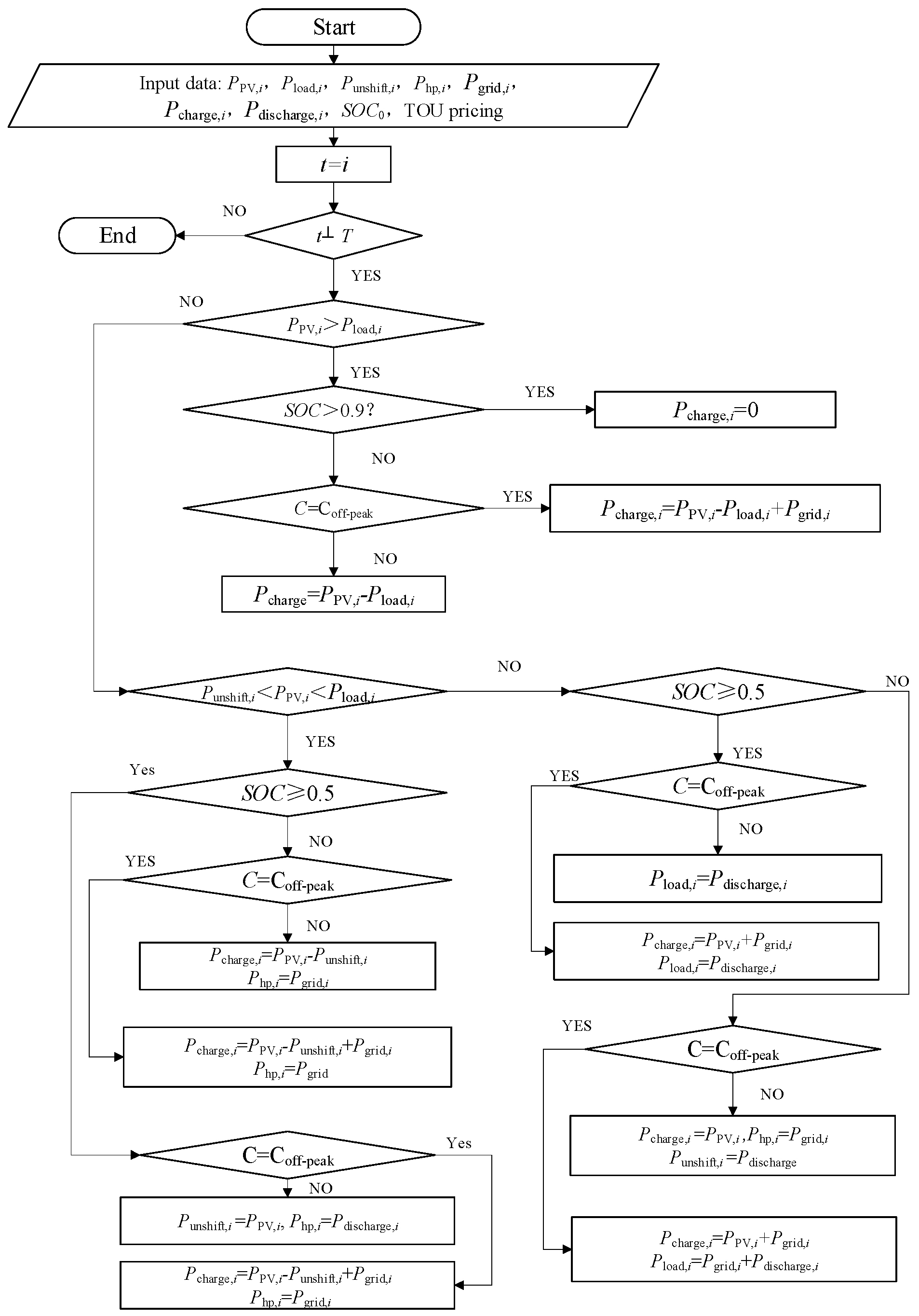
3.1. Flexible Energy Use Hierarchical Scheduling Strategy
3.2. Supply-Demand Matching and ESS Constraints
3.2.1. Energy Balance Relationship
3.2.2. Constraints for the Election of ESS Capacity
3.3. Description of the Case
3.3.1. Simulation Case Setting
3.3.2. Input Data
4. Results and Discussion
4.1. Evaluation of the Effectiveness of the Energy Use Hierarchical Scheduling Strategy
4.1.1. Energy Production and Consumption Curves and Load Characteristics
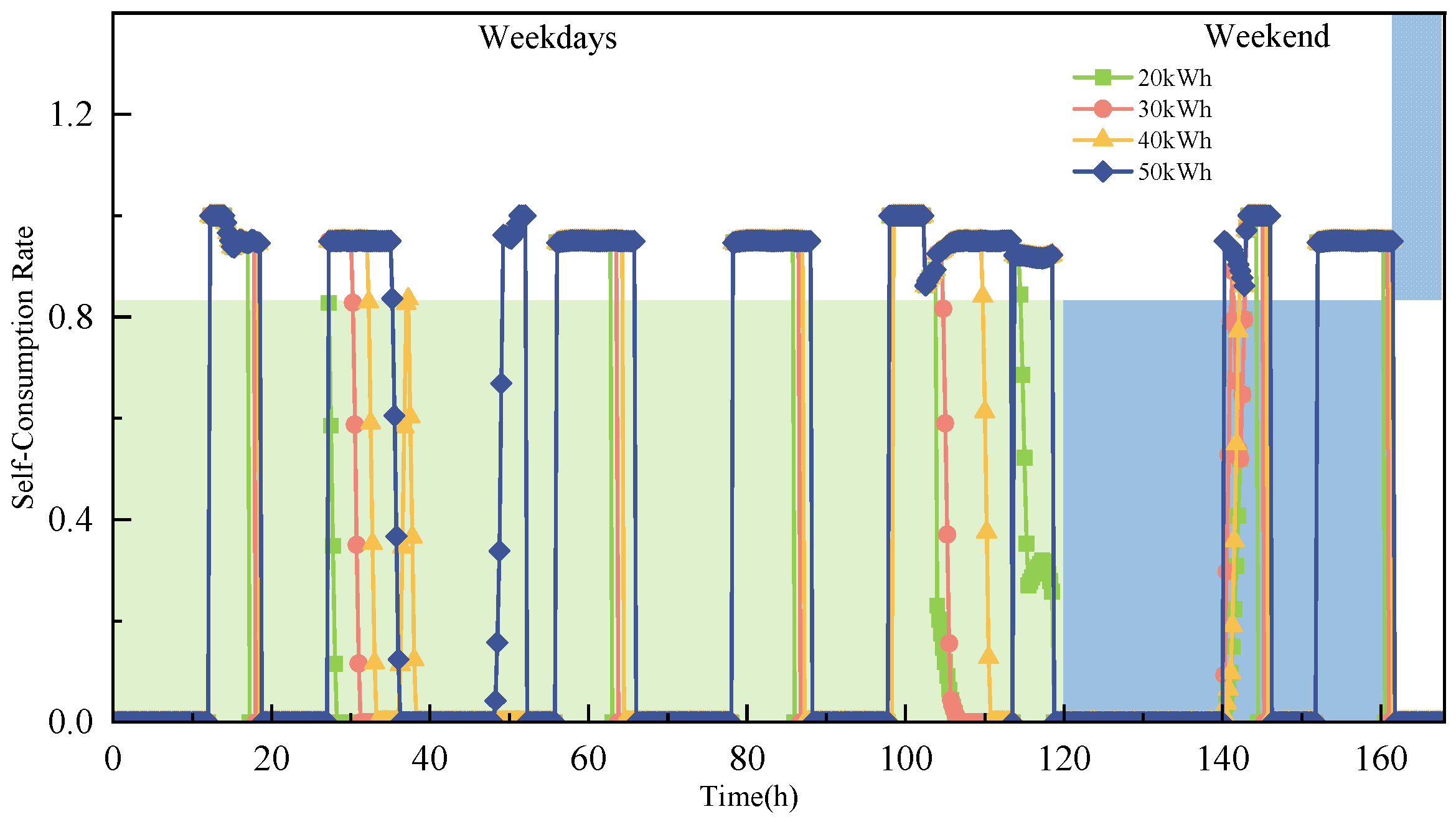
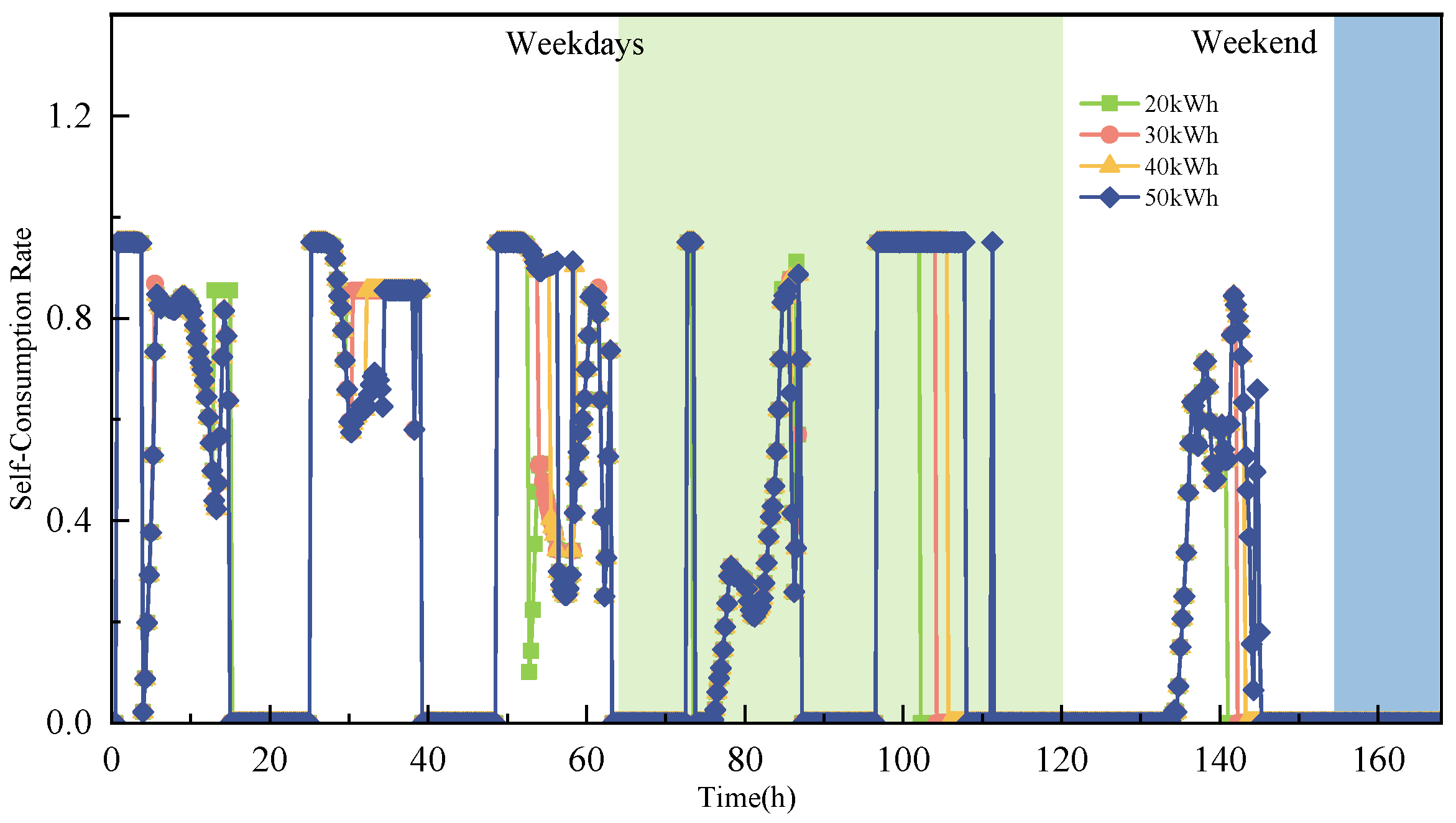
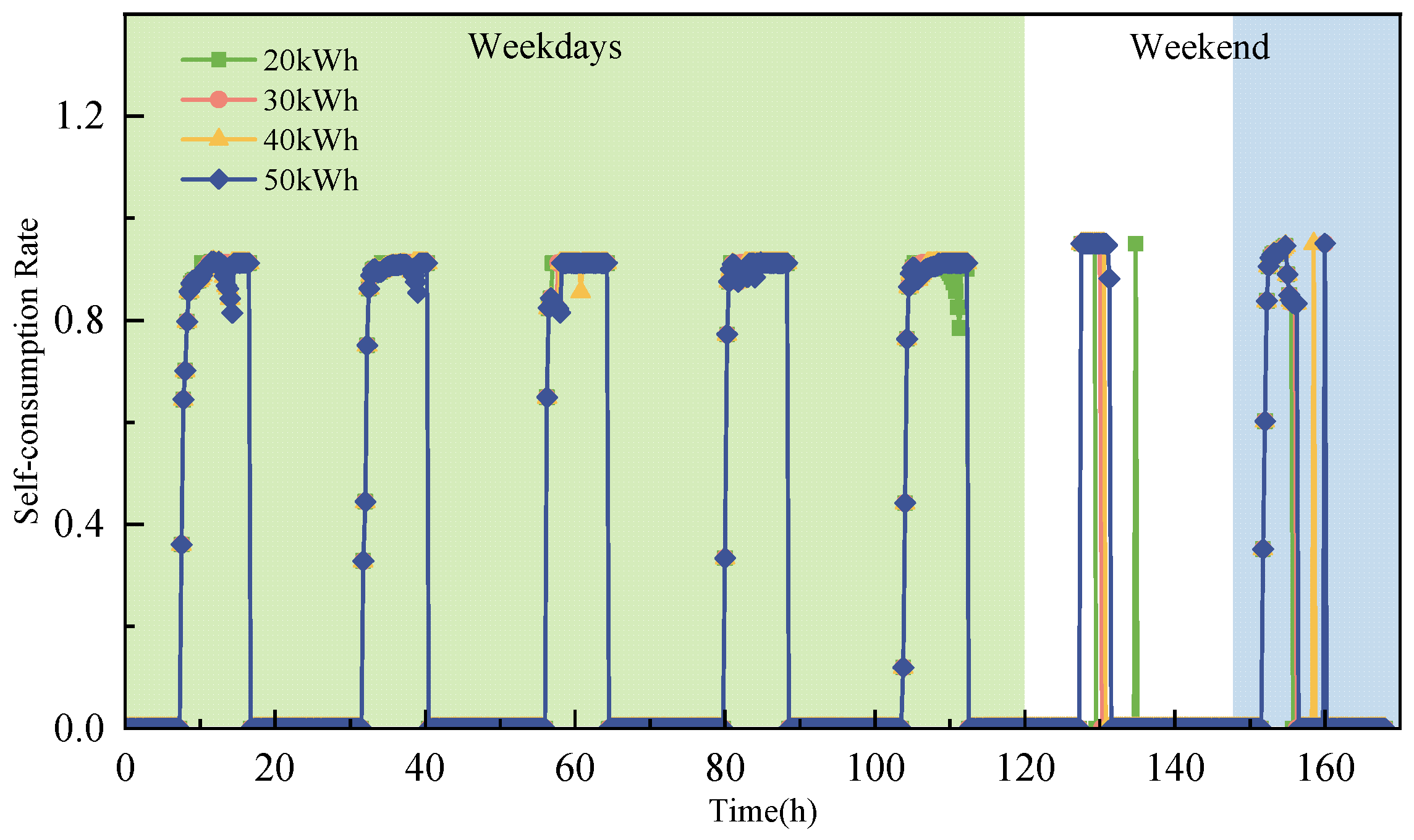
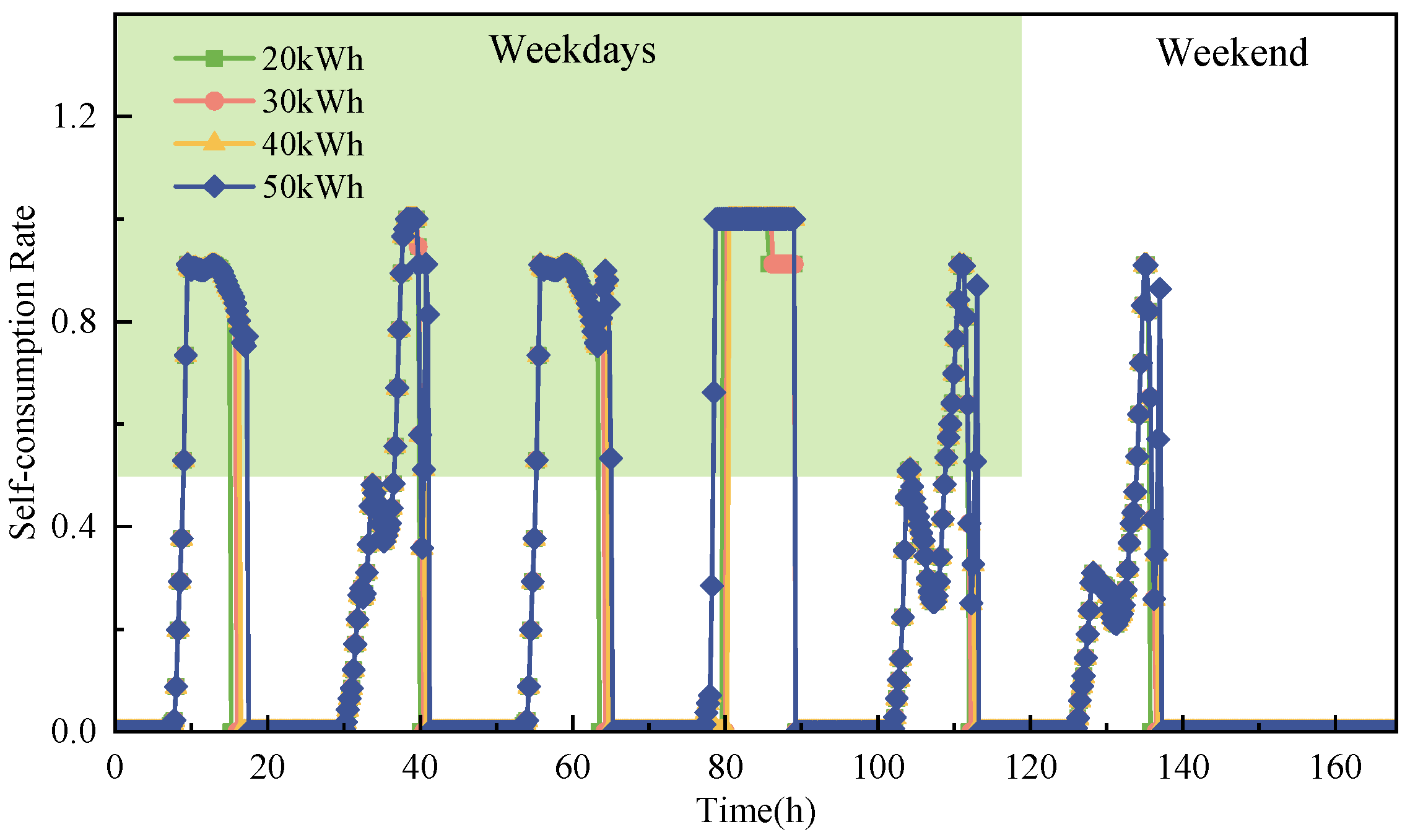
4.1.2. The Impact of Energy Storage Capacity on Photovoltaic Utilization
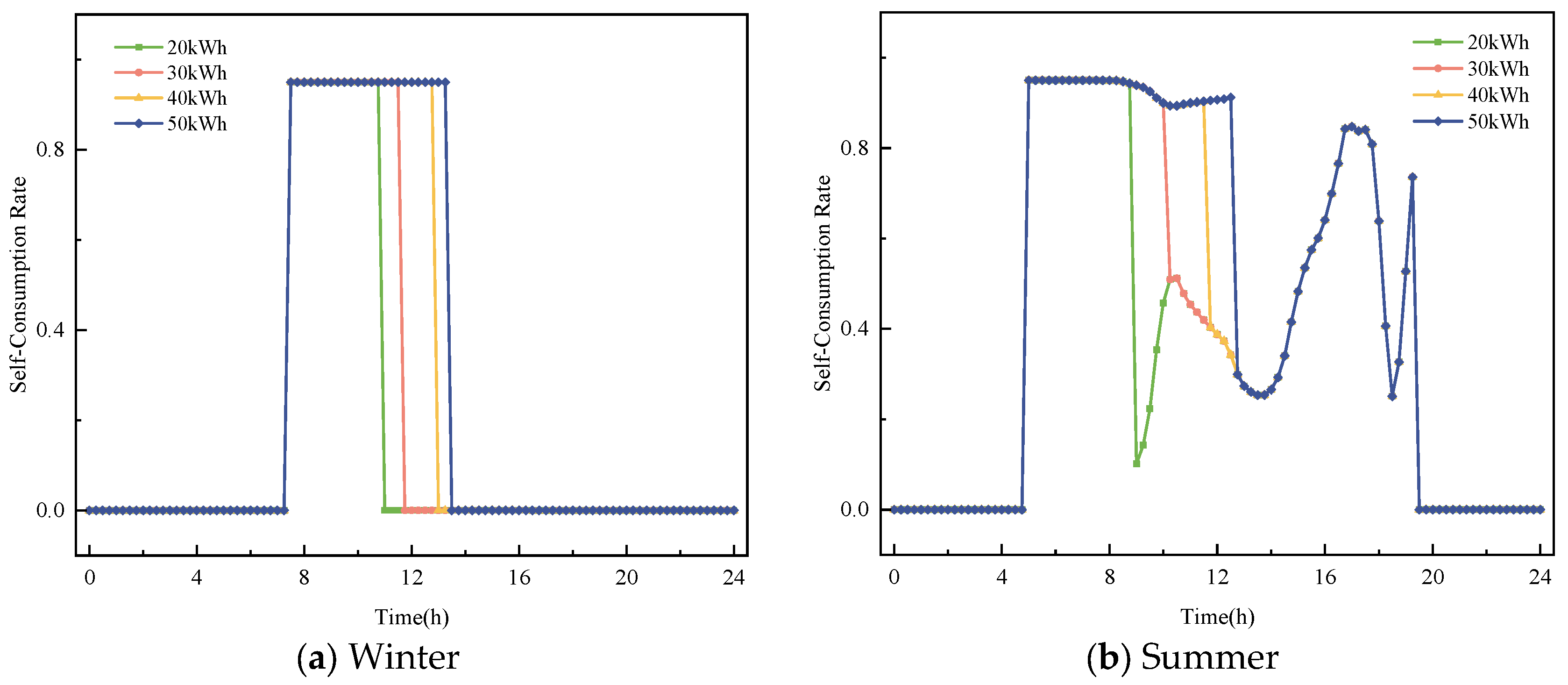
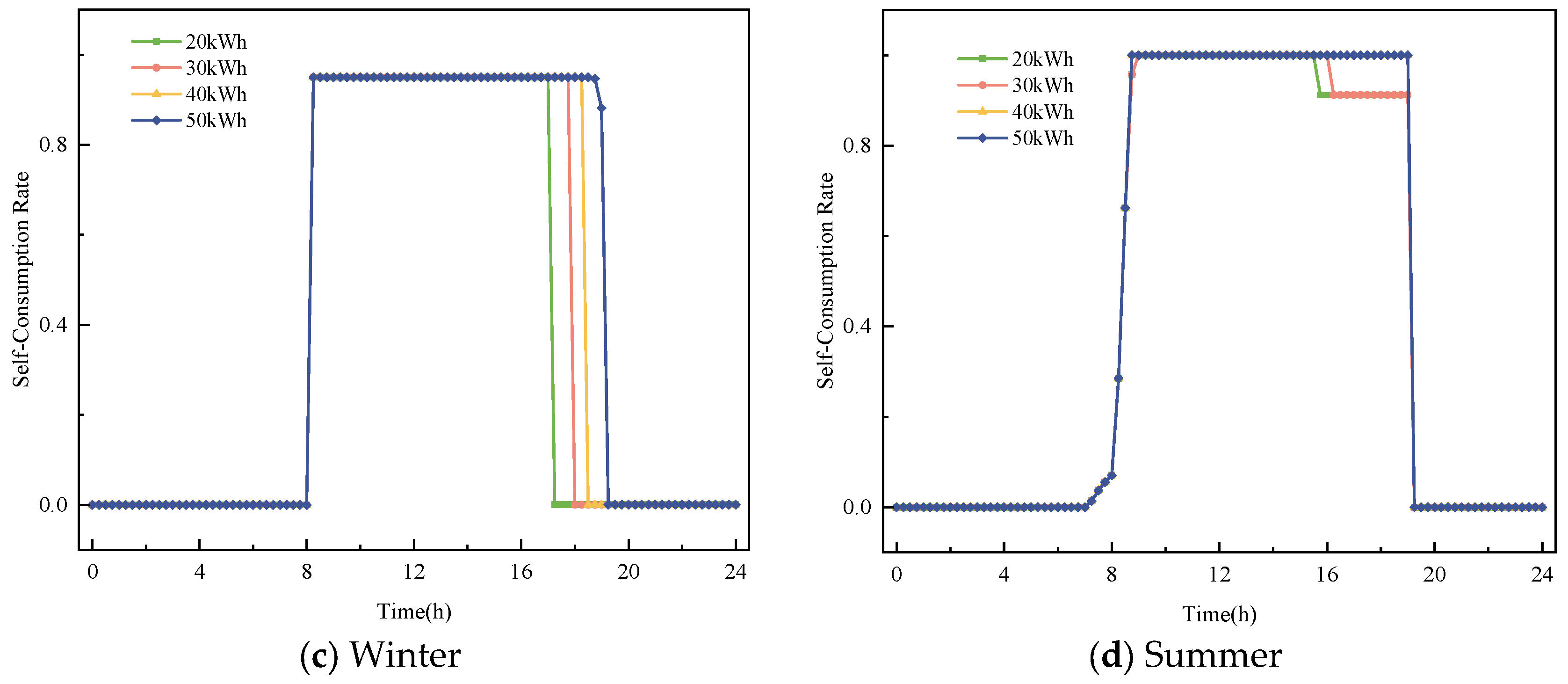
4.1.3. The Impact of Energy Storage Capacity on the System’s Response Capability
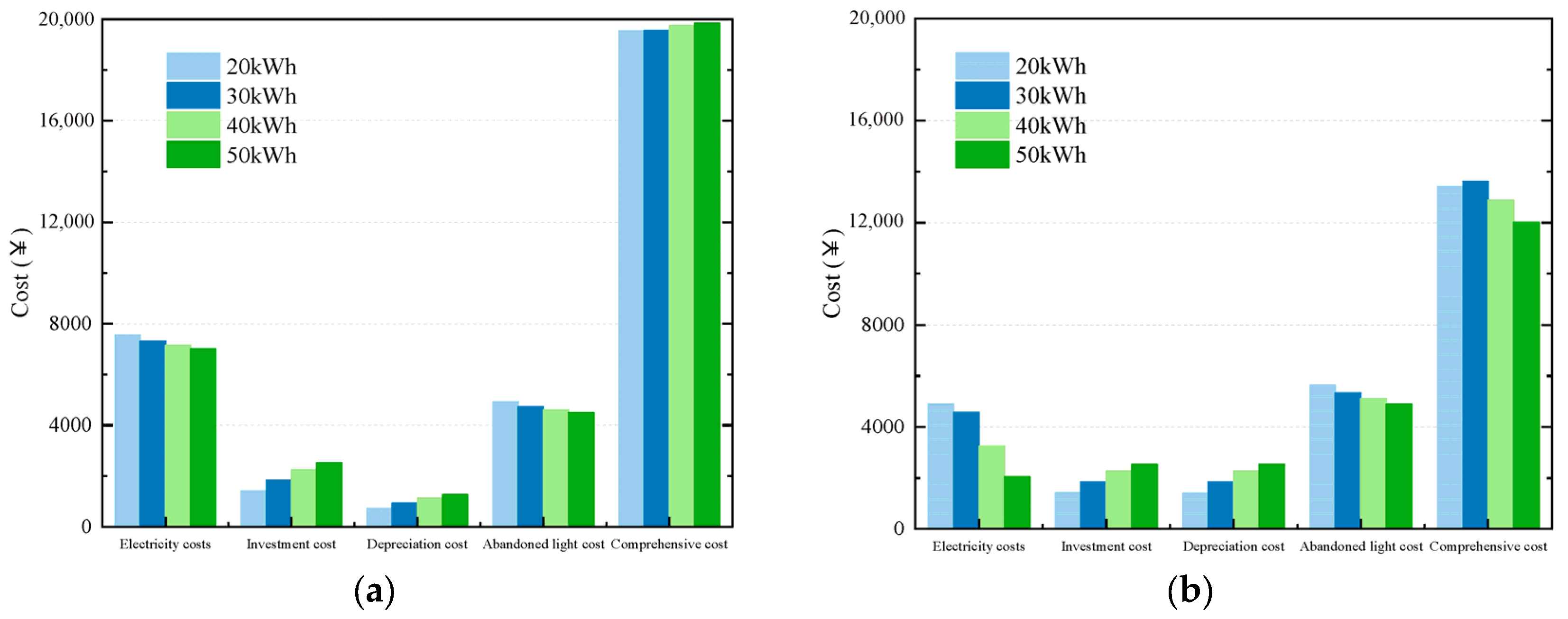
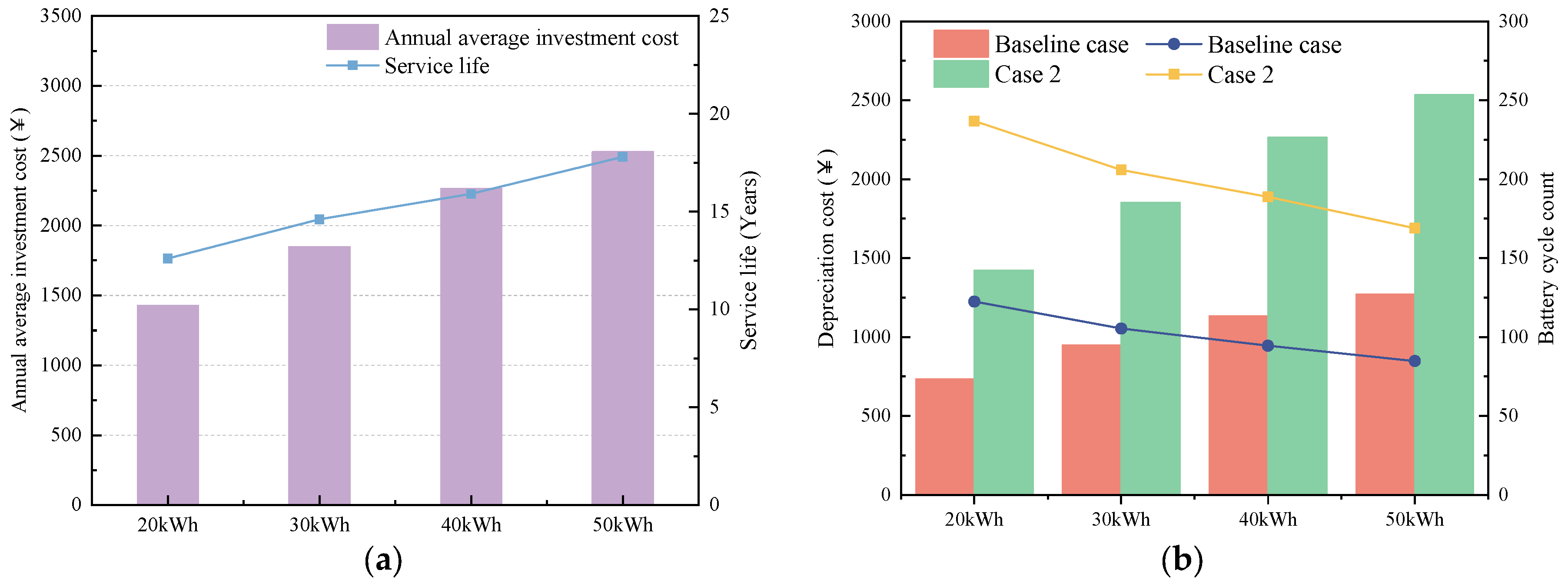
4.2. The Impact of Energy Storage Capacity on the Comprehensive Operating Cost of the System
5. Conclusions
- The flexible energy management strategy significantly improves the PV energy absorption. The implementation of this strategy increases the annual PV consumption by 35.29%, with the PV self-consumption rate improving by up to 4.07% as ESS capacity increases. After adopting this strategy, the system effectively reduces PV waste caused by variability and intermittency. A larger ESS capacity provides greater flexibility for energy absorption, strengthening the system’s operational security and adaptability.
- Analysis of the ESS charge and discharge curves shows that the system’s responsiveness improves under the flexible energy management strategy. As ESS capacity increases, the system is better able to respond to fluctuations in PV power generation. The system’s ability to adapt and respond strengthens continuously, with the increase in storage capacity playing a vital role in enhancing system stability and regulatory capabilities.
- In terms of overall costs, while the degradation costs during operation slightly rise with the implementation of the flexible energy management strategy, the total cost decreases by 65.13%. A comparison of different capacities shows that the cost differences between various ESS sizes are within 1.48%, indicating that, within a certain range, the choice of ESS capacity should balance both system performance and economic feasibility.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IES | Integrated energy systems |
| ESS | Energy storage systems |
| SCR | Self-consumption rate |
| DSM | Demand-side management |
| DR | Demand response |
References
- Jensen, S.Ø.; Marszal-Pomianowska, A.; Lollini, R.; Pasut, W.; Knotzer, A.; Engelmann, P.; Stafford, A.; Reynders, G. IEA EBC Annex 67 Energy Flexible Buildings. Energy Build. 2017, 155, 25–34. [Google Scholar] [CrossRef]
- Camarasa, C.; Mata, É.; Navarro, J.P.J.; Reyna, J.; Bezerra, P.; Angelkorte, G.B.; Feng, W.; Filippidou, F.; Forthuber, S.; Harris, C.; et al. A Global Comparison of Building Decarbonization Scenarios by 2050 towards 1.5–2 °C Targets. Nat. Commun. 2022, 13, 3077. [Google Scholar] [CrossRef]
- Mittelviefhaus, M.; Georges, G.; Boulouchos, K. Electrification of Multi-Energy Hubs under Limited Electricity Supply: De-/Centralized Investment and Operation for Cost-Effective Greenhouse Gas Mitigation. Adv. Appl. Energy 2022, 5, 100083. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The Role of Renewable Energy in the Global Energy Transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Lv, F.; Tang, H. Assessing the Impact of Climate Change on the Optimal Solar–Wind Hybrid Power Generation Potential in China: A Focus on Stability and Complementarity. Renew. Sustain. Energy Rev. 2025, 212, 115429. [Google Scholar] [CrossRef]
- Wang, J.; Kontar, R.E.; Jin, X.; King, J. Electrifying High-Efficiency Future Communities: Impact on Energy, Emissions, and Grid. Adv. Appl. Energy 2022, 6, 100095. [Google Scholar] [CrossRef]
- Aruta, G.; Ascione, F.; Fistola, R.; Iovane, T. The City as a Power Hub for Boosting Renewable Energy Communities: A Case Study in Naples. Sustainability 2024, 16, 7988. [Google Scholar] [CrossRef]
- McGarry, C.; Dixon, J.; Flower, J.; Bukhsh, W.; Brand, C.; Bell, K.; Galloway, S. Electrified Heat and Transport: Energy Demand Futures, Their Impacts on Power Networks and What It Means for System Flexibility. Appl. Energy 2024, 360, 122836. [Google Scholar] [CrossRef]
- Zhang, P.; Mansouri, S.A.; Rezaee Jordehi, A.; Tostado-Véliz, M.; Alharthi, Y.Z.; Safaraliev, M. An ADMM-Enabled Robust Optimization Framework for Self-Healing Scheduling of Smart Grids Integrated with Smart Prosumers. Appl. Energy 2024, 363, 123067. [Google Scholar] [CrossRef]
- Wack, Y.; Sollich, M.; Salenbien, R.; Diriken, J.; Baelmans, M.; Blommaert, M. A Multi-Period Topology and Design Optimization Approach for District Heating Networks. Appl. Energy 2024, 367, 123380. [Google Scholar] [CrossRef]
- Bao, M.; Hui, H.; Ding, Y.; Sun, X.; Zheng, C.; Gao, X. An Efficient Framework for Exploiting Operational Flexibility of Load Energy Hubs in Risk Management of Integrated Electricity-Gas Systems. Appl. Energy 2023, 338, 120765. [Google Scholar] [CrossRef]
- Rotas, R.; Fotopoulou, M.; Drosatos, P.; Rakopoulos, D.; Nikolopoulos, N. Adaptive Dynamic Building Envelopes with Solar Power Components: Annual Performance Assessment for Two Pilot Sites. Energies 2023, 16, 2148. [Google Scholar] [CrossRef]
- Zhang, H.; Hao, S.; Wen, M.; Bai, X.; Liu, L.; Zhang, P. Optimization of Ground Source Heat Pump System Based on TRNSYS in Hot Summer and Cold Winter Region. Buildings 2024, 14, 2764. [Google Scholar] [CrossRef]
- Saleh, A. Experimental Performance Evaluation of Water Source Heat Pumps in Different Circumstances and Comparison to Air Source Heat Pumps. J. Therm. Eng. 2023, 9, 954–967. [Google Scholar] [CrossRef]
- Hosseinnia, S.M.; Sorin, M. Energy Targeting Approach for Optimum Solar Assisted Ground Source Heat Pump Integration in Buildings. Energy 2022, 248, 123528. [Google Scholar] [CrossRef]
- Mayer, M.J.; Szilágyi, A.; Gróf, G. Environmental and Economic Multi-Objective Optimization of a Household Level Hybrid Renewable Energy System by Genetic Algorithm. Appl. Energy 2020, 269, 115058. [Google Scholar] [CrossRef]
- Erdinç, F.G.; Çiçek, A.; Erdinç, O. Resiliency-Sensitive Decision Making Mechanism for a Residential Community Enhanced with Bi-Directional Operation of Fuel Cell Electric Vehicles. Energies 2022, 15, 8729. [Google Scholar] [CrossRef]
- Tang, H.; Wang, S.; Li, H. Flexibility Categorization, Sources, Capabilities and Technologies for Energy-Flexible and Grid-Responsive Buildings: State-of-the-Art and Future Perspective. Energy 2021, 219, 119598. [Google Scholar] [CrossRef]
- Lamnatou, C.; Chemisana, D.; Cristofari, C. Smart Grids and Smart Technologies in Relation to Photovoltaics, Storage Systems, Buildings and the Environment. Renew. Energy 2022, 185, 1376–1391. [Google Scholar] [CrossRef]
- Saberi-Derakhtenjani, A.; Barbosa, J.D.; Rodriguez-Ubinas, E. Energy Flexibility Strategies for Buildings in Hot Climates: A Case Study for Dubai. Buildings 2024, 14, 3008. [Google Scholar] [CrossRef]
- Mlecnik, E.; Parker, J.; Ma, Z.; Corchero, C.; Knotzer, A.; Pernetti, R. Policy Challenges for the Development of Energy Flexibility Services. Energy Policy 2020, 137, 111147. [Google Scholar] [CrossRef]
- Nolzen, N.; Leenders, L.; Bardow, A. Flexibility-Expansion Planning of Multi-Energy Systems by Energy Storage for Participating in Balancing-Power Markets. Front. Energy Res. 2023, 11, 1225564. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Zhao, Y.; Sun, Q.; Wang, F. A Robust Flexibility Evaluation Method for Distributed Multi-Energy Microgrid in Supporting Power Distribution System. Front. Energy Res. 2023, 10, 1021627. [Google Scholar] [CrossRef]
- Antoniadou-Plytaria, K.; Steen, D.; Tuan, L.A.; Carlson, O.; Fotouhi Ghazvini, M.A. Market-Based Energy Management Model of a Building Microgrid Considering Battery Degradation. IEEE Trans. Smart Grid 2021, 12, 1794–1804. [Google Scholar] [CrossRef]
- Lu, F.; Yu, Z.; Zou, Y.; Yang, X. Energy Flexibility Assessment of a Zero-Energy Office Building with Building Thermal Mass in Short-Term Demand-Side Management. J. Build. Eng. 2022, 50, 104214. [Google Scholar] [CrossRef]
- Shakeri, M.; Shayestegan, M.; Abunima, H.; Reza, S.M.S.; Akhtaruzzaman, M.; Alamoud, A.R.M.; Sopian, K.; Amin, N. An Intelligent System Architecture in Home Energy Management Systems (HEMS) for Efficient Demand Response in Smart Grid. Energy Build. 2017, 138, 154–164. [Google Scholar] [CrossRef]
- Gupta, R.; Pena-Bello, A.; Streicher, K.N.; Roduner, C.; Farhat, Y.; Thöni, D.; Patel, M.K.; Parra, D. Spatial Analysis of Distribution Grid Capacity and Costs to Enable Massive Deployment of PV, Electric Mobility and Electric Heating. Appl. Energy 2021, 287, 116504. [Google Scholar] [CrossRef]
- Li, Y.; Lu, Y.; Sun, J.; Wang, T.; Zong, S.; Zhou, T.; Wang, X. Operational Strategy of a DC Inverter Heat Pump System Considering PV Power Fluctuation and Demand-Side Load Characteristics. Buildings 2024, 14, 1139. [Google Scholar] [CrossRef]
- Gradwohl, C.; Maxim, D.C.; Islam, S.; Kienberger, T. Unlocking Heat Pump Flexibility: A Multi-Objective Optimisation Approach for Self Sufficiency and Energy Costs. Energy Convers. Manag. 2025, 334, 119822. [Google Scholar] [CrossRef]
- Xue, T.; Jokisalo, J.; Kosonen, R. Demand Response Potential of an Educational Building Heated by a Hybrid Ground Source Heat Pump System. Energies 2024, 17, 5428. [Google Scholar] [CrossRef]
- Dong, X.; Liu, Y.; Pu, Z.; Zhang, L. Experimental Investigation of an Off-Grid Photovoltaic Heat Pump Collection System with Heat Collecting as a Core. Appl. Therm. Eng. 2025, 260, 125004. [Google Scholar] [CrossRef]
- Tan, K.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Kasinathan, P.; Solanki, S.G.; Raveendran, S.K. Empowering Smart Grid: A Comprehensive Review of Energy Storage Technology and Application with Renewable Energy Integration. J. Energy Storage 2021, 39, 102591. [Google Scholar] [CrossRef]
- Fan, M.; Cao, S.; Lu, S. Optimal Allocation of Multiple Energy Storage in the Integrated Energy System of a Coastal Nearly Zero Energy Community Considering Energy Storage Priorities. J. Energy Storage 2024, 87, 111323. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Du, E.; Fan, C.; Wu, Z.; Yao, Y.; Liu, L.; Zhang, N. A Review and Outlook on Cloud Energy Storage: An Aggregated and Shared Utilizing Method of Energy Storage System. Renew. Sustain. Energy Rev. 2023, 185, 113606. [Google Scholar] [CrossRef]
- Li, J.; Guo, Q.; Wang, X.; Tu, C.; Xiao, F.; Hou, Y.; Shen, X. Parallel-Execute-Based Real-Time Energy Management Strategy for FTPSS Integrated PV and ESS. Appl. Energy 2025, 385, 125538. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.R.; Tharumalingam, E.; Dusseault, M.B.; Fraser, R. Study of Energy Storage Systems and Environmental Challenges of Batteries. Renew. Sustain. Energy Rev. 2019, 104, 192–208. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The Lithium-Ion Battery: State of the Art and Future Perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Sandoval, D.; Goffin, P.; Leibundgut, H. How Low Exergy Buildings and Distributed Electricity Storage Can Contribute to Flexibility within the Demand Side. Appl. Energy 2017, 187, 116–127. [Google Scholar] [CrossRef]
- Hannan, M.A.; Faisal, M.; Jern Ker, P.; Begum, R.A.; Dong, Z.Y.; Zhang, C. Review of Optimal Methods and Algorithms for Sizing Energy Storage Systems to Achieve Decarbonization in Microgrid Applications. Renew. Sustain. Energy Rev. 2020, 131, 110022. [Google Scholar] [CrossRef]
- Li, Y.; Peng, J.; Jia, H.; Zou, B.; Hao, B.; Ma, T.; Wang, X. Optimal Battery Schedule for Grid-Connected Photovoltaic-Battery Systems of Office Buildings Based on a Dynamic Programming Algorithm. J. Energy Storage 2022, 50, 104557. [Google Scholar] [CrossRef]
- Cruz, C.; Tostado-Véliz, M.; Palomar, E.; Bravo, I. Pattern-Driven Behaviour for Demand-Side Management: An Analysis of Appliance Use. Energy Build. 2024, 308, 113988. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Yang, M.; Xu, H. Hybrid Active and Passive Strategies for Chance-Constrained Bilevel Scheduling of Community Multi-Energy System Considering Demand-Side Management and Consumer Psychology. Appl. Energy 2023, 349, 121646. [Google Scholar] [CrossRef]
- Iranpour Mobarakeh, A.; Sadeghi, R.; Saghafi Esfahani, H.; Delshad, M. Optimal Planning and Operation of Energy Hub by Considering Demand Response Algorithms and Uncertainties Based on Problem-Solving Approach in Discrete and Continuous Space. Electr. Power Syst. Res. 2023, 214, 108859. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Hong, T.; Piette, M.A. Energy Flexibility of Residential Buildings: A Systematic Review of Characterization and Quantification Methods and Applications. Adv. Appl. Energy 2021, 3, 100054. [Google Scholar] [CrossRef]
- Ali, S.; Rehman, A.U.; Wadud, Z.; Khan, I.; Murawwat, S.; Hafeez, G.; Albogamy, F.R.; Khan, S.; Samuel, O. Demand Response Program for Efficient Demand-Side Management in Smart Grid Considering Renewable Energy Sources. IEEE Access 2022, 10, 53832–53853. [Google Scholar] [CrossRef]
- Zulfiqar, M.; Ul Abdeen, Z.; Kamran, M. Optimizing Electric Vehicle Charging Scheduling Using Enhanced Multi-Agent Neural Networks with Dynamic Pricing. J. Energy Storage 2024, 99, 113317. [Google Scholar] [CrossRef]
- Asadinejad, A.; Tomsovic, K. Optimal Use of Incentive and Price Based Demand Response to Reduce Costs and Price Volatility. Electr. Power Syst. Res. 2017, 144, 215–223. [Google Scholar] [CrossRef]
- Alipour, M.; Zare, K.; Seyedi, H.; Jalali, M. Real-Time Price-Based Demand Response Model for Combined Heat and Power Systems. Energy 2019, 168, 1119–1127. [Google Scholar] [CrossRef]
- Rehman, A.U.; Hafeez, G.; Albogamy, F.R.; Wadud, Z.; Ali, F.; Khan, I.; Rukh, G.; Khan, S. An Efficient Energy Management in Smart Grid Considering Demand Response Program and Renewable Energy Sources. IEEE Access 2021, 9, 148821–148844. [Google Scholar] [CrossRef]
- Sarsabahi, Y.; Safari, A.; Quteishat, A.; Salehi, J. Strategic Energy Storage Scheduling with Fast Acting Demand Side Schemes to Improve Flexibility of Hybrid Renewable Energy System. J. Energy Storage 2024, 92, 112182. [Google Scholar] [CrossRef]
- Jiang, H.; Lu, S.; Li, B.; Wang, R. The Power Regulation Characteristics, Key Challenges, and Solution Pathways of Typical Flexible Resources in Regional Energy Systems. Energies 2025, 18, 3830. [Google Scholar] [CrossRef]
- Shi, M.; Wang, H.; Lyu, C.; Xie, P.; Xu, Z.; Jia, Y. A Hybrid Model of Energy Scheduling for Integrated Multi-Energy Microgrid with Hydrogen and Heat Storage System. Energy Rep. 2021, 7, 357–368. [Google Scholar] [CrossRef]
- De Carli, M.; Galgaro, A.; Pasqualetto, M.; Zarrella, A. Energetic and Economic Aspects of a Heating and Cooling District in a Mild Climate Based on Closed Loop Ground Source Heat Pump. Appl. Therm. Eng. 2014, 71, 895–904. [Google Scholar] [CrossRef]
- Jonban, M.S.; Romeral, L.; Akbarimajd, A.; Ali, Z.; Ghazimirsaeid, S.S.; Marzband, M.; Putrus, G. Autonomous Energy Management System with Self-Healing Capabilities for Green Buildings (Microgrids). J. Build. Eng. 2021, 34, 101604. [Google Scholar] [CrossRef]

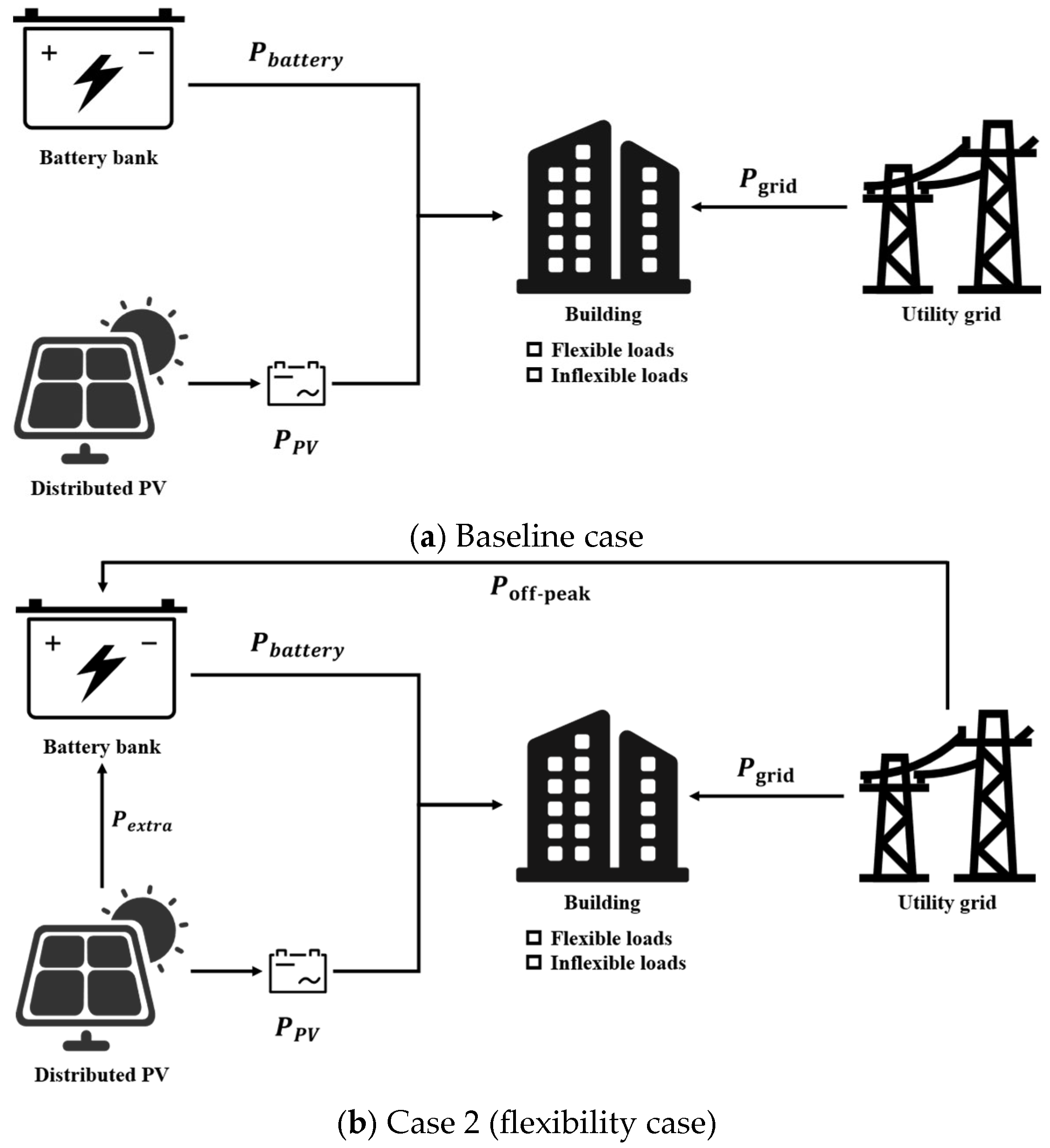
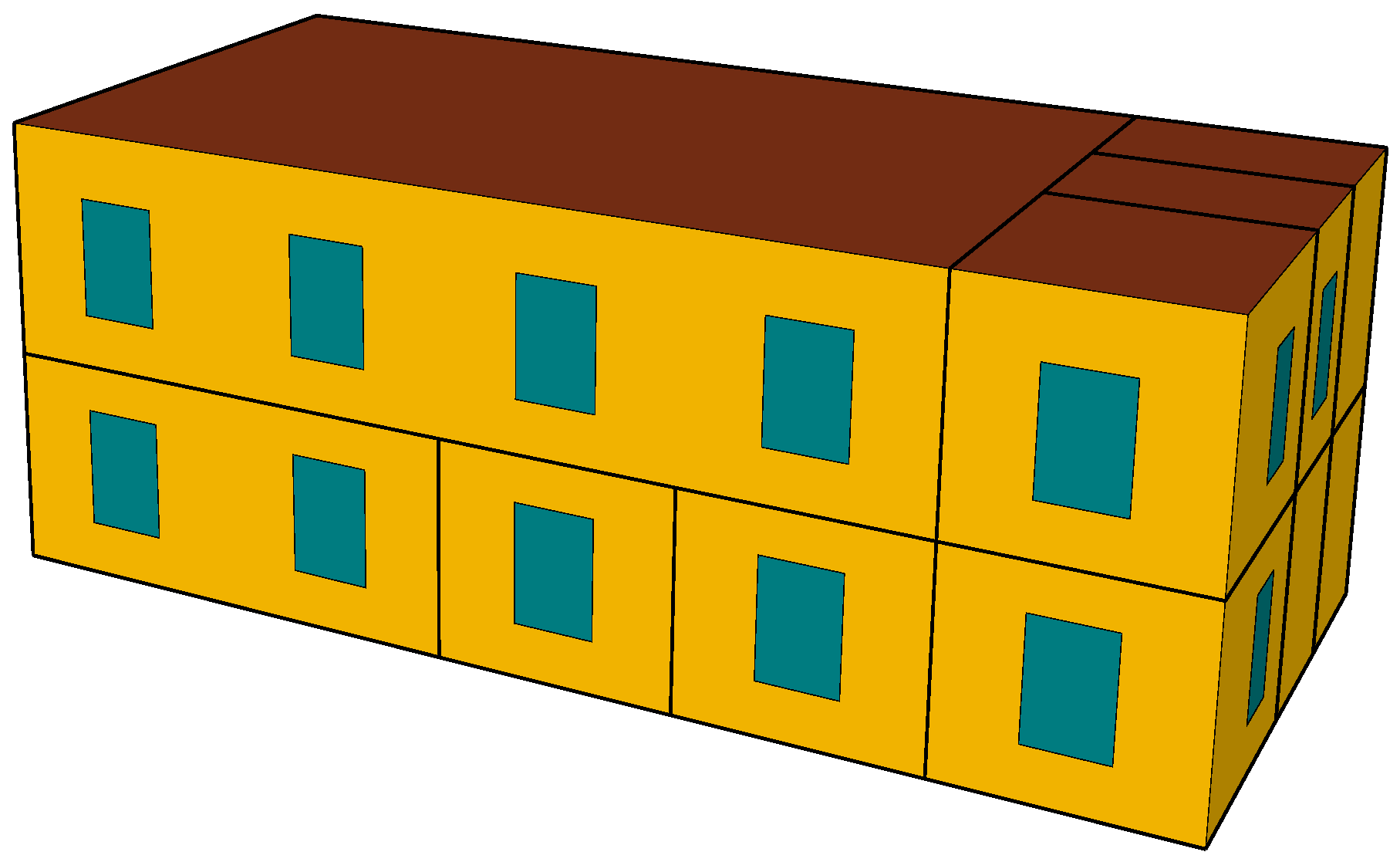
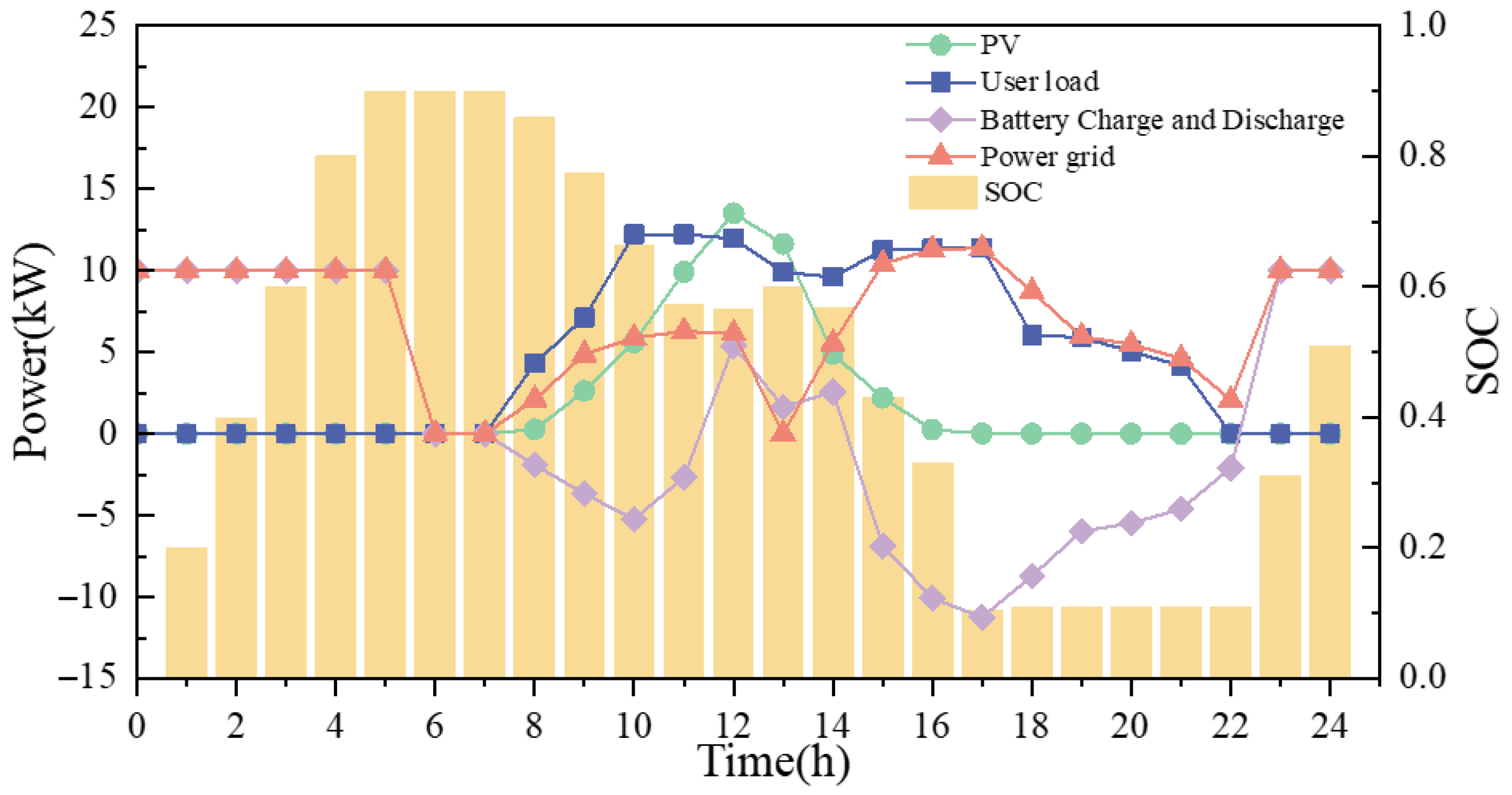
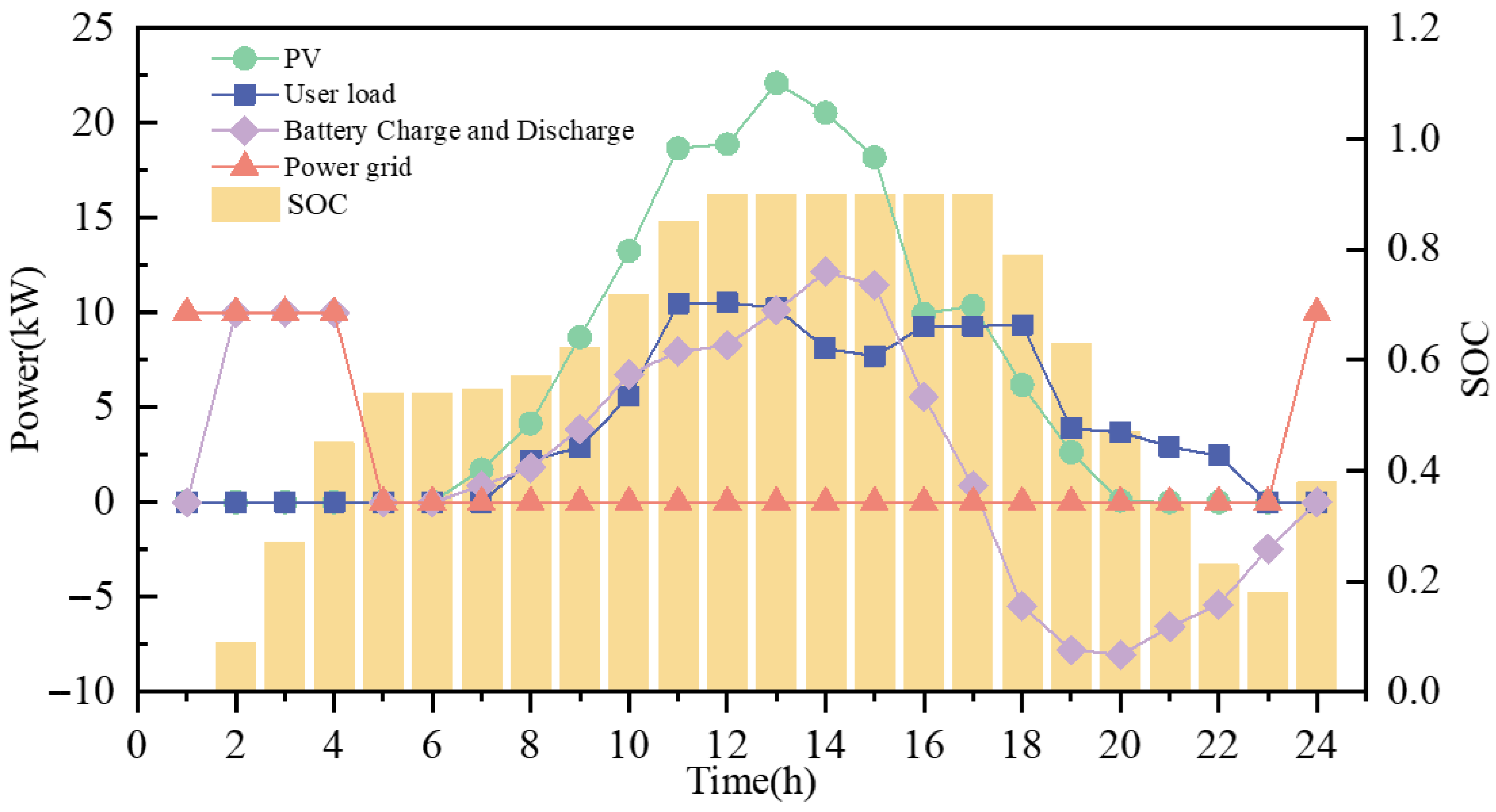
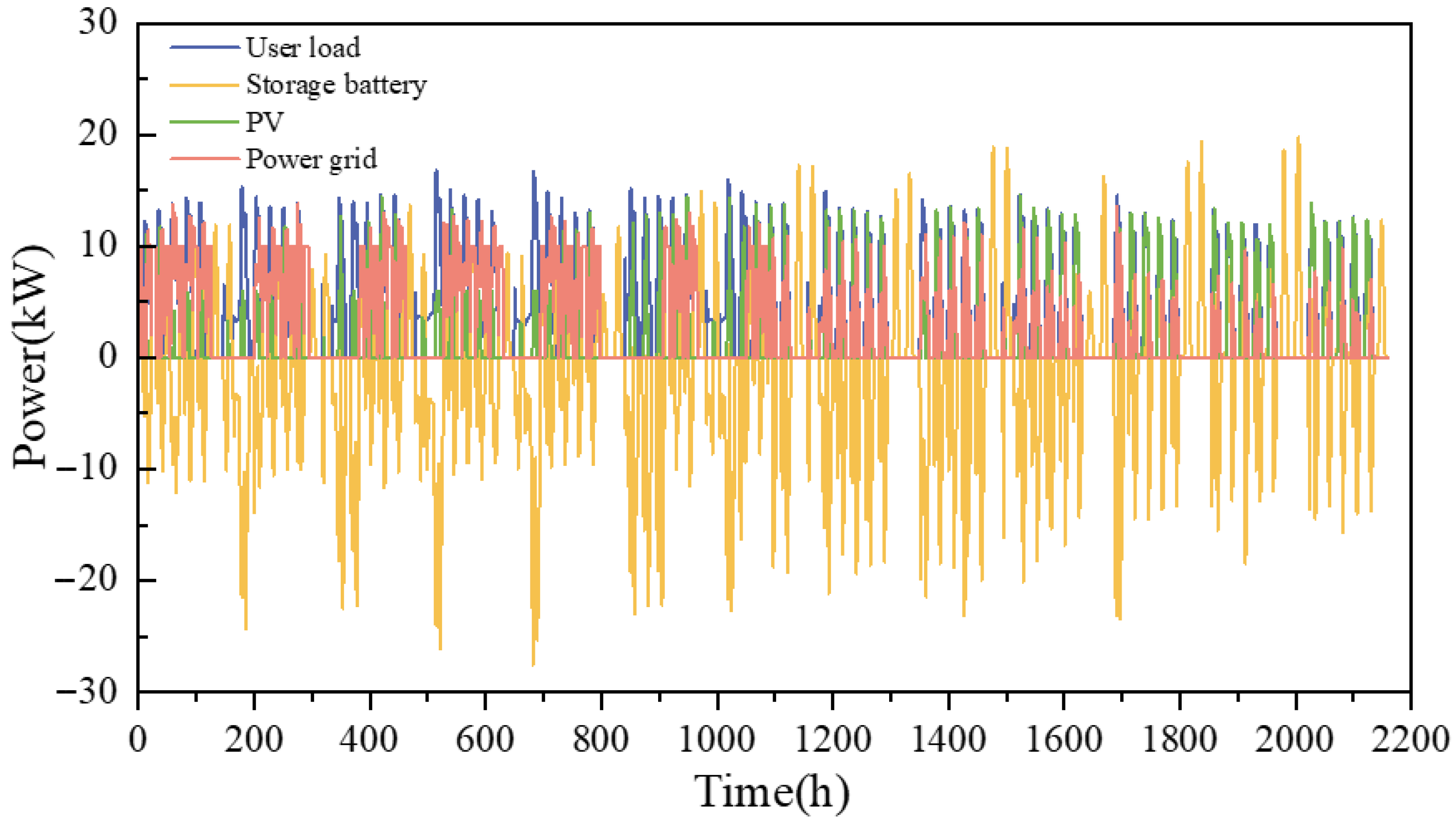


| PV | ESS | Power Grid | |
|---|---|---|---|
| Baseline case | √ | √ | × |
| Case 2 (Flexibility case) | √ | √ | √ |
| Energy System Module | Parameters |
|---|---|
| PV | Monocrystalline silicon photovoltaic panels, 5 × 10 pieces, 45° south |
| ESS | 20/30/40/50 kWh lithium battery, discharge efficiency 0.9, SOC ∈ (0.1, 0.9) |
| GSHP | Single U-shaped ground heat exchanger, with a unit rated heating capacity of 42.78 kWh and a rated cooling capacity of 34.22 kWh. |
| Time (h) | 1–6 | 7 | 8 | 9–11 | 12–13 | 14–17 | 18–19 | 20–24 |
|---|---|---|---|---|---|---|---|---|
| Weekday Usage Proportion (%) | 0 | 10 | 50 | 95 | 80 | 95 | 30 | 0 |
| Holiday Usage Proportion (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Time Period | Price (Yuan) | Time Slot |
| Peak Period | 1.267688 | 17:00–19:00 |
| High Peak Period | 1.020915 | 7:30–11:30, 19:00–21:00 |
| Off-Peak Period | 0.691885 | 5:00–7:30, 11:30–17:00, 21:00–5:00 (next day) |
| 20 kWh | 30 kWh | 40 kWh | 50 kWh | |
| Total annual PV self-consumption | 22,111.14 | 22,639.99 | 23,170.60 | 23,750.45 |
| Annual PV self-consumption rate | 0.68 | 0.70 | 0.71 | 0.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, F.; Yu, S. Quantifying the Impact of Energy Storage Capacity on Building Energy Flexibility: A Case Study of the PV-ESS-GSHP System. Buildings 2025, 15, 3536. https://doi.org/10.3390/buildings15193536
Han F, Yu S. Quantifying the Impact of Energy Storage Capacity on Building Energy Flexibility: A Case Study of the PV-ESS-GSHP System. Buildings. 2025; 15(19):3536. https://doi.org/10.3390/buildings15193536
Chicago/Turabian StyleHan, Fuhong, and Shui Yu. 2025. "Quantifying the Impact of Energy Storage Capacity on Building Energy Flexibility: A Case Study of the PV-ESS-GSHP System" Buildings 15, no. 19: 3536. https://doi.org/10.3390/buildings15193536
APA StyleHan, F., & Yu, S. (2025). Quantifying the Impact of Energy Storage Capacity on Building Energy Flexibility: A Case Study of the PV-ESS-GSHP System. Buildings, 15(19), 3536. https://doi.org/10.3390/buildings15193536





