Theoretical Method for Calculating the Second-Order Effect and Reinforcement of Reinforced Concrete Box Section Columns
Abstract
1. Introduction
2. Calculation of Cross-Sectional Internal Force
2.1. Basic Assumptions
2.2. Constitutive Relationship
2.3. Cross-Sectional Strain Region and Geometric Relationship of the Section
- (1)
- As shown in the box-shaped cross-section in Figure 2a, the black circular dots represent the steel reinforcement bars, and the gray areas indicate the concrete.
- (2)
- Region 1: The neutral axis descends from an infinite position above the cross-section to the upper edge thereof. The stress state undergoes a transformation from uniformly distributed tension to tension with minor eccentricity. At the left boundary of the region, the strain distribution manifests as uniform tension, wherein the strain values of all reinforcing steels attain a specific magnitude .
- (3)
- Region 2, 3, and 4: A portion of the cross-section experiences compressive stresses, with the neutral axis migrating into the cross-section and progressively descending from the upper edge to the lower edge. The load scenarios transition sequentially from tension with minor eccentricity to tension with substantial eccentricity, pure bending, compression with substantial eccentricity, and compression with a minor eccentricity, successively.
- (4)
- Region 5: The right boundary line of Region 4 concurrently serves as the boundary line for Region 5. It rotates counterclockwise around point A to the vertical position (point A can be calculated from the geometric relationship between the upper and lower edge strains of the right boundary line of Region 4). The entire cross-section is subjected to compressive stresses; the neutral axis moves from the bottom of the cross-section to an infinite position below it. The load cases transition from compression with a minor eccentricity to uniform compression.
- (5)
- Strain Continuity and Load Transition: The strain changes continuously from Region 1 to Region 5, and the corresponding load cases also gradually transition.
2.4. Internal Force Calculation of Concrete
2.5. The Internal Force Calculation of Reinforcing Steels
- (1)
- The upper and lower edges: ignoring the influence of the size of the reinforcing steel, the strain at the centre of the reinforcing steels ( and ) can be calculated as follows based on Figure 3:
- (2)
- The webs: to simplify the calculation, the scattered reinforcing steels are simplified into reinforcing steel strips with the same area as the original reinforcing steels, as shown in Figure 3. The per unit length area of the reinforcing steel strips can be written as follow:
2.6. Calculation of the Full Cross-Section Resistance
2.7. Relationship Between the Mechanical Ratio of Reinforcement and Dimensionless Ultimate Eccentricity
2.8. Relationship Between Normal Relative Force and Dimensionless Ultimate Curvature
3. Simplified Calculations of the Second-Order Effect of Columns (In Terms of Members)
4. Equilibrium of Internal Resistance and External Effect
4.1. The Equilibrium of the Second-Order Bending Moment of the Member and the Internal Force of the Cross-Section
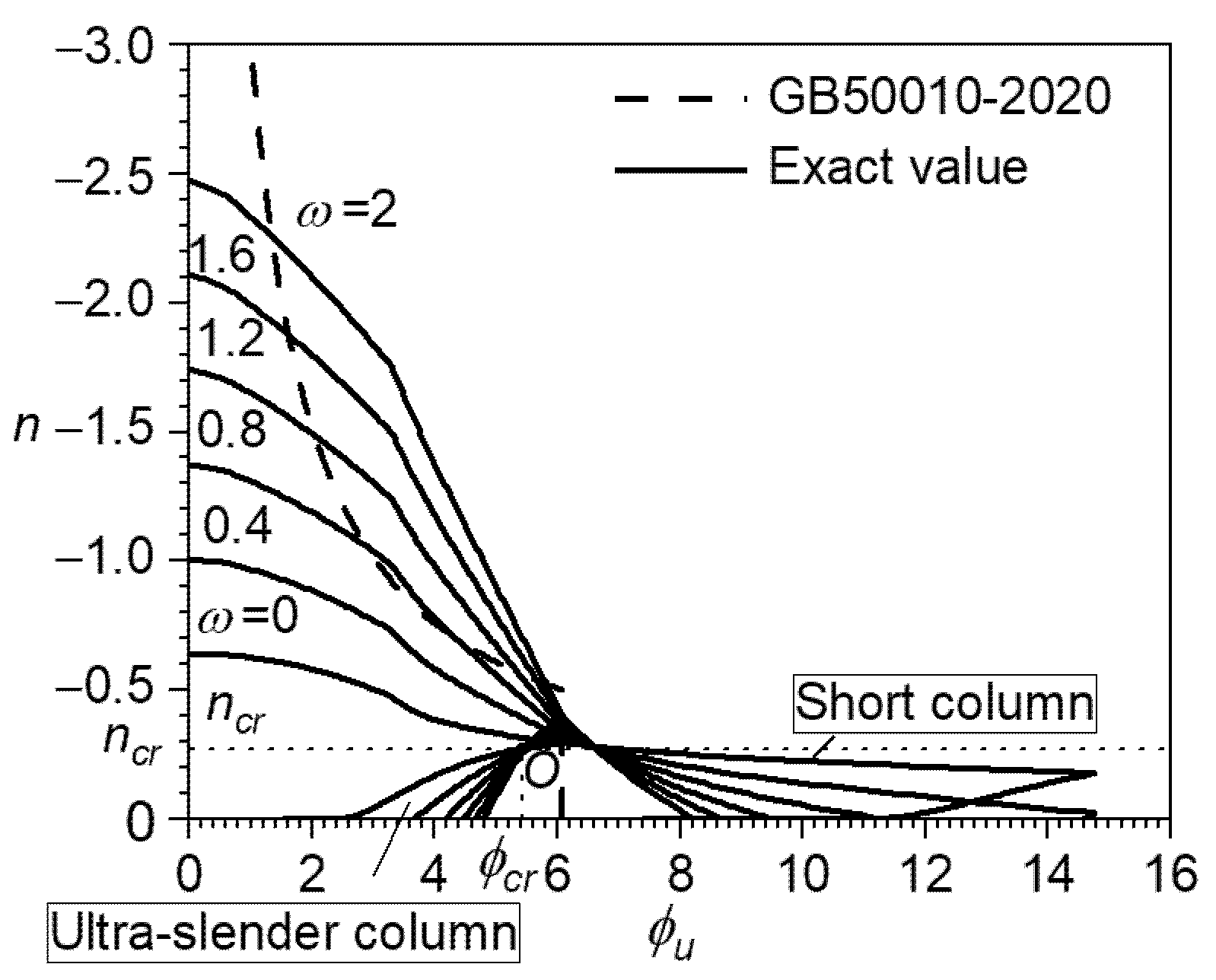
4.2. Simplification of Dimensionless Ultimate Curvature
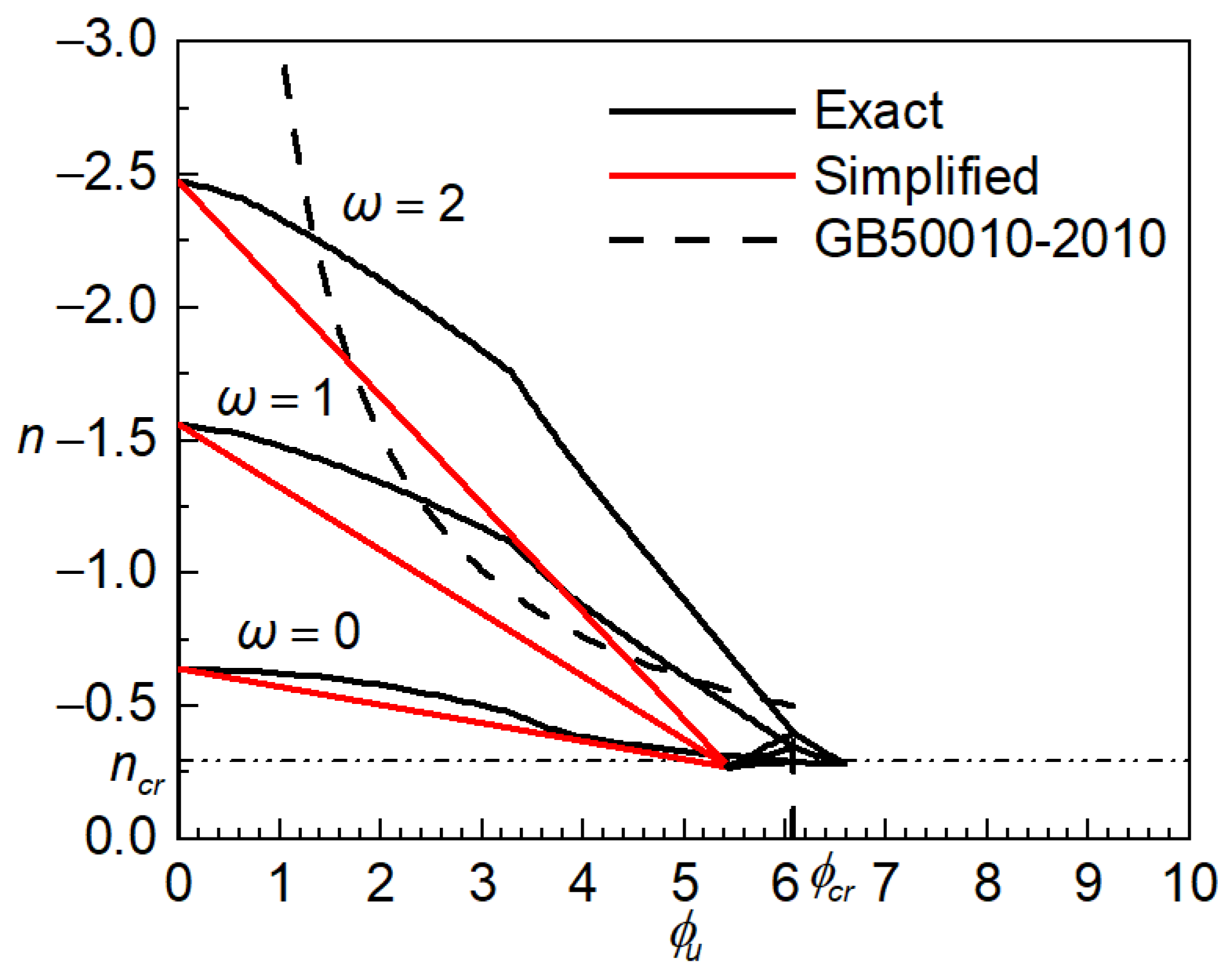
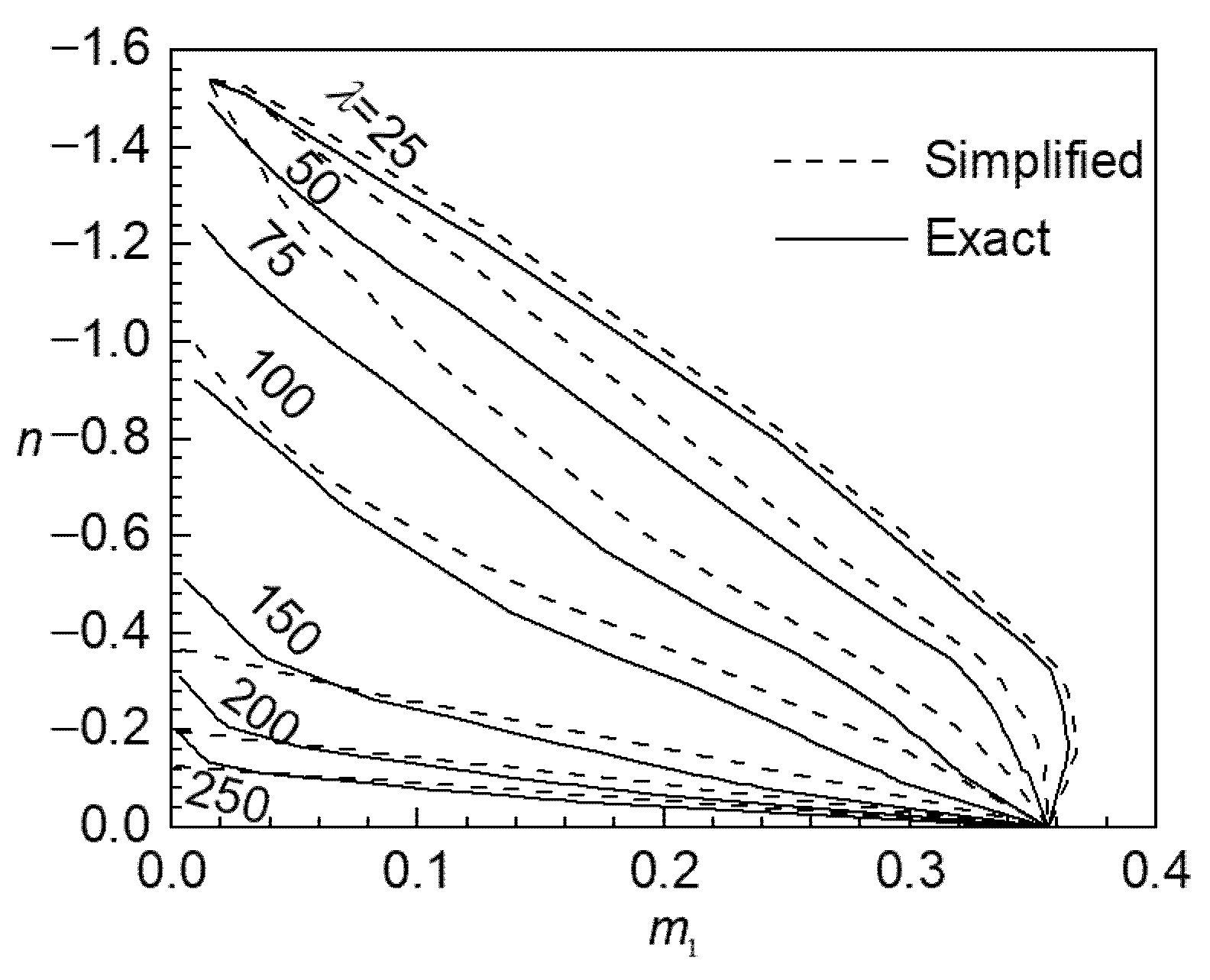
4.3. Error Analysis of Calculating Column Bearing Capacity with Simplified Ultimate Curvature
5. Nomograms for Calculating the Mechanical Ratio of Reinforcement and Second Effect of Columns
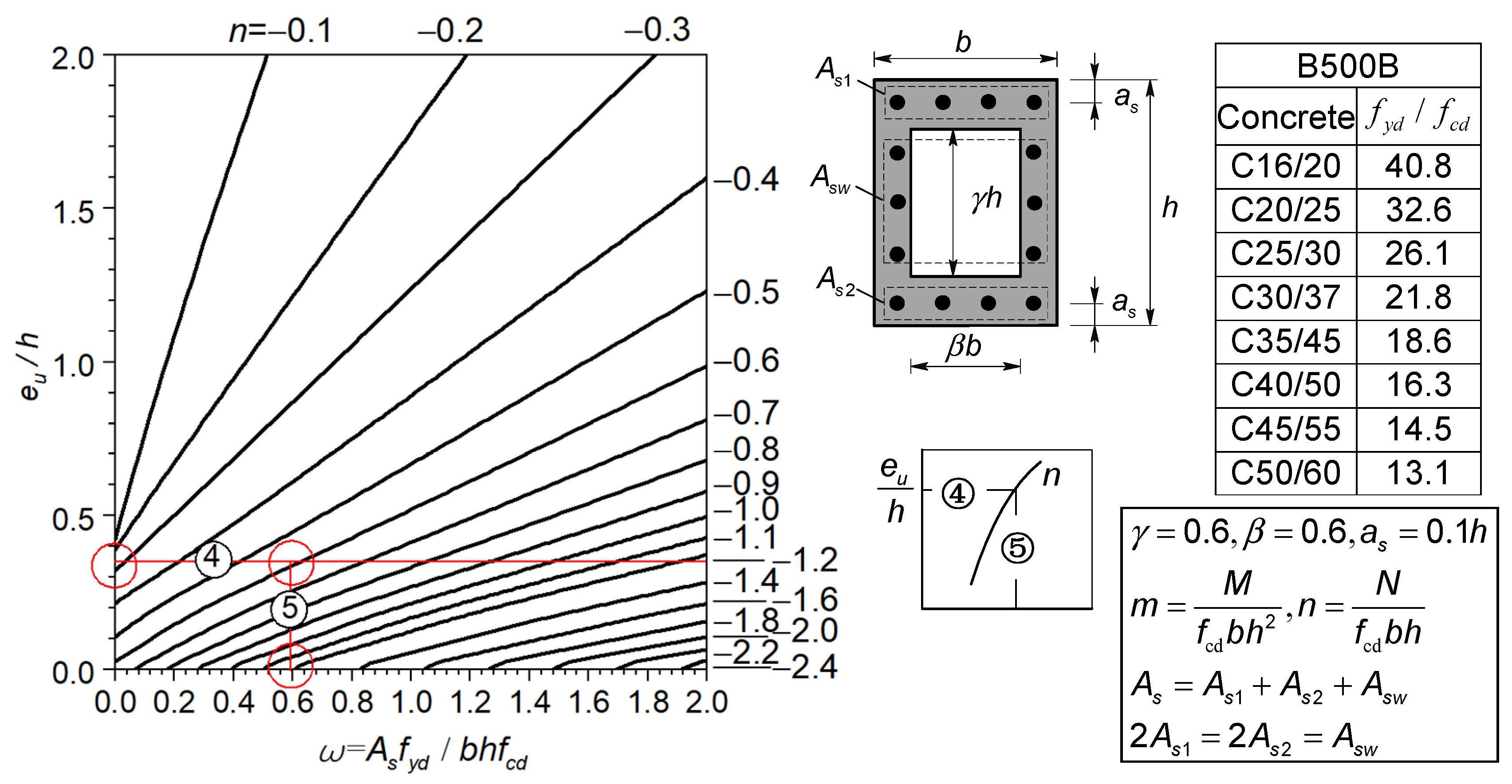
5.1. Drawing Method of the Nomogram
- (1)
- The slope of the external effect line in Figure 7 can be obtained by Equation (23):
- (2)
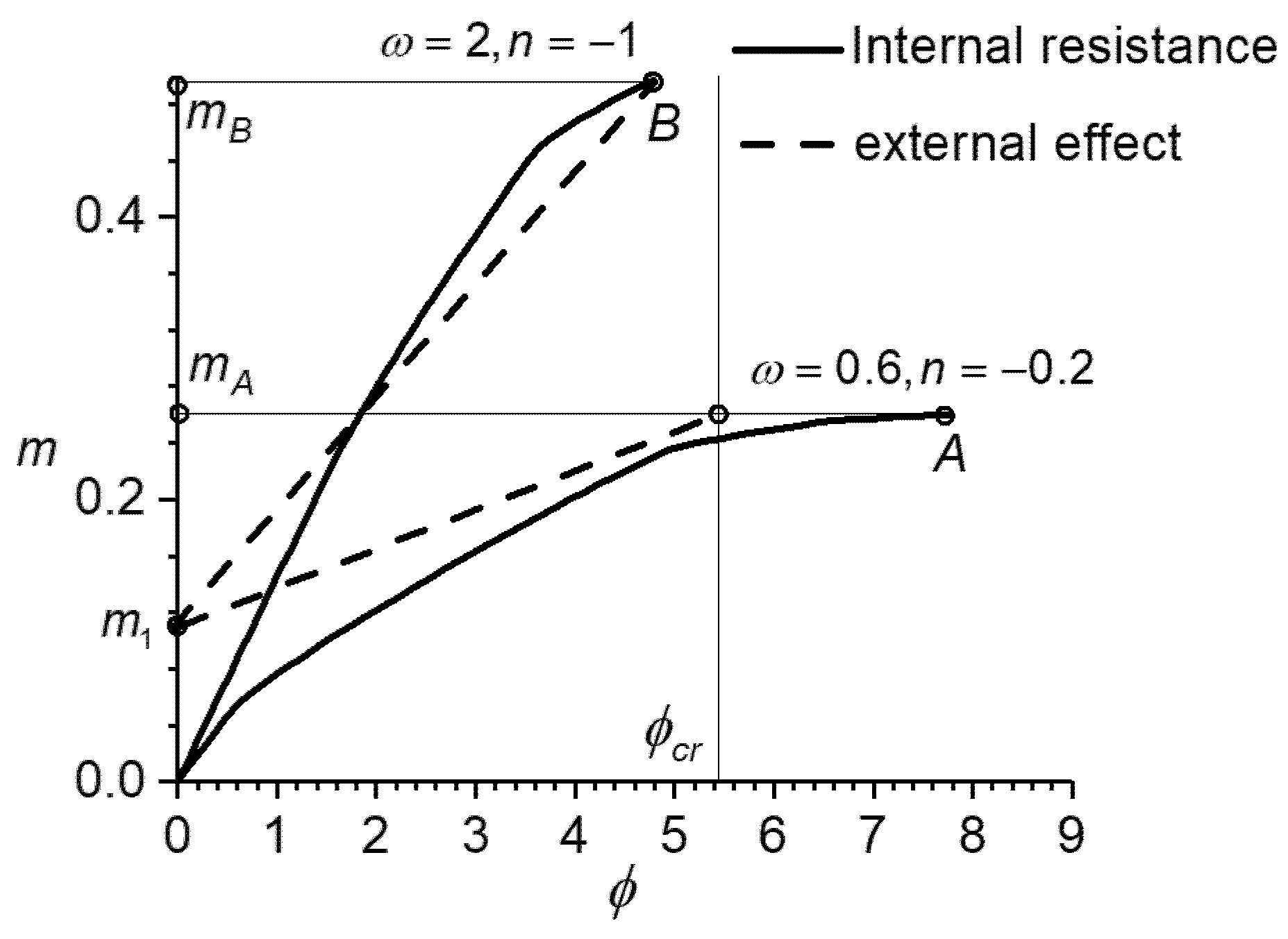
- The part of internal resistance: each value of n is selected from −0.1 to −2.4 and is fixed, then we let increase from 0 to 2 with the steps of 0.01, thus of the cross-section can be calculated with calculation methods presented in Section 2.6, and the simplified dimensionless ultimate curvature can be calculated by Equation (24). Curves can be drawn with as the abscissa and as the ordinate, as shown in Figure 10.
5.2. The Specific Steps of Using the Nomograms
- (1)
- Compute , , and according to the known load and component size.In Figure 10:
- (2)
- Draw line ① by known ;
- (3)
- Draw line ② by making the parallel line of line ① through ;
- (4)
- Draw a horizontal line ③ through the intersection point of line ② and the known n curve to find the value of ;
- (5)
- Calculate using the following equations: , ;In Figure 4:
- (6)
- Draw horizontal line ④ by known ;
- (7)
- Draw a vertical line ⑤ through the intersection point of line ④ and the known curve to the abscissa to find .
5.3. Comparison of Nomograms and GB 50010-2010
- (1)
- Calculate using the nomogramsFirst-order dimensionless eccentricity is:Normal relative force is:Dimensionless first-order bending moment is:
- (2)
- Calculate using GB 50010-2010
- (3)
- Comparison of the two methods
- (1)
- The dimensionless ultimate curvature calculated by GB 50010-2010 is only related to the normal relative force. When , the simplified ultimate curvature values calculated by GB 50010-2010 and the nomograms are both fixed values, as shown in Figure 8. At this time, the values of calculated by the two methods are very close. In examples 1 and 2, the difference is within 6%. As the increases, the difference in decreases, while the difference in increases.
- (2)
- In Example 3, the difference in and calculated by the two methods is 5% and −12%, respectively. Although the and calculated by GB 50010-2010 are larger than that calculated by nomograms, the calculated by GB 50010-2010 is smaller than those calculated by nomograms. It shows that the difference between the two methods is reflected in the value of and of the column, and also in the internal force calculation of the cross-section.
- (3)
- Only when the and are both small, as in Example 1, is as calculated by the nomograms more economical, and, in other cases, it is safer.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
List of Abbreviations
| Total reinforcement area | |
| Total area of upper reinforcement | |
| Total area of lower reinforcement | |
| The total area of the web reinforcing steel strips | |
| The per unit length area of the web reinforcing steel strips | |
| Distance between the longitudinal reinforcement force point and the near edge of the section | |
| The width of the cross-section | |
| Elastic modulus of reinforcement | |
| Flexural rigidity of section | |
| First-order eccentric distance | |
| Second-order eccentric distance | |
| Total eccentric distance | |
| Ultimate eccentric distance | |
| Lateral concentrated force | |
| Design compressive strength of concrete | |
| Design tensile (compressive) strength of reinforcement | |
| The height of the cross-section | |
| The height of the web reinforcing steel strips | |
| Effective height of the cross-section | |
| Simplified slope of the external action curve | |
| Length of column | |
| Effective length of column | |
| Total bending moment distributed along the length of the member | |
| First-order bending moment | |
| Second-order bending moment | |
| Bending moment of concrete | |
| Bending moment of reinforcing steel | |
| Bending moment of reinforcing steel at the upper and lower edges | |
| Bending moment of the web reinforcing steel strips | |
| Maximum bending moment distributed along the length of the member | |
| Ultimate bending moment of the cross-section | |
| Dimensionless bending moment () | |
| Dimensionless first-order bending moment | |
| Dimensionless second-order bending moment | |
| Dimensionless bending moment of concrete | |
| Dimensionless bending moment of reinforcing steel | |
| Dimensionless maximum bending moment distributed along the length of the member | |
| Dimensionless ultimate bending moment | |
| Axial force | |
| Axial force of concrete | |
| Axial force of reinforcing steel | |
| Axial force of reinforcing steel at the upper and lower edges | |
| Axial force of the web reinforcing steel strips | |
| Ultimate axial force | |
| Dimensionless axial force/axial tension ratio/axial compression ratio () | |
| Dimensionless resultant force of concrete | |
| Critical dimensionless axial force at strain of | |
| The dimensionless resultant force of reinforcement in reinforced concrete section | |
| Dimensionless deflection coordinate | |
| Dimensionless length coordinate | |
| Geometric parameters of the cross-section: The height ratio between the hollow part and the exterior of the box-shaped cross-section | |
| Geometric parameters of the cross-section: The width ratio between the hollow part and the exterior of the box-shaped cross-section | |
| Strain | |
| Design compressive strain of concrete | |
| Concrete strain at any location of cross-section | |
| Upper edge strain of concrete section | |
| Lower edge strain of concrete section | |
| Strain at any location of cross section | |
| Design compressive strain of reinforcing steel | |
| Reinforcing steel strain at any location of cross-section | |
| Upper reinforcement strain of reinforced concrete section | |
| Lower reinforcement strain of reinforced concrete section | |
| Design yield strain of reinforcing steel | |
| Slenderness ratio () | |
| Stress | |
| Stress of concrete | |
| Stress of upper concrete in reinforced concrete section | |
| Stress of lower concrete in reinforced concrete section | |
| Stress of reinforcing steel | |
| Stress of upper reinforcing steel in reinforced concrete section | |
| Stress of lower reinforcing steel in reinforced concrete section | |
| Curvature | |
| Dimensionless curvature () | |
| Critical dimensionless yield curvature at strain of | |
| Dimensionless ultimate curvature | |
| Dimensionless yield curvature | |
| Mechanical reinforcement ratio of total reinforcing steel () | |
| Mechanical reinforcement ratio of upper reinforcing steel () | |
| Mechanical reinforcement ratio of lower reinforcing steel () | |
| Mechanical reinforcement ratio of web reinforcing steel strips () |
References
- Xu, J.; Gong, J. Nonlinear Second-Order Effect of Non-Sway Columns. ACI Struct. J. 2013, 110, 755–765. [Google Scholar]
- Babazadeh, A.; Burgueno, R.; Silva, P.F. P-δ Effects on the Plastic Region of RC Bridge Columns: Closed-Form Solution. J. Struct. Eng. 2016, 142, 04016116. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2010.
- Dundar, C.; Sahin, B. Arbitrarily shaped reinforced concrete members subject to biaxial bending and axial load. Comput. Struct. 1993, 49, 643–662. [Google Scholar] [CrossRef]
- Dündar, C. Concrete box sections under biaxial bending and axial load. Struct. Eng. 1990, 116, 860–865. [Google Scholar] [CrossRef]
- Pisani, M.A. A numerical method to analyse compact cross-sections. Comput. Struct. 1996, 59, 1063–1072. [Google Scholar] [CrossRef]
- Sousa, J.B.M.; Muniz, C.F.D.G. Analytical integration of cross section properties for numerical analysis of reinforced concrete, steel and composite frames. Eng. Struct. 2007, 29, 618–625. [Google Scholar] [CrossRef]
- Qiu, F.; Li, W.; Pan, P.; Qian, J. Experimental tests on reinforced concrete columns under biaxial quasi-static loading. Eng. Struct. 2002, 24, 419–428. [Google Scholar] [CrossRef]
- Hong, H.P. Strength of Slender Reinforced Concrete Columns under Biaxial Bending. J. Struct. Eng. 2001, 127, 758–762. [Google Scholar] [CrossRef]
- Chang, S.-Y. Experimental Studies of Reinforced Concrete Bridge Columns under Axial Load Plus Biaxial Bending. J. Struct. Eng. 2010, 136, 12–25. [Google Scholar] [CrossRef]
- Di Ludovico, M.; Verderame, G.M.; Prota, A.; Manfredi, G.; Cosenza, E. Experimental Behavior of Nonconforming RC Columns with Plain Bars under Constant Axial Load and Biaxial Bending. J. Struct. Eng. 2013, 139, 897–914. [Google Scholar] [CrossRef]
- Kwak, H.-G.; Kwak, J.-H. An improved design formula for a biaxially loaded slender RC column. Eng. Struct. 2010, 32, 226–237. [Google Scholar] [CrossRef]
- Barrera, A.C.; Bonet, J.L.; Romero, M.L.; Fernández, M. Ductility of slender reinforced concrete columns under monotonic flexure and constant axial load. Eng. Struct. 2012, 40, 398–412. [Google Scholar] [CrossRef]
- Dundar, C.; Tokgoz, S.; Tanrikulu, A.K.; Baran, T. Behaviour of reinforced and concrete-encased composite columns subjected to biaxial bending and axial load. Build. Environ. 2008, 43, 1109–1120. [Google Scholar] [CrossRef]
- Guan, Z.; Zhang, J.; Li, J. A Robust Computational Method for Ultimate Strength Analysis of Arbitrary Reinforced Concrete and Composite Sections Subjected to Axial Force and Biaxial Bending. Adv. Struct. Eng. 2014, 17, 83–96. [Google Scholar] [CrossRef]
- Perdomo, C.; Monteiro, R. Simplified damage models for circular section reinforced concrete bridge columns. Eng. Struct. 2020, 217, 110794. [Google Scholar] [CrossRef]
- Laora, R.D.; Galasso, C.; Mylonakis, G.; Cosenza, E. A simple method for N-M interaction diagrams of circular reinforced concrete cross sections. Struct. Concr. 2020, 21, 48–55. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Sextos, A.G. Design charts for rectangular R/C columns under biaxial bending: A historical review toward a Eurocode-2 compliant update. Eng. Struct. 2016, 115, 196–206. [Google Scholar] [CrossRef]
- Klempka, K.; Jędrzejczak, M. Design of Slender Reinforced Concrete Columns of Annular Cross-Section According to the Nominal Curvature Method and the Exact Method. In Proceedings of the 2017 Baltic Geodetic Congress (BGC Geomatics), Gdansk, Poland, 22–25 June 2017; pp. 143–147. [Google Scholar]
- Wang, J.; Wang, X.; Duan, Y.; Su, Y.; Yi, X. The Investigation on Mechanical Performances of High-Strength Steel Reinforced Concrete Composite Short Columns under Axial Load. Materials 2022, 15, 329. [Google Scholar] [CrossRef]
- Lechman, M. Cross-Sectional Analysis of the Resistance of RC Members Subjected to Bending with/without Axial Force. Materials 2022, 15, 1957. [Google Scholar] [CrossRef]
- Zhou, D.H.; Wang, Q.F.; Fan, J.; Gao, Q.X.; Wang, H.Y. A new method for the calculation of reinforcement of concrete: General dimensionless designing diagram. Eng. Mech. 2010, 27, 162–172. [Google Scholar]
- Wei, W.; Zhu, A.; Liu, Y.; Bai, S. Design methods of reinforced concrete frame column considering P-δ effect. J. Build. Struct. 2006, 27, 64–71. [Google Scholar]
- Wei, W.; Qin, H.P.; Yu, D.J. Design method of multiple-story column considering second-order effect in frame structure. J. Build. Struct. 2018, 39, 135–142. [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity; Xu, Z.L.; Wang, Y.Z., Translators; People’s Education Press: China, Beijing, 1964. [Google Scholar]
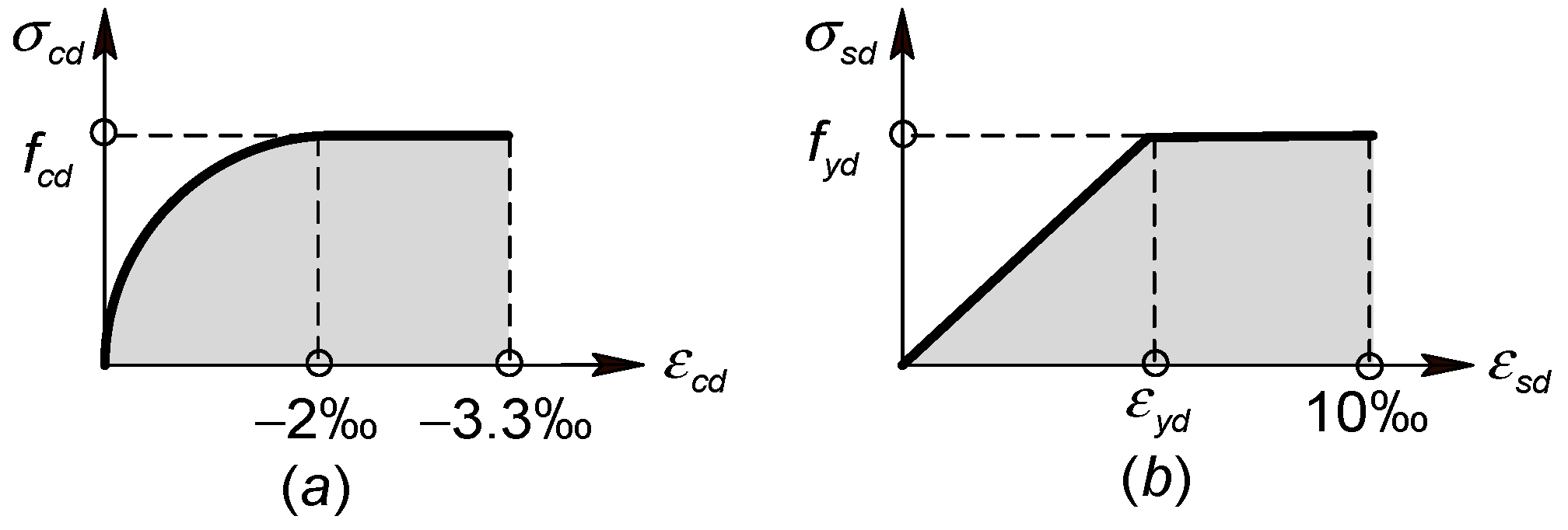

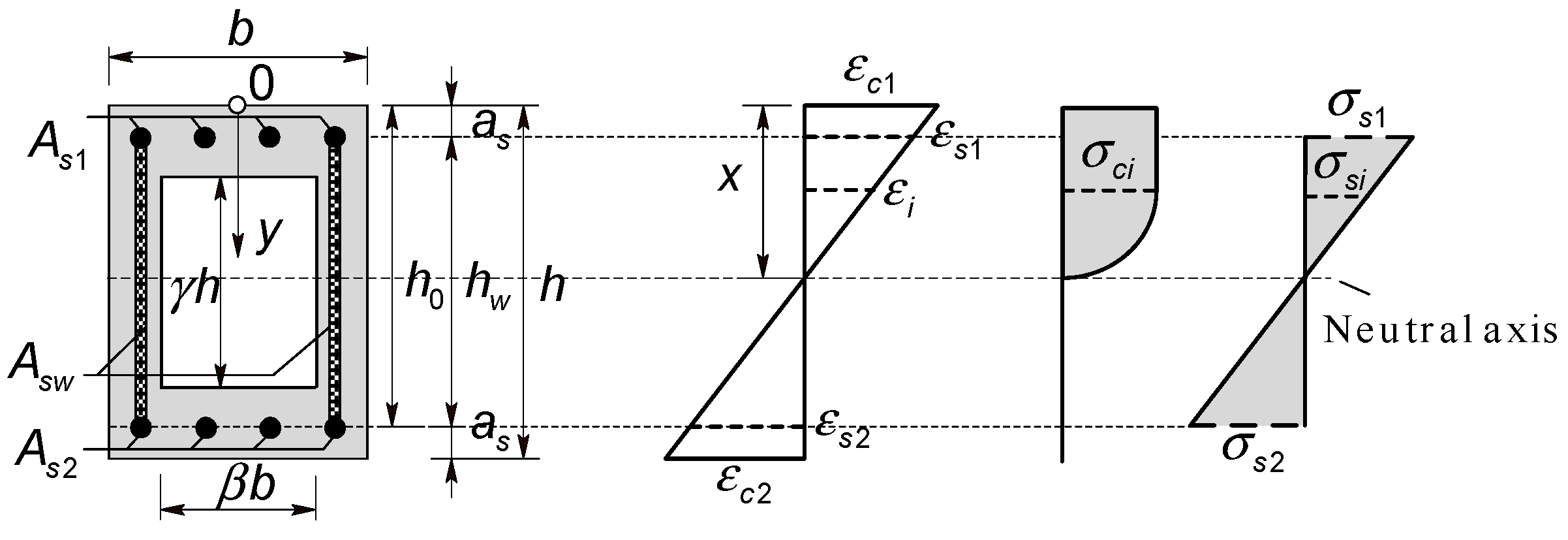
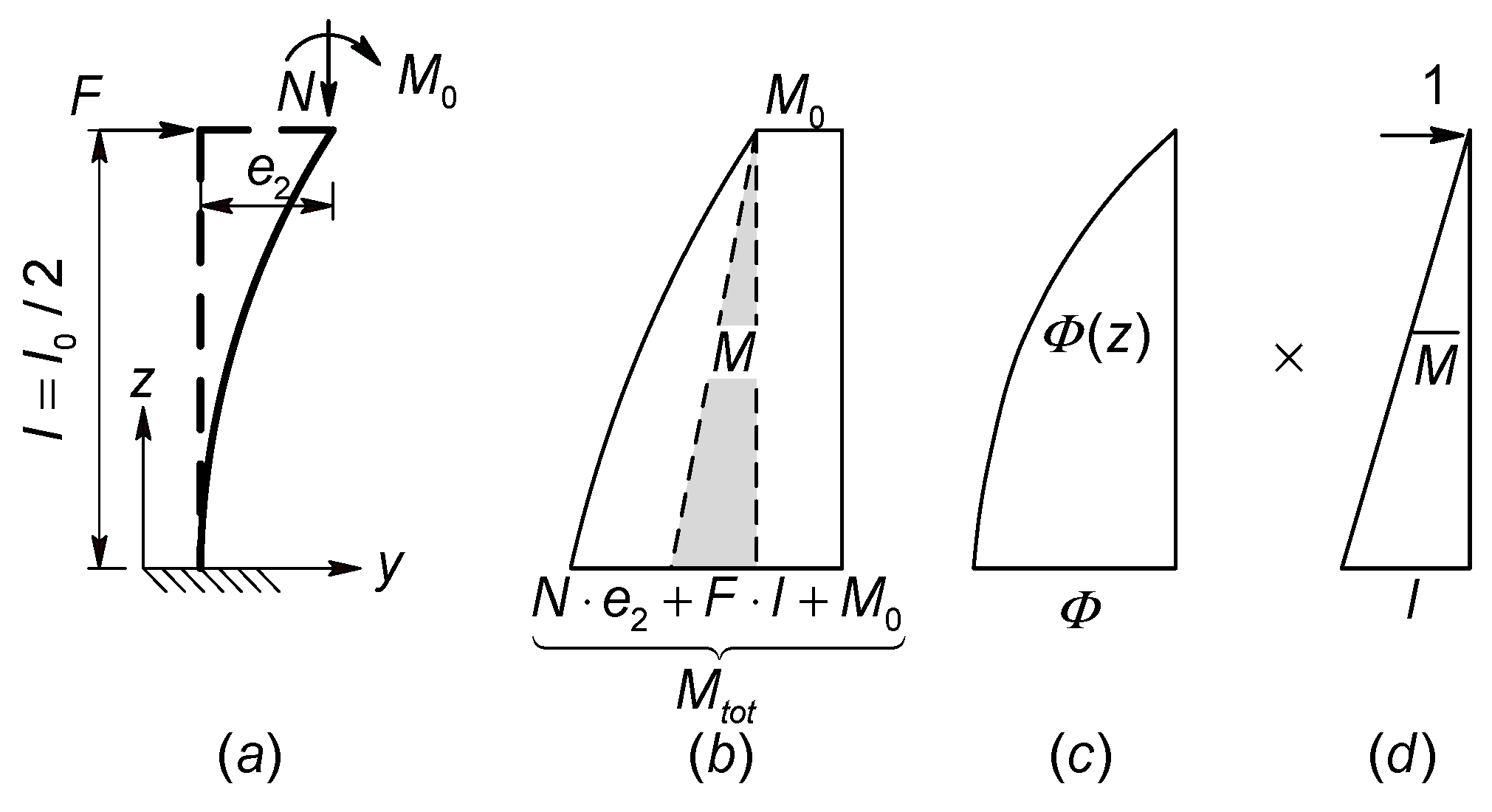

| Examples | (mm)2 | (Code) | (Nomogram) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) Code | (2) Nomogram | (1) Code | (2) Nomogram | ||||||||
| 1 | −0.2 | 0.1 | 20 | 0.152 | 0.145 | 1.05 | 1684 | 1603 | 1.05 | 6.30 | 5.44 |
| 2 | −0.2 | 0.5 | 20 | 0.555 | 0.545 | 1.02 | 11,992 | 12,759 | 0.94 | 6.30 | 5.44 |
| 3 | −0.6 | 0.3 | 20 | 0.430 | 0.408 | 1.05 | 9353 | 10,602 | 0.88 | 5.25 | 4.32 |
| 4 | −1 | 0.1 | 20 | 0.204 | 0.191 | 1.07 | 6162 | 7310 | 0.84 | 3.15 | 2.19 |
| 5 | −1 | 0.3 | 20 | 0.425 | 0.446 | 0.95 | 11,418 | 14,344 | 0.80 | 3.15 | 3.49 |
| 6 | −2 | 0.1 | 20 | 0.183 | 0.189 | 0.97 | 13,369 | 15,286 | 0.87 | 1.58 | 1.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Chen, G.; Zhou, D.; Guo, X. Theoretical Method for Calculating the Second-Order Effect and Reinforcement of Reinforced Concrete Box Section Columns. Buildings 2025, 15, 3528. https://doi.org/10.3390/buildings15193528
Li L, Chen G, Zhou D, Guo X. Theoretical Method for Calculating the Second-Order Effect and Reinforcement of Reinforced Concrete Box Section Columns. Buildings. 2025; 15(19):3528. https://doi.org/10.3390/buildings15193528
Chicago/Turabian StyleLi, Lu, Gang Chen, Donghua Zhou, and Xuefeng Guo. 2025. "Theoretical Method for Calculating the Second-Order Effect and Reinforcement of Reinforced Concrete Box Section Columns" Buildings 15, no. 19: 3528. https://doi.org/10.3390/buildings15193528
APA StyleLi, L., Chen, G., Zhou, D., & Guo, X. (2025). Theoretical Method for Calculating the Second-Order Effect and Reinforcement of Reinforced Concrete Box Section Columns. Buildings, 15(19), 3528. https://doi.org/10.3390/buildings15193528





