Investigation on the Mechanical Response of a Prefabricated Underground Pipe Gallery with a Flexible Energy Dissipation Node: An Experimental Study
Abstract
1. Introduction
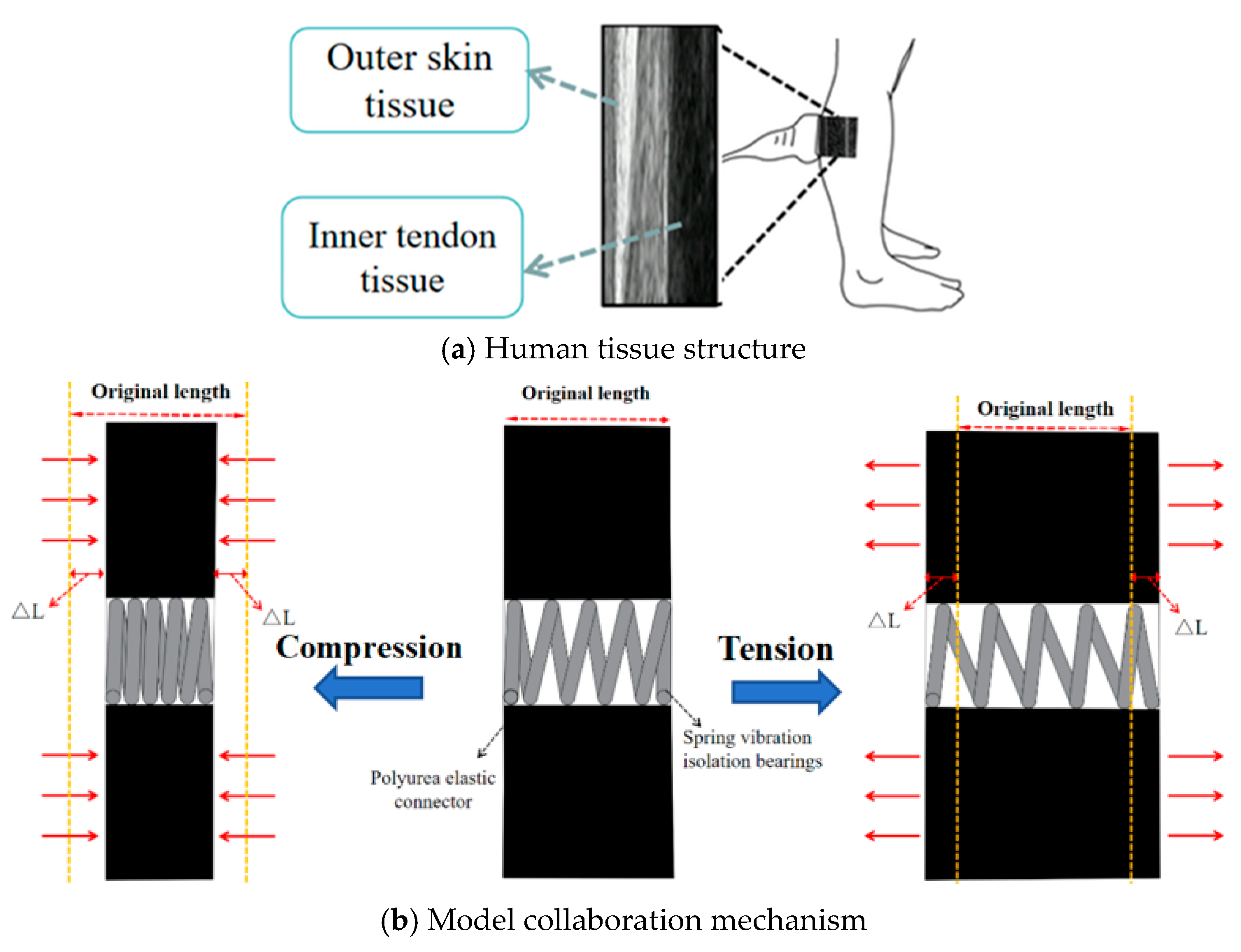
2. The Concept of a “Skin-Tendon” Flexible-Connection Structure
2.1. Source of Inspiration
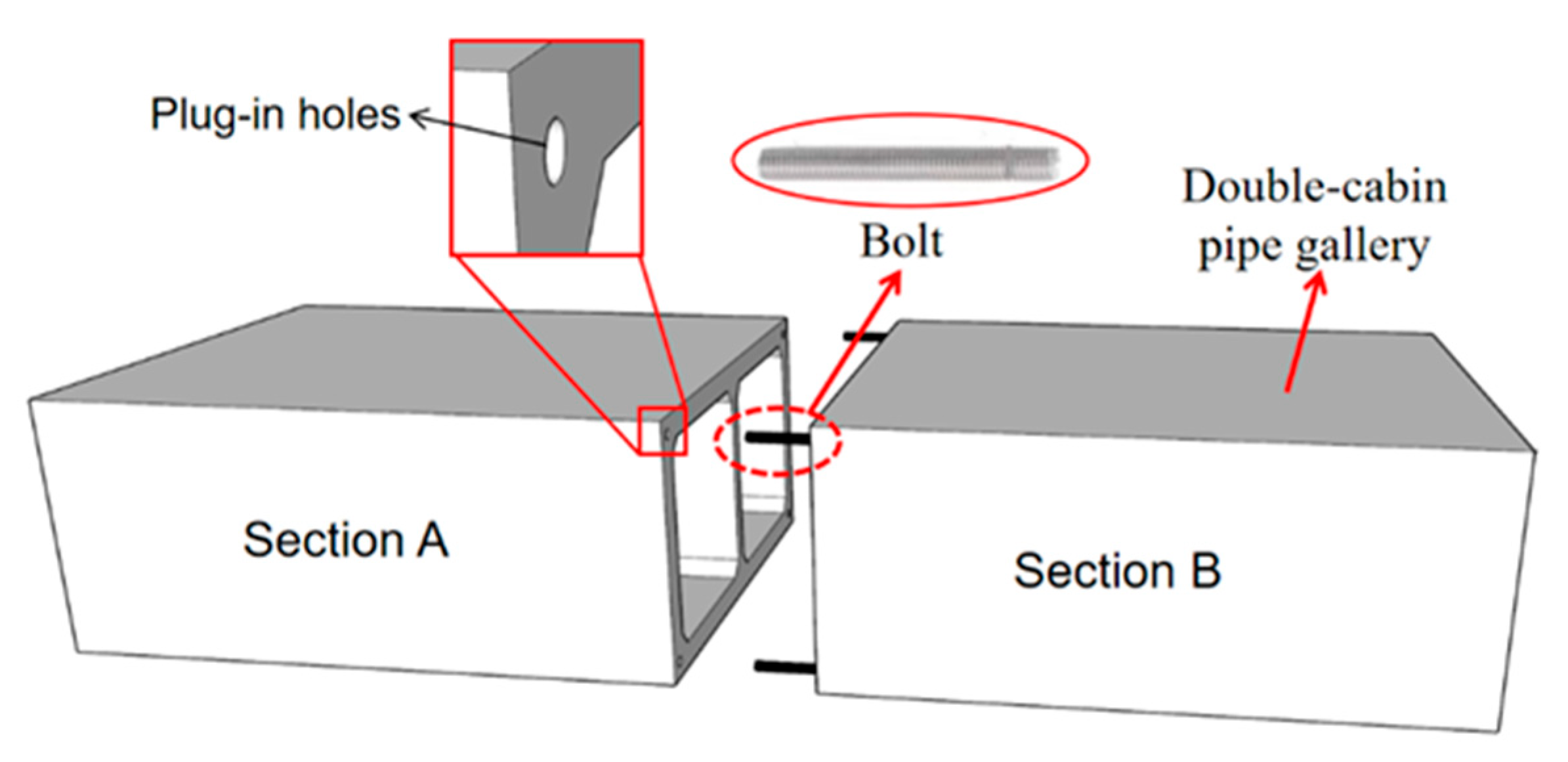
2.2. Construction of Rigid-Connection and Flexible-Connection Nodes
2.3. Joint Connection Material
- (1)
- Polyurea elastic connector material
- (2)
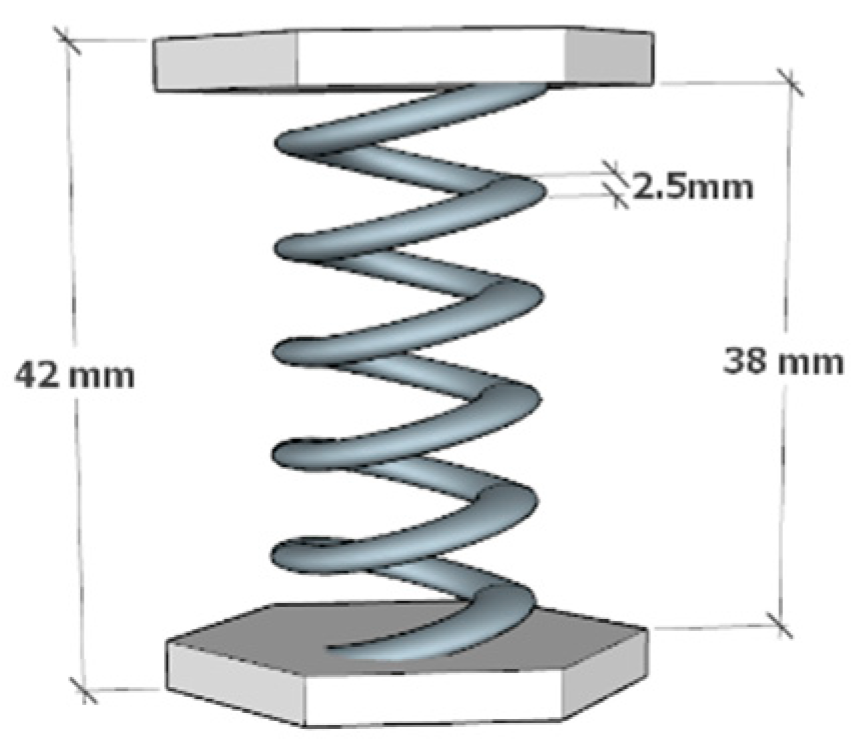
- Spring vibration isolation bearing
- (3)
- Material behavior of embedded bolt
3. Design of Model Test
3.1. Similarity Relation of Physical Quantity in Model Test
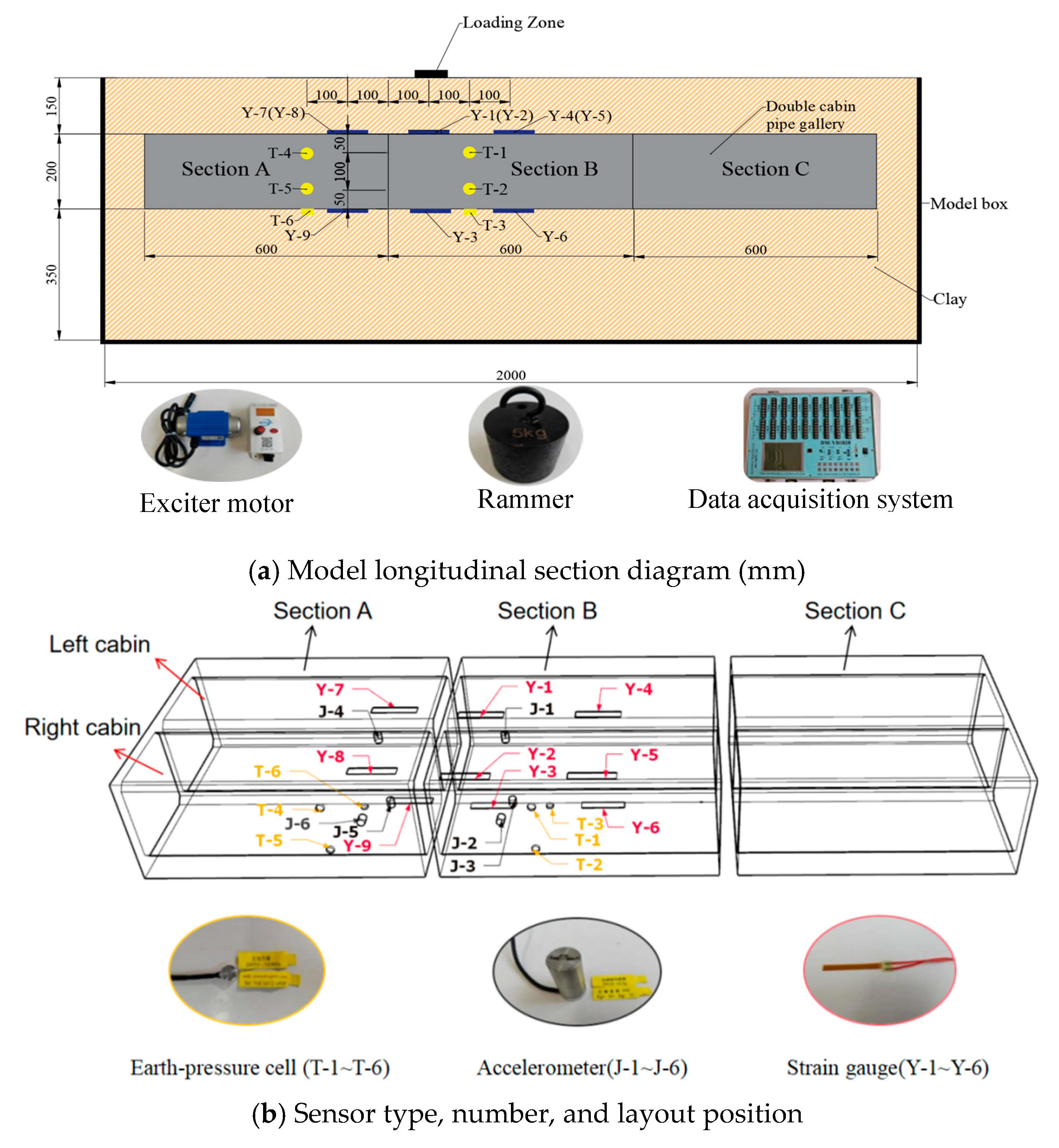
3.2. Model Test System and Sensor Layout
3.3. Installation Steps of the Pipe Gallery
3.4. Test Scheme
4. Results
4.1. Response Analysis of the Pipe Gallery Under Machine Vibration
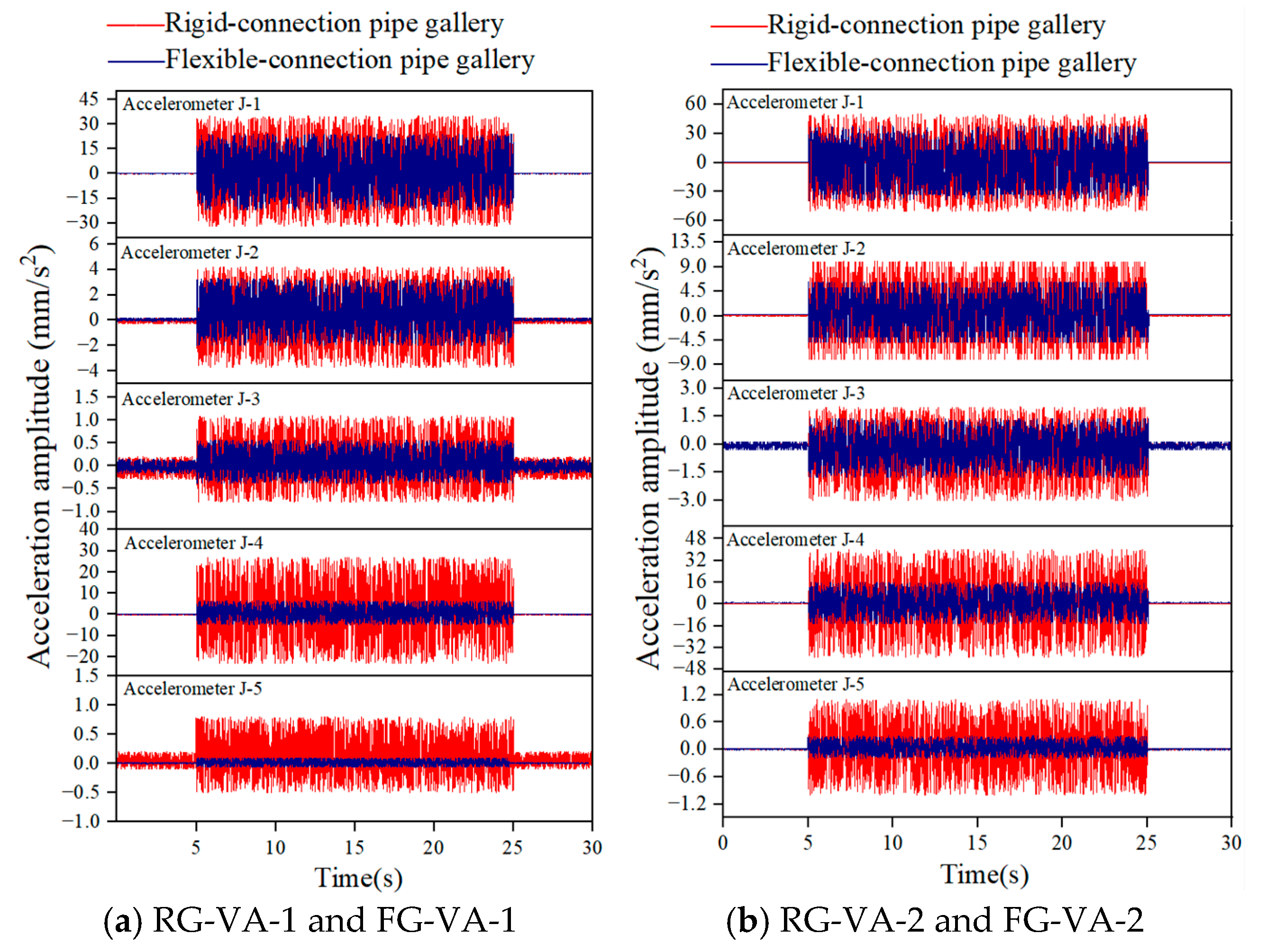
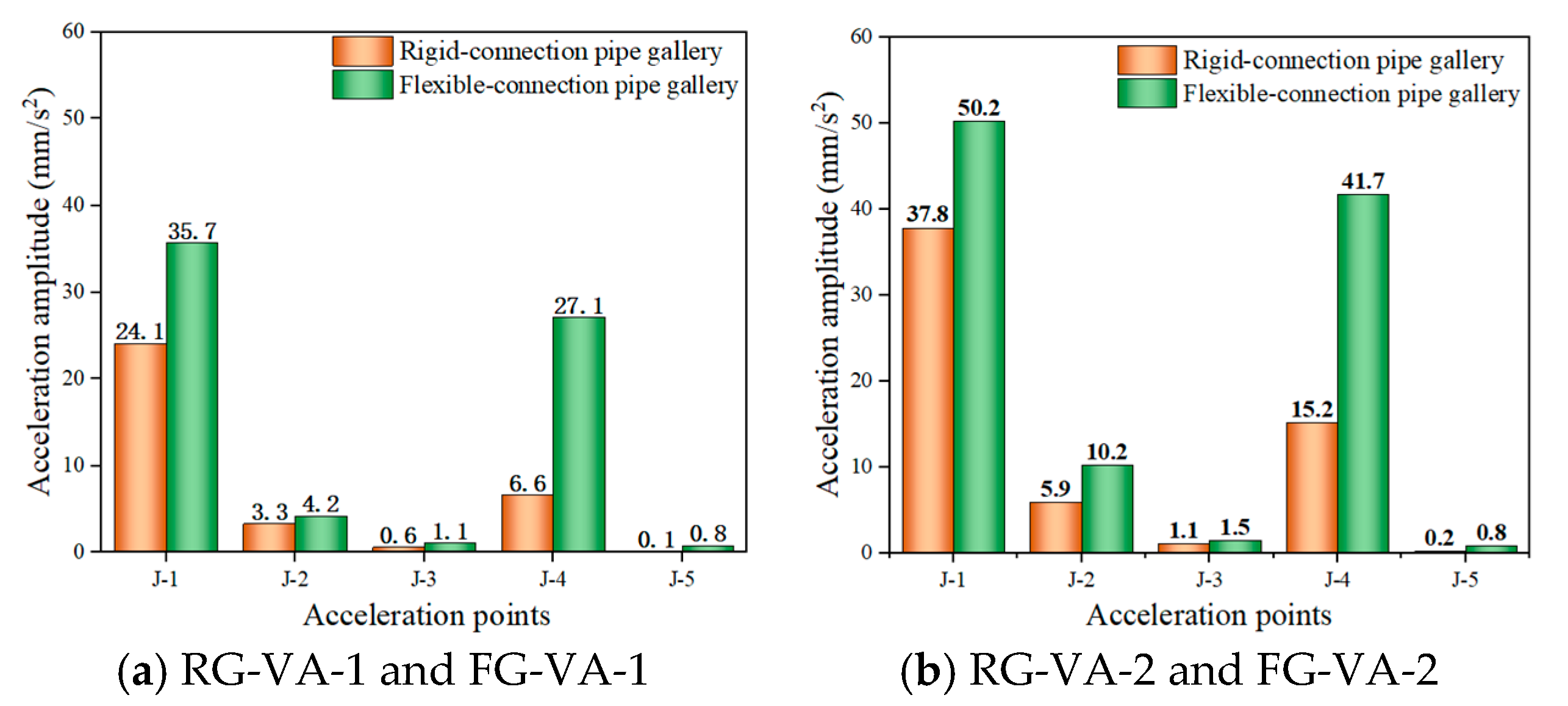
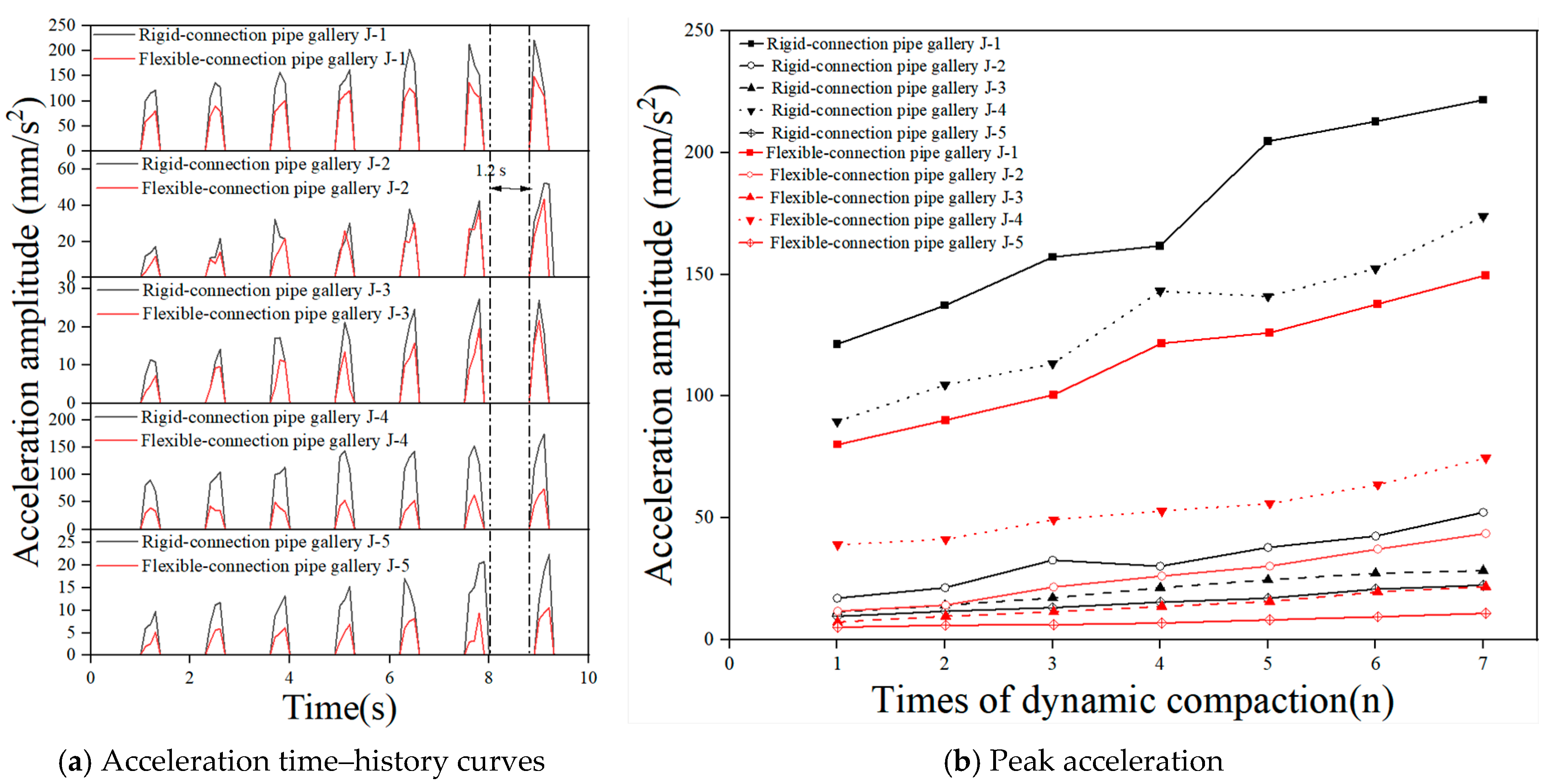
4.1.1. Acceleration
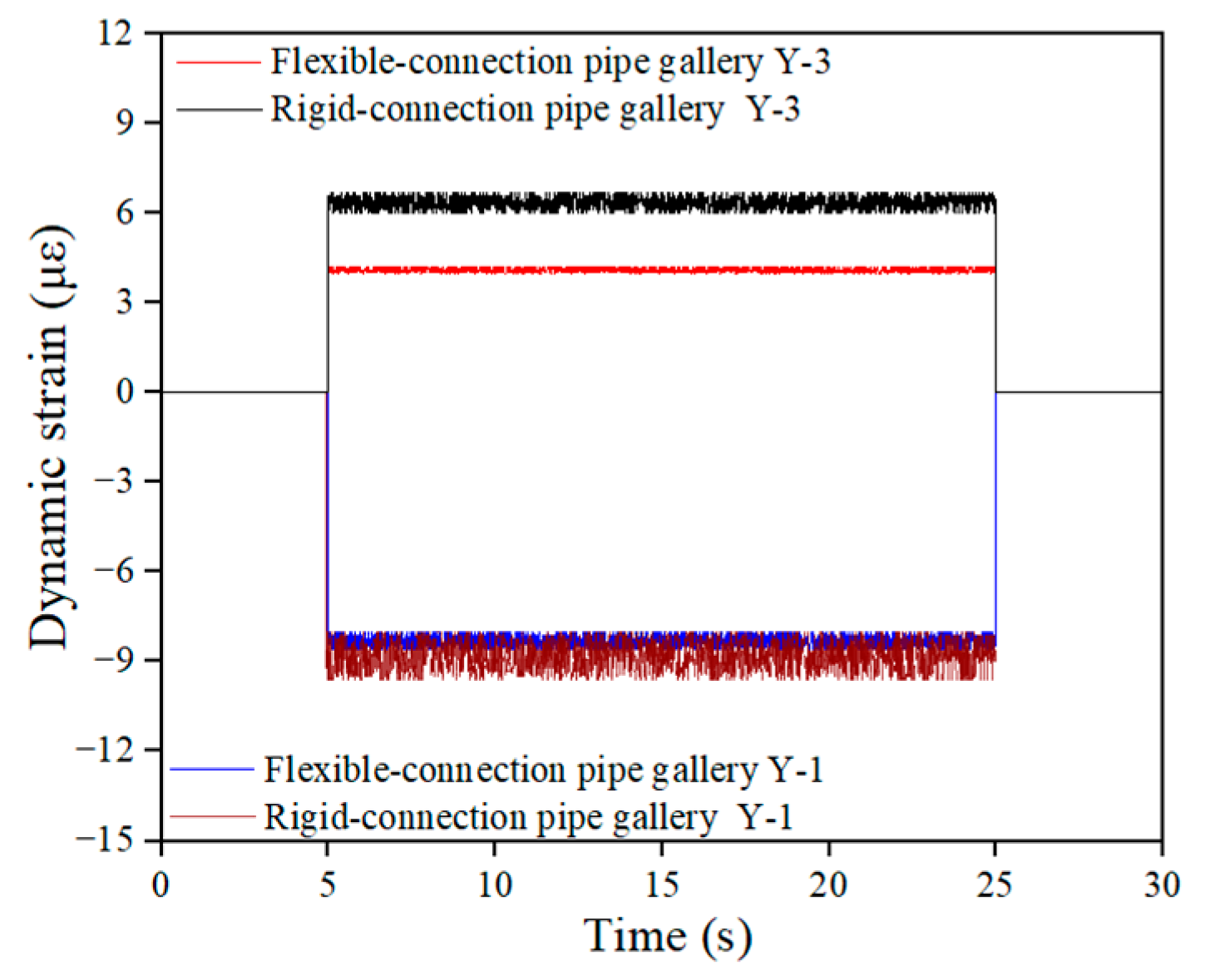
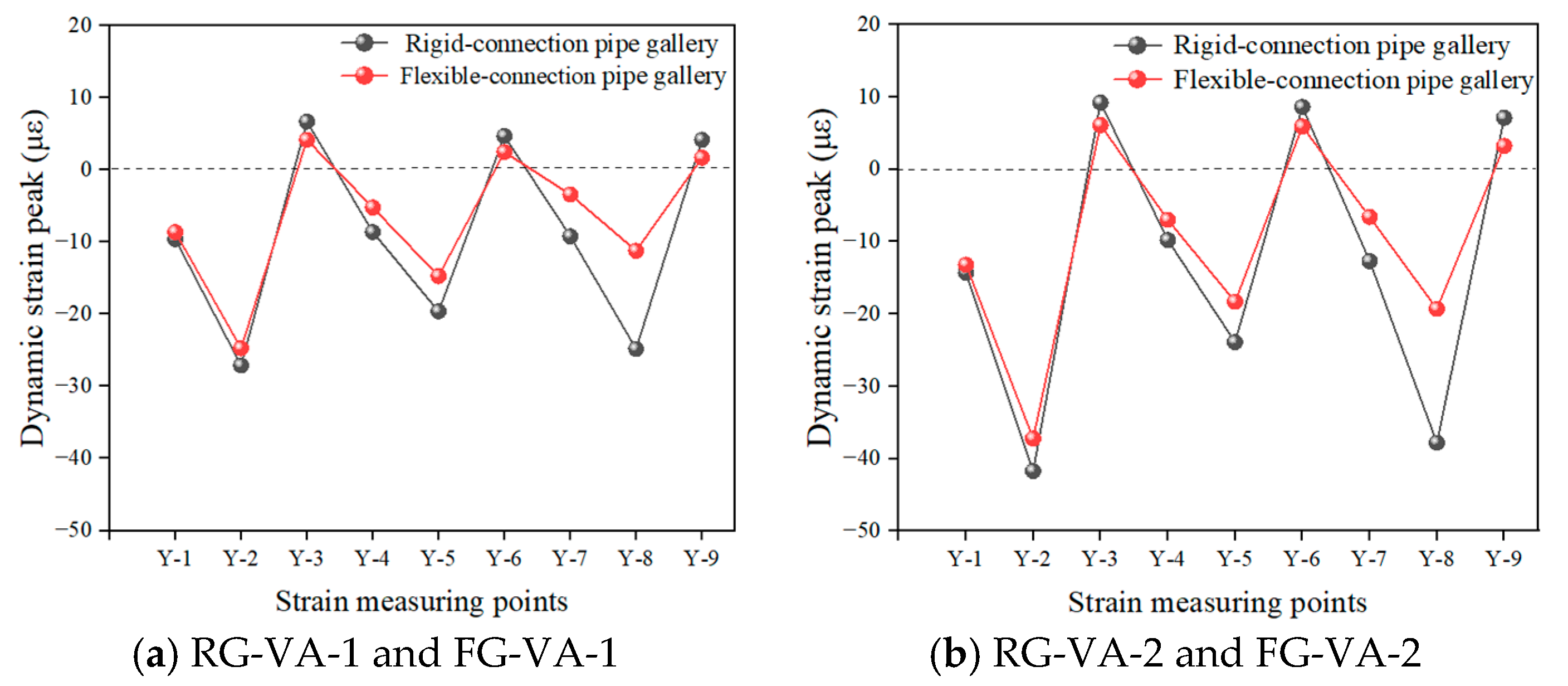
4.1.2. Dynamic Strain Response
4.1.3. Dynamic Earth Pressure
4.2. Response Analysis of Pipe Gallery Under Dynamic Compaction
4.2.1. Acceleration
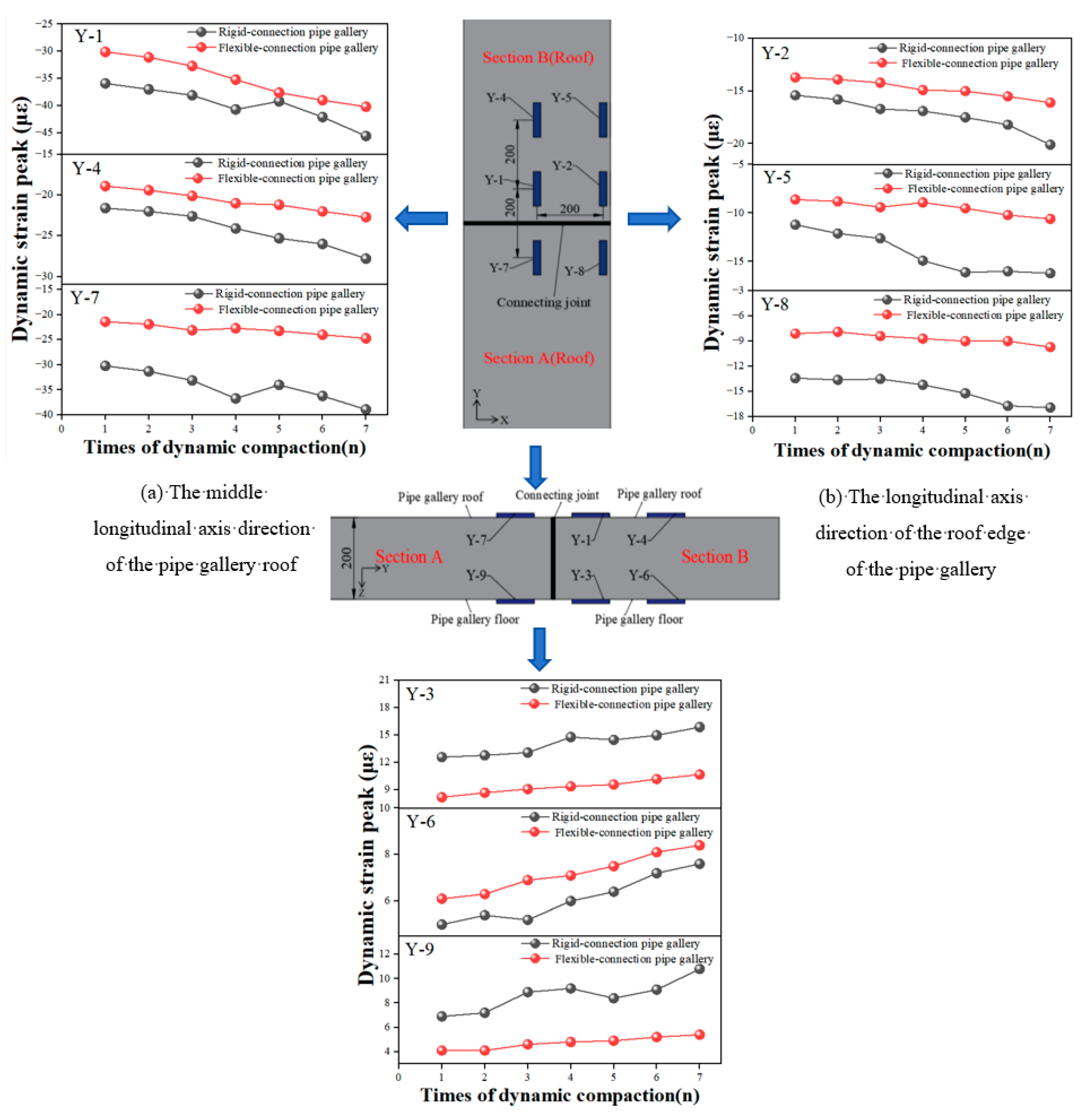
4.2.2. Dynamic Strain Response
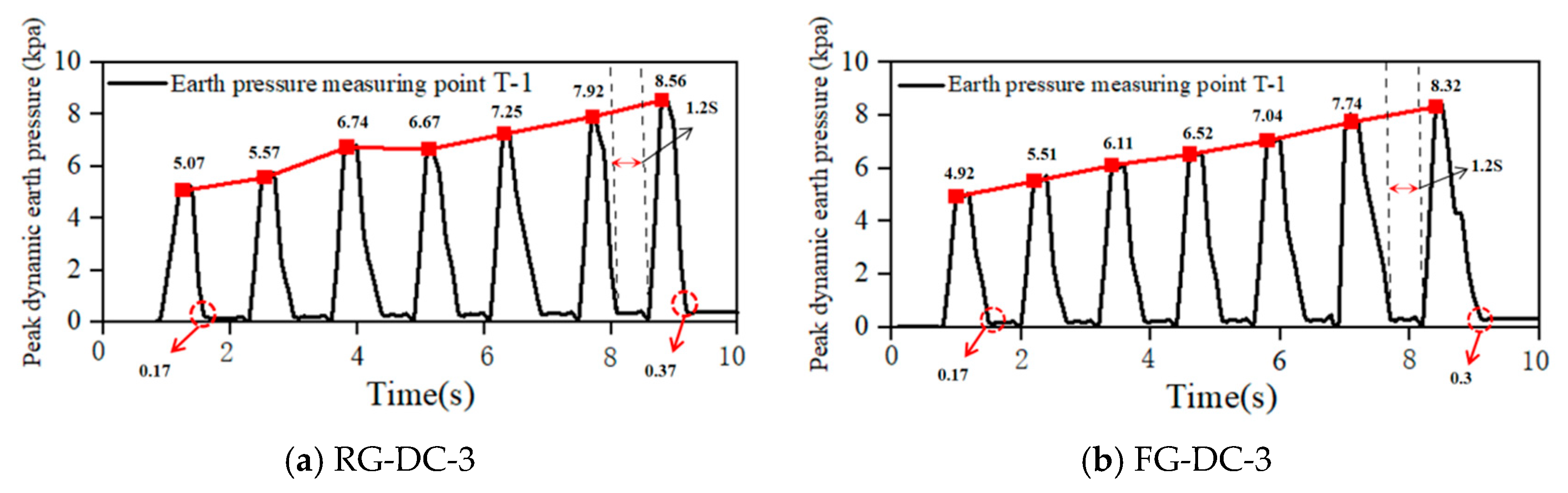
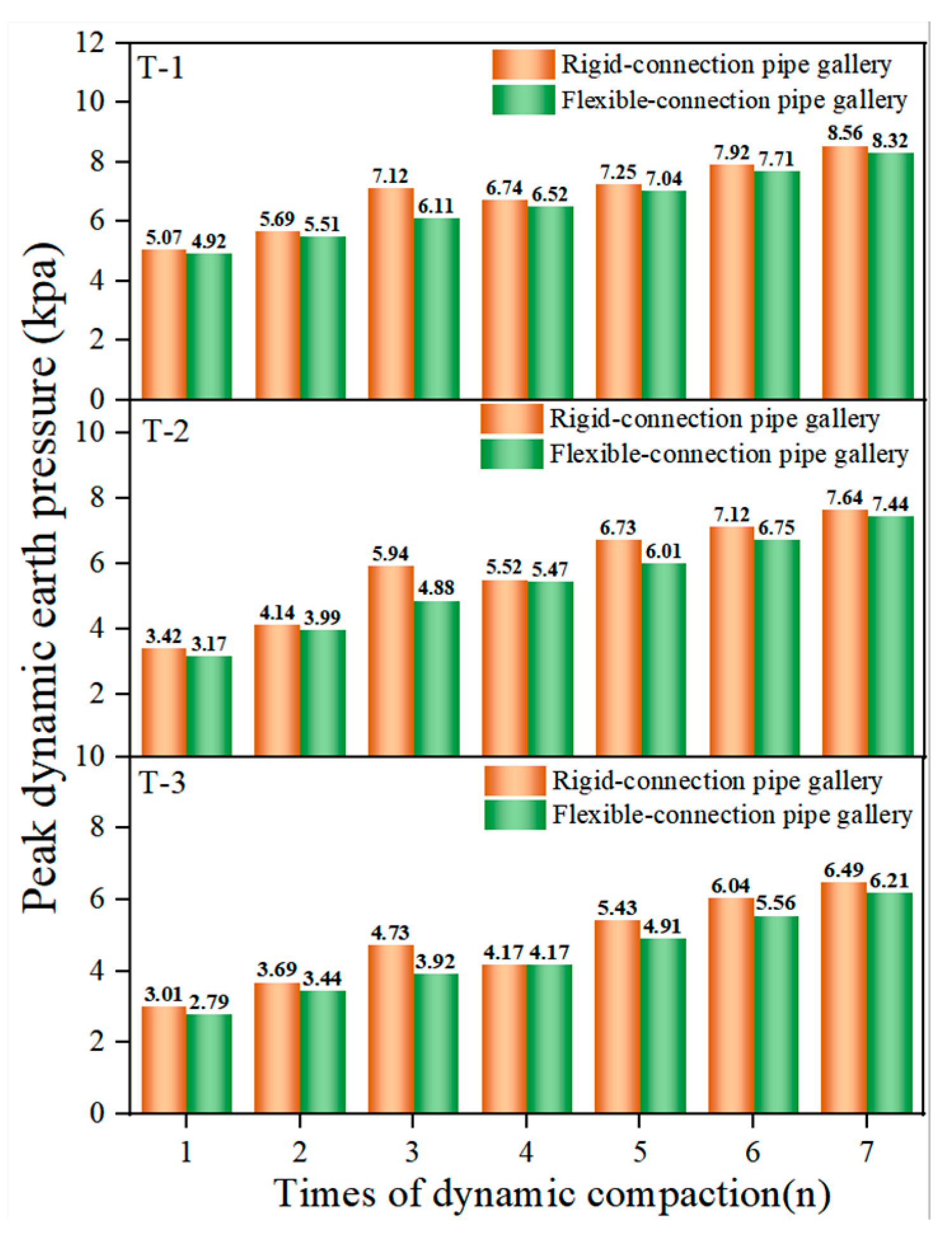
4.2.3. Dynamic Earth Pressure
5. Discussion
5.1. Result Analysis
5.2. Energy Attenuation Mechanism
5.3. Long-Term Performance
6. Conclusions
- (1)
- A flexible-connection node of “skin-tendon” for the pipe gallery structure has been proposed. The node is composed of an “outer skin” made by a polyurea grouting slurry and an “inner rib” composed of the spring vibration isolation bearing.
- (2)
- Under dynamic compaction, the maximum attenuation rates of acceleration and the dynamic strain of flexible-connection nodes are 51.4% and 42.2%, respectively, while those of rigid-connection nodes are only 21.5% and 14.6%, respectively. Under machine vibration, the maximum attenuation rates of acceleration and the dynamic strain of flexible-connection nodes are 72.6% and 60.4%, respectively. However, those of rigid-connection nodes are only 24.1% and 11.1%, respectively.
- (3)
- Under identical load conditions, the earth pressure measured at the pipe gallery structure with flexible nodes is smaller than that with rigid nodes, with a reduction range of 2.2–7.9%. Additionally, dynamic compaction generates residual earth pressure, leading to increased pressure on the side walls of the pipe gallery. Therefore, the reinforcement ratio of the pipe gallery structure should be increased to enhance the load-bearing capacity.
- (4)
- There may be scaling effects in the model test, but the mechanical properties and response laws of the prototype can still be basically revealed. The combination structure of “skin-tendon” flexible-connection nodes is not unique, and different materials with a similar performance can be used in combination to ensure the energy efficiency of the nodes. Future research will aim to establish theory and numerical models to conduct a quantitative analysis; at the same time, the feasibility of the flexible-connection node under complex loading would be verified.
- (5)
- Although this study incorporates bionic principles, verification for the self-recovery capability of flexible-connection nodes after vibration is also lacking. The current sensor layout mainly focuses on capturing global strain responses, and energy dissipation during load propagation is neglected. To capture energy changes in the underground pipe gallery accurately during load propagation, the installation distance between sensors should be reduced. These improvements will bridge the gap between the model test and engineering practice and provide guides for the design of underground pipe gallery structures more effectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Canto-Perello, J.; Curiel-Esparza, J. Assessing governance issues of urban utility tunnels. Tunn. Undergr. Space Technol. 2013, 33, 82–87. [Google Scholar] [CrossRef]
- Legrand, L.; Blanpain, O.; Buyle-Bodin, F. Promoting the urban utilities tunnel technique using a decision-making approach. Tunn. Undergr. Space Technol. 2004, 19, 79–83. [Google Scholar] [CrossRef]
- Zhang, W.; Han, L.; Feng, L.; Ding, X.; Wang, L.; Chen, Z.; Liu, H.; Aljarmouzi, A.; Sun, W. Study on seismic behaviors of a double box utility tunnel with joint connections using shaking table model tests. Soil Dyn. Earthq. Eng. 2020, 136, 106118. [Google Scholar] [CrossRef]
- Tian, T.; Yao, A.; Li, Y.; Gong, Y. Seismic response of utility tunnels with different burial depths at the non-homogeneous liquefiable site. Appl. Sci. 2022, 12, 11767. [Google Scholar] [CrossRef]
- Darli, C.M.; Tang, A.; Huang, D.; Zhang, J. Large-scale shaking table model test and analysis on seismic response of utility tunnel in non-homogeneous soil. Earthq. Eng. Eng. Vib. 2021, 20, 505–515. [Google Scholar] [CrossRef]
- Deng, B.; Zheng, X.; Shen, C.; Fu, Y. Study on dynamic response characteristics of shallow buried pipe gallery structure under vehicle vibration load. Soil Dyn. Earthq. Eng. 2024, 181, 108597. [Google Scholar] [CrossRef]
- Wang, G.; Yin, Y.; Wang, J. Vibration safety evaluation and vibration isolation control measures for buried oil pipelines under dynamic compaction: A case study. Soil. Dyn. Earthq. Eng. 2023, 167, 107783. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Z.; He, J.; Huang, Z. Experimental Study on Seismic Performance of Prefabricated Joints of Underground Utility Tunnel. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 042109. [Google Scholar] [CrossRef]
- Li, D.; Liang, J.; Dong, B.; Ba, Z. A multi-scale model for longitudinal seismic design of prefabricated utility tunnel based on multi-point constraints. Structures 2024, 62, 106176. [Google Scholar] [CrossRef]
- Wu, X.; Nie, C.; Li, D.; Qiu, F.; Tang, Y. Structural response of a prefabricated utility tunnel subject to a reverse fault. Buildings 2022, 12, 1086. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Huang, W.; Shan, H.; Zhu, L.; Song, G. Research on natural foundation bearing capacity and foundation pit settlement of prefabricated utility tunnel. Adv. Civ. Eng. 2022, 2022, 5361199. [Google Scholar] [CrossRef]
- Yang, M.; Li, H.; Li, N.; Yang, S.; Dede, T. Effect of subway excavation with different support pressures on existing utility tunnel in Xi’an loess. Adv. Civ. Eng. 2020, 2020, 8818949. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Z.; Zhang, H. Numerical analysis on the features of road deformation in the construction process of heat supply pipeline works. Alex. Eng. J. 2020, 60, 159–171. [Google Scholar] [CrossRef]
- Yang, M.; Li, H.; Li, N.; Yang, S.; Hao, X. Influence of Utility Tunnel on the Lower Part of the Existing Double-Track Shield Tunnel in Loess Soil. Adv. Mater. Sci. Eng. 2021, 2021, 9927245. [Google Scholar] [CrossRef]
- Deng, B.-T.; Li, P.; Li, X.; Tian, J.-T.; Zhi, B. Mechanical behavior of underground pipe gallery structure considering ground fissure. J. Mt. Sci. 2022, 19, 547–562. [Google Scholar] [CrossRef]
- Ma, J.; Cui, G.; He, S.; Liu, X. Application of isolation technology in shallow super-large comprehensive pipe galleries in seismically vulnerable areas with weak soils. Appl. Rheol. 2023, 33, 20220150. [Google Scholar] [CrossRef]
- Zhao, C.; Lei, M.; Shi, C.; Cao, H.; Yang, W.; Deng, E. Function mechanism and analytical method of a double layer pre-support system for tunnel underneath passing a large-scale underground pipe gallery in water-rich sandy strata: A case study. Tunn. Undergr. Space Technol. 2021, 115, 104041. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Q.; Hu, Z.; Yang, S.; Peng, C.; Zhang, X.; Li, Z.; Wang, X.; Xie, Z. Research on the influence of groundwater in coastal areas on the stress and deformation characteristics of integrated pipe gallery. Geofluids 2022, 2022, 3463752. [Google Scholar] [CrossRef]
- Duan, X.; Dong, Q.; Ye, W. Experimental study on seismic performance of prefabricated utility tunnel. Adv. Civ. Eng. 2019, 2019, 8968260. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, J.; Dong, B.; Xu, A.; Ba, Z. Shaking table test on the seismic performance of prefabricated utility tunnel passing through hard-soft strata under longitudinal excitation. Soil Dyn. Earthq. Eng. 2024, 183, 108788. [Google Scholar] [CrossRef]
- Li, J.; Yue, Q. Research on shaking-table test and finite element numerical simulation of utility tunnel. J. Earthq. Eng. Eng. Vib. 2009, 29, 41–45. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Q. Comparison between the seismic performance of buried pipes and pipes in a utility tunnel. CMES-Comp. Model. Eng. 2020, 123, 661–690. [Google Scholar] [CrossRef]
- Wei, G.; Qiu, H.J.; Wei, X.J. Analysis of settlement control measures in immersed tunnel. Appl. Mech. Mater. 2012, 204, 1449–1453. [Google Scholar] [CrossRef]
- Xiang, B.; Liu, Y.; Cui, J.; Yang, Z. Analytical Solution for the Deformation of Pipe Galleries Adjacent to Deep Excavation. Buildings 2024, 14, 1103. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Z.-D.; Sun, B.; Liu, X.; Xu, D. Spatiotemporal state assessment for the underground pipe gallery: Physical model and experimental verification. Tunn. Undergr. Space Technol. 2024, 143, 105474. [Google Scholar] [CrossRef]
- Zhang, C.; Li, X.; Pang, Y.; Xu, Y. Mechanical Response and deformation mechanism of the utility tunnel crossing an earth fissure. Structures 2024, 64, 106587. [Google Scholar] [CrossRef]
- Dong, L.; Yao, A.; Zhou, D.; Zhang, G.; Zhang, P. Experimental study on seismic behavior of T-joints of composite shell system with prefabricated underground pipe gallery. Structures 2023, 58, 105572. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, J.; Dong, B.; Xu, A.; Ba, Z. Shaking table tests on the seismic performance of prefabricated T-shaped cross utility tunnel. Structures 2023, 58, 105516. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, Z.; Zhang, C.; Pang, Y.; Liu, T. Bearing Capacities and Failure Behaviors of F-Type Socket Joint in Rectangular Pipe Jacking Tunnel. Appl. Sci. 2023, 13, 5442. [Google Scholar] [CrossRef]
- Chen, H.; Liang, J.; Li, D.; Ba, Z. Transverse seismic analysis method of underground interchange prefabricated utility tunnel. Structures 2024, 68, 107112. [Google Scholar] [CrossRef]
- Zhu, L.; Shangguan, S.; Yu, H.; Guo, Y.; Chen, Z.; An, D.; Zhang, X. Quasi-Static Test Study on Seismic Behavior of Large-Section Fabricated Utility Tunnel. Shock Vib. 2022, 2022, 8679189. [Google Scholar] [CrossRef]
- Faux-Dugan, L.; Piazza, S.J. Correlations between Achilles tendon moment arm and plantarflexor muscle architecture variables. PLoS ONE 2024, 19, e0309406. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Sun, X.; Pi, D. An experimental study on the resistance of a polyurea-sprayed structure to low-speed drop hammer impact. Constr. Build. Mater. 2024, 435, 136915. [Google Scholar] [CrossRef]
- Davidson, S.J.; Porter, R.J.; Dinan, J.R. Explosive Testing of Polymer Retrofit Masonry Walls. J. Perform. Constr. Face 2004, 18, 100–106. [Google Scholar] [CrossRef]
- Yu, C.; Guo, H.; Sun, M. Tensile Mechanical Properties and Dynamic Constitutive Model of Polyurea Elastomer under Different Strain Rates. Polymers 2022, 14, 3579. [Google Scholar] [CrossRef]
- Yan, X.; Yu, C.; Zhai, S. Experimental study on segment joint’s mechanical properties of split-type prefabricated municipal tunnel. Sichuan Build. Sci. 2017, 43, 28–31. (In Chinese) [Google Scholar]
- GB/50838-2015; Technical Standard for Urban Pipe Gallery Engineering. China Planning Press: Beijing, China, 2015. (In Chinese)
- JGJ79-2012; Technical Code for Building Foundation Treatment. China Planning Press: Beijing, China, 2012. (In Chinese)
- GB/T 1239.6-2012; Cold Coiled Helical Compressions Springs-Technical Specifications. Standards Press of China: Beijing, China, 2012. (In Chinese)


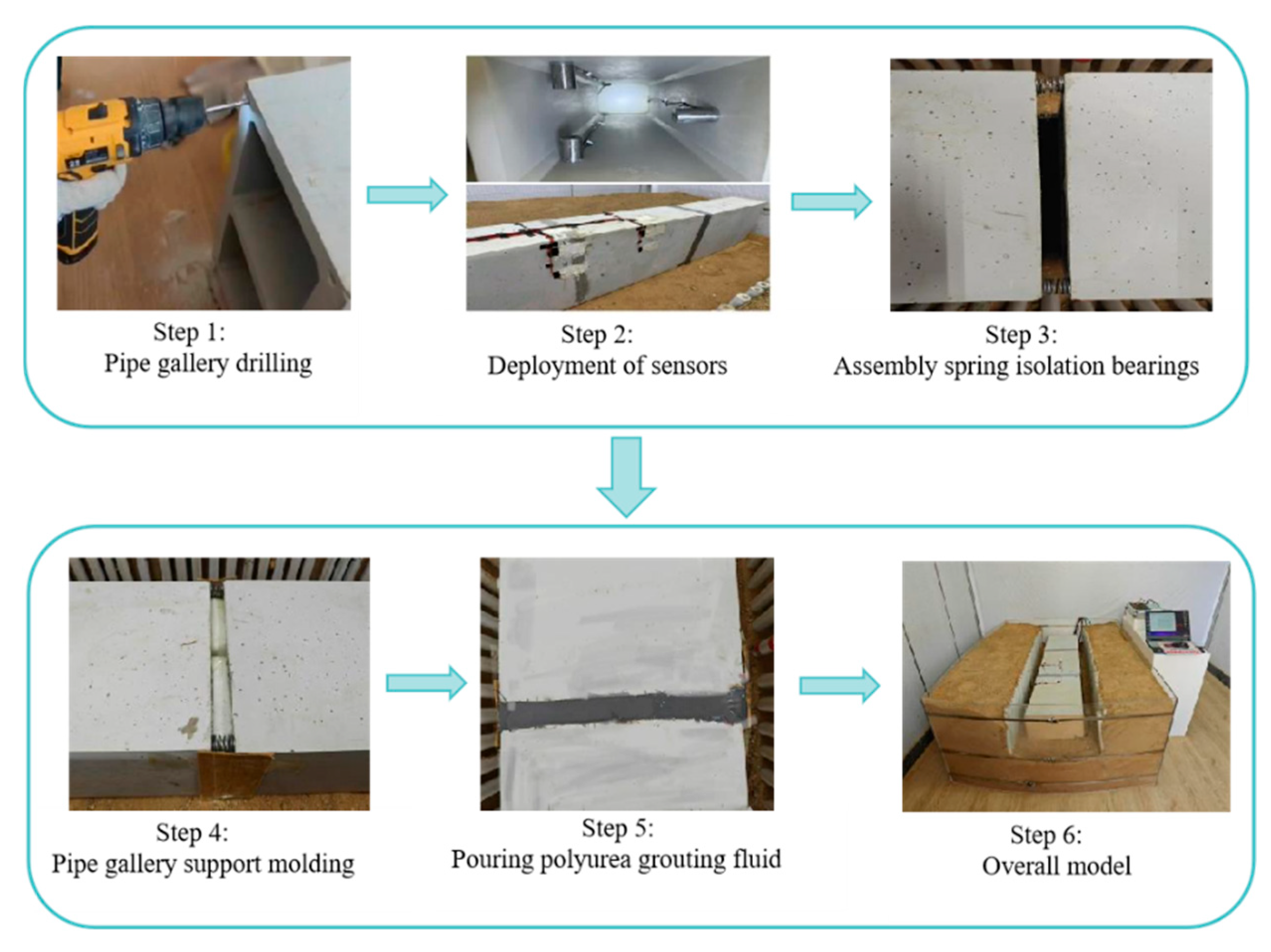

| Parameters | Values |
|---|---|
| Density (g/cm3) | 1.1 |
| Stickiness (mPa·s) | 2000 |
| Curing time (min) | 120 |
| Durometer (HBa) | 90 |
| Tensile strength (MPa) | 20 |
| Elongation at break (%) | 300 |
| Tear strength (N/mm) | 50 |
| Abrasion resistance (mg/1000 r) | 40 |
| Wire Diameter/mm | Spring Height/mm | Total Height/mm | Lap Number/n | Weight-Bearing Load/kg | Vertical Stiffness N/mm | Horizontal Stiffness N/mm | |
|---|---|---|---|---|---|---|---|
| Stainless steels | 2.5 | 38 | 42 | 6 | 10–15 | 21 | 10 |
| Physical Quantity | Dimension | Resemblance | Similarity Ratio | Physical Quantity | Dimension | Resemblance | Similarity Ratio |
|---|---|---|---|---|---|---|---|
| Length (L) | [L] | 15 | Strain (ε) | - | 1 | ||
| Quality (m) | [M] | 4050 | Time (s) | [T] | 9.49 | ||
| Density () | [M] [L]−3 | 1.2 | Concentrated load (F) | [M] [L] [T]−2 | 675 | ||
| Elastic modulus (E) | [M] [L]−1 [T]−2 | 3 | Acceleration (a) | [L] [T]−2 | 0.17 | ||
| Stress (σ) | [M] [L]−1 [T]−2 | 3 | Frequency (ƒ) | [T]−1 | 0.11 |
| (a) | ||||
| Component | Actual Working Conditions and Model Material | Density (kg/m3) | Elastic Modulus (Gpa) | |
| Pipe Gallery Section | Prototype Material | C35 Concrete | 2500 | 31.5 |
| Model Material | Cement Mortar (water–mud–sand = 0.65:1:3) | 2000 | 10.5 | |
| (b) | ||||
| Density | Moisture Content | Elastic Modulus | Cohesion | Internal Friction Angle |
| 1875 | 7.66 | 30 | 7.33 | 25.74 |
| Site Dynamic Compaction Weight/kg | Quality Similarity Ratio | Model Dynamic Compaction Weight/kg | Site Dynamic Compaction Height/m | Length Similarity Ratio | Model Dynamic Compaction Height/m | Model Dynamic Compaction Energy/(N·m) |
|---|---|---|---|---|---|---|
| 20,250 | 4050 | 5 | 9 | 15 | 0.6 | 30 |
| 12 | 0.8 | 40 | ||||
| 15 | 1 | 50 |
| Site Vibration Load/kN | Similarity Ratio of Concentrated Load | Model Vibration Load/kN | Site Vibration Frequency/Hz | Frequency Similarity Ratio | Model Vibration Frequency/Hz |
|---|---|---|---|---|---|
| 90 | 675 | 0.134 | 20 | 0.11 | 220 |
| 140 | 0.207 | 30 | 330 |
| Test Type | Number | Working Condition | Perturbation Mode |
|---|---|---|---|
| Rigid-connection pipe gallery | RG-DC-1 | 5 kg × 60 cm | Number of dynamic compactions: 7 times |
| RG-DC-2 | 5 kg × 80 cm | ||
| RG-DC-3 | 5 kg × 100 cm | ||
| RG-VA-1 | 220 Hz/0.134 kN | Vibration action time: 20 S | |
| RG-VA-2 | 330 Hz/0.207 kN | ||
| Flexible-connection pipe gallery | FG-DC-1 | 5 kg × 60 cm | Number of dynamic compactions: 7 times |
| FG-DC-2 | 5 kg × 80 cm | ||
| FG-DC-3 | 5 kg × 100 cm | ||
| FG-VA-1 | 220 Hz/0.134 kN | Vibration action time: 20 S | |
| FG-VA-2 | 330 Hz/0.207 kN |
| Monitoring Indicators | Sensor Measuring Point | RG-VA-1 | FG-VA-1 | RG-VA-2 | FG-VA-2 |
|---|---|---|---|---|---|
| Acceleration amplitude (mm/s2) | J-1 | 35.7 | 24.1 | 50.2 | 37.8 |
| J-4 | 27.1 | 6.6 | 41.7 | 15.2 | |
| Attenuation rate (%) | 24.1% | 72.6% | 16.9% | 59.7% | |
| Dynamic strain amplitude (με) | Y-1 | 9.6 | 8.6 | 14.3 | 13.2 |
| Y-7 | 9.2 | 3.4 | 12.7 | 6.6 | |
| Attenuation rate (%) | 4.1% | 60.4% | 11.1% | 50% |
| Monitoring Indicators | Sensor Measuring Point | RG-DC-1 | FG-DC-1 | RG-DC-2 | FG-DC-2 | RG-DC-3 | FG-DC-3 |
|---|---|---|---|---|---|---|---|
| Acceleration amplitude (mm/s2) | J-1 | 152.4 | 107.4 | 182.1 | 120.4 | 221.7 | 149.7 |
| J-4 | 127.3 | 52.1 | 143.9 | 60.2 | 173.9 | 74.6 | |
| Attenuation rate (%) | 16.4% | 51.4% | 20.9% | 50% | 21.5% | 50.1% | |
| Dynamic strain amplitude (με) | Y-1 | 36.1 | 31.7 | 40.2 | 36.1 | 45.6 | 40.2 |
| Y-7 | 32.1 | 18.3 | 35.6 | 21.7 | 38.9 | 24.7 | |
| Attenuation rate (%) | 11% | 42.2% | 11.4% | 39.8% | 14.6% | 38.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Cao, H.; Wang, P.; Zhao, Z.; Liu, J. Investigation on the Mechanical Response of a Prefabricated Underground Pipe Gallery with a Flexible Energy Dissipation Node: An Experimental Study. Buildings 2025, 15, 3521. https://doi.org/10.3390/buildings15193521
Zhang E, Cao H, Wang P, Zhao Z, Liu J. Investigation on the Mechanical Response of a Prefabricated Underground Pipe Gallery with a Flexible Energy Dissipation Node: An Experimental Study. Buildings. 2025; 15(19):3521. https://doi.org/10.3390/buildings15193521
Chicago/Turabian StyleZhang, Enhua, Haiying Cao, Ping Wang, Zhen Zhao, and Jiefeng Liu. 2025. "Investigation on the Mechanical Response of a Prefabricated Underground Pipe Gallery with a Flexible Energy Dissipation Node: An Experimental Study" Buildings 15, no. 19: 3521. https://doi.org/10.3390/buildings15193521
APA StyleZhang, E., Cao, H., Wang, P., Zhao, Z., & Liu, J. (2025). Investigation on the Mechanical Response of a Prefabricated Underground Pipe Gallery with a Flexible Energy Dissipation Node: An Experimental Study. Buildings, 15(19), 3521. https://doi.org/10.3390/buildings15193521





