Abstract
Cracks are vital warning signs to reflect the structural deterioration in concrete constructions and buildings. However, their diverse and complex morphologies make accurate segmentation challenging. Deep learning-based methods effectively alleviate the low accuracy of traditional methods, while they are limited by the receptive field and computational efficiency, resulting in suboptimal performance. To address this challenging problem, we propose a novel framework termed High-frequency Refined Mamba with Snake Perception Attention module (HFR-Mamba) for more accurate crack segmentation. HFR-Mamba effectively refines Mamba’s global dependency modeling by extracting frequency domain features and the attention mechanism. Specifically, HFR-Mamba consists of the High-frequency Refined Mamba encoder, the Snake Perception Attention (SPA) module, and the Multi-scale Feature Fusion decoder. The encoder uses Discrete Wavelet Transform (DWT) to extract high-frequency texture features and utilizes the Refined Visual State Space (RVSS) module to fuse spatial features and high-frequency components, which effectively refines the global modeling process of Mamba. The SPA module integrates snake convolutions with different directions to filter background noise from the encoder and highlight cracks for the decoder. For the decoder, it adopts a multi-scale feature fusion strategy and a strongly supervised approach to enhance decoding performance. Extensive experiments show HFR-Mamba achieves state-of-the-art performance in IoU, DSC, Recall, Accuracy, and Precision indicators with fewer parameters, validating its effectiveness in crack segmentation.
1. Introduction
Cracks serve as vital warning signs of structural deterioration in concrete constructions and buildings [1,2]. These fractures, often triggered by excessive loads, environmental erosion, and temperature variations, pose significant risks by undermining the structural integrity and compromising the safety of key infrastructures such as bridges and roads. Consequently, accurate crack segmentation plays an indispensable role in empowering timely repair and safeguarding public safety [3,4,5].
However, the long-distance distribution and varied morphologies of cracks pose a significant challenge. Specifically, cracks commonly exhibit elongated and irregular shapes in morphology. Different types of cracks share a common characteristic of strong contextual dependency, which requires the algorithms to consider the global connectivity of cracks. To address this challenging problem, traditional algorithms [6,7,8] primarily utilize classic image processing techniques to extract cracks, which are straightforward and efficient. Nevertheless, they often struggle with irregular morphology of cracks, which limits their effectiveness in complex real-world scenarios.
Recently, Artificial Intelligence has attracted widespread attention in various fields [9,10,11,12]. As one of the core techniques, deep learning is commonly used in the computer vision tasks including crack segmentation task. They can primarily be categorized into CNN-based networks and Transformer-based variants. CNN-based methods [13,14,15] can capture local crack-related features, while the limited receptive field poses a significant challenge when dealing with the diverse and complex crack patterns. Transformer-based methods [16,17,18] excel in modeling long-range dependencies, and thereby can capture global features of long-spanned cracks with high precision. Nevertheless, the quadratic computational complexity imposes a significant burden on Transformers, necessitating reliance on high-capacity hardware.
More recently, Mamba [19] has achieved significant success in the field of Natural Language Processing (NLP) due to its linear computational complexity and precise global modeling capabilities. Compared to CNN-based and Transformer-based models, Mamba-based methods [20,21,22] can achieve higher accuracy with lower computational complexity. However, these methods require converting the image into sequences and then modeling the global dependencies between the sequences by the state space model. As a result, during the conversion process, the contextual spatial information of the cracks is disrupted, leading to suboptimal performance in segmentation. Despite the loss of spatial information, the image-level semantics can still be explored from the frequency domain features. Motivated by this, we employ the Discrete Wavelet Transform (DWT) to explore the frequency domain features while recovering the lost spatial features, so as to refine the encoding process of Mamba.
In this paper, we aim to introduce the high-frequency features into Mamba to refine the spatial modeling process and enhance the performance of crack segmentation. Specifically, we use Discrete Wavelet Transform (DWT) to decouple the features into high-frequency and low-frequency components. Since the low-frequency components primarily contain background information, we discard these features. In contrast, we retain the high-frequency components, which contain a significant amount of texture features, helping to refine Mamba’s global representation of cracks. Notably, the high-frequency components obtained from DWT are in three different directions. To avoid unnecessary texture loss, we integrate these high-frequency semantics into new features. Subsequently, by injecting these high-frequency textures into Mamba’s encoding process, we effectively enhance the feature extraction accuracy of the encoder. In addition, considering that shallow features contain uncertain background noise, we specifically designed a Snake Perception Attention (SPA) module. By embedding this module into the skip connections between the encoder and decoder, it effectively filters out background-related noise. Meanwhile, by integrating snake convolutions in different directions with global max pooling operations, the SPA module highlights cracks effectively in both spatial and channel dimensions, thus enhancing the decoder’s performance.
In summary, this paper makes the following contributions:
- We propose a novel framework called HFR-Mamba, which effectively integrates frequency domain information to enhance Mamba’s performance in the spatial domain.
- The Refined Visual State Space (RVSS) module is embedded into the Mamba encoder to fuse high-frequency and spatial features for representative features. In addition, the decoder uses a strongly supervised approach and feature fusion to improve decoding performance.
- We introduce a novel Snake Perception Attention (SPA) module between the encoder and decoder, which can filter the background-related noise while highlighting the crack textures.
- Extensive experiments are conducted on three public datasets, and the results show that our proposed HFR-Mamba achieves the highest scores of IoU, DSC, Recall, Accuracy, and Precision metrics with fewer parameters.
2. Related Work
In this section, we review the development of crack segmentation and provide a brief overview of the Mamba-based networks in image segmentation.
2.1. Crack Segmentation Algorithms
Crack segmentation has been a fundamental problem and drawn sustained attention in civil engineering. Existing methods can be broadly categorized into two groups: traditional crack segmentation algorithms and deep learning-based crack segmentation networks. Traditional algorithms primarily rely on techniques such as threshold segmentation [6], detection operators [7], structure propagation [8], and morphological processing [23] to segment cracks. While these methods are fast and accurate, they are highly susceptible to interference from the image background, lighting, and noise, resulting in unstable segmentation performance. Consequently, our research focuses on deep learning-based crack segmentation methods.
Recently, deep learning techniques have been widely used in computer vision community [24,25]. Motivated by this, crack segmentation algorithms have extended the CNN framework to identify a wide variety of cracks. These CNN-based methods can be broadly classified into high-accuracy networks and real-time models. The former focuses on enhancing the contextual understanding of cracks by exploring effective feature aggregation strategies [13], designing robust attention modules [14], and developing feature extraction methods tailored to crack morphology [15]. For example, Yu et al. [15] designed a novel terrain surface crack detection network by analyzing the spatial characteristics of cracks and introducing adaptive deformable convolutions. On the other hand, some CNN-based methods focus on extending lightweight backbone networks with decoders and segmentation heads for real-time crack segmentation [26,27,28]. For instance, Zhang et al. [28] proposed an efficient crack segmentation network named ECSNet to accelerate real-time pavement crack segmentation by introducing small kernel convolutional layers and parallel max pooling. While these CNN-based models can segment cracks with high accuracy, their inherent limitations in the receptive field hinder their further development.
To address this issue, Transformers [16,17,18,29,30] have been introduced into crack segmentation. Wang et al. [16] proposed a novel SegCrack model by utilizing a hierarchical Transformer encoder and multi-scale feature fusion to segment cracks in diverse inspection scenarios. Shamsabadi et al. [18] proposed a Vision Transformer (ViT)-based framework for crack detection on asphalt and concrete surfaces by incorporating transfer learning and a differentiable Intersection over Union (IoU) loss function. A hybrid semantic segmentation model termed SCDeepLab [29] was proposed by integrating Swin Transformer [31] and CNN based on the DeepLabv3+ framework [32] for tunnel lining crack detection. These Transformer-based variants have demonstrated remarkable potential in crack segmentation tasks. However, the quadratic computational complexity of Transformers limits their application in general-purpose crack segmentation, particularly in real-time scenarios.
2.2. Mamba-Based Segmentation Methods
Recently, Mamba [19] has gained significant attention due to its achievements in the field of Natural Language Processing (NLP). Building on this success, its linear computational complexity and precise global dependency modeling have been investigated to enhance the efficiency and accuracy of image segmentation. Inspired by ViT [33], Zhu et al. [34] proposed Vision Mamba (Vim) for image segmentation. Vim employs patching and flattening operations to convert images into vectors, embeds positional information into these vectors, and uses bidirectional state space modeling (SSM) to capture long-range dependencies. Different from Vim, Liu et al. [35] introduced a novel VMamba by integrating a more efficient four-way scanning strategy into Visual State Space (VSS) blocks, which significantly improved the performance of Mamba in the field of computer vision [36]. However, the four-way scanning strategy is not universally effective, as different scanning orders may imply varying regional dependency relationships.
To address this issue, Fan et al. [37] proposed SliceMamba for medical image segmentation, ensuring that spatially adjacent features remain tightly coupled in the scanning sequence. For crack segmentation, Zuo et al. [21] also designed a task-specific scanning mechanism based on the morphological characteristics of cracks, achieving state-of-the-art performance. These Mamba-based variants achieve precise segmentation of specific targets by incorporating various scanning strategies. However, for diverse types of crack curves, focusing solely on the design of scanning strategies into Mamba proves insufficient to boost performance. Moreover, severe artifacts and noise interference intertwined with cracks pose significant challenges for achieving accurate crack segmentation.
3. Method
The proposed method adopts the classic encoder–decoder architecture to segment the cracks. It consists of a High-frequency Refined Mamba Encoder and Multi-scale Feature Fusion Decoder. To mitigate the impact of background noise, we specially design a novel Snake Perception Attention Module between the encoder and decoder to filter noise and highlight crack-related textures. The architecture of the proposed method is shown in Figure 1.
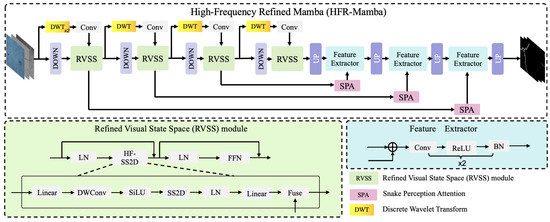
Figure 1.
Pipeline of the High-Frequency Refined Mamba (HFR-Mamba).
3.1. High-Frequency Refined Mamba Encoder
Mamba is efficient in modeling long-range dependency with linear computational overhead. However, the sequential scanning mechanism makes it easy for Mamba to encounter discontinuities when extracting elongated cracks, leading to the formation of suboptimal representations. Therefore, we fully explore the semantic information in the image from the frequency domain perspective, proposing the High-frequency Refined Mamba Encoder to effectively model long-range dependencies in cracks.
Specifically, the proposed encoder mainly consists of a high-frequency decoupling branch and a spatial modeling branch. Given the input image , it is sent in parallel to the spatial modeling branch and the high-frequency decoupling branch. For the high-frequency decoupling branch, it utilizes the Discrete Wavelet Transform (DWT), which can reduce the image resolution while preserving the textures. Note that the first high-frequency decoupling branch adopts two cascaded DWT operations, while the others use only one. Based on the DWT operation and convolution, we can disentangle the high-frequency component and obtain to further refine Mamba, which can be reformulated as:
where is the operation of fusing high-frequency components. For the spatial modeling branch, motivated by [35], it primarily uses a downsampling operation to reduce the image resolution and Refined Visual State Space (RVSS) module for global modeling. In the encoder, the first downsampling module performs downsampling at a 4× rate, while the others perform at a 2× downsampling rate. After the first downsampling module, we obtain , which is then sent to the RVSS module for global modeling, which can be calculated as:
where represents the RVSS module. Different from the Visual State Space module [35], the RVSS module can model global dependencies while simultaneously introducing high-frequency features to enhance texture representation. The RVSS module is comprised of Layer Normalization, a High-frequency Fused SS2D (HF-SS2D) module, and a Feed-Forward Network (FFN). Layer Normalization is employed to standardize the data distribution, and the FFN is used to integrate features. The RVSS module adopts a sequential scanning strategy combined with a state space module to model global dependencies, while incorporating high-frequency textures to further refine the global modeling. Similar to the Visual State Space module [35], the RVSS module adopts a four-directional scanning strategy to capture sequential relationships across different patches, as illustrated in Figure 2:

Figure 2.
Illustration of the direction of the RVSS module.
By repeatedly applying the above operations, we can refine the encoding efficiency of Mamba and output hierarchical multi-scale features (where i represents the encoding stage).
3.2. Snake Perception Attention Module
Fusing multi-scale features of the encoder and decoder through skip connections is a commonly used technique in the encoder–decoder architecture [38]. It can complement deep features with spatial textures and improve segmentation performance. However, for crack images, due to numerous uncertain interference factors in the shooting environment, directly merging shallow and deep features may cause the continuity of cracks to be disrupted by noise. Therefore, inspired by the morphological structure of cracks, we specifically design a Snake Perception Attention (SPA) module to filter noise and highlight texture information from both spatial and channel dimensions, as shown in Figure 3.
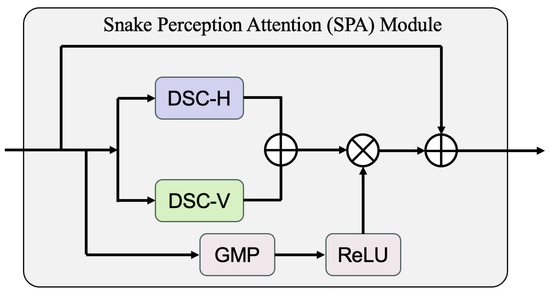
Figure 3.
Illustration of the Snake Perception Attention (SPA) module. Note that GMP is global max pooling.
The SPA module consists of three branches, including the channel excitation branch, the snake convolution branch, and the skip connection branch. The channel excitation branch primarily utilizes global max pooling and the ReLU activation function to integrate important channel feature information into the snake convolution branch, which can be reformulated as:
For snake convolution [39], due to its strong feature extraction capability for curved structures, we apply it to the spatial feature extraction of cracks. Specifically, given the layer feature from the encoder, we use two snake convolutions in different directions to extract features along the horizontal and vertical axes, respectively. We assume that the center of the snake convolution kernel K is and its receptive field size is . The generation process of the receptive field of snake convolution in the horizontal and vertical directions can be calculated as:
where represents the offset and . c is the receptive field range and ∑ means the accumulation process. By combining two snake convolutions in different directions, we can effectively detect crack branches in different orientations. The skip connection branch adds the input features to the enhanced features, helping to alleviate the vanishing gradient problem. The whole process of the SPA module can be reformulated as:
where ‘⊙’ is element-wise multiplication.
3.3. Multi-Scale Feature Fusion Decoder
To enhance the decoding performance, we design a Multi-scale Feature Fusion Decoder to restore feature resolution and decode crack semantics. The proposed decoder consists of three decoding stages. Each stage employs two cascaded convolution operations, a ReLU activation function, and Batch Normalization to integrate the upsampled deep features, which can be reformulated as:
where is the Snake Perception Attention module. Based on repeating the above process, the decoder can generate multi-scale features (when , is the result output by the proposed model). Before feature integration, the decoder employs bilinear interpolation to restore the resolution. The factors of the first three upsampling operations are set to , while the last upsampling operation uses a factor of , corresponding to the downsampling operations in the encoder. After feature integration, each stage of the decoder computes the loss by comparing the layer outputs with the downsampled ground truth, which can be reformulated as:
where means the ground truth. Based on this strongly supervised approach, the decoder can effectively improve the final segmentation accuracy.
3.4. Loss Function
In this paper, we primarily use the Dice loss to supervise the coverage between the segmentation results and the ground truth. Motivated by [40], we employ Cross-Entropy loss to encourage the accuracy during the segmentation process to closely approximate the ground truth. Therefore, the total loss function can be reformulated as follows:
where i represent the i-th pixel and N means the total pixels of the image. The details of the Dice loss and Cross-Entropy loss are shown in Equations (10) and (11), respectively.
4. Experiments
4.1. Datasets
Rissbilder Dataset [41]. The Rissbilder dataset contains 2736 images of different types of cracks collected from buildings such as walls and bridges, along with their corresponding label images. The original resolution of the images in the dataset is . The proportion of cracks in the images is approximately 2.70%, and some of the images have distortion issues. In the experiment, we randomly divided the dataset into training, validation, and test sets in a 6:1:3 ratio.
CrackTree200 Dataset [42]. The CrackTree200 dataset contains 175 images of cracks collected from pavement and building surfaces, along with manually annotated label images. The original resolution of the images is . The proportion of crack pixels in the images is relatively low, approximately 0.31%. Additionally, the images in this dataset contain interference factors such as shadows, occlusions, low contrast, and noise. For the division of the training, validation, and test sets, we followed a 6:1:3 ratio.
GAPS384 Dataset [43]. The GAPS384 dataset contains 383 crack images collected during the summer of 2015 under dry and warm environmental conditions. Due to the specific constraints applied to the image collection environment, the dataset has minimal image noise caused by harsh weather conditions such as rain glare and mud obstruction. However, the dataset is still challenging due to random thickening distortions of the cracks. The original resolution of the images is . Since the proportion of crack pixels in the images is 1.21%, it is classified as a low-crack-ratio dataset.
4.2. Performance Metrics
To comprehensively evaluate the proposed method, referenced by [44,45], we selected five commonly used metrics in semantic segmentation to quantify the differences between the prediction and the ground truth. Specifically, we chose and indicators to calculate the overlap ratio between the prediction and the ground truth, which can be calculated as:
where , , , are true positives, false positives, true negatives, and false negatives, respectively. We also compute the mean IoU
() for parts of the datasets, which is obtained by averaging the IoU of the foreground and background. To focus on the pixels that are missed, we also introduce the , Precision , and Accuracy metrics, which can be reformulated as:
4.3. Implementation Details
All experiments were conducted on an Ubuntu 22.04 system. The hardware supporting this system includes an Intel i5-12600KF CPU, an NVIDIA 3090 GPU, and a 1200 W power supply. Additionally, the software supporting the training process includes Anaconda version 22.3.1, PyTorch framework version 2.0, and PyCharm version 2023.1 (community version). Before the training, we applied data augmentation strategies to improve the model’s performance, including random flipping, random cropping, and random deformation. For the hyperparameters in the experiments, we set the batch size to 4, resized all images to a resolution of , initialized the learning rate to 0.0001, set the total number of training iterations to 80,000, and selected the Adam optimizer to promote model convergence. We set the regularization parameter in the loss function to 0.4. We set the weights for the fusion factor of the high-frequency branch and spatial branch in the encoder to 0.6, respectively.
4.4. Comparison Experiments
To evaluate the segmentation performance of our proposed HFR-Mamba, we compared it with eight state-of-the-art methods as competitors including U-Net [46], DeepLabv3 [47], Vision Transformer [33], Swin Transformer [31], CrackSegNet [48], DECSNet [49], RHACrackNet [50], and CarNet [51] across the public Rissbilder, CrackTree200, and GAPS384 datasets. Among these competitors, U-Net, DeepLabv3, Vision Transformer, and Swin Transformer are commonly used benchmark methods for general semantic segmentation, while the CrackSegNet, DECSNet, RHACrackNet, and CarNet models are state-of-the-art methods specifically designed for crack segmentation tasks. To explore the performance of these methods, we recorded their results with and without loading of the pretrained weight from the ImageNet-1K dataset [52]. Note that our proposed HFR-Mamba was not pretrained.
The performances of HFR-Mamba and other competitors on the Rissbilder dataset are recorded in Table 1. We observed that our proposed HFR-Mamba achieves the SOTA performance on all metrics. In terms of CarNet, which ranked second and was specifically designed for crack segmentation, our proposed HFR-Mamba model outperformed it by 2.71%, 2.25%, 2.28%, 0.19%, and 2.04% in the mIoU, DSC, Recall, Acc, and Precision metrics, respectively. Additionally, we found that loading pretrained weights from the ImageNet-1K dataset significantly improves the model’s segmentation performance, suggesting that pretraining on large-scale datasets can enhance the model’s accuracy in segmenting crack structures. To provide a more intuitive comparison, we visualized the segmentation results of HFR-Mamba and the top-performing models, as shown in Figure 4. From the comparison, we observed that HFR-Mamba is able to capture the fine-grained structures of cracks more accurately. In contrast, other methods, such as the Swin Transformer model, demonstrate suboptimal performance in segmenting curved areas, suggesting that general segmentation models require specialized techniques when dealing with cracks. Overall, our proposed HFR-Mamba model can accurately segmenting crack structures on the Rissbilder dataset.

Table 1.
Performance (%) of the methods on the Rissbilder dataset [41].
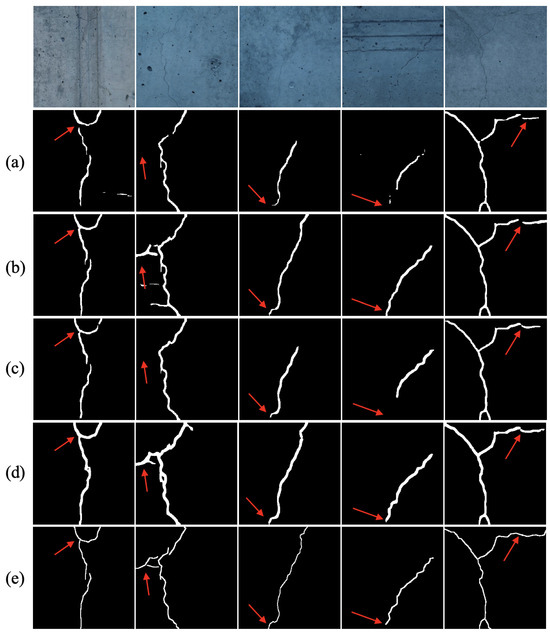
Figure 4.
Comparison of HFR-Mamba with SOTA methods on the Rissbilder. (a) DECSNet. (b) Swin Transformer. (c) CarNet. (d) HFR-Mamba. (e) Label. Arrows mean the distinguishing areas.
To evaluate the performance of the proposed method on the CrackTree200 dataset, we recorded the scores of all models on the IoU, DSC, Recall, Accuracy, and Precision metrics. The CrackTree200 dataset primarily consists of tree-like crack images, which pose a challenge for models requiring global dependency modeling. As shown in Table 2, our HFR-Mamba achieved an IoU score of 79.34%, a DSC score of 81.02%, a Recall score of 87.30%, an Accuracy score of 99.83%, and a Precision score of 78.94%, outperforming all other models and achieving state-of-the-art performance across all metrics. On a broader scale, the segmentation performance of Transformers outperforms that of CNNs, validating our hypothesis that extracting crack contextual features requires long-range dependency modeling. To provide a deeper comparison of the segmentation performance, we visualized the results of the proposed HFR-Mamba and the top-performing segmentation models. As shown in Figure 5, the proposed HFR-Mamba accurately captures the tree-like crack structures, demonstrating its ability to model the relationships between crack structures and indicating its strong contextual modeling capability. In contrast, CarNet, which is specifically designed for crack segmentation, focuses solely on spatial feature extraction and neglects the advantages of frequency domain representations in capturing textures. As a result, it performs suboptimally in segmenting fine-grained features.

Table 2.
Performance (%) of the methods on the CrackTree200 dataset [42].
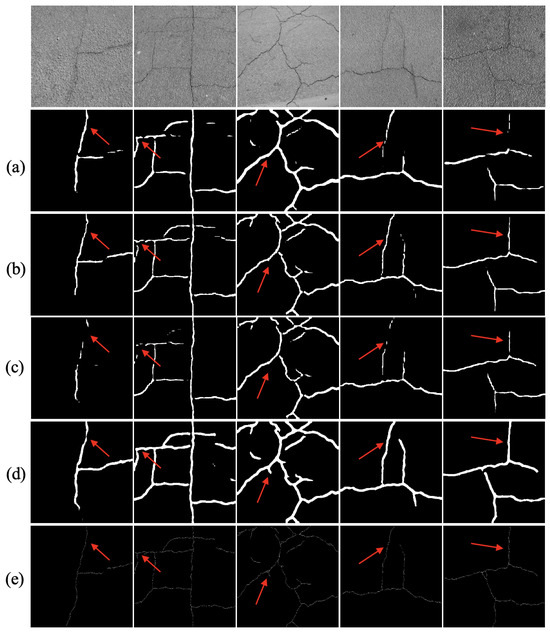
Figure 5.
Comparison of HFR-Mamba with SOTA methods on the CrackTree200. (a) DECSNet. (b) Swin Transformer. (c) CarNet. (d) HFR-Mamba. (e) Label. Arrows mean the distinguishing areas.
The segmentation performance of all models on the GAPS384 dataset is analyzed both qualitatively and quantitatively in Table 3 and Figure 6. By comparing with other methods, we found that the proposed HFR-Mamba achieved the highest scores across all metrics. Specifically, HFR-Mamba obtained 71.27%, 81.88%, 84.31%, 99.52%, and 77.58% in mIoU, DSC, Recall, Accuracy, and Precision, respectively. Compared to the dedicated segmentation model CarNet, HFR-Mamba outperforms it by 2.29%, 2.62%, 3.51%, 0.18%, and 1.76% in mIoU, DSC, Recall, Accuracy, and Precision, respectively. Furthermore, for the general segmentation method Swin Transformer, HFR-Mamba surpasses it by 3.16%, 4.41%, 4.40%, 0.32%, and 3.44% in mIoU, DSC, Recall, Accuracy, and Precision, respectively. By comparing these models designed for different purposes, the superiority of the proposed method is effectively validated. Figure 6 visualizes the segmentation results of the proposed HFR-Mamba and the top-performing models. By comparison, we observed that HFR-Mamba exhibits a clear advantage in crack segmentation. It is capable of recognizing slender curves while preserving key fine-grained features. Therefore, the proposed method shows great potential for application in crack detection across other scenarios.

Table 3.
Performance (%) of the methods on the GAPS384 dataset [43].
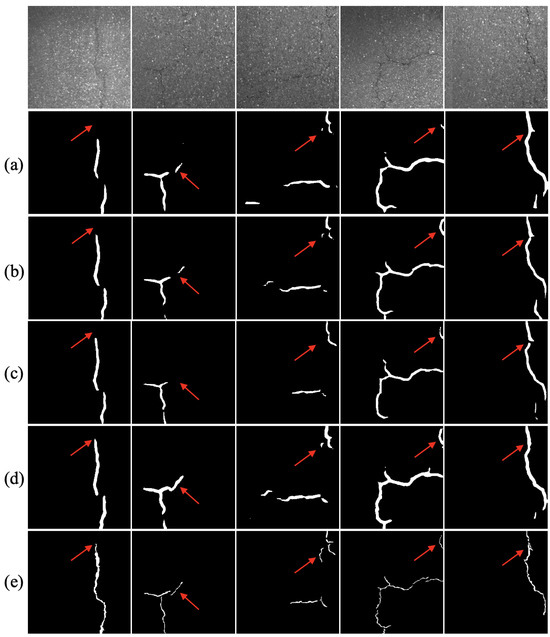
Figure 6.
Comparison of HFR-Mamba with SOTA methods on the GAPS384 dataset. (a) DECSNet. (b) Swin Transformer. (c) CarNet. (d) HFR-Mamba. (e) Label. Arrows mean the distinguishing areas.
To provide a comprehensive comparison of all methods, we calculated their model parameters, FLOPs, FPS, and other efficiency-related metrics. As shown in Table 4, the proposed HFR-Mamba has 22.1 M parameter counts. Compared to Transformer-based models, such as ViT, the Mamba-based approach shows a clear advantage. Although the number of parameters in HFR-Mamba is not the lowest, our aim in this work is to achieve more precise segmentation. Additionally, the proposed HFR-Mamba method has a FLOPs value of 21.9 G, indicating its higher computational efficiency. Regarding the FPS metric, the proposed method is only slightly lower than the lightweight CarNet, suggesting that HFR-Mamba demonstrates good real-time performance. Thus, our proposed HFR-Mamba can achieve more accurate segmentation performance with lower computational overhead.

Table 4.
The parameter counts, FLOPs value, and FPS of the proposed HFR-Mamba and competitors.
4.5. Ablation Study
In this subsection, we conducted ablation experiments on the individual components of the proposed HFR-Mamba to evaluate their effectiveness. Given the complexity of the crack structures in the CrackTree200 dataset, all ablation experiments are performed on this dataset. First, we removed the high-frequency refinement branch from the encoder and used the remaining part as the backbone. As shown in Table 5, by directly upsampling the segmentation results from the backbone, we achieved an IoU score of 76.74%. After incorporating the high-frequency features into the encoder, we observed a 1.08% increase in the IoU score. This validates the necessity of introducing high-frequency information into Mamba for crack segmentation. Next, we added the decoder. By comparing with the direct upsampling method, we found that the progressive decoder significantly improves crack segmentation, achieving a 0.54% increase in IoU. Additionally, we verified the contribution of the proposed SPA module. By comparing the performance of HFR-Mamba before and after adding the module, we found that the SPA module increased the IoU score by 0.66%. To visually assess the high-frequency branch, we performed a heatmap visualization of HFR-Mamba before and after adding the branch. As shown in Figure 7, we observed that the high-frequency branch enables HFR-Mamba to capture changes in the fine-grained branches of cracks and improves the global continuity. Thus, these results demonstrate that each component of HFR-Mamba plays a crucial role in crack segmentation tasks.

Table 5.
Ablation study for components of the proposed method on the CrackTree200 dataset. ‘w/’ and ‘w/o’ mean with and without, respectively.

Figure 7.
Heatmap visualization of the high-frequency branch. (a) and (b) are the original image and ground truth, respectively. (c) and (d) show the heatmaps of HFR-Mamba without and with the high-frequency branch, respectively.
We also conducted the corresponding ablation study for the hyperparameter . As shown in Table 5, adding extra supervision to the decoder’s layer features led to a further improvement. We also conducted ablation experiments on the weights of the supervisory branch in the decoder. As shown in Figure 8, through comparison, we found that when is set to 0.4, HFR-Mamba performs best across the three public datasets. This is because the higher weight for Dice Loss encourages the model to focus more on the overall integrity and consistency of the target region, which performs better for imbalanced data. Meanwhile, the lower weight for Cross-Entropy Loss ensures the proposed model maintains accuracy in boundary details without overfitting, thus improving the overall region segmentation. This setting helps enhance the overall performance of crack segmentation tasks, especially when dealing with complex backgrounds.
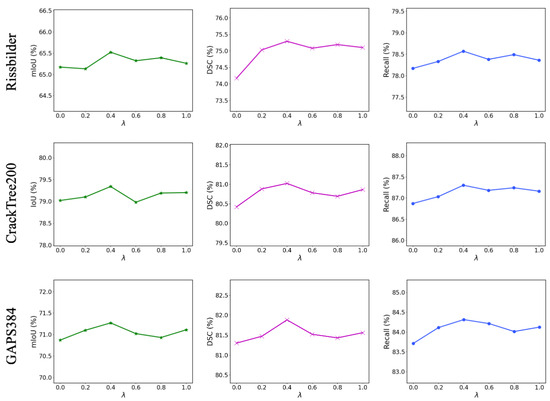
Figure 8.
Comparison of different hyperparameter on three public crack datasets.
To explore the optimal fusion strategy of spatial and frequency domain features, we compared three methods: pixel-wise addition, tensor multiplication, and weighted fusion. As shown in Table 6, we observed that by multiplying the aforementioned features, HFR-Mamba achieved IoU, DSC, Recall, Accuracy, and Precision scores of 78.82%, 80.07%, 86.45%, 99.71%, and 78.13%, respectively. Next, we experimented with adding the two feature sets together and found a slight improvement in segmentation accuracy. Subsequently, we employed a weighted fusion strategy to combine the two feature sets. We compared three strategies: emphasizing the frequency domain while weakening the spatial features (EFWS), equalizing the frequency and spatial features (EFS), and weakening the frequency domain while emphasizing the spatial features (WFES). We set the weight of the high-frequency branch as . As shown in Figure 9, when , the proposed method shows relatively lower performance on the three public datasets. This indicates that the fusion approach, which amplifies spatial features while reducing the importance of frequency domain features, is not suitable for crack segmentation tasks. This is because the spatial domain may contain background and noise, and amplifying these features can interfere with the semantics in the high-frequency features. In contrast, when , the proposed method performs better on the three public datasets. This once again confirms the necessity of introducing high-frequency features. Additionally, we observed that when , the performance of the proposed method was better than when . This suggests that excessively amplifying frequency domain features while compressing spatial features can also negatively affect the segmentation performance. Since we only introduce high-frequency features while discarding low-frequency features, this inevitably leads to the loss of some background-related semantics, thereby impacting the model’s ability to recognize the contextual features of the cracks. Therefore, when , the encoder is able to effectively fuse spatial features and high-frequency semantics, improving the segmentation performance.

Table 6.
Ablation study for the fusion manner of high-frequency and spatial features on the CrackTree200 dataset. Note that ‘★’ represents the proposed method.
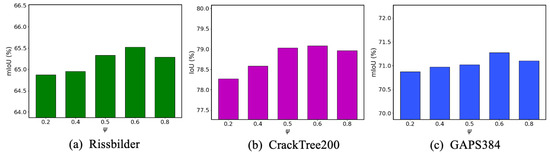
Figure 9.
Comparison of different fusion factor between spatial branch and high-frequency branch.
To evaluate the performance of the SPA module, we conducted ablation experiments on it. Specifically, we compared its structure with three commonly used attention modules: the Squeeze-and-Excitation (SE) attention module [53], the Strip Pooling module [54], and the self-attention module [55] on the CrackTree200 dataset. As shown in Table 7, replacing the SPA module with the SE module resulted in a decrease of 1.13%, 0.68%, 0.63%, 0.14%, and 0.70% in IoU, DSC, Recall, Accuracy, and Precision, respectively. This demonstrates that simply increasing the model’s attention to channel features is not the optimal approach for crack segmentation. Next, we compared two spatial attention methods, and found that the Strip Pooling and self-attention modules significantly improved the model’s segmentation performance over the channel attention module. Finally, we compared these methods with the proposed SPA module. By observation, we found that our method achieved state-of-the-art performance across all metrics. This indicates that incorporating both channel and spatial attention in the HFR-Mamba model is well-suited for crack segmentation tasks.

Table 7.
Ablation study for the SPA module on the CrackTree200. ‘★’ means the proposed method.
Additionally, we conducted ablation experiments on the resolution of the input images. As shown in Table 8, we resized the original images to , , , and . From the comparison, we found that resizing the images to small resolutions significantly impacted the model’s accuracy in crack segmentation. This suggests that excessive downsampling disrupts the contextual relationships between crack structures, making precise segmentation more challenging. Due to memory constraints, we did not experiment with resolutions higher than . Therefore, among all the tested resolutions, we found that can effectively maximize the potential of HFR-Mamba for crack segmentation.

Table 8.
Ablation study for the resolution of input images on the CrackTree200 dataset. Note that ‘★’ represents the proposed method.
5. Conclusions
This study focuses on addressing the challenge of accurate crack segmentation in concrete constructions and buildings. To address this challenging problem, we propose a High-frequency Refined Mamba with Snake Perception Attention Module (HFR-Mamba), which can refine the global modeling of Mamba and alleviate the problems of limited receptive field and insufficient computational overhead in deep learning methods. We have verified that mining high-frequency features from the frequency domain is one of the effective methods to improve the efficiency of Mamba encoding. To explore the fusion of frequency domain features and the high-dimensional features of Mamba encoding, we investigated their integration strategies. The results demonstrated that the optimal approach is to emphasize the frequency domain while weakening the spatial features, which is a superior feature fusion method. Additionally, the proposed Snake Perception Attention (SPA) module fully utilizes the dynamic snake convolution to capture features of curvilinear structures. Corresponding experiments have shown that, compared to commonly used general attention modules, this module achieves superior performance in crack segmentation tasks.
Limitations: Although the proposed algorithm achieves SOTA performance, the lack of hardware has prevented us from deploying the algorithm to drone systems or embedded systems to evaluate its performance in real-world scenarios. Additionally, there is still room for improvement in the model’s real-time performance.
Author Contributions
Conceptualization, H.L.; methodology, H.L.; software, H.L.; validation, L.C.; formal analysis, T.W.; investigation, T.W.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, L.C.; visualization, H.L.; supervision, L.C.; project administration, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Three public datasets are used to evaluate our proposed method in this paper, which are termed the Rissbilder Dataset, the Cracktree200 dataset, and the GAPS384 Dataset. The Cracktree200 and the GAPS384 Datasets can be downloaded from https://github.com/fyangneil/pavement-crack-detection?tab=readme-ov-file (accessed on 15 May 2025), and the Rissbilder Dataset can be downloaded from https://data.lib.vt.edu/articles/dataset/Concrete_Crack_Conglomerate_Dataset/16625056?file=30916681 (accessed on 15 May 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zheng, J.; Lv, H.; Song, H.; Li, J.; Bai, R.; Chen, L.; Chen, Q.; Jiang, L. FMANet: Fused mamba attention model with multi-type preprocessing for simulated crack-contaminated complex environments. Adv. Eng. Inform. 2026, 69, 103808. [Google Scholar] [CrossRef]
- Ye, Z.; Lovell, L.; Faramarzi, A.; Ninić, J. Sam-based instance segmentation models for the automation of structural damage detection. Adv. Eng. Inform. 2024, 62, 102826. [Google Scholar] [CrossRef]
- Chen, Z.; Lai, Z.; Chen, J.; Li, J. Mind marginal non-crack regions: Clustering-inspired representation learning for crack segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 12698–12708. [Google Scholar]
- Inam, H.; Islam, N.U.; Akram, M.U.; Ullah, F. Smart and automated infrastructure management: A deep learning approach for crack detection in bridge images. Sustainability 2023, 15, 1866. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Wang, J.; Chen, Q.; Huang, X.; Jiang, L. Knowledge distillation with T-Seg guiding for lightweight automated crack segmentation. Autom. Constr. 2024, 166, 105585. [Google Scholar] [CrossRef]
- Oliveira, H.; Correia, P.L. Automatic road crack segmentation using entropy and image dynamic thresholding. In Proceedings of the 2009 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 622–626. [Google Scholar]
- Lopez-Molina, C.; De Baets, B.; Bustince, H.; Sanz, J.; Barrenechea, E. Multiscale edge detection based on Gaussian smoothing and edge tracking. Knowl.-Based Syst. 2013, 44, 101–111. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, Y.; Sun, H.; Huang, W. Pavement crack detection using hessian structure propagation. Adv. Eng. Inform. 2021, 49, 101303. [Google Scholar] [CrossRef]
- Sun, L.; Shi, W.; Tian, X.; Li, J.; Zhao, B.; Wang, S.; Tan, J. A plane stress measurement method for CFRP material based on array LCR waves. NDT E Int. 2025, 151, 103318. [Google Scholar] [CrossRef]
- Hao, H.; Yao, E.; Pan, L.; Chen, R.; Wang, Y.; Xiao, H. Exploring heterogeneous drivers and barriers in MaaS bundle subscriptions based on the willingness to shift to MaaS in one-trip scenarios. Transp. Res. A Policy Pract. 2025, 199, 104525. [Google Scholar] [CrossRef]
- Guan, A.; Zhou, S.; Gu, W.; Wu, Z.; Gao, M.; Liu, H.; Zhang, X.-p. Dynamic Simulation and Parameter Calibration-Based Experimental Digital Twin Platform for Heat-Electric Coupled System. IEEE Trans. Sustain. Energy. 2025, 1–14. [Google Scholar] [CrossRef]
- Liu, P.; Li, S.; Jin, H.; Tian, X.; Liu, G. Shape parameterization method and hydrodynamic noise characteristics of low-noise toroidal propeller. Ocean Eng. 2025, 328, 121088. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1525–1535. [Google Scholar] [CrossRef]
- Qu, Z.; Wang, C.Y.; Wang, S.Y.; Ju, F.R. A method of hierarchical feature fusion and connected attention architecture for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16038–16047. [Google Scholar] [CrossRef]
- Yu, D.; Ji, S.; Li, X.; Yuan, Z.; Shen, C. Earthquake crack detection from aerial images using a deformable convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4412012. [Google Scholar] [CrossRef]
- Wang, W.; Su, C. Automatic concrete crack segmentation model based on transformer. Autom. Constr. 2022, 139, 104275. [Google Scholar] [CrossRef]
- Beyene, D.A.; Maru, M.B.; Kim, T.; Park, S.; Park, S. Unsupervised domain adaptation-based crack segmentation using transformer network. J. Build. Eng. 2023, 80, 107889. [Google Scholar] [CrossRef]
- Shamsabadi, E.A.; Xu, C.; Rao, A.S.; Nguyen, T.; Ngo, T.; Dias-da Costa, D. Vision transformer-based autonomous crack detection on asphalt and concrete surfaces. Autom. Constr. 2022, 140, 104316. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Zhou, H.Y.; Xi, Y.; Yu, L.; Li, C.; Liang, Y.; Shi, G.; Yu, Y.; Zhang, S.; et al. Swin-umamba: Mamba-based unet with imagenet-based pretraining. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Marrakesh, Morocco, 6–10 October 2024; Springer: Cham, Switzerland, 2024; pp. 615–625. [Google Scholar]
- Zuo, X.; Sheng, Y.; Shen, J.; Shan, Y. Topology-aware mamba for crack segmentation in structures. Autom. Constr. 2024, 168, 105845. [Google Scholar] [CrossRef]
- Cai, W.; Wang, X.; Xue, Y.; Ma, Y.; Wu, J.; Ge, Z.; Wang, B. CrackMamba with Normalized Soft-Frangi-Filter Enhancement towards Accurate Crack Segmentation. In Proceedings of the 2025 International Conference on Multimedia Retrieval, Chicago, IL, USA, 30 June–3 July 2025; pp. 43–51. [Google Scholar]
- Landstrom, A.; Thurley, M.J. Morphology-based crack detection for steel slabs. IEEE J. Sel. Top. Signal Process. 2012, 6, 866–875. [Google Scholar] [CrossRef]
- Lu, W.; Wang, J.; Wang, T.; Zhang, K.; Jiang, X.; Zhao, H. Visual style prompt learning using diffusion models for blind face restoration. Pattern Recognit. 2025, 161, 111312. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, H.; Yu, D.; Cheng, J.; Li, J. Outlier detection method based on high-density iteration. Inf. Sci. 2024, 662, 120286. [Google Scholar] [CrossRef]
- Ye, X.; Luo, K.; Wang, H.; Zhao, Y.; Zhang, J.; Liu, A. An advanced AI-based lightweight two-stage underwater structural damage detection model. Adv. Eng. Inform. 2024, 62, 102553. [Google Scholar] [CrossRef]
- Liao, J.; Yue, Y.; Zhang, D.; Tu, W.; Cao, R.; Zou, Q.; Li, Q. Automatic tunnel crack inspection using an efficient mobile imaging module and a lightweight CNN. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15190–15203. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, D.; Lu, Y. ECSNet: An accelerated real-time image segmentation CNN architecture for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15105–15112. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Gong, C. Hybrid semantic segmentation for tunnel lining cracks based on Swin Transformer and convolutional neural network. Comput.-Aided Civ. Infrastruct. Eng. 2023, 38, 2491–2510. [Google Scholar] [CrossRef]
- Guo, F.; Qian, Y.; Liu, J.; Yu, H. Pavement crack detection based on transformer network. Autom. Constr. 2023, 145, 104646. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision mamba: Efficient visual representation learning with bidirectional state space model. arXiv 2024, arXiv:2401.09417. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Jiao, J.; Liu, Y. Vmamba: Visual state space model. In Proceedings of the 38th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 10–15 December 2024. [Google Scholar]
- Hu, Q.; Peng, Y.; U, K.; Zhao, S. Infrared and Visible Image Fusion Using a State-Space Adversarial Model with Cross-Modal Dependency Learning. Mathematics 2025, 13, 2333. [Google Scholar] [CrossRef]
- Fan, C.; Yu, H.; Huang, Y.; Wang, L.; Yang, Z.; Jia, X. Slicemamba with neural architecture search for medical image segmentation. IEEE J. Biomed. Health Inform. 2025, 1–13. [Google Scholar] [CrossRef]
- Hu, Q.; Peng, Y.; Zheng, Z. A deep learning framework for gender sensitive speech emotion recognition based on MFCC feature selection and SHAP analysis. Sci. Rep. 2025, 15, 28569. [Google Scholar] [CrossRef]
- Qi, Y.; He, Y.; Qi, X.; Zhang, Y.; Yang, G. Dynamic snake convolution based on topological geometric constraints for tubular structure segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 6070–6079. [Google Scholar]
- Yadav, D.P.; Kishore, K.; Gaur, A.; Kumar, A.; Singh, K.U.; Singh, T.; Swarup, C. A novel multi-scale feature fusion-based 3SCNet for building crack detection. Sustainability 2022, 14, 16179. [Google Scholar] [CrossRef]
- Pak, M.; Kim, S. Crack detection using fully convolutional network in wall-climbing robot. In Advances in Computer Science and Ubiquitous Computing: CSA-CUTE 2019; Springer: Singapore, 2021; pp. 267–272. [Google Scholar]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Eisenbach, M.; Stricker, R.; Seichter, D.; Amende, K.; Debes, K.; Sesselmann, M.; Ebersbach, D.; Stoeckert, U.; Gross, H.M. How to get pavement distress detection ready for deep learning? A systematic approach. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2039–2047. [Google Scholar]
- Hu, Q.; Peng, Y.; Zhang, C.; Lin, Y.; U, K.; Chen, J. Building Instance Extraction via Multi-Scale Hybrid Dual-Attention Network. Buildings 2025, 15, 3102. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.; Chen, N.; Chen, Q.; Miao, Q.; Jin, H.; Jiang, L.; Ngo, T. Crack semantic segmentation performance of various attention modules in different scenarios. Struct. Concr. 2024, 26, 4409–4430. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, J.; Hong, Z.; Lu, W.; Yin, J.; Zou, L.; Shen, X. Image-based concrete crack detection in tunnels using deep fully convolutional networks. Constr. Build. Mater. 2020, 234, 117367. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, Z.; Sharma, P.K.; Alfarraj, O.; Tolba, A.; Wang, J. A dual encoder crack segmentation network with Haar wavelet-based high–low frequency attention. Expert Syst. Appl. 2024, 256, 124950. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, J.; Fan, Z.; Yuan, D.; Ma, P.; Wang, M.; Sheng, W.; Wang, K.C. A lightweight encoder–decoder network for automatic pavement crack detection. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 1743–1765. [Google Scholar] [CrossRef]
- Li, K.; Yang, J.; Ma, S.; Wang, B.; Wang, S.; Tian, Y.; Qi, Z. Rethinking lightweight convolutional neural networks for efficient and high-quality pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2024, 25, 237–250. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 248–255. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Hou, Q.; Zhang, L.; Cheng, M.M.; Feng, J. Strip pooling: Rethinking spatial pooling for scene parsing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4003–4012. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).