Axial Force Analysis and Geometric Nonlinear Beam-Spring Finite Element Calculation of Micro Anti-Slide Piles
Abstract
1. Introduction
2. Analysis of Axial Force Mobilization of Micropiles
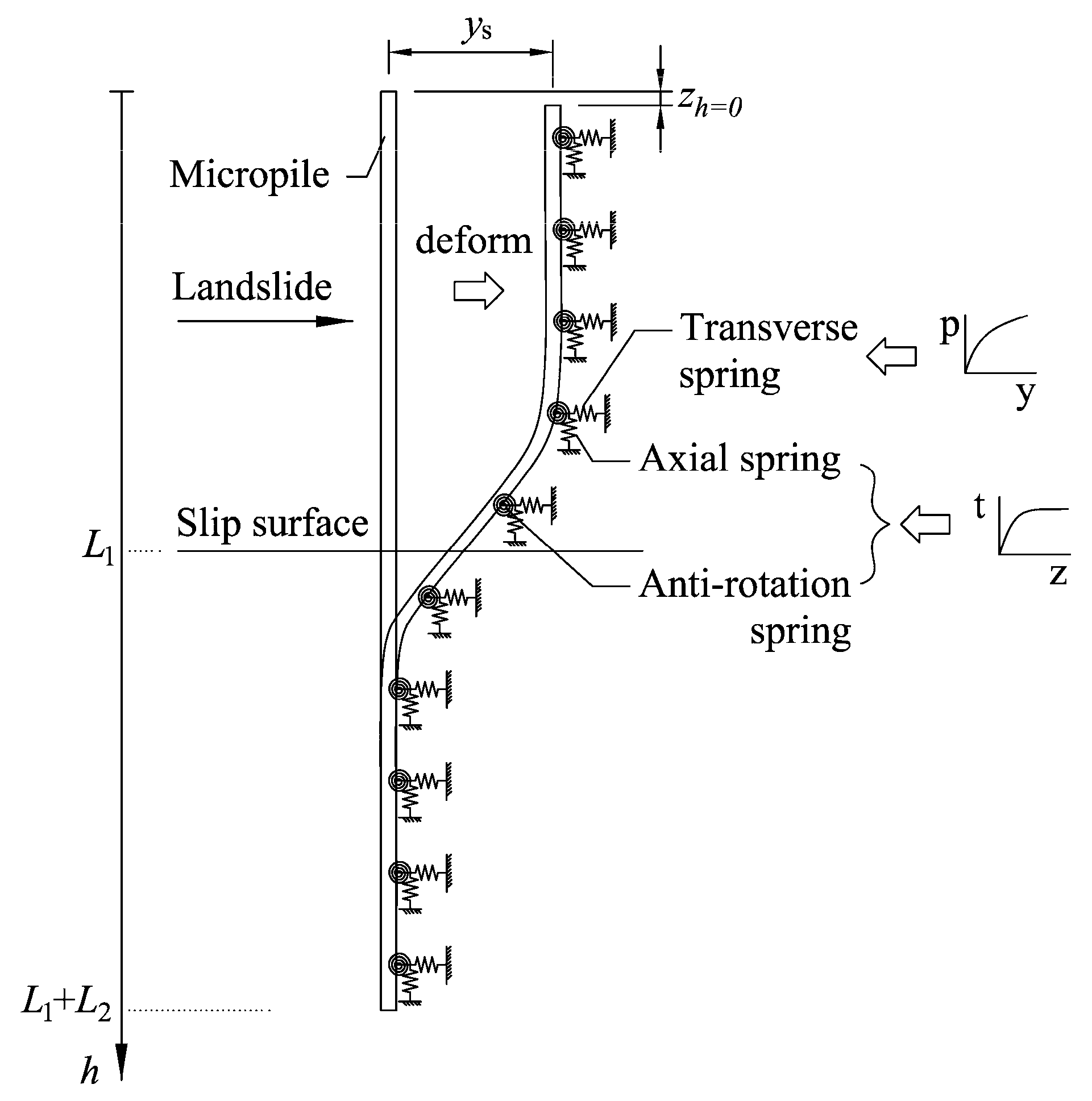
2.1. Numerical Model
2.2. Axial Force Development
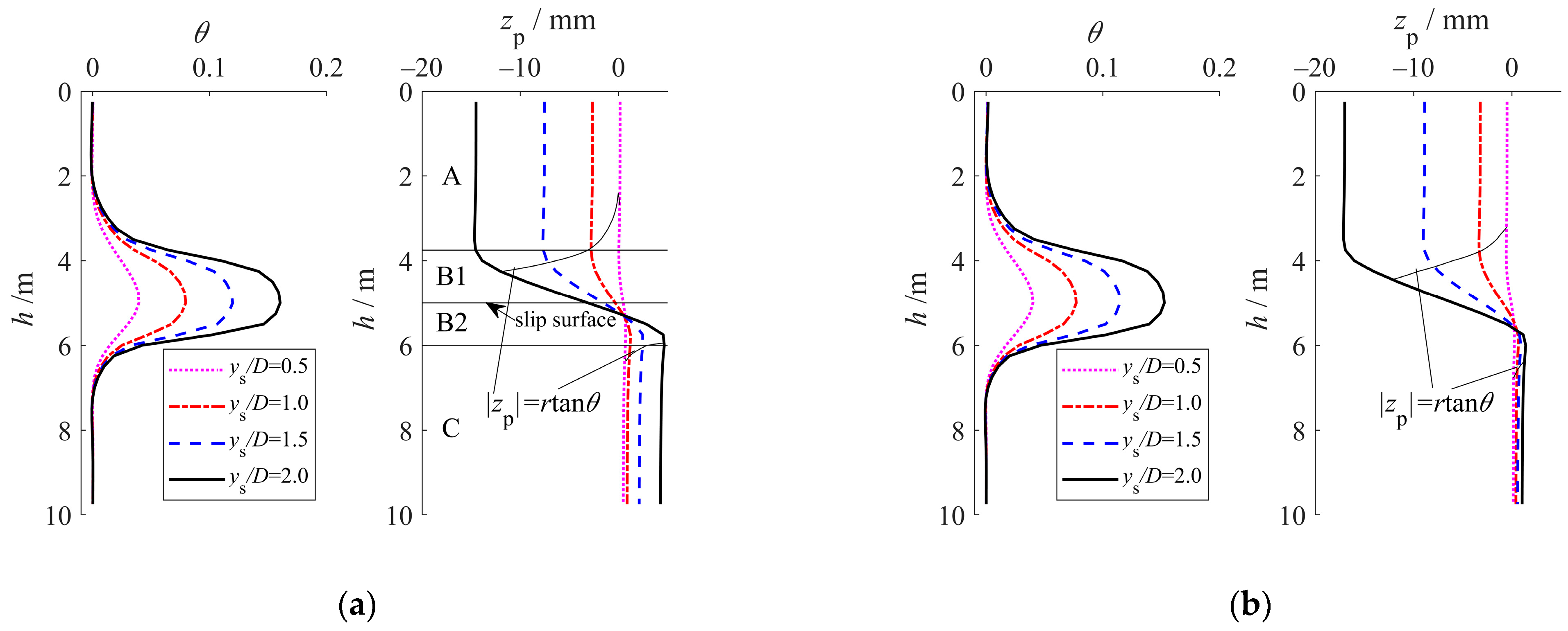
2.3. Pile Displacements
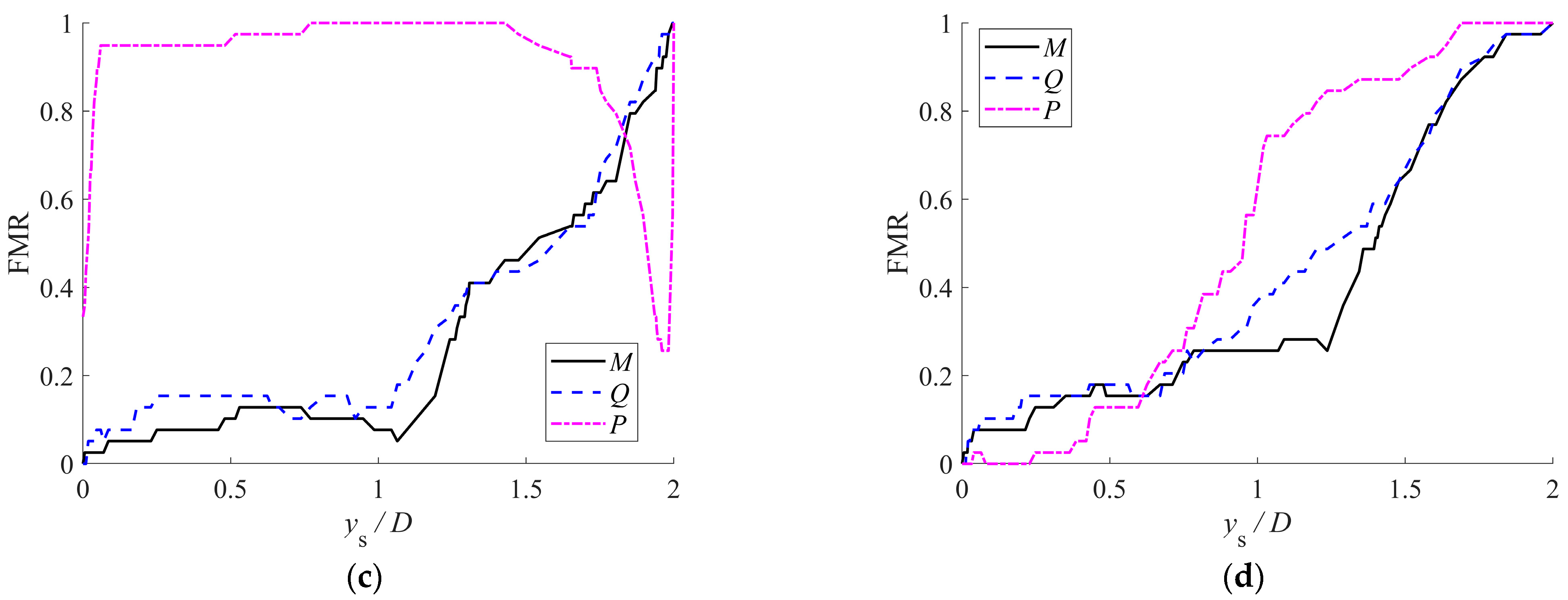
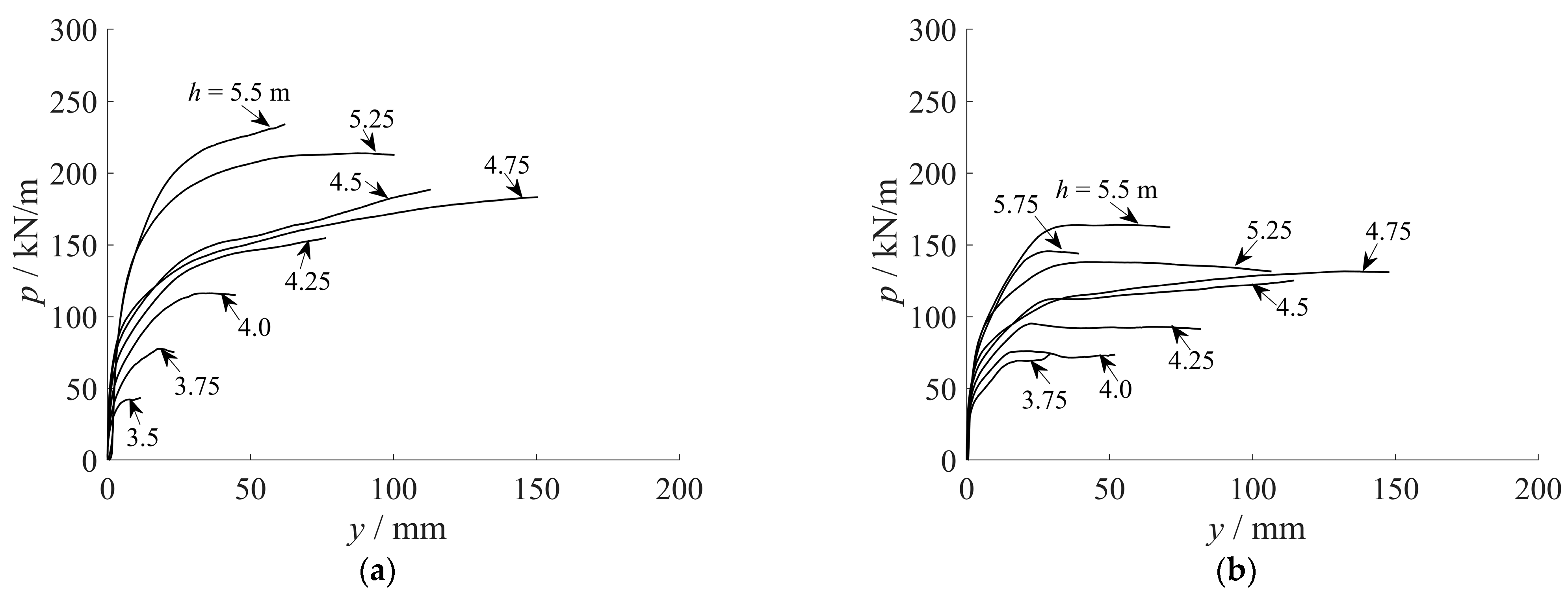
2.4. p-y and t-z Curves
3. Soil Resistance Models and Parameters
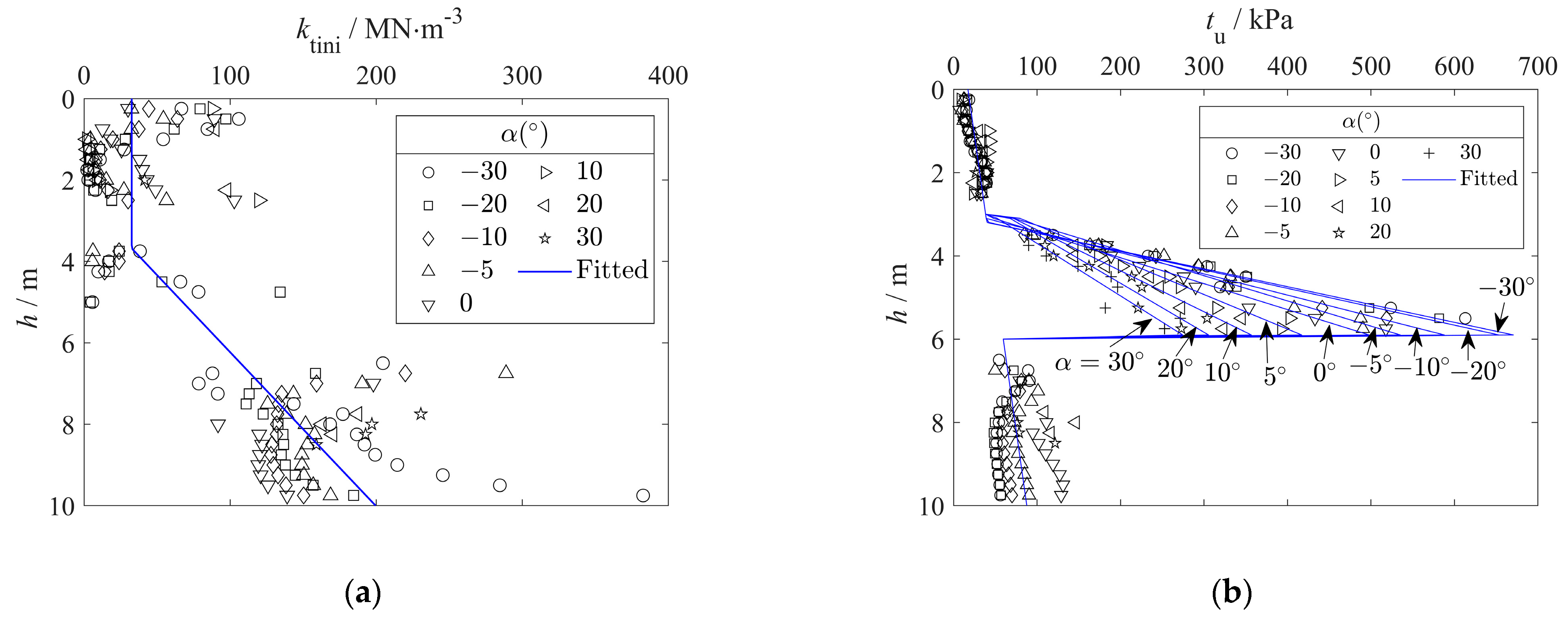
3.1. p-y Model and Parameter Calibration
3.2. t-z and Anti-Rotation Models
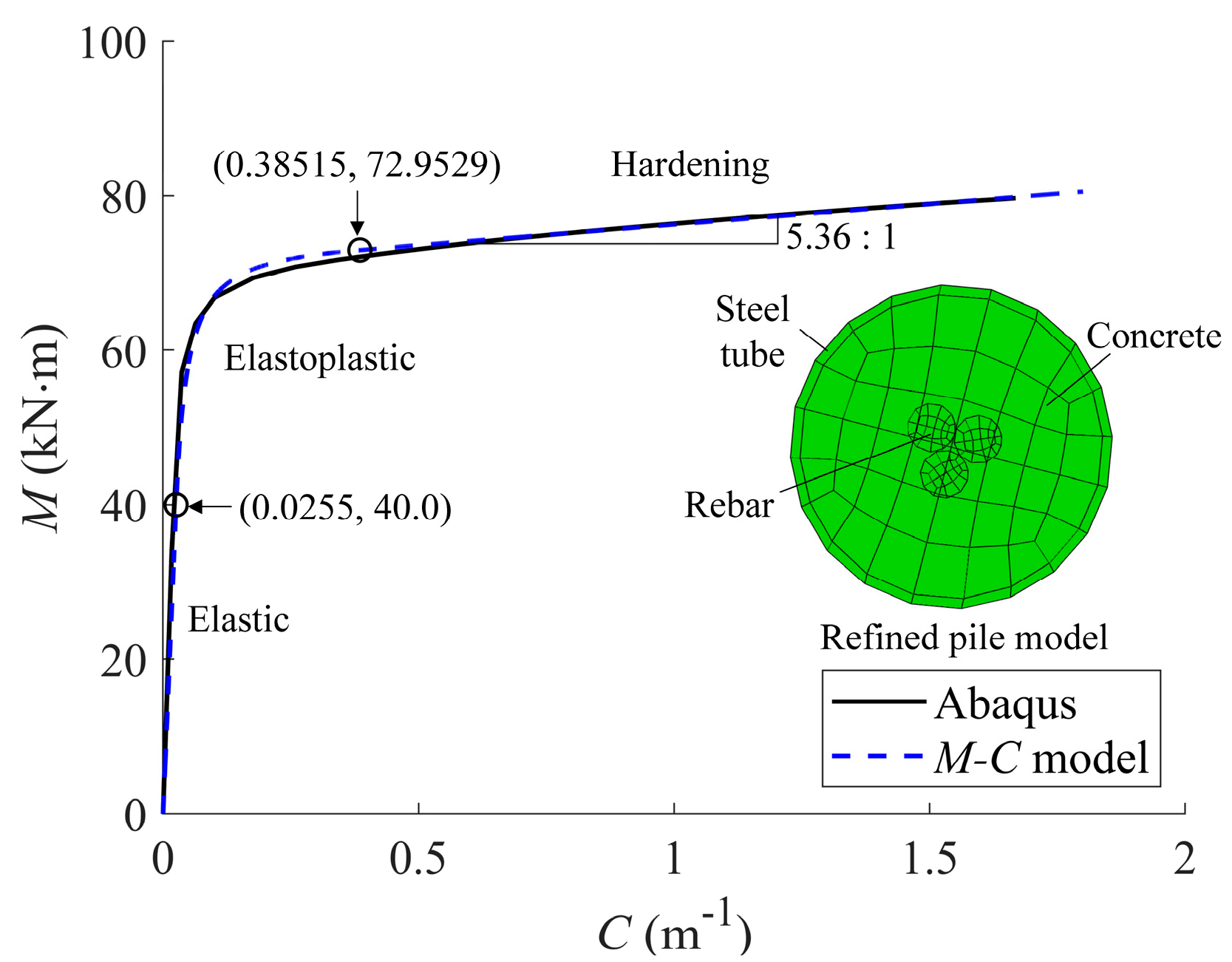
3.3. Parameter Calibration for the t-z Model
4. Beam-Spring Finite Element Method (BSFEM)
4.1. Geometric Nonlinear Finite Element Formulation
4.2. Beam-Spring Finite Element Calculation Driven by Soil Displacements
5. Verifications
5.1. Verification Against Abaqus
5.1.1. Lateral Pile Responses
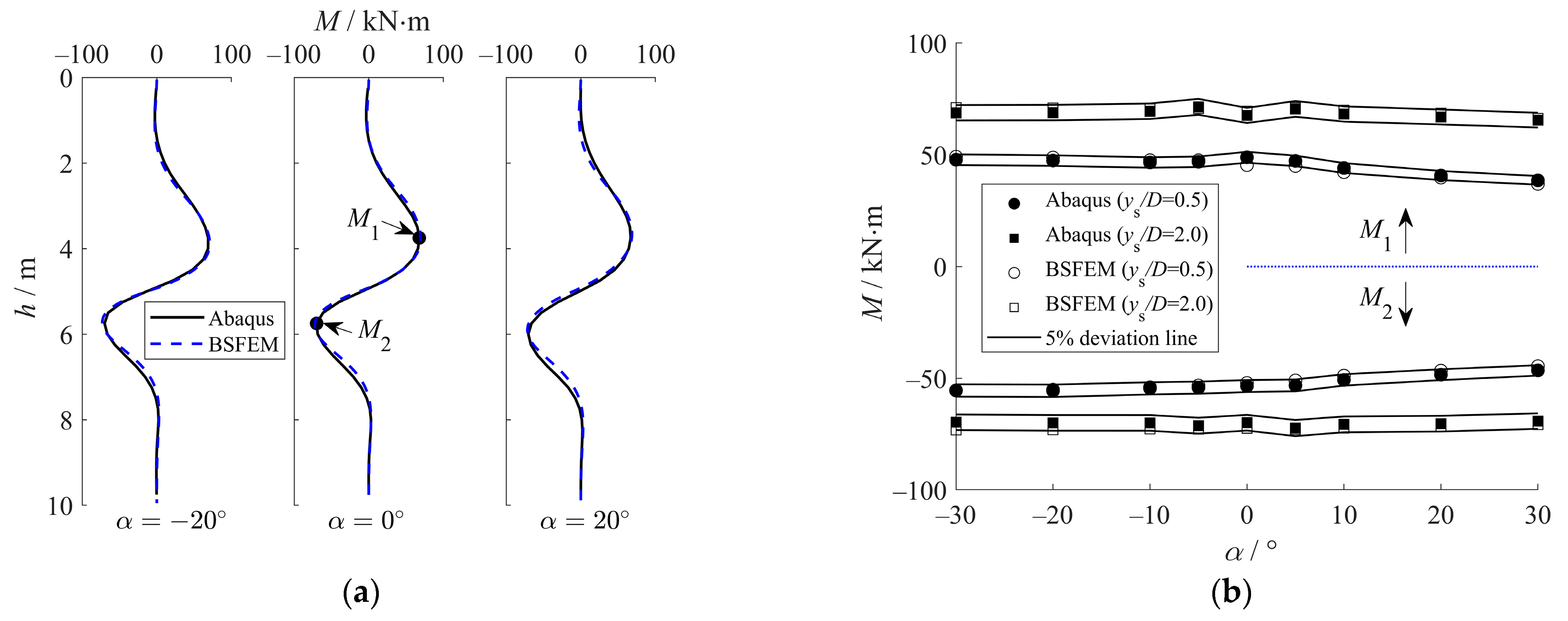
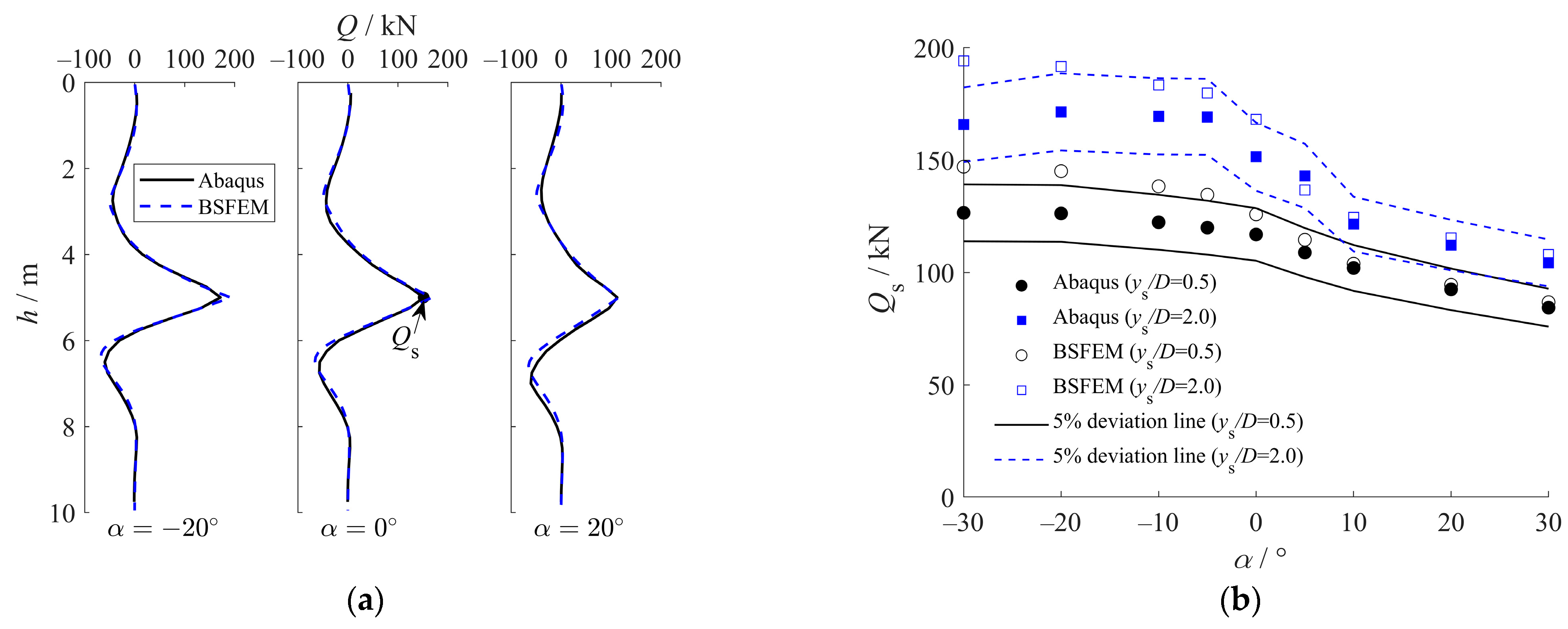
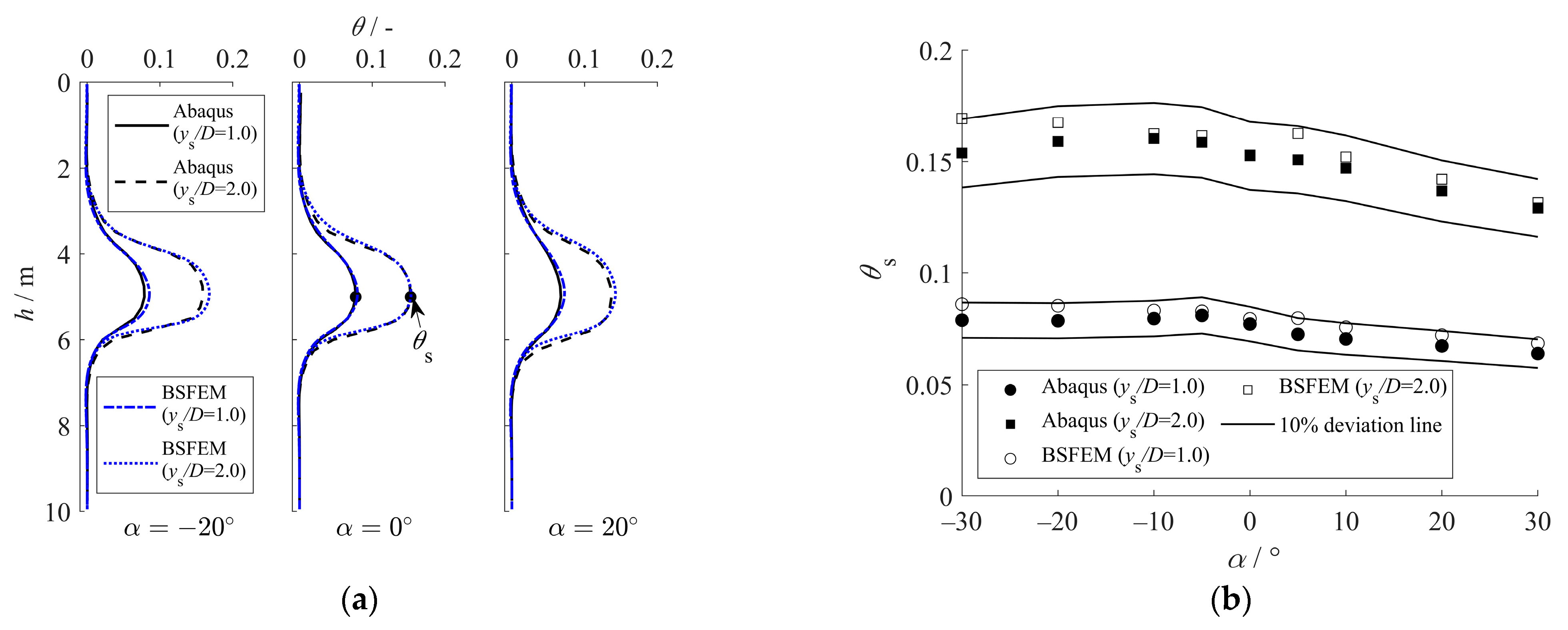
5.1.2. Axial Pile Responses
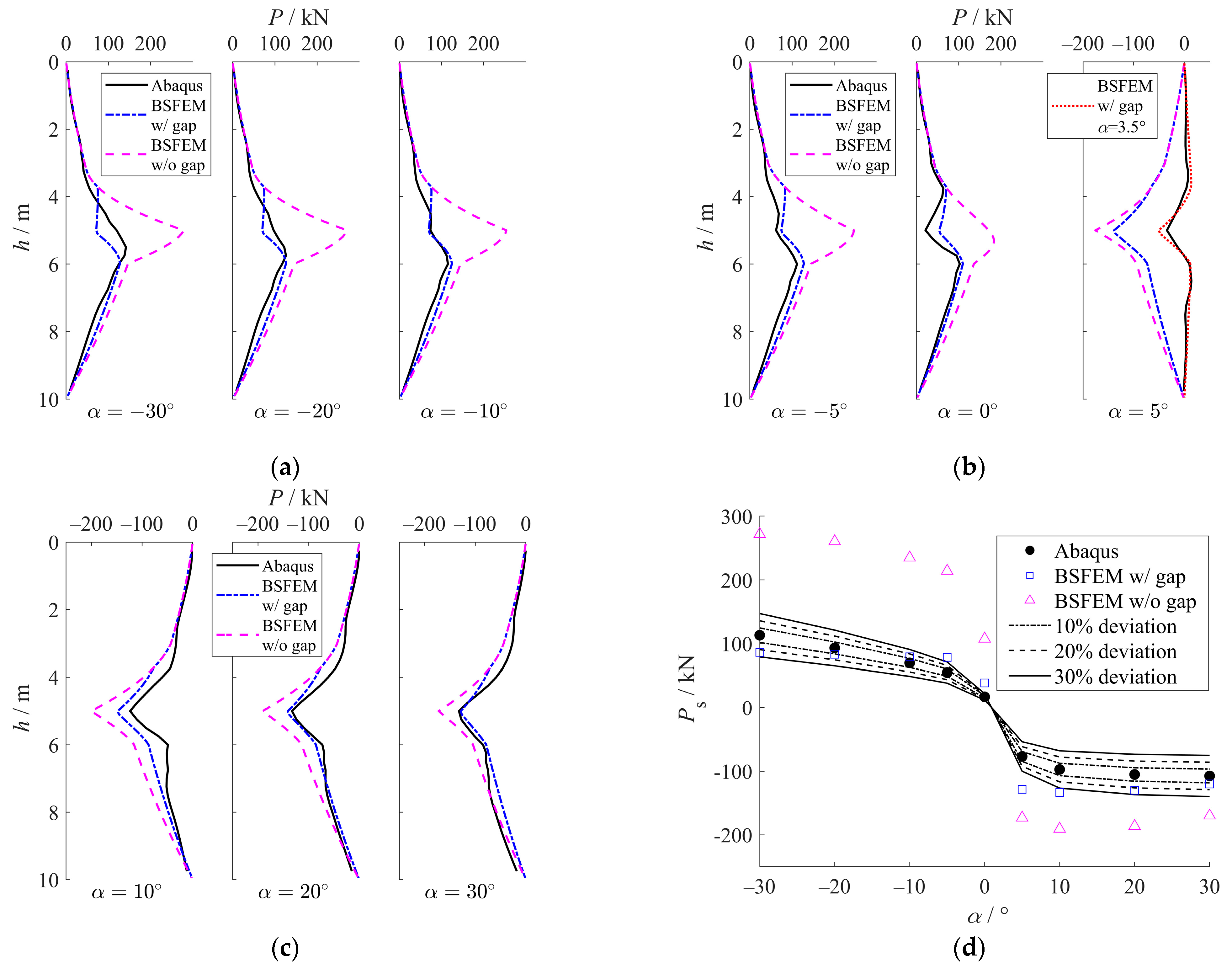

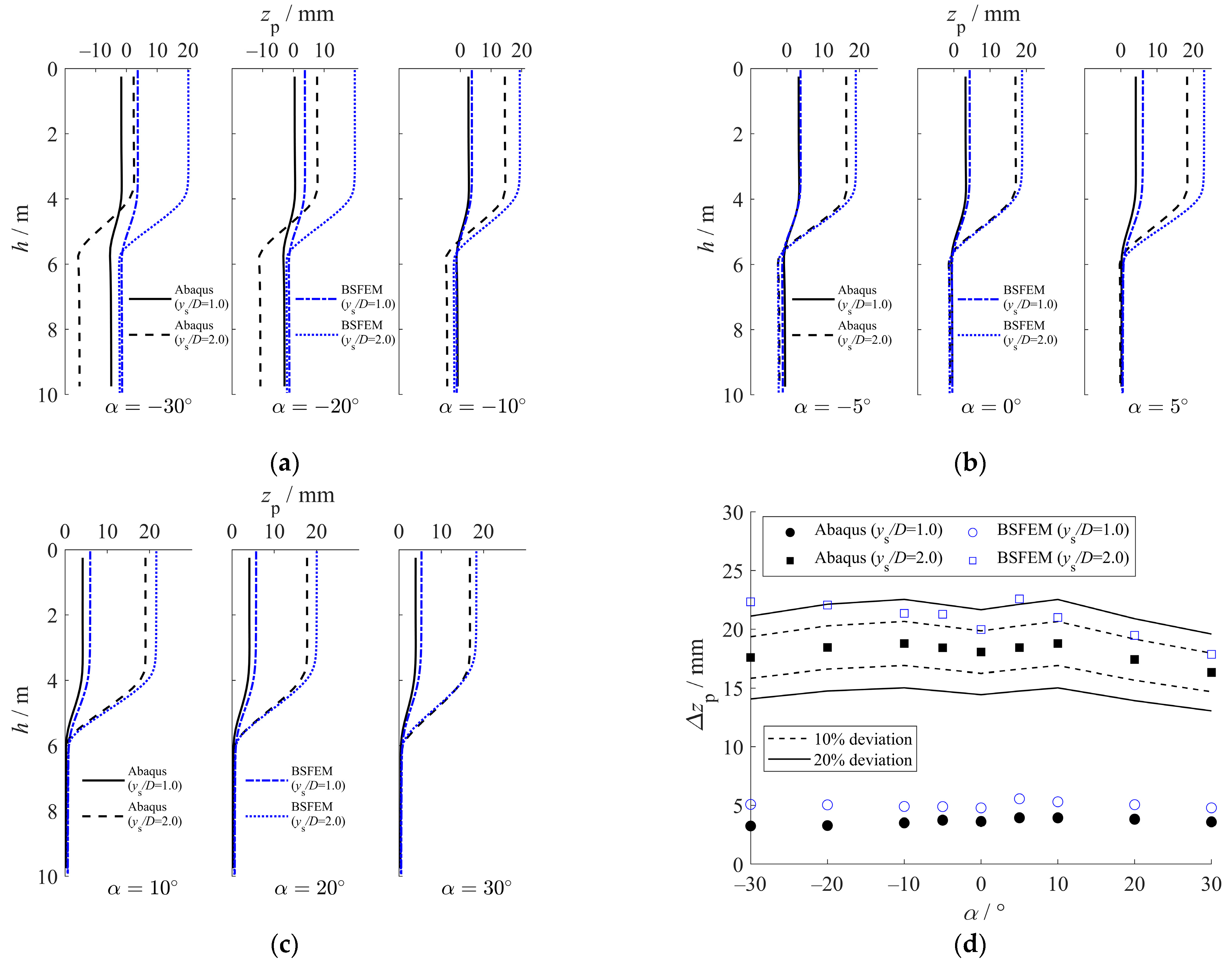
5.1.3. Discussion
5.2. Verification Against Field Measurements
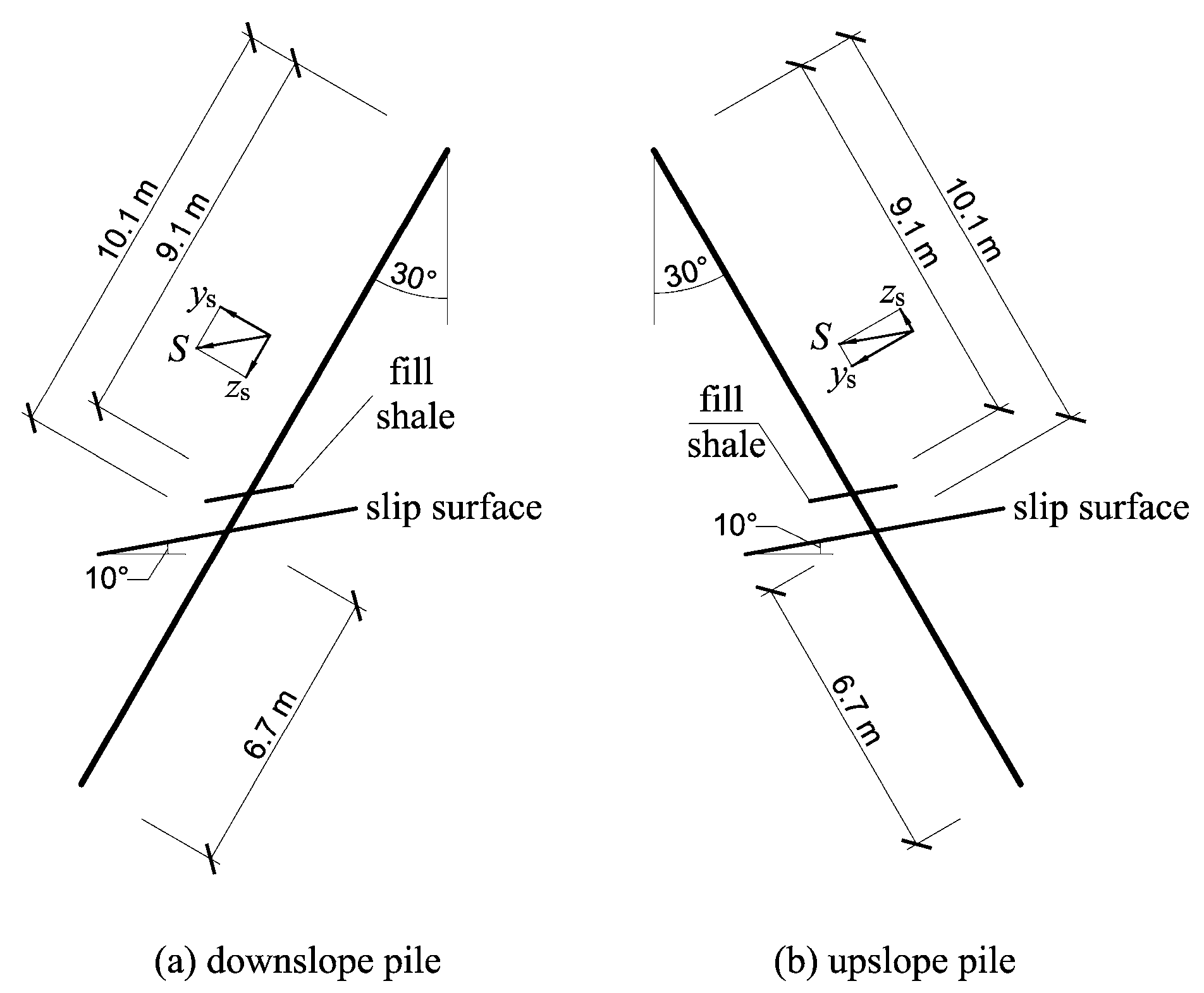
6. Conclusions
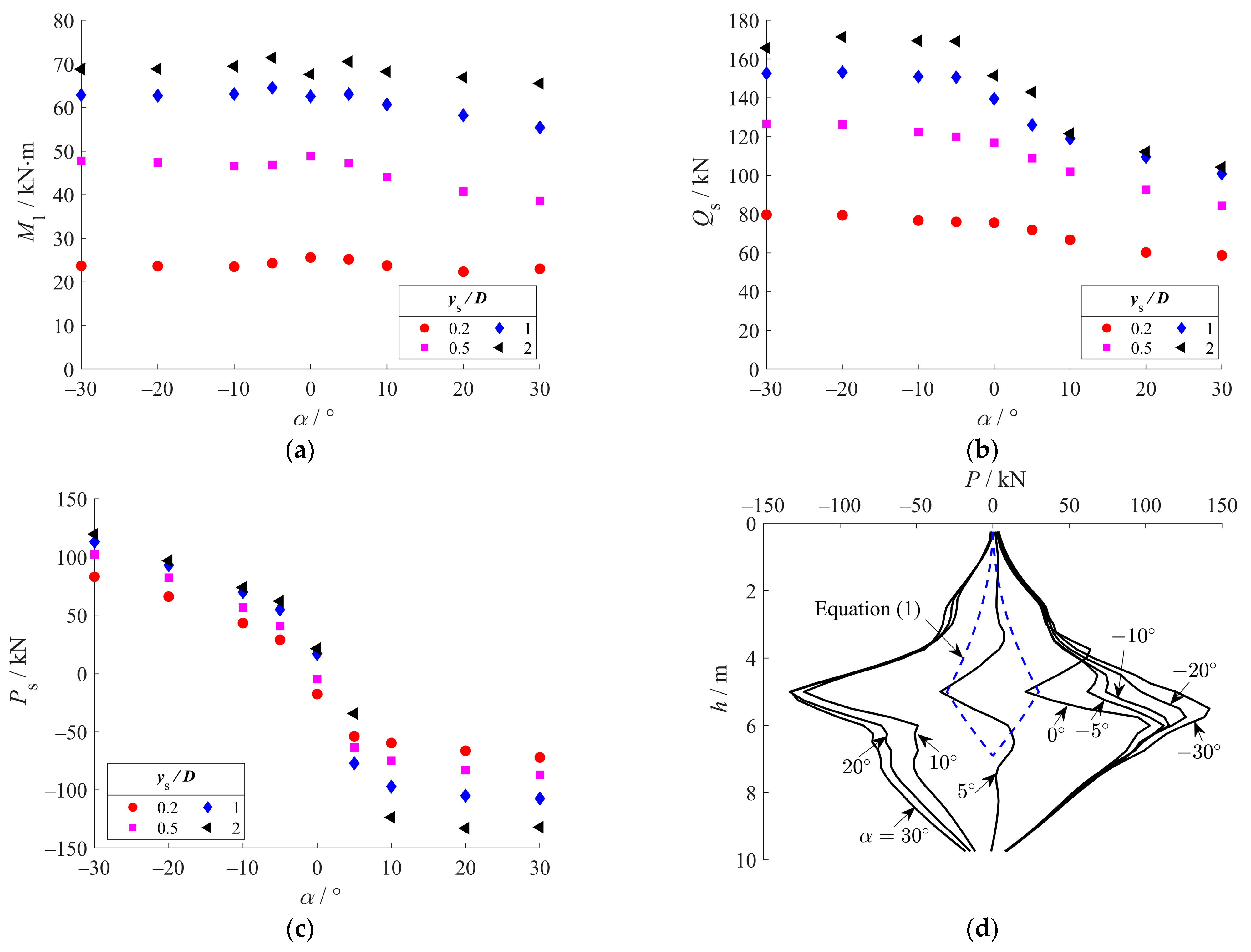
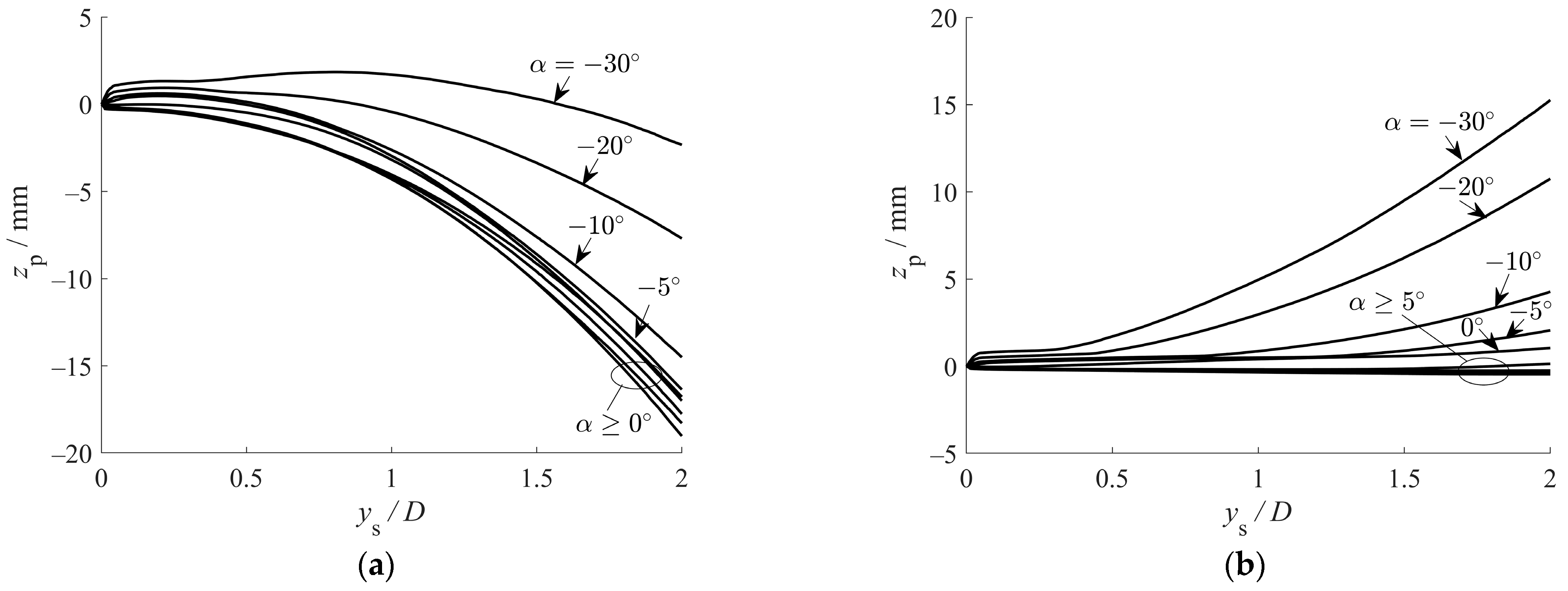
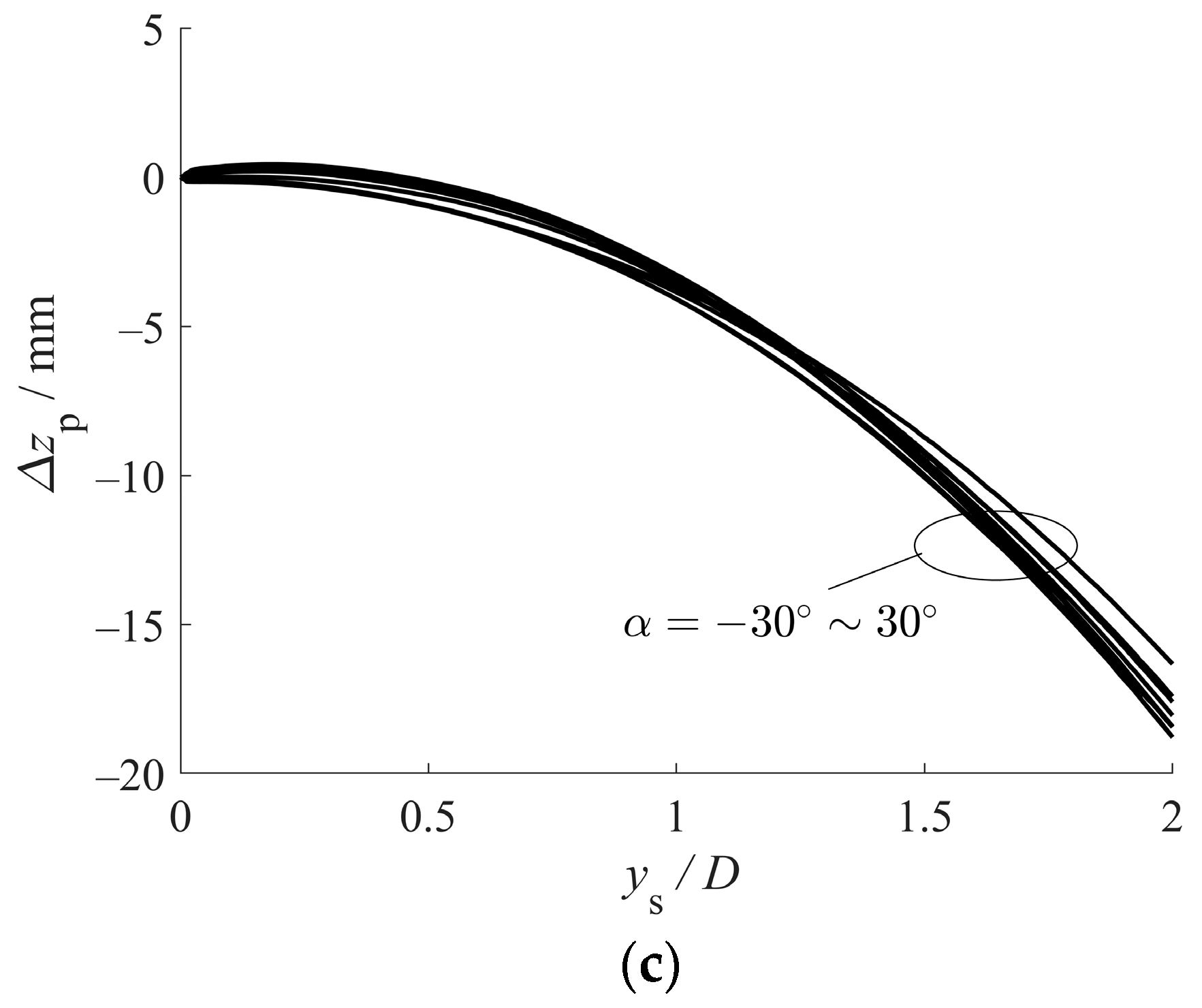
- Axial force (P) in a micro anti-slide pile develops through two primary mechanisms: axial soil displacement () and pile kinematics. As the sliding angle () transitions from negative to positive values, P shifts from tension to mainly compression, highlighting the predominant role of in axial force generation. In contrast, the kinematically induced axial force remains consistently tensile, opposing the compressive influence of when is positive. The case where serves as an approximate transition point at which these opposing effects effectively cancel each other. The two mechanisms governing axial force development also demonstrate distinct mobilization behaviors: the zs-induced axial force mobilizes earlier than both bending moment and shear force, whereas kinematically induced axial force mobilizes considerably later.
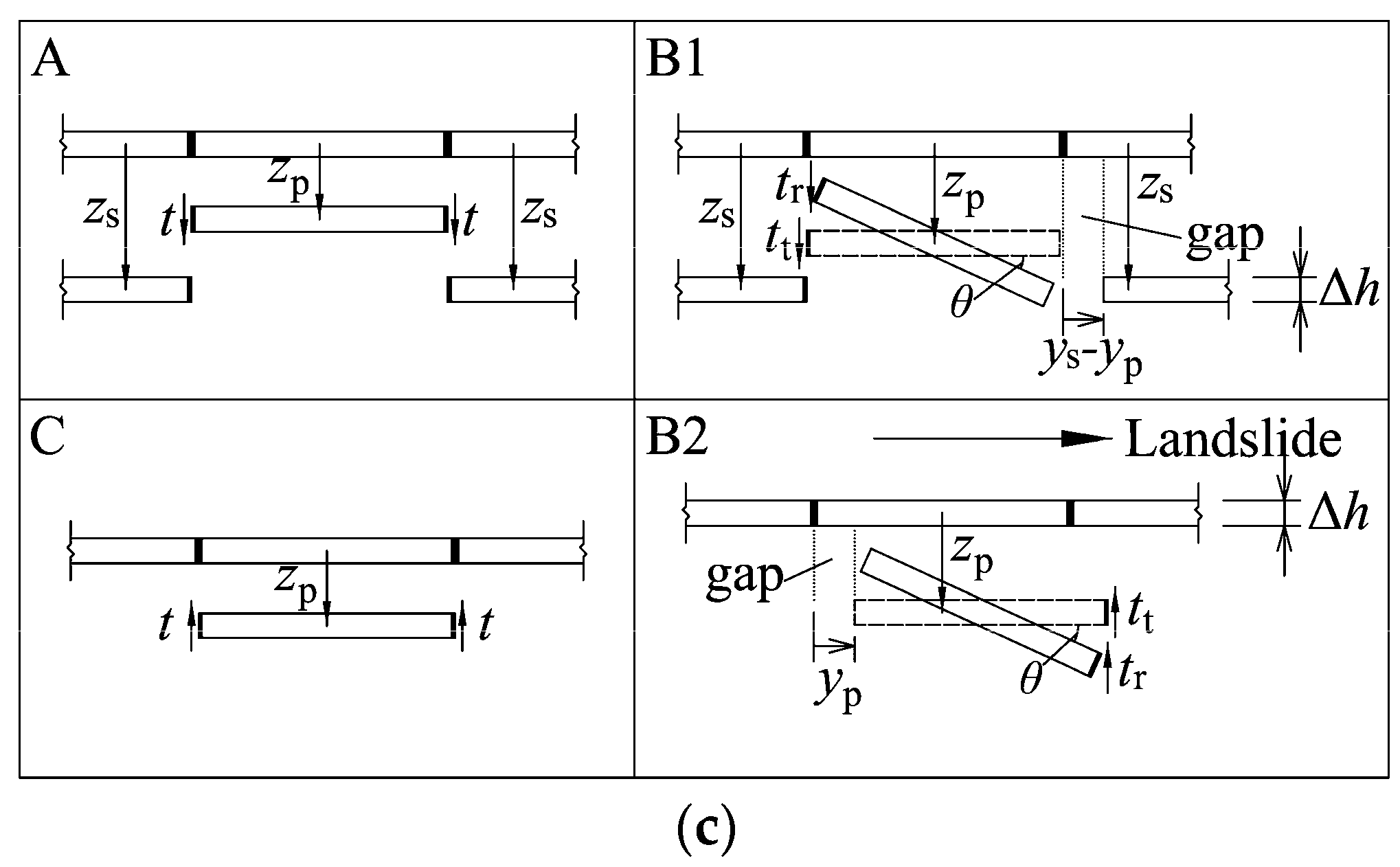
- Based on displacement characteristics, the micropile is divided into three segments: Segments A and C away from the slip surface show axial displacement governed by rigid cross-section translation, while Segment B near the slip surface exhibits rotation-dominated axial displacement accompanied by partial soil–pile separation due to large lateral displacements—significantly complicating predictions of axial friction magnitude and direction. A detailed analysis of axial frictional resistance was conducted for each segment, taking into account the influence of varying sliding angles ().
- Both the p-y and t-z relationships were modeled using a hyperbolic formulation. For Segment B, the derived soil resistance equations explicitly account for two key mechanisms: cross-sectional rotation effects and soil-pile separation behavior. Model parameters for both the p-y and t-z curves were calibrated through inverse analysis based on numerically simulated response data. The results indicate that both the ultimate lateral soil resistance () and the ultimate shaft resistance () exhibit clear dependence on the sliding angle ().
- This study developed a novel beam-spring finite element method (BSFEM) that incorporates both geometric and material nonlinearities of the pile behavior, featuring a soil displacement-driven solution algorithm. The proposed BSFEM demonstrates good agreement with Abaqus simulations in capturing the distribution and evolution of axial deformation and force in micropiles under varying soil movement conditions.
- The proposed methodology has been successfully validated against field monitoring data from an actual engineering application. The advantage over conventional 3D finite element approaches is its ability to predict pile responses efficiently without explicitly simulating complex soil behavior. To fully realize this potential, future work should focus on: (1) incorporating field cases with larger soil displacements, and (2) performing comprehensive numerical simulations to systematically establish reliable p-y and t-z parameter determination methods for micro anti-slide piles, ultimately improving their practical design and application in slope stabilization engineering.
- The developed numerical model and Segment B soil resistance formulations are particularly appropriate for cohesive soils, where significant soil-pile separation develops under lateral soil movements. However, for cohesionless granular materials or cases involving post-separation gap infilling, the observed axial force distribution patterns near the slip surface may deviate from the current findings. In such scenarios, modifications to the soil resistance models would be necessary to account for these differing mechanical behaviors.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Wasowski, J.; Juang, C.H. Geohazards in the Three Gorges Reservoir Area, China—Lessons Learned from Decades of Research. Eng. Geol. 2019, 261, 105267. [Google Scholar] [CrossRef]
- Tang, H.; Wang, L.; Li, C.; Zou, Z. Key Techniques of Prevention and Control for Reservoir Landslides Based on Evolutionary Process. In Progress in Landslide Research and Technology, Volume 1 Issue 2, 2022; Alcántara-Ayala, I., Arbanas, Ž., Huntley, D., Konagai, K., Mikoš, M., Sassa, K., Sassa, S., Tang, H., Tiwari, B., Eds.; Progress in Landslide Research and Technology; Springer International Publishing: Cham, Switzerland, 2023; pp. 11–28. ISBN 978-3-031-18470-3. [Google Scholar]
- Sun, S.-W.; Zhu, B.-Z.; Wang, J.-C. Design Method for Stabilization of Earth Slopes with Micropiles. Soils Found. 2013, 53, 487–497. [Google Scholar] [CrossRef]
- Lei, G.; Su, D.; Cabrera, M.A. Non-Dimensional Solutions for the Stabilising Piles in Landslides in Layered Cohesive Soils Considering Non-Linear Soil–Pile Interactions. Géotechnique 2022, 72, 737–751. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Tang, H.; Wang, J.; Chen, F.; Liang, D. A Novel Optimal Plane Arrangement of Stabilizing Piles Based on Soil Arching Effect and Stability Limit for 3D Colluvial Landslides. Eng. Geol. 2015, 195, 236–247. [Google Scholar] [CrossRef]
- Xiang, B.; Zhang, L.M.; Zhou, L.-R.; He, Y.-Y.; Zhu, L. Field Lateral Load Tests on Slope-Stabilization Grouted Pipe Pile Groups. J. Geotech. Geoenviron. Eng. 2015, 141, 04014124. [Google Scholar] [CrossRef]
- Zeng, J.; Xiao, S. A Simplified Analytical Method for Stabilizing Micropile Groups in Slope Engineering. Int. J. Civ. Eng. 2020, 18, 199–214. [Google Scholar] [CrossRef]
- Yang, T.; Men, Y.; Rutherford, C.J.; Zhang, Z. Static and Dynamic Response of Micropiles Used for Reinforcing Slopes. Appl. Sci. 2021, 11, 6341. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Liu, K.; Su, Y. Experimental Investigation on Anti-Sliding Performance of Grouted Micro-Pipe Pile Groups. Nat. Hazards 2022, 113, 1367–1384. [Google Scholar] [CrossRef]
- Zhang, C.; Yin, Y.; Yan, H.; Zhu, S.; Li, B.; Hou, X.; Yang, Y. Centrifuge Modeling of Multi-Row Stabilizing Piles Reinforced Reservoir Landslide with Different Row Spacings. Landslides 2023, 20, 559–577. [Google Scholar] [CrossRef]
- Zhang, C.; Yin, Y.; Yan, H.; Zhu, S.; Zhang, M.; Wang, L. Centrifuge Modeling of Unreinforced and Multi-Row Stabilizing Piles Reinforced Landslides Subjected to Reservoir Water Level Fluctuation. J. Rock Mech. Geotech. Eng. 2024, 16, 1600–1614. [Google Scholar] [CrossRef]
- Loehr, J.E.; Brown, D.A. A Method for Predicting Mibilization of Resistance for Micropiles Used in Slope Stabilization Applications. Report Submitted to the Joint ADSC/DFI Micropile Committee. 2008. Available online: https://danbrownandassociates.com/wp-content/uploads/2008/01/a-method-for-predicting-mobilization-of-resistance-for-micropiles-used-in-slope-stabilization-applications-loher_brown-adsc-dfi-micropile-committee-report-jan-08.pdf (accessed on 12 September 2025).
- Han, M.; Jia, J. Nonlinear Response of Micropile Groups Stabilizing Landslides Considering Pile–Soil Interactions. Int. J. Geomech. 2024, 24, 04024109. [Google Scholar] [CrossRef]
- White, D.J.; Thompson, M.J.; Suleiman, M.T.; Schaefer, V.R. Behavior of Slender Piles Subject to Free-Field Lateral Soil Movement. J. Geotech. Geoenviron. Eng. 2008, 134, 428–436. [Google Scholar] [CrossRef]
- API. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms-Working Stress Design; American Petroleum Institute: Washington, DC, USA, 2000. [Google Scholar]
- Bateman, A.H.; Crispin, J.J.; Vardanega, P.J.; Mylonakis, G.E. Theoretical T-z Curves for Axially Loaded Piles. J. Geotech. Geoenviron. Eng. 2022, 148, 04022052. [Google Scholar] [CrossRef]
- Boeckmann, A.Z. Load Transfer in Micropiles for Slope Stabilization from Tests of Large Scale Physic Models. Master’s Thesis, University of Missouri, Columbia, MO, USA, 2006. [Google Scholar]
- Su, D.; Li, J.H. Three-Dimensional Finite Element Study of a Single Pile Response to Multidirectional Lateral Loadings Incorporating the Simplified State-Dependent Dilatancy Model. Comput. Geotech. 2013, 50, 129–142. [Google Scholar] [CrossRef]
- Kourkoulis, R.; Gelagoti, F.; Anastasopoulos, I.; Gazetas, G. Hybrid Method for Analysis and Design of Slope Stabilizing Piles. J. Geotech. Geoenviron. Eng. 2012, 138, 1–14. [Google Scholar] [CrossRef]
- Kourkoulis, R.; Gelagoti, F.; Anastasopoulos, I.; Gazetas, G. Slope Stabilizing Piles and Pile-Groups: Parametric Study and Design Insights. J. Geotech. Geoenviron. Eng. 2011, 137, 663–677. [Google Scholar] [CrossRef]
- Lei, G.; Wu, Z.; Su, D.; Mo, Y.; Cheng, M. A p-y method for calculating micro anti-slide piles considering pile material nonlinearity. Rock Soil Mech. 2024, 45, 337–348. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced Seismic Analysis of Soil-Foundation-Structure Interaction for Shallow and Pile Foundations in Saturated and Dry Deposits: Insights from 3D Parallel Finite Element Modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of Seismic Soil–Pile–Structure Interaction on Mid- and High-Rise Steel Buildings Resting on a Group of Pile Foundations. Int. J. Geomech. 2018, 18, 04018103. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, X.; Zhou, H.; Chai, J. Numerical Modeling of Progressive Failure of Rigid Piles under Embankment Load. Can. Geotech. J. 2019, 56, 23–34. [Google Scholar] [CrossRef]
- Su, D.; Huang, J.J.; Yan, W.M. Parametric Investigation on the Responses of Laterally Loaded Piles in Overconsolidated Clay Using Nondimensional Solutions Addressing Nonlinear Soil-Pile Interaction. Comput. Geotech. 2018, 96, 203–214. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, G. New P-y Curve Model Considering Vertical Loading for Piles of Offshore Wind Turbine in Sand. Ocean. Eng. 2020, 203, 107228. [Google Scholar] [CrossRef]
- Byrne, B.W.; Houlsby, G.T.; Burd, H.J.; Gavin, K.G.; Igoe, D.J.P.; Jardine, R.J.; Martin, C.M.; McAdam, R.A.; Potts, D.M.; Taborda, D.M.G.; et al. PISA Design Model for Monopiles for Offshore Wind Turbines: Application to a Stiff Glacial Clay Till. Géotechnique 2020, 70, 1030–1047. [Google Scholar] [CrossRef]
- Abchir, Z.; Burlon, S.; Frank, R.; Habert, J.; Legrand, S. T–z Curves for Piles from Pressuremeter Test Results. Géotechnique 2016, 66, 137–148. [Google Scholar] [CrossRef]
- Kraft, L.M.; Ray, R.P.; Kagawa, T. Theoretical t–z Curves. J. Geotech. Engrg. Div. 1981, 107, 1543–1561. [Google Scholar] [CrossRef]
- Zhu, H.; Chang, M.-F. Load Transfer Curves along Bored Piles Considering Modulus Degradation. J. Geotech. Geoenviron. Eng. 2002, 128, 764–774. [Google Scholar] [CrossRef]
- Rangel, R.L. Educational Tool for Structural Analysis of Plane Frame Models with Geometric Nonlinearity. Master’s Thesis, Pontifical Catholic University of Rio de Janeiro, Rio de Janeiro, Brazil, 2019. [Google Scholar]
- Brown, D.A.; Chancellor, K. Instrumentation, Monitoring and Analysis of the Performance of a Type-A Insert Wall—Littleville, Alabama; Highway Research Center, Harbert Engineering Center, Auburn University: Auburn, AL, USA, 1997. [Google Scholar]








| Stratum | Unit Weight (kN·m−3) | Elastic Modulus (MPa) | Poisson’s Ratio (-) | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|
| Silty clay | 18.2 | 60 | 0.30 | 25 | 18 |
| Fully weathered bedrock | 20.0 | 100 | 0.25 | 30 | 20 |
| Stratum | kpini (kPa) | pu (kN/m) | ktini (kN/m3) | tu (kPa) |
|---|---|---|---|---|
| Fill | 2718.53 | 29.92 | 1.722 × 105 | 88.66 |
| Shale | 7087.59 | 78.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, G.; Yuan, D.; Wu, Z.; Liu, F. Axial Force Analysis and Geometric Nonlinear Beam-Spring Finite Element Calculation of Micro Anti-Slide Piles. Buildings 2025, 15, 3498. https://doi.org/10.3390/buildings15193498
Lei G, Yuan D, Wu Z, Liu F. Axial Force Analysis and Geometric Nonlinear Beam-Spring Finite Element Calculation of Micro Anti-Slide Piles. Buildings. 2025; 15(19):3498. https://doi.org/10.3390/buildings15193498
Chicago/Turabian StyleLei, Guoping, Dongmei Yuan, Zexiong Wu, and Feifan Liu. 2025. "Axial Force Analysis and Geometric Nonlinear Beam-Spring Finite Element Calculation of Micro Anti-Slide Piles" Buildings 15, no. 19: 3498. https://doi.org/10.3390/buildings15193498
APA StyleLei, G., Yuan, D., Wu, Z., & Liu, F. (2025). Axial Force Analysis and Geometric Nonlinear Beam-Spring Finite Element Calculation of Micro Anti-Slide Piles. Buildings, 15(19), 3498. https://doi.org/10.3390/buildings15193498






