Spring-Based Soil–Structure Interaction Modeling of Pile–Abutment Joints in Short-Span Integral Abutment Bridges with LR and RSM
Abstract
1. Introduction
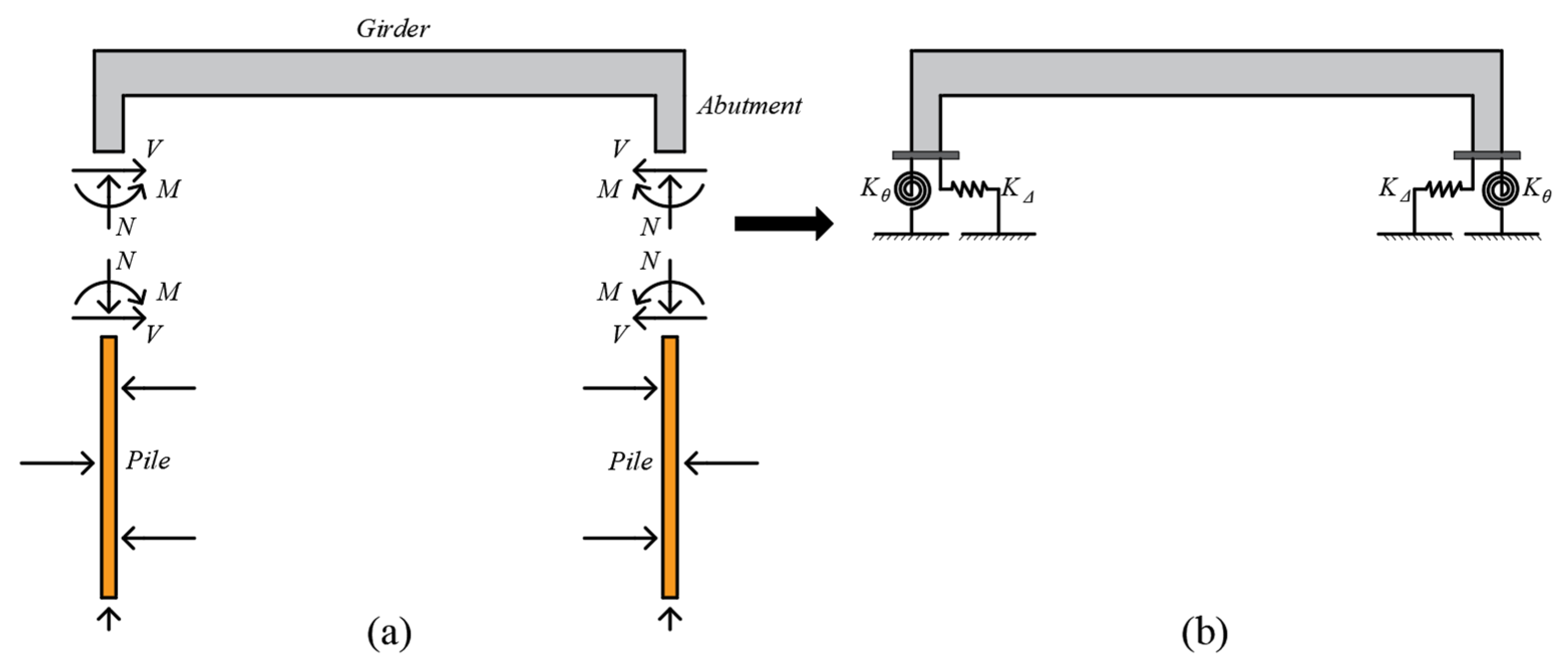
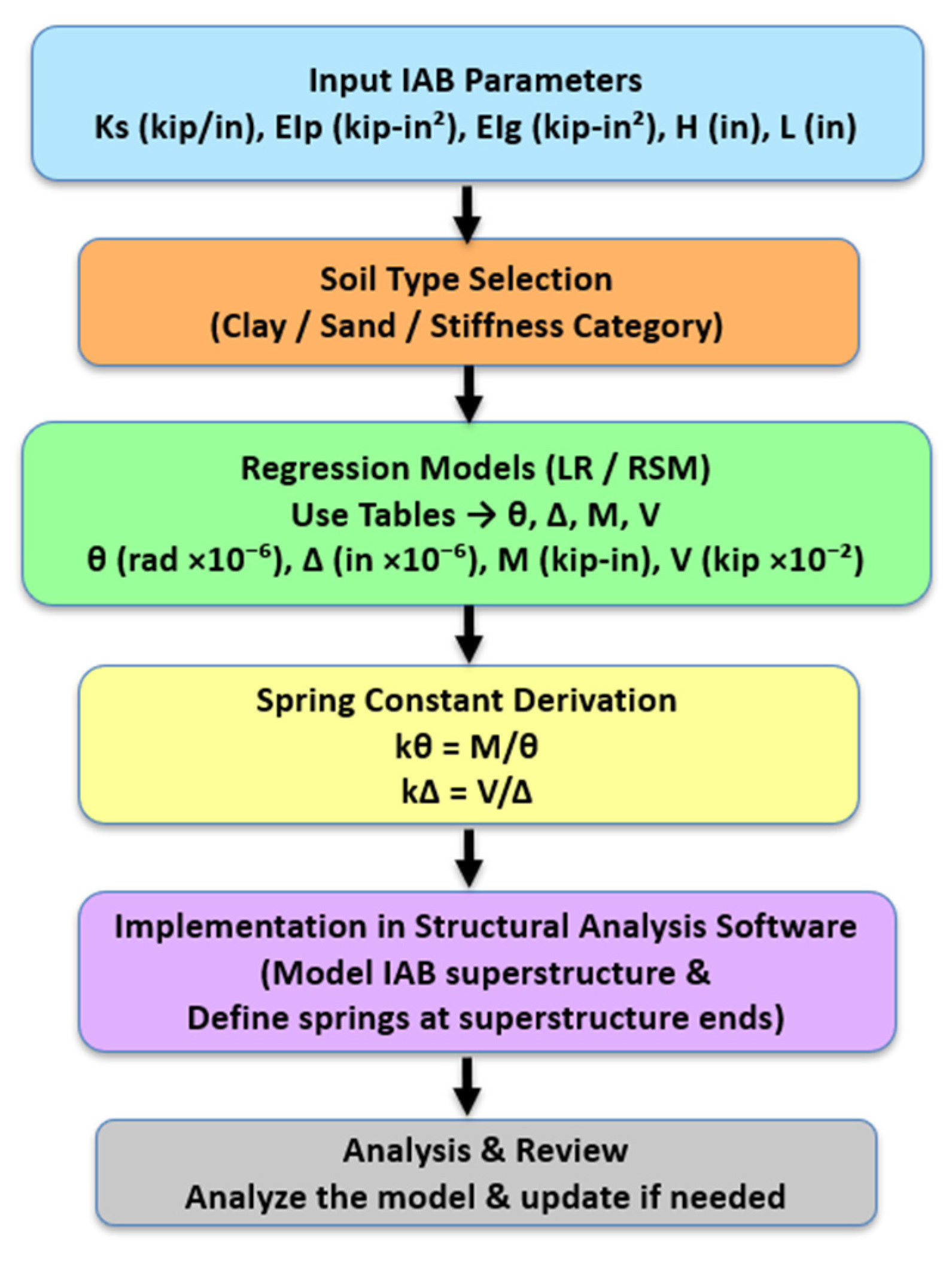
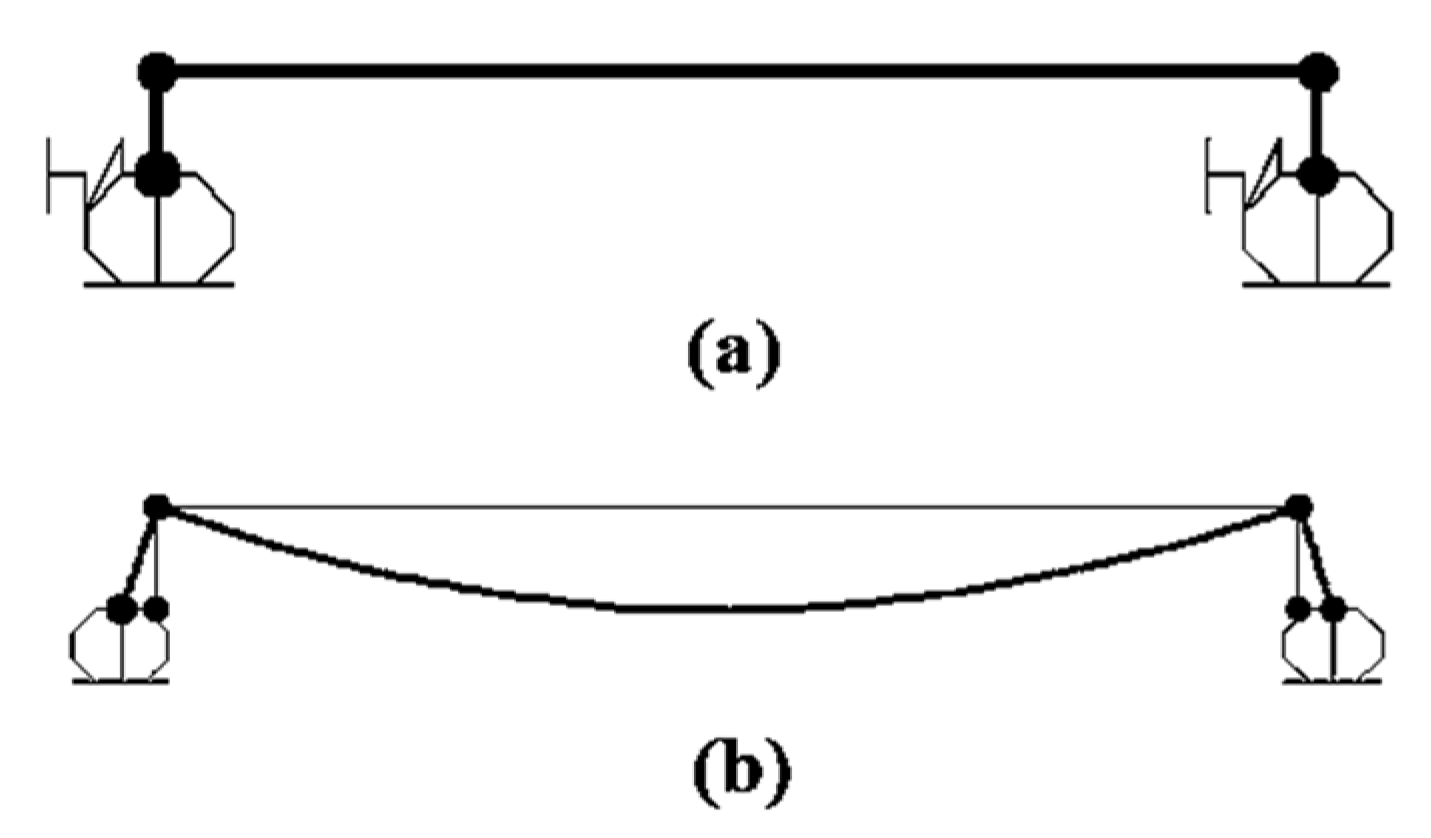
2. Proposed Spring Model
3. Reference Bridge Models
4. Experimental Design Using RSM, LR
4.1. Application of RSM
4.2. Central Composite Design
5. Finite Element Modeling
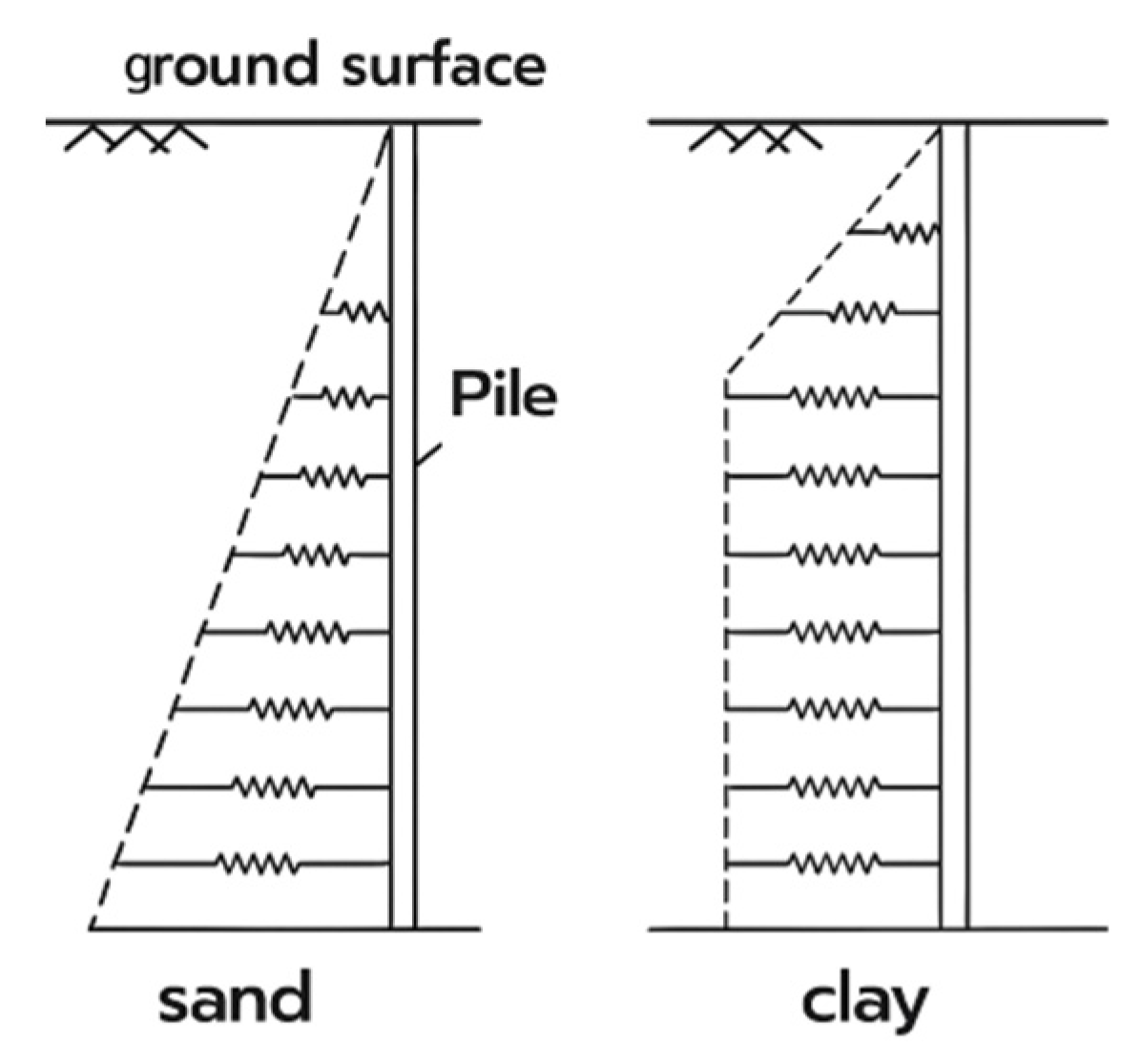
5.1. Pile-Soil Interaction
P-Y Method
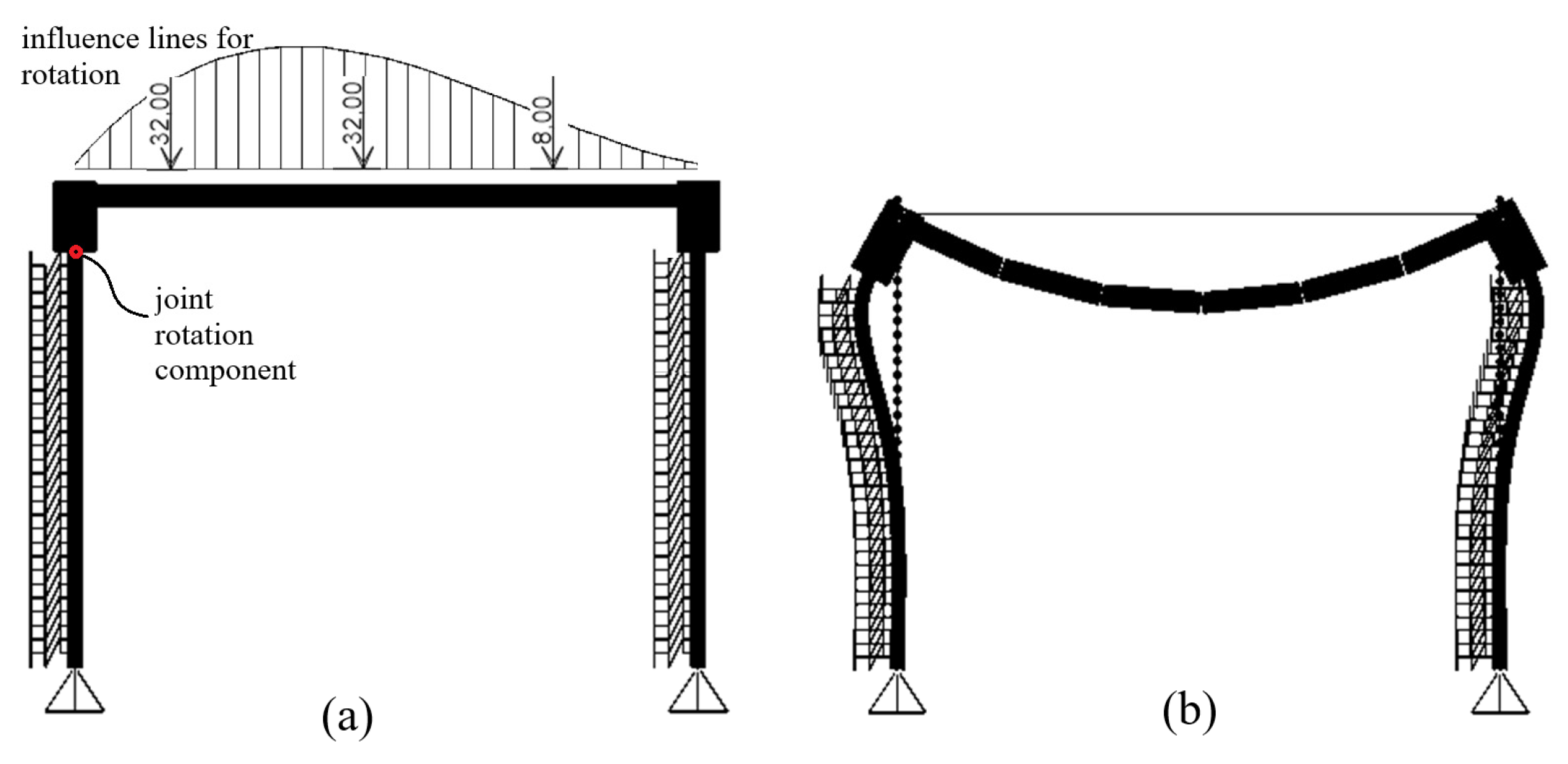
5.2. Two-Dimensional Frame Modeling of Bridges
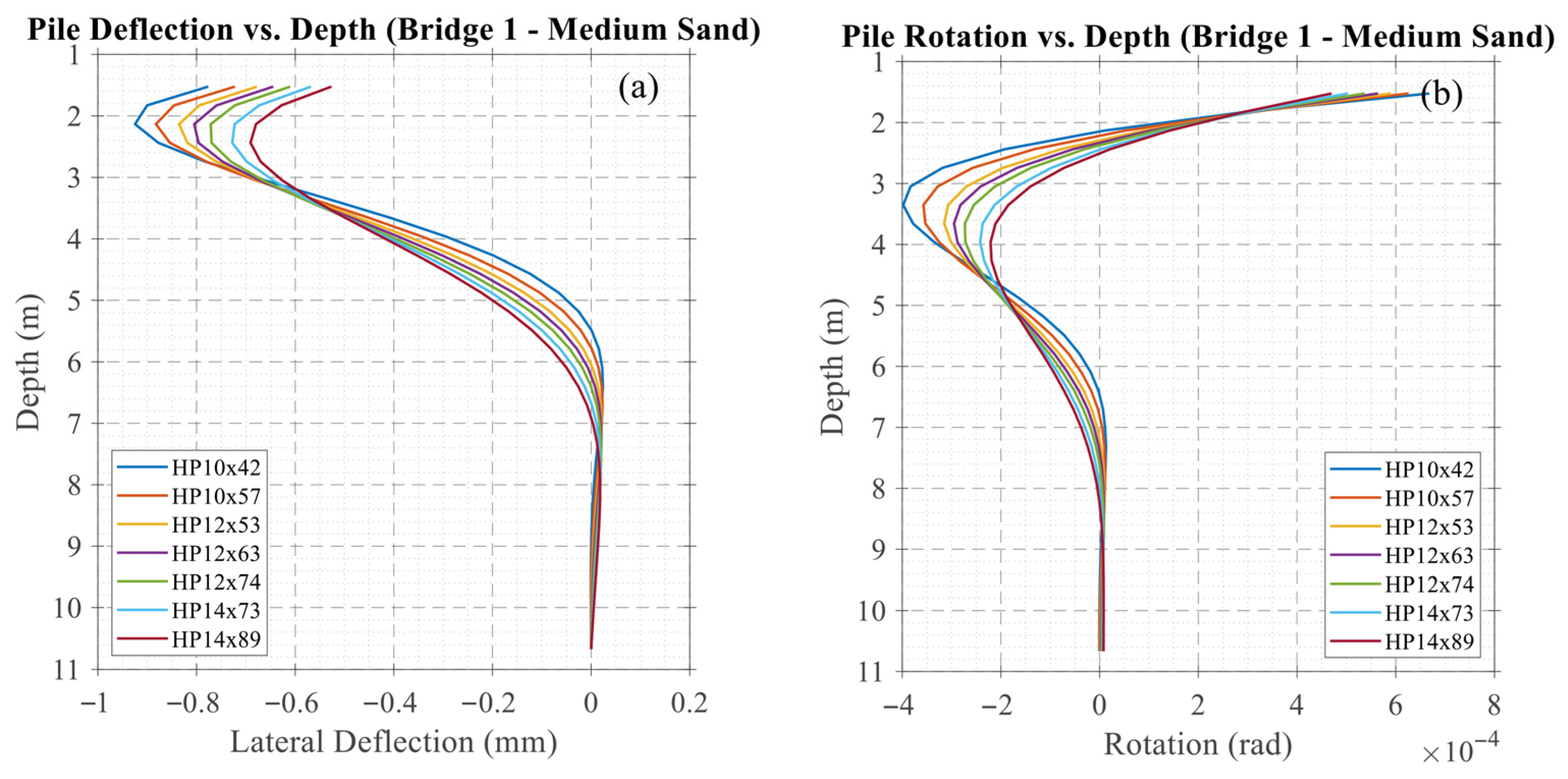
5.3. Typical Pile Response and Spring Model Representation
6. Design Optimization Using LR and RSM
6.1. Development of Predictive Equations Using LR and RSM
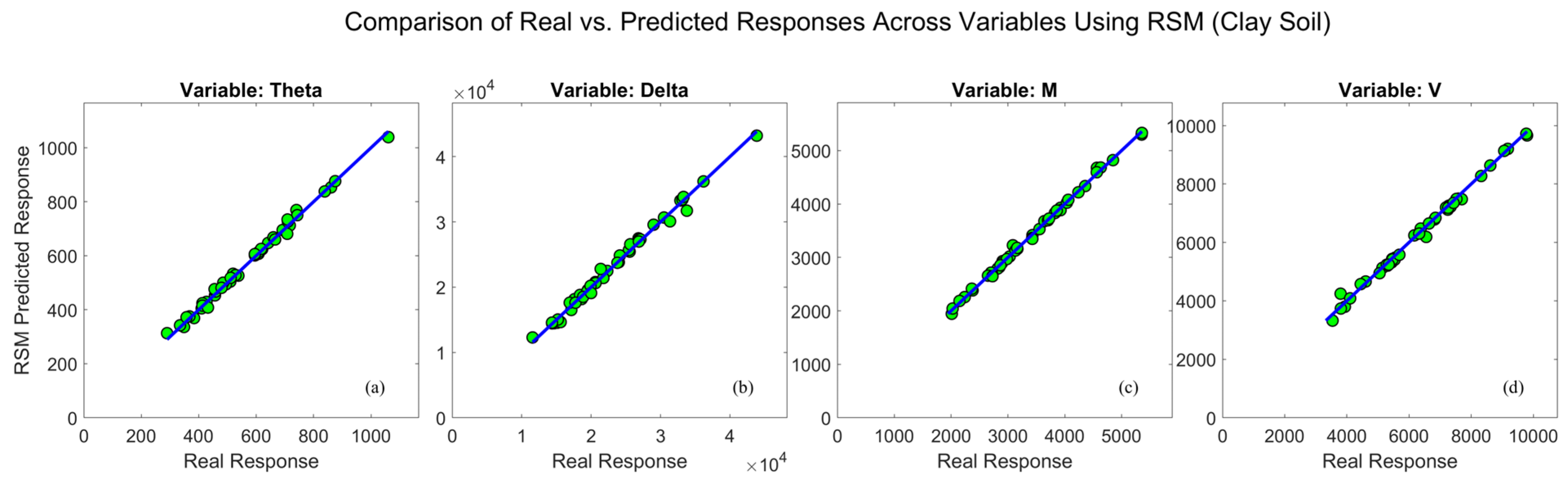
6.2. RSM and LR Predicted Response
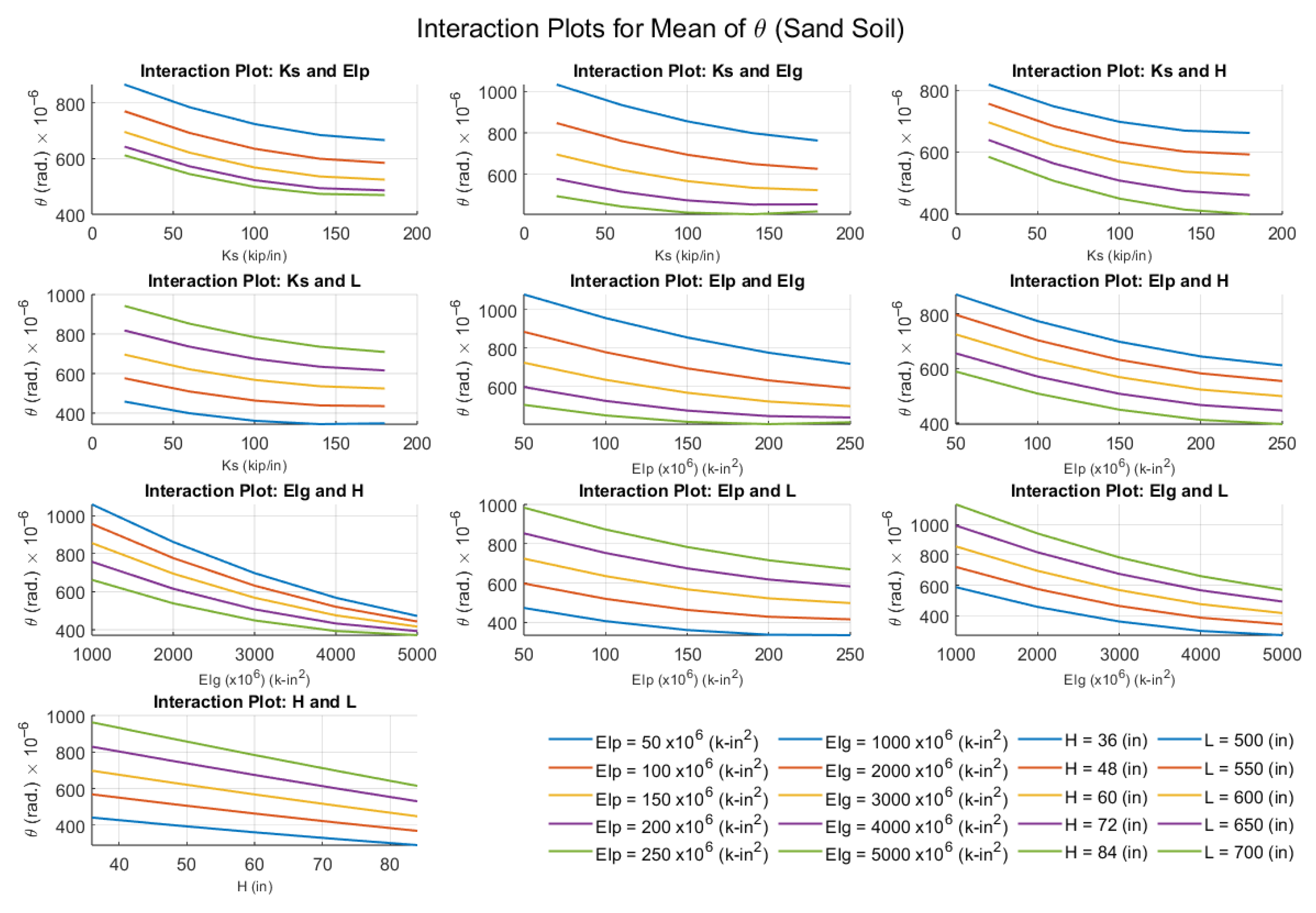
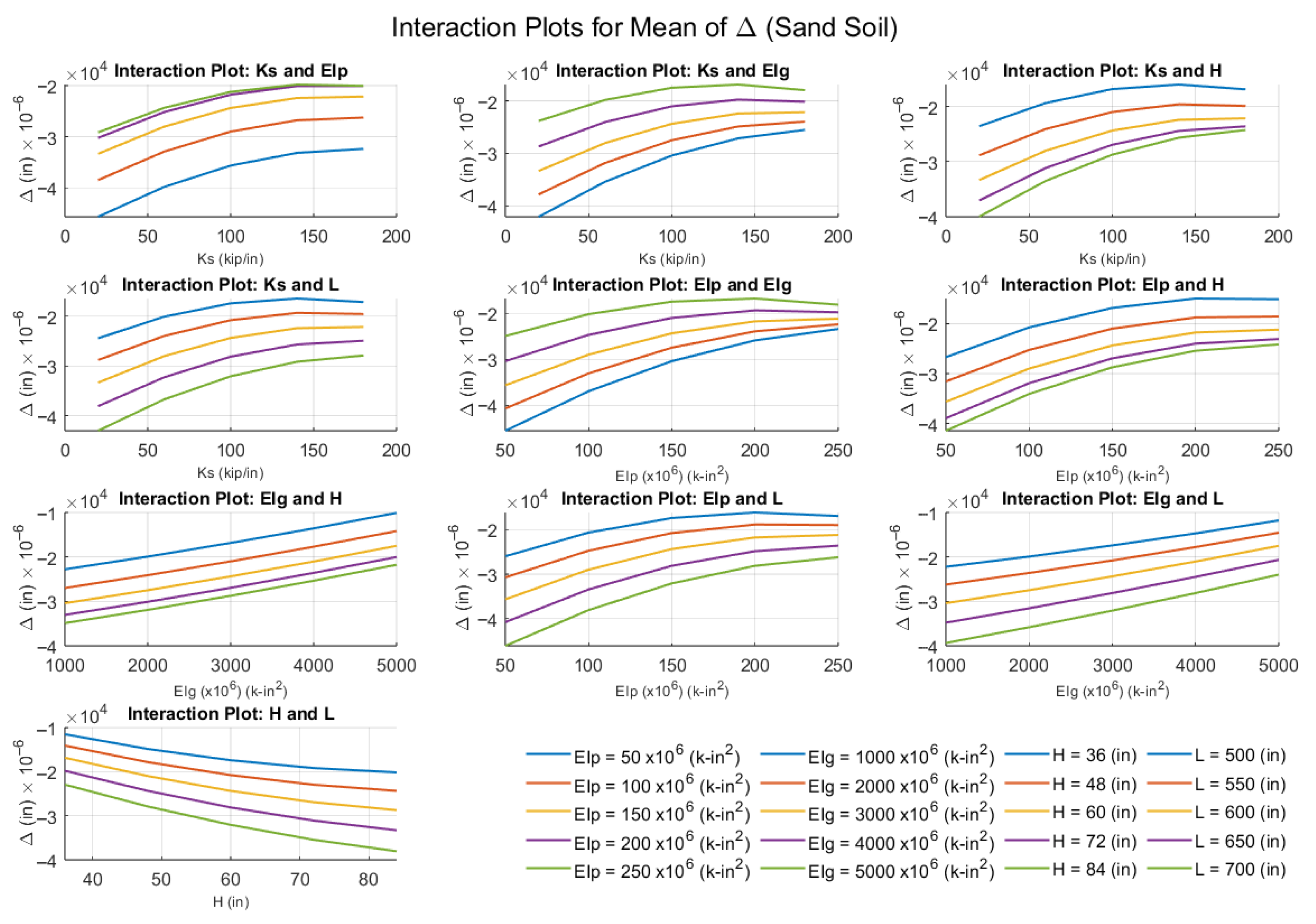
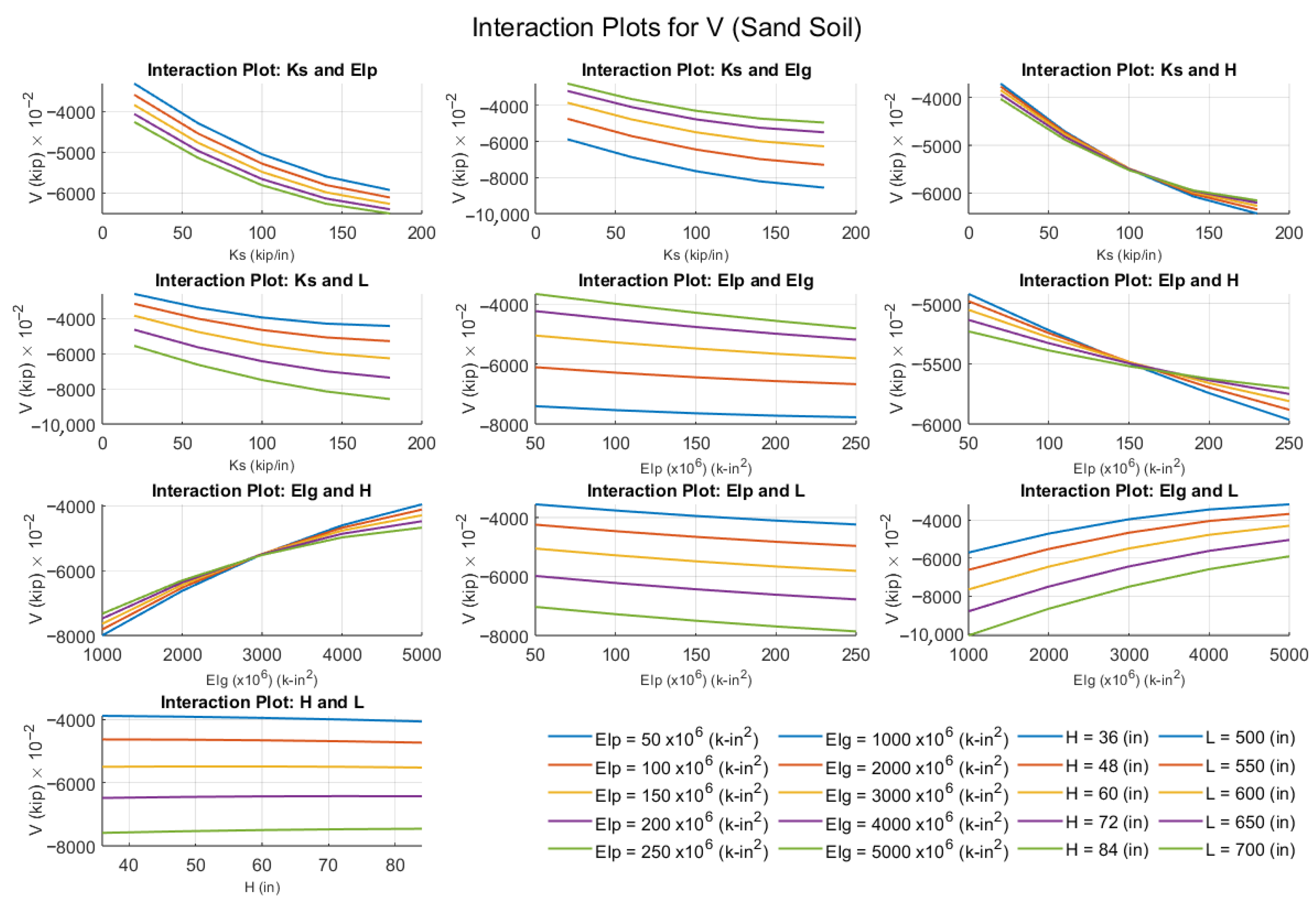
6.3. Interaction of Variables with Responses Obtained by RSM
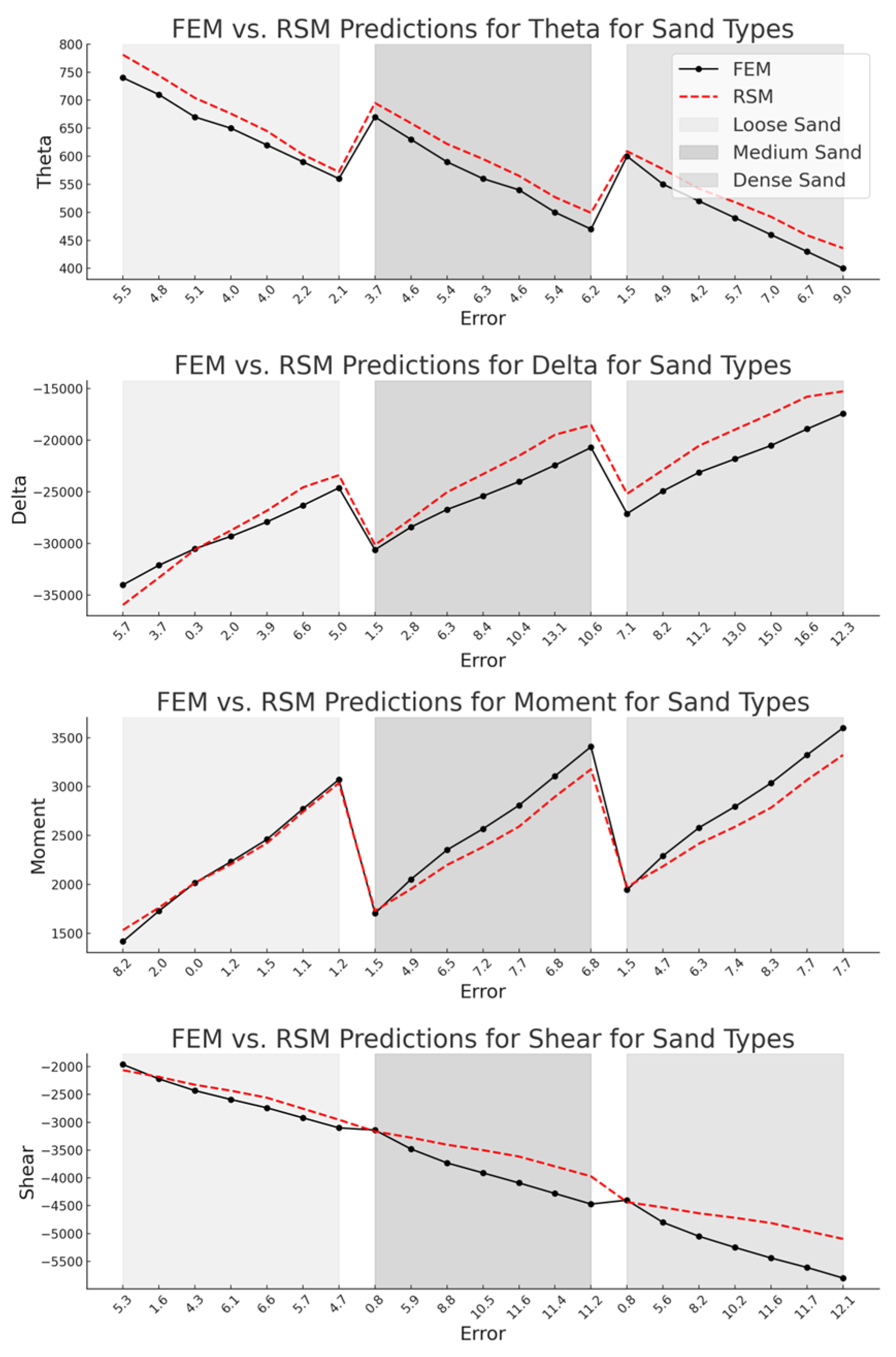
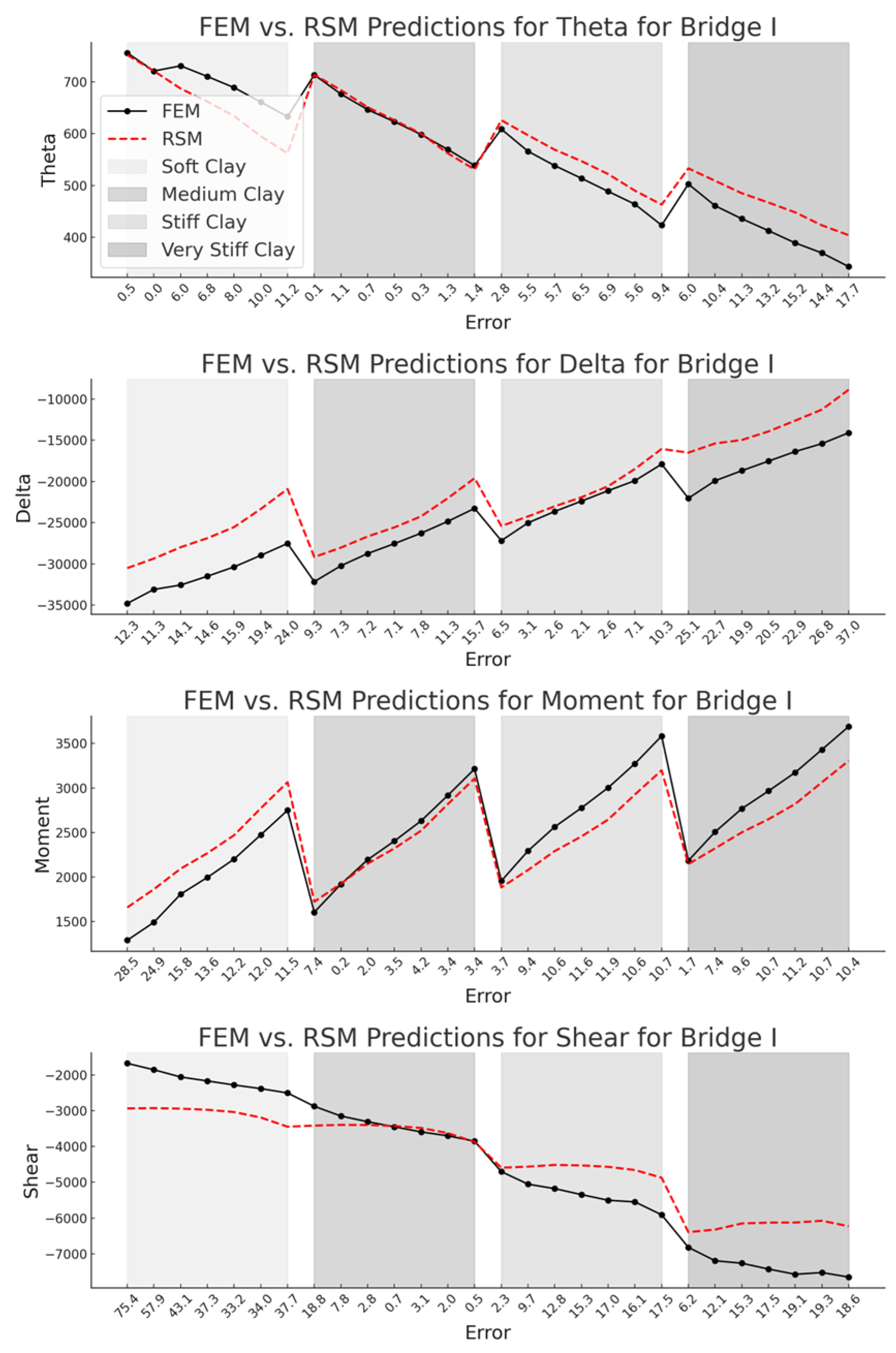
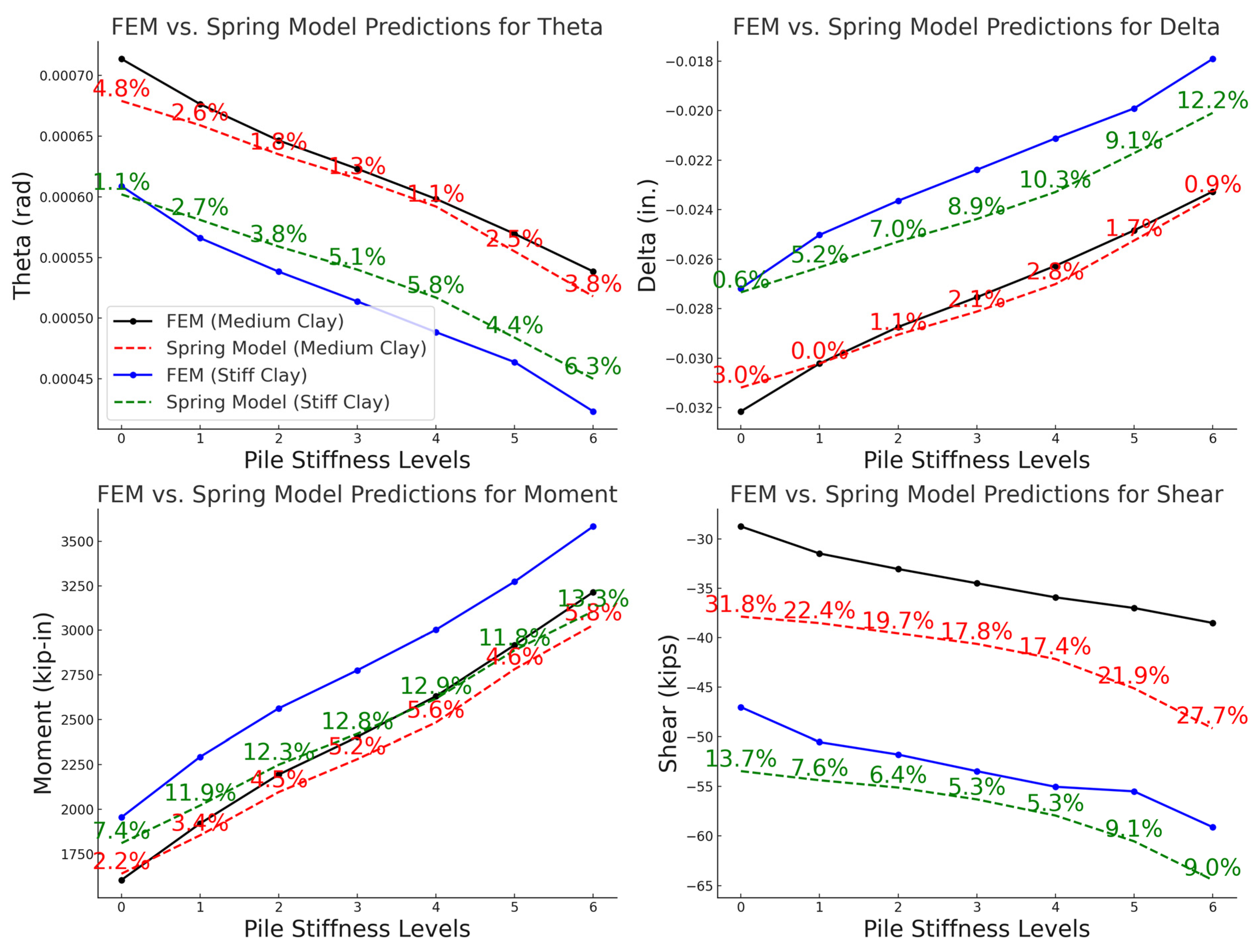
7. FEM vs. RSM Predictions
8. Implementation of Spring Model for Pile-Abutment Joint
9. Conclusions
- The complex and nonlinear behavior of pile–soil interaction can be effectively approximated using the proposed spring models, in which stiffness values are derived from RSM equations.
- RSM provides better prediction accuracy for pile–abutment responses of short-span IABs under live loads and varying soil and structural conditions, significantly outperforming LR in capturing complex parameter interactions.
- The novelty of this study lies in deriving regression-based spring constants calibrated against FEM analyses, which is a practical and resilience-oriented technique for bridge designers. Unlike prior studies relying solely on FEM or traditional p–y curves, the proposed model enables direct use of predictive spring constants in design software.
- Prediction errors for soft clay and very stiff clay exceed 20% in some cases, reaching up to 27% for very stiff clays. Extrapolation to high-stiffness soils should therefore be applied cautiously, with engineering judgment and conservatism as required by design codes.
- For other soil conditions, prediction errors remain below 20% for rotation and deflection, and below 15% for moment and shear. The models are most reliable within the ranges Ks = 20–180 kip/in (3.5–31.5 kN/mm), EIp = 50–250 × 106 kip·in2 (0.14–0.72 × 106 kN·m2), EIg = 1000–5000 × 106 kip·in2 (2.9–14.3 × 106 kN·m2), H = 3–7 ft (0.91–2.13 m), and L = 42–58 ft (12.7–17.8 m). A design safety factor of 1.2–1.3 is recommended when applying regression-derived stiffness values.
- Sensitivity analyses revealed that increasing soil stiffness reduces pile–abutment rotation and deflection, slightly increases moments, but considerably raises shear demand.
- Increasing pile rigidity reduces joint rotation and deflection but increases moments and shear forces.
- Increasing girder flexural rigidity reduces joint rotation, deflection, moments, and shear forces.
- Increasing abutment height slightly reduces moments and joint rotation but increases deflection, with negligible influence on shear.
- Increasing span length amplifies joint rotation, deflection, moments, and shear forces due to larger lever arms and higher load demands.
- Prediction errors increase with span length due to amplified lever-arm effects and greater sensitivity of pile-abutment responses to geometric nonlinearity. Regression models capture these effects within the studied range of 42–58 ft (12.7–17.8 m), but extrapolation to longer spans introduces cumulative deviations.
- The proposed regression-based spring model is restricted to static analysis of short-span IABs. It does not capture dynamic effects such as seismic or thermal cycling, nor does it consider pile-to-pile interaction effects. These aspects should be addressed in future research.
- The findings regarding the influence of soil stiffness on pile–abutment rotation, deflection, moment, and shear are valid only for the dry/static soil conditions modeled herein. Pore pressure evolution, seasonal groundwater fluctuations, and long-term environmental effects are not accounted for in this study, as they are beyond its scope.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Soil Spring Parameters Used in p-y Method Correlations
| Nomenclature | Description | Units/Values |
|---|---|---|
| Soil stiffness | - | |
| Pu | Ultimate soil resistance | kip/ft (kN/m) |
| cu | Undrained shear strength of clay | Refer to Table 4 |
| Bp | Pile width | ft (m) |
| ɣ | Effective unit weight of the soil | pcf (N/m3) |
| z | Depth of soil spring from ground surface | ft (m) |
| y50 | Displacement at one-half of the ultimate soil reaction | ft (m): 2.5Bpε50 for soft and stiff clay 2Bpε50 for very stiff clay |
| ε50 | Axial strain at one-half of the peak stress difference from a triaxial test | 0.02 for soft clay 0.01 for stiff clay 0.005 for very stiff clay |
| J | Soil parameter | 200 for loose sand 600 for medium sand 1500 for dense sand |
| Clay Consistency | Average Undrained Shear Strength, cu (kPa) | ε50 |
|---|---|---|
| Soft Clay | 12–24 | 0.02 |
| Medium Clay | 24–48 | 0.01 |
| Stiff Clay | 48–96 | 0.007 |
| Very Stiff Clay | 96–192 | 0.005 |
| Hard Clay | 192–383 | 0.04 |
References
- Kunin, J.; Alampalli, S. Integral abutment bridges: Current practice in United States and Canada. J. Perform. Constr. Facil. 2000, 14, 104–111. [Google Scholar] [CrossRef]
- Khodair, Y.; Abdel-Mohti, A. Numerical analysis of pile–soil interaction under axial and lateral loads. Int. J. Concr. Struct. Mater. 2014, 8, 239–249. [Google Scholar] [CrossRef]
- Allen, C.A. Research Pays Off: Jointless Bridge Research Pays Dividends for Vermont. TR News 2010, 267, 51–53. [Google Scholar]
- White, H. Integral Abutment Bridges: Comparison of Current Practice Between European Countries and the United States of America; Transportation Research and Development Bureau, New York State Department of Transportation: Albany, NY, USA, 2007. [Google Scholar]
- Maruri, R.F.; Petro, S.H. Integral Abutments and Jointless Bridges (IAJB) 2004 Survey Summary. In Proceedings of the Integral Abutment and Jointless Bridges (IAJB 2005), Federal Highway AdministrationWest Virginia Department of Transportation, Baltimore, MD, USA, 16–18 March 2005. [Google Scholar]
- Arsoy, S.; Barker, R.M.; Duncan, J.M. The behavior of Integral Abutment Bridges; Virginia Transportation Research Council (VTRC): Charlottesville, VA, USA, 1999. [Google Scholar]
- Huang, J. Behavior of Concrete Integral Abutment Bridges. Doctoral Dissertation, University of Minnesota, Minneapolis, MN, USA, 2004. [Google Scholar]
- Burke, M.P., Jr. Integral and Semi-Integral Bridges; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kuntoğlu, M.; Aslan, A.; Pimenov, D.Y.; Giasin, K.; Mikolajczyk, T.; Sharma, S. Modeling of cutting parameters and tool geometry for multi-criteria optimization of surface roughness and vibration via response surface methodology in turning of AISI 5140 steel. Materials 2020, 13, 4242. [Google Scholar] [CrossRef] [PubMed]
- Adamu, M.; Ayeni, K.O.; Haruna, S.I.; Mansour, Y.E.-H.I.; Haruna, S. Durability performance of pervious concrete containing rice husk ash and calcium carbide: A response surface methodology approach. Case Stud. Constr. Mater. 2021, 14, e00547. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, X.; Chen, X.; Lu, K. Mix design for recycled aggregate pervious concrete based on response surface methodology. Constr. Build. Mater. 2020, 259, 119776. [Google Scholar] [CrossRef]
- Ghorbani, J.; Kodikara, J. Thermodynamically consistent effective stress formulation for unsaturated soils across a wide range of soil saturation. Comput. Mech. 2024, 73, 1077–1094. [Google Scholar] [CrossRef]
- Borja, R.I. Cam-Clay plasticity. Part V: A mathematical framework for three-phase deformation and strain localization analyses of partially saturated porous media. Comput. Methods Appl. Mech. Eng. 2004, 193, 5301–5338. [Google Scholar] [CrossRef]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 10th ed.; AASHTO: Washington, DC, USA, 2024. [Google Scholar]
- Pando, M.A.; Ealy, C.D.; Filz, G.M.; Lesko, J.; Hoppe, E. A Laboratory and Field Study of Composite Piles for Bridge Substructures; United States Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2006. [Google Scholar]
- Reese, L.C.; Van Impe, W.F. Single Piles and Pile Groups Under Lateral Loading; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Rajapakse, R.A. Pile Design and Construction Rules of Thumb; Butterworth-Heinemann: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Sabetamal, H.; Nazem, M.; Sloan, S.W.; Carter, J.P. Frictionless contact formulation for dynamic analysis of nonlinear saturated porous media based on the mortar method. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 25–61. [Google Scholar] [CrossRef]
- Ghorbani, J.; Nazem, M.; Kodikara, J.; Wriggers, P. Finite element solution for static and dynamic interactions of cylindrical rigid objects and unsaturated granular soils. Comput. Methods Appl. Mech. Eng. 2021, 384, 113974. [Google Scholar] [CrossRef]
- Polat, E. Finite Element Analysis of Integral Abutment Bridges. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2013. [Google Scholar]
- Fennema, J.L.; Laman, J.A.; Linzell, D.G. Predicted and measured response of an integral abutment bridge. J. Bridge Eng. 2005, 10, 666–677. [Google Scholar] [CrossRef]
- Kim, W.; Laman, J.A.; Jeong, Y.; Ou, Y.-C.; Roh, H. Comparative study of integral abutment bridge structural analysis methods. Can. J. Civ. Eng. 2016, 43, 378–389. [Google Scholar] [CrossRef]
- Polat, E.; Polat, E.G. Predicting and optimizing maximum flexural strength of planar composite plate shear walls—concrete filled with the application of LR and RSM. Structures 2024, 69, 107353. [Google Scholar] [CrossRef]
- Greimann, L.; Abendroth, R.; Johnson, D.; Ebner, P. Pile Design and Tests for Integral Abutment Bridges; Final Report; Iowa Department of Transportation: Ames, IA, USA, 1987. [Google Scholar]
- Alin, A. Minitab. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 723–727. [Google Scholar] [CrossRef]
- Matlock, H. Correlation for Design of Laterally Loaded Piles in Soft Clay. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 21–23 April 1970; p. OTC–1204-MS. [Google Scholar]
- Hannigan, P.J.; Rausche, F.; Likins, G.; Robinson, B.; Becker, M.; Berg, R.R. Design and Construction of Driven Pile Foundations—Volume I; National Highway Institute: Vienna, VA, USA, 2016. [Google Scholar]



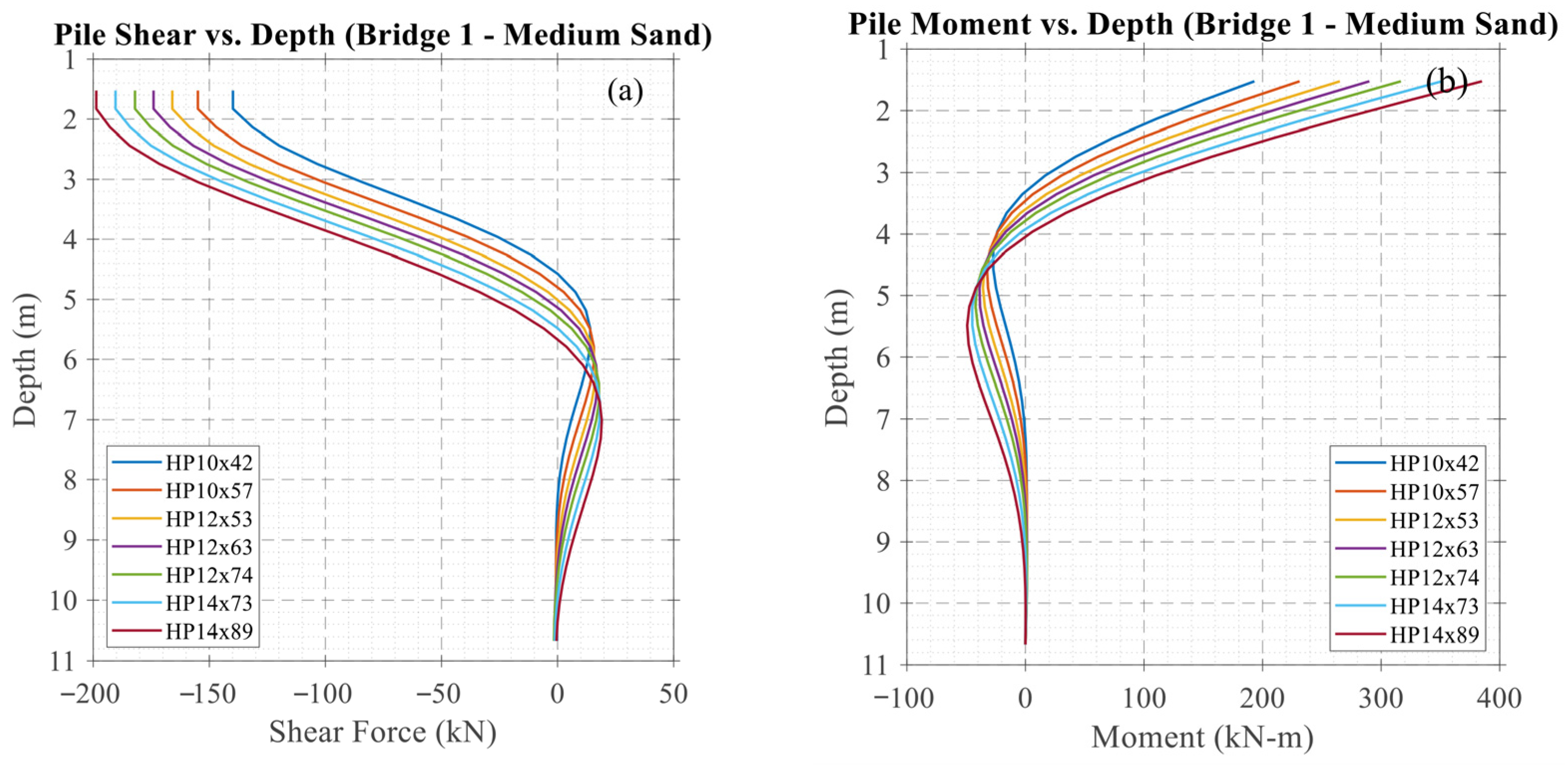
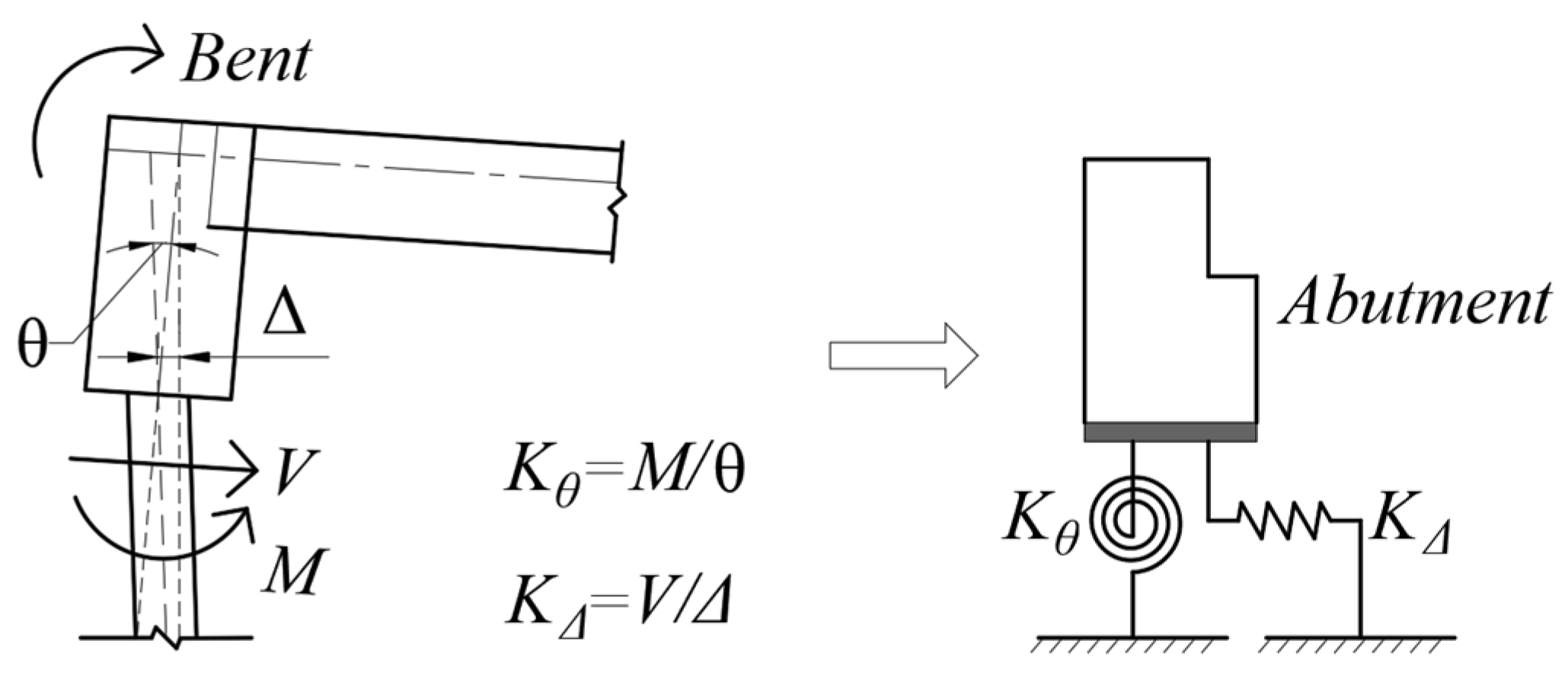

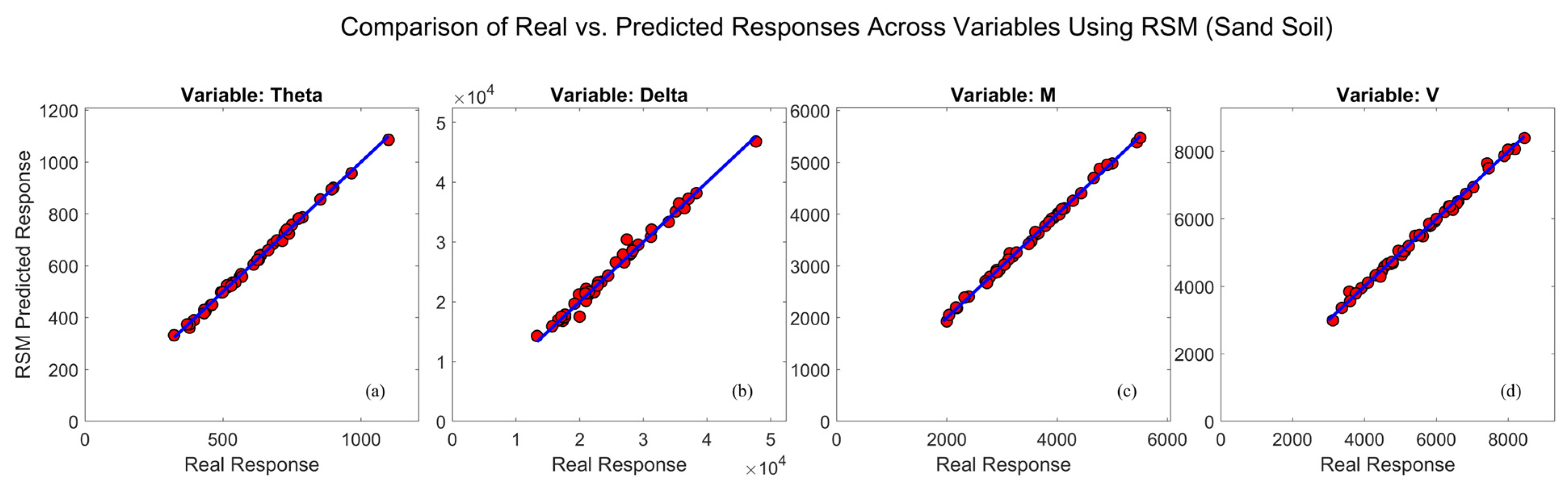
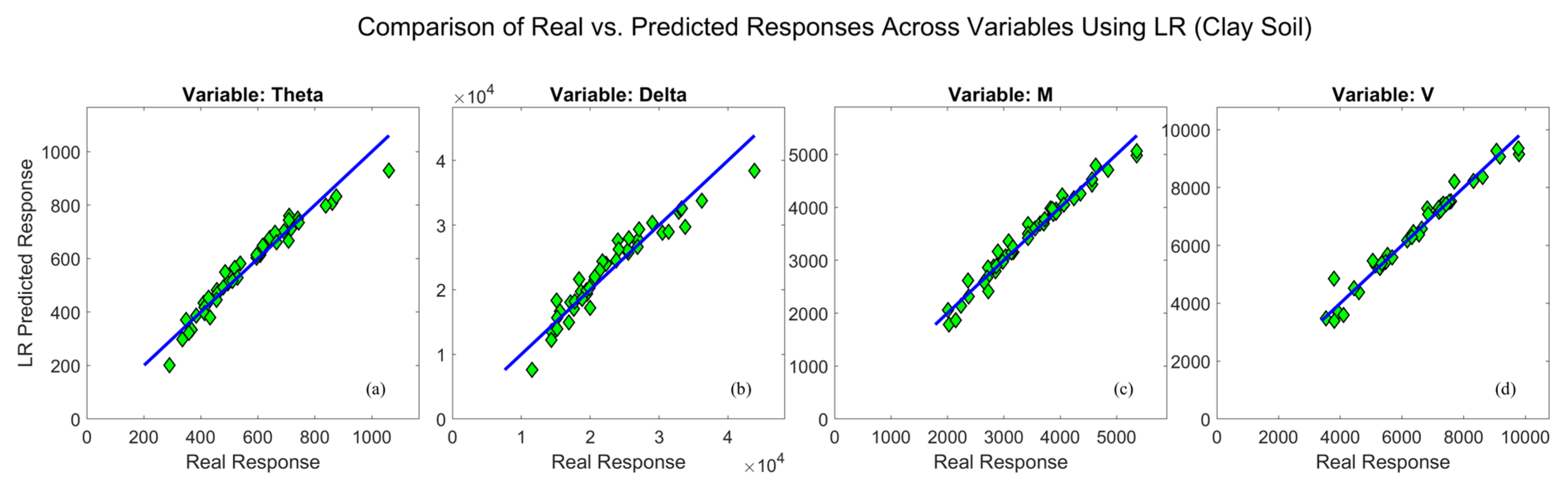

| Property | Bridge I | Bridge II |
|---|---|---|
| Span length | 45 ft (13.7 m) | 50 ft (15.2 m) |
| Bridge width | 32 ft (9.8 m) | 46 ft (14.0 m) |
| Girder type | Channel | Concrete slab |
| Girder width | 4 ft (1.2 m) | - |
| Girder height | 28 in (711 mm) | - |
| Slab thickness | 8 in (203 mm) | 26.4 in (670 mm) |
| Abutment height | 5 ft (1.5 m) | 10 ft (3.0 m) |
| Abutment thickness | 3 ft (914 mm) | 2.5 ft (762 mm) |
| Number of piles | 8 HP steel | 10 HP steel |
| Pile length | 30 ft (9.1 m) | 30 ft (9.1 m) |
| Girder concrete strength (fc′) | 5000 psi (34.5 MPa) | - |
| Girder modulus of elasticity (Ec) | 4286 ksi (29.6 GPa) | - |
| Deck concrete strength (fc′) | 4000 psi (27.6 MPa) | 4000 psi (27.6 MPa) |
| Deck modulus of elasticity (Ec) | 3834 ksi (26.4 GPa) | 3834 ksi (26.4 GPa) |
| Substructure concrete strength (fc′) | 4000 psi (27.6 MPa) | 3500 psi (24.1 MPa) |
| Substructure modulus of elasticity (Ec) | 3834 ksi (26.4 GPa) | 3587 ksi (24.7 GPa) |
| Composite Section M.of.Inertia (Ig) | 86,988 in2 (561,000 cm2) | - |
| Levels | |||||||
|---|---|---|---|---|---|---|---|
| No | Variables | Units (US/SI) | Axial | Factorial | Axial | ||
| (−2) | Low (−1) | Center (0) | High (1) | (+2) | |||
| 1 | Soil stiffness (Sand), Ks | kip/in (kN/m) | 20 (3504) | 60 (10,512) | 100 (17,520) | 140 (24,528) | 180 (31,536) |
| 2 | Pile flexural rigidity, EIp | 106 k-in2 (109 N-m2) | 50 (5.65) | 100 (11.3) | 150 (16.95) | 200 (22.6) | 250 (28.25) |
| 3 | Girder flexural rigidity, EIg | 106 k-in2 (109 N-m2) | 1000 (113) | 2000 (226) | 3000 (339) | 4000 (452) | 5000 (565) |
| 4 | Abutment height, H | in. (mm) | 36 (914.4) | 48 (1219.2) | 60 (1524) | 72 (1828.8) | 84 (2133.6) |
| 5 | Bridge span, L | in. (mm) | 500 (12,700) | 550 (13,970) | 600 (15,240) | 650 (16510) | 700 (17,780) |
| 2-D IAB Model Properties | Analyses Results (Sand) | Analyses Results (Clay) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case No | |||||||||||||
| (Sand) | × 106 | × 106 | × 10−6 | × 10−6 | × 10−2 | × 10−6 | × 10−6 | × 10−2 | |||||
| kip/in | kip-in2 | kip-in2 | in. | in. | rad | in. | kip-in | kips | rad | in. | kip-in | kips | |
| 1 | 100 | 150 | 1000 | 60 | 600 | 853 | −27,410 | 4772 | −7411 | 740 | −30,500 | 4565 | −8322 |
| 2 | 60 | 100 | 2000 | 48 | 550 | 774 | −28,310 | 3053 | −4734 | 743 | −26,830 | 3030 | −5291 |
| 3 | 140 | 100 | 2000 | 48 | 550 | 681 | −23,440 | 3196 | −5946 | 608.1 | −19,530 | 3166 | −7201 |
| 4 | 60 | 200 | 2000 | 48 | 550 | 638 | −21,340 | 3935 | −5124 | 620.8 | −20,620 | 3875 | −5552 |
| 5 | 140 | 200 | 2000 | 48 | 550 | 561 | −17,350 | 4015 | −6234 | 509.7 | −14,710 | 3924 | −7274 |
| 6 | 140 | 100 | 2000 | 48 | 650 | 966 | −31,200 | 4436 | −8184 | 860.6 | −25,550 | 4359 | −9798 |
| 7 | 60 | 100 | 2000 | 48 | 650 | 1100 | −38,340 | 4287 | −6604 | 1060 | −36,190 | 4240 | −7344 |
| 8 | 60 | 200 | 2000 | 48 | 650 | 900 | −27,900 | 5445 | −7027 | 875 | −26,970 | 5353 | −7589 |
| 9 | 140 | 200 | 2000 | 48 | 650 | 788 | −22,300 | 5506 | −8451 | 716.8 | −18,640 | 5357 | −9774 |
| 10 | 140 | 200 | 2000 | 72 | 550 | 437 | −21,000 | 3621 | −5968 | 383.6 | −17,150 | 3431 | −6824 |
| 11 | 60 | 200 | 2000 | 72 | 550 | 517 | −26,900 | 3660 | −5041 | 494.5 | −25,440 | 3555 | −5440 |
| 12 | 60 | 100 | 2000 | 72 | 550 | 634 | −35,600 | 2923 | −4790 | 595.4 | −32,860 | 2851 | −5306 |
| 13 | 140 | 100 | 2000 | 72 | 550 | 534 | −28,100 | 2955 | −5823 | 456.4 | −22,330 | 2820 | −6850 |
| 14 | 140 | 100 | 2000 | 72 | 650 | 750 | −37,100 | 4038 | −7888 | 641.4 | −29,000 | 3826 | −9179 |
| 15 | 60 | 200 | 2000 | 72 | 650 | 724 | −35,100 | 5000 | −6823 | 692 | −33,160 | 4848 | −7337 |
| 16 | 60 | 100 | 2000 | 72 | 650 | 894 | −47,700 | 4040 | −6576 | 838.6 | −43,860 | 3926 | −7246 |
| 17 | 140 | 200 | 2000 | 72 | 650 | 611 | −27,000 | 4906 | −7990 | 537.9 | −21,770 | 4632 | −9063 |
| 18 | 100 | 150 | 3000 | 36 | 600 | 696 | −16,700 | 3604 | −5408 | 659.9 | −15,110 | 3641 | −6375 |
| 19 | 100 | 150 | 3000 | 60 | 500 | 379 | −17,700 | 2399 | −3912 | 348.7 | −15,610 | 2378 | −4603 |
| 20 | 20 | 150 | 3000 | 60 | 600 | 715 | −34,000 | 3139 | −3577 | 708 | −33,790 | 3087 | −3798 |
| 21 | 100 | 250 | 3000 | 60 | 600 | 493 | −19,880 | 4133 | −5843 | 458.2 | −17,610 | 4037 | −6642 |
| 22 | 100 | 50 | 3000 | 60 | 600 | 739 | −36,470 | 2321 | −4942 | 665.7 | −31,370 | 2365 | −6170 |
| 23 | 180 | 150 | 3000 | 60 | 600 | 515 | −21,000 | 3531 | −6457 | 455 | −16,920 | 3427 | −7697 |
| 24 | 100 | 150 | 3000 | 60 | 600 | 566 | −24,470 | 3484 | −5624 | 519.3 | −21,380 | 3429 | −6552 |
| 25 | 100 | 150 | 3000 | 60 | 700 | 775 | −31,300 | 4661 | −7456 | 710.2 | −27,100 | 4563 | −8615 |
| 26 | 100 | 150 | 3000 | 84 | 600 | 460 | −28,390 | 3264 | −5529 | 410.1 | −23,990 | 3132 | −6326 |
| 27 | 140 | 100 | 4000 | 48 | 550 | 456 | −16,640 | 2185 | −4096 | 420.3 | −14,380 | 2239 | −5142 |
| 28 | 60 | 200 | 4000 | 48 | 550 | 436 | −15,680 | 2741 | −3600 | 426.9 | −15,220 | 2719 | −3935 |
| 29 | 140 | 200 | 4000 | 48 | 550 | 395 | −13,310 | 2903 | −4556 | 367.5 | −11,570 | 2905 | −5457 |
| 30 | 60 | 100 | 4000 | 48 | 550 | 499 | −19,180 | 2000 | −3120 | 485.3 | −18,400 | 2012 | −3538 |
| 31 | 140 | 200 | 4000 | 48 | 650 | 569 | −17,700 | 4085 | −6348 | 528 | −15,200 | 4062 | −7525 |
| 32 | 140 | 100 | 4000 | 48 | 650 | 664 | −22,900 | 3116 | −5799 | 608.8 | −19,440 | 3163 | −7189 |
| 33 | 60 | 100 | 4000 | 48 | 650 | 731 | −26,800 | 2887 | −4478 | 709.2 | −25,640 | 2893 | −5052 |
| 34 | 60 | 200 | 4000 | 48 | 650 | 630 | −21,300 | 3898 | −5083 | 617.1 | −20,640 | 3859 | −5535 |
| 35 | 140 | 200 | 4000 | 72 | 550 | 323 | −17,120 | 2781 | −4645 | 289.7 | −14,370 | 2703 | −5470 |
| 36 | 60 | 100 | 4000 | 72 | 550 | 432 | −25,670 | 2042 | −3370 | 412.6 | −24,140 | 2027 | −3806 |
| 37 | 140 | 100 | 4000 | 72 | 550 | 379 | −21,420 | 2167 | −4310 | 334.8 | −17,750 | 2148 | −5283 |
| 38 | 60 | 200 | 4000 | 72 | 550 | 370 | −20,880 | 2701 | −3760 | 357.5 | −19,920 | 2649 | −4105 |
| 39 | 140 | 100 | 4000 | 72 | 650 | 545 | −29,200 | 3039 | −6001 | 479.2 | −23,790 | 2981 | −7257 |
| 40 | 60 | 200 | 4000 | 72 | 650 | 530 | −28,300 | 3786 | −5232 | 511.2 | −26,880 | 3705 | −5688 |
| 41 | 60 | 100 | 4000 | 72 | 650 | 625 | −35,600 | 2902 | −4764 | 595.2 | −33,310 | 2867 | −5347 |
| 42 | 140 | 200 | 4000 | 72 | 650 | 461 | −22,800 | 3855 | −6378 | 412.7 | −18,850 | 3723 | −7431 |
| 43 | 100 | 150 | 5000 | 60 | 600 | 432 | −20,000 | 2728 | −4445 | 432 | −20,000 | 2728 | −4445 |
| Soil Type | Unit Weight (ɣ) | Cohesion (c) | Angle of Internal Friction (Ø) | Strain at 50% Strength (ε50) |
|---|---|---|---|---|
| (pcf)/(N/m3) | (Psi)/(MPa) | (Deg) | ||
| Soft Clay | 120/18,852 | 2.6/0.018 | - | 0.02 |
| Medium Clay | 120/18,852 | 5.2/0.036 | - | 0.01 |
| Stiff Clay | 120/18,852 | 10.4/0.072 | - | 0.007 |
| Very Stiff Clay | 120/18,852 | 20.8/0.143 | - | 0.005 |
| Loose Sand | 120/18,852 | - | 30 | - |
| Medium Sand | 120/18,852 | - | 35 | - |
| Dense Sand | 120/18,852 | - | 40 | - |
| Sand Soil | Clay Soil | |||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Θ (rad × 10−6) | Δ (in × 10−6) | M (kip-in) | V (kip × 10−2) | Θ (rad × 10−6) | Δ (in × 10−6) | M (kip-in) | V (kip × 10−2) |
| R2 (%) | 98.84 | 92.73 | 97.21 | 97.13 | 94.99 | 91.90 | 96.87 | 97.08 |
| Constants | 256.3 | 5748 | −2657 | 4705 | 293.2 | −1020 | −2323 | 5187 |
| Linear Terms | ||||||||
| (kip/in) | −1.071 | 70.01 | 1.430 | −15.157 | −1.49 | 99.87 | 1.069 | −22.75 |
| (kip-in2) | −1.133 | 72.20 | 8.598 | −3.789 | −0.962 | 59.71 | 8.048 | −2.057 |
| (kip-in2) | −0.10765 | 3.225 | −0.5504 | 0.8399 | −0.09235 | 2.903 | −0.5053 | 0.9265 |
| (in) | −5.196 | −248.3 | −8.23 | −0.45 | −5.467 | −193.4 | −11.42 | 3.46 |
| (in) | 2.107 | −73.25 | 11.436 | −17.799 | 1.95 | −63.32 | 11.055 | −19.952 |
| Sand Soil | Clay Soil | |||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Θ (rad × 10−6) | Δ (in × 10−6) | M (kip-in) | V (kip × 10−2) | Θ (rad × 10−6) | Δ (in × 10−6) | M (kip-in) | V (kip × 10−2) |
| R2 (%) | 99.81 | 98.82 | 99.58 | 99.78 | 99.61 | 99.55 | 99.79 | 99.79 |
| Constants | −609 | 12,769 | 276 | −2372 | −268 | 68,654 | −342 | −3510 |
| Linear Terms | ||||||||
| (kip/in) | −1042 | 28.4 | 6.44 | −14.74 | −1.667 | −16.1 | 9.77 | −22.15 |
| (kip-in2) | −1412 | 66.4 | 5.38 | −4.95 | −1.608 | 31.9 | 5.13 | −1.51 |
| (kip-in2) | −0.2014 | 3.30 | −0.567 | 0.842 | −0.1992 | 8.96 | −0.583 | 0.458 |
| (in) | 0.75 | −384 | 11.3 | −9.9 | −1.37 | −686 | 15.4 | −12.4 |
| (in) | 4.80 | −71 | −0.46 | 7.2 | 3.98 | −247.4 | 1.29 | 12.7 |
| Quadratic Terms | ||||||||
| 0.00659 | −0.529 | −0.01033 | 0.0669 | 0.00967 | −0.4537 | −0.01524 | 0.0871 | |
| 0.00432 | −0.406 | −0.01741 | 0.0053 | 0.00423 | −0.2039 | −0.01536 | −0.0101 | |
| 0.000017 | 0.000103 | 0.000087 | −0.000121 | 1.70 × 10−5 | −0.0007 | 0.000073 | −0.000020 | |
| 0.0090 | 2.73 | 0.0571 | −0.041 | 0.0267 | 5.04 | 0.0554 | −0.079 | |
| 0.00042 | −0.038 | 0.01289 | −0.0239 | 0.00098 | 0.1096 | 0.01159 | −0.0304 | |
| Interaction Terms | ||||||||
| 0.001781 | −0.1309 | −0.00769 | 0.0114 | 0.00282 | −0.2011 | −0.01066 | 0.02081 | |
| 0.000306 | −0.01670 | 0.000659 | 0.000812 | 0.000415 | −0.02223 | 0.001059 | 0.000867 | |
| −0.00378 | 1.172 | −0.0578 | 0.0779 | −0.00285 | 1.502 | −0.0884 | 0.159 | |
| −0.003844 | 0.2447 | −0.00050 | −0.0377 | −0.00542 | 0.3558 | −0.00322 | −0.05547 | |
| 0.000338 | −0.01911 | −0.000467 | −0.000969 | 0.000274 | −0.01468 | −0.000476 | −0.001184 | |
| 0.00698 | 0.592 | −0.0606 | 0.0597 | 0.00828 | 0.37 | −0.06 | 0.0522 | |
| −0.004375 | 0.2708 | 0.02375 | −0.00374 | −0.00371 | 0.2181 | 0.0227 | 0.00137 | |
| 0.001542 | 0.0022 | 0.005698 | −0.00725 | 0.001521 | −0.00518 | 0.006161 | −0.00935 | |
| −0.000307 | 0.00619 | −0.001407 | 0.002036 | −0.000277 | 0.00479 | −0.001274 | 0.002065 | |
| −0.02052 | −0.673 | −0.0477 | 0.0322 | −0.02136 | −0.503 | −0.0569 | 0.0496 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polat, E.; Göçmen Polat, E. Spring-Based Soil–Structure Interaction Modeling of Pile–Abutment Joints in Short-Span Integral Abutment Bridges with LR and RSM. Buildings 2025, 15, 3493. https://doi.org/10.3390/buildings15193493
Polat E, Göçmen Polat E. Spring-Based Soil–Structure Interaction Modeling of Pile–Abutment Joints in Short-Span Integral Abutment Bridges with LR and RSM. Buildings. 2025; 15(19):3493. https://doi.org/10.3390/buildings15193493
Chicago/Turabian StylePolat, Erkan, and Elifcan Göçmen Polat. 2025. "Spring-Based Soil–Structure Interaction Modeling of Pile–Abutment Joints in Short-Span Integral Abutment Bridges with LR and RSM" Buildings 15, no. 19: 3493. https://doi.org/10.3390/buildings15193493
APA StylePolat, E., & Göçmen Polat, E. (2025). Spring-Based Soil–Structure Interaction Modeling of Pile–Abutment Joints in Short-Span Integral Abutment Bridges with LR and RSM. Buildings, 15(19), 3493. https://doi.org/10.3390/buildings15193493






