Experimental and Numerical Investigations on Load Capacity of SRC Beams with Various Sections
Abstract
1. Introduction
2. Experimental Setup
2.1. Specimen Preparation
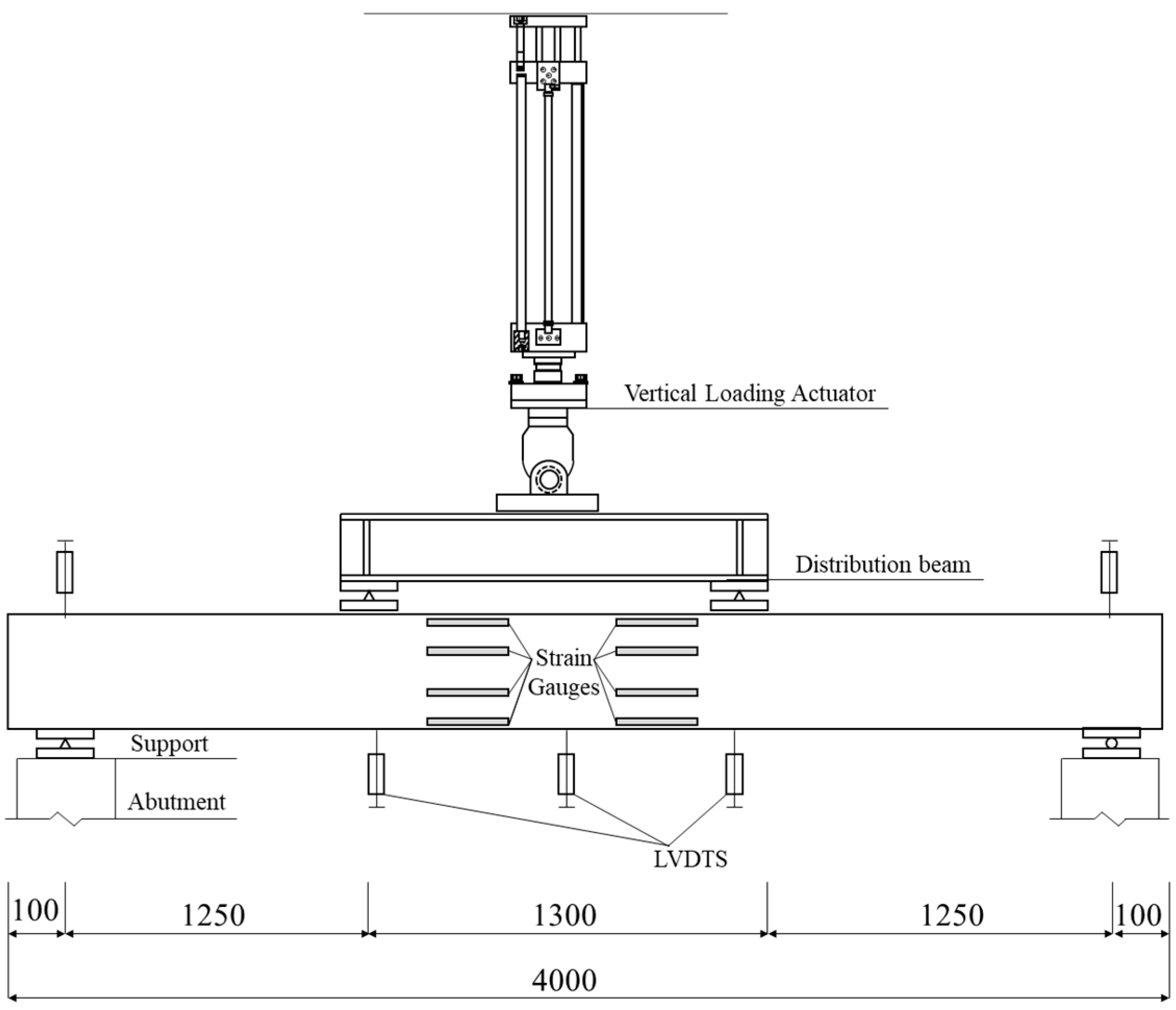
2.2. Instrumentation and Measurement
2.3. Testing Procedure
3. Experimental Test
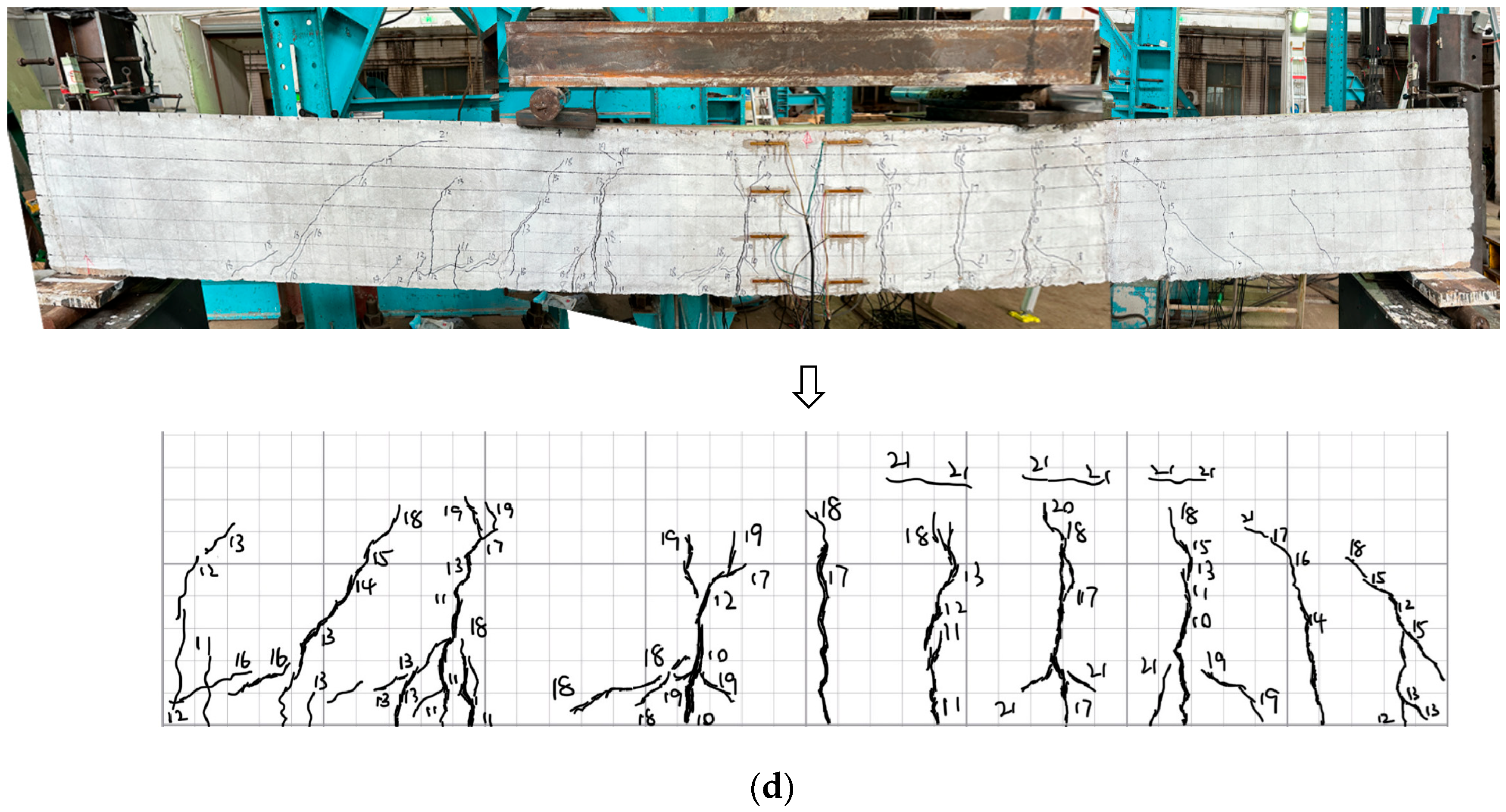
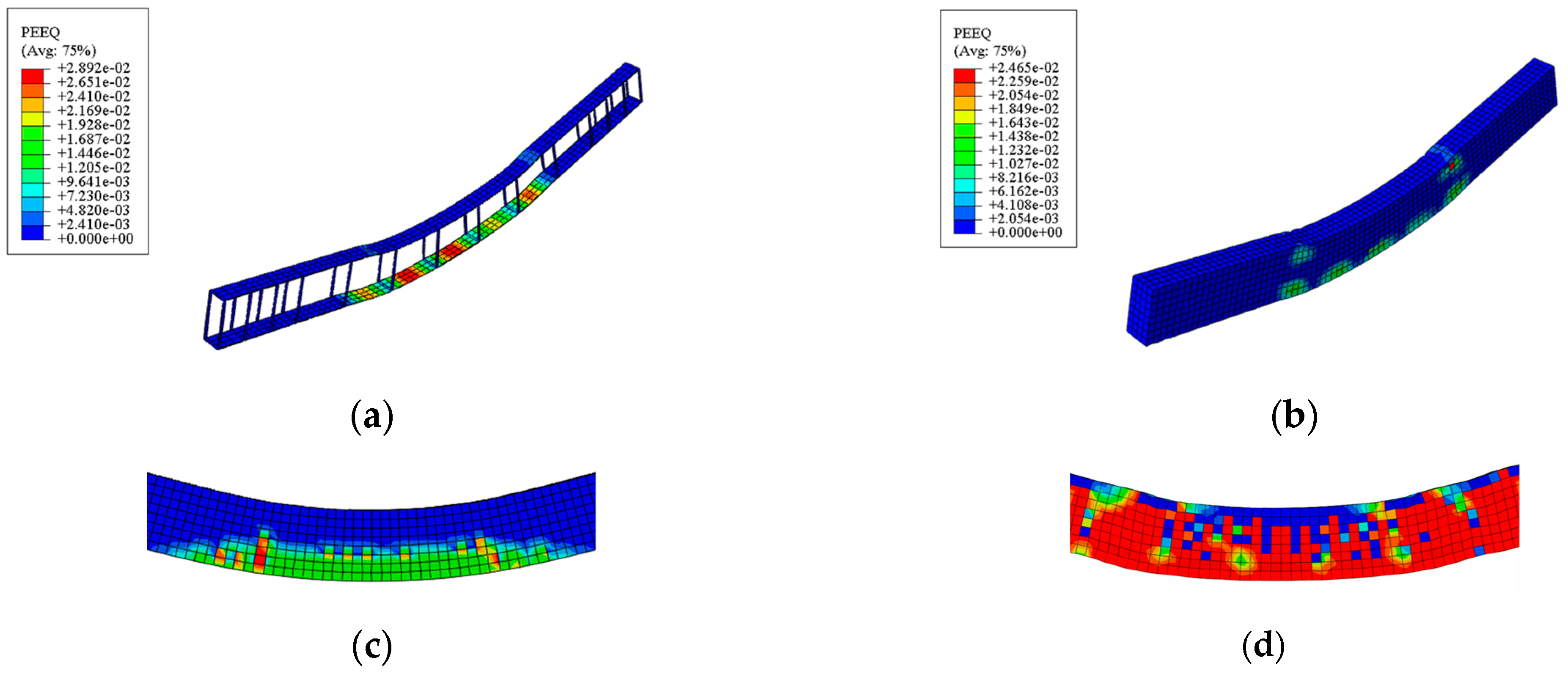
3.1. Crack Pattern and Failure Modes
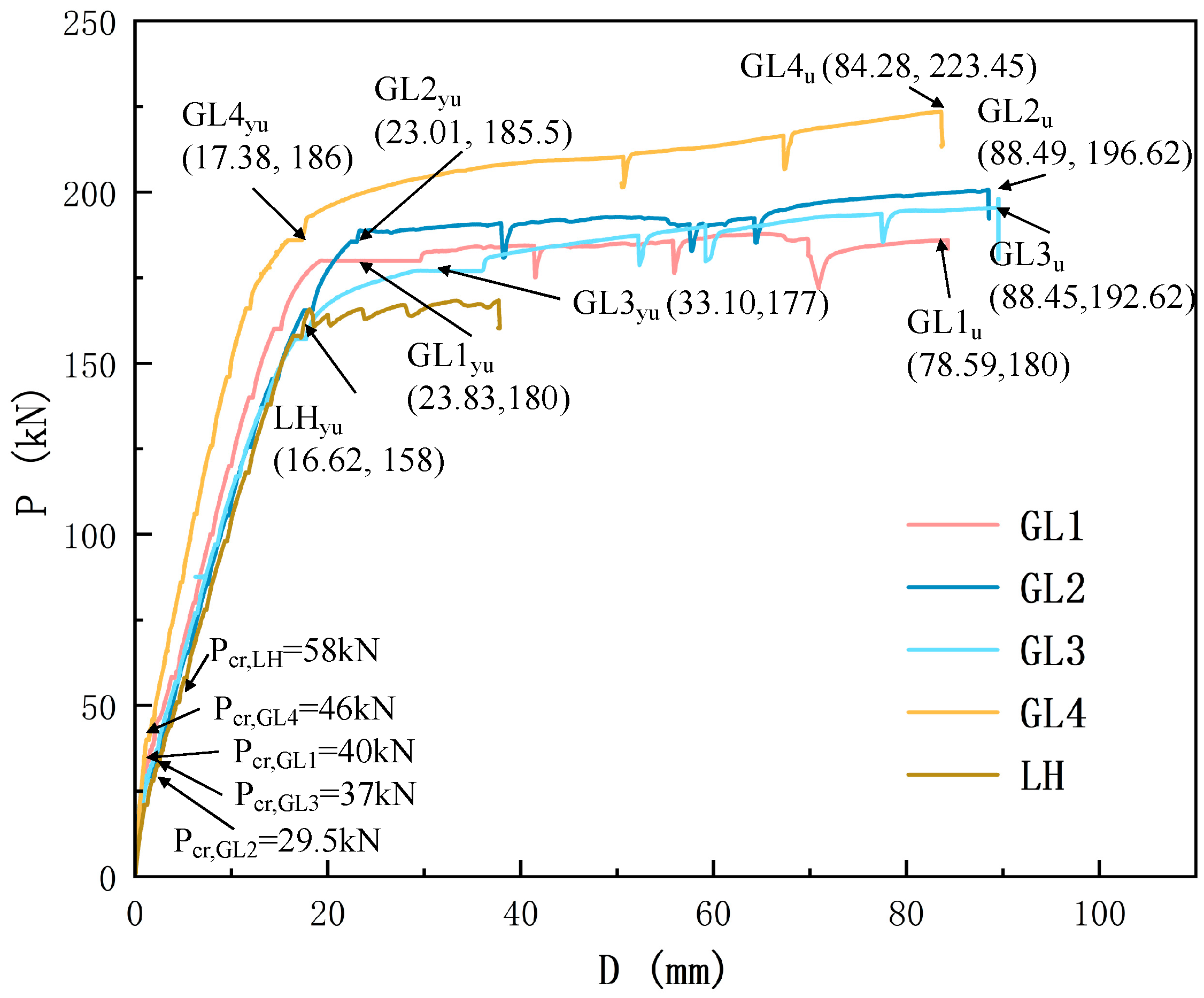
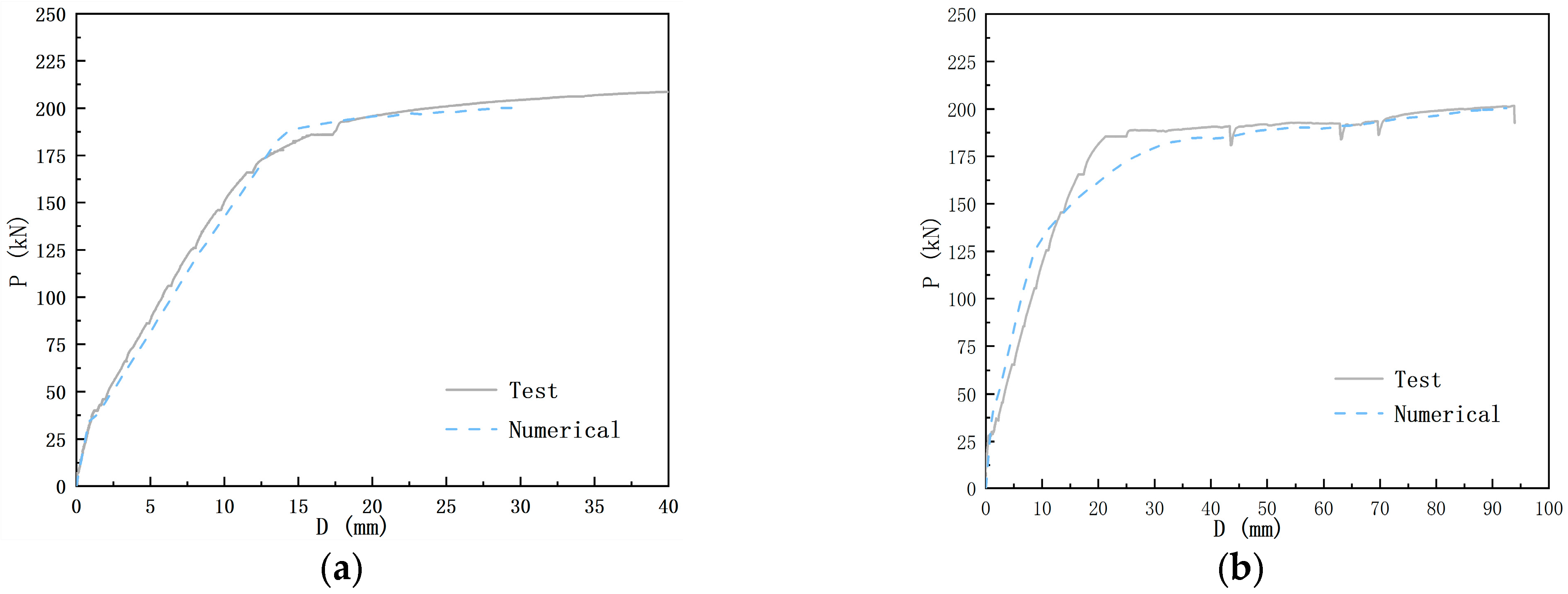
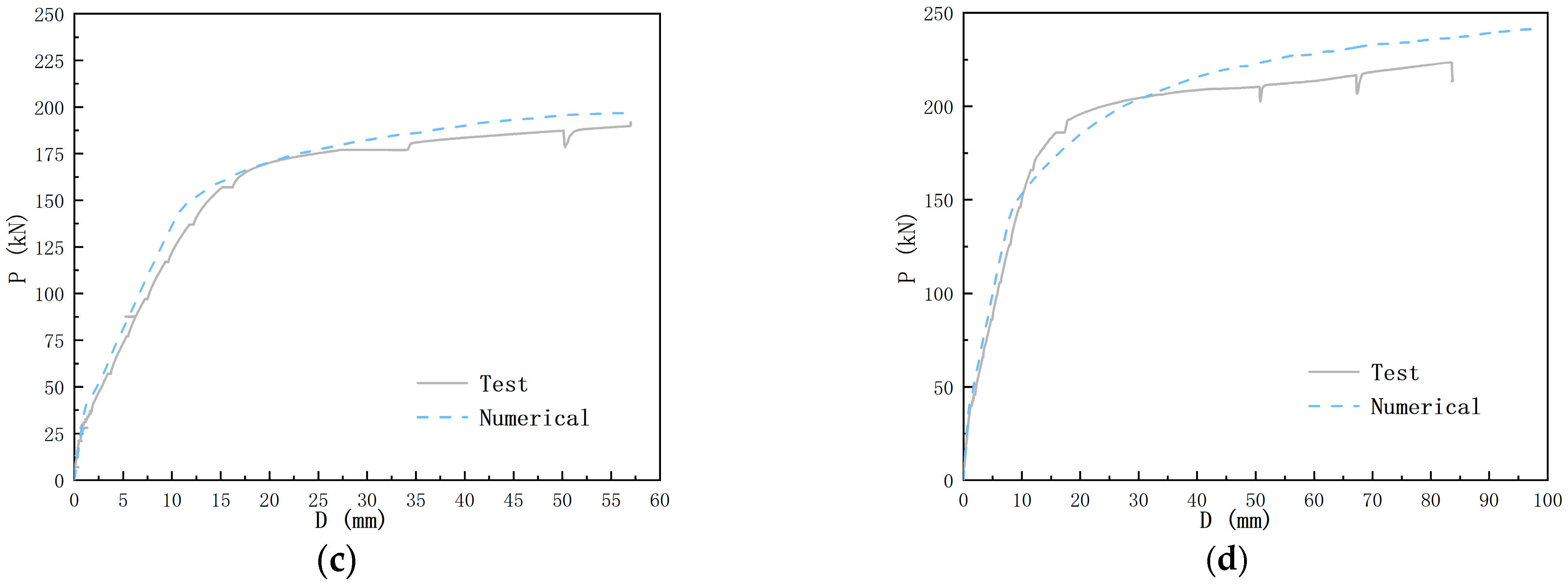
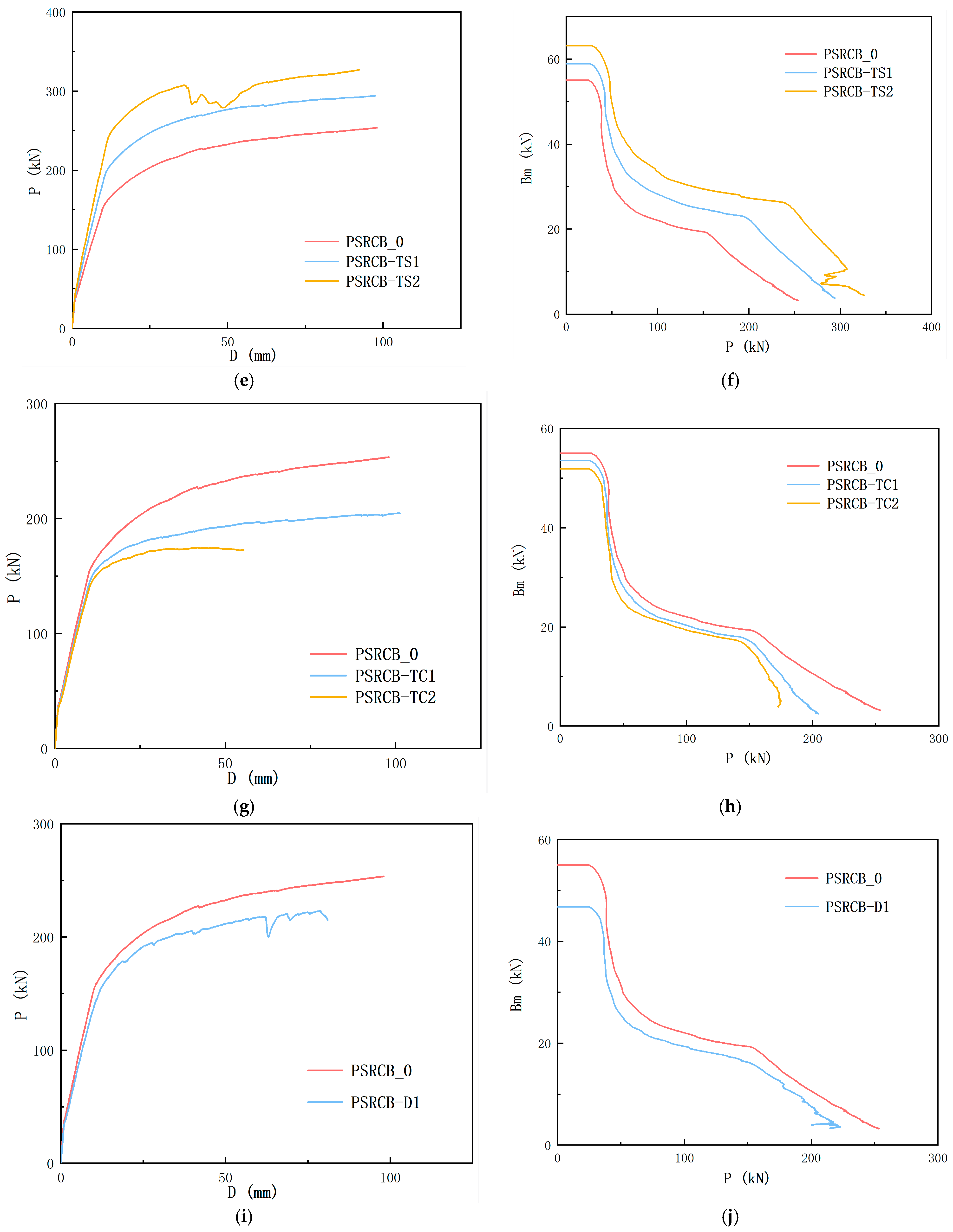
3.2. Load–Displacement Curve
3.3. Strain Development
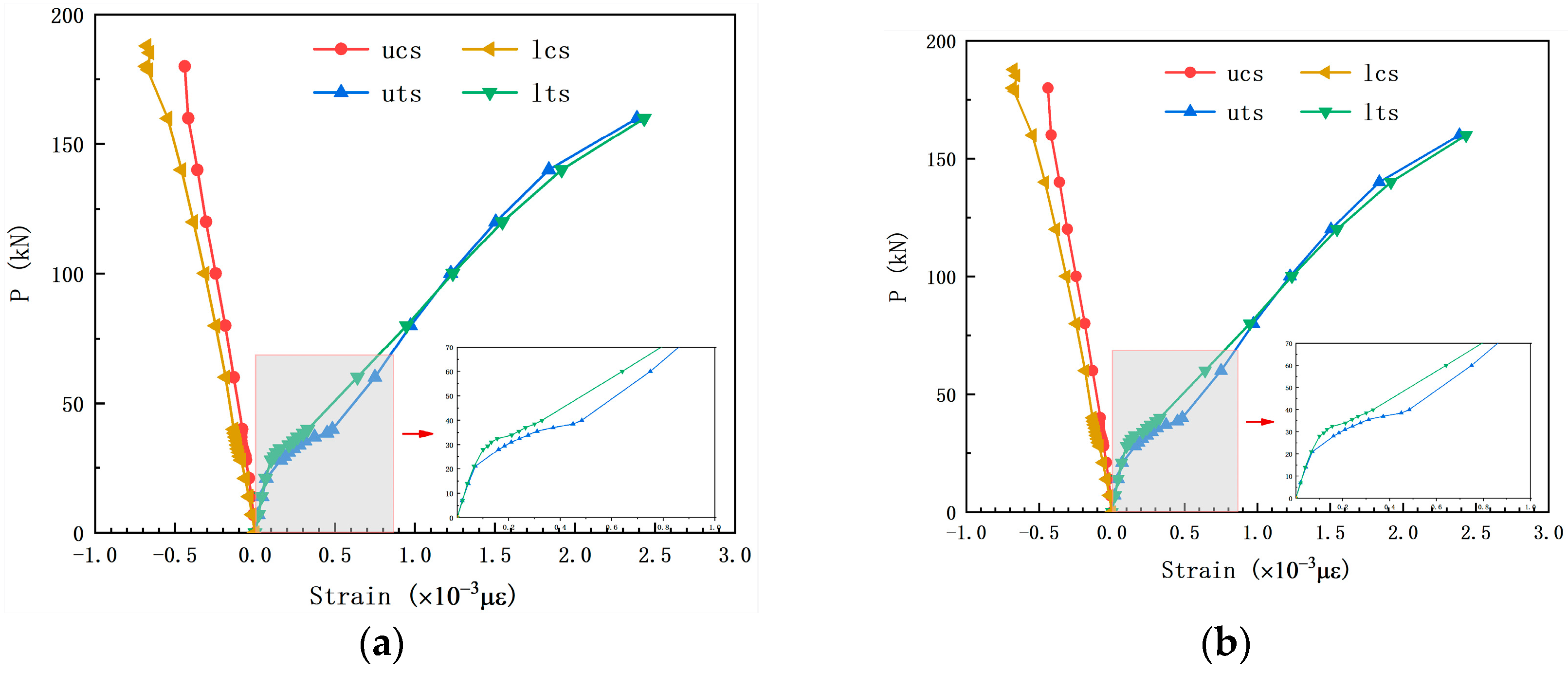
3.3.1. Steel Strain Behavior
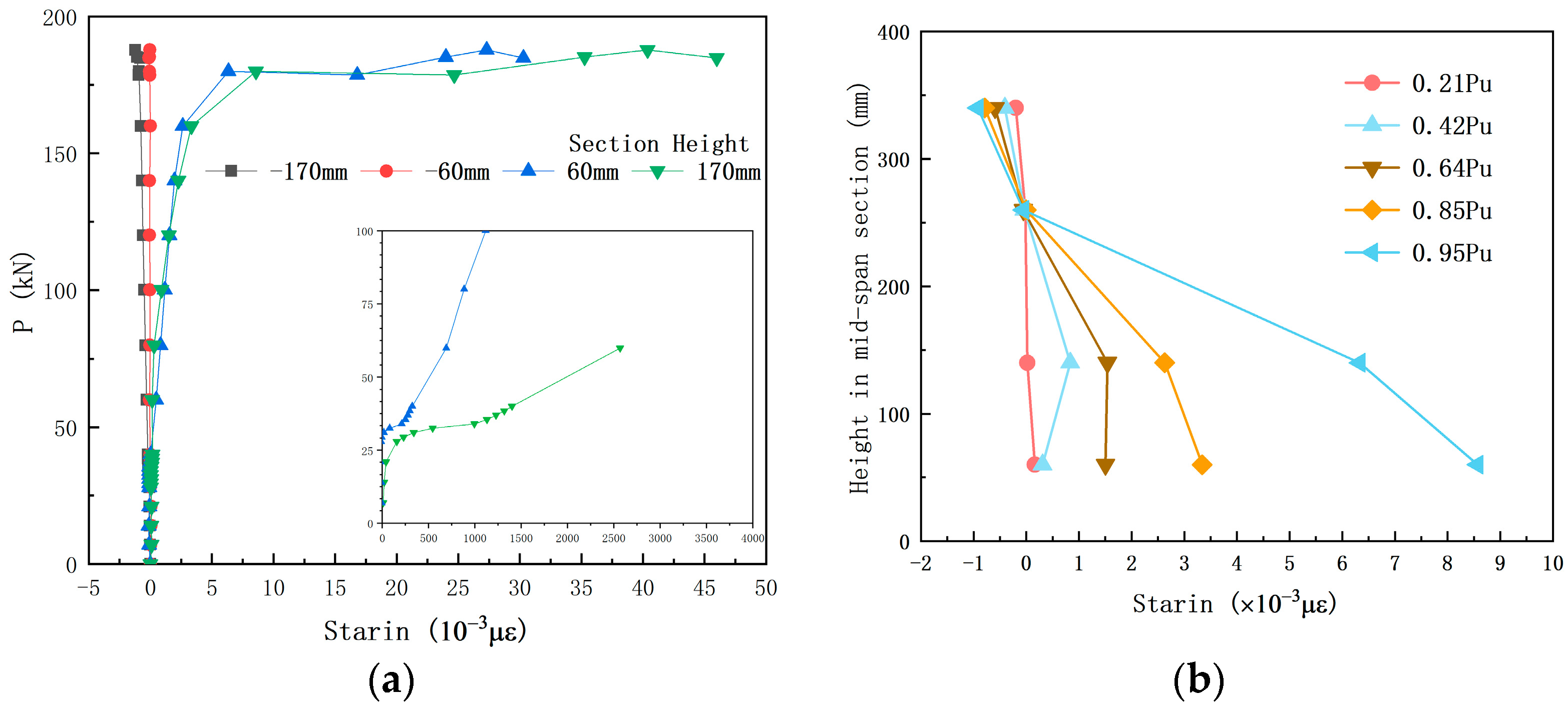
3.3.2. Concrete Strain Behavior
4. Numerical Analysis
4.1. Model Verification
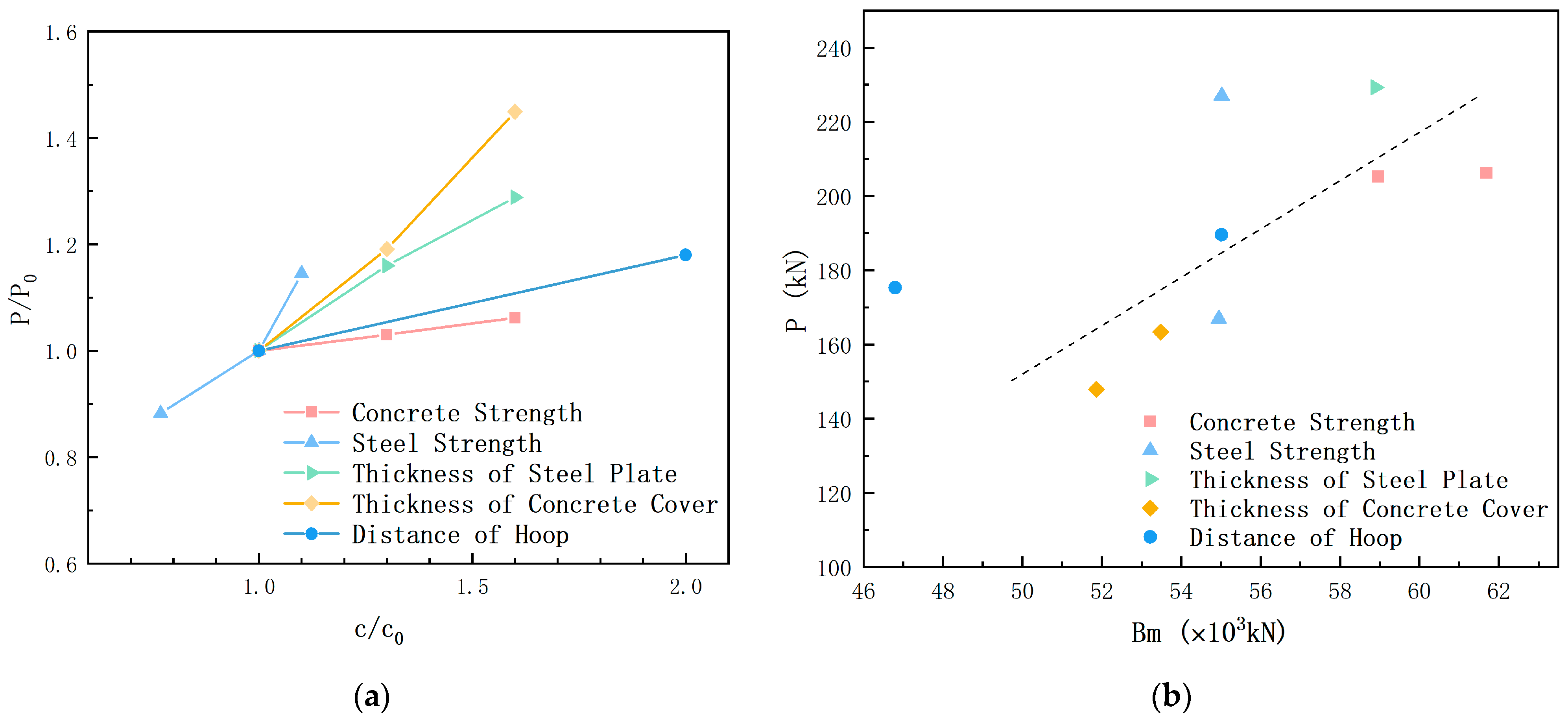
4.2. Parameter Analysis
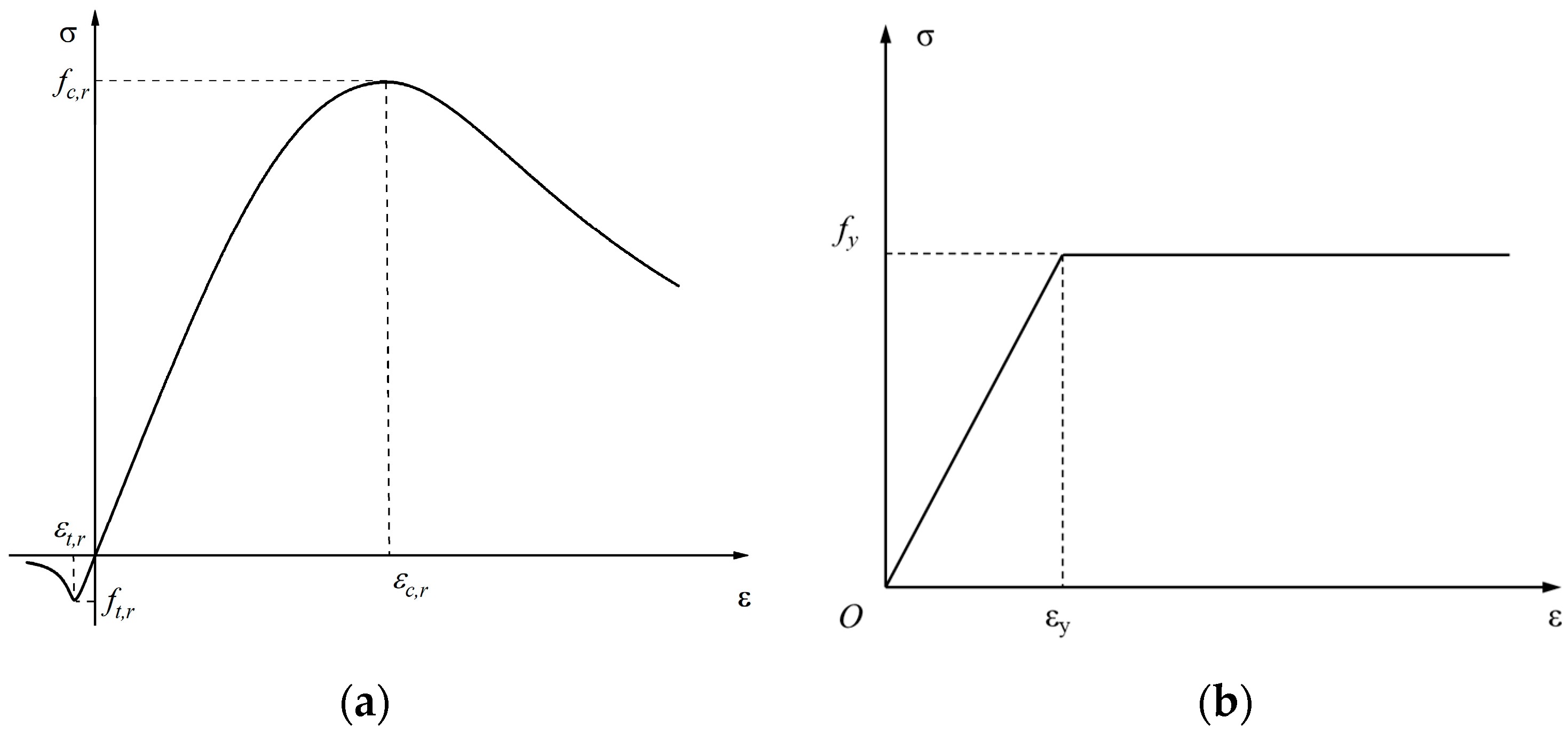
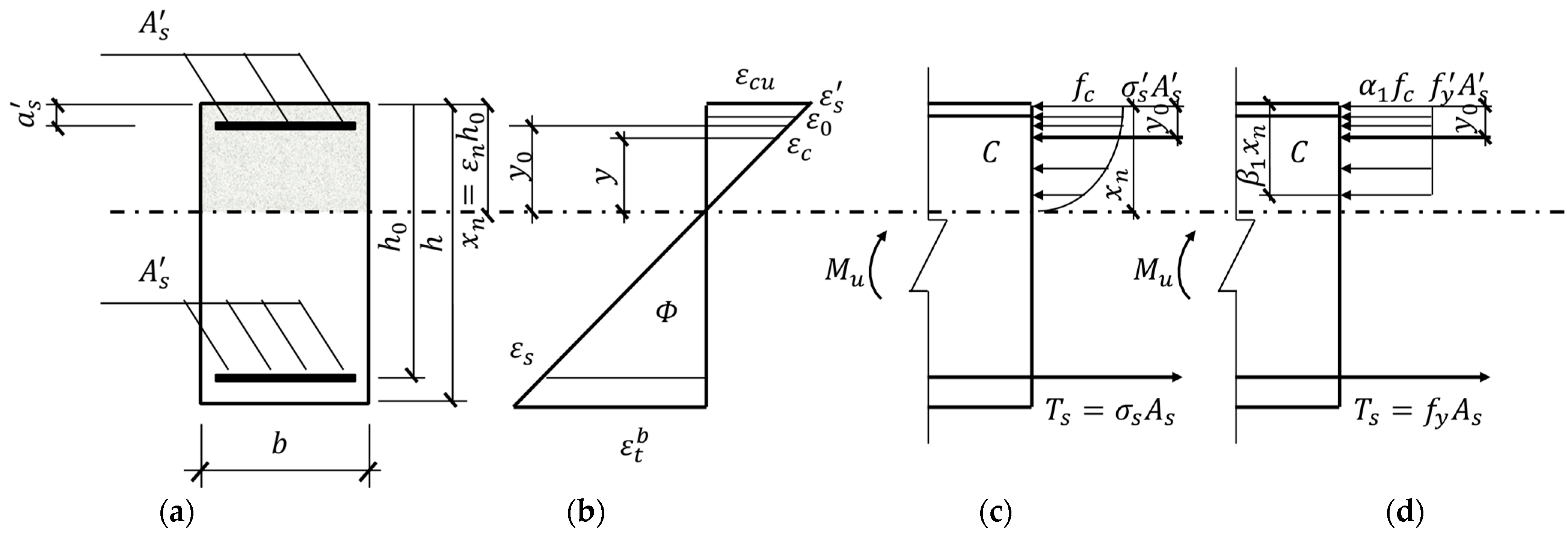
4.3. Basic Assumption
4.4. Prediction and Validation
4.5. Design Recommendations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A








Appendix B
References
- Sun, H.; Shen, W. Stiff reinforced concrete structures—A promising structural type. Build. Sci. 1992, 2, 15–20. [Google Scholar]
- Sadoughi, A.; Kouhirostami, M.; Kouhirostamkolaei, M.; Qi, B.; Costin, A. Autonomous Building Design for Manufacturing and Assembly: A Systematic Review of Design Application, Challenges, and Opportunities. J. Constr. Eng. Manag. 2024, 150, 03124006. [Google Scholar] [CrossRef]
- Li, X.; Wang, C.; Alashwal, A.; Bora, S. Game analysis on prefabricated building evolution based on dynamic revenue risks in China. J. Clean. Prod. 2020, 267, 121730. [Google Scholar] [CrossRef]
- Ferdous, W.; Bai, Y.; Ngo, T.D.; Manalo, A.; Mendis, P. New advancements, challenges and opportunities of multi-storey modular buildings—A state-of-the-art review. Eng. Struct. 2019, 183, 883–893. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Zhao, L.; Chen, M. Analysis of Factors Affecting Prefabricated Building Quality Based on ISM-BN. Sustainability 2023, 15, 9682. [Google Scholar] [CrossRef]
- Kurama, Y.C.; Sritharan, S.; Fleischman, R.B.; Restrepo, J.I.; Henry, R.S.; Cleland, N.M.; Ghosh, S.K.; Bonelli, P. Seismic-Resistant Precast Concrete Structures: State of the Art. J. Struct. Eng. 2018, 144, 03118001. [Google Scholar] [CrossRef]
- Vähä, P.; Heikkilä, T.; Kilpeläinen, P.; Järviluoma, M.; Gambao, E. Extending automation of building construction—Survey on potential sensor technologies and robotic applications. Autom. Constr. 2013, 36, 168–178. [Google Scholar] [CrossRef]
- Wu, C.; Liu, L.; Mou, B.; Pan, W.; Liu, J. Experimental and theoretical study on seismic behavior of connection between prefabricated steel-reinforced concrete column and base. Eng. Struct. 2023, 274, 115169. [Google Scholar] [CrossRef]
- Lou, G.; Li, Y.; Jia, G.; Chen, P. Research on bending behavior of angle steel lattice concrete composite beam. J. Build. Struct. 2024, 45, 230–242. [Google Scholar]
- Guo, X.; Gao, S.; Wang, L.; Bui, T.N. Bearing capacity of embedded channel-shaped steel connections at precast concrete beam end. Eng. Struct. 2018, 175, 177–190. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, Y.; Tan, B.; Liu, Y.; Xue, Y. Experiments and FE Modeling on the Seismic Behavior of Partially Precast Steel-Reinforced Concrete Squat Walls. Buildings 2024, 14, 3441. [Google Scholar] [CrossRef]
- Chen, H.B.; Wu, L.W.; Jiang, H.; Liu, Y. Seismic performance of prefabricated middle frame composed of special-shaped columns with built-in lattice concrete-filled circular steel pipes. Structures 2021, 34, 1443–1457. [Google Scholar] [CrossRef]
- Tang, X.; Sun, H. Experimental research and design suggestion on static behavior of spatial steel frame concrete simply supported deep beam. J. Build. Struct. 2010, 31, 108–116. [Google Scholar]
- Tang, X.R.; He, B.L. Experimental study and design recommendations on seismic behavior of spatial steel frame concrete frame structures. J. Build. Struct. 2009, 30, 45–52. [Google Scholar]
- Wu, C.L.; Liu, J.M.; Tan, W.Y.; Wang, P.F. Seismic behavior of composite interior joints of prefabricated H-shaped steel reinforced concrete column—Steel beam. Structures 2020, 23, 558–572. [Google Scholar] [CrossRef]
- Wu, C.; Liu, Z.; Men, J.; Li, Z.; Ding, H.; Xiong, C.; Wang, X. Analysis of stress mechanism in a new prefabricated SRC composite column. Structures 2024, 59, 105695. [Google Scholar] [CrossRef]
- Xu, Z.-H.; Bai, G.L.; Zhao, J.Q.; Liu, B. Study on seismic performance of SRC leaning beam-column exterior joints in the main workshop of CAP1400 nuclear power plant. Structures 2021, 34, 2721–2734. [Google Scholar] [CrossRef]
- Xu, Z.H.; Bai, G.L.; Zhao, J.Q.; Liu, B. Study on seismic performance of SRC special-shaped interior joints in NPP. Eng. Struct. 2021, 234, 111736. [Google Scholar] [CrossRef]
- Tang, B.; Ruan, H.; Li, Y. Design and construction of 24 m-long-span lattice SRC transfer structure. Ind. Constr. 2008, 38, 96–98. [Google Scholar]
- Eom, T.S.; Hwang, H.J.; Park, H.G.; Lee, C.N.; Kim, H.S. Flexural Test for Steel-Concrete Composite Members Using Prefabricated Steel Angles. J. Struct. Eng. 2014, 140, 04013094. [Google Scholar] [CrossRef]
- Xue, J.; Qi, L.; Gao, L.; Liu, Z. Mechanical behavior of lattice steel reinforced concrete inner frame with irregular section columns under cyclic reversed loading. Eng. Struct. 2016, 128, 225–236. [Google Scholar] [CrossRef]
- Ding, J.; Zou, Y.; Wang, C.Q.; Zhou, H.F.; Li, T.Q. Investigation on flexural behavior of a new-type composite column with steel angles. J. Asian Archit. Build. Eng. 2020, 19, 458–479. [Google Scholar] [CrossRef]
- Kim, H.-J.; Hwang, H.-J.; Park, H.-G. Flexural testing for composite members with bolt-connected steel angles. Eng. Struct. 2021, 230, 111638. [Google Scholar] [CrossRef]
- JGJ369-2016; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2016.
- GB 55008-2021; General Code for Concrete Structures. China Architecture & Building Press: Beijing, China, 2021.
- GB/T 50152-2012; Standard for Test Method of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012.
- Guo, J.Q.; Xiong, E.G.; Yang, K. Analysis and calculation for flexural capacity of symmetrically reinforced concrete beams. J. Chang’An Univ. Nat. Sci. Ed. 2011, 31, 72–76. [Google Scholar]

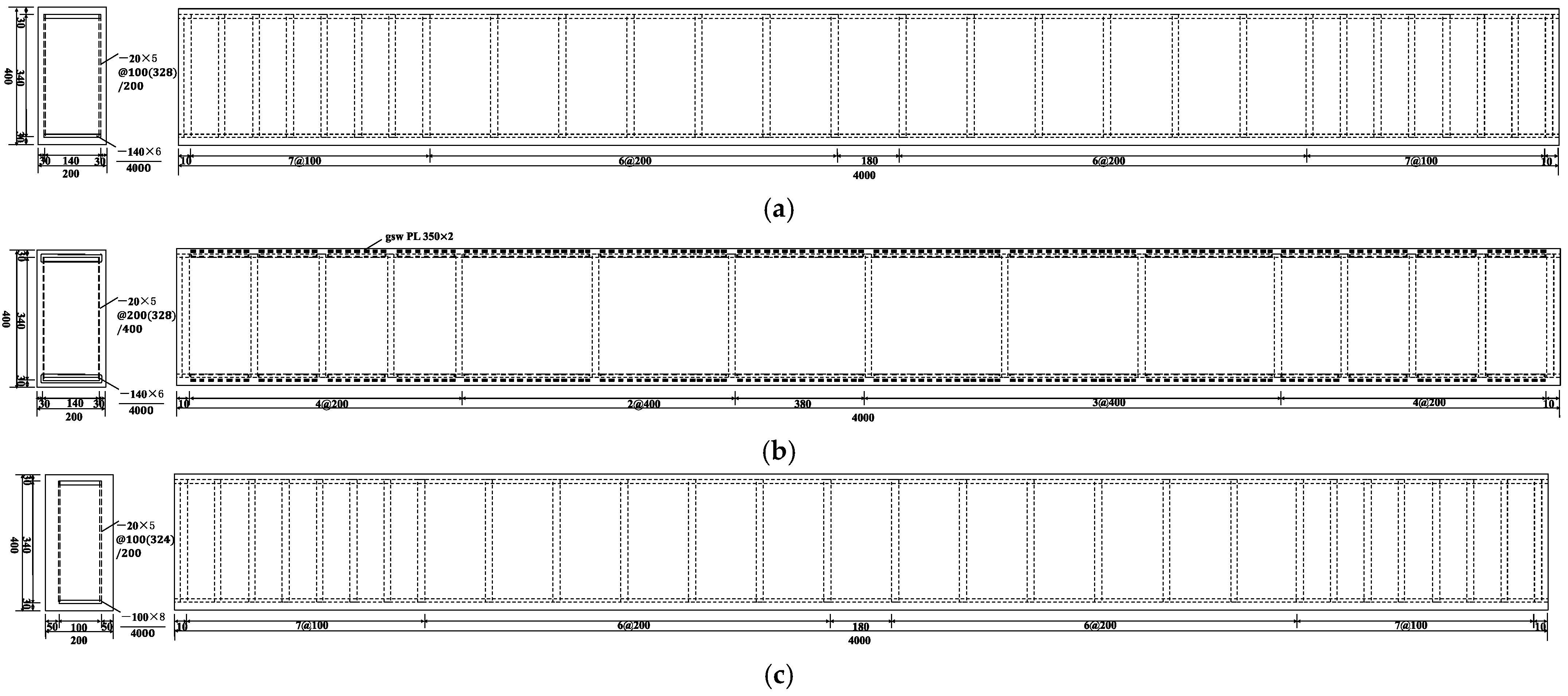



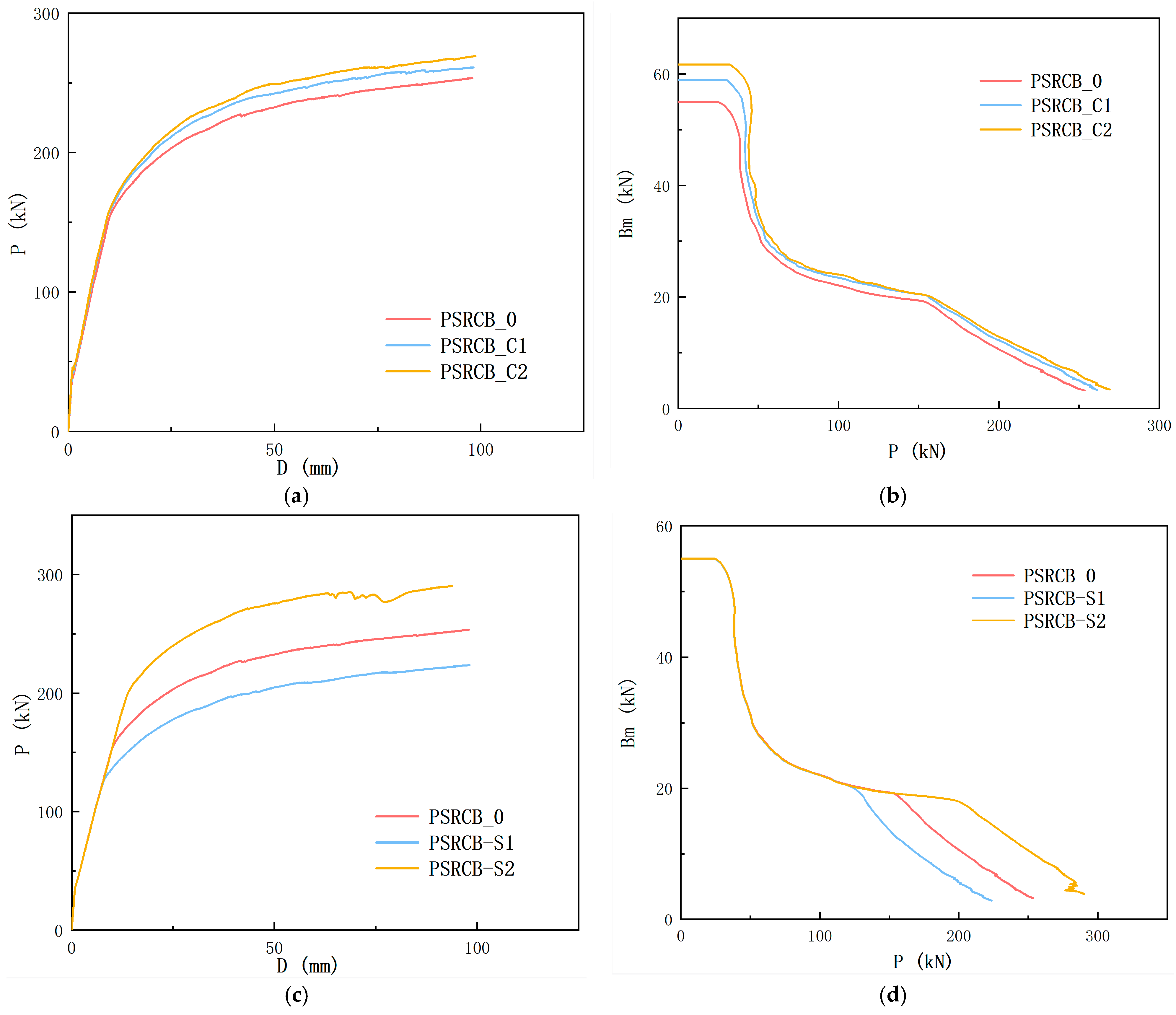
| Label | Beam Section b × h × l (mm) | Steel | Thickness of Steel tw (mm) | Steel Wire Mesh | Width of Cover cl (mm) | Strips/Hoop (mm) |
|---|---|---|---|---|---|---|
| GL1 | 200 × 400 × 4000 | Q355 | 6 | 30 | −20 × 5@100/200 | |
| GL2 | 200 × 400 × 4000 | Q355 | 6 | √ | 30 | −20 × 5@200/400 |
| GL3 | 200 × 400 × 4000 | Q355 | 8 | 50 | −20 × 5@100/200 | |
| GL4 | 200 × 400 × 4000 | Q355 | 6 | √ | 30 | −20 × 5@100/200 |
| LH | 200 × 400 × 4000 | HRB 400 | 8 | 30 | Ф8@100/200 |
| Material | Thickness (mm) | fy (MPa) | fu (MPa) | fc (MPa) |
|---|---|---|---|---|
| Steel (Q235) | 6 | 335 | 417 | - |
| Steel (Q355) | 10 | 399 | 522 | - |
| Concrete (C30) | - | - | - | 32.5 |
| Label | GL1 | GL2 | GL3 | GL4 |
|---|---|---|---|---|
| Upper steel plate | 6.10 (1.67%) | 5.97 (0.50%) | 7.98 (0.25%) | 5.92 (1.33%) |
| Below steel plate | 5.83 (2.83%) | 5.97 (0.50%) | 7.97 (0.38%) | 5.94 (1.00%) |
| Length of the specimen | 4008.8 (0.2%) | 4008.4 (0.2%) | 4010.1 (0.3%) | 3991.8 (0.2%) |
| Height of sections | 400.1 (0.03%) | 403.6 (9.0%) | 401.4 (0.4%) | 399.7 (0.08%) |
| Width of sections | 201.1 (0.6%) | 201.4 (0.7%) | 202.7 (1.35%) | 199.8 (0.1%) |
| Label | Pcr (kN) | Pyu (kN) | Dyu (mm) | Pu (kN) | Du (mm) | k1 (×103 kN/m) | Du/Dy |
|---|---|---|---|---|---|---|---|
| GL1 | 40 | 180 | 23.83 | 187.54 | 78.59 | 37.42 | 3.3 |
| GL2 | 29.5 | 185.5 | 23.01 | 196.62 | 88.49 | 41.31 | 3.8 |
| GL3 | 37 | 177 | 33.10 | 192.62 | 88.45 | 38.68 | 2.7 |
| GL4 | 46 | 186 | 17.38 | 223.45 | 84.28 | 38.08 | 4.8 |
| LH | 58 | 158 | 16.62 | 164.98 | 37.75 | 27.66 | 2.3 |
| Label | Concrete | Steel | Thickness of Steel (mm) | Thickness of Cover (mm) | Distance of Hoop (mm) |
|---|---|---|---|---|---|
| PSRCB-0 | C30 | Q355 | 6 | 30 | 20 |
| PSRCB-C1/C2 | C40, C50 | Q355 | 6 | 30 | 20 |
| PSRCB-S1/S2 | C30 | Q275, Q390 | 6 | 30 | 20 |
| PSRCB-TS1/TS2 | C30 | Q335 | 8, 10 | 30 | 20 |
| PSRCB-TC1/TC2 | C30 | Q335 | 6 | 40, 50 | 20 |
| PSRCB-D1 | C30 | Q335 | 6 | 30 | 40 |
| Label | Ultimate Capacity Fu (kN) | Calculation Capacity Fc (kN) | Ding et al. [22] | Kim et al. [23] |
|---|---|---|---|---|
| SRCB-0 | 189.54 | 172.41 (0.91) | 150.38 (0.79) | 158.48 (0.83) |
| SRCB-C1 | 205.26 | 174.05 (0.85) | 150.38 (0.73) | 158.48 (0.77) |
| SRCB-C2 | 206.25 | 175.69 (0.85) | 150.38 (0.72) | 158.48 (0.76) |
| SRCB-S1 | 166.94 | 145.99 (0.87) | 134.67 (0.80) | 141.93 (0.85) |
| SRCB-S2 | 227.03 | 193.17 (0.85) | 179.56 (0.79) | 189.24 (0.83) |
| SRCB-TS1 | 229.28 | 192.45 (0.84) | 199.31 (0.86) | 210.71 (0.91) |
| SRCB-TS2 | 269.01 | 236.40 (0.88) | 247.63 (0.92) | 262.64 (0.97) |
| SRCB-TC1 | 163.33 | 129.63 (0.79) | 123.37 (0.75) | 133.72 (0.81) |
| SRCB-TC2 | 147.91 | 120.65 (0.82) | 109.86 (0.74) | 122.47 (0.82) |
| SRCB-D1 | 175.32 | 172.41 (0.98) | 150.38 (0.85) | 158.48 (0.90) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Wang, P.; Chen, H.; Ge, J.; Peng, C. Experimental and Numerical Investigations on Load Capacity of SRC Beams with Various Sections. Buildings 2025, 15, 3473. https://doi.org/10.3390/buildings15193473
Yang B, Wang P, Chen H, Ge J, Peng C. Experimental and Numerical Investigations on Load Capacity of SRC Beams with Various Sections. Buildings. 2025; 15(19):3473. https://doi.org/10.3390/buildings15193473
Chicago/Turabian StyleYang, Bin, Peiyang Wang, Haizhou Chen, Jiqian Ge, and Chengxin Peng. 2025. "Experimental and Numerical Investigations on Load Capacity of SRC Beams with Various Sections" Buildings 15, no. 19: 3473. https://doi.org/10.3390/buildings15193473
APA StyleYang, B., Wang, P., Chen, H., Ge, J., & Peng, C. (2025). Experimental and Numerical Investigations on Load Capacity of SRC Beams with Various Sections. Buildings, 15(19), 3473. https://doi.org/10.3390/buildings15193473







