Data Augmentation Using Multivariate Time Series Decomposition for Predicting Daily Energy Consumption of New Buildings
Abstract
1. Introduction
2. Literature Review
2.1. Deep Learning in Building Energy Use Prediction
2.2. Time-Series Decomposition for Enhanced Predictive Modeling
3. Overview of Case Building
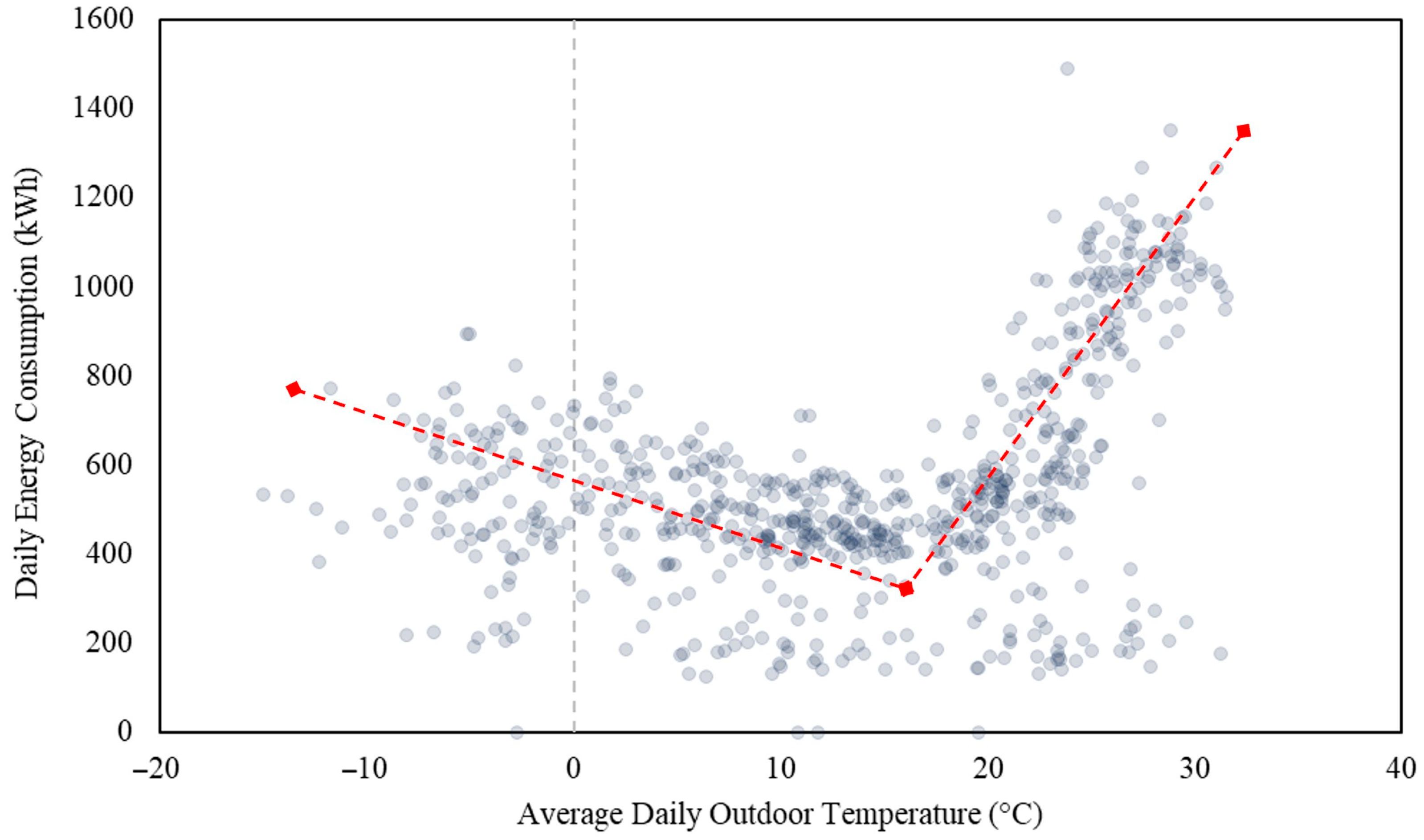
- Average daily outdoor temperature (OT): Mean ambient temperature recorded outside the case building over a 24 h period and had numerical values (e.g., 17 °C),
- Average daily relative humidity (RH): Mean atmospheric moisture content relative to the maximum possible at the same temperature, calculated over each day and has numerical values (e.g., 68%),
- Average daily solar insolation (SI): Total incident solar radiation energy per unit area accumulated throughout the day and had numerical values (e.g., 185 kWh/m2),
- Day type (DT): A categorical variable representing the day of the week with possible values including Monday (1), Tuesday (2), Wednesday (3), Thursday (4), Friday (5), Saturday (6), and Sunday (7),
- Temperature difference (TD): Difference between average daily outdoor temperature and the 18 °C (e.g., −5 °C or 25 °C), and
- Daily energy consumption (E): Total amount of energy consumed by the case building within a 24 h period (e.g., 24 kWh), which includes heating, cooling, lighting, plug loads, and equipment.
- : Covariance of and ,
- : Standard deviation of , and
- : Standard deviation of .
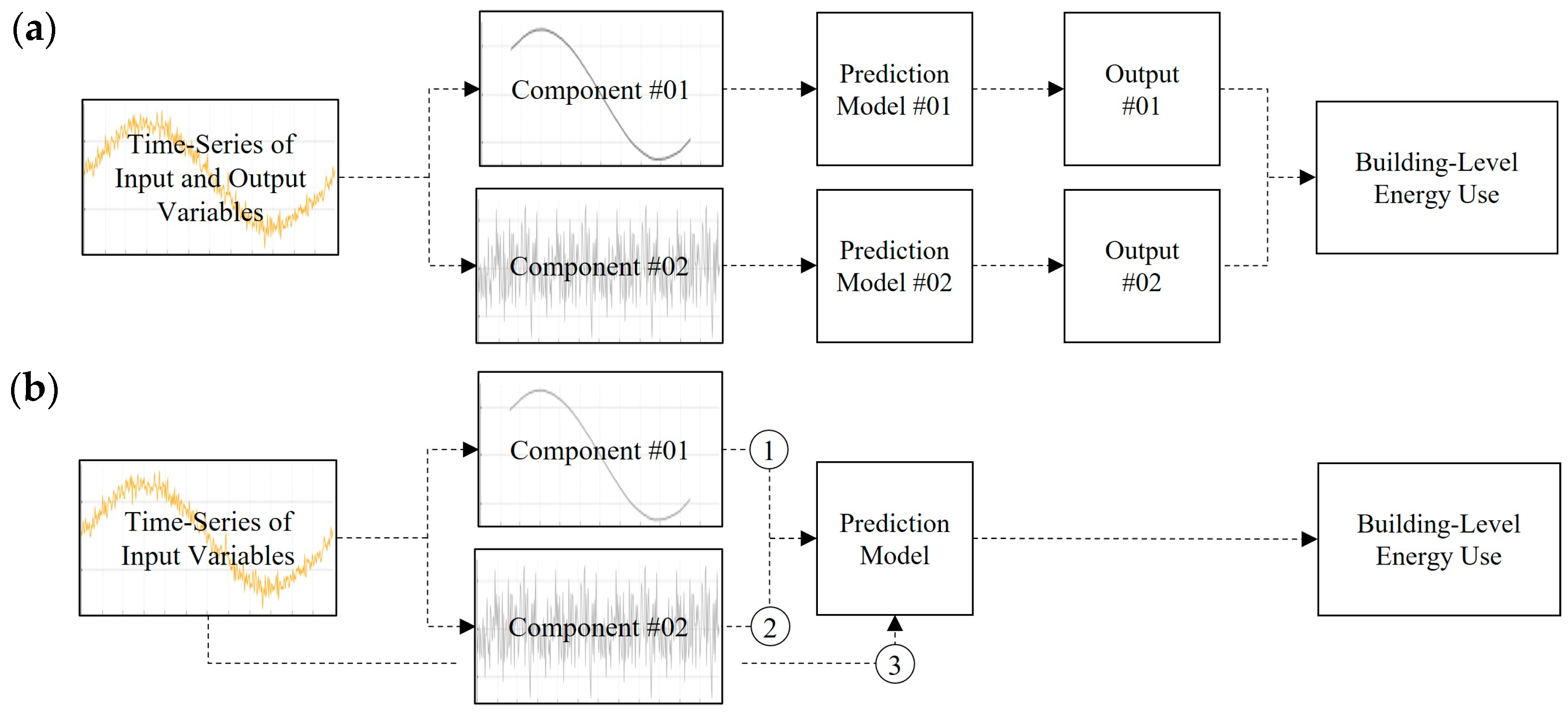
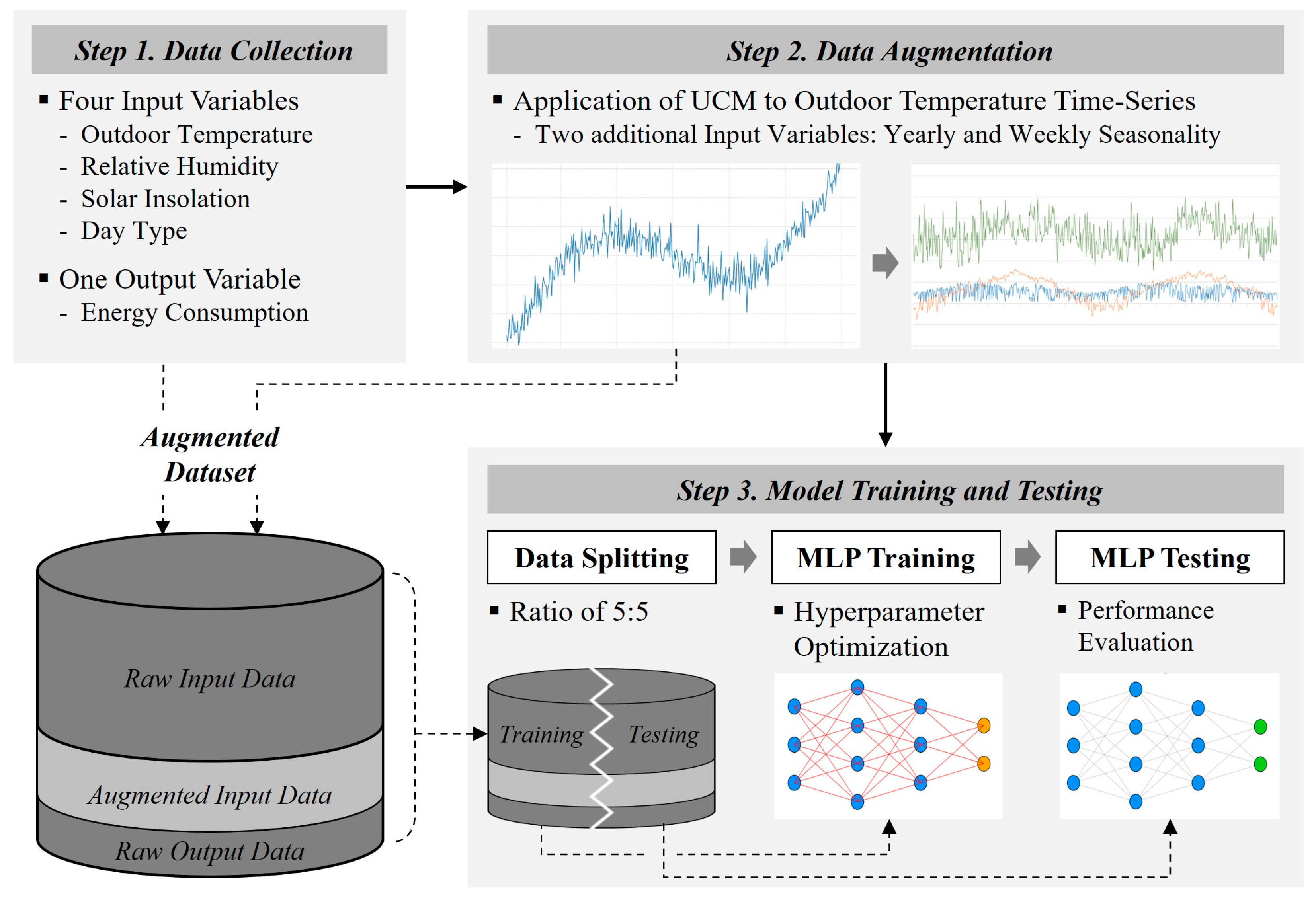
4. Model Development
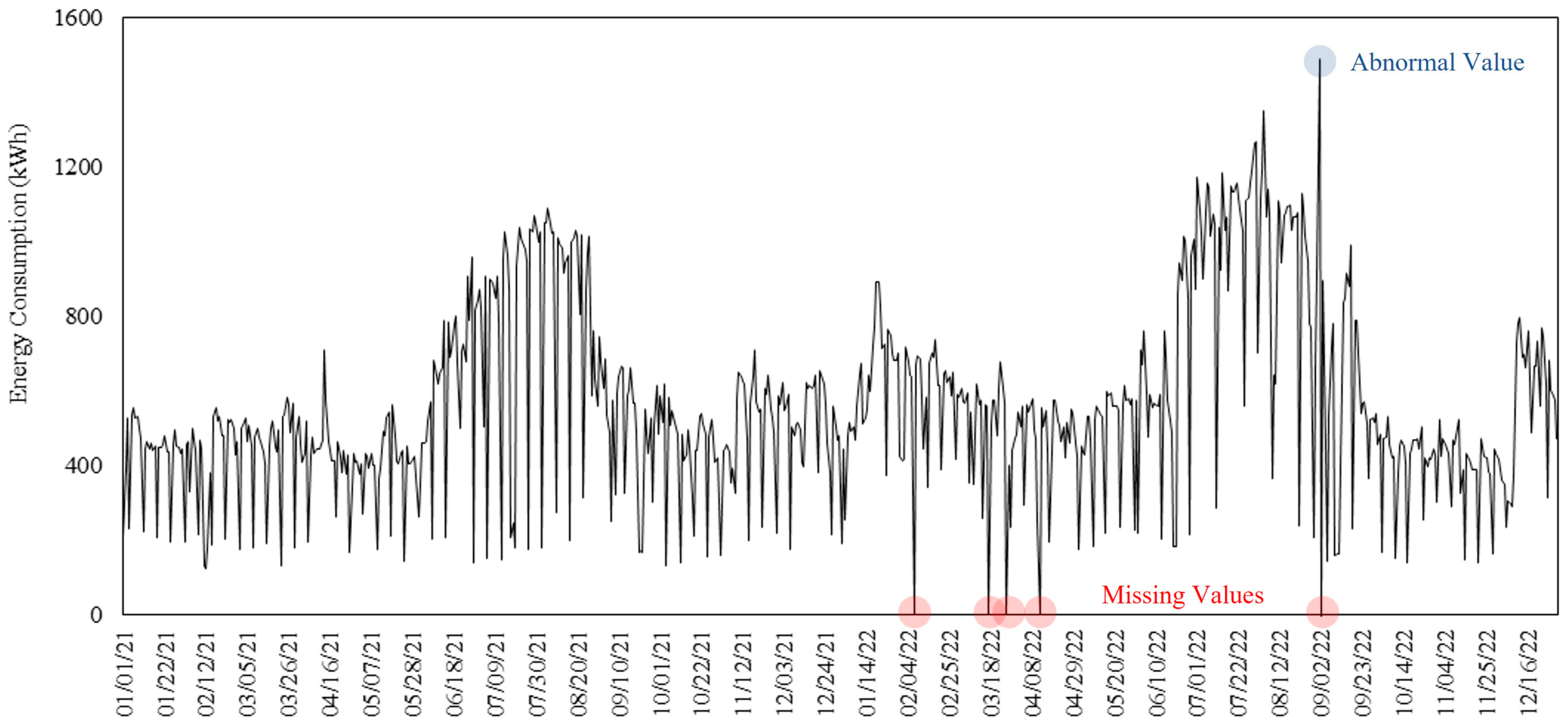
4.1. Data Acquisition
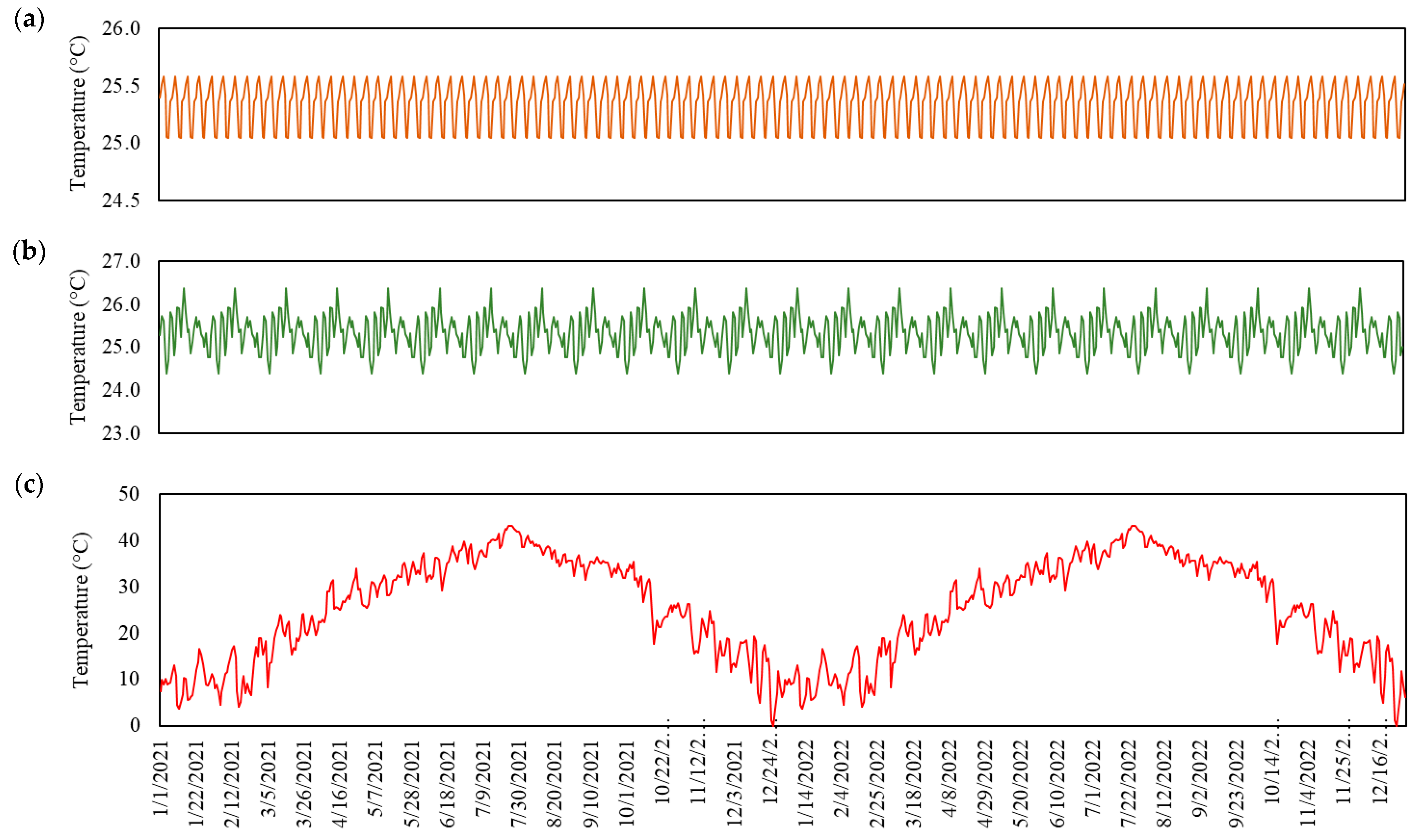
4.2. Data Augmentation
- : Trend component of outdoor temperature time-series which captures long-term changes overs time. This allowed us to flexibly capture long-term temperature trends that change over time,
- : Seasonality component of outdoor temperature time-series which represents recurring patterns within a year. To model the multiple seasonalities evident in the data, three stochastic seasonal factors with weekly (7 days), monthly (approximately 30 days), and yearly (365.25 days) cycles were used together,
- : Cyclical component of outdoor temperature time-series which reflects longer-term cycles,
- : Autoregressive component which models the influence of past values of outdoor temperature time series on the current value,
- : Regression component of outdoor temperature time-series which capture the effect of external explanatory variables , and
- : Irregular (noise) component of outdoor temperature time-series which accounts for random fluctuations not explained by the other components.
4.3. Model Training and Testing
- : Actual energy consumption at time t,
- : Predicted energy consumption at time t,
- : Average value of actual energy consumption during the prediction period n.
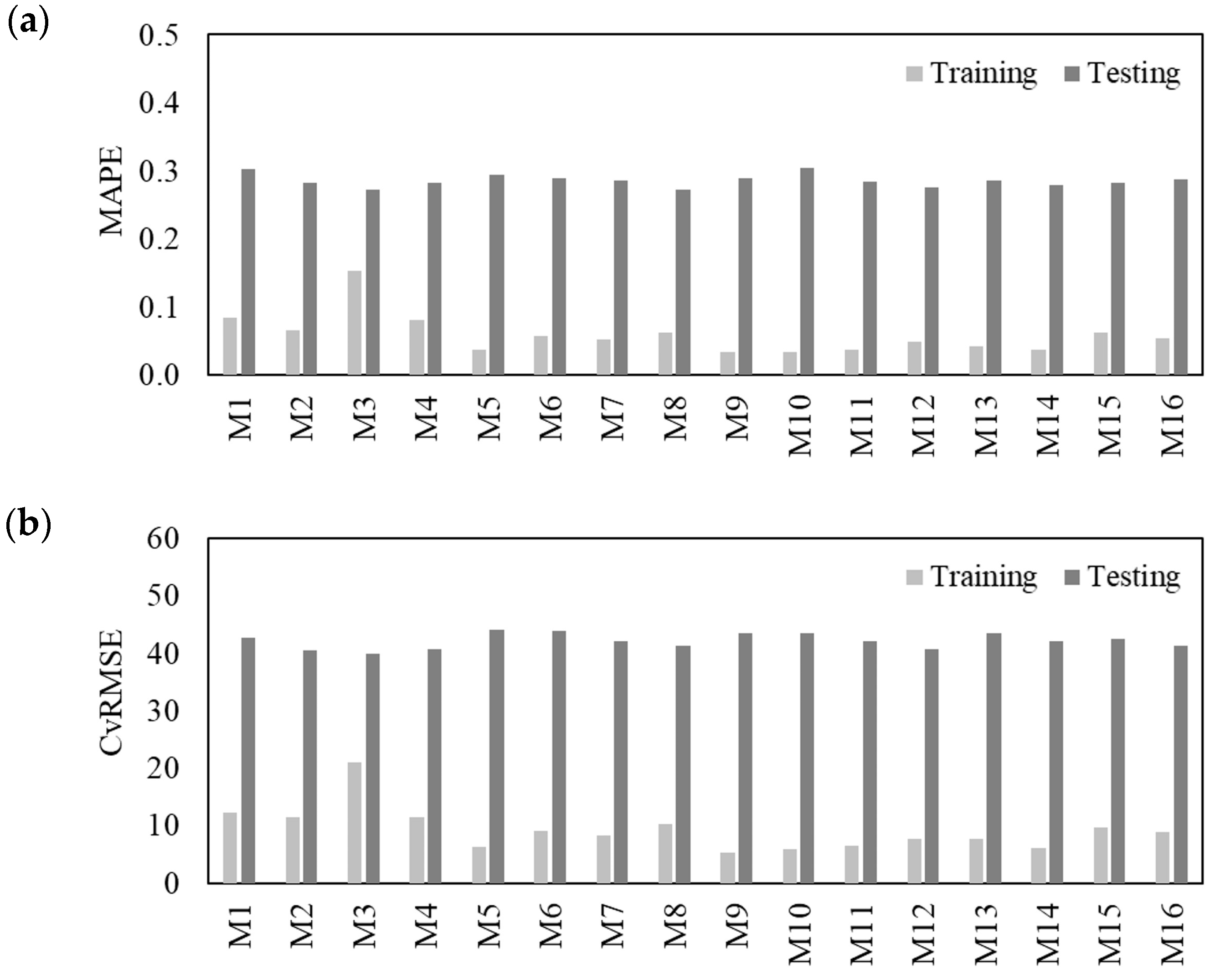
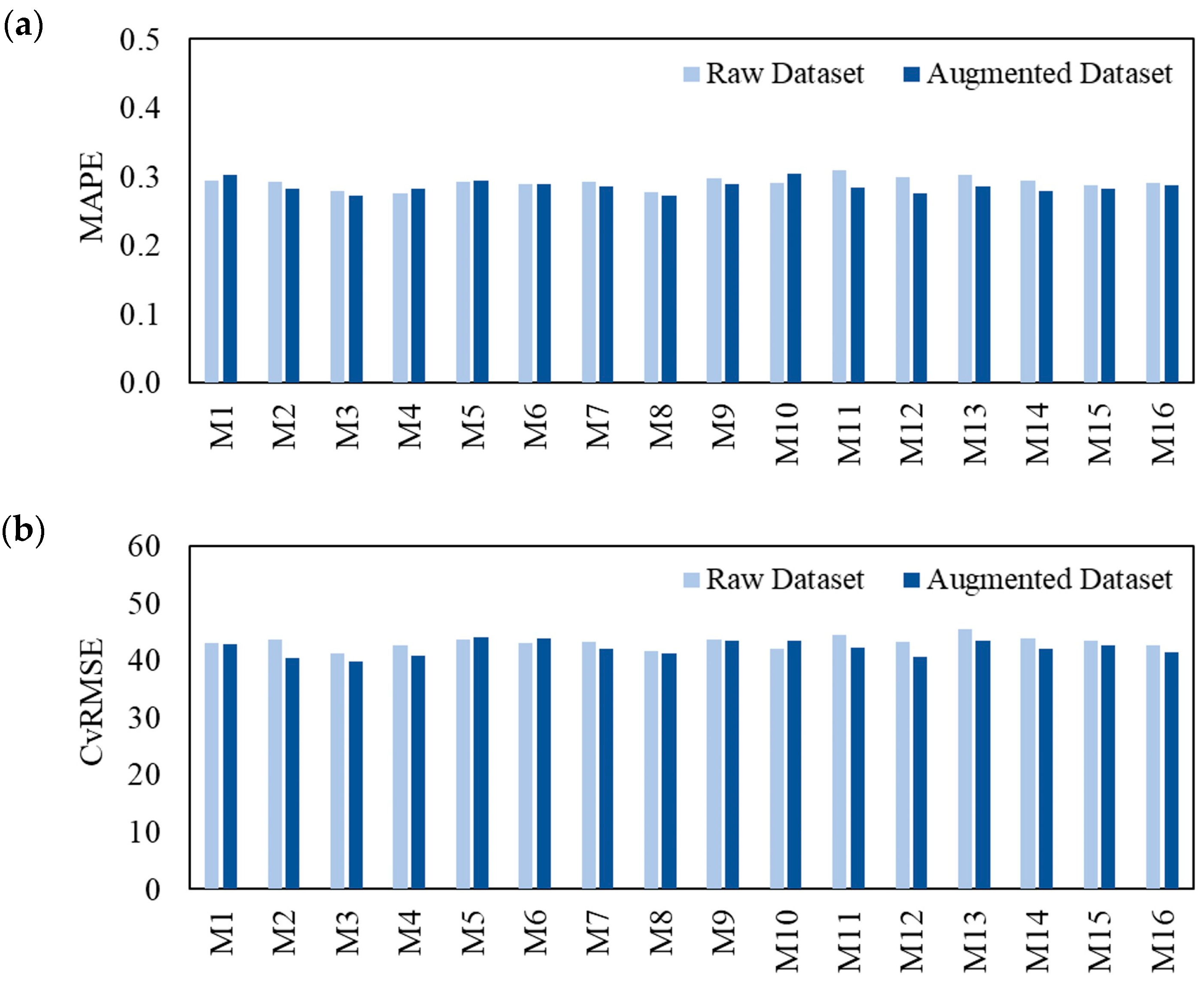
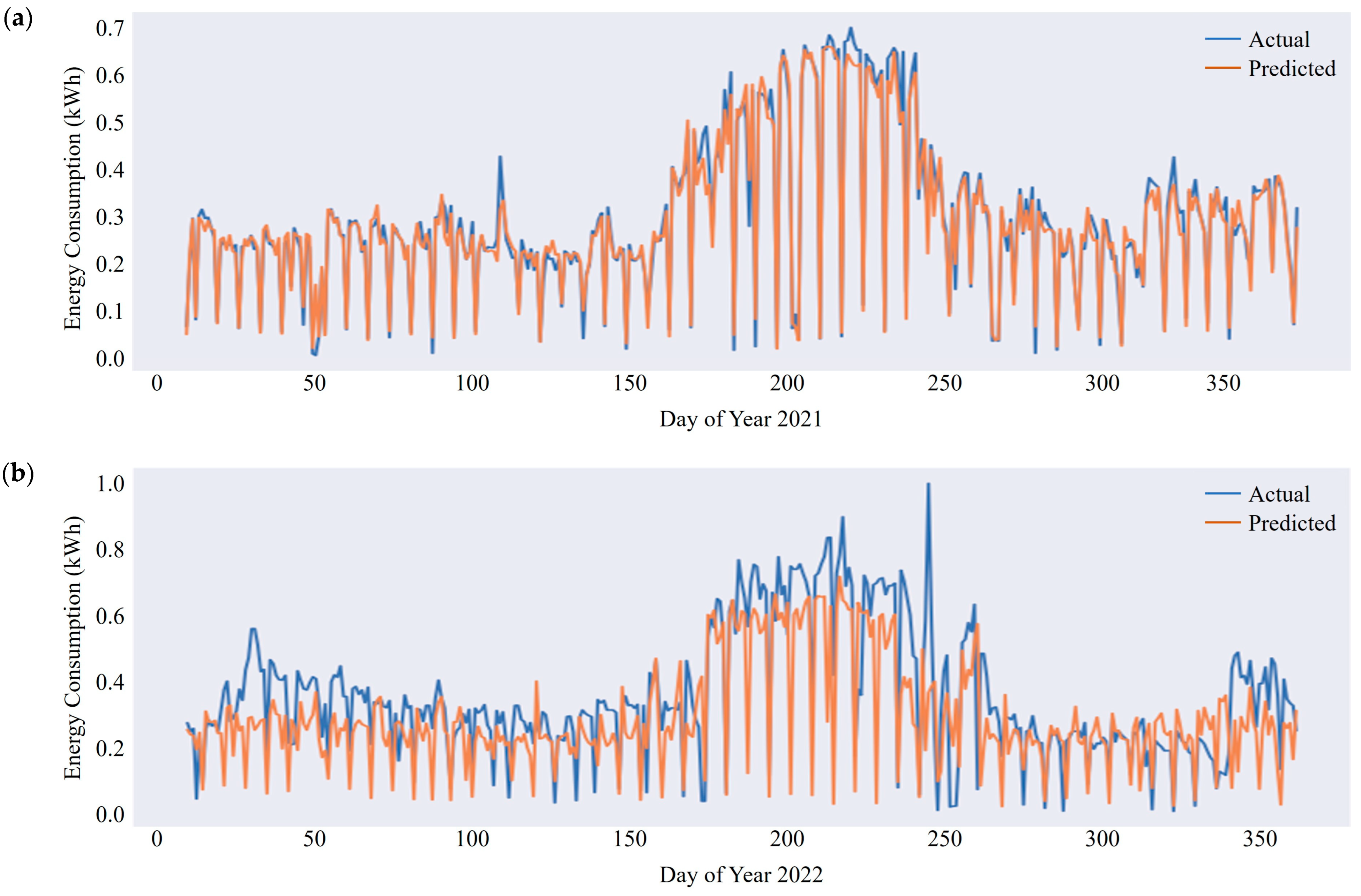
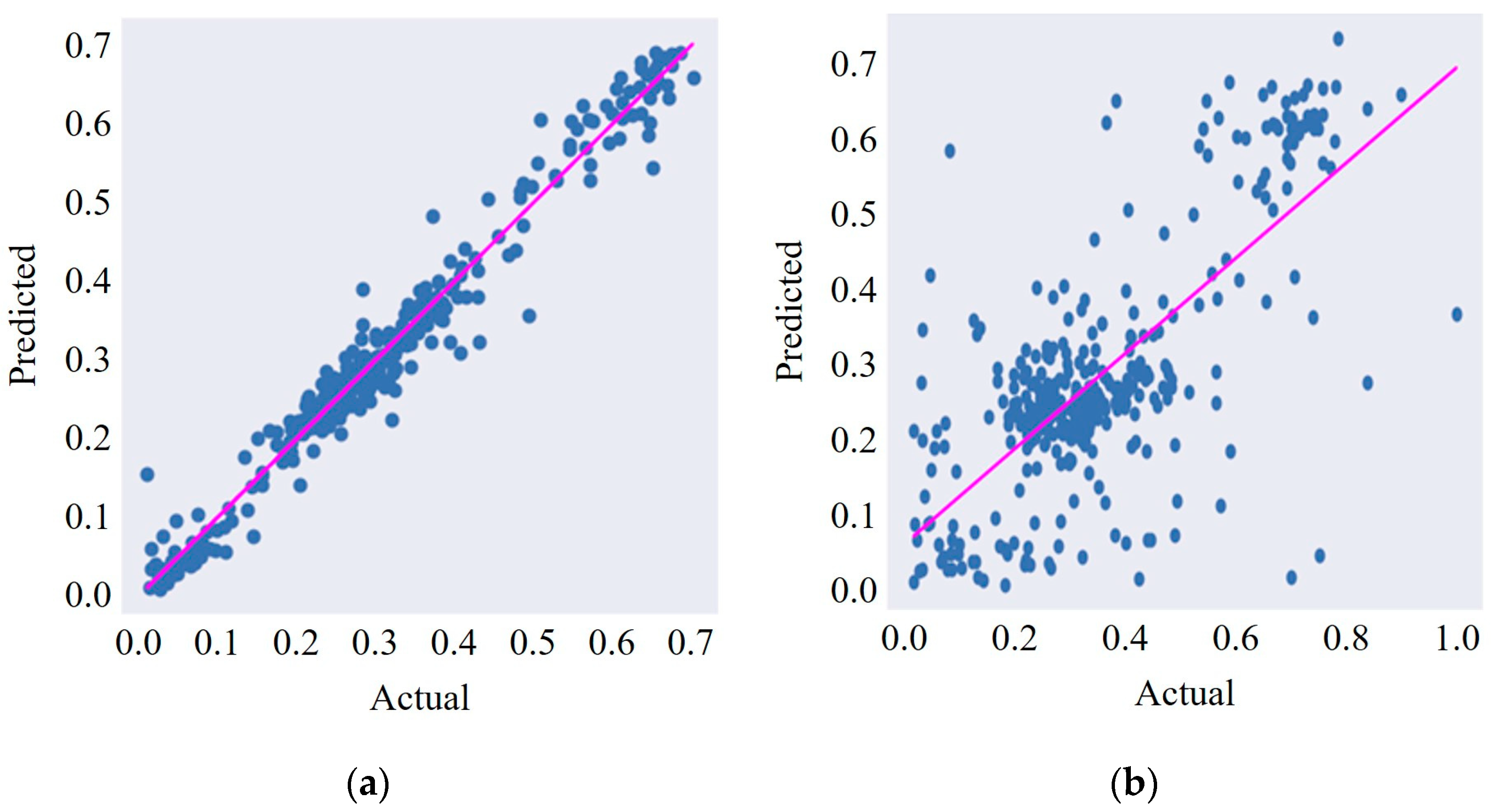
5. Results
5.1. Prediction Performance by Dataset Type
5.2. Prediction Performance of Top-Performing MLP Network
6. Discussions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korea Energy Economics Institute. Energy Status of Korea 2023; Korea Energy Economics Institute: Ulsan, Republic of Korea, 2023. [Google Scholar]
- Nasir, T.; Bukhari, S.S.H.; Raza, S.; Munir, H.M.; Abrar, M.; Muqeet, H.A.U.; Bhatti, K.L.; Ro, J.S.; Masroor, R. Recent Challenges and Methodologies in Smart Grid Demand Side Management: State-of-the-Art Literature Review. Math. Probl. Eng. 2021, 2021, 5821301. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration Demand-Side Management Programs Save Energy and Reduce Peak Demand. Available online: https://www.eia.gov/ (accessed on 2 March 2023).
- Chen, C.F.; Xu, X.; Cao, Z.; Mockus, A.; Shi, Q. Analysis of Social–Psychological Factors and Financial Incentives in Demand Response and Residential Energy Behavior. Front. Energy Res. 2023, 11, 932134. [Google Scholar] [CrossRef]
- Song, K.; Kwon, N.; Anderson, K.; Park, M.; Lee, H.-S.; Lee, S. Predicting Hourly Energy Consumption in Buildings Using Occupancy-Related Characteristics of End-User Groups. Energy Build. 2017, 156, 121–133. [Google Scholar] [CrossRef]
- Neto, A.H.; Fiorelli, F.A.S. Comparison between Detailed Model Simulation and Artificial Neural Network for Forecasting Building Energy Consumption. Energy Build. 2008, 40, 2169–2176. [Google Scholar] [CrossRef]
- Yun, K.; Luck, R.; Mago, P.J.; Cho, H. Building Hourly Thermal Load Prediction Using an Indexed ARX Model. Energy Build. 2012, 54, 225–233. [Google Scholar] [CrossRef]
- Li, K.; Hu, C.; Liu, G.; Xue, W. Building’s Electricity Consumption Prediction Using Optimized Artificial Neural Networks and Principal Component Analysis. Energy Build. 2015, 108, 106–113. [Google Scholar] [CrossRef]
- Guo, J.; Lin, P.; Zhang, L.; Pan, Y.; Xiao, Z. Dynamic Adaptive Encoder-Decoder Deep Learning Networks for Multivariate Time Series Forecasting of Building Energy Consumption. Appl. Energy 2023, 350, 121803. [Google Scholar] [CrossRef]
- Fang, L.; He, B. A Deep Learning Framework Using Multi-Feature Fusion Recurrent Neural Networks for Energy Consumption Forecasting. Appl. Energy 2023, 348, 121563. [Google Scholar] [CrossRef]
- Heidari, A.; Khovalyg, D. Short-Term Energy Use Prediction of Solar-Assisted Water Heating System: Application Case of Combined Attention-Based LSTM and Time-Series Decomposition. Sol. Energy 2020, 207, 626–639. [Google Scholar] [CrossRef]
- Gao, Y.; Ruan, Y. Interpretable Deep Learning Model for Building Energy Consumption Prediction Based on Attention Mechanism. Energy Build. 2021, 252, 111379. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, J.; Liu, B.; Li, K.; Li, X. Hourly Energy Consumption Prediction of an Office Building Based on Ensemble Learning and Energy Consumption Pattern Classification. Energy Build. 2021, 241, 110929. [Google Scholar] [CrossRef]
- Shakeel, H.M.; Iram, S.; Hill, R.; Athar Farid, H.M.; Sheikh-Akbari, A.; Saleem, F. A Machine Learning-Based Intelligent Framework for Predicting Energy Efficiency in Next-Generation Residential Buildings. Buildings 2025, 15, 1275. [Google Scholar] [CrossRef]
- Riyadh Baqer, N.; Rashidi-Khazaee, P. Residential Building Energy Usage Prediction Using Bayesian-Based Optimized XGBoost Algorithm. IEEE Access 2025, 13, 36036–36049. [Google Scholar] [CrossRef]
- Harvey, A.C.; Peters, S. Estimation Procedures for Structural Time Series Models. J. Forecast. 1990, 9, 89–108. [Google Scholar] [CrossRef]
- Jiao, Y.; Tan, Z.; Zhang, D.; Zheng, Q.P. Short-Term Building Energy Consumption Prediction Strategy Based on Modal Decomposition and Reconstruction Algorithm. Energy Build. 2023, 290, 113074. [Google Scholar] [CrossRef]
- Masrur Ahmed, A.A.; Bailek, N.; Abualigah, L.; Bouchouicha, K.; Kuriqi, A.; Sharifi, A.; Sareh, P.; Al khatib, A.M.G.; Mishra, P.; Colak, I.; et al. Global Control of Electrical Supply: A Variational Mode Decomposition-Aided Deep Learning Model for Energy Consumption Prediction. Energy Rep. 2023, 10, 2152–2165. [Google Scholar] [CrossRef]
- Li, F.; Wan, Z.; Koch, T.; Zan, G.; Li, M.; Zheng, Z.; Liang, B. Improving the Accuracy of Multi-Step Prediction of Building Energy Consumption Based on EEMD-PSO-Informer and Long-Time Series. Comput. Electr. Eng. 2023, 110, 108845. [Google Scholar] [CrossRef]
- Wei, S.; Bai, X. Multi-Step Short-Term Building Energy Consumption Forecasting Based on Singular Spectrum Analysis and Hybrid Neural Network. Energies 2022, 15, 1743. [Google Scholar] [CrossRef]
- Chou, S.Y.; Dewabharata, A.; Zulvia, F.E.; Fadil, M. Forecasting Building Energy Consumption Using Ensemble Empirical Mode Decomposition, Wavelet Transformation, and Long Short-Term Memory Algorithms. Energies 2022, 15, 1035. [Google Scholar] [CrossRef]
- Fernández-Martínez, D.; Jaramillo-Morán, M.A. Multi-Step Hourly Power Consumption Forecasting in a Healthcare Building with Recurrent Neural Networks and Empirical Mode Decomposition. Sensors 2022, 22, 3664. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, M.; Wan, N.; Deng, Z.; He, Z.; Luo, J. Missing Measurement Data Recovery Methods in Structural Health Monitoring: The State, Challenges and Case Study. Measurement 2024, 231, 114528. [Google Scholar] [CrossRef]
- Chai, J.; Zeng, H.; Li, A.; Ngai, E.W.T. Deep Learning in Computer Vision: A Critical Review of Emerging Techniques and Application Scenarios. Mach. Learn. Appl. 2021, 6, 100134. [Google Scholar] [CrossRef]
- Rojas-Carabali, W.; Agrawal, R.; Gutierrez-Sinisterra, L.; Baxter, S.L.; Cifuentes-González, C.; Wei, Y.C.; Abisheganaden, J.; Kannapiran, P.; Wong, S.; Lee, B.; et al. Natural Language Processing in Medicine and Ophthalmology: A Review for the 21st-Century Clinician. Asia-Pac. J. Ophthalmol. 2024, 13, 100084. [Google Scholar] [CrossRef]
- Lian, H.; Wei, H.; Wang, X.; Chen, F.; Ji, Y.; Xie, J. Research on Real-Time Energy Consumption Prediction Method and Characteristics of Office Buildings Integrating Occupancy and Meteorological Data. Buildings 2025, 15, 404. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Y.; Wang, Y.; Du, C.; Li, H.; Zhang, Z. A Deep Belief Network-Based Energy Consumption Prediction Model for Water Source Heat Pump System. Appl. Therm. Eng. 2024, 255, 124000. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, D.; Zhao, L. Short-Term Energy Consumption Prediction of Large Public Buildings Combined with Data Feature Engineering and Bilstm-Attention. Appl. Sci. 2024, 14, 2137. [Google Scholar] [CrossRef]
- Jana, R.K.; Ghosh, I.; Sanyal, M.K. A Granular Deep Learning Approach for Predicting Energy Consumption. Appl. Soft Comput. 2020, 89, 106091. [Google Scholar] [CrossRef]
- Zheng, P.; Zhou, H.; Liu, J.; Nakanishi, Y. Interpretable Building Energy Consumption Forecasting Using Spectral Clustering Algorithm and Temporal Fusion Transformers Architecture. Appl. Energy 2023, 349, 121607. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Identification of Relevant Input Variables for Prediction of 1-Minute Time-Step Photovoltaic Module Power Using Artificial Neural Network and Multiple Linear Regression Models. Renew. Sustain. Energy Rev. 2017, 77, 955–969. [Google Scholar] [CrossRef]
- Harvey, A.C. Forecasting, Structural Time Series Models and the Kalman Filter; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Maddala, G.S.; Nimalendran, M. An Unobserved Component Panel Data Model to Study the Effect of Earnings Surprises on Stock Prices, Trading Volumes, and Spreads. J. Econ. 1995, 68, 229–242. [Google Scholar] [CrossRef]
- Smith, W.R.; Bauserman, R.L.; Ballas, S.K.; McCarthy, W.F.; Steinberg, M.H.; Swerdlow, P.S.; Waclawiw, M.A.; Barton, B.A. Climatic and Geographic Temporal Patterns of Pain in the Multicenter Study of Hydroxyurea. Pain 2009, 146, 91–98. [Google Scholar] [CrossRef] [PubMed]
- Bian, Z.; Zhang, Z.; Liu, X.; Qin, X. Unobserved Component Model for Predicting Monthly Traffic Volume. J. Transp. Eng. A Syst. 2019, 145, 04019052. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Elhabyb, K.; Baina, A.; Bellafkih, M.; Deifalla, A.F. Machine Learning Algorithms for Predicting Energy Consumption in Educational Buildings. Int. J. Energy Res. 2024, 2024, 6812425. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating, and Air-Conditioning Engineers (ASHRAE). ASHRAE Handbook Fundamentals; American Society of Heating, Refrigerating, and Air-Conditioning Engineers (ASHRAE): Atlanta, GA, USA, 2009. [Google Scholar]
- Sasu, G.-V.; Ciubotaru, B.-I.; Goga, N.; Vasilățeanu, A. Addressing Missing Data Challenges in Geriatric Health Monitoring: A Study of Statistical and Machine Learning Imputation Methods. Sensors 2025, 25, 614. [Google Scholar] [CrossRef]
- Xu, D.; Hu, P.J.-H.; Fang, X. Deep Learning-Based Imputation Method to Enhance Crowdsourced Data on Online Business Directory Platforms for Improved Services. J. Manag. Inf. Syst. 2023, 40, 624–654. [Google Scholar] [CrossRef]




| No | Number of Nodes in Hidden Layers | Dropout | Batch Size |
|---|---|---|---|
| M1 | [12, 16, 32, 16, 12, 6] | 0.00 | 32 |
| M2 | 64 | ||
| M3 | 0.01 | 32 | |
| M4 | 64 | ||
| M5 | [18, 24, 48, 24, 18, 12] | 0.00 | 32 |
| M6 | 64 | ||
| M7 | 0.01 | 32 | |
| M8 | 64 | ||
| M9 | [24, 32, 64, 32, 24, 18] | 0.00 | 32 |
| M10 | 64 | ||
| M11 | 0.01 | 32 | |
| M12 | 64 | ||
| M13 | [12, 16, 32, 64, 32, 16, 12] | 0.00 | 32 |
| M14 | 64 | ||
| M15 | 0.01 | 32 | |
| M16 | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, T.; Song, K. Data Augmentation Using Multivariate Time Series Decomposition for Predicting Daily Energy Consumption of New Buildings. Buildings 2025, 15, 3467. https://doi.org/10.3390/buildings15193467
Kang T, Song K. Data Augmentation Using Multivariate Time Series Decomposition for Predicting Daily Energy Consumption of New Buildings. Buildings. 2025; 15(19):3467. https://doi.org/10.3390/buildings15193467
Chicago/Turabian StyleKang, Taewook, and Kwonsik Song. 2025. "Data Augmentation Using Multivariate Time Series Decomposition for Predicting Daily Energy Consumption of New Buildings" Buildings 15, no. 19: 3467. https://doi.org/10.3390/buildings15193467
APA StyleKang, T., & Song, K. (2025). Data Augmentation Using Multivariate Time Series Decomposition for Predicting Daily Energy Consumption of New Buildings. Buildings, 15(19), 3467. https://doi.org/10.3390/buildings15193467







