Seismic Performance Evaluation of RC–Masonry Hybrid Systems: A Comparative Study with İsa Divanli Mosque as a Case Example

Abstract

Reinforced concrete (RC)–masonry hybrid systems are commonly found in both historical renovations and modern constructions, particularly in seismic regions. While combining the ductility of RC with the mass and stiffness of masonry offers potential advantages, these systems often exhibit complex and unpredictable seismic behavior due to the differing mechanical characteristics of the two materials. This study aims to evaluate the benefits and drawbacks of RC–masonry hybrid systems by performing a comparative numerical analysis of three structural configurations. As a representative case study, the historical İsa Divanlı Mosque in Kahramanmaraş, Turkey—severely damaged during the 6 February 2023 earthquakes—is modeled under three scenarios: (Configuration A) full RC structure with shear walls, (Configuration B) unreinforced masonry, and (Configuration C) the existing hybrid form with an RC dome and slabs over masonry walls. Finite element models were developed for each case, and their seismic responses were analyzed under identical loading conditions. The maximum spectral displacements were 55.3 mm, 45.8 mm, and 59.5 mm for the RC, masonry, and hybrid configurations, respectively. The Normalized Displacement Index (NDI) values reached 0.666 mm/MPa for the RC and hybrid systems, while the masonry configuration remained at 0.528 mm/MPa, reflecting its brittle behavior. The findings highlight the influence of structural typology on seismic vulnerability and demonstrate the potential risks and disadvantages of hybrid systems. This study contributes to the understanding of hybrid structural behavior and offers recommendations for the design and retrofit of such systems in seismic regions.

1. Introduction

Hybrid structural systems, combining reinforced concrete (RC) and masonry elements, are frequently employed in both historical and modern constructions. These systems offer the strength and durability of RC while preserving the traditional and aesthetic qualities of masonry. However, the seismic performance of such systems presents unique challenges due to the inherent differences in mechanical properties between RC and masonry, particularly in terms of stiffness, ductility, and deformation capacity. This discrepancy in material behavior under dynamic loads often results in poor interaction, leading to structural vulnerabilities during seismic events.

RC, with its high compressive and tensile strength, is commonly used for modern structural elements due to its ability to resist both vertical and lateral forces. Conversely, masonry, while known for its compressive strength and historical significance, is brittle and less capable of withstanding tensile and shear stresses. When combined in hybrid systems, the differential stiffness and load-carrying capacities of these materials often create challenges in force transfer and energy dissipation during earthquakes. This interaction problem can result in severe damage, particularly in regions of high seismic activity, where dynamic forces expose the limitations of such systems.

The seismic performance of hybrid structural systems composed of reinforced concrete (RC) and masonry elements has been the subject of increasing attention due to their widespread use and vulnerability in seismic regions. These systems, whether intentionally designed or developed through later modifications in historical or informal constructions, pose unique challenges because of their heterogeneous behavior under dynamic loading. Hybrid systems suffer from discontinuities in both lateral and vertical load paths, particularly at the interface between RC and masonry components. Zhang et al. (2025) [1] showed through shaking table experiments that confined masonry elements in hybrid buildings tend to fail earlier than RC components, resulting in a progressive collapse mechanism. They advocate for re-evaluating seismic design assumptions where masonry is often underrepresented or treated as non-structural. Abrams et al. (2016) [2] conducted a series of full-scale experimental studies on hybrid masonry systems, particularly focusing on their use with steel or RC frames. These studies illustrated how detailing, connector design, and force transfer mechanisms critically affect the overall performance. Their findings highlight that hybrid systems can be competitive with traditional systems—if designed properly. Likewise, Zheng et al. (2019) [3] explored frame–masonry horizontal hybrid structures common in rural China, demonstrating how torsional effects and irregular stiffness distribution significantly exacerbate seismic vulnerabilities. Their study combines shaking table tests and FE modeling, offering valuable insights into structural behavior, including story drift and stress concentration at beam–column joints. Retrofitting hybrid structures presents another layer of complexity. Noori et al. (2025) [4] introduced the Thick Hybrid Wall (THW) technique, which was proven to significantly increase shear strength and ductility of URM-infilled RC frames. Their cyclic loading tests validated an analytical model that predicts failure mechanisms considering axial–shear–flexural interaction. This technique demonstrates promise as a low-cost alternative, especially for pilotis-type and soft-story buildings. A similar line of work by Gora et al. (2021) [5] evaluated RC–masonry hybrid buildings in Nepal, concluding that the addition of RC elements does not always yield improved performance unless holistic integration is ensured. Their nonlinear static analysis highlighted significant failure at RC–masonry junctions due to differential stiffness. Past earthquake events in various regions have revealed recurring patterns of damage in masonry buildings with later-added RC components. For example, post-earthquake surveys following the 2015 Gorkha earthquake in Nepal (Dizhur et al., 2016 [6]; Gautam and Rodrigues, 2018 [7]), the 2016 Central Italy earthquakes (Saretta et al., 2021 [8]; Acito et al., 2023 [9]), the 2022 Düzce-Golyaka earthquake and 2023 Kahramanmaraş earthquakes in Türkiye (Isik et al., 2023 [10]; Dedeoglu et al., 2024 [11], Kahya et al., 2024 [12]) indicated that rigid RC components often induced stress concentrations in masonry structures, leading to severe cracking or partial collapse. Similar observations were reported in heritage structures affected by the 1999 Kocaeli earthquake in Türkiye (Sezen et al., 2000 [13]; Saatcioglu et al., 2001 [14]), the 2009 L’Aquila earthquake in Italy (Indirli et al., 2013 [15]; Palermo et al., 2014 [16]), and the 2010 Maule earthquake in Chile (Astroza et al., 2012 [17]).

Despite the growing body of literature [18,19,20,21], detailed comparative studies assessing different hybrid configurations in existing buildings—particularly historical ones—are still limited. This research addresses this gap by focusing on the İsa Divanlı Mosque, a historical structure in Kahramanmaraş, Turkey, that experienced severe damage during the 6 February 2023 earthquakes. Originally constructed as a masonry building, the mosque was later modified with RC domes and slabs. These events highlight that the interaction between masonry and RC elements is a global issue that requires detailed investigation. While several studies have explored the seismic behavior of hybrid systems, only a few works focus on historically modified structures using calibrated finite element models informed by actual earthquake damage data. This research directly addresses this gap by applying a validated FEM approach to the İsa Divanlı Mosque.

In this study, three structural configurations of the mosque are modeled and analyzed: (1) a full RC structure with shear walls, (2) a full masonry structure, and (3) the current hybrid system. The goal is to evaluate and compare their seismic responses using finite element modeling and analyses. Through this comparison, the study aims to offer practical insights into the seismic vulnerabilities and strengths of hybrid systems and contribute to better design and retrofitting strategies for such buildings.

2. Historical İsa Divanlı Mosque

Kahramanmaraş has been an important center of life for many different civilizations and cultures throughout history. The structures built in various architectural styles within the city limits are some of the most prominent examples that showcase this rich historical heritage. The historical İsa Divanlı Mosque, located in the heart of Kahramanmaraş and examined in this report, holds a special place among these structures (Figure 1). This mosque, situated in the city center, is also known as “Uyuz Pınarı Mosque.”

The İsa Divanlı Mosque, built in the mid-16th century, is one of the first mosques constructed by the Ottoman Empire in the city. According to the construction inscription on the mosque’s mihrab, the mosque was commissioned during the reign of Sultan Suleiman the Magnificent by Hacı Osman, the son of Hacı İsa Divan. However, it is understood that Hacı Osman passed away during the construction, and the mosque was completed during the reign of Sultan Selim II in the year 976 AH (1568–1569 AD). One of the repair inscriptions found in various parts of the building indicates that the mosque was destroyed in the 1795 earthquake, which caused significant damage in the city, and was rebuilt in 1797 with the help of the community. This inscription marks an important restoration period in the mosque’s history and highlights the community’s contribution to preserving and rebuilding this historic structure. After undergoing several repairs, the İsa Divanlı Mosque remained largely faithful to its original form until 1959. However, in 1959, the prayer hall was significantly damaged and was demolished and rebuilt by the local residents. It is understood that the mosque completely lost its original character during the reconstruction efforts after 1959. The work conducted at that time ignored the mosque’s original architectural identity, which was in harmony with other examples in the city and resulted in the construction of a completely different mosque design. As seen in Figure 2, the mosque originally had a wooden roof system, but after 1960, the wooden roof was removed and replaced with a reinforced concrete dome system.

3. Current Condition of the Mosque

In the structural damage assessment, a detailed investigation of the structural load-bearing elements of the historical monument was conducted, analyzing these components both geometrically and structurally in detail. During this investigation, the geometric properties, structural defects, and all visible damage of the load-bearing system were meticulously identified and documented. Additionally, the damages that occurred in various parts of the structure following the 6 February 2023 Kahramanmaraş Earthquakes were carefully examined. It was determined that the minaret and the main walls of the structure suffered significant damage (Figure 3).

Examinations inside and outside the mosque revealed severe displacements in the walls, as well as separations, shifts, and fractures in the upper sections of the body. Furthermore, cracks of various lengths and widths were observed between the main walls of the structure. Particularly, significant damage was identified around the window and door openings (Figure 3).

During the structural inspections, material defects were also observed, with certain areas showing a loss of mechanical strength. The defects identified in the minaret, as a result of these investigations, were found to have the potential to cause significant problems in the future, increasing the risk of further damage to the structure.

4. Material Characterization Tests

A comprehensive material characterization study was conducted to accurately represent the mechanical properties of the existing materials used in the hybrid structure of the İsa Divanlı Mosque. This chapter outlines the procedures undertaken for sampling, testing, and evaluating both the reinforced concrete (RC) and masonry elements of the building. The acquired data were instrumental in calibrating the numerical models and interpreting the structural performance under seismic actions.

4.1. Concrete Elements

To assess the condition and mechanical properties of the existing reinforced concrete components, core samples were extracted in accordance with relevant testing standards (TS EN 12504-1 [23], TS EN 1992-1-1 [24]). Cylindrical core specimens with a diameter of 100 mm were taken from various parts of the structure, particularly from RC columns. These core samples were subjected to uniaxial compressive strength testing to determine the compressive strength of the concrete. Additionally, surface stripping was carried out at select regions to expose the embedded reinforcement. This allowed for visual inspection of the reinforcement condition, evaluation of corrosion levels, and identification of possible deficiencies such as insufficient cover or discontinuities. Following this, a detailed reinforcement mapping was performed using a non-destructive testing method: Ferroscan scanning. The Ferroscan provided spatial information on the position, diameter, and spacing of rebars, allowing for the generation of a comprehensive reinforcement layout, which was later incorporated into the finite element model (Figure 4).

4.2. Masonry Elements

Masonry materials from various parts of the mosque were also sampled to determine the physical and mechanical properties of the stone and mortar used in the historic structure. Extracted stones were shaped into two standardized specimen types: (i) cubic samples of 5 cm × 5 cm × 5 cm and (ii) prismatic samples of 4 cm × 4 cm × 16 cm. These specimens were subjected to a series of laboratory tests (Figure 5 and Figure 6), including:

• Apparent Density Test: Conducted in accordance with TS EN 1936 [25], this test aimed to determine the bulk density and porosity of the masonry stones.
• Uniaxial Compression Test: Following TS EN 1926 [26], both cube and prism specimens were tested to determine their compressive strength under axial loading.
• Flexural Strength Test: Prismatic specimens were tested for flexural (bending) strength in compliance with TS EN 12372 [27] to assess their tensile behavior across joints and bedding planes.

These results provided valuable input for defining the mechanical parameters used in the modeling of unreinforced masonry (URM) elements and understanding the variability of material quality across different parts of the structure. The results of the material characterization tests are presented in

Table 1. Material characterization test results.

	Apparent Density	Uniaxial Compressing Strength		Apparent Density	Uniaxial Compressing Strength
Sample No	kg/m3	MPa	Sample No	kg/m3	MPa
Wall Sample 1	1950	39.17	Minaret Sample 1	2256	1.83
Wall Sample 2	2241	38.08	Minaret Sample 2	2258	2.91
Wall Sample 3	2034	31.47	Minaret Sample 3	2276	5.96
Wall Sample 4	2066	35.69	Minaret Sample 4	2400	3.00
Wall Sample 5	2040	48.15	Minaret Sample 5	2397	5.77
Wall Sample 6	1977	40.19	Minaret Sample 6	2442	2.68
Wall Sample 7	1906	48.01	Minaret Sample 7	2277	1.56
Wall Sample 8	1749	38.78	Minaret Sample 8	2067	2.45
Wall Sample 9	2050	34.66	Minaret Sample 9	2109	1.08
Average Value	2002	39.36	Average Value	2276	3.03
Standard Deviation	133.67	5.62	Standard Deviation	127.37	1.73

. These parameters were directly used in the development and calibration of the finite element models described in the subsequent chapters.

5. Structural Configurations of the Mosque

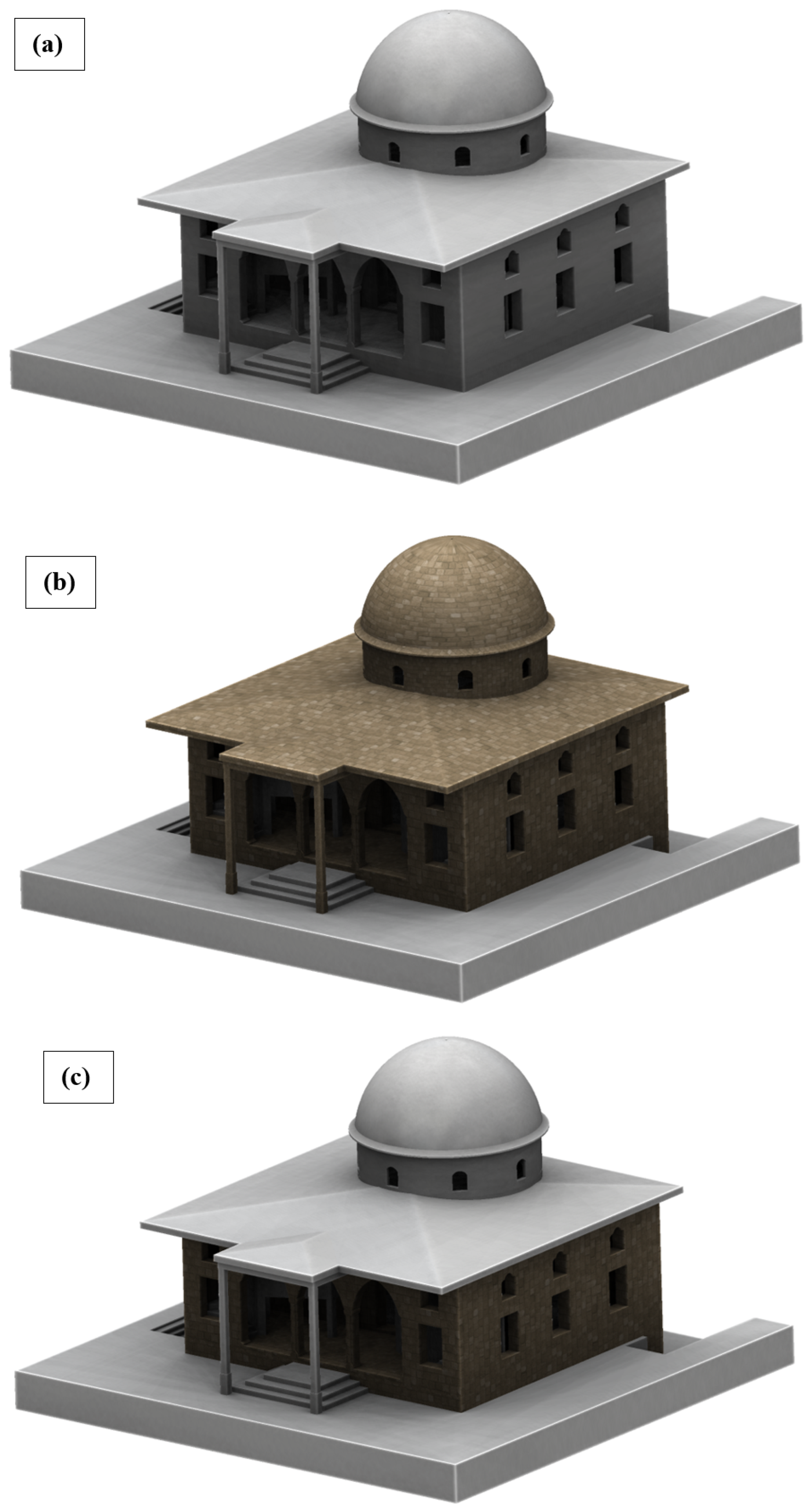
In order to assess the seismic performance of various structural typologies, three distinct configurations of the İsa Divanlı Mosque were developed and analyzed. Each configuration reflects a realistic structural system either currently present in the building or commonly observed in similar historical or hybrid structures (Figure 7). These models were subjected to identical seismic loading conditions to ensure a consistent comparison framework. The configurations are described as follows:

• Configuration A—Fully Reinforced Concrete (RC) Structure:

This model represents a modern structural typology in which all vertical and horizontal load-bearing elements are composed of RC, including shear walls strategically placed to enhance lateral stiffness and energy dissipation. It serves as a benchmark for assessing the highest expected seismic performance among the scenarios.

2.

Configuration B—Fully Unreinforced Masonry (URM) Structure:

This model reflects the original construction of the mosque, where all vertical and horizontal elements are composed of unreinforced stone masonry. Due to its brittle nature, low tensile strength, and lack of ductility, this configuration is particularly vulnerable to seismic loads and offers insight into the original performance limitations of the structure.

3.

Configuration C—Existing Hybrid Configuration (RC Dome and Slabs over Masonry Walls):

The current state of the mosque includes reinforced concrete dome and slab elements added atop existing masonry walls. This hybrid system combines materials with contrasting stiffness and deformation capacities, leading to discontinuities in force transfer and potential damage concentration at the RC–masonry interfaces. The model reflects the actual damage-prone behavior observed after the 2023 earthquakes and serves as the primary subject of investigation in this study.

Each of these configurations was translated into a finite element model and analyzed using finite element analyses to evaluate drift ratios, stress distributions, failure mechanisms, and overall dynamic response. The comparative results offer valuable insight into the strengths and limitations of each structural typology in seismic zones. The undamaged state of the structure was assumed by using average intact material parameters obtained from laboratory tests. In the comparative modeling, only the masonry and reinforced concrete components were modified across the configurations. All other structural parts of the mosque were kept unchanged. By holding these elements constant, the effect of masonry and reinforced concrete behavior on seismic performance could be clearly observed.

6. Finite Element Model (FEM)

6.1. Finite Element Modeling

Advancements in computer technology have facilitated the numerical analysis of the behavior of structures and soils. Numerical (mathematical) modeling enables the observation of the real behavior of an entire structure or a specific part under various loads or physical effects. Therefore, the use of finite element methods in numerical modeling studies is a highly effective and widely adopted approach. The finite element method (FEM) provides a mathematical representation of a physical structure and offers a reliable solution framework for a broad range of engineering problems. At its core, FEM simplifies complex problems by dividing them into smaller, manageable subdomains known as elements, which are connected at discrete points called nodes. These elements allow the discretization of a continuum, enabling the approximation of its behavior through algebraic expressions derived from the governing physical laws. In the structural analysis and evaluation of the historical monument’s load-bearing system, FEM was employed to construct the numerical model of the structure. ANSYS Workbench (19.1 release) software was utilized for this purpose, and the entire structure was modeled in three dimensions (Figure 8). Following the development of the model, environmental vibration data collected from the site were used to validate the model by comparing the natural frequencies. Calibration studies ensured that the numerical model’s fundamental periods closely matched the experimental results. Upon successful validation, linear and modal finite element analyses were carried out.

The modeling process was guided by several key considerations and assumptions:

• While preparing the finite element model, aspects such as the quantity of masonry units, their repetitive pattern, the geometric configuration of the structure, construction period, and block arrangement were considered.
• The macro-modeling approach, widely used for the analysis of masonry structures, was adopted.
• The material properties used in the model were determined based on laboratory testing and on-site vibration measurements.
• The three-dimensional models consisted of 425,707 nodes and 226,180 elements for each configuration (Figure 8, Figure 9 and Figure 10).
• RC joints were modeled as rigid connections. RC–masonry interfaces were represented by contact surfaces allowing discontinuities to simulate realistic force transfer limitations.
• The analyses were performed using an implicit time-integration scheme. All structural components were modeled using 20-node solid elements. Reinforcement in RC components was represented through equivalent smeared properties calibrated with Ferroscan data.
• The mosque is located on an alluvial deposit classified as soil type ZD according to Turkey Building Earthquake Code (TBEC, 2018) [28]. Shear wave velocity (Vs30 ≈ 280 m/s) was adopted to define the site-specific spectrum.
• Non-structural elements such as finishes and secondary infills were excluded, focusing the model on the primary load-bearing system.

To deepen the understanding of the structural behavior and to ensure analytical consistency, the finite element formulation is elaborated below.

The governing equation of the entire structural system under static or dynamic loading conditions can be expressed as:

$$Ku=f$$

(1)

where $K$ is the global stiffness matrix, $u$ is the nodal displacement vector, $f$ is the vector of externally applied nodal forces.

Each finite element contributes to the global system through its own stiffness matrix. Within each element, the displacement field is approximated by:

$$u(\xi ,\eta ,\zeta )=\sum _{i=1}^n{N}_i\left(\xi ,\eta ,\zeta \right)u_i=N(\xi ,\eta ,\zeta )u_e$$

(2)

where $\xi ,\eta ,\zeta$ are the natural coordinates in the isoparametric domain, $N_i$ are the interpolation (shape) functions, $u_e$ is the nodal displacement vector of the element, $N$ is the matrix of shape functions for all nodes.

The strain vector ε within an element is obtained using the differential operator matrix $B$:

$$\epsilon =B{u}_e$$

(3)

To evaluate spatial derivatives in global coordinates, the Jacobian matrix $\mathit{J}$ is used to transform the local derivatives as follows:

$$\left[\begin{array}{c}{\displaystyle \frac{\partial }{{\partial }_x}}\\ {\displaystyle \frac{\partial }{{\partial }_y}}\\ {\partial }_z\end{array}\right]={\mathit{J}}^{-1}\left[\begin{array}{c}{\displaystyle \frac{\partial }{{\partial }_{\xi }}}\\ {\displaystyle \frac{\partial }{{\partial }_{\eta }}}\\ {\displaystyle \frac{\partial }{{\partial }_{\zeta }}}\end{array}\right]$$

(4)

where the Jacobian matrix is defined by:

$$\mathit{J}=\left[\begin{array}{ccc}{\displaystyle \frac{{\partial }_x}{{\partial }_{\xi }}}& {\displaystyle \frac{{\partial }_x}{{\partial }_{\eta }}}& {\displaystyle \frac{{\partial }_x}{{\partial }_{\zeta }}}\\ {\displaystyle \frac{{\partial }_y}{{\partial }_{\xi }}}& {\displaystyle \frac{{\partial }_y}{{\partial }_{\eta }}}& {\displaystyle \frac{{\partial }_y}{{\partial }_{\zeta }}}\\ {\displaystyle \frac{{\partial }_z}{{\partial }_{\xi }}}& {\displaystyle \frac{{\partial }_z}{{\partial }_{\eta }}}& {\displaystyle \frac{{\partial }_z}{{\partial }_{\zeta }}}\end{array}\right]$$

(5)

The constitutive relationship for isotropic linear elastic masonry is defined by:

$$\sigma =D\epsilon$$

(6)

where $D$ is the elasticity matrix dependent on Young’s modulus $E$ and Poisson’s ratio $\nu$. For 3D problems:

$$\mathit{D}={\displaystyle \frac{E}{\left(1+\nu \right)\left(1-2\nu \right)}}\left[\begin{array}{cccccc}1-\nu & \nu & \nu & 0& 0& 0\\ \nu & 1-\nu & \nu & 0& 0& 0\\ \nu & \nu & 1-\nu & 0& 0& 0\\ 0& 0& 0& {\displaystyle \frac{1-2\nu }{2}}& 0& 0\\ 0& 0& 0& 0& {\displaystyle \frac{1-2\nu }{2}}& 0\\ 0& 0& 0& 0& 0& {\displaystyle \frac{1-2\nu }{2}}\end{array}\right]$$

(7)

Substituting the above relations, the stiffness matrix of a single element becomes:

$$K_e={\int }_{V_e}{B}^{T}DBdV$$

(8)

Using Gauss quadrature for numerical integration, this equation is approximated as:

$$K_e=\sum _{i=1}^{n_g}{B}^T\left({\xi }_i,{\eta }_i,{\zeta }_i\right)DB\left({\xi }_i,{\eta }_i,{\zeta }_i\right)\mid J\left({\xi }_i,{\eta }_i,{\zeta }_i\right)\mid {\omega }_i$$

(9)

where n_g is the number of Gauss integration points, and ${\omega }_i$ are their associated weights.

After calculating individual element stiffness matrices, they are assembled into the global stiffness matrix $K$ through a connectivity mapping. The resulting system of equations was solved to evaluate the static and dynamic behavior of the structure.

This integrated approach allowed for an accurate representation of the historic structure’s response under various loading scenarios, particularly for earthquake-induced dynamic effects. The model thus served both as a simulation platform and a decision-making tool for assessing structural safety and formulating potential strengthening strategies.

6.2. Calibration of the Finite Element Model

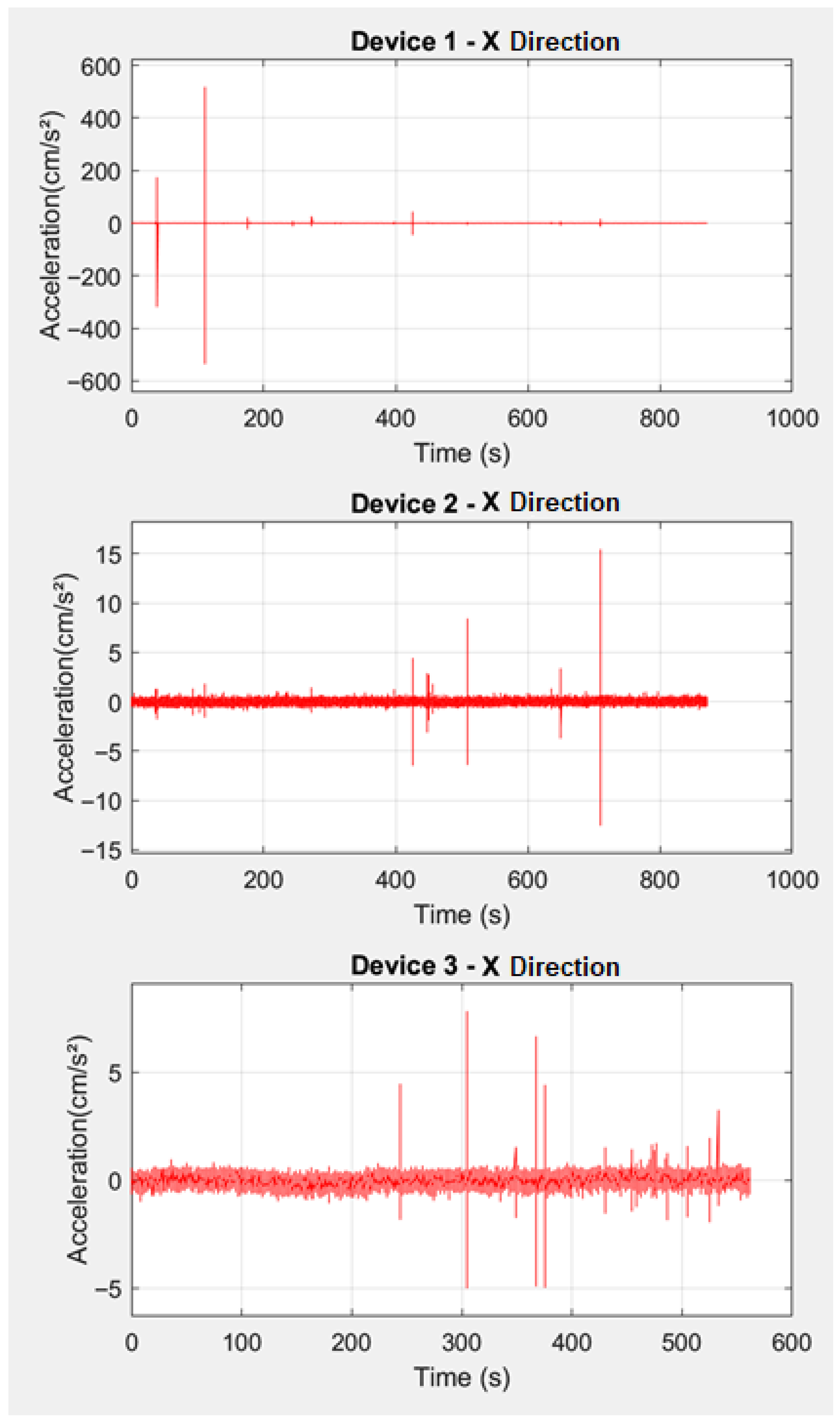
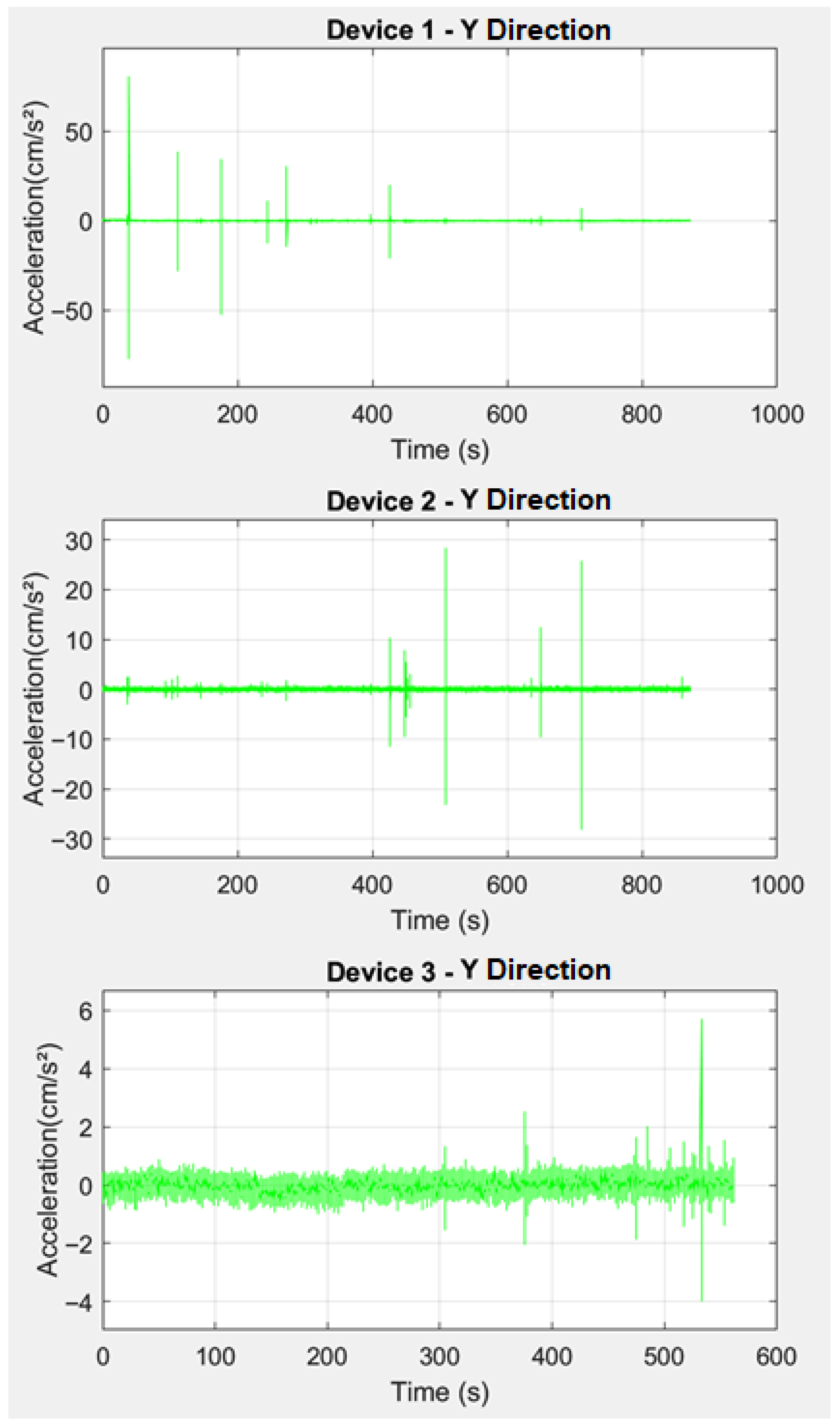
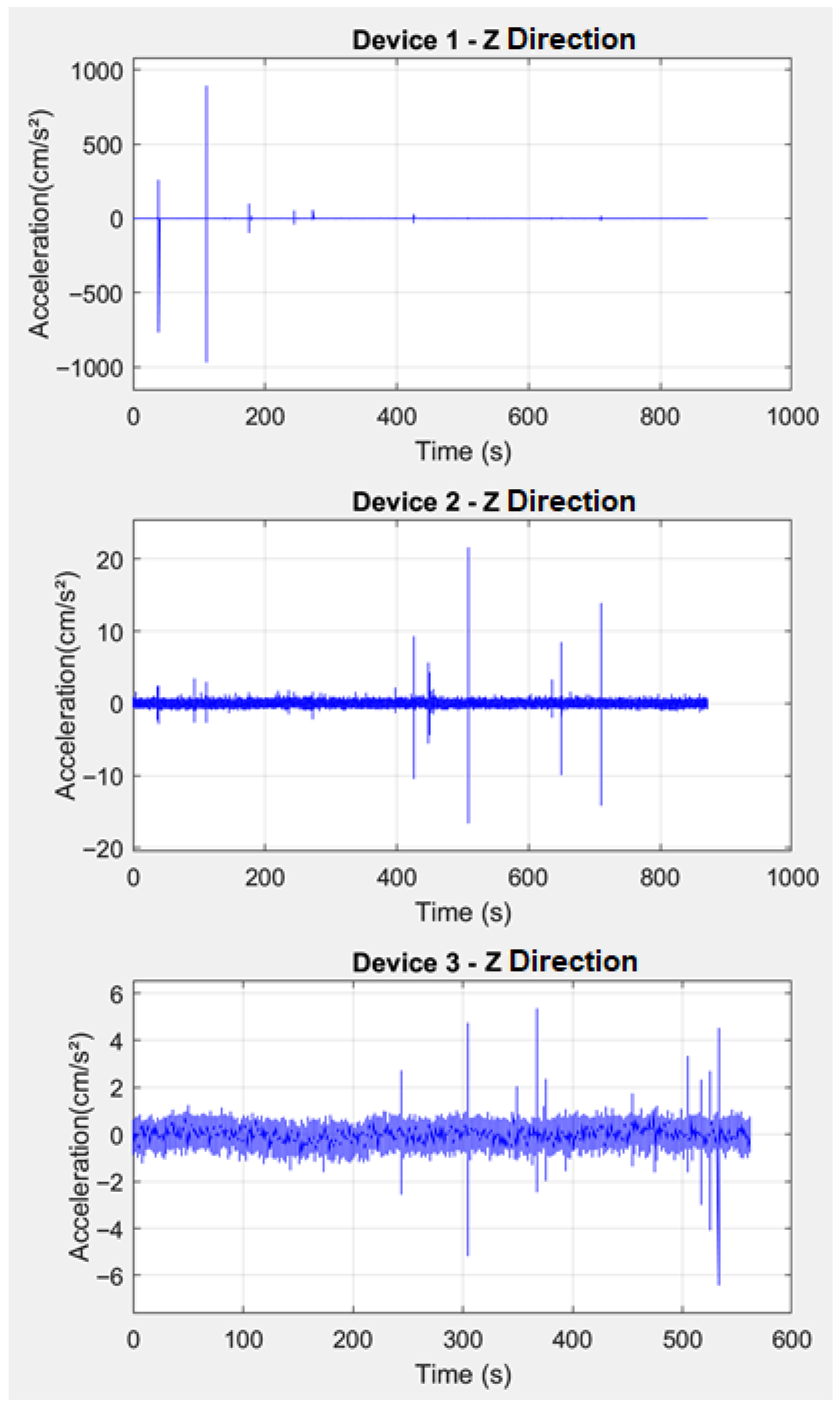
Calibration studies were first conducted on the finite element model prepared to observe the structural behavior of the historic building. At this stage, environmental vibration data were recorded from the site using three-axis accelerometers and the dominant frequency of the structure was determined based on these data.

The locations of the accelerometers were strategically chosen to capture the most relevant structural responses of the historic building. The three-axis accelerometers were placed in key positions to accurately record environmental vibration data (Figure 11):

Minaret: One accelerometer was placed at the top section of the minaret to capture vibrations affecting the upper part, while another was positioned at the base to monitor the overall behavior of the structure under different vibration modes.

Main structure of the mosque: Accelerometers were placed at critical points, such as:

Roof level: To observe the dynamic response of the roof, where significant movement could occur.

Wall junctions: Especially near areas with visible cracks or structural weaknesses, ensuring that any localized movements were accurately recorded.

Foundation level: To capture the overall vibration response of the building as a whole, providing a baseline for comparison with the other measurement points.

These specific positions were selected to ensure the best possible calibration of the finite element model, accurately reflecting the real structural behavior of both the minaret and the mosque. The obtained ambient vibration and force vibration data were given in Figure 12, Figure 13 and Figure 14. In the calibration stage, Full cracking and deformations were modeled by using as-built drawings and calibration was performed within the deformed model.

To perform calibration, the modal properties (natural frequencies and mode shapes) of the finite element model were compared with those obtained experimentally from ambient vibration tests. In finite element analysis, modal characteristics are extracted by solving the eigenvalue problem derived from the undamped free vibration equation:

$$M\ddot{u}+Ku=0$$

(10)

Assuming a harmonic solution of the form $u\left(t\right)=\varphi e^{iwt}$, the classical eigenvalue formulation was obtained:

$$\left(K-{\omega }^{2}M\right)\varphi =0$$

(11)

where $K$ is global stiffness matrix, M is global mass matrix, ω is natural angular frequency (ω = 2πf), ϕ is mode shape vector.

The solutions of this problem provide the natural frequencies f_i and corresponding mode shapes ϕ_i of the structure. To compare the measured and computed frequencies, the following modal correlation coefficient (MAC—Modal Assurance Criterion) can be used to quantify the agreement between mode shapes:

$$MAC({\varphi }_{exp},{\varphi }_{num})={\displaystyle \frac{{\left|{\varphi }_{exp}^T{\varphi }_{num}\right|}^2}{\left({\varphi }_{exp}^T{\varphi }_{exp}\right)\left({\varphi }_{num}^T{\varphi }_{num}\right)}}$$

(12)

A MAC value closer to 1 indicates a stronger correlation. As a result of the revision studies, the frequency values obtained from the minaret (3.125 Hz) and the frequency values obtained from the numerical modal analyses (3.397 Hz) were found to have a correlation of over 90%. When examining the frequency values obtained from the main mosque structure, the experimental frequency (18.457 Hz) (Figure 15) and the numerical frequency (18.381 Hz) showed a correlation greater than 95%.

The error percentage between analytical and experimental frequencies can also be calculated as:

$${\epsilon }_f=\left|{\displaystyle \frac{f_{num}-f_{exp}}{f_{exp}}}\right|\times 100\mathrm{\%}$$

(13)

For the minaret:

$${\epsilon }_f=\left|{\displaystyle \frac{3.397-3.125}{3.125}}\right|\times 100\mathrm{\%}\approx 8.7\mathrm{\%}$$

(14)

For the mosque:

$${\epsilon }_f=\left|{\displaystyle \frac{18.381-18.457}{18.457}}\right|\times 100\mathrm{\%}\approx 0.4\mathrm{\%}$$

(15)

This close correlation between the numerical and experimental modal characteristics validated the accuracy of the finite element models. As such, the calibrated models were deemed reliable and used in subsequent structural performance analyses under static and dynamic loads.

7. Finite Element Analyses (FEA)

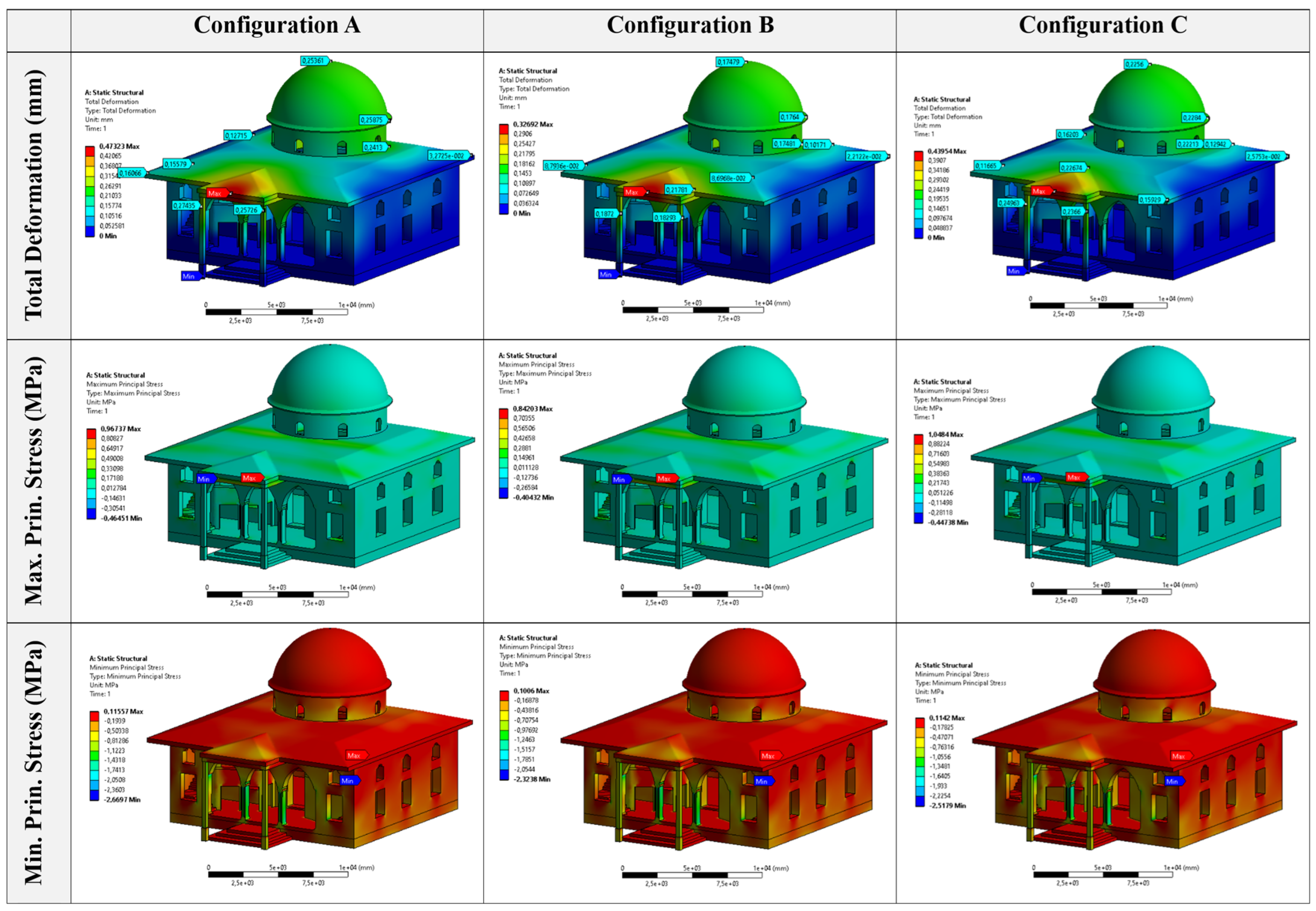
7.1. Static Analyses

The static analyses were carried out to evaluate the stress distribution, displacement characteristics, and potential damage mechanisms of the three structural configurations under gravity and lateral (seismic) loads. The linear static analysis was performed using the calibrated finite element models, incorporating the self-weight of the structure, imposed dead loads, and an equivalent lateral force representing the seismic action as per (TBEC, 2018) [29]. Stress concentrations and displacement magnitudes were extracted and compared across configurations. Principal stresses were visualized to identify critical zones (Figure 16).

7.2. Eigenvalue Analyses

In the second stage, Eigenvalue analyses were conducted to determine the fundamental dynamic characteristics of each structural configuration, including their natural frequencies and corresponding mode shapes. This type of analysis plays a critical role in understanding how the structure will behave under dynamic loads such as earthquakes, as it reveals the vibration modes that are most likely to be activated.

For each of the three structural models—Configuration A, B, C—a set of dominant vibration modes was extracted (Figure 17). These modes were used to assess whether the structural behavior is primarily translational or torsional and to identify irregularities or concentrations of dynamic response. Particular attention was given to how the different material compositions affected the distribution and symmetry of mode shapes. In addition to identifying mode shapes, the analysis calculated the participation of each mode in the total dynamic response. The mass participation ratios were used to determine how many modes should be included in the subsequent seismic analysis in order to capture an adequate portion of the structure’s dynamic behavior. These results formed the basis for the Response Spectrum Analysis presented in the following section.

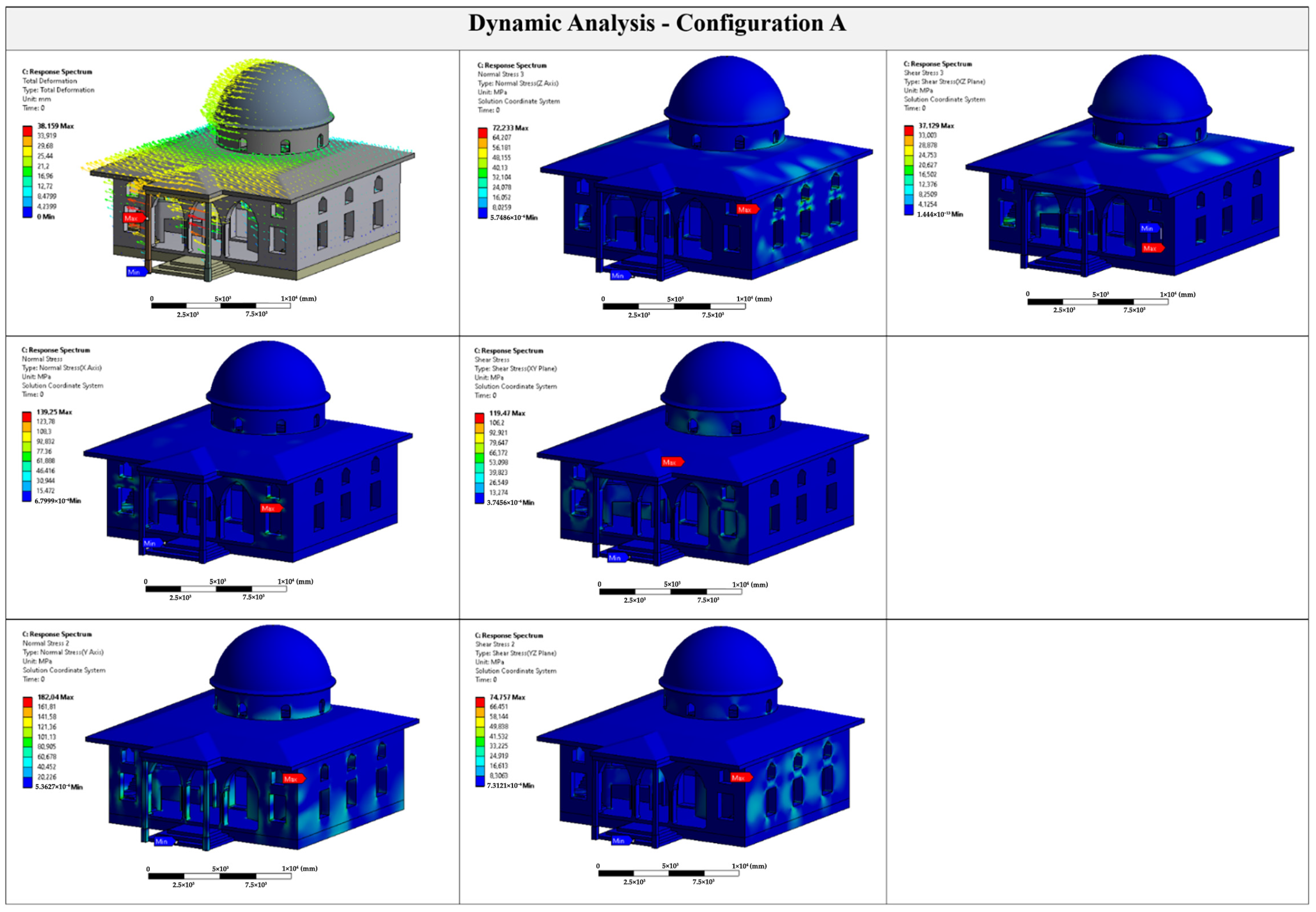
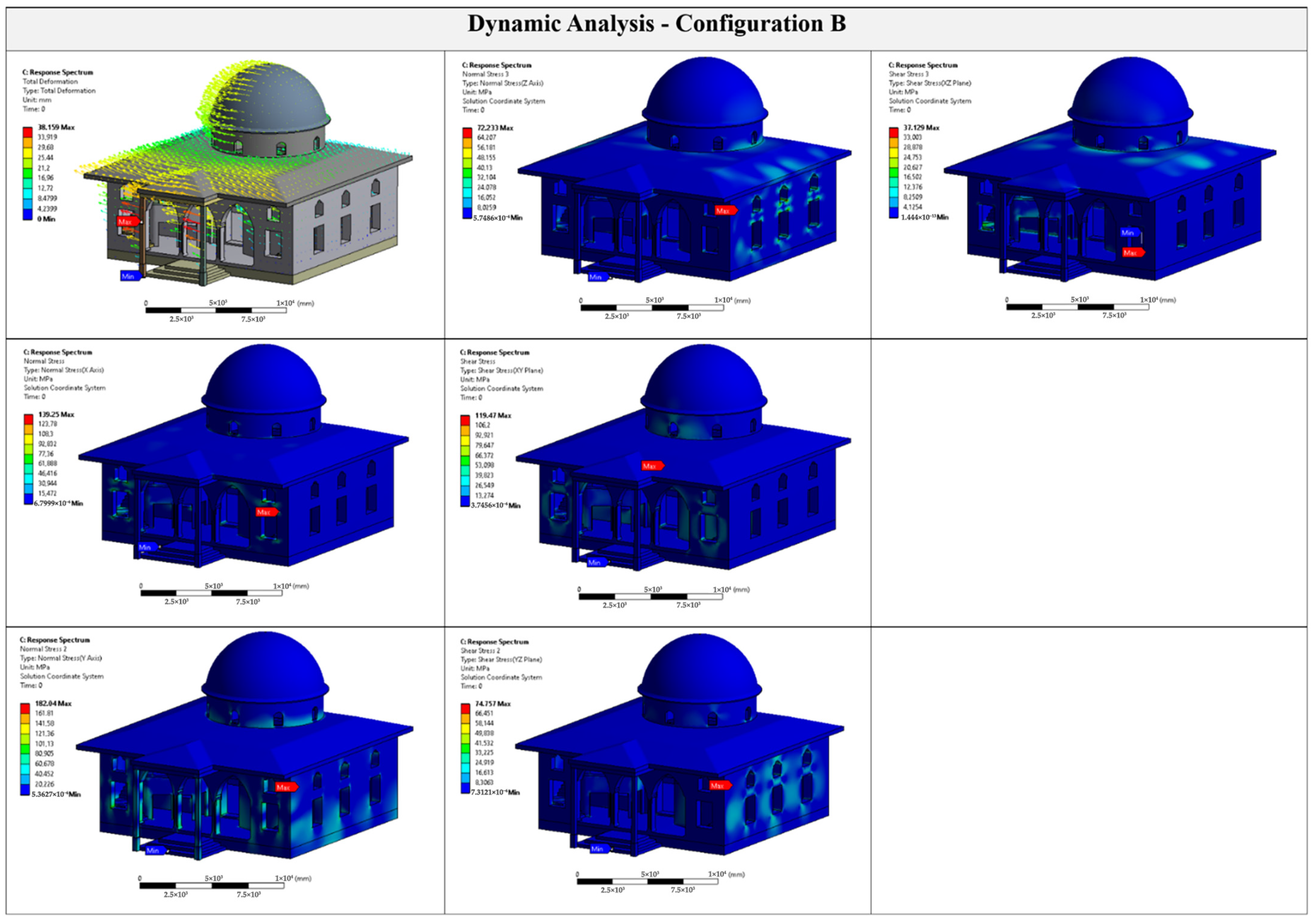
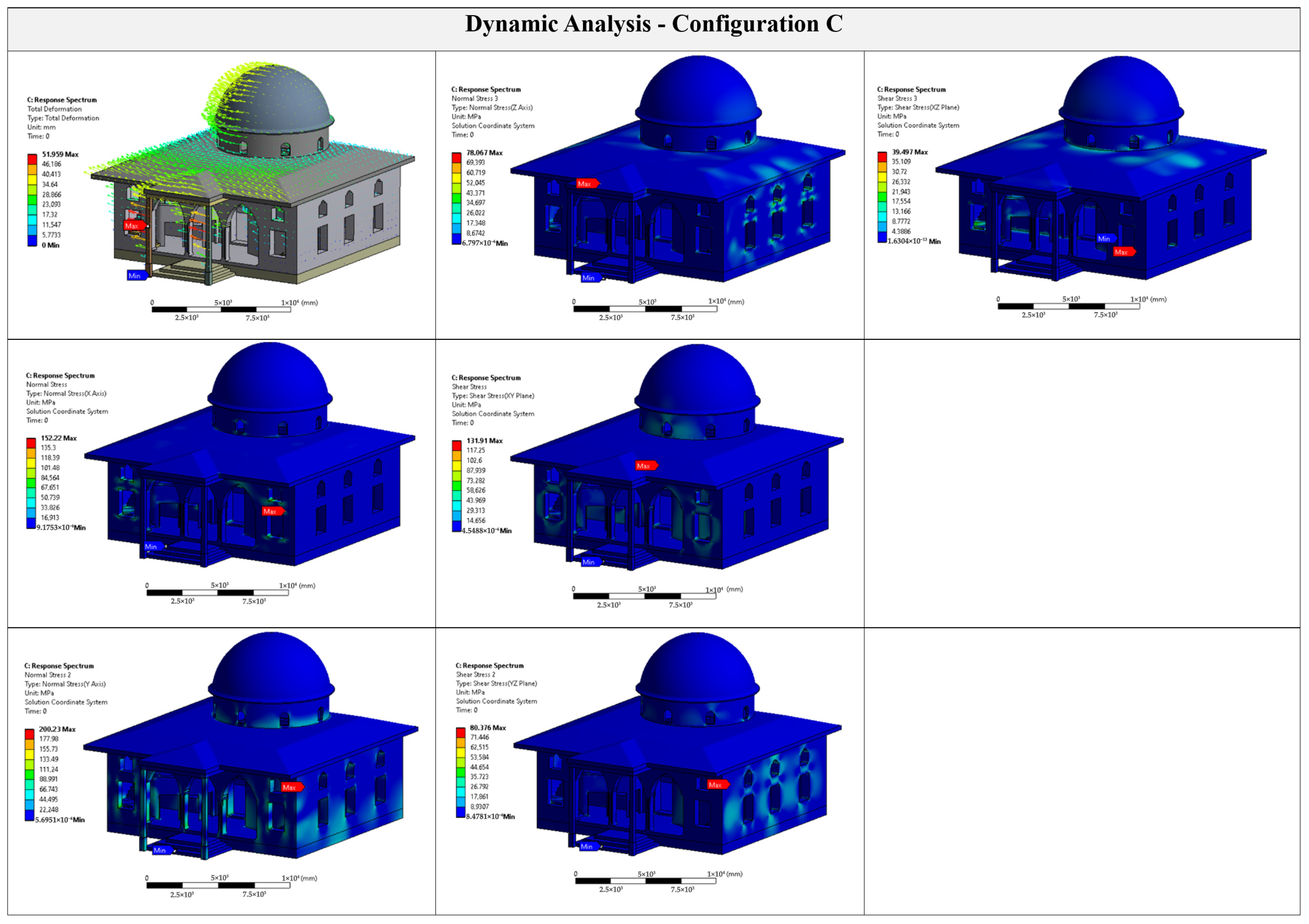
7.3. Dynamic Analyses

Dynamic analyses were carried out using the Response Spectrum Analysis (RSA) method to estimate the maximum structural response under seismic loading conditions. The analysis was conducted in accordance with the TBEC [29], incorporating site-specific spectrum parameters for Kahramanmaraş.

The response spectrum $S_a\left(T\right)$ used in the analyses is defined as:

$$S_a\left(T\right)=\left\{\begin{array}{cc}\hfill SDS.{\displaystyle \frac{T}{T_B}},& 0<T\le T_B\hfill \\ \hfill SDS,& T_B<T\le T_C\hfill \\ \hfill SDS.{\displaystyle \frac{T_c}{T}},& T_C<T\le T_D\hfill \\ \hfill SDS.{\displaystyle \frac{T_c{T}_D}{T^2}},& T>T_D\hfill \end{array}\right.$$

(16)

where $SDS$ is the design spectral acceleration for short periods, and $T_B$, $T_c$, $T_D$ are the characteristic periods defined by TBEC [29], respectively.

The total structural response was computed using the Square Root of Sum of Squares (SRSS) method, under the assumption that the vibration modes are statistically independent:

$$U_{TOTAL}=\sqrt{\sum _{i=1}^n{U}_i^2}$$

(17)

The dynamic analysis results are given in Figure 18, Figure 19 and Figure 20.

8. Results and Discussion

This section presents a comprehensive evaluation of the seismic performance of the three structural configurations (A: Reinforced Concrete, B: Unreinforced Masonry, C: Hybrid RC–masonry) based on static, modal, and response spectrum analyses. The findings are interpreted using quantitative indices, notably the Normalized Displacement Index (NDI), and illustrated through comparative graphs.

Under static loading, the maximum total displacements were recorded as 0.47 mm for Configuration A, 0.33 mm for Configuration B, and 0.44 mm for Configuration C. While the URM configuration (Configuration B) exhibited the lowest displacement, this outcome reflects high stiffness and brittle behavior rather than improved seismic capacity. The RC system (Configuration A), although slightly more deformable, showed superior stress redistribution and ductile energy dissipation. Configuration C exhibited stress concentrations at RC–masonry interfaces, indicating poor material compatibility. The observed deformation in Configuration C is only 7% lower than Configuration A, yet it arises from stiffness discontinuities and modal irregularities, compromising structural safety.

The first natural frequencies were found to be 16.5 Hz (Configuration A), 19.8 Hz (Configuration B), and 15.2 Hz (Configuration C). Configuration B exhibited the highest frequency due to its overall rigidity, yet its lack of ductility poses critical seismic vulnerability. Configuration C had the lowest frequency, suggesting dynamic softening due to irregular stiffness and mass distribution. Compared to RC, the hybrid system showed a 7.9% lower natural frequency, making it more susceptible to resonance effects and higher modal participation during seismic excitation.

The maximum spectral displacements were 55.3 mm (Configuration A), 45.8 mm (Configuration B), and 59.5 mm (Configuration C). Although the URM model displayed lower displacements, it also reached high stress magnitudes near failure thresholds. The RC model exhibited balanced behavior, whereas the hybrid configuration demonstrated the most unfavorable performance, combining high displacements and localized stress peaks.

To gain a direction-specific understanding of seismic deformation efficiency, the NDI was calculated separately for the horizontal principal stress directions (X and Z) and the XY shear plane. This metric, defined as:

$${NDI}_{\alpha }={\displaystyle \frac{U_{max}}{{\sigma }_{\alpha ,max}}}$$

(18)

where $U_{max}$ is the total peak displacement and σα, max denotes the peak normal (or shear) stress in direction α, allows comparative evaluation of stress-driven displacements under multi-directional seismic actions.

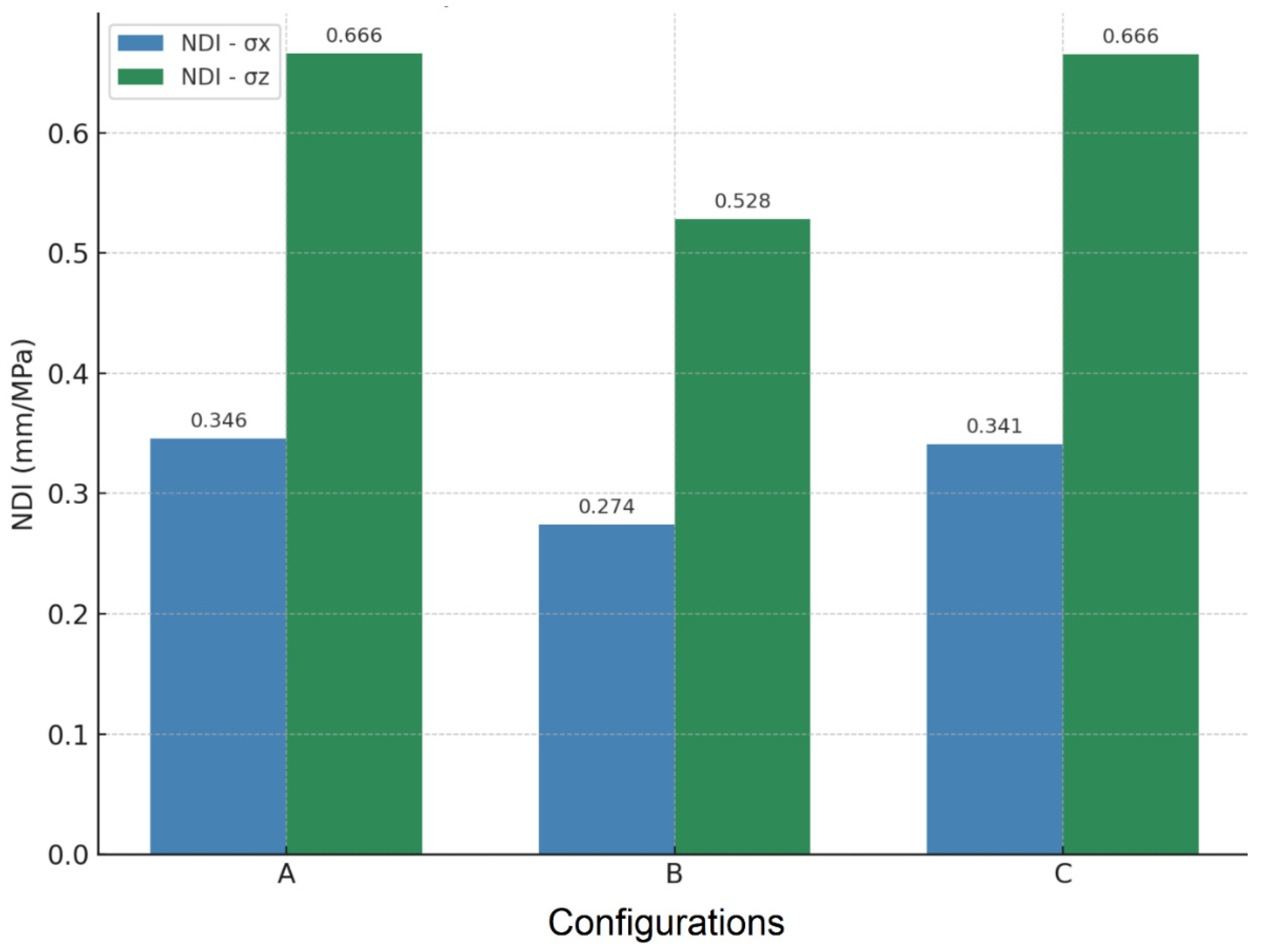
In the X-direction, all three systems exhibited similar NDI values (0.27–0.35 mm/MPa), but the hybrid system (Configuration C) displayed a value very close to the RC configuration (Configuration A), implying a comparable deformation level per unit of horizontal stress. However, the structural mechanism behind this is fundamentally different: while RC systems distribute stresses through ductile elements, the hybrid system exhibits significant stress concentration at the material interfaces, thus producing similar displacements at a higher cost of structural integrity.

In the Z-direction, both RC and hybrid systems reached nearly identical NDI values (~0.666 mm/MPa), approximately 26% higher than that of the masonry system. This indicates that hybrid systems experience much larger displacements in longitudinal directions under relatively similar stress magnitudes—suggesting significant modal participation and possible asymmetry in stiffness (Figure 21). In the XY shear plane, NDI values ranged between 0.32 and 0.40 mm/MPa, with the masonry structure showing the lowest shear-based displacement capacity. The hybrid system, again, approached the RC system (Configuration A) in numeric value, but the underlying mechanics suggest greater vulnerability due to uneven stiffness gradients and incompatible deformation modes (Figure 22).

These findings underline the importance of the NDI as more than a simple numerical index. Unlike raw displacement or stress values, the NDI captures the relationship between demand and resistance, thereby offering a normalized measure of seismic efficiency. It reveals not only how much a system displaces under stress but also the cost of that displacement in terms of structural reliability. For historical structures and hybrid systems in particular, the NDI provides an invaluable benchmark, enabling the comparison of systems with different material properties on a common scale. Moreover, it highlights hidden vulnerabilities that may not be evident in displacement values alone, such as stress concentration zones, stiffness incompatibilities, and premature damage initiation at interfaces. Thus, the NDI can be regarded as a diagnostic tool for both researchers and practitioners, guiding design decisions, prioritizing retrofit strategies, and offering a quantitative basis for evaluating the seismic resilience of hybrid structural systems.

The URM system (Configuration B) recorded the lowest indices in both directions, with 0.274 mm/MPa (${\sigma }_x$) and 0.528 mm/MPa (${\sigma }_z$). This behavior reflects its stiff but brittle nature, characterized by limited deformation capacity under high stress concentrations, thereby increasing the likelihood of localized cracking and potential collapse initiation.

The hybrid system (Configuration C) exhibited values of 0.341 mm/MPa (${\sigma }_x$) and 0.666 mm/MPa (${\sigma }_z$), closely approaching those of the RC system in numerical terms. However, this similarity is misleading. Unlike the RC configuration, which achieves a uniform and ductile stress distribution, the hybrid system suffers from stress amplification at the interfaces between RC domes and masonry walls. The nearly identical Z-direction NDI to that of RC indicates that the hybrid system undergoes comparable global displacements, yet the mechanism is governed by irregular stiffness transitions and concentrated stress fields, making the response less reliable. Overall, the comparative results highlight distinct behavioral patterns among the three configurations. RC systems demonstrate the most favorable seismic performance owing to their ductility, stiff consistency, and capacity for uniform stress redistribution. In contrast, unreinforced masonry systems are prone to brittle failure due to their inability to accommodate deformation under increasing seismic demand. Hybrid systems fall in between, but their discontinuities, incompatible deformation modes, and dynamic irregularities render them vulnerable despite numerically comparable indices. These findings confirm that achieving high seismic performance requires the use of a single, compatible structural material. Hybrid RC–masonry systems should be avoided in new constructions unless rigorous detailing ensures stiffness compatibility and adequate interface reinforcement. For existing structures, retrofitting strategies must address these interface vulnerabilities to prevent premature failure.

Finally, the finite element results were validated by comparing simulated damage zones with the actual earthquake-induced damages observed in the mosque during the 2023 Kahramanmaraş earthquakes, ensuring the practical reliability of the analyses. This validation further reinforces the conclusion that while hybrid systems may appear close to RC systems in performance indices, their structural mechanisms are inherently less robust, often requiring more demanding retrofit measures. Such insights provide practical guidance for seismic design and conservation, emphasizing the prioritization of RC or confined masonry systems over hybrid configurations.

9. Conclusions

This study provided a comparative seismic performance evaluation of three structural configurations—reinforced concrete (RC), unreinforced masonry (URM), and a hybrid RC–masonry system—using static, modal, and response spectrum analyses. A key contribution was the use of the NDI to quantify deformation demand relative to stress capacity in different directions, offering deeper insights into directional vulnerabilities and stiffness compatibility.

The findings revealed that the RC configuration consistently outperformed the others across all analyses. It exhibited controlled deformation, ductile energy dissipation, and uniform stress distribution, supported by relatively high natural frequencies and balanced dynamic response. The URM configuration, while showing lower displacement values, was characterized by high stiffness and brittle failure potential, particularly under shear. The hybrid system, although numerically similar to RC in some performance indices, suffered from modal softening, stress amplification at material interfaces, and stiffness discontinuities—resulting in a less reliable structural response. The results emphasize that hybrid RC–masonry systems should be avoided in new seismic constructions unless strict detailing ensures stiffness compatibility and reliable force transfer mechanisms.

A major conclusion is that material compatibility and continuity are critical to seismic resilience. Hybrid RC–masonry systems introduce discontinuities in both stiffness and deformation behavior, which significantly impair their dynamic performance. Even when global displacement values appear acceptable, the underlying stress mechanisms often reveal concentration zones that may lead to early failure. Therefore, for high seismic performance and structural reliability, systems constructed with a single, compatible material, either RC or confined masonry, should be preferred. Hybrid systems should only be employed when detailed engineering ensures proper integration, stiffness transition, and interface reinforcement. For existing historical structures, retrofit measures such as steel ties, RC jacketing, and grout injection are recommended to mitigate stiffness discontinuities and enhance seismic resilience.