Efficient Lightweight CNN and 2D Visualization for Concrete Crack Detection in Bridges
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Augmentation
2.2. Image Grayscaling and Normalization
3. Establishment of Models
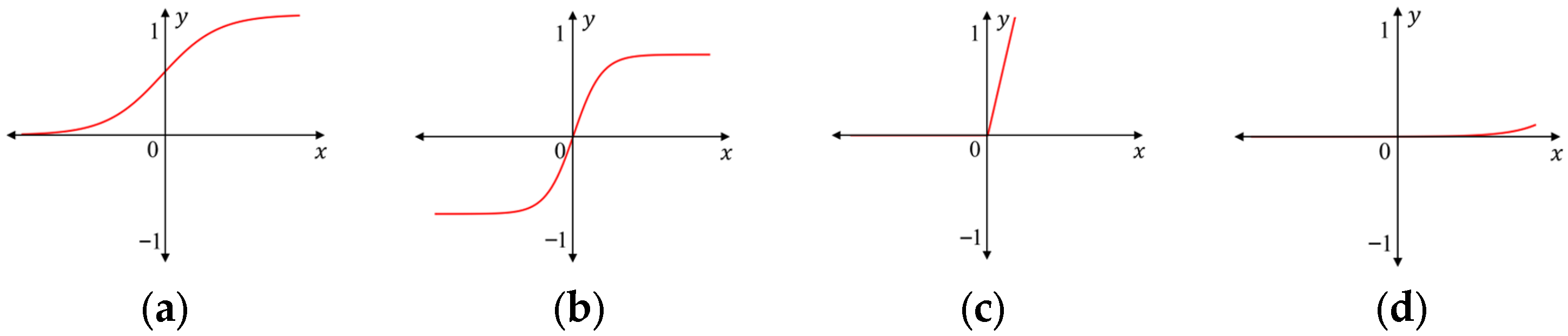
3.1. Architecture of Networks
3.1.1. Global Average Pooling (GAP) Layer
3.1.2. Dropout Method
3.1.3. L2 Regularization
3.1.4. Adding Early Stopping Mechanism
3.2. Optimization of Hyperparameters
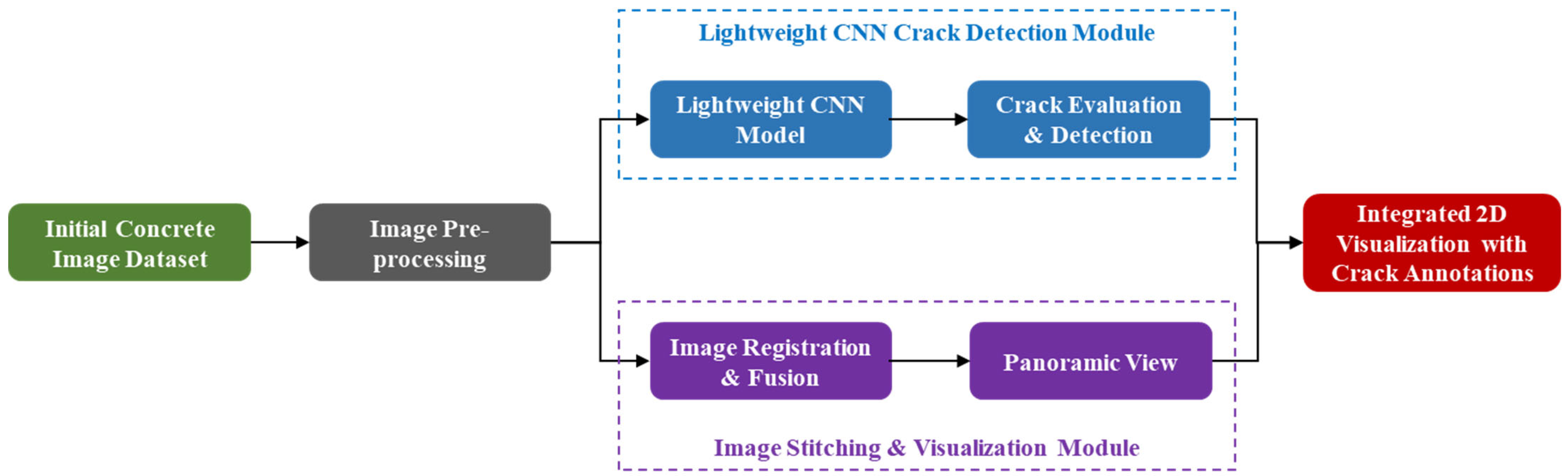
4. Visualization of Detection Results Based on Image Stitching
4.1. Image Preprocessing
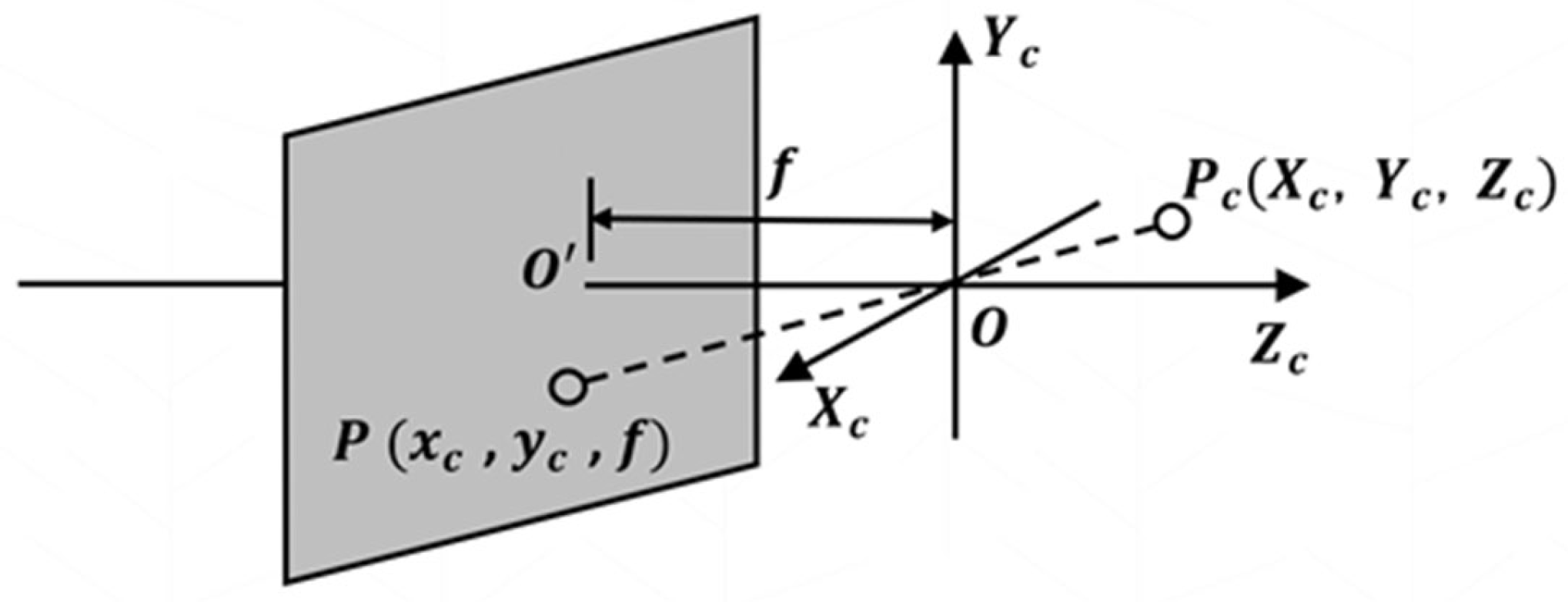
4.1.1. Camera Distortion Correction
4.1.2. Lighting Correction
4.2. Feature Detection
4.3. Image Registration
4.3.1. Direct Registration
4.3.2. Feature-Based Registration
Approximate Nearest Neighbor (ANN) Matching
Random Sample Consensus (RANSAC) Algorithm
5. Test and Results Analysis
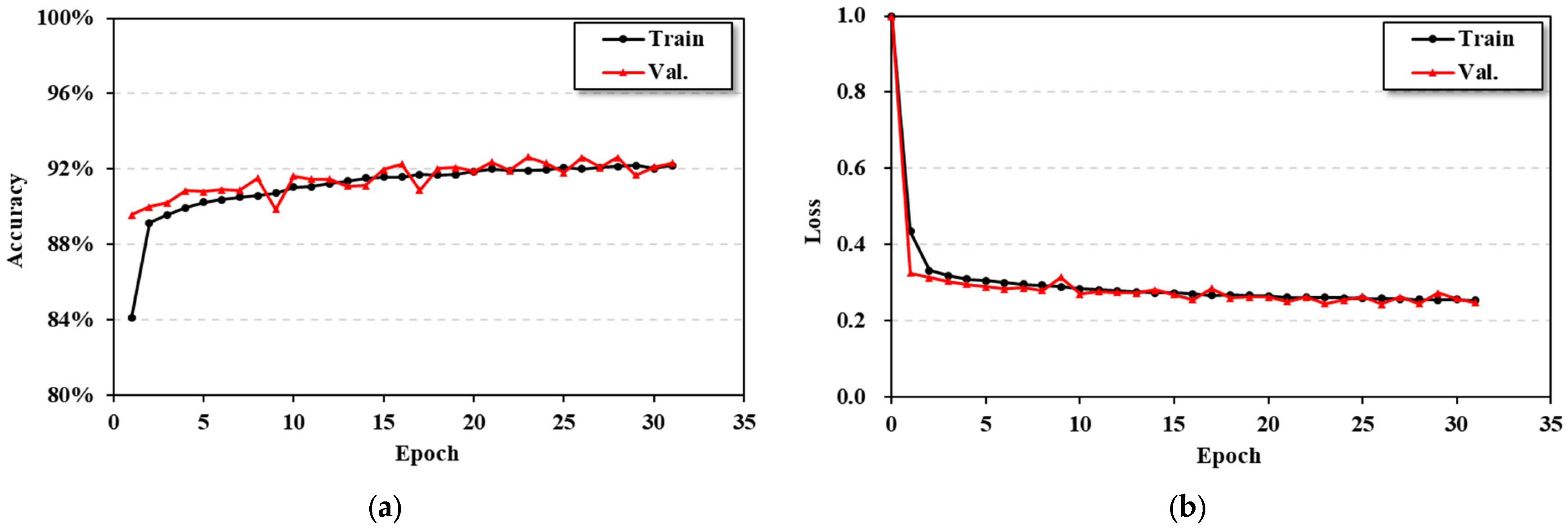
5.1. Model Training
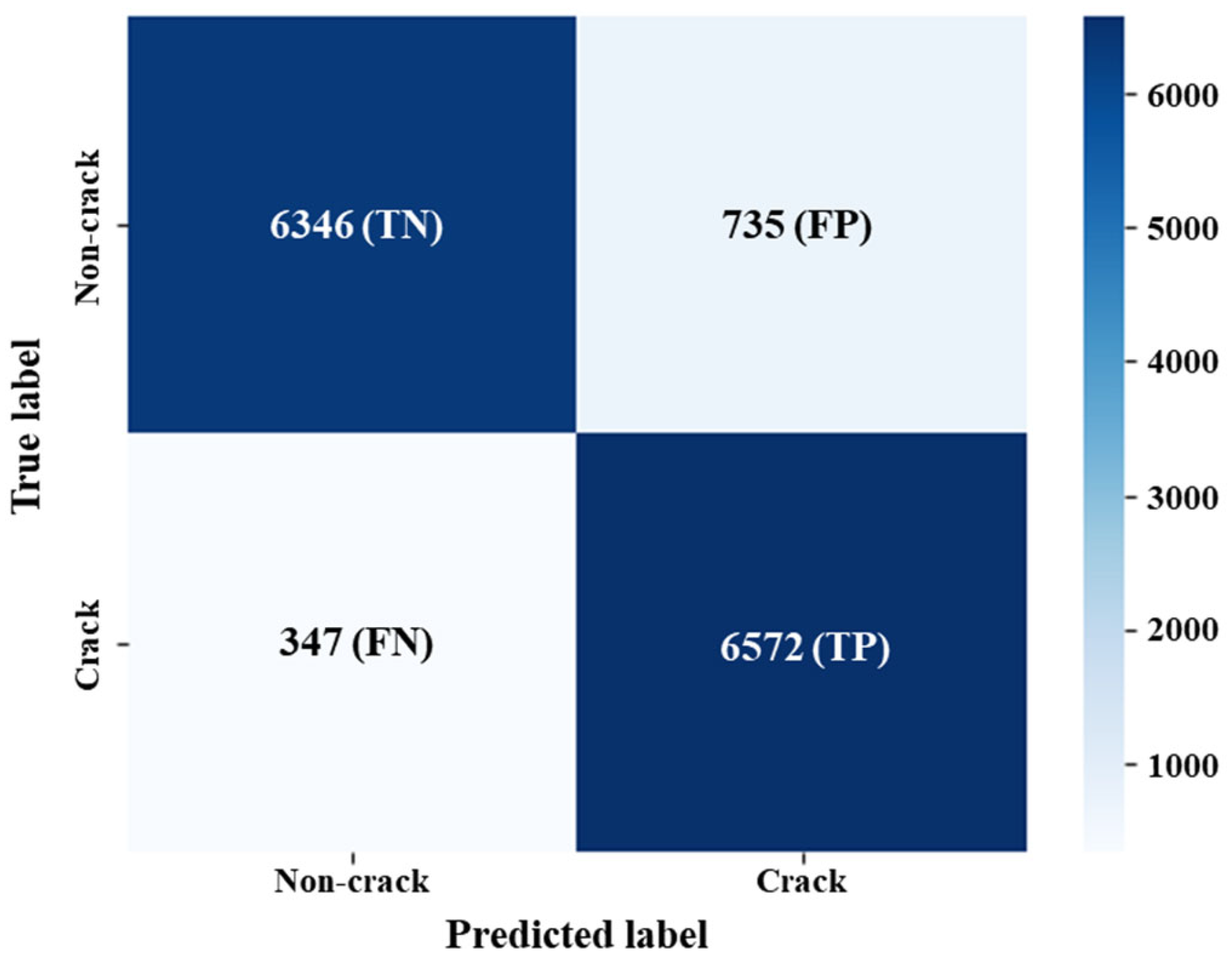
5.2. Index of Performance of Models
- True Negative (TN): The number of samples predicted as negative and are actually negative.
- True Positive (TP): The number of samples predicted as positive and are actually positive.
- False Negative (FN): The number of samples predicted as negative but are actually positive.
- False Positive (FP): The number of samples predicted as positive but are actually negative.
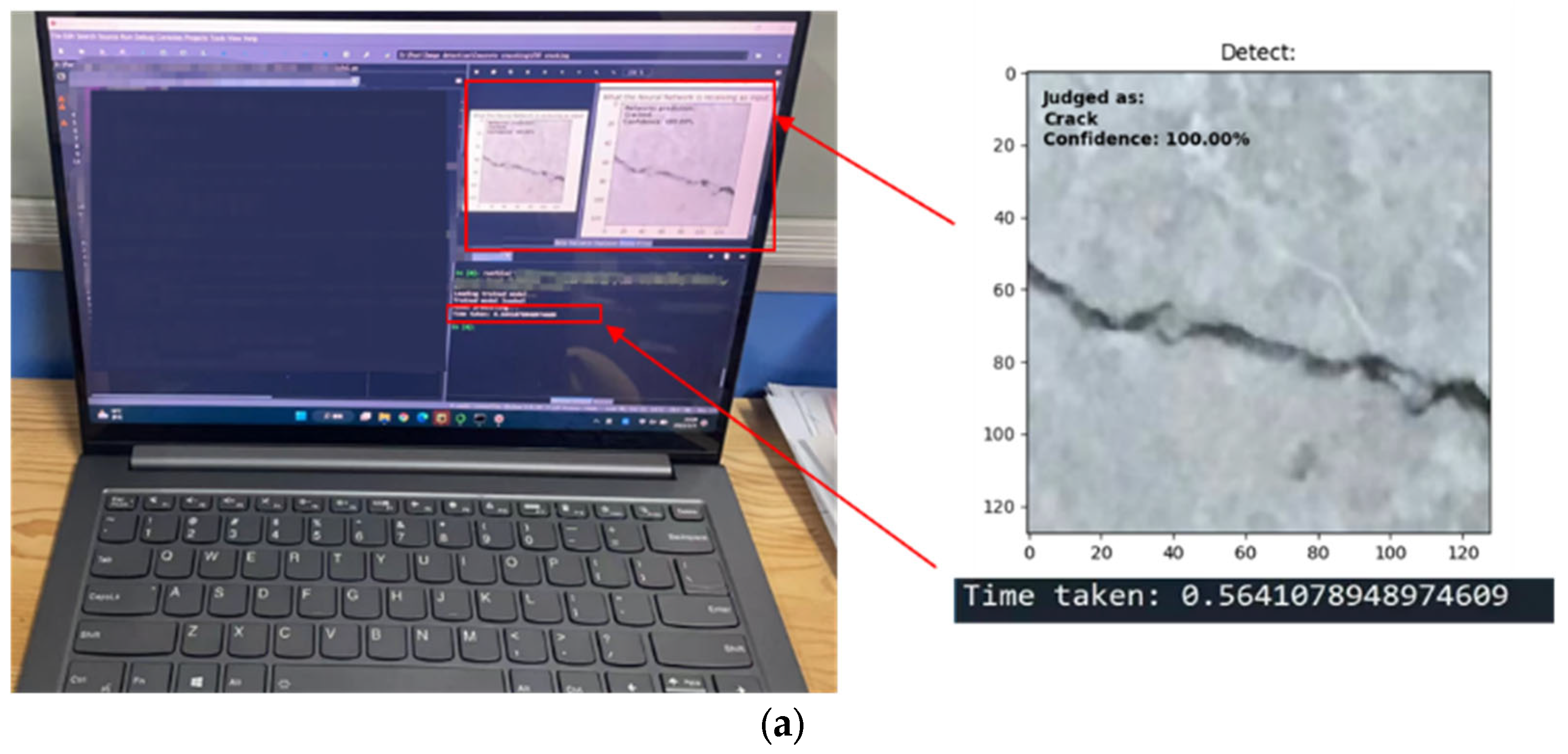
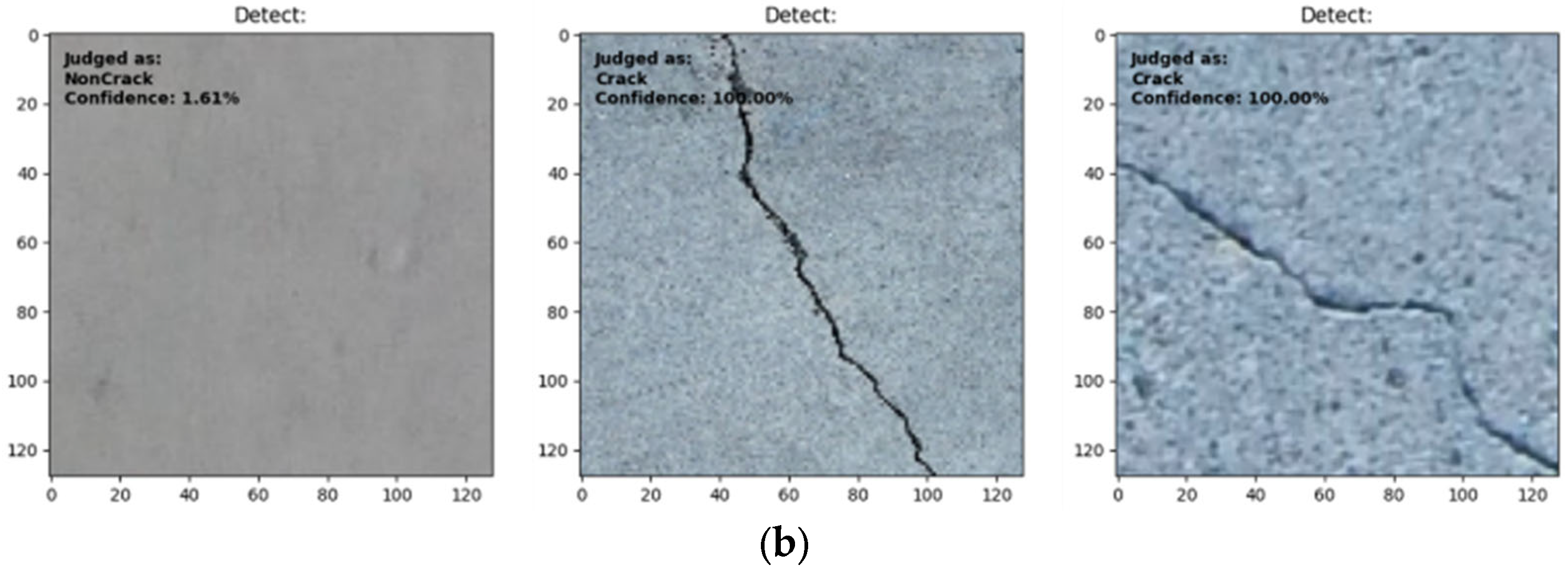
5.3. Model Qualitative Evaluation
5.4. Image Stitching Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Peter, E.; Fanning, P. Vibration Based Condition Monitoring: A Review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar]
- David, M. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Roberts, L. Machine Perception of Three-Dimensional Solids; Massachusetts Institute of Technology: Cambridge, MA, USA, 1965. [Google Scholar]
- Oshima, M.; Shirai, Y. Object Recognition Using Three-dimensional Information. IEEE Trans. Pattern Anal. Mach. Intell. 1983, PAMI-5, 353–361. [Google Scholar] [CrossRef]
- Brown, C.; Karuna, R.; Evans, R. Monitoring of Structures Using the Global Positioning System. Proc. Inst. Civ. Eng. 1999, 134, 97–105. [Google Scholar] [CrossRef]
- Zhang, J.; Wan, C.; Sato, T. Advanced Markov Chain Monte Carlo Approach for Finite Element Calibration under Uncertainty. Comput.-Aided Civ. Infrastruct. Eng. 2013, 28, 522–530. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, S.; Zhou, Y.; Zhang, J. A Quantum-Inspired Genetic Algorithm-Based Optimization Method for Mobile Impact Test Data Integration. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 411–422. [Google Scholar] [CrossRef]
- Zhang, J.; Sato, T.; Lai, S. Support Vector Regression for On-line Health Monitoring of Large-scale Structures. Struct. Saf. 2006, 28, 392–406. [Google Scholar] [CrossRef]
- Liu, Y.F. Multi-Scale Structural Damage Assessment Based on Model Updating and Image Processing; Tsinghua University: Peking, China, 2016. (In Chinese) [Google Scholar]
- Wang, R.; Qi, T.Y. Study on crack characteristics based on machine vision detection. China Civ. Eng. J. 2016, 49, 123–128. (In Chinese) [Google Scholar]
- Han, X.J.; Zhao, Z.C. Structural surface crack detection method based on computer vision technology. J. Build. Struct. 2018, 39, 418–427. (In Chinese) [Google Scholar]
- Fan, Y.; Zhao, Q.; Ni, S.; Rui, T.; Ma, S.; Pang, N. Crack Detection Based on the Mesoscale Geometric Features for Visual Concrete Bridge Inspection. J. Electron. Imaging 2018, 27, 53011. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, J.; Zhu, B. A Research on an Improved UNet-based Concrete Crack Detection Algorithm. Struct. Health Monit. 2020, 20, 1864–1879. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Büyüköztürk, O. Deep learning-based crack damage detection using convolutional neural networks. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Liu, Z.; Yeoh, J.K.W.; Gu, X.; Dong, Q.; Chen, Y.; Wu, W.; Wang, L.; Wang, D. Automatic pixel-level detection of vertical cracks in asphalt pavement based on GPR investigation and improved mask R-CNN. Autom. Constr. 2023, 146, 104689. [Google Scholar] [CrossRef]
- Deng, L.; Chu, H.H.; Shi, P.; Wang, W.; Kong, X. Region-based CNN method with deformable modules for visually classifying concrete cracks. Appl. Sci. 2020, 10, 2528. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X. Thoughts on the Development of Bridge Technology in China. Engineering 2019, 5, 11. [Google Scholar] [CrossRef]
- Mohammadkhorasani, A.; Malek, K.; Mojidra, R.; Li, J.; Bennett, C.; Collins, W.; Moreu, F. Augmented reality-computer vision combination for automatic fatigue crack detection and localization. Comput. Ind. 2023, 149, 103936. [Google Scholar] [CrossRef]
- Ai, D.; Jiang, G.; Lam, S.K.; He, P.; Li, C. Computer vision framework for crack detection of civil infrastructure—A review. Eng. Appl. Artif. Intell. 2023, 117, 105478. [Google Scholar] [CrossRef]
- Sutherland, I.E. The ultimate display. In Proceedings of the IFIP Congress, New York, NY, USA, 24–29 May 1965; Volume 2, pp. 506–508. [Google Scholar]
- Reddy, B.; Chatterji, B. An FFT-based Technique for Translation, Rotation, and Scale-invariant Image Registration. IEEE Trans. Image Process. 1996, 5, 1266–1271. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D. Recognising Panoramas. In Proceedings of the Proceedings Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; pp. 1218–1225. [Google Scholar]
- Liu, Y.; Yao, J.; Liu, K.; Lu, X. Optimal Image Stitching for Concrete Bridge Bottom Surfaces Aided by 3d Structure Lines. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B3, 527–534. [Google Scholar] [CrossRef][Green Version]
- Jiang, T.; Frøseth, G.T.; Rønnquist, A. A robust bridge rivet identification method using deep learning and computer vision. Eng. Struct. 2023, 283, 115809. [Google Scholar] [CrossRef]
- Yang, K.; Ding, Y.; Sun, P.; Jiang, H.; Wang, Z. Computer vision-based crack width identification using F-CNN model and pixel nonlinear calibration. Struct. Infrastruct. Eng. 2023, 19, 978–989. [Google Scholar] [CrossRef]
- Bianchi, E.; Hebdon, M. Visual structural inspection datasets. Autom. Constr. 2022, 139, 104299. [Google Scholar] [CrossRef]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic road crack detection using random structured forests. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, F.; Zhang, Y.D.; Zhu, Y.J. Road crack detection using deep convolutional neural network. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3708–3712. [Google Scholar]
- Eisenbach, M.; Stricker, R.; Seichter, D.; Amende, K.; Debes, K.; Sesselmann, M.; Ebersbach, D.; Stoeckert, U.; Gross, H.-M. How to get pavement distress detection ready for deep learning? A systematic approach. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2039–2047. [Google Scholar]
- Huethwohl, P. Cambridge Bridge Inspection Dataset; University of Cambridge Repository: Cambridge, UK, 2017. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Dorafshan, S.; Thomas, R.J.; Maguire, M. SDNET2018: An annotated image dataset for non-contact concrete crack detection using deep convolutional neural networks. Data Brief 2018, 21, 1664–1668. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Mosalam, K.M. Deep transfer learning for image-based structural damage recognition. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 748–768. [Google Scholar] [CrossRef]
- Li, S.; Zhao, X. Image-based concrete crack detection using convolutional neural network and exhaustive search technique. Adv. Civ. Eng. 2019, 2019, 6520620. [Google Scholar] [CrossRef]
- Hüthwohl, P.; Lu, R.; Brilakis, I. Multi-classifier for reinforced concrete bridge defects. Autom. Constr. 2019, 105, 102824. [Google Scholar] [CrossRef]
- Xu, H.; Su, X.; Xu, H.; Li, H. Autonomous bridge crack detection using deep convolutional neural networks. In Proceedings of the 3rd International Conference on Computer Engineering, Information Science & Application Technology (ICCIA 2019), Chongqing, China, 30–31 May 2019; Atlantis Press: Dordrecht, The Netherlands, 2019; pp. 274–284. [Google Scholar]
- Mundt, M.; Majumder, S.; Murali, S.; Panetsos, P.; Ramesh, V. Meta-learning convolutional neural architectures for multi-target concrete defect classification with the concrete defect bridge image dataset. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11196–11205. [Google Scholar]
- Liu, Y.; Yao, J.; Lu, X.; Xie, R.; Li, L. DeepCrack: A deep hierarchical feature learning architecture for crack segmentation. Neurocomputing 2019, 338, 139–153. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1525–1535. [Google Scholar] [CrossRef]
- Arya, D.; Maeda, H.; Ghosh, S.K.; Toshniwal, D.; Sekimoto, Y. RDD2020: An annotated image dataset for automatic road damage detection using deep learning. Data Brief 2021, 36, 107133. [Google Scholar] [CrossRef]
- Narazaki, Y.; Hoskere, V.; Yoshida, K.; Spencer, B.F.; Fujino, Y. Synthetic environments for vision-based structural condition assessment of Japanese high-speed railway viaducts. Mech. Syst. Signal Process. 2021, 160, 107850. [Google Scholar] [CrossRef]
- Bai, M.; Sezen, H. Detecting cracks and spalling automatically in extreme events by end-to-end deep learning frameworks. In Proceedings of the ISPRS Annals of Photogrammetry and Remote Sensing Spatial Information Science, XXIV ISPRS Congress, International Society for Photogrammetry and Remote Sensing, Nice, France, 5–9 July 2021. [Google Scholar]
- Ye, X.W.; Jin, T.; Li, Z.X.; Ma, S.Y.; Ding, Y.; Ou, Y.H. Structural crack detection from benchmark data sets using pruned fully convolutional networks. J. Struct. Eng. 2021, 147, 04721008. [Google Scholar] [CrossRef]
- Bianchi, E.; Hebdon, M. Labeled Cracks in the Wild (LCW) Dataset; University Libraries, Virginia Tech: Blacksburg, VA, USA, 2021. [Google Scholar]
- Xie, X.; Cai, J.; Wang, H.; Wang, Q.; Xu, J.; Zhou, Y.; Zhou, B. Sparse-sensing and superpixel-based segmentation model for concrete cracks. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 1769–1784. [Google Scholar] [CrossRef]
- Wyszecki, G.; Stiles, W.S. Color Science: Concepts and Methods, Quantitative Data and Formulae; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 1–26 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Kilian, Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Milgram, D.L. Computer methods for creating photomosaics. IEEE Trans. Comput. 1975, 100, 1113–1119. [Google Scholar] [CrossRef]
- Peleg, S. Elimination of seams from photomosaics. Comput. Graph. Image Process. 1981, 16, 90–94. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Yu, B.; Guo, L.; Qian, X.L.; Zhao, T.-Y. A New Adaptive Bilateral Filtering. J. Appl. Sci. 2012, 30, 517–523. [Google Scholar]
- Oliveira, M.; Sappa, A.D.; Santos, V.M.F. Color Correction Using 3D Gaussian Mixture Models. In Proceedings of the International Conference Image Analysis and Recognition, Aveiro, Portugal, 25–27 June 2012; pp. 97–106. [Google Scholar]
- Sun, L.; Tang, C.; Xu, M.; Lei, Z. Non-uniform illumination correction based on multi-scale Retinex in digital image correlation. Appl. Opt. 2021, 60, 5599–5609. [Google Scholar] [CrossRef]
- Li, W.; Kang, C.; Guan, H.; Huang, S.; Zhao, J.; Zhou, X.; Li, J. Deep Learning Correction Algorithm for the Active Optics System. Sensors 2020, 20, 6403. [Google Scholar] [CrossRef]
- Hum, Y.C.; Lai, K.W.; Mohamad Salim, M.I. Multiobjectives bihistogram equalization for image contrast enhancement. Complexity 2014, 20, 22–36. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. Lect. Notes Comput. Sci. 2006, 3951, 404–417. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2564–2571. [Google Scholar]
- Ma, C.; Hu, X.; Xiao, J.; Zhang, G.; Owolabi, T. Homogenized ORB algorithm using dynamic threshold and improved Quadtree. Math. Probl. Eng. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Li, T.; Wang, J.; Yao, K. Subpixel image registration algorithm based on pyramid phase correlation and upsampling. Signal Image Video Process. 2022, 16, 1973–1979. [Google Scholar] [CrossRef]
- Förstner, W.; Gülch, E. A fast operator for detection and precise location of distinct points, corners and centres of circular features. In Proceedings of the ISPRS Intercommission Conference on Fast Processing of Photogrammetric Data, Interlaken, Switzerland, 2–4 June 1987; Volume 6, pp. 281–305. [Google Scholar]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Huber, P.J. Robust statistics. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1248–1251. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]











| Activation Function | Learning Rate | Dropout | L2 Regularization Coefficient |
|---|---|---|---|
| ReLU | 0.001 | 0.3 | 0.001 |
| Compile Software | Python | TensorFlow | Keras | CDUA | CuDNN |
|---|---|---|---|---|---|
| PyCharm | 3.9 | 2.6.0 | 2.6.0 | 11.2.0 | 8.1.0 |
| Operating System | CPU | GPU | Memory |
|---|---|---|---|
| Windows 10 | Intel® Xeon® W-2255 | NVIDIA GeForce RTX 3090 | DDR4 64 GB |
| Accuracy Rate | Recall | F1 Score |
|---|---|---|
| 92.27% | 94.98% | 92.39% |
| Operating System | CPU | GPU | Memory |
|---|---|---|---|
| Windows 11 | AMD R7-4800H | Integrated graphics | DDR4 16 GB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, F.; Zou, X. Efficient Lightweight CNN and 2D Visualization for Concrete Crack Detection in Bridges. Buildings 2025, 15, 3423. https://doi.org/10.3390/buildings15183423
Wang X, Zhang F, Zou X. Efficient Lightweight CNN and 2D Visualization for Concrete Crack Detection in Bridges. Buildings. 2025; 15(18):3423. https://doi.org/10.3390/buildings15183423
Chicago/Turabian StyleWang, Xianqiang, Feng Zhang, and Xingxing Zou. 2025. "Efficient Lightweight CNN and 2D Visualization for Concrete Crack Detection in Bridges" Buildings 15, no. 18: 3423. https://doi.org/10.3390/buildings15183423
APA StyleWang, X., Zhang, F., & Zou, X. (2025). Efficient Lightweight CNN and 2D Visualization for Concrete Crack Detection in Bridges. Buildings, 15(18), 3423. https://doi.org/10.3390/buildings15183423






