Abstract
To address the limitations of traditional models in capturing complex features for concrete strength prediction, this study proposes a hybrid deep learning approach that integrates multiple attention mechanisms with gated recurrent units (GRU). The methodology employs a multi-scale validation framework, conducting three-dimensional validation across three datasets: the Kaggle standard dataset, the lightweight foam concrete dataset, and the self-compacting concrete dataset. Six attention mechanisms (SE attention, dot-product attention, self-attention, etc.) are comprehensively compared to optimise the GRU network structure. A Newton–Raphson-based optimiser (NRBO) enables hyperparameter adaptive tuning. Experimental results show significant improvements over the baseline GRU model: mean R2 increased by 6.99%, while RMSE and MAE decreased by 38.5% and 37.5%, respectively. SHAP interpretability analysis confirms that attention mechanisms effectively capture key parameters like SP and VMA in the self-compacting concrete dataset. Based on the findings, this study recommends using self-attention for datasets smaller than 200 samples and selecting the higher-accuracy model between self-attention and stacked attention mechanisms for larger datasets.
1. Introduction
Concrete, a construction material used extensively worldwide, directly influences the safety, durability, and economic efficiency of building structures. In concrete mix design, three core performance indicators are considered: strength, workability, and durability. Among these, compressive strength, as a key parameter for evaluating the mechanical properties of concrete, has always been a focal point in the engineering community [1]. However, concrete strength is influenced by multiple complex factors, such as raw material proportions, curing conditions, and age, leading to instabilities in prediction results and poor generalisation capabilities in traditional prediction methods that rely heavily on empirical formulas or regression analysis [2,3,4]. Consequently, the establishment of an efficient and precise concrete strength prediction model is of great significance for optimising construction processes and ensuring engineering quality.
In the early stages of research, statistical methods such as linear and multiple nonlinear regressions were predominantly employed. These methods involve the use of either single indicators or a combination of indicators, including cement content and the water–cement ratio. The construction of predictive models was the primary focus of these studies. However, it should be noted that these methods are susceptible to overfitting or underfitting when handling high-dimensional nonlinear data [5,6]. Moreover, such methodologies have a limited capacity to capture complex interactions, such as the synergistic effects between mineral and chemical admixtures [7]. Furthermore, in instances where data are insufficient or distributed unevenly, prediction stability is significantly diminished. To address this issue, researchers have proposed the implementation of machine learning techniques, including support vector machines (SVM) [8], light gradient boosting machines (LGBM) [9], and extreme learning machines (ELM) [10]. In addition, the introduction of deep learning frameworks, such as convolutional neural networks (CNN) and recurrent neural networks (RNN) [11], has further contributed to the advancement of this field. Although deep learning frameworks have significant advantages in data processing, when data is insufficient, single deep learning models still cannot work effectively. The advent of deep learning frameworks has further enhanced the data processing capabilities and ability to capture the nonlinear relationships of predictive models. The extant literature confirms that data-driven methods have significant advantages in predicting concrete strength.
However, when confronted with complex patterns, traditional machine learning methods are unable to fully capture the intricate features that influence concrete compressive strength. The capacity of deep learning models to extract complex features is contingent on an increase in network complexity. However, in instances where the available concrete compressive strength data are limited, a single deep learning model, such as a deep neural network (DNN) [12,13], convolutional neural network (CNN) [14], or long short-term memory (LSTM) network [15], will encounter issues with information deficiency. Therefore, introducing hybrid deep learning models has become key to solving the problems of low data efficiency and improving model performance. Attention mechanisms, a common component of hybrid models, have been introduced and applied in various industries, including wind speed prediction [16], short-term power load prediction [17], and post-earthquake loss prediction [18]. However, research on hybrid deep learning models for predicting concrete strength remains limited.
Therefore, this study proposes a range of attention mechanisms for predicting the compressive strength of concrete. The core principle of the attention mechanism is to enable the model to focus on key information in the input data by dynamically allocating the weights. Mathematically, this is equivalent to a weighted summation of the input features, where the weights are calculated based on the similarity between the query and key vectors and normalised using the softmax function [19]. The introduction of the attention mechanism avoids the uniform processing of all data in traditional models, such as RNN/LSTM, significantly reducing redundant calculations. The transformer model uses self-attention and cross-attention to achieve bilingual word alignment in natural language processing (NLP), significantly improving translation quality [20]. SE improves the classification performance in computer vision (CV) by introducing a channel attention mechanism [21]. This demonstrates that the effective application of the attention mechanism can enhance a model’s data processing, feature extraction, and learning capabilities. However, attention mechanisms exhibit a high degree of diversity, and no study has yet identified the most suitable mechanism for predicting concrete strength. Furthermore, the selection of an appropriate model for different data scenarios requires systematic exploration.
Although deep learning frameworks have significant advantages in data processing, their “black box” characteristics remain a bottleneck for applications in the engineering field. To this end, the Kaggle benchmark dataset [22] was used to validate the fundamental performance, the lightweight foam concrete dataset [7] was employed to simulate small-sample scenarios, and the self-compacting concrete dataset [23] was used to assess the sparse data processing capability. Based on these three datasets and the GRU model, this study presents a novel and systematic comparison of the performance of attention mechanisms, including SE [24], dot-product [25], and self-attention [26], in concrete strength prediction. Moreover, existing studies are deficient in systematic comparisons of the specific applications of attention mechanisms in concrete materials, resulting in limitations in model interpretability and predictive accuracy. Therefore, the proposed fusion GRU-based framework also reveals the differentiated effects of different mechanisms on feature extraction through SHAP analysis. Furthermore, the NRBO algorithm [27] was implemented as a hyperparameter tuning tool for each model, with the objective of ensuring the validity of the comparison. Finally, the SHAP method was adopted to quantitatively analyse the model’s prediction decision process, improving model transparency and reliability, making the concrete strength prediction model not only highly accurate but also providing clear feature influence analysis. The proposed GRU network based on attention mechanisms effectively avoids overfitting and improves prediction accuracy in sparse data and small sample situations, validating its advantages in complex material systems.
2. Data Description and Analysis
To validate the performance and effectiveness of the attention mechanism in concrete strength prediction, this study selected three representative datasets from the academic literature and public platforms. The selection of these datasets was made with the aim of verifying the universality of the model and the robustness of the algorithm in a variety of data, thus providing a multidimensional empirical basis for the combination of the attention mechanism and GRU networks. The datasets under consideration consisted of three typical materials: lightweight foam concrete, self-compacting concrete, and high-performance concrete, corresponding to low-density, high-flowability, and high-strength application scenarios, respectively. Furthermore, the datasets encompass both small-scale (44 cases) and large-scale (1030 cases) datasets, with feature dimensions ranging from four to eleven. This allows for a comprehensive evaluation of the adaptability of the model to tasks of varying complexities.
2.1. Data Statistic
The Kaggle concrete strength dataset [22] was sourced from the open-source platform of the University of California, Irvine Machine Learning Repository and is widely recognised as a benchmark dataset in the field of concrete strength prediction. The input features included eight core parameters: cement, water, fine aggregate, coarse aggregate, fly ash, slag, superplasticiser, and age, with a total of 1030 samples. The data were uniformly distributed and covered a broad range of mixing ratios and curing conditions, as illustrated in Table 1. This dataset was used as the benchmark platform for algorithm comparison in this study, thereby facilitating end-to-end validation from traditional machine learning models to deep learning models and providing a standardised reference for model performance evaluation.

Table 1.
Detailed statistics of the input and output parameters for the Kaggle concrete strength dataset.
The lightweight foam concrete dataset was extracted from the Yaseen team [7], which focused on the strength prediction task of low-density foam concrete. The input features included four key parameters: cement content, foam volume, dry density, and water–cement ratio, with a total of 44 samples, as illustrated in Table 2. The data exhibited significant nonlinear correlations (e.g., foam volume was negatively correlated with strength) and a small sample size, posing challenges to the generalisation ability of the model under extreme density conditions. The present study utilises these distinctive characteristics to validate the merits of attention mechanisms in capturing nonlinear relationships and small-sample learning.

Table 2.
Detailed statistics of the input and output parameters for the lightweight foam concrete dataset.
The dataset pertaining to self-compacting concrete was derived from a neural network prediction study by Asteris et al. [23], which focused on the optimisation of the mix design for high-flowability self-compacting concrete. The input features included 11 component ratios, such as cement, aggregate, water, limestone powder, and fly ash, with 205 samples, as illustrated in Table 3. Some features (e.g., silica fume and rice husk ash) exhibited many zero values, resulting in significant data sparsity and increasing the difficulty of feature extraction for the model. The present study employs the aforementioned dataset to assess the feature selection capability of the attention-GRU network in complex material systems and analyses the impact of sparsity on model interpretability.

Table 3.
Detailed statistics of the input and output parameters for the self-compacting concrete dataset.
2.2. Correlation Measures
Pearson’s correlation coefficient was used to analyse the correlations between the three datasets referenced in the preceding section. A correlation heat map is shown in Figure 1. In this study, an analysis was conducted on the eight input variables of the Kaggle concrete strength dataset to ascertain their linear correlations with concrete compressive strength. The results of this analysis are shown in Figure 1a. The heatmap demonstrates that cement content (Cement) exhibits a significant positive correlation (r = 0.50) with compressive strength, while fly ash (Fly Ash) shows a weak negative correlation (r = −0.29) with strength. Notably, water (Water) and superplasticiser (Superplasticiser) exhibited a strong negative correlation (r = −0.66), indicating an interactive effect between the two in the mix design. It is evident that the majority of the variables exhibit correlation coefficients that are less than 0.3, which is consistent with the optimisation requirements of machine learning models for systems that exhibit weak correlation. However, the presence of strong local correlations (e.g., water and superplasticiser) suggests the necessity of feature engineering to mitigate the multicollinearity effects. The correlation analysis results indicate that, although most variables exhibit weak linear associations with strength, the attention mechanism can still improve the prediction accuracy by capturing local nonlinear relationships. Furthermore, variable pairs that exhibit strong correlations (e.g., water and superplasticiser) necessitate weight adjustments during the feature selection stage to prevent model overfitting.
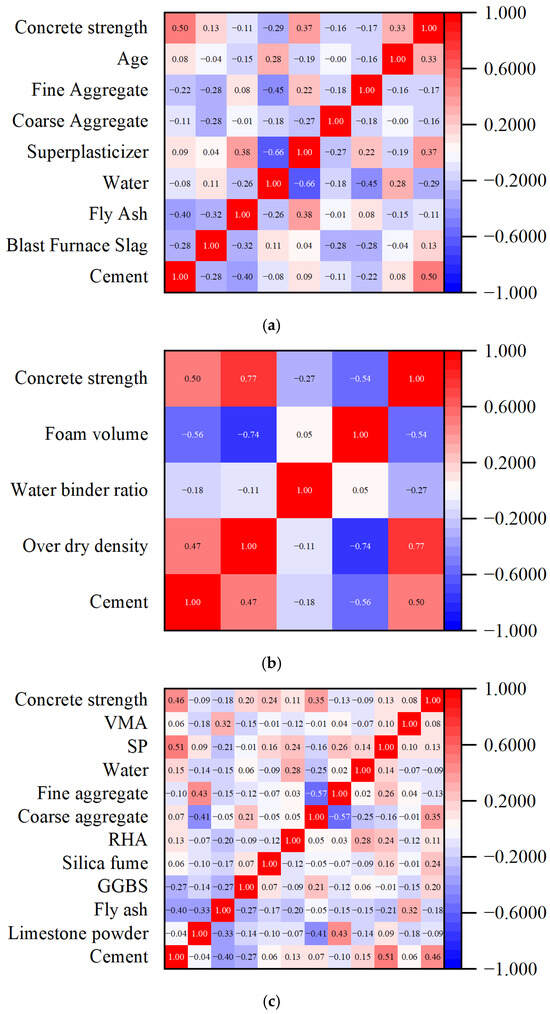
Figure 1.
Correlation matrix of the dataset. (a) Kaggle concrete strength dataset. (b) Self-compacting concrete dataset. (c) Lightweight foam concrete dataset.
The correlation analysis of the lightweight foam concrete dataset is shown in Figure 1b. The cement content demonstrated a significant positive correlation with compressive strength (r = 0.46), whereas the coarse aggregate exhibited a negative correlation with strength (r = −0.57). This confirms the bidirectional influence of aggregate gradation on the mechanical properties. Water (Water) and high-efficiency water-reducing agent (SP) exhibited a strong negative correlation (r = −0.66), suggesting that the design should balance the workability and strength development. The synergistic effect between fly ash (Fly Ash) and limestone powder (Limestone Powder) (r = 0.43) provides a basis for optimising the composite cementitious system. Although most correlation coefficients between variables were below 0.3, the overall data still met the optimisation requirements of machine learning models for low-correlation data. However, strong local correlations (for example, Water-SP) necessitate weight adjustment through the use of feature selection algorithms.
Similarly, the correlation analysis of the self-compacting concrete dataset is shown in Figure 1c. Concrete strength was significantly positively correlated with foam volume (r = 0.77), indicating that foam content is the primary factor influencing the strength of lightweight concrete. The findings indicate a robust negative correlation between dry density and foam volume (r = −0.74), thereby substantiating the dilution effect of foam on material density. The water-to-binder ratio (W/B ratio) demonstrated a correlation below 0.3 with most variables, underscoring the necessity of an attention mechanism to assign dynamic weights and avert information loss. This finding indicates that the prediction of the performance of lightweight concrete necessitates the consideration of both linearly correlated variables (e.g., foam volume) and nonlinear interaction terms (e.g., the W/B ratio). The model’s capacity to accommodate intricate material behaviour can be optimised through the dynamic adjustment of feature weights using the attention mechanism.
3. Methodology
This study proposes a novel integration of SE attention [24], dot-product attention [25], self-attention [26], causal attention [19], and global attention [28] within a single-layer GRU model. These attention mechanisms form a progressive enhancement system where each builds upon the limitations of the previous ones to better capture the complex relationships in concrete strength prediction. The incorporation of attention layers within these models has been demonstrated to significantly enhance the capacity of the model for feature extraction. The integration of these attention mechanisms creates a hierarchical understanding system: SE attention identifies important features, dot-product attention finds relevant patterns, self-attention captures internal relationships, causal attention respects temporal constraints, global attention provides comprehensive context, and transformer coordinates all these processes for optimal concrete strength prediction. To validate the performance enhancement resulting from the incorporation of the attention mechanism within concrete strength prediction models, this study introduced GRU, CNN-GRU, and transformer-GRU as comparison models. In Section 3.1, the attention mechanisms introduced in this study are described in detail.
3.1. Overview of Attention Mechanism
3.1.1. SE Attention
Squeeze-and-excitation attention (SE attention) [24], as shown in Figure 2, involves the implementation of a squeeze operation on feature U to acquire global features at the channel level. This is followed by the execution of an excitation operation on the global features, with the purpose of establishing the relationships between channels and determining the weights of different channels. Finally, these are multiplied by the original feature U to obtain the final features. In concrete strength prediction, SE attention acts as a feature selector that identifies which material properties (cement content, water–cement ratio, aggregate properties) are most relevant for strength prediction at each prediction step. In essence, the SE module performs attention or gating operations in the channel dimension. This mechanism enables the model to concentrate on the most informative channel features while suppressing less significant ones. Another salient point is that the SE module is universal, meaning that it can be embedded into existing network architectures.
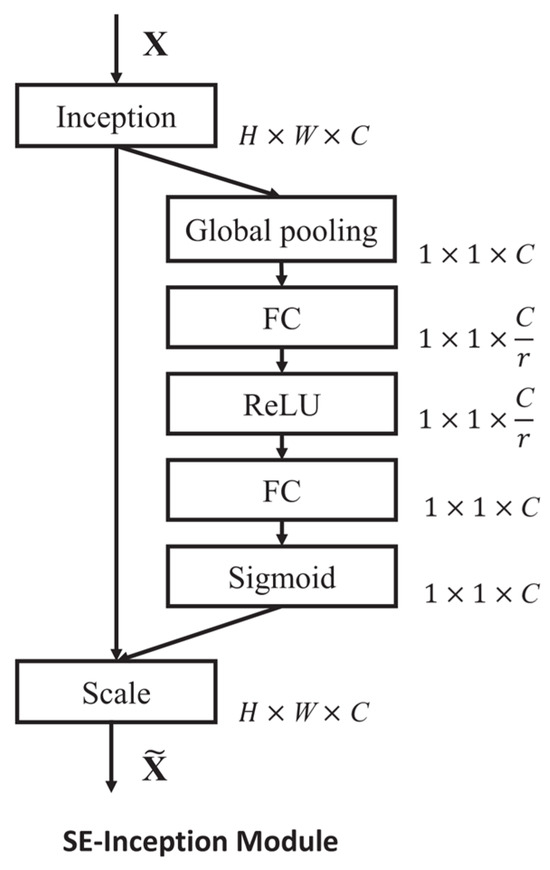
Figure 2.
The schema of the SE Inception module [24].
In the squeeze operation, feature U is compressed using the squeeze operation, which aggregates feature maps across spatial dimensions H × W to generate a channel descriptor, H × W × C → 1 × 1 × C. Simply put, this process compresses all spatial information about concrete mix components into channel-wise summaries, similar to how engineers summarise multiple test results into key performance indicators. As demonstrated above, global spatial information is compressed into the channel descriptors. This enables the utilisation of the channel descriptors by their respective input layers. In this instance, the global average pooling method was employed to achieve the desired outcome. Subsequently, an excitation operation is performed. To reduce the complexity of the model and enhance its generalisation capabilities, a bottleneck structure comprising two fully connected layers was employed. The primary function of the first FC layer is to reduce the dimensionality of the data, with the reduction coefficient r being a hyperparameter. Subsequently, the ReLU activation function was employed. Finally, the FC layer restores the original dimension, and the activation values (sigmoid activation, values 0–1) learned from each channel are multiplied by the original features on U. This excitation process is analogous to an experienced engineer assigning importance weights to different concrete ingredients based on their contribution to final strength. The entire operation can be viewed as learning the weight coefficients of each channel, thereby enabling the model to better distinguish the features of each channel.
3.1.2. Dot-Product Attention
Building upon SE attention’s channel-wise feature selection, dot-product attention introduces a more sophisticated similarity-based weighting system. The attention mechanism is predicated on the degree of focus (importance) attributed to disparate pieces of information through weight allocation. The attention mechanism can be conceptualised as a multi-layer perceptron (MLP) comprising a query matrix (Q), keys (K), and weighted averages. In concrete engineering terms, Q represents the current prediction target (desired strength), K represents available historical data patterns, and V contains the actual strength values corresponding to those patterns. The notion of attention bears resemblance to that of addressing the user’s needs. In the event of an element Q being present in the target, the similarity or correlation between Q and each K is calculated to obtain the weight coefficient of each K corresponding to the value (V). Subsequently, the value of V is weighted and summed to yield the final attention value. Therefore, the attention mechanism can be considered as the weighted sum of the V values of the elements in the source. For concrete strength prediction, this mechanism allows the model to find similar mix designs from historical data and weight their influence based on similarity to the current mix being predicted. In this regard, Q and K are employed to calculate the weight coefficients corresponding to the V. Dot-product attention [25], regarded as the most basic attention mechanism, permits Q, K, and V to span different sequences. The scalar product attention mechanism is initiated through the utilisation of the scalar product to calculate the similarity between quantities:
This equation calculates how similar each historical concrete mix (K) is to the target mix (Q), then uses these similarities as weights to combine the corresponding strength values (V).
To prevent the result of the dot product from becoming too large and causing the gradient to disappear, it is necessary to scale similar calculation results:
In this instance, dk is the feature dimension of K. The scaling factor √dk prevents numerical instability, similar to how engineers use normalised ratios (like water–cement ratio) rather than absolute values to ensure consistent comparisons across different mix scales. Consequently, the similarity is converted into attention weights through the softmax normalisation function:
3.1.3. Self-Attention
While dot-product attention compares current predictions with historical data, self-attention advances this concept by allowing different components within the same concrete mix to influence each other. The dot-product attention mechanism primarily employs matrix multiplication for its computational processes, leveraging GPU acceleration to optimise efficiency. The similarity matrix intuitively reflects the strength of the association between the queries and keys and is interpretable to a certain degree. However, it is important to note that a single calculation may result in the loss of the feature diversity. In concrete terms, a single attention head might focus only on the cement–water relationship while missing important interactions between aggregates and admixtures. To mitigate this issue, a scaling factor is required to prevent the gradients from disappearing. Based on the aforementioned points, a multi-head attention mechanism was developed, with dot-product attention constituting the fundamental unit. Multi-head attention facilitates the parallel learning of features from different subspaces.
In the multi-head attention mechanism, Q, K, and V are divided into h groups, with each group performing independent dot-product attention calculation. Finally, the calculation results were concatenated and underwent a linear transformation. Restricting the input to the same input sequence has been demonstrated to facilitate the concurrent calculation of feature matrices for all positions. This, in turn, has been shown to accelerate the training process. This multi-head attention mechanism, which restricts the inputs Q, K, and V to the same input sequence, is also called the self-attention mechanism [26]. For concrete strength prediction, self-attention captures how cement content influences water demand, how aggregate size affects workability, and how these interdependent relationships collectively determine final strength. The self-attention mechanism does not function as an attention mechanism between the output and input; rather, it is an attention mechanism that occurs between elements within the input or between elements within the output. By capturing complex dependencies through global interactions and multi-head mechanisms, the model can dynamically focus on other positions within the sequence when processing sequences, thereby capturing global dependencies. Compared with dot-product attention, it exhibits a larger receptive field and can acquire more contextual information. The introduction of the self-attention mechanism has demonstrated the ability to overcome the limitations of the sequential processing inherent to RNNs.
3.1.4. Causal Attention
Expanding upon self-attention’s global view, causal attention introduces temporal constraints that are particularly relevant for concrete curing processes. Causal attention [19] builds upon self-attention by introducing a mask matrix to restrict the model to focus only on the current time step and previous content when computing attention at each time step. Causal attention enforces unidirectionality through masking, sacrificing some information utilisation capabilities in exchange for prediction rationality. The direct causal attention masking method involves multiplying the attention weight matrix by a mask matrix. The mask matrix is a triangular matrix with negative infinity above the diagonal, and the masked attention weight matrix is obtained through this process. Subsequently, each element of the masked attention weight matrix is divided by the sum of all elements in its row. Thereafter, the unmasked attention weights are renormalised such that the sum of all attention weights in each row of the masked attention weight matrix equals 1. This mathematical constraint ensures that the model respects the chronological nature of concrete curing, where early-age properties influence later strength development but not vice versa. The calculation principle is as follows:
where M is a mask matrix that sets future positions to negative infinity, ensuring that strength predictions at any curing age only consider information from previous time steps.
3.1.5. Global Attention
While causal attention respects temporal constraints, it may miss important long-range dependencies in concrete behaviour. Global attention addresses this limitation by providing comprehensive feature integration. In contrast, causal attention focuses on information prior to the current position and is suitable for generation tasks. However, it has been demonstrated that this may result in semantic loss due to information truncation. As demonstrated in [28], global attention circumvents this issue and exhibits superior performance in tasks that require a comprehensive understanding (e.g., text classification and reading comprehension). Similarly, concrete strength prediction requires understanding the complete picture of how all mix components, curing conditions, and time factors interact throughout the entire development process. To achieve this, the model must possess the capability to capture global features. Nevertheless, despite the fact that self-attention is global in nature, it cannot effectively capture dependencies between distant elements when dealing with complex patterns. Consequently, global attention was initiated. The utilisation of global attention within the model facilitates access to the entire input sequence during the processing of each position, thereby ensuring the effective capture of dependencies between distant elements.
The calculation of global attention is based on the output latent variable ht of the current decoder and all the latent variables in the encoder, as per the attention model. This results in at. Subsequently, ct is obtained by weighting at and latent variables in the preceding encoders. The ct is then concatenated with ht and subsequently encoded through a layer to obtain the output vector and value. Three possible methodologies can be used to establish a global attention model:
The three methods for calculating at are called dot, general, and concat. The current output is derived by incorporating an attention mechanism, which differs from the previous version. Concurrently, the model has the capacity to flexibly adapt to varying task requirements while maintaining a global perspective by combining dot products and other calculation methods (e.g., additive attention).
3.1.6. Transformer
The transformer architecture, as shown in Figure 3, represents the culmination of attention mechanism evolution, integrating all previous concepts into a unified framework that can handle the complex, multi-faceted nature of concrete strength prediction. The transformer [19] is a sequence modelling architecture based on a self-attention mechanism. Its core structure consists of stacked encoders and decoders which, through a multi-head self-attention mechanism, capture long-range dependencies between arbitrary positions in a sequence, thereby replacing the sequential computation pattern of traditional recurrent neural networks (RNNs). The encoder maps the input sequence to hidden representations, and the decoder combines the encoder output with the generated sequence to perform an autoregressive prediction. Positional encoding preserves the sequence order information, and residual connections and layer normalisation ensure training stability. Multi-head attention enables the model’s multiple parallel attention layers to capture different feature subspaces, thereby improving its expressiveness and generalisation ability. Each attention head can specialise in different aspects: mechanical properties, chemical reactions, physical transformations, and environmental effects, providing comprehensive coverage of all factors influencing concrete strength. Additionally, Transformers lack inherent temporal or sequential awareness; therefore, positional encoding is introduced to explicitly inject sequence position information. Furthermore, fully connected feedforward neural networks were embedded within the encoder and decoder to extract local features.
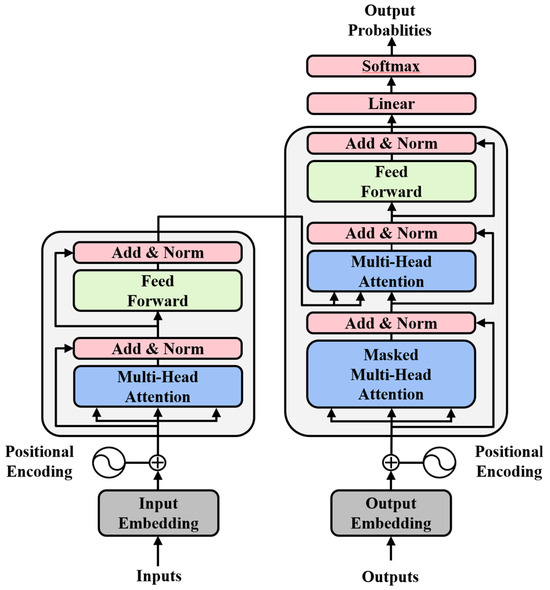
Figure 3.
Transformer model structure diagram [19].
3.2. Attention-Based GRU Network
Building upon the aforementioned overview of attention mechanisms, this section introduces the attention-based gated recurrent unit (GRU) network, a hybrid architecture designed to enhance temporal feature extraction and interpretability in concrete strength prediction. The integration of attention mechanisms with GRU units addresses the limitations of standalone recurrent networks, particularly in capturing long-range dependencies and prioritising critical time steps in sequential datasets.
Gated recurrent units (GRUs) were selected as the foundational recurrent architecture owing to their simplicity and computational efficiency compared with long short-term memory (LSTM) networks. GRUs utilise a single gating mechanism (the update gate) to regulate information flow, thereby reducing parameter complexity while retaining the ability to model long-term dependencies. This makes GRUs less prone to overfitting, especially when the training data are limited, which is a common challenge in materials science datasets. Furthermore, GRUs demonstrate performance comparable to that of LSTMs in sequence modelling tasks, making them a pragmatic choice for concrete strength prediction, where computational resources and data volume may be constrained.
A single-layer GRU network consists of a series of GRU units, each comprising an update gate, reset gate, and candidate hidden state. The hidden state of the GRU is processed further via an attention mechanism, with the aim of emphasising task-relevant objectives. The complete architecture of the attention-GRU network, ordered by data flow, includes a feature input layer, an attention layer/feature extraction layer, a GRU layer, a fully connected layer, and a regression layer. Following the encoding of the raw data within the feature input layer, the attention layer/feature extraction layer extracts latent features from the data before feeding them into the GRU layer. The GRU then captures relationships between features and predicted targets through its gating mechanisms. The fully connected layer integrates outputs from each GRU unit, applying a linear combination to produce the final output. Finally, the regression layer calculates the loss function value, governing the network’s overall updates and iterations.
Below, we provide a detailed integration of the five attention variants, as illustrated in Figure 4. In addition to the GRU model, this study introduced eight other models: SE-GRU, DPA-GRU, SA-GRU, CA-GRU, GA-GRU, CA-SA-GRU, transformer-GRU, and CNN-GRU. The CA-SA-GRU is a causal attention–self-attention stacking model derived from the transformer model.
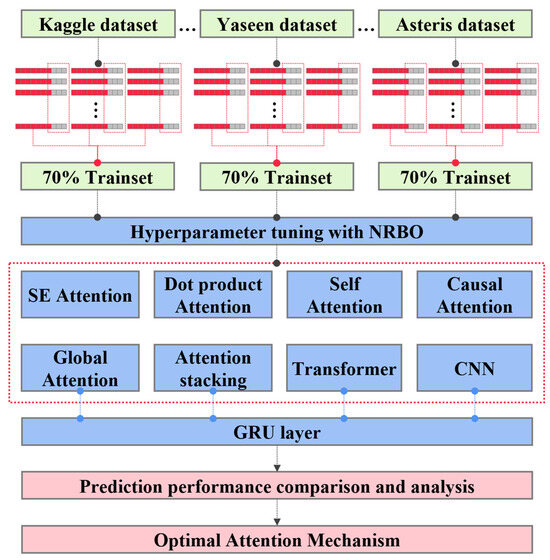
Figure 4.
The overall architecture of training the process and concrete strength prediction.
To prevent overfitting of the model, five-fold cross-validation was used. And the mean value was used as the optimisation function for NRBO, where the mean value was calculated excluding the highest and lowest values to prevent the model from overfitting. The training and test sets were divided in a 7:3 ratio, respectively. The prediction models were trained separately for each dataset. The experiment was conducted on an NVIDIA RTX5080 GPU using the TensorFlow 2.8.0 and CUDA 12.0 frameworks. All computing is run under MATLAB 2024b and Windows 11 24H2.
4. Implementation
4.1. Tuning Hyperparameters Using Newton–Raphson-Based Optimiser (NRBO)
Before training a deep learning prediction model, it is necessary to set hyperparameters, such as the maximum number of epochs, initial learning rate, number of neurones in the hidden layers, and parameters of the attention mechanism. These hyperparameters cannot be obtained through data learning and are set before the model training. They directly affect the convergence speed, complexity, and generalisation ability of the model. When the parameter space is large, manual adjustment can be time-consuming, and it is easy to overlook the optimal combination. In addition, different data types can exhibit varying sensitivities to hyperparameters. To ensure a reasonable number of iterations (epochs) and maintain the model performance, the training time can be reduced. To systematically and automatically improve the performance, adaptability, and efficiency of various prediction models, this study employs the NRBO algorithm [27] for hyperparameter tuning.
The NRBO algorithm optimises problems by simulating the allocation and utilisation of resources in nature. The core concept involves defining the solution space using a set of vectors and searching it using operators such as the natural resource strategy (NRS) and the trap avoidance operator (TAO). During the initialisation stage, the algorithm randomly generates an initial population according to the following rules:
In these formulas, xjn represents the position of the nth individual in the population in the jth dimension, rand represents a random number between 0 and 1, and lb and ub represent the upper and lower bounds of the variable, respectively. dim represents the number of optimisation dimensions. The population matrix for all dimensions is expressed as follows:
The core strategy of the NBRO algorithm is the NRSR search rule. This strategy is used to guide the population search process of the algorithm, facilitating the exploration of the solution space. During the solution search process, the NRSR algorithm retains and explores solutions that exhibit higher fitness. Specifically, it replaces the position of xn − Δx with the position of Xb, where Xb represents a position within its neighbourhood that is better than xn. In addition, it simultaneously retains some inferior solutions to help avoid getting stuck in local optima and promote population diversity. The algorithm replaces the position of xn + Δx with the position of Xw, where Xw represents a position in its neighbourhood that is worse than xn. Here, xn represents the current position, and Δx = rand (1,dim) × abs (Xb − XnIT) represents the perturbation quantity.
During the search process, the algorithm updates the position of the solution according to the following equation:
To prevent the algorithm from becoming trapped in a local optimum, the NBRO algorithm employs a trap avoidance operator strategy. The solution update rule is as follows:
4.2. Model Performance Evaluation Indicators
To evaluate the accuracy of the predictions, this study used three common evaluation indicators: R-squared (R2), root mean square error (RMSE), and mean absolute error (MAE).
The value of R2 ranges from 0 to 1, with a value closer to 1 indicating a superior model fit.
The RMSE is a common measure of the discrepancy between an observed value and a true value. A lower RMSE value indicates a smaller deviation between the observed and true values.
The MAE was calculated as the mean of the absolute value of the difference between the predicted and actual values. Additionally, the MAE was calculated as the mean of the absolute value as a proportion of the actual value. It is desirable for these values to be as small as possible:
4.3. Evaluation of Models with SHapley Additive exPlanations
Although the proposed attention-based GRU model demonstrates significant advantages in predicting concrete strength, the complexity of its network structure results in a ‘black box’ characteristic in the prediction process. To meet the stringent requirements for prediction transparency in the engineering field, this study employs a game theory-based Shapley additive explanation (SHAP) [1,29] method to explain the proposed attention-based GRU model and quantify the contribution of each feature to the prediction results.
SHAP explains the decision-making process of machine learning models by calculating the contribution value (Shapley value) of each feature to the model prediction. Specifically, this method uses the global average prediction value of the training dataset as a baseline without features. It generates feature subset combinations through Monte Carlo sampling and calculates the weighted average of the marginal effects of each feature in all possible feature sequences as follows:
where ϕi is the Shapley value of the ith feature, and S is the subset of features excluding feature i. f(S) denotes the output of the prediction model using feature S as input. denotes the total number of features, which is 15 in this study. The combination coefficients were normalised and weighted using binomial coefficients. By constructing feature contribution plots, this study achieved multidimensional visualisation from global feature importance ranking to local sample interpretation.
5. Results
5.1. Performance Evaluation of Hyperparameter Optimisation
This study focused on predicting the concrete strength. Following Section 4.1, this study performed systematic hyperparameter tuning on six attention mechanism models (SE attention, dot-product-attention, self-attention, etc.) and six benchmark models (GRU, transformer-GRU, and CNN-GRU). The optimisation process used the NRBO algorithm to search for optimal parameter combinations over 15 iterations. Table 4 summarises the optimal values of the key hyperparameters. The learning rate (initial learning rate) and number of hidden layer units (Hidden Units) significantly influence the model’s convergence speed. In self-attention, the number of attention heads (Num Heads) requires a balance between computational complexity and the ability to capture features.

Table 4.
Hyperparameters with optimal values.
Hyperparameter optimisation was used to determine the optimal configuration of each model (see Table 4), providing a reliable benchmark for subsequent feature importance analysis and mechanism explanation. For the GRU-based models, the hidden unit range (64–256) was selected based on the principle that too few units cannot capture the complex nonlinear relationships in concrete mix design, while too many units risk overfitting given the relatively small dataset sizes typical in concrete research. The learning rate range (0.0001–0.01) was determined through gradient analysis, where values below 0.0001 resulted in slow convergence and values above 0.01 caused training instability. The max epochs (50–150) balances computational efficiency with gradient estimation quality, considering that concrete datasets often have fewer samples than typical deep learning applications. For attention mechanisms, the attention head numbers (2 to the power of 7–10) were selected based on the multi-faceted nature of concrete strength prediction, where different heads can focus on mechanical, chemical, physical, and temporal aspects. The attention dimension ranges were constrained to ensure that the total parameter count remains manageable while providing sufficient representational capacity for capturing feature interactions in concrete materials. The experimental results demonstrate that the hybrid model combining NRBO optimisation and the attention mechanism (e.g., CA-SA) offers significant advantages in concrete strength prediction.
5.2. Comparison of Attention’s Performance
Figure 5 shows the three radar charts corresponding to the Kaggle, lightweight foam concrete, and self-compacting concrete datasets. Each group includes the performance of the training (red) and test (blue) sets for the GRU, CNN-GRU, and transformer-GRU models improved with the attention mechanism. The performance of each model on the Kaggle dataset is shown in Figure 5a. The differences in R2, RMSE, and MAE between the training and test sets were small, suggesting that there was no overfitting. The SE-attention-GRU exhibited the best performance among all models, with R2, RMSE, and MAE values of 0.89, 5.97, and 4.41, respectively, in the test set. Meanwhile, the global attention-GRU performed the worst, with R2, RMSE, and MAE reaching only 0.83, 6.81, and 5.38 in the test set, respectively. However, although the R2 and RMSE of transformer-GRU and GRU reached relatively high levels, their MAE showed an abnormal increase in the test set. This indicates that although the transformer-GRU and GRU models can capture the overall features between the participating concrete and concrete strength, their ability to learn local features is relatively weak.
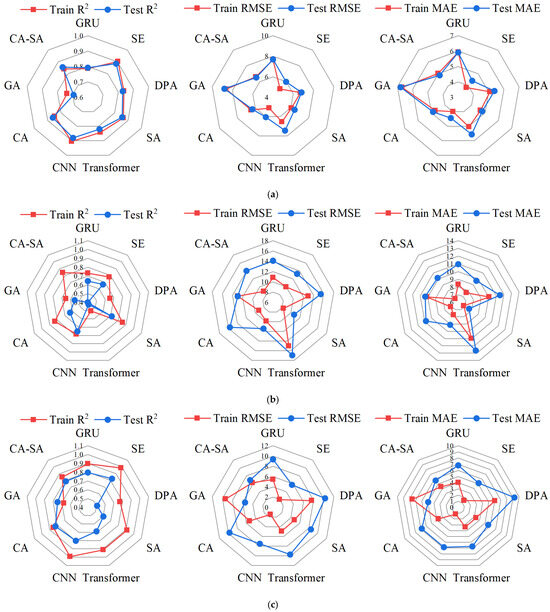
Figure 5.
Radar plot for model comparison based on R2, RMSE, and MAE. (a) Prediction performance in the Kaggle concrete strength dataset. (b) Prediction performance in the lightweight foam concrete dataset. (c) Prediction performance in the self-compacting concrete dataset.
However, the performance of various models fluctuated significantly in the lightweight foam concrete and self-compacting concrete datasets. For example, in the lightweight foam concrete dataset, the R2 value of the transformer-GRU model was only 0.50. Additionally, the differences in R2, RMSE, and MAE between the training and test sets were small, suggesting that all models exhibited some degree of overfitting. Kaggle has a large sample size (n = 1030), which supports the training of complex models. However, lightweight foam data contain nonlinear parameters such as foam volume, and the dataset is very small. Attention mechanisms capture interaction terms and require large amounts of data to function effectively. This resulted in insufficient feature learning and reduced prediction accuracy in the transformer and CA-SA models, which were built using stacked attention mechanisms.
Figure 6c shows that the average number of hidden layer neurones across all models in the Kaggle dataset was 179.3. This is lower than the values of 185.8 and 193 for the lightweight foam and self-compacting concrete datasets, respectively. As the number of neurones decreases, the model complexity also decreases. In the Kaggle dataset, models with lower complexity achieved higher prediction accuracy. Additionally, as illustrated in Figure 1a, the strong correlation between the parameters and concrete strength significantly enhances the training quality of the prediction model. This indicates that the data in the Kaggle dataset were highly consistent. In this case, a larger initial learning rate and maximum epoch helped the prediction model capture the global data features.
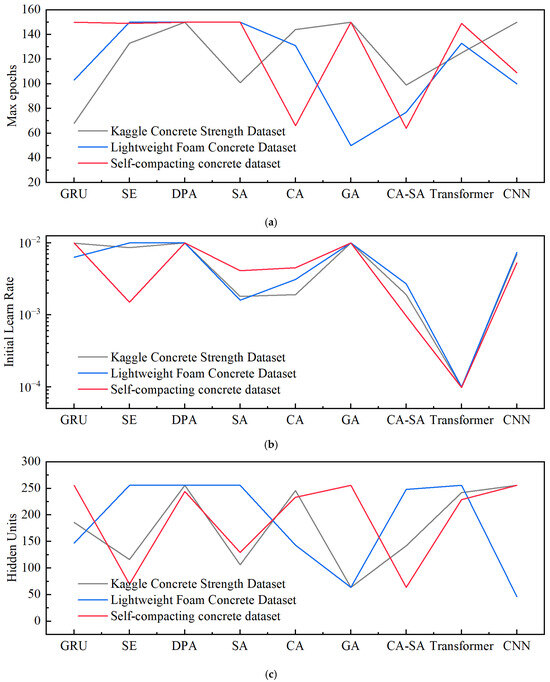
Figure 6.
Comparison of key hyperparameters in all three datasets. (a) Optimal max epoch changes in the three datasets. (b) Optimal initial learn rate changes in the three datasets. (c) Optimal hidden units change in the three datasets.
In the lightweight foam concrete dataset, neither the initial learning rate nor the maximum epoch changed significantly compared with the Kaggle dataset. This may be due to the insufficient complexity of the single-layer attention mechanism and the single-layer GRU hybrid model. In contrast, the more complex transformer-GRU and causal attention self-attention stack-GRU models exhibited overfitting and error anomalies owing to insufficient data. In addition, the average number of hidden layer neurones increased by 3.59% to 193, resulting in a slight increase in the model complexity. This suggests that there are more hidden features in the dataset. However, this dataset contains only five parameters, each of which is highly correlated with the concrete strength, as shown in Figure 1b. Together with the decrease in the prediction model accuracy, this suggests that the dataset has an insufficient sample size or missing auxiliary parameters, which led to the use of a single-layer attention mechanism and a single-layer GRU hybrid model to capture the features of the dataset by increasing the model complexity. This resulted in overfitting issues for all the models. Conversely, reducing the model complexity in the relatively more complex transformer-GRU and causal attention-self-attention stack-GRU models prevented overfitting.
The self-compacting concrete dataset contained a large number of deliberately set missing values. This makes it more difficult for the model to extract the features. However, on average, the model complexity increased by only 7.62% compared to the Kaggle dataset, whereas the GRU model complexity increased by 37.6%. This suggests that introducing an attention mechanism significantly improves the model’s ability to extract features. However, overfitting was particularly severe in this dataset compared to the other two datasets. Additionally, the average maximum epoch decreased by 10%, indicating a faster model convergence. This suggests that, except for the causal attention–self-attention stack–GRU model, the other models prioritised noncritical features as inputs. Therefore, further research on model interpretability is required to investigate changes in key model parameters and overfitting issues in the aforementioned dataset by incorporating the SHAP interpretability theory.
5.3. Relative Feature Importance and Feature Dependence
As outlined in Section 4.3, the SHAP feature contributions were calculated for each model across the three datasets, and the results are presented in Table 5, Table 6 and Table 7, and Figure 7 shows the feature contribution ratios for each model. Because only material usage parameters are involved and material strength parameters are not considered in these datasets, the models inferred that concrete strength is primarily associated with the water–cement ratio and the usage and ratio of coarse and fine aggregates. In the Kaggle dataset, all models identified superplasticiser, coarse aggregate, and fine aggregate as the primary features, which is consistent with the traditional concrete strength design theory. In terms of SHAP contribution percentages for these three parameters, the CNN and SE models, which achieved the highest accuracy, accounted for 70.67% and 76.90% of the total contribution, respectively; the SE model exhibited stronger model-inferred associations, allocating 74.3% of its attention to superplasticiser and fine aggregate. The GA model, which achieved the lowest accuracy, showed the strongest model-inferred association with the fly ash feature, which contradicts the physical principles. This may be because the GA model focuses excessively on global features during training, capturing and retaining correlations between random data points.

Table 5.
SHAP contributions for each parameter in the Kaggle concrete strength dataset.

Table 6.
SHAP contributions for each parameter in the lightweight foam concrete dataset.

Table 7.
SHAP contributions for each parameter in the self-compacting concrete dataset.
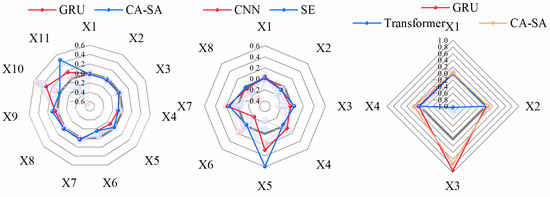
In the lightweight foam concrete dataset, all models used the water-to-binder ratio as the primary feature, which is consistent with the conclusions drawn from the experiments on lightweight concrete. However, the bubble content is negatively correlated with the concrete strength. However, in the CA-SA, CNN, GA, GRU, and SE models, the SHAP contributions for this parameter were all positive, indicating that although these models identified the primary features, they did not establish model-inferred associations that reflect the correct mapping relationship between concrete strength and the parameters. This has also contributed to severe overfitting issues.
In the self-compacting concrete dataset, the models inferred that the main associated features were SP and VMA. These two components are important factors in regulating concrete fluidity and significantly affect concrete strength. However, this dataset contains many deliberately set missing values. This contributed to severe overfitting of the GA, SE and transformer models that showed model-inferred associations primarily with SP and VMA as the main features, while CNN models exhibited overfitting due to limitations in their feature extraction capabilities, despite showing an increase in the contribution of other features. In contrast, CA-SA reduced the data requirements for transformer models while retaining most of their feature extraction and learning capabilities. This model avoided overfitting and achieved extremely high accuracy on this dataset. This suggests that attention mechanisms are necessary for processing complex data.
5.4. Exploitation for the Best Attention Mechanism
In terms of concrete strength prediction, the optimal attention mechanism should be highly accurate and able to generalise well. As a specialised model, the ability to learn global features can improve the prediction accuracy while ensuring the model’s generalisation ability. However, this requires a large dataset. The prediction accuracies of the CA-SA and transformer models mentioned above support this conclusion. However, owing to data limitations, the transformer model was unable to demonstrate its full performance. Although increasing the volume of data can improve the model performance, the diversity of concrete types means that a general concrete strength prediction model would result in a large number of missing values. This increases both the data requirements and computational costs. Therefore, this study recommends, based on experience, prioritising self-attention when the data volume is less than 200 and considering CA-SA models when accuracy is comparable.
6. Discussion
This study has explored the application of hybrid deep learning models, particularly the attention-based gated recurrent units (GRU), to predict the compressive strength of concrete. While the proposed model demonstrated improved performance compared to traditional methods, several limitations are inherent in its design and application. These limitations, as discussed below, provide valuable insights into the scope of future research.
One of the major limitations identified in this study is the reliance on large datasets for training the hybrid models, particularly the transformer-GRU and CA-SA models. While these models performed well with large, well-distributed datasets like the Kaggle concrete strength dataset, their performance significantly deteriorated when tested on smaller datasets such as the lightweight foam concrete dataset. The small sample size in such datasets often leads to poor generalisation and overfitting, which compromises model robustness. This suggests that attention mechanisms require large volumes of data to effectively capture complex features. Thus, when applied to smaller datasets, the models may not fully leverage the data’s potential, leading to suboptimal performance.
To address the challenge posed by small datasets, future work could explore techniques like transfer learning or few-shot learning. These approaches could help improve model performance even with limited data by leveraging pre-trained models or fine-tuning models on smaller, domain-specific datasets. Additionally, synthetic data generation methods, such as data augmentation or generative adversarial networks (GANs), could be employed to increase the size and diversity of training data, ultimately improving model generalisation.
On the other hand, although the use of SHAP (Shapley additive explanations) provided insights into the feature importance for each model, the complexity of the hybrid models with attention mechanisms can still pose challenges to interpretability. The intricate interactions between features captured by the attention mechanisms may make it difficult to intuitively understand the reasoning behind the model’s predictions. This lack of transparency is a significant drawback, especially in engineering applications where model explainability is crucial for trust and adoption.
Thus, the need for explainability in engineering models is crucial, especially for safety-critical applications like concrete strength prediction. Future research could focus on developing more interpretable attention mechanisms that provide clear and actionable insights into how the model arrives at its predictions. Techniques such as attention visualisation, saliency maps, or rule-based models could be integrated into the existing framework to enhance model transparency.
7. Conclusions
This study systematically investigates the effectiveness of attention mechanisms in predicting the strength of concrete and proposes a multi-attention mechanism fusion prediction framework based on GRU networks. Three public concrete strength datasets were analysed: the Kaggle standard dataset, the lightweight foam concrete dataset, and the self-compacting concrete dataset. Six attention variants—SE attention, dot-product attention, self-attention, etc.—were validated for their performance in concrete strength prediction tasks, and the prediction results were evaluated for accuracy and model comparison using R2, RMSE, and MAE. Finally, the model reliability was verified using the SHAP explainability theory. The specific findings were as follows:
- (1)
- The Kaggle concrete strength, lightweight foam concrete, and self-compacting concrete datasets were collected and analysed for correlation. The principles of SE Attention, dot-product attention, self-attention, causal attention, global attention, CA-SA and transformer algorithms were introduced.
- (2)
- By using hybrid attention mechanisms and the NRBO algorithm, the proposed model can overcome the fundamental limitations of traditional prediction methods, achieving substantial improvements of 6.99% in R2, 38.5% in RMSE, and 37.5% in MAE compared to baseline GRU models. These improvements represent a significant advancement in prediction accuracy that directly translates to enhanced reliability in concrete mix design and quality control processes.
- (3)
- In the lightweight foam concrete dataset, the lightweight attention mechanism exhibited significant benefits in scenarios with a small sample size. In the self-compacting concrete dataset, the introduction of the attention mechanism maintained the prediction accuracy and prevented overfitting, even under sparse data conditions. This proves that the channel spatial attention fusion strategy can effectively capture multi-scale features.
- (4)
- The SHAP-based interpretability analysis bridges the critical gap between AI model predictions and engineering understanding. By revealing that parameters like superplasticiser and viscosity-modifying agent dominate strength development in self-compacting concrete, our approach transforms black-box predictions into actionable engineering insights. This interpretability is essential for gaining practitioner confidence and enabling model-guided mix optimisation.
- (5)
- Through a comprehensive evaluation across nine attention mechanisms, this study reveals that attention mechanisms provide adaptive solutions for varying data scenarios: self-attention excels for small datasets (<200 samples), while stacked attention mechanisms optimise performance for larger datasets. This data-driven guidance enables practitioners to select optimal modelling approaches based on their specific application requirements, maximising both prediction accuracy and computational efficiency.
Author Contributions
Conceptualization, Z.J. and N.A.M.N.; Methodology, Z.J.; Software, Z.J.; Resources, N.A.B.; Data curation, N.A.M.N.; Writing—original draft, Z.J.; Writing—review & editing, N.A.M.N.; Visualization, N.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is unavailable due to privacy or ethical restrictions.
Acknowledgments
The authors gratefully acknowledge all support for this research provided by Universiti Putra.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hariri-Ardebili, M.A.; Mahdavi, P.; Pourkamali-Anaraki, F. Benchmarking AutoML Solutions for Concrete Strength Prediction: Reliability, Uncertainty, and Dilemma. Constr. Build. Mater. 2024, 423, 135782. [Google Scholar] [CrossRef]
- Chung, K.L.; Wang, L.; Ghannam, M.; Guan, M.; Luo, J. Prediction of Concrete Compressive Strength Based on Early-Age Effective Conductivity Measurement. J. Build. Eng. 2021, 35, 101998. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Z.; Bian, Z. Prediction on Compressive Strength Concrete Using Modified Pull-off Testing Method (MPTM). Constr. Build. Mater. 2020, 250, 118834. [Google Scholar] [CrossRef]
- Murad, Y. Compressive Strength Prediction for Concrete Modified with Nanomaterials. Case Stud. Constr. Mater. 2021, 15, e00660. [Google Scholar] [CrossRef]
- Yang, J.H.; Chen, T.; Barroso-Luque, L.; Jadidi, Z.; Ceder, G. Approaches for Handling High-Dimensional Cluster Expansions of Ionic Systems. npj Comput. Mater. 2022, 8, 133. [Google Scholar] [CrossRef]
- Chakraborty, S. Bayesian Multiple Response Kernel Regression Model for High Dimensional Data and Its Practical Applications in near Infrared Spectroscopy. Comput. Stat. Data Anal. 2012, 56, 2742–2755. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting Compressive Strength of Lightweight Foamed Concrete Using Extreme Learning Machine Model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Salami, B.A.; Olayiwola, T.; Oyehan, T.A.; Raji, I.A. Data-Driven Model for Ternary-Blend Concrete Compressive Strength Prediction Using Machine Learning Approach. Constr. Build. Mater. 2021, 301, 124152. [Google Scholar] [CrossRef]
- Le Nguyen, K.; Shakouri, M.; Ho, L.S. Investigating the Effectiveness of Hybrid Gradient Boosting Models and Optimization Algorithms for Concrete Strength Prediction. Eng. Appl. Artif. Intell. 2025, 149, 110568. [Google Scholar] [CrossRef]
- Al-Shamiri, A.K.; Kim, J.H.; Yuan, T.-F.; Yoon, Y.S. Modeling the Compressive Strength of High-Strength Concrete: An Extreme Learning Approach. Constr. Build. Mater. 2019, 208, 204–219. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, H.; Guan, T.; Chen, P.; Ren, B.; Guo, Z. Intelligent Prediction of Compressive Strength of Concrete Based on CNN-BiLSTM-MA. Case Stud. Constr. Mater. 2025, 22, e04486. [Google Scholar] [CrossRef]
- Oyebisi, S.; Alomayri, T. Artificial Intelligence-Based Prediction of Strengths of Slag-Ash-Based Geopolymer Concrete Using Deep Neural Networks. Constr. Build. Mater. 2023, 400, 132606. [Google Scholar] [CrossRef]
- Choi, J.-H.; Kim, D.; Ko, M.-S.; Lee, D.-E.; Wi, K.; Lee, H.-S. Compressive Strength Prediction of Ternary-Blended Concrete Using Deep Neural Network with Tuned Hyperparameters. J. Build. Eng. 2023, 75, 107004. [Google Scholar] [CrossRef]
- Lv, Z.; Jiang, A.; Liang, B. Development of Eco-Efficiency Concrete Containing Diatomite and Iron Ore Tailings: Mechanical Properties and Strength Prediction Using Deep Learning. Constr. Build. Mater. 2022, 327, 126930. [Google Scholar] [CrossRef]
- Joshi, D.A.; Menon, R.; Jain, R.K.; Kulkarni, A.V. Deep Learning Based Concrete Compressive Strength Prediction Model with Hybrid Meta-Heuristic Approach. Expert Syst. Appl. 2023, 233, 120925. [Google Scholar] [CrossRef]
- Liu, W.; Bai, Y.; Yue, X.; Wang, R.; Song, Q. A Wind Speed Forcasting Model Based on Rime Optimization Based VMD and Multi-Headed Self-Attention-LSTM. Energy 2024, 294, 130726. [Google Scholar] [CrossRef]
- Wang, Z.; Ying, Y.; Kou, L.; Ke, W.; Wan, J.; Yu, Z.; Liu, H.; Zhang, F. Ultra-Short-Term Offshore Wind Power Prediction Based on PCA-SSA-VMD and BiLSTM. Sensors 2024, 24, 444. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Z.; Zhang, R.; Yao, L.; Wu, G. Attention Mechanism Based Neural Networks for Structural Post-Earthquake Damage State Prediction and Rapid Fragility Analysis. Comput. Struct. 2023, 281, 107038. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems, NIPS 2017, Long Beach, CA, USA, 4–9 December 2017; Neural Information Processing Systems Foundation: Long Beach, CA, USA, 2017; pp. 5999–6009. [Google Scholar]
- Tetko, I.V.; Karpov, P.; Van Deursen, R.; Godin, G. State-of-the-Art Augmented NLP Transformer Models for Direct and Single-Step Retrosynthesis. Nat. Commun. 2020, 11, 5575. [Google Scholar] [CrossRef]
- Swapno, S.M.M.R.; Nobel, S.M.N.; Islam, M.B.; Bhattacharya, P.; Mattar, E.A. ViT-SENet-Tom: Machine Learning-Based Novel Hybrid Squeeze–Excitation Network and Vision Transformer Framework for Tomato Fruits Classification. Neural Comput. Appl. 2025, 37, 6583–6600. [Google Scholar] [CrossRef]
- I-Cheng, Y. Concrete Compressive Strength Data Set. Available online: https://archive.ics.uci.edu/dataset/165/concrete+compressive+strength (accessed on 12 July 2025).
- Asteris, P.G.; Kolovos, K.G. Self-Compacting Concrete Strength Prediction Using Surrogate Models. Neural Comput. Appl. 2019, 31, 409–424. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef]
- Leelaluk, S.; Minematsu, T.; Taniguchi, Y.; Okubo, F.; Yamashita, T.; Shimada, A. Scaled-Dot Product Attention for Early Detection of At-Risk Students. In Proceedings of the 11th IEEE International Conference on Teaching, Assessment and Learning for Engineering, TALE 2022, Online, 4–7 December 2022; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022; pp. 316–322. [Google Scholar]
- Bian, T.; Chen, F.; Xu, L. Self-Attention Based Speaker Recognition Using Cluster-Range Loss. Neurocomputing 2019, 368, 59–68. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-Based Optimizer: A New Population-Based Metaheuristic Algorithm for Continuous Optimization Problems. Eng. Appl. Artif. Intell. 2024, 128, 107532. [Google Scholar] [CrossRef]
- Li, C.; Xuan, S.; Liu, F.; Chang, E.; Wu, H. Global Attention Network for Collaborative Saliency Detection. Int. J. Mach. Learn. Cybern. 2023, 14, 407–417. [Google Scholar] [CrossRef]
- Su, Y.; Wang, X.; Fu, Y.; Zheng, X.; You, G. Research on Surface Settlement Prediction Based on the Combination Prediction Model of S-Shaped Growth Curves. Geosystem Eng. 2018, 21, 236–241. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).