Interpretable ML Model for Predicting Magnification Factors in Open Ground-Storey Columns to Prevent Soft-Storey Collapse

Abstract

Open Ground-Storey (OGS) buildings, widely adopted for functional openness, are highly vulnerable to seismic collapse due to stiffness irregularity at the ground storey (GS). The magnification factor (MF), defined as the amplification applied to GS column design forces, acts as a practical strengthening measure to enhance GS stiffness and thereby mitigate the soft storey failure mechanism. While earlier studies recommended fixed MF values, their lack of adaptability often left stiffness deficiencies unresolved. This study develops a rational framework to quantify and predict the required MF for OGS columns, enabling safe yet functionally efficient design. A comprehensive set of three-dimensional reinforced concrete OGS models was analyzed under seismic loads, covering variations in plan geometry, ground-to-upper-storey height ratio (Hr), and GS infill percentage. Iterative stiffness-based evaluations established the MF demand needed to overcome stiffness deficiencies. To streamline prediction, advanced machine learning (ML) models were applied. Among these, black-box models achieved high predictive accuracy, but Symbolic Regression (SR) offered an interpretable closed-form equation that balances accuracy with transparency, making it suitable for design practice. A sensitivity analysis confirmed the Hr as the most influential parameter, with additional contributions from other variables. Validation on additional OGS configurations confirmed the reliability of the SR model, while seismic response comparisons showed that Modified OGS (MOGS) frames with the proposed MF achieved improved stiffness, reduced lateral displacements, uniform drift distribution, and shorter fundamental periods. The study highlights the novelty of integrating interpretable ML into structural design, providing a codifiable and practical tool for resilient OGS construction.

1. Introduction

1.1. Background and Relevance of OGS Structures

Functionally efficient buildings provide a viable solution to address the increasing demand for urban development, especially in the context of rising population density and limited land resources. These structures are designed to accommodate more occupants while satisfying diverse functional requirements, making them highly desirable. However, architectural modifications aimed at improving space efficiency may sometimes compromise structural safety. Among such structural forms, Open Ground-Storey (OGS) buildings have gained considerable popularity due to their capacity to optimize usable space. The ground storey (GS), typically kept open for vehicle parking, is also frequently adapted for commercial or social purposes, offering multiple benefits to occupants. To achieve such open configurations, masonry infill walls at the GS are commonly omitted. This omission leads to a significant reduction in lateral stiffness at the ground level compared to the upper storeys, making OGS buildings particularly susceptible to seismic damage due to this stiffness irregularity.

Moreover, architectural trends often demand increased GS height for both aesthetic and functional flexibility. However, increasing the storey height further diminishes the lateral stiffness of GS columns, even when modeled as bare frames. The combined absence of infill walls and increased slenderness of columns at the ground level results in reduced stiffness and higher flexibility, significantly amplifying the inter-storey drift under lateral seismic loading. This makes OGS structures highly vulnerable to collapse when subjected to earthquake forces. Various international design codes identify this type of stiffness irregularity, often using criteria based on inter-storey drift and relative stiffness [1]. In the current study, IS 1893:2016 [2] is adopted for identifying soft-storey conditions, which classifies a storey as a soft storey if its stiffness is less than that of the storey directly above.

1.2. Seismic Vulnerability and Design Challenges of OGS Structures

Numerous past investigations have highlighted the vulnerability of OGS buildings, particularly at the ground level, under seismic excitations. These studies consistently report that GS columns are more likely to fail due to excessive lateral deformations and elevated axial force demands [3,4,5,6,7]. Experimental shake table tests further validate that inter-storey drift is disproportionately higher at the GS level than at upper levels [8]. Nonlinear static pushover analyses have also demonstrated the poor seismic performance of reinforced concrete (RC) frames when a soft storey is present. Specifically, structures with a soft storey at the ground level are found to be the most critically deficient in terms of seismic safety [9,10,11]. Columns in these configurations are highly prone to plastic hinge formation, frequently failing to satisfy safety requirements. Hence, careful attention must be paid to the seismic design of OGS buildings.

Since the soft-storey behavior in such buildings is directly attributable to inadequate stiffness at the ground level, storey stiffness emerges as the fundamental parameter governing structural vulnerability. Researchers have proposed various methods to estimate storey stiffness, including models based on lateral mode shapes [12], the distribution of seismic forces at the center of mass of each storey, and the use of unmodified frame models [13]. Additionally, the effective stiffness of RC members under seismic loading has been examined with respect to influencing factors like reinforcement ratio, axial load ratio, the compressive strength of concrete, and the presence of shallow beams [14].

1.3. Strengthening Strategies and Code Provisions of OGS Structures

One of the most widely accepted and practical approaches for countering the soft-storey problem is enhancing the lateral stiffness of the GS through strengthening measures. Extensive studies have investigated this, resulting in significant improvements in seismic resilience. Common strengthening techniques include magnifying OGS column sizes, increasing column count, incorporating diagonal bracings, providing lateral buttresses, and using confinement solutions such as steel jacketing and fiber-reinforced polymer (FRP) sheets [10,15,16,17,18,19,20,21,22,23,24,25]. Moreover, confinement-based retrofit strategies such as RC or steel jacketing and externally bonded FRP wraps, have been shown to improve the seismic performance of under-designed RC frames prone to soft-storey mechanisms. On a plan-wise irregular RC building tested at JRC-ELSA, selective RC jacketing (to relocate strength or stiffness and reduce torsion) combined with FRP wrapping (to raise column ductility) markedly improved global response in nonlinear time-history and pushover assessments. Likewise, comparative analyses on a benchmark RC frame confirmed that FRP or RC-jacketing schemes effectively reduce inter-storey drifts and demand-to-capacity ratios when evaluated alongside other retrofit options [26,27]. In addition, passive vibration control strategies have been studied, including base isolation [28], energy dissipation using compact steel sections combined with shape memory alloys (SMA) for re-centering [29], pin-supported energy dissipation devices [30], and hybrid systems integrating hysteretic dampers with GS column strengthening [31]. Recent studies have systematically explored diverse retrofitting strategies for soft-storey and seismically deficient RC buildings. Conventional approaches such as RC jacketing or FRP wrapping enhance column stiffness and axial capacity, though they may shift weaknesses to higher stories if not carefully designed [32]. Steel bracing, buttresses, and supplemental damping devices improve lateral resistance and energy dissipation but can compromise architectural openness and increase construction complexity. Base isolation systems, as comprehensively reviewed by Ghafar et al. (2025) [33], offer superior performance by decoupling structures from ground motion, significantly reducing inertial forces and safeguarding both structural and non-structural components. However, isolation retrofits are often limited by high cost, technical feasibility, and foundation requirements. However, the application of such techniques often necessitates specialized technical expertise, making them less feasible for standard design practice. Moreover, arbitrary column magnification alone may offer limited improvements and is typically insufficient to fully address the soft-storey vulnerability [3].

1.4. Need for Prediction of Improved Magnification Factor (MF) Demand by OGS Columns

A more practical and engineering-friendly approach is to magnify GS columns by an optimal magnification factor (MF) to enhance stiffness while bypassing the challenges mentioned in previous article, retaining functional efficiency and conventional construction practices. While earlier versions of Indian seismic codes (IS 1893:2002) recommended a fixed MF of 2.5 [34], the revised IS 1893:2016 [2] removed this provision. Other global codes suggest varied values; Eurocode 8 (2003) [35] recommends increasing design forces by a factor of 1.5 to 4.68; Israel’s SI 413 (1995) proposes MFs in the range of 2.1–3 [36], and the Bulgarian code (1987) suggests a value of 3 [37]. While several studies have attempted to recommend suitable MF values, these findings are often confined to specific building geometries and lack general applicability [38]. Also, the performance of predefined MFs, such as those in IS 1893:2002 [34], has been shown to be unsatisfactory in eliminating stiffness deficiencies, especially in buildings exceeding two storeys [20,39]. Compared with the strengthening methods described in Section 1.3, the MF approach proposed in this study provides a simple, stiffness-targeted alternative that preserves functional openness, requires minimal intervention, and can be readily adapted to existing design practices. Thus, MF-based strengthening can serve as a practical complement to traditional retrofitting solutions, especially where space, economy, or construction constraints restrict the adoption of isolation or heavy retrofits.

The MF required for OGS columns can vary widely depending on building geometry, layout, and GS proportions. Yet, deriving an MF that is universally applicable across multiple configurations involves substantial computational effort, often making it impractical for routine design. As a result, engineers may neglect this critical design aspect, inadvertently compromising structural safety. Therefore, a simplified yet reliable method for MF estimation is necessary, particularly one that considers configuration-sensitive variables such as storey height ratios.

Moreover, studies have demonstrated that maintaining a completely open GS is not essential to preserve the functional advantages of OGS buildings. Partial infill with strategically placed masonry walls can improve GS stiffness without impeding usability. This partial infill approach effectively reduces the MF required, contributing to a more economical and efficient design [40]. Ghosh et al. [41] proposed a method to predict MF considering different plan configurations, but did not include the variation in GS height. Since the GS height varies based on functional needs, a taller GS leads to increased flexibility and reduced stiffness. This, combined with the OGS configuration, may significantly exacerbate soft-storey vulnerabilities. Thus, incorporating the GS height ratio into MF prediction is essential for realistic and robust design.

The novelty of this work lies in developing a generalized framework for MF estimation that incorporates configuration-sensitive parameters such as the ground-to-upper-storey height ratio (Hr) and varying percentage of partial GS infill, which were often overlooked in earlier studies. By analyzing a large set of 216 systematically designed OGS models, this study bridges the gap between limited, geometry-specific MF recommendations and the need for a universally applicable, stiffness-based approach.

1.5. Role of Machine Learning and Symbolic Regression in MF Prediction

Considering the above, the present research aims to develop a predictive model for determining the minimum required MF based on geometric parameters of the building, including ground-to-upper-storey height ratio (Hr). These parameters can be readily extracted from architectural drawings. To address the complexity of the underlying relationships among variables, advanced ML techniques, including Ridge and Lasso Regression, Decision Trees, Random Forests, Gradient Boosting, and Neural Networks are employed to predict MF values. These algorithms were selected for their ability to capture intricate, nonlinear patterns in the data and to minimize prediction errors effectively [42]. Model validation is performed using cross-validation techniques to ensure both generalizability and robustness.

While ML methods offer high predictive performance, their “black-box” nature often limits interpretability, which is crucial for engineering design applications. To overcome this limitation, the study incorporates Symbolic Regression (SR), an ML technique that discovers explicit mathematical expressions representing the relationship between inputs and outputs. SR enables the derivation of human-readable, physics-informed equations that offer both accuracy and interpretability [43]. By integrating SR with traditional ML models, this study presents a transparent, simplified empirical equation for MF prediction, which can be directly used in routine design without the need for advanced computational tools.

The derived empirical model is validated against various structural configurations and benchmarked against ML-based predictions. Results demonstrate that the SR-based equation closely aligns with MFs obtained through detailed seismic analyses. Furthermore, comparative structural assessments with and without MF underscore the effectiveness of the proposed approach in mitigating soft-storey effects, reducing seismic vulnerability, and improving the overall performance of OGS buildings.

Unlike previous works that either relied on fixed MF provisions or black-box machine learning models, this study introduces SR to derive a transparent, closed-form predictive equation for MF. This is a key contribution, as it ensures both accuracy and interpretability, enabling its straightforward adoption in routine design practice and potential integration into building codes. The combined use of advanced ML methods for benchmarking and SR for codifiable output represents a novel contribution to the seismic design of OGS structures, directly addressing the soft-storey problem with a practical, engineer-friendly solution.

The significance of this contribution is twofold, firstly, it enhances the seismic safety and resilience of OGS structures by offering a rational method to eliminate stiffness irregularity; and secondly, it advances the state of practice by bridging data-driven ML methods with codifiable, interpretable design tools, thereby providing a foundation for future updates to seismic design codes in seismic regions.

2. Frame Configuration Details Considered in the Study

A total of 216 distinct three-dimensional OGS structural models were developed and analyzed in this study. Each model set consists of three variants: the bare frame model, base OGS model and a modified OGS (MOGS) model with magnified GS columns to improve stiffness. All the models had fixed-base conditions. The structural configurations were defined by varying several geometric parameters: the number of bays in the X-direction (Nx) and Y-direction (Ny), bay widths in both directions X and Y (Wx, Wy), total structural height (H), number of storeys (Nz), the height ratio between the GS and the immediate upper-storey (Hr), and the percentage of infill masonry at the GS level (I). The values adopted for these variables are summarized in

Table 1. Range of structural parameters considered in the study.

Nx	Wx (m)	Ny	Wy (m)	H (m)	Nz	Hr	I
3, 5	3, 5	3, 5	3, 5	9, 10, 11, 15, 16, 17, 21, 22, 23	3, 5, 7	1.00, 1.33, 1.67	0, 16, 33

. The 3D RC OGS models were developed in ETABS v2021 [44] and SAP2000 v24 [45], following IS 1893:2016 and IS 456:2000 [46] provisions, with masonry infill walls idealized through the equivalent diagonal strut method, as recommended in IS 1893:2016. The validity of this approach for OGS buildings is already cited in the manuscript and was further checked here through stiffness-ratio evaluation, drift patterns, and a comparison of fundamental periods with code-based estimates. The primary parametric study employed linear elastic analysis to derive stiffness-driven MF predictions, complemented by nonlinear pushover and time history analyses on a representative model to confirm similar response trends under inelastic demand. Soil–structure interaction (SSI) was not explicitly modeled in the parametric study. As highlighted by Bagheri et al. (2018) [47], SSI mainly amplifies drift demands in soft soils rather than altering intrinsic stiffness ratios, and therefore SSI and detailed infill degradation are considered future extensions of the proposed MF framework.

The selected parameter set was defined in accordance with the geometric and detailing provisions of IS 1893:2016 [2], IS 456:2000 [46], and IS 13920:2016 [48]. Building heights (9–23 m), bay widths (3–5 m), and ground-to-upper-storey height ratios (1.0–1.67) reflect practical design scenarios that comply with IS 456 column slenderness limits. GS infill percentages of 0–33% capture the open and partially infilled cases permitted in practice. To focus on stiffness irregularities, the models were restricted to plan-regular configurations and did not incorporate setbacks or torsional irregularities, which are separately classified in IS 1893 as vertical or plan irregularities. This ensured that the dataset conformed to codified provisions while isolating the effects of the OGS condition.

In this study, stiffness irregularity is defined strictly in accordance with IS 1893:2016 [2] as the condition where the GS stiffness is less than that of the storey above, which arises due to the absence of or reduction in infill walls in the GS (OGS condition). Among the parameters studied, the ground-to-upper-storey height ratio (Hr) and GS infill percentage (I) directly influence this stiffness irregularity. Other geometric parameters (Nx, Ny, Wx, Wy, Nz, H) primarily affect the global flexibility and dynamic response of the building, but were also varied to ensure the dataset spanned a realistic design space. Plan asymmetries and torsional irregularities were not explicitly modeled in this parametric study, consistent with the scope of isolating the stiffness irregular mechanism. Broader irregularities, including torsional and soil–foundation–structure interaction effects [49], are identified as potential extensions for future work.

2.1. Justification for the Selection of Structural Parameters

The height of all storeys above the ground floor was maintained at 3 m. The values chosen for each variable were carefully selected to reflect typical design configurations encountered in real-world RC OGS buildings. The combinations of bay numbers and bay widths (Nx, Ny, Wx, Wy) covered both compact and elongated plan layouts, facilitating an assessment of plan geometry’s influence on lateral stiffness. The variation in total height (H) and number of storeys (Nz) spanned 9 m to 23 m and three to seven storeys, respectively, representing low- to mid-rise buildings commonly used in practice.

The GS-to-upper-storey height ratios (Hr = 1.00, 1.33, 1.67) were incorporated to reflect the effect of increased GS height, a condition often present in buildings designed for commercial or parking functions. Likewise, different infill wall percentages at the GS (I = 0%, 16%, 33%) were included to capture the range of practical infill configurations, as increased infill enhances stiffness at the cost of reducing functional openness. The maximum GS infill considered was 33.33%, beyond which usability as an OGS space becomes impractical [40]. This variation enables assessment of how partial infill can improve lateral stiffness and thereby reduce the required magnification factor. The adopted ranges align with field observations and previous analytical studies on OGS irregularities cited in the introduction section. They therefore represent both typical practice and extreme yet plausible configurations encountered in seismic design and assessment.

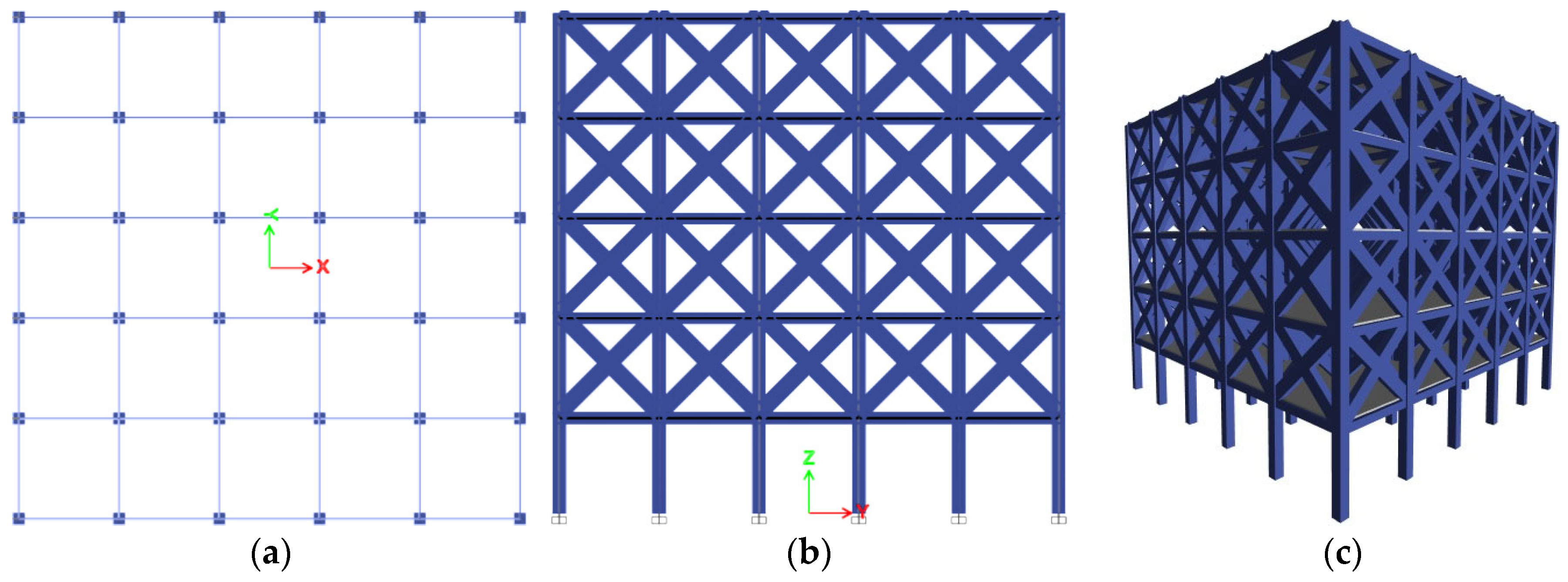
The selected parameter set is intended to comprehensively represent typical OGS designs encountered in engineering practice, ensuring that the conclusions of this study and the derived MF prediction model remain applicable under realistic conditions and in line with national building codes and engineering guidelines. The plan view, elevation, and three-dimensional schematic of a representative OGS model are shown in Figure 1. In this model, all storeys above the GS are infilled with masonry walls, represented using the equivalent diagonal strut technique, while the GS remains open to reflect the soft-storey configuration.

2.2. Material Properties and Load Consideration

The structural design of each model incorporated a range of material properties, load combinations, and seismic parameters as per code-based design practice to ensure realistic performance assessment under seismic conditions. These specifications are listed in

Table 2. Structural design parameters and material properties.

Parameter	Value
Material Strengths
Concrete (fck)	30 N/mm2
Steel (fy)	415 N/mm2
Brick Masonry (fm)	4.1 N/mm2
Unit Weights
Concrete	25 kN/m3
Masonry	21.2 kN/m3
Load Considerations
Dead Loads (DL)	Beams, Columns, Slabs, Wall Loads
Live Load (LL) on Floors	3 kN/m2
Live Load (LL) on Roof	1.5 kN/m2
Wall Load (WL)	Included in DL
Mass Source	1.0 DL + 1.0 WL + 0.25 LL
Seismic Design Parameters
Zone Factor (Z)	0.36
Soil Type	Medium
Damping Ratio	5%
Structural System	Special Moment-Resisting Frame (SMRF)
Response Reduction Factor (R)	5
Importance Factor (If)	1
Structural Dimensions
Beam Sections	250 mm × 300 mm
Column Sections (initial)	350 mm × 350 mm
Slab Thickness	150 mm
Parapet Wall Height	1000 mm

.

Masonry infill walls were simulated using an equivalent diagonal strut model, represented by pin-ended two-node elements. This modeling approach was adopted because it is explicitly recommended in IS 1893 (Part 1): 2016 [2], which specifies the use of the equivalent diagonal strut method for simulating masonry infill contribution in reinforced concrete frames. As a code-prescribed method, it ensures compliance with national standards while providing a balance between accuracy and computational efficiency. More detailed micro-modeling techniques, such as continuum finite element models, can capture localized nonlinear behavior but are computationally prohibitive for large-scale studies involving hundreds of models. Therefore, the equivalent diagonal strut representation offered a code-compatible and computationally feasible method for realistically simulating infill contribution in this study. The effective width of unreinforced masonry (URM) struts, denoted as $w_{\mathrm{d}\mathrm{s}}$, was computed using the empirical formulation provided in IS 1893 (Part 1): 2016 [2], as presented in Equation (1).

$$w_{\mathrm{d}\mathrm{s}}=0.175{\alpha }_h^{-0.4}{L}_{\mathrm{d}\mathrm{s}},$$

(1)

where

$${\alpha }_h=h\left(\sqrt[4]{{\displaystyle \frac{E_{m}t\mathit{sin}2\theta }{4E_f{I}_{c}h}}}\right)$$

In the above, E_m and E_f represent the modules of elasticity of URM infill and RC frame members. I_c is the moment of inertia of the adjoining columns, t is the thickness of the infill walls, θ is the angle of diagonal strut with horizontal, h is the height of the URM infill walls, and L_ds is the length of the diagonal strut. The material parameters for unreinforced masonry were taken from Kaushik et al. (2007) [50], which provides a detailed experimental evaluation of URM behavior.

2.3. Details of Models

A comprehensive parametric study was conducted involving a total of 216 three-dimensional OGS structural models. These models systematically varied across key geometric parameters, including the Nx, Ny, Wx, Wy, Nz, H, Hr, and I. To improve readability and prevent overloading the main body with extensive data, a condensed summary of the models is presented in

Table 3. Summarized table of the 216 model configurations.

Set No.	Hr	I	Nz	Model No.	Model Count
1	1.00	0.00	3	1–8	8
2			5	9–16	8
3			7	17–24	8
4		16.67	3	25–32	8
5			5	31–40	8
6			7	41–48	8
7		33.33	3	49–56	8
8			5	57–64	8
9			7	65–72	8
10	1.33	0.00	3	73–80	8
11			5	81–88	8
12			7	89–96	8
13		16.67	3	97–104	8
14			5	105–112	8
15			7	113–120	8
16		33.33	3	121–128	8
17			5	129–136	8
18			7	137–144	8
19	1.67	0.00	3	145–152	8
20			5	153–160	8
21			7	161–168	8
22		16.67	3	169–176	8
23			5	177–184	8
24			7	185–192	8
25		33.33	3	193–200	8
26			5	201–208	8
27			7	209–216	8

. This summary categorizes the configurations based on Hr, I, and Nz parameters that play a dominant role in influencing the stiffness behavior of the GS. Each configuration is uniquely labeled using a structured identifier in the format IMHr-NxWxNyWyNz, where each embedded variable corresponds to a specific structural attribute. This structured identifier format improves traceability by embedding key geometric and infill parameters directly into the model label, allowing for immediate recognition of the configuration without cross-checking external tables. It also enhances reproducibility by enabling other researchers to reconstruct the model setup unambiguously. Such a coding scheme could be readily adapted for future OGS studies to facilitate cross-study comparisons and data-sharing, provided that the definition of each identifier component is clearly documented. For example, the model designation 16M1-53357 denotes an OGS structure with 16.67% infill at the GS (I = 16.67), a GS-to-upper-storey height ratio Hr = 1.00, five bays in the X direction (Nx = 5), a 3 m bay width (Wx = 3 m), three bays in the Y direction (Ny = 3), a 5 m bay width (Wy = 5 m), and a total of seven storeys (Nz = 7).

This systematic coding format ensures that each model can be easily traced and referenced based on its geometric properties, enabling efficient comparison and organized analysis across varying structural configurations. The complete listing of all 216 model configurations, along with additional geometric identifiers, such as plan dimensions in the X and Y directions (Lx, Ly), ground- and upper-storey heights (H_G, H_G+1), total and infilled panel counts (TPG, IPG), and model designation, is provided in Appendix A (

Table A1. Complete details of all 216 OGS model configurations.

Model No.	Model Designation	Nx	Wx	Ny	Wy	Lx	Ly	α	H	Nz	HG	HG+1	Hr	I	TPG	IPG
1	0M1-33333	3	3	3	3	9	9	1.00	9	3	3	3	1.00	0.00	24	0.00
2	0M1-35353	3	5	3	5	15	15	1.00	9	3	3	3	1.00	0.00	24	0.00
3	0M1-35333	3	5	3	3	15	9	1.67	9	3	3	3	1.00	0.00	24	0.00
4	0M1-53353	5	3	3	5	15	15	1.00	9	3	3	3	1.00	0.00	38	0.00
5	0M1-53333	5	3	3	3	15	9	1.67	9	3	3	3	1.00	0.00	38	0.00
6	0M1-53533	5	3	5	3	15	15	1.00	9	3	3	3	1.00	0.00	60	0.00
7	0M1-55333	5	5	3	3	25	9	2.78	9	3	3	3	1.00	0.00	38	0.00
8	0M1-55553	5	5	5	5	25	25	1.00	9	3	3	3	1.00	0.00	60	0.00
9	0M1-33335	3	3	3	3	9	9	1.00	15	5	3	3	1.00	0.00	24	0.00
10	0M1-35355	3	5	3	5	15	15	1.00	15	5	3	3	1.00	0.00	24	0.00
11	0M1-35335	3	5	3	3	15	9	1.67	15	5	3	3	1.00	0.00	24	0.00
12	0M1-53355	5	3	3	5	15	15	1.00	15	5	3	3	1.00	0.00	38	0.00
13	0M1-53335	5	3	3	3	15	9	1.67	15	5	3	3	1.00	0.00	38	0.00
14	0M1-53535	5	3	5	3	15	15	1.00	15	5	3	3	1.00	0.00	60	0.00
15	0M1-55335	5	5	3	3	25	9	2.78	15	5	3	3	1.00	0.00	38	0.00
16	0M1-55555	5	5	5	5	25	25	1.00	15	5	3	3	1.00	0.00	60	0.00
17	0M1-33337	3	3	3	3	9	9	1.00	21	7	3	3	1.00	0.00	24	0.00
18	0M1-35357	3	5	3	5	15	15	1.00	21	7	3	3	1.00	0.00	24	0.00
19	0M1-35337	3	5	3	3	15	9	1.67	21	7	3	3	1.00	0.00	24	0.00
20	0M1-53357	5	3	3	5	15	15	1.00	21	7	3	3	1.00	0.00	38	0.00
21	0M1-53337	5	3	3	3	15	9	1.67	21	7	3	3	1.00	0.00	38	0.00
22	0M1-53537	5	3	5	3	15	15	1.00	21	7	3	3	1.00	0.00	60	0.00
23	0M1-55337	5	5	3	3	25	9	2.78	21	7	3	3	1.00	0.00	38	0.00
24	0M1-55557	5	5	5	5	25	25	1.00	21	7	3	3	1.00	0.00	60	0.00
25	16M1-33333	3	3	3	3	9	9	1.00	9	3	3	3	1.00	16.67	24	4.00
26	16M1-35353	3	5	3	5	15	15	1.00	9	3	3	3	1.00	16.67	24	4.00
27	16M1-35333	3	5	3	3	15	9	1.67	9	3	3	3	1.00	16.67	24	4.00
28	16M1-53353	5	3	3	5	15	15	1.00	9	3	3	3	1.00	16.67	38	6.33
29	16M1-53333	5	3	3	3	15	9	1.67	9	3	3	3	1.00	16.67	38	6.33
30	16M1-53533	5	3	5	3	15	15	1.00	9	3	3	3	1.00	16.67	60	10.00
31	16M1-55333	5	5	3	3	25	9	2.78	9	3	3	3	1.00	16.67	38	6.33
32	16M1-55553	5	5	5	5	25	25	1.00	9	3	3	3	1.00	16.67	60	10.00
33	16M1-33335	3	3	3	3	9	9	1.00	15	5	3	3	1.00	16.67	24	4.00
34	16M1-35355	3	5	3	5	15	15	1.00	15	5	3	3	1.00	16.67	24	4.00
35	16M1-35335	3	5	3	3	15	9	1.67	15	5	3	3	1.00	16.67	24	4.00
36	16M1-53355	5	3	3	5	15	15	1.00	15	5	3	3	1.00	16.67	38	6.33
37	16M1-53335	5	3	3	3	15	9	1.67	15	5	3	3	1.00	16.67	38	6.33
38	16M1-53535	5	3	5	3	15	15	1.00	15	5	3	3	1.00	16.67	60	10.00
39	16M1-55335	5	5	3	3	25	9	2.78	15	5	3	3	1.00	16.67	38	6.33
40	16M1-55555	5	5	5	5	25	25	1.00	15	5	3	3	1.00	16.67	60	10.00
41	16M1-33337	3	3	3	3	9	9	1.00	21	7	3	3	1.00	16.67	24	4.00
42	16M1-35357	3	5	3	5	15	15	1.00	21	7	3	3	1.00	16.67	24	4.00
43	16M1-35337	3	5	3	3	15	9	1.67	21	7	3	3	1.00	16.67	24	4.00
44	16M1-53357	5	3	3	5	15	15	1.00	21	7	3	3	1.00	16.67	38	6.33
45	16M1-53337	5	3	3	3	15	9	1.67	21	7	3	3	1.00	16.67	38	6.33
46	16M1-53537	5	3	5	3	15	15	1.00	21	7	3	3	1.00	16.67	60	10.00
47	16M1-55337	5	5	3	3	25	9	2.78	21	7	3	3	1.00	16.67	38	6.33
48	16M1-55557	5	5	5	5	25	25	1.00	21	7	3	3	1.00	16.67	60	10.00
49	33M1-33333	3	3	3	3	9	9	1.00	9	3	3	3	1.00	33.33	24	8.00
50	33M1-35353	3	5	3	5	15	15	1.00	9	3	3	3	1.00	33.33	24	8.00
51	33M1-35333	3	5	3	3	15	9	1.67	9	3	3	3	1.00	33.33	24	8.00
52	33M1-53353	5	3	3	5	15	15	1.00	9	3	3	3	1.00	33.33	38	12.67
53	33M1-53337	5	3	3	3	15	9	1.67	9	3	3	3	1.00	33.33	38	12.67
54	33M1-53533	5	3	5	3	15	15	1.00	9	3	3	3	1.00	33.33	60	20.00
55	33M1-55337	5	5	3	3	25	9	2.78	9	3	3	3	1.00	33.33	38	12.67
56	33M1-55553	5	5	5	5	25	25	1.00	9	3	3	3	1.00	33.33	60	20.00
57	33M1-33335	3	3	3	3	9	9	1.00	15	5	3	3	1.00	33.33	24	8.00
58	33M1-35355	3	5	3	5	15	15	1.00	15	5	3	3	1.00	33.33	24	8.00
59	33M1-35335	3	5	3	3	15	9	1.67	15	5	3	3	1.00	33.33	24	8.00
60	33M1-53355	5	3	3	5	15	15	1.00	15	5	3	3	1.00	33.33	38	12.67
61	33M1-53335	5	3	3	3	15	9	1.67	15	5	3	3	1.00	33.33	38	12.67
62	33M1-53535	5	3	5	3	15	15	1.00	15	5	3	3	1.00	33.33	60	20.00
63	33M1-55335	5	5	3	3	25	9	2.78	15	5	3	3	1.00	33.33	38	12.67
64	33M1-55555	5	5	5	5	25	25	1.00	15	5	3	3	1.00	33.33	60	20.00
65	33M1-33337	3	3	3	3	9	9	1.00	21	7	3	3	1.00	33.33	24	8.00
66	33M1-35357	3	5	3	5	15	15	1.00	21	7	3	3	1.00	33.33	24	8.00
67	33M1-35337	3	5	3	3	15	9	1.67	21	7	3	3	1.00	33.33	24	8.00
68	33M1-53357	5	3	3	5	15	15	1.00	21	7	3	3	1.00	33.33	38	12.67
69	33M1-53337	5	3	3	3	15	9	1.67	21	7	3	3	1.00	33.33	38	12.67
70	33M1-53537	5	3	5	3	15	15	1.00	21	7	3	3	1.00	33.33	60	20.00
71	33M1-55337	5	5	3	3	25	9	2.78	21	7	3	3	1.00	33.33	38	12.67
72	33M1-55557	5	5	5	5	25	25	1.00	21	7	3	3	1.00	33.33	60	20.00
73	0M1.33-33333	3	3	3	3	9	9	1.00	10	3	4	3	1.33	0.00	24	0.00
74	0M1.33-35353	3	5	3	5	15	15	1.00	10	3	4	3	1.33	0.00	24	0.00
75	0M1.33-35333	3	5	3	3	15	9	1.67	10	3	4	3	1.33	0.00	24	0.00
76	0M1.33-53353	5	3	3	5	15	15	1.00	10	3	4	3	1.33	0.00	38	0.00
77	0M1.33-53333	5	3	3	3	15	9	1.67	10	3	4	3	1.33	0.00	38	0.00
78	0M1.33-53533	5	3	5	3	15	15	1.00	10	3	4	3	1.33	0.00	60	0.00
79	0M1.33-55333	5	5	3	3	25	9	2.78	10	3	4	3	1.33	0.00	38	0.00
80	0M1.33-55553	5	5	5	5	25	25	1.00	10	3	4	3	1.33	0.00	60	0.00
81	0M1.33-33335	3	3	3	3	9	9	1.00	16	5	4	3	1.33	0.00	24	0.00
82	0M1.33-35355	3	5	3	5	15	15	1.00	16	5	4	3	1.33	0.00	24	0.00
83	0M1.33-35335	3	5	3	3	15	9	1.67	16	5	4	3	1.33	0.00	24	0.00
84	0M1.33-53355	5	3	3	5	15	15	1.00	16	5	4	3	1.33	0.00	38	0.00
85	0M1.33-53335	5	3	3	3	15	9	1.67	16	5	4	3	1.33	0.00	38	0.00
86	0M1.33-53535	5	3	5	3	15	15	1.00	16	5	4	3	1.33	0.00	60	0.00
87	0M1.33-55335	5	3	3	3	15	9	1.67	16	5	4	3	1.33	0.00	38	0.00
88	0M1.33-55555	5	5	5	5	25	25	1.00	16	5	4	3	1.33	0.00	60	0.00
89	0M1.33-33337	3	3	3	3	9	9	1.00	22	7	4	3	1.33	0.00	24	0.00
90	0M1.33-35357	3	5	3	5	15	15	1.00	22	7	4	3	1.33	0.00	24	0.00
91	0M1.33-35337	3	5	3	3	15	9	1.67	22	7	4	3	1.33	0.00	24	0.00
92	0M1.33-53357	5	3	3	5	15	15	1.00	22	7	4	3	1.33	0.00	38	0.00
93	0M1.33-53337	5	3	3	3	15	9	1.67	22	7	4	3	1.33	0.00	38	0.00
94	0M1.33-53537	5	3	5	3	15	15	1.00	22	7	4	3	1.33	0.00	60	0.00
95	0M1.33-55337	5	5	3	3	25	9	2.78	22	7	4	3	1.33	0.00	38	0.00
96	0M1.33-55557	5	5	5	5	25	25	1.00	22	7	4	3	1.33	0.00	60	0.00
97	16M1.33-33333	3	3	3	3	9	9	1.00	10	3	4	3	1.33	16.67	24	4.00
98	16M1.33-35353	3	5	3	5	15	15	1.00	10	3	4	3	1.33	16.67	24	4.00
99	16M1.33-35333	3	5	3	3	15	9	1.67	10	3	4	3	1.33	16.67	24	4.00
100	16M1.33-53353	5	3	3	5	15	15	1.00	10	3	4	3	1.33	16.67	38	6.33
101	16M1.33-53333	5	3	3	3	15	9	1.67	10	3	4	3	1.33	16.67	38	6.33
102	16M1.33-53533	5	3	5	3	15	15	1.00	10	3	4	3	1.33	16.67	60	10.00
103	16M1.33-55333	5	5	3	3	25	9	2.78	10	3	4	3	1.33	16.67	38	6.33
104	16M1.33-55553	5	5	5	5	25	25	1.00	10	3	4	3	1.33	16.67	60	10.00
105	16M1.33-33335	3	3	3	3	9	9	1.00	16	5	4	3	1.33	16.67	24	4.00
106	16M1.33-35355	3	5	3	5	15	15	1.00	16	5	4	3	1.33	16.67	24	4.00
107	16M1.33-35335	3	5	3	3	15	9	1.67	16	5	4	3	1.33	16.67	24	4.00
108	16M1.33-53355	5	3	3	5	15	15	1.00	16	5	4	3	1.33	16.67	38	6.33
109	16M1.33-53335	5	3	3	3	15	9	1.67	16	5	4	3	1.33	16.67	38	6.33
110	16M1.33-53535	5	3	5	3	15	15	1.00	16	5	4	3	1.33	16.67	60	10.00
111	16M1.33-55335	5	5	3	3	25	9	2.78	16	5	4	3	1.33	16.67	38	6.33
112	16M1.33-55555	5	5	5	5	25	25	1.00	16	5	4	3	1.33	16.67	60	10.00
113	16M1.33-33337	3	3	3	3	9	9	1.00	22	7	4	3	1.33	16.67	24	4.00
114	16M1.33-35357	3	5	3	5	15	15	1.00	22	7	4	3	1.33	16.67	24	4.00
115	16M1.33-35337	3	5	3	3	15	9	1.67	22	7	4	3	1.33	16.67	24	4.00
116	16M1.33-53357	5	3	3	5	15	15	1.00	22	7	4	3	1.33	16.67	38	6.33
117	16M1.33-53337	5	3	3	3	15	9	1.67	22	7	4	3	1.33	16.67	38	6.33
118	16M1.33-53537	5	3	5	3	15	15	1.00	22	7	4	3	1.33	16.67	60	10.00
119	16M1.33-55337	5	5	3	3	25	9	2.78	22	7	4	3	1.33	16.67	38	6.33
120	16M1.33-55557	5	5	5	5	25	25	1.00	22	7	4	3	1.33	16.67	60	10.00
121	33M1.33-33333	3	3	3	3	9	9	1.00	10	3	4	3	1.33	33.33	24	8.00
122	33M1.33-35353	3	5	3	5	15	15	1.00	10	3	4	3	1.33	33.33	24	8.00
123	33M1.33-35333	3	5	3	3	15	9	1.67	10	3	4	3	1.33	33.33	24	8.00
124	33M1.33-53353	5	3	3	5	15	15	1.00	10	3	4	3	1.33	33.33	38	12.67
125	33M1.33-53333	5	3	3	3	15	9	1.67	10	3	4	3	1.33	33.33	38	12.67
126	33M1.33-53533	5	3	5	3	15	15	1.00	10	3	4	3	1.33	33.33	60	20.00
127	33M1.33-55333	5	5	3	3	25	9	2.78	10	3	4	3	1.33	33.33	38	12.67
128	33M1.33-55553	5	5	5	5	25	25	1.00	10	3	4	3	1.33	33.33	60	20.00
129	33M1.33-33335	3	3	3	3	9	9	1.00	16	5	4	3	1.33	33.33	24	8.00
130	33M1.33-35355	3	5	3	5	15	15	1.00	16	5	4	3	1.33	33.33	24	8.00
131	33M1.33-35335	3	5	3	3	15	9	1.67	16	5	4	3	1.33	33.33	24	8.00
132	33M1.33-53355	5	3	3	5	15	15	1.00	16	5	4	3	1.33	33.33	38	12.67
133	33M1.33-53335	5	3	3	3	15	9	1.67	16	5	4	3	1.33	33.33	38	12.67
134	33M1.33-53535	5	3	5	3	15	15	1.00	16	5	4	3	1.33	33.33	60	20.00
135	33M1.33-55335	5	5	3	3	25	9	2.78	16	5	4	3	1.33	33.33	38	12.67
136	33M1.33-55555	5	5	5	5	25	25	1.00	16	5	4	3	1.33	33.33	60	20.00
137	33M1.33-33337	3	3	3	3	9	9	1.00	22	7	4	3	1.33	33.33	24	8.00
138	33M1.33-35357	3	5	3	5	15	15	1.00	22	7	4	3	1.33	33.33	24	8.00
139	33M1.33-35337	3	5	3	3	15	9	1.67	22	7	4	3	1.33	33.33	24	8.00
140	33M1.33-53357	5	3	3	5	15	15	1.00	22	7	4	3	1.33	33.33	38	12.67
141	33M1.33-53337	5	3	3	3	15	9	1.67	22	7	4	3	1.33	33.33	38	12.67
142	33M1.33-53537	5	3	5	3	15	15	1.00	22	7	4	3	1.33	33.33	60	20.00
143	33M1.33-55337	5	5	3	3	25	9	2.78	22	7	4	3	1.33	33.33	38	12.67
144	33M1.33-55557	5	5	5	5	25	25	1.00	22	7	4	3	1.33	33.33	60	20.00
145	0M1.67-33333	3	3	3	3	9	9	1.00	11	3	5	3	1.67	0.00	24	0.00
146	0M1.67-35353	3	5	3	5	15	15	1.00	11	3	5	3	1.67	0.00	24	0.00
147	0M1.67-35333	3	5	3	3	15	9	1.67	11	3	5	3	1.67	0.00	24	0.00
148	0M1.67-53353	5	3	3	5	15	15	1.00	11	3	5	3	1.67	0.00	38	0.00
149	0M1.67-53333	5	3	3	3	15	9	1.67	11	3	5	3	1.67	0.00	38	0.00
150	0M1.67-53533	5	3	5	3	15	15	1.00	11	3	5	3	1.67	0.00	60	0.00
151	0M1.67-55333	5	5	3	3	25	9	2.78	11	3	5	3	1.67	0.00	38	0.00
152	0M1.67-55553	5	5	5	5	25	25	1.00	11	3	5	3	1.67	0.00	60	0.00
153	0M1.67-33335	3	3	3	3	9	9	1.00	17	5	5	3	1.67	0.00	24	0.00
154	0M1.67-35355	3	5	3	5	15	15	1.00	17	5	5	3	1.67	0.00	24	0.00
155	0M1.67-35335	3	5	3	3	15	9	1.67	17	5	5	3	1.67	0.00	24	0.00
156	0M1.67-53355	5	3	3	5	15	15	1.00	17	5	5	3	1.67	0.00	38	0.00
157	0M1.67-53335	5	3	3	3	15	9	1.67	17	5	5	3	1.67	0.00	38	0.00
158	0M1.67-53535	5	3	5	3	15	15	1.00	17	5	5	3	1.67	0.00	60	0.00
159	0M1.67-55335	5	5	3	3	25	9	2.78	17	5	5	3	1.67	0.00	38	0.00
160	0M1.67-55555	5	5	5	5	25	25	1.00	17	5	5	3	1.67	0.00	60	0.00
161	0M1.67-33337	3	3	3	3	9	9	1.00	23	7	5	3	1.67	0.00	24	0.00
162	0M1.67-35357	3	5	3	5	15	15	1.00	23	7	5	3	1.67	0.00	24	0.00
163	0M1.67-35337	3	5	3	3	15	9	1.67	23	7	5	3	1.67	0.00	24	0.00
164	0M1.67-53357	5	3	3	5	15	15	1.00	23	7	5	3	1.67	0.00	38	0.00
165	0M1.67-53337	5	3	3	3	15	9	1.67	23	7	5	3	1.67	0.00	38	0.00
166	0M1.67-53537	5	3	5	3	15	15	1.00	23	7	5	3	1.67	0.00	60	0.00
167	0M1.67-55337	5	5	3	3	25	9	2.78	23	7	5	3	1.67	0.00	38	0.00
168	0M1.67-55557	5	5	5	5	25	25	1.00	23	7	5	3	1.67	0.00	60	0.00
169	16M1.67-33333	3	3	3	3	9	9	1.00	11	3	5	3	1.67	16.67	24	4.00
170	16M1.67-35353	3	5	3	5	15	15	1.00	11	3	5	3	1.67	16.67	24	4.00
171	16M1.67-35333	3	5	3	3	15	9	1.67	11	3	5	3	1.67	16.67	24	4.00
172	16M1.67-53353	5	3	3	5	15	15	1.00	11	3	5	3	1.67	16.67	38	6.33
173	16M1.67-53333	5	3	3	3	15	9	1.67	11	3	5	3	1.67	16.67	38	6.33
174	16M1.67-53533	5	3	5	3	15	15	1.00	11	3	5	3	1.67	16.67	60	10.00
175	16M1.67-55333	5	5	3	3	25	9	2.78	11	3	5	3	1.67	16.67	38	6.33
176	16M1.67-55553	5	5	5	5	25	25	1.00	11	3	5	3	1.67	16.67	60	10.00
177	16M1.67-33335	3	3	3	3	9	9	1.00	17	5	5	3	1.67	16.67	24	4.00
178	16M1.67-35355	3	5	3	5	15	15	1.00	17	5	5	3	1.67	16.67	24	4.00
179	16M1.67-35335	3	5	3	3	15	9	1.67	17	5	5	3	1.67	16.67	24	4.00
180	16M1.67-53355	5	3	3	5	15	15	1.00	17	5	5	3	1.67	16.67	38	6.33
181	16M1.67-53335	5	3	3	3	15	9	1.67	17	5	5	3	1.67	16.67	38	6.33
182	16M1.67-53535	5	3	5	3	15	15	1.00	17	5	5	3	1.67	16.67	60	10.00
183	16M1.67-55335	5	5	3	3	25	9	2.78	17	5	5	3	1.67	16.67	38	6.33
184	16M1.67-55555	5	5	5	5	25	25	1.00	17	5	5	3	1.67	16.67	60	10.00
185	16M1.67-33337	3	3	3	3	9	9	1.00	23	7	5	3	1.67	16.67	24	4.00
186	16M1.67-35357	3	5	3	5	15	15	1.00	23	7	5	3	1.67	16.67	24	4.00
187	16M1.67-35337	3	5	3	3	15	9	1.67	23	7	5	3	1.67	16.67	24	4.00
188	16M1.67-53357	5	3	3	5	15	15	1.00	23	7	5	3	1.67	16.67	38	6.33
189	16M1.67-53337	5	3	3	3	15	9	1.67	23	7	5	3	1.67	16.67	38	6.33
190	16M1.67-53537	5	3	5	3	15	15	1.00	23	7	5	3	1.67	16.67	60	10.00
191	16M1.67-55337	5	5	3	3	25	9	2.78	23	7	5	3	1.67	16.67	38	6.33
192	16M1.67-55557	5	5	5	5	25	25	1.00	23	7	5	3	1.67	16.67	60	10.00
193	33M1.67-33333	3	3	3	3	9	9	1.00	11	3	5	3	1.67	33.33	24	8.00
194	33M1.67-35353	3	5	3	5	15	15	1.00	11	3	5	3	1.67	33.33	24	8.00
195	33M1.67-35333	3	5	3	3	15	9	1.67	11	3	5	3	1.67	33.33	24	8.00
196	33M1.67-53353	5	3	3	5	15	15	1.00	11	3	5	3	1.67	33.33	38	12.67
197	33M1.67-53333	5	3	3	3	15	9	1.67	11	3	5	3	1.67	33.33	38	12.67
198	33M1.67-53533	5	3	5	3	15	15	1.00	11	3	5	3	1.67	33.33	60	20.00
199	33M1.67-55333	5	5	3	3	25	9	2.78	11	3	5	3	1.67	33.33	38	12.67
200	33M1.67-55553	5	5	5	5	25	25	1.00	11	3	5	3	1.67	33.33	60	20.00
201	33M1.67-33335	3	3	3	3	9	9	1.00	17	5	5	3	1.67	33.33	24	8.00
202	33M1.67-35355	3	5	3	5	15	15	1.00	17	5	5	3	1.67	33.33	24	8.00
203	33M1.67-35335	3	5	3	3	15	9	1.67	17	5	5	3	1.67	33.33	24	8.00
204	33M1.67-53355	5	3	3	5	15	15	1.00	17	5	5	3	1.67	33.33	38	12.67
205	33M1.67-53335	5	3	3	3	15	9	1.67	17	5	5	3	1.67	33.33	38	12.67
206	33M1.67-53535	5	3	5	3	15	15	1.00	17	5	5	3	1.67	33.33	60	20.00
207	33M1.67-55335	5	5	3	3	25	9	2.78	17	5	5	3	1.67	33.33	38	12.67
208	33M1.67-55555	5	5	5	5	25	25	1.00	17	5	5	3	1.67	33.33	60	20.00
209	33M1.67-33337	3	3	3	3	9	9	1.00	23	7	5	3	1.67	33.33	24	8.00
210	33M1.67-35357	3	5	3	5	15	15	1.00	23	7	5	3	1.67	33.33	24	8.00
211	33M1.67-35337	3	5	3	3	15	9	1.67	23	7	5	3	1.67	33.33	24	8.00
212	33M1.67-53357	5	3	3	5	15	15	1.00	23	7	5	3	1.67	33.33	38	12.67
213	33M1.67-53337	5	3	3	3	15	9	1.67	23	7	5	3	1.67	33.33	38	12.67
214	33M1.67-53537	5	3	5	3	15	15	1.00	23	7	5	3	1.67	33.33	60	20.00
215	33M1.67-55337	5	5	3	3	25	9	2.78	23	7	5	3	1.67	33.33	38	12.67
216	33M1.67-55557	5	5	5	5	25	25	1.00	23	7	5	3	1.67	33.33	60	20.00

). This approach maintains clarity in the main manuscript while ensuring full technical transparency and accessibility for detailed reference by readers and reviewers.

2.4. Analysis Procedure of the Structural Models Considered in the Present Study

A comprehensive three-dimensional structural response evaluation was performed of all the models presented in Table A1 of Appendix A, using ETABS 2021, employing both the Equivalent Static Force Method (ESFM) and the Response Spectrum Method (RSM). Since mode shapes obtained through RSM are typically normalized, the RSM base shear outputs were appropriately scaled to match those from ESFM, in accordance with the guidelines specified in IS 1893:2016 [2]. For the ESFM, multiple load combinations were considered; however, the combinations 1.5 (DL ± ELx ± 0.3 ELy) and 1.5 (DL ± ELy ± 0.3 ELx) were found to be the most influential in governing the response.

In addition to the linear static and dynamic analyses, nonlinear seismic evaluations were also conducted for representative models to complement and validate the elastic results. The nonlinear static (pushover) analysis was performed using SAP2000 v24, following the provisions of ATC-40 [51] and ASCE 41-13 [52], to capture the evaluate structural capacity and identify the performance point. Furthermore, nonlinear time history analyses were carried out using ground-motion records (Kobe and El Centro earthquakes) that were scaled to the design spectrum. These analyses provided additional insights into inelastic displacement demands, inter-storey drift concentration at the GS, and the effectiveness of the proposed MF in reducing nonlinear deformation.

3. Determination of Required MF by OGS Columns

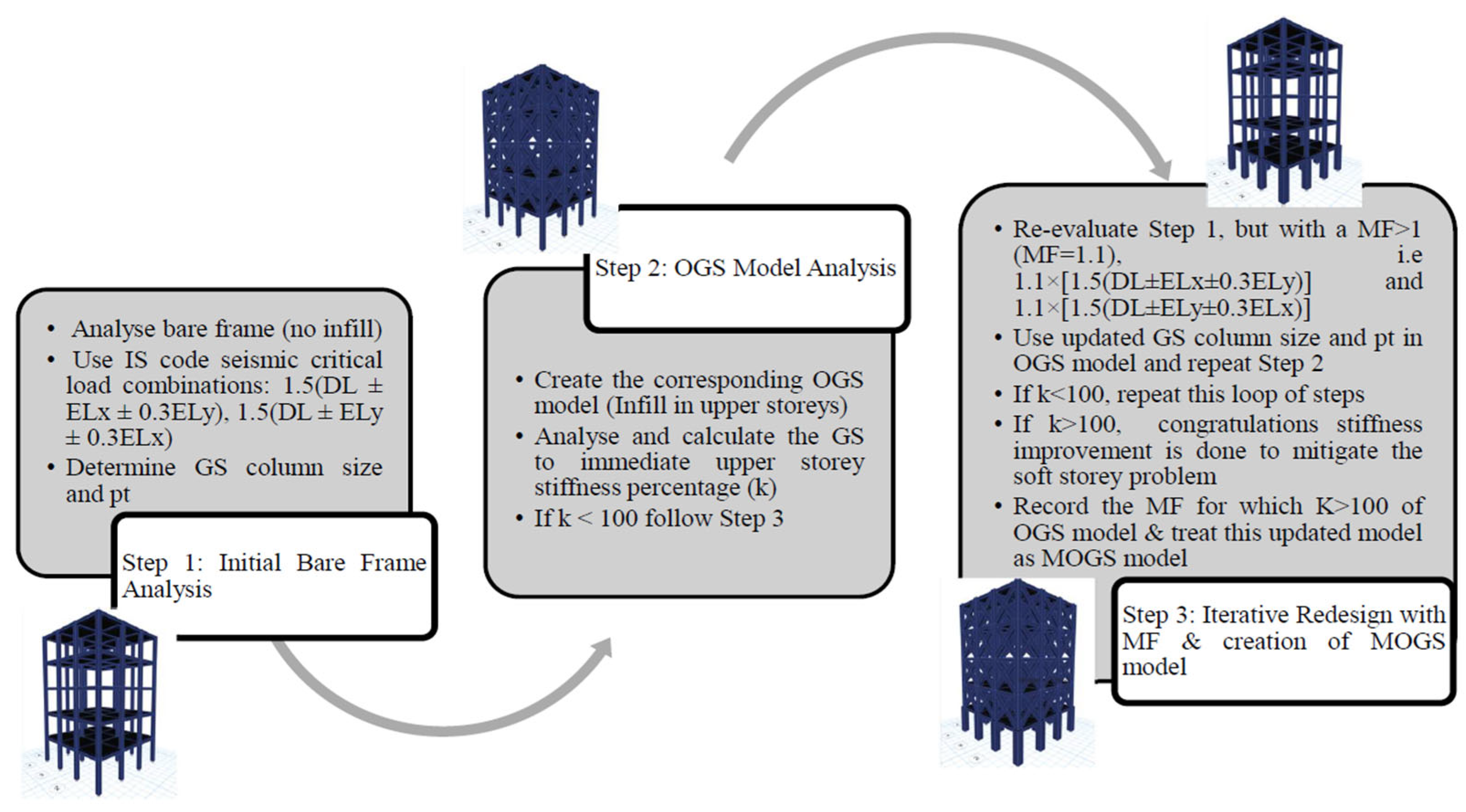
Several seismic design codes recommend applying an appropriate MF to the GS columns of OGS buildings in order to achieve a stiffness level at the GS that is at least equal to the storey immediately above. This ensures that the stiffness ratio between the GS and the upper-storey is not less than 1.0, which is essential for effectively mitigating the soft-storey condition. The procedure for determining this required MF follows the approach proposed by Ghosh et al. [41] and involves two main stages.

• Step 1: Initial Bare Frame Analysis without Infill Stiffness

A bare frame model, matching the geometric configuration of the OGS structure, is analyzed under the governing seismic load combinations, as detailed in the IS code provisions. In this stage, infill wall stiffness is excluded from the analysis. Among the various combinations, the critical ones found to induce the most significant effects are 1.5 (DL ± ELx ± 0.3 Ely) and 1.5 (DL ± ELy ± 0.3 ELx).

From this analysis, the required cross-sectional dimensions and reinforcement percentages (p_t) for the GS columns are determined. These column properties are then used in a corresponding OGS model where infill stiffness is now considered. The stiffness ratio between the GS and the storey immediately above is then computed based on the OGS model.

• Step 2: Iterative Redesign with Applied MF

Next, the bare frame model is re-evaluated by amplifying the governing load combinations using a trial MF value greater than 1. For instance, with an initial MF of 1.1, the modified combinations become 1.1 × [1.5 (DL ± ELx ± 0.3 ELy)] and 1.1 × [1.5 (DL ± ELy ± 0.3 ELx)]. Based on these amplified load cases, the GS columns are redesigned, resulting in updated cross-sectional areas and reinforcement requirements. These newly designed, magnified GS columns are incorporated into the OGS model and the GS stiffness ratio is recalculated. The process is repeated iteratively by increasing the MF in successive trials until the GS stiffness exceeds that of the storey above (i.e., stiffness ratio > 1.0). When this condition is met, the structure is reclassified as a Modified OGS (MOGS) model.

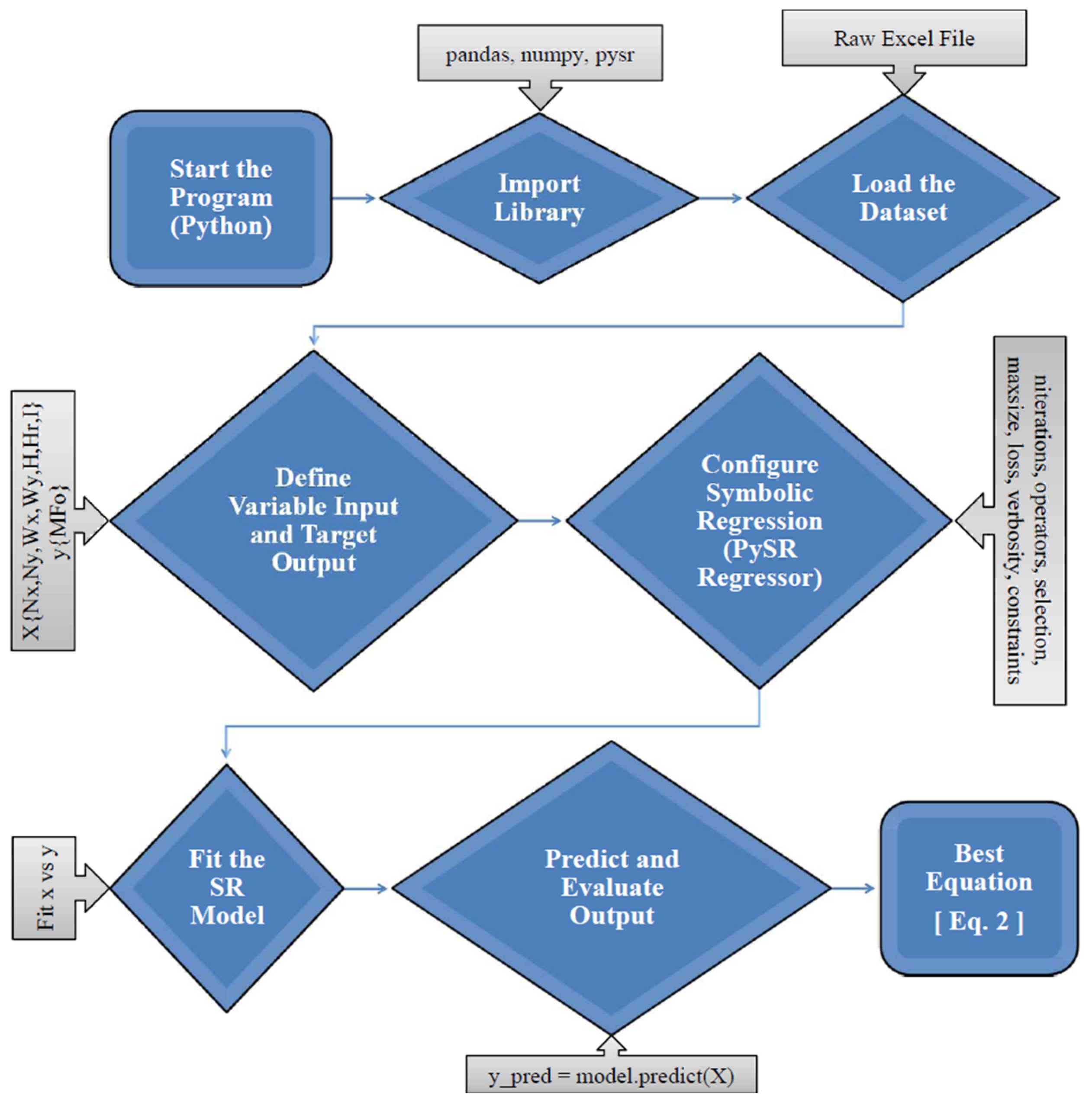
This complete procedure is summarized in the visual flowchart shown in Figure 2, which serves as a graphical representation of the sequential methodology.

In this study, the MF is determined by iteratively increasing GS column sizes until the GS stiffness exceeded that of the immediate upper storey. This condition is chosen as a conservative benchmark because it directly removes the stiffness irregularity identified in IS 1893:2016 [2], which classify a storey as “soft” if its stiffness falls below of that of the storey above. By ensuring the soft-storey mechanism is suppressed, a rational and code-consistent basis for MF determination is established.

If the initially assumed GS column sections prove inadequate during this iterative redesign, larger column sizes are adopted as a new starting point. It is noteworthy that the MF is not predefined in this method; instead, it is determined through trial and error, ensuring that the desired stiffness enhancement is achieved and the soft-storey effect is effectively mitigated.

4. Results and Discussion

4.1. Results of Structural Analysis

The GS-to-upper-storey stiffness percentage was computed for each OGS model. The complete list of model configurations used for this analysis is presented in Table A1 in Appendix A. These percentages were generally found to be less than 100%, indicating insufficient GS stiffness. To rectify this, the GS columns were redesigned using MFs derived through the iterative methodology described in Section 3. This led to the formation of MOGS models where stiffness ratios exceeded 100%, thus effectively mitigating the soft-storey effect.

Table 4. Condensed summary of stiffness percentage and details of columns for a few representative models.

Model No.	Model	OGS Stiffness %		MOGS Stiffness %		MFo	Column Dimensions
		kx	ky	kx	ky		Initial	Final
8	0M1-55553	19.072	19.072	110.577	110.577	2.762	350	730
9	0M1-33335	29.142	29.142	109.360	109.360	3.150	350	615
17	0M1-33337	29.805	29.805	111.330	111.323	2.665	350	615
25	16M1-33333	43.912	43.912	110.531	110.531	3.364	350	585
33	16M1-33335	44.050	44.050	108.260	108.260	2.906	350	580
41	16M1-33337	45.532	45.532	108.471	108.471	2.514	350	575
49	33M1-33333	59.223	59.223	111.878	111.862	3.149	350	550
57	33M1-33335	50.023	50.023	111.633	111.633	3.200	350	650
65	33M1-33337	61.181	61.181	107.029	107.029	2.329	350	530
73	0M1.33-33333	15.643	15.643	109.445	109.441	5.390	350	800
81	0M1.33-33335	14.937	14.937	112.598	112.592	3.810	350	810
89	0M1.33-33337	15.229	15.229	110.732	110.724	3.320	350	800
97	16M1.33-33333	24.540	24.540	109.946	109.946	5.225	350	780
105	16M1.33-33335	24.503	24.505	109.378	109.378	3.650	350	780
117	16M1.33-53337	38.812	40.645	110.308	122.542	3.300	350	810
121	33M1.33-33333	34.309	34.389	111.961	111.949	5.070	350	760
130	33M1.33-35355	34.554	34.728	110.656	110.589	2.485	350	845
141	33M1.33-53337	53.135	61.806	111.597	124.553	3.214	350	790
145	0M1.67-33333	9.491	9.491	109.949	109.945	5.931	350	970
153	0M1.67-33335	8.923	8.923	111.053	111.047	4.439	350	975
161	0M1.67-33337	9.075	9.075	114.773	114.763	3.901	350	980
169	16M1.67-33333	15.326	15.328	111.520	111.520	6.340	350	960
177	16M1.67-33335	15.231	15.232	110.933	110.931	4.346	350	960
185	16M1.67-33337	15.825	15.826	109.549	109.545	3.750	350	950
193	33M1.67-33333	21.964	22.022	110.841	110.833	6.972	350	940
201	33M1.67-33335	21.888	21.920	110.141	110.126	4.231	350	940
214	33M1.67-53537	20.213	20.321	109.706	109.645	3.700	350	965

presents a condensed summary featuring representative models selected from each of the 27 sets outlined in Table 3. For each selected model, the table reports the initial and final GS stiffness percentages (OGS Stiffness % and MOGS Stiffness %) in both the X direction (kx) and Y direction (ky), the required MF (MFo), and the corresponding change in column dimensions resulting from redesign. The complete dataset of all 216 model configurations is provided in

Table A2. Stiffness percentage and details of columns for all 216 models.

Sl No.	Model	OGS Stiffness %		MOGS Stiffness %		MFo	Column Dimensions
		kx	ky	kx	ky		Initial	Final
1	0M1-33333	29.967	29.967	111.349	111.349	3.600	350	618
2	0M1-35353	21.036	21.036	112.465	112.465	2.767	350	715
3	0M1-35333	21.104	29.916	107.314	152.379	3.552	350	703
4	0M1-53353	26.794	21.142	150.435	114.707	3.585	350	720
5	0M1-53333	26.844	29.987	112.174	121.378	4.571	350	640
6	0M1-53533	26.862	26.862	110.652	110.652	4.493	350	635
7	0M1-55333	19.114	29.932	112.107	171.887	3.651	350	735
8	0M1-55553	19.072	19.072	110.577	110.577	2.762	350	730
9	0M1-33335	29.142	29.142	109.360	109.360	3.150	350	615
10	0M1-35355	19.979	19.979	109.620	109.620	2.192	350	710
11	0M1-35335	19.963	29.163	109.116	157.329	2.811	350	710
12	0M1-53355	25.690	19.994	146.822	111.656	2.805	350	715
13	0M1-53335	25.683	29.159	112.461	123.231	3.333	350	645
14	0M1-53535	25.698	25.698	110.839	110.839	3.130	350	640
15	0M1-55335	17.927	29.164	112.637	176.691	2.900	350	740
16	0M1-55555	17.959	17.959	109.249	109.249	2.212	350	730
17	0M1-33337	29.805	29.805	111.330	111.323	2.665	350	615
18	0M1-35357	19.992	19.992	110.446	110.024	1.815	350	725
19	0M1-35337	19.955	29.848	112.130	163.614	2.100	350	715
20	0M1-53357	25.798	19.988	145.237	110.326	2.135	350	710
21	0M1-53337	25.776	29.826	110.951	123.134	2.730	350	640
22	0M1-53537	25.796	25.796	111.471	111.456	2.673	350	640
23	0M1-55337	17.748	29.863	110.623	177.081	2.450	350	735
24	0M1-55557	17.802	17.802	111.599	111.558	1.810	350	735
25	16M1-33333	43.912	43.912	110.531	110.531	3.364	350	585
26	16M1-35353	35.627	35.627	111.192	111.192	2.625	350	680
27	16M1-35333	35.745	43.809	111.031	151.790	3.437	350	680
28	16M1-53353	37.312	34.781	139.779	111.623	3.371	350	680
29	16M1-53333	38.725	41.006	107.259	114.792	4.272	350	600
30	16M1-53533	43.143	43.143	110.528	110.528	4.196	350	595
31	16M1-55333	32.249	40.270	110.249	161.382	3.468	350	700
32	16M1-55553	37.086	37.086	110.900	111.197	2.576	350	685
33	16M1-33335	44.050	44.050	108.260	108.260	2.906	350	580
34	16M1-35355	35.186	35.186	110.495	110.495	2.100	350	680
35	16M1-35335	35.226	44.010	110.167	152.813	2.700	350	680
36	16M1-53355	37.435	33.973	138.953	110.749	2.668	350	680
37	16M1-53335	38.138	40.904	109.429	119.015	3.000	350	610
38	16M1-53535	41.915	41.915	110.206	110.206	2.927	350	600
39	16M1-55335	31.328	41.750	110.266	165.982	2.750	350	704
40	16M1-55555	35.578	35.578	110.815	110.815	2.090	350	690
41	16M1-33337	45.532	45.532	108.471	108.471	2.514	350	575
42	16M1-35357	35.695	35.695	111.472	111.472	1.698	350	680
43	16M1-35337	35.712	45.517	111.077	155.978	2.255	350	680
44	16M1-53357	37.696	30.956	140.163	111.655	2.229	350	680
45	16M1-53337	38.812	40.645	112.079	124.052	2.615	350	615
46	16M1-53537	42.222	42.222	110.757	110.757	2.532	350	600
47	16M1-55337	31.423	41.981	112.792	173.576	2.345	350	710
48	16M1-55557	35.432	35.432	109.055	109.055	1.695	350	685
49	33M1-33333	59.223	59.223	111.878	111.862	3.149	350	550
50	33M1-35353	46.838	59.357	111.315	111.250	2.386	350	635
51	33M1-35333	51.679	58.425	111.149	143.897	3.140	350	635
52	33M1-53353	51.424	51.424	131.895	110.753	3.058	350	630
53	33M1-53337	52.958	59.275	110.068	119.892	4.072	350	570
54	33M1-53533	47.054	52.139	110.312	110.244	3.970	350	560
55	33M1-55337	46.838	59.424	110.311	156.710	3.218	350	660
56	33M1-55553	49.956	55.827	111.633	111.365	2.405	350	650
57	33M1-33335	50.023	50.023	111.633	111.633	3.200	350	650
58	33M1-35355	51.121	51.121	110.449	110.449	1.934	350	635
59	33M1-35335	51.281	58.974	110.108	144.504	2.484	350	635
60	33M1-53355	52.561	51.684	132.987	111.281	2.458	350	635
61	33M1-53335	52.428	59.796	108.417	119.695	2.825	350	570
62	33M1-53535	55.479	55.479	110.364	110.364	2.785	350	565
63	33M1-55335	45.982	59.982	111.938	163.054	2.602	350	670
64	33M1-55555	49.287	49.287	110.067	110.067	1.945	350	650
65	33M1-33337	61.181	61.181	107.029	107.029	2.329	350	530
66	33M1-35357	51.913	51.913	111.336	111.336	1.575	350	635
67	33M1-35337	52.041	60.966	110.937	147.321	2.100	350	635
68	33M1-53357	53.291	52.543	131.916	110.417	2.043	350	630
69	33M1-53337	53.135	61.806	110.757	123.775	2.475	350	575
70	33M1-53537	56.286	56.286	109.417	109.417	2.400	350	560
71	33M1-55337	46.161	62.029	110.405	163.820	2.175	350	665
72	33M1-55557	49.540	49.540	110.242	109.943	1.580	350	650
73	0M1.33-33333	15.643	15.643	109.445	109.441	5.390	350	800
74	0M1.33-35353	10.998	10.998	111.294	111.294	3.300	350	910
75	0M1.33-35333	21.104	29.916	111.460	156.509	4.215	350	910
76	0M1.33-53353	13.733	11.083	139.839	107.897	4.080	350	900
77	0M1.33-53333	13.786	15.611	109.835	119.120	5.400	350	825
78	0M1.33-53533	13.765	13.765	110.113	110.098	5.340	350	825
79	0M1.33-55333	9.929	15.539	109.797	167.320	4.210	350	930
80	0M1.33-55553	9.843	9.843	109.782	109.782	3.278	350	930
81	0M1.33-33335	14.937	14.937	112.598	112.592	3.810	350	810
82	0M1.33-35355	10.253	10.253	114.895	114.876	2.700	350	920
83	0M1.33-35335	19.963	29.163	110.796	157.994	3.410	350	910
84	0M1.33-53355	12.926	10.275	146.377	112.909	3.373	350	915
85	0M1.33-53335	25.683	29.159	111.852	122.882	3.897	350	835
86	0M1.33-53535	12.922	12.922	114.053	114.038	3.770	350	840
87	0M1.33-55335	17.927	29.164	110.356	172.042	3.430	350	935
88	0M1.33-55555	9.097	9.097	112.695	112.650	2.656	350	940
89	0M1.33-33337	15.229	15.229	110.732	110.724	3.320	350	800
90	0M1.33-35357	10.214	10.214	110.118	110.097	2.180	350	905
91	0M1.33-35337	19.955	29.848	109.785	158.622	2.860	350	905
92	0M1.33-53357	12.929	10.224	142.802	109.993	2.830	350	905
93	0M1.33-53337	25.776	29.826	110.589	123.029	3.370	350	830
94	0M1.33-53537	12.919	12.919	110.923	110.905	3.320	350	830
95	0M1.33-55337	17.748	29.863	110.575	175.748	2.923	350	935
96	0M1.33-55557	8.972	8.972	111.166	111.118	2.220	350	935
97	16M1.33-33333	24.540	24.540	109.946	109.946	5.225	350	780
98	16M1.33-35353	22.332	22.349	113.843	113.845	3.220	350	890
99	16M1.33-35333	22.458	24.451	110.472	149.513	4.060	350	880
100	16M1.33-53353	20.454	18.684	139.498	112.329	4.002	350	885
101	16M1.33-53333	21.310	22.606	111.167	119.737	5.314	350	810
102	16M1.33-53533	24.078	24.078	114.318	114.318	5.250	350	810
103	16M1.33-55333	20.237	22.241	108.593	158.413	4.052	350	900
104	16M1.33-55553	23.673	23.673	114.546	114.546	3.173	350	905
105	16M1.33-33335	24.503	24.505	109.378	109.378	3.650	350	780
106	16M1.33-35355	22.104	22.114	111.696	111.697	2.710	350	885
107	16M1.33-35335	35.226	44.010	111.687	152.840	3.287	350	885
108	16M1.33-53355	20.133	18.281	136.686	110.169	3.240	350	880
109	16M1.33-53335	38.138	40.904	111.405	121.950	3.780	350	815
110	16M1.33-53535	23.175	23.413	109.041	109.044	3.660	350	800
111	16M1.33-55335	31.328	41.750	110.803	165.540	3.328	350	910
112	16M1.33-55555	22.611	23.474	109.884	109.922	2.554	350	895
113	16M1.33-33337	25.405	25.407	111.341	111.340	3.230	350	780
114	16M1.33-35357	22.499	22.507	112.711	112.711	2.135	350	885
115	16M1.33-35337	35.712	45.517	110.891	153.529	2.782	350	880
116	16M1.33-53357	20.212	18.184	135.640	109.463	2.738	350	875
117	16M1.33-53337	38.812	40.645	110.308	122.542	3.300	350	810
118	16M1.33-53537	23.327	23.506	109.563	109.551	3.210	350	800
119	16M1.33-55337	31.423	41.981	111.054	169.354	2.838	350	910
120	16M1.33-55557	22.514	23.230	111.752	111.720	2.134	350	900
121	33M1.33-33333	34.309	34.389	111.961	111.949	5.070	350	760
122	33M1.33-35353	34.755	35.053	112.724	112.666	3.075	350	850
123	33M1.33-35333	51.679	58.425	111.267	142.379	3.905	350	845
124	33M1.33-53353	30.412	35.236	127.876	109.126	3.785	350	835
125	33M1.33-53333	52.958	59.275	111.092	120.870	5.100	350	785
126	33M1.33-53533	32.479	32.164	111.956	111.905	4.883	350	780
127	33M1.33-55333	46.838	59.424	111.201	156.123	3.930	350	875
128	33M1.33-55553	33.765	34.629	110.068	109.868	3.010	350	860
129	33M1.33-33335	34.406	34.449	111.373	111.351	3.550	350	760
130	33M1.33-35355	34.554	34.728	110.656	110.589	2.485	350	845
131	33M1.33-35335	51.281	58.974	110.486	143.227	3.150	350	845
132	33M1.33-53355	29.953	34.961	130.952	111.278	3.124	350	845
133	33M1.33-53335	52.428	59.796	110.996	122.379	3.650	350	790
134	33M1.33-53535	31.786	31.961	110.248	110.181	3.544	350	780
135	33M1.33-55335	45.982	59.982	111.411	160.039	3.216	350	880
136	33M1.33-55555	33.272	33.776	111.867	111.649	2.450	350	870
137	33M1.33-33337	35.669	35.702	113.292	113.258	3.150	350	760
138	33M1.33-35357	35.185	35.326	111.579	111.494	2.048	350	845
139	33M1.33-35337	52.041	60.966	111.335	146.036	2.683	350	845
140	33M1.33-53357	30.400	35.562	128.057	109.016	2.628	350	835
141	33M1.33-53337	53.135	61.806	111.597	124.553	3.214	350	790
142	33M1.33-53537	32.293	32.434	114.117	114.022	3.170	350	790
143	33M1.33-55337	46.161	111.601	163.398	163.820	2.745	350	880
144	33M1.33-55557	33.491	33.912	110.568	110.334	2.057	350	865
145	0M1.67-33333	9.491	9.491	109.949	109.945	5.931	350	970
146	0M1.67-35353	6.674	6.674	109.930	109.912	4.041	350	1086
147	0M1.67-35333	21.104	29.916	111.689	156.018	4.965	350	1090
148	0M1.67-53353	8.197	6.738	142.604	110.994	4.900	350	1088
149	0M1.67-53333	13.786	15.611	115.753	125.814	6.105	350	1015
150	0M1.67-53533	8.221	8.221	110.792	110.776	5.941	350	1000
151	0M1.67-55333	9.929	15.539	112.154	170.336	5.061	350	1120
152	0M1.67-55553	5.906	5.906	111.752	111.692	4.094	350	1120
153	0M1.67-33335	8.923	8.923	111.053	111.047	4.439	350	975
154	0M1.67-35355	6.127	6.127	109.487	109.470	3.151	350	1085
155	0M1.67-35335	19.963	29.163	116.370	164.923	4.076	350	1105
156	0M1.67-53355	7.597	6.145	143.161	111.223	3.975	350	1090
157	0M1.67-53335	25.683	29.159	112.453	123.838	4.553	350	1010
158	0M1.67-53535	7.592	7.592	111.892	111.875	4.498	350	1008
159	0M1.67-55335	17.927	29.164	111.017	172.585	3.089	350	1120
160	0M1.67-55555	5.373	5.373	109.512	109.467	3.184	350	1115
161	0M1.67-33337	9.075	9.075	114.773	114.763	3.901	350	980
162	0M1.67-35357	6.082	6.082	110.517	110.494	2.583	350	1085
163	0M1.67-35337	19.955	29.848	115.578	165.909	3.426	350	1100
164	0M1.67-53357	7.574	6.093	142.252	110.450	3.333	350	1085
165	0M1.67-53337	25.776	29.826	109.632	122.248	3.911	350	1000
166	0M1.67-53537	7.564	7.564	111.517	111.496	3.872	350	1005
167	0M1.67-55337	17.748	29.863	111.259	176.311	3.464	350	1120
168	0M1.67-55557	5.278	5.278	111.583	111.531	2.647	350	1120
169	16M1.67-33333	15.326	15.328	111.520	111.520	6.340	350	960
170	16M1.67-35353	15.259	15.272	112.138	112.136	3.966	350	1070
171	16M1.67-35333	22.458	24.451	110.878	149.947	4.818	350	1065
172	16M1.67-53353	12.652	12.253	139.510	112.428	4.795	350	1070
173	16M1.67-53333	21.310	22.606	118.280	128.332	6.074	350	1010
174	16M1.67-53533	14.983	15.278	110.531	110.575	5.810	350	980
175	16M1.67-55333	20.237	22.241	109.572	161.062	4.871	350	1090
176	16M1.67-55553	16.373	17.502	110.976	111.056	3.918	350	1085
177	16M1.67-33335	15.231	15.232	110.933	110.931	4.346	350	960
178	16M1.67-35355	15.143	15.151	110.319	110.316	3.080	350	1065
179	16M1.67-35335	35.226	44.010	115.355	158.058	3.950	350	1080
180	16M1.67-53355	12.369	12.393	139.020	112.058	3.885	350	1070
181	16M1.67-53335	38.138	40.904	110.149	121.019	4.490	350	990
182	16M1.67-53535	14.287	14.448	110.294	110.297	4.397	350	985
183	16M1.67-55335	31.328	41.750	111.619	167.451	3.990	350	1100
184	16M1.67-55555	15.584	16.303	111.453	111.445	3.091	350	1090
185	16M1.67-33337	15.825	15.826	109.549	109.545	3.750	350	950
186	16M1.67-35357	15.466	15.473	109.738	109.734	2.513	350	1060
187	16M1.67-35337	35.712	45.517	116.374	161.359	3.340	350	1080
188	16M1.67-53357	12.459	12.049	136.129	109.885	3.242	350	1060
189	16M1.67-53337	38.812	40.645	119.328	132.927	3.969	350	1015
190	16M1.67-53537	14.377	14.496	110.839	110.821	3.799	350	985
191	16M1.67-55337	31.423	41.981	110.294	168.507	3.362	350	1095
192	16M1.67-55557	15.526	16.133	110.162	110.117	2.541	350	1085
193	33M1.67-33333	21.964	22.022	110.841	110.833	6.972	350	940
194	33M1.67-35353	24.882	25.145	110.745	110.704	3.813	350	1035
195	33M1.67-35333	51.679	58.425	116.965	150.946	4.770	350	1055
196	33M1.67-53353	19.128	25.168	129.710	110.210	4.583	350	1030
197	33M1.67-53333	52.958	59.275	113.798	123.925	5.880	350	980
198	33M1.67-53533	20.223	20.456	110.897	110.864	5.680	350	965
199	33M1.67-55333	46.838	59.424	108.740	153.350	4.700	350	1060
200	33M1.67-55553	24.029	24.810	111.165	111.005	3.805	350	1060
201	33M1.67-33335	21.888	21.920	110.141	110.126	4.231	350	940
202	33M1.67-35355	24.718	24.873	110.391	110.339	2.984	350	1035
203	33M1.67-35335	51.281	58.974	110.371	144.025	3.770	350	1035
204	33M1.67-53355	18.716	24.939	132.869	112.400	3.760	350	1040
205	33M1.67-53335	52.428	59.796	108.981	120.315	4.375	350	970
206	33M1.67-53535	19.880	20.013	110.676	110.629	4.305	350	970
207	33M1.67-55335	45.982	59.982	110.357	159.327	3.855	350	1070
208	33M1.67-55555	23.669	24.136	111.609	111.441	3.005	350	1065
209	33M1.67-33337	22.741	22.766	111.988	111.964	3.703	350	940
210	33M1.67-35357	25.224	25.353	112.842	112.770	2.461	350	1040
211	33M1.67-35337	52.041	60.966	111.222	146.881	3.190	350	1035
212	33M1.67-53357	19.003	25.436	133.927	113.267	3.174	350	1040
213	33M1.67-53337	53.135	61.806	111.103	124.167	3.805	350	975
214	33M1.67-53537	20.213	20.321	109.706	109.645	3.700	350	965
215	33M1.67-55337	46.161	62.029	112.050	164.937	3.286	350	1075
216	33M1.67-55557	23.853	23.853	111.898	111.710	2.486	350	1065

of Appendix B for detailed reference.

As evident from Table 4 and further substantiated by the full dataset in Table A2 of Appendix B, the GS-to-immediate upper-storey stiffness percentages for all OGS models (OGS Stiffness %) fall well below 100%. This clearly indicates a significant stiffness deficiency at the ground level, which is a primary contributor to soft-storey collapse under seismic loading.

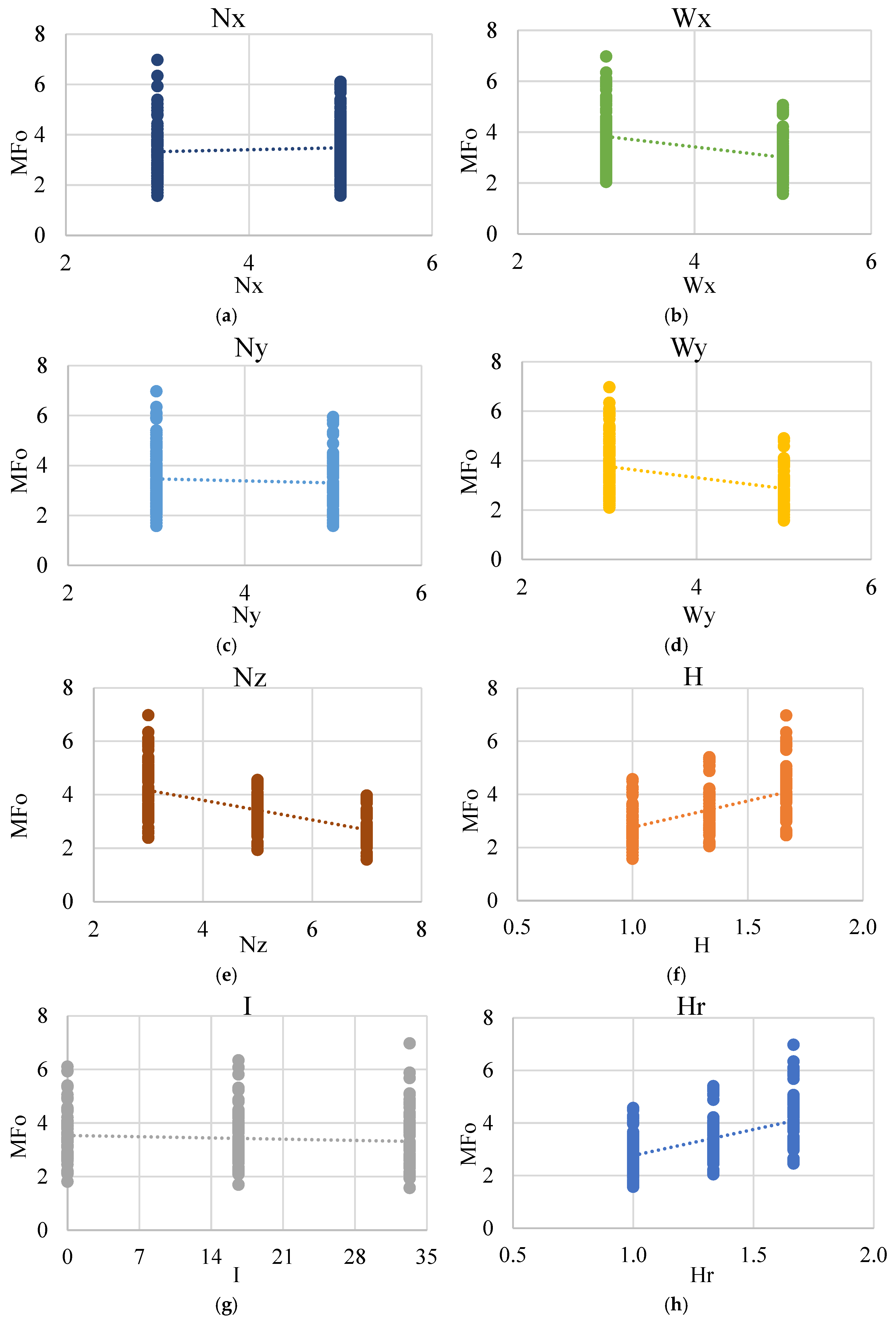
The influence of bay numbers (Nx, Ny) and bay widths (Wx, Wy) on the global lateral stiffness of the OGS models was evaluated. Variations in these parameters produced only minimal changes in GS stiffness percentages compared to the dominant effects of overall height, height ratio, and infill percentage. For this reason, only H, Nz, I, and Hr are highlighted in Figure 3, while the variation in required MF considering all variables (including Nx, Ny, Wx, and Wy) is presented in Figure 4. All models were kept plan-symmetric to isolate the stiffness irregularity mechanism; torsional irregularities and explicit plan-asymmetry effects were not evaluated in this study and are noted as a limitation for future work.

Figure 3 illustrates the variation in GS stiffness across all model configurations with respect to four key parameters, such as H, Nz, I, and Hr. The observed trends reveal that an increase in the overall structural height results in a slight reduction in stiffness percentage. Conversely, a higher number of storeys tends to enhance stiffness. As expected, increasing the percentage of masonry infill at the GS contributes positively to stiffness due to the added lateral resistance provided by the infill walls. Notably, a decrease in stiffness percentage is prominently associated with higher storey height ratios (Hr), underscoring that the stiffness deficiency is not solely attributed to the absence of infill walls. Even in the presence of partial infill, a tall GS introduces slenderness effects that significantly reduce lateral stiffness. This emphasizes that Hr is a critical parameter influencing GS stiffness, and must be carefully considered during the seismic design of OGS buildings to mitigate the soft-storey effect.

To mitigate stiffness deficiencies, it is crucial to improve the GS stiffness in both the X and Y directions. Accordingly, MFos were chosen to ensure that the stiffness percentage of the GS relative to the storey above exceeded 100% in both directions. As evident from Table 4 and the comprehensive data in Table A2 of Appendix B, all MOGS models successfully achieve GS stiffness percentages well above 100% in both directions following the application of appropriate MFs.

Figure 4 presents the variation in the required magnification factor (MFo) with respect to individual structural parameters. It can be observed that the number of bays has a relatively minor influence on MFo. In contrast, increasing the bay widths in both X and Y directions tends to lower the MFo requirement, while a taller overall building height leads to an increase in MFo. Interestingly, the opposite trend is noted with the number of storeys, where a greater number of storeys results in reduced MF demand. As anticipated, the presence of infill walls at the GS enhances the initial stiffness of OGS models and concurrently decreases the required MF for corresponding MOGS models, and higher infill percentages lead to noticeably lower MFo values. While the direct contribution of infill percentage to MFo reduction may appear modest, its influence remains significant. Furthermore, as highlighted earlier, the height ratio between the GS and the upper storey (Hr) plays a vital role in reducing GS stiffness. This reduction translates to a substantial increase in MFo as Hr increases, reinforcing the importance of incorporating Hr as a key parameter in the development of the MF prediction model.

4.2. Requirements of the MF Evaluation by ML

The application of MFs across the full range of geometric configurations demonstrates a marked enhancement in GS stiffness. In every MOGS model, the GS stiffness exceeds that of the storey directly above, thereby effectively addressing the soft-storey vulnerability and significantly improving the seismic resilience of the structure. Ghosh et al. [41] developed a predictive relation for estimating the required MF based on plan-related parameters, demonstrating good alignment with the analytical results. However, their approach did not account for the variation in GS height, which can significantly influence MF demand. In practical scenarios, GS height often varies to meet functional needs, and an increase in this height leads to greater flexibility and a corresponding reduction in storey stiffness. Given that OGS structures inherently exhibit reduced stiffness at the GS level, an increase in GS height exacerbates the issue due to slenderness effects. The combined influence of an open configuration and increased storey height further aggravates the soft-storey problem, raising critical safety concerns. As such, the inclusion of the GS-to-upper-storey height ratio (Hr) in MF prediction is essential for a more accurate and realistic evaluation, which is an aspect addressed in the present study.

Since determining the appropriate MF for a specific structural configuration typically demands significant computational time and effort, this study utilizes ML techniques, particularly SR, to develop a simplified and interpretable predictive model. The resulting expression reliably estimates the required MF, and its application ensures that the GS stiffness percentage exceeds 100%, thereby mitigating the soft-storey effect and enhancing the seismic performance of OGS structures.

5. Proposed Model for Required MF by Incorporating ML Techniques

To establish a relationship between the required MF for OGS columns and the structural geometric characteristics of building frames, a comprehensive ML analysis was performed. In this approach, parameters such as Nx, Wx, Ny, Wy, H, Hr, and I were considered as input features, while the required MFo was treated as the target output.

5.1. ML Techniques Adopted in This Present Study

It is important to note that selecting the most appropriate ML technique depends on the nature of the dataset, the analytical objectives, and the complexity of the relationships among variables [42]. In this study, the dataset comprises continuous numerical variables, making it suitable for advanced ML techniques such as Random Forest, Gradient Boosting, and Neural Networks, which are capable of capturing intricate and nonlinear dependencies often overlooked by simpler models. These methods also facilitate the discovery of hidden patterns and interactions, thereby enhancing predictive accuracy. Furthermore, feature selection approaches such as Lasso and Ridge, along with embedded techniques in decision tree-based models, aid in refining the model by eliminating irrelevant or redundant features, thereby improving efficiency and clarity [53]. Notably, Symbolic Regression (SR) was also employed for its ability to derive interpretable, human-readable expressions that preserve physical relevance while maintaining high predictive performance [43]. Validating all models using unseen data ensures robustness and generalizability, making these ML approaches valuable for advancing the understanding of structural behavior under seismic loading.

5.2. Execution of ML Techniques and Results

All the aforementioned ML techniques were implemented using the Python v3.10.11 programming environment. The modeling workflow was executed using widely adopted libraries such as pandas for data handling, NumPy for numerical operations, scikit-learn for model training and evaluation, and PySR for symbolic regression. The complete dataset, including all geometric parameters of the OGS models, was compiled as described in Table A1 of Appendix A and Table A2 of Appendix B. The structural parameters Nx, Wx, Ny, Wy, H, Hr, and I, as outlined in Appendix A, were treated as independent input features, while the required MF (MFo) was used as the target variable, sourced from Appendix B. The dataset of 216 OGS models spans a wide range of configurations, including plan dimensions of 3–5 bays, total building heights of 9–23 m, ground-to-upper-storey height ratios of 1.0–1.67, and GS infill conditions between 0 and 33%. These configuration ranges, summarized in Table 1 and detailed in Appendix A and Appendix B, were selected to capture realistic geometric ratios and infill scenarios, thereby supporting the generalizability of the ML predictions and the derived SR equation within the stated domain. This approach is consistent with the emphasis on representative training datasets for robust surrogate modeling, as also highlighted by Jahangiri et al. (2025) [54].

Model development included preprocessing the data, splitting data into training and testing sets, performing normalization where necessary, and tuning hyperparameters through cross-validation. SR was specifically performed using PySR to derive interpretable mathematical expressions for MF prediction. Model performance was quantitatively assessed using three evaluation metrics, Root Mean Squared Error (RMSE), Residual Standard Error (RSE), and Coefficient of Determination (R²), as presented in Figure 5. These metrics collectively provide a robust understanding of each model’s predictive accuracy, goodness-of-fit, and reliability [55,56].

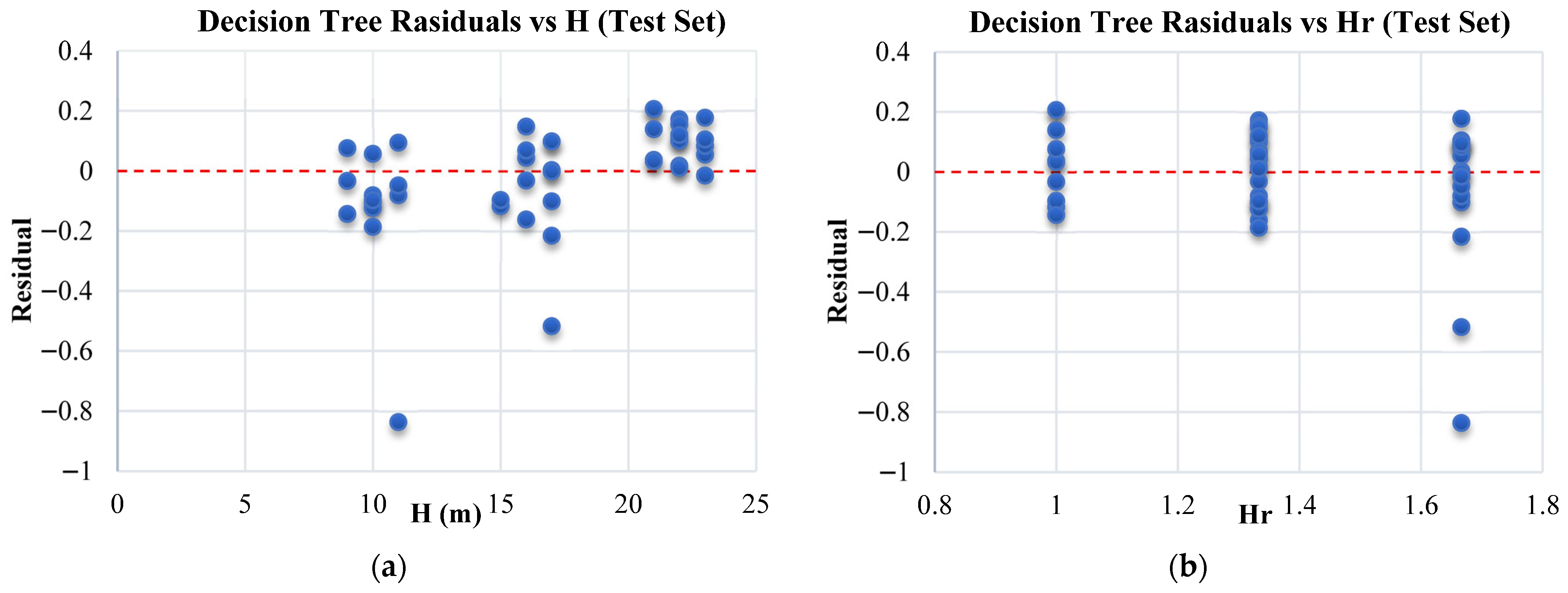
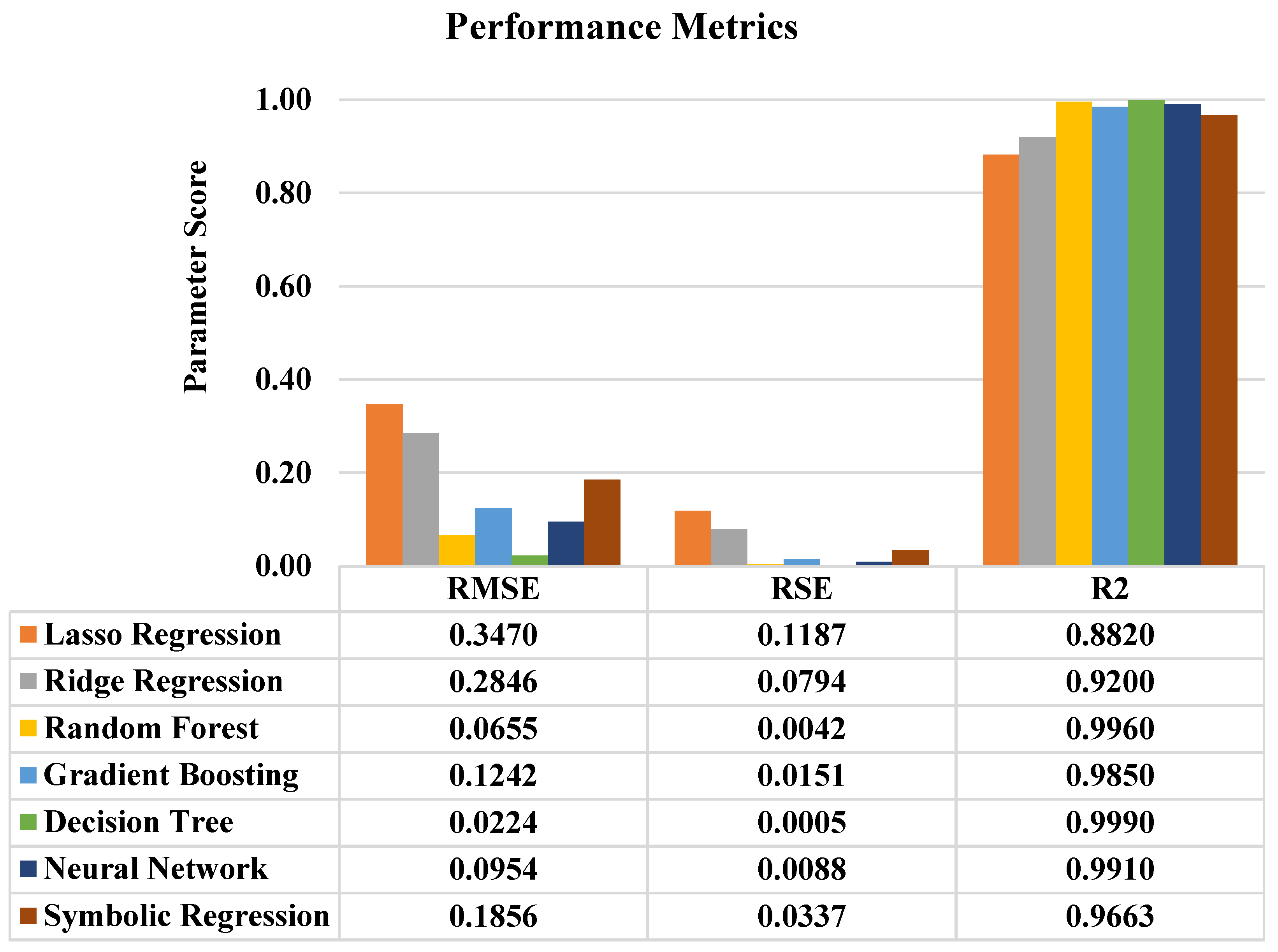
The comparative analysis of ML techniques, illustrated in Figure 5, highlights their relative effectiveness in predicting the required MF in OGS structures. The Decision Tree model exhibits excellent performance with an exceptionally high coefficient of determination (R² = 0.999) and the lowest RMSE (0.0224). However, this near-perfect fit should be interpreted with caution, as Decision Trees are susceptible to overfitting, especially with complex datasets. Nevertheless, their rule-based output provides good interpretability for early-stage insights. The results in Figure 5 correspond to model performance when evaluated on the entire dataset, whereas Appendix C,

Table A3. Cross-validation summary (five-fold on training set).

ML Model	CV R2 (Mean ± Std)	CV RMSE (Mean ± Std)	CV MAE (Mean ± Std)
Lasso	0.873 ± 0.08	0.36 ± 0.08	0.25 ± 0.05
Ridge	0.897 ± 0.07	0.33 ± 0.07	0.24 ± 0.05
Decision Tree	0.977 ± 0.03	0.16 ± 0.05	0.11 ± 0.04
Random Forest	0.993 ± 0.01	0.09 ± 0.02	0.06 ± 0.02
Gradient Boosting	0.985 ± 0.02	0.13 ± 0.03	0.09 ± 0.02
Neural Network	0.986 ± 0.02	0.12 ± 0.03	0.08 ± 0.02

and

Table A4. Test Set Performance (80/20 split).

Model	Test R2	Test RMSE	Test MAE
Lasso	0.882	0.340	0.240
Ridge	0.905	0.320	0.230
Decision Tree	0.990	0.090	0.060
Random Forest	0.995	0.070	0.050
Gradient Boosting	0.989	0.100	0.070
Neural Network	0.993	0.080	0.060
Symbolic Regression	0.964	0.190	0.130

, presents five-fold cross-validation and held-out test set results. The latter provide a more realistic estimate of generalization ability and highlight that models such as Decision Tree, while nearly perfect in-sample, display higher variance under cross-validation due to overfitting tendencies. Further details, including the Decision Tree learning curve and residual analyses, are provided in Appendix C. Lasso and Ridge Regression apply regularization to manage model complexity and highlight relevant features. Lasso performs feature selection by promoting sparsity, while Ridge shrinks coefficients without excluding variables. Both yielded moderate performance (R² ≈ 0.85–0.90) and higher residual errors than nonlinear models, indicating limitations in capturing the underlying relationships using linear assumptions. Random Forest and Gradient Boosting exhibit strong generalization with R² values above 0.98, a low RMSE, and stable RSE. These ensemble methods leverage Decision Tree combinations to model nonlinear dependencies effectively. Random Forest uses bootstrap aggregation, while Gradient Boosting sequentially reduces residual errors, making both ideal for structural systems with complex parameter interactions. Among all, the Neural Network model achieved the highest overall predictive accuracy (R² = 0.9910; RMSE = 0.0954; RSE = 0.0088). Its ability to model highly nonlinear input–output relationships make it highly suitable where prediction precision is critical. However, its black-box nature limits its interpretability, which is a concern for design applications unless complemented by explainability tools.

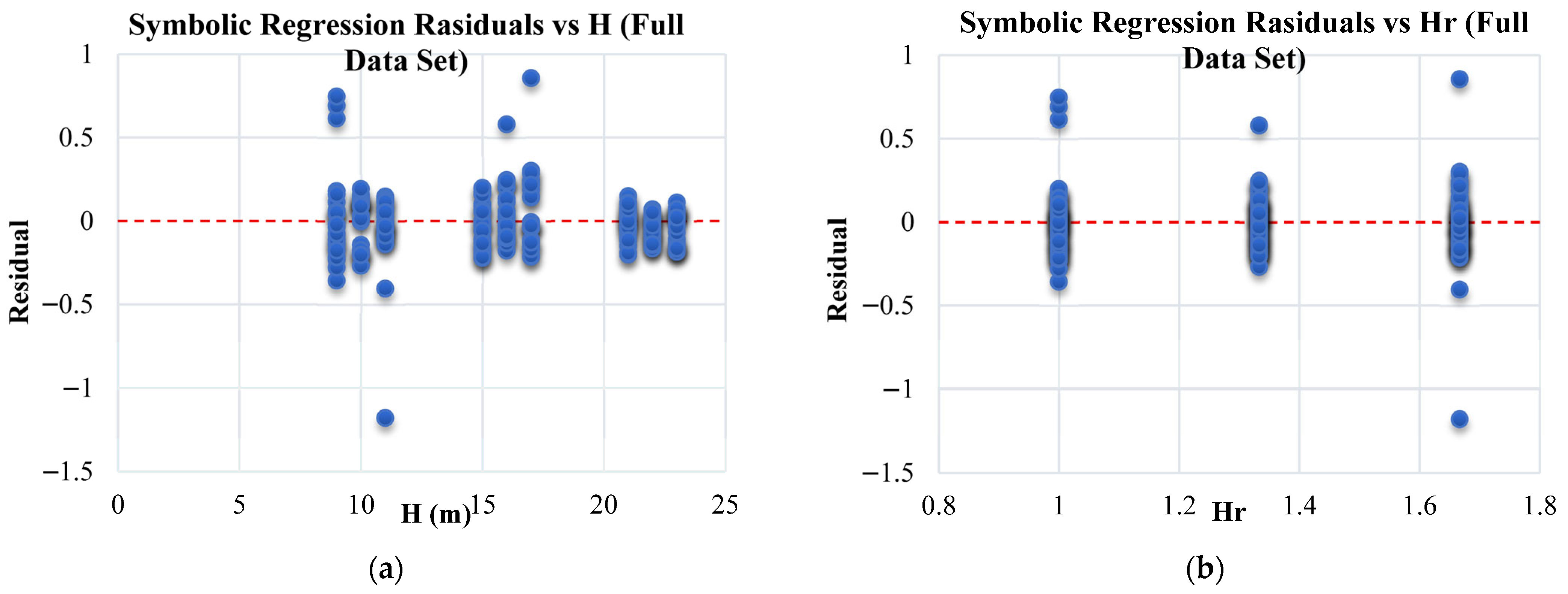
In contrast, Symbolic Regression (SR) stands out as a benchmark technique for its interpretability and transparency. With R² = 0.9663, RMSE = 0.1856, and RSE = 0.0337, it strikes a practical balance between accuracy and understanding. Its closed-form, physics-consistent equations are invaluable for validation, parametric analysis, and design code integration, making SR indispensable for engineering applications where explainability is key.

The results highlight the fundamental trade-off between predictive accuracy and interpretability in ML-based modeling. While Neural Networks achieved the highest accuracy, their ‘black-box’ nature limits direct codification. In contrast, SR provides an interpretable closed-form equation, which is slightly less accurate but transparent, reproducible, and readily auditable for design purposes. For engineering code integration, interpretability and consistency often take precedence over marginal gains in accuracy, since closed-form relations allow for peer review, regulatory acceptance, and conservative safety checks. Therefore, the SR model is recommended as a practical codifiable tool, while higher-accuracy black-box models can still serve as benchmarks or decision-support tools in research or performance assessment.

5.3. Expression of MF via Symbolic Regression

Based on the symbolic regression analysis, a closed-form predictive equation for the required MF is formulated as Equation (2). For better visual interpretability, the process of symbolic regression is presented in the form of a flowchart in Figure 6.

$$\mathbf{M}\mathbf{F}=\mathbf{0.396}+\mathbf{2.478}(\mathbf{H}\mathbf{r}·\mathsf{\alpha }-\mathsf{\beta }){\displaystyle \frac{\mathbf{ln}\mathbf{H}}{\mathbf{H}\sqrt{\mathbf{W}\mathbf{y}}}}$$

(2)

where

$$\mathsf{\alpha }=13.929-\mathrm{W}\mathrm{x}\mathrm{and}\mathsf{\beta }=0.02736·\mathrm{I}$$

The logarithmic term in Equation (2) is the natural logarithm (ln, base-e). The variable H must be expressed in meters, so that direct substitution yields meaningful values of MF. The equation was trained using the range of structural parameters listed in Table 1 and detailed in Table A1 of Appendix A and Table A2 of Appendix B, where they were used as features for training the ML models, as described in Section 5.2. The MF is dimensionless, and all terms in Equation (2) yield dimensionless contributions. The logarithmic term uses the natural logarithm (ln), with H expressed in meters, consistent with the training dataset. Composite terms such as $\mathrm{H}\sqrt{\mathrm{W}\mathrm{y}}$ carry units of m^1.5, but their fitted coefficients in Equation (2) have reciprocal units so that the resulting product is dimensionless. Similarly, all other coefficients ensure unit balance. For consistency, inputs must use the same units used in training: H, Wx, Wy in meters, Hr dimensionless, and I in percent. With this convention, MF remains dimensionless and properly scaled.

To verify the physical monotonicity of Equation (2), a one-at-a-time (OAT) sweep is performed and presented in

Table 5. One-at-a-time sensitivity for Equation (2).

Variable	Range Tested	MF (min)	MF (mid)	MF (max)	Trend (OAT)
H (m)	9 → 17 → 23	3.4907	2.5086	2.1241	Monotonic ↓
Hr (–)	1.00 → 1.33 → 1.67	1.9643	2.5086	3.0693	Monotonic ↑
I (%)	0 → 16 → 33	2.5894	2.5086	2.4227	Monotonic ↓
Wx (m)	3 → 4 → 5	2.9998	2.7542	2.5086	Monotonic ↓
Wy (m)	3 → 4 → 5	3.1233	2.7579	2.5086	Monotonic ↓

. Baseline values were fixed at H = 17 m, Hr = 1.33, Wx = 5 m, Wy = 5 m, and I = 16%. Each variable is then varied across its training range while others are held fixed, and MF was computed from Equation (2) (with ln as the natural log and inputs in the stated units).

The sensitivity results in Table 5 indicate that Equation (2) provides physically consistent and monotonic trends across the admissible ranges of the input variables. The MF increases with the Hr, confirming that taller ground-storeys have higher strengthening demands, which decrease with the GS infill percentage (I), as expected when additional masonry infill enhances stiffness. A mild decreasing trend is observed with overall building height (H), which is explained by the lnH/H term in the regression form, while both bay widths (Wx and Wy) also show decreasing effects when considered in isolation. Importantly, no non-physical reversals were noted, and the monotonic behavior across all parameters ensures the robustness of Equation (2). It is further noted that the dataset trends shown in Figure 4f represent marginal effects where parameters co-vary, whereas the sensitivity panel reflects one-at-a-time partial effects, thereby explaining the differences in the observed direction of variation.

This equation reflects the most influential structural parameters affecting MF demand, namely, Hr, H, Wx, Wy, and I. Notably, the plan dimensions Nx and Ny were automatically excluded by the symbolic regression process due to their negligible contribution to predictive accuracy. This balance of performance and interpretability makes the SR-derived model particularly suited for engineering applications where transparency, physical relevance, and potential for design codification are critical. Its concise form allows for direct implementation in design workflows while maintaining predictive fidelity.

The scope of validity and a worked application of Equation (2) on a representative model are presented in Appendix D, which defines the applicability envelope and demonstrates, step-by-step, how the SR-predicted MF is applied in design to achieve stiffness regularization in compliance with code provisions.

5.4. Sensitivity Analysis on ML Techniques

To better understand the relative influence of key structural parameters on the required MF for OGS columns, a sensitivity analysis was conducted on selected ML models. This analysis helps quantify how changes in input variables affect MF predictions, offering deeper interpretability and aiding in the identification of the most influential design factors [57]. Among the models, Decision Tree, Random Forest, and Gradient Boosting were deliberately excluded from the sensitivity analysis. These models operate using discrete splits and hierarchical rule structures, which do not provide smooth gradients or consistent global feature importance in the continuous domain, which are needed for interpreting stiffness sensitive variables. For tree-based models (Decision Tree, Random Forest, Gradient Boosting), split-based structures complicate direct sensitivity analysis. However, model-agnostic feature importance methods, such as permutation importance (evaluating loss of accuracy upon shuffling features), SHAP values (quantifying per-feature contribution to predictions), or accumulated local effects (ALE) plots, could be applied to extract meaningful insights into parameter influence. While these techniques were not implemented in the present study, they are identified as valuable tools for future work to complement the symbolic regression-based sensitivity assessment. Instead, the analysis focused on Lasso Regression, Ridge Regression, Neural Network, and Symbolic Regression, all of which are capable of providing either direct coefficient-based sensitivities or analytic expressions suitable for perturbation-based analysis. This perturbation-based approach is inherently local and may not fully capture the nonlinear interdependencies between parameters. The incorporation of global sensitivity methods such as Sobol indices, variance-based decomposition, or SHAP interaction values is identified as a direction for future work.

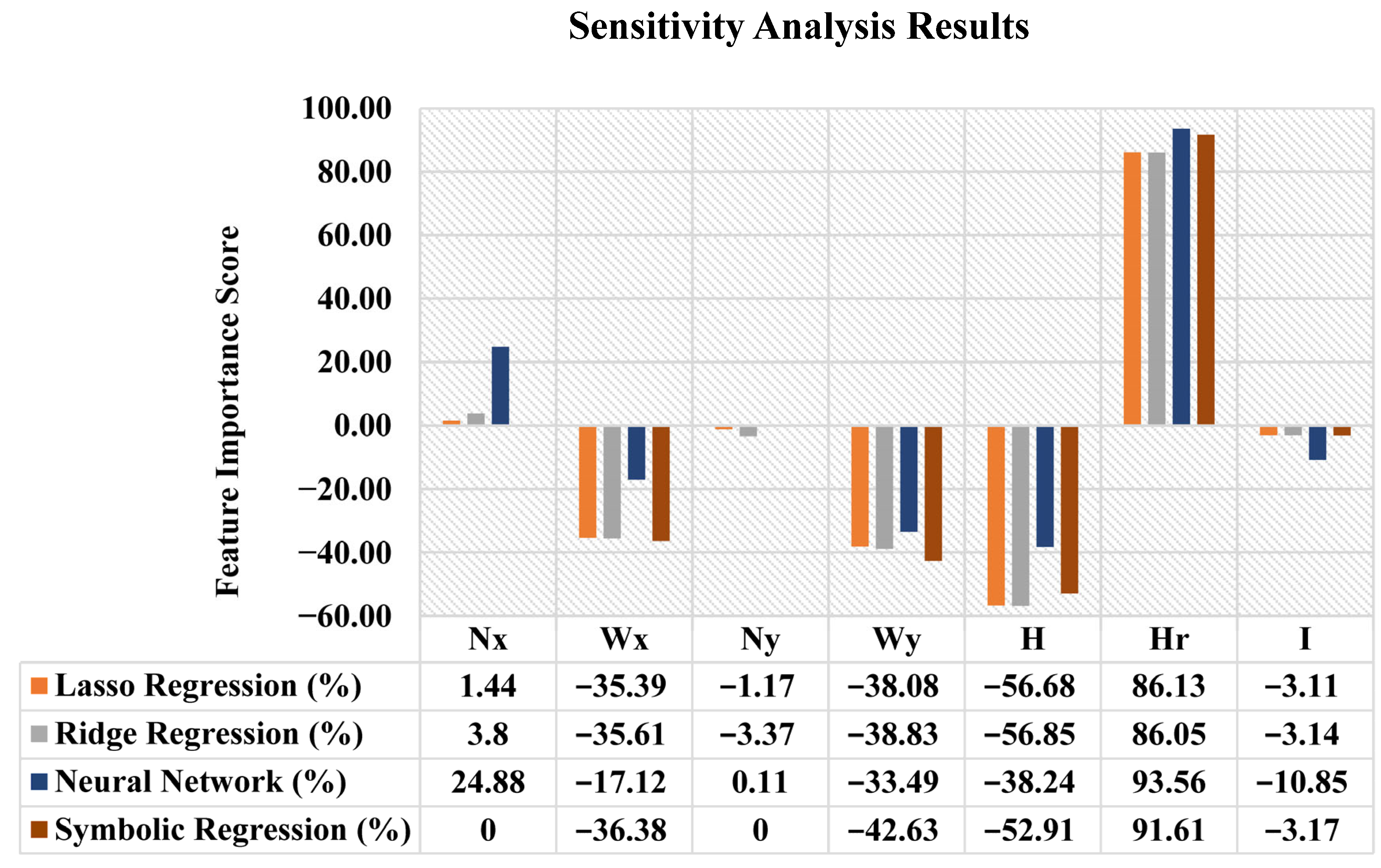
The sensitivity evaluation was performed using the Python programming environment, with essential packages including scikit-learn for regression models and PySR for symbolic regression. Perturbation-based approaches were used depending on model type. The results are graphically summarized in Figure 7, with feature influence values scaled to percentage scores for comparison. To enable direct comparison across these approaches, sensitivities are expressed on a standardized, unitless scale: coefficients from Lasso and Ridge were taken as absolute standardized values, Neural Network sensitivities were derived through perturbation-based gradients, and Symbolic Regression sensitivities were computed from the global normalized derivatives of the closed-form equation. This allowed the results to be reconciled into a unified ranking of key design parameters. As shown in Figure 7, all models consistently identify the ground-to-upper-storey height ratio (Hr) as the most influential factor, followed by overall height (H) and plan bay widths (Wx, Wy), while parameters such as bay numbers (Nx, Ny) and GS infill percentage (I) exhibit minimal influence.

The sensitivity analysis clearly identifies the Hr as the most dominant factor influencing stiffness deficiency in OGS structures. It consistently exhibits high scaled sensitivity across all models, peaking at 93.56% in the Neural Network, highlighting its critical role in determining the required MF. This aligns with structural behavior, as taller ground storeys relative to upper storeys result in increased flexibility and lower stiffness, making the structure more prone to soft-storey failure. The H also shows a significant negative influence, indicating that as overall height increases, base stiffness tends to decrease due to increased flexibility. While not as critical as Hr, it remains an essential parameter in evaluating MF demand.

The influence of I at the GS, though moderate (ranging between −3% and −10%), contributes positively to stiffness and hence reduces MFo demand. This confirms the structural benefit of even partial masonry infill in enhancing GS stiffness. Bay widths (Wx, Wy) show limited and inconsistent sensitivity, with minor negative effects in some models and minimal overall influence. As such, they are acknowledged but not emphasized in the final model interpretation. Notably, the number of bays (Nx, Ny) were found to have negligible impact and were automatically excluded by symbolic regression from the final predictive equation. This reinforces the view that when span dimensions and height proportions are considered, the bay count adds little predictive value for MF estimation.

The interpretable equation (Equation (2)) not only reflects the dominant influence of Hr, H, Wy, Wx, and I, but also validates the elimination of Nx and Ny. The symbolic structure allows for direct analytical sensitivity, which complements the empirical results and further underscores the importance of using interpretable ML tools like symbolic regression in structural engineering. This strengthens the credibility of the symbolic regression model and provides engineers with actionable insights for improving the seismic resilience of OGS buildings.

5.5. Comparison of Actual and Predicted MF Using ML Techniques

A plot of actual vs. predicted MFo values is presented in Figure 8. By using this graph alongside other metrics, a comprehensive evaluation of the model’s effectiveness and reliability is carried out.

The plot in Figure 8 provides a visual comparison of actual MF (MFo) versus predicted MF (MFp) for multiple nonlinear machine learning models. The predictions generated by the Neural Network model exhibit the closest clustering around the ideal fit line, highlighting its superior predictive accuracy and ability to generalize complex relationships between input features and MFo. Symbolic Regression, while slightly less tight in its clustering, still maintains a highly consistent trend with actual values, offering an excellent compromise between accuracy and interpretability, making it particularly valuable for engineering applications where transparency is crucial. Tree-based ensemble models such as Random Forest and Gradient Boosting also deliver strong predictive alignment, although some points deviate marginally at the extremes. These methods leverage multiple weak learners to enhance robustness and handle nonlinearity effectively. The Decision Tree model shows discrete prediction steps and, while it aligns well in most regions, slight overfitting tendencies are visible, especially where it perfectly hits individual points but lacks general smoothness across the dataset. Overall, the visualization affirms that Neural Networks are the top-performing model for accuracy-driven tasks, and SR provides a dependable, codifiable alternative with strong alignment with the actual values, making it a benchmark for interpretable ML in structural engineering.

6. Validation of the Proposed Symbolic Regression Model

To further evaluate the reliability of the developed model in predicting suitable MFs, a validation exercise is conducted using five additional OGS frame configurations. These configurations, characterized by varied geometric parameters, were intentionally excluded from the training dataset. As such, they serve as unseen data for assessing the model’s predictive accuracy and generalization ability. Detailed descriptions of these validation models are provided in

Table 6. Details of validated models.

Model Designation	Nx	Wx	Ny	Wy	Lx	Ly	α	H	Nz	HG	HG+1	Hr	I	TPG	IPG
V1	4	4.0	4	4.0	16	16	1.000	12.5	4	3.5	3	1.167	10	40	4
V2	4	3.0	4	3.0	12	12	1.000	13.5	4	4.5	3	1.500	20	40	8
V3	4	3.5	4	3.5	14	14	1.000	18.2	6	3.2	3	1.067	15	40	6
V4	5	4.0	5	3.5	20	17.5	1.143	19.2	6	4.2	3	1.400	13	60	8
V5	5	4.0	3	4.0	20	12	1.667	12.5	4	3.5	3	1.167	26	38	10

.

The required magnification factors (MFo) for the five new models are calculated using the method outlined in Section 3. Additionally, the predicted magnification factors (MFp) were obtained using the SR model (Equation (2)), as well as the Random Forest and Neural Network models, which demonstrated the highest accuracy among all ML techniques in this study. These MFp calculations for those ML techniques are performed using Python programming. The details of MFo and MFp for the new models are presented in

Table 7. Details of observed and predicted MFs for the validated modes.

Model Designation	MFo	MFp
		Symbolic Regression	Random Forest	Neural Network
V1	3.300	3.230	3.420	3.300
V2	4.237	4.770	4.700	4.550
V3	2.671	2.660	2.800	2.650
V4	3.144	3.160	3.350	3.200
V5	3.175	3.120	3.380	3.250

.

The MF determination technique, as well as the proposed MF equation, is stiffness-driven and therefore independent of the seismic demand scalars R, Z, soil type (I—hard; II—medium; III—soft), and importance factor (I_f). These parameters influence the amplitude of seismic demand but do not alter the structural stiffness that governs soft-storey behavior. Soil flexibility (SSI) can influence the seismic response of structures, but not the intrinsic structural stiffness unless foundation flexibility is explicitly modeled. The present MF prediction was validated for soil types and the considered seismic demand scalars, while extensions to cases with significant SSI effects are identified as a direction for future work.

To assess the predictive accuracy of different modeling approaches, the predicted MFs (MFps) from Symbolic Regression, Random Forest, and Neural Network are compared against the actual MFo values of five newly adopted models. For each model, the absolute error is calculated as the absolute difference between the predicted MFp and the actual MFo. The model yielding the smallest absolute error for a given data point is considered to have the most accurate prediction. Based on this analysis, Symbolic Regression (SR) provided the closest match to MFo in three out of five cases, while the Neural Network model was closest in the remaining two cases. The Random Forest model did not yield the closest prediction in any instance. These results suggest that SR demonstrates a strong generalization capability and reliable accuracy across varying structural configurations, while Neural Networks remain competitive, particularly in scenarios involving higher predicted values.

Additionally,

Table 8. Stiffness percentage, Mfo, and details of columns for the validated models.

Model Designation	OGS Stiffness %		MF	MOGS Stiffness %		Column Dimensions
	kx	ky		kx	ky	Initial	Final
V1	23.289	23.289	3.230	112.957	112.957	350	780
V2	21.056	21.195	4.237	110.250	110.222	350	880
V3	34.552	33.154	2.650	112.471	111.470	350	675
V4	18.509	19.280	3.144	111.838	121.315	350	910
V5	30.926	43.402	3.120	111.251	129.930	350	760

presents the GS to immediate upper-storey stiffness percentages for both OGS and MOGS models, along with the corresponding cross-sectional details of the GS columns.

These values were derived using the minimum required MF from Table 7, ensuring a precise assessment of stiffness variations across different structural configurations. It was observed that the predicted MF (MFp) obtained from both the proposed SR relationship (Equation (2)) and the Neural Network model is effective in addressing the stiffness shortfall. Specifically, the stiffness percentages of the MOGS models exceed 100% when the lowest MF values from Table 7 are applied, indicating that the soft-storey condition is adequately corrected. This outcome validates the efficacy of the proposed data-driven approaches in mitigating stiffness deficiencies and improving the seismic performance of OGS buildings.

6.1. Seismic Response Analysis of the Validated Structural Models

Further, to assess the impact of MFs, the response parameters for OGS and MOSG of validated models are evaluated in Figure 9, Figure 10 and Figure 11.

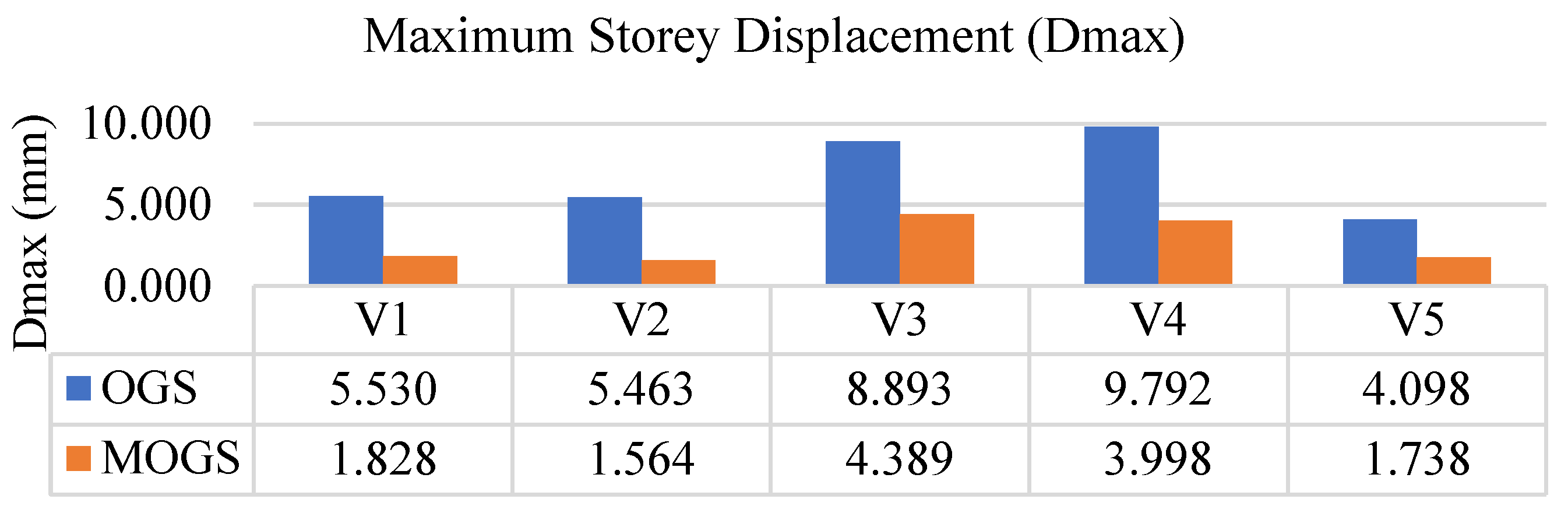
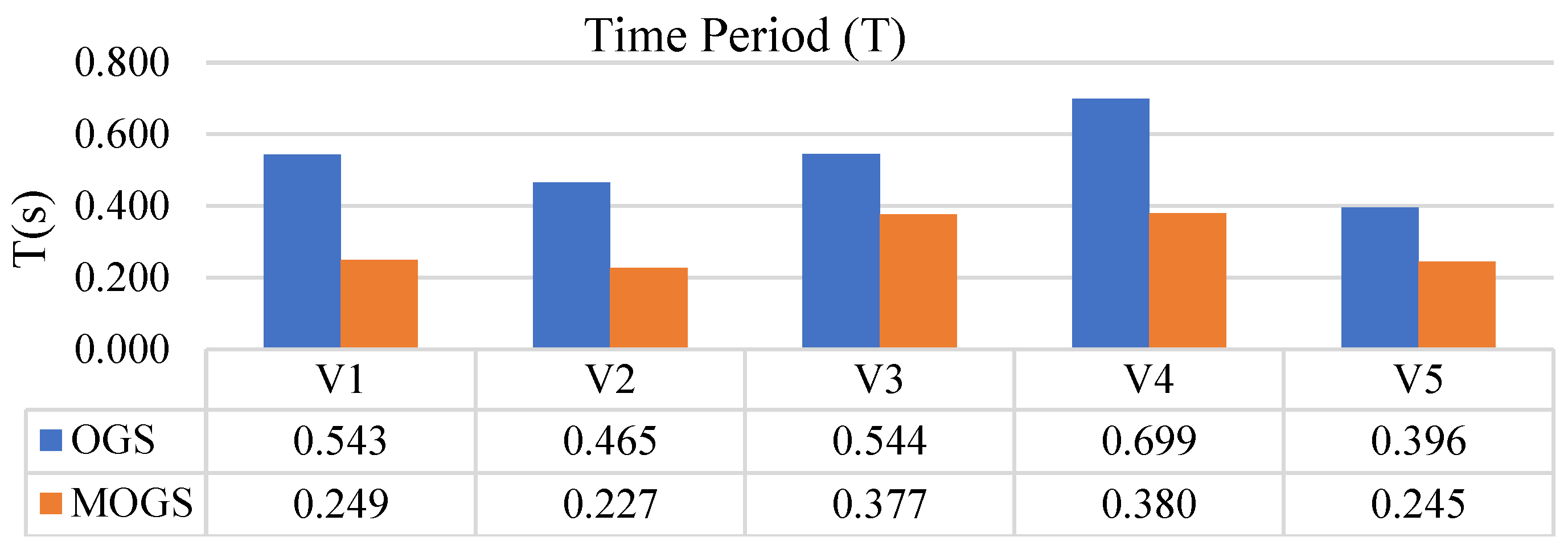
The presented figures (Figure 9, Figure 10 and Figure 11) provide a comparative evaluation of the seismic behavior of OGS and MOGS models, focusing on three key parameters: maximum storey displacement, inter-storey drift, and the fundamental time period. In this study, maximum storey displacement refers to the lateral displacement measured at the top storey, which represents the largest overall deflection of the structure relative to the fixed base under seismic excitation. Inter-storey drift is defined as the relative displacement between two consecutive floors normalized by the storey height, and is a critical indicator of the soft-storey mechanism. The maximum inter-storey drift for OGS buildings is specifically recorded at the GS to immediate upper-floor level, as this location consistently exhibits the highest relative deformation due to the stiffness discontinuity. The findings clearly demonstrate that MOGS models exhibit superior seismic performance, primarily attributed to their enhanced stiffness. For maximum storey displacement, OGS models show significantly larger lateral deflections, mainly due to the absence of infill walls at the GS level, which increases flexibility and vulnerability to lateral forces. In contrast, the application of MFs in MOGS models results in stiffer GS columns, thereby reducing displacements and improving resistance against lateral seismic loads. The inter-storey drift analysis further reinforces this outcome. For a quantitative performance evaluation, the inter-storey drift ratios of the MOGS models were compared against those of the initial OGS models. The results are presented in Figure 10, highlighting the reduction in drift concentration at the GS through MF application. OGS configurations tend to develop pronounced drift at the GS, a key indicator of the soft-storey mechanism. However, MOGS models exhibit a more uniform drift distribution, mitigating stress concentrations and enhancing structural continuity. Additionally, the dynamic characteristics assessed through fundamental time period analysis indicate that OGS models have longer periods due to reduced stiffness, making them more susceptible to unfavorable dynamic behavior, such as excessive GS drift, larger fundamental time periods, and amplified seismic demand, which collectively increase their vulnerability during earthquakes. In contrast, MOGS models display shorter time periods as a result of increased ground-storey stiffness, contributing to a more stable dynamic response. MOGS models effectively address the soft-storey vulnerability by improving GS stiffness through the application of MF. This leads to reduced lateral displacement, controlled inter-storey drift, and improved dynamic characteristics, specifically reflected in shorter fundamental time periods and a more stable overall seismic response. These improvements underscore the importance of adopting MFs in the design of OGS buildings for enhanced seismic safety and reliability.

To complement the elastic spectrum-based analysis and provide further confidence in the findings, a nonlinear pushover and nonlinear time history evaluation was carried out for one representative 0M1-53535 OGS model and its corresponding MOGS configuration.

6.2. Nonlinear Pushover Analysis

The analysis was performed in SAP2000 v24 software using a displacement-controlled procedure, following the guidelines of ATC-40 [51] and ASCE 41-13 [52]. The primary objective is to evaluate global seismic performance by incrementally applying lateral loads and tracking hinge formation and progression until target displacement or collapse is reached.

In SAP2000, lateral load is applied gradually at the roof-level control node until a specified displacement demand is achieved. Plastic hinge properties are assigned to structural members based on ASCE 41-13 [52]: nonlinear moment hinges (M3) at both ends of beams and columns, shear hinges (V2/V3) in select elements prone to shear failure, and user-defined axial hinges (P-M2-M3 interaction type) at the center of equivalent diagonal struts to represent the nonlinear axial behavior of masonry infill panels. Automatic step-size adjustments ensure numerical convergence at each increment, and the performance point is identified using the capacity spectrum method as defined in ATC-40 [51].

The resulting pushover curves (Figure 12) demonstrate a marked contrast between the OGS and MOGS systems. The OGS curve rises slowly to a limited peak force and then declines, reflecting its lack of reserve strength and poor post-yield performance. By contrast, the MOGS model achieves significantly higher lateral capacity, with smoother strength degradation after peak and more stable post-yield behavior, indicating improved ductility and robustness. The magnified columns in the MOGS configuration clearly enhance both initial stiffness and energy absorption capacity.

Key performance parameters derived from the pushover analysis are summarized in

Table 9. Critical parameters of pushover analysis.

Models	δy	δu	µ	Vy	Vu	δpp	Vpp
OGS	0.0151	0.0464	3.7276	2633.093	3066.337	0.111	2870.10
MOGS	0.0302	0.0789	2.6149	9321.023	11,345.240	0.053	10,561.29

. The OGS model exhibited a substantially lower yielding force (Vy) at yield displacement (δy), ultimate force (Vu) at ultimate displacement (δu), and performance point capacity (Vpp) at performance point displacement (δpp) than the MOGS model, confirming its high seismic vulnerability. Conversely, the MOGS frame displayed markedly higher strength values and improved global behavior, although its ductility ratio (µ) was slightly lower due to the higher stiffness of the magnified columns.

These results confirm that the OGS model suffers from limited lateral resistance and poor deformation capacity, whereas the MOGS configuration achieves a much higher base shear capacity and stable nonlinear response. The findings from this representative nonlinear analysis are consistent with the elastic spectrum-based evaluations, providing additional validation that the proposed MF-based strengthening effectively mitigates the soft-storey collapse mechanism.

6.3. Nonlinear Time History Analysis

To further examine the seismic performance of OGS and MOGS systems, nonlinear dynamic analyses were performed using real earthquake records scaled to the design spectrum specified in IS 1893 (Part 1): 2016 [2]. The models incorporated nonlinear hinges assigned to beams, columns, and diagonal strut elements to capture inelastic behavior. The analysis was executed in SAP2000 through direct time integration of the equations of motion, employing either the Hilber–Hughes–Taylor (HHT) or Newmark-beta algorithms with small time steps (0.005–0.01 s) to ensure accuracy. Ground motions from the 1995 Kobe earthquake and the 1940 El Centro earthquake were selected as input excitations, representing strong and well-documented seismic events.

The results, expressed in terms of maximum roof displacement and maximum inter-storey drift, are presented in Figure 13.

For both earthquakes, the OGS model exhibits significantly higher displacements and drifts, reaffirming its seismic vulnerability. Under the Kobe record, the OGS frame reached a maximum roof displacement of 0.1463 m and an inter-storey drift of 0.0339, whereas the MOGS frame recorded substantially lower values (0.0581 m displacement; 0.0066 drift). This clearly demonstrates the effectiveness of column magnification in restraining inelastic deformations.

The El Centro record showed similar trends. The OGS frame showed maximum displacement and drift values of 0.0257 m and 0.0048, respectively, while the MOGS frame achieved much lower responses (0.0136 m displacement; 0.0017 drift). The reduced values highlight the role of the MF-strengthened GS columns in enhancing stiffness and ductility, thereby limiting damage under nonlinear seismic demand.

Overall, the nonlinear time history analyses corroborate the findings of the pushover study. The OGS configuration is consistently inadequate under strong ground motions, while the MOGS model demonstrates markedly improved stiffness, controlled drift, and reduced displacement demands, confirming the validity of appropriate MF-based strengthening as a reliable approach to mitigate soft-storey collapse.

7. Constructability of Magnified OGS Columns, Code-Integration Framework, and Practical Implications

7.1. Construction Technique of Magnified OGS Columns

At the intersection of the GS and the floor directly above, a variation in the column cross-section is observed due to the amplification of OGS columns by the MF. To simplify construction, this issue can be resolved by ensuring that the core column dimensions in the GS remain consistent with the gross column dimensions in the upper floors, along with maintaining uniform reinforcement details [41].

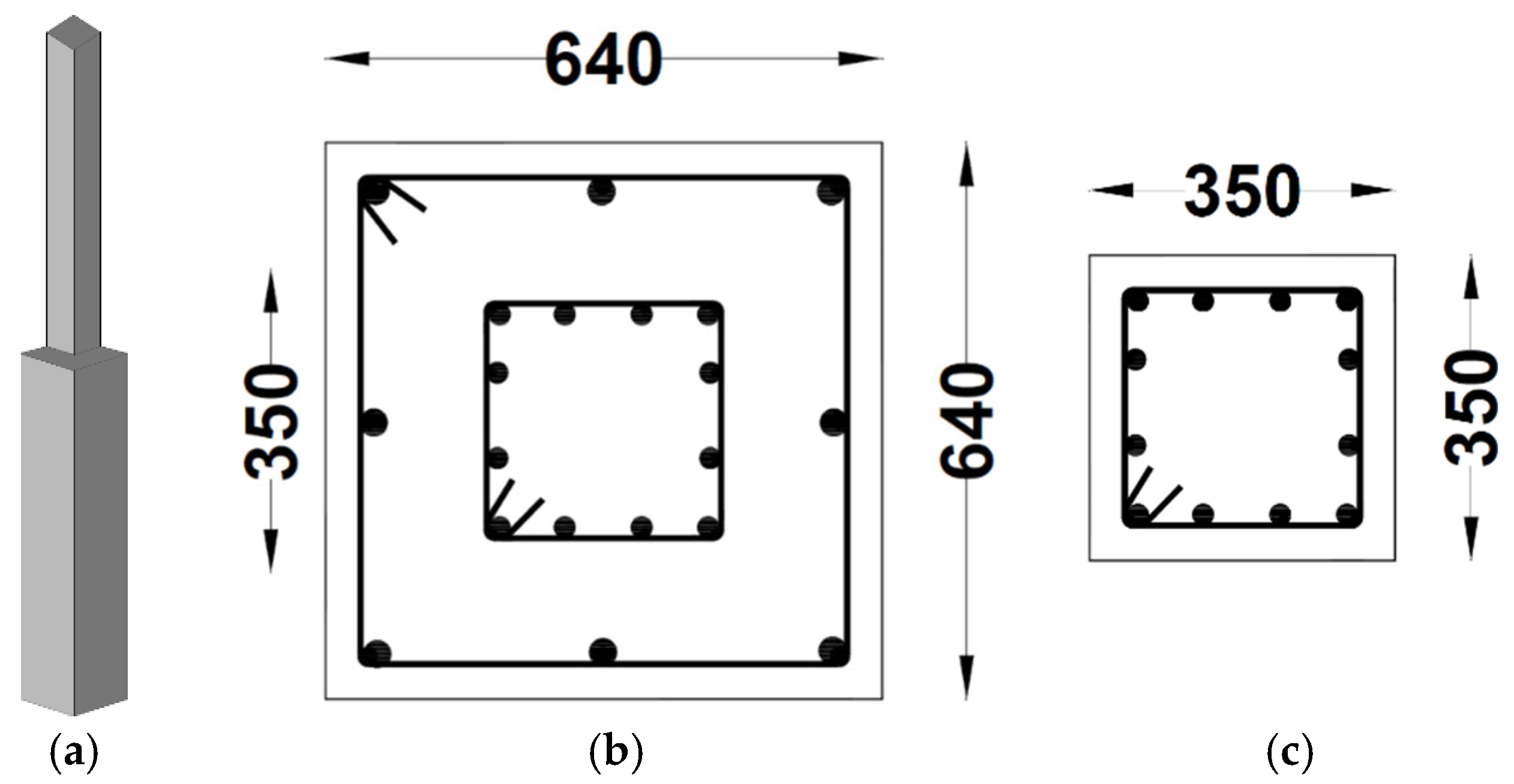
For instance, in model 0M1-53535, the GS column is magnified to 640 mm × 640 mm, with a steel reinforcement percentage (p_t) of 1.4%. A two-layer reinforcement approach was adopted, where the core layer matches the gross section of the upper-storey columns (350 mm × 350 mm with the required pt), as depicted in Figure 14. The magnified OGS column (640 mm × 640 mm) is reinforced with 8–25 mm∅ bars in the outer layer and 12–16 mm∅ bars in the core layer, resulting in a total p_t of 1.55% at the GS level. This GS column terminates at the base of the immediate upper storey, allowing only the core section to extend to the top level. By ensuring that the core section of GS columns aligns with the gross cross-section of upper-storey columns, while following the design specifications for reinforcement, the construction process can be significantly streamlined. This method can be effectively implemented in other models to facilitate easier construction.

It is acknowledged that several predicted MFs lead to larger GS column dimensions in the range of 800–910 mm. Such large cross-sections raise practical concerns regarding floor-plan utilization, architectural clearances, and construction detailing. From a structural standpoint, the increased column size directly enhances GS stiffness and shear capacity; however, it also imposes challenges such as beam–column joint detailing, increased shear demand at joints, potential bar congestion, and lap splice management. These issues necessitate careful detailing using staggered splices, confinement reinforcement, and optimized bar placement to maintain constructability. From an architectural perspective, the larger GS columns may intrude into parking or open spaces, and early coordination with architects is essential to integrate them within functional layouts. Despite these constraints, column magnification offers important advantages, such as preserving the overall building footprint and openness of the ground floor, requiring no introduction of shear walls or bracing elements that obstruct space, and being able to be implemented with conventional reinforced concrete construction practices. A comparative perspective highlights that RC shear walls provide strong stiffness but significantly reduce GS openness; buckling-restrained braces (BRBs) offer efficient energy dissipation but are not commonly codified in practice; and column jacketing is typically used for retrofitting existing buildings, not for new designs. In contrast, MF-based column magnification offers a simpler, codifiable, and cost-effective alternative that aligns with standard design and construction methods. While it requires attention to detailing and coordination, it provides a rational balance of seismic safety, functional openness, and construction economy.

To confirm code compliance, the magnified GS column designs are checked against the relevant provisions of IS 1893 (Part 1): 2016 [2] and IS 13920: 2016 [48] for Special Moment Resisting Frames (SMRFs). These checks include drift limits, strong-column/weak-beam requirement, confinement reinforcement, longitudinal reinforcement ratios, and shear strength. A compact summary for the representative model 0M1-53535 is presented in

Table 10. Code-compliance checks for magnified OGS columns.

Check	IS Provision (Code Clause)	Result for MOGS Model	Status
Maximum inter-storey drift	Δ/h ≤ 0.004 (IS 1893:2016 [2], Cl. 7.11.1)	0.000443	OK
Strong-column/weak-beam ratio	[∑Mc/∑Mb] ≥ 1.4 (IS 13920:2016 [48], Cl. 7.2)	1.476 (Least)	OK
Longitudinal reinforcement ratio	0.8% ≤ pt ≤ 6% (IS 456:2000 [46], Cl. 26.5.3.1)	1.4%	OK
Shear strength vs. demand	Vu (col) = factored shear force demand as per linear structural analysis (IS 13920:2016 [48], Cl. 7.5)	Safe	OK

. The results confirm that (i) the inter-storey drifts under design-level earthquake remain within the 0.004 h storey drift limit prescribed by IS 1893 (Part 1): 2016 [2], (ii) the strong-column/weak-beam ratio exceeds 1.4, as required by IS 13920: 2016 [48], (iii) longitudinal reinforcement lies between the code-specified minimum (0.8%) and maximum (6%) limits, and (iv) shear demand is safely resisted by the designed shear capacity with appropriate stirrup detailing. These checks collectively demonstrate that the MF-based magnified GS column designs remain consistent with seismic code provisions.

7.2. Proposed Code-Integration Framework for Sensitivity Results

The reconciled sensitivity results identify Hr as the primary driver of MF demand, with secondary influence from H and Wx, Wy, and minor influence from Nx, Ny, I. To embed these findings in practice without eroding safety or constructability, the following workflow is proposed:

• Applicability envelope: State the valid ranges (Table 1; Section 2) and regularity assumptions. If a design lies outside this envelope or exhibits strong SSI/torsion, revert to the stiffness-iteration method (Figure 2; Section 3).
• Base predictor (MF): Compute MF using the SR equation. For edge cases (e.g., very high Hr), take the max of SR-based MF and stiffness-iteration MF.
• Priority checks aligned with sensitivity: Since Hr dominates, require an explicit check of GS-to-upper-storey stiffness percentage ≥ 100% after applying MF. Second-tier checks focus on H and Wx, Wy (global flexibility); then, verify the drift limit Δ/h ≤ 0.004 and confirm the time period reduction is reasonable.
• Mandatory ductile detailing: Enforce IS 13920: 2016 [2] provisions after magnification: SC/WB at joints, confinement spacing limits, shear capacity (including capacity-based joint/column shear), longitudinal steel ratio bounds, and lap-splice location/length.
• Constructability gate: Cap column sizes and reinforcement congestion: clear cover, bar layering, joint shear stirrup density, and parking/functional clearances; if exceeded, trigger alternative measures (e.g., limited RC shear walls or steel jacketing) with the same stiffness target.
• Documentation and traceability: Record the model ID (IMHr–NxWxNyWyNz), inputs, SR-MF, final sizes, and pass/fail status of checks; include one worked sheet per project.
• Exception/edge-case rule: For SSI or plan-irregular frames, require a targeted nonlinear verification (pushover or a small set of compatible time histories) to confirm drifts and local demands after applying MF.
• Update loop: Encourage periodic re-calibration of MF and envelopes as more data accumulate.

This framework preserves code conservatism (Via MF, max-of-two rule, and mandatory checks), keeps designs buildable (constructability gate), and remains auditable (traceability pack). The proposed framework offers a codifiable pathway for design codes, while the worked example (Appendix D) illustrates its immediate practical application.

7.3. Practical Implications

This research provides the engineering community with a rational and interpretable framework for addressing the soft-storey vulnerability of OGS buildings, a configuration widely used in urban areas for parking and functional space. The SR equation offers a transparent and codifiable tool for estimating the required MF for OGS columns, enabling engineers to achieve stiffness regularization without resorting to trial-and-error or arbitrary assumptions. By integrating this predictive approach with sensitivity findings, practitioners can prioritize the most influential parameters during design, ensuring both safety and efficiency. The methodology is consistent with IS 1893:2016 [2], IS 456:2000 [46] and IS 13920:2016 [48] provisions, making it directly adaptable to practice. Furthermore, the proposed code-integration framework, along with the applicability envelope and worked application of proposed SR equation, provides a clear pathway for incorporating MF predictions into future design standards, balancing accuracy, interpretability, and constructability. Collectively, these contributions reduce design uncertainty, support performance-based seismic design, and enhance the resilience of OGS structures in high-seismicity regions.

8. Summary and Conclusions

This study developed a rational and interpretable framework for predicting the magnification factor (MF) required to strengthen ground-storey (GS) columns of Open Ground-Storey (OGS) buildings in order to mitigate the soft-storey failure mechanism. A comprehensive dataset of 216 three-dimensional RC OGS models was generated, incorporating variations in plan geometry, ground-to-upper-storey height ratio, and infill percentage. Iterative stiffness-based evaluations were performed to determine the minimum MF necessary to ensure that the GS stiffness exceeds that of the immediate upper storey, thereby eliminating the stiffness irregularity responsible for soft-storey vulnerability. To generalize this process for practical application, advanced machine learning (ML) models were developed. While black-box models such as Neural Networks achieved the highest predictive accuracy, Symbolic Regression (SR) yielded an interpretable closed-form equation that balances accuracy with transparency, making it particularly suitable for codification and design practice. Validation using additional OGS configurations confirmed the robustness of the proposed SR model, and seismic response evaluations demonstrated that Modified OGS (MOGS) frames incorporating the predicted MF exhibited reduced lateral displacements, controlled inter-storey drifts concentrated at the GS, and shorter fundamental time periods, collectively indicating improved dynamic performance. The main novelty of this work lies in establishing a stiffness-based MF prediction methodology that integrates large-scale parametric structural analysis with interpretable machine learning, resulting in a design-oriented predictive equation that is both accurate and transparent.

Despite these contributions, the study has limitations. Although a representative nonlinear pushover and time history analysis were performed for one representative structural model, the broader framework remains primarily based on elastic response-spectrum evaluations. The nonlinear checks confirmed the effectiveness of the proposed MF-based strengthening, and a similar response is expected across other model configurations; however, this cannot be fully generalized without additional nonlinear analyses. Moreover, plastic hinge cyclic degradation, P–Δ effects, cumulative damage, and the progressive cracking of masonry infills are not explicitly modeled. Soil–structure interaction (SSI) is also excluded, which may influence the seismic structure. These limitations are acknowledged, and future research is planned to expand nonlinear evaluations across multiple configurations and incorporate SSI to further generalize and refine the proposed framework.

In addition, the further optimization of MF demand is considered a promising area of future study. Such optimization may be explored through the partial replacement of masonry infill walls at the GS level with RC shear walls through the steel tube jacketing of columns or by employing other advanced strengthening strategies. Here, optimization refers to establishing the minimum strengthening requirement that restores GS stiffness without resorting to over-design, thereby achieving a rational balance between seismic safety and construction economy. Such approaches could complement the MF-based determination method proposed in this study and lead to more efficient solutions for improving the seismic resilience of OGS buildings.

For clarity and an at-a-glance description of practical impact, the key contributions and findings of this study are summarized below:

• Stiffness-targeted MF workflow (simple and codifiable): GS columns were redesigned until the GS stiffness exceeded that of the storey above; across 216 models, the validated set shows GS stiffness was increased from ~18–35% (OGS) to ≥110% (MOGS) in both directions when the required MF was applied.
• Interpretable MF predictor within a stated envelope: The SR equation provides a closed-form MF estimate in the training envelope (Table 1), and, on the validated set, matched MFo the most often (3/5 cases), with the NN performing best in 2/5 cases; both reliably cleared the stiffness deficit.
• Demonstrated demand reductions after MF application: In the five validated frames, MOGS reduced roof displacement by ≈51–71% and inter-storey drift by ≈75–83% relative to OGS; fundamental periods were consistently shorter, reflecting increased stiffness.
• Nonlinear checks corroborate trends: Under the Kobe record, OGS vs. MOGS peak roof displacement (0.1463→0.0581 m, ~60%) and drift (0.0339→0.0066, ~80%) confirm the effective control of inelastic response; El Centro shows similar reductions.
• Design/code compliance and constructability: Post-magnification drifts in validated cases (Dr ≈ 0.000186–0.000357) were comfortably below the IS 1893:2016 [2] limit (0.004 h), and redesigned GS columns remained detail-able; where final sizes are large, stepped columns, joint shear checks, lap-splice relocation, and bar layering mitigate congestion while preserving clearances.
• Limitations and future work: The current results address regular RC without explicit torsion and SSI modeling; extending the MF framework to strong torsional irregularity and SSI conditions (with targeted nonlinear verification) is a priority for future research. In addition, plastic hinge cyclic degradation, P–Δ effects, cumulative damage, and the progressive cracking of masonry infills and further optimization of MF demand are considered promising areas of future study.

In summary, this work demonstrates that integrating Symbolic Regression with stiffness-based evaluations provides a codifiable, interpretable, and technically robust tool for determining the required MF demand in OGS columns. The framework offers a viable pathway for enhancing seismic resilience, with potential applicability in performance-based seismic design and future code development.