Statistical Characteristics of Soil Dynamics in the Beijing-Tianjin-Hebei Region and Their Impacts on Structural Seismic Analyses

Abstract

The dynamic shear modulus ratios and dynamic damping ratios of soil are critical parameters for soil seismic response analyses and seismic safety evaluation of engineering sites. This study utilized dynamic triaxial test and resonant column test data of 5208 soil samples collected from more than 2500 boreholes across the Beijing-Tianjin-Hebei (BTH) region. Statistical analyses were conducted for five typical soil types (silty clay, clay, silt, silty sand, and fine sand), focusing on their dynamic shear modulus ratios and dynamic damping ratios. Key parameters representing the characteristics of soil dynamics, including the reference strain, the maximum damping ratio, and the damping ratio nonlinearity coefficient, were statistically evaluated. Median values, as well as the values corresponding to 84% and 16% exceedance probabilities, were provided. The median values of the reference strain, the maximum damping ratio, and the damping ratio nonlinearity coefficient were 13.43 × 10⁻⁴, 0.2155, and 0.7799 for silty clay; 16.47 × 10⁻⁴, 0.2266, and 0.7722 for clay; 10.64 × 10⁻⁴, 0.2012, and 0.7856 for silt; 11.98 × 10⁻⁴, 0.1842, and 0.7911 for silty sand; and 12.73 × 10⁻⁴, 0.1803, and 0.8064 for fine sand. Based on these statistics, the influence of various factors on the reference shear strain, maximum damping ratio, and damping ratio nonlinearity coefficient were investigated. The results showed considerable variability, and weak correlations were observed between these parameters and site-related factors such as sampling depth, shear wave velocity at sampling depth, overburden thickness, 30 m average shear wave velocity (V_S30), and 20 m equivalent shear wave velocity (V_se). The coefficients of determination for the linear regressions considering each factor were between 0.001 and 0.274, which were sufficiently close to 0 and indicated a weak predictive ability of the model considering only one factor. Furthermore, multivariate linear regression models incorporating all five influencing factors also achieved a slight reduction in standard deviation compared with directly adopting the mean values—by <5.5% for the reference shear strain, <3.9% for the maximum damping ratio, and <7.3% for the damping ratio nonlinearity coefficient. A case study was conducted to demonstrate the impact of the variability in soil dynamic parameters on both site seismic response and structural seismic response. For the selected ground motion inputs, site model, and structural model, differences in soil dynamic parameters led to variations in structural seismic response up to 54.5%. Comparative analyses with recommended values from existing studies indicate that the dynamic parameters of the five typical soil types in the BTH region investigated exhibited distinct regional characteristics: the dynamic shear modulus ratios were significantly lower, while the dynamic damping ratios were significantly higher. Comparisons with results from other studies on soil dynamic parameters in China showed that the dynamic shear modulus ratios derived from this study were noticeably smaller, while the dynamic damping ratios were significantly larger. At least one of the three soil dynamic parameters for each soil type failed to pass two-side t-tests, which indicated that the statistical data were from two distributions, that is, soil dynamic properties were intrinsically linked to sedimentary environments, exhibiting distinct regional specificity. Therefore, for boreholes lacking laboratory dynamic test data of soil in the BTH region, it was recommended to use the median values of reference shear strains, maximum damping ratios, and damping ratio nonlinearity coefficients provided in this study for the estimation of dynamic shear modulus ratios and dynamic damping ratios, while their variability must be taken into consideration.

1. Introduction

The dynamic shear modulus ratio and dynamic damping ratio are two fundamental parameters that characterize the dynamic behavior of soils. They serve as essential inputs for both seismic response analysis of soil layers and seismic safety evaluation of engineering sites. The accuracy with which these parameters are determined directly influences the reliability of the analytical results. Typically, the dynamic shear modulus ratios decrease with increasing shear strain, while the dynamic damping ratios increase accordingly. Research on the variation patterns of the soil dynamic shear modulus ratio and dynamic damping ratio with shear strain originated in the 1970s. In a pioneering study published in 1970, Seed et al. [1] first proposed curves describing the relationship between dynamic shear modulus ratios and dynamic damping ratios with shear strain for both sandy and cohesive soils. Since then, numerous researchers [2,3,4,5,6] have conducted extensive investigations into the empirical relationships between these soil dynamic parameters and shear strain, resulting in significant progress in this research field.

Due to differences in regional soil formation and sedimentary environments, the dynamic shear modulus ratios and dynamic damping ratio exhibit significant regional variability. Consequently, many researchers have determined these parameters for typical regional soils based on experimental data. Yuan et al. [7] proposed the recommended values for dynamic shear modulus ratios and dynamic damping ratios across different depths for six soil types based on resonant column test data from multiple regions including Beijing and Shanghai. Chen et al. [6,8,9] developed fitted curves and corresponding parameter recommendations for the variation in dynamic shear modulus ratio and dynamic damping ratio with shear strain based on free-vibration column tests conducted on typical soils from Nanjing and its surrounding regions. Shi et al. [10] carried out a statistical analysis of the average dynamic shear modulus ratios and dynamic damping ratios of silty clay in the Beijing region across different depths. Liu et al. [11] statistically analyzed the nonlinear dynamic parameters of soils in the New Region of Xiong’an. Chen [12], Zhang et al. [13], Lian et al. [14], Cai et al. [15], Shi et al. [16], and Xia et al. [17] conducted statistical analyses on experimental data for typical soils from different coastal regions of China and proposed corresponding recommended values for the dynamic shear modulus ratio and dynamic damping ratio. Lu et al. [18] and Wu et al. [19] conducted experimental studies on the dynamic shear modulus ratios and dynamic damping ratios of representative marine soils in China. Wu [20] performed experimental research on the dynamic shear modulus ratios and dynamic damping ratios of frozen soils on the Qinghai-Tibet Plateau.

Although extensive research has been conducted on the dynamic parameters of typical soils across various regions, samples targeting specific regions remained relatively limited, particularly in the Beijing-Tianjin-Hebei (BTH) region. With the rapid advancement of regional integration and large-scale infrastructure development, there was an increasing need to accurately determine soil dynamic parameters in this region. This study aimed to utilize laboratory dynamic test data of five representative soil types from the BTH region, in combination with statistical analyses and numerical modeling, to derive the statistical characteristics of key parameters that described the dynamic shear modulus ratio and dynamic damping ratio. The study further investigated the influencing factors of these parameters and evaluated their impacts on structural seismic response, with the goal of providing a practical method for selecting soil dynamic parameters in site seismic response analyses for boreholes lacking laboratory test data.

This paper introduced firstly the spatial distributions of the statistical data as well as their shear velocity and depth, and then the Hardin–Drnevich Hyperbolic Model and its modified version was used to describe the trends of dynamic shear modulus and dynamic damping ratios with shear strain. Nonlinear parameters including the reference shear strain, maximum damping ratio, and damping ratio nonlinearity coefficient were calculated from the statistical data, and their statistical characteristics and the correlations between nonlinear parameters and site factors including sampling depth, shear wave velocity at the sampling depth, overburden thickness, 30 m average shear wave velocity, and 20 m equivalent shear wave velocity were obtained. The dynamic response of a two-storied structure on a one-dimensional site model was conducted in order to reveal the influence of the variations in soil dynamic parameters on the seismic response of structures founded on these soils. Finally, according to the comparisons between different studies, a method to predict the dynamic shear modulus ratio and dynamic damping ratio of soil in the BTH region were proposed.

2. Data Overview

The statistical data were derived from dynamic triaxial tests and resonant column tests conducted on 5208 soil sample sets collected from 2500 boreholes located across Beijing, Tianjin, and Hebei Province in the northern part of the North China Plain. The samples included 564 clay specimens, 2483 silty clay specimens, 1029 silt specimens, 876 silty sand specimens, and 256 fine sand specimens.

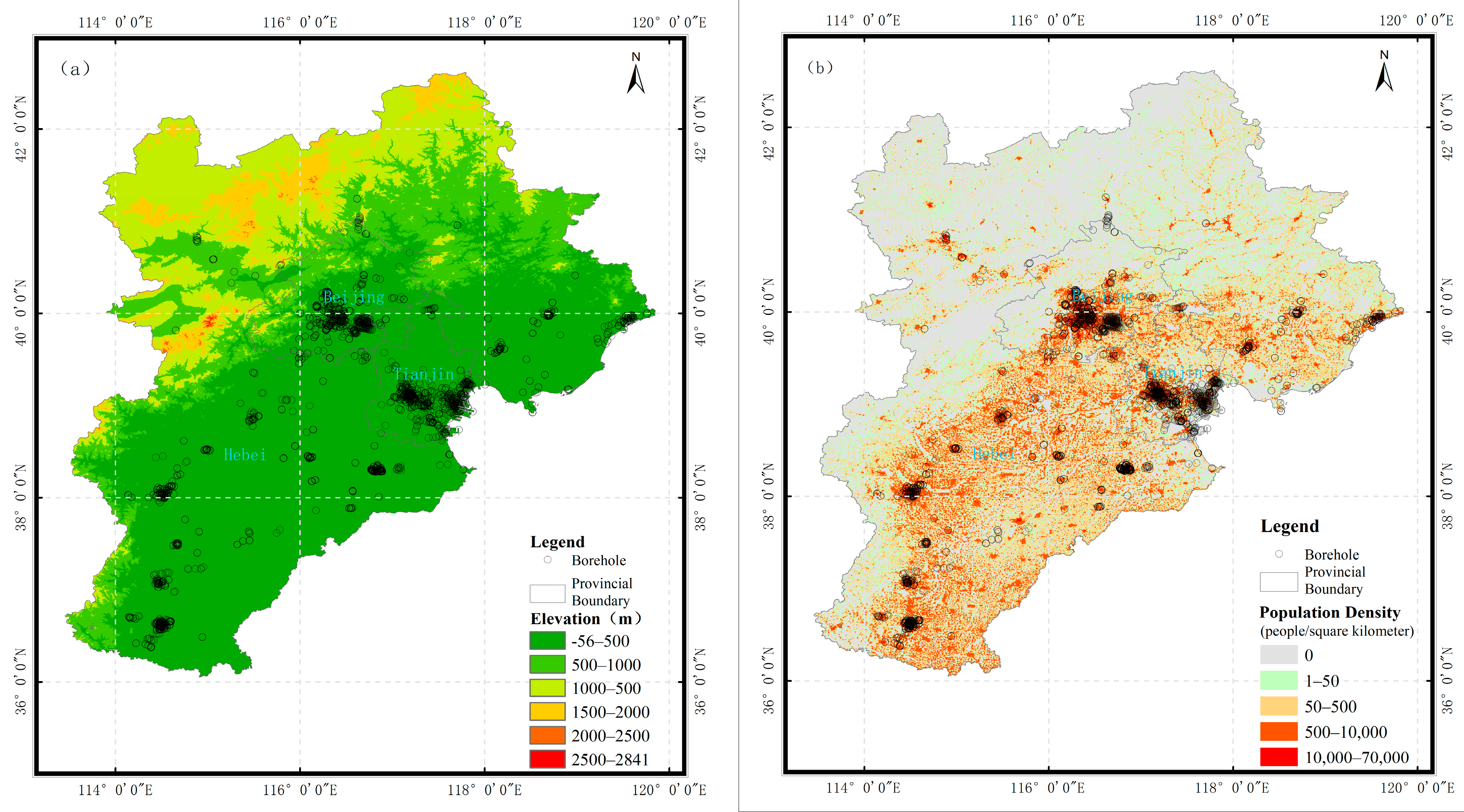
As shown in the borehole location distribution map (Figure 1), the boreholes were primarily concentrated in the southeastern plain areas of this region, particularly within medium and large-sized cities such as Beijing, Tianjin, and Shijiazhuang. In contrast, boreholes were sparsely distributed in other areas, with especially limited coverage in the northwestern mountainous regions. Based on this spatial distribution, the collected soil samples were considered representative of the dynamic properties of site soils in the densely populated southeastern plain but might not adequately reflect the geotechnical characteristics of the less populated northwestern mountainous zone.

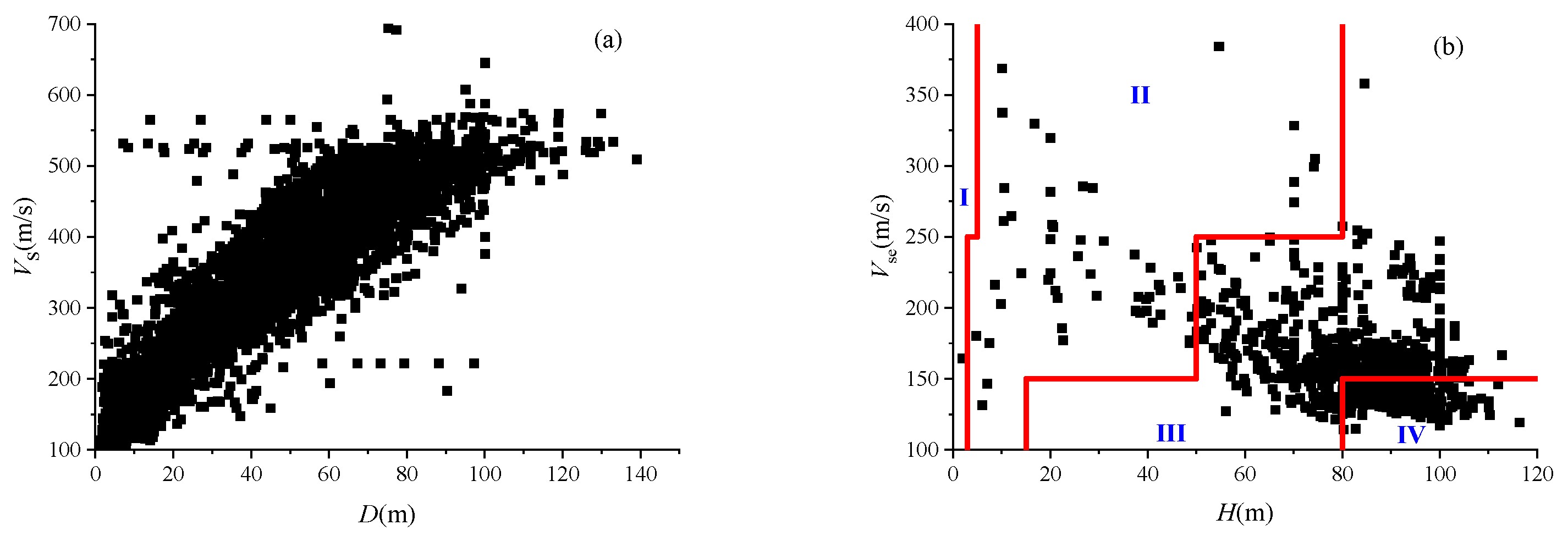
Based on the sampling depth of the soil specimens and the corresponding shear wave velocity at each sampling location (Figure 2a), it was observed that soil samples were distributed throughout depths less than 140 m, with a relatively uniform distribution within the depths less than 100 m. In terms of shear wave velocity, samples spanned the range of 100 to 700 m/s, with a more uniform distribution between 100 and 550 m/s. This comprehensive coverage indicated that the experimental soil data sufficiently represented the dynamic properties of the investigated soil types at various depths and across sites with different shear wave velocity conditions.

The relationship between overburden thickness and 20 m equivalent shear wave velocity (V_se), as revealed by the borehole data and illustrated in Figure 2b, showed that most sites had an overburden thickness between 50 and 110 m and a V_se range between 120 and 250 m/s. According to the site classification system defined in the Chinese Code for Seismic Design of Buildings (GB 50011) [21], these characteristics corresponded to Site Classes III and IV. Soil samples from Site Classes III and IV accounted for 57.8% and 39.6% of the total, respectively, whereas those from Site Classes I and II comprised only 0.1% and 2.5%. Consequently, the experimental data could be considered highly representative of the dynamic properties of soils in Site Classes III and IV. Conversely, the representativeness of the dataset for Site Classes I and II was limited.

3. Statistical Characteristics of Soil Dynamic Parameters

Currently, two empirical models have been widely adopted for describing the relationships between the dynamic shear modulus ratio and dynamic damping ratio with shear strain:

(1) Hardin–Drnevich Hyperbolic Model (H–D Model) [2]

$$\begin{array}{c}{G/G}_{\mathrm{m}\mathrm{a}\mathrm{x}}=1/(\gamma /{\gamma }_{\mathrm{r}})\end{array}$$

(1)

$$\lambda ={\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}(1-{G/G}_{\mathrm{m}\mathrm{a}\mathrm{x}})$$

(2)

where G is the dynamic shear modulus, G_max is the maximum dynamic shear modulus, γ is the dynamic shear strain, γ_r is the reference shear strain, λ is the dynamic damping ratio, and λ_max is the maximum dynamic damping ratio.

(2) Davidenkov Model [3]

$${\displaystyle \frac{G}{G_{\mathrm{m}\mathrm{a}\mathrm{x}}}}=1-{\left[{\displaystyle \frac{{(\gamma /{\gamma }_0)}^{2B}}{{1+(\gamma /{\gamma }_0)}^{2B}}}\right]}^A$$

(3)

$$\lambda ={\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}{\left\{{\left[{\displaystyle \frac{{(\gamma /{\gamma }_0)}^{2B}}{{1+(\gamma /{\gamma }_0)}^{2B}}}\right]}^A\right\}}^n$$

(4)

where G, G_max, γ, λ, and λ_max are defined as above. A, B, n, and γ₀ are fitting coefficients.

Among the two models, Model (1) was the standard empirical formulation for the relationship between shear modulus ratio, damping ratio, and shear strain used in seismic response analyses of soil layers as part of China’s seismic safety evaluation procedures [5] because Model (1) had less coefficients to be determined by soil tests. In comparison, Model (2) involved more fitting coefficients without standardized values, which could lead to irregular or inconsistent fitting results when dealing with large datasets [22]. Nevertheless, experimental data also indicated that the variation of soil damping ratio with shear strain was relatively complex and could not be fully captured by either the H–D model or the Davidenkov model [8]. More important, the coefficients in Model (1) were more easily obtainable, which was essential in engineering applications, so almost all of dynamic shear modulus curves and dynamic damping ratio curves in China were given by Model (1) or its modified version. Therefore, based on the experimental data compiled in this study, the dynamic damping ratio was expressed using the following empirical formula:

$$\lambda ={\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}(1-\alpha G/G_{\mathrm{m}\mathrm{a}\mathrm{x}})$$

(5)

where G, G_max, λ, λ_max are defined as previously. α denotes the damping ratio nonlinearity coefficient.

In this study, Equations (1) and (5) were employed to perform statistical analyses of the empirical relationships between the dynamic shear modulus ratios, dynamic damping ratio, and shear strain for typical soils in the BTH region. The results indicated that fitting the dynamic shear modulus ratio of each soil sample using Equation (1) yielded a maximum standard deviation of 0.011, while fitting the dynamic damping ratio using Equation (5) resulted in a maximum standard deviation of 0.021, both of which were within an acceptable accuracy range. Meanwhile, fitting the dynamic damping ratio using Equation (2) resulted in much larger standard deviations, whose mean value was 0.034. Small standard deviations also indicated that Equations (1) and (5) were adapted to the statistical data in the BTH region.

Figure 3 presents violin plots illustrating the distributions of nonlinear dynamic parameters across different soil types. As shown, nonlinear parameters such as the reference shear strain (γ_r), maximum damping ratio (λ_max), and damping ratio nonlinearity coefficient (α) exhibited considerable variability across soil types.

Table 1. Statistical characteristics of dynamic parameters for silty clay, clay, silt, silty sand, and fine sand.

No.	Soil Type	Reference Strain γr (×10−4)			Maximum Damping Ratio λmax			Damping Ratio Nonlinearity Coefficient α
		Median	84%	16%	Median	84%	16%	Median	84%	16%
1	Silty Clay	13.43	19.96	7.64	0.2155	0.2452	0.1886	0.7799	0.7228	0.8693
2	Clay	16.47	23.93	11.19	0.2266	0.2610	0.1993	0.7772	0.7331	0.8501
3	Silt	10.64	16.13	5.66	0.2012	0.2234	0.1790	0.7856	0.7434	0.8323
4	Silty Sand	11.98	16.43	7.97	0.1842	0.2133	0.1676	0.7911	0.7593	0.8373
5	Fine Sand	12.73	20.71	6.94	0.1803	0.2062	0.1644	0.8064	0.7711	0.8587

summarizes the median values of these parameters, along with the values corresponding to exceedance probabilities of 84% and 16%. Significant differences were observed among the three parameters. Therefore, further investigation into factors such as sampling depth, overburden thickness, and shear wave velocity were essential to improve the predictive accuracy of nonlinear soil dynamic parameters.

4. Analyses of Influencing Factors on Soil Dynamic Parameters

In this study, five factors characterizing the geological and geophysical conditions at the soil sampling locations were analyzed, which were sampling depth (D), shear wave velocity at the sampling depth (V_S), overburden thickness (H), 30 m average shear wave velocity (V_S30), and 20 m equivalent shear wave velocity (V_Se) defined in the Chinese Code for Seismic Design of Buildings (GB 50011) [21]. The influence of these factors on the soil dynamic parameters was analyzed, including reference shear strain (γ_r), maximum damping ratio (λ_max), and damping ratio nonlinearity coefficient (α).

4.1. Reference Shear Strain (γ_r)

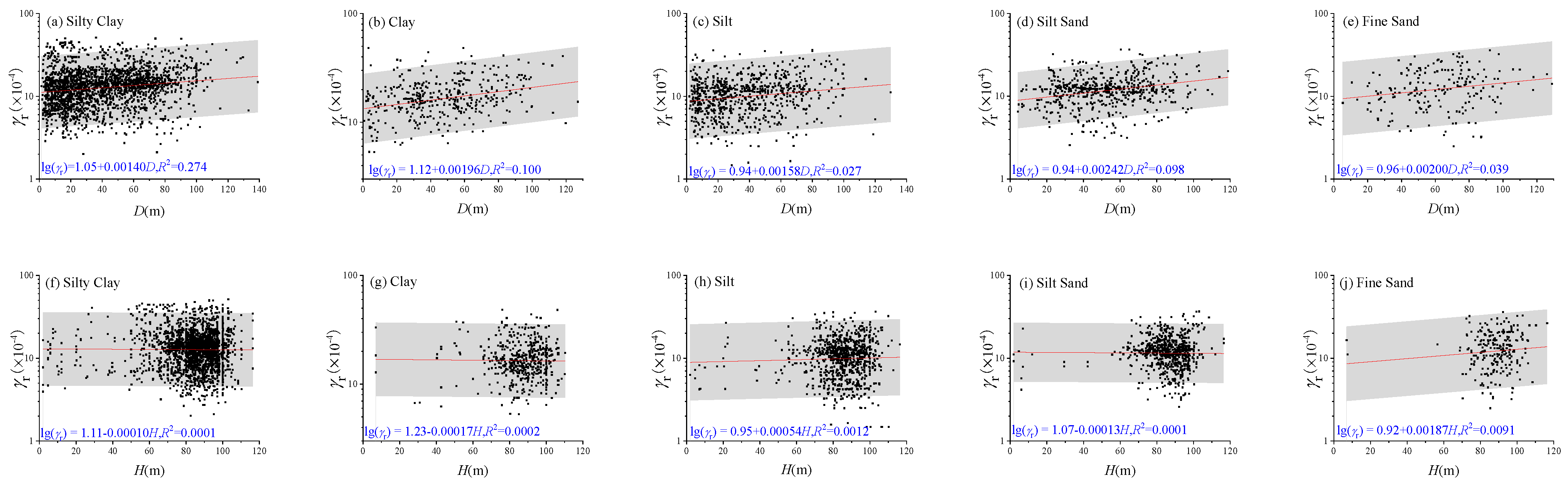
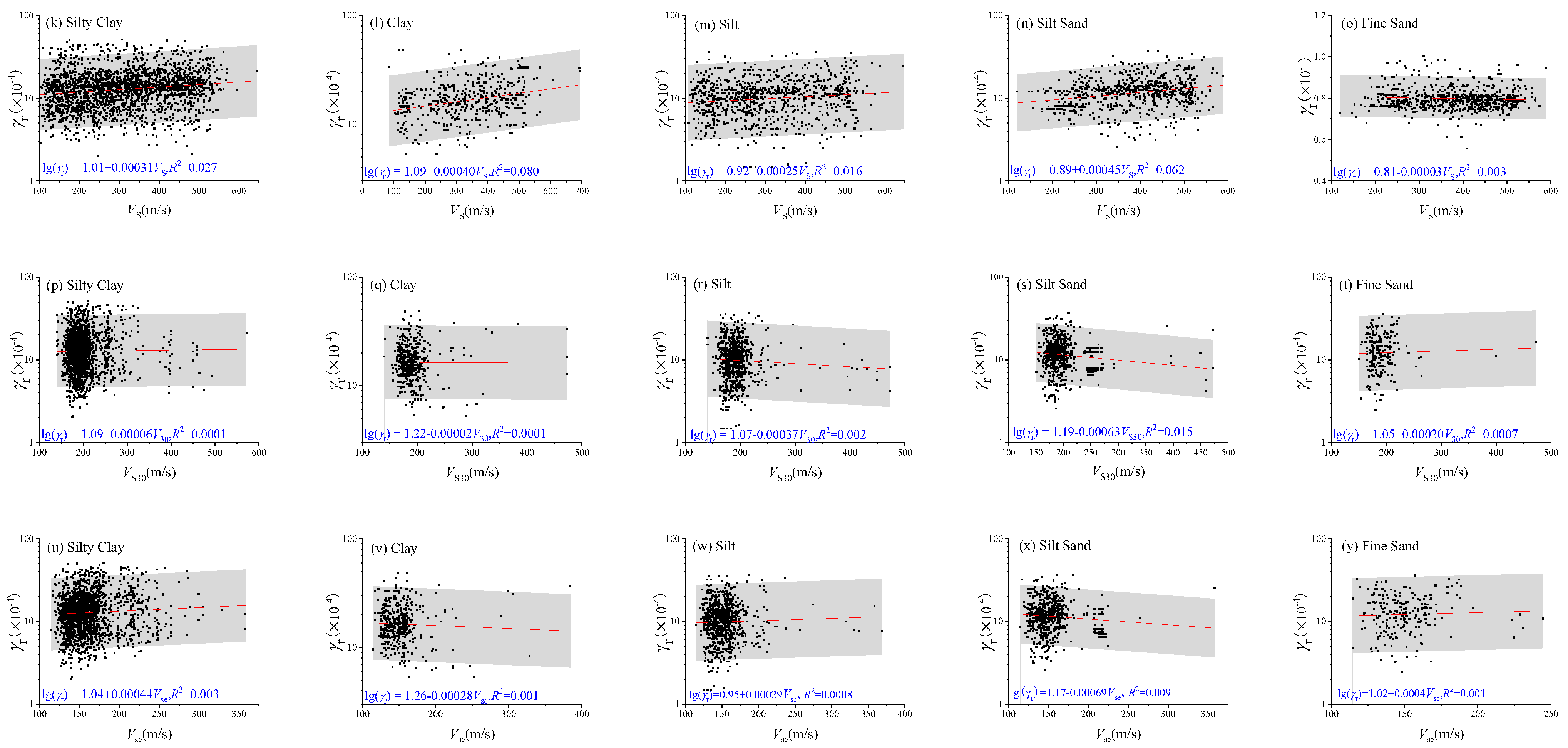
As shown in Figure 4, the correlations between the reference shear strain (γ_r) and various influencing factors exhibited considerable scatter. Despite the variability, γ_r tended to increase notably with both sampling depth (D) and the shear wave velocity (V_S) at the sampling depth across different soil types. In contrast, with increasing overburden thickness (H), 30 m average shear wave velocity (V_S30), and 20 m equivalent shear wave velocity (V_Se), no clear patterns were observed for most soil types, except for silty clay, which showed a distinct trend.

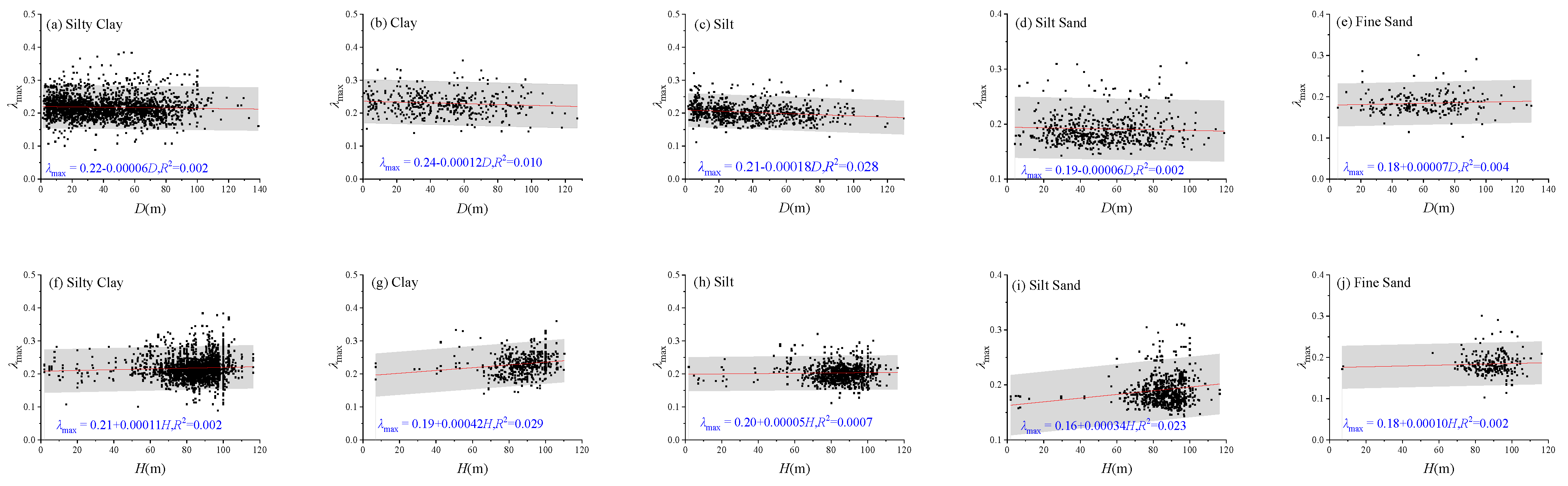
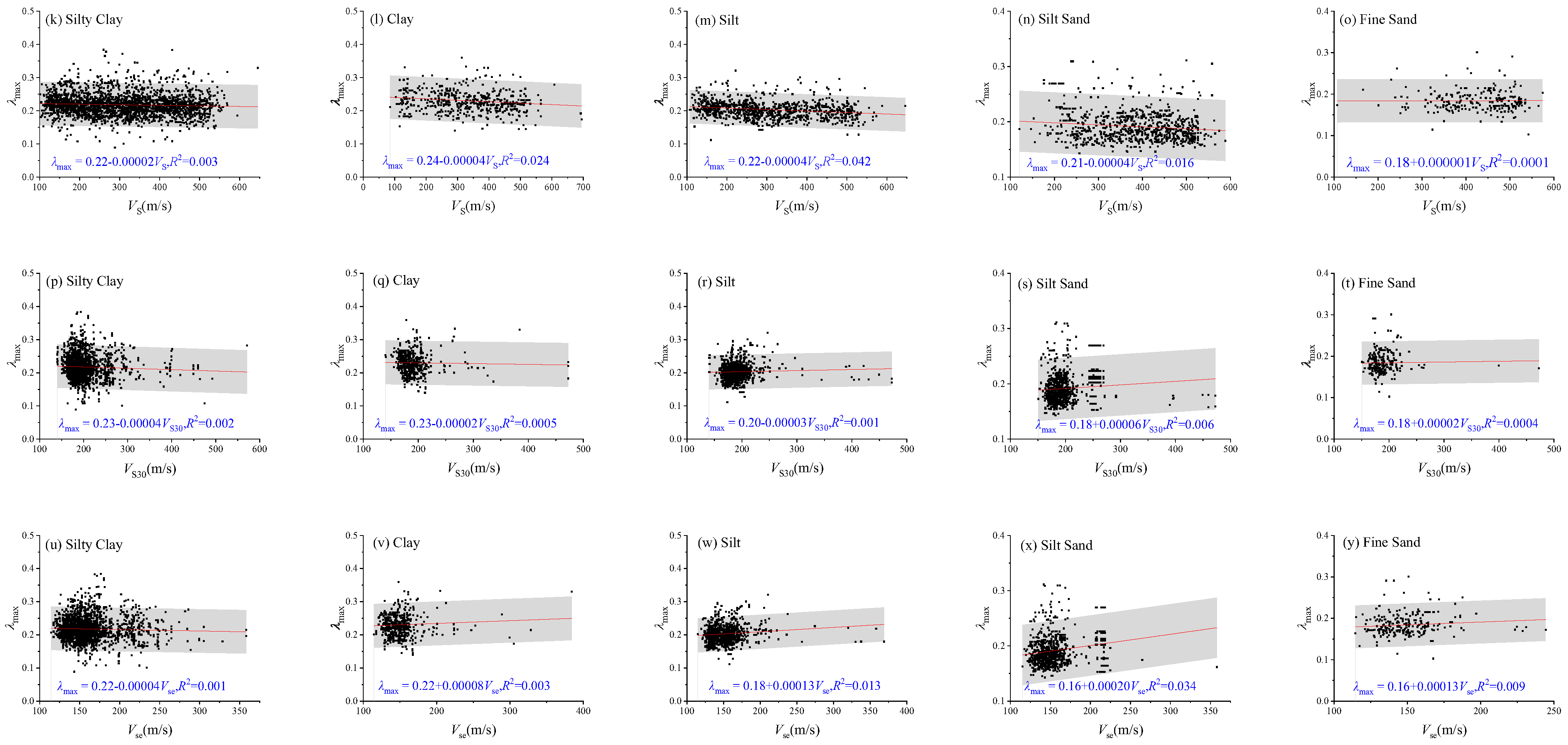
4.2. Maximum Damping Ratio (λ_max)

The correlation analyses between various influencing factors and the maximum ratio (λ_max), as presented in Figure 5, revealed significant scatter across all soil types. Specifically, λ_max generally exhibited a weak decreasing trend with increasing sampling depth (D) and shear wave velocity at the sampling depth (V_S) across most soil types, with the exception of fine sand. Conversely, a weak increasing trend of λ_max was observed with increasing overburden thickness (H). Additionally, for 30 m average shear wave velocity (V_S30) and 20 m equivalent shear wave velocity (V_Se), most soil types showed a weak increasing trend in λ_max, except for silty clay, which demonstrated atypical behavior relative to these parameters.

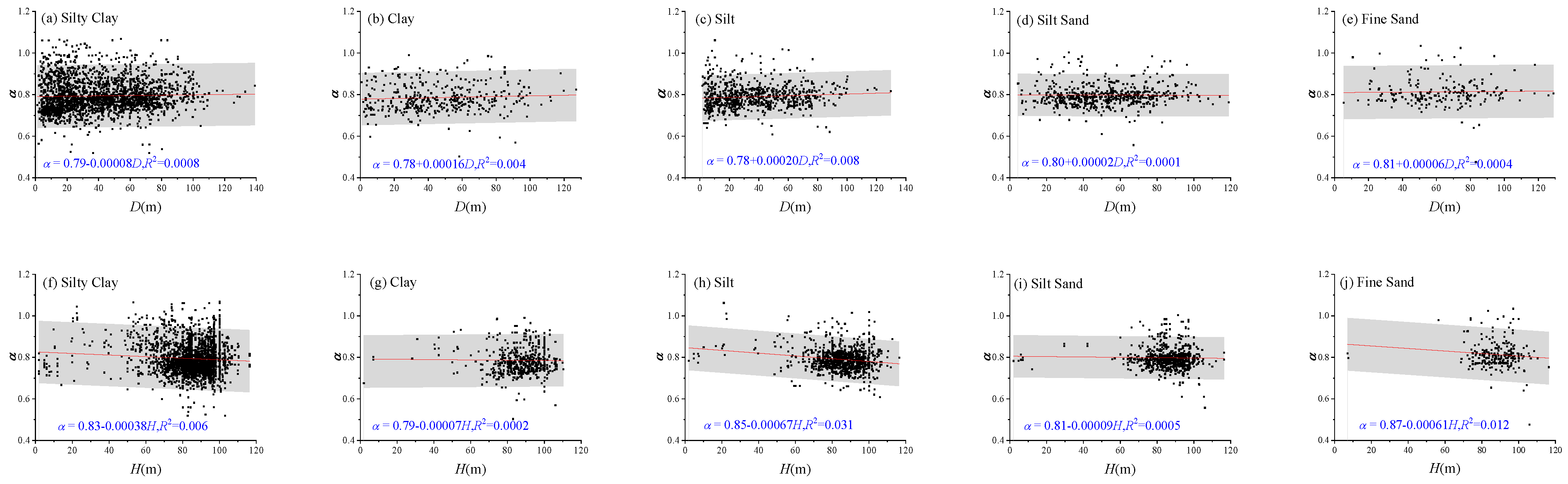
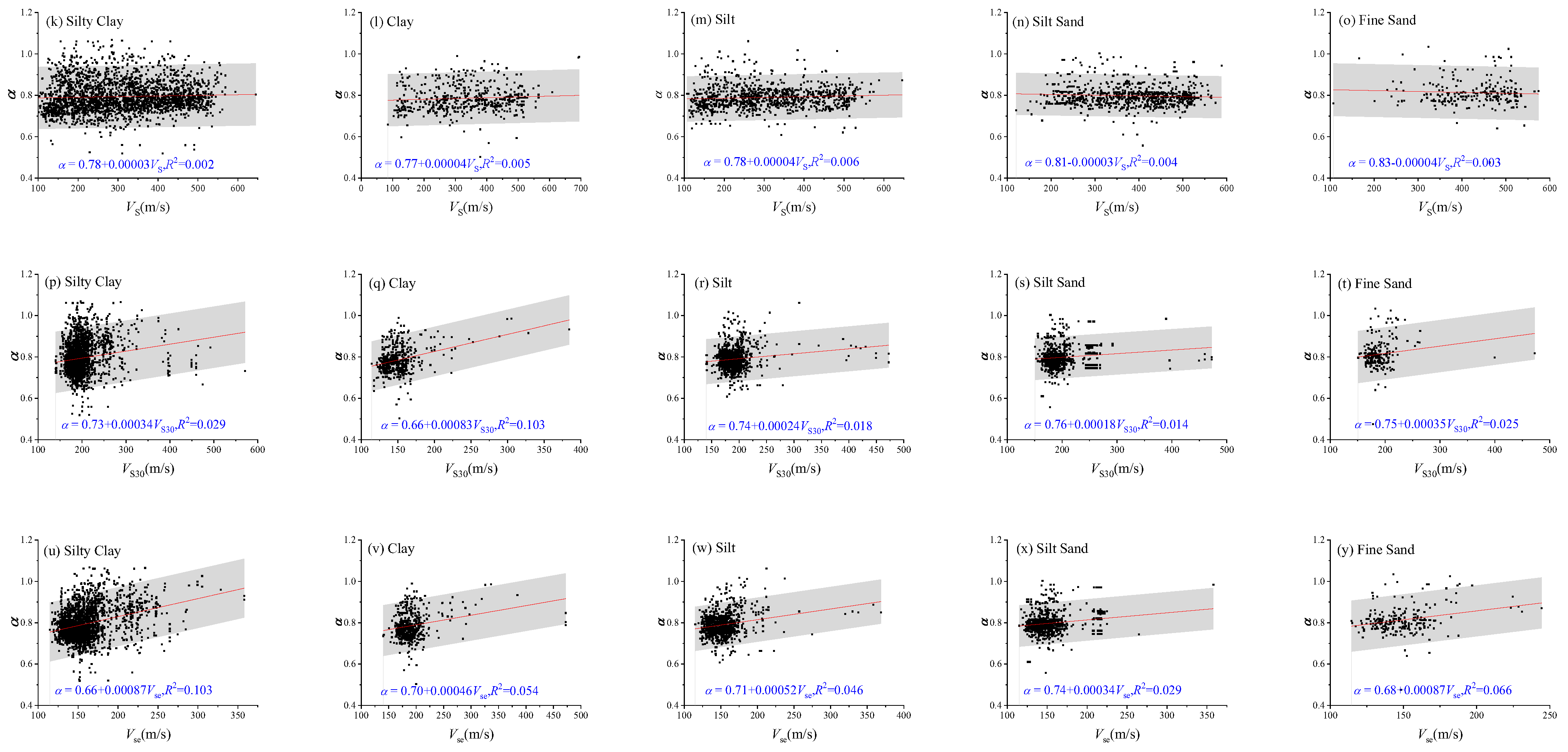
4.3. Damping Ratio Nonlinearity Coefficient (α)

The correlation analyses between various influencing factors and damping ratio nonlinearity coefficient (α), as presented in Figure 6, also revealed significant scatter across all soil types. Specifically, no clear trend was observed between α and sampling depth (D) or shear wave velocity at the sampling depth (V_S) across all soil types. Conversely, α exhibited a weak decreasing trend with increasing overburden thickness (H). Moreover, α showed an increasing trend with increasing 30 m average shear wave velocity (V_S30) and 20 m equivalent shear wave velocity (V_Se).

4.4. Recommendations for the Selection of Soil Dynamic Parameters

Multivariate linear regressions were performed using two sets of input variables: one considering all the five influencing factors and the other one considering only two factors, which were sampling depth (D) and overburden thickness (H). The regression coefficients were used to estimate the predicted values and standard deviations of the soil dynamic parameters.

As shown by the standard deviations of the prediction models (

Table 2. Standard deviations of different prediction methods.

No.	Soil Type	Reference Shear Strain (γr)			Maximum Damping Ratio (λmax)			Damping Ratio Nonlinearity Coefficient (α)
		Mean	5-Var Reg	2-Var Reg	Mean	5-Var Reg	2-Var Reg	Mean	5-Var Reg	2-Var Reg
1	Silty Clay	0.2176	0.2134	0.2142	0.0328	0.0327	0.0327	0.0750	0.0704	0.0747
2	Clay	0.1686	0.1597	0.1598	0.0330	0.0317	0.0324	0.0629	0.0583	0.0628
3	Silt	0.2293	0.2244	0.2261	0.0257	0.0250	0.0254	0.0546	0.0525	0.0535
4	Silty Sand	0.1776	0.1678	0.1686	0.0277	0.0267	0.0275	0.0507	0.0495	0.0507
5	Fine Sand	0.2257	0.2182	0.2212	0.0259	0.0257	0.0259	0.0636	0.0600	0.0632

), the multiple linear regression model incorporating all five influencing factors achieved a slight reduction in standard deviation compared with directly adopting the mean values—by approximately 1.9–5.5% for reference shear strain (γ_r), 0.3–3.9% for maximum damping ratio (λ_max), and 2.7–7.3% for the damping ratio nonlinearity coefficient (α).

In contrast, when only sampling depth (D) and overburden thickness (H) were included in the regression model, the reduction in standard deviation was more limited, with corresponding improvements of approximately 1.4–5.2%, 0.0–1.8%, and 0.0–6.3%, respectively. These results indicated that incorporating multiple influencing factors in the prediction of soil dynamic parameters did not lead to a substantial improvement in accuracy compared with using mean values.

Figure 7 illustrates the correlations among reference shear strain (γ_r), maximum damping ratio (λ_max), and damping ratio nonlinearity coefficient (α). As shown in the figure, λ_max increased noticeably with increasing reference shear strain (γ_r), while the damping ratio nonlinearity coefficient (α) showed a slight decrease with increasing reference shear strain (γ_r) but a more evident increase with increasing maximum damping ratio (λ_max), except for fine sand.

Therefore, it was recommended that γ_r, λ_max, and α could be selected based on the median or mean values for each soil type. Alternatively, as shown in the linear regression equations in Figure 7, the maximum damping ratio (λ_max) could be determined from the reference shear strain (γ_r), and the damping ratio nonlinearity coefficient (α) could be determined from the maximum damping ratio (λ_max). In either case, the variability of the data should be fully accounted for by incorporating the 84% and 16% exceedance probability values or by applying one standard deviation.

5. Impacts on Structural Seismic Analyses

To evaluate the impact of the variability in soil dynamic parameters on structural seismic analyses, a computational model was developed based on a selected borehole. The equivalent linearization method was applied to compute the acceleration time history of ground motions, followed by an analysis of the seismic response of an elastoplastic structural model.

5.1. One-Dimensional Borehole Model

The one-dimensional soil profile model and its corresponding parameters are summarized in

Table 3. Parameters of the borehole model for calculation.

No.	Layer Thickness (m)	Soil Type Code	Soil Type	Shear Wave Velocity (m/s)	Density (g/cm3)
1	4.0	1	Silty Clay	125	1.85
2	3.7	1	Silty Clay	133	1.85
3	8.1	2	Clay	165	1.85
4	8.4	1	Silty Clay	236	1.90
5	7.2	1	Silty Clay	266	1.90
6	6.3	2	Clay	288	1.90
7	7.1	3	Silt	288	1.90
8	5.6	4	Silty Sand	303	1.95
9	6.2	4	Silty Sand	355	1.95
10	8.2	5	Fine Sand	412	1.95
11	11.7	3	Clay	450	1.98
12	7.4	1	Silty Clay	465	1.98
13	8.0	3	Silt	465	1.98
14	10.5	5	Fine Sand	515	2.05

. The soil type, shear wave velocity, and density were based on in-situ measurements from borehole TJ0003. For each soil type, the reference shear strain (γ_r), maximum damping ratio (λ_max), and damping ratio nonlinearity coefficient (α) were selected based on the median values, as well as the values corresponding to the 84% and 16% exceedance probabilities listed in Table 1. These parameters were then used to determine the dynamic shear modulus ratio and dynamic damping ratio for each soil type. For cases where the dynamic shear modulus ratio was relatively large, the corresponding dynamic damping ratio was assigned a smaller value.

5.2. Two-Storied Structural Model

The structural model consisted of a two-storied reinforced concrete (RC) frame with a floor height of 3.0 m and a total of three spans. The side spans each had a length of 6.0 m, while the middle span measured 2.4 m. The structural model employed HPB300 steel [23] for transverse reinforcement and HRB335 steel [23] for longitudinal reinforcement, and the cement grade was C30 [23]. The cross-sectional dimensions and reinforcement details of the beams and columns are illustrated in Figure 8.

The open-source finite element software OpenSees version 3.8.0, widely recognized by international researchers, was employed as the computational platform for numerical modeling of the reinforced concrete frame structure. The modeling approach explicitly excluded non-structural elements. Concrete material was modeled using the Concrete02 material model, which accounts for the confinement effect provided by transverse reinforcement. Steel reinforcement was modeled using the Steel02 material model. Fiber sections were adopted for the cross-sections, and nonlinear beam–column elements based on force formulations were utilized. No special modeling was applied to beam–column joints, which were assumed to be rigidly connected. The column elements considered P-Delta effects, whereas the beam elements did not. Modal analysis results indicated that the fundamental period of the structure was approximately 0.43 s.

5.3. Analyses of Computational Results

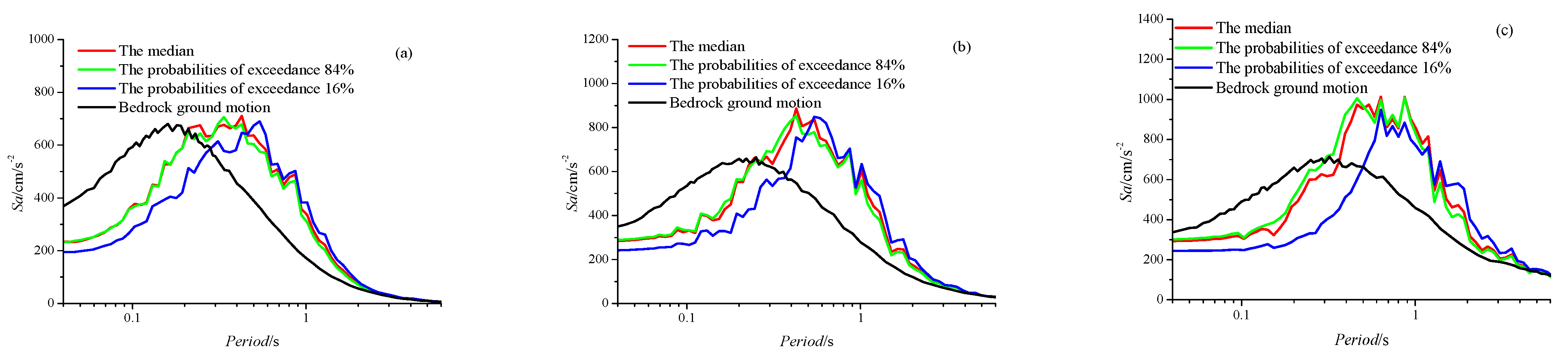
Three target sets of spectral accelerations were selected, representing motions rich in short-period components, motions with balanced low- and high-frequency content, and motions rich in long-period components. Artificially synthesized ground motion time histories matching these target spectral accelerations were used as seismic inputs. The ground motion was calculated using a one-dimensional equivalent linear analysis program. The resulting spectral accelerations are shown in Figure 9, where the black solid line denotes the spectral accelerations on bedrock site. As shown in Figure 9, soft overburden layers significantly amplify longer-period components (0.3–0.5 s < T < 2 s), with the amplification becoming more pronounced as the long-period content increased, while they substantially attenuates short-period motions. Regarding the selection of soil parameters, smaller dynamic shear modulus ratios and dynamic damping ratios (i.e., larger reference shear strain, smaller maximum damping ratio, and larger damping ratio nonlinearity coefficient) lead to greater suppression of short-period ground motions but stronger amplification of long-period components.

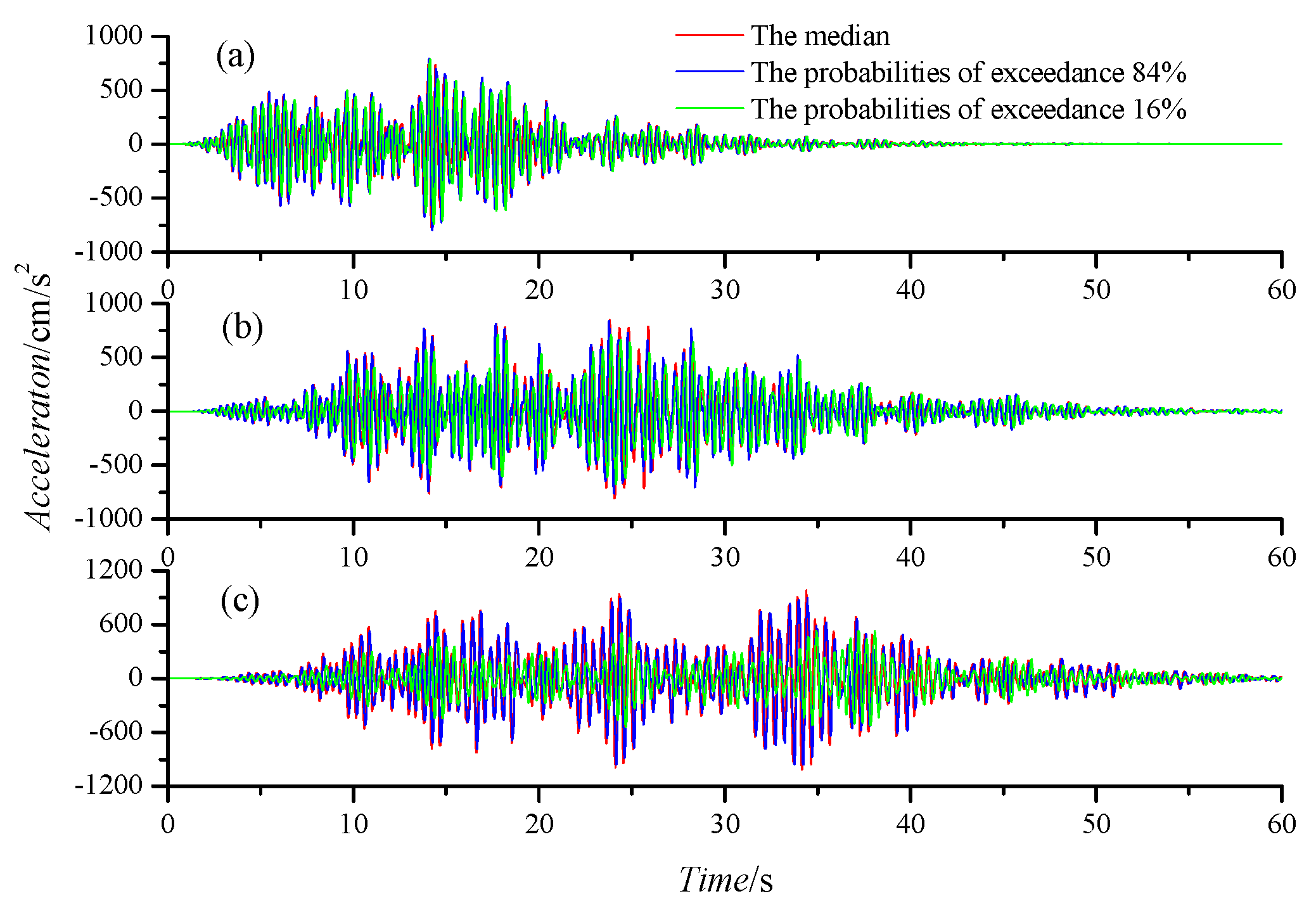
Using the acceleration time histories at the surface soil layer as input, seismic responses of the structural model were computed. The maximum seismic responses, represented by the rooftop acceleration time histories, are shown in Figure 10. It was observed from the figure that, under identical bedrock ground motion inputs, differences in site soil dynamic parameters led to significant variations in the seismic responses of the same structure. Moreover, the magnitude of these disparities correlated directly with the spectral characteristics of the input motions, exhibiting progressively more pronounced variations as the long-period content of ground motions intensified. For the three sets of ground motion inputs, the maximum inter-storey drift ratios of the structural model differed by up to 3.6%, 18.4%, and 54.5%, respectively. This indicated that variations in soil dynamic parameters have a non-negligible impact on the seismic response of structures founded on these soils.

6. Comparisons

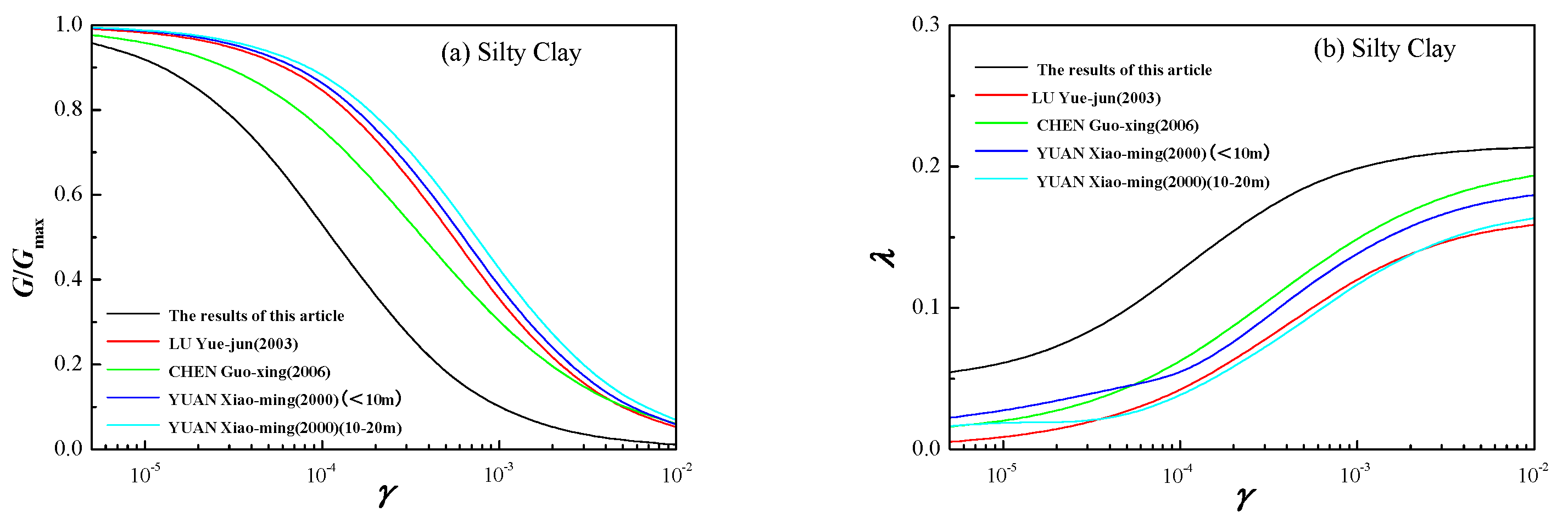
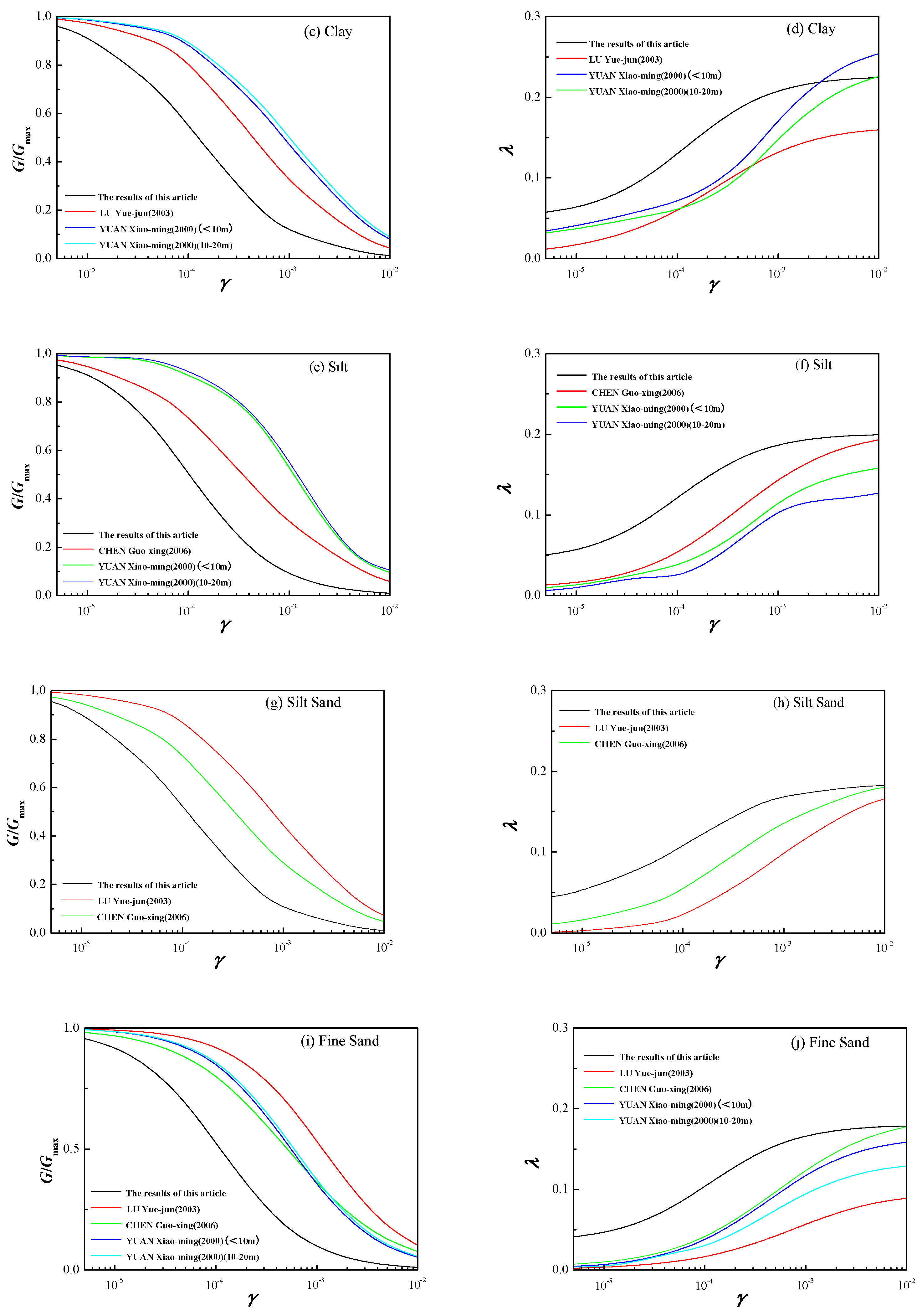
Compared with results from other studies (Figure 11), the dynamic shear modulus ratios and dynamic damping ratios of site soils derived from the statistical values of reference shear strain, maximum damping ratio, and damping ratio nonlinearity coefficient provided herein were noticeably smaller, while the dynamic damping ratios were significantly larger. Significance testing between this study and the proximate curves in other studies was performed by two-side t-tests. For clay and silt, the proximate curves were derived from soil samples in Bohai [18], while for the other three soil types, the proximate curves were derived from soil samples in Nanjing [6]. The t-test result (

Table 4. t-tests between this study and the proximate curve in other studies.

Soil Type	Parameter	Mean Value of Proximate Study	Degree of Freedom	t Value	t (p < 0.05) Value
Silty Clay	lg(γr/10−4)	0.8062		1.479	1.964
	λmax	0.2065	564	0.274
	α	0.9354		2.073
Clay	lg(γr/10−4)	0.6568		3.321	1.961
	λmax	0.1736	2483	1.606
	α	0.8742		1.542
Silt	lg(γr/10−4)	0.7892		1.037	1.962
	λmax	0.2028	1029	0.062
	α	0.9714		3.403
Silty Sand	lg(γr/10−4)	0.6936		2.167	1.963
	λmax	0.1886	876	0.159
	α	0.9671		3.471
Fine Sand	lg(γr/10−4)	0.9154		0.839	1.969
	λmax	0.1917	256	0.440
	α	0.9792		2.717

) showed that there were significant differences between the maximum damping ratio (λ_max) given in this study and those in other studies for clay and silty sand, and there were significant differences between the damping ratio nonlinearity coefficient (α) given in this study and those in other studies for silty clay, silt, silty sand, and fine sand, meaning the dynamic shear modulus ratios and dynamic damping ratios given in this study were significantly different from those in other studies at the inspection level of 5%. This observation underscores that soil dynamic properties were intrinsically linked to sedimentary environments, exhibiting distinct regional specificity. Consequently, the conclusions of this study were applicable primarily to Class III and IV building sites in the northern part of the North China Plain. Their applicability to other site classes and other regions required further verification.

7. Conclusions and Discussions

Statistical analyses of over 5000 sets of soil dynamic test data from the BTH region indicated that soil dynamic parameters such as reference shear strain, maximum damping ratio, and damping ratio nonlinearity coefficient exhibited significant variability. These parameters showed certain correlations with site geological and geotechnical factors including sampling depth, shear wave velocity at the sampling depth, overburden thickness, 30 m average shear wave velocity, and 20 m equivalent shear wave velocity. However, these correlations were generally weak, and multivariate linear regression did not significantly reduce the dispersion of the predictive models. For borehole site models where only stratigraphic logs and velocity data were available but no laboratory soil dynamic test data, it was recommended to adopt the median values of reference shear strain, maximum damping ratio, and damping ratio nonlinearity coefficient to account for soil nonlinearity while using the 84% and 16% exceedance probability values to incorporate the observed parameter variability.

Numerical modeling results indicated that variability in soil dynamic parameters had a clear impact on site seismic response, especially on the short-period portion of the spectral acceleration, and also influenced the seismic response of overlying structures. Consequently, the effects of parameter variability should be considered in site seismic response analyses. Moreover, the specific influence patterns of soil dynamic parameter variability on both borehole site models and structural seismic response depend on the characteristics of the site models and structural models. Thus, the conclusions derived from the case-specific numerical simulations presented herein lacked universality and should be interpreted within their modeling constraints.

In summary, given the strong variability of soil dynamic parameters revealed by the statistical data, it was recommended that laboratory tests on soil samples be conducted for each engineering site to obtain the site-specific dynamic shear modulus ratio and dynamic damping ratio curves. For Class III and IV building sites in the BTH region where no laboratory soil tests had been performed, the dynamic shear modulus ratio and dynamic damping ratio curves could be determined according to Table 1 of this study while explicitly accounting for parameter uncertainties.

This study had the limitation that the statistical data on Class I₁ and II building sites were insufficient, so the reliability of the statistical results in the BTH northwestern mountainous regions needed to be modified by more data. Furthermore, the statistical result that the soil dynamic shear modulus ratio and dynamic damping ratio were slightly related with site parameters including the sampling depth and the shear wave velocity at the sampling depth could not be explained by current understandings. More data were needed in order to discover the primary factor influencing the soil dynamic parameters and improve the accuracy of their prediction models.