Research on NSGA-II-Based Low-Carbon Retrofit of Rural Residential Building Envelope Structures in Low-Latitude, High-Altitude, Warm-Climate Regions
Abstract
1. Introduction
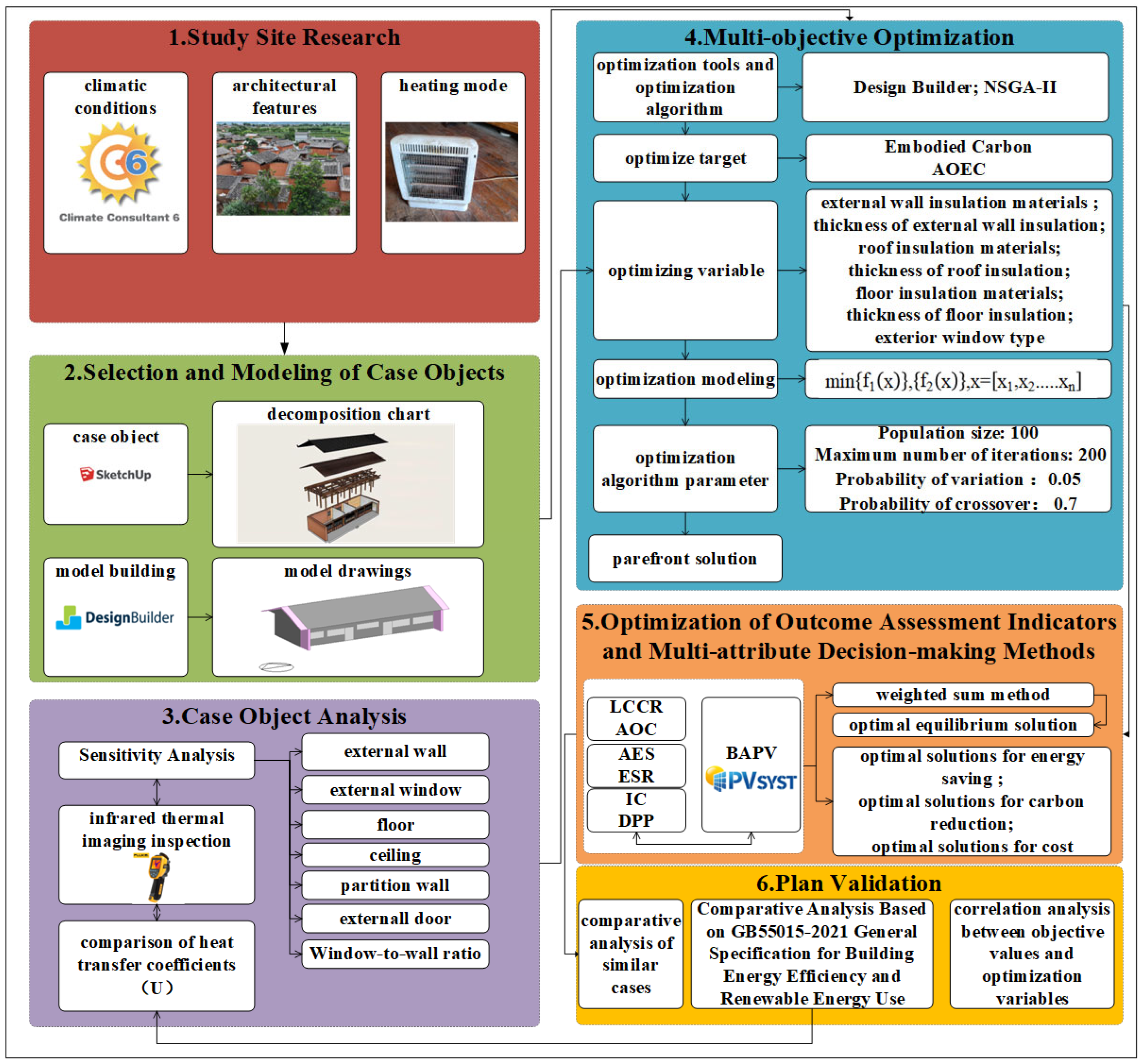
2. Methods
2.1. Research on Research Sites
2.1.1. Climatic Conditions
2.1.2. Architectural Features
2.1.3. Heating Patterns
2.2. Case Object Selection and Modelling
2.2.1. Case Object Selection
2.2.2. Modelling and Validation
2.3. Case Object Analysis
2.3.1. Single-Factor Sensitivity Analysis and Ranking of Key Parameters in Envelope Structures
2.3.2. Thermal Defect Analysis of Building Envelope Based on Infrared Thermal Spectroscopy
2.3.3. Comparative Analysis of Envelope Heat Transfer Coefficients Based on Building Energy Codes
2.4. Multi-Objective Optimization Modelling
2.4.1. Multi-Objective Optimization Tool and NSGA-II Algorithm
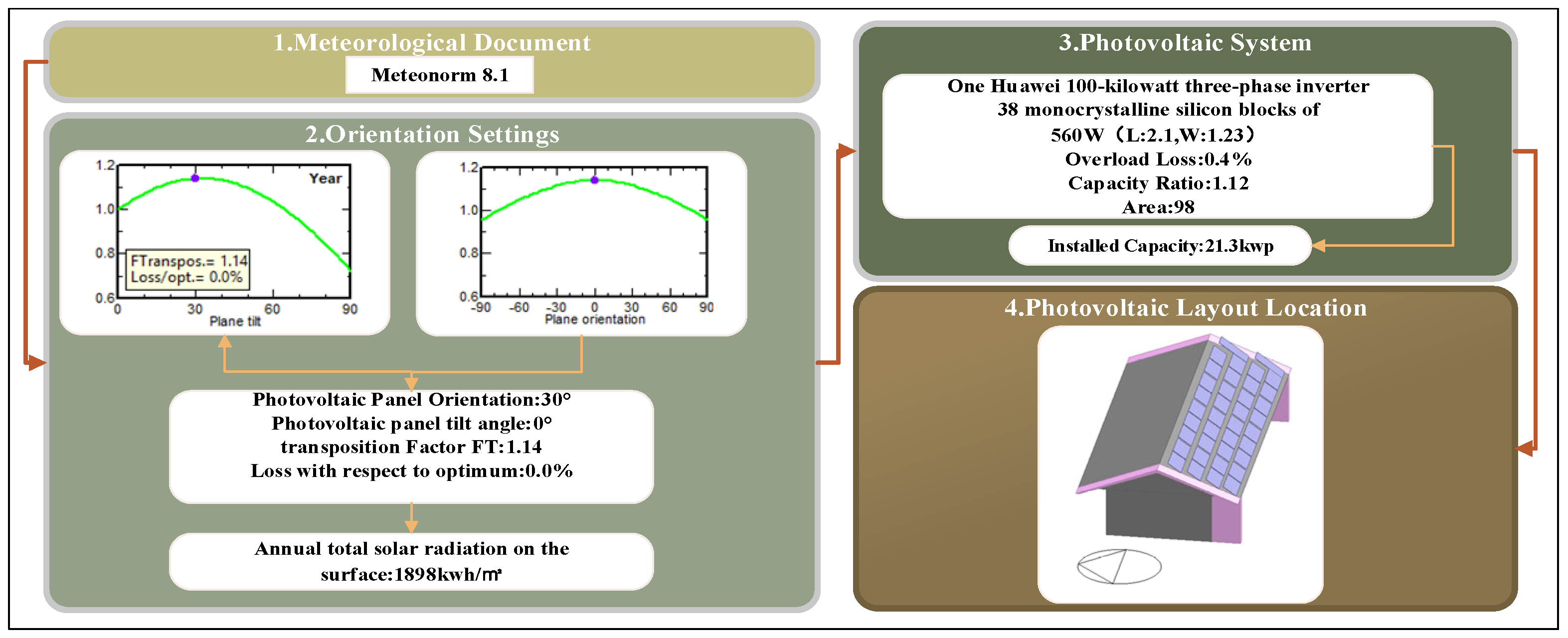
2.4.2. Optimization Variable Selection
2.4.3. Optimization Modelling
2.4.4. Setting of NSGA-II Algorithm Parameters
2.5. Optimization Results Evaluation Index Establishment
2.5.1. Life Cycle Carbon Reduction and Annual Operational Carbon
2.5.2. Annual Energy Savings and Energy Saving Rate
2.5.3. Incremental Cost and Dynamic Payback Period
2.6. Multi-Attribute Decision-Making Methods
3. Optimization Results and Analysis
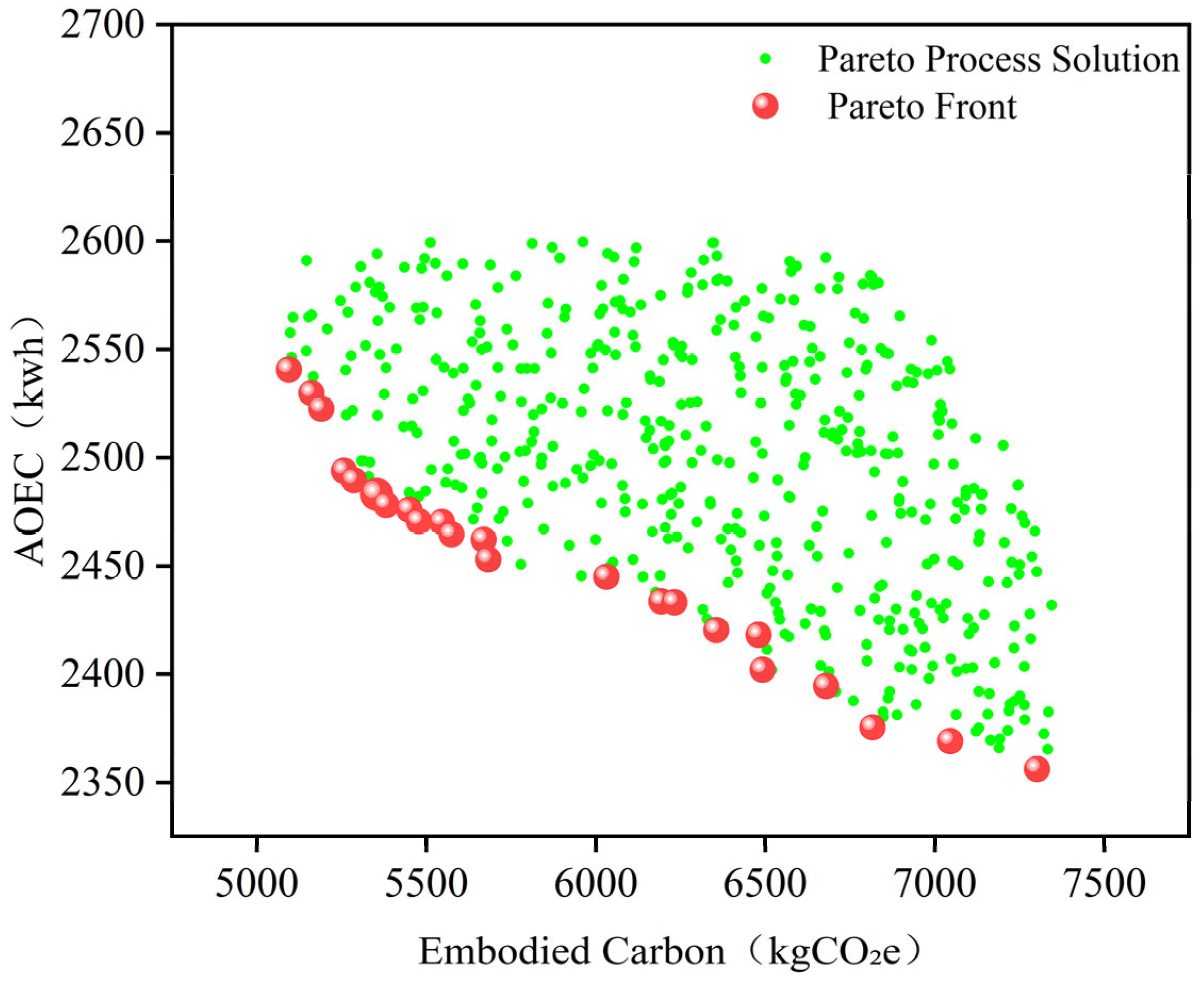
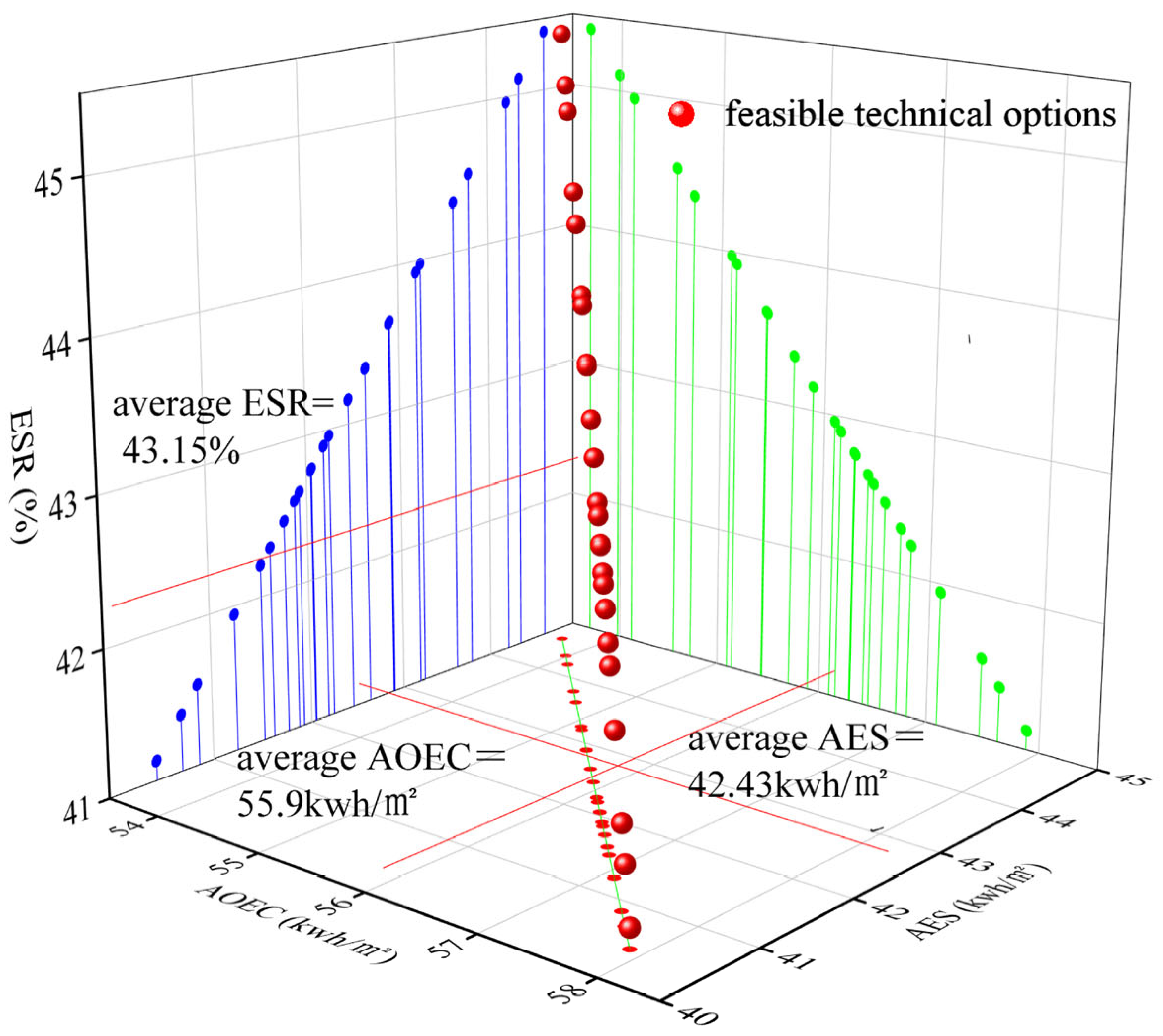
3.1. Optimal Results
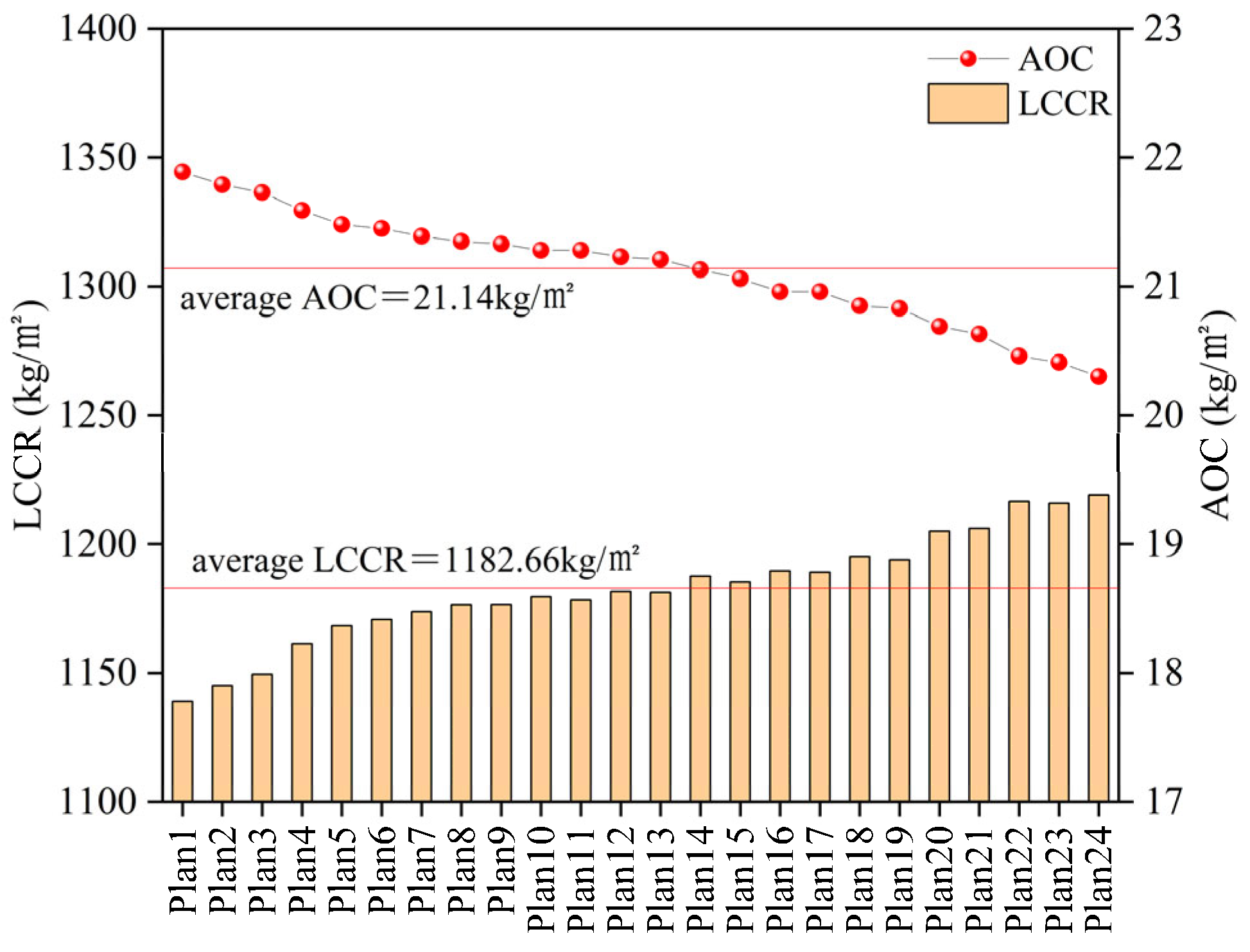
3.2. Optimization Effect Evaluation and Program Selection
3.2.1. Assessment of Carbon Reduction Effectiveness
3.2.2. Assessment of Energy Efficiency
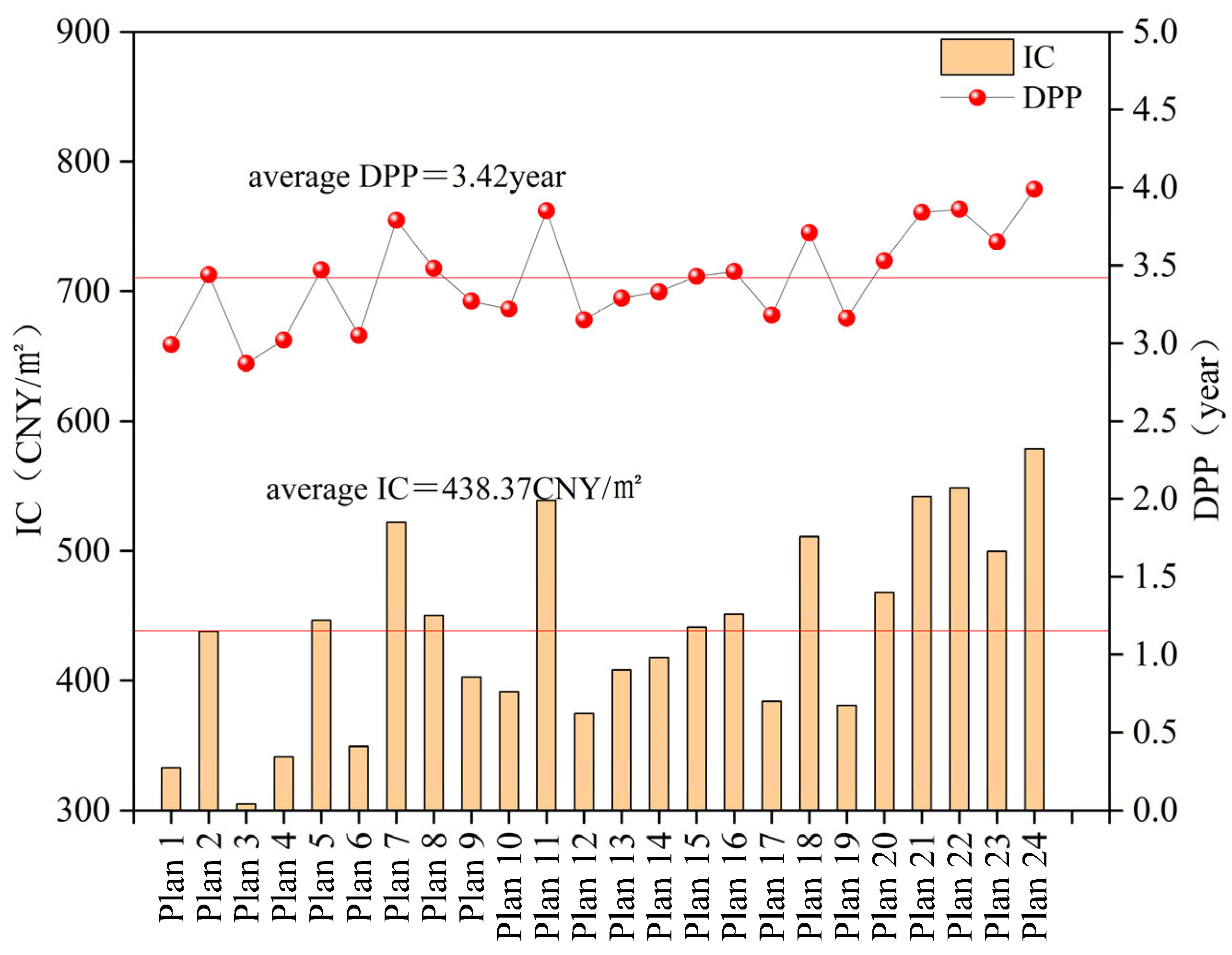
3.2.3. Economic Assessment
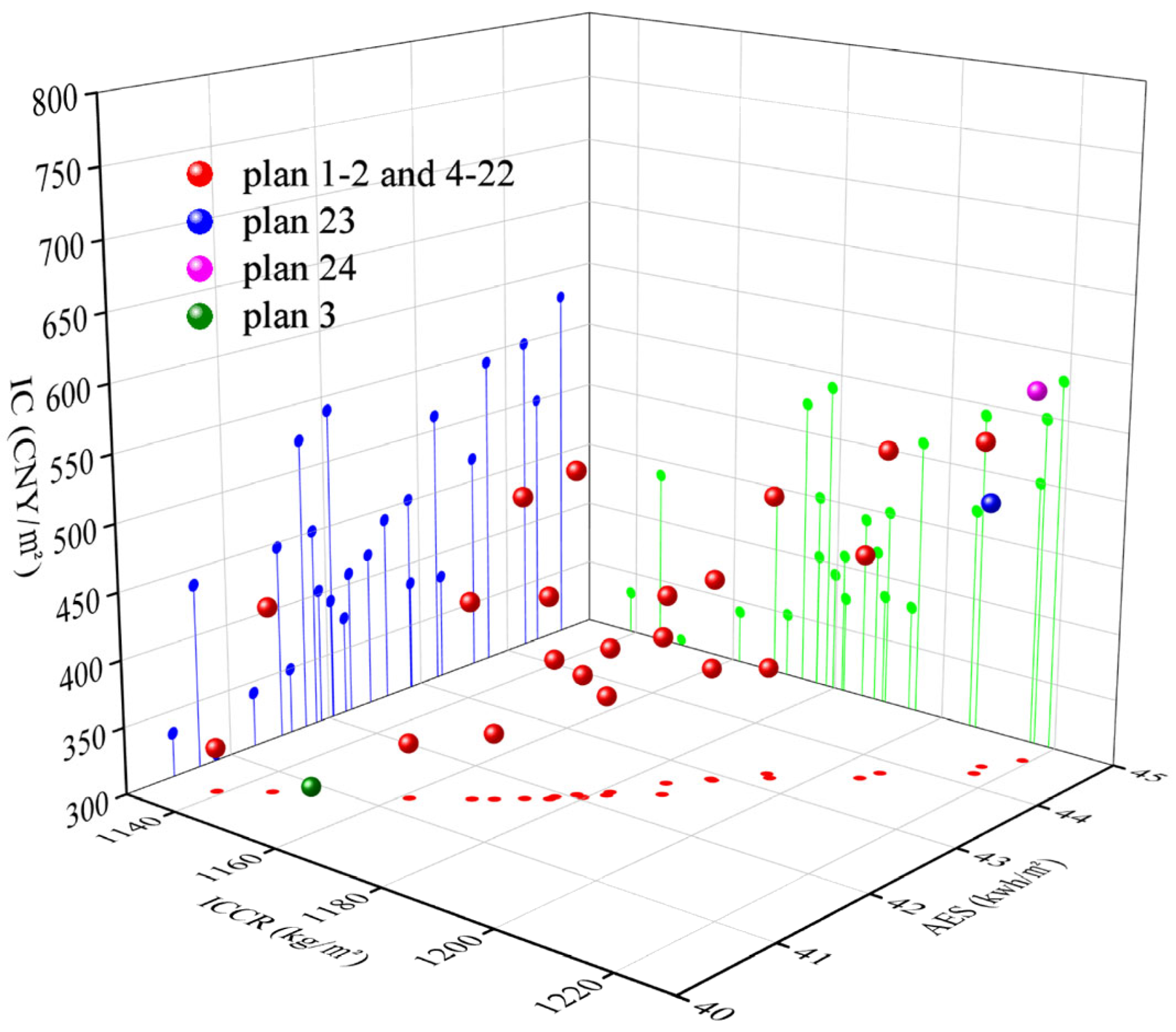
3.2.4. Integrated Impact Assessment
3.2.5. Review of Heat Transfer Coefficients for the Envelope of the Optimized Solution
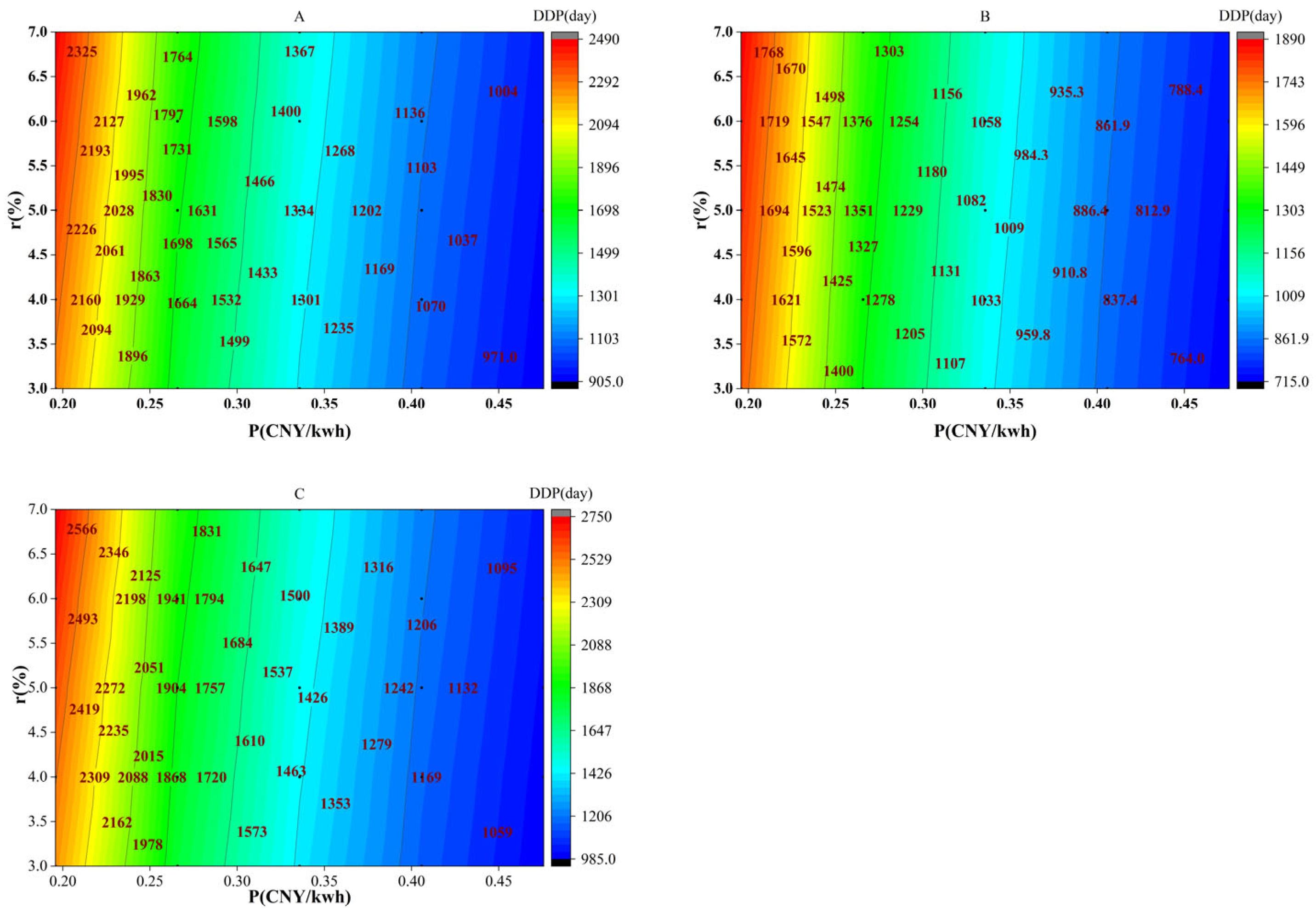
3.2.6. Dynamic Payback Period Evaluation of Schemes Based on Orthogonal Experimentation Methodology
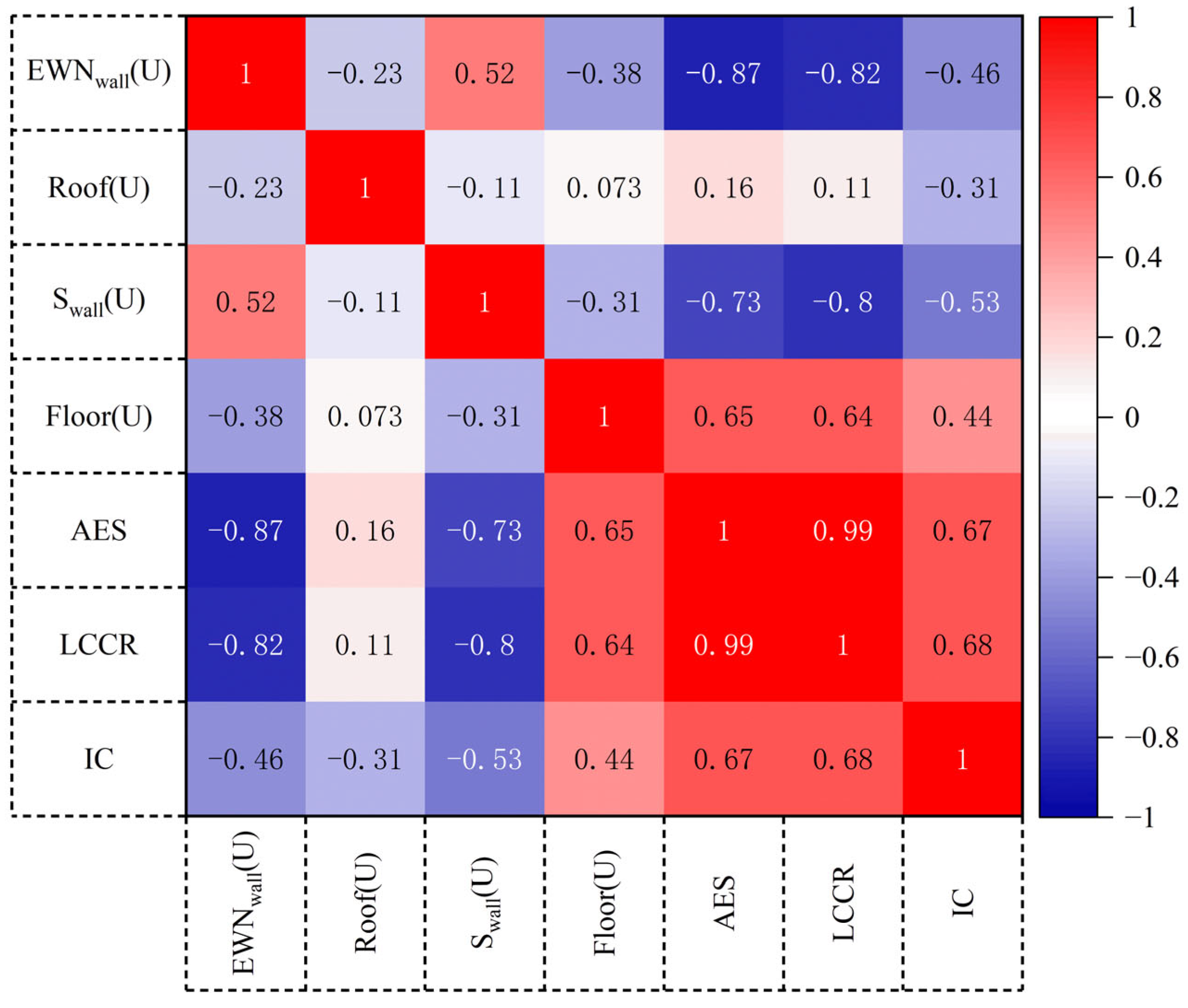
3.3. Correlation Analysis Between Optimization Variables and Optimization Objectives
3.3.1. Correlation Analysis Between Heat Transfer Coefficient of Insulation and Optimization Objective
3.3.2. Correlation Analysis of Insulation Thickness and Material Type with Optimization Objectives
4. Discussion
5. Conclusions
- (1)
- Optimized solution meeting government requirements: EWNwall insulation employs 200 mm-thick XPS insulation boards; Swall, roofs, and floor utilize 80 mm, 100 mm, and 20 mm-thick RW insulation materials, respectively. The exterior window type is 6Low-E + 12Ar + 6. The ESR, LCCR, and DPP are 45.11%, 1215.76 kg/m2, and 3.65 years, respectively.
- (2)
- Solution meeting the designer’s requirements: The EWNwall insulation layer is 220 mm thick, using XPS insulation material; the Swall, roof, and floor insulation layers increased by 100 mm, 140 mm, and 20 mm, respectively, using RW insulation material. The window type is 6Low-E + 12Ar + 6. The ESR, LCCR, and DPP are 45.41%, 1218.96 kg/m2, and 3.99 years, respectively.
- (3)
- Solution meeting farmer requirements: EWNwall, roof, and floor insulation thicknesses increased by 40 mm, 80 mm, and 20 mm, respectively, using EPS insulation material; Swall insulation thickness increased by 20 mm, using RW insulation material. The window type is 6 + 12A + 6. The ESR, LCCR, and DPP are 41.55%, 1149.46 kg/m2, and 2.87 years, respectively.
- (4)
- When energy conservation and emission reduction are the primary objectives, XPS should be selected for EWNwall insulation, while RW should be chosen for Swall, roof, and floor insulation. The optimization priority for the building envelope is EWNwall > Swall > roof > floor. If economic efficiency is the primary objective, EWNwall should not use RW or PU; Swall should use RW; and roofs and floors should not use PU. The optimization priority in this case is floor > roof > EWNwall > Swall.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LCCR | Life cycle carbon reduction |
| AOC | Annual operational carbon |
| AES | Annual energy savings |
| ESR | Energy saving rate |
| IC | Incremental cost |
| DPP | Dynamic payback period |
| AOEC | Annual operational energy consumption |
| EWNwall | East-, west-, and north-facing exterior walls |
| Swall | South-facing exterior wall |
| EPS | Expanded polystyrene |
| XPS | Extruded polystyrene |
| PU | Polyurethane |
| RW | Rock wool |
References
- Paris Agreement. Available online: https://unfccc.int/most-requested/key-aspects-of-the-paris-agreement (accessed on 5 February 2025).
- Unpacking China’s 2060 Carbon Neutrality Pledge. Available online: https://www.oxfordenergy.org/publications/unpacking-chinas-2060-carbon-neutrality-pledge/ (accessed on 6 February 2025).
- China Building Energy Efficiency Association Building Energy Consumption and Carbon Emissions Data Special Committee. China Urban and Rural Development Sector Carbon Emissions Research Report; Chongqing University Press: Chongqing, China, 2024. [Google Scholar]
- Thomsen, K.E.; Rose, J.; Mørck, O.; Jensen, S.Ø.; Østergaard, I.; Knudsen, H.N.; Bergsøe, N.C. Energy consumption and indoor climate in a residential building before and after comprehensive energy retrofitting. Energy Build. 2016, 123, 8–16. [Google Scholar] [CrossRef]
- Olonscheck, M.; Walther, C.; Lüdeke, M.; Kropp, J.P. Feasibility of energy reduction targets under climate change: The case of the residential heating energy sector of the Netherlands. Energy 2015, 90, 560–569. [Google Scholar] [CrossRef]
- Serrano-Jiménez, A.; Lizana, J.; Molina-Huelva, M. Barrios-Padura Á Decision-support method for profitable residential energy retrofitting based on energy-related occupant behaviour. J. Clean. Prod. 2019, 222, 622–632. [Google Scholar] [CrossRef]
- Abouaiana, A.; Battisti, A. Insights and Evidence on Energy Retrofitting Practices in Rural Areas: Systematic Literature Review. Buildings 2023, 13, 1586. [Google Scholar] [CrossRef]
- Xu, K.; Song, S.; Xiang, C. Parametric design for combined solar facades for high-rise residential buildings. Sustain. Energy Technol. Assess. 2025, 74, 104167. [Google Scholar] [CrossRef]
- Galimshina, A.; Moustapha, M.; Hollberg, A.; Lasvaux, S.; Sudret, B.; Habert, G. Strategies for robust renovation of residential buildings in Switzerland. Nat. Commun. 2024, 15, 2227. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Chai, X.; Jing, W.; Li, Y.; Li, C. Assessment of photovoltaic power generation and radiative cooling potentials in old residential districts: A case study of Shenzhen. Energy Build. 2024, 319, 114493. [Google Scholar] [CrossRef]
- Chen, R.; Feng, X.; Li, C.; Chen, H. Reduction in carbon dioxide emission and energy saving obtained by renovation of building envelope of existing residential buildings. Aerosol Air Qual. Res. 2021, 21, 210084. [Google Scholar] [CrossRef]
- Li, R.; Shari, Z.; Ab Kadir, M.Z.A. A review on multi-objective optimization of building performance-Insights from bibliometric analysis. Heliyon 2025, 11, e42480. [Google Scholar] [CrossRef]
- Echenagucia, T.M.; Moroseos, T.; Meek, C. On the tradeoffs between embodied and operational carbon in building envelope design: The impact of local climates and energy grids. Energ. Buildings 2023, 278, 112589. [Google Scholar] [CrossRef]
- Song, J.; Wang, W.; Ni, P.; Zheng, H.; Zhang, Z.; Zhou, Y. Framework on low-carbon retrofit of rural residential buildings in arid areas of northwest China: A case study of Turpan residential buildings. Build. Simul-China 2023, 16, 279–297. [Google Scholar] [CrossRef]
- Fang, H.; Li, W.K.; Dai, P. Parametric analysis of passive ultra-low energy building envelope performance in existing residential buildings. Sci. Rep. 2025, 15, 23407. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q.; Zhang, S.; Shan, M.; Li, J. Research on envelope thermal performance of ultra-low energy rural residential buildings in China. Sustainability 2023, 15, 6931. [Google Scholar] [CrossRef]
- Gao, P.; Nor, M.F.I.M. Climate-Responsive Envelope Retrofit Strategies for Aged Residential Buildings in China Across Five Climate Zones. Buildings 2025, 15, 2842. [Google Scholar] [CrossRef]
- Zhao, S.; Diao, J.; Yao, S.; Yuan, J.; Liu, X.; Li, M. Seasonal optimization of envelope and shading devices oriented towards low-carbon emission for premodern historic residential buildings of China. Case Stud. Therm. Eng. 2024, 64, 105452. [Google Scholar] [CrossRef]
- He, Q.; Ng, S.T.; Hossain, M.U.; Skitmore, M. Energy-efficient window retrofit for high-rise residential buildings in different climatic zones of China. Sustainability 2019, 11, 6473. [Google Scholar] [CrossRef]
- Xi, H.; Gao, H.; Hou, W.; Yin, B.; Zuo, J.; Zhao, H. Multi-objective optimization for winter heating retrofit in rural houses of cold regions: A case study in the Wusu Area. Appl. Sci. 2024, 14, 3760. [Google Scholar] [CrossRef]
- Rached, E.; Anber, M. Energy retrofitting strategies for office buildings in hot arid climate. Int. J. Low-Carbon. Tec. 2022, 17, 506–512. [Google Scholar] [CrossRef]
- Wang, D.; Dong, Q.; Sun, C. Evaluating the adaptation potential and retrofitting effectiveness of existing residential buildings in severe cold regions of China under climate change. Build. Environ. 2025, 278, 112982. [Google Scholar] [CrossRef]
- JGJ 475-2019; Energy Efficiency Design Standards for Residential Buildings in Temperate Regions. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- Yang, Z.; Xiao, H.; Shi, W.; Zhang, M.; Wang, B. Analysis and determination of a seasonal performance evaluation for air source heat pumps. J. Build. Eng. 2021, 43, 102574. [Google Scholar] [CrossRef]
- Chua, K.J.; Chou, S.K.; Yang, W.M. Advances in heat pump systems: A review. Appl. Energy 2010, 87, 3611–3624. [Google Scholar] [CrossRef]
- GB55015-2021; General Specifications for Energy Efficiency in Buildings and the Use of Renewable Energy. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2021.
- JGJ/T132-2009; Residential Building Energy Efficiency Testing Standards. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2009.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Evins, R. A review of computational optimisation methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Delgarm, S.; Kowsary, F. A novel approach for the simulation-based optimization of the buildings energy consumption using NSGA-II: Case study in Iran. Energy Build. 2016, 127, 552–560. [Google Scholar] [CrossRef]
- Chaudhari, P.; Thakur, A.K.; Kumar, R.; Banerjee, N.; Kumar, A. Comparison of NSGA-III with NSGA-II for multi objective optimization of adiabatic styrene reactor. Mater. Today 2022, 57, 1509–1514. [Google Scholar] [CrossRef]
- Reyes-Sierra, M.; Coello, C.C. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- GB/T 51366-2019; Building Carbon Emissions Calculation Standards. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- GB50797-2012; Photovoltaic Power Station Design Specifications. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
- Hao, Y.; He, Q.; Zhou, Q.; Du, D. Modeling and techno-economic analysis of a novel trans-critical carbon dioxide energy storage system based on life cycle cost method. Energy Storage 2020, 28, 101273. [Google Scholar] [CrossRef]
- Fernandes, W.S.; Greco, M.; Almeida, V.S. Application of the smooth evolutionary structural optimization method combined with a multi-criteria decision procedure. Eng. Struct. 2017, 143, 40–51. [Google Scholar] [CrossRef]
- Sun, B.; Zhong, C.; Yu, D.; Han, Q.; Tang, J. Life cycle carbon emission assessment and carbon payback period analysis for the regeneration of old residential areas in cold regions: Case study in Qingdao, China. Sustain. Cities Soc. 2024, 115, 105860. [Google Scholar] [CrossRef]
- Zou, D.; Sun, C.; Gao, D. Multi-Objective Optimization-Driven Research on Rural Residential Building Design in Inner Mongolia Region. Energies 2025, 18, 1867. [Google Scholar] [CrossRef]
- Zhao, D.; Mo, Y. Construction cost decomposition of residential building energy retrofit. Buildings 2023, 13, 1363. [Google Scholar] [CrossRef]
- Chiradeja, P.; Thongsuk, S.; Ananwattanaporn, S.; Ngaopitakkul, A. Renovation of an academic building’s envelope, lighting, and air conditioning system according to Thailand building energy code for energy consumption reduction. Sustainability 2023, 15, 15298. [Google Scholar] [CrossRef]
- Yang, H.; Kikuta, K.; Hayashi, M. Research on carbon reduction of residential buildings in severe cold regions based on renovation of envelopes. Energies 2022, 15, 1873. [Google Scholar] [CrossRef]
- Han, Y.; Yang, S.; Sun, Z.; Li, J. Research on the green retrofitting strategies of existing residential buildings in cold areas. Energ. Buildings 2025, 116320. [Google Scholar] [CrossRef]
- Charles, A.; Maref, W.; Ouellet-Plamondon, C.M. Case study of the upgrade of an existing office building for low energy consumption and low carbon emissions. Energy Build. 2019, 183, 151–160. [Google Scholar] [CrossRef]





| Item | Parameters |
|---|---|
| Living Room Area | 43–45 m2 |
| Bedroom Area | 22–24 m2 |
| Clear Ceiling Height | 2.2–2.4 m |
| EWNwall | 450–455 mm thick and painted with straw art paint |
| Swall | Constructed of pine wood; wall thickness 50–55 mm |
| Roof | Double-sloped roof; the main structure consists of wooden rafters, suspended boards and blue-grey shingles, with a suspended ceiling inside the house |
| Floor | Pine flooring with a thickness of 20 mm |
| Outer Door | 50 mm thick pine panel door |
| Exterior window | 6 mm thick single glazed timber windows using plain white lightly tinted plate glass |
| Enclosure Parts | Framework | U(W/(m2·K)) |
|---|---|---|
| EWNwall | 10 mm straw art paint + 400 mm adobe + plastering | 0.969 |
| Swall | 60 mm pine solid wood | 2.653 |
| Roof | 20 mm cold-laid green tiles | 3.39 |
| Floor | 20 mm pine solid wood | 4.185 |
| Exterior Window | 6 mm transparent glass | 5.36 |
| Outer Door | 50 mm pine solid wood | 2.92 |
| Item | Parameters |
|---|---|
| Density of Persons in Living Rooms | 0.05 person/m2 |
| Density of Persons in Bedrooms | 0.096 person/m2 |
| Living Room Occupancy and Time in Room | 50%, 8:00–2:00, 14:00–22:00 |
| Bedroom Occupancy and Time in Room | 100%, 00:00–8:00, 22:00–24:00; 50%, 12:00–14:00 |
| Living Room Lighting Time | 19:00–22:00 |
| Bedroom Lighting Hours | 22:00–22:30 |
| Power of Electrical Equipment | 3.8 w/m2 |
| Lighting Power Density | 5 w/m2 |
| Average Thermal Resistance of Winter Clothing | 1 |
| Average Summer Clothing Thermal Resistance | 0.5 |
| Number of Air Changes | 1 time/h |
| Interior Design Temperature | 18 °C |
| Item | Parameters |
|---|---|
| Air Source Heat Pumps + Radiators | COP = 3.2, Natural Ventilation |
| Name | Place of Origin/Manufacturer | Measurement Content | Sensor | Measurement Range | Inaccuracies |
|---|---|---|---|---|---|
| Testo174 | Shanghai, China/Testo SE & Co. KGaA | Temperature, humidity | - | (−40 °C, +150 °C) | ±0.05%, ±0.04 °C |
| JTSOFT–IAQ | Beijing, China/Beijing Century Janty Technology Co. | PMV | Wind Speed Sensor | (0.05 m/s, 5 m/s) | ±0.03 m/s |
| Humidity Sensor | (0% RH, +100% RH) | ±1.5% RH | |||
| Black Ball Temperature Sensor | (20 °C, +85 °C) | ±0.3 °C | |||
| Wet Bulb Temperature Sensor | (5 °C, +40 °C) | ±0.5 °C | |||
| Dry Bulb Temperature Sensor | (5 °C, +60 °C) | ±0.5 °C | |||
| Radiant Heat Sensor | (0 kw/m2, 2000 w/m2) | - |
| Factor | Limit Value | Reference Source | Range of Variation |
|---|---|---|---|
| EWNwall(U) | ≤0.6 w/(m2·k) | Table 3.1.8-10 | 0.969–0.6 w/(m2·k) |
| Swall(U) | ≤1.6 w/(m2·k) | Table 3.1.8-10 | 2.653–1.6 w/(m2·k) |
| Roof(U) | ≤0.4 w/(m2·k) | Table 3.1.8-10 | 3.39–0.4 w/(m2·k) |
| Floor(U) | ≤1.8 w/(m2·k) | Continued Table 3.1.8-10 | 4.185–1.8 w/(m2·k) |
| External door(U) | ≤2 w/(m2·k) | Continued Table 3.1.8-10 | 2.92–2 w/(m2·k) |
| Partition(U) | ≤1.52 w/(m2·k) | Continued Table 3.1.8-10 | 2.755–1.52 w/(m2·k) |
| External window(U) | ≤2.5 w/(m2·k) | Table 3.1.9-5 | 5.36–2.5 w/(m2·k) |
| WWR | 0.2 ≤ WWR ≤ 0.4 | Table 3.1.9-5 | 0.2−0.3 |
| Name | Place of Origin/Manufacturer | Measurement Content | Measurement Range | Inaccuracies |
|---|---|---|---|---|
| Fluke TiS20 | Shanghai, China/Fluke Corporation | Thermal Distribution | (−20 °C, +250 °C) | ±2 °C, 2% |
| Parts | Actual Value (W/(m2·K)) | Regulatory Limit (W/(m2·K)) | Does It Meet the Specification |
|---|---|---|---|
| EWNwall | 0.969 | 0.6 | Nonstandard |
| Swall | 2.653 | 1.6 | Nonstandard |
| Roof | 3.39 | 0.4 | Nonstandard |
| Exterior Window | 5.36 | 2.5 | Nonstandard |
| Variable Type | Practice | Materials | U (W/(m2·K)) |
|---|---|---|---|
| EWNwall; Swall; Roof; Floor | Insulation thickness change interval [0, 240] mm in 20 mm steps | Expanded Polystyrene (EPS) | 1.52–0.166 |
| Extruded Polystyrene (XPS) | 1.195–0.122 | ||
| Polyurethane (PU) | 0.997–0.098 | ||
| Rock Wool (RW) | 1.627–0.182 | ||
| Exterior Window | 6 mm transparent glass + 12 mm air + 6 mm transparent glass(6 + 12A + 6) | Glass | 2.5 |
| 6 mm Low-E glass + 12 mm air + 6 mm transparent glass (6 Low-E + 12A + 6) | 1.8 | ||
| 6 mm Low-E glass + 12 mm argon gas + 6 mm transparent glass (6 Low-E + 12Ar + 6) | 1.5 |
| Material Type | Density (kg/m3) | Production Phase (kgCO2e/m3) | Transportation Phase (kgCO2e/m3) | Embodied Carbon (kgCO2e/m3) |
|---|---|---|---|---|
| EPS | 18 | 90.36 | 3.01 | 93.37 |
| XPS | 25 | 153 | 4.17 | 157.17 |
| PU | 30 | 156.6 | 5.01 | 161.61 |
| RW | 95 | 188.1 | 15.86 | 203.96 |
| Glass | 2500 | 2767.5 | 417.5 | 3185 |
| Item | Population Size | Maximal Algebra | Crossover Probability | Probability of Mutation |
|---|---|---|---|---|
| Parameters | 100 | 200 | 0.7 | 0.05 |
| Item | Incremental Cost |
|---|---|
| EPS | 315 CNY/m3 |
| XPS | 389 CNY/m3 |
| PU | 972 CNY/m3 |
| RW | 527 CNY/m3 |
| 6 + 12A + 6 | 890 CNY/m2 |
| 6Low-E + 12A + 6 | 920 CNY/m2 |
| 6Low-E + 12Ar + 6 | 1200 CNY/m2 |
| Air Source Heat Pumps + Radiators | 5000 CNY/unit |
| Photovoltaic Module | 194 CNY/m2 |
| Optimization Objective | LCCR (kg/m2) | AES (kWh/m2) | IC (CNY/m2) |
|---|---|---|---|
| Scenario 1 | 0.33 | 0.33 | 0.33 |
| Scenario 2 | 0.5 | 0.3 | 0.2 |
| Scenario 3 | 0.2 | 0.3 | 0.5 |
| Parts | EWNwall (mm) | Swall (mm) | Roof (mm) | Floor (mm) | External Window |
|---|---|---|---|---|---|
| Scenario 1 | 200 XPS | 80 RW | 100 RW | 20 RW | 6Low-E + 12Ar + 6 |
| Scenario 2 | 220 XPS | 100 RW | 140 RW | 20 RW | 6Low-E + 12Ar + 6 |
| Scenario 3 | 40 EPS | 20 RW | 80 EPS | 20 EPS | 6 + 12A + 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Li, X. Research on NSGA-II-Based Low-Carbon Retrofit of Rural Residential Building Envelope Structures in Low-Latitude, High-Altitude, Warm-Climate Regions. Buildings 2025, 15, 3366. https://doi.org/10.3390/buildings15183366
Chen L, Li X. Research on NSGA-II-Based Low-Carbon Retrofit of Rural Residential Building Envelope Structures in Low-Latitude, High-Altitude, Warm-Climate Regions. Buildings. 2025; 15(18):3366. https://doi.org/10.3390/buildings15183366
Chicago/Turabian StyleChen, Limeng, and Xianqiu Li. 2025. "Research on NSGA-II-Based Low-Carbon Retrofit of Rural Residential Building Envelope Structures in Low-Latitude, High-Altitude, Warm-Climate Regions" Buildings 15, no. 18: 3366. https://doi.org/10.3390/buildings15183366
APA StyleChen, L., & Li, X. (2025). Research on NSGA-II-Based Low-Carbon Retrofit of Rural Residential Building Envelope Structures in Low-Latitude, High-Altitude, Warm-Climate Regions. Buildings, 15(18), 3366. https://doi.org/10.3390/buildings15183366






