Exploring the Nexus Between the Land and Housing Markets in Saudi Arabia Amid Transformative Regulatory Reforms

Abstract

Soaring housing prices worldwide are compromising housing affordability, potentially leading to significant economic, social, and health repercussions. Understanding the price discovery process within the real estate market is therefore crucial for policymakers. While the relationship between land and housing prices in urban residential markets has been widely examined in the literature, the results are often context-specific, leaving the question of whether the land market leads the housing market or vice versa open to debate. Saudi Arabia, with its rapidly growing real estate market, evolving demographics and urbanization trends, and transformative regulatory reforms, presents a compelling context for revisiting the land–housing nexus. This study examines the long-term relationship between land and housing markets and investigates the short-term price dynamics with the ultimate goal of understanding the price formation in the housing market. The study dataset comprises quarterly time-series price indices published by the General Authority for Statistics (GASTAT) in Saudi, representing the nation-wide price movements of residential lands and villas from 2014Q1 to 2025Q1. The study employs the Johansen cointegration method and the Granger causality testing. The results of cointegration analysis confirm a significant long-run equilibrium relationship between the two markets, while the error correction model reveals that both land and housing prices adjust to restore this equilibrium. Granger causality test results show a unidirectional relationship, where land prices predict future housing prices, consistent with the neoclassical rent theory. These findings reinforce the long-term, intrinsic link between land and housing markets observed in prior studies. The dynamics in the Saudi market are likely shaped by rapid urbanization that intensified speculation in the land market, and also the prevalence of self-building enabled by government-supported financing. This study underscores the importance of striking a delicate balance between supply and demand side policies in the real estate market while monitoring the impact of these policies on housing affordability.

1. Introduction

According to Maslow’s hierarchy of needs, shelter is one of the most fundamental human necessities. This notion has resonated in the 2030 Agenda for Sustainable Development, emphasizing the importance of ensuring access to adequate, safe, and affordable housing. Appropriate housing, thus, became key in accomplishing several Sustainable Development Goals (SDGs), being most closely linked to SDG 11, which prioritizes inclusive access to adequate, safe, and affordable housing. That said, there has been a worldwide prolonged upward trend in house prices in metropolitan areas, hindering the likelihood of meeting the 2030 target of achieving inclusive access to affordable housing. This challenge is not new, with the upward trend starting from the latter half of the 20th century in advanced economies [1], while transcending into several East Asian emerging economies over the past few decades (See Chen and Wen [2], Kim and Cho [3], KH and Cuervo [4] for a detailed account of the real estate booms in China, South Korea and Singapore, respectively). Housing prices in other emerging economies are not an exception, particularly in Saudi Arabia, which paints a similar story [5].

Indeed, the various factors contributing to the increasing housing prices have been extensively discussed in the literature. These factors are commonly classified into demand and supply side factors. While the bulk of the literature focuses on the demand side, notable studies highlight the importance of the supply side in explaining the workings of the housing market [6]. The demand side factors include the expansionary monetary policy [7,8] that led to low interest rates, combined with the advent of financial innovations and liberalization [9,10], and demographic changes as well as immigration [11,12,13,14]. On the supply side, Glaeser, et al. [15] suggest that land, construction cost, and building regulation approvals are the three main elements driving the housing supply. While construction costs (labor and building materials) have generally been stable, increases in land prices are the prime contributor to the surge in housing prices. This is mainly due to the stringent regulations on land use, which reduce the elasticity of supply, ultimately amplifying price increases during demand shocks [1,15,16].

Regardless of the causes of housing price escalations, they remain of wide concern to local communities and policymakers. This concern stems from the myriad consequences of rising housing prices, which extend beyond economic outcomes to encompass social and health ramifications. Indeed, the disparity between outright homeowners and home seekers concerning housing prices creates a dilemma that complicates the housing affordability problem. On the one hand, outright homeowners benefit from the growth in housing prices, enjoying a boost in wealth and increased demand and less price sensitivity [17,18] as well as improved physical health [19]. However, from the perspective of home seekers, the soaring housing prices reduce housing affordability and increase household debt [20], compromising financial stability and negatively affecting consumption, which ultimately undermines economic growth [21,22,23], and beyond that inflict negative health and social outcomes on homeowners and renters who live in unaffordable housing [19,24,25,26].

Against this backdrop, since a house is a composite of land and structures, it naturally follows that land and housing markets are interdependent and simultaneously driven by supply and demand forces. Therefore, understanding the long-run relationship between land and housing prices and the associated short-run dynamics is of great importance to policymakers. Leveraging the empirical findings vis-à-vis the interlinkages between land and housing prices, policymakers are better equipped to formulate targeted, evidence-based policies to address the problem of housing unaffordability and ensure sustainable urban development, thereby mitigating the negative consequences of housing unaffordability.

The theoretical foundation of the land–housing markets nexus is rooted in two conflicting theoretical perspectives. The first of these views is an analogy of the Ricardian causal ordering of the housing market put forward by Alyousha and Tsoukis [27]. Under this theory, the demand for land is a ‘derived’ demand because land is an integral input for housebuilding [28,29]. Therefore, if the land market is informationally efficient, a shock that increases demand for housing will lead to an increase in house prices, which will translate into higher demand for land and ultimately higher land prices. After all, developers commonly employ the residual valuation method for land appraisals [30]. This method ultimately determines the maximum price to be paid for the land, subject to the required profit after accounting for all projected development costs and estimating a selling price. So, the anticipated selling price of the house will, by and large, determine the developer’s bid for the plot of land (Grigson [31] as cited in Ooi and Lee [32]). Thus, according to this view, the changes in house prices are suggested to lead to the changes in land prices unilaterally.

The second view is based on the neoclassical rent theory, which posits that a house price, like any other product, is determined by its cost of production. The house price is composed of the cost of acquiring the land, construction cost, agency, legal and planning fees, finance costs, and other costs, in addition to the developer’s profits based on the anticipated sale price. Of all these costs, the cost of the land typically represents the lion’s share of the house price [1,33]. Consequently, the changes in land prices are suggested to lead to changes in house prices, while the converse is not true.

These two conflicting perspectives on the land–housing market nexus give rise to the following empirical research question: Do changes in land prices drive changes in house prices, or is it the other way around? While this question has been addressed, predominantly using cointegration analysis [34] and Granger causality testing [35], in the existing literature (for example, [27,28,32,36,37,38,39]), the mixed results obtained from these studies preclude a definitive answer. Although prior research focuses predominantly on advanced American and European economies, studies on emerging markets remain largely limited to East Asian countries. These countries, however, possess unique regulatory frameworks and demographics, which constrain the generalizability of their findings to other contexts. Therefore, revisiting this research question in a new context will advance our understanding of the land–housing nexus and ultimately yield fresh insights into the mechanisms driving the changes in land and house prices. To that end, this study aims to investigate the long-run relationship and the short-run dynamics between the land and housing markets in Saudi Arabia. In this context, I formulate the following hypotheses:

H1. 

There exists a long-run relationship between land and housing prices.

H2. 

There exists Granger causality between land and housing prices.

The novelty of the Saudi context stems from the fact that Saudi cities have experienced a rapid pace of urbanization over the past decades, becoming among the most urbanized countries in the world [40,41]. This urbanization trend had yielded fewer benefits than costs, exposing citizens to a chronic housing crisis [40]. The housing problem became pronounced in 2007, marked by steep increases in rent and house prices [42]. According to Al-Hamidy [42], supply bottlenecks and demographic pressures, combined with the strong demand due to increasing crude oil prices, are thought to be fueling the rising prices. Additionally, excessive delays in the government-led housing finance system—where government-backed interest-free loans are offered—have further exacerbated the problem. As a result, homeownership rates have stagnated at no more than 50% [43].

In response to the mounting housing challenges, the housing program was launched in 2018 as part of Saudi Vision 2030, enabling Saudi households to access affordable housing. As a result, the real estate market is undergoing transformative reforms to address the chronic housing crisis. These reforms are centered on improving housing affordability by increasing supply through regulatory measures. These measures include, among others, the exemption of first-home buyers from value added tax (VAT), the introduction of the White Land Tax Law and launching the developmental housing program [44]. On the demand side, the attention is directed towards strengthening the financial market via deepening the housing finance system by widening access to mortgages, improving refinancing mechanisms, and boosting private sector engagement in order to guarantee that citizens can obtain sustainable financing solutions (See the pillars of the housing program [45]).

While the program was successful in boosting homeownership (According to the housing program annual report, the percentage of house ownership among Saudi households reached 63.74% [45]), housing supply shortages remain in the face of the strong demand arising from the robust population growth, particularly in the capital city of Riyadh [46]. This growth trajectory is likely to be sustained by new reforms targeting visa policy and foreign ownership of real estate (The Cabinet has recently approved a new law regulating foreign ownership of real estate in Saudi, whereby non-Saudis are permitted to own property subject to the provisions of executive regulations [47]). Indeed, the consequences of the supply shortages manifest in the booming residential real estate prices [48], compromising housing affordability in metropolitan areas (See Knight Frank [49]). That said, the government remains committed to achieving the housing program’s ultimate goal of enhancing housing affordability by acknowledging the existing deficiencies and actively reforming the real estate market to resolve these problems. The seriousness of the government, on this respect, is evident by the recent Crown Prince’s action to balance the real estate sector [50], leading to the modification of existing regulations accordingly. The Council of Ministers has approved the modifications to the White Land Tax Law, through raising levies on undeveloped land from 2.5% to 10% and introducing a tax on long-vacant properties, in order to discourage speculation and free more land for development [51]. The Cabinet also has recently approved the proposed reduction in the down payment of the first home from 10% to 5% [52].

Besides the unfolding developments in the Saudi real estate market, the Saudi context differs from other markets in several aspects. One example is that in East Asian countries, viz., Hong Kong and Singapore, the supply of land is dominated by the government [32], while private ownership of land is not permitted at all in mainland China [28]. In contrast to these emerging economies, private ownership of land is permitted in Saudi Arabia, like other advanced economies. Indeed, private ownership induces monopolistic practices by landowners that are shown to undermine the supply of land in Saudi cities [53]. The impact of the resultant Land shortages on land prices is further amplified by the rapid paces of urbanization in Saudi cities, ultimately leading to land price increases that are transmitted, in turn, to housing prices in the absence of effective regulations. Another example is the prevalence of self-building in the Saudi context, which is also supported by the housing program [43], whereas it constitutes only a minor portion of the housing supply in most advanced economies [54]. In fact, the availability of self-building financing products in Saudi increases the demand for land. This is because ownership of land is a prerequisite for the eligibility to obtain this financing product. This could put upward pressure on land prices that ultimately feed into housing prices. Considering the above, I believe that the evolving nature of the Saudi residential real estate market, together with the differences from emerging and advanced markets, makes it conducive to expanding our understanding of the relationship between land and housing prices.

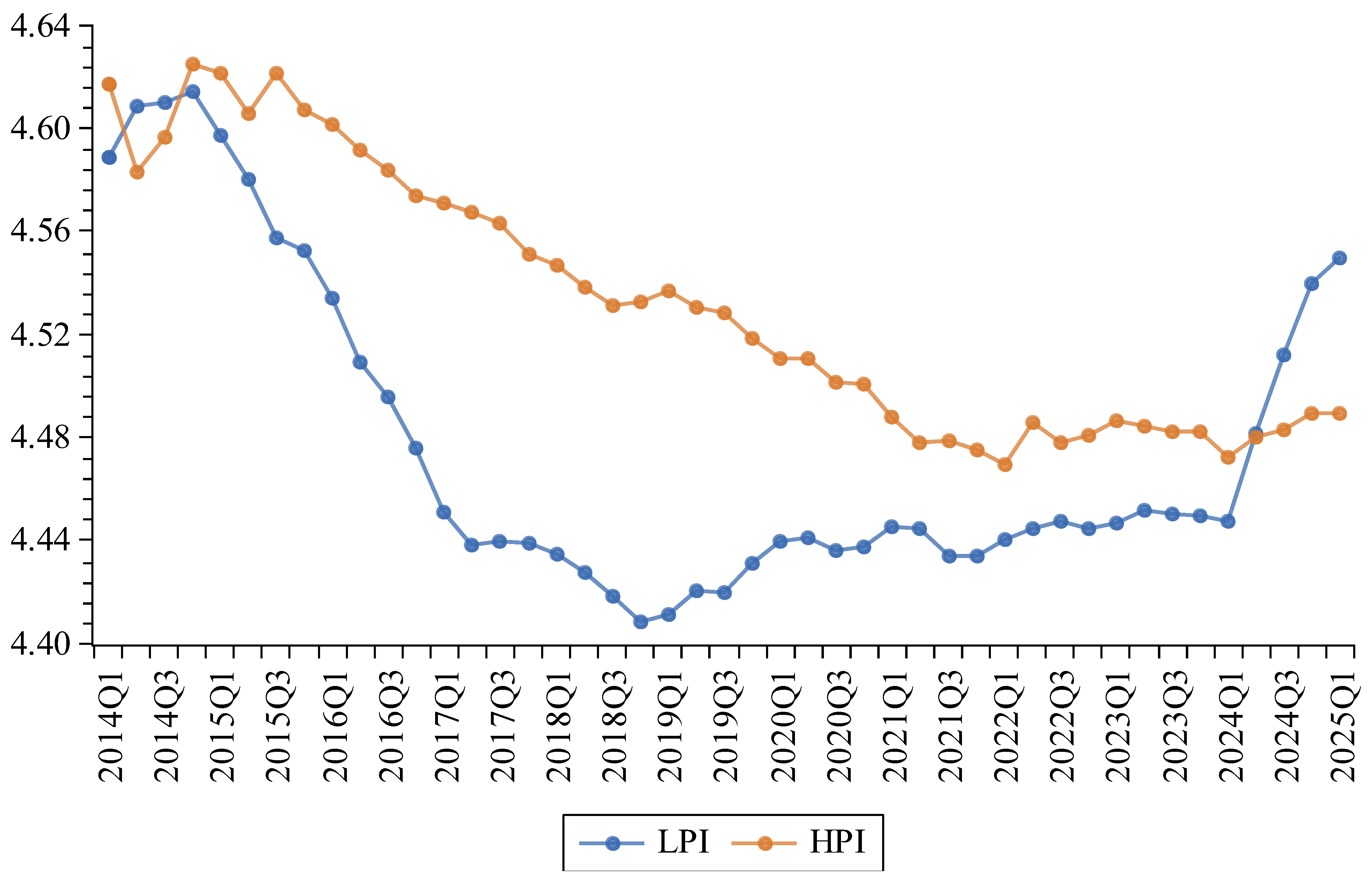
This study, thereby, contributes to the extant literature by being the first study to provide empirical evidence on the land–housing markets nexus in the Saudi economy. To achieve this objective, I use a sample based on the real estate price index statistics issued by the General Authority for Statistics in Saudi Arabia (GASTAT), comprising quarterly time-series price indices that represent the nation-wide price movements of residential lands and villas from 2014Q1 to 2025Q1. The econometric method employed to analyze the data is based on cointegration analysis and Granger causality testing. The empirical analysis commences with unit root testing to determine the series’ order of integration. Based on the outcome of the unit root testing, the appropriate cointegration testing approach is selected to determine whether a long-term equilibrium relationship exists between land and house prices. If cointegration is confirmed, I proceed to examine the short-term dynamics using an error correction model. Based on the error correction framework, I then conduct Granger causality tests to explore the direction of causality.

The unit root tests results show that land and villa series are both integrated of order one. This outcome enables the use of Johansen’s [55] cointegration approach whose results confirm the existence of a long-run relationship between the land and housing markets. The error correction model results indicate that both markets play a significant role in restoring equilibrium in the short run. Meanwhile, the Granger causality tests reveal a unidirectional causality running from the land market to the housing market. While both land and villas have a role to play to maintain their intrinsic long-run relationship, land market carries predictive power for future movements in the housing market but not vice versa. These findings align with the neoclassical rent theory, highlighting the relative importance of the land price in the housing market price formation as noted also by Knoll, Schularick and Steger [1] and Glaeser and Gyourko [16]. This outcome is consistent with my conjecture regarding the direction of causality—running from land to the housing market but not the reverse. This is justified by the features of the Saudi context, particularly the monopolistic practices of landowners, amplified by rapid urbanization and the prevalence of self-building.

These findings carry important implications for policymakers. They should strive to strike the right balance between demand and supply side regulations in the real estate market. Notably, Saudi regulatory authorities responsible for real estate appear to be carefully monitoring market developments and implementing largely harmonized modifications to existing regulations. This is evident, for instance, in the recent increase in the idle (white) land tax rate, which aims to expand the stock of residential land and curb monopolistic practices. Simultaneously, the mandated reduction in the minimum mortgage down payment is expected to stimulate demand by enabling a broader segment of society to achieve homeownership. However, the recently enacted law allowing foreign ownership of Saudi real estate could potentially drive-up property prices, further compromising housing affordability. Consequently, when drafting the executive regulations for this law, the relevant authorities must also ensure a careful balance between the anticipated benefits of attracting foreign direct investment and the potential price increases stemming from such investments in the real estate sector and their impact on housing affordability.

The rest of the paper is structured as follows: Section 2 discusses the theories and empirical evidence from prior studies. Section 3 defines the dataset and presents preliminary analyses. Section 4 outlines the research design. Section 5 presents the results and their interpretation. Section 6 provides robustness checks, and Section 7 concludes the paper with a discussion of the implications of the findings.

2. Literature Review

The body of literature on the interaction between residential land and housing markets is of moderate volume; however, most studies are conducted within unique institutional contexts, leading to conflicting findings and interpretations. These studies are rooted in two competing theoretical frameworks. The first is the Ricardian causal ordering, which some recent studies refer to as the derived demand perspective [56] or what Ball, Shepherd and Wyatt [29] term the professional literature. The second is the neoclassical rent theory, referred to in some studies as the cost-driven perspective [56] or what Ball, Shepherd and Wyatt [29] term the policy literature. Some authors, including Wen and Goodman [56] and Ball, Shepherd and Wyatt [29], attempt to reconcile these conflicting perspectives by suggesting the possibility of mutual or feedback causation between land and housing prices.

On the one hand, the Ricardian framework suggests that the demand for land is a derived demand, determined by its intended use. For residential land, this use is primarily housing. Consequently, a shock that increases housing demand will drive up housing prices, which, in turn, will raise land prices, as land is a fundamental input in house construction. Within this framework, the causal relationship between land and housing prices is expected to run from the housing market to the land market. On the other hand, Needham [57] argues that in the neoclassical rent theory, the price of a product is determined by its production costs. By the same token, since land cost constitutes the largest component of housing prices [1,33], higher land prices will push up the overall cost of housing, leading to higher housing prices.

Alternatively, the feedback perspective is justified on the following grounds. Wen and Goodman [56] argue that neither house prices nor land prices are the sole determinant of the other. Therefore, it is important to consider the dynamics of the relationship between the housing and land markets across different time periods, land use policies, and stages of real estate development. Likewise, Ball, Shepherd and Wyatt [29] argue for a bidirectional relationship between the land and housing markets, emphasizing that the two influence each other differently: housing prices affect land prices rapidly, while land prices impact house prices more gradually. Shifts in housing demand drive quick changes in house prices, leading to rapid adjustments in land prices, whereas the effect of land supply on house prices remains relatively sluggish and diluted.

The volume of empirical studies aimed at testing these theories through an analysis of the relationship between the land and housing markets is growing. Alyousha and Tsoukis [27] was the first to examine whether the Ricardian theory holds in the property market in England. This is achieved by examining whether housing prices can predict land prices. They use cointegration analysis (using both the Johansen and conventional residual-based tests) and Granger causality to analyze quarterly data of residential land and house price indices over the period 1981Q1 to 1994Q4. Their results indicate that while land and house prices are cointegrated, Granger causality test results fail to support the Ricardian conjecture in the short run. While the study reported the cointegration and Granger tests’ results, it did not provide the cointegrating regression parameters’ estimates nor the speed of adjustments parameters. Therefore, the persistence of the long-run relationship and the pace of adjustment toward equilibrium cannot be assessed.

A subsequent notable study conducted by Ooi and Lee [32] offered a detailed analysis of the land–housing market nexus in the Singaporean context. They utilize quarterly data of the residential property price index and construct a land index over the period between 1990 and 2005. Using Johansen’s cointegration and Granger causality tests, they find land and housing prices to be cointegrated and consequently estimate an error correction model based on which they test the Granger causality restrictions. Their results support a unidirectional Granger causality from house to land prices, thereby lending support to the Ricardian theory. However, the authors caution against ignoring the cross-market linkages between the land and housing markets. Despite the reported extensive testing results, the study did not provide the cointegrating regression parameters’ estimates. This omission limits the ability to evaluate the strength of the land–housing market nexus in the long run.

Another notable study examines the dynamics of the nexus between residential land and housing markets in the US real estate market [37]. Based on a sample comprising the largest 27 metropolitan statistical areas that differ in their land use regulations, Kim, Park, Shilling and Cho [37] consider quarterly data from the Davis and Palumbo [58] database over the period 1985 to 2004. Using Granger causality testing, they find evidence in favor of bidirectional feedback causality in both directions, with more restrictive land use regulation amplifying the impact of house prices on future land values. In a similar vein, Zhang and Hou [59] expanded the scope of their analysis of the dynamics of the land–housing relationship to rural areas. The objective of considering rural areas is to ascertain whether these dynamics differ across metro and rural areas. To that end, they use monthly vacant land and house sales data for 32 counties in the US state of Georgia over the period 1970–2011. The authors employ several econometric techniques, including Granger causality, 3-stage simultaneous equations, and cointegration analysis. Their results indicate that, while land and housing prices are cointegrated, short-run dynamics are context-dependent. In metropolitan areas, changes in housing prices drive changes in land prices, whereas in rural areas, the reverse is true. While the sample employed is based on a single state, the study provides valuable insights into land–housing market nexus in similar contexts.

A substantial thread in the literature focuses on the Chinese context. In this realm, the seminal studies are those of Du, Ma and An [28] and Wen and Goodman [56]. Motivated by the reforms in the Chinese land policy, Du, Ma and An [28] investigate the linkages between the residential land and housing markets in four major Chinese cities. Their sample comprises quarterly data on average land and house prices indices over the period 2001 to 2009. Using panel cointegration analysis and Granger causality, they find that land and housing prices are cointegrated, with the error correction parameters indicating that housing prices adjust more quickly than land prices. Additionally, their analysis reveals a unidirectional Granger causality from land prices to housing prices in the short run in line with the prediction of the neoclassical rent theory. They also find that the informational efficiency of both the land and housing markets is compromised by the advent of the new land-granting system, as reflected by the decline in the speed of adjustment in both markets. Based on a larger sample comprising 21 provincial Chinese cities over the period 2001 and 2005, Wen and Goodman [56] use the two-stage least squares (2SLS) to capture the mutual relationship between housing and land prices, considering the fundamental determinants of both markets. Their results reveal that land and housing prices are interrelated, with housing prices exerting a greater influence on land prices than the reverse. In a recent study, Su, et al. [60] investigate the relationship between the process of financialization in the land market and its connection to the housing market. Their sample covers urban cities in China over the period 2006 to 2015. Using several panel data estimation techniques, they find evidence proving the role of land financialization in increasing housing prices.

Indeed, there are only a few studies conducted in other advanced and emerging economies. Altuzarra and Esteban [38] analyze quarterly land price and housing price data for Spanish provinces from 2005 to 2010. They estimate a cointegrating model and an error correction model, using the latter to test Granger causality restrictions. Their results indicate bidirectional Granger causality, with housing price movements having a stronger impact on future land values. In an Australian context, Rossini and Kupke [39] examine the dynamics of land and housing prices in Adelaide’s metropolitan area from 1981 to 2010. They construct land and house price indices using transaction data. Cointegration analysis shows that land and house prices are cointegrated, while Granger causality tests reveal bidirectional predictive relationships—house prices lead to changes in land prices in the short run, while land prices forecast changes in house prices in the long run. Vergara-Perucich [36] analyzes the relationship between land and housing markets in the Chilean capital city of Santiago over the period 2008 to 2019. Using Granger causality testing, consistent with the Ricardian theory, they find that land prices exhibit a significant influence on apartment prices; however, their impact on house prices is comparatively less pronounced. Indeed, the findings of the latter two studies are based on a single city which could limit their generalizability.

On balance, the literature on the relationship between land and housing markets presents a nuanced and evolving understanding, characterized by areas of both consensus and divergence. Most studies confirm the presence of a long-run relationship between the two markets. However, findings differ significantly regarding short-run dynamics, which appear to be influenced by factors such as land use regulation, financialization, and the state of real estate development. Notably, this body of work often focuses on a limited number of geographic regions and institutional settings, likely due to data availability constraints. Many studies construct their own land and housing price indices rather than relying on standardized, readily available national statistics. Addressing these limitations by examining new market contexts could yield valuable insights. In this regard, the Saudi market—with its ongoing reforms under Vision 2030 and a booming real estate sector combined with the availability of official data—emerges as a particularly compelling case for further research.

3. Data Sources and Preliminary Analysis

3.1. Data Sources

The dataset that I use in empirical analysis is based on the real estate price index statistics issued by the General Authority for Statistics in Saudi Arabia. I focus on two types of real estate within the residential sector: residential land plots and villas. The choice of villas to represent residential properties in this context may be justified on the following grounds: first, according to the survey conducted by Knight Frank [49], there is a strong preference for villas as the property type of choice. Second, Apartments are typically a part of high-rise structures with a high floor area ratio (FAR), allowing greater density and better utilization of available space. In addition, many apartment complexes include tangible amenities like health clubs and facilities that affect the value of the apartment. These features can potentially make the link between apartments and the land on which they are constructed relatively less pronounced compared to villas whose FAR is much lower to provide more open space. Third, the distinguishing feature of self-building in the Saudi context, along with the associated financial support from the government, does not typically apply to apartments. This is because apartment complexes are usually constructed by developers.

I use two quarterly series of index numbers representing each of the two types of real estate aggregated across all provinces (regions) in Saudi Arabia (The indicator code is EfPi0401, and the base year is 2014). While the aggregation could, prima facie, average out provincial differences, in the Saudi context the housing program and real estate regulations apply to all provinces. In addition, the available provincial-level indices are also aggregated, covering both large cities and small towns. The data is retrieved from the statistical database maintained by the General Authority for Statistics in Saudi Arabia. The sample period starts from the inception of the indices in the first quarter of 2014 to the first quarter of 2025, leaving us with 45 quarterly observations for each series.

3.2. Preliminary Analysis

Before I proceed with econometric analysis, a word on data notations is warranted. Let ${LPI}_t$ and ${HPI}_t$ denote the natural logarithm of the quarterly real estate price indices levels of residential land plots and villas, respectively: ${LPI}_t=\mathit{log}(land {plot}_t)$ and ${HPI}_t=\mathit{log}({villa}_t)$. For a visual inspection, I plot the movements in residential land and villa price indices in Figure 1.

As a prerequisite for cointegration analysis, I must ascertain the order of integration of the two series, ${LPI}_t$ and ${HPI}_t$. To that end, I use the Augmented Dickey and Fuller [61] unit root test (ADF), in addition to the unit root test of Phillips and Perron (PP) [62]. The results that emerge from unit root testing dictate the cointegration technique to be used in modeling and testing the long-run relationship between the two series. The unit root testing results are reported in

Table 1. Standard unit root tests.

Series	ADF		PP
	Intercept	Intercept and Trend	Intercept	Intercept and Trend
Land
${LPI}_t$	−2.69 * [1]	−0.87 [1]	−1.58	0.43
$∆{LPI}_t$	−3.01 ** [0]	−4.69 *** [0]	−3.05 **	−4.85 ***
Villa
${HPI}_t$	−1.47 [0]	−1.15 [1]	−1.48	−1.15
$∆{HPI}_t$	−3.64 *** [2]	−7.86 *** [0]	−7.74 ***	−7.67 ***

Note: ADF = Augmented Dickey–Fuller [61]; PP = Philip-Perron [62]; the lag lengths for the ADF test are based on the Schwarz Information Criterion (SIC); the selected lag lengths are given in [ ]. ***, ** and * denote significance at the 1%, 5% and 10% levels, respectively.

.

A look at Table 1 reveals that both unit root tests consistently confirm that the natural logarithms of the index levels of both property types are integrated of order one (i.e., ${LPI}_t~ I\left(1\right)$ and ${HPI}_t ~ I\left(1\right)$), while the first differences are found to be stationary processes (i.e., ${∆LPI}_t~ I\left(0\right)$ and ${∆HPI}_t ~ I\left(0\right)$), at least at the 5% significance level. Therefore, I can safely conclude that ${LPI}_t$ and ${HPI}_t$ are both $I\left(1\right)$ processes.

4. Research Design

In the spirit of Alyousha and Tsoukis [27], Ooi and Lee [32], and Du, Ma and An [28], I use cointegration analysis to examine the relationship between residential land and housing markets. Cointegration analysis not only exploits long-run information in level data (rather than proceeding directly to take the first difference) but also evaluates the short-run dynamics in the land and housing markets and shows how short-run deviations from the long-run relation adjust to the long-run equilibrium through an error correction representation.

Like prior studies, including Alyousha and Tsoukis [27], Ooi and Lee [32], and Du, Ma and An [28], I also employ Granger causality analysis to gain additional insight into the interaction between the land and housing markets. Granger causality testing enables us to determine whether the information contained in the past values of prices in one market has any bearing on the prices in the other market.

4.1. Cointegration Analysis

As both the land and villa index series are integrated of the order of one $I\left(1\right)$, I employ Johansen’s [55] maximum likelihood approach to examine the presence of cointegration following Alyousha and Tsoukis [27] and Ooi and Lee [32]. In this approach, a system of endogenous variables with a vector error correction model (VECM) representation is given by:

$${\mathsf{\Delta }\mathrm{Y}}_{\mathrm{t}}=\mathsf{\Phi }{\mathrm{D}}_{\mathrm{t}}+\mathsf{\Pi }{\mathrm{Y}}_{\mathrm{t}-1}+{\mathsf{\Gamma }}_1{\mathsf{\Delta }\mathrm{Y}}_{\mathrm{t}-1}+\cdots +{\mathsf{\Gamma }}_{\mathrm{k}-1}{\mathsf{\Delta }\mathrm{Y}}_{\mathrm{t}-\mathrm{k}+1}+{\mathrm{e}}_{\mathrm{t}}$$

(1)

where ${\mathrm{Y}}_{\mathrm{t}}$ is an $m\times 1$ vector containing the series ${LPI}_t$ and ${HPI}_t$; $\mathsf{\Phi }$ is an $m\times 1$ vector of deterministic terms; $\mathsf{\Pi }$ and $\mathsf{\Gamma }$ are $m\times 2$ parameter matrices capturing, respectively, the long-run relationship and short-run dynamics, and ${\mathrm{e}}_{\mathrm{t}}$ is a Gaussian error term.

If rank $\left(\mathsf{\Pi }\right)=0$, then ${\mathrm{Y}}_{\mathrm{t}}$ is $I\left(1\right)$ and is not cointegrated, whereas when the rank $\left(\mathsf{\Pi }\right)>0=r<m$, $Y_t$ is $I\left(1\right)$ with $r$ linearly independent cointegrating vectors and share $m-r$ stochastic trends (unit roots). This allows the expression of $\mathsf{\Pi }$ as the product $\mathsf{\Pi }=\alpha {\beta }^{\prime }$, where $\alpha ={\left({\alpha }_1+{\alpha }_2\right)}^{\prime }$ and ${\beta }^{\prime }=\left(1,-\theta \right)$. The row of ${\beta }^{\prime }$ represents the cointegrating vector, and the elements of $\alpha$ are the error-correction parameters capturing the speed of adjustment toward the long-run equilibrium.

To test whether the two series are cointegrated, the number of non-zero eigenvalues of the $\mathsf{\Pi }$ matrix, which is also called the rank, is investigated. The number of nonzero eigenvalues represents the number of cointegrating vectors among the series. Two likelihood ratio statistics are normally used to test for non-zero eigenvalues, the trace and the maximum eigenvalue test statistics, which are, respectively, given by:

$${\lambda }_{trace}\left(r\right)=-T\sum _{i=r+1}^m\mathit{ln}\left(1-{\widehat{\lambda }}_i\right)$$

(2)

$${\lambda }_{max}\left(r,r+1 \right)=-T\ln \left(1-{\widehat{\lambda }}_{r+1}\right)$$

(3)

where ${\widehat{\lambda }}_i$ is the estimated eigenvalues attained from the estimated $\mathsf{\Pi }$ matrix, and $T$ is the number of observations. The number of cointegrating vectors is determined via Johansen’s sequential testing procedure. If the series are found to be cointegrated, Engle and Granger [34] posit that a valid error-correction representation must exist between ${LPI}_t$ and ${HPI}_t$, which can be expressed by the following simple specification:

$$∆{HPI}_t={\alpha }_1\left({HPI}_{t-1}-\gamma -{\theta LPI}_{t-1}\right)+e_{1t}$$

(4)

$$∆{LPI}_t={\alpha }_2\left({HPI}_{t-1}-\gamma -{\theta LPI}_{t-1}\right)+e_{2t}$$

(5)

These equations link the price changes in both series to the vector of lagged disequilibrium errors $\left({HPI}_{t-1}-\gamma -{\theta LPI}_{t-1}\right)$, where the parameters $\gamma$ and $\theta$ are the cointegrating (long-run) parameters with the long-run parameter on ${HPI}_{t-1}$ normalized to unity.

Since the series are in logarithmic form, the parameter $\theta$ is interpreted as the elasticity of ${HPI}_t$ with respect to ${LPI}_t$. The reaction of ${HPI}_t$ (${LPI}_t$) to disequilibrium errors is captured by the speed of the adjustment parameters ${\alpha }_1$(${\alpha }_2)$, and at least one of them must be statistically significant (i.e., either ${\alpha }_1\ne 0$ or ${\alpha }_2\ne 0$ or both) for equilibrium to be eventually restored.

Indeed, the VECM specification as presented by Equations (4) and (5) can be generalized by including a time trend in the cointegrating equation and lagged values of $∆{LPI}_t$ and $∆{HPI}_t$ as follows:

$$∆{HPI}_t={{\phi }_1+\alpha }_1\left({HPI}_{t-1}-\gamma -{\theta LPI}_{t-1}-\psi Trend\right)+\sum _{i=1}^{ k}{\delta }_{1i}{∆HPI}_{t-i}+\sum _{i=1}^{ k}{\varphi }_{1i}{∆LPI}_{t-i}+e_{1t}$$

(6)

$$∆{LPI}_t={\phi }_2+{\alpha }_2\left({HPI}_{t-1}-\gamma -{\theta LPI}_{t-1}-\psi Trend\right)+\sum _{i=1}^{ k}{\delta }_{2i}{∆HPI}_{t-i}+\sum _{i=1}^{ k}{\varphi }_{2i}{∆LPI}_{t-i}+e_{2t}$$

(7)

4.2. Granger Causality

Following Alyousha and Tsoukis [27] and Ooi and Lee [32], I test for Granger causality within the VECM framework. The null hypotheses ${\varphi }_{11}={\varphi }_{12}=\cdots ={\varphi }_{1k}=0$ and ${\delta }_{21}={\delta }_{22}=\cdots ={\delta }_{2k}=0$ imply that no Granger causality exists between the two markets. If the first null hypothesis pertaining to Equation (6) is rejected while insufficient evidence is found to reject the second null hypothesis for Equation (7), then I conclude that ${∆LPI}_t$ Granger-cause $∆{HPI}_t$. This implies that price formation initially takes place in the land market, thereby leading the housing market prices. On the contrary, if the opposite outcome is obtained, then I conclude that $∆{HPI}_t$ Granger-cause ${∆LPI}_t$, meaning that the housing market leads the land market. If both hypotheses are rejected, I conclude that there is feedback between the two markets.

5. Empirical Results and Discussion

Having established that the indices levels of both property types are integrated of the same order of one, I perform Johansen’s test of cointegration. To that end, I start by estimating the levels VAR with a maximum lag length of 4 (equivalent to a year) and select the optimal lag order based on the sequential modified likelihood ratio (LR) test recommended by Sims [63]. Then, I ensure that the VAR errors are not autocorrelated by means of the Lagrange multiplier (LM) test for autocorrelation. The results pertaining to the optimal lag length criteria and autocorrelation test are presented in

Table 2. Lag length selection criteria and VAR residual autocorrelation LM test.

Lag	Lag Length Criteria			LM Test
	LR	AIC	SIC	F-Statistic	p-Value
1	NA	−12.89	−12.73	0.23	[0.92]
2	25.41 a	−13.39 a	−13.05 a	0.3	[0.88]
3	1.64	−13.24	−12.74	0.68	[0.61]
4	0.29	−13.05	−12.38	1.71	[0.16]

Note: LR = the sequential modified likelihood ratio test statistic; AIC = Akaike information criterion and SIC = Schwarz information criterion. ^a indicates the corresponding lag order selected by each lag length selection criteria. LM= is the Lagrange multiplier test under the null of no autocorrelation in the VAR residuals, the F-statistic is the Roa F-statistic and p-values in [ ].

.

Based on Table 2, one can see that all lag length criteria agree on a lag length of 2 ($k=2$). The autocorrelation test reveals that the VAR (2) model seems sufficient to filter out autocorrelation from the residuals. The specification of the deterministic terms in Equation (1) depends on the trend behavior of ${\mathrm{Y}}_{\mathrm{t}}$ which can be classified into five cases (see, [64]). Looking at the data, case 4, whereby the cointegrating relationship includes a constant and trend and short-run dynamics include a constant seems to be reasonable. In addition, restricting the trend parameter to zero is strongly rejected (${\chi }^2\left(1\right)=8.41, \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}=0.004$). The results of Johansen’s trace and maximum eigenvalue tests are presented in

Table 3. Johansen’s trace and maximum eigenvalue tests.

Eigenvalue	${\mathit{\lambda }}_{\mathit{t}\mathit{r}\mathit{a}\mathit{c}\mathit{e}}$		${\mathit{\lambda }}_{\mathit{m}\mathit{a}\mathit{x}}$
${\widehat{\mathit{\lambda }}}_{\mathit{i}}$	$\mathit{r}=0$	$\mathit{r}\le 1$	$\mathit{r}=0$	$\mathit{r}=1$
${\widehat{\lambda }}_1=$0.40	27.40 **	5.96	21.44 **	5.96
${\widehat{\lambda }}_2=$0.13	[0.03]	[0.47]	[0.02]	[0.47]

Notes: ${\widehat{\lambda }}_i$ = is the estimated eigenvalues of $\mathsf{\Pi }$ matrix in Equation (1); ${\lambda }_{trace}=$ is the trace test statistic; ${\lambda }_{max}=$ is the maximum eigenvalue test statistic; p-values in [ ]. Max eigenvalue and Trace test p-values are from Mackinnon, et al. [65]; lag order is 4; restricted constant specification. ** denotes significance at the 5% level.

.

Based on Table 3, one can clearly see that both the ${\lambda }_{trace}$ and ${\lambda }_{max}$ statistics reject the null of no cointegration ($r=0$) against the alternatives of one or more cointegrating vectors, at the 5% significance level. Furthermore, both tests also fail to reject the null of at most one cointegrating vector at all conventional levels of significance. These results confirm the existence of one cointegrating vector (or long-run relation) between the housing and land market which is in line with the findings of Alyousha and Tsoukis [27], Ooi and Lee [32], Du, Ma and An [28] and Rossini and Kupke [39]. This means that housing and land prices move in tandem in the long run. I present the estimates of the cointegrating vector, and its short-run dynamics reflected in the error-correction representation in

Table 4. Long-run relationship and short-run dynamics.

Long-Run Relation		Error Correction Model
Cointegrating Vector		${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$
HPIt = 2.53 + 0.47LPIt − 0.004Trend		−0.17 ***	0.22 ***
(4.54) ***	(−7.01) ***	(−2.72)	(2.95)

Notes: t-statistics in ( ), *** denotes significance at the 1% level.

.

The left part of Table 4, pertaining to the estimates of cointegrating vector parameters, shows that the estimated slope parameter has the expected sign, displaying statistical significance at the 1% level. This implies that a 10% rise in land prices results in an increase of about 5% in housing prices in the long run. The magnitude of the slope indicates that while housing and land move together in the long run, they do not move in a one-to-one correspondence which is in accordance with the findings of Altuzarra and Esteban [38]. A plausible explanation is that despite the importance of land prices in determining housing prices, the price of land is not the sole determining factor of house prices. The current regulatory reforms aimed at increasing the supply of land and stimulating the demand for housing will continue to shape the intrinsic link between land and housing prices in the future.

The right part of Table 4, containing the estimates of error correction parameters, shows that the error correction parameters exhibit opposite signs and are highly significant at the 1% level. As such, the null of weak exogeneity is strongly rejected for both variables, suggesting that land and housing prices are important in adjusting toward the long-run equilibrium. A word on the interpretation of these parameters is warranted. When the two series drift away from equilibrium such that HPI_t > 2.53 + 0.47LPI_t − 0.004Trend, the disequilibrium is restored via a fall in HPI_t by 17% of the difference and a rise in LPI_t by 22% of the difference. Thus, the total adjustments add up to 39% per quarter toward the long-run equilibrium. This result implies that it takes nearly 8 months for housing prices to converge to their long-run equilibrium after a shock in the real estate market.

A comparison of our findings with those of Ooi and Lee [32] for the Singaporean market, Du, Ma and An [28] for the Chinese market, Altuzarra and Esteban [38] for the Spanish market, and Rossini and Kupke [39] for the Australian market reveals the presence of both similarities and differences. Our findings are consistent with these studies in rejecting the null of weak exogeneity for both variables, indicating that housing as well as land prices adjust in the short run in response to deviations from the long-run equilibrium. The Saudi real estate market adjusts faster than its Australian counterpart but slower overall compared to Singapore and China. However, like Singapore (but unlike China), Saudi Arabia’s land market adjusts faster than its housing market. Du, Ma and An [28] justify the slow adjustment for land price in China on the ground that the government rather than the market forces determines the supply of land in China.

All in all, our findings imply that the market mechanism operates reasonably efficiently in both markets in the short run, enforcing the reversion to the long-run equilibrium between the housing and land markets. However, the relatively sluggish pace of the overall correction in the real estate market compared to other financial markets is generally attributed to the inherent features of real estate like high transaction costs and taxes [66] as well as behavioral biases leading sellers to be reluctant to sell below their purchase price [67]. These features lead to price stickiness in the short run.

Table 5. Granger causality based on the VECM.

Null Hypothesis	Test Statistic	p-Value	Conclusion
${\varphi }_{11}={\varphi }_{12}=0$ $\left(LPI\nrightarrow HPI\right)$	7.87 **	[0.02]	$LPI\to HPI$
${\delta }_{21}={\delta }_{22}=0 \left(HPI\nrightarrow LPI\right)$	2.98	[0.22]	$HPI\nrightarrow LPI$

Notes: Test statistic is a Wald test statistic with ${\chi }^2\left(2\right)$ degrees of freedom. ** denotes significance at the 5% level.

offers another perspective into the short-run dynamics within the VECM using Granger causality testing. Table 5 shows that the Wald ${\chi }^2$ statistic pertaining to the restriction imposed on the parameters of the lagged changes in land prices in Equation (6) is statistically significant at the 5% level. On the other hand, insufficient evidence is found to reject the restriction imposed on lagged changes in housing price in Equation (7).

Taken altogether, these results are indicative of a unilateral Granger causality running from changes in land prices to the changes in housing prices, but not vice versa. This outcome is in line with the expectations of the neoclassical rent theory and is in accordance with the findings of Du, Ma and An [28]. Indeed, the predictive usefulness of land prices is hardly surprising given the rapid pace of urbanization, land monopolies and the prevalence of self-building in the Saudi context. Self-building starts technically with land acquisition; therefore, one would expect that changes in land price precede those of housing prices. This pattern is reinforced by government-subsidized financing for self-building, which requires land ownership as a prerequisite for financing approval.

6. Robustness Checks

To ensure that our main results are not driven by specific modeling choices, we conduct several robustness checks.

6.1. Unit Root Test with a Structural Break

The ADF test conducted over the entire sample period may potentially produce biased results towards the nonrejection of a unit root [68]. To guard against the potential bias in traditional unit root tests in series containing a structural change, I employ the Perron [69] unit root testing framework in the presence of a structural break at time period $t=\tau$. Here $t$ represents the usual time trend while $\tau$ is the exact point in time on which the break has occurred. The COVID-19 pandemic had unprecedented ramifications across all sectors of the economy, including real estate and construction. Therefore, I take it into account as the break point in this test. The World Health Organization declared COVID-19 a pandemic on 11 March 2020, and the global preventative measures that followed were reflected in the collapse of the crude oil market on 20 April 2020. Therefore, I set 2020Q2 as the exact break quarter in the present analysis. The second-quarter data for 2020 can be regarded as reflecting the initial economic impact of the pandemic and related policy responses. To perform this test, I use the unrestricted Dickey–Fuller specification as follows:

$$y_t=\mu +{\varrho y}_{t-1}+{\psi }_1{D}_p+{\psi }_2{D}_L+{\theta }_{1}t+{\theta }_2{t}_{break}\sum _{i=1}^k{{\beta }_i∆y}_{t-i}+{\epsilon }_t$$

(8)

where $D_p$ represents a pulse dummy variable that takes the value 1 if $t=\tau$ and zero otherwise, $D_L$ is a level dummy variable that takes the value 1 if $t\ge \tau$ and zero otherwise, For $t\ge \tau$, $t_{break}=(t-(\tau -1\left)\right)$ and zero otherwise. This specification yields a test of a random walk with drift against a trend stationary with intercept and trend break alternative. The null hypothesis that $\varrho =1$ is tested using the t-statistic. The number of lags $p$ is chosen using the SIC. The time of break relative to total sample size, $\lambda ={\displaystyle \frac{26}{45}}=0.58$. The estimation results of the test are presented in

Table 6. Perron’s unit root test with a structural break.

Parameter	Series
	Land	Villa
$\mu$	0.28	2.00 ***
	(0.78)	(3.43)
$\varrho$	0.94 ***	0.57 ***
	(12.29)	(4.52)
${\psi }_1$	0.002	0.01
	(0.16)	(1.39)
${\psi }_2$	0.00	−0.01 *
	(−0.71)	(−1.84)
${\theta }_1$	0.00	−0.002 ***
	(0.03)	(−3.34)
${\theta }_2$	0.001	0.002 ***
	(0.76)	(3.47)
$k$	1	0
Unit root test
$\varrho =1$	t-statistic = −0.82       Prob ≥ 0.5	t-statistic = −3.44       Prob ≥ 0.10

Note: t-statistics in (); $k=$ the lag lengths for the Perron [69] unit root test based on the SIC; The critical values are based on [69] asymptotic critical values as reported by the EViews 14 software (for $\lambda =0.58$ ) −4.88, −4.24 and −3.95 for the 1%, 5% and 10% levels, respectively. *** and * denote significance at the 1%and 10% levels, respectively.

.

Based on Table 6, Perron’s unit root tests statistics are lower than the corresponding critical values at all conventional significance levels, implying that there is insufficient evidence to reject the null of a unit root in both series. These results reaffirm the robustness of the traditional unit root tests’ results reported earlier in Table 1.

6.2. Cointegration Analysis with a Structural Break

A look at the results pertaining to the villa series in Table 6 reveals statistical significance for both the intercept and trend breaks at least at the 10% level. To allow for the presence of a structural break in the system during COVID-19, I employ Johansen, et al. [70] testing procedure as illustrated by Giles [71]. This procedure entails the inclusion of the deterministic variables that we constructed earlier in the VAR as exogenous variables. As previously stated, our VAR is of order 2, i.e., $k=2$. Therefore, the exogenous variables to be included in the VAR are ${D_L}_{t-2}$, $t\times {D_L}_{t-2}$, $D_p$ and ${D_p}_{t-1}$. Subsequently, the Johansen cointegration test is conducted in the same manner. Johansen, Mosconi and Nielsen [70] refer to the resulting tests as $H_l\left(r\right)$ and $H_c\left(r\right)$. Indeed, The asymptotic distribution of these tests will differ from those of the standard tests. Hence, I rely on the critical values reported in Giles and Godwin [72]. The results of Johansen’s cointegration test with a structural break are presented in

Table 7. Johansen’s cointegration test with a structural break.

Hypothesized No. of CE(s)	${\mathit{H}}_{\mathit{l}}\left(\mathit{r}\right)$	${\mathit{H}}_{\mathit{c}}\left(\mathit{r}\right)$
None (Zero)	39.78 **	33.91 ***
At most one	5.87	5.87

Note: The asymptotic critical values are obtained from Table 1 of the Giles and Godwin [72] paper. These asymptotic critical values depend on the time of break relative to total sample size, $\lambda$ which is denoted $v_1$ in their paper, and on $(p-r)$, where $p$ is the number of series in the VAR and $r$ is the cointegrating rank. In the present analysis, $p=2$ and $\lambda =v_1=0.58$. Since the table does not contain all possible values of $v_1$ and because values for $1-v_1$ are the same as $v_1$, I use $v_1=0.4$ as it is the closest to $1-0.58=0.42$. The corresponding critical values are: (p–r) Test 10% 5% 1%; 1: $H_l\left(r\right)$ 16.7 18.8 23.3; $H_c\left(r\right)$ 11.0 12.8 16.7; 2: $H_l\left(r\right)$ 34.2 37.4 43.1, $H_c\left(r\right)$ 23.8 26.3 31.5; *** and ** denote significance at the 1% and 5% levels, respectively.

.

A look at Table 7 shows that both tests reject the null of no cointegration against the alternatives of one or more cointegrating vectors, at least at the 5% significance level. Furthermore, both tests also fail to reject the null of at most one cointegrating vector at all conventional levels of significance (This conclusion will remain the same when using $v_1=0.5$, the most concervative critical values in Table 1 (see, [72])). These finding corroborate the robustness of the results pertaining to the traditional Johansen test reported in Table 3.

6.3. Toda and Yamamoto Granger Causality Test

I carry out a robustness check of the findings regarding the presence and direction of Granger causality between the housing and land market. To that end, I adopt the Toda and Yamamoto [73] procedure in performing Granger causality testing. Toda and Yamamoto [73] argue that the conventional Granger causality procedure that requires testing for unit root and cointegration suffers from pretest bias. Clarke and Mirza [74] show that pretesting for cointegration tends to significantly increase the likelihood of erroneously rejecting the null hypothesis of noncausality, while overfitting helps maintain better control over Type I error rates, often with minimal reduction in statistical power. Toda and Yamamoto [73] procedure overcomes the pretesting shortcomings by estimating a VAR in levels, with little concern about the order of integration and cointegration of the series. Then, imposing and testing restrictions on the parameters of the VAR model using Wald test statistics that will be asymptotically chi-square distributed with degrees of freedom $k$. For this purpose, a levels VAR model of order $k+d_{max}$ is specified as follows:

$${HPI}_t={\vartheta }_1+\sum _{i=1}^{ k+d_{max}}{\lambda }_{1i}{HPI}_{t-i}+\sum _{i=1}^{ k+d_{max}}{\rho }_{1i}{LPI}_{t-i}+e_{2t}$$

(9)

$${LPI}_t={\vartheta }_2+\sum _{i=1}^{ k+d_{max}}{\lambda }_{2i}{HPI}_{t-i}+\sum _{i=1}^{ k+d_{max}}{\rho }_{2i}{LPI}_{t-i}+e_{1t}$$

(10)

where $d_{max}$ is the maximum order of integration of the ${LPI}_t$ and ${HPI}_t$ series. Having established that land and housing prices are cointegrated and that there exists a unilateral Granger causality running from the land to the housing market, I can apply Granger causality testing using the Toda and Yamamoto [73] procedure. This procedure not only will offer an additional insight into the interaction between the land and housing markets but also will serve as a cross-check to the validity of cointegration and Granger causality results based on the VECM. As I have arrived at the appropriate lag length of the VAR model that is VAR ($k=2$), I include one additional lag given that our two series are $I\left(1\right)$ processes. So, I estimate a VAR (3) model and conduct Granger causality testing only based on the first $k$ parameters. The Granger causality results are presented in

Table 8. Granger causality based on levels VAR.

Null Hypothesis	Test Statistic	p-Value	Conclusion
${\rho }_{11}={\rho }_{12}=0 \left(LPI\nrightarrow HPI\right)$	6.03 **	[0.05]	$LPI\to HPI$
${\lambda }_{21}={\lambda }_{22}=0 \left(HPI\nrightarrow LPI\right)$	1.42	[0.49]	$HPI\nrightarrow LPI$

Notes: Test statistic is a Wald test statistic with ${\chi }^2\left(2\right)$ degrees of freedom. ** denotes significance at the 5% level.

.

A look at Table 8 corroborates the documented unilateral Granger causality extending from the land to the housing market at the 5% level.

7. Conclusions, Implications and Policy Recommendations

This study examines the strength of the long-run relationship between land and housing markets and analyzes how price dynamics in both markets behave in the short run. Using quarterly observations of Saudi Arabia’s official land and housing market indices, I conduct the Johansen cointegration test, estimating the cointegrating regression and the error correction model. Granger causality restrictions are tested within the error-correction framework.

The results from the Johansen test confirm the existence of a long-run relationship between the land and housing markets. The estimated error-correction model indicates that both markets exhibit significant error-correction parameters, suggesting that land and housing prices actively adjust to restore the long-run equilibrium. The Granger causality tests reveal that land prices predict future housing prices, but the reverse is not true, which aligns with the neoclassical rent theory. In fact, the cointegration between the two markets is a well-documented finding in the literature, reflecting the natural link between land and housing that holds across different contexts. However, the results concerning short-run dynamics—namely, the unidirectional Granger causality from the land market to the housing market—require further clarification. Given the rapid urbanization of Saudi metropolitan areas, this outcome is not surprising, particularly considering speculation in the land market and low land supply elasticity due to stringent land use policies. Additionally, the popularity of self-building in Saudi Arabia may have contributed to these dynamics.

The housing program under Vision 2030 acknowledges these challenges and is taking significant steps to address the housing problem. However, the government support program, which substantially reduces down payments for home loans, and the recently introduced law allowing foreign ownership could exert upward pressure on property prices. Regulators, therefore, must strike a delicate balance between reforms targeting the supply and demand side in the real estate market. This is achieved through careful monitoring of the impact of these policies and the preparedness to take corrective measures once they are needed.

The study has several caveats that should be considered when interpreting the findings. First, the analysis focuses on one type of residential property, namely villas. This choice was made because land represents a larger share of villa prices, suggesting a particularly strong link between land and villa prices. In addition, villas reflect the unique feature of self-building in the Saudi context, which does not typically apply to apartments. While this focus strengthens the study’s relevance to a key segment of the housing market, it does not capture potential dynamics between land and apartment prices. Future research could extend the analysis to other property types. Second, the study relies on aggregated data at the provincial level. This approach was necessary because city-specific housing indices are unavailable; the existing subnational indices combine large metropolitan areas with smaller towns within each province. Although this may dilute localized price movements, it allows for a nationwide perspective, which is appropriate given that all regions are subject to the Housing Program’s initiatives. Nevertheless, exploring regional heterogeneity in the land–housing nexus remains an important direction for future work.