Predicting the Effects of Nano Additives and Elevated Temperatures on Concrete Compressive Strength Utilizing Machine Learning
Abstract
1. Introduction
2. Research Significance
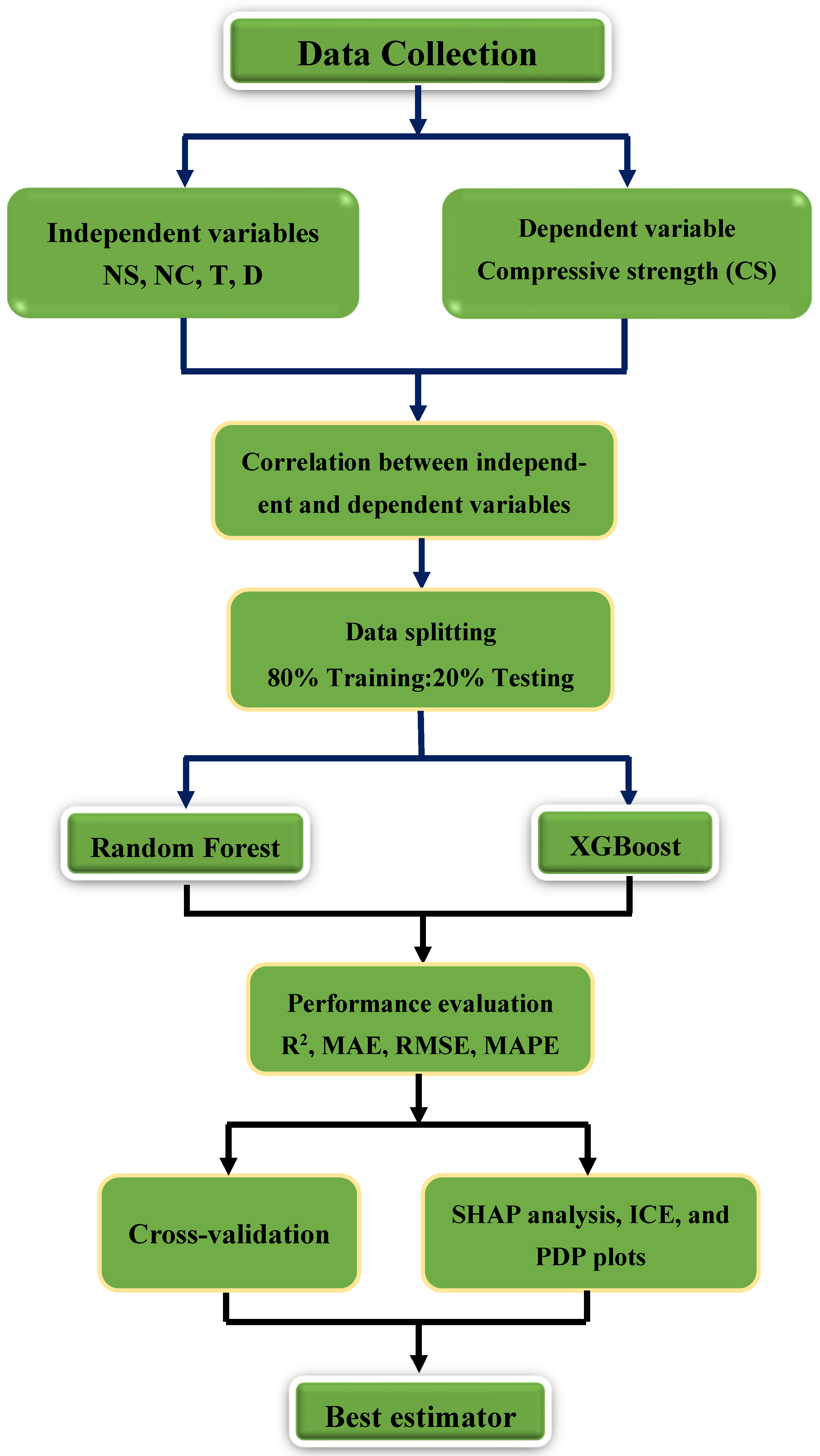
3. Materials and Methods
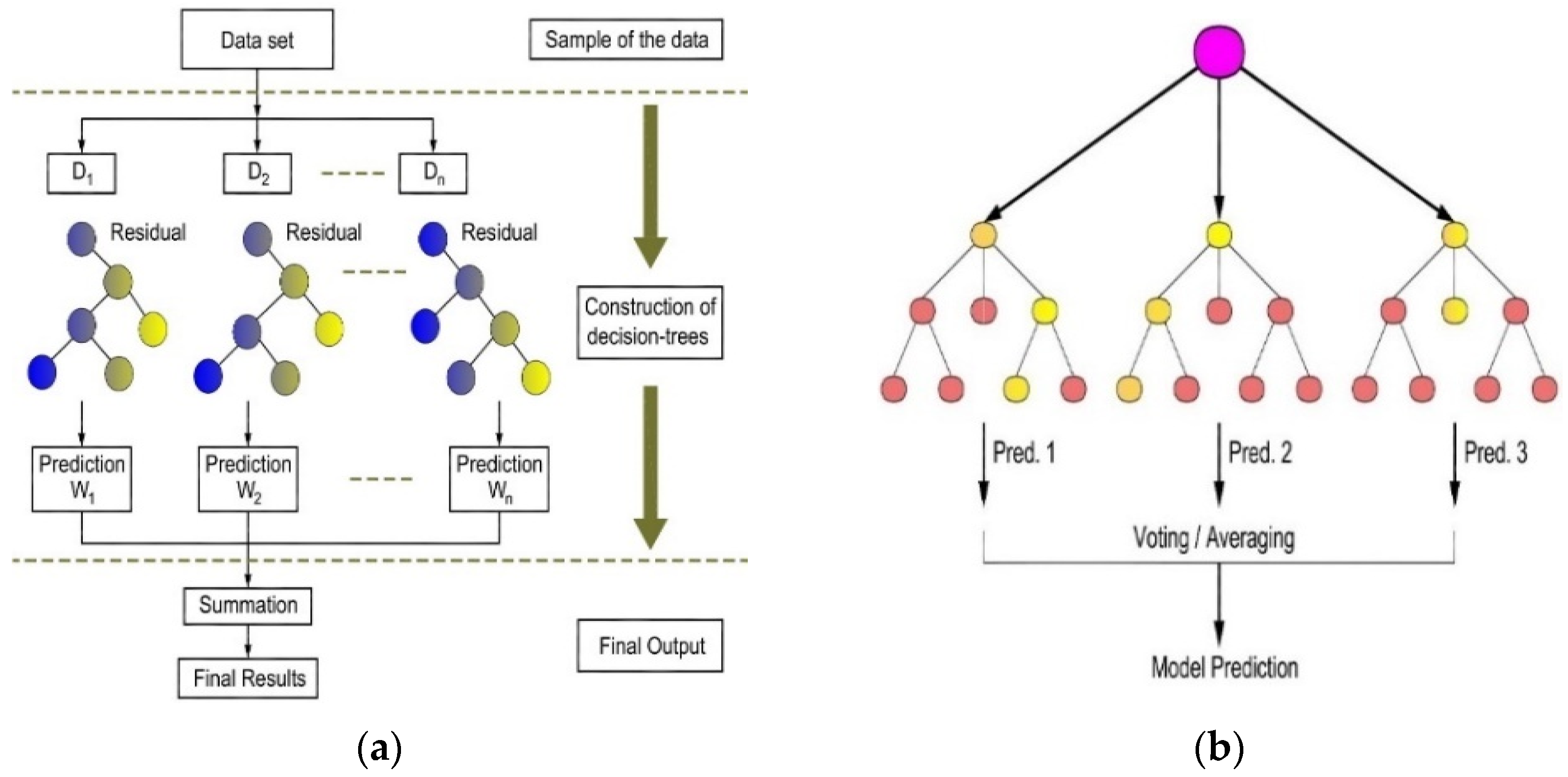
3.1. Machine Learning (ML) Techniques
3.2. Optimization of Hyperparameters
3.3. Model Efficiencies
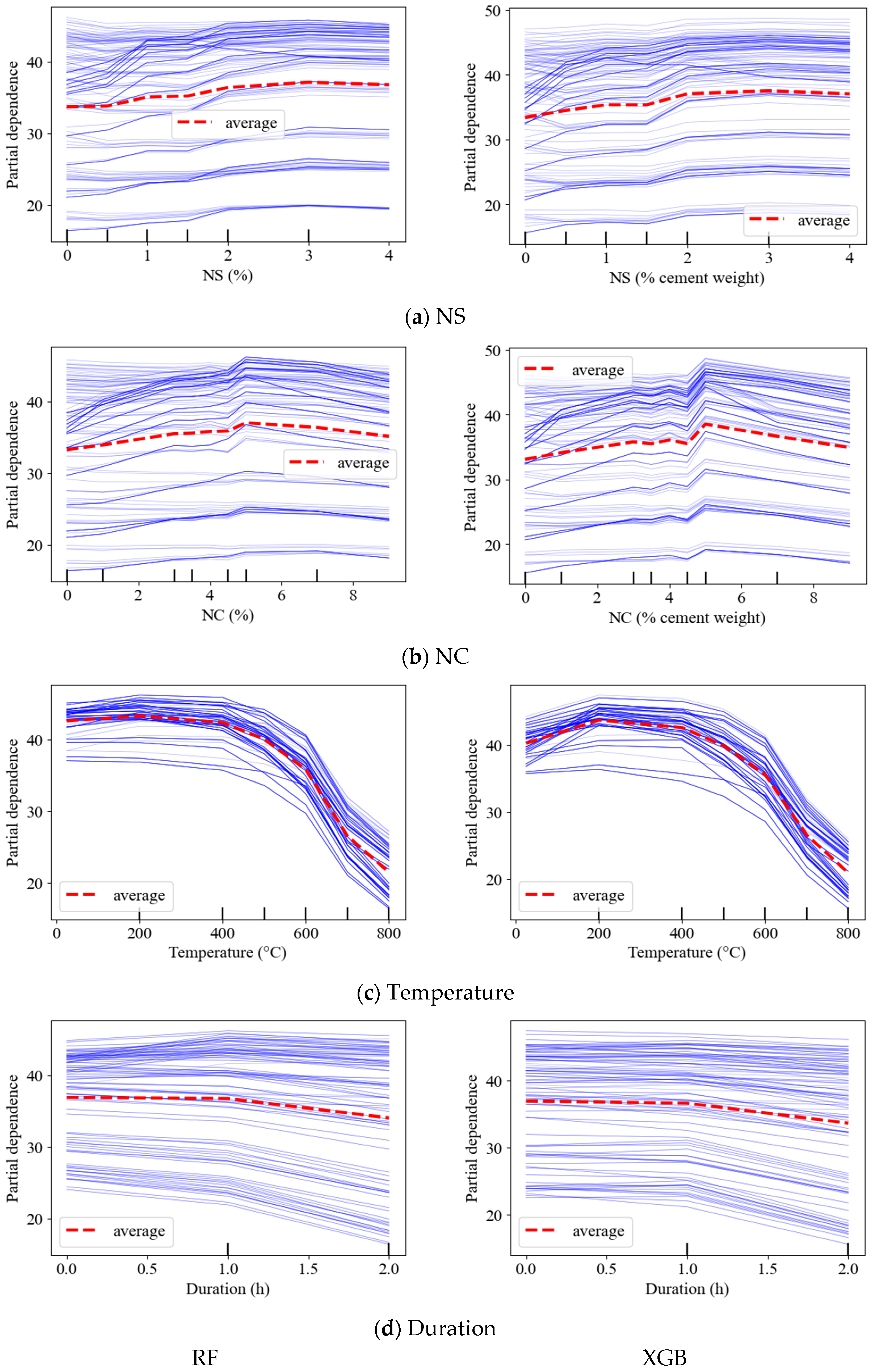
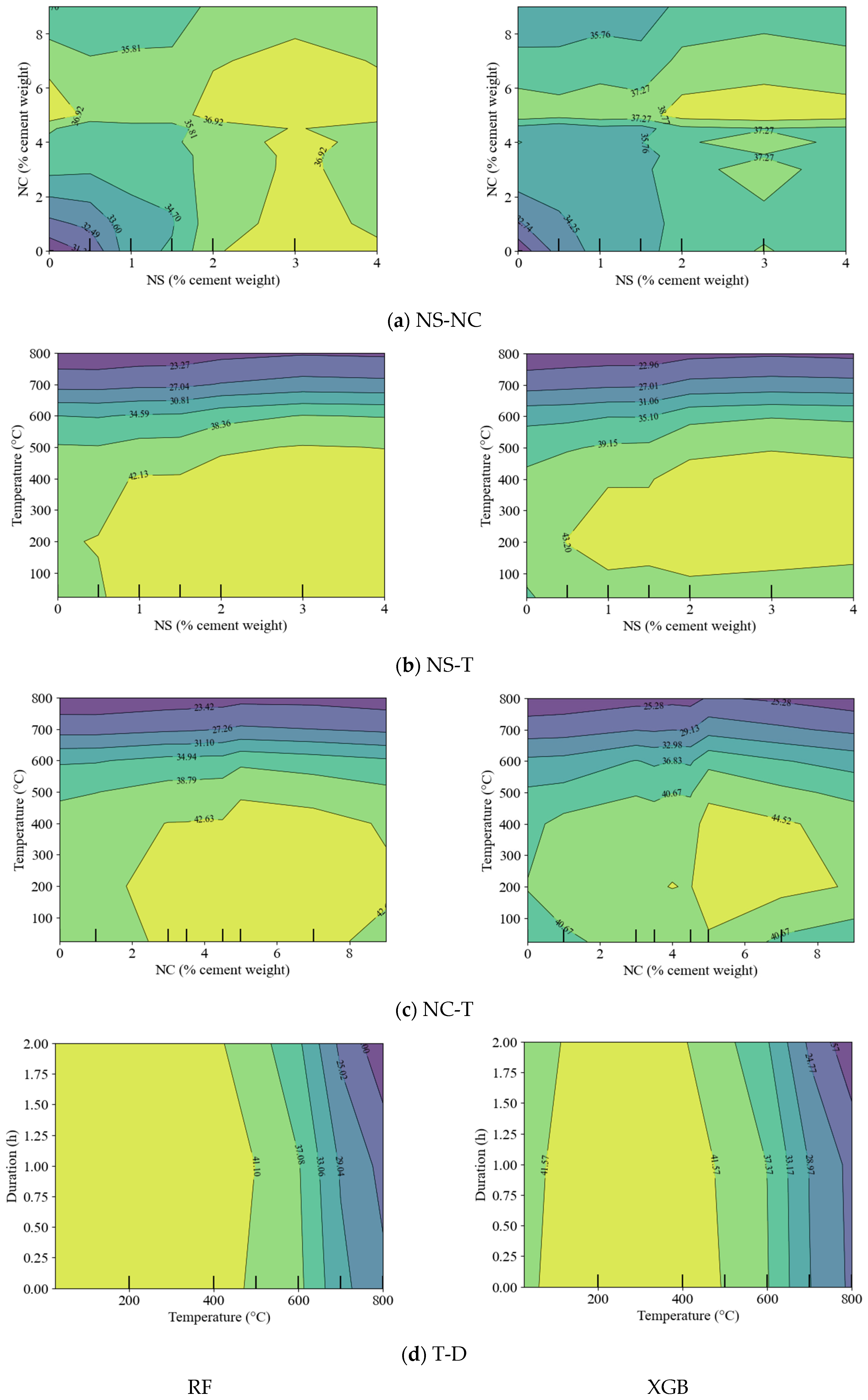
3.4. ICE with PDP
4. Results and Discussion
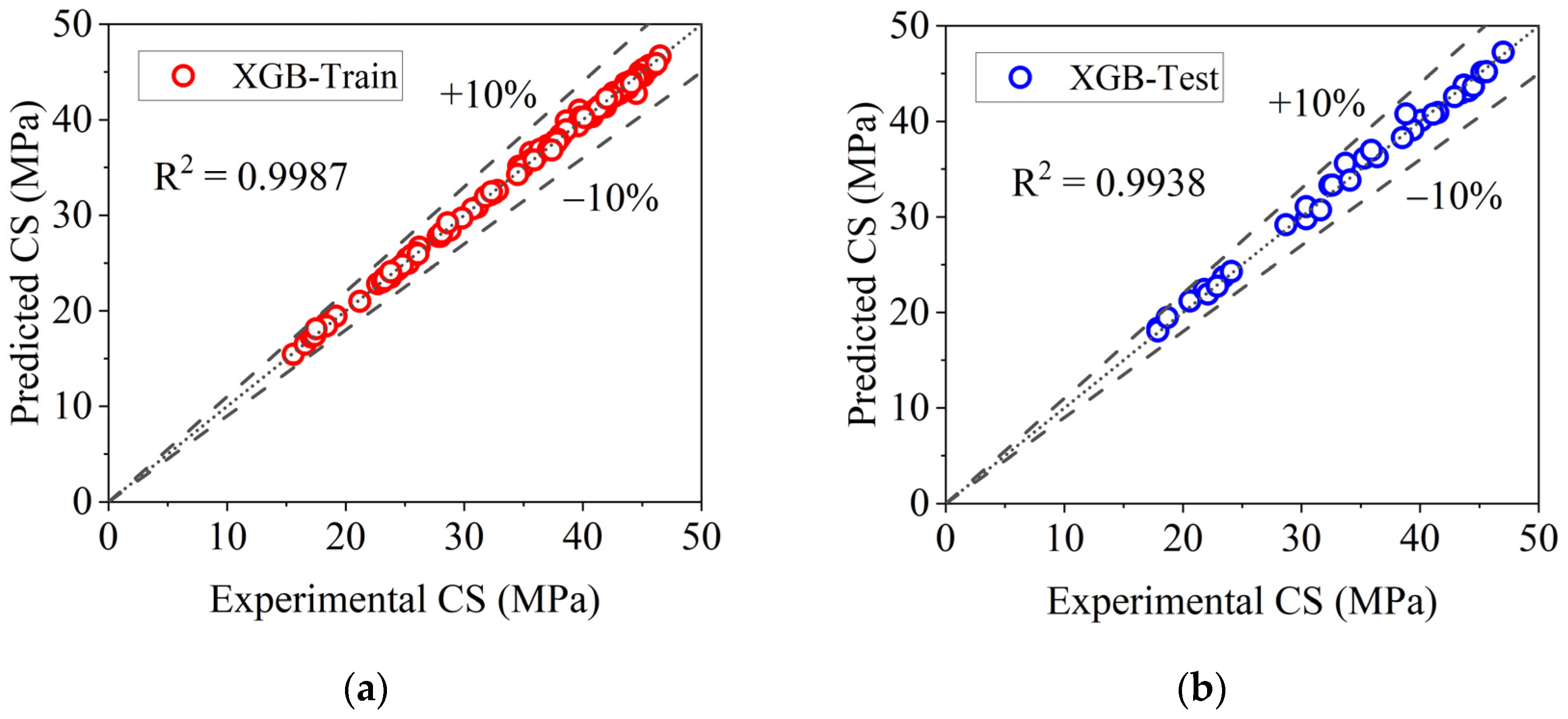
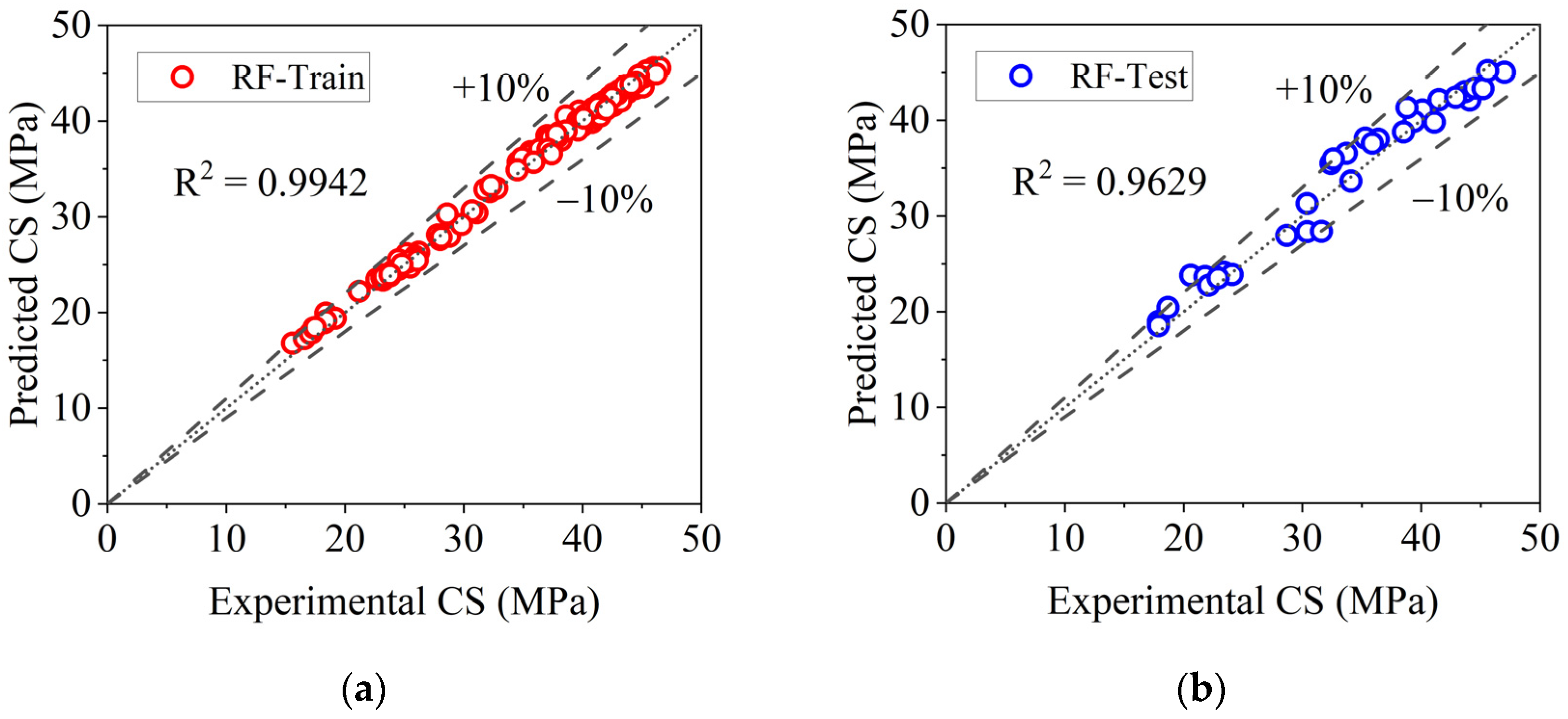
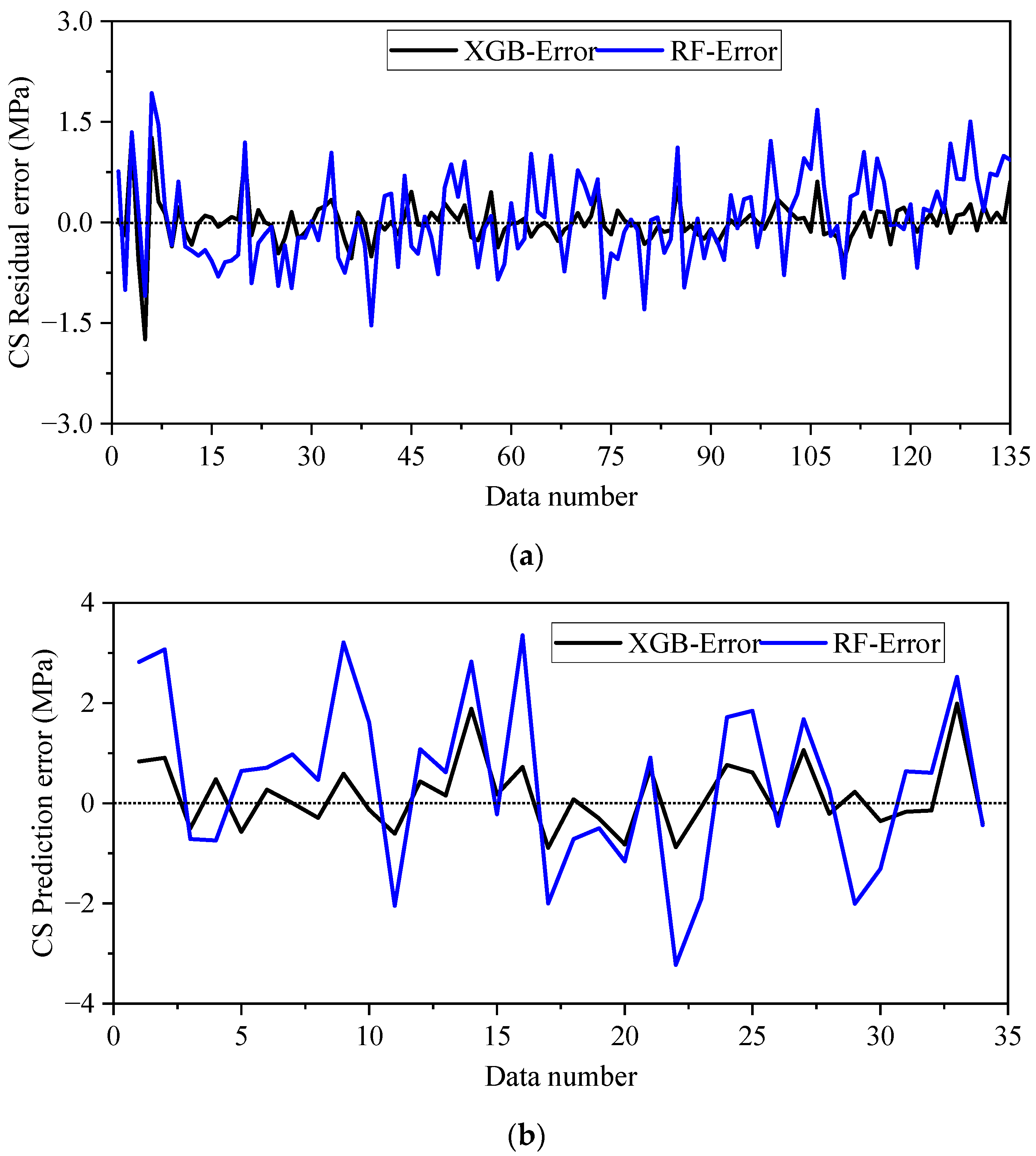
4.1. Performance of ML Models
4.2. Comparison Between the Developed Models
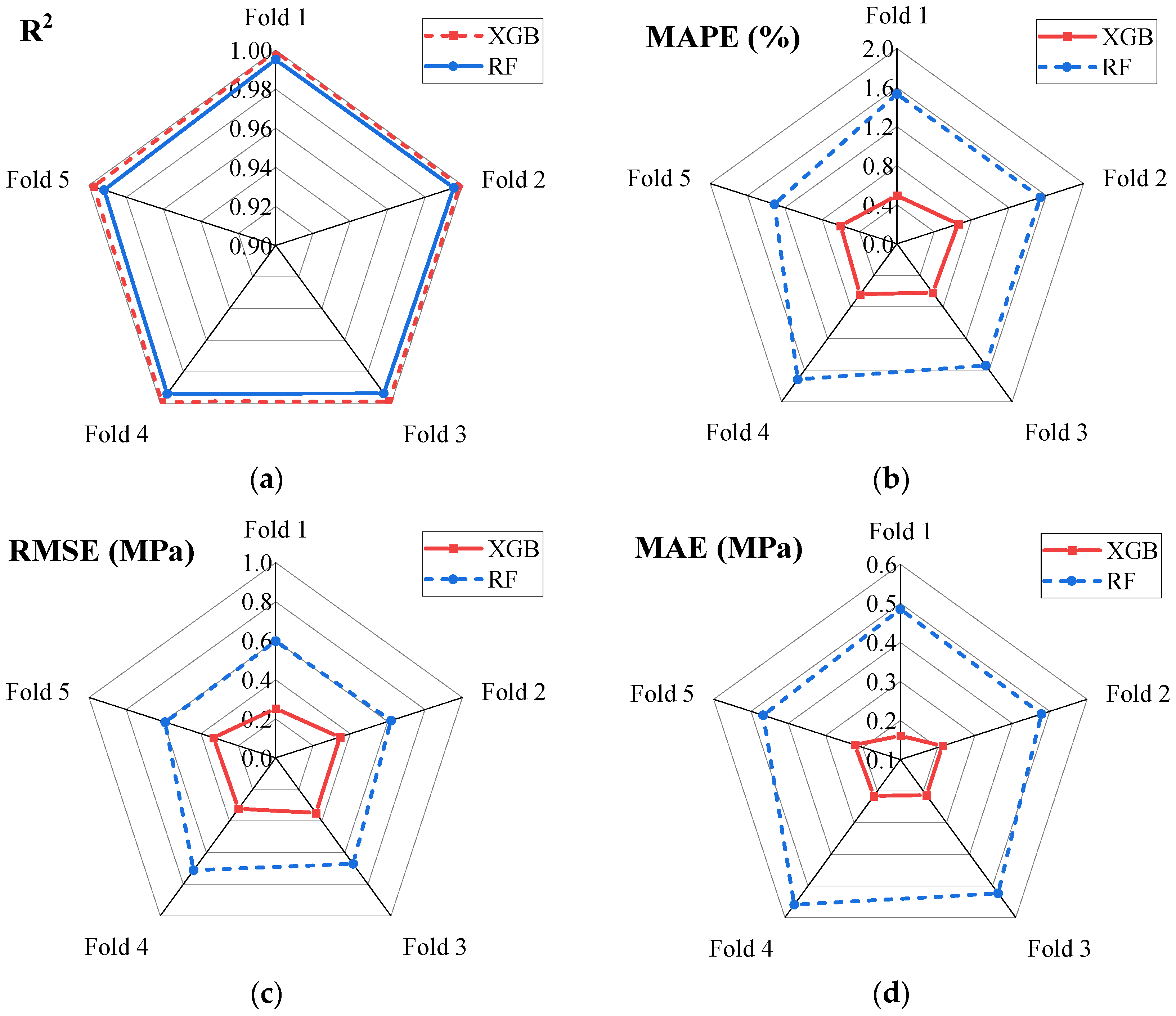
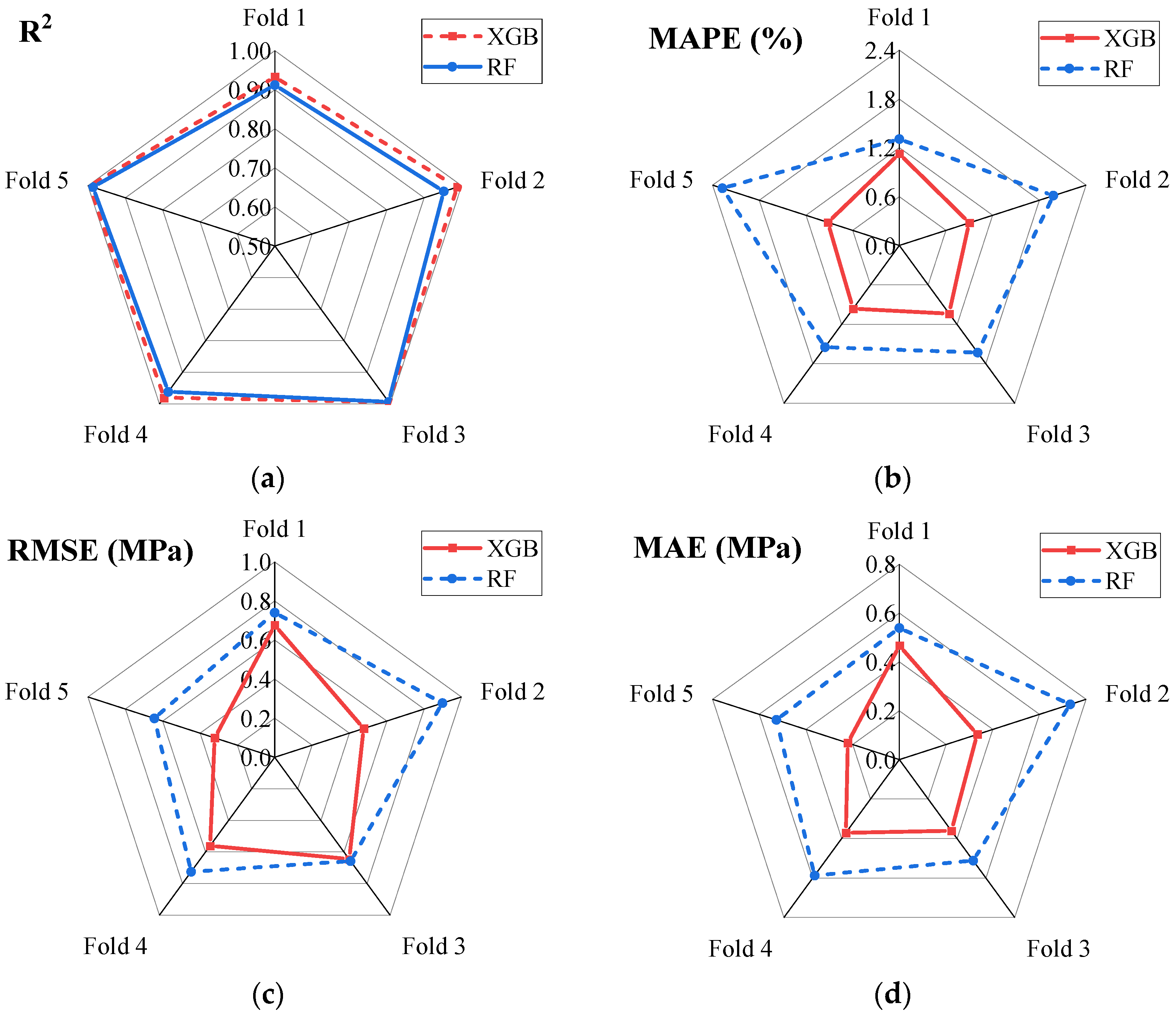
4.3. Cross-Validation
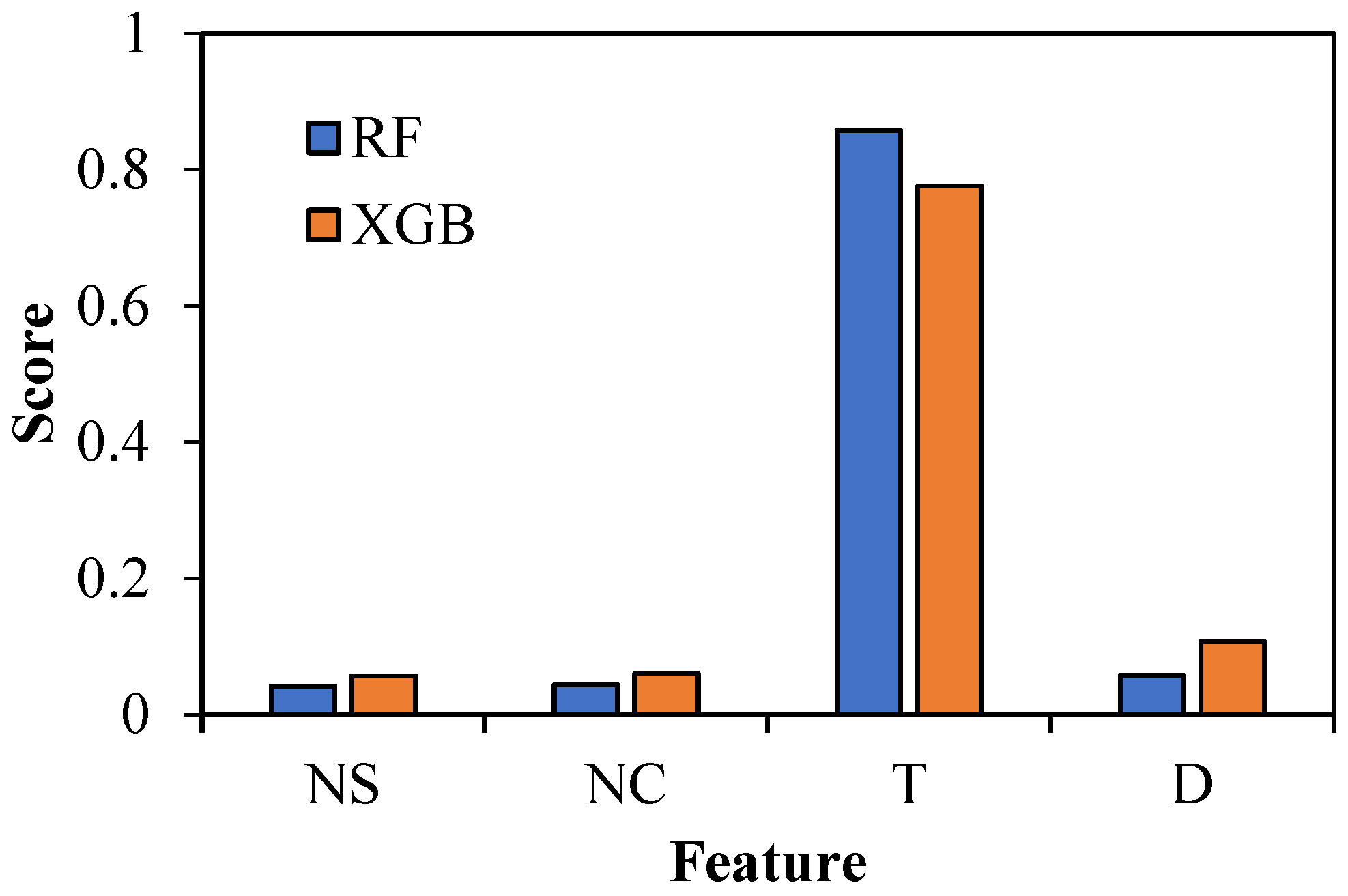
4.4. Feature Importance
4.5. SHAP Analysis
4.6. ICE with PDP
4.7. Comparisons with Previous Models
5. Conclusions
- The XGB prediction model attained accurate predictions and correlated well with the experimental data. R2 values of 0.9987 and 0.9938 were obtained for the training and testing data, respectively. The values of MAPE, RMSE, and MAE attained with the XGB model for the training dataset were 0.5955%, 0.3179 MPa, and 0.2015 MPa, respectively; meanwhile, for the testing dataset, these values were 1.7121%, 0.7054 MPa, and 0.5439 MPa, respectively.
- The XGB model showed better performance in terms of resilience and accuracy during the five-fold cross-validation compared to the RF model. In addition, the XGB model outperformed other earlier CS models: LR, QUAD, FQM, WCA, GA, ANN, and FLM.
- The results from the SHAP analysis, generated using the XGB and RF models, indicated that T had the highest negative impact on CS prediction, followed by D.
- The ICE and PDP plots showed that the optimal combined use of NS and NC as partial cement replacements by weight in concrete, which leads to maximum compressive strength (CS), occurs with an NS content between 2% and 4% and an NC content between 5% and 6%.
- The developed prediction models can be used as a tool for optimizing mix designs for specific fire resistance ratings, reducing the need for costly and time-consuming experimental trial programs.
6. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CH | calcium hydroxide |
| CSH | calcium–silicate hydrate |
| CS | compressive strength |
| CV | cross-validation |
| CNT | carbon nanotubes |
| D | exposure duration |
| FQM | full quadratic model |
| ICE | individual conditional expectation |
| LR | linear regression |
| LOI | loss on ignition |
| NS | nano-silica |
| NC | nano-clay |
| MAPE | mean absolute percentage error |
| MAE | mean absolute error |
| ML | machine learning |
| PDP | partial dependence plots |
| QUAD | quadratic |
| RF | random forest |
| R | correlation coefficients |
| R2 | coefficient of determination |
| RMSE | root mean squared error |
| SHAP | Shapley additive explanations |
| STD | standard deviation |
| T | temperature |
| VIF | variation inflation factor |
| XGB | extreme gradient boosting |
Appendix A
| NS (%) | NC (%) | T (°C) | D (h) | CS (MPa) | NS (%) | NC (%) | T (°C) | D (h) | CS (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 25 | 0 | 38 | 1 | 0 | 500 | 1 | 40 |
| 1 | 0 | 25 | 0 | 42.6 | 2 | 0 | 500 | 1 | 43.6 |
| 2 | 0 | 25 | 0 | 41.5 | 3 | 0 | 500 | 1 | 44.5 |
| 3 | 0 | 25 | 0 | 39.7 | 4 | 0 | 500 | 1 | 43.8 |
| 4 | 0 | 25 | 0 | 38.8 | 0 | 1 | 500 | 1 | 37 |
| 0 | 1 | 25 | 0 | 39.4 | 0 | 3 | 500 | 1 | 41 |
| 0 | 3 | 25 | 0 | 41.9 | 0 | 5 | 500 | 1 | 45.1 |
| 0 | 5 | 25 | 0 | 44.5 | 0 | 7 | 500 | 1 | 42.5 |
| 0 | 7 | 25 | 0 | 38.6 | 0 | 9 | 500 | 1 | 40.2 |
| 0 | 9 | 25 | 0 | 37 | 0.5 | 4.5 | 500 | 1 | 39.6 |
| 0.5 | 4.5 | 25 | 0 | 42.3 | 1 | 4 | 500 | 1 | 41.3 |
| 1 | 4 | 25 | 0 | 43.7 | 1.5 | 3.5 | 500 | 1 | 40.1 |
| 1.5 | 3.5 | 25 | 0 | 43.1 | 0 | 0 | 600 | 1 | 32.6 |
| 0 | 0 | 200 | 1 | 37.1 | 1 | 0 | 600 | 1 | 36.1 |
| 1 | 0 | 200 | 1 | 44.1 | 2 | 0 | 600 | 1 | 39.8 |
| 2 | 0 | 200 | 1 | 45.5 | 3 | 0 | 600 | 1 | 40.9 |
| 3 | 0 | 200 | 1 | 46 | 4 | 0 | 600 | 1 | 40.4 |
| 4 | 0 | 200 | 1 | 45.6 | 0 | 1 | 600 | 1 | 33.7 |
| 0 | 1 | 200 | 1 | 40.7 | 0 | 3 | 600 | 1 | 38.2 |
| 0 | 3 | 200 | 1 | 43.8 | 0 | 5 | 600 | 1 | 41.1 |
| 0 | 5 | 200 | 1 | 47 | 0 | 7 | 600 | 1 | 38.1 |
| 0 | 7 | 200 | 1 | 45.6 | 0 | 9 | 600 | 1 | 35.7 |
| 0 | 9 | 200 | 1 | 43.8 | 0.5 | 4.5 | 600 | 1 | 35.3 |
| 0.5 | 4.5 | 200 | 1 | 44 | 1 | 4 | 600 | 1 | 37.3 |
| 1 | 4 | 200 | 1 | 45.4 | 1.5 | 3.5 | 600 | 1 | 35.9 |
| 1.5 | 3.5 | 200 | 1 | 44.8 | 0 | 0 | 700 | 1 | 25.2 |
| 0 | 0 | 400 | 1 | 35.6 | 1 | 0 | 700 | 1 | 28 |
| 1 | 0 | 400 | 1 | 42.7 | 2 | 0 | 700 | 1 | 30.4 |
| 2 | 0 | 400 | 1 | 44.8 | 3 | 0 | 700 | 1 | 31.1 |
| 3 | 0 | 400 | 1 | 45.4 | 4 | 0 | 700 | 1 | 30.7 |
| 4 | 0 | 400 | 1 | 44.9 | 0 | 1 | 700 | 1 | 26.2 |
| 0 | 1 | 400 | 1 | 40.8 | 0 | 3 | 700 | 1 | 28.8 |
| 0 | 3 | 400 | 1 | 43.5 | 0 | 5 | 700 | 1 | 31.6 |
| 0 | 5 | 400 | 1 | 46.5 | 0 | 7 | 700 | 1 | 29.8 |
| 0 | 7 | 400 | 1 | 45.4 | 0 | 9 | 700 | 1 | 27.8 |
| 0 | 9 | 400 | 1 | 43.2 | 0.5 | 4.5 | 700 | 1 | 28 |
| 0.5 | 4.5 | 400 | 1 | 42.1 | 1 | 4 | 700 | 1 | 28.7 |
| 1 | 4 | 400 | 1 | 43.6 | 1.5 | 3.5 | 700 | 1 | 28.1 |
| 1.5 | 3.5 | 400 | 1 | 42.6 | 0 | 0 | 800 | 1 | 21.2 |
| 2 | 0 | 800 | 1 | 24.3 | 3 | 0 | 500 | 2 | 41.7 |
| 3 | 0 | 800 | 1 | 25.1 | 4 | 0 | 500 | 2 | 41.3 |
| 4 | 0 | 800 | 1 | 24.5 | 0 | 1 | 500 | 2 | 34.9 |
| 0 | 1 | 800 | 1 | 22.1 | 0 | 3 | 500 | 2 | 38.6 |
| 0 | 3 | 800 | 1 | 23.8 | 0 | 5 | 500 | 2 | 42 |
| 0 | 5 | 800 | 1 | 25.5 | 0 | 7 | 500 | 2 | 40.1 |
| 0 | 7 | 800 | 1 | 24.5 | 0 | 9 | 500 | 2 | 37.9 |
| 0 | 9 | 800 | 1 | 22.7 | 0.5 | 4.5 | 500 | 2 | 37.3 |
| 0.5 | 4.5 | 800 | 1 | 23.1 | 1 | 4 | 500 | 2 | 38.5 |
| 1 | 4 | 800 | 1 | 24.1 | 1.5 | 3.5 | 500 | 2 | 37.8 |
| 1.5 | 3.5 | 800 | 1 | 23.3 | 0 | 0 | 600 | 2 | 28.6 |
| 0 | 0 | 200 | 2 | 36.4 | 1 | 0 | 600 | 2 | 32.5 |
| 1 | 0 | 200 | 2 | 43.2 | 2 | 0 | 600 | 2 | 35.9 |
| 2 | 0 | 200 | 2 | 44.5 | 3 | 0 | 600 | 2 | 37.1 |
| 3 | 0 | 200 | 2 | 45.1 | 4 | 0 | 600 | 2 | 36.4 |
| 4 | 0 | 200 | 2 | 44.7 | 0 | 1 | 600 | 2 | 30.4 |
| 0 | 1 | 200 | 2 | 39.9 | 0 | 3 | 600 | 2 | 34.1 |
| 0 | 3 | 200 | 2 | 42.9 | 0 | 5 | 600 | 2 | 37.4 |
| 0 | 5 | 200 | 2 | 46.2 | 0 | 7 | 600 | 2 | 34.5 |
| 0 | 7 | 200 | 2 | 44.7 | 0 | 9 | 600 | 2 | 32.2 |
| 0 | 9 | 200 | 2 | 42.9 | 0.5 | 4.5 | 600 | 2 | 31.8 |
| 0.5 | 4.5 | 200 | 2 | 43.1 | 1 | 4 | 600 | 2 | 32.8 |
| 1 | 4 | 200 | 2 | 44.5 | 1.5 | 3.5 | 600 | 2 | 32.3 |
| 1.5 | 3.5 | 200 | 2 | 43.9 | 0 | 0 | 700 | 2 | 20.6 |
| 0 | 0 | 400 | 2 | 34.6 | 1 | 0 | 700 | 2 | 23.3 |
| 1 | 0 | 400 | 2 | 41.5 | 2 | 0 | 700 | 2 | 25.3 |
| 2 | 0 | 400 | 2 | 43.5 | 3 | 0 | 700 | 2 | 25.9 |
| 3 | 0 | 400 | 2 | 44.1 | 4 | 0 | 700 | 2 | 25.6 |
| 4 | 0 | 400 | 2 | 43.6 | 0 | 1 | 700 | 2 | 21.8 |
| 0 | 1 | 400 | 2 | 39.6 | 0 | 3 | 700 | 2 | 24 |
| 0 | 3 | 400 | 2 | 42.2 | 0 | 5 | 700 | 2 | 26.1 |
| 0 | 5 | 400 | 2 | 45.2 | 0 | 7 | 700 | 2 | 24.8 |
| 0 | 7 | 400 | 2 | 44.1 | 0 | 9 | 700 | 2 | 23.2 |
| 0 | 9 | 400 | 2 | 41.9 | 0.5 | 4.5 | 700 | 2 | 23.3 |
| 0.5 | 4.5 | 400 | 2 | 40.9 | 1 | 4 | 700 | 2 | 23.8 |
| 1 | 4 | 400 | 2 | 42.5 | 1.5 | 3.5 | 700 | 2 | 23.4 |
| 1.5 | 3.5 | 400 | 2 | 41.4 | 0 | 0 | 800 | 2 | 15.6 |
| 0 | 0 | 500 | 2 | 32.4 | 1 | 0 | 800 | 2 | 17.2 |
| 1 | 0 | 500 | 2 | 37.7 | 2 | 0 | 800 | 2 | 18.3 |
| 4 | 0 | 800 | 2 | 18.4 | 0 | 9 | 800 | 2 | 17.1 |
| 0 | 1 | 800 | 2 | 16.6 | 0.5 | 4.5 | 800 | 2 | 17.4 |
| 0 | 3 | 800 | 2 | 17.9 | 1 | 4 | 800 | 2 | 17.9 |
| 0 | 5 | 800 | 2 | 19.2 | 1.5 | 3.5 | 800 | 2 | 17.5 |
| 0 | 7 | 800 | 2 | 18.4 |
References
- Kodur, V. Properties of Concrete at Elevated Temperatures. ISRN Civ. Eng. 2014, 2014, 1–15. [Google Scholar] [CrossRef]
- Dahish, H.A.; Almutairi, A.D. Effect of elevated temperatures on the compressive strength of nano-silica and nano-clay modified concretes using response surface methodology. Case Stud. Constr. Mater. 2023, 18, e02032. [Google Scholar] [CrossRef]
- Aly Elsayd, A.; Fathy, I.N. Experimental Study of fire effects on compressive strength of normal-strength concrete supported with nanomaterials additives. IOSR J. Mech. Civ. Eng. (IOSR-JMCE) 2019, 16, 28–37. [Google Scholar] [CrossRef]
- Prasad Bhatta, D.; Singla, S.; Garg, R. Experimental investigation on the effect of Nano-silica on the silica fume-based cement composites. Mater. Today Proc. 2022, 57, 2338–2343. [Google Scholar] [CrossRef]
- Sivamani, J. Influence of nano-silica on the behaviour of high-performance concrete—Multiscale investigation on its mechanical, durability and microstructural properties. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 283. [Google Scholar] [CrossRef]
- Khosravi, H.; Toloue-Hassanpour, M.R.; Lezgy-Nazargah, M. Investigating the Effects of Nano-Materials on the Mechanical and Durability Properties of Self-Consolidating Concrete. CivilEng 2025, 6, 12. [Google Scholar] [CrossRef]
- Mokhtar, M.M.; Morsy, M.; Taha, N.A.; Ahmed, E.M. Investigating the mechanical performance of nano additives reinforced high-performance concrete. Constr. Build. Mater. 2022, 320, 125537. [Google Scholar] [CrossRef]
- Fallah-Valukolaee, S.; Mousavi, R.; Arjomandi, A.; Nematzadeh, M.; Kazemi, M. A comparative study of mechanical properties and life cycle assessment of high-strength concrete containing silica fume and nanosilica as a partial cement replacement. Structures 2022, 46, 838–851. [Google Scholar] [CrossRef]
- Kanagaraj, B.; Anand, N.; Cashell, K.A.; Andrushia, A.D. Post-fire behaviour of concrete containing nano-materials as a cement replacement material. Case Stud. Constr. Mater. 2023, 18, e02171. [Google Scholar] [CrossRef]
- Ghale Noee, A.; Nasiri Rajabli, J. The effect of nano-silica powder on mechanical and non-mechanical characteristics of self-consolidating concrete (SCC) and its impact on environment protection. Innov. Infrastruct. Solut. 2023, 8, 166. [Google Scholar] [CrossRef]
- Yassin, A.M.; Eldin, M.M.; Omar, M.S.; Hafez, M.A.; Elnaggar, M.A. Effect of nano-silica on the flexural behavior and mechanical properties of self-compacted high-performance concrete (SCHPC) produced by cement CEM II/A-P (experimental and numerical study). Case Stud. Constr. Mater. 2024, 21, e03490. [Google Scholar] [CrossRef]
- Noori, A.; Lu, Y.; Saffari, P.; Zhang, Y.; Wang, M. The optimum percentage of nano clay (NC) in both direct-additive and sonicated modes to improve the mechanical properties of self-compacting concrete (SCC). Case Stud. Constr. Mater. 2022, 17, e01493. [Google Scholar] [CrossRef]
- Amiri, Y.; Hassaninasab, S.; Chehri, K.; Zahedi, M. Investigating the effect of adding bacillus bacteria and nano-clay on cement mortar properties. Case Stud. Constr. Mater. 2022, 17, e01167. [Google Scholar] [CrossRef]
- Shah, S.P.; Hou, P.; Cheng, X. Durability of Cement-Based Materials and Nano-particles: A Review. In Nanotechnology in Construction; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 15–24. [Google Scholar] [CrossRef]
- Mohammed, B.S.; Achara, B.E.; Nuruddin, M.F.; Yaw, M.; Zulkefli, M.Z. Properties of nano-silica-modified self-compacting engineered cementitious composites. J. Clean. Prod. 2017, 162, 1225–1238. [Google Scholar] [CrossRef]
- Ashwini, R.M.; Potharaju, M.; Srinivas, V.; Kanaka Durga, S.; Rathnamala, G.V.; Paudel, A. Compressive and Flexural Strength of Concrete with Different Nanomaterials: A Critical Review. J. Nanomater. 2023, 2023. [Google Scholar] [CrossRef]
- Serag, M.I.; Yasien, A.M.; El-Feky, M.S.; Elkady, H. Effect of nano silica on concrete bond strength modes of failure. Int. J. GEOMATE 2017, 12, 73–80. [Google Scholar] [CrossRef]
- Hosseini, P.; Afshar, A.; Vafaei, B.; Booshehrian, A.; Molaei Raisi, E.; Esrafili, A. Effects of nano-clay particles on the short-term properties of self-compacting concrete. Eur. J. Environ. Civ. Eng. 2017, 21, 127–147. [Google Scholar] [CrossRef]
- Hakamy, A.; Shaikh, F.U.A.; Low, I.M. Effect of calcined nanoclay on microstructural and mechanical properties of chemically treated hemp fabric-reinforced cement nanocomposites. Constr. Build. Mater. 2015, 95, 882–891. [Google Scholar] [CrossRef]
- Hamed, N.; El-Feky, M.S.; Kohail, M.; Nasr, E.S.A.R. Effect of nano-clay de-agglomeration on mechanical properties of concrete. Constr. Build. Mater. 2019, 205, 245–256. [Google Scholar] [CrossRef]
- Ibrahem, A.M.; Al-Mishhadani, S.A.; H.Naji, Z. The Effect of Nano Metakaolin Material on Some Properties of Concrete. Diyala J. Eng. Sci. 2013, 6, 50–61. [Google Scholar] [CrossRef]
- Wang, Z.-H.; Bai, E.-L.; Xu, J.Y.; Du, Y.-H.; Zhu, J.S. Effect of nano-SiO2 and nano-CaCO3 on the static and dynamic properties of concrete. Sci. Rep. 2022, 12, 907. [Google Scholar] [CrossRef]
- Ghouchani, K.; Abbasi, H.; Najaf, E. Some mechanical properties and microstructure of cementitious nanocomposites containing nano-SiO2 and graphene oxide nanosheets. Case Stud. Constr. Mater. 2022, 17, e01482. [Google Scholar] [CrossRef]
- Arioz, O. Effects of elevated temperatures on properties of concrete. Fire Saf. J. 2007, 42, 516–522. [Google Scholar] [CrossRef]
- Malik, M.; Bhattacharyya, S.K.; Barai, S.V. Thermal and mechanical properties of concrete and its constituents at elevated temperatures: A review. Constr. Build. Mater. 2021, 270, 121398. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Fathy, I.N.; Tayeh, B.A.; Almeshal, I. Using artificial neural networks for predicting mechanical and radiation shielding properties of different nano-concretes exposed to elevated temperature. Constr. Build. Mater. 2022, 324, 126663. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Hughes, P.; Fan, Y. Mechanical properties and microstructure of basalt fibre and nano-silica reinforced recycled concrete after exposure to elevated temperatures. Constr. Build. Mater. 2020, 247, 118561. [Google Scholar] [CrossRef]
- Ibrahim, R.K.; Hamid, R.; Taha, M.R. Fire resistance of high-volume fly ash mortars with nanosilica addition. Constr. Build. Mater. 2012, 36, 779–786. [Google Scholar] [CrossRef]
- Wu, L.; Lu, Z.; Zhuang, C.; Chen, Y.; Hu, R. Mechanical properties of Nano SiO2 and carbon fiber reinforced concrete after exposure to high temperatures. Materials 2019, 12, 3773. [Google Scholar] [CrossRef] [PubMed]
- Polat, R.; Qarluq, A.W.; Karagöl, F. Influence of singular and binary nanomaterials on the physical, mechanical and durability properties of mortars subjected to elevated temperatures and freeze–thaw cycles. Constr. Build. Mater. 2021, 295, 123608. [Google Scholar] [CrossRef]
- He, C.; Makovicky, E.; Osbæck, B. Thermal stability and pozzolanic activity of calcined kaolin. Appl. Clay Sci. 1994, 9, 165–187. [Google Scholar] [CrossRef]
- Syamsunur, D.; Wei, L.; Ahmed Memon, Z.; Surol, S.; Md Yusoff, N.I. Concrete Performance Attenuation of Mix Nano-SiO2 and Nano-CaCO3 under High Temperature: A Comprehensive Review. Materials 2022, 15, 7073. [Google Scholar] [CrossRef]
- Ali, A.E.; Faried, A.S.; Osman, K.M. Effect of elevated temperature on properties of concrete containing different types of nano-materials. Constr. Build. Mater. 2024, 438, 136988. [Google Scholar] [CrossRef]
- Hassan, M.M.; Elyamany, M.A.; Khalil, A.E.-R.R.; Megahed, S.Y. Effect of High Elevated Temperature on the Behavior of Concrete Containing Slag and Nano Clay. Civ. Eng. Archit. 2025, 13, 2687–2702. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, Y.; Liu, S.; Chen, Z.; Su, H. Experimental Study on Mechanical Properties of Nano-Alumina-Modified Cement Composites Exposed to High Temperatures. Processes 2023, 12, 94. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Pereira, F.; Mitchell, T.; Botvinick, M. Machine learning classifiers and fMRI: A tutorial overview. Neuroimage 2009, 45, S199–S209. [Google Scholar] [CrossRef]
- Nazar, S.; Yang, J.; Ahmad, W.; Javed, M.F.; Alabduljabbar, H.; Deifalla, A.F. Development of the New Prediction Models for the Compressive Strength of Nanomodified Concrete Using Novel Machine Learning Techniques. Buildings 2022, 12, 2160. [Google Scholar] [CrossRef]
- Ali, R.; Muayad, M.; Mohammed, A.S.; Asteris, P.G. Analysis and prediction of the effect of Nanosilica on the compressive strength of concrete with different mix proportions and specimen sizes using various numerical approaches. Struct. Concr. 2023, 24, 4161–4184. [Google Scholar] [CrossRef]
- Nigam, M.; Verma, M. Prediction of compressive strength of nano-silica concrete by using random forest algorithm. Asian J. Civ. Eng. 2024, 25, 5205–5213. [Google Scholar] [CrossRef]
- Garg, A.; Aggarwal, P.; Aggarwal, Y.; Belarbi, M.O.; Chalak, H.D.; Tounsi, A.; Gulia, R. Machine learning models for predicting the compressive strength of concrete containing nano silica. Comput. Concr. 2022, 30, 33–42. [Google Scholar] [CrossRef]
- Murad, Y. Compressive strength prediction for concrete modified with nanomaterials. Case Stud. Constr. Mater. 2021, 15, e00660. [Google Scholar] [CrossRef]
- Zeyad, A.M.; Mahmoud, A.A.; El-Sayed, A.A.; Aboraya, A.M.; Fathy, I.N.; Zygouris, N.; Asteris, P.G.; Agwa, I.S. Compressive strength of nano concrete materials under elevated temperatures using machine learning. Sci. Rep. 2024, 14, 24246. [Google Scholar] [CrossRef]
- Alkharisi, M.K.; Dahish, H.A.; Youssf, O. Prediction models for the hybrid effect of nano materials on radiation shielding properties of concrete exposed to elevated temperatures. Case Stud. Constr. Mater. 2024, 21, e03750. [Google Scholar] [CrossRef]
- Das, P.; Kashem, A.; Hasan, I.; Islam, M. A comparative study of machine learning models for construction costs prediction with natural gradient boosting algorithm and SHAP analysis. Asian J. Civ. Eng. 2024, 25, 3301–3316. [Google Scholar] [CrossRef]
- BS 1881 P 116; Testing Concrete. Method for Determination of Compressive Strength of Concrete Cubes. BSI: London, UK, 1983.
- Khan, M.A.; Farooq, F.; Javed, M.F.; Zafar, A.; Ostrowski, K.A.; Aslam, F.; Malazdrewicz, S.; Maślak, M. Simulation of Depth of Wear of Eco-Friendly Concrete Using Machine Learning Based Computational Approaches. Materials 2021, 15, 58. [Google Scholar] [CrossRef] [PubMed]
- Anaconda Inc. Anaconda Individual Edition, Anaconda Website. 2024. Available online: https://www.anaconda.com/products/individual (accessed on 14 January 2025).
- Kutner, M.H.; Nachtsheim, C.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill Irwin: New York, NY, USA, 2005. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Wu, J.; Ma, D.; Wang, W. Leakage Identification in Water Distribution Networks Based on XGBoost Algorithm. J. Water Resour. Plan. Manag. 2022, 148. [Google Scholar] [CrossRef]
- Wang, T.; Bian, Y.; Zhang, Y.; Hou, X. Classification of earthquakes, explosions and mining-induced earthquakes based on XGBoost algorithm. Comput. Geosci. 2023, 170, 105242. [Google Scholar] [CrossRef]
- Ansari, S.S.; Ibrahim, S.M.; Hasan, S.D. Interpretable Machine-Learning Models to Predict the Flexural Strength of Fiber-Reinforced SCM-Blended Concrete Composites. J. Struct. Des. Constr. Pract. 2025, 30. [Google Scholar] [CrossRef]
- Quan Tran, V. Machine learning approach for investigating chloride diffusion coefficient of concrete containing supplementary cementitious materials. Constr. Build. Mater. 2022, 328, 127103. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Dahish, H.A. Predicting the Compressive Strength of Concrete Modified by Nanoparticles and Exposed to Fire. IOSR J. Mech. Civ. Eng. (IOSR-JMCE) 2022, 19, 37–50. [Google Scholar] [CrossRef]






| Formula | Concentration (%) | ||
|---|---|---|---|
| Cement | NC | NS | |
| SiO2 | 20.22 | 51.52 | 99.85 |
| Fe2O3 | 3.3 | 1.23 | 0.01 |
| Al2O3 | 6.05 | 40.18 | 0.02 |
| CaO | 62.75 | 2 | 0.03 |
| K2O | 0.85 | 0.53 | 0.01 |
| MgO | 1.8 | 0.12 | 0.01 |
| Na2O | 0.79 | 0.08 | 0.01 |
| SO3 | 2.25 | -- | -- |
| TiO2 | 0.2 | 2.27 | -- |
| LOI | 1.77 | 2.01 | 0.04 |
| Parameters | Unit | Min. | Max. | Mean | SD | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Nano-silica dose (NS) | %wt. of cement | 0.00 | 4.00 | 1.000 | 1.259 | 1.176 | 0.264 |
| Nano-clay dose (NC) | %wt. of cement | 0.00 | 9.00 | 2.846 | 2.893 | 0.645 | −0.649 |
| Temperature (T) | °C | 25.0 | 800 | 494.2 | 233.6 | −0.485 | −0.767 |
| Duration (D) | hour | 0.00 | 2.00 | 1.385 | 0.627 | −0.508 | −0.629 |
| Compressive strength (CS) | MPa | 15.6 | 47.0 | 35.22 | 8.853 | −0.636 | −0.901 |
| Feature | NS | NC | T | D |
|---|---|---|---|---|
| VIF | 1.4148 | 1.4148 | 1.1606 | 1.1606 |
| ML Approach | Hyperparameter | Range | Optimized Value |
|---|---|---|---|
| XGB | n_estimators | [10, 600] | 91 |
| max_depth | [10, 30] | 18 | |
| learning_rate | [0.01, 0.3] | 0.1 | |
| Subsample | [0.1, 1.0] | 0.4 | |
| RF | n_estimators | [10, 200] | 89 |
| max_depth | [10, 30] | 12 | |
| min_samples_split | [2, 20] | 2 | |
| ′min_samples_leaf | [1, 10] | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahish, H.A.; Alturki, M. Predicting the Effects of Nano Additives and Elevated Temperatures on Concrete Compressive Strength Utilizing Machine Learning. Buildings 2025, 15, 3349. https://doi.org/10.3390/buildings15183349
Dahish HA, Alturki M. Predicting the Effects of Nano Additives and Elevated Temperatures on Concrete Compressive Strength Utilizing Machine Learning. Buildings. 2025; 15(18):3349. https://doi.org/10.3390/buildings15183349
Chicago/Turabian StyleDahish, Hany A., and Mansour Alturki. 2025. "Predicting the Effects of Nano Additives and Elevated Temperatures on Concrete Compressive Strength Utilizing Machine Learning" Buildings 15, no. 18: 3349. https://doi.org/10.3390/buildings15183349
APA StyleDahish, H. A., & Alturki, M. (2025). Predicting the Effects of Nano Additives and Elevated Temperatures on Concrete Compressive Strength Utilizing Machine Learning. Buildings, 15(18), 3349. https://doi.org/10.3390/buildings15183349






