Research on Construction Period Optimization of High-Rise Buildings Based on Integrated Building Platform Applications
Abstract
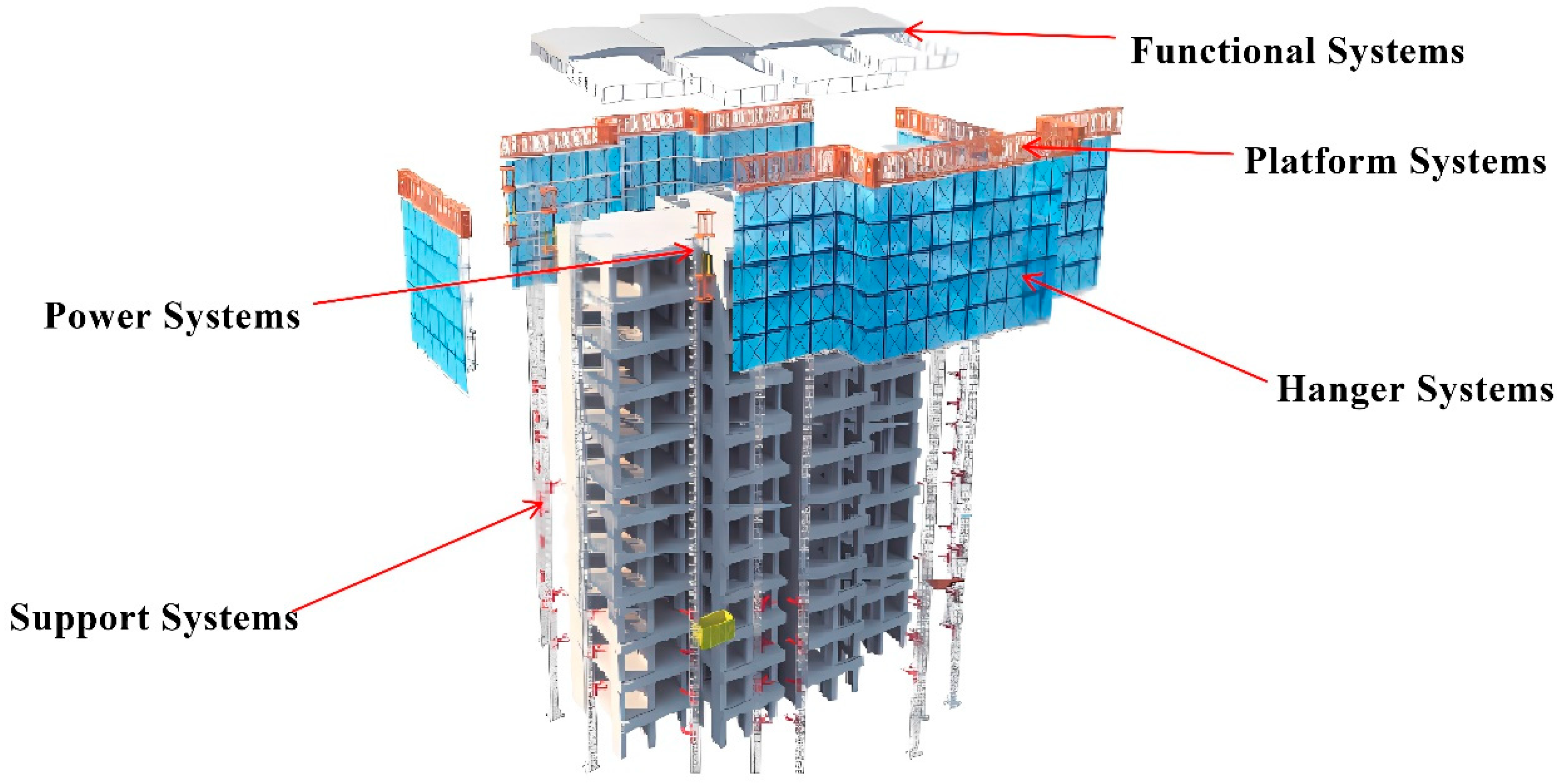
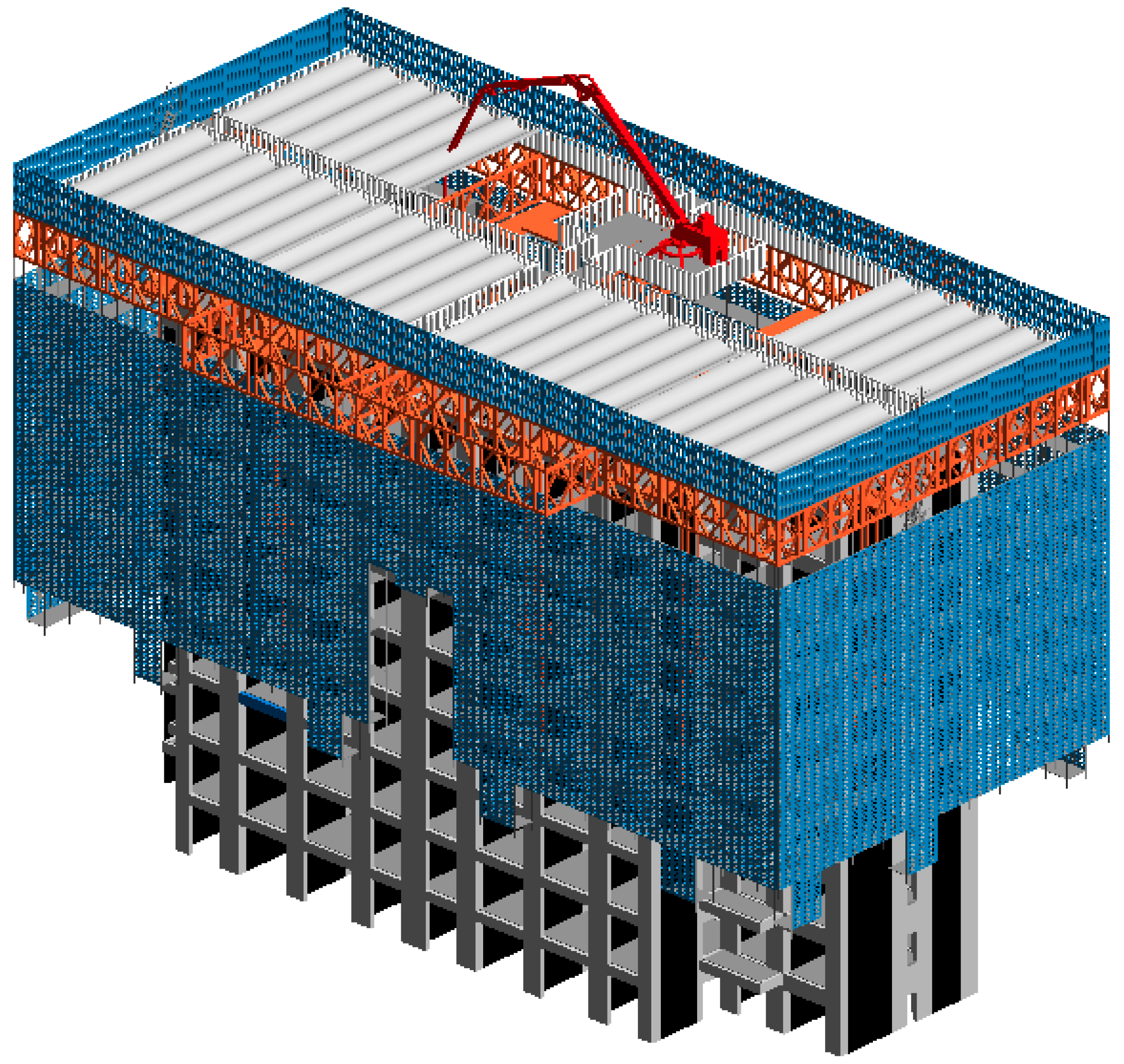
1. Introduction
- Developing a novel GA-based optimization model that integrates overlap network theory to enable parallel, multi-layer construction processes under IBP constraints, addressing both intra- and inter-layer workflow dependencies.
- Providing empirical validation through a real-world case study, demonstrating a 33.3% reduction in standard-floor duration and 41% idle-time reduction—outcomes surpassing traditional sequential methods.
- Advancing practical applications by defining ten standardized workflow states to guide dynamic resource allocation, a contribution absent in prior IBP literature.
2. Literature Review
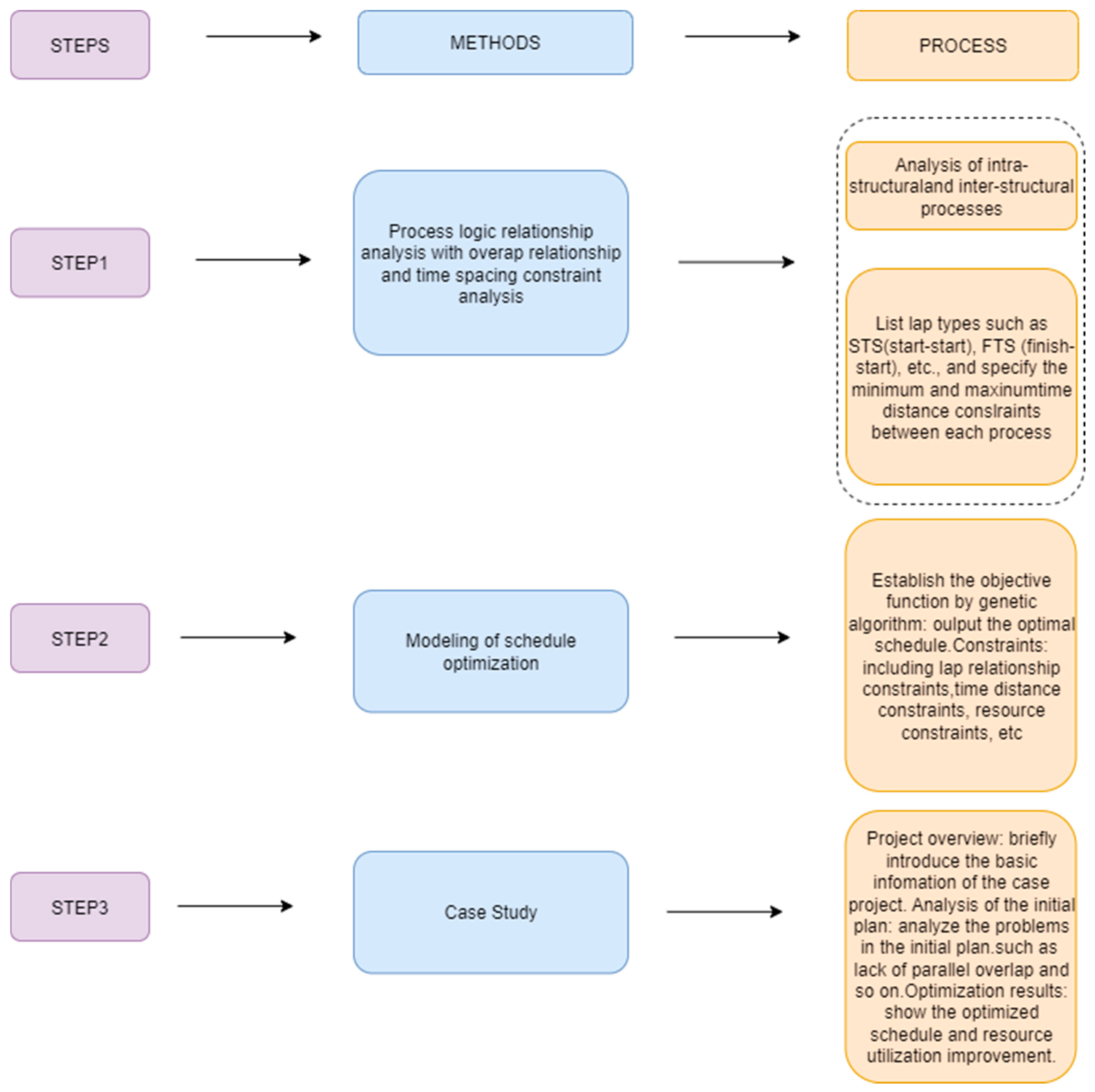
3. Methods
- 1.
- Encoding and Decoding
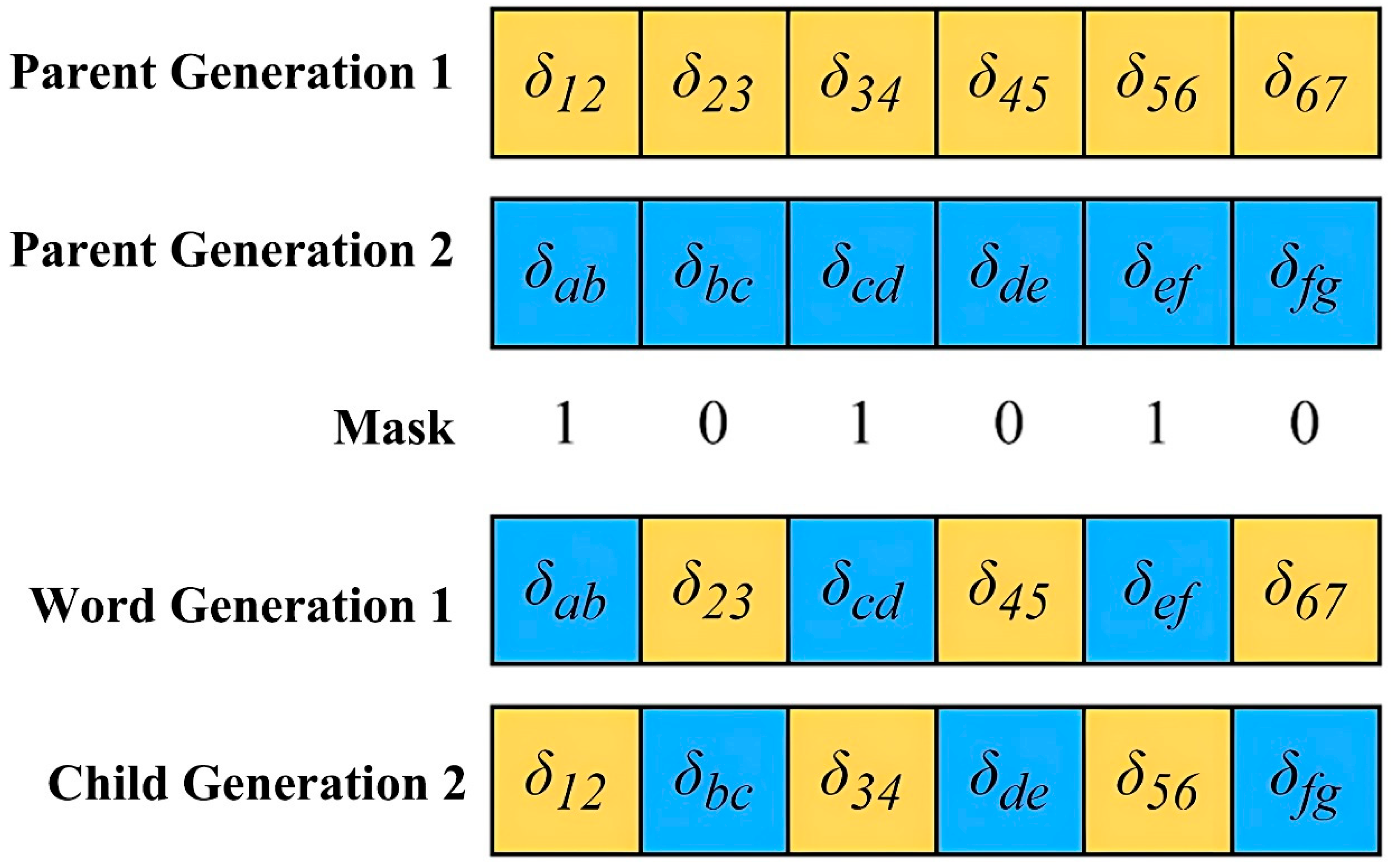
- Crossover: Uniform crossover exchanges δij values between parent chromosomes using a randomly generated mask.
- Mutation: Each gene δij has a 10% probability of being regenerated as a random value within [δijmin, δijmax].
- 2.
- Initial Population Generation
- 3.
- Fitness Function Design
- (1)
- Decoding: Extract all δij values from the chromosome.
- (2)
- Schedule Calculation:
- Initialize S1 = 0.
- Compute each Sj = max (Si + Di + δij) for all predecessor processes i.
- (3)
- Duration Calculation:
- T = max (Si + Di) ∀i ∈ processes.
- (4)
- Fitness Assignment:
- Fitness = 1/T (if all constraints are satisfied).
- Fitness = 0 (if any constraint is violated).
- (5)
- Constraint Checking:
- Verify δijmin ≤ δij ≤ δijmax.
- Check resource usage ∑Rr ≤ Cr at each time t (Equation (6)).
- 4.
- Alternative Formal Phrasing
- 5.
- Crossover Operation
- 6.
- Mutation Operation
- 7.
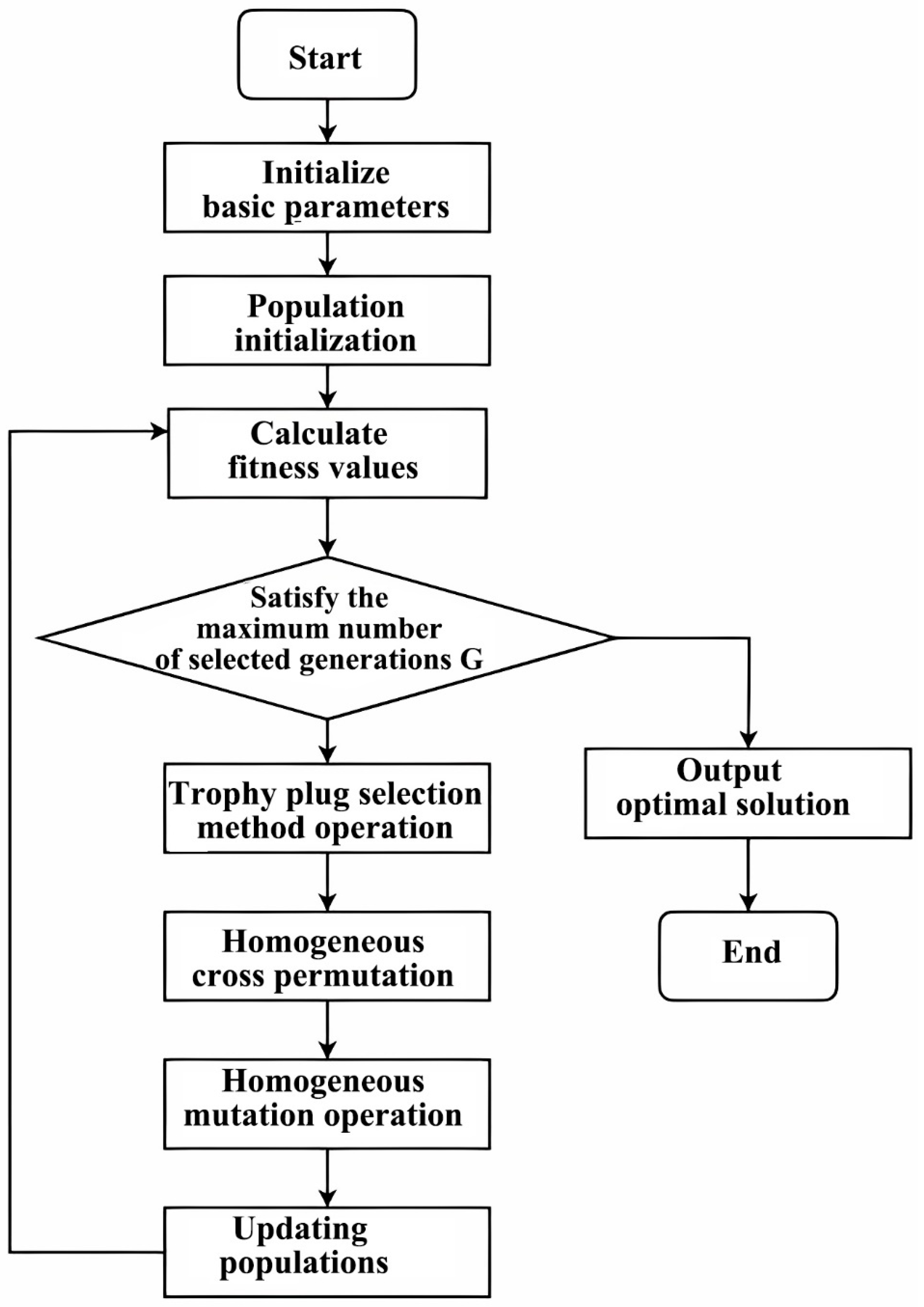
- Termination Criteria and Algorithmic Flow
- Step 1:
- Initialize basic parameters. Including the basic information of each process, the labor resource demand R of each process, the total labor resource Cr, the overlap relationship between processes, and the constraint of the overlap time window δij. The initial population size NP, maximum iteration times G, tournament selection scale k, crossover probability Pc, mutation probability Pm, and other basic information of the genetic algorithm.
- Step 2:
- Population initialization. According to the encoding strategy, randomly generate an initial population P (0) of N chromosomes.
- Step 3:
- Calculate fitness. For each chromosome in population P (g), calculate its fitness value according to the formula.
- Step 4:
- Select the operation. Using the tournament selection operator, N individuals are selected from population P (g) to form the intermediate population Q (g).
- Step 5:
- Cross operation. Perform a uniform crossover operation on individuals in population Q (g) based on crossover probability Pc to generate new individuals.
- Step 6:
- Mutation operation. Perform a uniform mutation operation on individuals in population Q (g) based on mutation probability Pm to generate new individuals.
- Step 7:
- Update the population. Merge individuals in Q (g) with individuals in P (g), select N optimal individuals based on fitness values, and form a new population P (g + 1).
- Step 8:
- Termination condition judgment. If the maximum iteration count G is reached, stop the calculation; otherwise, let g = g + 1. Return to step three. The flowchart of genetic algorithm optimization design and implementation is shown in Figure 6.
4. Analysis of Process Logic and Overlapping Relationships
4.1. Analysis of the Logical Relationship Between the Construction Sequences of Work Processes
- (1)
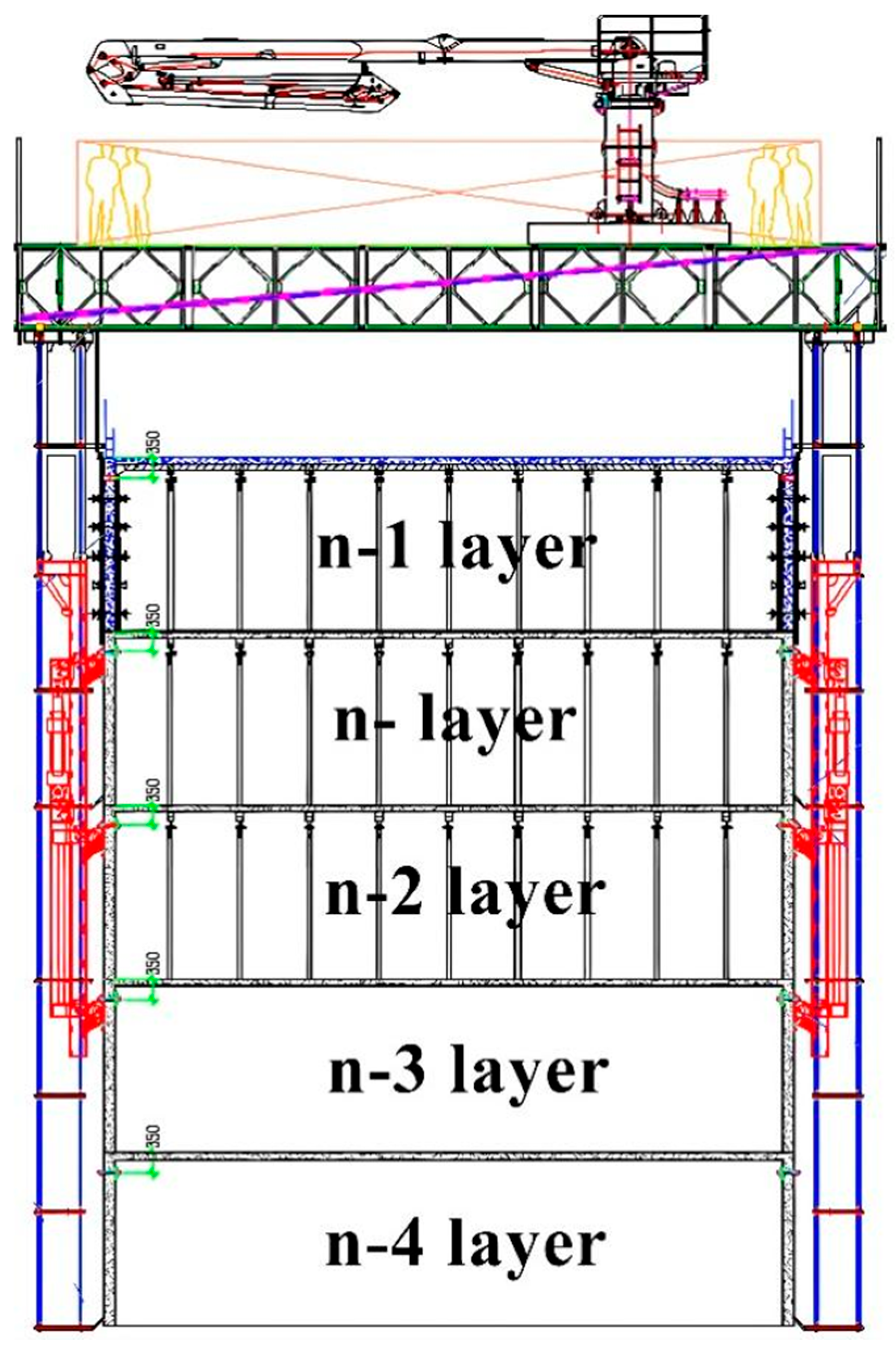
- Analysis of the contents of construction operations within each structural layer
- (2)
- Process sequential logical relationship analysis
4.2. Adaptable Working Relationship Analysis
- STS: Start-To-Start;
- FTS: Finish-To-Start;
- FTF: Finish-To-Finish;
- STF: Start-To-Finish.
- (1)
- Analysis of work overlap relationships within structural layers
- (2)
- Analysis of overlap relationships between structural layers
- (3)
- Constraints on the value of lap spacing between processes
5. Duration Optimization Model Based on Genetic Algorithm
- (1)
- Analysis of constraintsLap parallelism of processes by adjusting work relationships to optimize the duration is achieved by considering constraints such as the type of lap logic between processes, constraints on the value of the lap spacing between processes, and the demand for labor resources.
- ①
- Lap relationship constraintsFor each pair of processes i and j with overlapping relationships, constraints are defined according to the type of overlap:STS (Start-To-Start)-type lap relationship, with the following constraint equation:The FTS (Finish-To-Start)-type lap relationship is constrained by the following equation.FTF (Finish-To-Finish)-type lap relationship, whose constraint equation is as follows:The STF (Start-To-Finish)-type lap relationship is constrained by the following equations:This type of lapping relationship is not addressed in this study, so the subsequent model is constructed without this constraint.
- ②
- Lap spacing time window constraintFor each pair of processes i and j with a lap relationship, the lap time distance δij must satisfy the lap time distance time window constraint equation as follows:
- ③
- Resource constraintsWhen adjusting work relationships, all processes in the overlap process occur at the same time to occupy each labor resource and cannot exceed the total amount of labor resources to ensure that parallel processes will not be interrupted due to resource conflicts.At any moment t, the total use of each of the labor resources r does not exceed the total of the resources in the following formula:
- (2)
- Objective function analysisAll processes aim at the minimum completion time of the construction duration of the standard floor of the main structure under the constraints of lap relationship constraints, lap time distance constraints, and resource constraints. The formula for minimizing the total duration is as follows:
- (3)
- Construction of a construction period optimization model for the standard floor of the main structureAccording to the analysis of the objective function and constraints, the construction duration optimization model of the standard layer of the main structure based on the integrated platform established in this paper is as follows:
6. Case Study
6.1. Project Overview
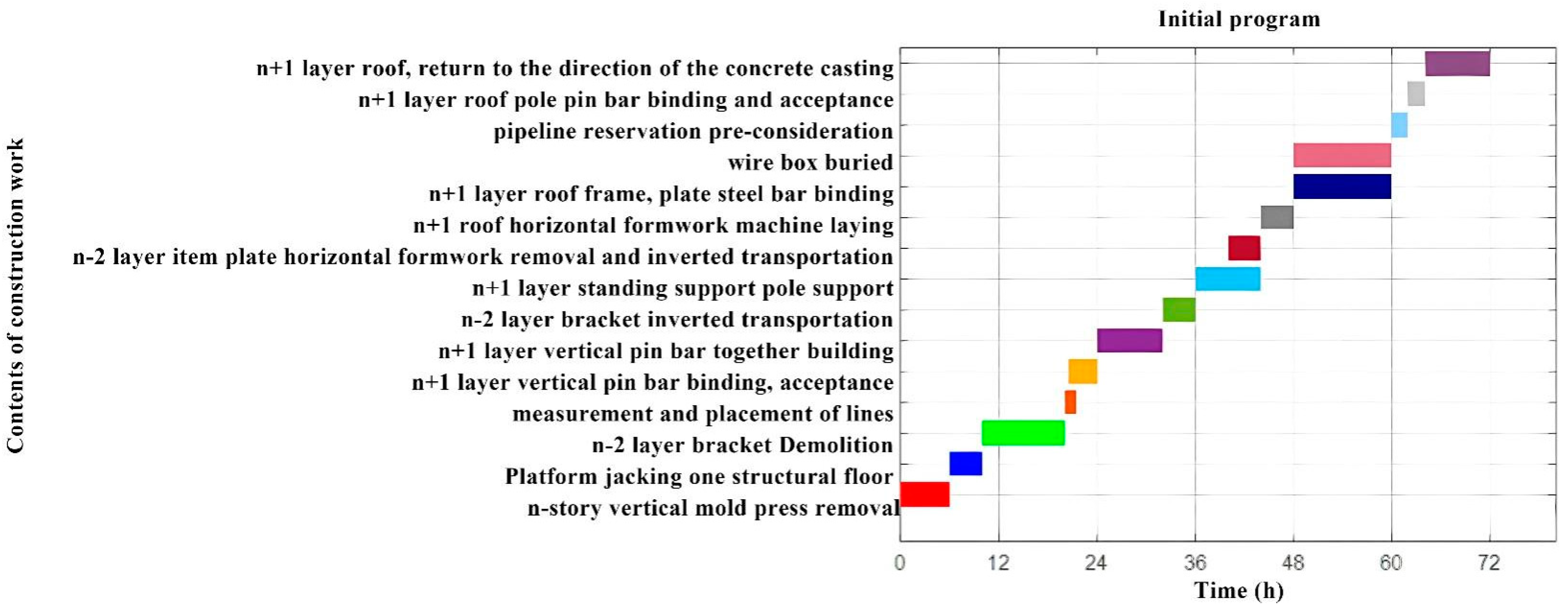
6.2. Analysis of Problems with the Standard Floor Construction Schedule Program
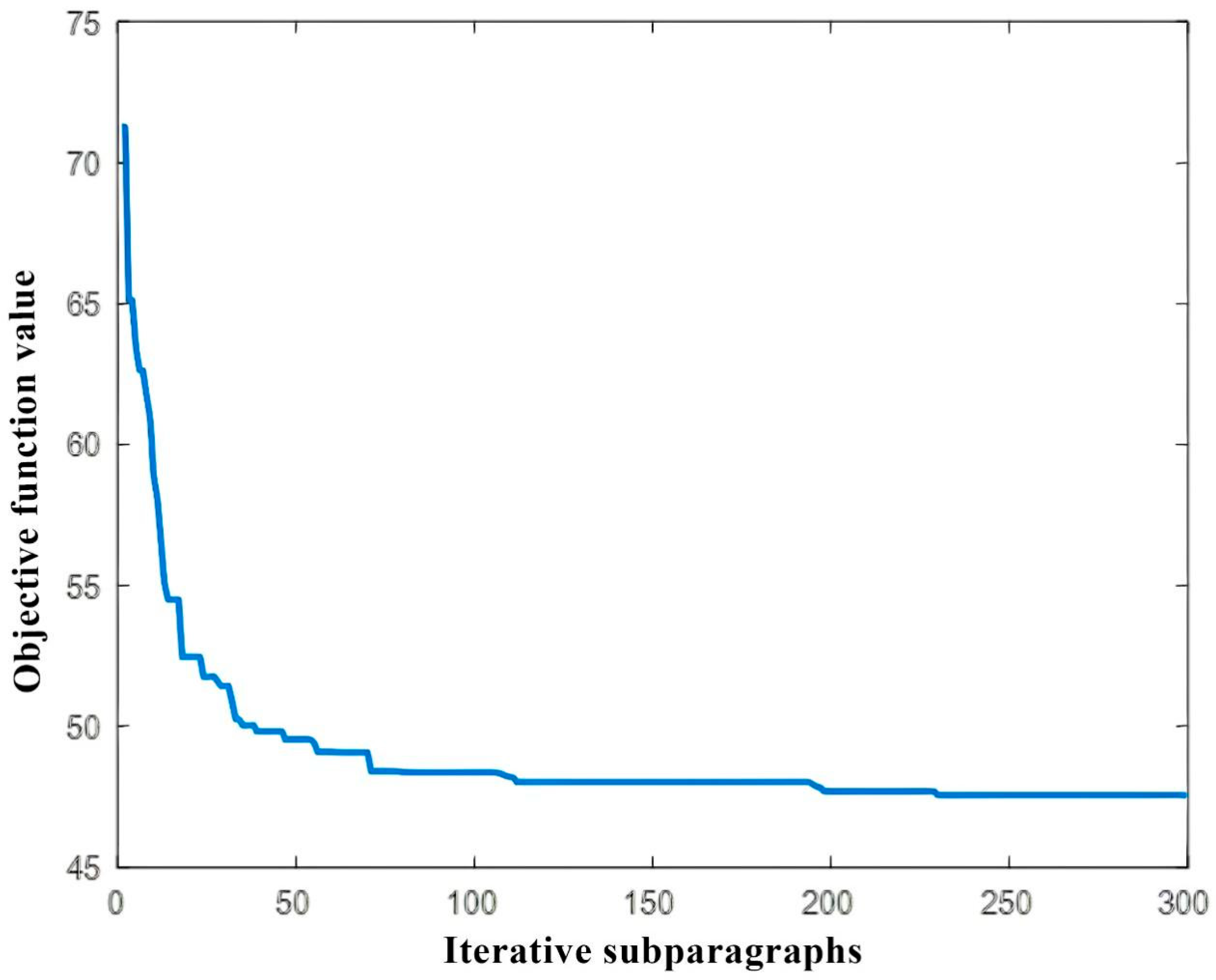
6.3. Optimization Results and Analysis Based on Genetic Algorithm
- Population size (50): Determined via incremental testing (20–100), where 50 achieved a balance between diversity and computational cost.
- Crossover (Pc = 1): Adopted studies to ensure thorough solution–space exploration.
- Mutation (Pm = 0.1): Validated through sensitivity analysis (Figure 9), with higher values (>0.2) causing divergence.
- Termination (300 iterations): Selected after observing convergence plateaus beyond 250 iterations in 90% of trials.
7. Discussion
8. Conclusions
- (1)
- Through detailed analysis of integrated platform construction workflows, this study establishes clear sequential relationships between intra- and inter-layer processes (e.g., N-layer concrete pouring as a prerequisite for platform jacking). These defined logic rules prevent construction conflicts while ensuring safety and workflow continuity.
- (2)
- Applying overlap network theory, the research identifies adjustable process overlaps (e.g., STS-type between platform jacking and rebar work) across vertical and horizontal dimensions. This precise mapping of parallel potentials enables targeted schedule compression.
- (3)
- A genetic algorithm model incorporating process logic, spacing constraints, and labor demands was tested on Wuhan Building #1. Results show that standard floor duration was reduced to 33.3% (6 → 4 days), process idle time was cut by 41%, and 3D platform resource utilization was significantly enhanced.
- (4)
- Building on this study’s framework, future research should focus on the following: 1. Extend the GA model to simultaneously optimize duration, cost, and carbon emissions, aligning with sustainable construction goals. 2. Test the model’s adaptability to diverse building types (e.g., steel-framed offices, irregular mixed-use towers) by recalibrating process logic relationships (Table 2) and spatial constraints (Table 7). 3. Develop automated workflows to translate BIM 4D/5D data into model inputs (e.g., auto-generating process dependencies in Table 2), reducing manual calibration efforts.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.Y. Green design of high-rise buildings under the “double carbon” target. Sichuan Shuini 2023, 5, 172–174. [Google Scholar]
- Kim, K.; Teizer, J. Automatic design and planning of scaffolding systems using building information modeling. Adv. Eng. Inform. 2014, 28, 66–80. [Google Scholar] [CrossRef]
- Kim, K.; Cho, Y.K.; Kim, K. BIM-based decision-making framework for scaffolding planning. J. Manag. Eng. 2018, 34, 04018046. [Google Scholar] [CrossRef]
- Yu, Z. The road to development of scaffolding and formwork technology. Chin. Build. Met. Strut. 2008, 38–40. [Google Scholar]
- Xu, M. Application of Attached Lifting Scaffold in Construction Technology of High-rise Building. Jiangxi Build. Mater. 2022, 8, 270–272. [Google Scholar]
- Guo, F.Y.; Liu, S.P.; Fu, S.; Xu, J.; Sun, J. Digitalization paths for aerial building machine construction technology. Sci. Technol. Eng. 2025, 25, 3840–3850. [Google Scholar]
- Lian, J.; Jiang, J.D.; Liu, H.; Zhang, B.Y.; Liu, K.; Hu, Z.M. Application of residential building making machine in construction process. Constr. Technol. 2022, 51, 45–48. [Google Scholar]
- Zhu, J.W.; Ouyang, M.Y. Explore the super high-rise construction tool jacking platform system. Constr. Architect. 2018, 20, 64–66. [Google Scholar]
- Liu, X.Z. Research on the analysis and construction technology of key system of intelligent construction machine for super high-rise buildings. Xi’an Univ. Technol. 2023. [Google Scholar]
- Wang, H. Research and application of key construction technology for high-rise residential buildings. Residence 2024, 6, 56–59. [Google Scholar]
- Hao, H.M. Research on digital climbing technology of integral molding system for super high-rise buildings. Qingdao Univ. Technol. 2023. [Google Scholar]
- Li, S.; Yu, Z.; Meng, Z.; Han, G.; Huang, F.; Zhang, D.; Zhang, Y.; Zhu, W.; Wei, D. Study on construction technology of hydraulic climbing formwork for super high-rise building under aluminum formwork system. IOP Conf. Ser. Earth Environ. Sci. 2021, 769, 032062. [Google Scholar] [CrossRef]
- Wakisaka, T.; Furuya, N.; Inoue, Y.; Shiokawa, T. Automated construction system for high-rise reinforced concrete buildings. Autom. Constru. 2018, 9, 229–250. [Google Scholar] [CrossRef]
- Xu, G.W.; Deng, H.W.; Chen, D.; Liu, K.; Li, L. Application of lightweight swingable high-efficiency construction integrated platform in house building construction. Constr. Technol. 2021, 50, 9–11+18. [Google Scholar]
- Gong, J.; Fang, T.; Yang, D.; Feng, Y.; Zhu, Y. Research on Integrated Technology of Integral Aerial Building Formwork Equipment and Large Tower Crane. Structures 2024, 60, 105771. [Google Scholar] [CrossRef]
- Liao, H.; Du, F.; Yuan, Y. Design and Construction Technology of lntegrated Construction Platform System of Chongqing IFS. Constr. Technol. 2016, 45, 117–120. [Google Scholar]
- Oltra-Badenes, R.; Guerola-Navarro, V.; Gil-Gómez, J.-A.; Botella-Carrubi, D. Design and implementation of teaching–learning activities focused on improving the knowledge, the awareness and the perception of the relationship between the SDGs and the future profession of university students. Sustainability 2023, 15, 5324. [Google Scholar] [CrossRef]
- Hong, Q.; Dong, X.B. Research on the application of critical chain technology in project schedule management. Light Text. Ind. Technol. 2017, 46, 30–31. [Google Scholar]
- Damci, A.; Polat, G. Impacts of different objective functions on resource leveling in construction projects: A case study. J. Civ. Eng. Manag. 2014, 20, 537–547. [Google Scholar] [CrossRef]
- Sonmez, R.; Bettemir, O.H. A hybrid genetic algorithm for the discrete time-cost trade-off problem. Exp. Syst. Appl. 2012, 39, 11428–11434. [Google Scholar] [CrossRef]
- Yuan, Y.; Ye, S.; Lin, L.; Gen, M. Multi-objective multi-mode resource-constrained project scheduling with fuzzy activity durations in prefabricated building construction. Comput. Ind. Eng. 2021, 158, 107316. [Google Scholar] [CrossRef]
- Alsayegh, H.; Hariga, M. Hybrid meta-heuristic methods for the multi-resource leveling problem with activity splitting. Autom. Constr. 2012, 27, 89–98. [Google Scholar] [CrossRef]
- Ma, Z.; Demeulemeester, E.; He, Z.; Wang, N. A computational experiment to explore better robustness measures for project scheduling under two types of uncertain environments. Comput. Ind. Eng. 2019, 131, 382–390. [Google Scholar] [CrossRef]
- Tian, J.; Hao, X.; Gen, M. A hybrid multi-objective EDA for robust resource constraint project scheduling with uncertainty. Comput. Ind. Eng. 2019, 130, 317–326. [Google Scholar] [CrossRef]
- Ujong, J.A.; Mbadike, E.M.; Alaneme, G.U. Prediction of cost and duration of building construction using artificial neural network. Asian J. Civ. Eng. 2022, 23, 1117–1139. [Google Scholar] [CrossRef]
- Sonmez, R.; Gurel, M. Hybrid optimization method for large-scale multimode resource-constrained project scheduling problem. J. Manag. Eng. 2016, 32, 04016020. [Google Scholar] [CrossRef]
- Parihar, S.; Bhar, C. Project scheduling management: Analyzing the risks present in the on-time project completion in electrical power distribution projects. FILB Bus. Rev. 2015, 4, 80–90. [Google Scholar] [CrossRef]
- Feng, C.W.; Liu, L.; Burns, S.A. Using genetic algorithms to solve construction time-cost trade-off problems. J. Comput. Civ. Eng. 1997, 11, 184–189. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Du, Z.D.; Zhou, H. Resource leveling optimization for construction projects based on particle swarm algorithm. China Civ. Eng. J. 2017, 2, 93–96. [Google Scholar]
- El-Diraby, T.; Krijnen, T.; Papagelis, M. BIM-based collaborative design and sociotechnical analytics of green buildings. Autom. Constr. 2017, 82, 59–74. [Google Scholar] [CrossRef]
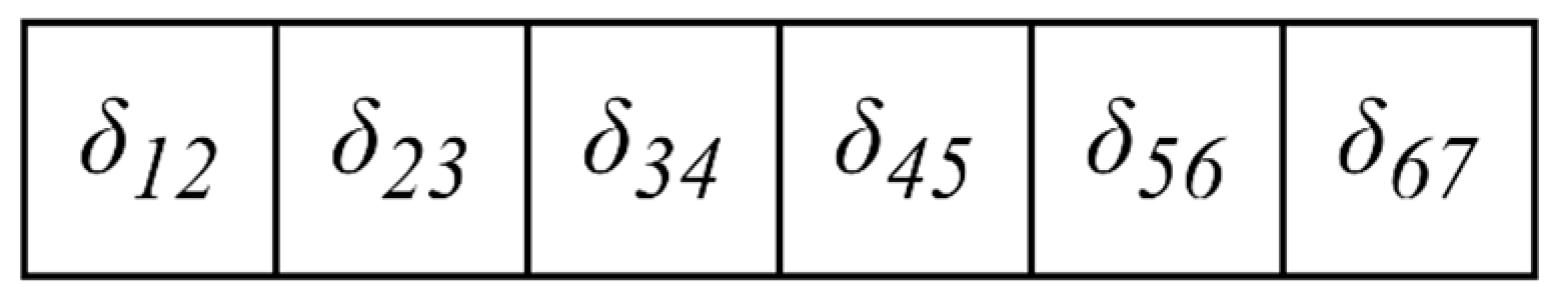
| Aspect | Traditional Methods | Integrated Platform Methods |
|---|---|---|
| Safety | Lower | Enclosed workspace, higher safety |
| Efficiency | Moderate | High, leveraging automation and digital technologies |
| Sustainability | Limited | Better, reusable components |
| Quality | High | Higher |
| Structural Layer | Serial Number | Process Name | Pre-Processing |
|---|---|---|---|
| N + 1 floor | A | Elevation of N + 1 floor platform moldings | M |
| B | Measurement and placement of the N + 1 floor | A | |
| C | Vertical reinforcement binding and acceptance at the N + 1 level | A, B | |
| D | N + 1 floor vertical reinforcement co-molding | A, C | |
| E | N + 1 floor riser support | D, O | |
| F | Horizontal formwork laying for N + 1 floor roof slabs | E, P | |
| G | N + 1 floor top slab beam and plate reinforcement binding | F | |
| H | N + 1 layer wire box burial | F | |
| I | N + 1 floor piping pre-reservation and pre-embedding | G, H | |
| J | N + 1 floor top plate slab reinforcement binding and acceptance | I | |
| K | N + 1 floor top slab, vertical concrete pouring | J | |
| N-layer | L | N-story top slab, N-story vertical concrete pouring | / |
| M | Removal of vertical formwork at N level | L | |
| N − 2nd floor | N | Removal of N − 2 floor supports | / |
| O | N − 2 level support reversal | N, D | |
| P | Removal and transportation of horizontal formwork at the top of the N − 2 floor | O, E |
| Working Procedure | Process Number | Overlapping Work | Connecting Logical Relationships |
|---|---|---|---|
| Elevation of N + 1 floor platform moldings | A | B | STS |
| C | STS | ||
| D | FTS | ||
| Measurement and placement of the N + 1 floor | B | C | STS |
| Vertical reinforcement binding and acceptance at the N + 1 level | C | D | FTS |
| N + 1 floor vertical reinforcement co-molding | D | E | STS |
| N + 1 floor riser support | E | F | STS |
| Horizontal formwork laying for N + 1 floor roof slabs | F | G | FTS |
| H | FTS | ||
| N + 1 floor top slab beam and plate reinforcement binding | G | / | / |
| N + 1 layer wire box burial | H | G | FTF |
| I | FTS | ||
| N + 1 floor pipeline pre-reservation and pre-embedding | I | J | FTS |
| N + 1 floor top plate slab reinforcement binding and acceptance | J | K | FTS |
| N + 1 floor top slab, vertical concrete pouring | K | / | / |
| Working Procedure | Process Number | Immediately After Work | Connecting Logical Relationships |
|---|---|---|---|
| N-story top slab, N-story vertical concrete pouring | L | M | FTS |
| Removal of vertical formwork at N level | M | / | / |
| Working Procedure | Process Number | Overlapping Work | Connecting Logical Relationships |
|---|---|---|---|
| N − 2nd floor Bracket removal | N | O | FTS |
| N − 2 level support reversal | O | P | FTS |
| Removal and transportation of horizontal formwork at the top of the N − 2 floor | P | / | / |
| Working Procedure | Process Number | Overlapping Work | Connecting Logical Relationships |
|---|---|---|---|
| Elevation of N + 1 floor moldings | A | / | / |
| Measurement and placement of the N + 1 floor | B | / | / |
| Vertical reinforcement binding and acceptance at the N + 1 level | C | / | / |
| N + 1 floor vertical reinforcement co-molding | D | O | STS |
| N + 1 floor riser support | E | P | STS |
| Horizontal formwork laying for N + 1 floor roof slabs | F | / | / |
| N + 1 floor top slab beam and plate reinforcement binding | G | / | / |
| N + 1 layer wire box burial | H | / | / |
| N + 1 floor pipeline pre-reservation and pre-embedding | I | / | / |
| N + 1 floor top plate slab reinforcement binding and acceptance | J | / | / |
| N + 1 floor top slab, vertical concrete pouring | K | / | / |
| N-story top slab, N-story vertical concrete pouring | L | B | FTS |
| Removal of vertical formwork at the N level | M | A | FTS |
| N | STS | ||
| Removal of N − 2 floor supports | N | A | STS |
| N − 2 level support reversal | O | E | STS |
| Removal and transportation of horizontal formwork at the top of the N − 2 floor | P | F | STS |
| Working Procedure | Overlapping Work | Connecting Logical Relationships | ||
|---|---|---|---|---|
| A | B | STS | 2 | 4 |
| A | C | STS | 2 | 4 |
| A | D | FTS | 0 | / |
| B | C | STS | 0.5 | 1.5 |
| C | D | FTS | 0 | / |
| D | o | STS | 0 | 8 |
| D | E | STS | 2 | 8 |
| E | P | STS | 0 | 8 |
| E | F | STS | 0 | 8 |
| F | G | FTS | 0 | / |
| F | H | FTS | 0 | / |
| H | G | FTF | 0 | / |
| H | I | FTS | 0 | / |
| I | J | FTS | 0 | / |
| J | K | FTS | 0 | / |
| L | B | FTS | 12 | / |
| L | M | FTS | 12 | / |
| M | A | FTS | 0 | / |
| M | N | STS | 0 | 6 |
| N | A | STS | 0 | 10 |
| N | O | FTS | 0 | / |
| O | P | FTS | 0 | / |
| O | E | STS | 2 | 4 |
| P | F | STS | 2 | 4 |
| Notation | Hidden Meaning |
|---|---|
| i | denotes the process i |
| j | denotes the process j |
| denotes the start time of process i | |
| Indicates the start time of process j | |
| denotes the duration of process i | |
| denotes the duration of process j | |
| denotes the demand of process i for resource r | |
| total resources for labor resources r | |
| Active (t) | the set of processes that are under construction at time t |
| denotes the constraint on the value of the lap spacing between process i and process j. | |
| T | indicates the total duration (objective function to be minimized) |
| Contents of Construction Work | Start Time–End Time | Operating Time/h |
|---|---|---|
| Removal of vertical formwork at the N level | 1 d/06:00 to 1 d/12:00 | 6 |
| Integrated platform mold jacking | 1 d/12:00 to 1 d/16:00 | 4 |
| Removal of N − 2 floor supports | 1 d/16:00 to 2 d/14:00 | 10 |
| N + 1 measurement and release | 2 d/14:00 to 2 d/15:30 | 1.5 |
| Vertical reinforcement binding and acceptance at the N + 1 level | 2 d/14:30 to 2 d/18:00 | 3.5 |
| N + 1 floor vertical reinforcement co-molding | 3 d/06:00 to 3 d/14:00 | 8 |
| N − 2 level support reversal | 3 d/14:00 to 3 d/18:00 | 4 |
| N + 1 floor riser support | 4 d/06:00 to 4 d/14:00 | 8 |
| Removal and transportation of horizontal formwork at the top of the N − 2 floor | 4 d/10:00 to 4 d/14:00 | 4 |
| Horizontal formwork laying for N + 1 floor roof slabs | 4 d/14:00 to 4 d/18:00 | 4 |
| N + 1 floor top slab beam and plate reinforcement binding | 5 d/06:00 to 5 d/18:00 | 12 |
| N + 1 wire box burial | 5 d/06:00 to 5 d/18:00 | 12 |
| N + 1 piping reservation and embedding | 6 d/06:00 to 6 d/08:00 | 2 |
| N + 1 floor top plate slab reinforcement binding and acceptance | 6 d/08:00 to 6 d/10:00 | 2 |
| N + 1 floor top slab and vertical concrete pouring | 6 d/10:00 to 6 d/18:00 | 8 |
| Contents of Construction Work | Timing |
|---|---|
| Removal of vertical formwork at the N level | 1 d/06:00 to 1 d/12:00 |
| Removal of N − 2 floor supports | 1 d/06:00 to 1 d/12:00 |
| Platform mold jacking | 1 d/12:00 to 1 d/16:00 |
| Removal of N − 2 floor supports | 1 d/12:00 to 1 d/16:00 |
| Measurement and placement of the N + 1 floor | 1 d/14:00 to 1 d/15:30 |
| N + 1 floor vertical reinforcement binding and acceptance | 1 d/14:30 to 1 d/18:00 |
| N + 1 floor vertical reinforcement co-molding | 2 d/06:00 to 2 d/14:00 |
| N − 2 level support reversal | 2 d/06:00 to 2 d/10:00 |
| N + 1 floor partially supported by uprights | 2 d/8:00 to 2 d/12:00 |
| N + 1 floor riser support | 2 d/12:00 to 2 d/16:00 |
| Removal and transportation of horizontal formwork at the top of the N − 2 floor | 2 d/12:00 to 2 d/16:00 |
| Horizontal formwork laying for N + 1 floor roof slabs | 2 d/14:00 to 2 d/18:00 |
| N + 1 floor top slab beam and plate reinforcement binding | 3 d/06:00 to 3 d/18:00 |
| N + 1 layer wire box burial | 3 d/06:00 to 3 d/18:00 |
| N + 1 floor piping pre-reservation and pre-embedding | 4 d/06:00 to 4 d/08:00 |
| N + 1 floor top plate slab reinforcement binding and acceptance | 4 d/08:00 to 4 d/10:00 |
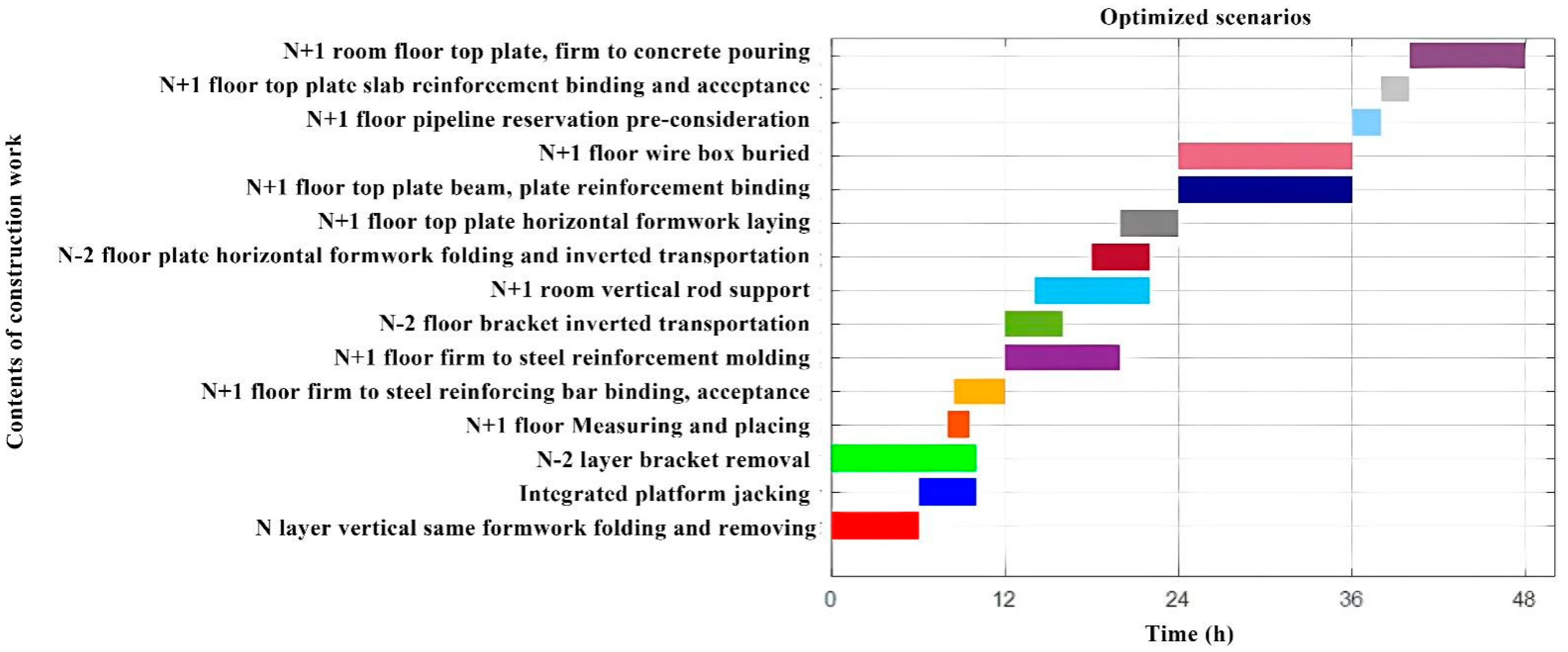
| N + 1 floor top slab and vertical concrete pouring | 4 d/10:00 to 4 d/18:00 |
| State of Affairs | Timing | Contents of Construction Work |
|---|---|---|
| Status I: Initial state | 1 d/10:00 to 1 d/18:00 | N-story top slab and N-story vertical concrete pouring |
| Status II: Vertical demolding | 1 d/06:00 to 1 d/12:00 | Removal of vertical formwork at the N level and removal of bracing at the N − 2 level |
| Status III: Ejector mold frame | 1 d/12:00 to 1 d/16:00 | Mold jacking one structural level and N − 2 level bracket removal (continued) |
| Status IV: Vertical reinforcement binding | 1 d/14:00 to 1 d/18:00 | Measuring and placing; N + 1 floor vertical reinforcement binding and acceptance |
| Status V: Vertical formwork closing | 2 d/06:00 to 2 d/14:00 | N + 1 floor vertical reinforcement molding, N − 2 floor support inverted, and N + 1 floor part of the vertical rod support |
| Status VI: Horizontal formwork removal and laying | 2 d/12:00 to 2 d/18:00 | N + 1 floor erection of vertical rods, removal and transportation of horizontal formwork for N floor roof, and laying of horizontal formwork for N + 1 floor roof |
| Status VII: Beam and slab reinforcement binding | 3 d/06:00 to 3 d/18:00 | N + 1 floor roof beam, plate reinforcement binding, and wire box embedding |
| Status eight: Pipeline pre-reservation and pre-embedding | 4 d/06:00 to 4 d/08:00 | N + 1 floor pipeline pre-reservation and pre-embedding |
| Status IX: Reinforcing steel binding and acceptance | 4 d/08:00 to 4 d/10:00 | N + 1 floor top plate slab reinforcement binding and acceptance |
| Status Ten: Concrete pouring | 4 d/10:00 to 4 d/18:00 | N + 1 floor top slab and vertical concrete pouring |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Hu, C.; Wu, Q. Research on Construction Period Optimization of High-Rise Buildings Based on Integrated Building Platform Applications. Buildings 2025, 15, 3338. https://doi.org/10.3390/buildings15183338
Wang S, Hu C, Wu Q. Research on Construction Period Optimization of High-Rise Buildings Based on Integrated Building Platform Applications. Buildings. 2025; 15(18):3338. https://doi.org/10.3390/buildings15183338
Chicago/Turabian StyleWang, Shuqiang, Chenxi Hu, and Qingqing Wu. 2025. "Research on Construction Period Optimization of High-Rise Buildings Based on Integrated Building Platform Applications" Buildings 15, no. 18: 3338. https://doi.org/10.3390/buildings15183338
APA StyleWang, S., Hu, C., & Wu, Q. (2025). Research on Construction Period Optimization of High-Rise Buildings Based on Integrated Building Platform Applications. Buildings, 15(18), 3338. https://doi.org/10.3390/buildings15183338





