Analysis of Vehicle-Induced Vibration Response and Impact Coefficient for Composite Truss Bridge with Partially Concrete-Filled Rectangular Steel Tube Members
Abstract
1. Introduction
2. Method for Solving Vehicle–Bridge Coupled Vibration
2.1. Vehicle Model
2.2. Bridge Model
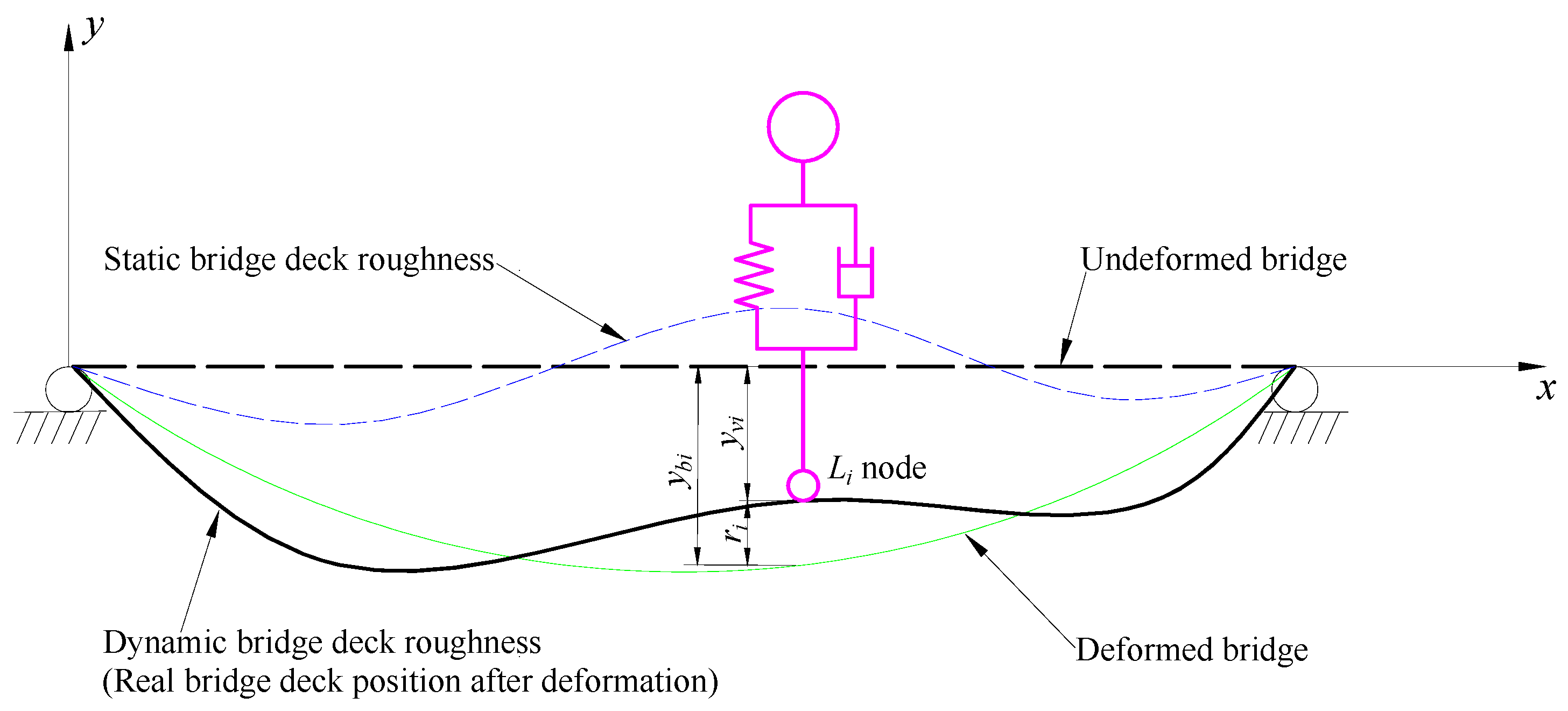
2.3. Bridge Deck Roughness Model
2.4. Displacement Compatibility Relation of Vehicle–Bridge Coupled System and Its Implementation
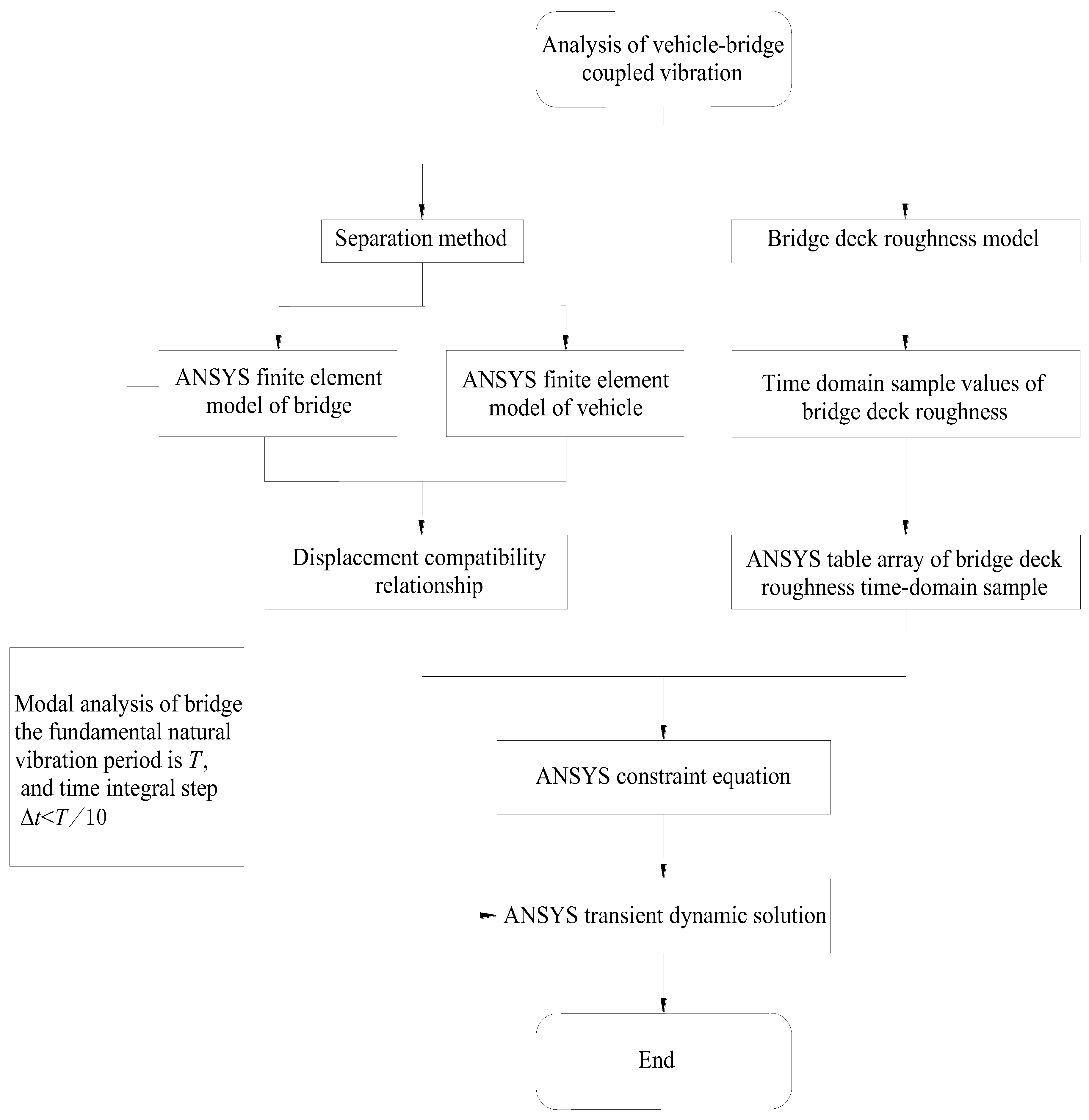
2.5. Solution Steps of Vehicle–Bridge Coupled Vibration Problem in ANSYS
- Step 1:
- In the ANSYS software, the bridge finite element model and vehicle finite element model are established.
- Step 2:
- Based on the inverse Fourier transform method, the time-domain sample data of bridge deck roughness are obtained using MATLAB M-files, which are then read into ANSYS tables. As a result, the surface roughness time-domain sample value at the position of a vehicle–bridge interaction at any time is determined using the index rule of “0 row, 0 column” of the ANSYS table array and its automatic interpolation function.
- Step 3:
- The modal solution of the finite element model of the bridge is conducted, and the fundamental frequency and natural vibration period of the bridge structure can be determined. The appropriate time integral step length for transient dynamic calculation can be selected, and the general time integral step length can be taken as .
- Step 4:
- By using the ANSYS constraint equation, the vertical displacement constraint conditions of the contact point between the wheel tire and the bridge deck at any given time can be determined according to Equation (7) (the geometric displacement compatibility relation between the vehicle and bridge). The dynamic time-history analysis of the vehicle crossing the bridge is realized based on the transient dynamic analysis function of the ANSYS software.
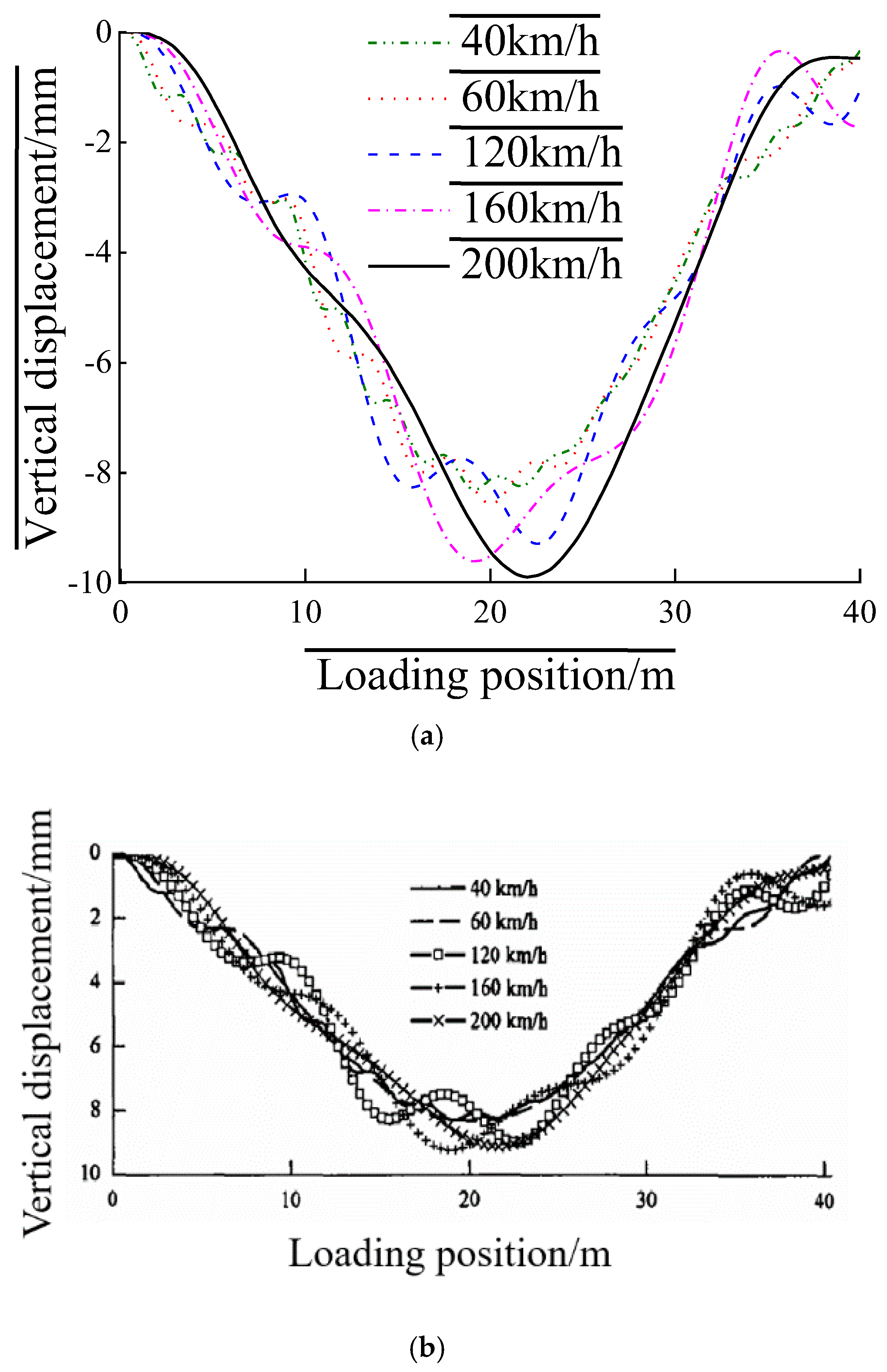
2.6. Verification of the Method
3. Vehicle-Induced Vibration Response of Composite Truss Bridge with Partially Concrete-Filled Rectangular Steel Tube Members
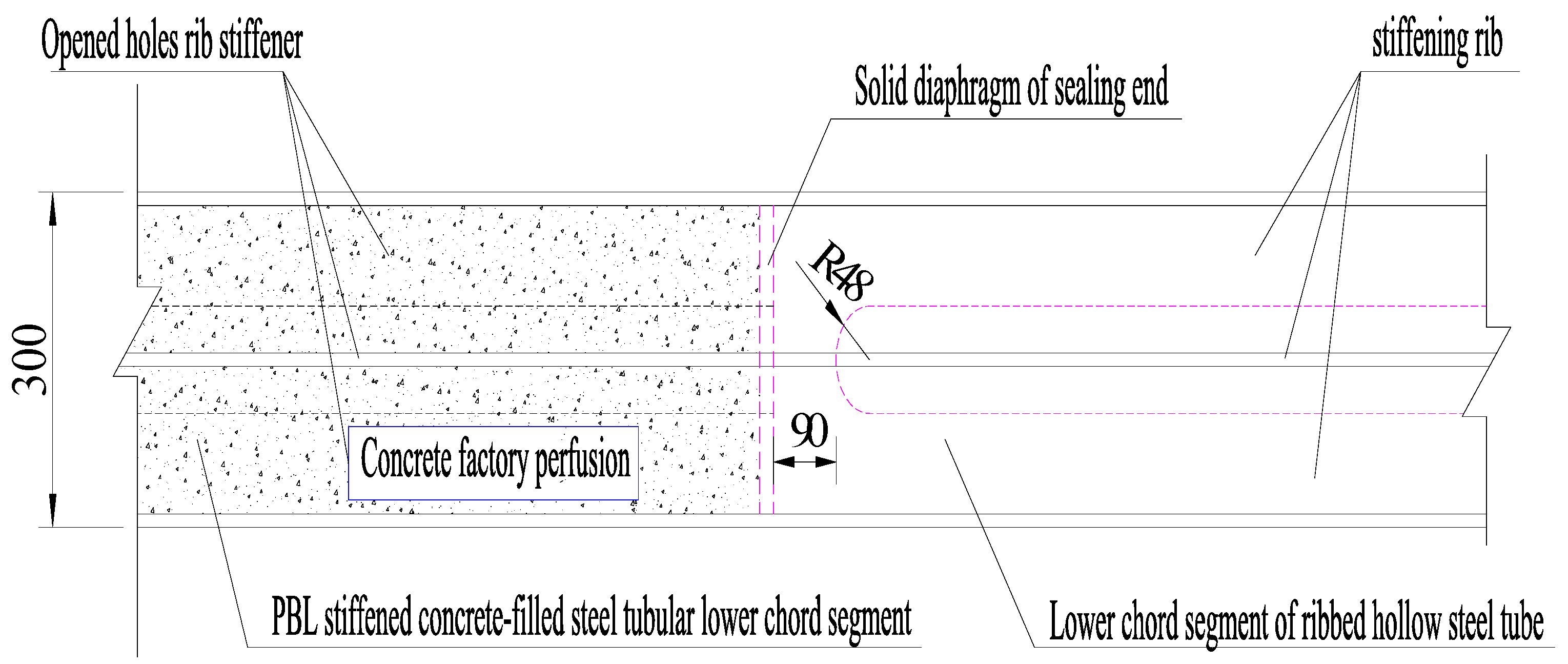
3.1. Engineering Overview
3.2. Finite Element Model
3.3. Analysis of Vehicle-Induced Vibration Response
4. Influence of Concrete-Filled Segment Length on Dynamic Response of Composite Truss Bridge
4.1. Concrete Filling Coefficient
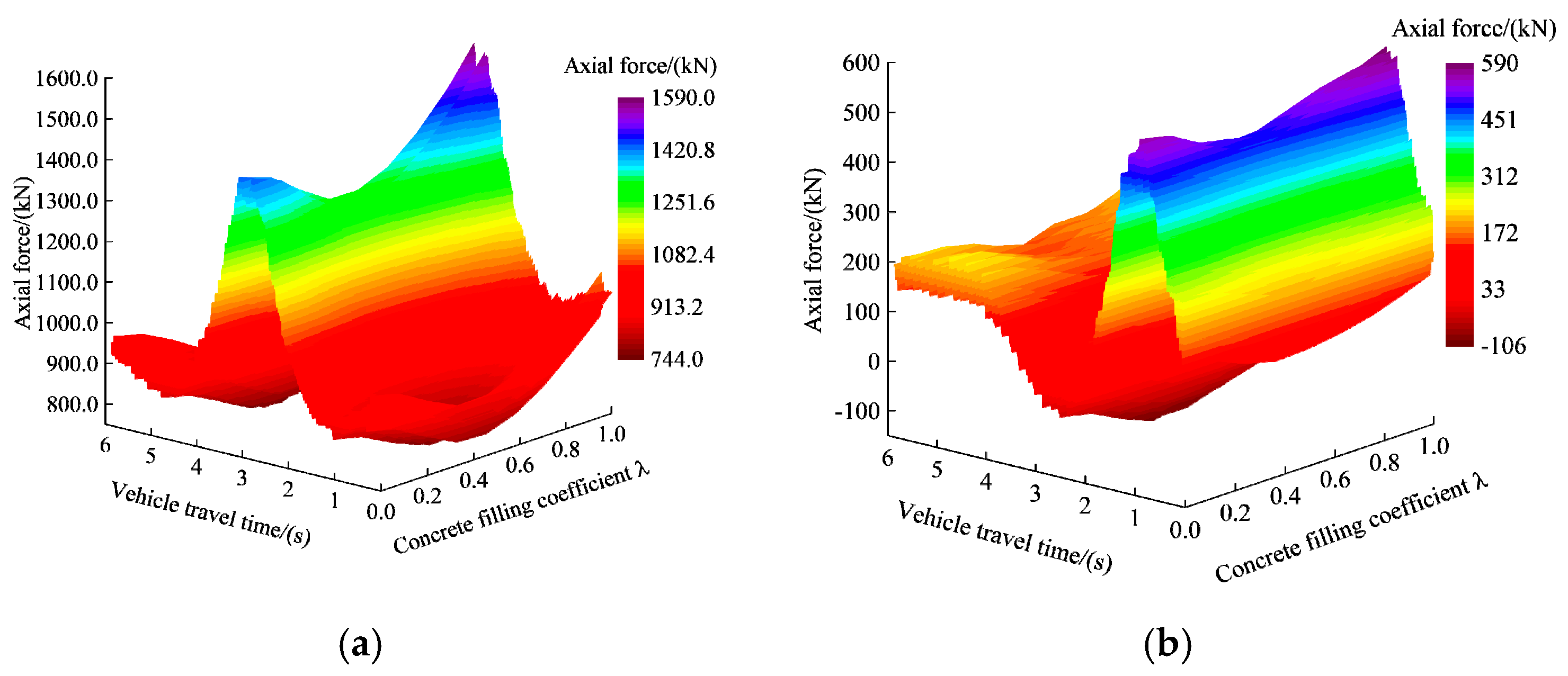
4.2. Dynamic Response Analysis of the Composite Truss Bridge Under Nine Concrete Filling Coefficients
5. Impact Coefficient of the Composite Truss Bridge with Partially Concrete-Filled Rectangular Steel Tube Members
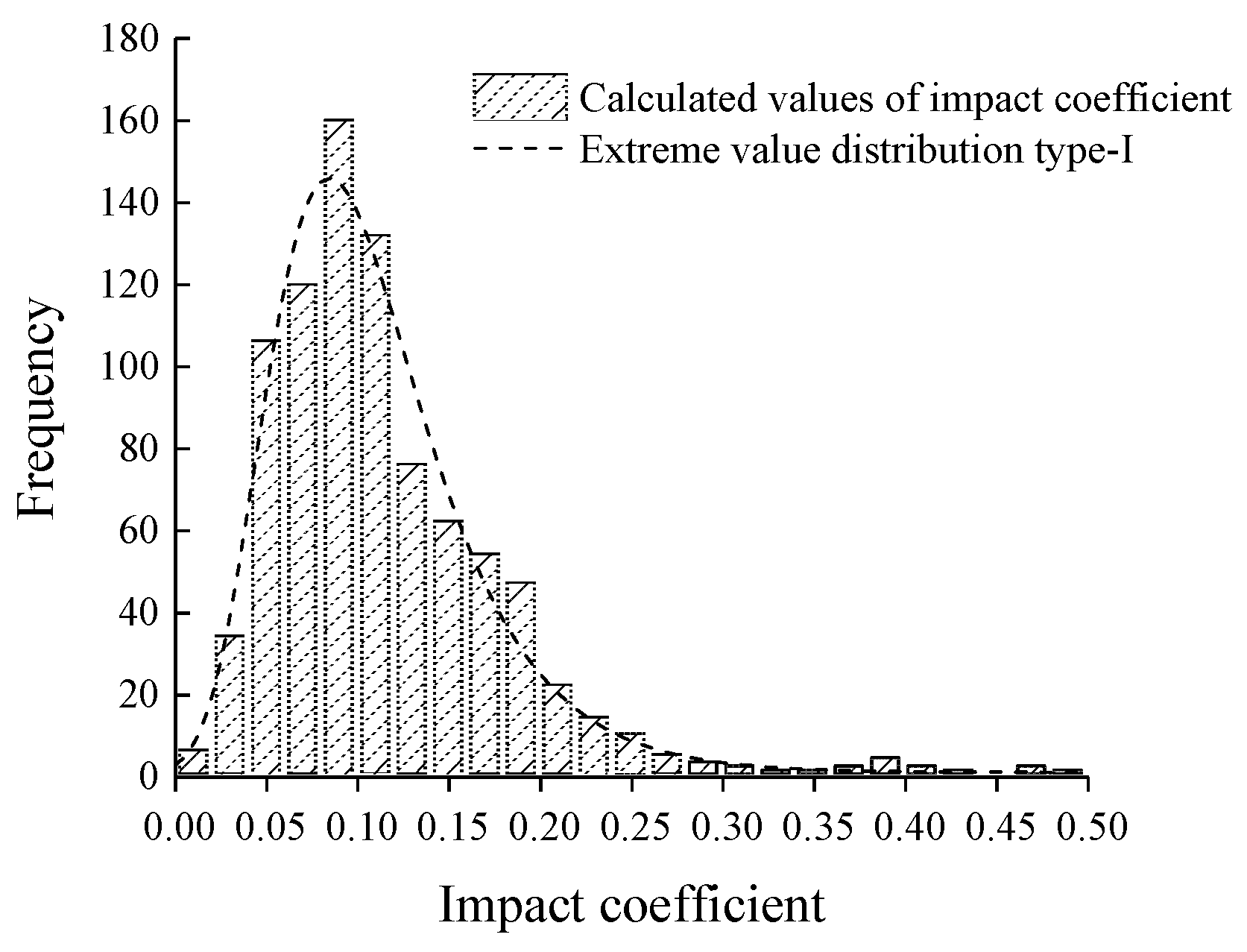
5.1. Impact Coefficient of Bridge
5.2. Influence of Concrete-Filled Length on Impact Coefficient of Composite Truss Bridge
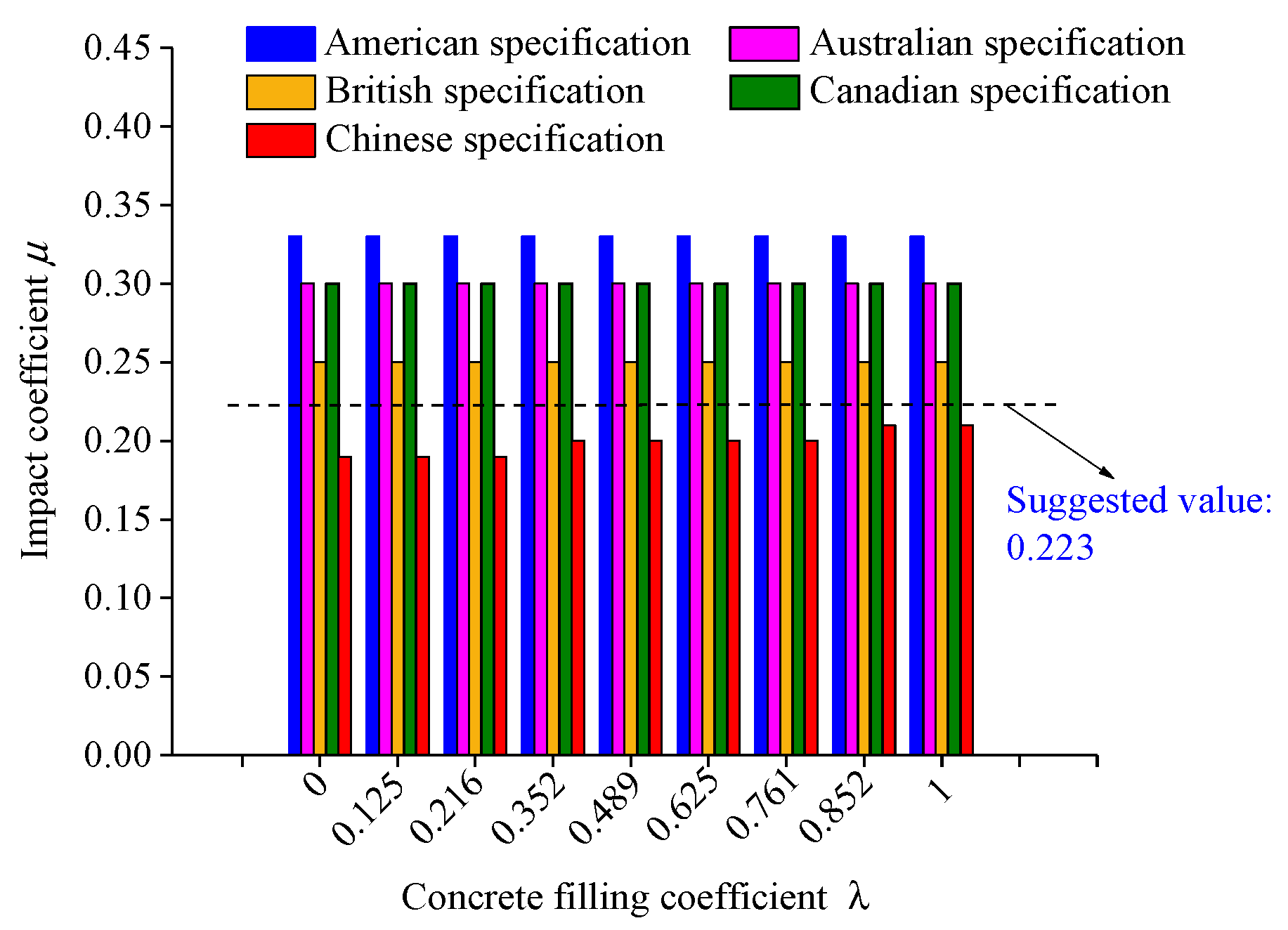
5.3. Suggested Value of Impact Coefficient
6. Conclusions
- The method in this paper is used to calculate the simply supported beam in the literature. The calculation results of the midspan deflection of the bridge are highly consistent with the literature results, and the maximum relative error is less than 5% at different speeds. The accuracy and reliability of the method were verified. For vehicle–bridge coupling vibration analysis, this method eliminates the need for engineers to design complicated programming programs, resulting in greatly improved efficiency.
- The partial concrete filling of a bridge does not change the shape of the time history curve of the dynamic responses of the lower chords of the bridge and has little impact on the position at which the maximum dynamic responses occur. In composite truss bridges, the partial concrete filling can improve the vertical dynamic stiffness, reduce its dynamic response, and improve fatigue resistance.
- The concrete filling can change the relative stiffness of the chord and the bridge. With the increase in the concrete filling coefficient, the axial forces of the midspan lower chords at both the middle-span and side-span first decrease and then increase for the composite truss bridge. The recommended concrete filling coefficient for the composite truss bridge with partially concrete-filled rectangular steel tube members is in the range of 0.35 to 0.5.
- A goodness-of-fit test was conducted on 867 calculated values of the impact coefficient of the new bridge under nine concrete filling coefficients, and the fitting results were submitted to the extreme value distribution type-I. At a 95% guarantee rate, the impact coefficient of the composite truss bridge was 0.223, which was the suggested value of the impact coefficient. The suggested value of the impact coefficient was less than the value of the impact coefficient in the American specification, Australian specification, British specification, and Canadian specification, but greater than the value of the impact coefficient in the Chinese specification, and should be highly valued by bridge designers.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dauner, H.G.; Oribasi, A.; Wery, D. The lully viaduct, a composite bridge with steel tube truss. J. Constr. Steel Res. 1998, 46, 67–68. [Google Scholar] [CrossRef]
- Mato, F.M.; Cornejo, M.O.; Rubio, L.M. Viaduct over river ulla: An outstanding composite (steel and concrete) high-speed railway viaduct. Struct. Eng. Int. 2014, 24, 131–136. [Google Scholar] [CrossRef]
- Wu, Q.X.; Huang, Y.F.; Chen, B.C. Shaking tables testing study of lightweight bridge with CFST composite truss girder and lattice pier. Eng. Mech. 2014, 31, 89–96. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.J.; Yang, Y.H.; Cao, M.M.; Wang, K.N. Design of PBL-stiffened steel truss-concrete composite girder bridge with truss made of rectangular steel tubes. Bridge Constr. 2019, 49, 97–102. [Google Scholar] [CrossRef]
- Xie, X.; Huang, Y.; Qin, X. A new composite truss bridge and a study on its dynamic characteristics with FE and experimental methods. KSCE J. Civ. Eng. 2021, 25, 931–947. [Google Scholar] [CrossRef]
- Nazari, H.; Babaei, M.; Kiarasi, F. Geometrically nonlinear dynamic analysis of functionally graded material plate excited by a moving load applying first-order shear deformation theory via generalized differential quadrature method. SN Appl. Sci. 2021, 3, 847. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.J.; Zhou, X.H.; Li, Z.; Wang, K.N. Design of mid-span fabricated RCFST composite truss bridge. J. Traffic Transp. Eng. 2017, 17, 20–31. [Google Scholar] [CrossRef]
- Liu, Y.J.; Ma, Y.P.; Tian, Z.J.; Yuan, Z.Y.; Xiong, Z.H.; Yang, J. Field test of rectangular concrete filled steel tubular composite truss bridge with continuos rigid system. China J. Highw. Transp. 2018, 31, 53–62. [Google Scholar] [CrossRef]
- Gao, Y.M.; Liu, Y.J.; Jiang, L.; Liu, J.P.; Liu, X.H. Experiment on flexural behaviour of rectangular concrete filled steel tubular truss stiffened with PBL. J. Archit. Civ. Eng. 2017, 34, 171–180. [Google Scholar] [CrossRef]
- Gao, Y.M.; Liu, Y.J.; Zhou, X.H.; Liu, B.; Jiang, L.; Xiong, Z.H. High-performance CFST composite truss bridge. China J. Highw. Transp. 2018, 31, 174–187. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, Y.J.; Long, X.; Wang, W.S.; Ma, Y.P. Fatigue assessment of joints in concrete-filled rectangular hollow section composite truss bridges based on hot spot stress method. J. Traffic Transp. Eng. 2020, 20, 104–116. [Google Scholar] [CrossRef]
- Liu, Y.J.; Long, X.; Jiang, L.; Liu, Z.B. Comparison on fatigue structural details of CFST welded joints based on hot spot stress method. J. Archit. Civ. Eng. 2020, 37, 1–12. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, Y.J.; Long, X.; Liu, B.; Liu, Z.B. Experimental study on stress concentration characteristics of joints in concrete-filled rectangular steel tubular truss. J. Build. Struct. 2022, 43, 184–196+214. [Google Scholar] [CrossRef]
- Liu, Y.J.; Zhou, X.H. Composite Truss Bridge with Concrete-Filled Rectangular Steel Tube Members; China Communications Press Co., Ltd.: Beijing, China, 2021. [Google Scholar]
- Chatterjee, P.K.; Datta, T.K.; Surana, C.S. Vibration of continuous bridges under moving vehicles. J. Sound Vib. 1994, 169, 619–632. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wu, Y.S. A versatile element for analyzing vehicle–bridge interaction response. Eng. Struct. 2001, 23, 452–469. [Google Scholar] [CrossRef]
- Wyss, J.C.; Di, S.; Fujino, Y. Prediction of vehicle-induced local responses and application to a skewed girder bridge. Eng. Struct. 2011, 33, 1088–1097. [Google Scholar] [CrossRef]
- Huang, X.Y.; Zhuo, W.D.; Shang, G.P. ANSYS-based spatial coupled vibration analysis method of vehicle-bridge interaction system. Key Eng. Mater. 2014, 2614, 117–126. [Google Scholar] [CrossRef]
- Ettefagh, M.M.; Behkamkia, D.; Pedrammehr, S.; Asadi, K. Reliability analysis of the bridge dynamic response in a stochastic vehicle-bridge interaction. KSCE J. Civ. Eng. 2015, 19, 220–232. [Google Scholar] [CrossRef]
- Jin, Z.B.; Pei, S.L.; Asce, M.; Li, X.Z.; Qiang, S.Z. Vehicle-induced lateral vibration of railway bridges: An analytical-solution approach. J. Bridge Eng. 2016, 21, 04015038. [Google Scholar] [CrossRef]
- Hou, W.Q.; Li, Y.K.; Guo, W.; Li, J.L.; Chen, Y.H.; Duan, X.X. Railway vehicle induced vibration energy harvesting and saving of rail transit segmental prefabricated and assembling bridges. J. Clean. Prod. 2018, 182, 946–959. [Google Scholar] [CrossRef]
- Li, Y.; Qin, L.H.; Li, Z.; Yang, T.T. Dynamic performance of strengthened concrete-filled steel tubular arch bridge due to moving vehicles. J. Aerosp. Eng. 2019, 32, 4018113. [Google Scholar] [CrossRef]
- Hou, J.L.; Xu, W.B.; Chen, Y.J.; Zhang, K.D.; Sun, H.; Li, Y. Typical diseases of a long-span concrete-filled steel tubular arch bridge and their effects on vehicle-induced dynamic response. Front. Struct. Civ. Eng. 2020, 14, 867–887. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, J. Structural flexibility identification via moving-vehicle-induced time-varying modal parameters. J. Sound Vib. 2020, 474, 115264. [Google Scholar] [CrossRef]
- Shen, H.P.; Chen, X.J.; Lu, K.; Huang, H. A new vehicle-bridge coupling analysis method based on model polycondensation. KSCE J. Civ. Eng. 2021, 25, 245–255. [Google Scholar] [CrossRef]
- Angelo Aloisio, M.A.; Alaggio, R. Probabilistic comparative analysis of vehicle–bridge interaction models for predicting bridge response under moving vehicles. J. Eng. Mech. 2024, 150, 04023121. [Google Scholar] [CrossRef]
- Yu, P.; Yu, C.; Ren, Z. Vehicle–bridge coupling vibration of long-span concrete-filled steel tubular arch bridge. Int. J. Struct. Stab. Dyn. 2025, 25, 2550064. [Google Scholar] [CrossRef]
- Shen, H.M.; Xiao, X.B. Numerical method for vehicle-bridge coupled vibrations. J. Southwest Jiaotong Univ. 2003, 38, 658–662. [Google Scholar] [CrossRef]
- GB/T7031-2005; Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. Standards Press of China: Beijing, China, 2005.
- Yu, F.; Lin, Y. Dynamics of the Vehicle’s System; Machine Press: Beijing, China, 2005. [Google Scholar]
- Yang, S.; Chen, L.; Li, S. Dynamics of Vehicle-Road Coupled System; Science Press: Beijing, China, 2012. [Google Scholar]
- Wang, X.M.; Li, Y.Q.; Xu, H.W. Element Types for Structural Analysis in Ansys and Their Applications; China Communications Press Co., Ltd.: Beijing, China, 2011. [Google Scholar]
- Gui, S.R.; Chen, S.S.; Tang, Z.J. Numerical simulation based on Fourier inverse transform and analysis of testing of road surface roughness on bridge. Highw. Eng. 2007, 32, 39–43. [Google Scholar] [CrossRef]
- Wang, X.M. ANSYS Numerical Analysis of Engineering Structures; China Communications Press Co., Ltd.: Beijing, China, 2007; pp. 385–409. [Google Scholar]
- Deng, L.; Chen, Y.X.; Han, W.S.; Wang, W. Studying impact factors for short-and medium-span simply supported concrete highway bridges and its suggested values. China J. Highw. Transp. 2020, 33, 69–78. [Google Scholar] [CrossRef]
- Deng, L.; Cai, C.S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges. Eng. Struct. 2010, 32, 21–31. [Google Scholar] [CrossRef]
- JTG D60-2015; General Specifications for Design of Highway Bridges and Culverts. China Communications Press Co., Ltd.: Beijing, China, 2015.

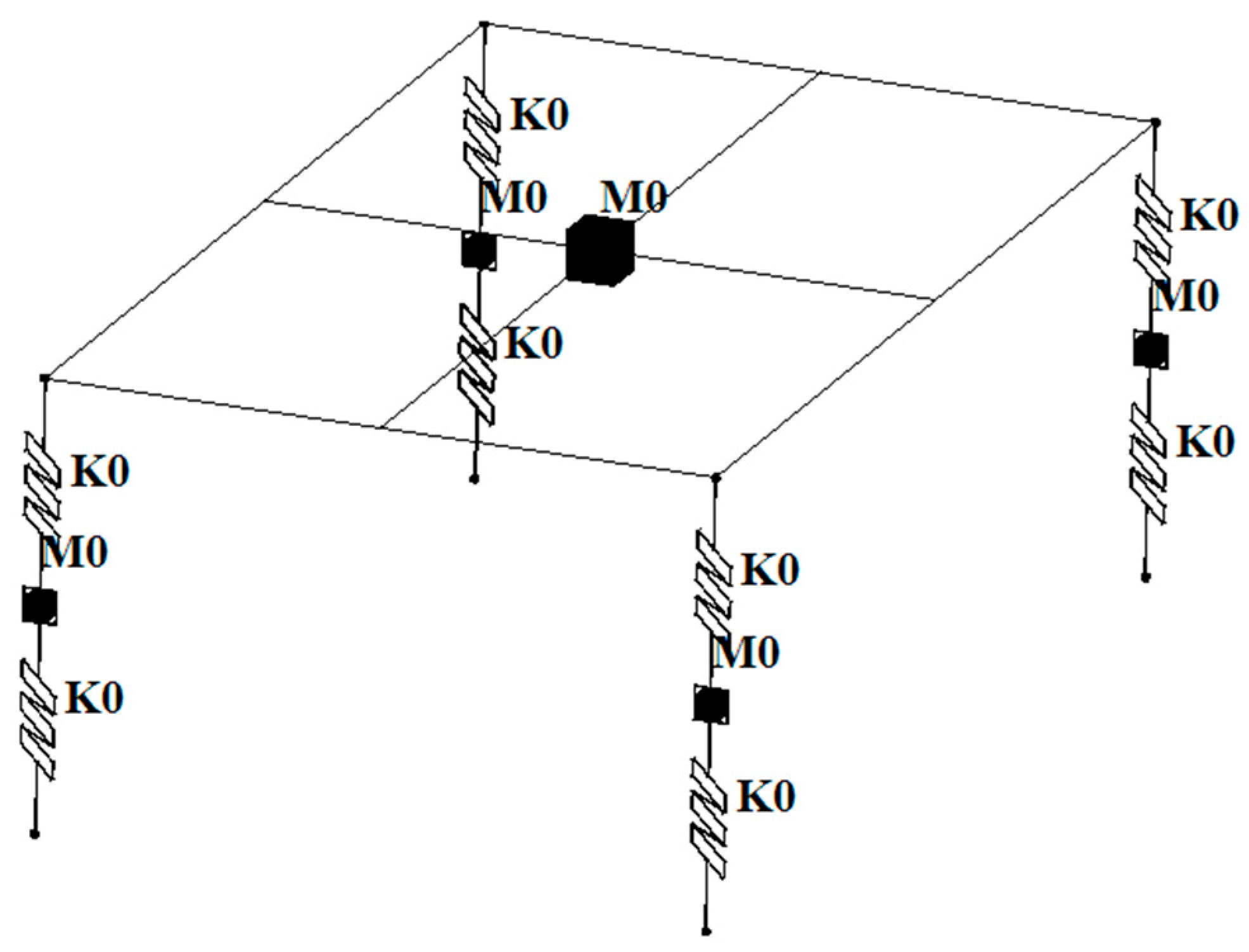
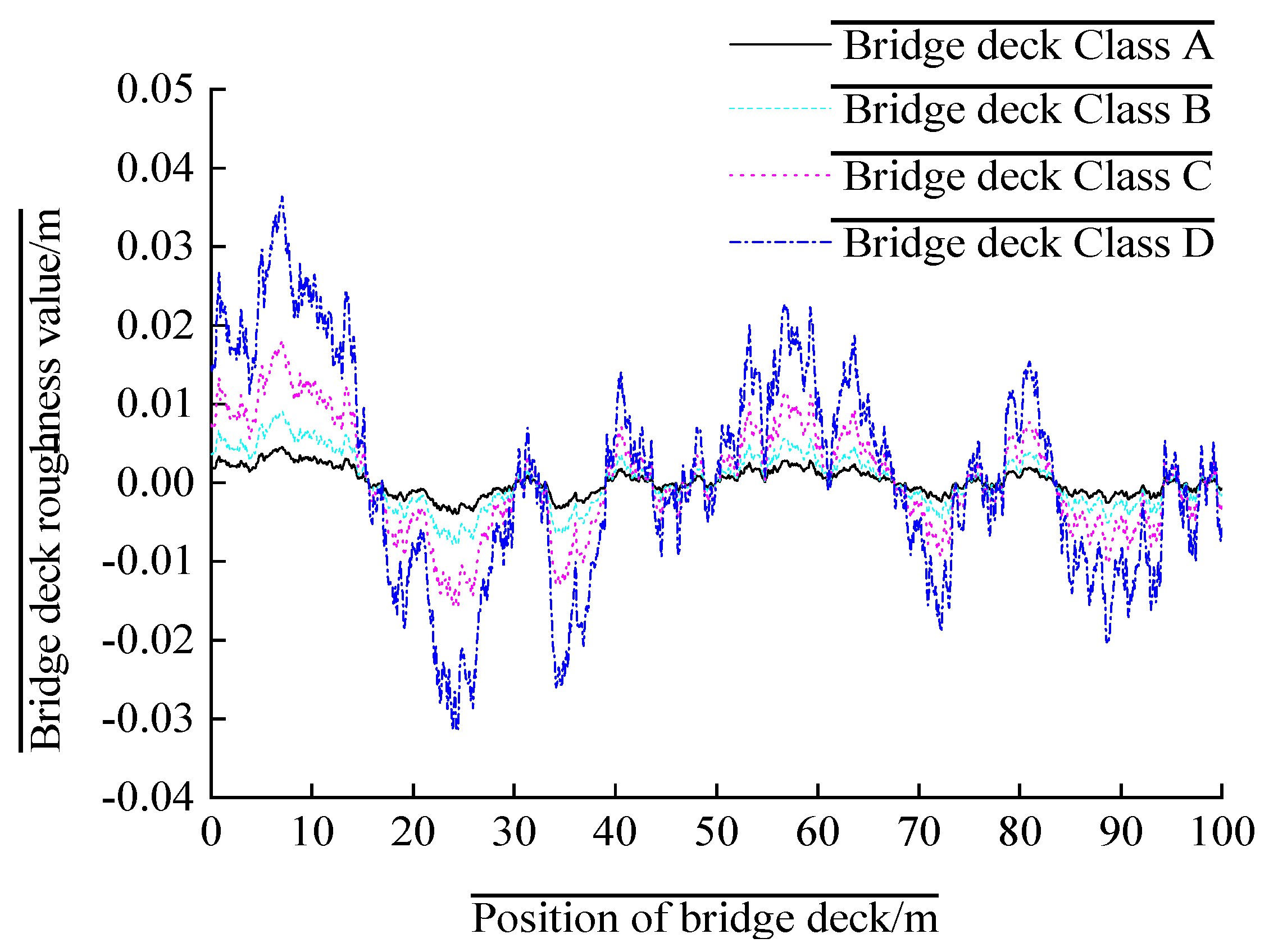
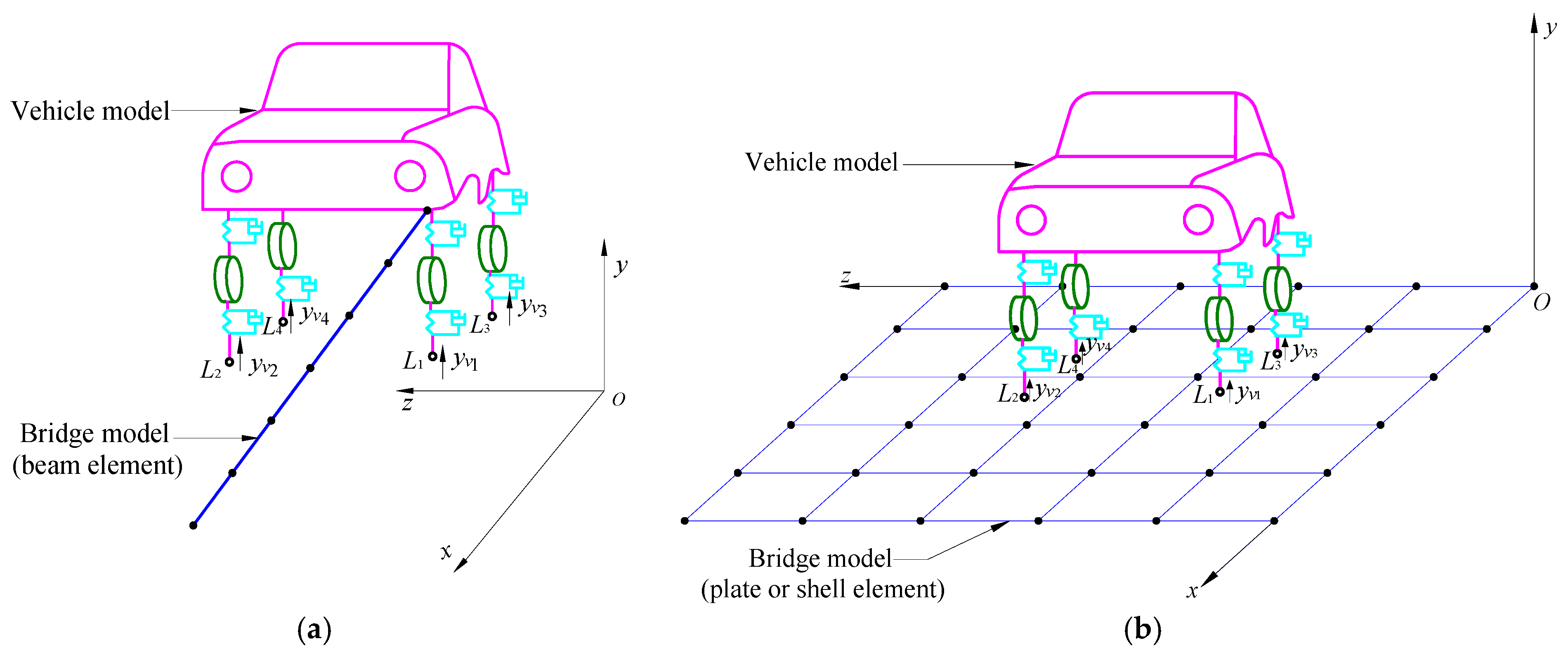
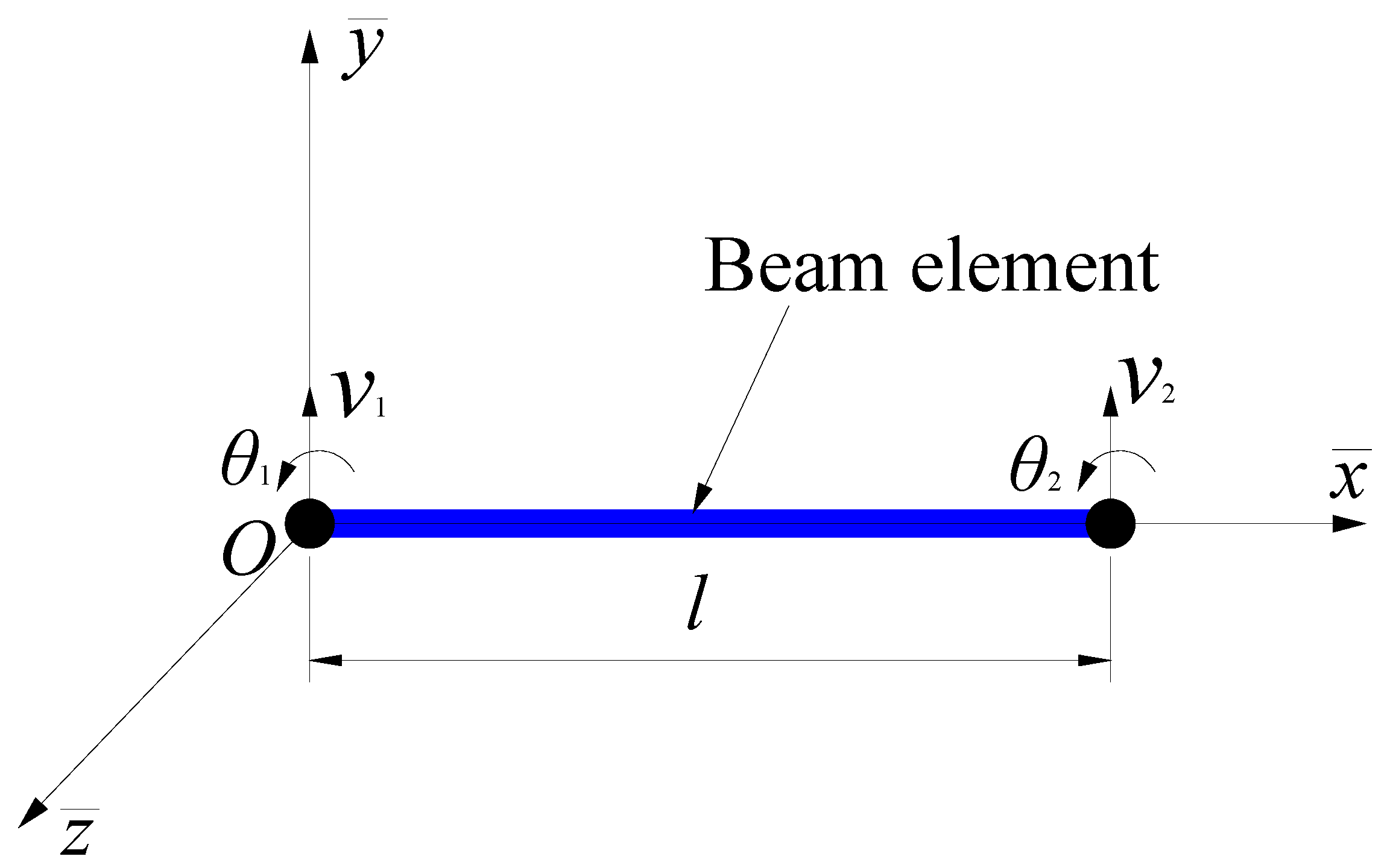







| Components of Vehicle | ANSYS Element Type | ANSYS Element Option |
|---|---|---|
| The vehicle body | MASS21 | KEYOPT(3) = 0 |
| The wheel | MASS21 | KEYOPT(3) = 2 |
| The suspension and wheel tire | COMBIN14 | KEYOPT(2) = 2 |
| Rigid beam | MPC184 | KEYOPT(1) = 1 |
| Technical Parameters | Value |
|---|---|
| Mass of vehicle body /kg | 38,500 |
| Rotational inertia /kg·m2 | 2,446,000 |
| Rotational inertia /kg·m2 | 1,223,000 |
| Mass of wheel /kg | 2165 |
| Tire stiffness /N·m−1 | 2,140,000 |
| Tire damping /kg·s−1 | 49,000 |
| Suspension stiffness /N·m−1 | 1,267,500 |
| Suspension damping /kg·s−1 | 98,000 |
| Wheel base /m | 8.4 |
| wheel track /m | 3.0 |
| Dynamic Response | Partially Concrete-Filled | Non-Filled |
|---|---|---|
| Vertical displacement/mm | −29.29 | −31.77 |
| Axial force/kN | 1317.59 | 1436.24 |
| Dynamic Parameters | Partially Concrete-Filled | Non-Filled | |
|---|---|---|---|
| Midspan of midddle-span | Increment of vertical displacement/mm | −0.46 | −0.52 |
| Increment of axial force/kN | 41.93 | 46.80 | |
| Midspan of side-span | Increment of vertical displacement/mm | −0.41 | −0.43 |
| Increment of axial force/kN | 57.85 | 58.58 | |
| Concrete-Filled Segment Length/m | ||
|---|---|---|
| 0 | 0 | 0 |
| 0.125 | 2.5 | 3.0 |
| 0.216 | 2.5 | 7.0 |
| 0.352 | 2.5 | 13.0 |
| 0.489 | 2.5 | 19.0 |
| 0.625 | 2.5 | 25.0 |
| 0.761 | 2.5 | 31.0 |
| 0.852 | 2.5 | 35.0 |
| 1 | 2.5 | 41.5 |
| Midspan of the Middle-Span | Midspan of the Side-Span | |||
|---|---|---|---|---|
| Vertical Displacement/ mm | Axial Force/kN | Vertical Displacement/mm | Axial Force/kN | |
| 0 | −31.77 | 1436.24 | −6.91 | 561.26 |
| 0.125 | −31.27 | 1411.08 | −6.86 | 547.60 |
| 0.216 | −30.43 | 1374.70 | −6.78 | 520.56 |
| 0.352 | −29.29 | 1317.59 | −6.76 | 505.30 |
| 0.489 | −29.11 | 1311.89 | −6.68 | 494.17 |
| 0.625 | −28.99 | 1346.27 | −6.63 | 518.68 |
| 0.761 | −28.45 | 1413.48 | −6.30 | 542.53 |
| 0.852 | −27.79 | 1470.96 | −6.25 | 555.55 |
| 1 | −26.33 | 1588.02 | −6.19 | 589.54 |
| Statistical Parameters | Value |
|---|---|
| Mean value | 0.114 |
| Standard deviation | 0.058 |
| Concrete Filling Coefficient | Fundamental Frequency of Bridge | Value of Impact Coefficient |
|---|---|---|
| 0 | 3.21 | 0.19 |
| 0.13 | 3.23 | 0.19 |
| 0.22 | 3.26 | 0.19 |
| 0.35 | 3.31 | 0.20 |
| 0.49 | 3.35 | 0.20 |
| 0.63 | 3.39 | 0.20 |
| 0.76 | 3.45 | 0.20 |
| 0.85 | 3.50 | 0.21 |
| 1 | 3.58 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhang, R.; Ge, J.; Li, Z.; Zhang, C. Analysis of Vehicle-Induced Vibration Response and Impact Coefficient for Composite Truss Bridge with Partially Concrete-Filled Rectangular Steel Tube Members. Buildings 2025, 15, 3330. https://doi.org/10.3390/buildings15183330
Liu S, Zhang R, Ge J, Li Z, Zhang C. Analysis of Vehicle-Induced Vibration Response and Impact Coefficient for Composite Truss Bridge with Partially Concrete-Filled Rectangular Steel Tube Members. Buildings. 2025; 15(18):3330. https://doi.org/10.3390/buildings15183330
Chicago/Turabian StyleLiu, Shizhong, Ruiyin Zhang, Jialin Ge, Zhanlong Li, and Chuanchuan Zhang. 2025. "Analysis of Vehicle-Induced Vibration Response and Impact Coefficient for Composite Truss Bridge with Partially Concrete-Filled Rectangular Steel Tube Members" Buildings 15, no. 18: 3330. https://doi.org/10.3390/buildings15183330
APA StyleLiu, S., Zhang, R., Ge, J., Li, Z., & Zhang, C. (2025). Analysis of Vehicle-Induced Vibration Response and Impact Coefficient for Composite Truss Bridge with Partially Concrete-Filled Rectangular Steel Tube Members. Buildings, 15(18), 3330. https://doi.org/10.3390/buildings15183330






