Innovative Retrofitting for Disaster Resilience: Optimizing Steel Plate Grade and Scheme in RC Non-Seismic Frames to Prevent Progressive Collapse
Abstract
1. Introduction
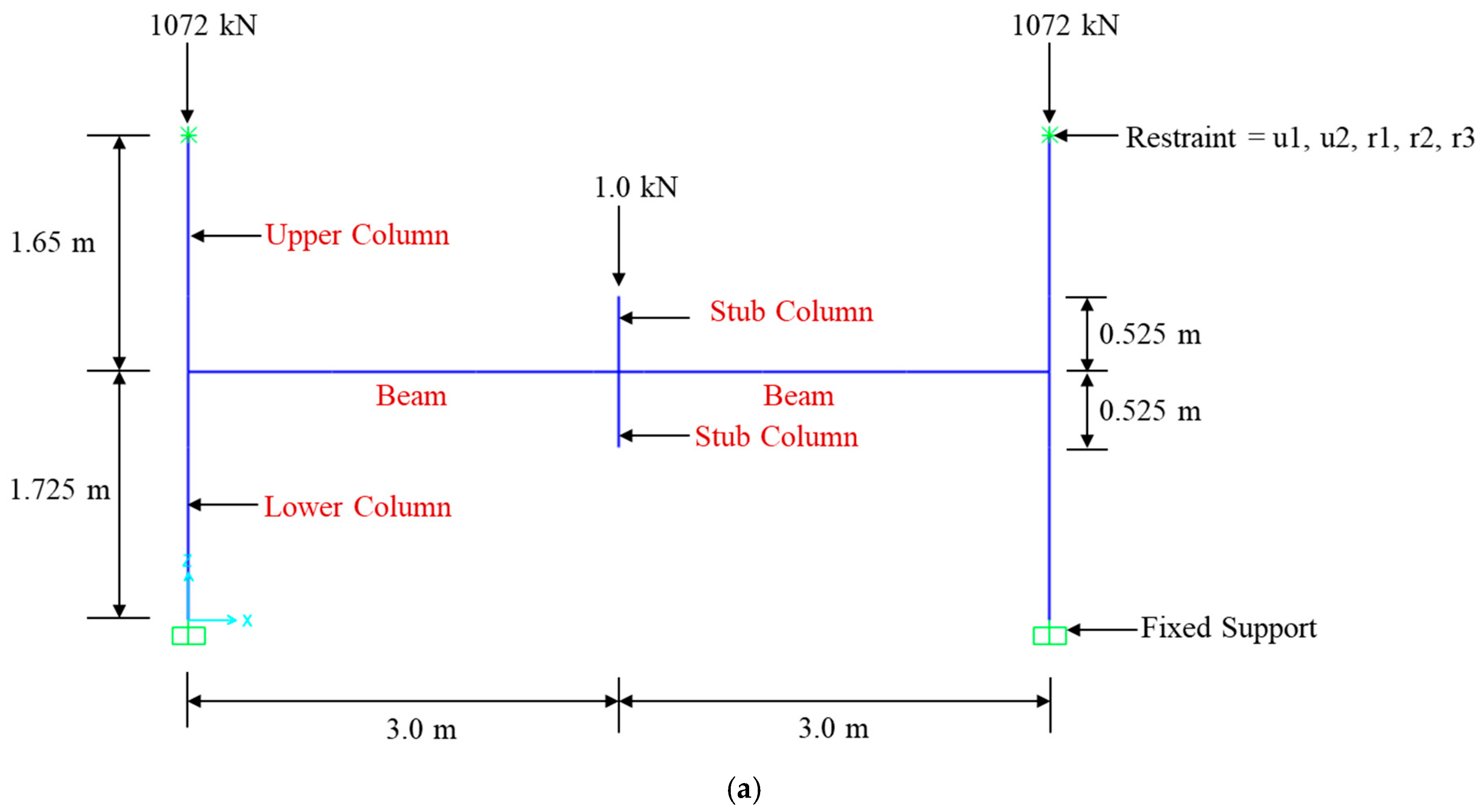
2. FE Analysis Matrix
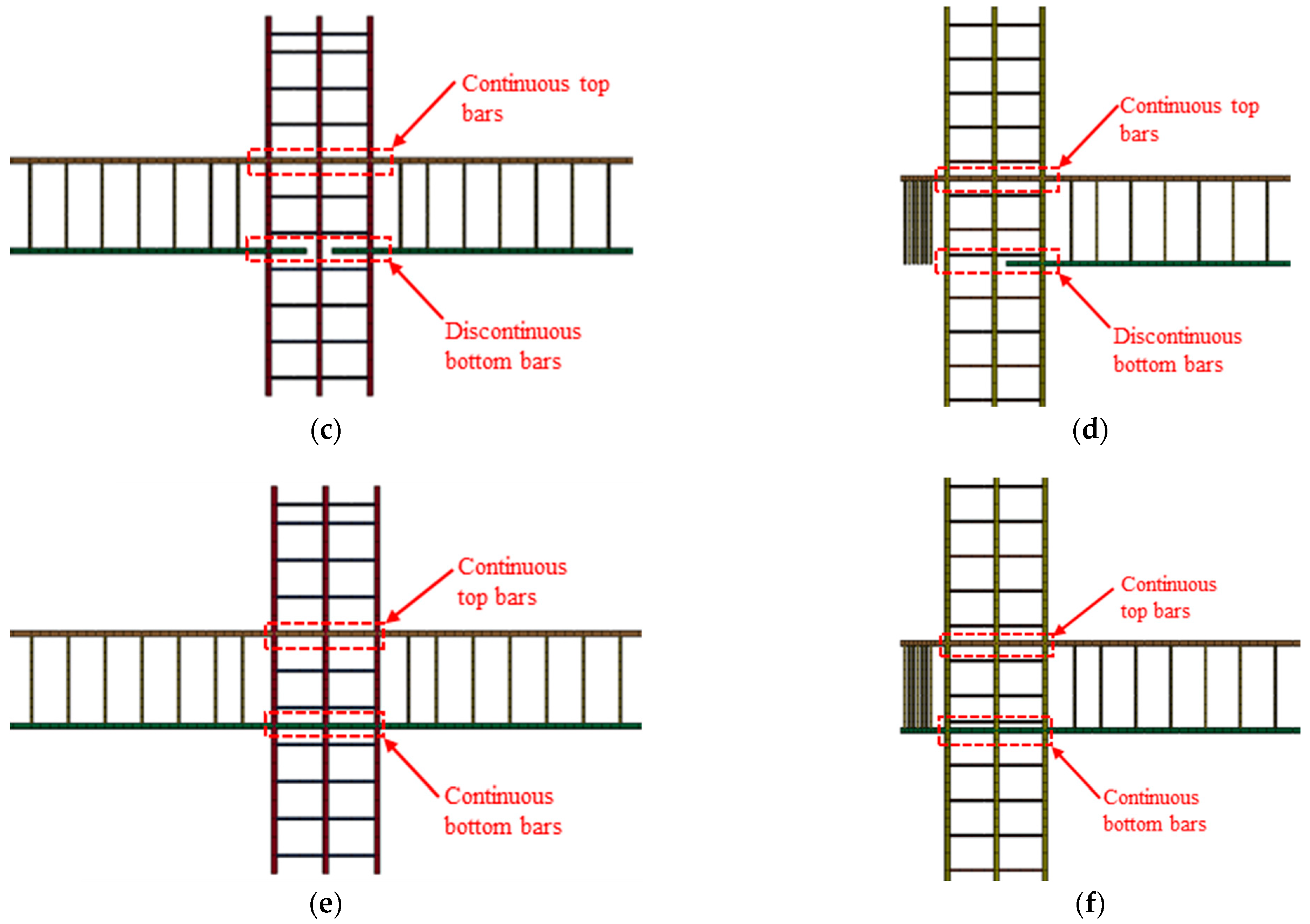
2.1. Control Specimens
2.2. Strengthened Specimens
3. FE Analysis
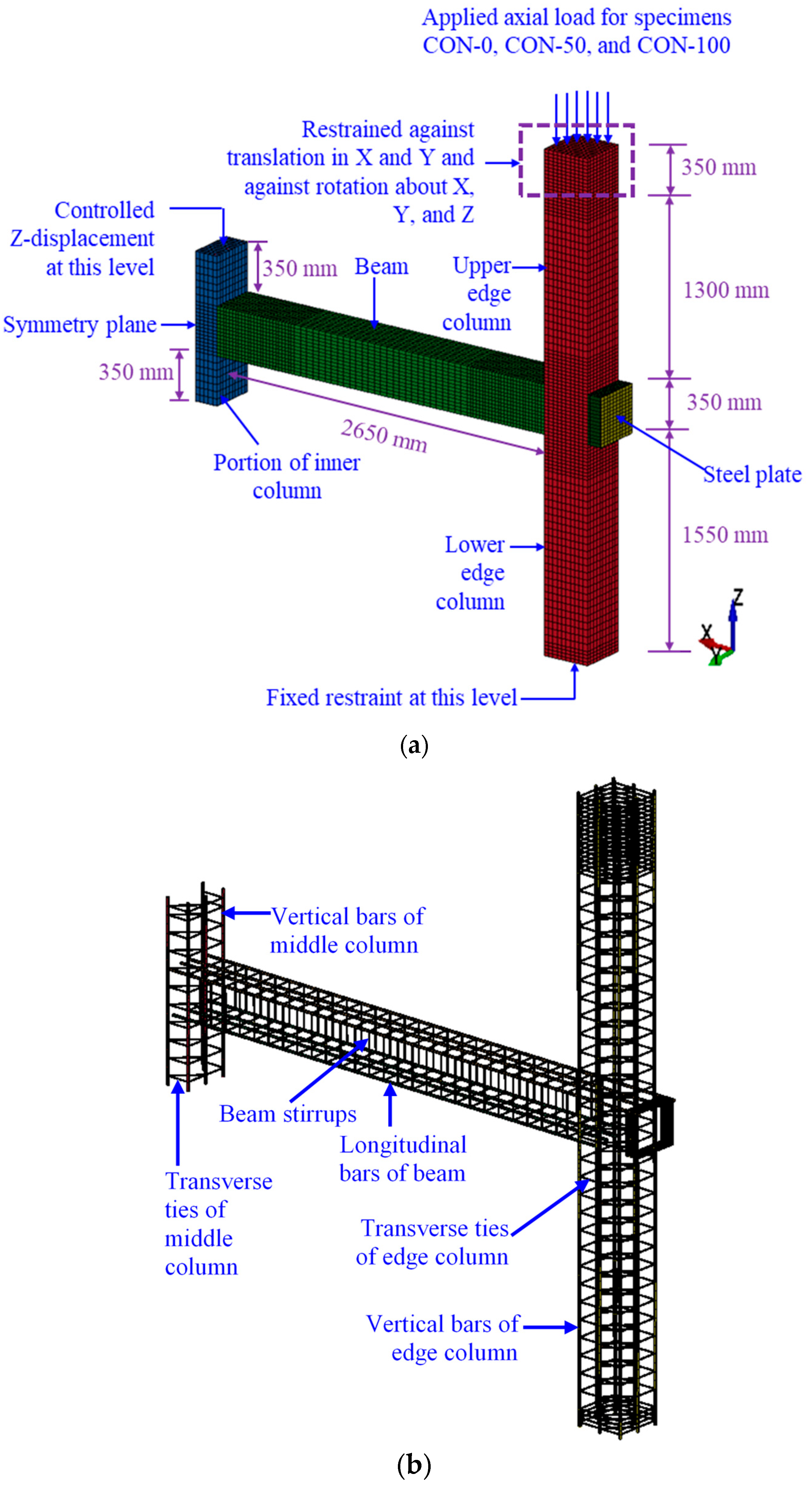
3.1. Mesh Generation
3.2. Constitutive Models
3.3. One-Dimensional Contact Model
3.4. Modeling of Contact Between Plates and Concrete
3.5. Boundary Conditions
3.6. Loading Strategy
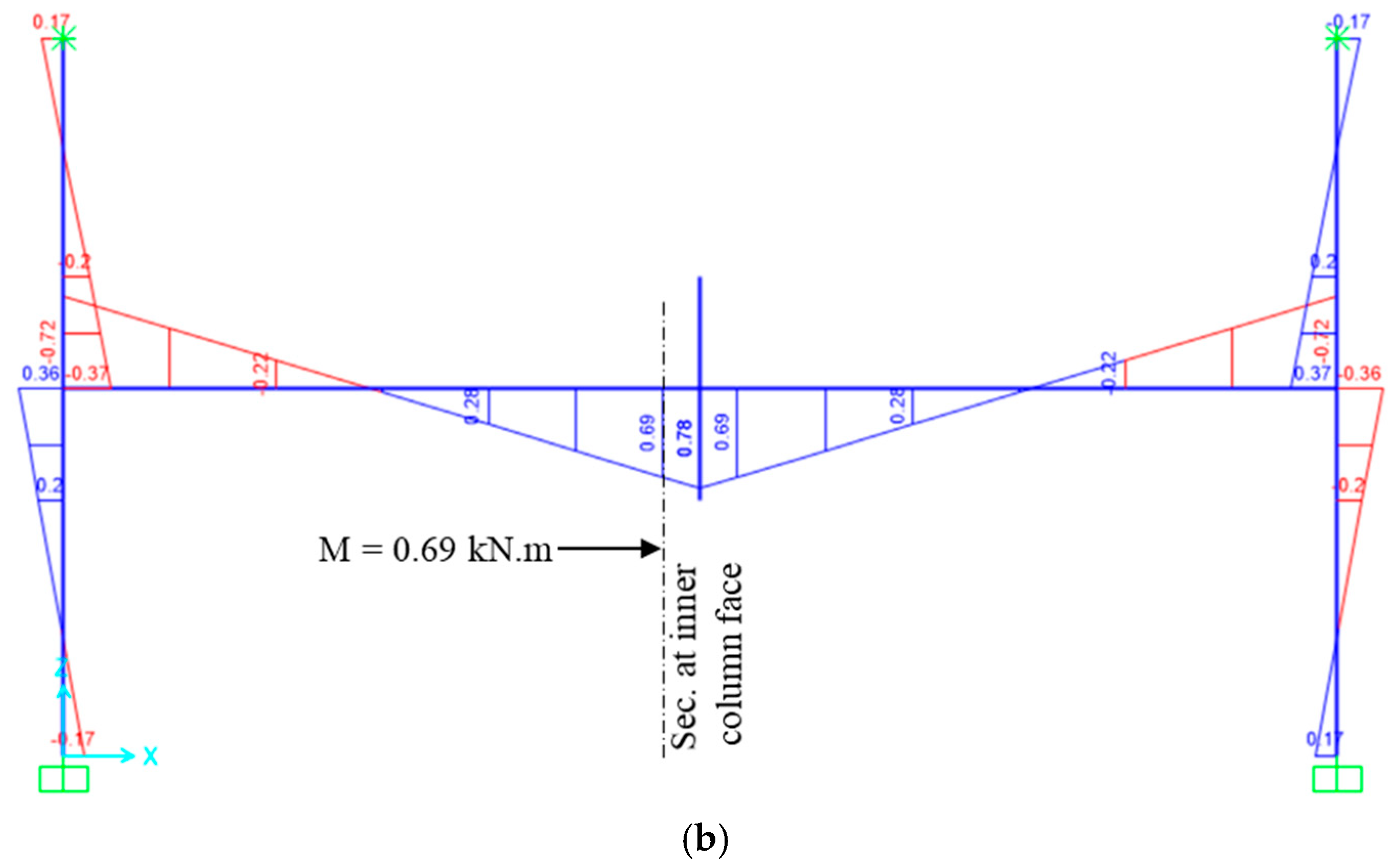
3.7. Validation of FE Models
4. Discussion of FE Findings
4.1. Failure Pattern
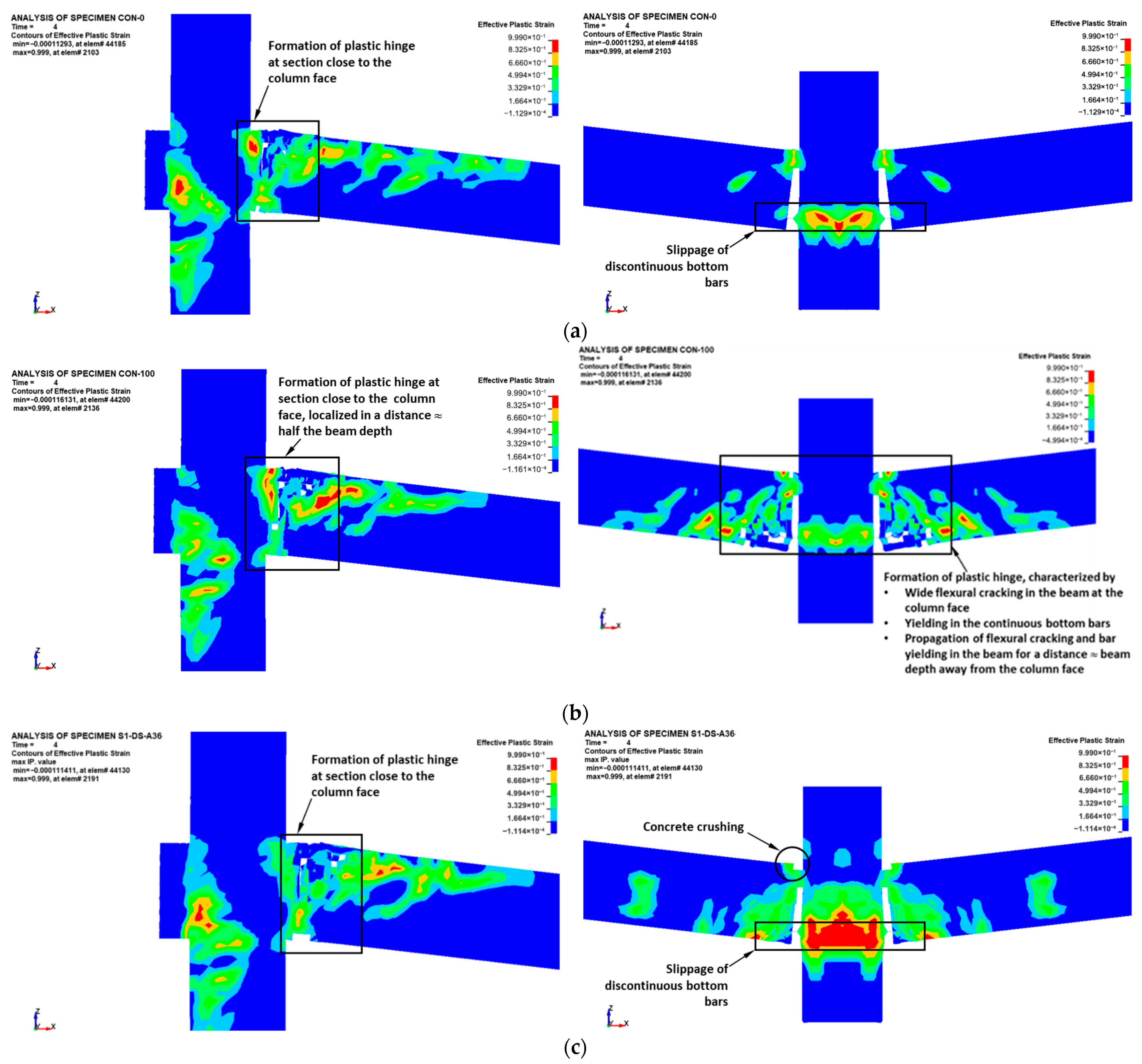
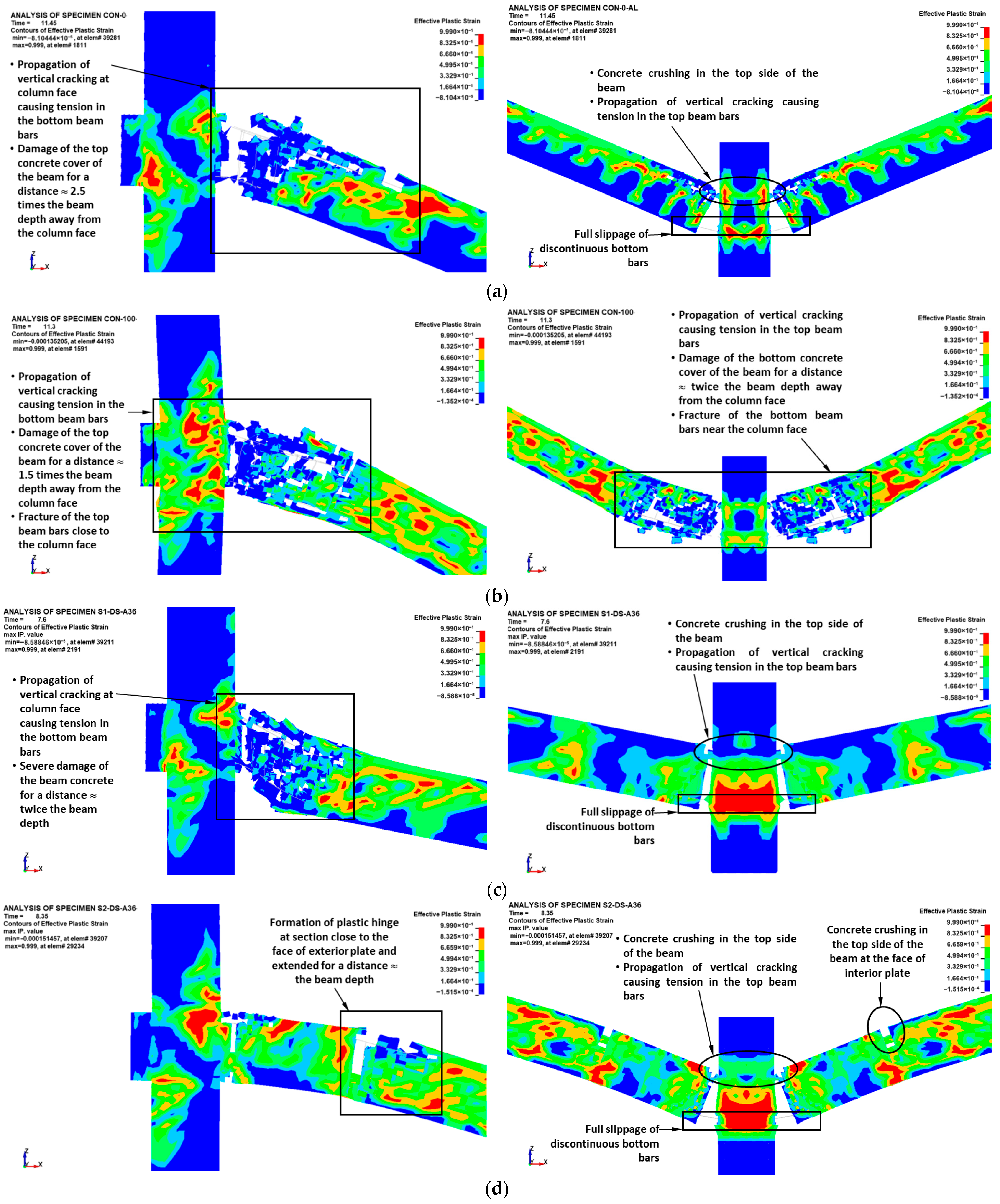
4.1.1. Control Specimens
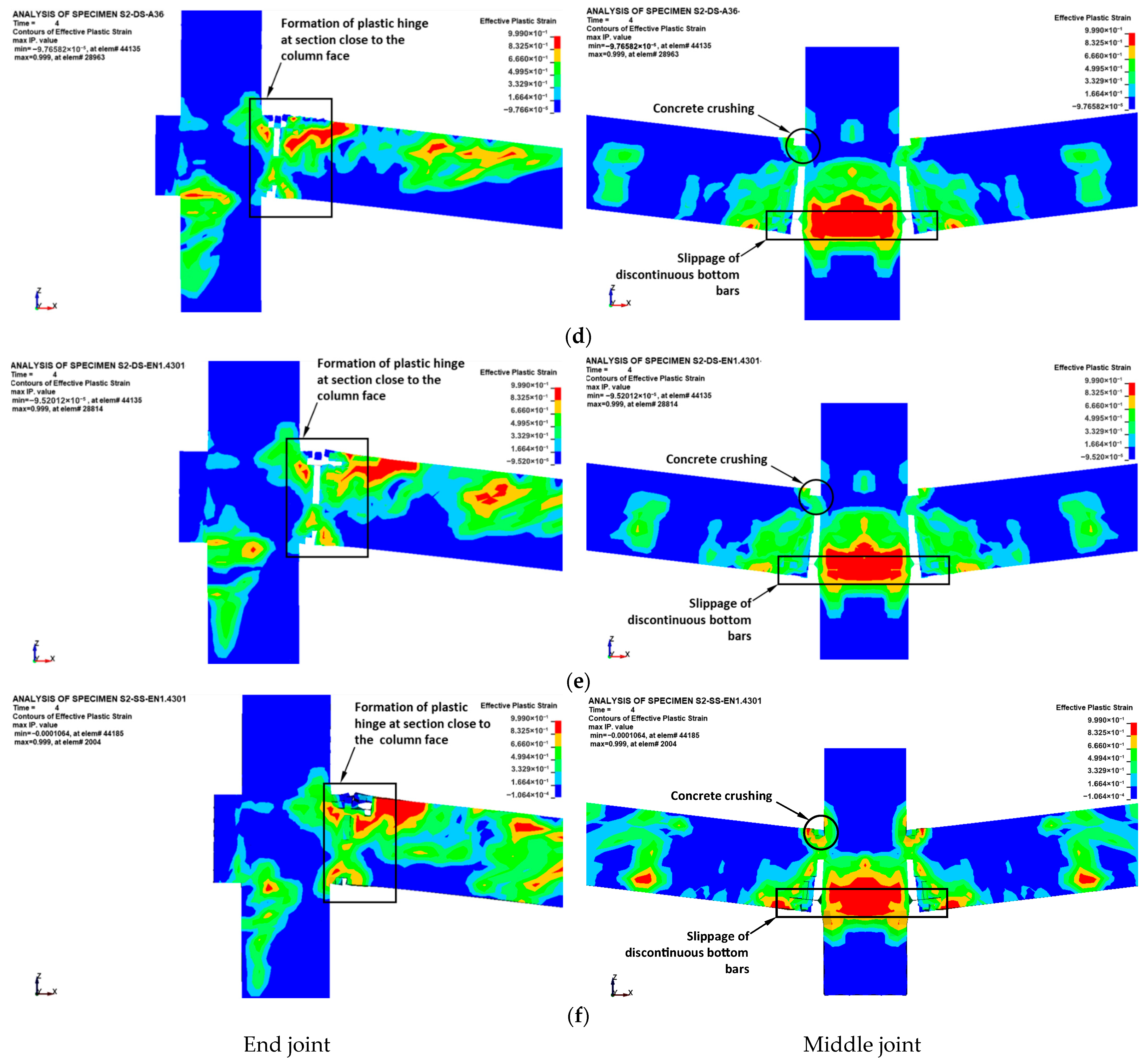
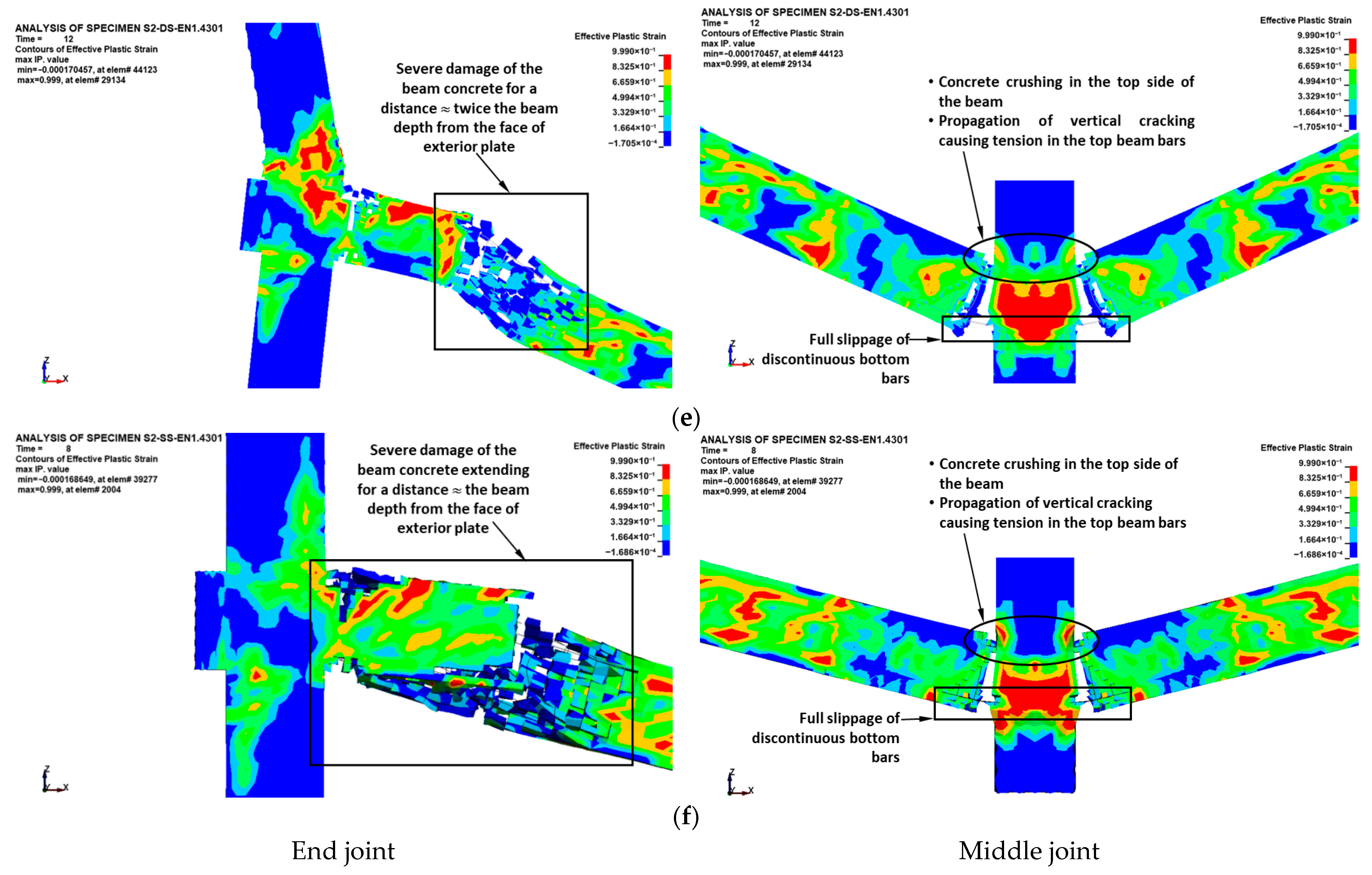
4.1.2. Strengthened Specimens
4.2. Load–Displacement Pattern
4.3. Limitations and Practical Applications of Bolted Steel Plate Retrofitting
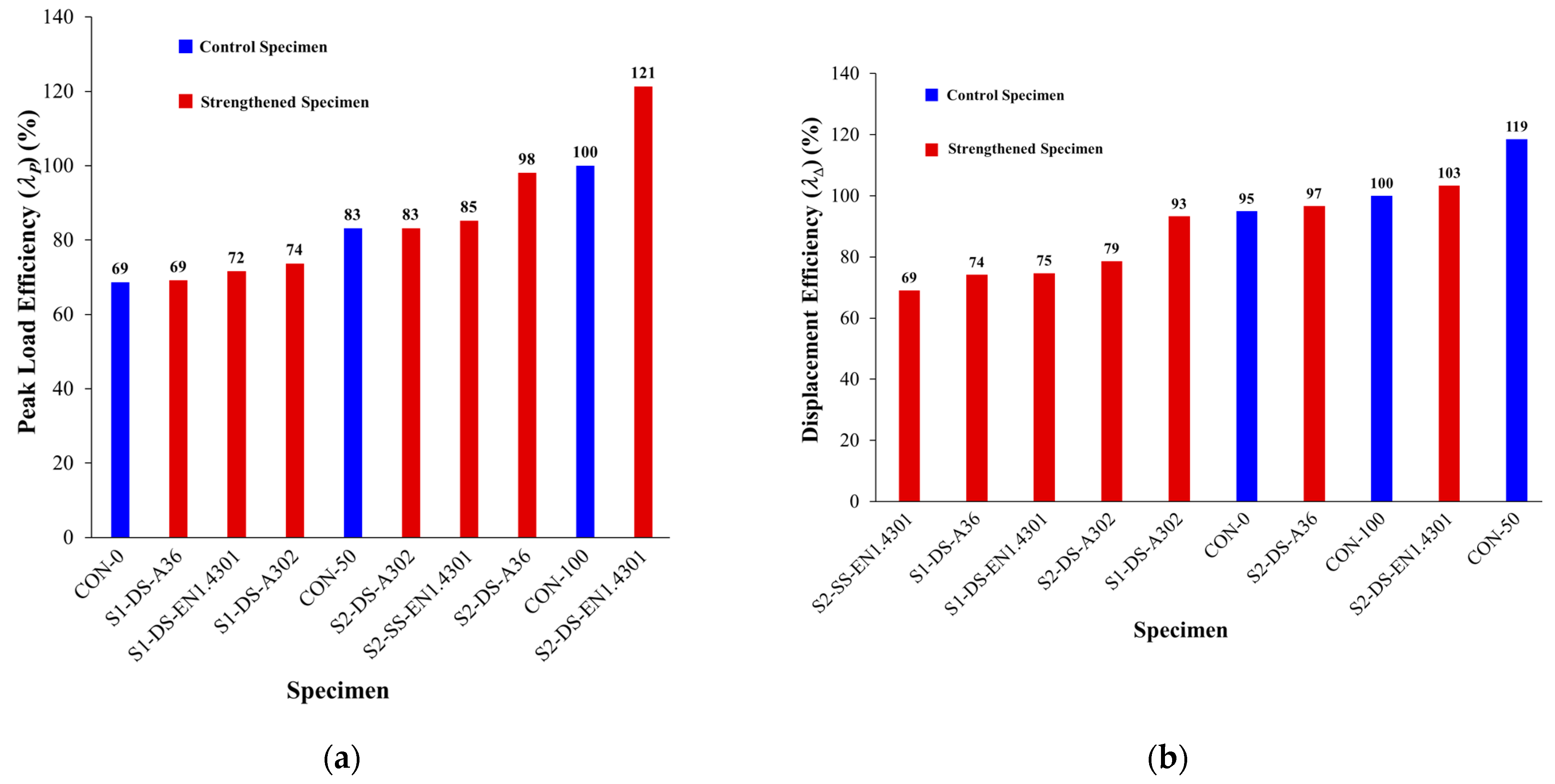
5. Comparison of Strengthening Schemes
6. Conclusions
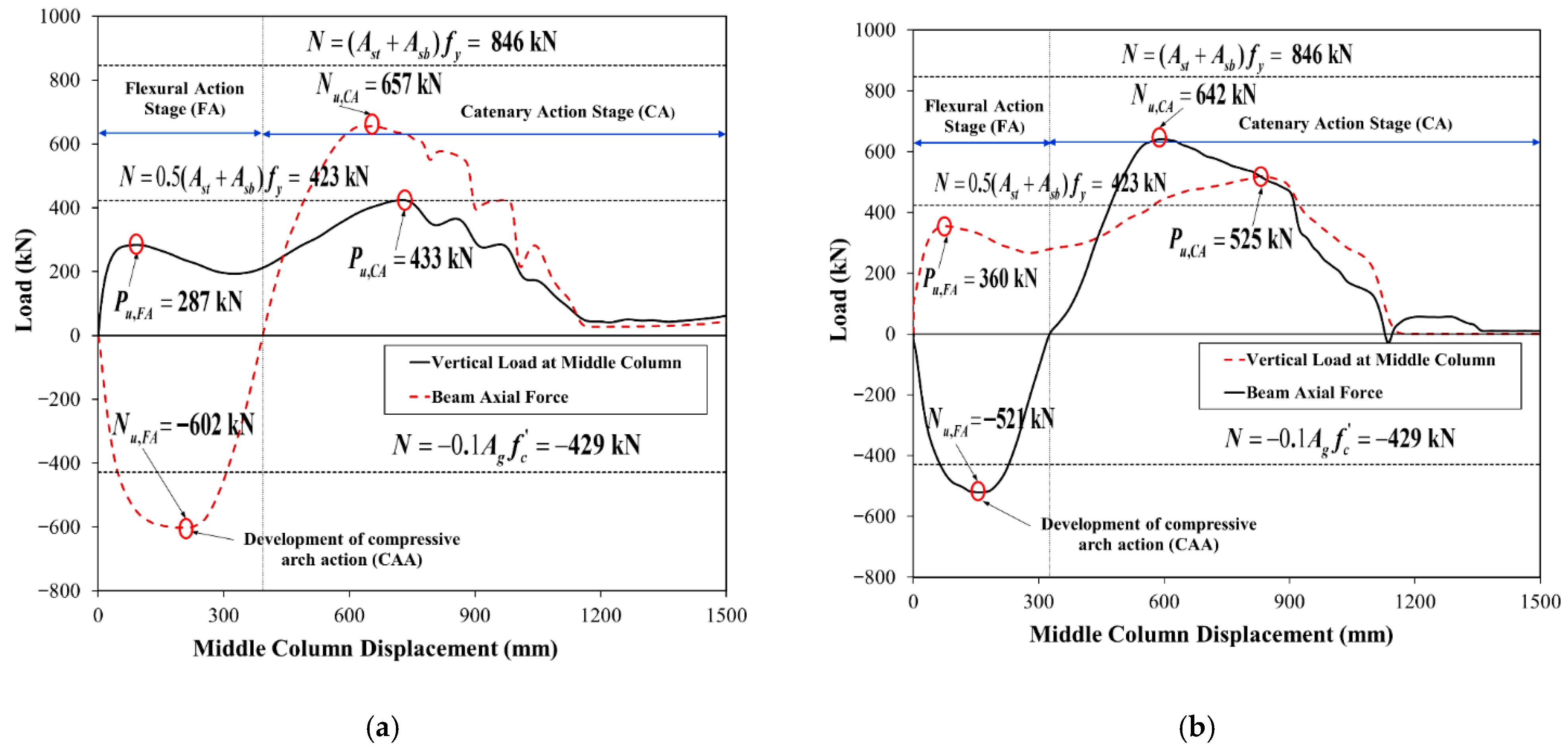
- In the behavior of control and strengthened specimens under middle column loss, two discrete phases were identified. These are the flexural and catenary stages. Considerable axial compressive forces in the beams were created during the flexural action stage. These forces exceeded 10% of the beam section’s axial capacity, promoting the formation of compressive arch action in the beams.
- Concrete damage contours of upgraded specimens were almost identical to those of control specimens with discontinuous bottom beam bars. The discontinuous beam bars at the middle column interface experienced slippage at low displacement levels of the middle column during the flexural stage. Full slippage of the discontinuous bottom bars occurred at large displacements during the catenary action phase. The flexural cracks near the center column face extended nearly vertically, inducing tension in the continuous top bars and partially triggering the establishment of the catenary stage. The ultimate failure pattern of steel plates added at the middle connection was due to either plate fracture or local plate buckling near the middle column face.
- Strengthening of RC non-seismic assemblies using bolted steel plates considerably enhanced their load–displacement response, especially in the flexural phase. The maximum load of strengthened specimens in the flexural action phase was higher than that of the control specimen with continuous beam bars (CON-100) by 1% to 25%.
- For upgrading schemes S1-DS and S2-DS, the steel grade has a slight influence on the percent enhancement in the maximum load at the flexural action stage. This is because at such a stage, the load resistance relied on the yield strength of the plate, and the plate thickness was different for each grade to have almost the same flexural capacity as the control specimen with continuous beam bars (CON-100).
- The progressive collapse capacity of specimens upgraded with scheme S2-DS is generally better than that of scheme S1-DS. When compared with scheme S1-DS, adding steel plates at the outer joints in scheme S2-DS increased the strength and stiffness of the outer beam–column joints and, hence, enhanced the maximum load of the assembly at the two action phases.
- Among all studied schemes and grades, the best progressive collapse performance was provided by specimens upgraded with EN1.4301 steel plates of scheme S2-DS. This is attributed to the high fracture strain of 45% for EN1.4301 steel, which helped the upgraded assembly to have large deformation in the catenary action phase without premature failure owing to plate fracture.
- Even though the results of this study are based on modeling of 2D assemblies, in which the effects of RC slabs and transverse RC beams were not included, the 2D assemblies provided lower-bound values for the progressive collapse resistance. For more accurate analysis, it is highly recommended in the future to model 3D assemblies with slabs and transverse beams in the event of middle column loss.
- This study confirmed that bolted steel plates are an effective strengthening method for mitigating progressive collapse in RC frames, with scheme S2-DS using EN 1.4301 stainless steel showing superior performance. Bolted plates offer practical advantages, such as ease of installation, adaptability, and reversibility. While EN 1.4301 has higher upfront costs, its corrosion resistance and durability improve long-term cost-effectiveness, making it a sustainable retrofitting option.
- The upgraded schemes suggested in this study may be considered innovative owing to that (i) the use of bolted steel plates has not been used in the previous literature for mitigating progressive collapse in non-seismic RC frames; (ii) the schemes were added on the sides of the beam without increasing its depth, which could be practical in real-world applications; and (3) the EN 1.4301 stainless steel employed in this study was not commonly used in strengthening applications.
- Future studies should focus on experimental validation of strengthening schemes, assessment of long-term performance under service loads, investigation of combined extreme loading scenarios, and evaluation of cost–benefit and construction feasibility aspects for the proposed bolted steel plate retrofitting techniques.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pearson, C.; Delatte, N. Lessons from the progressive collapse of the Ronan Point apartment tower. Forensic Eng. 2003, 190–200. [Google Scholar] [CrossRef]
- Kazemi-Moghaddam, A.; Sasani, M. Progressive collapse evaluation of Murrah Federal Building following sudden loss of column G20. Eng. Struct. 2015, 89, 162–171. [Google Scholar] [CrossRef]
- Işık, E.; Avcil, F.; Hadzima-Nyarko, M.; İzol, R.; Büyüksaraç, A.; Arkan, E.; Radu, D.; Özcan, Z. Seismic performance and failure mechanisms of reinforced concrete structures subject to the earthquakes in Türkiye. Sustainability 2024, 16, 6473. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete and Commentary; ACI 318–19; American Concrete Institute: Detroit, MI, USA, 2019. [Google Scholar]
- ASCE (American Society of Civil Engineers). Minimum Design Loads and Associated Criteria for Buildings and Other Structures (ASCE/SEI 7–16); American Society of Civil Engineers: Reston, VA, USA, 2016. [Google Scholar]
- DOD (Department of Defense). Unified Facilities Criteria, Design of Building to Resist Progressive Collapse; Department of Defense: Arlington, VA, USA, 2005. [Google Scholar]
- GSA (General Service Administration). Alternate Path Analysis & Design Guidelines for Progressive Collapse Resistance; The U.S. General Services Administration: Washington, DC, USA, 2016. [Google Scholar]
- Pearson, C.; Delatte, N. Ronan point apartment tower collapse and its effect on building codes. J. Perform. Constr. Facil. 2005, 19, 172–177. [Google Scholar] [CrossRef]
- Alshaikh, I.M.; Bakar, B.A.; Alwesabi, E.A.; Zeyad, A.M.; Magbool, H.M. Finite element analysis and experimental validation of progressive collapse of reinforced rubberized concrete frame. Structures 2021, 33, 2361–2373. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Almusallam, T.H.; Al-Salloum, Y.A.; Abbas, H. Investigation of precast RC beam-column assemblies under column-loss scenario. Constr. Build. Mater. 2017, 142, 552–571. [Google Scholar] [CrossRef]
- Feng, D.C.; Shi, H.R.; Parisi, F.; Brunesi, E.; Wang, C.L. Efficient numerical model for progressive collapse analysis of prestressed concrete frame structures. Eng. Fail. Anal. 2021, 129, 105683. [Google Scholar] [CrossRef]
- Kim, J.; An, D. Evaluation of progressive collapse potential of steel moment frames considering catenary action. Struct. Des. Tall Spec. Build. 2009, 18, 455–465. [Google Scholar] [CrossRef]
- Sasani, M.; Bazan, M.; Sagiroglu, S. Experimental and analytical progressive collapse evaluation of actual reinforced concrete structure. ACI Struct. J. 2007, 104, 731–739. Available online: https://www.proquest.com/scholarly-journals/experimental-analytical-progressive-collapse/docview/198350832/se-2 (accessed on 10 September 2025). [CrossRef] [PubMed]
- Kim, J.; Yu, J. Analysis of reinforced concrete frames subjected to column loss. Mag. Concr. Res. 2012, 64, 21–33. [Google Scholar] [CrossRef]
- Azar, A.B.; Sari, A. Reinforcement of arch structures under blast loads: A sustainable approach to structural enhancement. J. Struct. Integr. Maint. 2025, 10, 2457913. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Almusallam, T.H.; Ngo, T.; Abbas, H. Assessment of progressive collapse potential of special moment resisting RC frames–Experimental and FE study. Eng. Fail. Anal. 2019, 105, 896–918. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual; Version R11; LSTC: Livermore, CA, USA, 2018; Volume 1–3. [Google Scholar]
- Bao, Y.; Lew, H.S.; Kunnath, S.K. Modeling of reinforced concrete assemblies under column-removal scenario. J. Struct. Eng. 2014, 140, 04013026. [Google Scholar] [CrossRef]
- ASCE/SEI 41-06; Seismic Rehabilitation of Existing Buildings. American Society of Civil Engineers: Reston, VA, USA, 2006.
- Lim, N.S.; Tan, K.H.; Lee, C.K. Experimental studies of 3D RC substructures under exterior and corner column removal scenarios. Eng. Struct. 2017, 150, 409–427. [Google Scholar] [CrossRef]
- Lu, X.; Lin, K.; Li, Y.; Guan, H.; Ren, P.; Zhou, Y. Experimental investigation of RC beam-slab substructures against progressive collapse subject to an edge-column-removal scenario. Eng. Struct. 2017, 149, 91–103. [Google Scholar] [CrossRef]
- Yu, J.; Luo, L.; Li, Y. Numerical study of progressive collapse resistance of RC beam-slab substructures under perimeter column removal scenarios. Eng. Struct. 2018, 159, 14–27. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine learning-based seismic fragility and seismic vulnerability assessment of reinforced concrete structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Valente, M. Seismic upgrading strategies for non-ductile plan-wise irregular R/C structures. Procedia Eng. 2013, 54, 539–553. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Alternative retrofitting strategies to prevent the failure of an under-designed reinforced concrete frame. Eng. Fail. Anal. 2018, 89, 271–285. [Google Scholar] [CrossRef]
- Teng, J.G.; Chen, J.F.; Smith, S.T.; Lam, L. Behaviour and strength of FRP-strengthened RC structures: A state-of-the-art review. Proc. Inst. Civ. Eng. Struct. Build. 2003, 156, 51–62. [Google Scholar] [CrossRef]
- Liu, X.; Lu, Z.D.; Li, L.Z. The use of bolted side plates for shear strengthening of RC beams: A review. Sustainability 2018, 10, 4658. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A.; Alrubaidi, M.A.; Elsanadedy, H.M.; Almusallam, T.H.; Iqbal, R.A. Strengthening of precast RC beam-column connections for progressive collapse mitigation using bolted steel plates. Eng. Struct. 2018, 161, 146–160. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Alrubaidi, M.A.; Almusallam, T.H.; Abbas, H. Finite element analysis for progressive collapse potential of precast concrete beam-to-column connections strengthened with steel plates. J. Build. Eng. 2021, 34, 101875. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. Part B Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- Shang, X.Y.; Yu, J.T.; Li, L.Z.; Lu, Z.D. Strengthening of RC structures by using engineered cementitious composites: A review. Sustainability 2019, 11, 3384. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Alrubaidi, M.A.; Almusallam, T.H.; Siddiqui, N.A.; Abbas, H. Upgrading of precast RC beam-column joints using innovative FRP/steel hybrid technique for progressive collapse prevention. Constr. Build. Mater. 2021, 268, 121130. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Abadel, A.A. High-fidelity FE models for assessing progressive collapse robustness of RC ordinary moment frame (OMF) buildings. Eng. Fail. Anal. 2022, 136, 106228. [Google Scholar] [CrossRef]
- ASTM A302/A302M-17; Standard Specification for Pressure Vessel Plates, Alloy Steel, Manganese-Molybdenum and Manganese-Molybdenum-Nickel. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM A36/A36M-19; Standard Specification for Carbon Structural Steel. ASTM International: West Conshohocken, PA, USA, 2019.
- EN 10088-1:2023; Stainless Steels—Part 1: List of Stainless Steels. CEN: Brussels, Belgium, 2023.
- Karjalainen, L.P.; Taulavuori, T.; Sellman, M.; Kyröläinen, A.J. Some strengthening methods for austenitic stainless steels. Steel Res. Int. 2008, 79, 404–412. [Google Scholar] [CrossRef]
- Computers and Structures Inc. SAP2000 Ultimate 64-bit—Version 21.2.0; CSI: Berkeley, CA, USA, 2019. [Google Scholar]
- Belytschko, T.B.; Tsay, C.S. Explicit algorithms for nonlinear dynamics of shells. Nonlinear finite element analysis of plates and shells. J. Appl. Mech. 1981, 48, 209–231. [Google Scholar]
- Murray, Y.D.; Abu-Odeh, A.; Bligh, R. Evaluation of Concrete material Model 159; Report No. FHWA-HRT-05-063; US Department of Transportation, Federal Highway Administration National Transportation Systems Center: Washington, DC, USA, 2007. Available online: https://www.fhwa.dot.gov/publications/research/infrastructure/structures/05063/05063.pdf (accessed on 13 September 2025).
- ACI Committee 408. Bond and Development of Straight Reinforcing Bars in Tension; ACI 408R-03; American Concrete Institute: Detroit, MI, USA, 2003. [Google Scholar]
- NZS 4203; Code of Practice for General Structural Design and Design Loadings for Buildings 1. New Zealand Standard (NZS): Wellington, New Zealand, 1992.
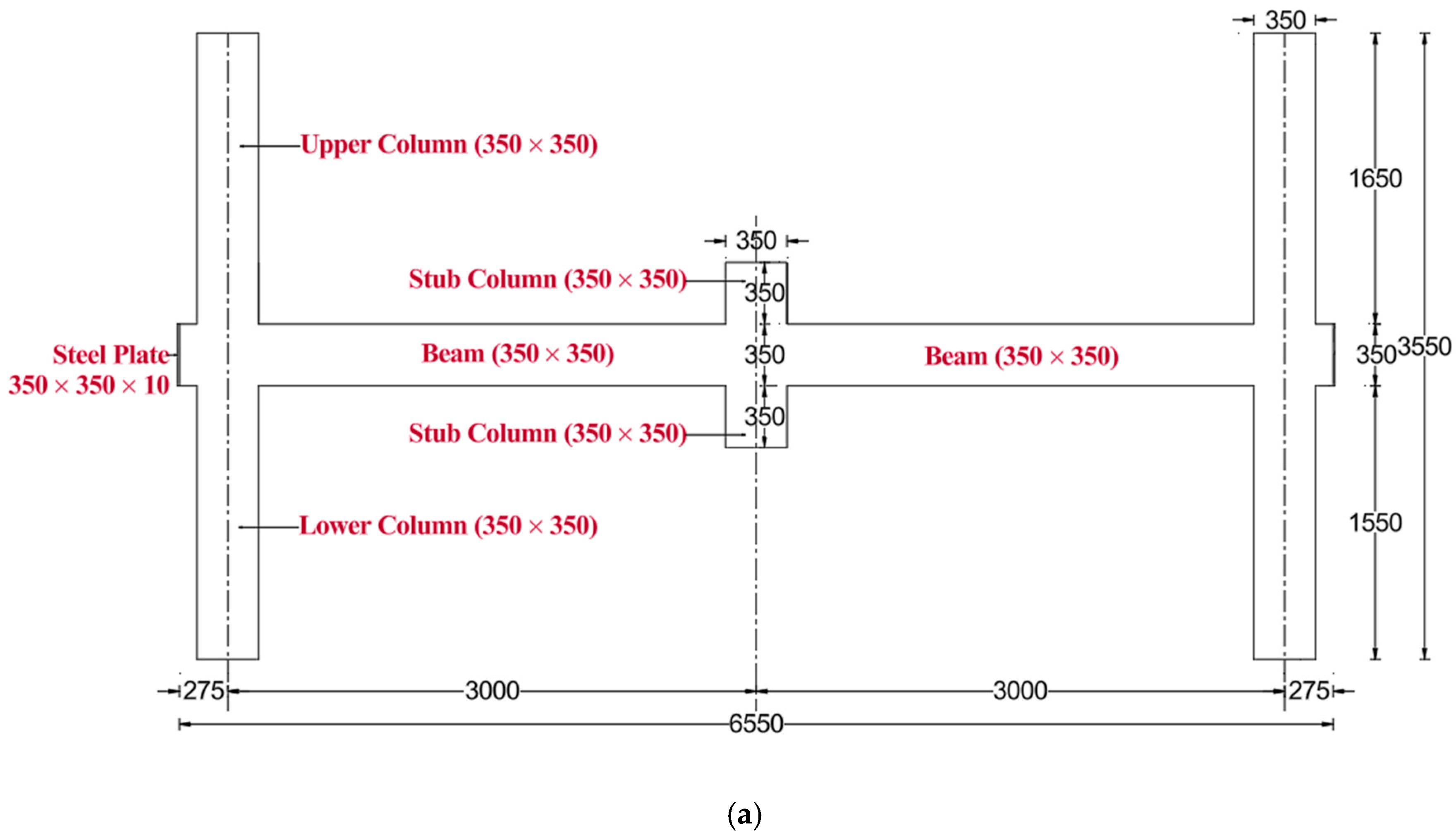
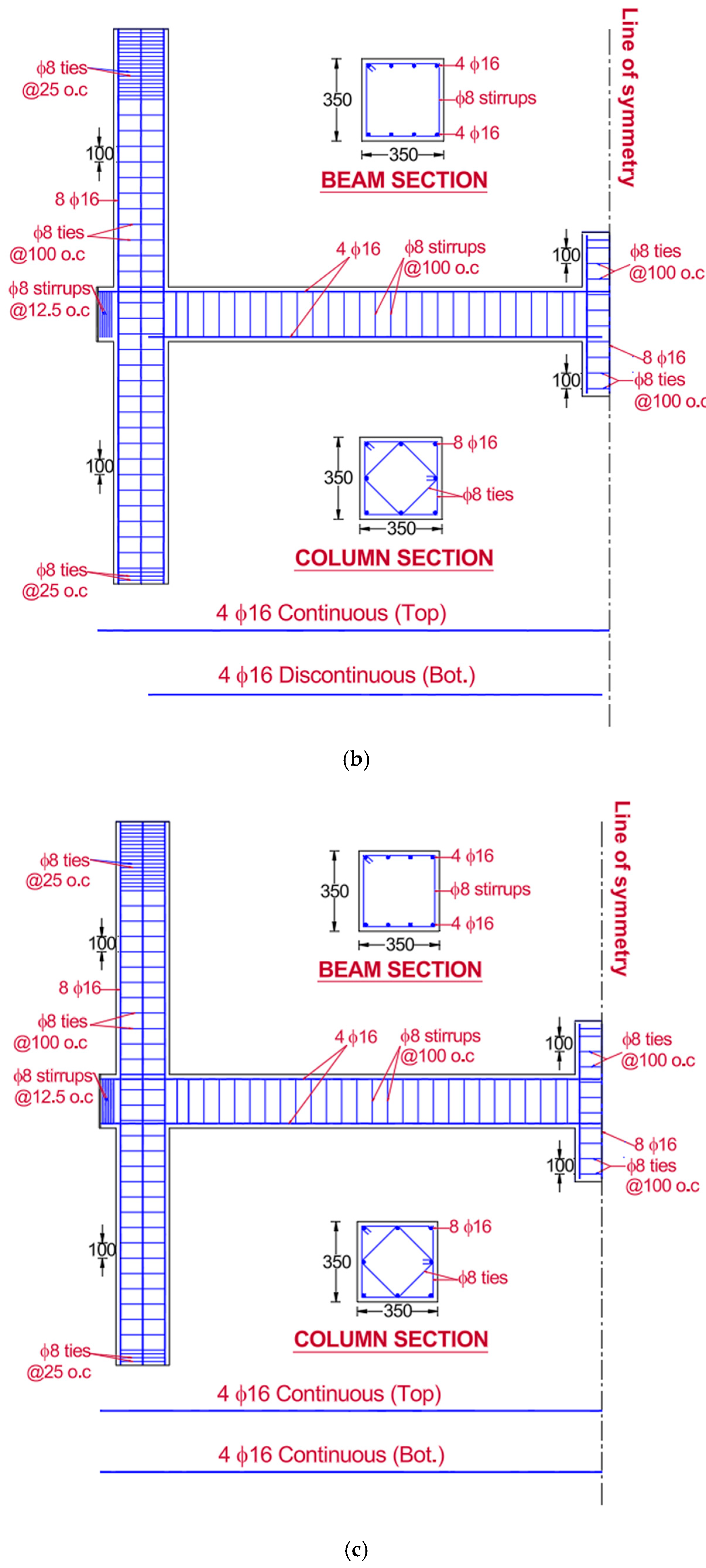


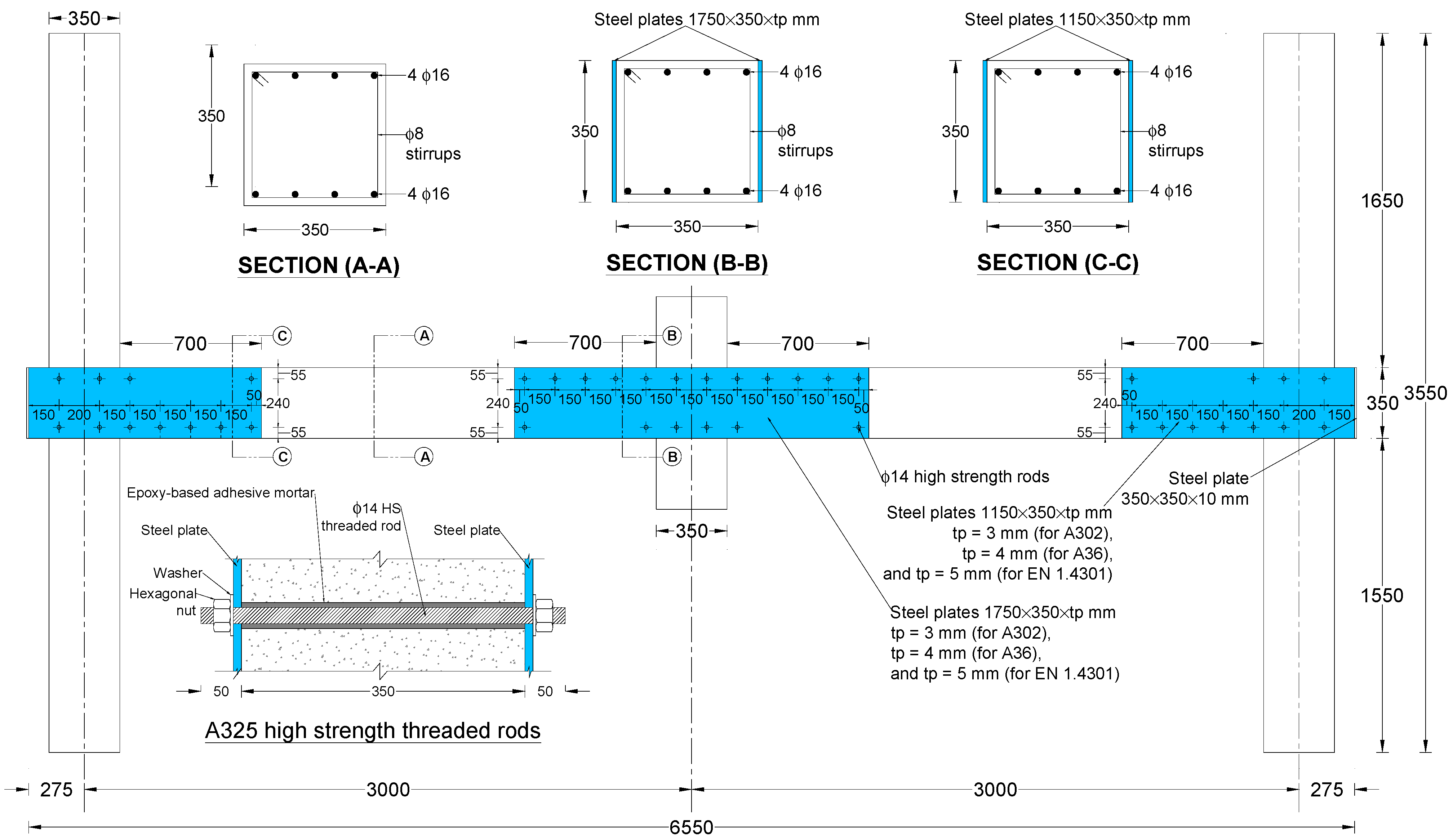
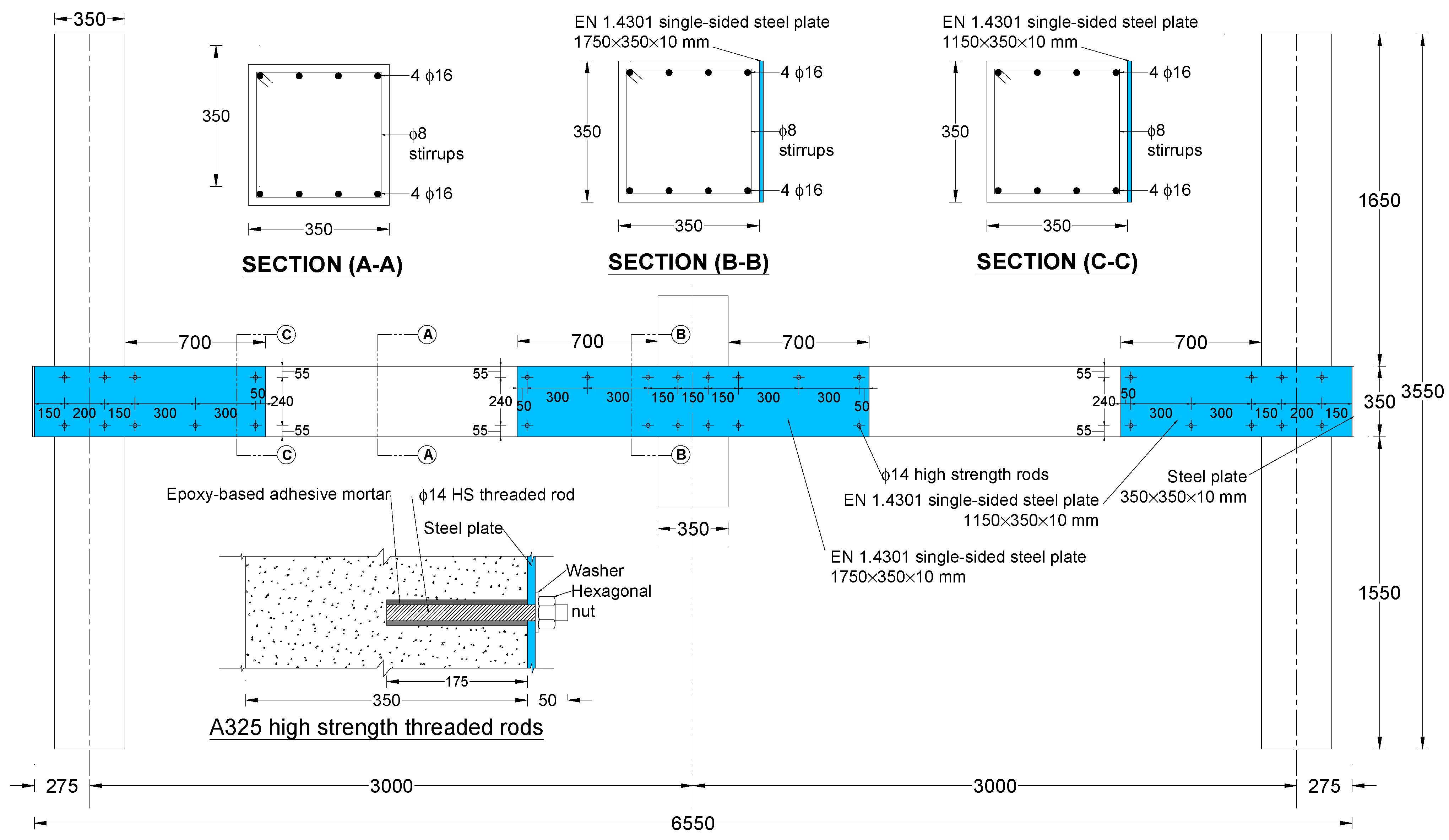
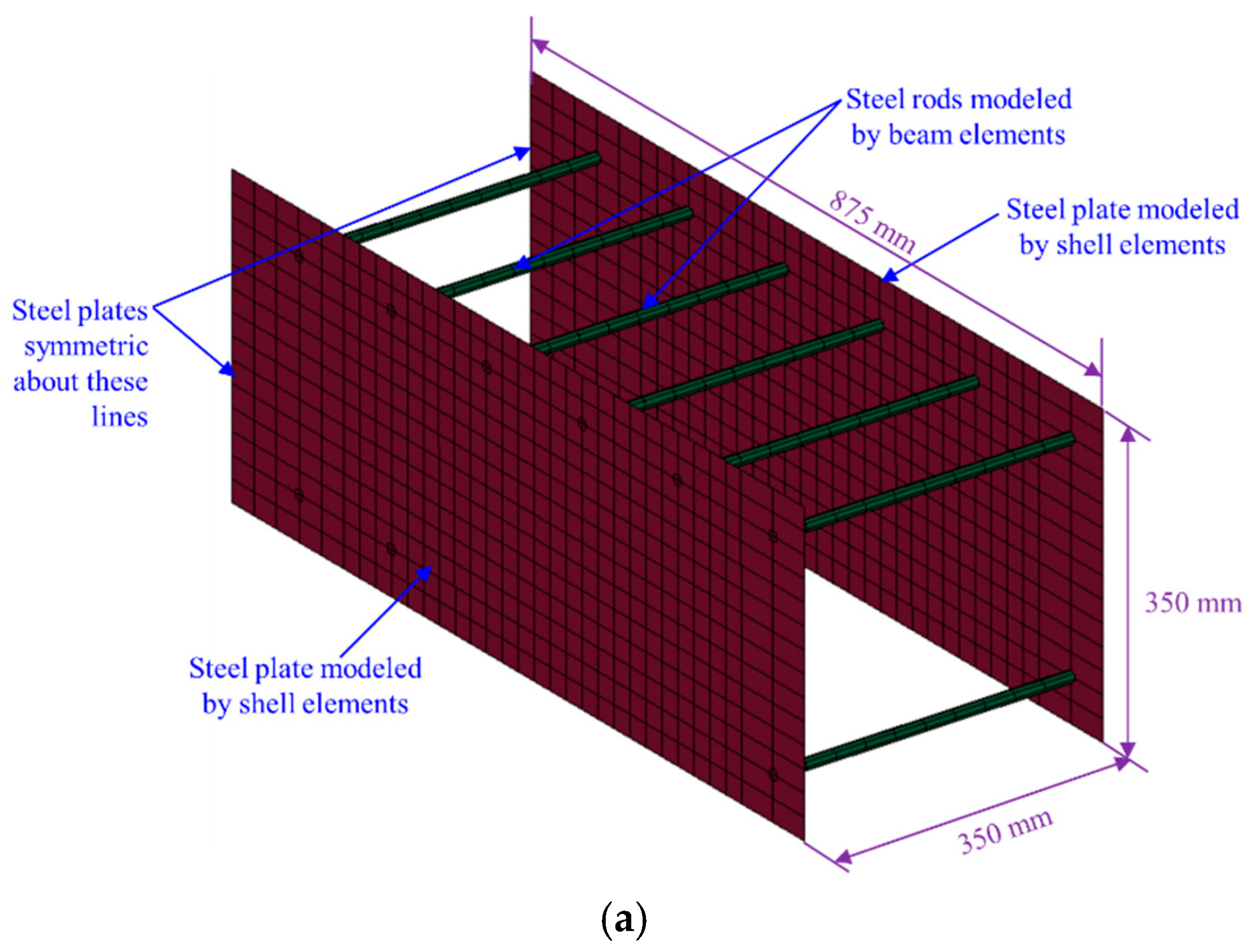
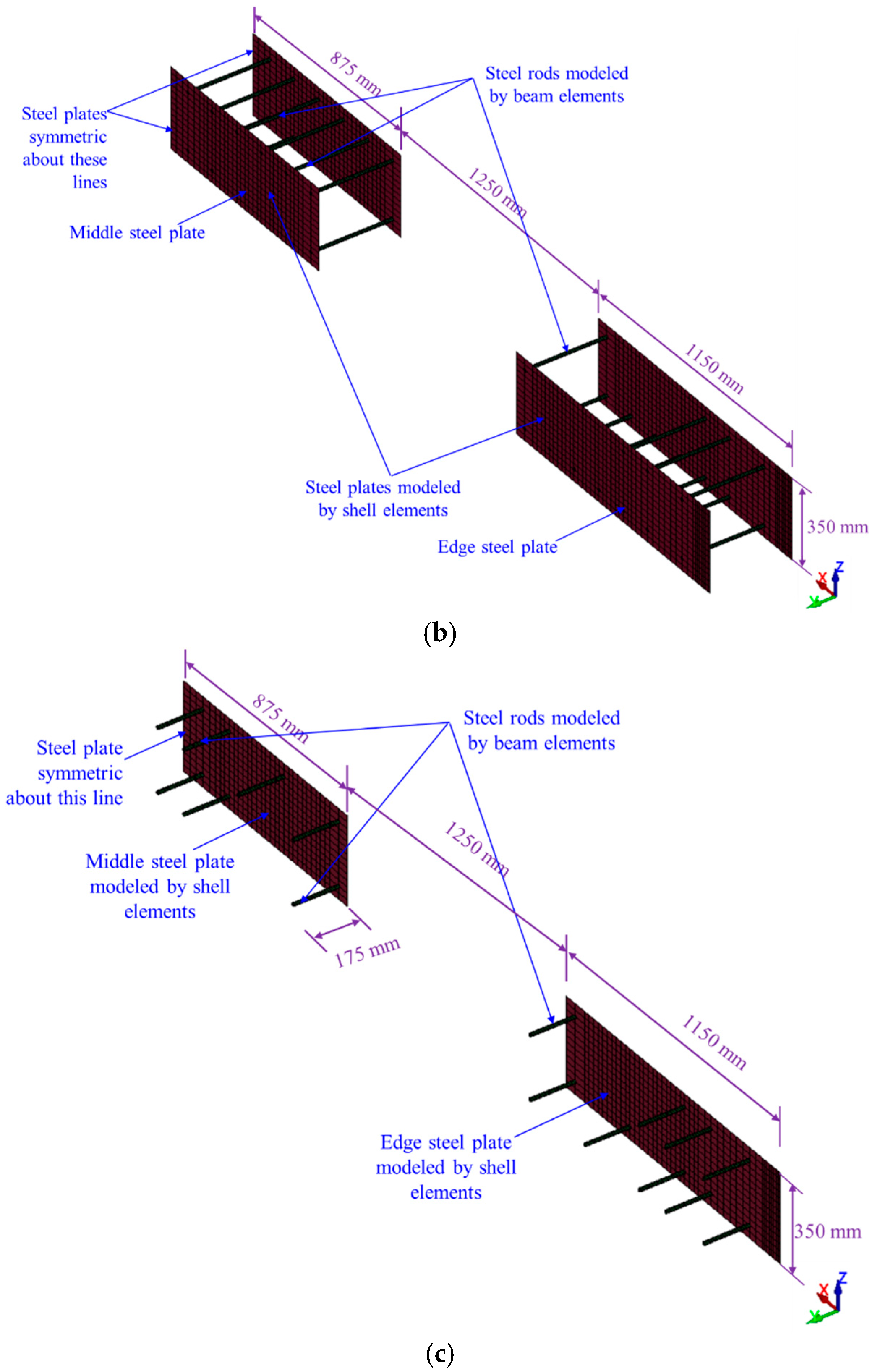
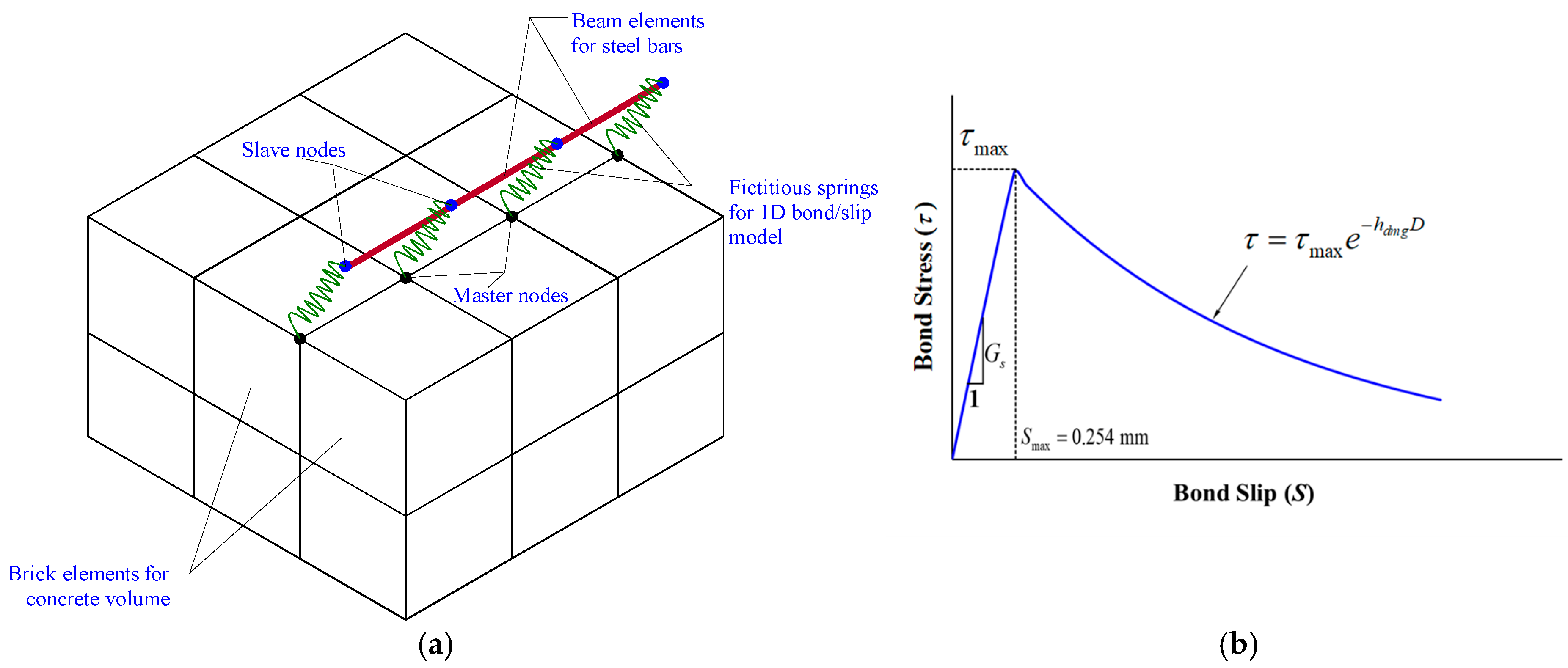
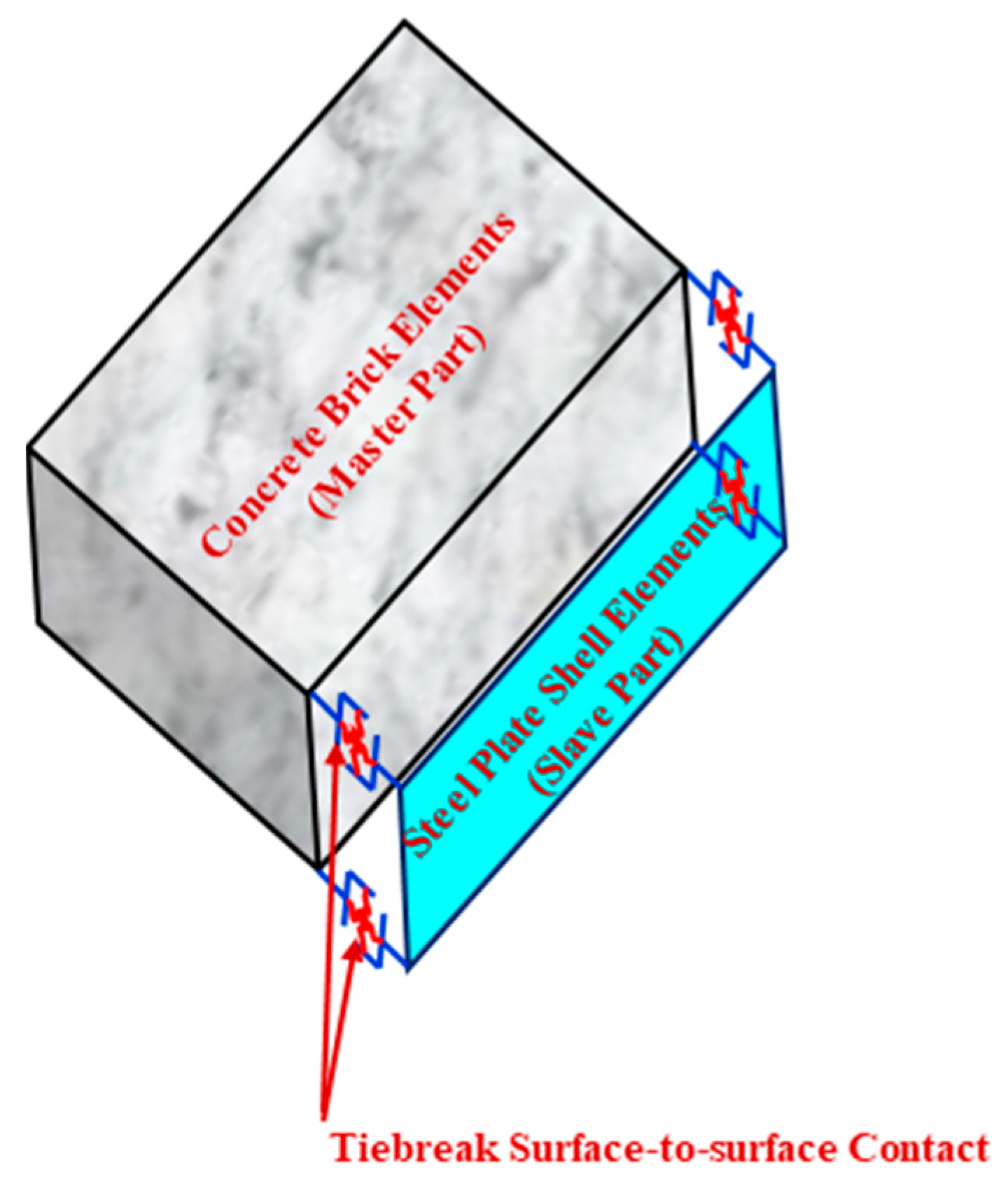

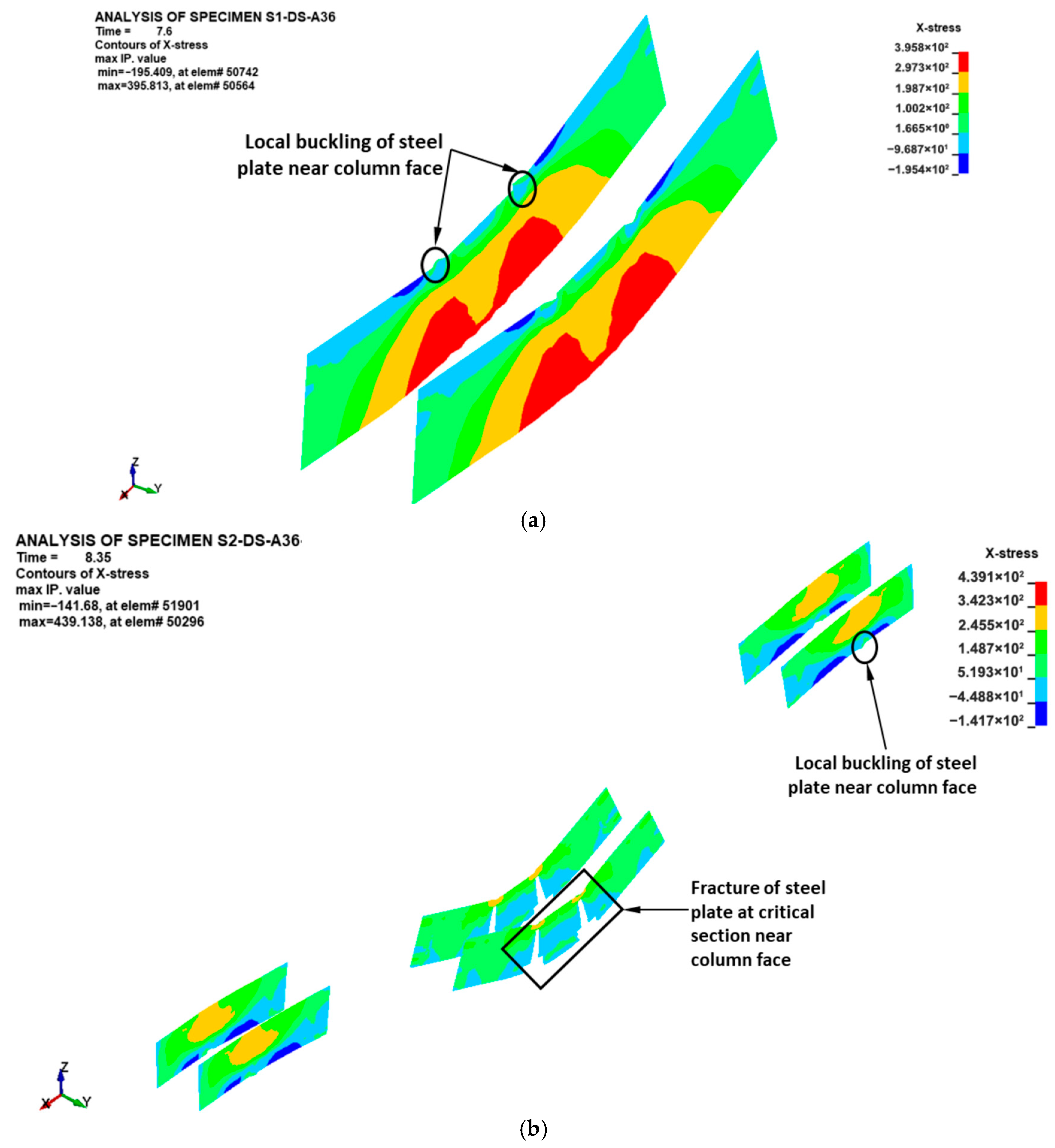
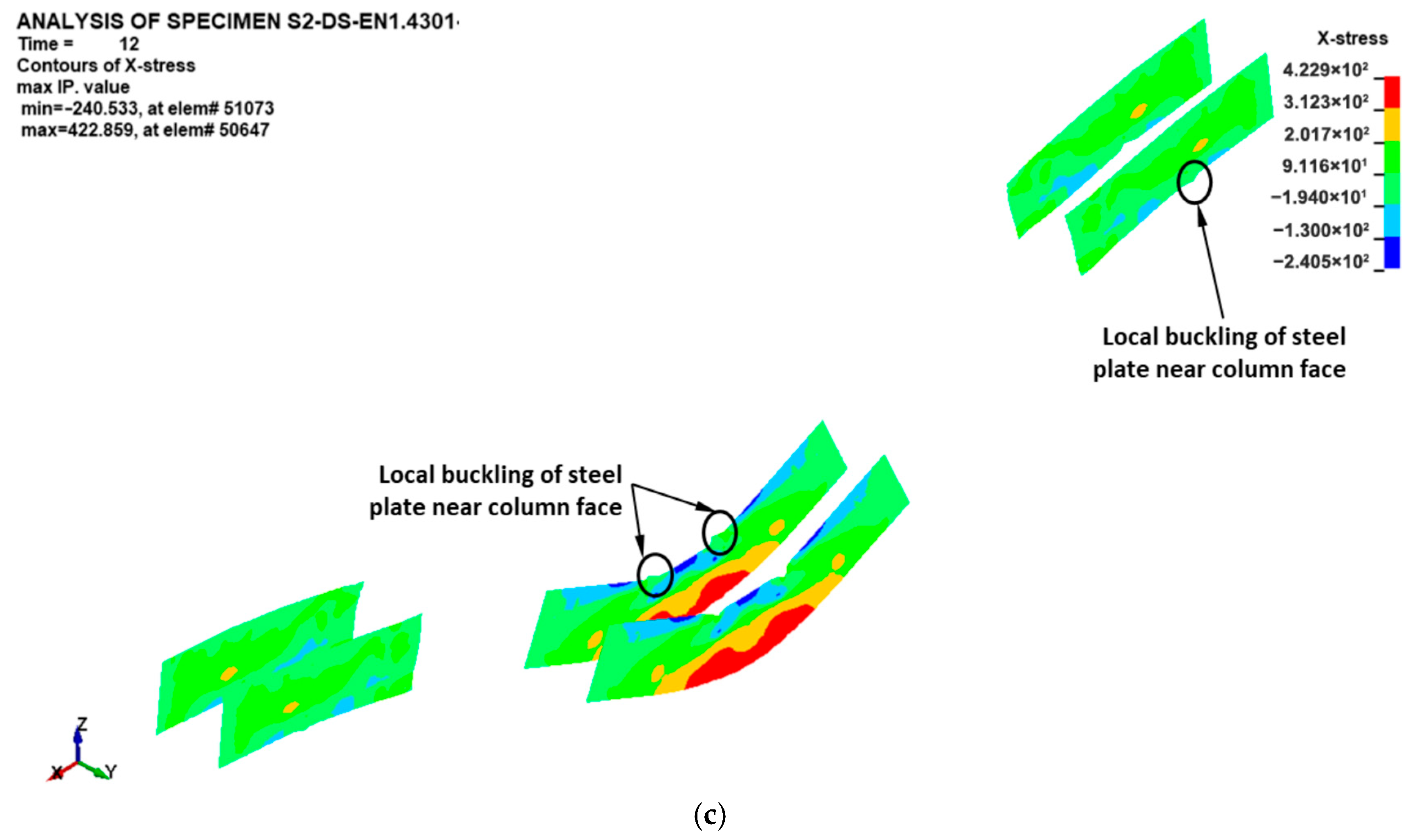
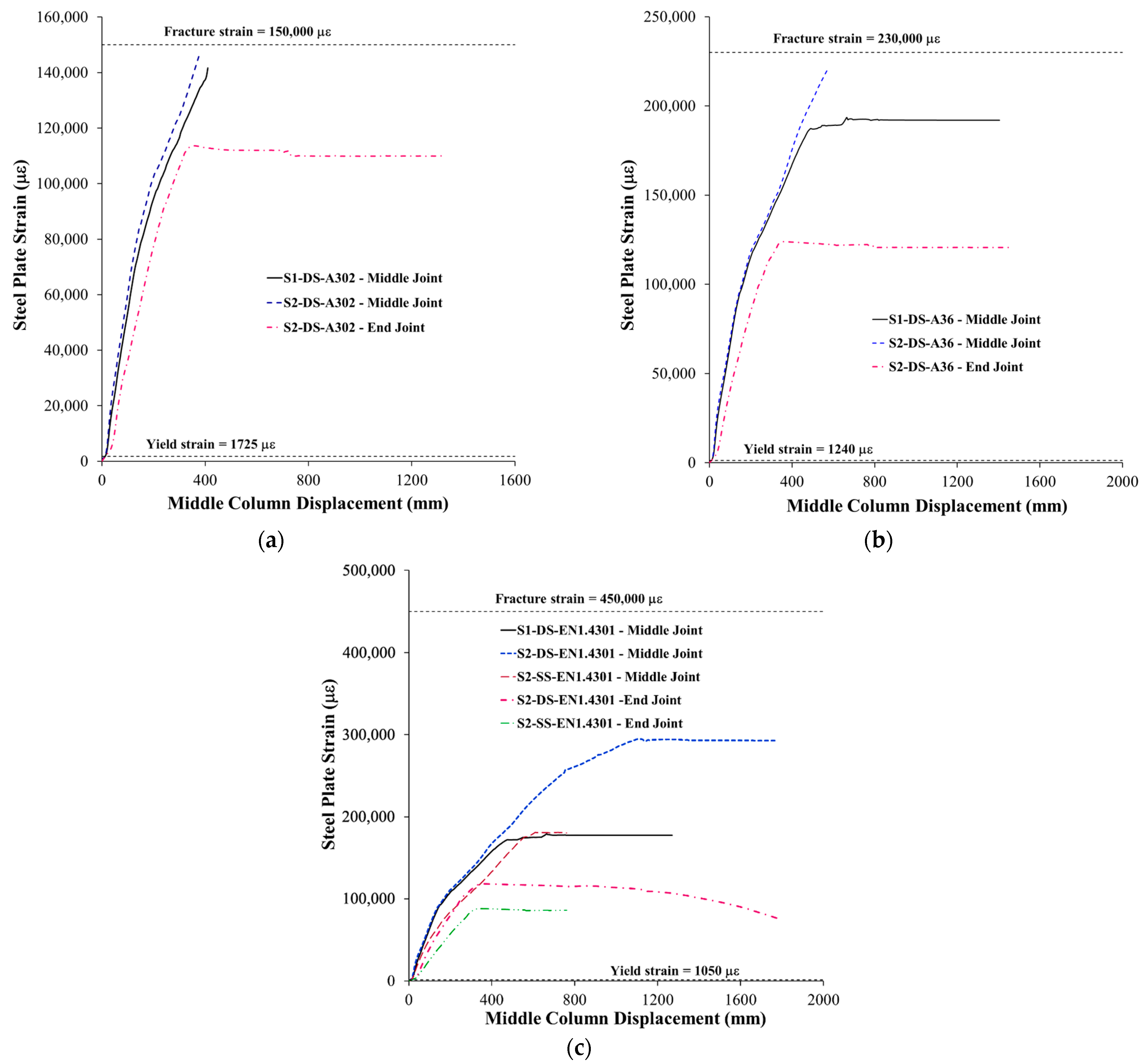




| Specimen ID | % of Continuous Bottom Beam Bars at Beam–Column Connection | Details |
|---|---|---|
| CON-0 | 0% | See Figure 1 and Figure 2 |
| CON-50 | 50% | See Figure 1 and Figure 2 |
| CON-100 | 100% | See Figure 1 and Figure 2 |
| Specimen ID | Upgrading Scheme | Steel Plate Configuration | Details | ||
|---|---|---|---|---|---|
| Thickness (mm) | Grade | Location | |||
| S1-DS-A302 | S1-DS | 3 | ASTM A302, Grade B [34] | Both sides of the specimen at the middle joint | See Figure 3 |
| S2-DS-A302 | S2-DS | 3 | ASTM A302, Grade B | Both sides of the specimen at the middle and end joints | See Figure 4 |
| S1-DS-A36 | S1-DS | 4 | ASTM A36 [35] | Both sides of the specimen at the middle joint | See Figure 3 |
| S2-DS-A36 | S2-DS | 4 | ASTM A36 | Both sides of the specimen at the middle and end joints | See Figure 4 |
| S1-DS-EN1.4301 | S1-DS | 5 | EN 1.4301 [36] | Both sides of the specimen at the middle joint | See Figure 3 |
| S2-DS-EN1.4301 | S2-DS | 5 | EN 1.4301 | Both sides of the specimen at the middle and end joints | See Figure 4 |
| S2-SS-EN1.4301 | S2-SS | 10 | EN 1.4301 | One side of the specimen at the middle and end joints | See Figure 5 |
| Concrete | ||||||
|---|---|---|---|---|---|---|
| Material model | Type 159—continuous surface cap | |||||
| Compressive strength (MPa) | 35 | |||||
| Rate effect included | Yes | |||||
| Erosion type and threshold | Maximum principal strain—erosion limit = 5% | |||||
| Maximum size of coarse aggregate (mm) | 10 | |||||
| Steel bars, plates, and rods | ф8 bars | ф16 bars | A302 plates | A36 plates | EN 1.4301 plates | HS rods |
| Material model | Type 24—piecewise linear plasticity | |||||
| Elastic modulus (MPa) | 2 × 105 | 2 × 105 | 2 × 105 | 2 × 105 | 2 × 105 | 2 × 105 |
| Poisson’s ratio | 0.3 | 0.3 | 0.29 | 0.3 | 0.29 | 0.3 |
| Strain rate parameter, α | 250 | 250 | 250 | 250 | 250 | 250 |
| Strain rate parameter, β | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 |
| Yield stress (MPa) | 525 | 526 | 345 | 248 | 210 | 711 |
| Tangent modulus (MPa) | 127 | 1065 | 1396 | 664 | 691 | 0 |
| Ultimate plastic strain (%) | 19.70 | 11.70 | 14.70 | 22.80 | 44.70 | 6.60 |
| Specimen ID | Py (kN) | Δy (mm) | Pu-FA (kN) | Δc-FA (mm) | Nu-FA (kN) | Formation of Compressive Arch Action in Beams |
|---|---|---|---|---|---|---|
| CON-0 | NY | NY | 204 | 55 | −611 | Yes |
| CON-50 | 164 | 15 | 250 | 75 | −606 | Yes |
| CON-100 | 218 | 20 | 287 | 85 | −602 | Yes |
| S1-DS-A302 | 197 | 15 | 301 | 60 | −601 | Yes |
| S2-DS-A302 | 212 | 14 | 360 | 85 | −525 | Yes |
| S1-DS-A36 | 148 | 9 | 291 | 85 | −604 | Yes |
| S2-DS-A36 | 174 | 10 | 351 | 65 | −525 | Yes |
| S1-DS-EN1.4301 | 198 | 13 | 305 | 60 | −599 | Yes |
| S2-DS-EN1.4301 | 167 | 9 | 360 | 65 | −521 | Yes |
| S2-SS-EN1.4301 | 133 | 7 | 346 | 75 | −514 | Yes |
| Specimen ID | Catenary Action Phase | Ultimate State | εb,u-DIS-MCF (µε) | εb,u-CONT-MCF (µε) | εsp,u-MCF (µε) | εt,u-ECF (µε) | εsp,u-ECF (µε) | Pu (kN) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Development | Pu-CA (kN) | Pu-CA/Pu-FA | Δc-CA (mm) | Nu-FA (kN) | Δu (mm) | Eu (kN.m) | |||||||
| CON-0 | Partial | 297 | 1.46 | 800 | 465 | 845 | 158 | 2023 | - | - | 121,308 | - | 297 |
| CON-50 | Partial | 360 | 1.44 | 975 | 472 | 1055 | 242 | 2087 | 115,945 | - | 119,584 | - | 360 |
| CON-100 | Partial | 433 | 1.51 | 740 | 657 | 890 | 292 | - | 107,709 | - | 120,917 | - | 433 |
| S1-DS-A302 | Partial | 319 | 1.06 | 805 | 488 | 830 | 201 | 1759 | - | 141,669 | 141,960 | - | 319 |
| S2-DS-A302 | Partial | 312 | 0.87 | 685 | 535 | 700 | 195 | 1965 | - | 145,716 | 90,347 | 113,644 | 360 |
| S1-DS-A36 | Partial | 299 | 1.03 | 485 | 467 | 660 | 165 | 1889 | - | 193,607 | 124,557 | - | 299 |
| S2-DS-A36 | Partial | 425 | 1.21 | 570 | 646 | 860 | 243 | 1834 | - | 221,224 | 91,325 | 123,916 | 425 |
| S1-DS-EN1.4301 | Partial | 310 | 1.02 | 540 | 461 | 665 | 167 | 1806 | - | 178,951 | 125,431 | - | 310 |
| S2-DS-EN1.4301 | Partial | 525 | 1.46 | 835 | 642 | 920 | 350 | 1793 | - | 294,855 | 88,987 | 118,359 | 525 |
| S2-SS-EN1.4301 | Partial | 369 | 1.07 | 555 | 525 | 615 | 186 | 2296 | - | 181,095 | 128,763 | 87,998 | 369 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsanadedy, H.M.; Almusallam, T.H.; Abbas, H.; Al-Salloum, Y.A. Innovative Retrofitting for Disaster Resilience: Optimizing Steel Plate Grade and Scheme in RC Non-Seismic Frames to Prevent Progressive Collapse. Buildings 2025, 15, 3325. https://doi.org/10.3390/buildings15183325
Elsanadedy HM, Almusallam TH, Abbas H, Al-Salloum YA. Innovative Retrofitting for Disaster Resilience: Optimizing Steel Plate Grade and Scheme in RC Non-Seismic Frames to Prevent Progressive Collapse. Buildings. 2025; 15(18):3325. https://doi.org/10.3390/buildings15183325
Chicago/Turabian StyleElsanadedy, Hussein M., Tarek H. Almusallam, Husain Abbas, and Yousef A. Al-Salloum. 2025. "Innovative Retrofitting for Disaster Resilience: Optimizing Steel Plate Grade and Scheme in RC Non-Seismic Frames to Prevent Progressive Collapse" Buildings 15, no. 18: 3325. https://doi.org/10.3390/buildings15183325
APA StyleElsanadedy, H. M., Almusallam, T. H., Abbas, H., & Al-Salloum, Y. A. (2025). Innovative Retrofitting for Disaster Resilience: Optimizing Steel Plate Grade and Scheme in RC Non-Seismic Frames to Prevent Progressive Collapse. Buildings, 15(18), 3325. https://doi.org/10.3390/buildings15183325






