Experimental and Numerical Study on the Impact of Multi-Line TBM Tunneling in Fractured Zones on Building Deformation
Abstract
1. Introduction
2. Project Overview
3. Materials and Methods
3.1. Similarity Ratio Design and Stratum Materials
3.2. Model Test Apparatus
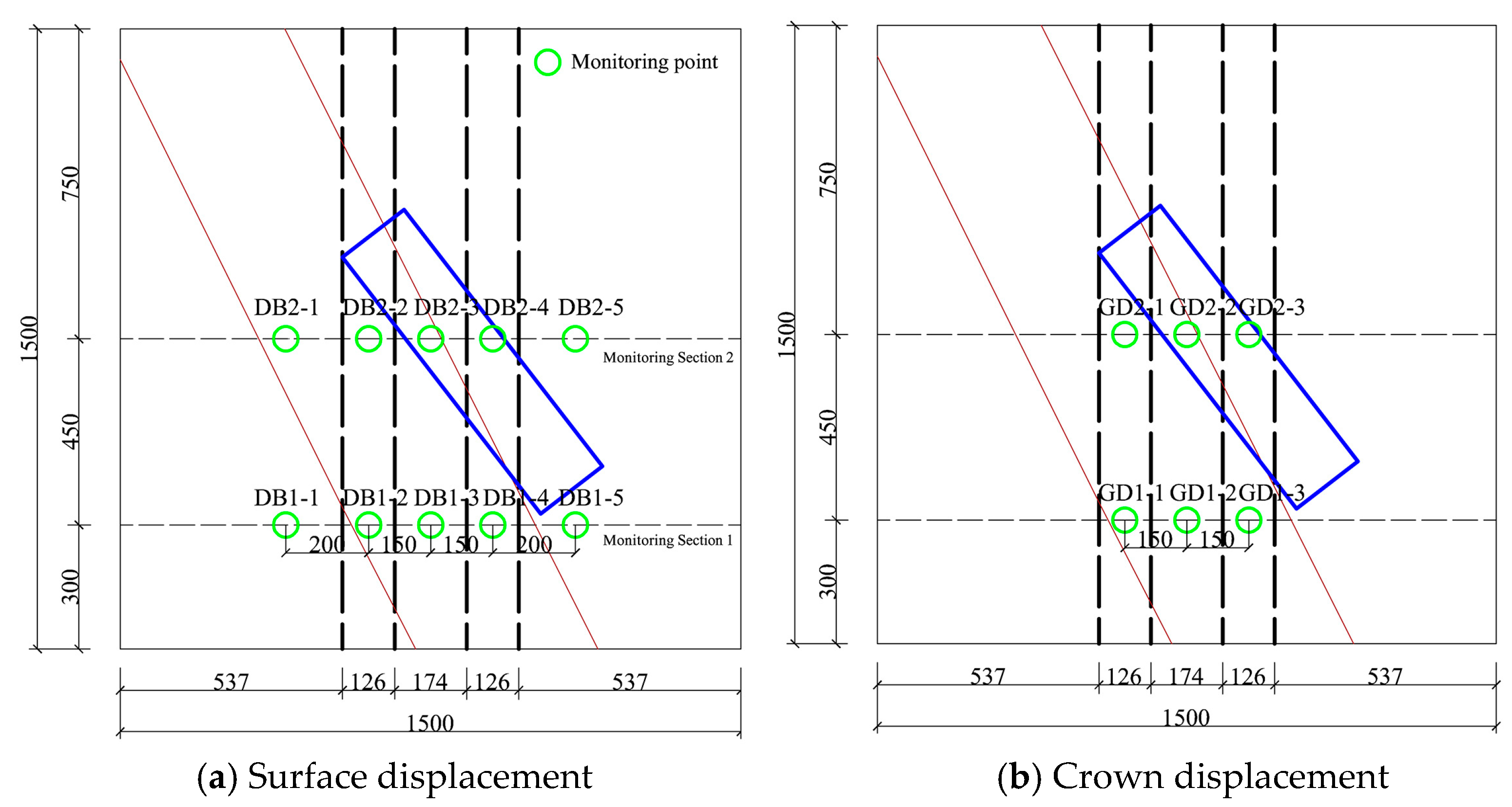
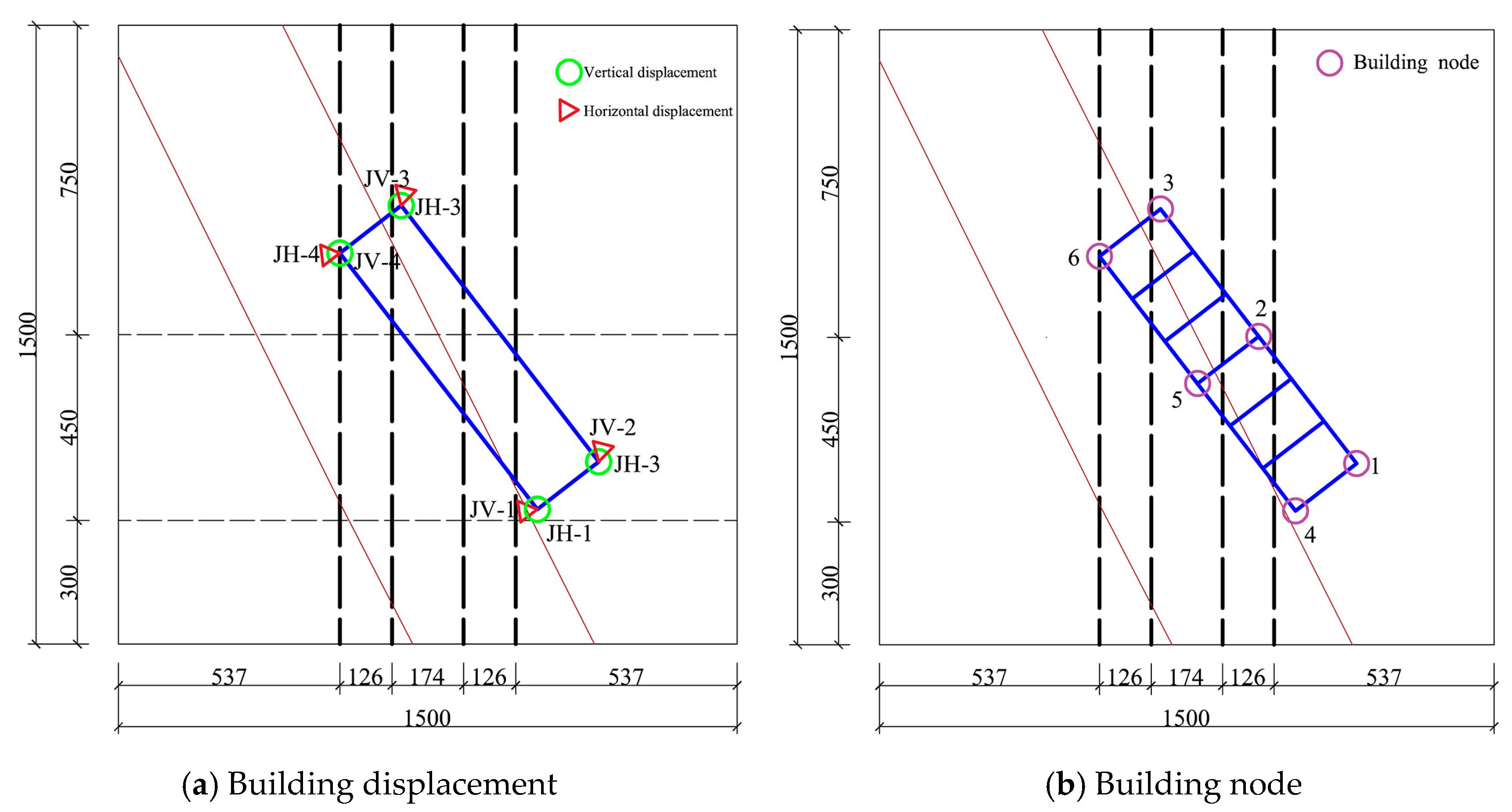
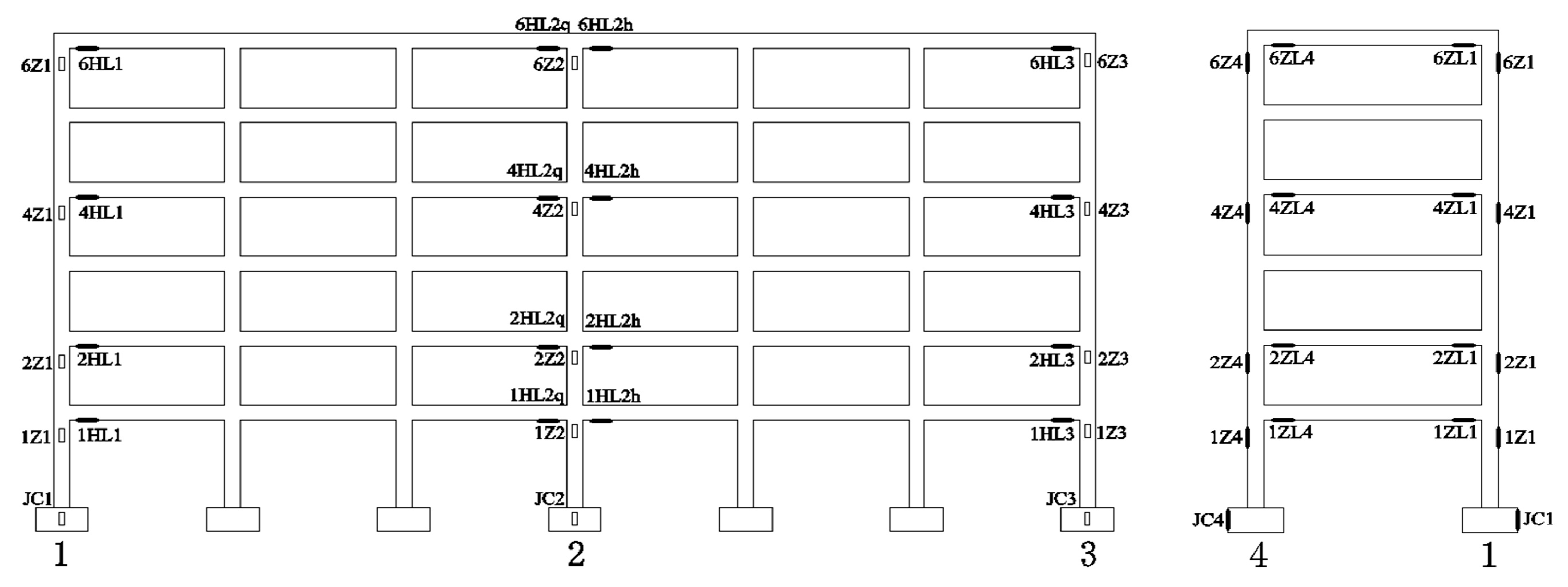
3.3. Model Test Measurement
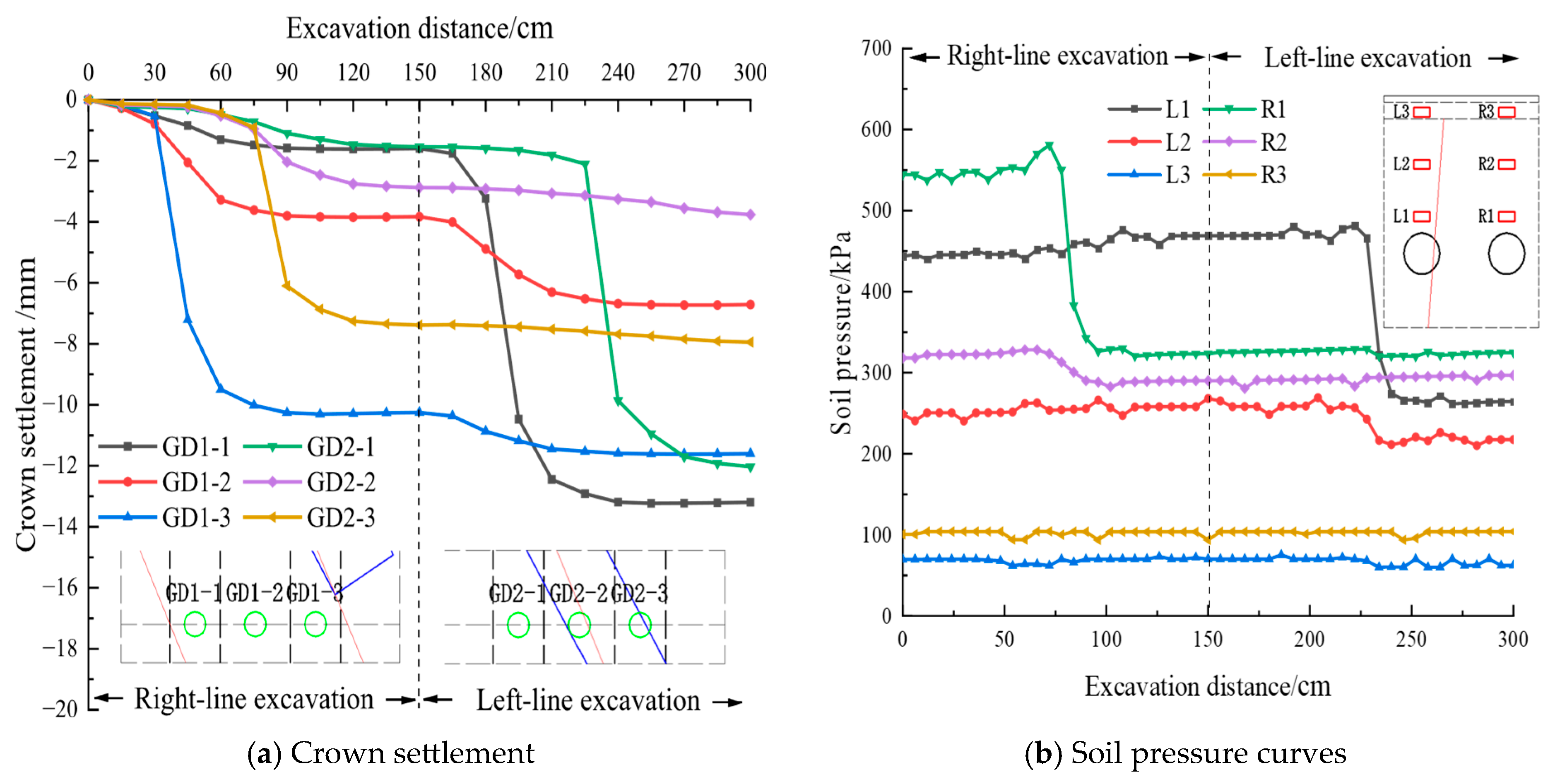
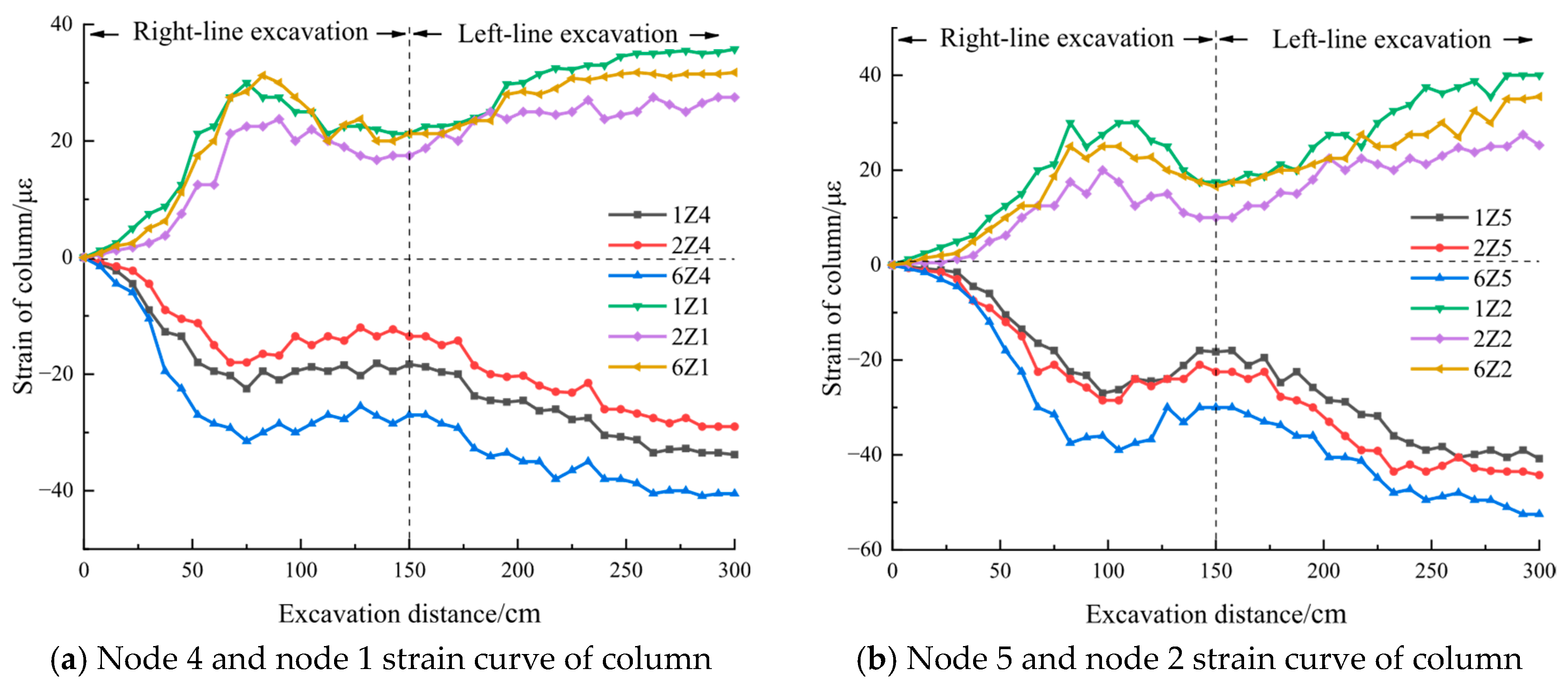
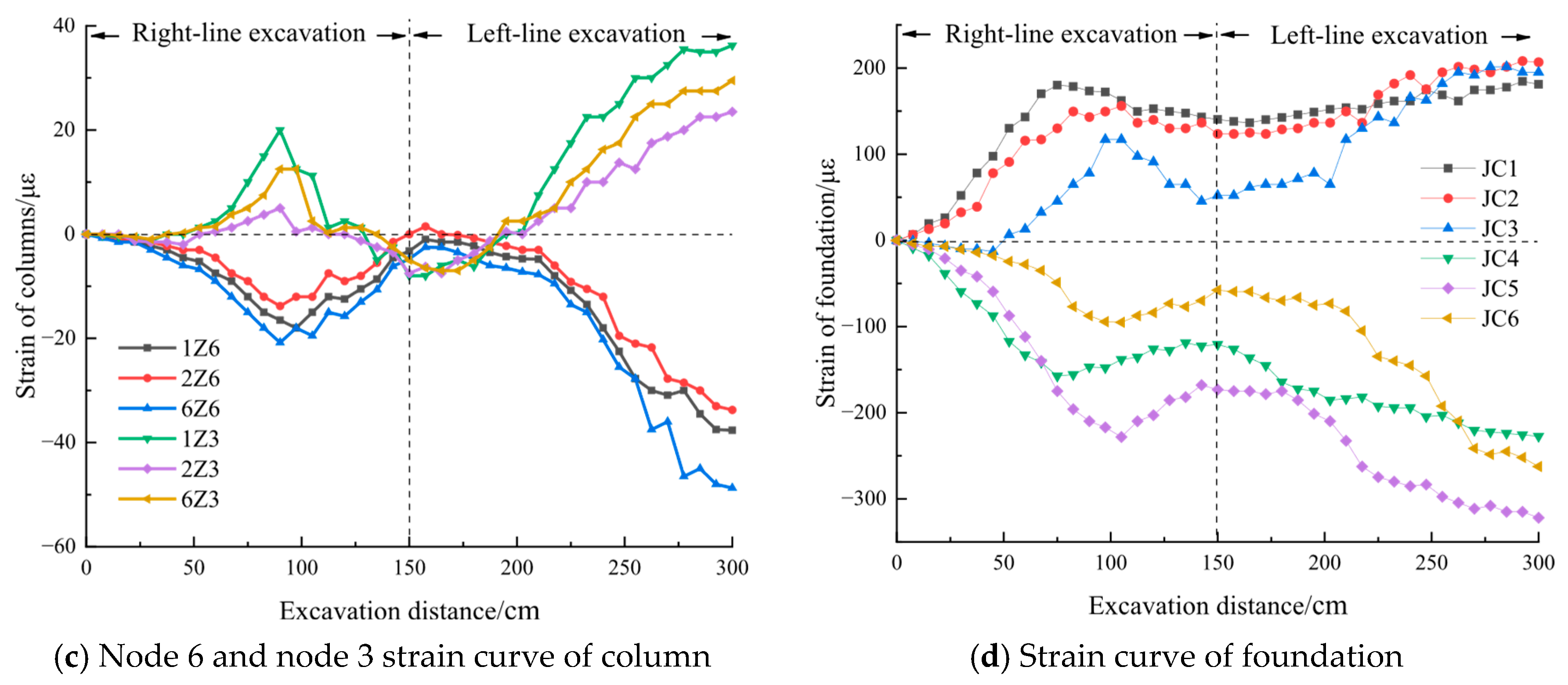
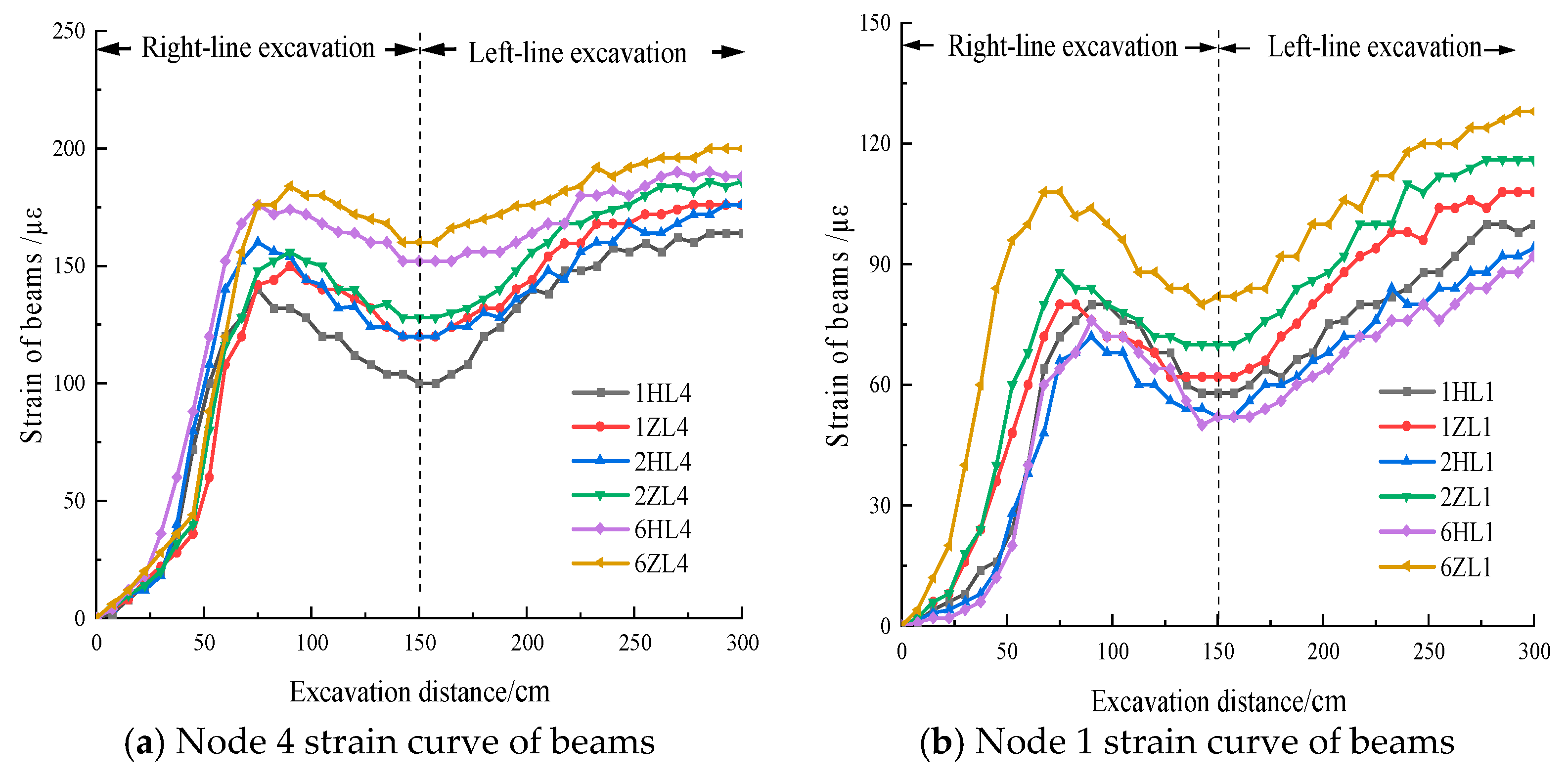
4. Model Test Results
5. Numerical Model
5.1. The Establishment of Numerical Models
5.2. Mesh Generation, Boundary Conditions, and Simulation Steps
- The lining segments, shield, and grouting layer are deactivated. Gravity and boundary conditions are applied, the building is activated, its loads are imposed, and the initial stress equilibrium is established.
- Stress release is simulated using the modulus-softening method. After reducing the elastic modulus by 40%, excavation is performed with the model change technique. During excavation, thrust and jacking pressure are applied at the face, while the cutterhead, front shield, and tail shield are progressively generated.
- When excavation reaches the TBM length, lining segments are installed sequentially, and a grouting pressure of 0.3 MPa is applied between the segments and the tunnel wall.
- After the lining extends 20 rings beyond the tail shield, backfilling is simulated by adjusting the grouting parameters.
- The process is repeated until both tunnels are completed.
5.3. Comparative of Numerical Simulation, Model Test Results, and Monitoring
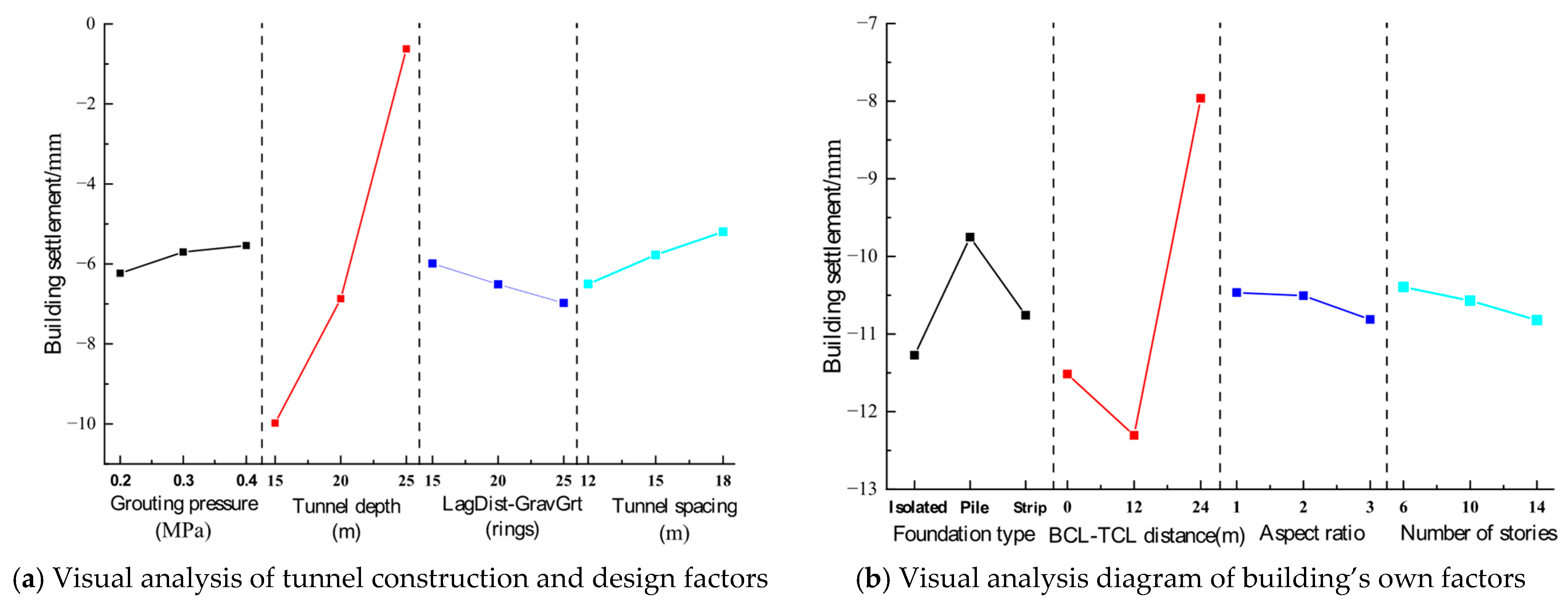
5.4. Sensitivity Analysis
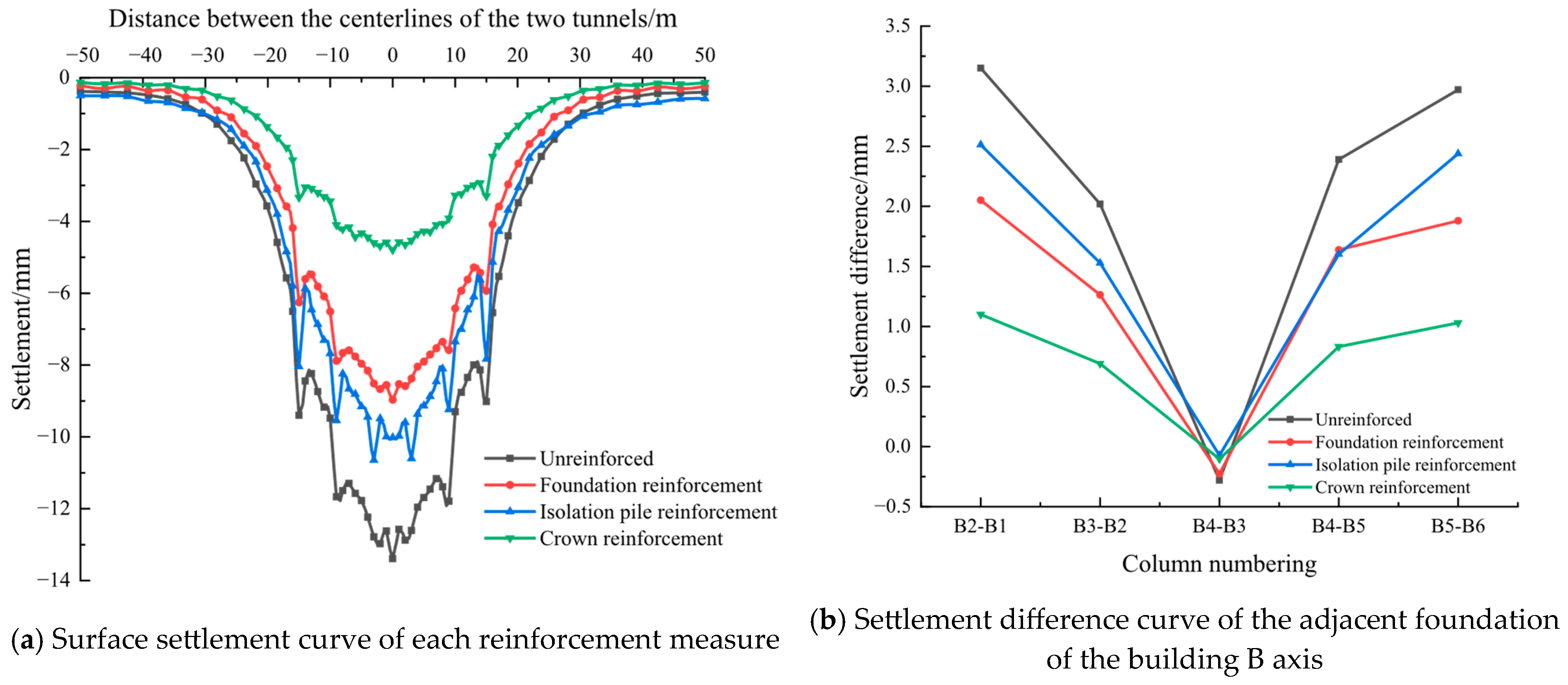
5.5. Deformation Control Measures
- Foundation reinforcement: Foundation-zone grouting with a plan width of 34 m and a thickness of 2 m beneath the foundation was evaluated;
- Crown reinforcement: Tunnel crown grouting beneath the building across 180° of the crown, 3 m thick and 14 m in length was evaluated;
- Sensitivity analysis shows that tunnel depth, grouting pressure, and the relative position between building and tunnel are the dominant factors affecting building settlement, highlighting their importance for risk control and design optimization.
- Isolation reinforcement: An isolation barrier of drilled, grouted piles 1.0 m in diameter at 1.2 m spacing, 25 m long, located 2 m outside the building perimeter was evaluated.
6. Discussion
7. Conclusions
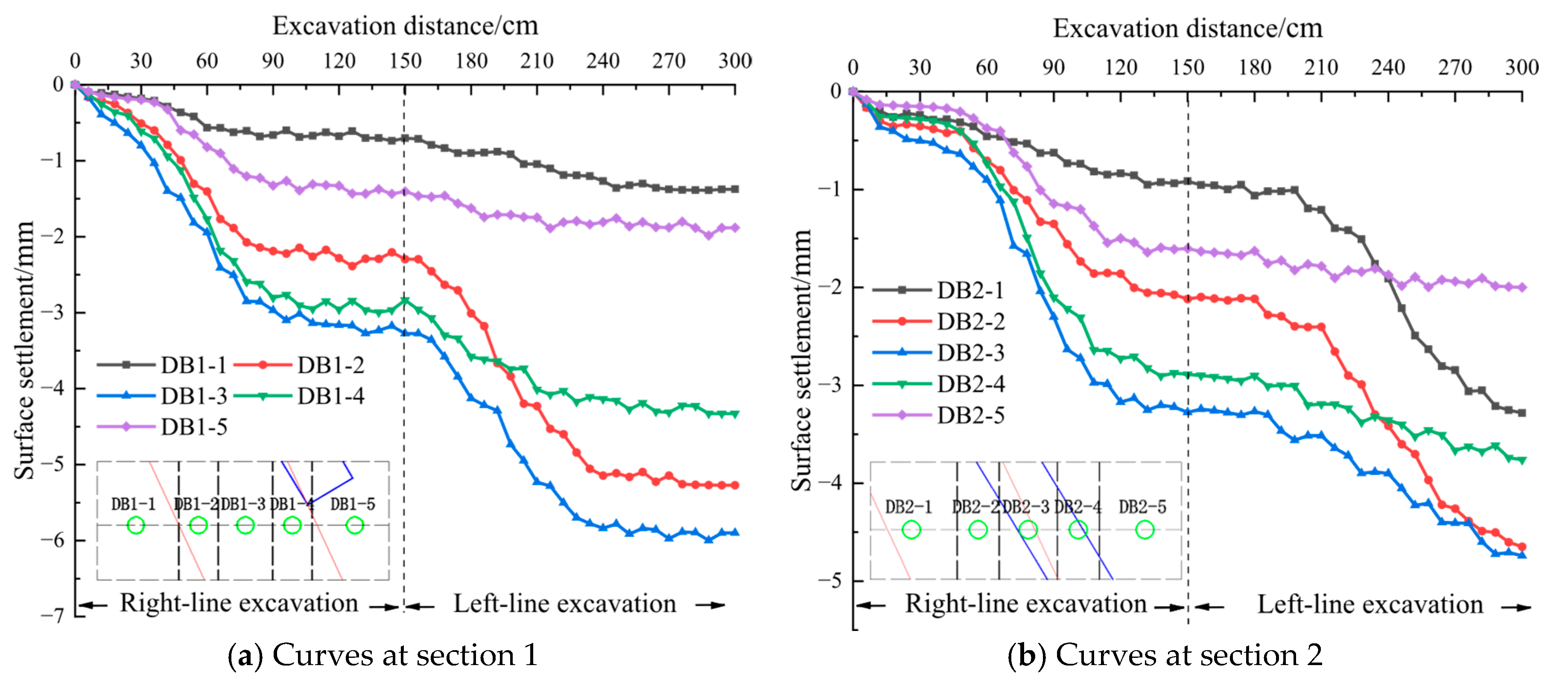
- After TBM excavation, surface settlement is larger in the center and smaller on both sides, with increased settlement closer to the tunnel centers and above the fractured zone. Settlement near the building is also greater. Before reaching the monitoring section, slight settlement occurs, which increases after passing the section. Once excavation exceeds 3.5 times the tunnel diameter, settlement stabilizes. The results show minimal deviation from numerical simulations and field monitoring, with consistent trends across all methods.
- The strain patterns of the building’s frame columns, beams, and foundation align with the settlement patterns. On the fractured zone side, compression occurs at the foundation and outer columns, while tension is observed on the opposite side. Strain values are influenced by factors such as load distribution, fractured zone position, and strata settlement, resulting in complex strain variations in the building’s components.
- Sensitivity analysis shows that the tunnel depth, grouting pressure, and the relative position between the building and tunnel are the dominant factors affecting building settlement, highlighting their importance for risk control and design optimization.
- Reinforcement measures such as grouting beneath the foundation, isolation piles, and crown grouting can all mitigate the structural response to excavation disturbances to varying degrees. Among these, crown grouting is the most effective in controlling settlement magnitude and deformation differences, and is recommended as the preferred method when tunneling directly beneath the building.
Author Contributions
Funding
Data Availability Statements
Acknowledgments
Conflicts of Interest
References
- Akl, S.A.Y.; Kohail, A.; Shazly, M.; Abukiefa, M. Testing and modeling clay behavior subjected to high strain rate loading in a tunneling problem. Ain Shams Eng. J. 2022, 13, 101764. [Google Scholar] [CrossRef]
- Fang, Q.; Du, J.-M.; Li, J.-Y.; Zhang, D.-L.; Cao, L.-Q. Settlement characteristics of large-diameter shield excavation below existing subway in close vicinity. J. Cent. South Univ. 2021, 28, 882–897. [Google Scholar] [CrossRef]
- Fang, Q.; Zhang, D.; Li, Q.; Wong, L.N.Y. Effects of twin tunnels construction beneath existing shield-driven twin tunnels. Tunn. Undergr. Space Technol. 2015, 45, 128–137. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Lin, X.-T.; Chen, R.-P.; Wu, H.-N.; Cheng, H.-Z. Deformation behaviors of existing tunnels caused by shield tunneling undercrossing with oblique angle. Tunn. Undergr. Space Technol. 2019, 89, 78–90. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, H.; Xu, Y.; Li, H. A case study on performances of overlying pipelines due to shallow tunnels excavation in water-rich gravel ground. Ain Shams Eng. J. 2022, 13, 101746. [Google Scholar] [CrossRef]
- Zhao, R.; Zheng, Y.; Guo, Y.; Luan, S.; Zhang, S. Experiments Studying the Instability Process of a Subway Tunnel in Soil–Rock Composite Strata Influenced by Defects. Buildings 2025, 15, 878. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, D.; Fang, Q.; Yu, L. Movements of ground and existing structures induced by slurry pressure-balance tunnel boring machine (SPB TBM) tunnelling in clay. Tunn. Undergr. Space Technol. 2020, 97, 103278. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, W.; Wu, S.; Wu, P.; Xu, S.; Yao, Z.; Sun, J. Research on Strata Deformation Induced by EPB Tunneling in Round Gravel Stratum and Its Control Technology. Appl. Sci. 2022, 12, 10553. [Google Scholar] [CrossRef]
- Lin, Q.; Lu, D.; Lei, C.; Tian, Y.; Gong, Q.; Du, X. Model test study on the stability of cobble strata during shield under-crossing. Tunn. Undergr. Space Technol. 2021, 110, 103807. [Google Scholar] [CrossRef]
- Gue, C.Y.; Wilcock, M.J.; Alhaddad, M.M.; Elshafie, M.Z.E.B.; Soga, K.; Mair, R.J. Tunnelling close beneath an existing tunnel in clay—Perpendicular undercrossing. Geotechnique 2017, 67, 795–807. [Google Scholar] [CrossRef]
- Islam, M.S.; Iskander, M. Twin tunnelling induced ground settlements: A review. Tunn. Undergr. Space Technol. 2021, 110, 103614. [Google Scholar] [CrossRef]
- Junjie, J.; Wenhao, S.; Yuan, W. A risk assessment approach for road collapse along tunnels based on an improved entropy weight method and K-means cluster algorithm. Ain Shams Eng. J. 2024, 15, 102805. [Google Scholar] [CrossRef]
- Junwei, Z.; Xutao, Z.; Yang, T. Analytical solution for deep pressure tunnels using composite stratum under a groundwater table. Ain Shams Eng. J. 2021, 12, 1419–1434. [Google Scholar] [CrossRef]
- Franzius, J.N.; Potts, D.M.; Addenbrooke, T.I.; Burland, J.B. The influence of building weight on tunnelling-induced ground and building deformation. Soils Found. 2004, 45, 166–167. [Google Scholar] [CrossRef][Green Version]
- Verruijt, A.; Booker, J.R. Surface settlements due to deformation of a tunnel in an elastic half plane. Géotechnique 1996, 46, 753–756. [Google Scholar] [CrossRef]
- Potts, D.M.; Addenbrooke, T.I. A Structure’s Influence on Tunnelling-Induced Ground Movements. Proc. Inst. Civ. Eng. Geotech. Eng. 1997, 125, 109–125. [Google Scholar] [CrossRef]
- Pinto, F.; Whittle, A.J. Ground Movements due to Shallow Tunnels in Soft Ground. I: Analytical Solutions. J. Geotech. Geoenviron. Eng. 2014, 140, 04013040. [Google Scholar] [CrossRef]
- Karakus, M. Appraising the methods accounting for 3D tunnelling effects in 2D plane strain FE analysis. Tunn. Undergr. Space Technol. 2007, 22, 47–56. [Google Scholar] [CrossRef]
- Bayati, M.; Khademi Hamidi, J. A case study on TBM tunnelling in fault zones and lessons learned from ground improvement. Tunn. Undergr. Space Technol. 2017, 63, 162–170. [Google Scholar] [CrossRef]
- Anato, N.J.; Chen, J.; Tang, A.; Assogba, O.C. Numerical Investigation of Ground Settlements Induced by the Construction of Nanjing WeiSanLu Tunnel and Parametric Analysis. Arab. J. Sci. Eng. 2021, 46, 11223–11239. [Google Scholar] [CrossRef]
- Hou, M.; Yang, C.; Yang, J.; Zeng, Y.; Zhu, Z. Analysis the Mechanical Response of Tunnels Under the Action of Vertical Jacking in Shield Construction and Research on Reinforcement. Buildings 2025, 15, 2321. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, J.; Wang, Z.; Liu, C. Model Test on the Collapse Evolution Law of Tunnel Excavation in Composite Strata with a Cavity. Buildings 2024, 14, 932. [Google Scholar] [CrossRef]
- Fang, Q.; Liu, X.; Zeng, K.; Zhang, X.; Zhou, M.; Du, J. Centrifuge modelling of tunnelling below existing twin tunnels with different types of support. Undergr. Space 2022, 7, 1125–1138. [Google Scholar] [CrossRef]
- Kim, S.; Burd, H.; Milligan, G. Model testing of closely spaced tunnels in clay. Geotechnique 1998, 48, 375–388. [Google Scholar] [CrossRef]
- Chenjie, L.I.; Bo, L.I.; Congan, L.I.; Zhipeng, W. Centrifuge Model Test of the Influence of Tunnel Excavation with Different Spacings on Existing Tunnels. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2024. [Google Scholar]
- Boonyarak, T.; Ng, C.W.W. Three-dimensional influence zone of new tunnel excavation crossing underneath existing tunnel. Jpn. Geotech. Soc. Spec. Publ. 2016, 2, 1513–1518. [Google Scholar] [CrossRef]
- Lu, H.; Shi, J.; Wang, Y.; Wang, R. Centrifuge modeling of tunneling-induced ground surface settlement in sand. Undergr. Space 2019, 4, 302–309. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Wei, J.; Li, X.; Lu, P. Centrifugal model test of group tunneling with small spacing beneath existing tunnels. Chin. J. Geotech. Eng. 2018, 40, 1507–1514. [Google Scholar] [CrossRef]
- Jiang, B.; Chen, L.; Yang, J.S.; Wang, S.; Ng, C.W.W. Effects of twin-tunnel excavation on an existing horseshoe-shaped tunnel considering the influence of a settlement joint. Can. Geotech. J. 2017, 54, 1346–1355. [Google Scholar] [CrossRef]
- Mair, R.J. Centrifuge Modelling of Tunnel Construction in Soft Clay. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1979. [Google Scholar]
- Lee, C.J.; Wu, B.R.; Chen, H.T.; Chiang, K.H. Tunnel stability and arching effects during tunneling in soft clayey soil. Tunn. Undergr. Space Technol. 2006, 21, 119–132. [Google Scholar] [CrossRef]
- Jacobsz, S.W.; Standing, J.R.; Mair, R.J.; Hagiwara, T.; Sugiyama, T. Centrifuge modelling of tunnelling near driven piles. J. Jpn. Geotech. Soc. 2004, 44, 49–56. [Google Scholar] [CrossRef]
- Idinger, G.; Aklik, P.; Wu, W.; Borja, R.I. Centrifuge model test on the face stability of shallow tunnel. Acta Geotech. 2011, 6, 105–117. [Google Scholar] [CrossRef]
- Li, P.; Du, S.-J.; Ma, X.-F.; Yin, Z.-Y.; Shen, S.-L. Centrifuge investigation into the effect of new shield tunnelling on an existing underlying large-diameter tunnel. Tunn. Undergr. Space Technol. 2014, 42, 59–66. [Google Scholar] [CrossRef]
- Fu, J.; Yu, Z.; Wang, S.; Yang, J. Numerical analysis of framed building response to tunnelling induced ground movements. Eng. Struct. 2018, 158, 43–66. [Google Scholar] [CrossRef]
- Ayasrah, M.; Qiu, H.; Zhang, X. Influence of Cairo Metro Tunnel Excavation on Pile Deep Foundation of the Adjacent Underground Structures: Numerical Study. Symmetry 2021, 13, 426. [Google Scholar] [CrossRef]
- Soomro, M.A.; Hong, Y.; Ng, C.W.W.; Lu, H.; Peng, S. Load transfer mechanism in pile group due to single tunnel advancement in stiff clay. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2015, 45, 63–72. [Google Scholar] [CrossRef]
- Simic-Silva, P.-T.; Martínez-Bacas, B.; Galindo-Aires, R.; Simic, D. 3D simulation for tunnelling effects on existing piles—ScienceDirect. Comput. Geotech. 2020, 124, 103625. [Google Scholar] [CrossRef]
- Burland, J.; Potts, D.; Franzius, J. The response of surface structures to tunnel construction. Proc. Inst. Civ. Eng. Geotech. Eng. 2006, 159, 3–17. [Google Scholar] [CrossRef]
- Mroueh, H.; Shahrour, I. A full 3-D finite element analysis of tunneling–adjacent structures interaction. Comput. Geotech. 2003, 30, 245–253. [Google Scholar] [CrossRef]
- Lee, G.T.K.; Ng, C.W.W. Effects of Advancing Open Face Tunneling on an Existing Loaded Pile. J. Geotech. Geoenviron. Eng. 2005, 131, 193–201. [Google Scholar] [CrossRef]
- Mroueh, H.; Shahrour, I. Three-dimensional finite element analysis of the interaction between tunneling and pile foundations. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 217–230. [Google Scholar] [CrossRef]
- Basile, F. Effects of tunnelling on pile foundations. Soils Found. 2014, 54, 280–295. [Google Scholar] [CrossRef]
- Fan, Y.; Cai, J.; Wang, J. An Analytical Method Evaluating the Evolution of Group Effect for Vertically Loaded Pile Groups Subjected to Tunnel Excavation. Appl. Sci. 2023, 13, 517. [Google Scholar] [CrossRef]
- Chapman, D.; Ahn, S.; Hunt, D.; Chan, A. The use of model tests to investigate the ground displacement associated with multiple tunnel construction in soil. Tunn. Undergr. Space Technol. 2006, 21, 413. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, X.; De Corte, W.; Taerwe, L. Numerical Simulation on the Leakage-Induced Collapse of Segmental Tunnels. Appl. Sci. 2024, 14, 3796. [Google Scholar] [CrossRef]
- Taylor, R.N. Geotechnical Centrifuge Technology; CRC Press: London, UK, 1994; Volume 1, p. 296. [Google Scholar]
- Han, X.; Standing, J.R.; Li, N. Analysis of tunnelling induced twist defomm ation of buildings. China Civ. Eng. J. 2010, 43, 82–88. [Google Scholar] [CrossRef]
- Peck, R.B. Deep excavations and tunnelling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 1969; Sociedad Mexicana de Mecanica de Suelos: Mexico City, Mexico, 1969. [Google Scholar]
- Loganathan, N.; Poulos, H.G. Analytical Prediction for Tunneling-Induced Ground Movements in Clays. J. Geotech. Geoenviron. Eng. 1998, 124, 846–856. [Google Scholar] [CrossRef]
- Zhang, K.; Chavez Torres, J.L.; Zang, Z. Numerical Analysis of Pipelines Settlement Induced by Tunneling. Adv. Civ. Eng. 2019, 2019, 13. [Google Scholar] [CrossRef]
- Chiang, K.-H.; Lee, C.-J. Responses of single piles to tunneling-induced soil movements in sandy ground. Can. Geotech. J. 2007, 44, 1224–1241. [Google Scholar] [CrossRef]
- Schlicke, M.; Wannenmacher, H.; Nübel, K. Advancing TBM Performance: Integrating Shield Friction Analysis and Machine Learning in Geotechnical Engineering. Geotechnics 2024, 4, 194–208. [Google Scholar] [CrossRef]




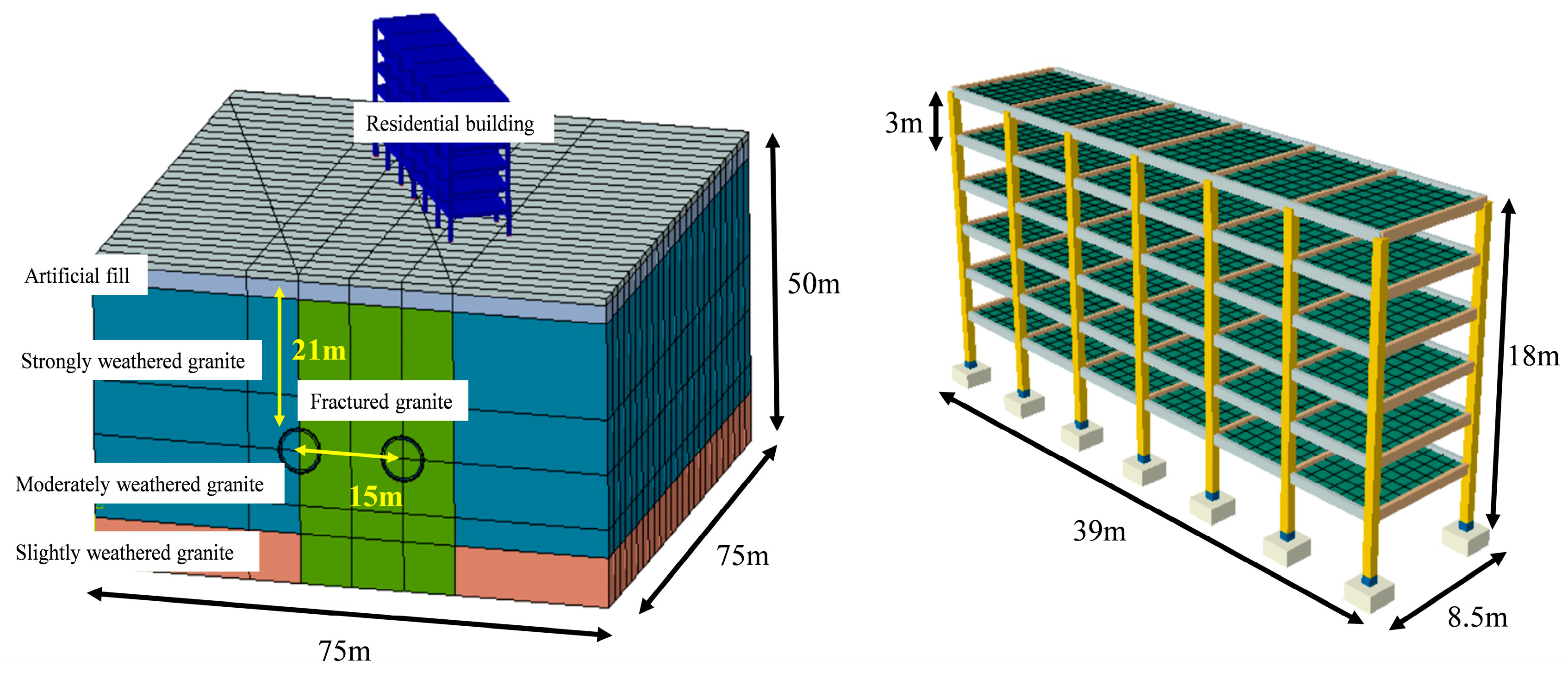


| Physical Quantity | Similarity Coefficient | Similarity Constant |
|---|---|---|
| Geometry l | Cl | 50 |
| Cohesion c | Cc | 50 |
| Elastic modulus E | CE | 50 |
| Unit weight γ | Cγ | 1 |
| Poisson’s ratio μ | Cμ | 1 |
| Internal friction angle φ | Cφ = 1 | 1 |
| Strain ε | Cε = 1 | 1 |
| Displacement u | Cu = Cl | 50 |
| Stress σ | Cσ = Cc | 50 |
| Materials | Strongly Weathered Granite | Moderately Weathered Granite | Slightly Weathered Granite | Fractured Granite |
|---|---|---|---|---|
| Quartz sand–iron powder–barite powder | 1:0.63:0.94 | 1:1.04:1.56 | 1:1:1 | 1:1.05:2.45 |
| Rosin/(rosin + alcohol) | 0.02 | 0.1 | 0.14 | 0.06 |
| Monitoring Point | |Mean| (mm) | |Standard Deviation| (mm) | |95% Confidence Interval| (mm) |
|---|---|---|---|
| DB1-1 | 2.995 | 1.727 | 0.195 |
| DB1-2 | 2.250 | 1.323 | 0.150 |
| DB1-3 | 2.682 | 1.541 | 0.174 |
| DB1-4 | 1.780 | 1.053 | 0.119 |
| DB1-5 | 1.484 | 0.859 | 0.097 |
| DB2-1 | 2.238 | 1.303 | 0.147 |
| DB2-2 | 2.699 | 1.567 | 0.177 |
| DB2-3 | 2.548 | 1.487 | 0.168 |
| DB2-4 | 2.088 | 1.226 | 0.139 |
| DB2-5 | 1.950 | 1.139 | 0.129 |
| Monitoring Point | |Mean| (mm) | |Standard Deviation| (mm) | |95% Confidence Interval| (mm) |
|---|---|---|---|
| GD1-1 | 4.917 | 3.611 | 13.042 |
| GD1-2 | 2.783 | 1.934 | 3.742 |
| GD1-3 | 1.867 | 1.299 | 1.687 |
| GD2-1 | 4.667 | 2.823 | 7.967 |
| GD2-2 | 3.017 | 1.84 | 3.386 |
| GD2-3 | 2.033 | 1.178 | 1.387 |
| Monitoring Point | |Mean| (kPa) | |Standard Deviation| (kPa) | |95% Confidence Interval| (kPa) |
|---|---|---|---|
| L1 | 420 | 92.646 | 8583.333 |
| L2 | 247.3 | 12.798 | 163.789 |
| L3 | 64.8 | 4.367 | 19.067 |
| R1 | 476 | 126.618 | 16,032.22 |
| R2 | 291.5 | 28.438 | 808.722 |
| R3 | 97.5 | 3.028 | 9.167 |
| Monitoring Point | Settlement Values (mm) | |||
|---|---|---|---|---|
| Excavation of the Right Tunnel: 75 cm | Completion of the Right Tunnel Excavation | Excavation of the Left Tunnel: 75 cm | Completion of the Left Tunnel Excavation | |
| JV1 | 2.79 | 3.30 | 4.24 | 4.41 |
| JV2 | 1.77 | 2.30 | 2.80 | 2.92 |
| JV3 | 0.38 | 1.95 | 2.20 | 4.89 |
| JV4 | 0.48 | 1.66 | 1.95 | 5.09 |
| Maximum | 2.79 | 3.30 | 4.24 | 5.09 |
| Minimum | 0.38 | 1.66 | 1.95 | 2.92 |
| Mean | 1.36 | 2.30 | 2.80 | 4.33 |
| Standard deviation | 1.05 | 0.66 | 0.97 | 1.04 |
| Excavation Distance | Settlement Difference (mm) | Distortion Value (mm−1) | |||
|---|---|---|---|---|---|
| S2—S1 | S3—S4 | S4—S1 | S3—S2 | ||
| Excavation of the right tunnel: 75 cm | −1.02 | −0.10 | −2.31 | −1.39 | −6.938 × 10−6 |
| Completion of the right tunnel excavation | −1.00 | 0.29 | −1.64 | −0.35 | −9.729 × 10−6 |
| Excavation of the left tunnel: 75 cm | −1.44 | 0.25 | −2.29 | −0.60 | −12.745 × 10−6 |
| Completion of the left tunnel excavation | −1.49 | −0.20 | 0.68 | 1.97 | −9.729 × 10−6 |
| |Maximum| | 1.49 | 0.29 | 2.31 | 1.97 | 12.745 × 10−6 |
| |Minimum| | 1.00 | 0.10 | 0.68 | 0.35 | 6.938 × 10−6 |
| |Mean| | 1.24 | 0.21 | 1.73 | 1.08 | 9.785 × 10−6 |
| |Standard deviation| | 0.23 | 0.16 | 0.72 | 0.93 | 2.500 × 10−6 |
| Monitoring Point | |Mean| (μs) | |Standard Deviation| (μs) | |95% Confidence Interval| (μs) |
|---|---|---|---|
| JC1 | 129 | 61.183 | 3743.333 |
| JC2 | 135 | 72.457 | 5250.000 |
| JC3 | 92 | 46.857 | 2195.556 |
| JC4 | 90 | 60.553 | 3666.667 |
| JC5 | 120 | 73.786 | 5444.444 |
| JC6 | 76.5 | 53.751 | 2889.167 |
| Node Number | Monitoring Point | |Mean| (μs) | |Standard Deviation| (μs) | |95% Confidence Interval| (μs) |
|---|---|---|---|---|
| Node 4 | 1HL-4 | 116.667 | 61.033 | 3725 |
| 1ZL-4 | 124.444 | 62.322 | 3884.028 | |
| 2HL-4 | 132.222 | 63.792 | 4069.444 | |
| 2ZL-4 | 139.444 | 65.069 | 4234.028 | |
| 6HL-4 | 148.333 | 67.777 | 4593.75 | |
| 6ZL-4 | 156.111 | 69.632 | 4848.611 | |
| Node 1 | 1HL-1 | 6.222 | 3.492 | 12.194 |
| 1ZL-1 | 7.111 | 3.723 | 13.861 | |
| 2HL-1 | 8.141 | 3.969 | 15.75 | |
| 2ZL-1 | 8.889 | 4.226 | 17.861 | |
| 6HL-1 | 9.778 | 4.494 | 20.194 | |
| 6ZL-1 | 10.667 | 4.77 | 22.75 |
| Category | γ (kN/m3) | E (MPa) | c kPa | φ (°) | μ | Element Type |
|---|---|---|---|---|---|---|
| Artificial fill | 18.5 | 8.5 | 10 | 12 | 0.4 | 3D solid |
| Strongly weathered granite | 25 | 150 | 200 | 32 | 0.35 | |
| Moderately weathered granite | 25.7 | 5000 | 800 | 40 | 0.28 | |
| Fractured zone | 24.5 | 500 | 300 | 35 | 0.33 | |
| Slightly weathered granite | 25.8 | 10,000 | 1500 | 47.5 | 0.25 | |
| Shield | 78.5 | 210,000 | - | - | 0.3 | |
| Segment | 25 | 34,500 | - | - | 0.2 | |
| Backfill layer (ungrouted) | 18 | 200 | - | - | 0.4 | |
| Backfill layer (grouted) | 24 | 1000 | - | - | 0.3 | |
| Beam, column | 25 | 30,000 | - | - | 0.2 | Beam |
| Plate | 25 | 30,000 | - | - | 0.2 | Shell |
| Foundation | 25 | 31,500 | - | - | 0.2 | Beam |
| Series | Sim-Field Error % (R) | Sim-Field Error % (L) | Test-Field Error % (R) | Test-Field Error % (L) |
|---|---|---|---|---|
| DB | 18.559 | 17.259 | 19.438 | 24.777 |
| GD | 21.005 | 25.329 | 20.247 | 19.007 |
| JV | 16.356 | 23.945 | 24.581 | 28.133 |
| JH | 20.114 | 20.947 | 22.441 | 25.425 |
| Number | Grouting Pressure (MPa) | Tunnel Depth (m) | Lag Distance of Gravel Grouting (Rings) | Tunnel Spacing (m) |
|---|---|---|---|---|
| 1 | 0.2 | 15 | 15 | 12 |
| 2 | 0.2 | 20 | 25 | 15 |
| 3 | 0.2 | 25 | 20 | 18 |
| 4 | 0.3 | 15 | 25 | 18 |
| 5 | 0.3 | 20 | 20 | 12 |
| 6 | 0.3 | 25 | 15 | 15 |
| 7 | 0.4 | 15 | 20 | 15 |
| 8 | 0.4 | 20 | 15 | 18 |
| 9 | 0.4 | 25 | 25 | 12 |
| Number | Foundation Type | Distance Between the Building Centerline and Tunnel Centerline (m) | Building Aspect Ratio | Number of Stories |
|---|---|---|---|---|
| a | Isolated | 0 | 1 | 6 |
| b | Isolated | 12 | 3 | 10 |
| c | Isolated | 24 | 2 | 14 |
| d | Pile | 0 | 3 | 14 |
| e | Pile | 12 | 2 | 6 |
| f | Pile | 24 | 1 | 10 |
| g | Strip | 0 | 2 | 10 |
| h | Strip | 12 | 1 | 14 |
| i | Strip | 24 | 3 | 6 |
| Number of Level Groups | Grouting Pressure (MPa) | Tunnel Depth (m) | Lag Distance of Gravel Grouting (Rings) | Tunnel Spacing (m) |
|---|---|---|---|---|
| 1 | 6.23 | 9.98 | 5.99 | 6.50 |
| 2 | 5.70 | 6.87 | 6.51 | 5.78 |
| 3 | 5.54 | 0.63 | 6.98 | 5.20 |
| Range R | 0.69 | 9.35 | 0.99 | 1.31 |
| Number of Level Groups | Foundation Type | Distance Between the Building Centerline and Tunnel Centerline (m) | Building Aspect Ratio | Number of Stories |
|---|---|---|---|---|
| 1 | 11.27 | 11.52 | 10.47 | 10.39 |
| 2 | 9.75 | 12.31 | 10.51 | 10.57 |
| 3 | 10.76 | 7.96 | 10.81 | 10.82 |
| Range R | 1.52 | 4.34 | 0.35 | 0.43 |
| Type | γ (kN/m3) | E (MPa) | μ | c (kPa) | φ (°) |
|---|---|---|---|---|---|
| Foundation reinforcement | 25 | 170 | 0.32 | 200 | 37 |
| Crown reinforcement | 26 | 300 | 0.27 | 400 | 42 |
| Isolation reinforcement | 25 | 31,500 | 0.2 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Hao, R.; Zhang, T.; Huang, D.; Xiong, Z. Experimental and Numerical Study on the Impact of Multi-Line TBM Tunneling in Fractured Zones on Building Deformation. Buildings 2025, 15, 3322. https://doi.org/10.3390/buildings15183322
Wu Y, Hao R, Zhang T, Huang D, Xiong Z. Experimental and Numerical Study on the Impact of Multi-Line TBM Tunneling in Fractured Zones on Building Deformation. Buildings. 2025; 15(18):3322. https://doi.org/10.3390/buildings15183322
Chicago/Turabian StyleWu, Yankai, Runmin Hao, Tong Zhang, Daokuan Huang, and Zaiyong Xiong. 2025. "Experimental and Numerical Study on the Impact of Multi-Line TBM Tunneling in Fractured Zones on Building Deformation" Buildings 15, no. 18: 3322. https://doi.org/10.3390/buildings15183322
APA StyleWu, Y., Hao, R., Zhang, T., Huang, D., & Xiong, Z. (2025). Experimental and Numerical Study on the Impact of Multi-Line TBM Tunneling in Fractured Zones on Building Deformation. Buildings, 15(18), 3322. https://doi.org/10.3390/buildings15183322






