Effects of Near-Fault Vertical Ground Motion on Seismic Response and Damage in High-Speed Railway Isolated Track–Bridge Systems
Abstract
1. Introduction
2. The Structural Dynamic Analysis Model
2.1. Simulation of HSR Track–Bridge System
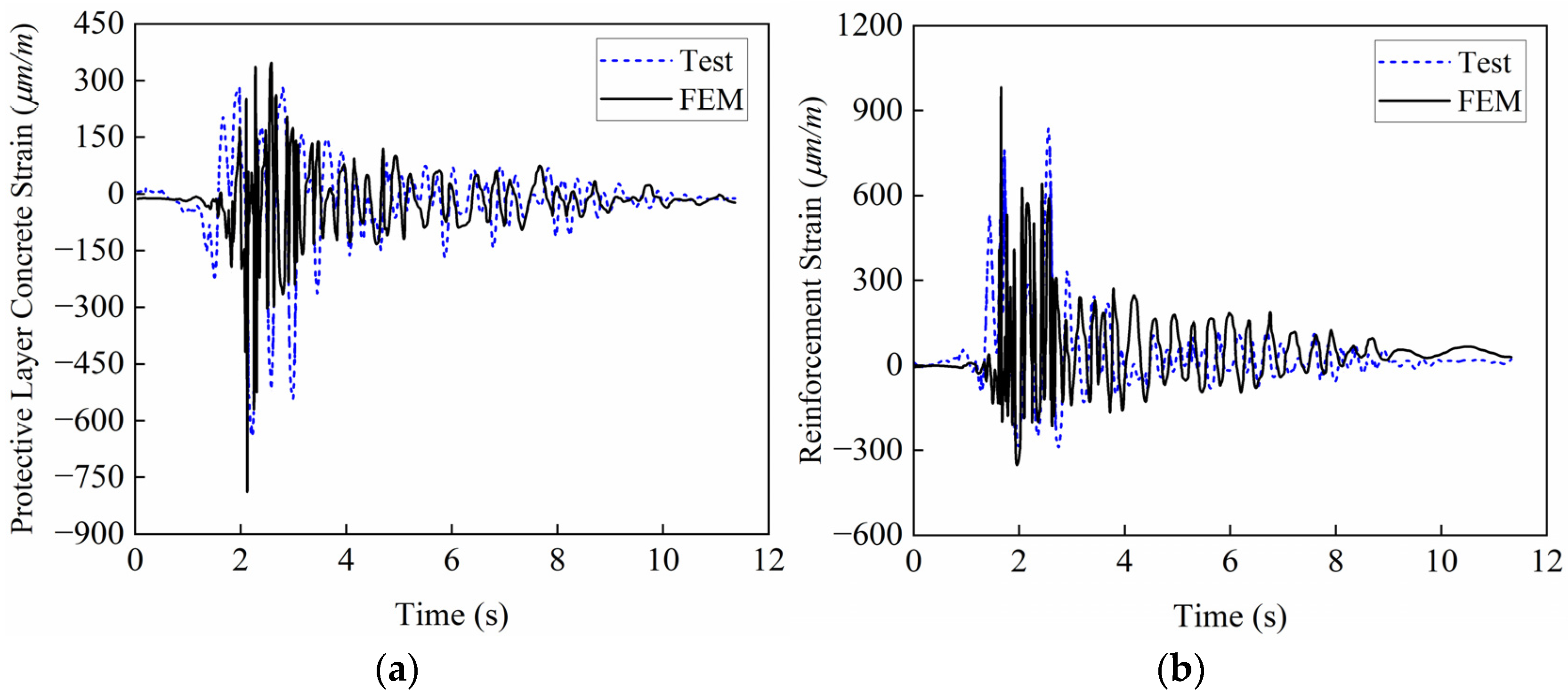
2.2. Verification of Finite Element Model
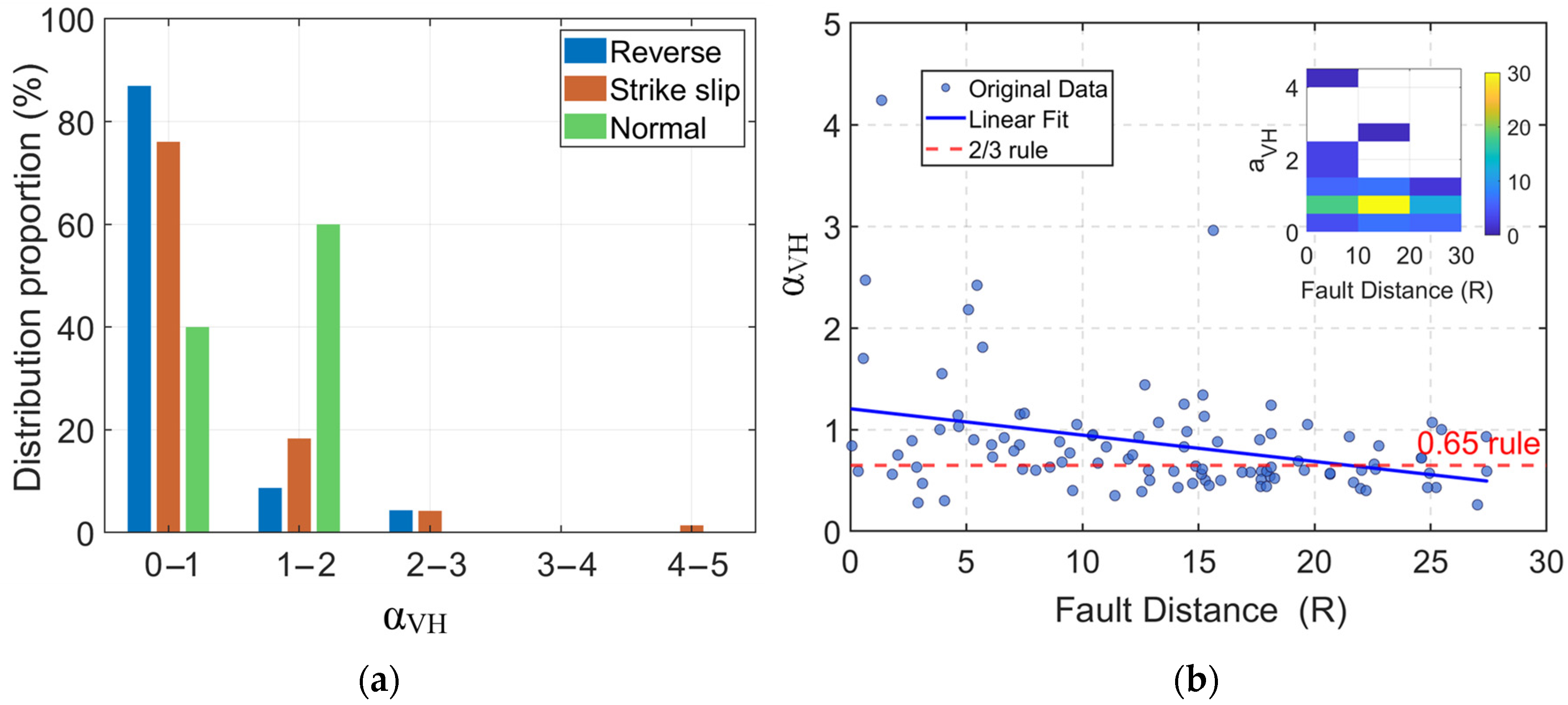
2.3. Near-Fault Ground Motions and Distribution of αVH
3. Influence of Near-Fault VGM on the Longitudinal Responses of Components
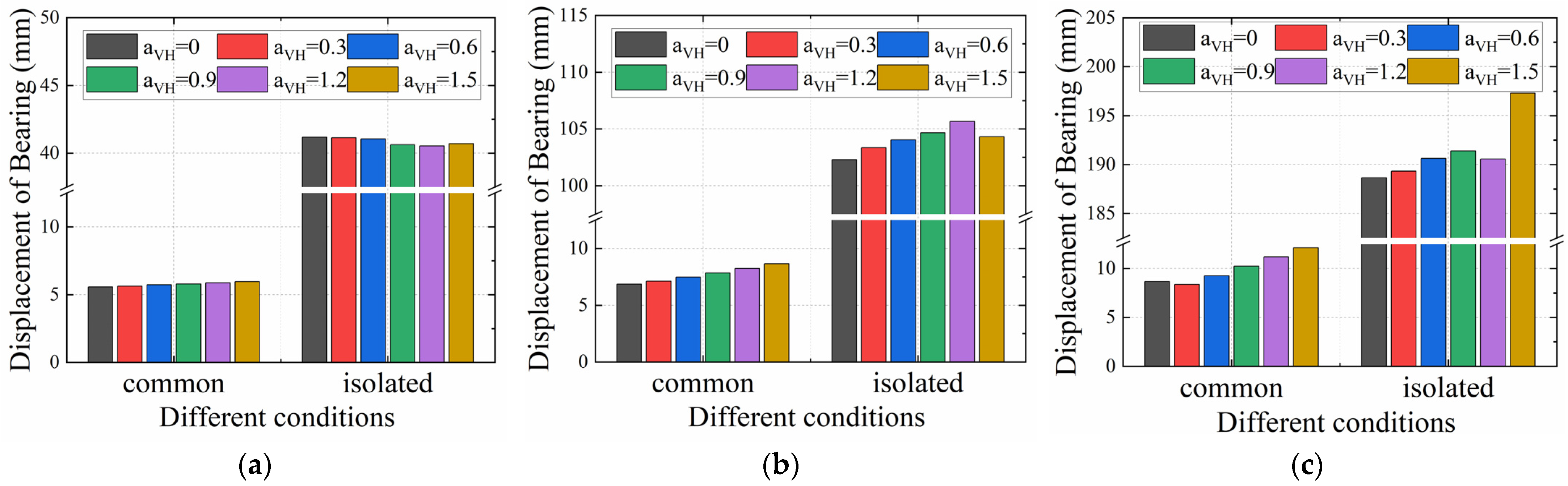
3.1. Impact on the Seismic Performance of Bearings and Piers
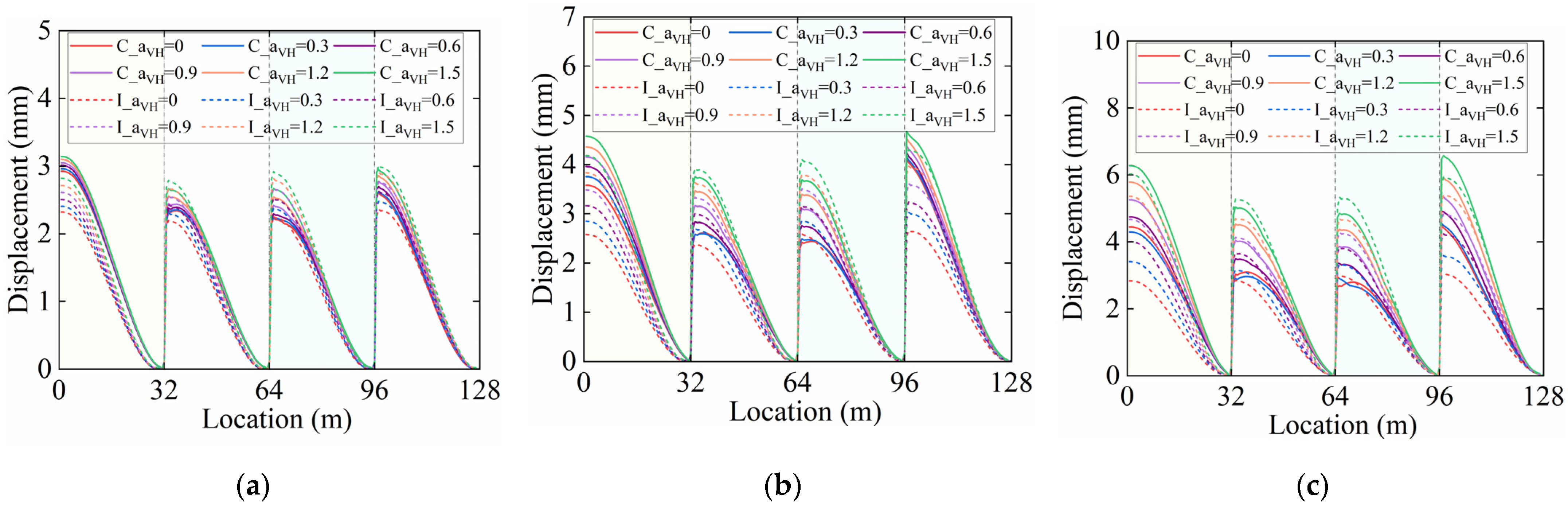
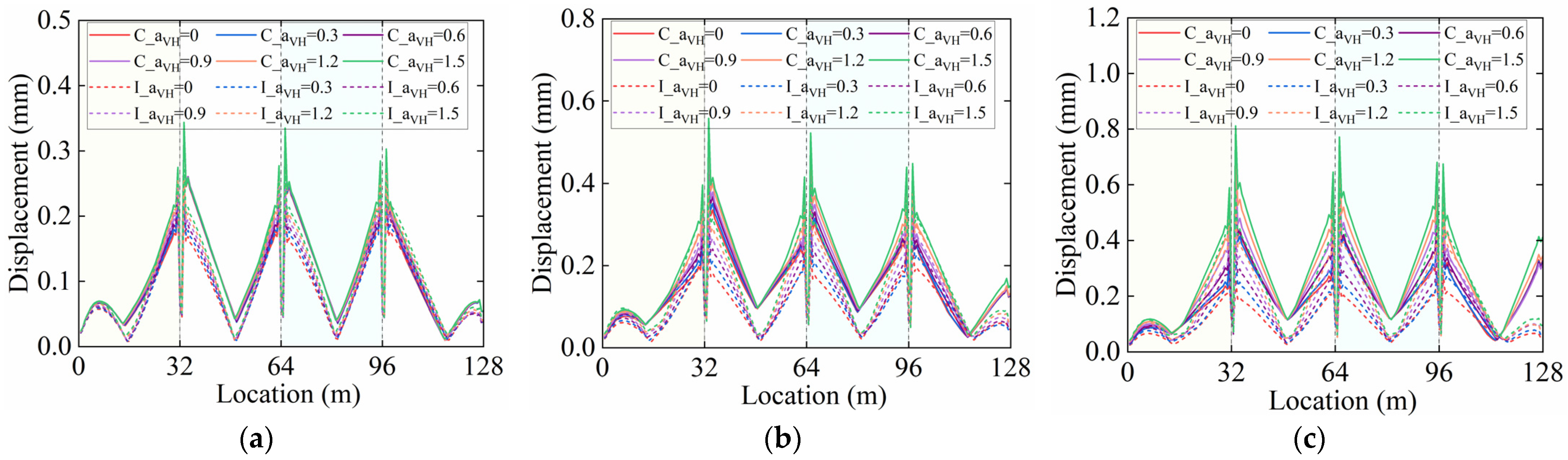
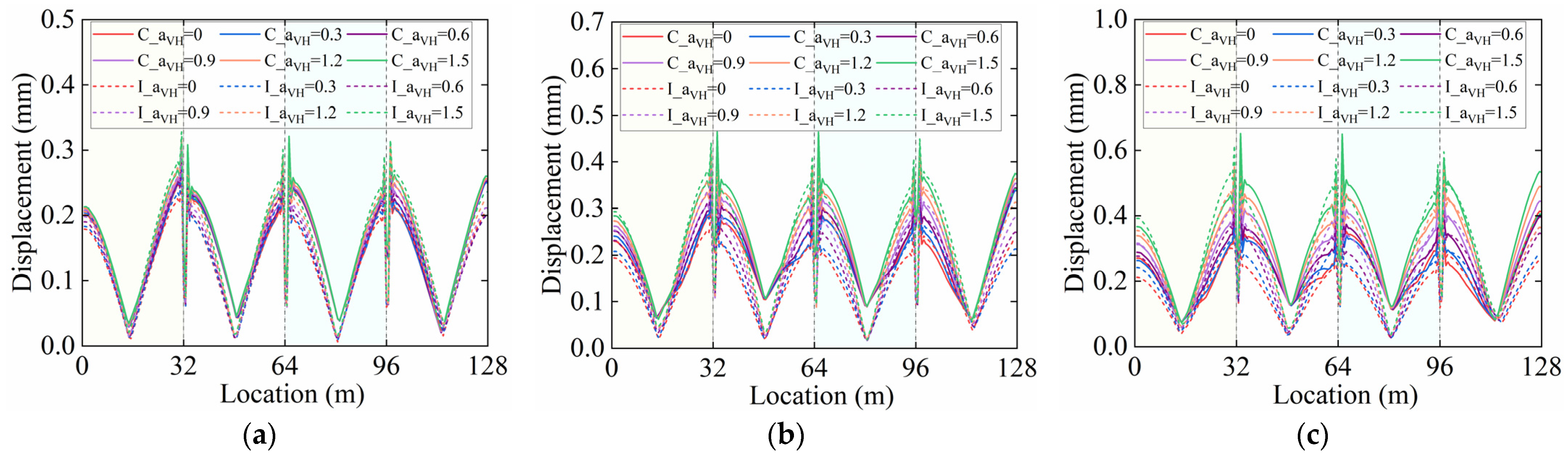
3.2. Effect of Seismic Response on Interlayer Components in Track Structure
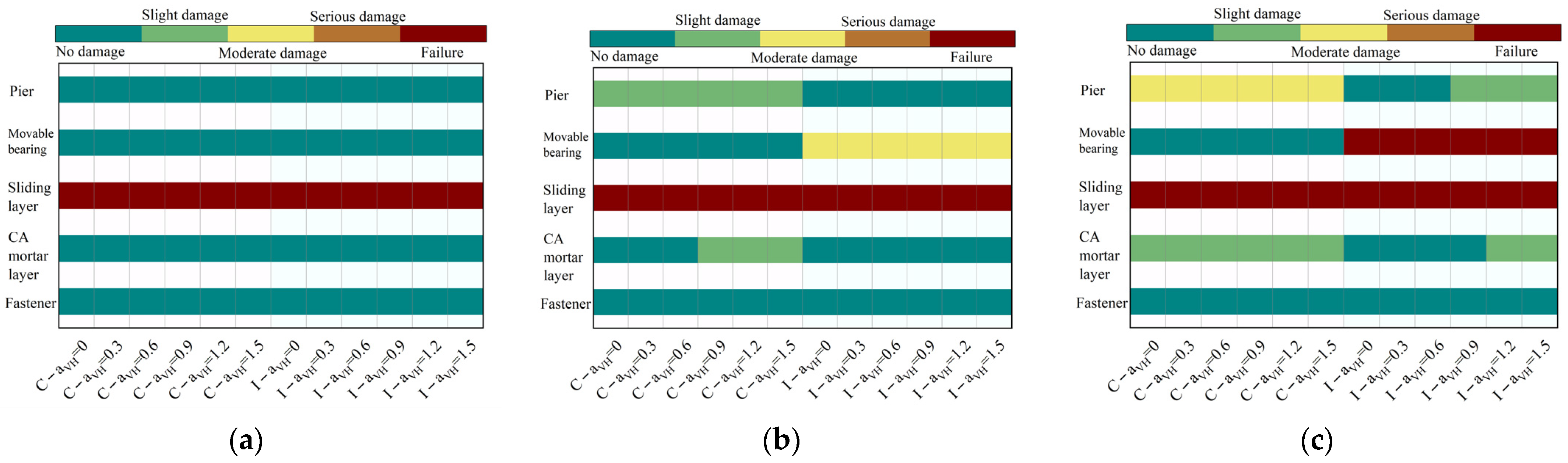
4. Damage Analysis of Components Under Different αVH Ratios
4.1. Displacement Response and Damage Degree Analysis
4.2. Recommended Values for αVH in Near-Fault Regions
5. Conclusions
- αVH distribution differs significantly from code-specified values: Statistics show that for reverse faults and strike-slip faults, αVH is mainly distributed in the interval of 0–1 (accounting for 75–85%), while for normal faults, it is concentrated in the interval of 1–2 (approximately 60%). Moreover, the measured αVH values are densely distributed in the range of 0.5–1.5, which is significantly different from the unified value of 0.65 specified in the code.
- αVH’s influence strengthens with seismic intensity: Under FE, the structural response is not sensitive to changes in αVH; under DE, an increase in αVH exacerbates damage in the common condition, while the isolated condition can delay such damage; under RE, the amplification effect of αVH is significant—the common condition suffers severe damage, while the isolated condition can significantly reduce the damage level. This confirms that the VGM in near-fault regions cannot be ignored in seismic analysis.
- Isolation offers differentiated protection: By utilizing large deformations of friction pendulum bearings for energy dissipation, isolation reduces displacements and damage in main structural components. However, it may lead to greater displacements in sliding layers of mid-span sections compared to non-isolated cases. Under rare earthquakes, isolation bearings themselves are prone to failure, necessitating optimized deformation control strategies.
- Tiered αVH design recommendations: Based on the principle of balancing damage control and economy, and guided by the framework of Chinese seismic design codes, it is suggested that αVH values under frequent, design, and rare earthquakes should be set to 0.65, 0.9, and 1.2, respectively. The value of 0.65 for frequent earthquakes is consistent with the specification in GB 50011-2010. For design and rare earthquake levels, the recommended values of 0.9 and 1.2 exceed the corresponding values of 0.85 (for 0.30 g) and 1.00 (for 0.40 g) suggested in GB 50909-2014 for general sites, which is justified by the higher intensity levels considered in this study (0.30 g for DE and 0.57 g for RE) and the specific near-fault conditions under investigation. Compared with the current code, this value system can more accurately reflect the characteristics of VGM in near-fault regions and provide a theoretical basis and practical reference for the seismic design of HSR projects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HSR | High-speed railway |
| VGM | Vertical ground motion |
| FEM | Finite element model |
| PGA | Peak ground acceleration |
| FPB | Friction pendulum bearing |
| FE | Frequent earthquake |
| DE | Design earthquake |
| RE | Rare earthquake |
References
- He, X.; Wu, T.; Zou, Y.; Chen, Y.F.; Guo, H.; Yu, Z. Recent developments of high-speed railway bridges in China. Struct. Infrastruct. Eng. 2017, 13, 1584–1595. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Carvalho, H.; Ribeiro, D.; Calçada, R.; Tokunaga, M.; Tanabe, M.; Zhai, W. Assessment of train running safety on bridges: A literature review. Eng. Struct. 2021, 241, 112425. [Google Scholar] [CrossRef]
- Billah, M.; Alam, M.S.; Bhuiyan, A. Fragility analysis of retrofitted multicolumn bridge bent subjected to near-fault and far-field ground motion. J. Bridge Eng. 2013, 18, 992–1004. [Google Scholar] [CrossRef]
- Taslimi, A.; Petrone, F.; Pitarka, A. Characteristics of Vertical Ground Motions and Their Effect on the Seismic Response of Bridges in the Near-Field: A State-of-the-Art Review. J. Bridge Eng. 2024, 29, 03124001. [Google Scholar] [CrossRef]
- Li, X.; Dou, H.; Zhu, X. Engineering characteristics of near-fault vertical ground motions and their effect on the seismic response of bridges. Earthq. Eng. Eng. Vib. 2007, 6, 345–350. [Google Scholar] [CrossRef]
- Malhotra, P.K. Response of buildings to near-field pulse-like ground motions. Earthq. Eng. Struct. Dyn. 1999, 28, 1309–1326. [Google Scholar] [CrossRef]
- MAKRIS, N. Rigidity–plasticity–viscosity: Can electrorheological dampers protect base-isolated structures from near-source ground motions? Earthq. Eng. Struct. Dyn. 1997, 26, 571–591. [Google Scholar] [CrossRef]
- Shaohui, L.; Lizhong, J.; Wangbao, Z.; Jian, Y.; Feng, Y.; Zhenbin, R. Influence of velocity pulse effect on earthquake-induced track irregularities of high-speed railway track–bridge system under near-fault ground motions. Arch. Civ. Mech. Eng. 2024, 24, 70. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, N.; Jiang, L.; Zeng, Z.; Chen, G.; Guo, W. Near-fault directivity pulse-like ground motion effect on high-speed railway bridge. J. Cent. South Univ. 2014, 21, 2425–2436. [Google Scholar] [CrossRef]
- Adanur, S.; Altunişik, A.; Bayraktar, A.; Akkose, M. Comparison of near-fault and far-fault ground motion effects on geometrically nonlinear earthquake behavior of suspension bridges. Nat. Hazards 2012, 64, 593–614. [Google Scholar] [CrossRef]
- Phan, V.; Saiidi, S.; Anderson, J.; Ghasemi, H. Near-Fault Ground Motion Effects on Reinforced Concrete Bridge Columns. J. Struct. Eng. 2007, 133, 982–989. [Google Scholar] [CrossRef]
- Zhang, J.; Huo, Y. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method. Eng. Struct. 2009, 31, 1648–1660. [Google Scholar] [CrossRef]
- Liu, X.; Wang, W.; Li, J. Full-scale shaking table tests and numerical studies of structural frames with a hybrid isolation system. Eng. Struct. 2023, 292, 116545. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, J. Design and Optimization of Seismic Isolation and Damping Devices for Highway Bridges Based on Probabilistic Repair Cost Ratio. J. Struct. Eng. 2018, 144, 04018125. [Google Scholar] [CrossRef]
- Papazoglou, A.; Elnashai, A. Analytical and field evidence of the damaging effect of vertical earthquake ground motion. Earthq. Eng. Struct. Dyn. 1996, 25, 1109–1137. [Google Scholar] [CrossRef]
- Tao, Y.; Yuan, X.; Zhong, J. Near-fault pulse seismic ductility spectra for bridge columns based on machine learning. Soil Dyn. Earthq. Eng. 2023, 164, 107582. [Google Scholar]
- Jiang, L.; Zhong, J.; Yuan, W. The pulse effect on the isolation device optimization of simply supported bridges in near-fault regions. Structures 2020, 27, 853–867. [Google Scholar] [CrossRef]
- Ismail, M.; Rodellar, J.; Pozo, F. An isolation device for near-fault ground motions. Struct. Control Health Monit. 2014, 21, 249–268. [Google Scholar] [CrossRef]
- Dicleli, M.; Buddaram, S. Equivalent linear analysis of seismic-isolated bridges subjected to near-fault ground motions with forward rupture directivity effect. Eng. Struct. 2007, 29, 21–32. [Google Scholar] [CrossRef]
- Jiang, L.; Duan, H.; Wen, T.; Jiang, L. Effects of Near-Fault Pulse-Like Ground Motions and Pulse Parameters on a High-Speed Railway Long-Span Arch Bridge–Track System. J. Bridge Eng. 2025, 30, 04024112. [Google Scholar] [CrossRef]
- Guo, W.; Yang, S.; Jiang, L.; Yu, Z.; Zeng, C.; Wang, Y.; Huang, R.; Wu, S.; Ren, S. Effect of near-fault vertical seismic excitation on running safety of trains on high-speed railway bridges. Eng. Struct. 2023, 296, 116880. [Google Scholar] [CrossRef]
- Ryan, K.; Mojidra, R. Analysis of effect of vertical ground shaking in bridges isolated with spherical sliding bearings. Earthq. Eng. Struct. Dyn. 2023, 52, 5010–5032. [Google Scholar] [CrossRef]
- Shao, Y.; Wei, Y.; Yang, T.; Ni, M.; Zhong, J. Empirical models of bridge seismic fragility surface considering the vertical effect of near-fault ground motions. Structures 2021, 34, 2962–2973. [Google Scholar] [CrossRef]
- Wei, B.; Zuo, C.; He, X.; Jiang, L.; Wang, T. Effects of vertical ground motions on seismic vulnerabilities of a continuous track-bridge system of high-speed railway. Soil Dyn. Earthq. Eng. 2018, 115, 281–290. [Google Scholar] [CrossRef]
- Zhou, F.; Tan, P.; Chen, Y.; Liu, Y. Recent Development and Application on Seismic Isolation, Energy Dissipation and Vibration Control in China. In Seismic Isolation, Energy Dissipation and Active Vibration Control of Structures; WCSI 2022. Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2023; Volume 309. [Google Scholar]
- Wang, D.; Guo, X.; Sun, Z.; Meng, Q.; Yu, D.; Li, X. Damage to highway bridges during wenchuan earthquake. J. Earthq. Eng. Eng. Vib. 2009, 29, 84–94. (In Chinese) [Google Scholar]
- Hu, S.; Yang, M.; Hao, H. Parameter Optimization of the Combined Viscous-Steel Damping System for Dual Vibration Control in Long-Span Suspension Bridges Under Traffic and Seismic Excitations. Int. J. Struct. Stab. Dyn. 2025, 2540027. [Google Scholar] [CrossRef]
- Hu, R.; Yang, M.; Meng, D.; Cucuzza, R.; Domaneschi, M. Robustness investigation of Horizontal Bidirectional Hybrid Damping System applied to long-span bridges under near-fault pulse-like earthquakes. Soil Dyn. Earthq. Eng. (1984) 2024, 184, 108803. [Google Scholar] [CrossRef]
- Hu, S.; Yang, M.; Zhang, H.; Meng, D.; Li, X. Numerical and experimental study of a suspension bridge with combined viscous-steel damping system under train and seismic loads. Struct. Infrastruct. Eng. 2024, 4, 1–14. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, L.; Qin, H.; Zhang, N.; Ling, L.; Zhang, Q.; Li, Q.; Cao, D. Nonlinear seismic assessment of isolated high-speed railway bridge subjected to near-fault earthquake scenarios. Struct. Infrastruct. Eng. 2019, 15, 1529–1547. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, J.; Mao, N.; Mao, Y.; Mao, J. Design and Seismic Performance Study of Multistage Controllable Isolation Bearing for High-Speed Railway Simply Supported Beam. Buildings 2024, 14, 3539. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Mao, J.; Spencer, B.F. Effect of seismic isolation on random seismic response of High-Speed railway bridge based on probability density evolution method. Structures 2021, 29, 1032–1046. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Mao, J.; Jiang, L. Nonlinear random seismic analysis of 3D high-speed railway track-bridge system based on OpenSEES. Structures 2020, 24, 87–98. [Google Scholar] [CrossRef]
- Wei, B.; Yang, Z.; Fu, Y.; Xiao, B.; Jiang, L. Seismic displacement response analysis of Friction Pendulum Bearing under friction coupling and collision effects. Eng. Struct. 2024, 310, 118128. [Google Scholar] [CrossRef]
- Loghman, V.; Khoshnoudian, F.; Banazadeh, M. Effect of vertical component of earthquake on seismic responses of triple concave friction pendulum base-isolated structures. J. Vib. Control 2015, 21, 2099–2113. [Google Scholar] [CrossRef]
- Zhong, J.; Zhu, Y.; Han, Q. Impact of vertical ground motion on the statistical analysis of seismic demand for frictional isolated bridge in near-fault regions. Eng. Struct. 2023, 278, 115512. [Google Scholar] [CrossRef]
- Xiao, B.; Wei, B.; Zhao, H.; Zheng, X.; Zhang, R.; Chen, J.; Jiang, L. Effect of seismic isolation parameters on component damage and running safety performance of high-speed railway bridge-track system under near-fault earthquakes. Eng. Struct. 2025, 328, 119712. [Google Scholar] [CrossRef]
- Wei, B.; Wang, W.; Wang, P.; Yang, T.; Jiang, L.; Wang, T. Seismic Responses of a High-speed Railway (HSR) Bridge and Track Simulation under Longitudinal Earthquakes. J. Earthq. Eng. 2020, 26, 4449–4470. [Google Scholar] [CrossRef]
- JTG/T 2231-01-2020; Code for Seismic Design of Highway Bridges. China Communications Press: Beijing, China, 2020.
- Castaldo, P.; Tubaldi, E. Influence of FPS bearing properties on the seismic performance of base-isolated structures. Earthq. Eng. Struct. Dyn. 2015, 44, 2817–2836. [Google Scholar] [CrossRef]
- Hu, Z. Study on Key Parameters of Seismic Vulnerability and Risk Analysis of High-Speed Railway Bridge-Track Structure. Doctoral Thesis, Central South University, Changsha, China, 2022. [Google Scholar]
- Hu, Z.; Wei, B.; Jiang, L.; Li, S. Research on damage quantification of high-speed railway bridge piers. Chin. Civ. Eng. J. 2023, 56, 60–68. (In Chinese) [Google Scholar]
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2016.
- GB 50909-2014; Code for Seismic Design of Urban Rail Transit Structures. China Planning Press: Beijing, China, 2014.

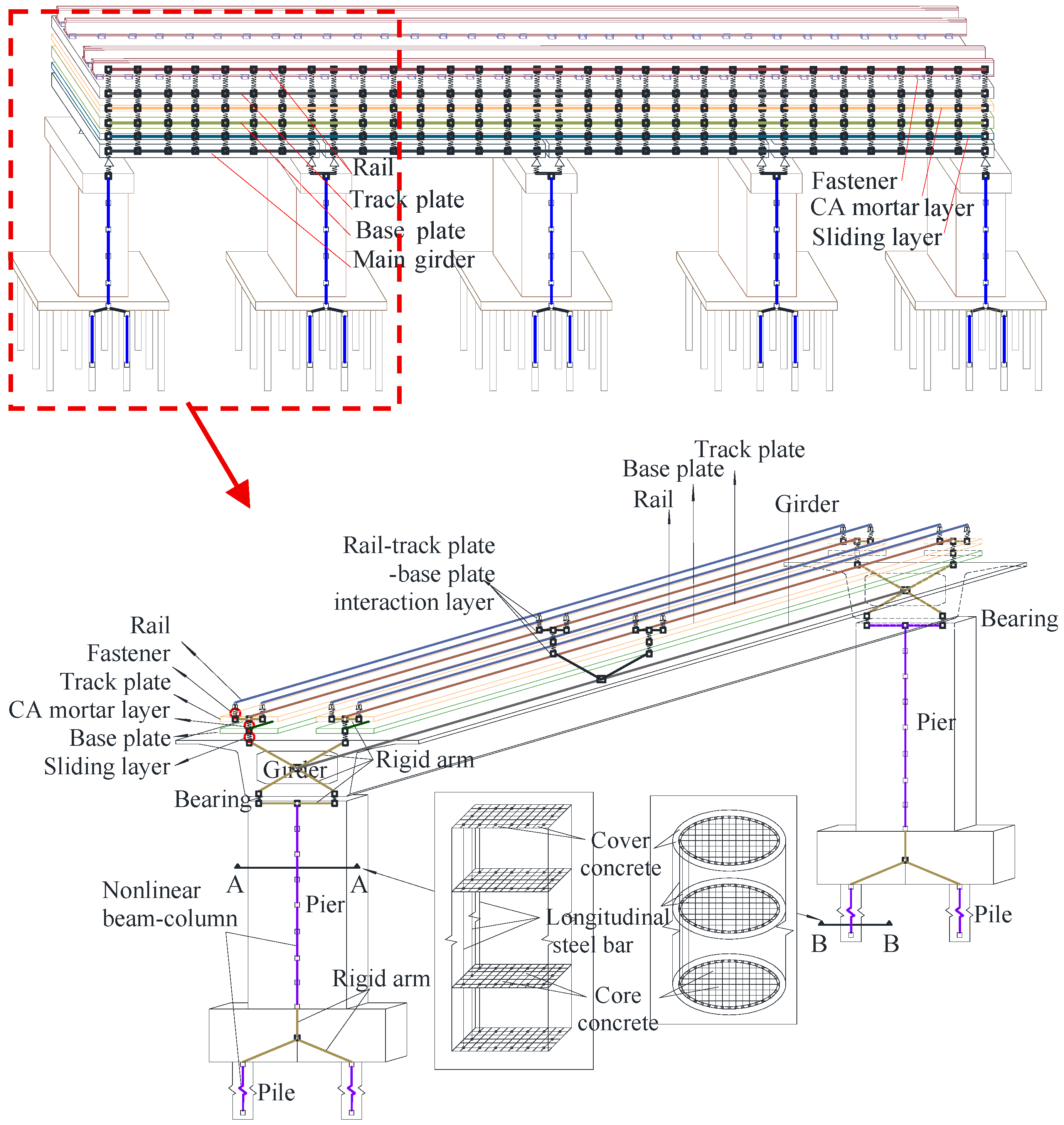
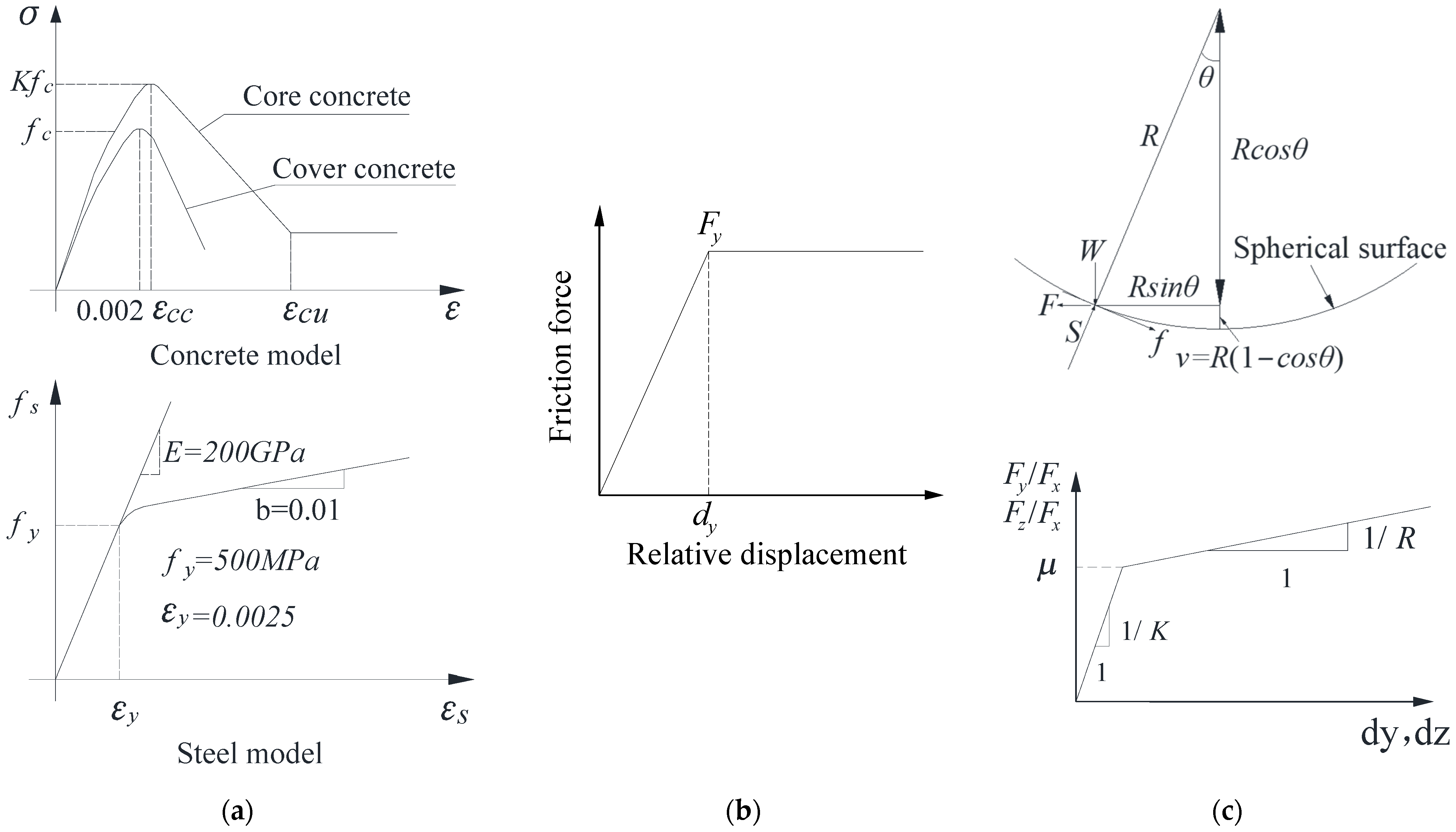
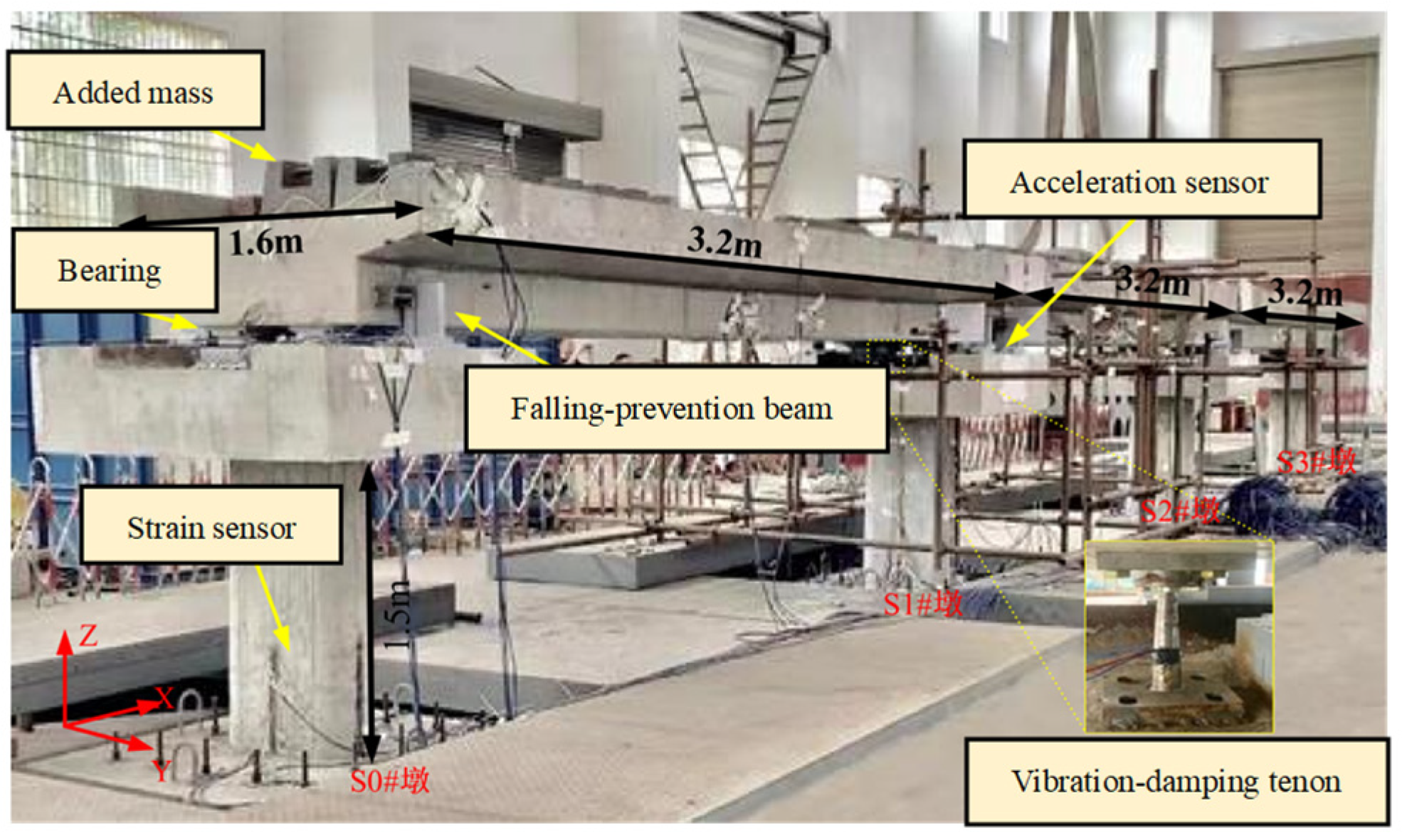
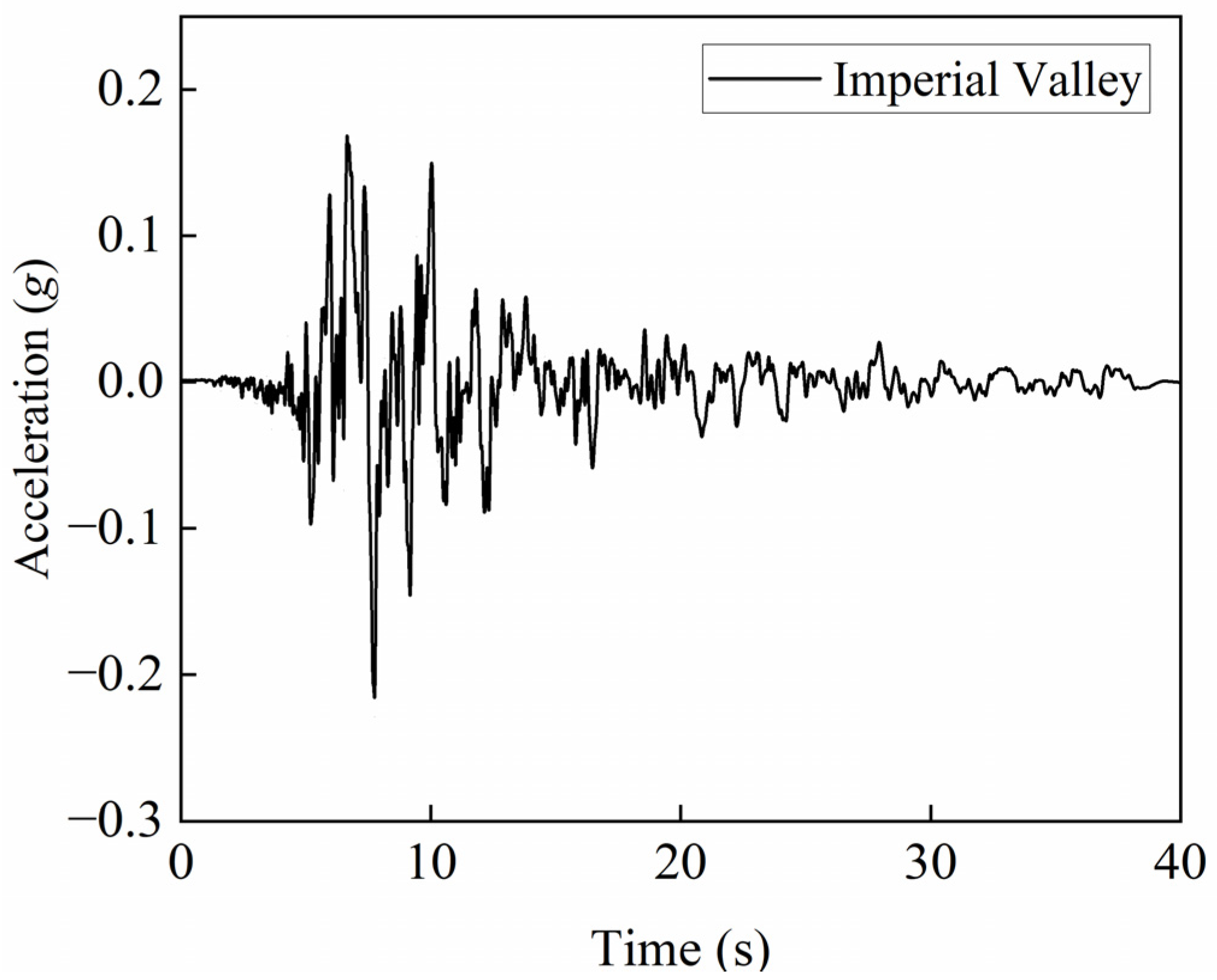


| Component | Sectional Area /m2 | Elastic Modulus /kN/m2 | Shear Modulus /kN/m2 | Torque /kN∙m | Inertia Moment 1 /m4 | Inertia Moment 2 /m4 |
|---|---|---|---|---|---|---|
| Main girder | 9.06 | 3.45 × 107 | 1.44 × 107 | 2.26 × 101 | 1.10 × 101 | 9.48 × 101 |
| Rail | 7.75 × 10−3 | 2.06 × 108 | 8.05 × 106 | 2.00 × 10−6 | 3.20 × 10−5 | 5.00 × 10−6 |
| Base plate | 5.61 × 10−1 | 3.00 × 107 | 1.25 × 107 | 6.74 × 10−3 | 1.69 × 10−3 | 4.06 × 10−1 |
| Track plate | 5.10 × 10−1 | 3.55 × 107 | 1.48 × 107 | 6.80 × 10−3 | 1.70 × 10−3 | 2.76 × 10−1 |
| Component | Fy/kN | dy/mm | Fz/kN | dz/mm |
|---|---|---|---|---|
| Sliding layer | 6 | 0.5 | 6 | 0.5 |
| CA layer | 41.5 | 0.5 | 41.5 | 0.5 |
| Fastener | 15 | 2 | 15 | 2 |
| Shear reinforcement | 22.5 | 0.075 | 22.5 | 0.075 |
| Lateral block | 453 | 2 | 453 | 2 |
| Fixed spherical steel bearing | 5000 | 2 | 5000 | 2 |
| Sliding spherical steel bearing | 470 | 2 | 470 | 2 |
| Indicator | Unit | FEM Calculation | Test Result | Relative Error |
|---|---|---|---|---|
| Protective layer concrete strain | μm/m | 791.07 | 653.12 | 17.44% |
| Reinforcement strain | μm/m | 1025.59 | 837.45 | 18.34% |
| Damage Indices | DT1 | DT2 | DT3 | DT4 |
|---|---|---|---|---|
| Fastener disp (mm) | 2 | 3 | 4 | 5 |
| CA layer disp (mm) | 0.5 | 1 | 1.5 | 2 |
| Sliding layer disp (mm) | 0.5 | 1 | 1.5 | 2 |
| Common movable bearing disp (mm) | 100 | 130 | 160 | 200 |
| FPB bearing disp (mm) | 80 | 100 | 130 | 160 |
| Pier drift ratio (%) | 0.13 | 0.34 | 0.95 | 2.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Ma, J.; Yu, Z.; Mao, J. Effects of Near-Fault Vertical Ground Motion on Seismic Response and Damage in High-Speed Railway Isolated Track–Bridge Systems. Buildings 2025, 15, 3320. https://doi.org/10.3390/buildings15183320
Li H, Ma J, Yu Z, Mao J. Effects of Near-Fault Vertical Ground Motion on Seismic Response and Damage in High-Speed Railway Isolated Track–Bridge Systems. Buildings. 2025; 15(18):3320. https://doi.org/10.3390/buildings15183320
Chicago/Turabian StyleLi, Haiyan, Jinyu Ma, Zhiwu Yu, and Jianfeng Mao. 2025. "Effects of Near-Fault Vertical Ground Motion on Seismic Response and Damage in High-Speed Railway Isolated Track–Bridge Systems" Buildings 15, no. 18: 3320. https://doi.org/10.3390/buildings15183320
APA StyleLi, H., Ma, J., Yu, Z., & Mao, J. (2025). Effects of Near-Fault Vertical Ground Motion on Seismic Response and Damage in High-Speed Railway Isolated Track–Bridge Systems. Buildings, 15(18), 3320. https://doi.org/10.3390/buildings15183320





