A Study on the Supply–Demand Matching and Spatial Value Effects of Community Public Service Facilities: A Case Study of Wuchang District, Wuhan
Abstract
1. Introduction
- Supply–demand evaluation dimension: Under the context of high-density urban development, what are the spatial equity patterns of different types of community public service facilities?
- Value effects dimension: Do significant spatial mismatches exist between facility accessibility and housing prices, and do the capitalization effects of different facility types exhibit spatial heterogeneity?
2. Literature Review
2.1. Progress in Research on Supply–Demand Matching of Public Service Facilities
2.2. Progress in Research on the Effect Mechanisms of Public Service Facilities on Housing Prices
2.3. Summary of Research Progress
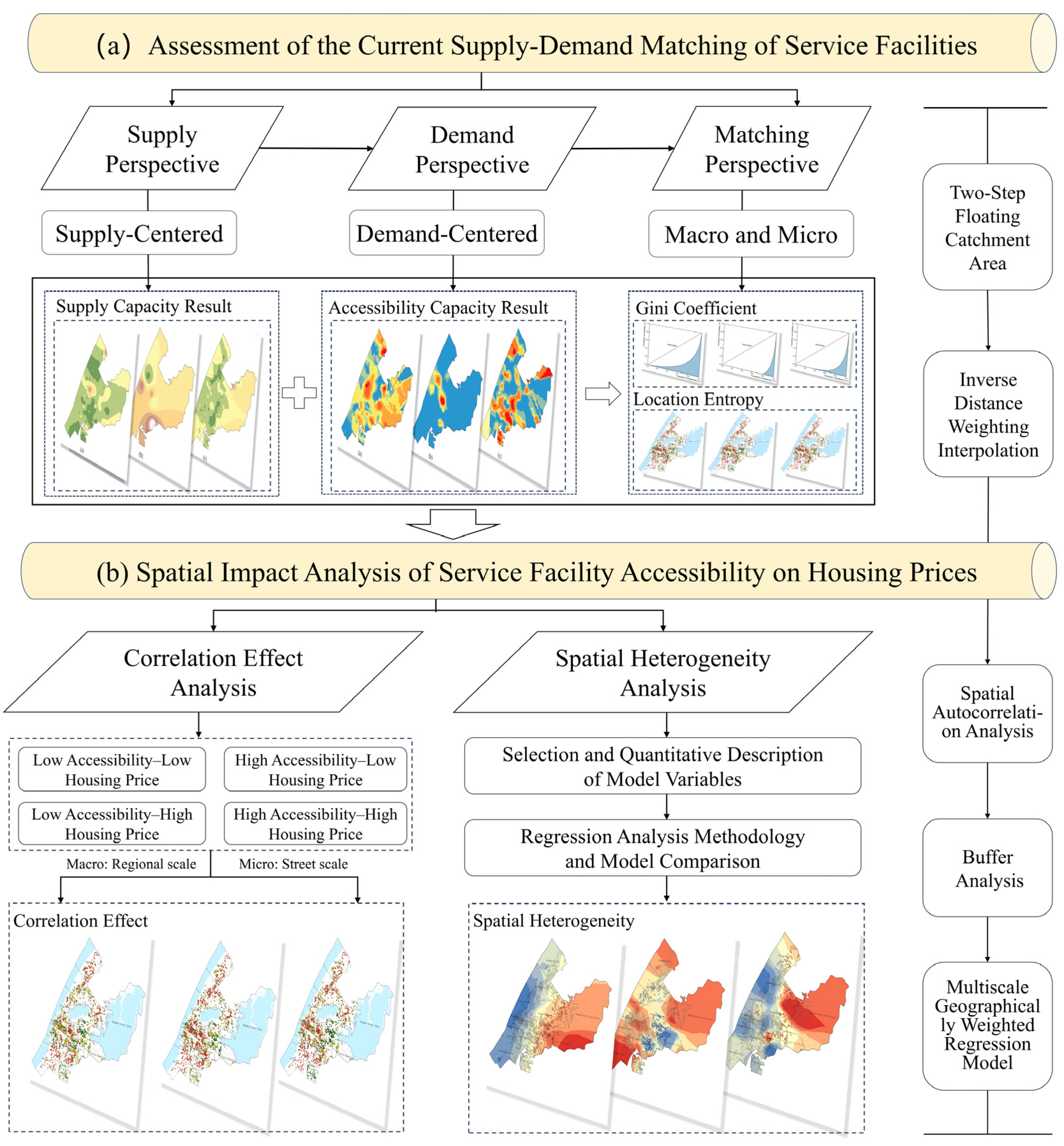
3. Data and Methodology
3.1. Study Area and Objects
3.2. Data Sources
3.3. Research Methods
3.3.1. Improved Two-Step Floating Catchment Area (2SFCA) Method
3.3.2. Inverse Distance Weighting Interpolation (IDW)
3.3.3. Spatial Autocorrelation Analysis
3.3.4. Buffer Analysis Method
3.3.5. Multiscale Geographically Weighted Regression Model (MGWR)
4. Results and Analysis
4.1. Assessment of the Current Supply–Demand Matching of Community Public Service Facilities
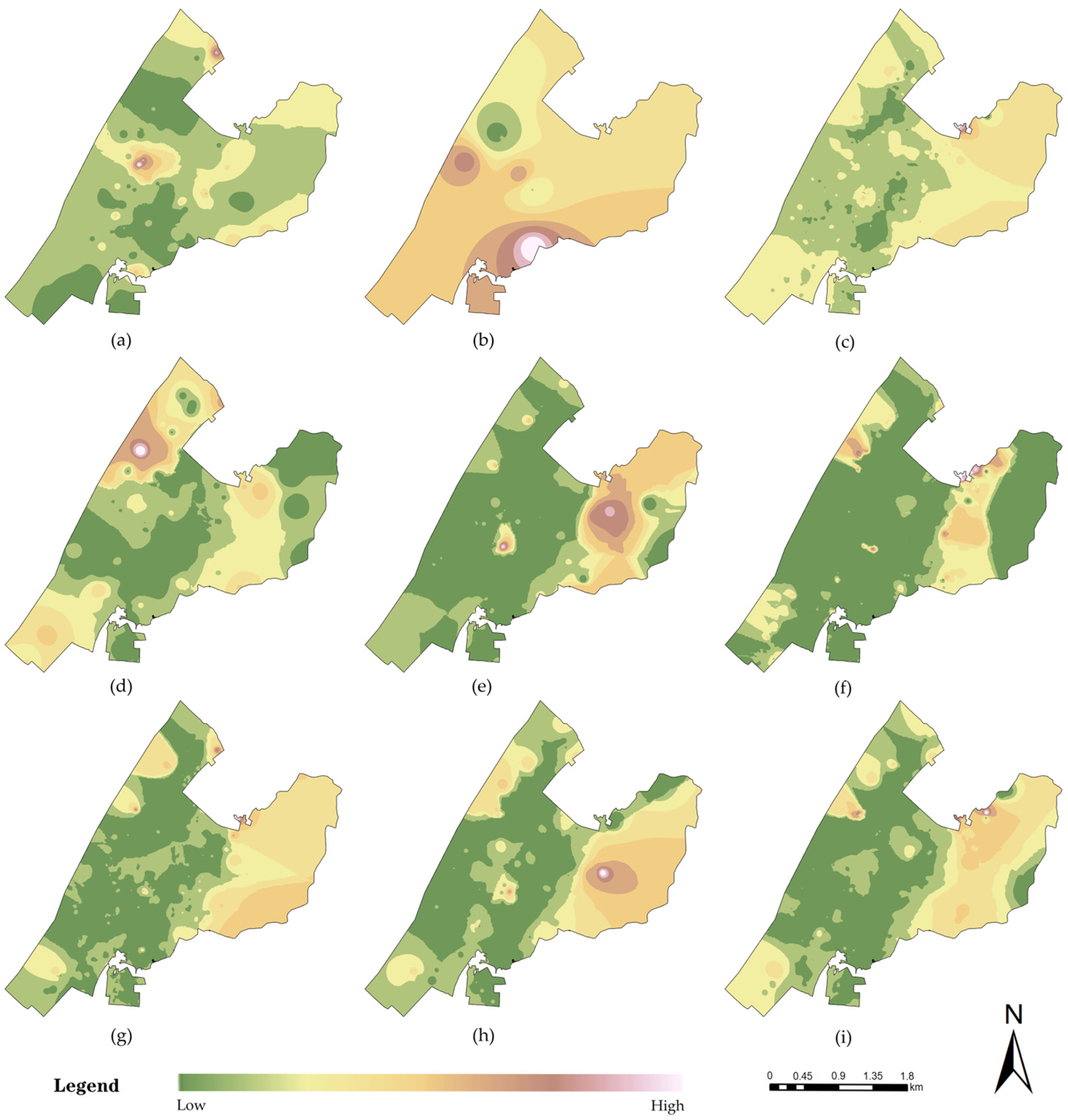
4.1.1. Supply-Side Perspective: Evaluation of Service Facility Provision
4.1.2. Demand-Side Perspective: Accessibility Assessment of Residential Communities
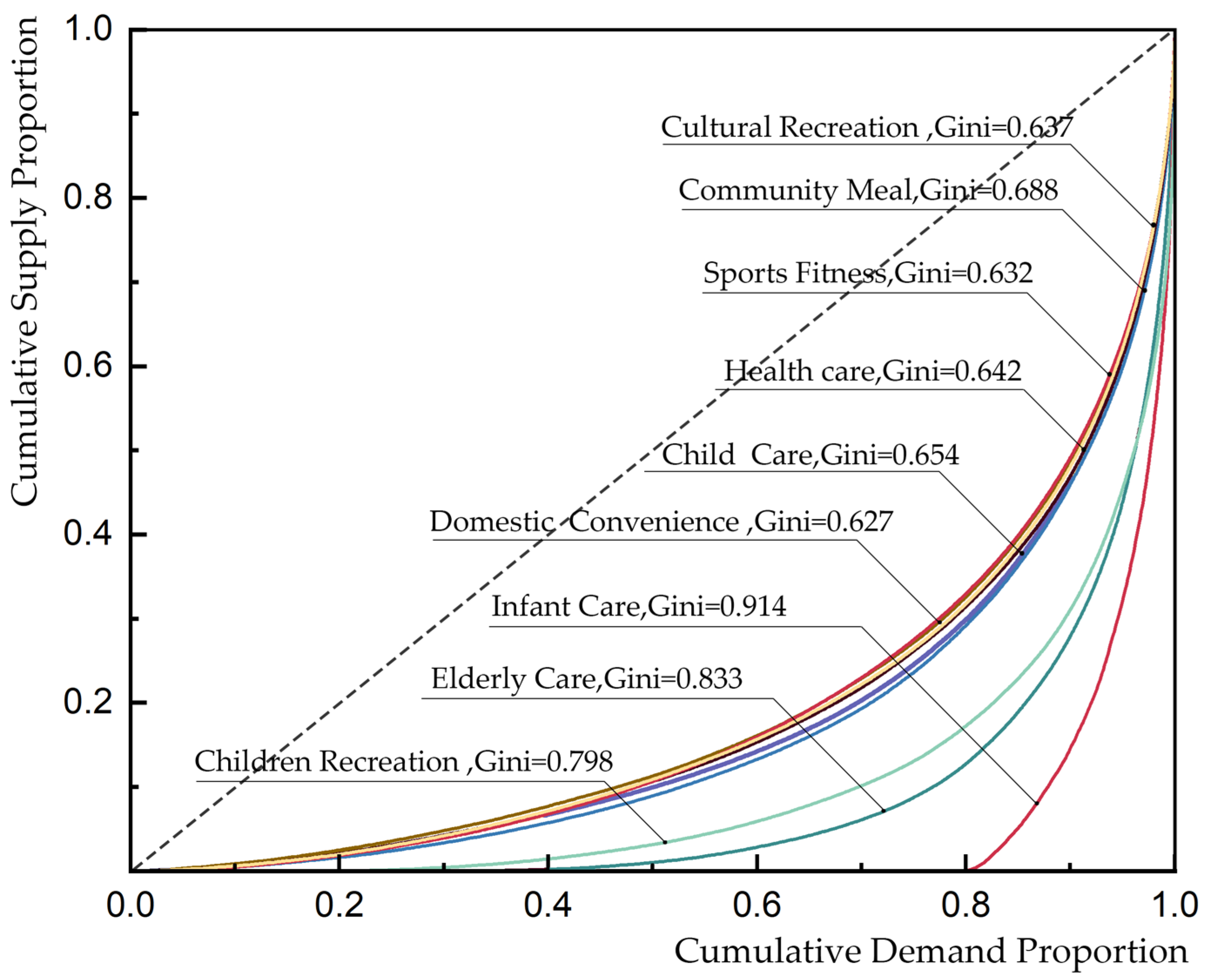
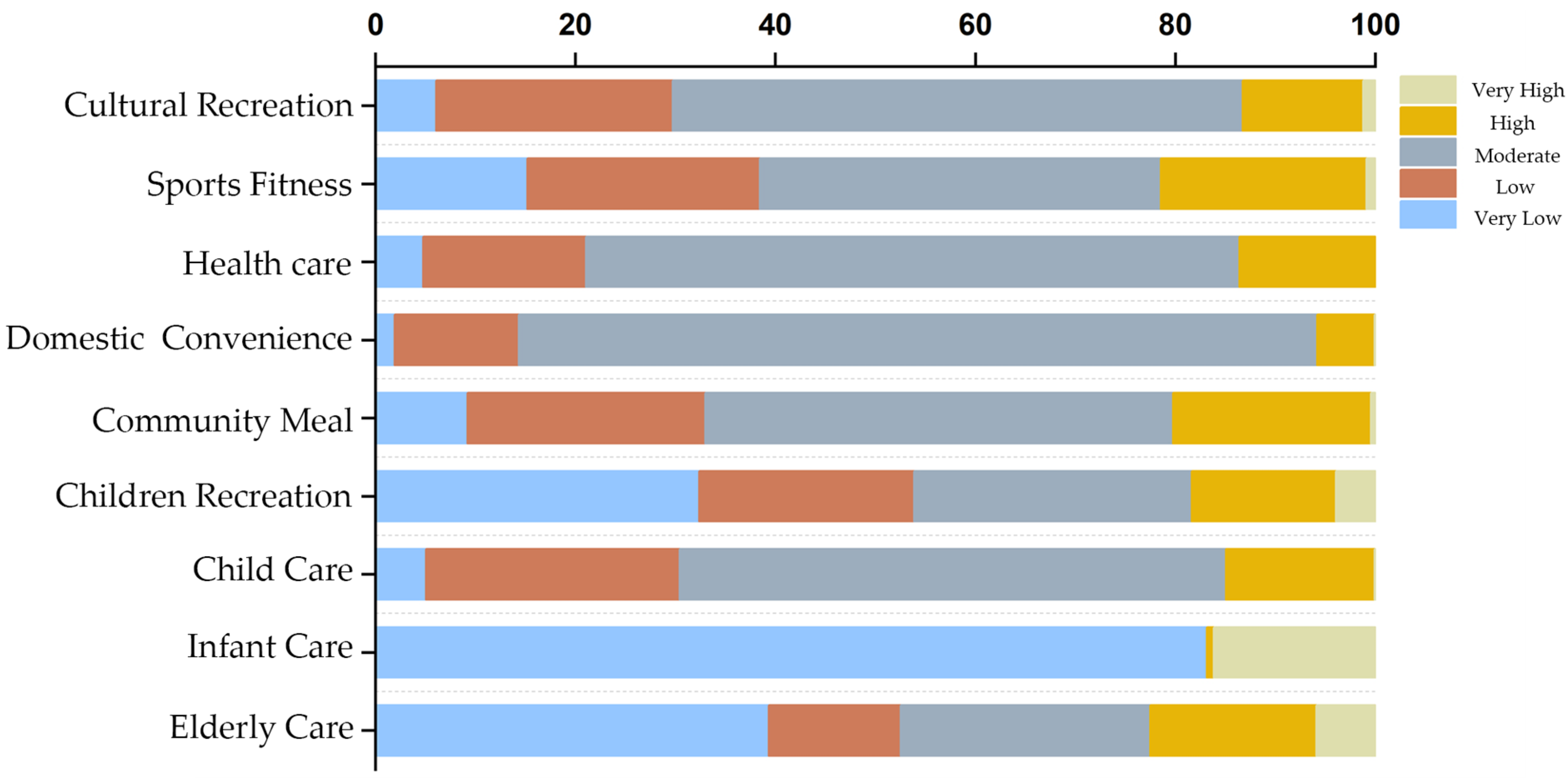
4.1.3. Matching Perspective: Spatial Equity Analysis of Service Facilities
- (1)
- Macro-Level Evaluation of Supply–Demand Spatial Distribution Based on the Gini Coefficient
- (2)
- Micro-Level Evaluation of Supply–Demand Spatial Distribution Based on Location Entropy
- (1)
- Low-value dominated type: Elderly care facilities, infant care facilities, and child recreation facilities
- (2)
- Median-stable type: Children care facilities, domestic convenience facilities, health care facilities, and cultural recreation facilities
- (3)
- High-value driven type: community meal facilities and sports fitness facilities
4.2. Analysis of the Spatial Value Effect of Community Public Service Facility Accessibility on Housing Prices
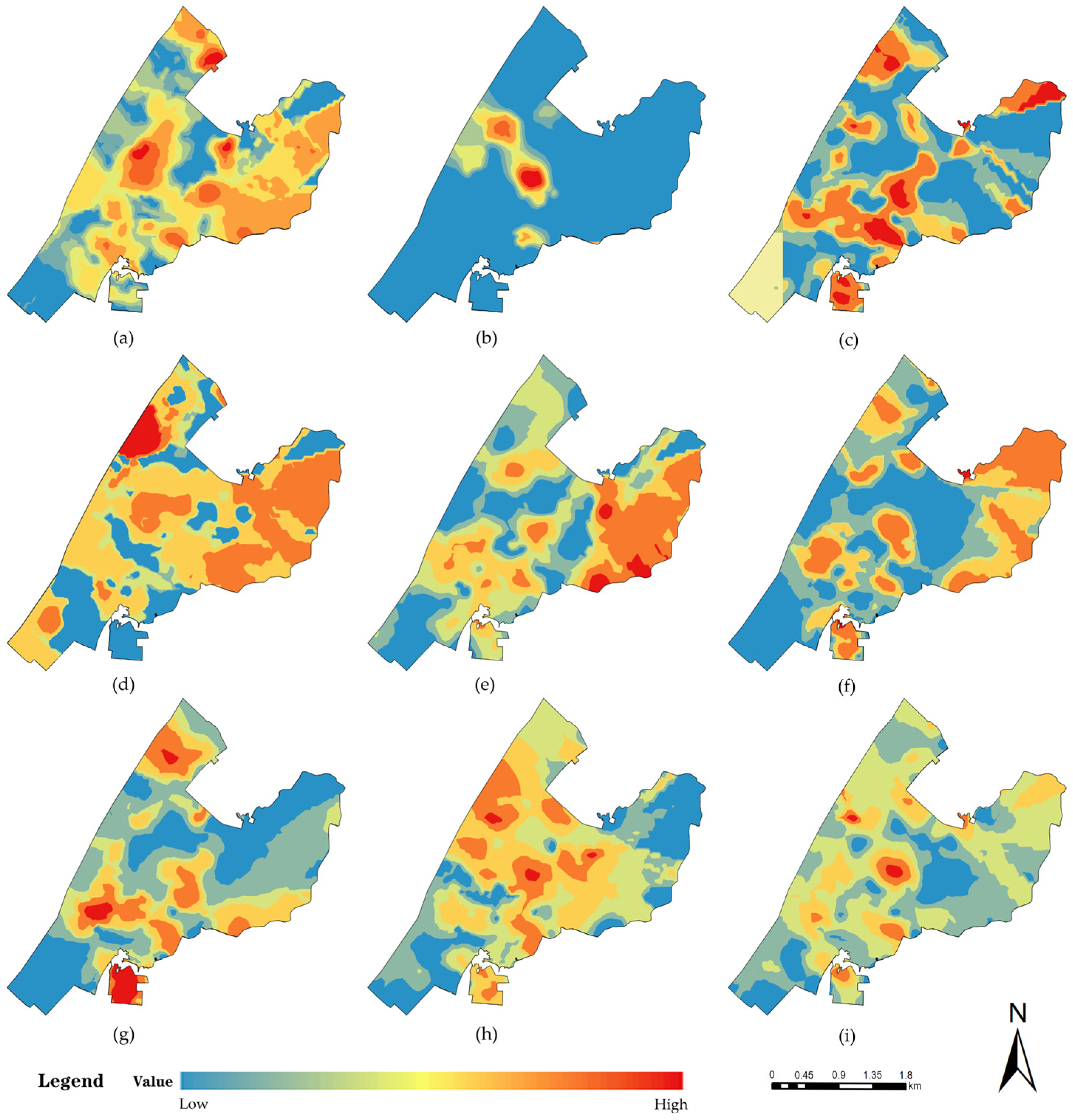
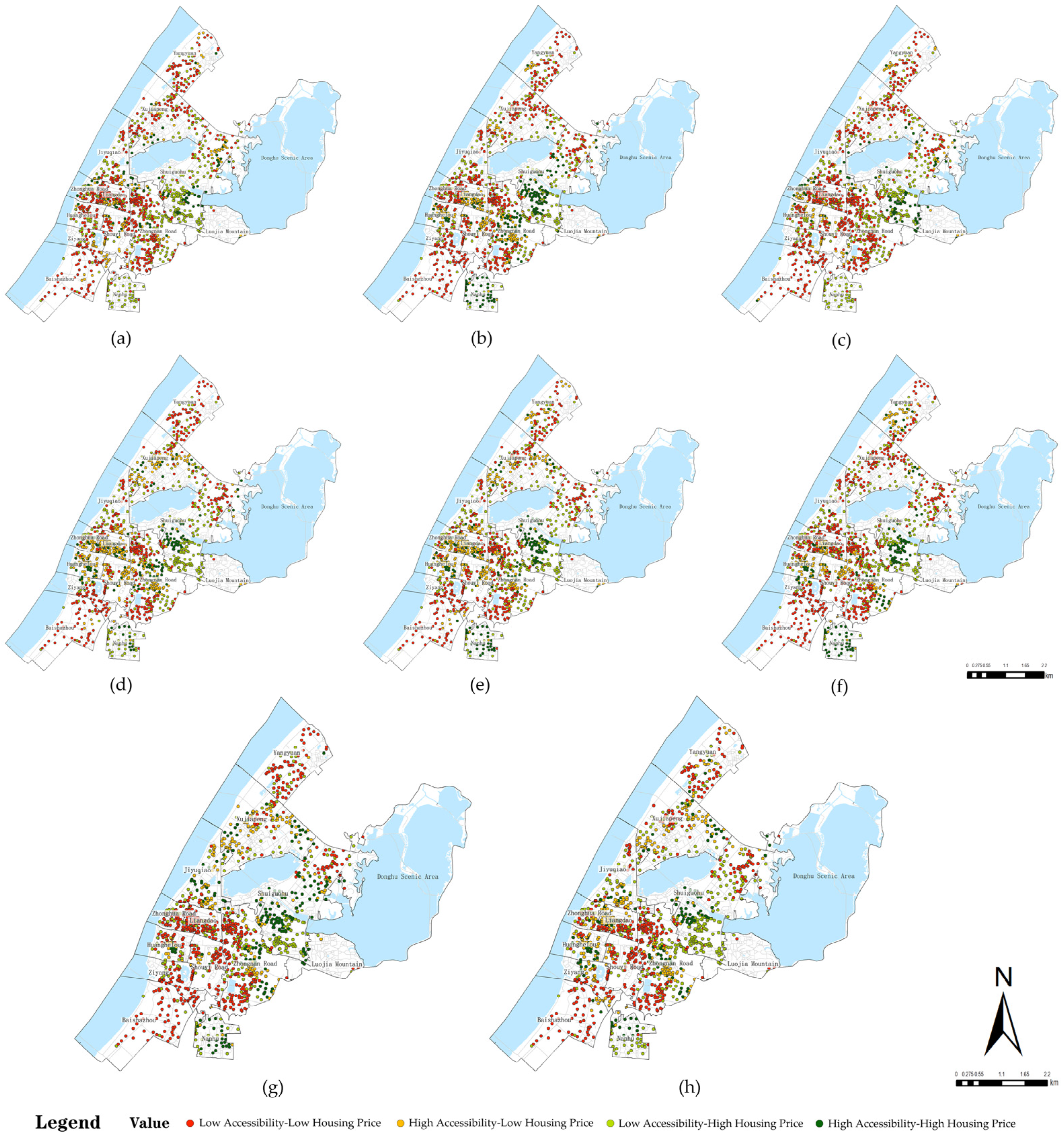
4.2.1. Spatial Correlation Analysis Between Community Public Service Facility Accessibility and Housing Prices
4.2.2. Spatial Heterogeneity Analysis of the Effect of Community Public Service Facility Accessibility on Housing Prices
5. Discussion
5.1. Key Findings and Summary
5.2. Contributions to Theory and Method
5.3. Practical Implications
5.4. Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, X.; Zhou, Y.; Yuan, X.; Zhu, M. The coordination relationship between urban development and urban life satisfaction in Chinese cities-An empirical analysis based on multi-source data. Cities 2024, 150, 105016. [Google Scholar] [CrossRef]
- Wen, C.; Albert, C.; Von Haaren, C. The elderly in green spaces: Exploring requirements and preferences concerning nature-based recreation. Sustain. Cities Soc. 2018, 38, 582–593. [Google Scholar] [CrossRef]
- Zang, Y.; Wang, H.; Huang, J.; Liu, G.; Li, J. Community disaster resilience assessment and external association characteristics analysis based on accessibility of service facilities: From the perspective of 15-minute life circle. Sustain. Cities Soc. 2025, 118, 106051. [Google Scholar] [CrossRef]
- Dong, S.; Esmalian, A.; Farahmand, H.; Mostafavi, A. An integrated physical-social analysis of disrupted access to critical facilities and community service-loss tolerance in urban flooding. Comput. Environ. Urban. Syst. 2020, 80, 101443. [Google Scholar] [CrossRef]
- Luo, Y.; Zou, G.; Liu, Q. Relationships between community public service facilities and social capital: An exploratory study of Harbin, China. PLoS ONE 2025, 20, e0318144. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Wang, N.; Li, Y.; Sun, D. 15-min pedestrian distance life circle and sustainable community governance in Chinese metropolitan cities: A diagnosis. Humanit. Soc. Sci. Commun. 2023, 10, 1–14. [Google Scholar] [CrossRef]
- Wei, W.; Ren, X.; Guo, S. Evaluation of public service facilities in 19 large cities in China from the perspective of supply and demand. Land 2022, 11, 149. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, R.; Qian, L.; Yang, X.; Dong, L.; Zhang, G. Supply-demand balance and spatial distribution optimization of primary care facilities in highland cities from a resilience perspective: A study of Lhasa, China. Front. Public Health 2023, 11, 1131895. [Google Scholar] [CrossRef]
- Wang, M.; Yuan, H.; Zhang, D.; Qi, J.; Rao, Q.; Li, J.; Tan, S. Supply-demand measurement and spatial allocation of Sponge facilities for Sponge city construction. Ecol. Indic. 2023, 148, 110141. [Google Scholar] [CrossRef]
- Song, L.; Kong, X.; Cheng, P. Supply-demand matching assessment of the public service facilities in 15-minute community life circle based on residents’ behaviors. Cities 2024, 144, 104637. [Google Scholar] [CrossRef]
- Fei, H.; Renchao, L. Matching of supply and demand for community service-oriented home care facilities based on accessibility measurement: A case study of Nanjing. Econ. Geogr. 2020, 40, 91–101. [Google Scholar]
- Wang, F. Inverted two-step floating catchment area method for measuring facility crowdedness. Prof. Geogr. 2018, 70, 251–260. [Google Scholar] [CrossRef]
- Fedotenkov, I.; Idrisov, G. A supply-demand model of public sector size. Econ. Syst. 2021, 45, 100869. [Google Scholar] [CrossRef]
- Qi, Z.; Li, Q.; Huang, Q.; Wu, T. Evaluation of supply and demand balance and spatial spillover effect of age-friendly environment. Sustainability 2023, 15, 11810. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, X.; Lv, D.; Wang, Q. Evaluation of urban green space supply and demand based on mobile signal data: Taking the central area of Shenyang city as an example. Land 2023, 12, 1742. [Google Scholar] [CrossRef]
- Soler, I.; Gemar, G.; Correia, M.; Serra, F. Algarve hotel price determinants: A hedonic pricing model. Tourism Manag. 2019, 70, 311–321. [Google Scholar] [CrossRef]
- Wei, C.; Fu, M.; Wang, L.; Yang, H.; Tang, F.; Xiong, Y. The research development of hedonic price model-based real estate appraisal in the era of big data. Land 2022, 11, 334. [Google Scholar] [CrossRef]
- Morano, P.; Tajani, F.; Guarini, M.R.; Di Liddo, F.; Anelli, D. A multivariate econometric analysis for the forecasting of the interdependences between the housing prices and the socio-economic factors in the city of Barcelona (Spain). In Computational Science and Its Applications—ICCSA 2019; Misra, S., Gervasi, O., Murgante, B., Stankova, E., Korkhov, V., Torre, C., Rocha, A.M.A.C., Taniar, D., Apduhan, B.O., Tarantino, E., Eds.; Springer: Cham, Switzerland, 2019; pp. 13–22. [Google Scholar]
- Charlton, M.; Brunsdon, C.; Fotheringham, A. Geographically weighted regression-modelling spatial non-stationarity. J. R. Stat. Soc. Ser. D Stat. 1998, 47, 431–443. [Google Scholar]
- Fotheringham, A.; Yang, W.; Kang, W. Multiscale geographically weighted regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Liu, L.; Yu, H.; Zhao, J.; Wu, H.; Peng, Z.; Wang, R. Multiscale effects of multimodal public facilities accessibility on housing prices based on MGWR: A case study of Wuhan, China. ISPRS Int. J. Geo-Inf. 2022, 11, 57. [Google Scholar] [CrossRef]
- Hansen, W.G. How accessibility shapes land use. J. Am. Inst. Plann. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Wei, Z.; Bai, J.; Feng, R. Evaluating the spatial accessibility of medical resources taking into account the residents’ choice behavior of outpatient and inpatient medical treatment. Socio-Econ. Plan. Sci. 2022, 83, 101336. [Google Scholar] [CrossRef]
- Li, Z.H.A.O.; Diaoxia, H.E.; Jian, Z.H.A.O. Spatial Distribution and Factors Influencing Elderly Care Service Facilities based on Accessibility Evaluation—Taking Wuxi City as an Example. J. Resour. Ecol. 2024, 15, 130–139. [Google Scholar] [CrossRef]
- Doi, S.; Ide, H.; Takeuchi, K.; Fujita, S.; Takabayashi, K. Estimation and evaluation of future demand and supply of healthcare services based on a patient access area model. Int. J. Environ. Res. Public Health 2017, 14, 1367. [Google Scholar] [CrossRef] [PubMed]
- Geletu, G.M. The qualitative and quantitative measurements of quality education for-and-against standards and indicators of high, medium and low performing primary schools in Oromia Regional State, Ethiopia. Education 2024, 3–13, 1–18. [Google Scholar] [CrossRef]
- Zhou, Y.; Xie, H.; Liu, X.; Wang, X.; Wang, Z. From service capacity to spatial equity: Accurately and comprehensively evaluating urban park green space distribution under multi-trips mode. PLoS ONE 2024, 19, e0296629. [Google Scholar] [CrossRef]
- Li, X.; Zhu, J.; Wan, J.; Wang, Z. Equilibrium in adversity: Balancing public service supply and demand during population decline. Humanit. Soc. Sci. Commun. 2024, 11, 1–15. [Google Scholar] [CrossRef]
- Liu, L.; Lyu, H.; Zhao, Y.; Zhou, D. An improved two-step floating catchment area (2SFCA) method for measuring spatial accessibility to elderly care facilities in Xi’an, China. Int. J. Environ. Res. Public Health 2022, 19, 11465. [Google Scholar] [CrossRef] [PubMed]
- Wachs, M.; Kumagai, T.G. Physical accessibility as a social indicator. Socio-Econ. Plan. Sci. 1973, 7, 437–456. [Google Scholar] [CrossRef]
- Peng, R.; Huang, J.; Deng, X. Spatiotemporal evolution and influencing factors of the allocation of social care resources for the older adults in China. Int. J. Equity Health 2023, 22, 222. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Li, Y.; Ji, Q.; Zhao, J.; Ge, Z.; Zhou, Q.; Sun, Q. A research on spatial configuration characteristics and social performance evaluation of public sports facilities in shanghai based on geographic information system (GIS). PLoS ONE 2025, 20, e0310585. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Gesang, D.; Zhou, G.; Li, Y. Spatial disparities and dynamic evolution of professional public health resource supply level in Beijing, China. BMC Public Health 2024, 24, 2524. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Liu, T.; Wang, J.; Liu, L.; Peng, Z.; Wu, H. What Are the Pivotal Factors Influencing Housing Prices? A Spatiotemporal Dynamic Analysis Across Market Cycles from Upturn to Downturn in Wuhan. Land 2025, 14, 356. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. External effects of neighbourhood parks and landscape elements on high-rise residential value. Land Use Policy 2010, 27, 662–670. [Google Scholar] [CrossRef]
- Dambon, J.A.; Fahrländer, S.S.; Karlen, S.; Lehner, M.; Schlesinger, J.; Sigrist, F.; Zimmermann, A. Examining the vintage effect in hedonic pricing using spatially varying coefficients models: A case study of single-family houses in the Canton of Zurich. Swiss J. Econ. Stat. 2022, 158, 2. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, Y.; Zhang, L. Do educational facilities affect housing price? An empirical study in Hangzhou, China. Habitat Int. 2014, 42, 155–163. [Google Scholar] [CrossRef]
- Peng, T.C.; Chiang, Y.H. The non-linearity of hospitals’ proximity on property prices: Experiences from Taipei, Taiwan. J. Prop. Res. 2015, 32, 341–361. [Google Scholar] [CrossRef]
- An, S.; Jang, H.; Kim, H.; Song, Y.; Ahn, K. Assessment of street-level greenness and its association with housing prices in a metropolitan area. Sci. Rep. 2023, 13, 22577. [Google Scholar] [CrossRef]
- Yu, P.; Yung, E.H.; Chan, E.H.; Zhang, S.; Wang, S.; Chen, Y. The spatial effect of accessibility to public service facilities on housing prices: Highlighting the housing equity. ISPRS Int. J. Geo-Inf. 2023, 12, 228. [Google Scholar] [CrossRef]
- Lee, H.; Han, H.; Pettit, C. Capturing the distance decay effect of amenities on housing price using explainable artificial intelligence. Appl. Geogr. 2025, 174, 103486. [Google Scholar] [CrossRef]
- Soltani, A.; Heydari, M.; Aghaei, F.; Pettit, C.J. Housing price prediction incorporating spatio-temporal dependency into machine learning algorithms. Cities 2022, 131, 103941. [Google Scholar] [CrossRef]
- Sharma, H.; Harsora, H.; Ogunleye, B. An optimal house price prediction algorithm: XGBoost. Analytics 2024, 3, 30–45. [Google Scholar] [CrossRef]
- Li, T.; Xu, H.; Sun, H. Spatial Patterns and Multi-Dimensional Impact Analysis of Urban Street Quality Perception under Multi-Source Data: A Case Study of Wuchang District in Wuhan, China. Appl. Sci. 2023, 13, 11740. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, K.; Bi, Q.; Cui, W.; Li, G. Landscape patterns and building functions for urban land-use classification from remote sensing images at the block level: A case study of Wuchang District, Wuhan, China. Remote Sens. 2020, 12, 1831. [Google Scholar] [CrossRef]
- Yang, X.; Cao, Y.; Wu, A.; Guo, M.; Dong, Z.; Tang, L. Accessibility assessment of buildings based on multi-source spatial data: Taking Wuhan as a case study. ISPRS Int. J. Geo-Inf. 2021, 10, 701. [Google Scholar] [CrossRef]
- National Development and Reform Commission (NDRC); Ministry of Housing and Urban-Rural Development (MOHURD); Ministry of Natural Resources (MNR). Guidelines for the Construction of Embedded Community Service Facilities in Urban Communities (Trial); Government of China: Beijing, China, 2021. [Google Scholar]
- Ministry of Natural Resources of the People’s Republic of China. Technical Guidelines for Community Life Circle Planning; China Standards Press: Beijing, China, 2024. [Google Scholar]
- Wang, J.; Zhou, J. Spatial evaluation of the accessibility of public service facilities in Shanghai: A community differentiation perspective. PLoS ONE 2022, 17, e0268862. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Wang, F. Measures of spatial accessibility to health care in a GIS environment: Synthesis and a case study in the Chicago region. Environ. Plan. B Plan. Des. 2003, 30, 865–884. [Google Scholar] [CrossRef]
- Lei, Z.; Lei, P. An Improved Algorithm for Accessibility of Public Transport Stations Based on Two Step Moving Search Method. World Sci. Res. 2024, 10, 25–34. [Google Scholar]
- Tao, Z.; Cheng, Y.; Liu, J. Hierarchical two-step floating catchment area (2SFCA) method: Measuring the spatial accessibility to hierarchical healthcare facilities in Shenzhen, China. Int. J. Equity Health 2020, 19, 164. [Google Scholar] [CrossRef]
- Tao, Z.; Yao, Z.; Kong, H.; Duan, F.; Li, G. Spatial accessibility to healthcare services in Shenzhen, China: Improving the multi-modal two-step floating catchment area method by estimating travel time via online map APIs. BMC Health Serv. Res. 2018, 18, 345. [Google Scholar] [CrossRef]
- Tercan, E.; Eymen, A.; Urfalı, T.; Saracoglu, B. A sustainable framework for spatial planning of photovoltaic solar farms using GIS and multi-criteria assessment approach in Central Anatolia, Turkey. Land Use Policy 2021, 102, 105272. [Google Scholar] [CrossRef]
- Ogryzek, M.; Jaskulski, M. Applying methods of exploratory data analysis and methods of modeling the unemployment rate in spatial terms in Poland. Appl. Sci. 2025, 15, 4136. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, M.; Na, J.; Lang, Z.; Lu, Y.; Yang, J. Incorporation of spatially heterogeneous area partitioning into vector-based cellular automata for simulating urban land-use changes. Land 2023, 12, 1893. [Google Scholar] [CrossRef]
- Nie, X.; Li, M.; Lu, J.; Wang, B. Research on Buffer Calculation Model of Critical Chain Based on Adjacency Information Entropy. Buildings 2023, 13, 942. [Google Scholar] [CrossRef]
- Song, X.; Du, L.; Wang, Z. Correlation Analysis of Urban Road Network Structure and Spatial Distribution of Tourism Service Facilities at Multi-Scales Based on Tourists’ Travel Preferences. Buildings 2024, 14, 914. [Google Scholar] [CrossRef]
- Rey-Blanco, D.; Zofio, J.; Gonzalez-Arias, J. Improving hedonic housing price models by integrating optimal accessibility indices into regression and random forest analyses. Expert Syst. Appl. 2024, 235, 121059. [Google Scholar] [CrossRef]
- Cellmer, R.; Cichulska, A.; Bełej, M. Spatial analysis of housing prices and market activity with the geographically weighted regression. ISPRS Int. J. Geo-Inf. 2020, 9, 380. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, Z.; Lan, X. Impact of China’s referral reform on the equity and spatial accessibility of healthcare resources: A case study of Beijing. Soc. Sci. Med. 2019, 235, 112386. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Zheng, S.; Wang, R. The capitalization of subway access in home value: A repeat-rentals model with supply constraints in Beijing. Transp. Res. Part A Policy Pract. 2015, 80, 104–115. [Google Scholar] [CrossRef]
- Gu, Z.; Tang, M.; Luo, X.; Feng, J. Examination of the impacts of hospital accessibility on housing prices: Heterogeneity across attributes, space and price quantiles. J. Hous. Built Environ. 2024, 39, 179–200. [Google Scholar] [CrossRef]
- Yang, H.J.; Song, J.; Choi, M.J. Measuring the externality effects of commercial land use on residential land value: A case study of Seoul. Sustainability 2016, 8, 432. [Google Scholar] [CrossRef]
- Liu, Z.; Ye, J.; Ren, G.; Feng, S. The effect of school quality on house prices: Evidence from Shanghai, China. Land 2022, 11, 1894. [Google Scholar] [CrossRef]
- Huang, Y.; Dall’Erba, S. Does proximity to school still matter once access to your preferred school zone has already been secured? J. Real Estate Financ. Econ. 2021, 62, 548–577. [Google Scholar] [CrossRef]
- Rong, D.; Biscaya, S. Exploration of supply–demand gaps of urban community-based elderly care facilities in Shanghai. City Built Environ. 2025, 3, 10. [Google Scholar] [CrossRef]
- Hu, Y.; Sherlock, P.; Huang, J.; Knopf, H.T.; Hall, J.M. Unveiling spatial mismatch in childcare supply and demand: An excess commuting analysis of home-to-childcare distance in subsidized families. J. Transp. Geogr. 2024, 116, 103829. [Google Scholar] [CrossRef]
- Laziou, G.; Lemoy, R.; Texier, M.L. Radial analysis and scaling of housing prices in French urban areas. Environ. Plan. B Urban Anal. City Sci. 2025, 52, 1147–1162. [Google Scholar] [CrossRef]
- Daams, M.N.; Sijtsma, F.J.; Veneri, P. Mixed monetary and non-monetary valuation of attractive urban green space: A case study using Amsterdam house prices. Ecol. Econ. 2019, 166, 106430. [Google Scholar] [CrossRef]
- Mohammad, S.I.; Graham, D.J.; Melo, P.C.; Anderson, R.J. A Meta-Analysis of the Impact of Rail Projects on Land and Property Values. Transp. Res. Part A Policy Pract. 2013, 50, 158–170. [Google Scholar] [CrossRef]
- Liu, Y.; Gu, H.; Shi, Y. Spatial accessibility analysis of medical facilities based on public transportation networks. Int. J. Environ. Res. Public Health 2022, 19, 16224. [Google Scholar] [CrossRef]
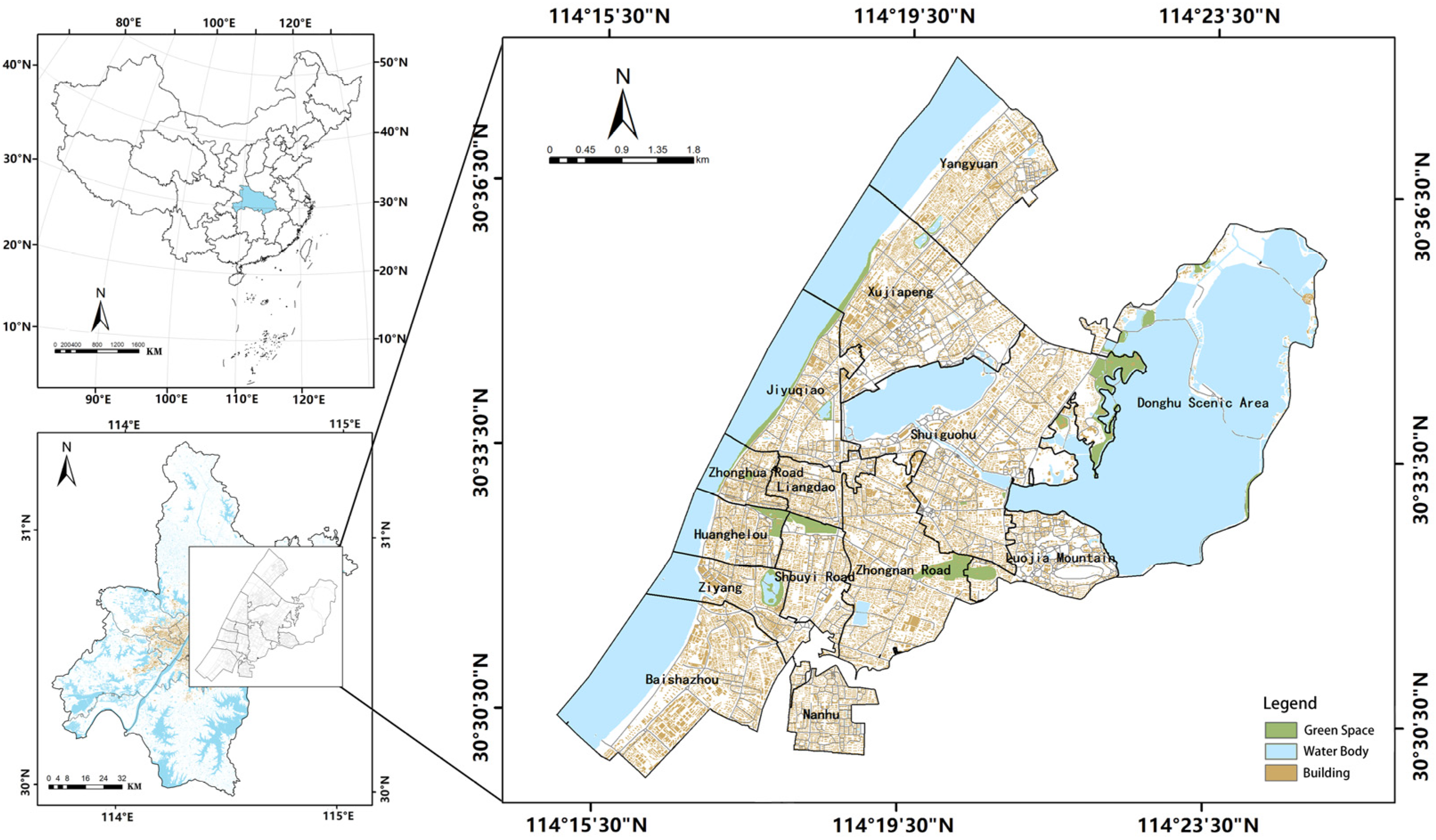
| Data Type | Source | Description | Year |
|---|---|---|---|
| Road Network Data | OSM Map | Includes expressways, main urban roads, secondary roads, local streets, rural roads, and pedestrian paths | 2024 |
| River and Water System Data | OSM Map | Includes the Yangtze River, Han River, and urban lakes | 2024 |
| Study Area Boundaries and Subdistricts | Amap Open Platform | Includes Wuchang District boundary and administrative boundaries of subdistricts | 2024 |
| Residential Community Data | Anjuke (Real Estate Platform) | Includes coordinates, number of households, greening ratio, and housing prices collected from listings | 2024 |
| POI Data for Public Service Facilities | Amap API Interface | POI data on community public service facilities | 2024 |
| Demographic Statistics | Wuchang District People’s Government | Subdistrict-level population size and average household size from the 7th National Census | 2020 |
| Category | Method | Function | Application |
|---|---|---|---|
| Supply–demand Evaluation | Improved 2SFCA | Integrates facility supply, population demand, and distance decay | Measures accessibility of multiple facility types |
| IDW | Estimates spatial values with distance weighting | Simulates the distribution of supply–demand ratios and accessibility values | |
| Value Effects | Spatial Autocorrelation | Identifies spatial clustering and dependence | Tests spatial clustering of housing price data |
| Buffer Analysis | Defines service areas based on threshold distance | Determines facility coverage areas | |
| MGWR | Identifies spatial heterogeneity at multiple scales | Examines variations in the effects of accessibility on housing prices |
| Value Range | Equity Level |
|---|---|
| 0 < G < 0.2 | Absolute equity |
| 0.2 ≤ G < 0.3 | Relatively equitable |
| 0.3 ≤ G < 0.4 | Moderately equitable |
| 0.4 ≤ G < 0.5 | Large disparity (Warning level) |
| 0.5 ≤ G < 1 | Severe disparity (Critical level) |
| Level | Entropy Value Range | Remarks |
|---|---|---|
| Very Low | <0.33 | Significantly below the district average |
| Low | 0.33–0.67 | Below the district average |
| Medium | 0.67–1.50 | Close to the district average |
| High | 0.67–1.50 | Above the district average |
| Very High | >3.00 | Significantly above the district average |
| Subdistrict | Low Accessibility—Low Price | High Accessibility—Low Price | Low Accessibility—High Price | High Accessibility—High Price |
|---|---|---|---|---|
| Nanhu | 0.84 | 0.28 | 4.32 | 2.56 |
| Shuiguohu | 1.60 | 0.48 | 3.72 | 2.19 |
| Donghu Scenic Area | 1.60 | 0.00 | 4.40 | 2.00 |
| Luojiashan | 1.20 | 1.20 | 3.90 | 1.70 |
| Huanghelou | 2.03 | 3.05 | 1.25 | 1.67 |
| Liangdaojie | 3.27 | 2.53 | 1.28 | 0.93 |
| Zhonghualu | 3.94 | 1.80 | 1.37 | 0.89 |
| Zhongnanlu | 4.06 | 1.19 | 1.93 | 0.83 |
| Xujiapeng | 3.18 | 1.92 | 2.16 | 0.74 |
| Shouyilu | 3.87 | 2.60 | 0.88 | 0.65 |
| Ziyang | 4.89 | 1.14 | 1.36 | 0.62 |
| Jiyuqiao | 3.54 | 1.45 | 2.41 | 0.60 |
| Yangyuan | 4.99 | 1.23 | 1.49 | 0.28 |
| Baishazhou | 6.78 | 0.40 | 0.76 | 0.07 |
| Total | 45.79 | 19.27 | 31.23 | 15.73 |
| Variable Type | Variable Code | Variable | Quantification Method | Expected Sign |
|---|---|---|---|---|
| Spatial Attributes | X1 | Floor Area Ratio | Actual value (unitless) | − |
| X2 | Green Coverage Ratio | Actual value (%) | + | |
| X3 | Building Height Category | Dummy variable: low-rise = 1, multi-storey = 2, mid-rise = 3, high-rise = 4, super high-rise = 5 | Uncertain | |
| X4 | Building Age | Actual value (years) | − | |
| Neighborhood Attributes | X5 | Distance to the nearest park or green space | Actual value (km) | − |
| X6 | Distance to the nearest hospital | Actual value (km) | Uncertain | |
| X7 | Number of primary and secondary schools within 1.5 km | Actual value (count) | + | |
| X8 | Distance to the nearest metro station | Actual value (km) | − | |
| X9 | Distance to the nearest commercial district | Actual value (km) | + | |
| Locational Attributes | X10 | Accessibility to elderly care facilities within a 15 min walking range | Actual value (unitless) | + |
| X11 | Accessibility to child care facilities within a 15 min walking range | Actual value (unitless) | + | |
| X12 | Accessibility to children recreation facilities within a 15 min walking range | Actual value (unitless) | + | |
| X13 | Accessibility to community meal facilities within a 15 min walking range | Actual value (unitless) | + | |
| X14 | Accessibility to domestic convenience facilities within a 15 min walking range | Actual value (unitless) | + | |
| X15 | Accessibility to health care facilities within a 15 min walking range | Actual value (unitless) | + | |
| X16 | Accessibility to sports fitness facilities within a 15 min walking range | Actual value (unitless) | + | |
| X17 | Accessibility to cultural recreation facilities within a 15 min walking range | Actual value (unitless) | + |
| Variable | Mean | Minimum | Maximum |
|---|---|---|---|
| X2 | 0.043 | 0.034 | 0.055 |
| X3 | 0.128 | −0.607 | 1.043 |
| X4 | −0.112 | −0.203 | −0.055 |
| X6 | 0.099 | 0.089 | 0.109 |
| X7 | −0.150 | −0.160 | −0.136 |
| X8 | −0.088 | −0.115 | −0.054 |
| X9 | 0.181 | −0.629 | 1.079 |
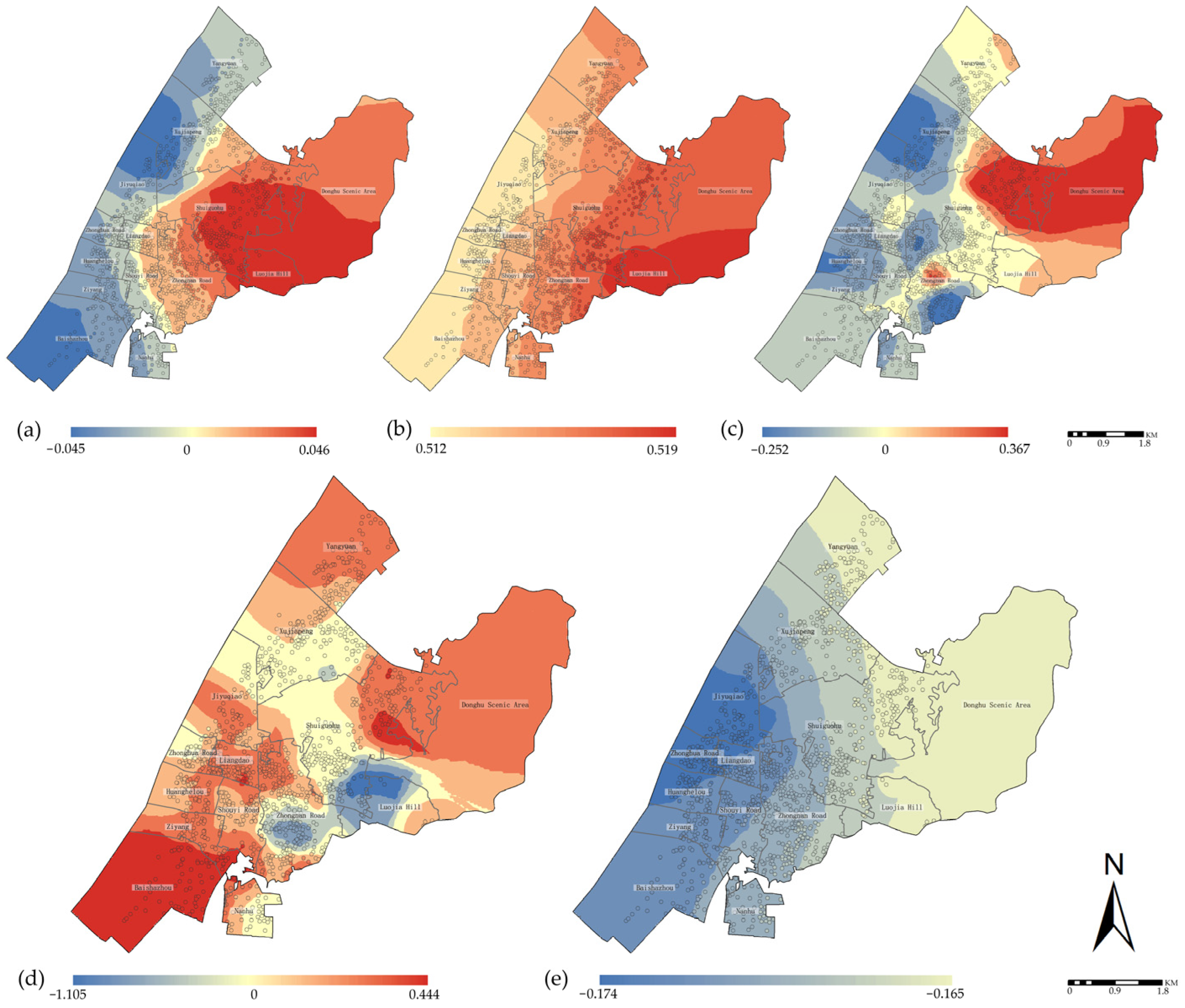
| X10 | 0.002 | −0.045 | 0.046 |
| X11 | 0.515 | 0.513 | 0.519 |
| X12 | −0.024 | −0.253 | 0.367 |
| X16 | −0.111 | −1.105 | 0.444 |
| X17 | −0.170 | −0.175 | −0.165 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Zhang, X.; Yu, X. A Study on the Supply–Demand Matching and Spatial Value Effects of Community Public Service Facilities: A Case Study of Wuchang District, Wuhan. Buildings 2025, 15, 3293. https://doi.org/10.3390/buildings15183293
Lin Y, Zhang X, Yu X. A Study on the Supply–Demand Matching and Spatial Value Effects of Community Public Service Facilities: A Case Study of Wuchang District, Wuhan. Buildings. 2025; 15(18):3293. https://doi.org/10.3390/buildings15183293
Chicago/Turabian StyleLin, Ying, Xian Zhang, and Xiao Yu. 2025. "A Study on the Supply–Demand Matching and Spatial Value Effects of Community Public Service Facilities: A Case Study of Wuchang District, Wuhan" Buildings 15, no. 18: 3293. https://doi.org/10.3390/buildings15183293
APA StyleLin, Y., Zhang, X., & Yu, X. (2025). A Study on the Supply–Demand Matching and Spatial Value Effects of Community Public Service Facilities: A Case Study of Wuchang District, Wuhan. Buildings, 15(18), 3293. https://doi.org/10.3390/buildings15183293







