Experimental Study on Local Bearing Capacity of Concrete Reinforced with Spiral Stirrups
Abstract
1. Introduction
2. Experimental Program
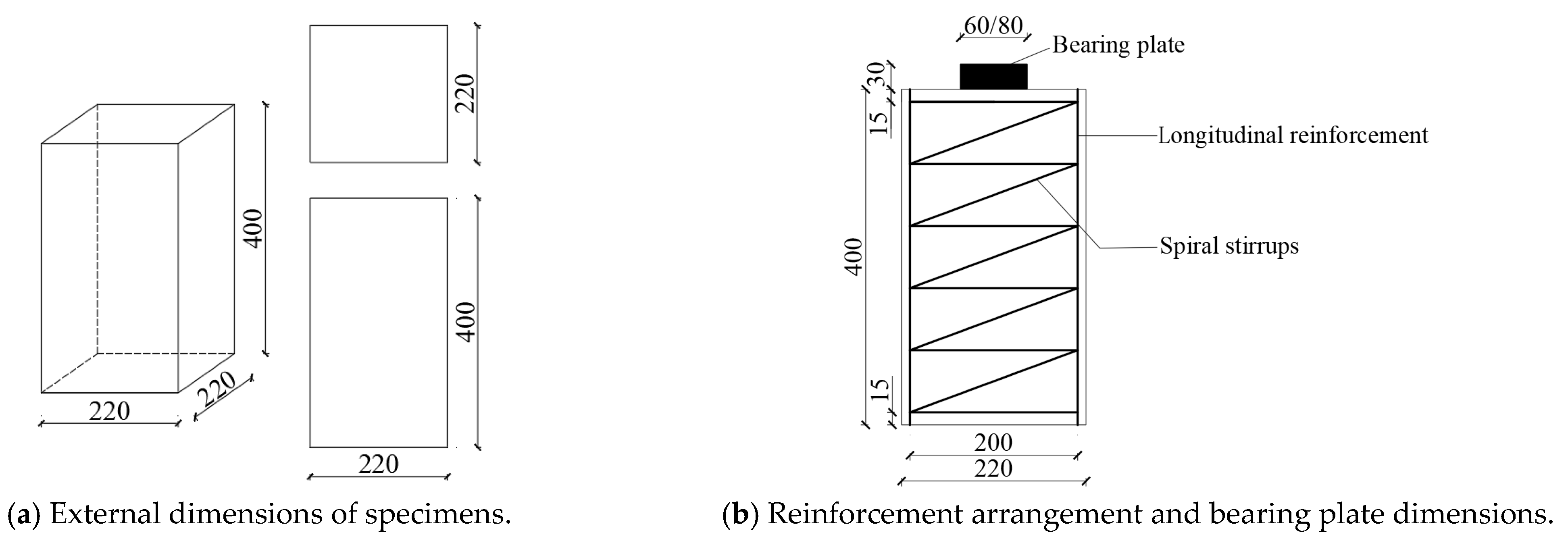
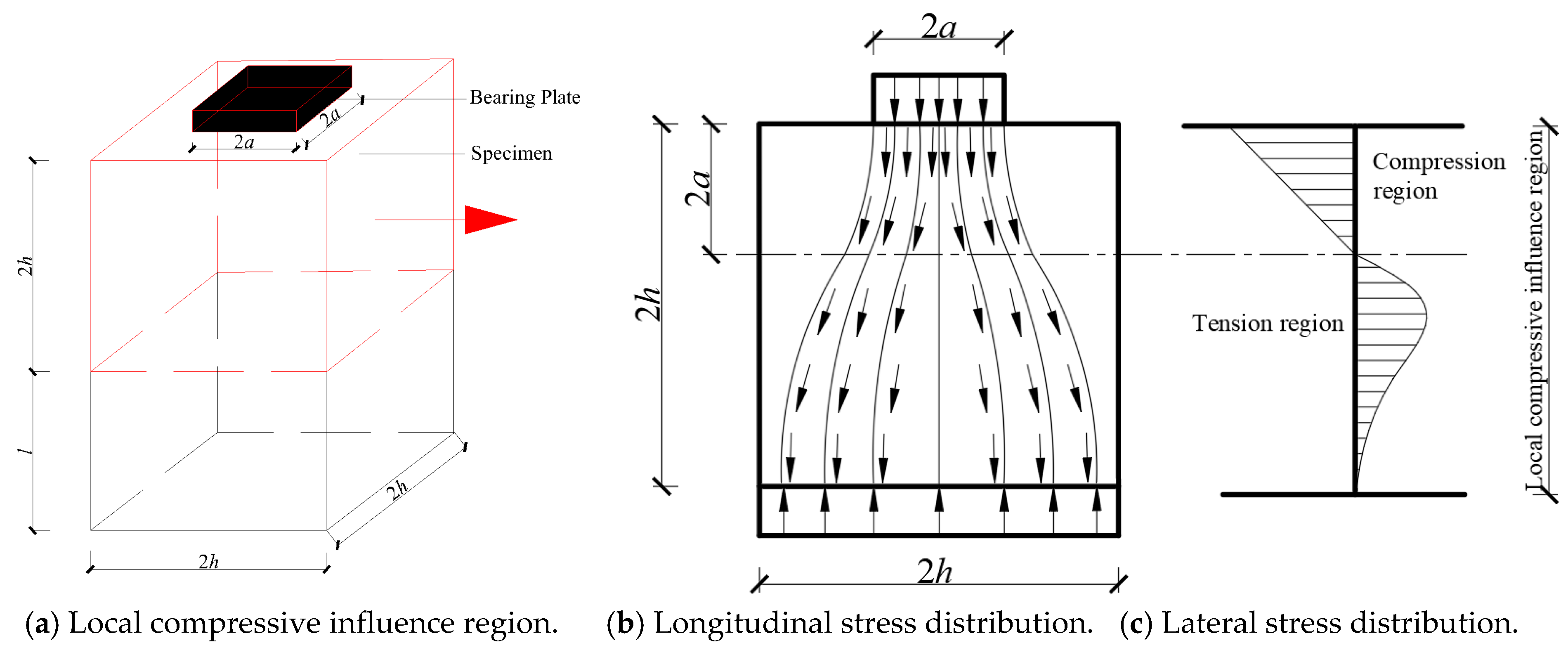
2.1. Specimen Design
2.2. Arrangement of Strain Gauges
2.3. Concrete Casting and Curing
2.4. Material Properties
2.5. Flowchart of Specimen Fabrication
3. Test Loading and Measurement Scheme
3.1. Test Loading Scheme
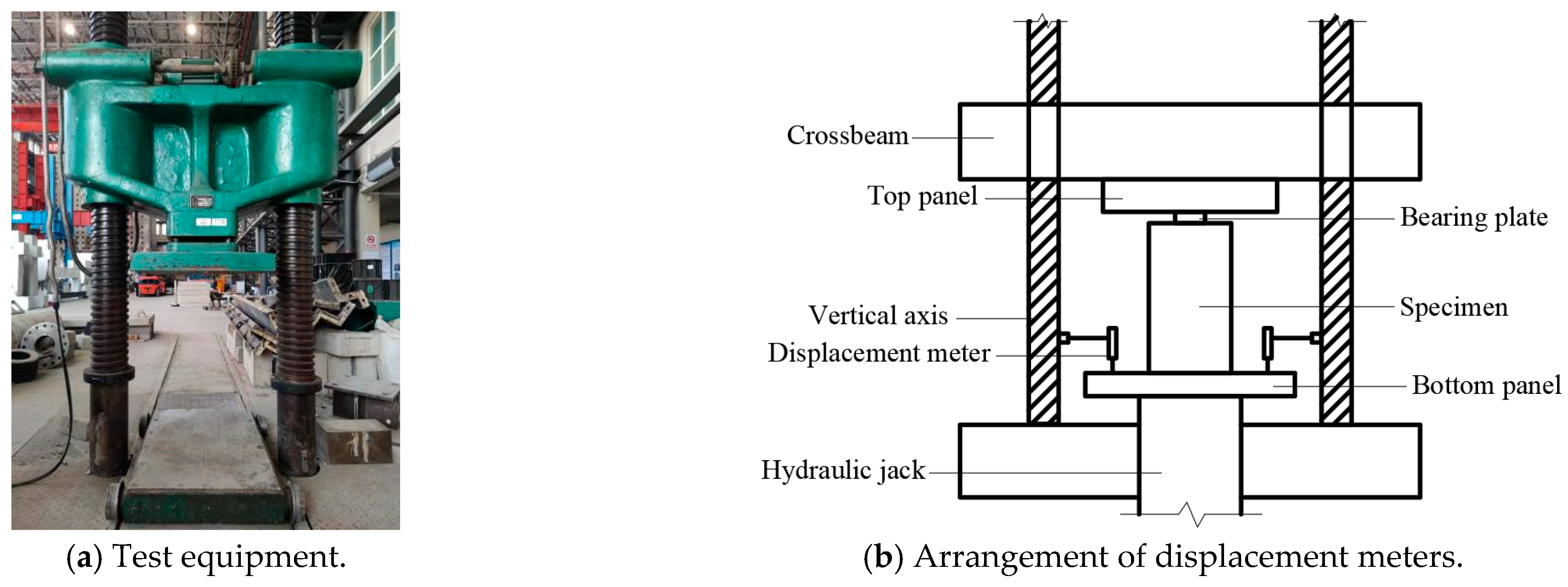
3.2. Test Measurement Scheme
4. Experimental Phenomena and Results
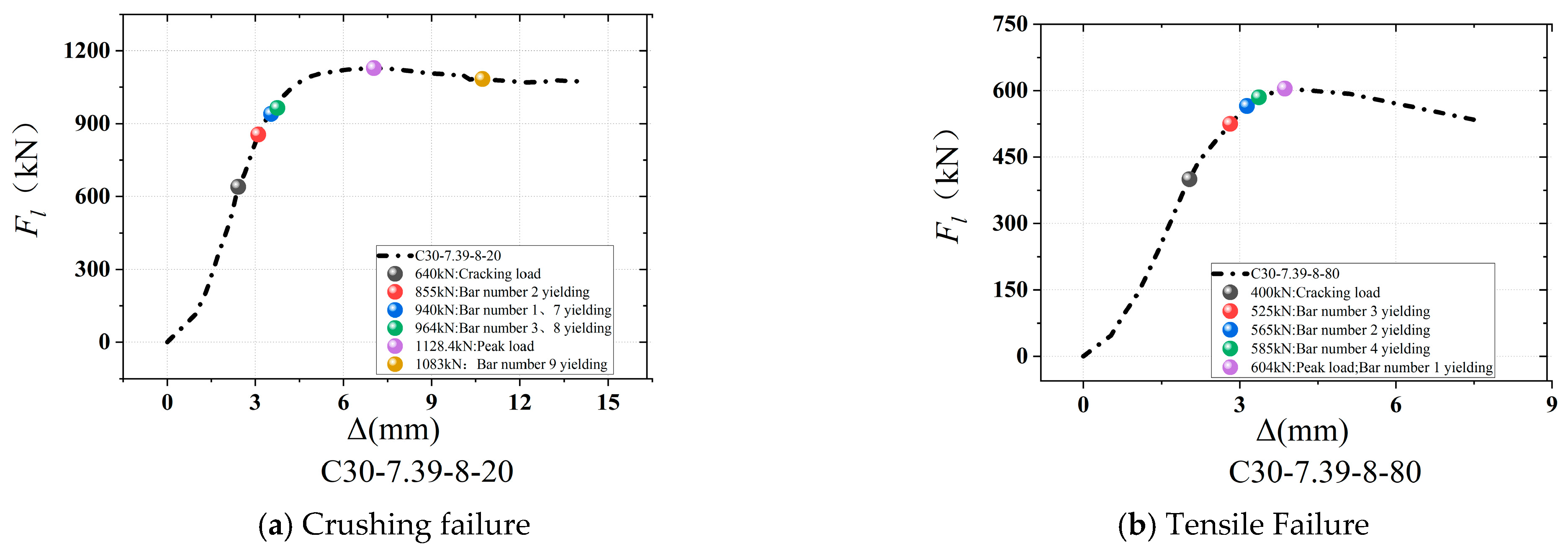
4.1. Crushing Failure
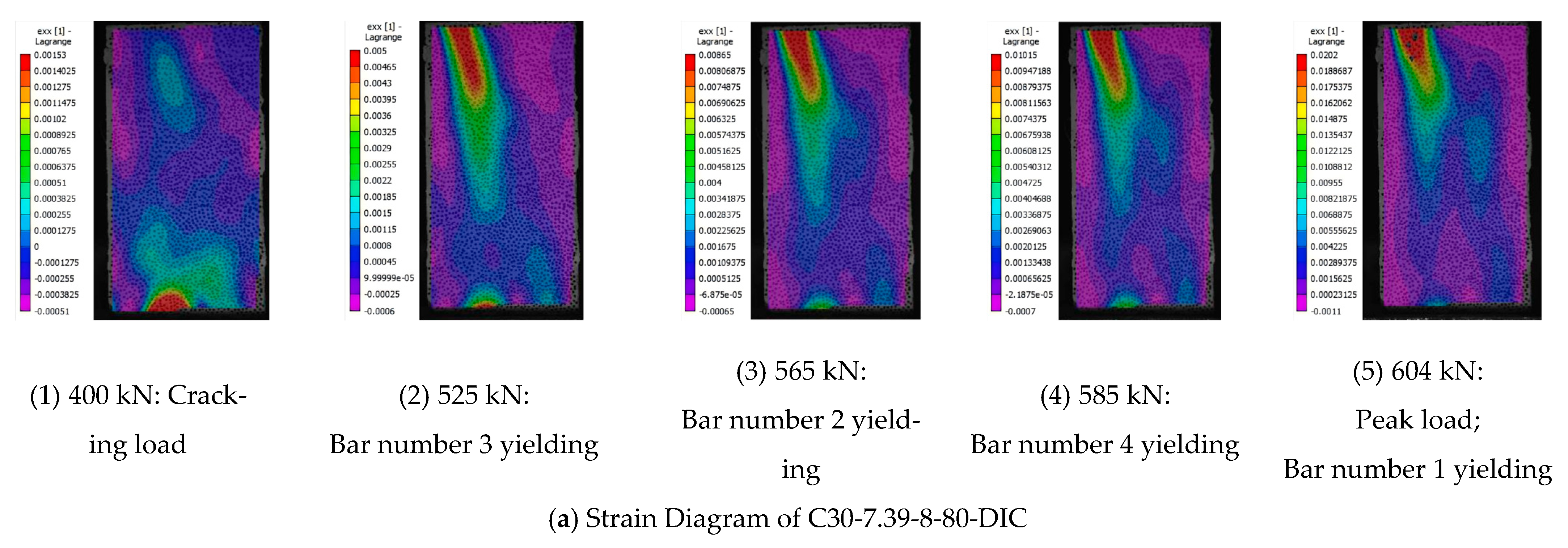
4.2. Tensile Failure
4.3. Experimental Results
5. Local Bearing Capacity Calculation
5.1. Theoretical Equation Calculation
5.2. Analysis of Influencing Factors
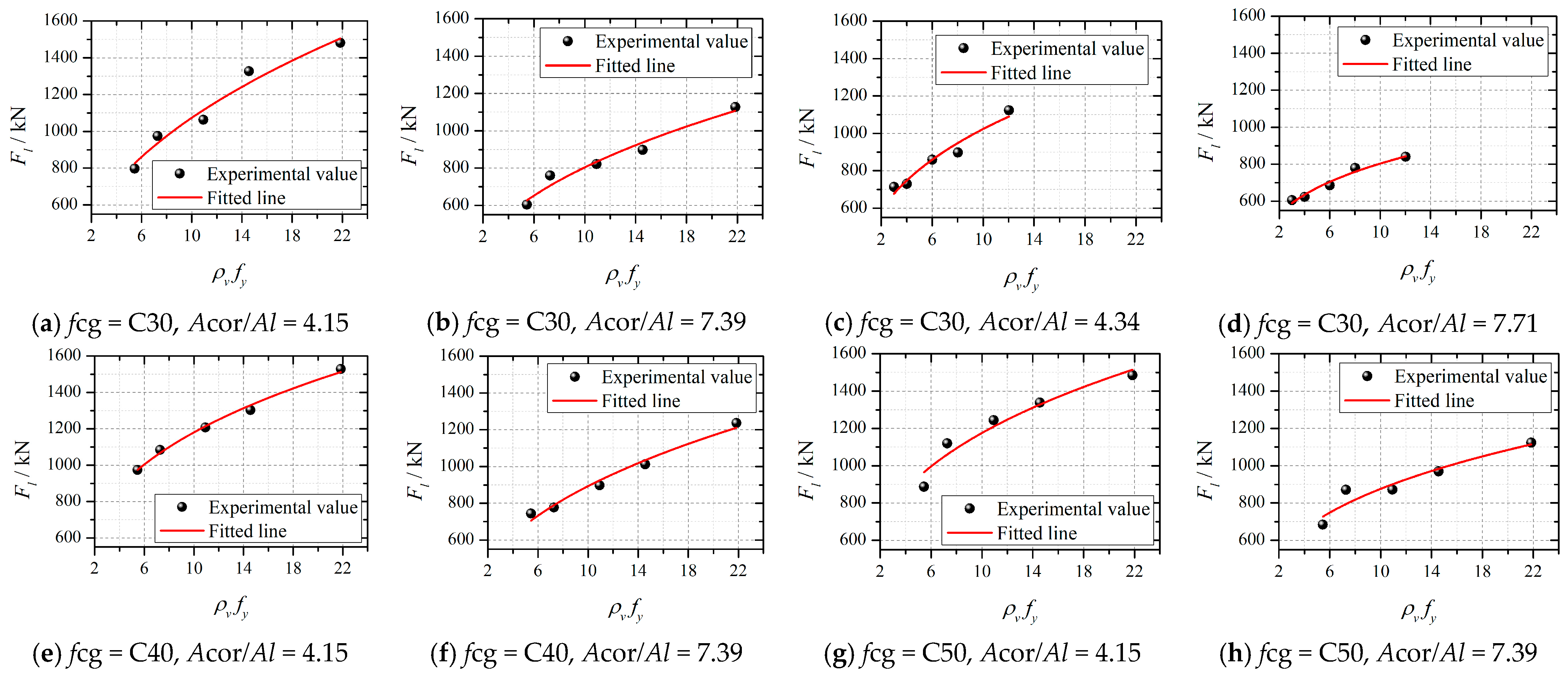
5.2.1. Influence of ρvfy
5.2.2. Influence of Acor/Al
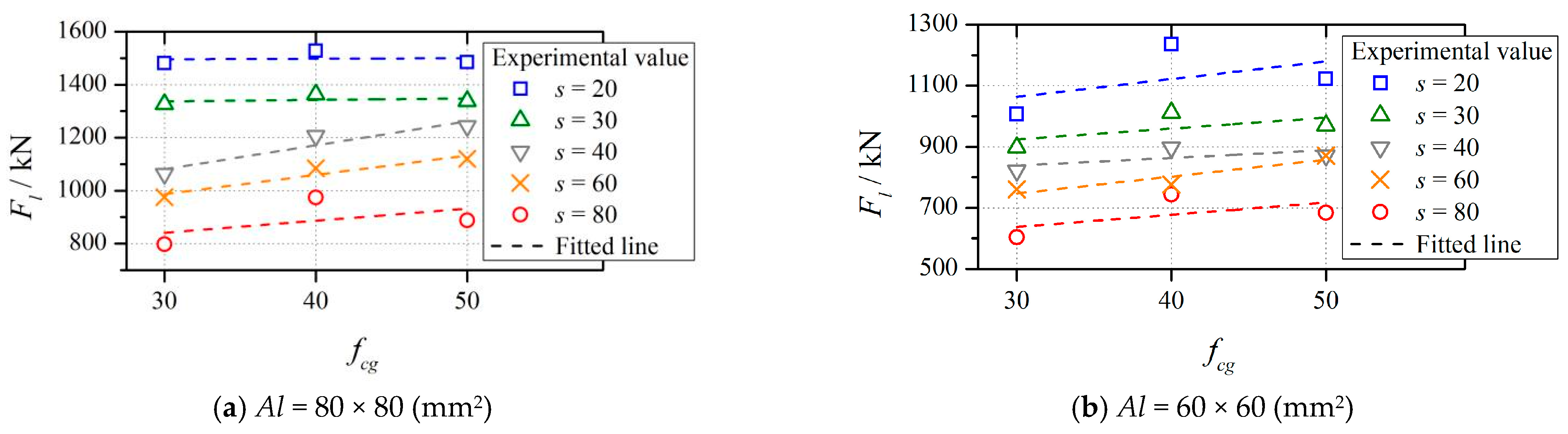
5.2.3. Influence of fcg
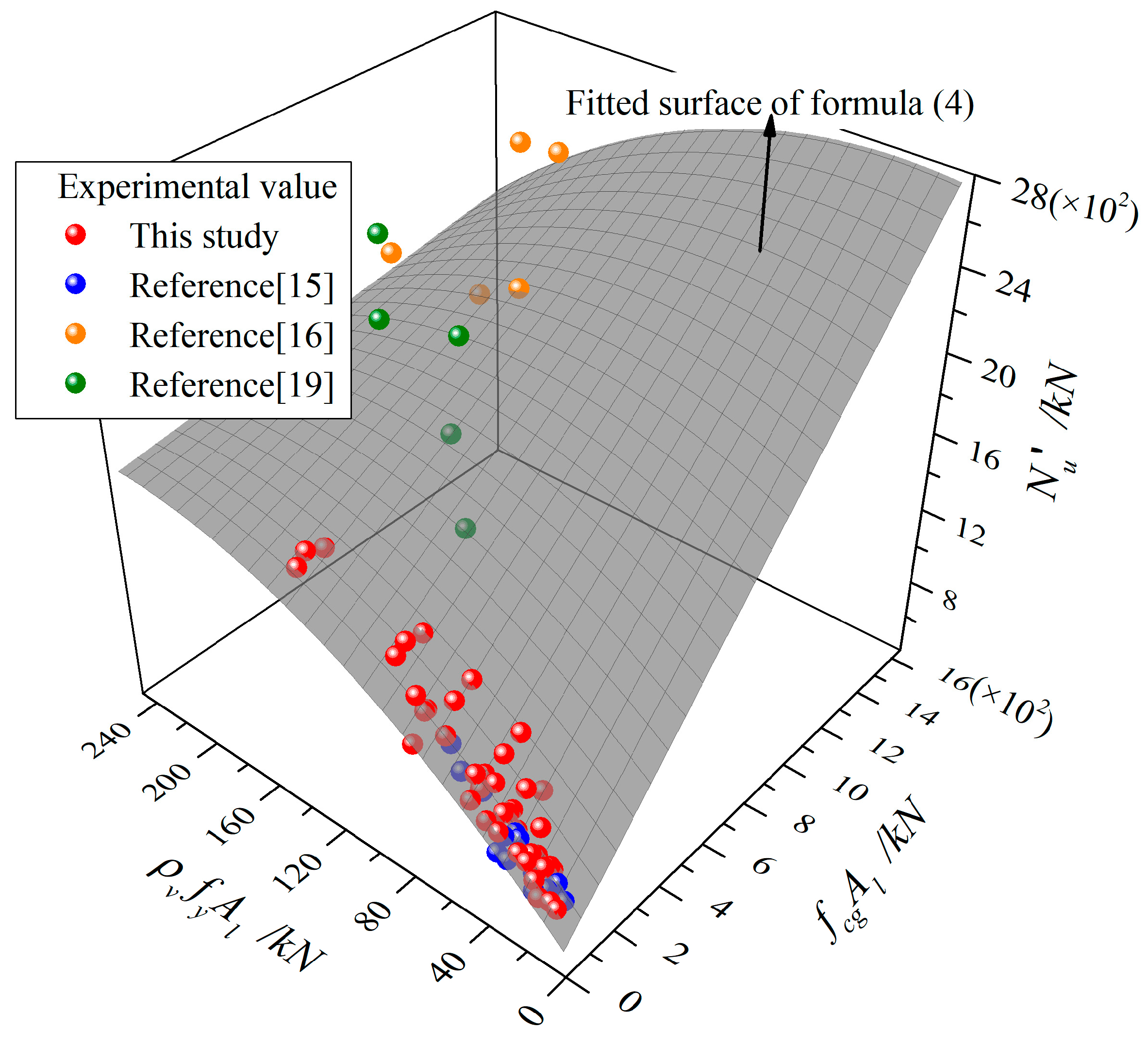
5.3. Fitting of Local Bearing Capacity Calculation Equation Nu’
5.4. Verification of the Equation
5.5. Discussion
6. Conclusions
- An analysis and classification of the failure types observed in the 40 specimens revealed two primary failure modes: tensile failure and crushing failure. The tensile failure occurred in the tension region, when the strength of the tensile region was lower than that of the compression region, and the crushing failure, which occurred in the compression region, when the strength of the tensile region was higher than that of the compression region.
- Based on analysis of the experimental parameters, it was found that the local bearing capacity of concrete Fl increases as the Acor/Al decreases, with an enhancement of 23.0%. Furthermore, a reduction in s would result in a 65.4% improvement in Fl compared to the initial value. Moreover, increasing the d results in a 24.7% improvement in Fl.
- Reducing the s increases the number of stirrups in the tension region, thereby enhancing the lateral restraint provided by the stirrups and further improving the strength of the tension region. It would contribute to an increase in the Fl. A smaller Acor/Al results in a larger proportion of the load area within the specimen, making its behavior more similar to axial compression and enhancing the Fl. Additionally, a larger d provided a stronger constraining effect on the concrete, which also improved the Fl.
- The experimental data indicated that there is a proportional relationship between fcg and Fl. A comparison of the local bearing capacities of C40 and C50 specimens revealed that the influence of concrete strength on bearing capacity must consider whether the spiral stirrups could fully exert their restraining effect on the concrete. During the experiments, single-point yielding of the stirrups was observed at crack locations in the C50 concrete specimens upon failure. Under the action of peak load, there were main cracks on the surface of the specimen. This indicated that the strain of the spiral stirrups was mainly concentrated at the main cracks. Therefore, the local bearing capacity of the C50 specimen failed to reach its maximum potential.
- Based on normative equation derived from theoretical research, the local bearing capacity Nu′ were recalculated. The calculation equation for Nu′ was developed in terms of fc,kAl and ρvfyAl. Subsequently, experimental data from studies on spiral stirrups reinforced concrete were collected to verify the accuracy and applicability of the proposed formula.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| fcg | Concrete strength grade | Es | Elastic modulus of spiral stirrup |
| d | Stirrup diameter | Nu′ | Local bearing capacity of calculation Equation (4) |
| ρv | Volumetric ratio of the spiral stirrups | Acor | Core area |
| Acor/Al | Ratio of core area to load area | Al | Load area |
| Fl | Local bearing capacity of experimental values | βc | Concrete strength influence coefficient |
| s | Stirrup spacing | α | Reduction coefficient |
| fcu,m | Measured compressive strength of concrete cubes | θc | Ratio between the experimental values and the theoretically calculated values |
| fc,m | Measured values for axial compressive strength of concrete | βl | Concrete strength grade adjustment coefficient |
| fc,k | Standard value for axial compressive strength of concrete | βcor | Coefficient for improving the local bearing capacity of indirect reinforcing |
| ft,k | Standard value of axial tensile strength of concrete | Nu | Local bearing capacity of calculation in Equation (1) |
| fy | Yield strength of spiral stirrup | θ | Ratio of calculated to experimental values. |
| fu | Ultimate strength of spiral stirrup | αc | Ratio of experimental values to calculated values |
References
- Musa, M.M.E.; Xiong, X.; Zhang, Y. Experiment and Validation of Local Bearing Capacity for Ultra-High-Performance Concrete Confined with Stirrups. Materials 2022, 15, 5869. [Google Scholar] [CrossRef] [PubMed]
- Niyogi, S.K. Bearing Strength of Reinforced Concrete Blocks. J. Struct. Div. 1975, 101, 1125–1137. [Google Scholar] [CrossRef]
- Liao, J.J.; Di, B.; Zheng, Y.; Xuan, Z.W.; Zeng, J.J. Shear behavior of circular concrete short columns reinforced with GFRP longitudinal bars and CFRP grid stirrups. Compos. Struct. 2024, 340, 118181. [Google Scholar] [CrossRef]
- ETAG 013-EOTA; ETAG 013 Guideline for European Technical Approval of Post-Tensioning Kits for Prestressing of Structures. European Organisation for Technical Approvals: Brussels, Belgium, 2002.
- Marchao, C.; Lúcio, V.; Ganz, H.R. Efficiency of the confinement reinforcement in anchoragezones of posttensioning tendons. Struct. Concr. 2019, 20, 1182–1198. [Google Scholar] [CrossRef]
- Cai, S.H. Local compressive strength of concrete and reinforced concrete. J. Civ. Eng. 1963, 9, 1–10. [Google Scholar]
- Liu, Y.; Guan, J.; Zhou, F.L.; Wang, C.Z. Methods for controlling tensioning cracks on the end faces of prestressed concrete members. Build. Str. 1980, 3, 9–15. [Google Scholar]
- Cao, S.Y.; Yang, X.K. Working mechanism and strength theory of concrete under local pressure. J. Harbin Univ. Civ. Eng. Archit. 1982, 3, 44–53. [Google Scholar]
- Yang, X.K.; Yang, B.; Meng, F.S. Several problems on local compression of concrete and reinforced concrete. Low Temp. Archit. Technol. 1999, 75, 8–10. [Google Scholar]
- Yang, X.K.; Yang, B.; Liu, L.N. Wedge theory of concrete and reinforced concrete under local pressure (I). Low Temp. Archit. Technol. 1999, 78, 10–12. [Google Scholar]
- Yang, X.K.; Yang, B.; Dong, L. Wedge theory of concrete and reinforced concrete under local pressure (II). Low Temp. Archit. Technol. 2000, 79, 18–19. [Google Scholar]
- Wei, S.M. The discussion of “local compressive strength and failure mechanism of concrete”. China Civ. Eng. J. 1985, 18, 82–87. [Google Scholar]
- Yang, Y.H.; Xue, A. Local compressive limit strength theory of high strength concrete. Sichuan Build. Sci. 1995, 4, 42–46. [Google Scholar]
- Yang, Y.H.; Xue, A. Analysis and calculation of local compressive cracking strength of high strength concrete. Sichuan Build. Sci. 1996, 1, 24–27. [Google Scholar]
- Cao, S.Y.; Yang, X.K.; Xu, K.Y. Experimental study on local bearing capacity of reinforced concrete. J. Harbin Univ. Civ. Eng. Archit. 1983, 2, 1–22. [Google Scholar]
- Zheng, W.Z.; Zhao, J.W.; Wang, Y.; Zhou, W. Local pressure test of concrete with Acor/Al < 1.35 and Ab extended to side beam. J. Harbin Inst. Technol. 2010, 42, 1536–1542. [Google Scholar]
- Zhao, J.W.; Zheng, W.Z. The calculation of the local compressive capacity of prestressed concrete and the configuration of indirect steel bars at the end. Ind. Constr. 2007, 11, 47–52. [Google Scholar]
- Gai, L.Q.; Zheng, W.Z.; Li, S. Indepth study on calculation method of local compression bearing capacity of concrete. J. Harbin Inst. Technol. 2021, 53, 1–11. [Google Scholar]
- Xiao, Z.M. Study on Local Compression Performance of HRB500 Reinforced Lightweight Aggregate Concrete Members. Master’s Thesis, Suzhou University of Science and Technology, Suzhou, China, 2017. [Google Scholar]
- Xiao, Z.M.; Sao, Y.J.; Lao, Y.H.; Zhang, C.Y. Calculation and analysis of local compression capacity of HRB500 reinforced lightweight aggregate concrete members. J. Guangxi Univ. 2018, 43, 103–110. [Google Scholar]
- Xiao, Z.M.; Sao, Y.J. Experimental study on local compression performance of HRB500 reinforced lightweight aggregate concrete beam ends. China Concr. Cem. Prod. 2018, 1, 68–72. [Google Scholar]
- Miao, T.M.; Yang, J.; Zhou, Y.; Zhan, M.Q.; Wang, B.; Zheng, W.Z. Model for calculating local bearing capacity of concrete with spiral stirrups. Constr. Build. Mater. 2023, 389, 131762. [Google Scholar] [CrossRef]
- Miao, T.M.; Zheng, W.Z. Local bearing capacity of concrete under the combined action of pressure force and bond stress. Constr. Build. Mater. 2019, 226, 152–161. [Google Scholar] [CrossRef]
- Miao, T.M.; Yang, J.; Zhou, Y.; Sha, L.R.; Zheng, W.Z. Method for calculating local bearing capacity of concrete under bond stress from reinforcement in straight anchor section. Structures 2022, 46, 1796–1807. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, H.B. Bearing capacity of steel fiber reinforced reactive powder concrete confined by spirals. Mater. Struct. 2015, 48, 2613–2628. [Google Scholar] [CrossRef]
- Wang, L.F.; Wu, H.Q.; Liu, L.; Xiao, Z.W. Enhancement of local concrete compression performance by incorporating ultra-high performance concrete (uhpc) tube. Multidiscip. Model. Mater. Struct. 2022, 18, 856–878. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.Z.; Xu, T.; Wang, Y. Artificial neural network model for predicting the local compression capacity of stirrups-confined concrete. Structures 2022, 41, 943–956. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.Z.; Zhou, W.; Wang, Y. General Prediction Models for Local Bearing Capacity of Concrete. KSCE J. Civ. Eng. 2023, 27, 4865–4875. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.Z.; Zhou, W. Compressive failure mechanism of ultra-high performance concrete with coarse aggregates with orthogonal reinforcements for predicting the bearing capacity: Experimental and numerical investigation. Eng. Fract. Mech. 2024, 298, 109915. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.Z.; Zhou, W.; Wang, Y. Local compression capacity of ultra-high performance concrete containing coarse aggregate: Testing and calculation method. J. Build. Eng. 2023, 76, 107411. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.Z.; Zhou, W.; Jiang, Z.S.; Cui, Y.N. Local compression capacity of steel fiber reinforced ultra-high performance concrete containing coarse aggregate. Compos. Struct. 2023, 318, 117084. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.Z.; Zhou, W.; Jiang, Z.S.; Wang, Y. Experiment and validation of local bearing capacity for reactive powder concrete confned with high strength spirals. Arch. Civ. Mech. Eng. 2022, 22, 40. [Google Scholar] [CrossRef]
- Li, H.D.; Zeng, J.; Ahmad, A. A study on improving energy flexibility in building engineering through generalized prediction models: Enhancing local bearing capacity of concrete for engineering structures. Eng. Struct. 2024, 303, 117051. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2015.
- Post-Tensioning Institute (PTI). Post-Tensioning Manual, 6th ed.; The USA: Post-Tensioning Institute: Phoenix, AZ, USA, 2006. [Google Scholar]
- Wu, C.; Su, Y.L.; Chen, T.; Sun, C.J.; Zhang, Z.H. Bearing capacity of post-tensioned concrete local anchorage zones under special bearing plates with multiple bearing surfaces. Eng. Struct. 2025, 335, 120338. [Google Scholar] [CrossRef]
- Yan, Y.; Jin, X.; Chang, W.; Wang, J.L.; Zheng, W.Z. Behavior of concrete-filled steel tube columns reinforced with steel-reinforced under local compression. J. Constr. Steel Res. 2025, 234, 109750. [Google Scholar] [CrossRef]
- Pohribnyi, V.; Dovzhenko, O.; Kuznietsova, I.; Usenko, D. The improved technique for calculating the concrete elements strength under local compression. MATEC Web Conf. 2018, 230, 02025. [Google Scholar] [CrossRef][Green Version]
- Wei, Y.Y.; Wu, Y.F. Experimental Study of Concrete Columns with Localized Failure. J. Compos. Constr. 2016, 20, 04016032. [Google Scholar] [CrossRef]
- Wu, Y.F.; Wei, Y.Y. Stress–Strain Modeling of Concrete Columns with Localized Failure: An Analytical Study. J. Compos. Constr. 2016, 20, 04015071. [Google Scholar] [CrossRef]
- Han, L.H.; Liu, W.; Yang, Y.F. Behaviour of concrete-filled steel tubular stub columns subjected to axially local compression. J. Constr. Steel Res. 2008, 64, 377–387. [Google Scholar] [CrossRef]
- Ganesh Prabhu, G.; Sundarraja, M.C. Design model for concrete-filled steel tube columns under full and local compression loads. Proc. Inst. Civ. Eng. Struct. Build. 2022, 175, 682–696. [Google Scholar] [CrossRef]
- JahanMohammadi, A.; Soltani, M. Toward combined local-average stress field modeling of reinforced concrete. Eng. Struct. 2016, 111, 394–410. [Google Scholar] [CrossRef]
- Chang, W.; Zheng, W.Z. A method for calculating the tensile stress of constrained stirrup under peak compressive load in a stirrup constrained concrete column. In Proceedings of the 33rd National Conference on Structural Engineering, Fuxin, China, 18 October 2024; Volume 1, pp. 254–260. [Google Scholar]
- Chang, W.; Zheng, W.Z.; Hao, M.J. Analytical models for stress–strain behaviour of UHPC confined with spiral stirrups. Constr. Build. Mater. 2023, 409, 133784. [Google Scholar] [CrossRef]
- Chang, W.; Hao, M.J.; Zheng, W.Z. Compressive behavior of UHPC confined by both spiral stirrups and carbon fiber-reinforced polymer (CFRP). Constr. Build. Mater. 2020, 230, 117007. [Google Scholar] [CrossRef]
- GB 50107-2010; Standard for Inspection and Assessment of Concrete Strength. Ministry of Housing and Urban-Rural Development of the People's Republic of China. China Architecture and Building Press: Beijing, China, 2010.
- GB/T 1499.2-2024; Steel for the Reinforcement of Concrete—Part 2: Hot Rolled Ribbed Bars. Standardization Administration of China. Standards Press of China: Beijing, China, 2024.
- Kabir, H.; Wu, J.; Dahal, S.; Joo, T.; Garg, N. Automated estimation of cementitious sorptivity via computer vision. Nat. Commun. 2024, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
- ACI 318-19; Building Code Requirements for Structural Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2019.









| Specimens | Acor/Al | Section Width /mm | Plate Width 2a /mm | Spiral Stirrups | Specimens | Acor/Al | Specimen Width /mm | Plate Width 2a /mm | Spiral Stirrups | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| d @ s /mm | ρv | d @ s /mm | ρv | ||||||||
| C30-4.15-d8-1 | 4.15 | 220 | 80 | 8@80 | 0.014 | C40-4.15-d8-21 | 4.15 | 220 | 80 | 8@80 | 0.014 |
| C30-4.15-d8-2 | 4.15 | 220 | 80 | 8@60 | 0.018 | C40-4.15-d8-22 | 4.15 | 220 | 80 | 8@60 | 0.018 |
| C30-4.15-d8-3 | 4.15 | 220 | 80 | 8@40 | 0.027 | C40-4.15-d8-23 | 4.15 | 220 | 80 | 8@40 | 0.027 |
| C30-4.15-d8-4 | 4.15 | 220 | 80 | 8@30 | 0.036 | C40-4.15-d8-24 | 4.15 | 220 | 80 | 8@30 | 0.036 |
| C30-4.15-d8-5 | 4.15 | 220 | 80 | 8@20 | 0.055 | C40-4.15-d8-25 | 4.15 | 220 | 80 | 8@20 | 0.055 |
| C30-7.39-d8-6 | 7.39 | 220 | 60 | 8@80 | 0.014 | C40-7.39-d8-26 | 7.39 | 220 | 60 | 8@80 | 0.014 |
| C30-7.39-d8-7 | 7.39 | 220 | 60 | 8@60 | 0.018 | C40-7.39-d8-27 | 7.39 | 220 | 60 | 8@60 | 0.018 |
| C30-7.39-d8-8 | 7.39 | 220 | 60 | 8@40 | 0.027 | C40-7.39-d8-28 | 7.39 | 220 | 60 | 8@40 | 0.027 |
| C30-7.39-d8-9 | 7.39 | 220 | 60 | 8@30 | 0.036 | C40-7.39-d8-29 | 7.39 | 220 | 60 | 8@30 | 0.036 |
| C30-7.39-d8-10 | 7.39 | 220 | 60 | 8@20 | 0.055 | C40-7.39-d8-30 | 7.39 | 220 | 60 | 8@20 | 0.055 |
| C30-4.34-d8-11 | 4.34 | 220 | 80 | 6@80 | 0.008 | C50-4.15-d8-31 | 4.15 | 220 | 80 | 8@80 | 0.014 |
| C30-4.34-d8-12 | 4.34 | 220 | 80 | 6@60 | 0.010 | C50-4.15-d8-32 | 4.15 | 220 | 80 | 8@60 | 0.018 |
| C30-4.34-d8-13 | 4.34 | 220 | 80 | 6@40 | 0.015 | C50-4.15-d8-33 | 4.15 | 220 | 80 | 8@40 | 0.027 |
| C30-4.34-d8-14 | 4.34 | 220 | 80 | 6@30 | 0.020 | C50-4.15-d8-34 | 4.15 | 220 | 80 | 8@30 | 0.036 |
| C30-4.34-d8-15 | 4.34 | 220 | 80 | 6@20 | 0.031 | C50-4.15-d8-35 | 4.15 | 220 | 80 | 8@20 | 0.055 |
| C30-7.71-d8-16 | 7.71 | 220 | 60 | 6@80 | 0.008 | C50-7.39-d8-36 | 7.39 | 220 | 60 | 8@80 | 0.014 |
| C30-7.71-d8-17 | 7.71 | 220 | 60 | 6@60 | 0.020 | C50-7.39-d8-37 | 7.39 | 220 | 60 | 8@60 | 0.018 |
| C30-7.71-d8-18 | 7.71 | 220 | 60 | 6@40 | 0.015 | C50-7.39-d8-38 | 7.39 | 220 | 60 | 8@40 | 0.027 |
| C30-7.71-d8-19 | 7.71 | 220 | 60 | 6@30 | 0.020 | C50-7.39-d8-39 | 7.39 | 220 | 60 | 8@30 | 0.036 |
| C30-7.71-d8-20 | 7.71 | 220 | 60 | 6@20 | 0.031 | C50-7.39-d8-40 | 7.39 | 220 | 60 | 8@20 | 0.055 |
| fcg (MPa) | Type of Cement | Material Consumption (kg/m3) | Water–Binder Ratio mw/mc | Sand–Stone Ratio ms/mg | |||
|---|---|---|---|---|---|---|---|
| Water mw | Cement mc | Sand ms | Stone mg | ||||
| C30 | P·O 42.5 | 190 | 400 | 615 | 1195 | 0.48 | 34% |
| C40 | P·O 42.5 | 170 | 430 | 610 | 1180 | 0.40 | 34% |
| C50 | P·O 42.5 | 155 | 430 | 617 | 1198 | 0.36 | 34% |
| fcg (MPa) | fcu,m/MPa | fc,m/MPa | fc,k/MPa | ft,k/MPa |
|---|---|---|---|---|
| C30 | 39.94 | 30.35 | 17.84 | 1.93 |
| C40 | 48.54 | 36.89 | 23.63 | 2.25 |
| C50 | 59.08 | 44.90 | 34.22 | 2.76 |
| Type | d/mm | fy/MPa | fu/MPa | Es/GPa |
|---|---|---|---|---|
| HRB400 | 6 | 459 | 635 | 210 |
| 8 | 445 | 620 | 210 |
| Specimen | fc,k/ MPa | βl | α | fy/ MPa | βcor | Nu/kN | Fl/kN | θc | Failure Mode |
|---|---|---|---|---|---|---|---|---|---|
| C30-4.15-d8-1 | 17.84 | 2.75 | 1.00 | 445 | 2.038 | 472.45 | 797.00 | 1.69 | Tensile failure |
| C30-4.15-d8-2 | 17.84 | 2.75 | 1.00 | 445 | 2.038 | 525.27 | 975.00 | 1.86 | Tensile failure |
| C30-4.15-d8-3 | 17.84 | 2.75 | 1.00 | 445 | 2.038 | 630.91 | 1063.00 | 1.68 | Tensile failure |
| C30-4.15-d8-4 | 17.84 | 2.75 | 1.00 | 445 | 2.038 | 736.56 | 1327.00 | 1.80 | Crushing failure |
| C30-4.15-d8-5 | 17.84 | 2.75 | 1.00 | 445 | 2.038 | 947.85 | 1481.00 | 1.56 | Crushing failure |
| C30-7.39-d8-6 | 17.84 | 3.67 | 1.00 | 445 | 2.717 | 354.34 | 604.00 | 1.70 | Tensile failure |
| C30-7.39-d8-7 | 17.84 | 3.67 | 1.00 | 445 | 2.717 | 393.95 | 760.00 | 1.93 | Tensile failure |
| C30-7.39-d8-8 | 17.84 | 3.67 | 1.00 | 445 | 2.717 | 473.19 | 822.00 | 1.74 | Tensile failure |
| C30-7.39-d8-9 | 17.84 | 3.67 | 1.00 | 445 | 2.717 | 552.42 | 898.00 | 1.63 | Crushing failure |
| C30-7.39-d8-10 | 17.84 | 3.67 | 1.00 | 445 | 2.717 | 710.88 | 1007.00 | 1.42 | Crushing failure |
| C30-4.34-d8-11 | 17.84 | 2.75 | 1.00 | 445 | 2.082 | 403.12 | 714.00 | 1.77 | Tensile failure |
| C30-4.34-d8-12 | 17.84 | 2.75 | 1.00 | 459 | 2.082 | 436.57 | 730.00 | 1.67 | Tensile failure |
| C30-4.34-d8-13 | 17.84 | 2.75 | 1.00 | 459 | 2.082 | 497.87 | 860.00 | 1.73 | Tensile failure |
| C30-4.34-d8-14 | 17.84 | 2.75 | 1.00 | 459 | 2.082 | 559.16 | 898.00 | 1.61 | Crushing failure |
| C30-4.34-d8-15 | 17.84 | 2.75 | 1.00 | 459 | 2.082 | 681.75 | 1124.00 | 1.65 | Crushing failure |
| C30-7.71-d8-16 | 17.84 | 3.67 | 1.00 | 459 | 2.776 | 304.44 | 605.00 | 1.99 | Tensile failure |
| C30-7.71-d8-17 | 17.84 | 3.67 | 1.00 | 459 | 2.776 | 327.43 | 623.00 | 1.90 | Tensile failure |
| C30-7.71-d8-18 | 17.84 | 3.67 | 1.00 | 459 | 2.776 | 373.40 | 685.00 | 1.83 | Crushing failure |
| C30-7.71-d8-19 | 17.84 | 3.67 | 1.00 | 459 | 2.776 | 419.37 | 779.00 | 1.86 | Crushing failure |
| C30-7.71-d8-20 | 17.84 | 3.67 | 1.00 | 459 | 2.776 | 511.31 | 840.00 | 1.64 | Crushing failure |
| C40-4.15-d8-21 | 23.63 | 2.75 | 1.00 | 445 | 2.038 | 574.27 | 974.30 | 1.70 | Tensile failure |
| C40-4.15-d8-22 | 23.63 | 2.75 | 1.00 | 445 | 2.038 | 627.09 | 1084.00 | 1.73 | Tensile failure |
| C40-4.15-d8-23 | 23.63 | 2.75 | 1.00 | 445 | 2.038 | 732.74 | 1207.00 | 1.65 | Tensile failure |
| C40-4.15-d8-24 | 23.63 | 2.75 | 1.00 | 445 | 2.038 | 838.38 | 1363.00 | 1.63 | Crushing failure |
| C40-4.15-d8-25 | 23.63 | 2.75 | 1.00 | 445 | 2.038 | 1049.67 | 1528.50 | 1.46 | Crushing failure |
| C40-7.39-d8-26 | 23.63 | 3.67 | 1.00 | 445 | 2.717 | 430.70 | 743.90 | 1.73 | Tensile failure |
| C40-7.39-d8-27 | 23.63 | 3.67 | 1.00 | 445 | 2.717 | 470.32 | 776.50 | 1.65 | Tensile failure |
| C40-7.39-d8-28 | 23.63 | 3.67 | 1.00 | 445 | 2.717 | 549.55 | 897.20 | 1.63 | Tensile failure |
| C40-7.39-d8-29 | 23.63 | 3.67 | 1.00 | 445 | 2.717 | 628.78 | 1012.00 | 1.61 | Crushing failure |
| C40-7.39-d8-30 | 23.63 | 3.67 | 1.00 | 445 | 2.717 | 787.25 | 1236.00 | 1.57 | Crushing failure |
| C50-4.15-d8-31 | 34.22 | 2.75 | 0.98 | 445 | 2.038 | 760.74 | 888.00 | 1.17 | Tensile failure |
| C50-4.15-d8-32 | 34.22 | 2.75 | 0.98 | 445 | 2.038 | 813.56 | 1120.00 | 1.38 | Tensile failure |
| C50-4.15-d8-33 | 34.22 | 2.75 | 0.98 | 445 | 2.038 | 919.20 | 1244.00 | 1.35 | Tensile failure |
| C50-4.15-d8-34 | 34.22 | 2.75 | 0.98 | 445 | 2.038 | 1024.85 | 1338.00 | 1.31 | Crushing failure |
| C50-4.15-d8-35 | 34.22 | 2.75 | 0.98 | 445 | 2.038 | 1236.13 | 1485.00 | 1.20 | Crushing failure |
| C50-7.39-d8-36 | 34.22 | 3.67 | 0.98 | 445 | 2.717 | 570.55 | 684.00 | 1.20 | Tensile failure |
| C50-7.39-d8-37 | 34.22 | 3.67 | 0.98 | 445 | 2.717 | 610.17 | 871.00 | 1.43 | Tensile failure |
| C50-7.39-d8-38 | 34.22 | 3.67 | 0.98 | 445 | 2.717 | 689.40 | 872.00 | 1.26 | Crushing failure |
| C50-7.39-d8-39 | 34.22 | 3.67 | 0.98 | 445 | 2.717 | 768.63 | 969.50 | 1.26 | Crushing failure |
| C50-7.39-d8-40 | 34.22 | 3.67 | 0.98 | 445 | 2.717 | 927.10 | 1123.00 | 1.21 | Crushing failure |
| Specimens | Reduction Rate of Fl | Specimens | Reduction Rate of Fl | Specimens | Reduction Rate of Fl | Specimens | Reduction Rate of Fl |
|---|---|---|---|---|---|---|---|
| C30-4.15-d8-1 | 24.2% | C30-4.34-d6-11 | 15.3% | C40-4.15-d8-21 | 23.6% | C50-4.15-d8-31 | 23.0% |
| C30-7.39-d8-6 | C30-7.71-d6-16 | C40-7.39-d8-26 | C50-7.39-d8-36 | ||||
| C30-4.15-d8-2 | 22.1% | C30-4.34-d6-12 | 14.7% | C40-4.15-d8-22 | 28.4% | C50-4.15-d8-32 | 22.2% |
| C30-7.39-d8-7 | C30-7.71-d6-17 | C40-7.39-d8-27 | C50-7.39-d8-37 | ||||
| C30-4.15-d8-3 | 22.7% | C30-4.34-d6-13 | 20.3% | C40-4.15-d8-23 | 25.7% | C50-4.15-d8-33 | 29.9% |
| C30-7.39-d8-8 | C30-7.71-d6-18 | C40-7.39-d8-28 | C50-7.39-d8-38 | ||||
| C30-4.15-d8-4 | 32.3% | C30-4.34-d6-14 | 13.3% | C40-4.15-d8-24 | 22.3% | C50-4.15-d8-34 | 27.5% |
| C30-7.39-d8-9 | C30-7.71-d6-19 | C40-7.39-d8-29 | C50-7.39-d8-39 | ||||
| C30-4.15-d8-5 | 23.8% | C30-4.34-d6-15 | 25.3% | C40-4.15-d8-25 | 19.1% | C50-4.15-d8-35 | 24.4% |
| C30-7.39-d8-10 | C30-7.71-d6-20 | C40-7.39-d8-30 | C50-7.39-d8-40 |
| Specimens | Nu′/kN | θ | Specimens | Nu′/kN | θ | Specimens | Nu′/kN | θ | Specimens | Nu′/kN | θ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C30-4.15-d8-1 | 863.58 | 0.92 | C30-4.34-d8-11 | 732.85 | 0.97 | C40-4.15-d8-21 | 909.44 | 1.07 | C50-4.15-d8-31 | 993.33 | 0.89 |
| C30-4.15-d8-2 | 944.85 | 1.03 | C30-4.34-d8-12 | 784.53 | 0.93 | C40-4.15-d8-22 | 988.62 | 1.10 | C50-4.15-d8-32 | 1068.69 | 1.05 |
| C30-4.15-d8-3 | 1110.48 | 0.96 | C30-4.34-d8-13 | 894.03 | 0.96 | C40-4.15-d8-23 | 1149.55 | 1.05 | C50-4.15-d8-33 | 1221.02 | 1.02 |
| C30-4.15-d8-4 | 1252.26 | 1.06 | C30-4.34-d8-14 | 995.70 | 0.90 | C40-4.15-d8-24 | 1286.63 | 1.06 | C50-4.15-d8-34 | 1349.50 | 0.99 |
| C30-4.15-d8-5 | 1473.26 | 1.01 | C30-4.34-d8-15 | 1175.54 | 0.96 | C40-4.15-d8-25 | 1497.71 | 1.02 | C50-4.15-d8-35 | 1542.42 | 0.96 |
| C30-7.39-d8-6 | 663.87 | 0.91 | C30-7.71-d8-16 | 586.63 | 1.03 | C40-7.39-d8-26 | 691.47 | 1.08 | C50-7.39-d8-36 | 741.95 | 0.92 |
| C30-7.39-d8-7 | 715.81 | 1.06 | C30-7.71-d8-17 | 614.70 | 1.01 | C40-7.39-d8-27 | 742.74 | 1.05 | C50-7.39-d8-37 | 792.01 | 1.10 |
| C30-7.39-d8-8 | 827.21 | 0.99 | C30-7.71-d8-18 | 683.16 | 1.00 | C40-7.39-d8-28 | 852.66 | 1.05 | C50-7.39-d8-38 | 899.21 | 0.97 |
| C30-7.39-d8-9 | 931.07 | 0.96 | C30-7.71-d8-19 | 749.13 | 1.04 | C40-7.39-d8-29 | 955.03 | 1.06 | C50-7.39-d8-39 | 998.86 | 0.97 |
| C30-7.39-d8-10 | 1125.54 | 0.89 | C30-7.71-d8-20 | 873.65 | 0.96 | C40-7.39-d8-30 | 1146.37 | 1.08 | C50-7.39-d8-40 | 1184.45 | 0.95 |
| No. | Acor/Al | Al/mm2 | fc,k/MPa | fy/MPa | ρv | s/mm | Fl/kN | Nu′/kN | αc | References |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.25 | 80 × 80 | 22.46 | 254.7 | 0.038 | 18 | 829.0 | 1050.12 | 0.79 | [15] |
| 2 | 6.25 | 80 × 80 | 19.2 | 254.7 | 0.043 | 16 | 909.0 | 1078.32 | 0.84 | |
| 3 | 6.25 | 80 × 80 | 24.23 | 254.7 | 0.049 | 14 | 960.0 | 1170.70 | 0.82 | |
| 4 | 11.11 | 60 × 60 | 29 | 233.4 | 0.017 | 40 | 589.0 | 650.53 | 0.91 | |
| 5 | 11.11 | 60 × 60 | 28.5 | 233.4 | 0.021 | 33 | 669.0 | 675.85 | 0.99 | |
| 6 | 11.11 | 60 × 60 | 25.6 | 233.4 | 0.026 | 27 | 620.0 | 696.15 | 0.89 | |
| 7 | 11.11 | 60 × 60 | 18.83 | 233.4 | 0.03 | 23 | 620.0 | 691.25 | 0.90 | |
| 8 | 11.11 | 60 × 60 | 25.7 | 233.4 | 0.034 | 20 | 660.0 | 750.27 | 0.88 | |
| 9 | 11.11 | 60 × 60 | 26.7 | 233.4 | 0.038 | 18 | 710.0 | 781.07 | 0.91 | |
| 10 | 11.11 | 60 × 60 | 25.5 | 233.4 | 0.043 | 16 | 800.0 | 807.75 | 0.99 | |
| 11 | 11.11 | 60 × 60 | 26.9 | 233.4 | 0.046 | 15 | 809.0 | 833.03 | 0.97 | |
| 12 | 11.11 | 60 × 60 | 18.43 | 233.4 | 0.046 | 15 | 700.0 | 795.11 | 0.88 | |
| 13 | 11.11 | 60 × 60 | 19.99 | 233.4 | 0.049 | 14 | 805.0 | 821.12 | 1.02 | |
| 14 | 11.11 | 60 × 60 | 18.75 | 233.4 | 0.053 | 13 | 700.0 | 840.71 | 0.87 | |
| 15 | 2.78 | 210 × 210 | 34.81 | 263.0 | 0.017 | 50 | 2336.0 | 2221.66 | 1.03 | [16] |
| 16 | 2.78 | 210 × 210 | 34.81 | 263.0 | 0.019 | 50 | 2315.0 | 2086.60 | 1.02 | |
| 17 | 4.24 | 170 × 170 | 36.48 | 263.0 | 0.021 | 50 | 2102.0 | 2088.75 | 1.05 | |
| 18 | 4.24 | 170 × 170 | 36.48 | 263.0 | 0.024 | 50 | 1988.0 | 2041.49 | 0.98 | |
| 19 | 4.24 | 170 × 170 | 36.48 | 263.0 | 0.031 | 50 | 2001.0 | 1857.83 | 0.95 | |
| 20 | 10.12 | 110 × 110 | 55.48 | 394.0 | 0.031 | 50 | 1720.0 | 1836.37 | 0.99 | [19] |
| 21 | 10.12 | 110 × 110 | 48.18 | 394.0 | 0.027 | 50 | 1400.0 | 1746.59 | 0.87 | |
| 22 | 7.25 | 130 × 130 | 47.18 | 394.0 | 0.024 | 50 | 2050.0 | 1922.94 | 1.11 | |
| 23 | 5.44 | 150 × 150 | 45.64 | 394.0 | 0.027 | 50 | 2100.0 | 1834.23 | 1.00 | |
| 24 | 7.25 | 130 × 130 | 47.18 | 394.0 | 0.031 | 50 | 1950.0 | 1865.14 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhou, Y.; Wang, S.; Ding, Y.; Jiang, D.; Miao, T.; Qie, R.; Bao, X.; Qian, Y.; Wang, B. Experimental Study on Local Bearing Capacity of Concrete Reinforced with Spiral Stirrups. Buildings 2025, 15, 3290. https://doi.org/10.3390/buildings15183290
Li H, Zhou Y, Wang S, Ding Y, Jiang D, Miao T, Qie R, Bao X, Qian Y, Wang B. Experimental Study on Local Bearing Capacity of Concrete Reinforced with Spiral Stirrups. Buildings. 2025; 15(18):3290. https://doi.org/10.3390/buildings15183290
Chicago/Turabian StyleLi, Hongbo, Ying Zhou, Shanshan Wang, Yongjian Ding, Deyu Jiang, Tianming Miao, Ruchen Qie, Xin Bao, Yongmei Qian, and Bo Wang. 2025. "Experimental Study on Local Bearing Capacity of Concrete Reinforced with Spiral Stirrups" Buildings 15, no. 18: 3290. https://doi.org/10.3390/buildings15183290
APA StyleLi, H., Zhou, Y., Wang, S., Ding, Y., Jiang, D., Miao, T., Qie, R., Bao, X., Qian, Y., & Wang, B. (2025). Experimental Study on Local Bearing Capacity of Concrete Reinforced with Spiral Stirrups. Buildings, 15(18), 3290. https://doi.org/10.3390/buildings15183290