Structural Behavior Analysis for Existing Pile Foundations Considering the Effects of Shield Tunnel Construction
Abstract
1. Introduction
1.1. Theoretical and Experimental Research on Tunnel Construction on Nearby Pile Foundations
1.2. Numerical Simulation Research on Tunnel Construction on Nearby Pile Foundations
1.3. Objectives and Scope of Work
- Developing a comprehensive FE model that incorporates geological conditions and construction processes, and validating its accuracy using published experimental data;
- Analyzing the structural performance of pile foundations in different construction stages based on FE results;
- Conducting a parametric FE method analysis to evaluate the structural behavior of pile foundations in tunnel construction, taking into account various horizontal distances between the tunnel and pile foundations, vertical distances between the tunnel and pile foundations, the stiffness of the pile foundations, and grouting pressures.
2. Finite Modeling of Shield Tunneling Beneath Bridge Foundations
2.1. Project Overview
2.2. Material Parameters
2.3. Modeling
2.4. Construction Phase Simulation
2.4.1. Shield Excavation
2.4.2. Segment Assembly and Synchronous Grouting
2.4.3. Hardening of Grouting Body
2.5. Calculation Assumption
- The rock and soil masses are modeled using the Mohr–Coulomb elastic–plastic constitutive model, with stratigraphic layers appropriately simplified based on the site geological investigation report.
- Groundwater effects are neglected due to the tunnel’s location beneath a river, the abundance of water resources in the surrounding area, and the predominance of saturated soil conditions.
- All materials are assumed to behave as homogeneous, isotropic, and continuous media. The relative displacement between the soil and tunnel or pile foundations is disregarded, implying a coupled soil–structure displacement response.
- During the construction of the shield tunnel segment beneath Haiqin Bridge, the existing bridge pile foundations are considered only under normal service conditions; seismic and civil defense scenarios are excluded from the analysis.
3. Numerical Verification
4. Numerical Calculation Results on the Bridge Pile
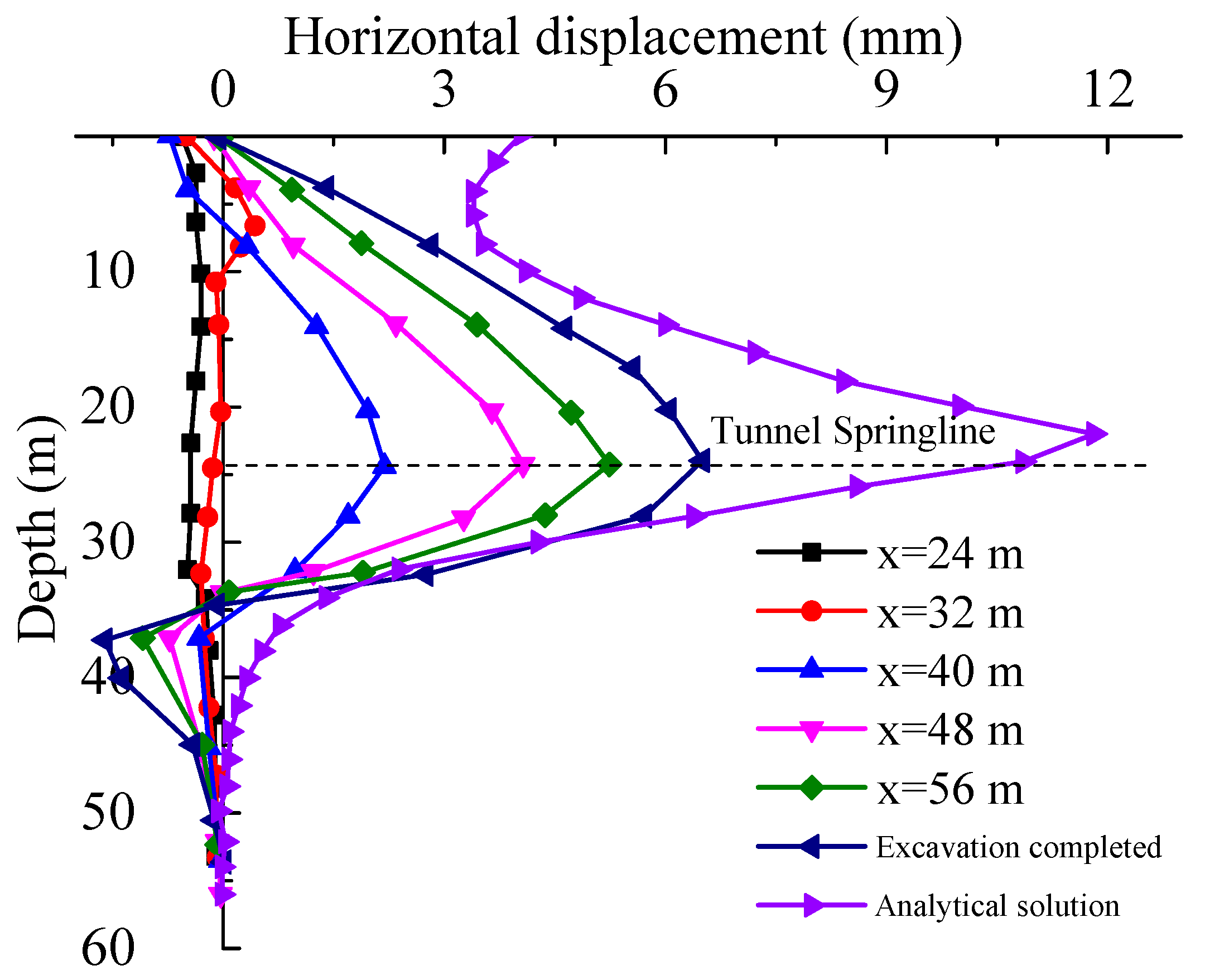
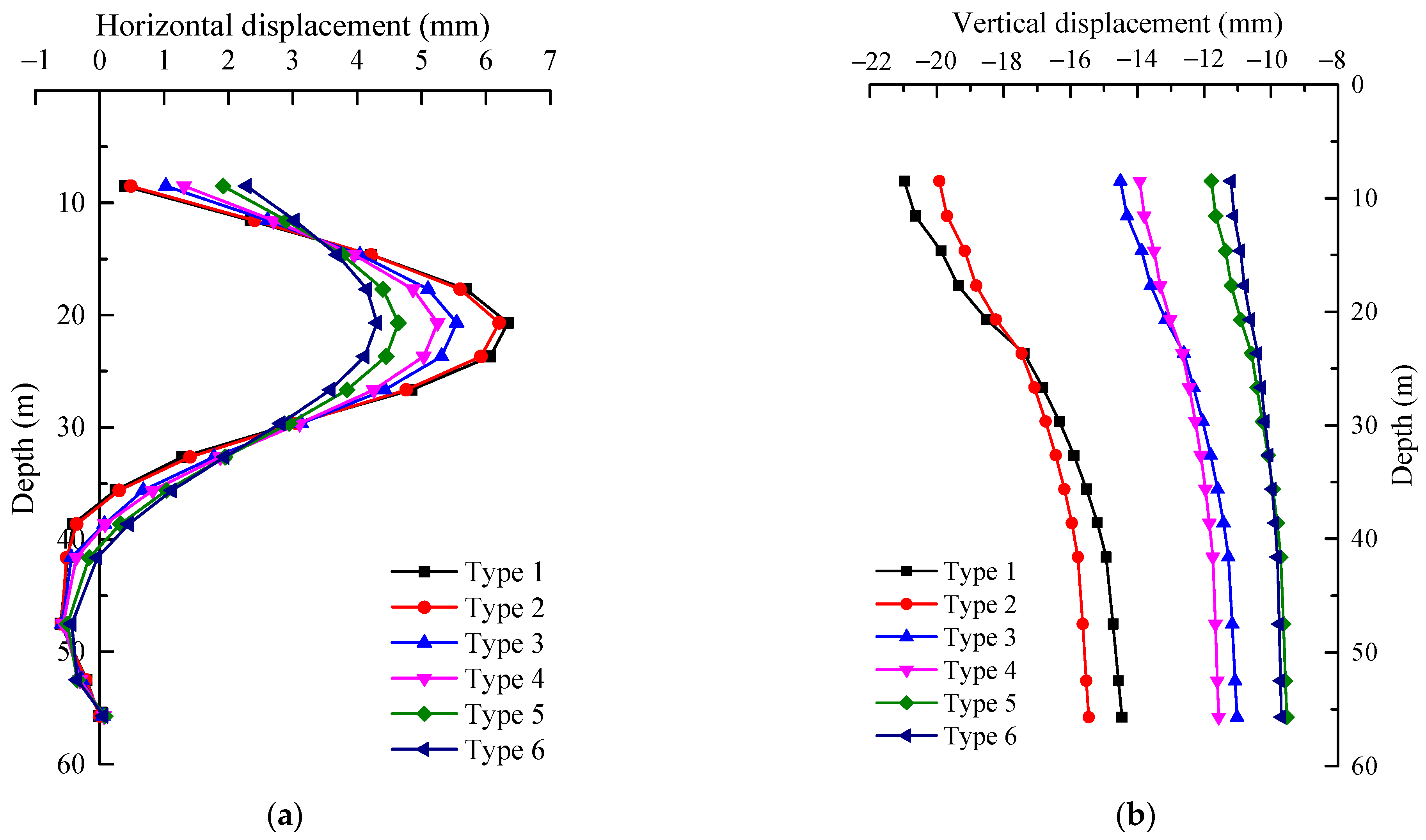
4.1. Horizontal Displacement
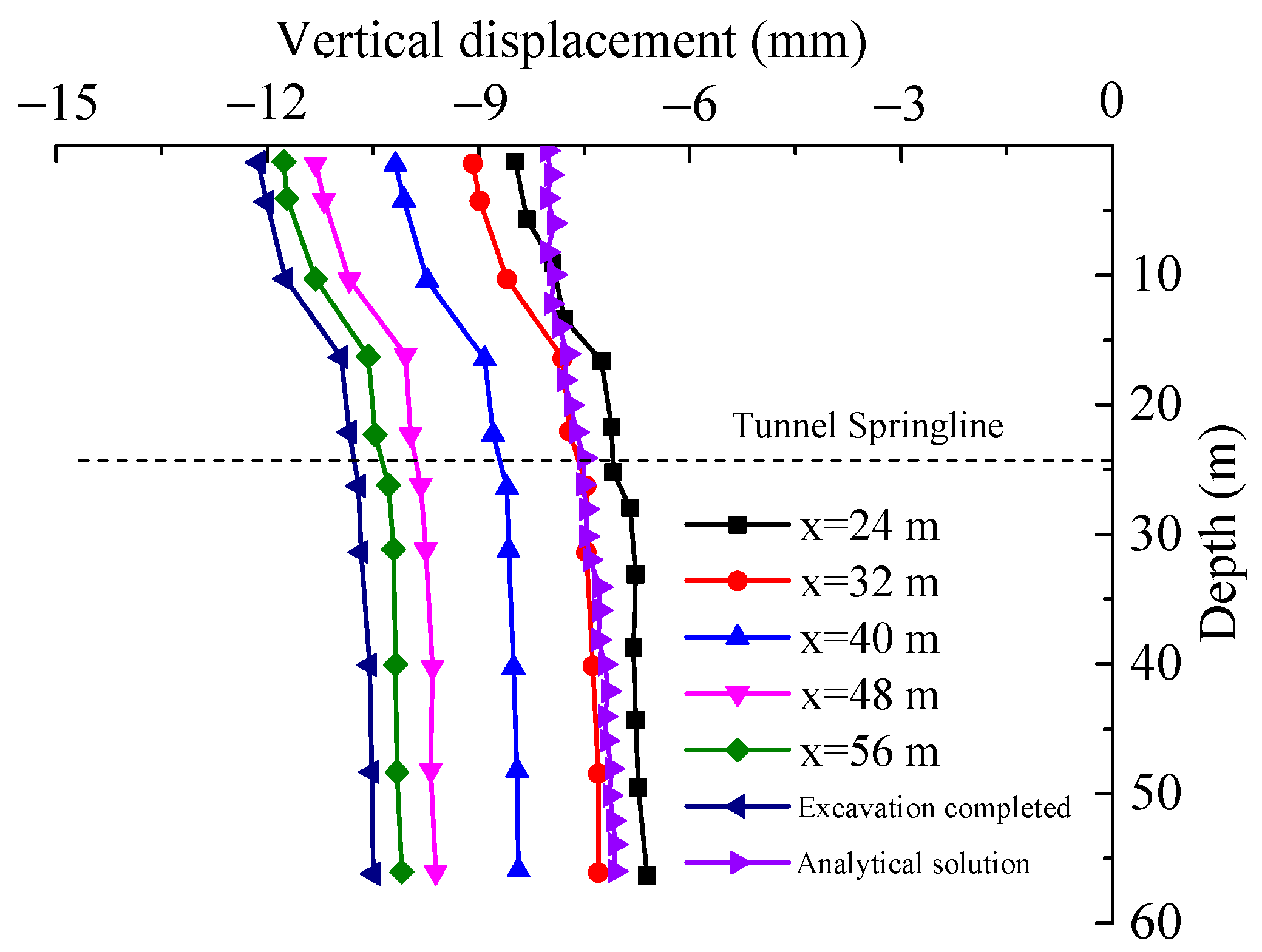
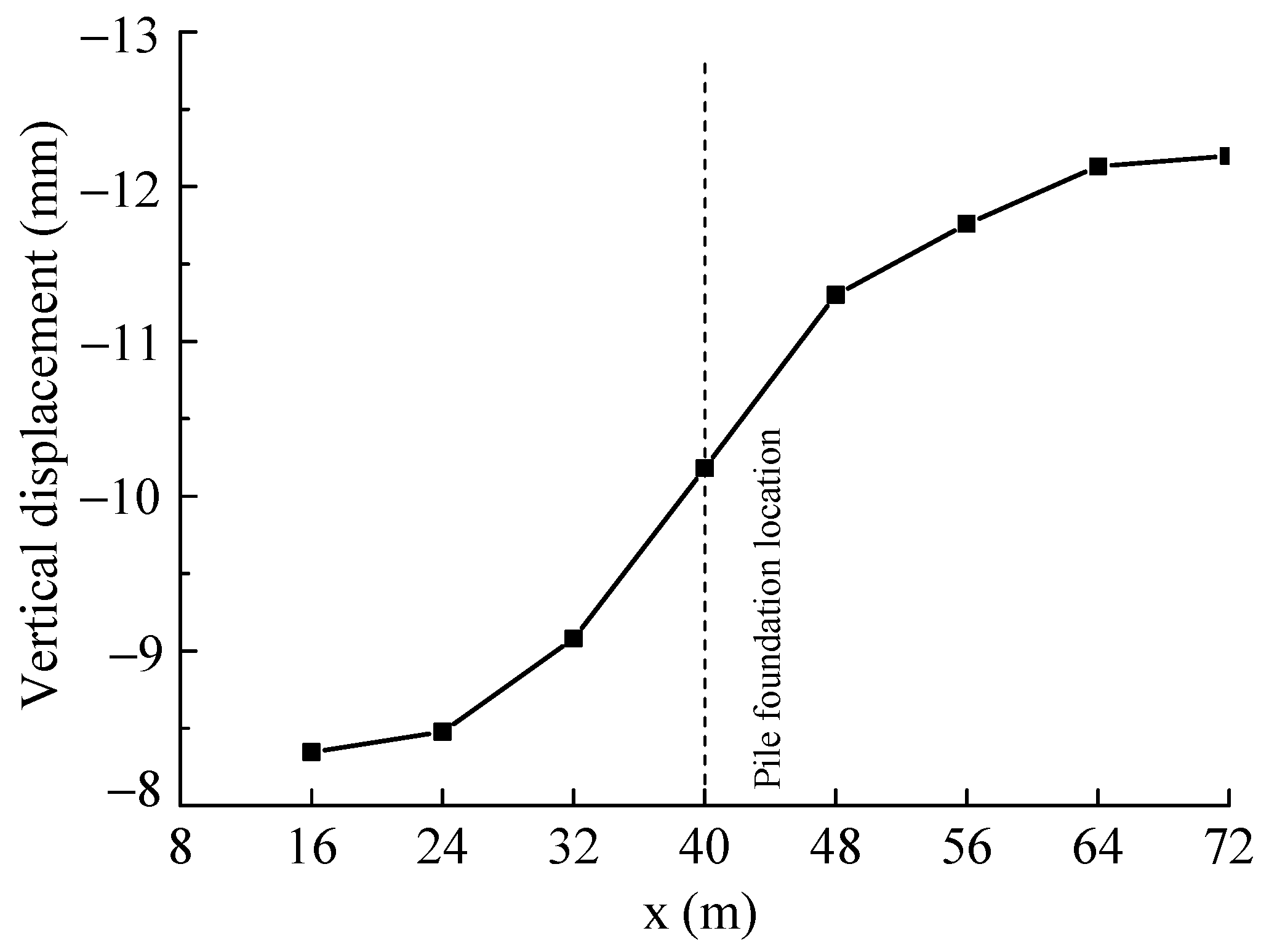
4.2. Vertical Displacement
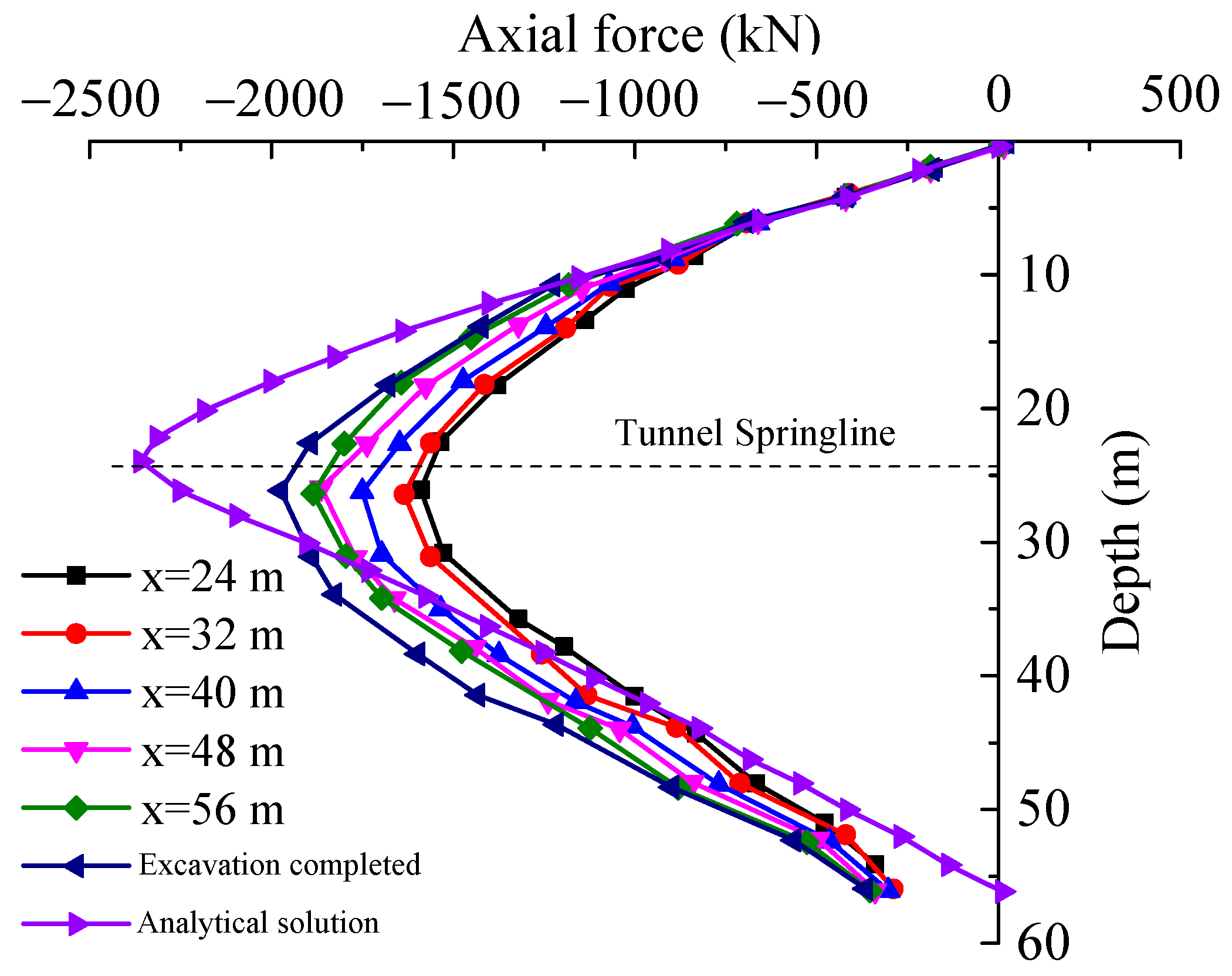
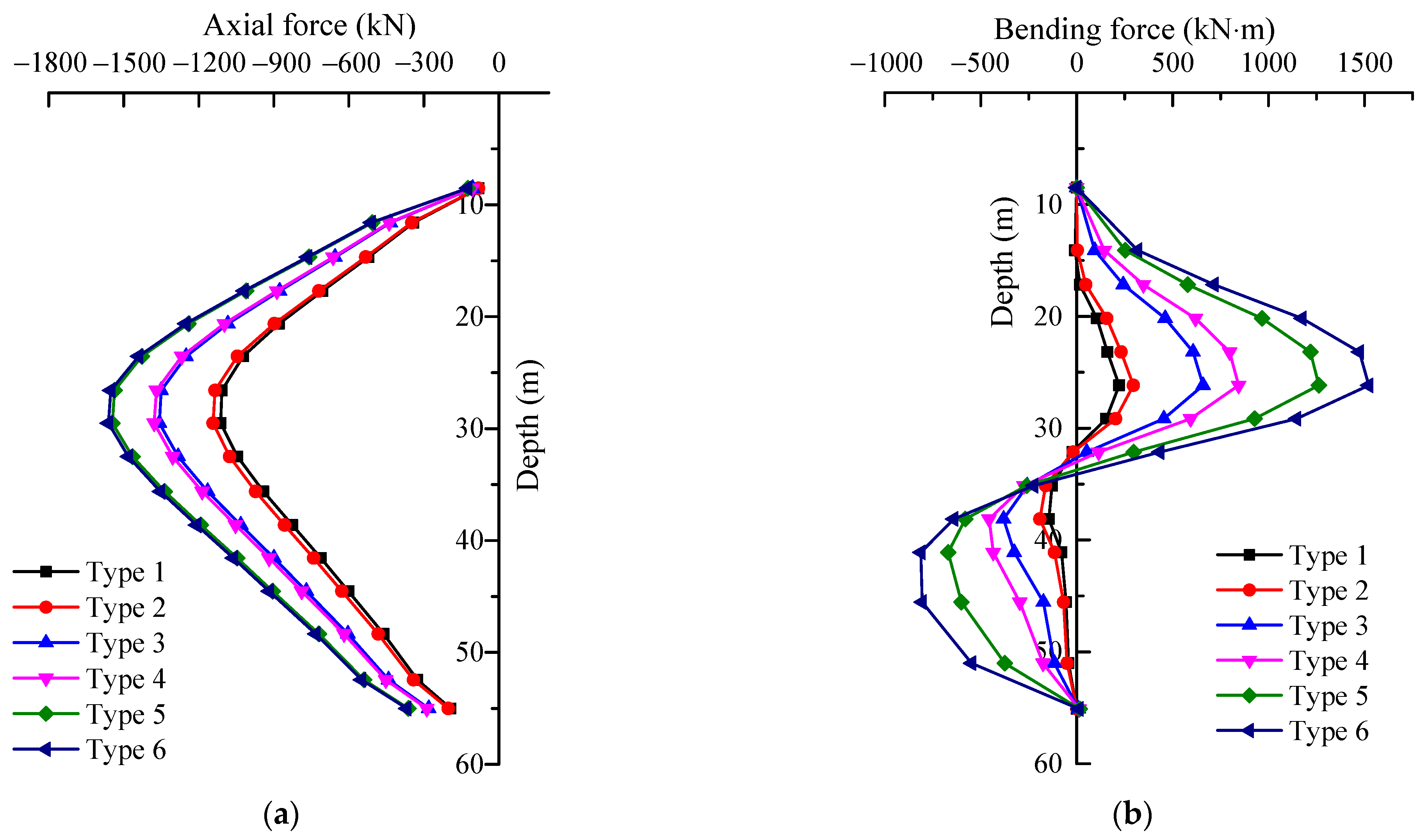
4.3. Axial Force
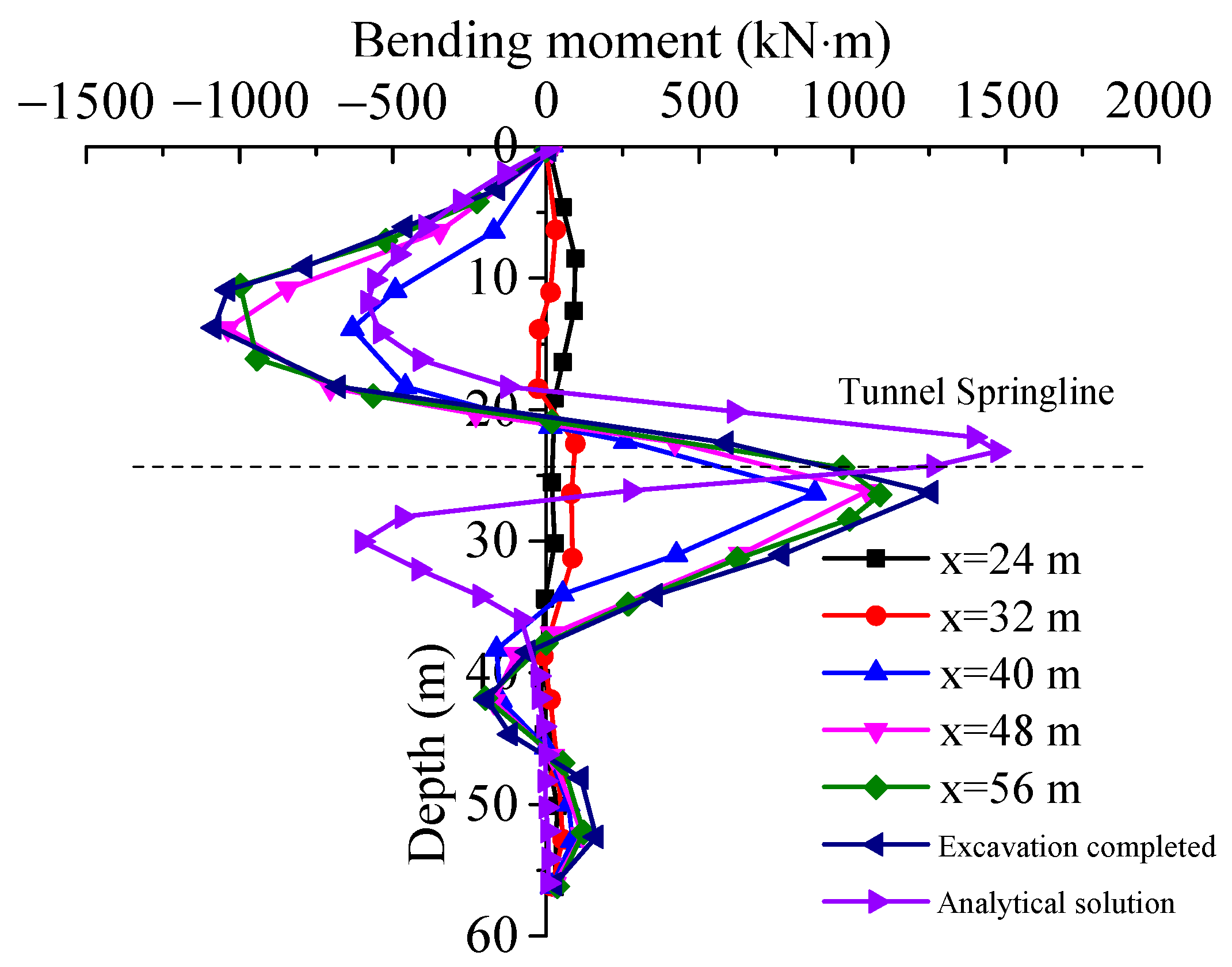
4.4. Bending Moment
5. Parametric Analysis
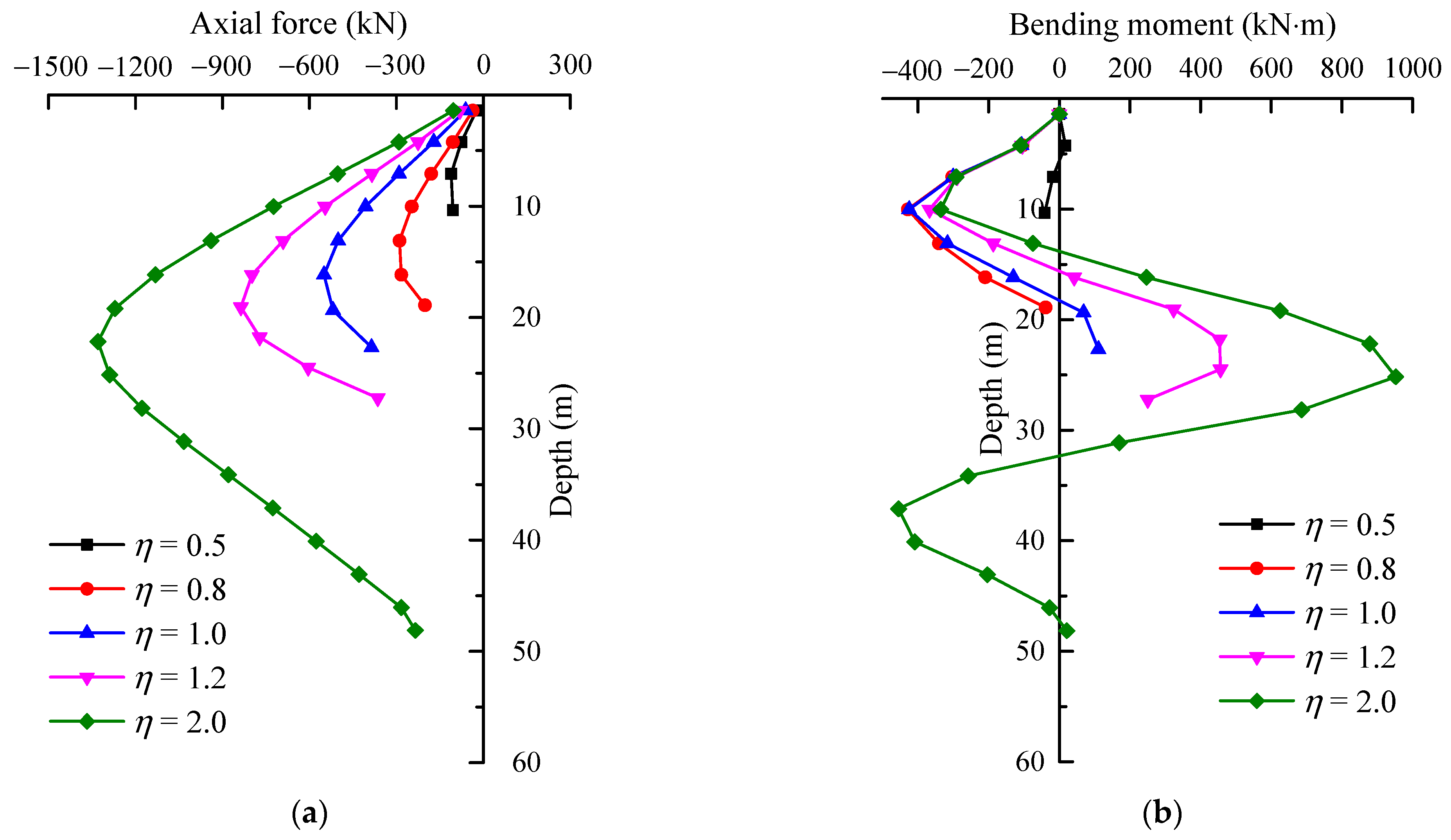
5.1. Vertical Relative Position of Tunnel–Pile Foundations
- η < 1.0 (Short piles)
- η = 1.0 (Medium-length piles)
- η > 1.0 (Long piles)
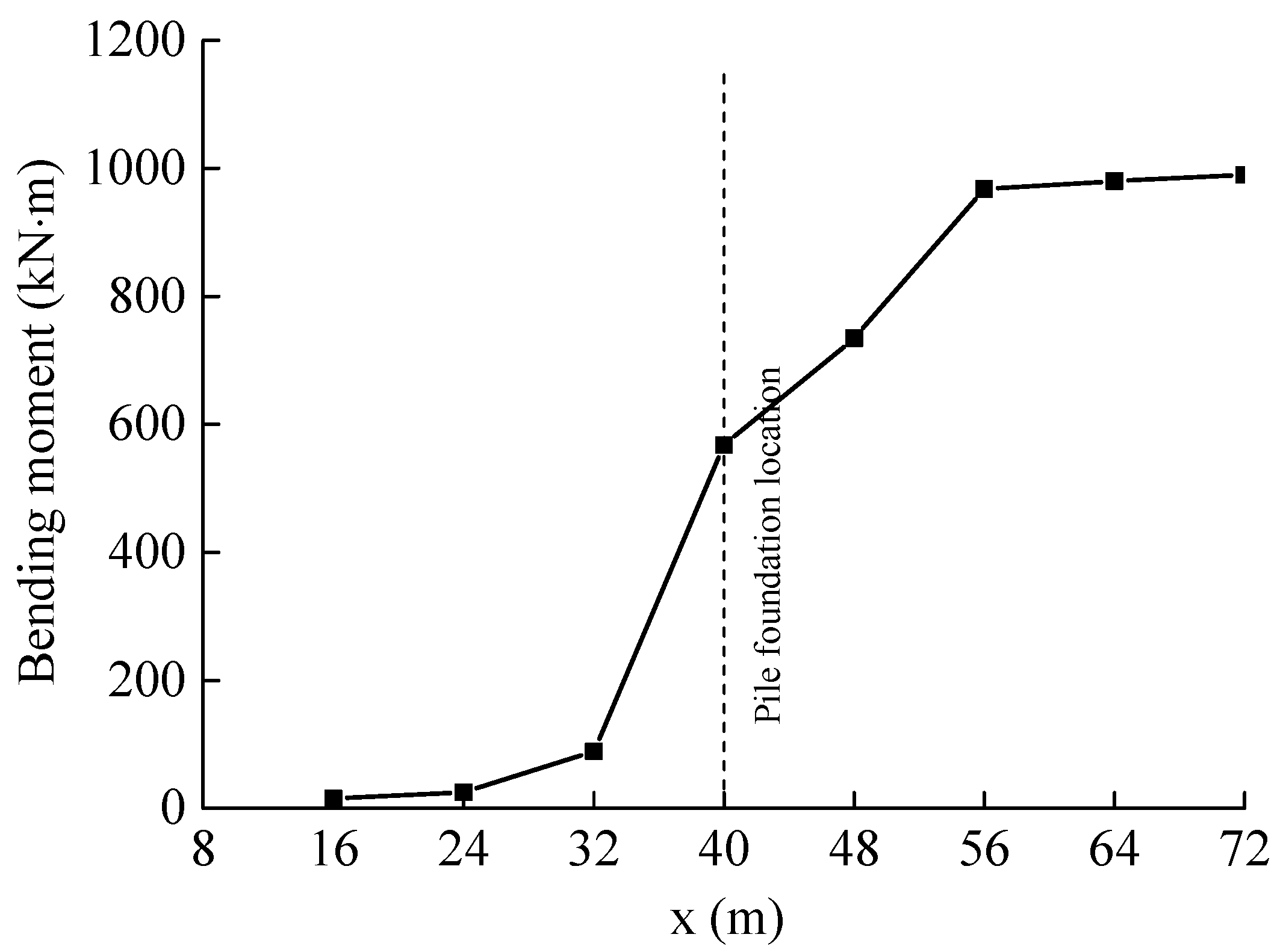
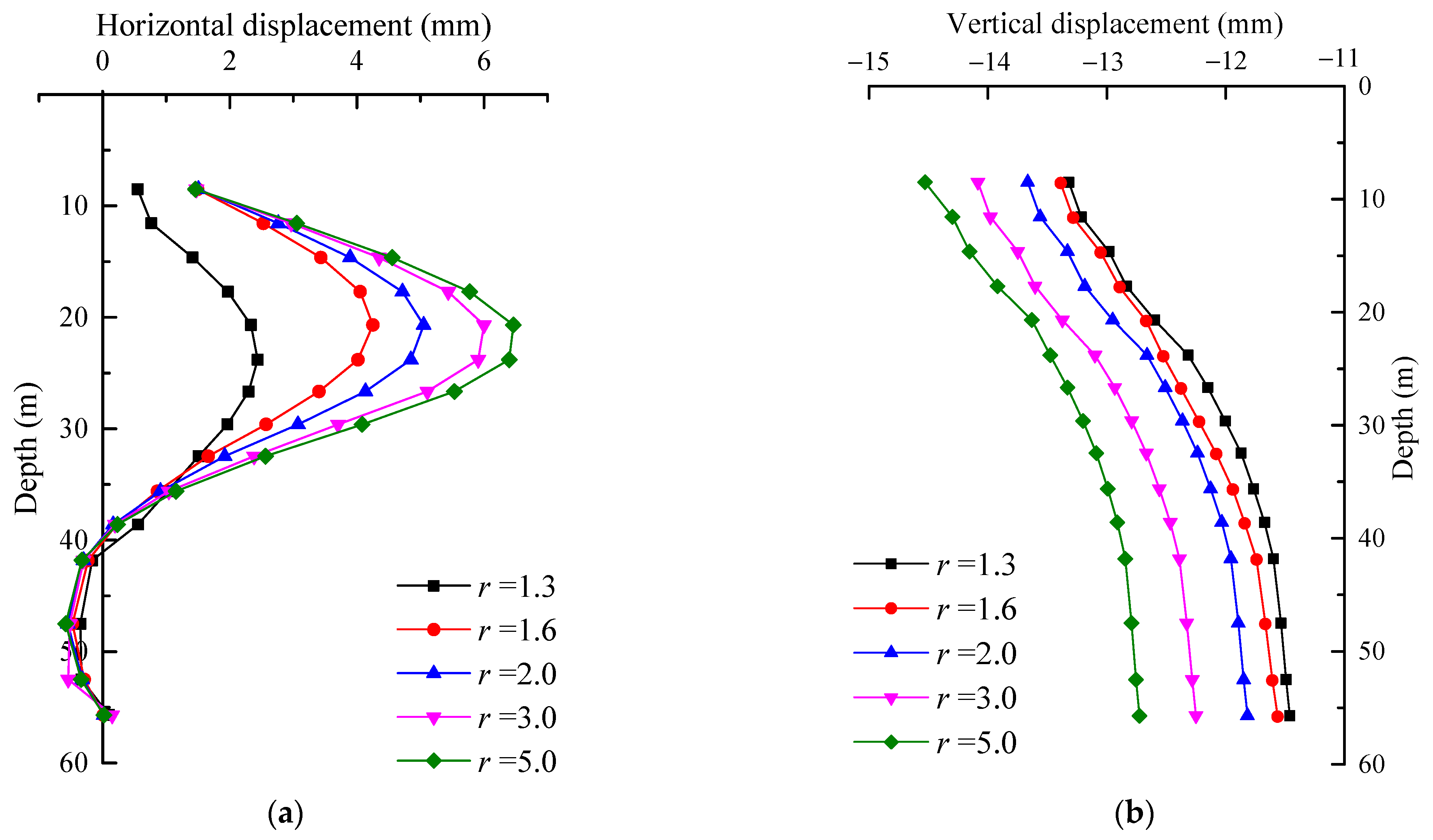
5.2. Horizontal Relative Position of Tunnel–Pile Foundations
5.3. Stiffness Coefficient of Pile Foundations
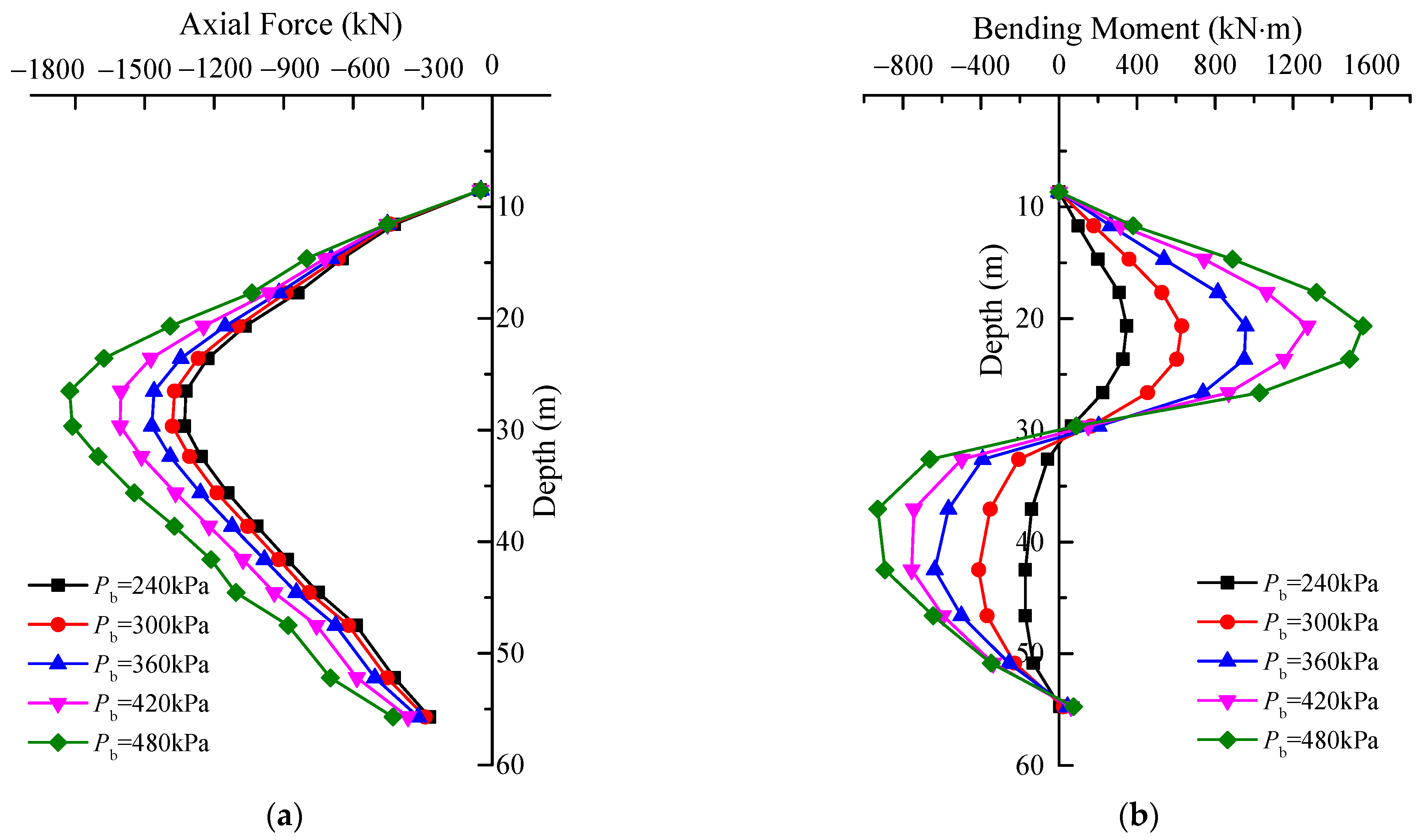
5.4. Grouting Pressures
6. Discussion
6.1. Findings
- The initial phase occurs before the shield tunneling construction reaches the pile foundation site. During this stage, the pile foundations are primarily affected by the propagation of soil pressure from the excavation face, resulting in slight deformations that are mainly directed away from the tunnel boundary.
- The second phase occurs as the shield tunneling process reaches and advances beyond the pile foundation. During this stage, the soil strata adjacent to the pile foundation on the tunnel side experience unloading, resulting in a significant reduction in the lateral constraint forces acting on the pile. Consequently, the pile foundation is subjected to a complex interaction of forces, including soil pressure from the excavation face, frictional resistance between the shield machine and the surrounding soil, and grouting pressure at the shield tail. These combined effects induce substantial bending deformation of the pile foundation toward the tunnel side, with internal forces and deformations reaching their maximum values near the tunnel axis. This observation aligns well with the findings reported by Zhang et al. [39]. Notably, the shield machine’s proximity within 1D of the foundation produces the most pronounced effects.
- The final stage involves the shield machine advancing beyond the pile foundation, during which the pile is primarily influenced by displacement effects caused by the grouting pressure at the shield tail. This results in the stabilization of internal forces and deformations within the pile. Throughout the tunnel construction process, the upper soil layer surrounding the pile experiences significant settlement, exerting downward negative skin friction along the pile shaft. Meanwhile, the pile toe is constrained by the deeper, less-displaced firm soil stratum. This combination of “pulling from above and supporting from below” places the pile in a state of tension and compression, resulting in greater settlement at the pile head than at the pile toe. In general, when the pile response is dominated by external soil displacement, the vertical displacement at the pile head is typically larger than that at the base. The development of vertical pile displacement due to soil settlement and skin friction has also been validated through a numerical simulation study carried out by Nabil et al. [40]. In summary, internal forces and displacements within the pile foundation progressively increase in tandem with the advancement of the shield tunneling process.
6.2. Limitations
7. Conclusions
- The published centrifuge test results validate the accuracy of the finite element modeling method used in this paper, which effectively simulates changes in the structural performance of adjacent pile foundations at various stages of tunnel construction.
- Finite element simulation results indicate that tunnel shield construction causes nearby bridge pile foundations to bend and deform toward the tunnel side. It should be noted that the bridge pile foundations experience the greatest horizontal displacement and internal forces in the same plane as the tunnel. The tunnel shield construction has the most significant impact on the internal forces and displacement of pile foundations within a range of 1D before and after the pile foundation location.
- As the vertical length-to-depth ratio (η) increases, indicating elongation of the pile length, the impact of tunnel construction on nearby pile foundations varies. When the pile toe is located above the tunnel axis burial depth (η < 1), the pile foundation primarily experiences settlement accompanied by negative frictional forces, with the greatest horizontal displacement observed at the pile toe. When the pile toe aligns with the tunnel axis (η = 1), the pile foundation begins to exhibit positive frictional forces, and the horizontal displacement reaches its maximum magnitude. When the pile toe extends below the tunnel axis burial depth (η > 1), the positive frictional forces within the pile foundation intensify further, while the maximum horizontal displacement decreases and shifts to the depth corresponding to the tunnel axis. Moreover, as the pile length increases, internal forces within the pile foundation amplify, whereas the overall settlement of the pile foundation decreases.
- The distribution patterns of internal forces and displacements along the pile foundation remain consistent subjected to different horizontal axial-to-clearance ratios (r). A decrease in the horizontal axial-to-clearance ratio (r) corresponds to a reduction in the internal forces and displacements experienced by the pile foundation. Furthermore, once the horizontal clearance reaches a specific threshold, tunnel construction no longer affects the structural behavior of the pile foundation.
- As the pile stiffness coefficient increases, the maximum displacement of the pile decreases, while the internal force in the pile shaft increases. Both the pile diameter and Young’s modulus affect the pile behavior similarly to the stiffness coefficient. However, the pile diameter has a greater influence compared to Young’s modulus.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mao, J.H.; Yuan, D.J.; Jin, D.L.; Zeng, J.F. Optimization and application of backfill grouting material for submarine tunnel. Constr. Build. Mater. 2020, 265, 120281. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; Zhang, Z.; Li, P.; Cui, J.; Liu, H.; Yang, Y. Model tests on tail-grouting process during URUP shield tunneling in soft soil. Tunn. Undergr. Space Technol. 2020, 103, 103451. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, S.; Li, Y.; Zhang, Y.; Tian, H.; Zhao, M. Deformation control strategies for shield tunnel underpassing viaduct of high-speed railway: A case study. Chin. J. Eng. Res. 2023, 13, 390–398. [Google Scholar] [CrossRef]
- Yan, B.; Wang, R.; Wang, Y. Deformation of adjacent buildings and ground settlement induced by shield construction of three-line small-spacing tunnels. Alex. Eng. J. 2023, 79, 237–251. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, Z. Analytical Method for Evaluating the Ground Surface Settlement Caused by Tail Void Grouting Pressure in Shield Tunnel Construction. Adv. Civ. Eng. 2018, 3729143. [Google Scholar] [CrossRef]
- Xie, X.; Yang, Y.; Ji, M. Analysis of ground surface settlement induced by the construction of a large-diameter shield-driven tunnel in Shanghai, China. Tunn. Undergr. Space Technol. 2016, 51, 120–132. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Demirci, H.E.; Nikitas, G.; Prakhya, G.; Lombardi, D.; Alexander, N.; Aleem, M.; Amani, S.; Mylonakis, G. Physical modeling ofinteractionproblems in geotechnical engineering. In Modeling in Geotechnical Engineering; Academic Press: Cambridge, MA, USA, 2021; pp. 205–256. [Google Scholar] [CrossRef]
- Fu, J.; Yang, J.; Zhang, X.; Klapperich, H.; Abbas, S.M. Response of the ground and adjacent buildings due to tunnelling in completely weathered granitic soil. Tunn. Undergr. Space Technol. 2014, 43, 377–388. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, Y.; Geng, D.; Huang, Z.; Ding, H. Numerical Investigation of the Combined Influence of Shield Tunneling and Pile Cutting on Underpinning Piles. Front. Earth Sci. 2022, 10, 896634. [Google Scholar] [CrossRef]
- Liang, F.; Zhang, H.; Yang, K. A variational solution for nonlinear response of laterally loaded piles with elasto-plastic winkler spring model. KSCE J. Civ. Eng. 2015, 19, 74–80. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Jiang, Y.; Wang, W. Simplified solution for tunnel-soil-pile interaction in Pasternak’s foundation model. Tunn. Undergr. Space Technol. 2018, 78, 146–158. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, C.; Jiang, K.; Wang, Z.; Jiang, Y.; Zhao, Q.; Lu, M. Analytical Prediction for Tunnel-Soil-Pile Interaction Mechanics based on Kerr Foundation Model. KSCE J. Civ. Eng. 2019, 23, 2756–2771. [Google Scholar] [CrossRef]
- Jia, H.; Wang, N.; Ding, H.; Guan, L. Impact of Tunneling on Adjacent Piles Based on the Kerr Foundation Model Considering the Influence of Lateral Soil. Buildings 2023, 13, 2548. [Google Scholar] [CrossRef]
- Wu, T.; Gao, Y.; Huang, C.; Jin, A.; Zhou, Y.; Li, J. Horizontal mechanical responses of single pile induced by adjacent tunneling considering the effect of multiple factors based on Timoshenko Beam-Kerr foundation model. Appl. Math. Model. 2025, 140, 115885. [Google Scholar] [CrossRef]
- Wang, C.; Zou, J.; Shu, D. A Method for Calculating the Deformation of Existing Bridge Pile Foundations Caused by the Oblique Crossing of Shield Tunnels. Int. J. Geomech. 2025, 25, 04025130. [Google Scholar] [CrossRef]
- Zhou, J.; Han, K.; Chen, W. Study on Influence Mechanism of Tunnel Construction on Adjacent Pile Foundation and Resilience Assessment. Buildings 2024, 14, 2818. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Lu, H.; Peng, S.Y. Three-dimensional centrifuge modelling of the effects of twin tunnelling on an existing pile. Tunn. Undergr. Space Technol. 2013, 35, 189–199. [Google Scholar] [CrossRef]
- Soomro, M.A.; Mangi, N.; Mangnejo, D.A.; Memon, N.A. 3D centrifuge and numerical modelling of lateral responses of a vertical loaded pile group to twin stacked tunnels. Eur. J. Environ. Civ. Eng. 2021, 26, 5517–5544. [Google Scholar] [CrossRef]
- Soomro, M.A.; Ng, C.W.W.; Memon, N.A.; Bhanbhro, R. Lateral behaviour of a pile group due to side-by-side twin tunnelling in dry sand: 3D centrifuge tests and numerical modelling. Comput. Geotech. 2018, 101, 48–64. [Google Scholar] [CrossRef]
- He, S.; Lai, J.; Li, Y.; Wang, K.; Wang, L.; Zhang, W. Pile group response induced by adjacent shield tunnelling in clay: Scale model test and numerical simulation-ScienceDirect. Tunn. Undergr. Space Technol. 2022, 120, 104039. [Google Scholar] [CrossRef]
- Su, J.; Pan, Y.; Niu, X.; Zhang, C. Effect of shield tunneling on adjacent pile foundations in water-rich strata. Transp. Geotech. 2025, 52, 101557. [Google Scholar] [CrossRef]
- Guo, C.; Yue, H.; Tao, Y.; Liu, G.; Kong, F.; Lu, D.; Du, X. Mechanical response of pile group and stratum induced by shallow tunneling based on the model test. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2025, 159, 106480. [Google Scholar] [CrossRef]
- Kitiyodom, P.; Matsumoto, T. A simplified analysis method for piled raft foundations in non-homogeneous soils. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 85–109. [Google Scholar] [CrossRef]
- Kitiyodom, P.; Matsumoto, T.; Kawaguchi, K. A simplified analysis method for piled raft foundations subjected to ground movements induced by tunnelling. Int. J. Numer. Anal. Methods 2005, 29, 1485–1507. [Google Scholar] [CrossRef]
- Asgarkhani, N.; Kazemi, F.; Jankowski, R. Machine-learning based tool for seismic response assessment of steel structures including asonry infill walls and soil-foundation-structure interaction. Comput. Struct. 2025, 317, 107918. [Google Scholar] [CrossRef]
- Lee, G.T.K.; Ng, C.W.W. Effects of advancing open face tunneling on an existing loaded pile. J. Geotech. Geoenviron. Eng. 2005, 131, 193–201. [Google Scholar] [CrossRef]
- Yang, X.J.; Deng, F.H.; Wu, J.J.; Liu, J.; Wang, F.Q. Response of carrying capacity of piles induced by adjacent Metro tunneling. Min. Sci. Technol. 2009, 19, 176–181. [Google Scholar] [CrossRef]
- Jongpradist, P.; Kaewsri, T.; Sawatparnich, A.; Suwansawat, S.; Youwai, S.; Kongkitkul, W.; Sunitsakul, J. Development of tunnelinginfluence zones for adjacent pile foundations by numerical analyses. Tunn. Undergr. Space Technol. 2013, 34, 96–109. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Z.X.; Regueiro, R.A. Pile and pile group response to tunnelling using a large diameter slurry shield-Case study in Shanghai. Comput. Geotech. 2014, 59, 21–43. [Google Scholar] [CrossRef]
- Boonyarak, T.; Phisitkul, K.; Ng, C.W.W.; Teparaksa, W.; Aye, Z.Z. Observed ground and pile group responses due to tunneling in Bangkok stiff clay. Can. Geotech. J. 2014, 51, 479–495. [Google Scholar] [CrossRef]
- Soomro, M.; Yi, H.; Ng, C.W.W.; Hu, L.; Peng, S. Load transfer mechanism in pile group due to single tunnel advancement in stiff clay. Tunn. Undergr. Space Technol. 2015, 45, 63–72. [Google Scholar] [CrossRef]
- Zidan, F.A.; Ramadan, M.O.O. Three dimensional numerical analysis of the effects of tunnelling near piled structures. KSCE J. Civ. Eng. 2015, 19, 917–928. [Google Scholar] [CrossRef]
- Li, H.J.; Tong, L.Y.; Liu, S.Y. Multistage-based evaluation of tunnelling effects onthe skin friction of adjacent building piles in layered media. Structures 2021, 32, 96–105. [Google Scholar] [CrossRef]
- Dai, X.; Cai, J.; Diao, Y.; Huo, H.; Xu, G. Influence of tunnelling on the deformation of the overlying excavation bracing system and analysis of countermeasures. Comput. Geotech. 2021, 134, 104089. [Google Scholar] [CrossRef]
- Huang, K.; Sun, Y.; Huang, X.; Li, Y.; Jiang, M.; Liu, R. Effects of different construction sequences on ground surface settlement and displacement of single long pile due to twin paralleled shield tunneling. Adv. Civ. Eng. 2021, 1–14. [Google Scholar] [CrossRef]
- Huang, K.; Sun, Y.W.; Zhou, D.Q.; Li, Y.J.; Jiang, M.; Huang, X.Q. Influence of water-rich tunnel by shield tunneling on existing bridge pile foundation in layered soils. J. Central South Univ. 2021, 28, 2574–2588. [Google Scholar] [CrossRef]
- Ayasrah, M.; Qiu, H.; Zhang, X.; Andrianov, I.V. Influence of cairo metro tunnel excavation on pile deep foundation of the adjacent underground structures: Numerical study. Symmerty 2021, 13, 426. [Google Scholar] [CrossRef]
- Lv, J.; Lin, D.; Wu, W.; Huang, J.; Li, Z.; Fu, H.; Li, H. Mechanical Responses of Slurry Shield Underpassing Existing Bridge Piles in Upper-Soft and Lower-Hard Composite Strata. Buildings 2022, 12, 1000. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Ning, X.; Lu, H.; Jiang, M.; Wei, S.; Xiao, X. Effect of Shield-Tunnel Construction on the Horizontal Response of Adjacent Piles in a Silty Layer. Buildings 2023, 13, 2455. [Google Scholar] [CrossRef]
- Nabil, M.H.; Tamir, A.; Abderahim, B. Three-dimensional numerical analyses of pile responses to tunneling-induced ground movements in bilayer soil. World J. Eng. 2024, 21, 71–90. [Google Scholar] [CrossRef]
- Jiao, N.; Ding, J.; Liao, Z.; Wan, X.; Gao, P. Impact of Double Shield Tunnel Construction on Adjacent Pile Foundation in Silty Fine Sand Strata. J. Perform. Constr. Facil. 2025, 39. [Google Scholar] [CrossRef]
- GB/T 50783-2012; Technical Code for Composite Foundation. China Planning Press: Beijing, China, 2012.
- Liu, W.; Zhao, L.; Yao, X.C.; Zheng, H.A.; Liu, W.L. Impact of Shield Tunnel Construction on Adjacent Railway Bridge: Protective Measures and Deformation Control. Buildings 2024, 14, 3024. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Z.; Xu, Y. Analysis on three-dimensional ground surface deformations due to shield tunnel. Chin. J. Rock Mech. Eng. 2002, 21, 388–392. [Google Scholar]
- Franzius, J.N.; Potts, D.M. Influence of mesh geometry on three-dimensional finite-element analysis of tunnel excavation. Int. J. Geomech. 2005, 5, 256–266. [Google Scholar] [CrossRef]
- Mair, R.J.; Taylor, R.N.; Bracegirdle, A. Subsurface settlement profiles above tunnels in clays. Geotechnique 1993, 43, 315–320. [Google Scholar] [CrossRef]
- Ren, R.; Zhong, Y.J.; Xu, S.S.; Ma, E.L.; Xie, Y. Numerical Simulation on Safety Influence of Shield TunnelingSide Crossing on Adjacent High Buildings of Steel Tower Atop. Highway 2018, 12, 318–324. [Google Scholar]
- Lin, C.; Jiang, R.; Xiao, S.; Wang, Z. Mechanism of influences of shield construction nearby friction pile foundation on its bearing capacity and its controlling techniques. Chin. J. Geotech. Eng. 2023, 45, 241–246. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Huang, M.S.; Wang, W.D. Additional stresses of disturbed soils induced by shield tunneling based on fictitious force method. Chin. J. Geotech. Eng. 2014, 36, 1235–1242. [Google Scholar] [CrossRef]
- Cao, S.; Qian, D.L.; Wei, X.Y.; Cheng, H.; Ma, X.F. Influence of deep foundation pit excavation on underlying metro tunnel and control measures. J. Hefei Univ. Technol. 2014, 37, 1479–1482. [Google Scholar] [CrossRef]
- Poulos, H.G.; Chen, L.T. Pile response due to excavation-induced lateral soil movement. J. Geotech. Geoenvironmental Eng. ASCE 1997, 123, 94–99. [Google Scholar] [CrossRef]
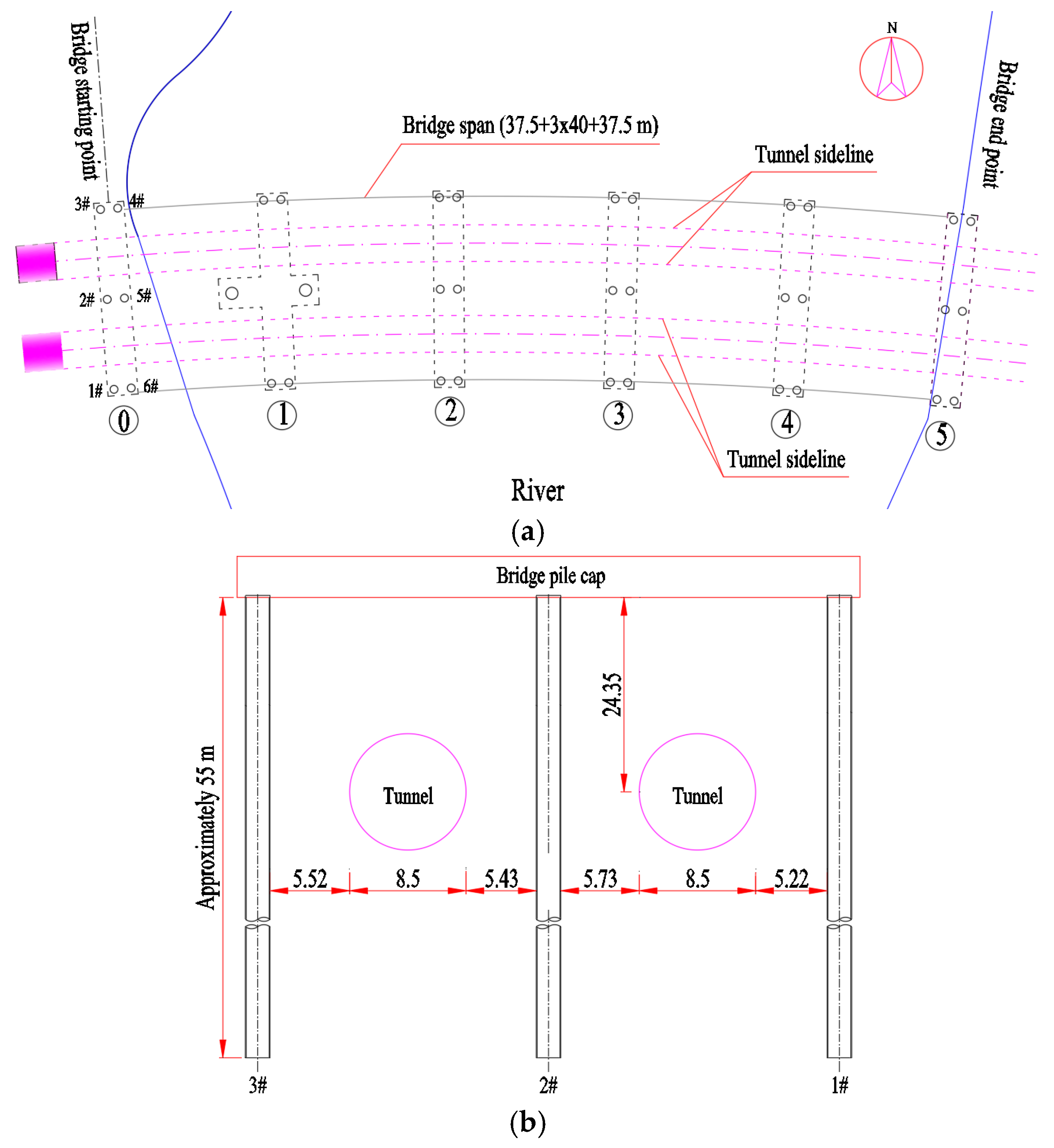


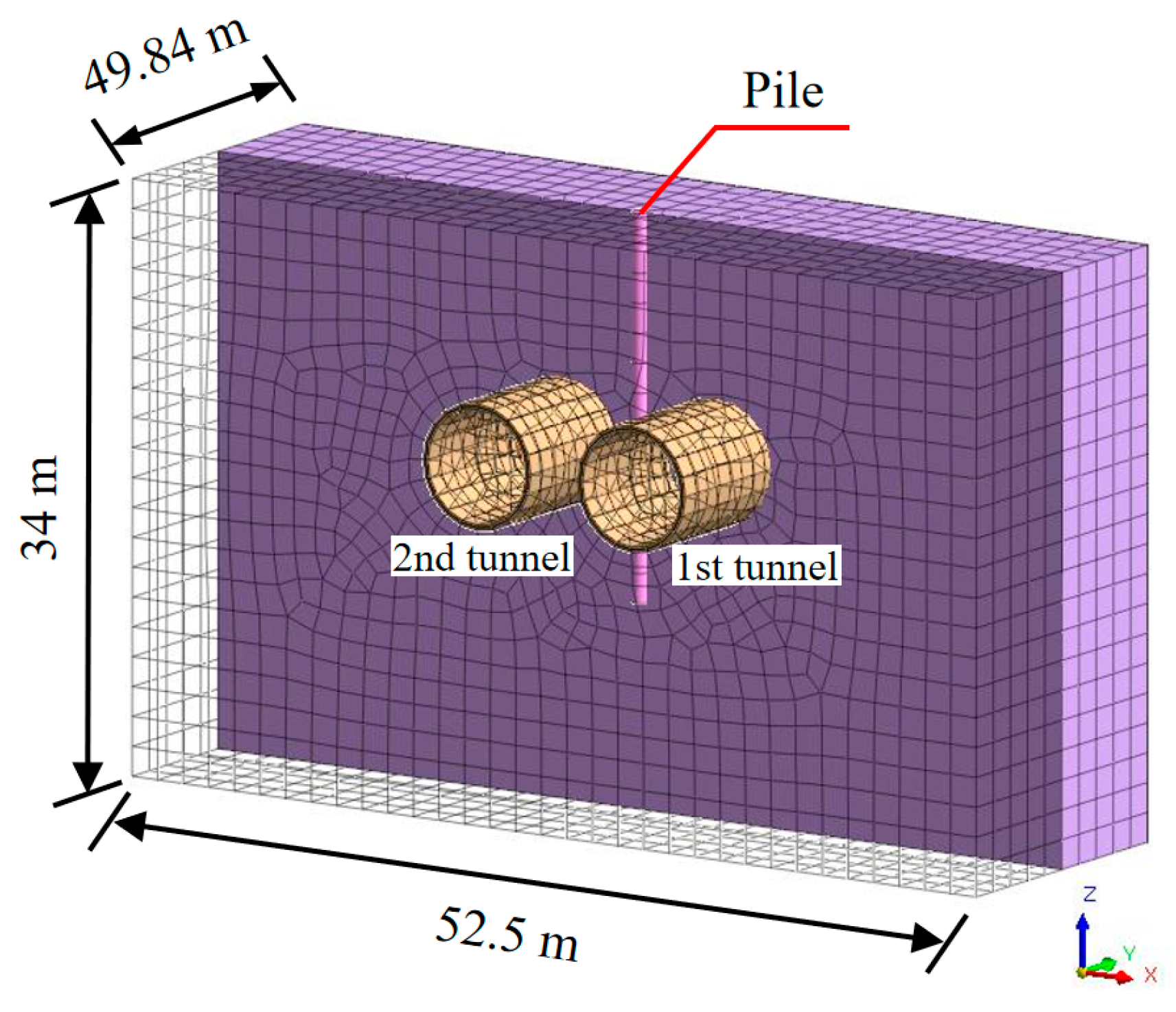
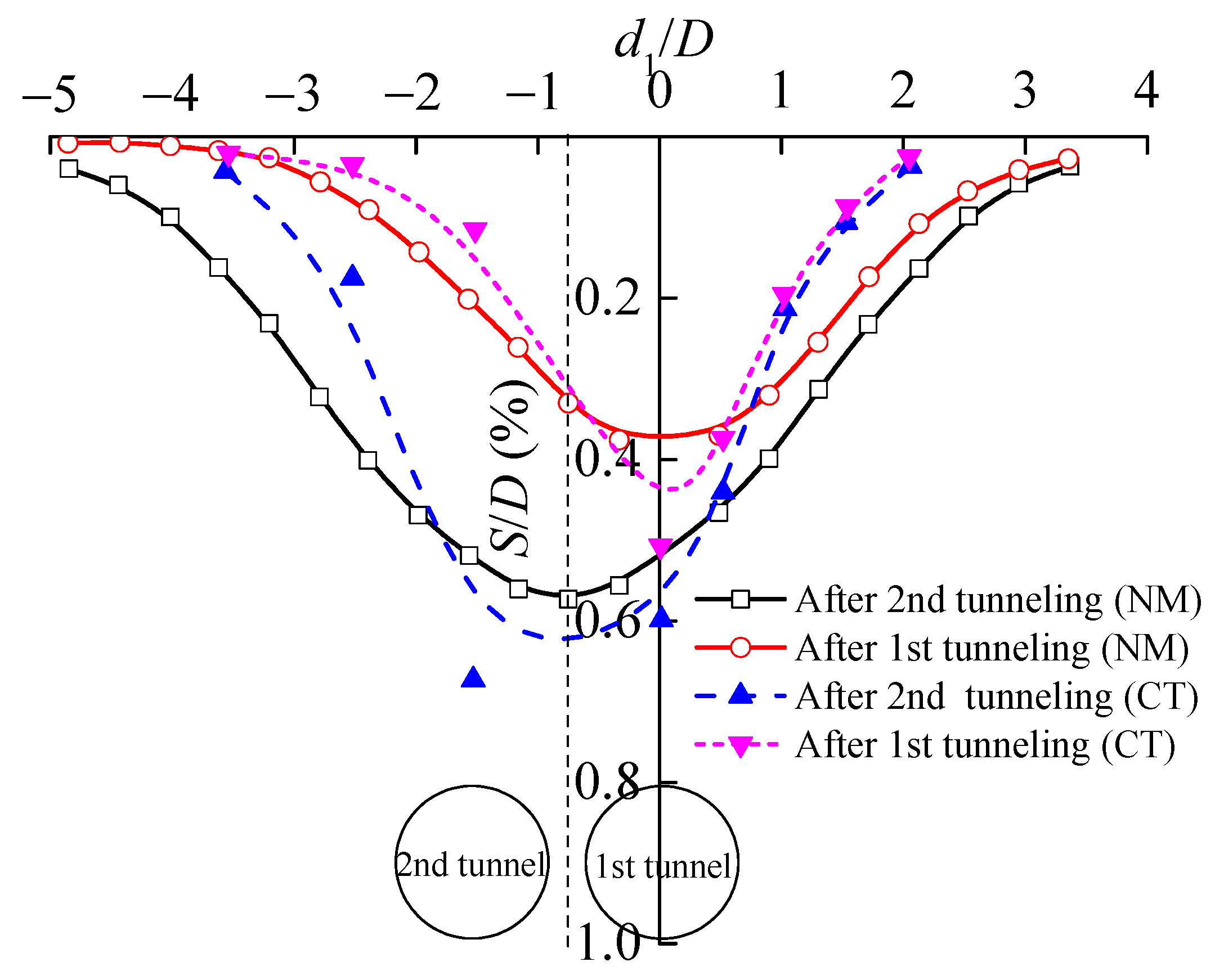

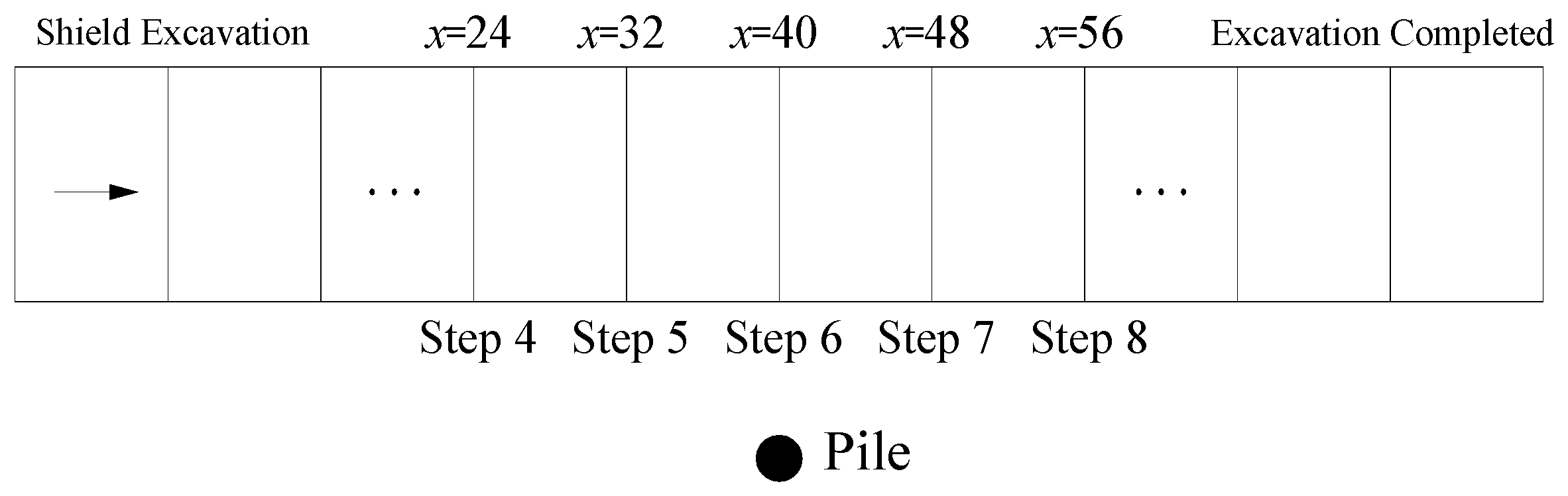





| Categories | Depth/m | Unit Weight/kN·m−3 | Compression Modulus/MPa | Poisson’s Ratio | Cohesion/kPa | Internal Friction/° |
|---|---|---|---|---|---|---|
| Artificial fill (after treatment) | 8.5 | 18 | 25.3 | 0.3 | 20 | 35 |
| Silt | 9.2 | 16.6 | 4.66 | 0.42 | 2.9 | 2.8 |
| Clay | 23.9 | 17.9 | 4.66 | 0.4 | 16.3 | 23.3 |
| Coarse sand | 5.9 | 19.5 | 30 | 0.3 | 0 | 38 |
| Sandy clay | 5 | 19 | 5.27 | 0.3 | 19 | 22.4 |
| Completely decomposed granite | 3.2 | 19 | 40 | 0.25 | 35 | 30 |
| Highly weathered granite | 5.3 | 20 | 2000 | 0.2 | 500 | 28 |
| Moderately weathered granite | — | 24 | 3000 | 0.15 | 1000 | 40 |
| Material Type | Unit Weight/kN·m−3 | Young’s Modulus/MPa | Poisson’s Ratio |
|---|---|---|---|
| Shield machine shell | 78 | 206,000 | 0.25 |
| Ling segment | 25 | 30,000 | 0.2 |
| Pile | 25 | 31,500 | 0.2 |
| Grouting body (initial set) | 22 | 1.8 | 0.2 |
| Grouting body (final set) | 22 | 400 | 0.2 |
| Material Type | Unit Weight /kN·m−3 | Young’s Modulus/MPa | Poisson’s Ratio | Cohesion/kPa | Internal Friction/° |
|---|---|---|---|---|---|
| Soil | 26.5 | 2 | 0.33 | 3 | 23 |
| Tunnel Lining | 25 | 30,000 | 0.2 | — | — |
| Pile | 25 | 25,000 | 0.2 | — | — |
| Pile Type | Young’s Modulus/GPa | Diameter/m | Cross-Sectional Area/m2 | Length/m | Stiffness Coefficient /kN·m−1 |
|---|---|---|---|---|---|
| Type 1 | 20 | 1.2 | 1.13 | 56 | 4.03 × 105 |
| Type 2 | 30 | 1.2 | 1.13 | 56 | 6.05 × 105 |
| Type 3 | 20 | 1.8 | 2.54 | 56 | 9.07 × 105 |
| Type 4 | 30 | 1.8 | 2.54 | 56 | 1.36 × 106 |
| Type 5 | 20 | 2.4 | 4.52 | 56 | 1.61 × 106 |
| Type 6 | 30 | 2.4 | 4.52 | 56 | 2.42 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Wei, J.; Liang, H.; Chen, Z.; Ding, W.; Li, B. Structural Behavior Analysis for Existing Pile Foundations Considering the Effects of Shield Tunnel Construction. Buildings 2025, 15, 3263. https://doi.org/10.3390/buildings15183263
He C, Wei J, Liang H, Chen Z, Ding W, Li B. Structural Behavior Analysis for Existing Pile Foundations Considering the Effects of Shield Tunnel Construction. Buildings. 2025; 15(18):3263. https://doi.org/10.3390/buildings15183263
Chicago/Turabian StyleHe, Cong, Jun Wei, Huan Liang, Zhongzhang Chen, Wenqi Ding, and Bin Li. 2025. "Structural Behavior Analysis for Existing Pile Foundations Considering the Effects of Shield Tunnel Construction" Buildings 15, no. 18: 3263. https://doi.org/10.3390/buildings15183263
APA StyleHe, C., Wei, J., Liang, H., Chen, Z., Ding, W., & Li, B. (2025). Structural Behavior Analysis for Existing Pile Foundations Considering the Effects of Shield Tunnel Construction. Buildings, 15(18), 3263. https://doi.org/10.3390/buildings15183263






