Post-Fire Performance of Bolted Steel T-Joints with Varying Coating Thicknesses: Experimental and Finite Element Analysis
Abstract
1. Introduction
1.1. Aim and Innovation of the Study
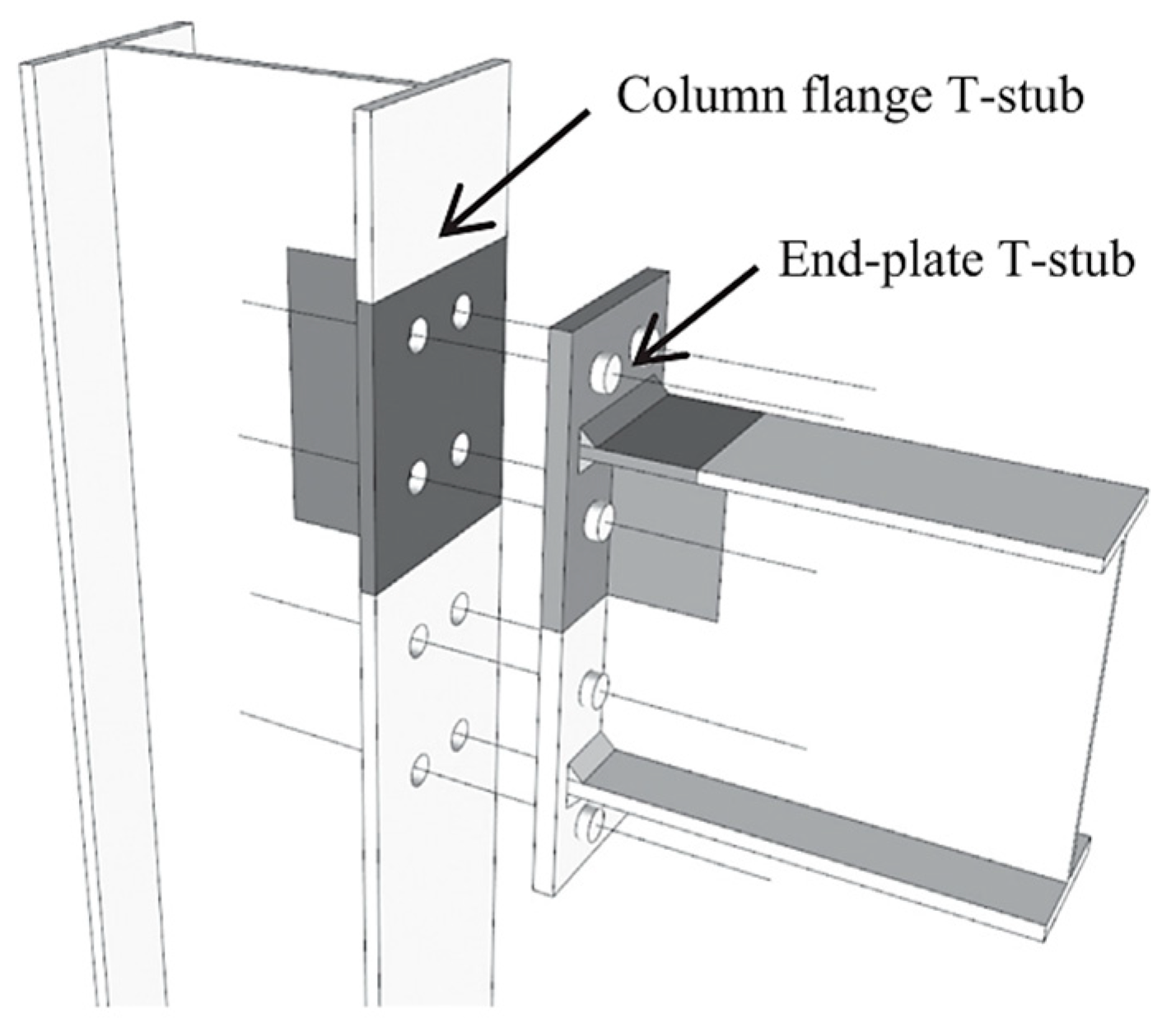
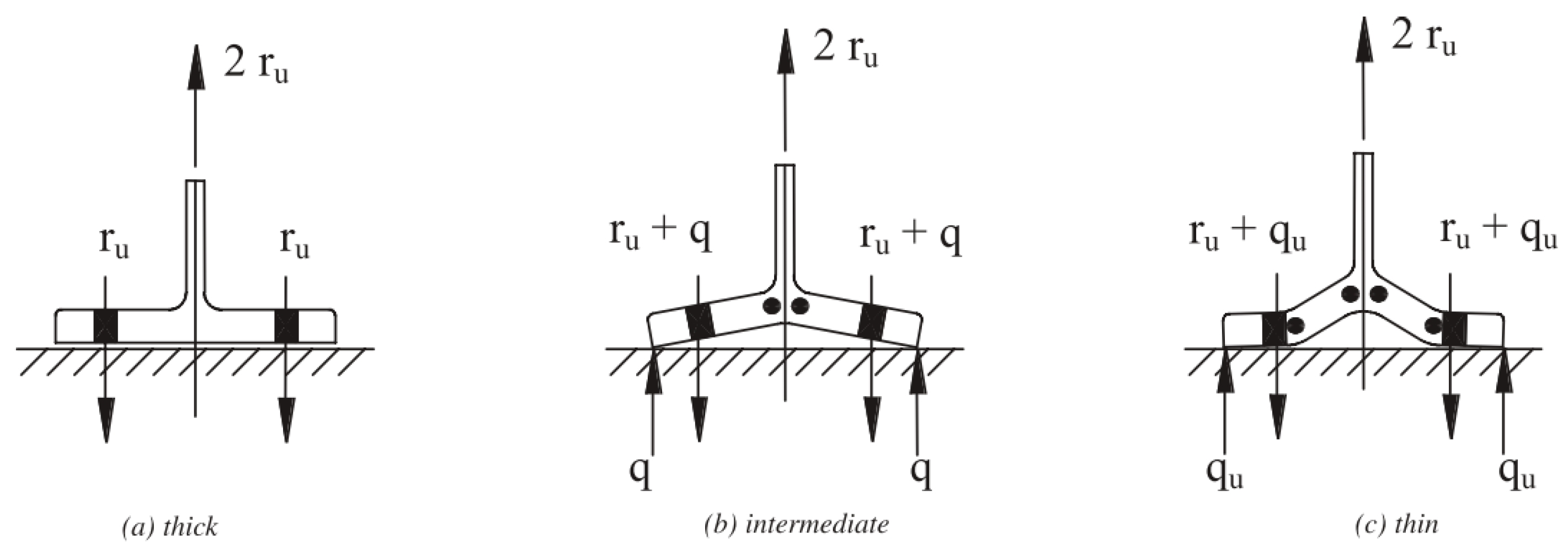
1.2. T-Stub Connections in Eurocode 3
2. Experimental Study
3. Experimental Results and Discussion
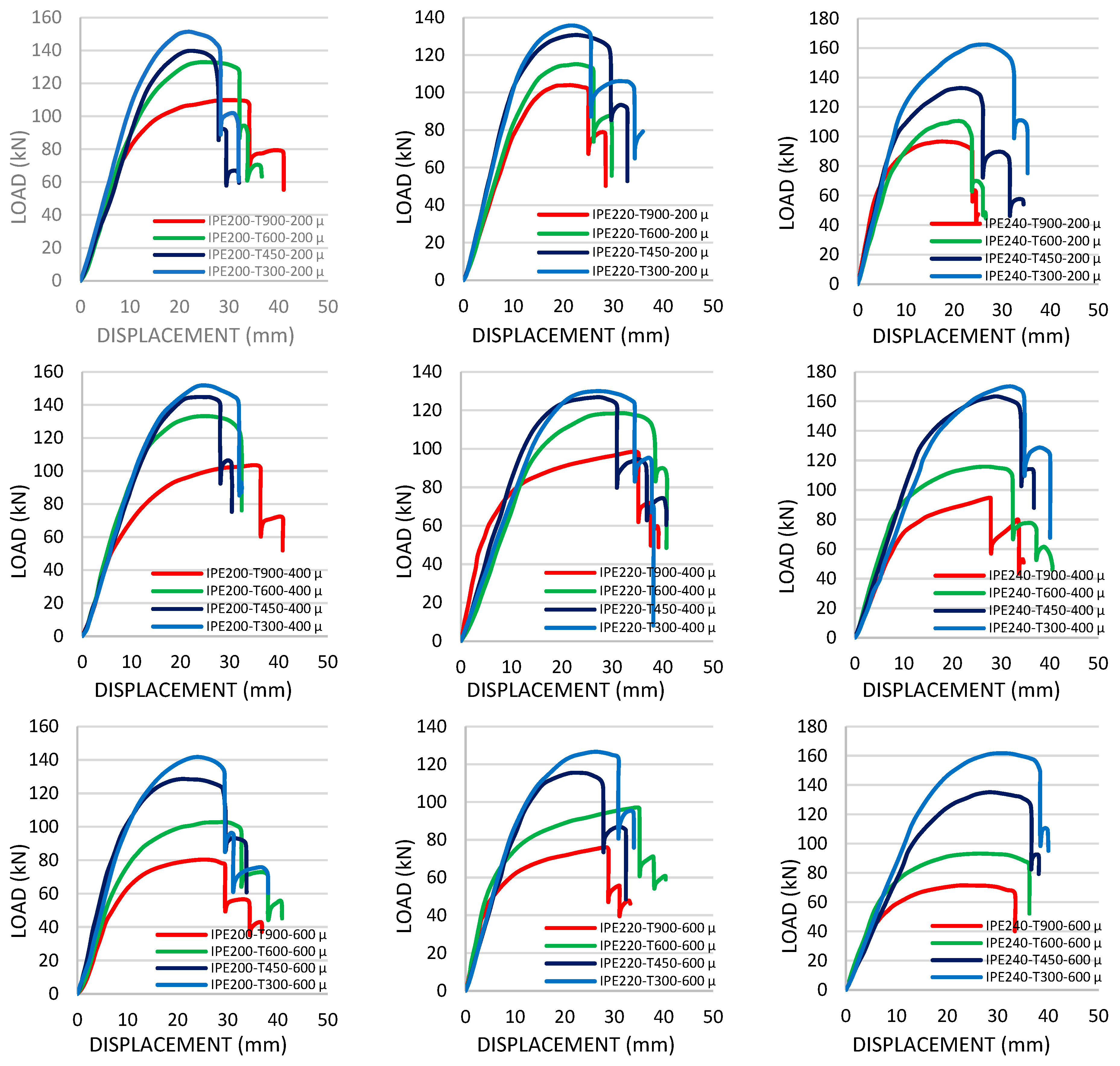
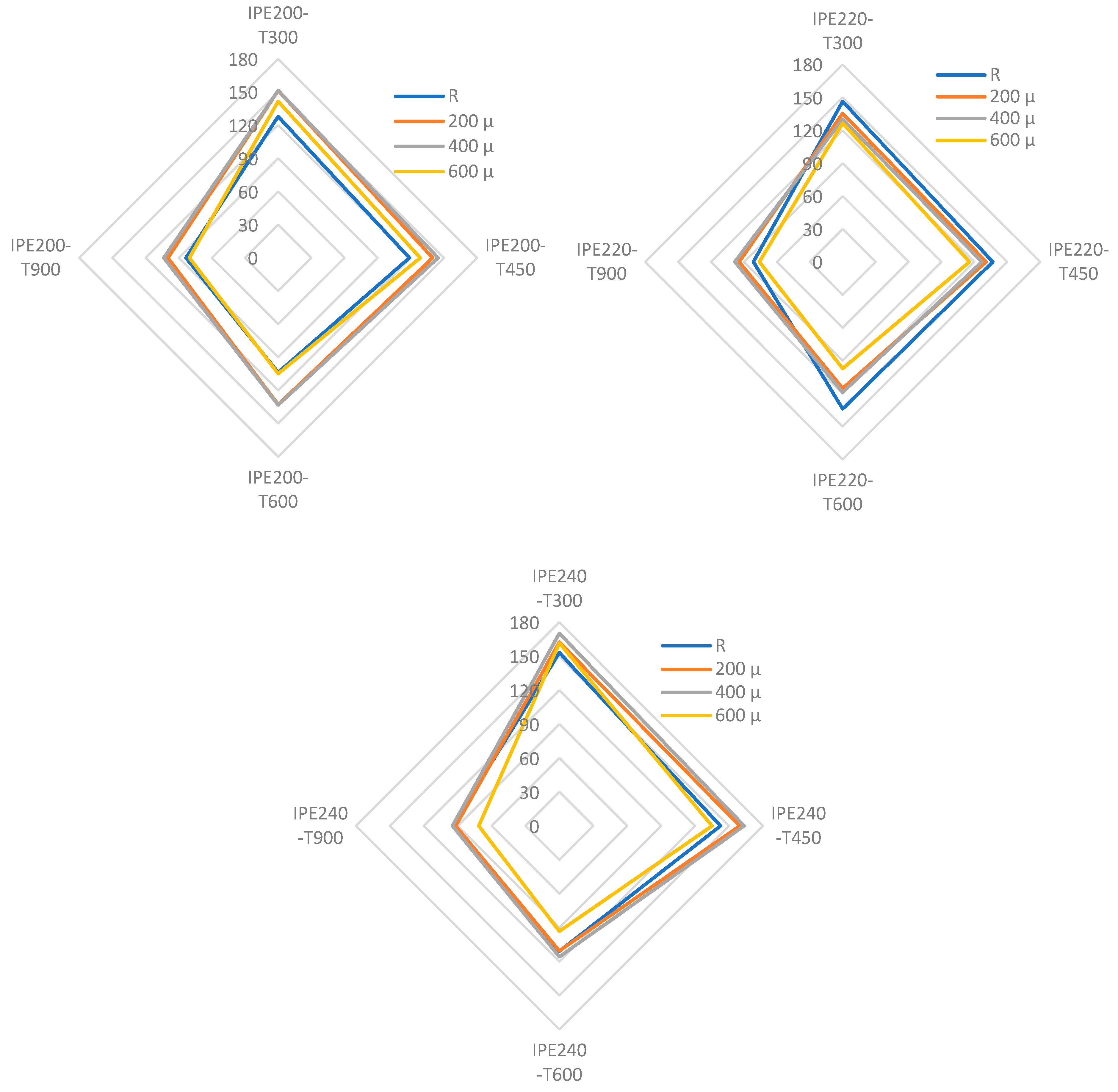
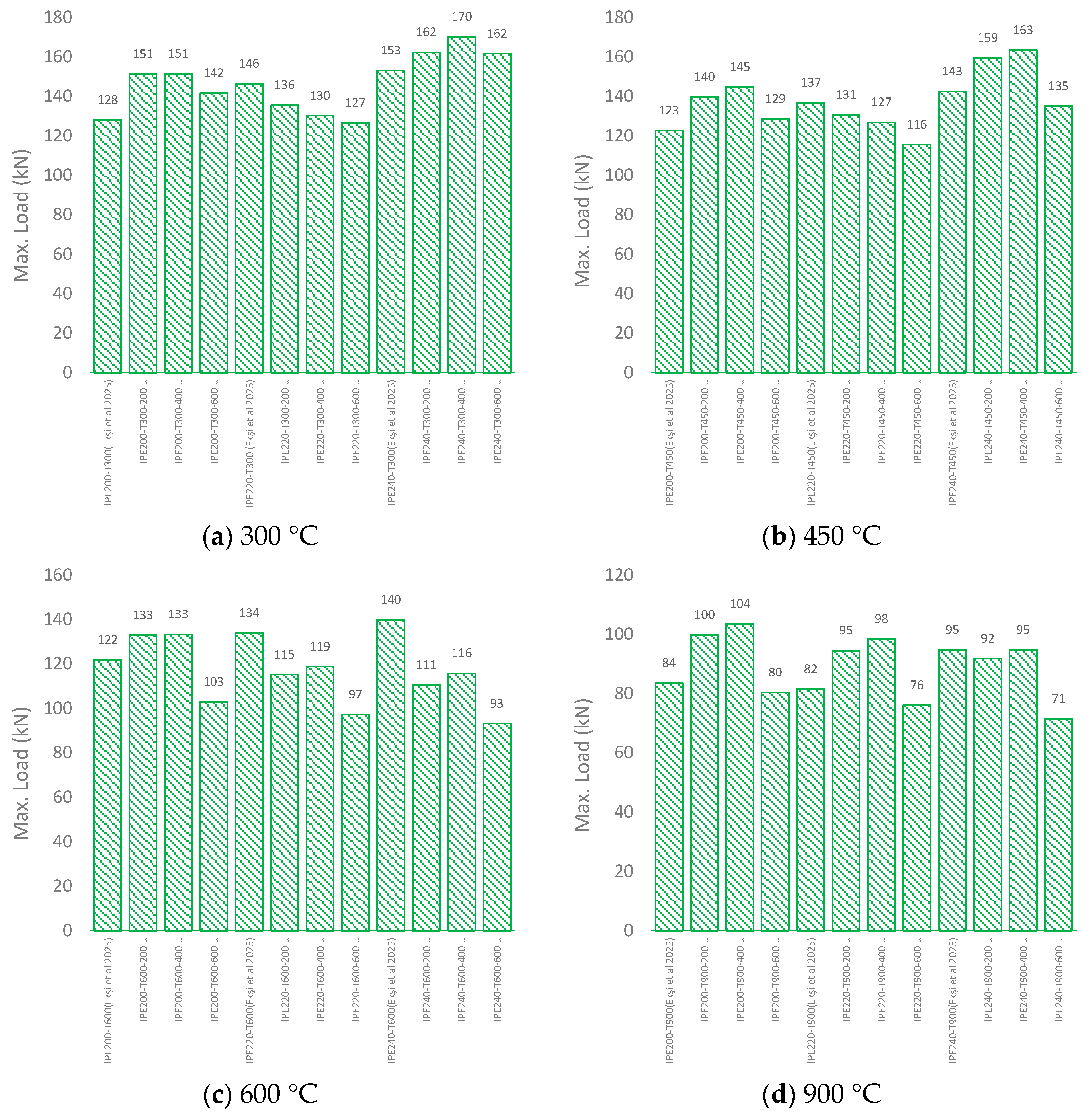
3.1. Load Carrying Capacity
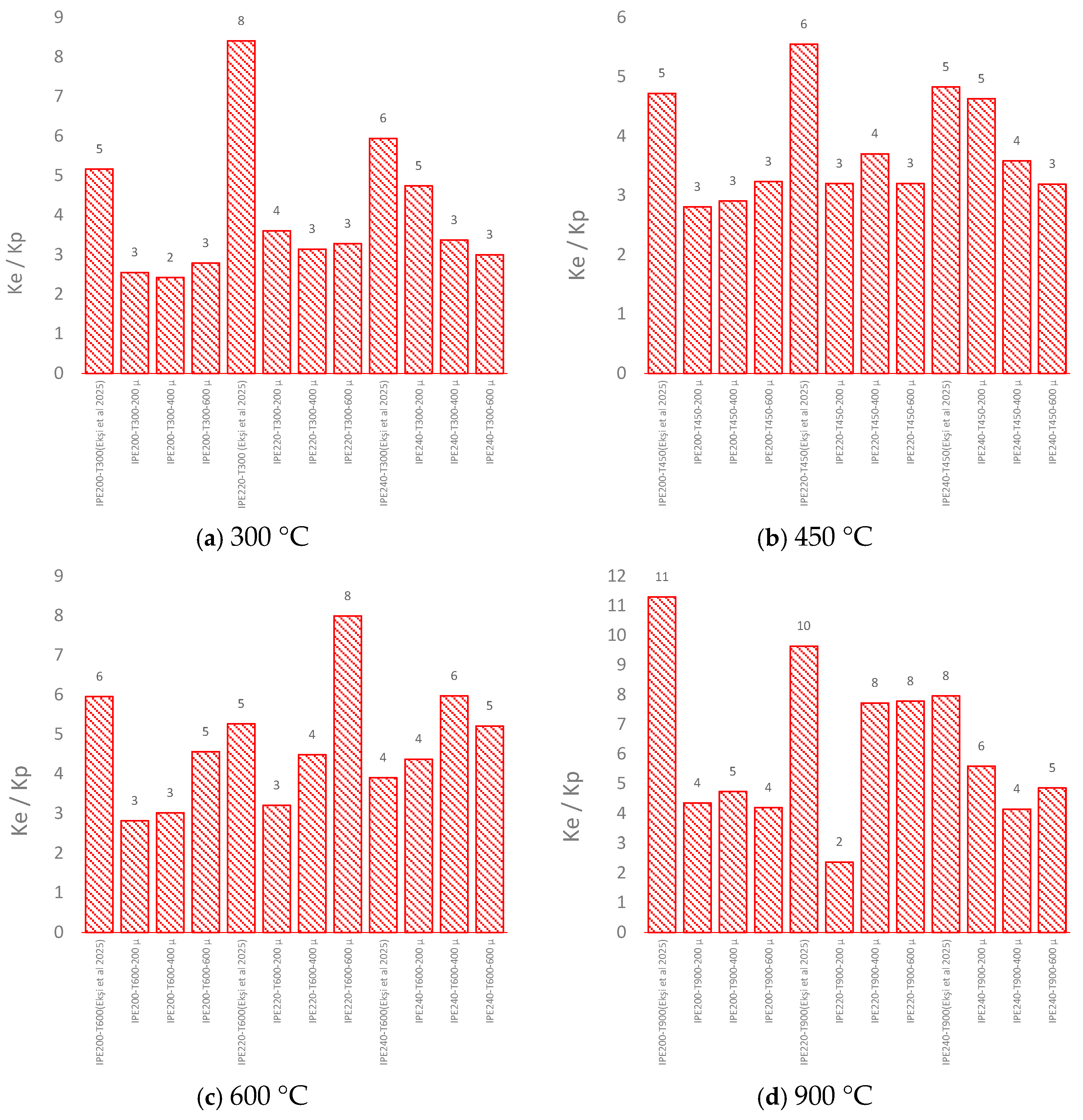
3.2. Stiffness (Ke/Kp)
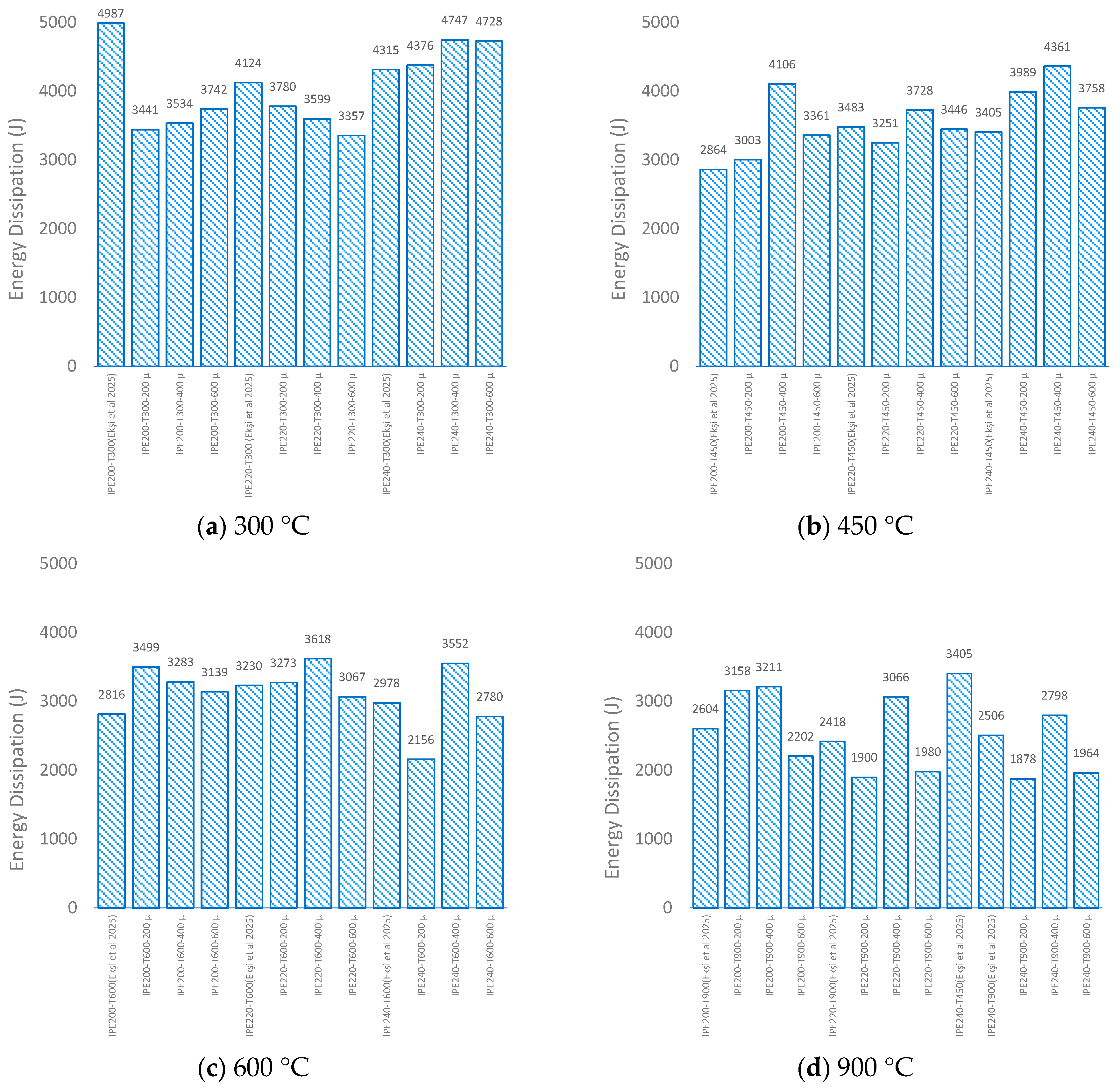
3.3. Energy Dissipation
4. Numerical Investigation
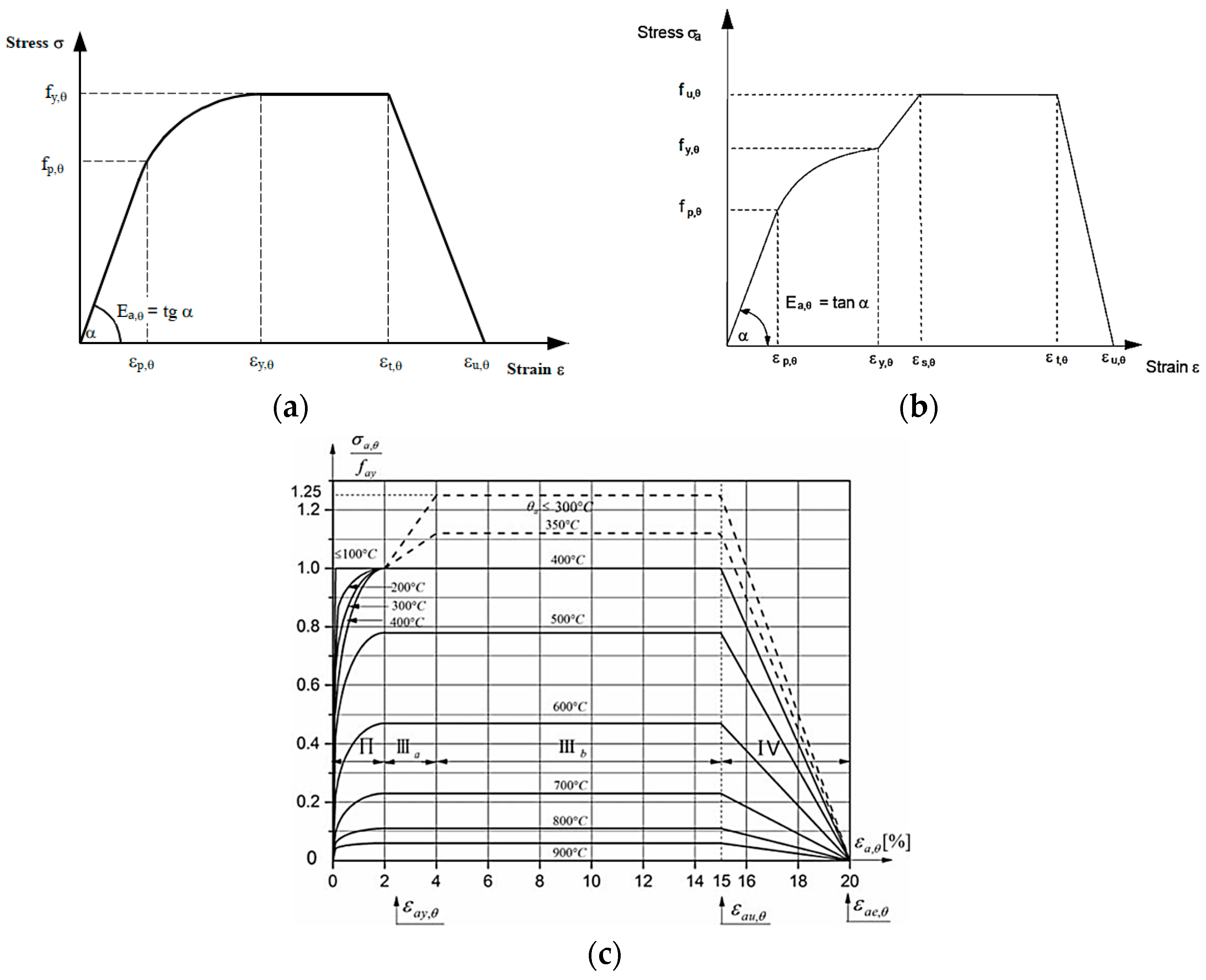
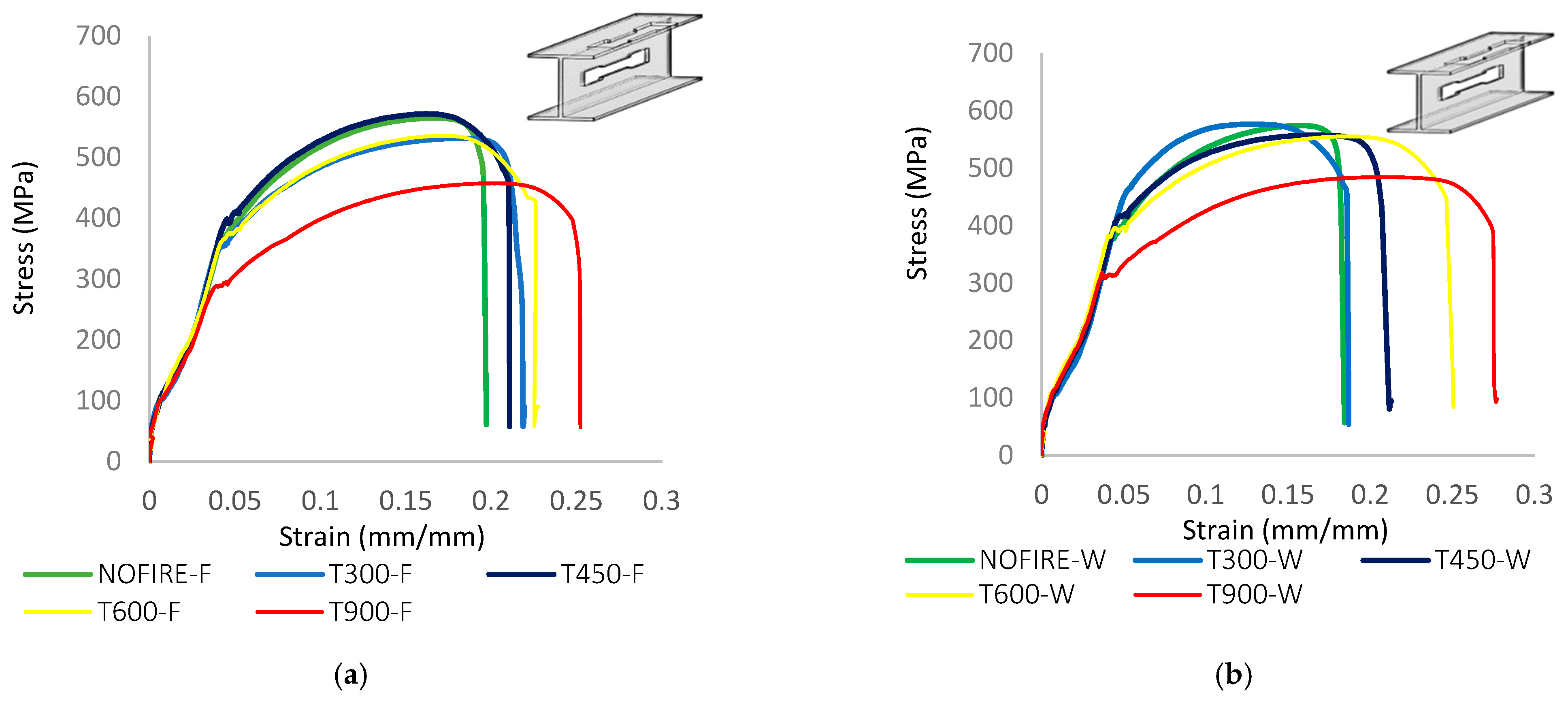
4.1. Material Properties, Element Type and Mesh Size
4.2. Boundary Conditions and Loading Procedure
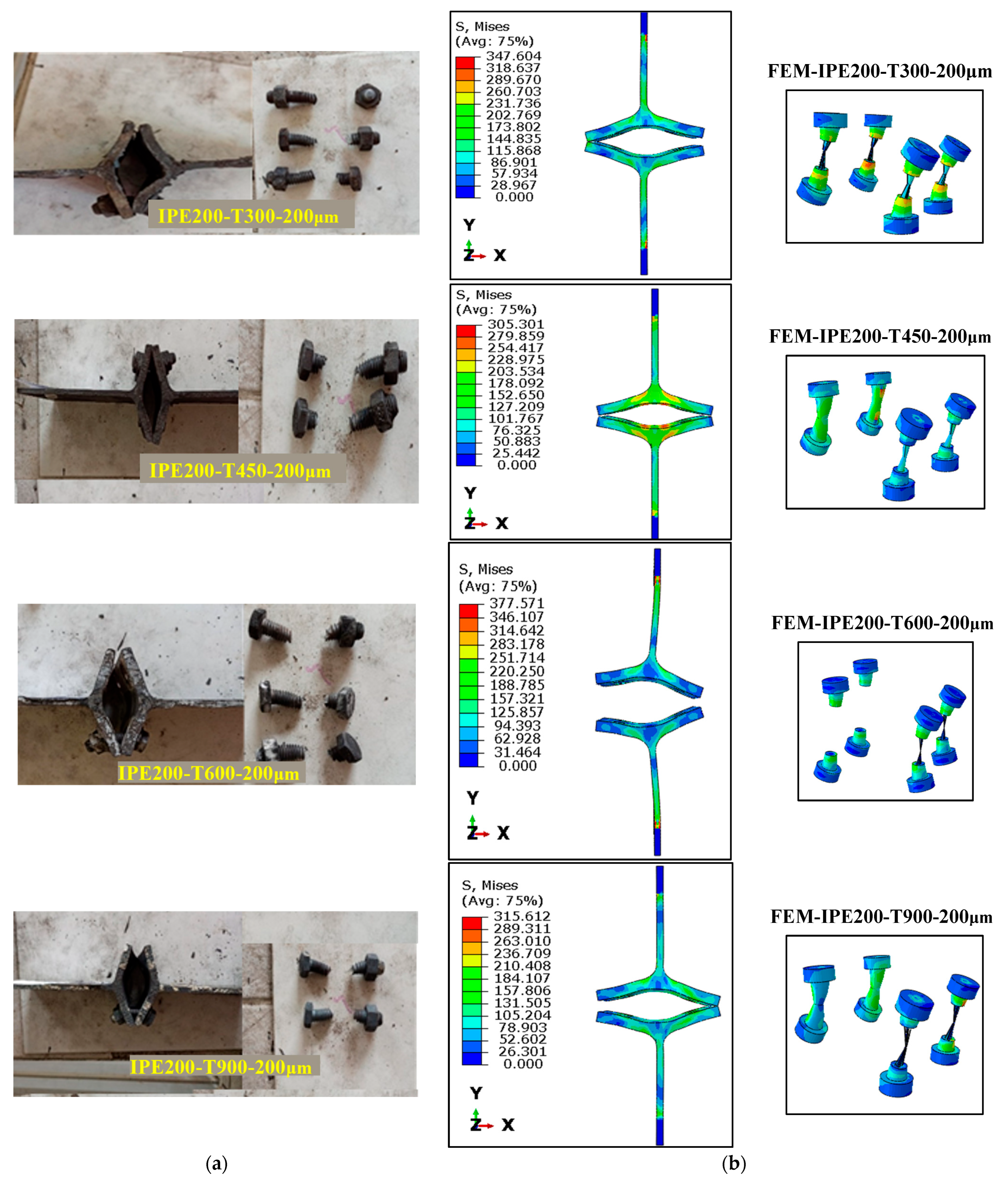
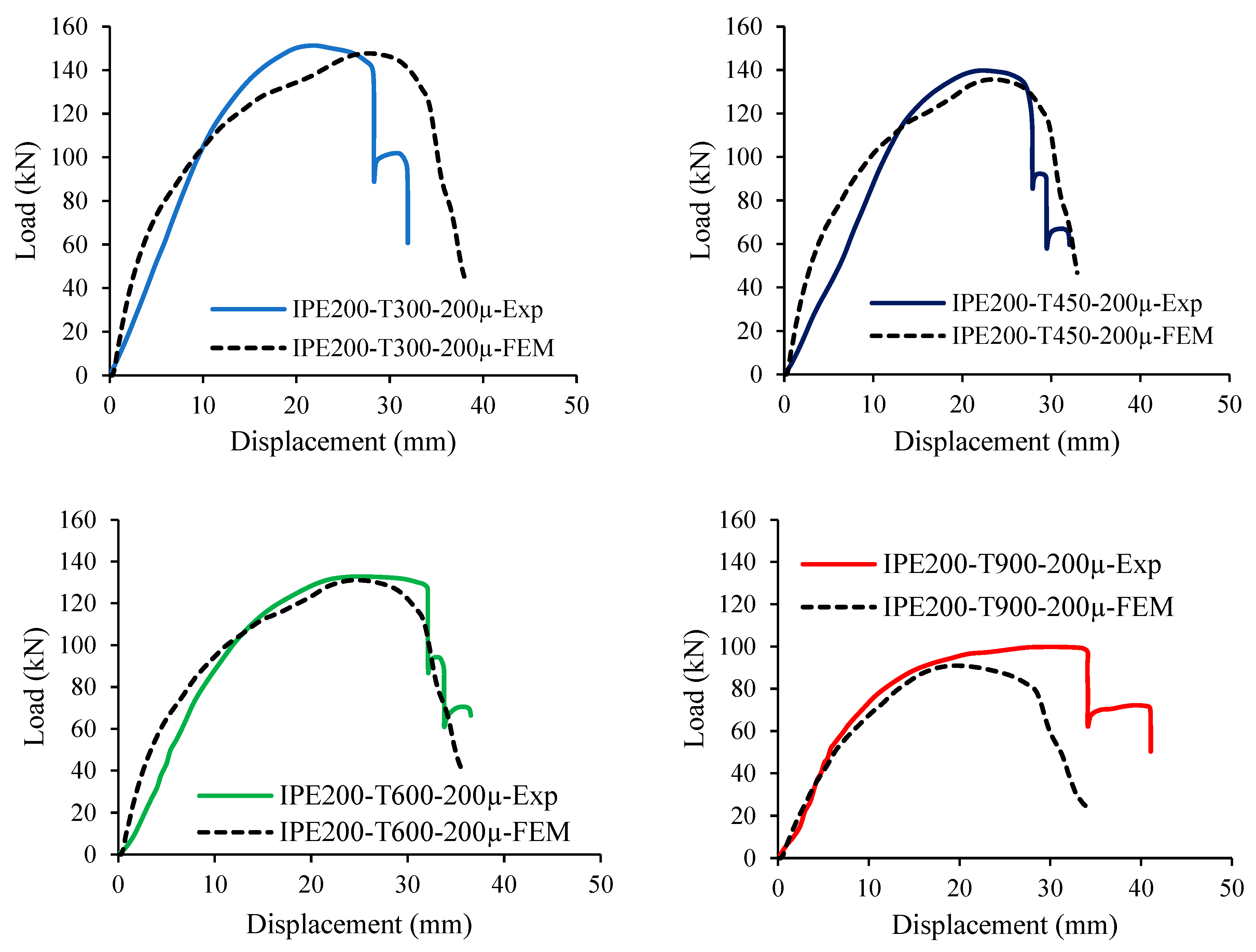
5. Validation of the Finite Element Method (FEM)
6. Conclusions
- The application of 200 μm and 400 μm fire-resistant paint at 300 °C and 450 °C led to significant improvements in axial load capacity—approximately 10% at 300 °C and 20% at 450 °C—compared to uncoated specimens.
- Under these conditions, the 200 μm and 400 μm fire-resistant coating maintained capacity after high production runs. This appeared to be due to two physiological factors:
- (a)
- Thermal lag, where the medium-trail coating slows down heat input, limiting strength loss in the steel and relaxation of the bolt pre-stressing.
- (b)
- Mechanical buffering, where the charred/swollen layer formed during the cooling phase acts as a compliant interlayer, reducing differential shrinkage and residual stresses.
- Protective coatings reduced the initial stiffness of the joints while increasing their post-limit stiffness, indicating a shift in mechanical behavior under elevated temperatures from elastic to more ductile response due to yield strength degradation.
- With increasing temperature and coating thickness, the elastic deformation ratio (Δe/Δmax) decreased, while the plastic deformation ratio (Δp/Δmax) increased, showing a tendency toward enhanced ductility at higher thermal exposure.
- IPE 200 specimens with 400 μm coatings showed maximum load capacity gains of 15.48%, 17.98%, 22.16%, and 19.28% at 300 °C, 450 °C, 600 °C, and 900 °C, respectively. These findings suggest that optimal fire resistance in terms of load-bearing performance can be achieved with 200–400 μm coatings and a tf/tw ratio below 0.63.
- Despite improved load capacity, stiffness ratios declined considerably with increased coating thickness up to 600 μm, especially at 600 °C and 900 °C. For effective fire resistance at these high temperatures, a coating thickness between 400 and 600 μm and a tf/tw ratio under 0.64 are recommended.
- Energy dissipation capacity increased with paint thickness up to 400 μm for specimens exposed to 450 °C and above. IPE 200 and IPE 220 specimens showed enhancements up to 30.25% and 21.14%, respectively, emphasizing the benefit of controlled coating application for structural resilience under fire.
- Finite element analyses performed using Abaqus demonstrated high agreement with experimental data, with deviations in maximum load and energy dissipation ranging from 0.97% to 9.73% and 1.18% to 42.13%, respectively. The FEM models accurately predicted deformation patterns and failure mechanisms, validating their reliability for simulating steel joints under fire exposure.
- Overall, this study highlights the effectiveness of fire-resistant coatings and geometric optimization in improving the structural performance of steel T-stub joints under elevated temperatures and demonstrates the accuracy of FEM tools in predicting their thermo-mechanical behavior.
- This study suggests that for bolted T-joints exposed to conditions similar to this one, a medium-thickness (200–400 μm) intumescent coating may provide an appropriate protection/thickness balance by balancing thermal retardation and coal layer integrity. In practice, designers and inspectors may prioritize verifying coal layer continuity/adhesion after fire, re-coating in areas experiencing coal loss, and considering the balance between thermal performance and mechanical strength of the coal layer when selecting coatings. While code/standard calibration is beyond the scope of this study, observed trends can inform coating selection and repair evaluations for similar connections.
Author Contributions
Funding
Conflicts of Interests
References
- Eurocode 3. EN1993 Design of Steel Structures; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Bezerra, L.M.; Bonilla, J.; Silva, W.A.; Matias, W.T. Experimental and numerical studies of bolted T-stub steel connection with different flange thicknesses connected to a rigid base. Eng. Struct. 2020, 218, 110770. [Google Scholar] [CrossRef]
- Özkılıç, Y.O. The capacities of thin plated stiffened T-stubs. J. Constr. Steel Res. 2021, 186, 106912. [Google Scholar] [CrossRef]
- Bezerra, L.M.; Bonilla, J.; Freitas, C.S.; Massicotte, B. Behavior of T-stub steel connections bolted to rigid bases. J. Constr. Steel Res. 2022, 192, 107242. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, S.; Guo, L.; Qu, J.; Wang, S. Ultimate tensile behavior of bolted T-stub connections with preload. J. Build. Eng. 2022, 47, 103833. [Google Scholar] [CrossRef]
- Stamatopoulos, G.N.; Ermopoulos, J.C. Influence of the T-stub flexibility on its strength. Int. J. Steel Struct. 2010, 10, 73–79. [Google Scholar] [CrossRef]
- Faralli, A.C.; Latour, M.; Tan, P.J.; Rizzano, G.; Wrobel, P. Experimental investigation and modelling of T-stubs undergoing large displacements. J. Constr. Steel Res. 2021, 180, 106580. [Google Scholar] [CrossRef]
- Liu, X.; Hao, Z.; Luo, X.; Jin, Z. Experimental behavior and modelling of steel bolted T-stub connections. Buildings 2023, 13, 575. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, L.; Wang, P.; Hou, G.; Cai, X.; He, M. Feasibility study of TSOB replacing standard high-strength bolt in T-stub connection. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 62, p. 106246. [Google Scholar] [CrossRef]
- Sarfarazi, S.; Shamass, R.; Guarracino, F.; Mascolo, I.; Modano, M. Exploring the stainless-steel beam-to-column connections response: A hybrid explainable machine learning framework for characterization. Front. Struct. Civ. Eng. 2025, 19, 34–59. [Google Scholar] [CrossRef]
- Shen, Y.; Li, M.; Li, Y. A reliable cyclic envelope model for partially-restrained steel beam-column bolted T-stub connections based on experimental data. Thin-Walled Struct. 2024, 200, 111951. [Google Scholar] [CrossRef]
- de Cisneros Fonfría, J.J.J.; Amador, A.M.G.; González, A.Q.; Fernández, L.P. Investigating the T-stub connection with different web-to-flange joint configurations. Eng. Struct. 2023, 294, 116715. [Google Scholar] [CrossRef]
- LaMalva, K.J.; Barnett, J.R.; Dusenberry, D.O. Failure analysis of the World Trade Center 5 building. J. Fire Prot. Eng. 2009, 19, 261–274. [Google Scholar] [CrossRef]
- Ahmadi, M.T.; Aghakouchak, A.A.; Mirghaderi, R.; Tahouni, S.; Garivani, S.; Shahmari, A.; Epackachi, S. Collapse of the 16-story Plasco building in Tehran due to fire. Fire Technol. 2020, 56, 769–799. [Google Scholar] [CrossRef]
- FEMA403; Federal Emergency Management Agency: Washington, DC, USA; New York, NY, USA, 2002. Available online: https://www.fema.gov/pdf/library/fema403_ch2.pdf (accessed on 1 February 2023).
- Meng, B.; Li, H.; Liew, J.Y.R.; Li, S.; Kong, D.Y. Enhancing the collapse resistance of a composite subassembly with fully welded joints using sliding inner cores. J. Struct. Eng. 2024, 150, 04024085. [Google Scholar] [CrossRef]
- Ketabdari, H.; Daryan, A.S.; Hassani, N. Predicting post-fire mechanical properties of grade 8.8 and 10.9 steel bolts. J. Constr. Steel Res. 2019, 162, 105735. [Google Scholar] [CrossRef]
- Wang, P.; You, Y.; Wang, Q.; Gu, H.; Wang, G.; Liu, Y.; Liu, F. Post-fire tensile behavior of hole-anchored bolted T-stub connection. J. Constr. Steel Res. 2021, 187, 106941. [Google Scholar] [CrossRef]
- Gao, F.; Liu, Z.; Guan, X. Fire resistance behavior of T-stub joint components under transient heat transfer conditions. Eng. Struct. 2021, 237, 112164. [Google Scholar] [CrossRef]
- Qiang, X.; Shu, Y.; Jiang, X.; Xiao, Y. Nonlinear analysis on mechanical behaviour of high strength steel extended endplate connections and equivalent T-stubs in fire considering axial force. Case Stud. Constr. Mater. 2023, 19, e02402. [Google Scholar] [CrossRef]
- Qiang, X.; Shu, Y.; Jiang, X. Mechanical behaviour of high strength steel T-stubs at elevated temperatures: Experimental study. Thin-Walled Struct. 2023, 182, 110314. [Google Scholar] [CrossRef]
- Irvani, M.; Ezati, H.; Khafajeh, R.; Jaari, V.R.K. Numerically study on the seismic response of partially restrained moment connection with structural fuse T-stub for European sections. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 35, pp. 82–105. [Google Scholar] [CrossRef]
- Wang, P.; You, Y.; Liu, M.; Zhang, B.; Zhou, S.; Chen, J. Behavior of thread-fixed one-side bolted T-stubs with backing plates at ambient and elevated temperatures. J. Constr. Steel Res. 2020, 170, 106093. [Google Scholar] [CrossRef]
- Sebbagh, H.R.; Kerdal, D.E.D.; Abidelah, A.; Bouchaïr, A. T-stubs with two and four bolts under monotonic and cyclic loading. J. Constr. Steel Res. 2021, 178, 106486. [Google Scholar] [CrossRef]
- Wang, P.; Sun, L.; Zhang, B.; Yang, X.; Liu, F.; Han, Z. Experimental studies on T-stub to hollow section column connection bolted by T-head square-neck one-side bolts under tension. J. Constr. Steel Res. 2021, 178, 106493. [Google Scholar] [CrossRef]
- Cai, W.Y.; Jiang, J.; Li, G.Q.; Wang, Y.B. Fracture behavior of high-strength bolted steel connections at elevated temperatures. Eng. Struct. 2021, 245, 112817. [Google Scholar] [CrossRef]
- AIJ.; Design Standard for Steel Structures–Based on Allowable Stress Concept. Architectural Institute of Japan: Tokyo, Japan, 2005.
- Standard, B. Eurocode 1: Actions on Structures; British Standard: London, UK, 2006. [Google Scholar]
- Wang, W.; Fang, H.; Wang, Z. Comprehensive studies on the behaviors of high strength steel T-stubs with thin-walled flange at elevated temperatures. Thin-Walled Struct. 2023, 190, 110998. [Google Scholar] [CrossRef]
- Meng, B.; Qiangqiang, D.; Zhong, W.; Tan, Z.; You, K. Tensile resistance and deformation of novel bending T-stub connections against progressive collapse. J. Constr. Steel Res. 2023, 201, 107733. [Google Scholar] [CrossRef]
- Khani, R.; Hosseinzadeh, Y.; Asl, M.H. Improving the T-stub component behavior tied to a rigid base. J. Constr. Steel Res. 2023, 211, 108199. [Google Scholar] [CrossRef]
- Zoetemeijer, P. A design method for the tension side of statically loaded, bolted beam-to-column connections. HERON 1974, 20, 1974. [Google Scholar]
- Khani, R.; Hosseinzadeh, Y.; Asl, M.H. Investigating the prying force magnitude and location in the T-stub connection based on the energy method. Eng. Struct. 2023, 280, 115655. [Google Scholar] [CrossRef]
- Hantouche, E.G.; Abboud, N.H. Stiffness modeling of bolted thick built-up T-stub connections including secondary prying effect. J. Constr. Steel Res. 2014, 95, 279–289. [Google Scholar] [CrossRef]
- Herrera, R.A.; Bravo, M.; Gómez, G.; Aedo, G. Performance of built-up T-stubs for Double T moment connections. J. Constr. Steel Res. 2013, 88, 289–295. [Google Scholar] [CrossRef]
- Nair, R.S.; Birkemoe, P.C.; Munse, W.H. High strength bolts subject to tension and prying. J. Struct. Div. 1974, 100, 351–372. [Google Scholar] [CrossRef]
- de la Croix Kombate, T.J.; Taşkın, K. State-of-the-art review on the behaviour of T-stubs and prying action. J. Constr. Steel Res. 2022, 191, 107203. [Google Scholar] [CrossRef]
- Hu, D.; Papadopoulos, J.; Adams, G.G. Prying action in an elastic T-stub tensile connection. J. Constr. Steel Res. 2020, 169, 106027. [Google Scholar] [CrossRef]
- Douty, R.T.; McGuire, W. High strength bolted moment connections. J. Struct. Div. 1965, 91, 101–128. [Google Scholar] [CrossRef]
- You, Y.; Liu, M.; Liu, Y.; Wang, P.; Zhou, S.; Chen, J. Experimental studies on thread-fixed one-side bolted T-stubs in tension at elevated temperatures. J. Constr. Steel Res. 2020, 171, 106139. [Google Scholar] [CrossRef]
- Both, I.; Duma, D.; Dinu, F.; Dubina, D.; Zaharia, R. The influence of loading rate on the ultimate capacity of bolted T-stubs at ambient and high temperature. Fire Saf. J. 2021, 125, 103438. [Google Scholar] [CrossRef]
- de Silva, D.; Alam, N.; Nadjai, A.; Nigro, E.; Ali, F. Finite element modelling for structural performance of slim floors in fire and influence of protection materials. Appl. Sci. 2021, 11, 11291. [Google Scholar] [CrossRef]
- Nazrun, T.; Hassan, M.K.; Hasnat, M.R.; Hossain, M.D.; Ahmed, B.; Saha, S. A comprehensive review on intumescent coatings: Formulation, manufacturing methods, research development, and issues. Fire 2025, 8, 155. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Y.; Li, M. Research on thermal response behavior of the intumescent coating at high temperature: An experimental and numerical study. Buildings 2022, 12, 1014. [Google Scholar] [CrossRef]
- Bogatu, N.; Buruiana, D.L.; Muresan, A.C.; Ghisman, V.; Lupu, A.; Mardare, L.; Herbei, E.E.; Basliu, V.; Ceoromila, A.; Florescu, S. Assessment of the Effectiveness of Protective Coatings in Preventing Steel Corrosion in the Marine Environment. Polymers 2025, 17, 378. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Liew, J.R.; Xiong, M.X.; Lai, B.L. Experimental investigation on fire resistance of high-strength concrete encased steel composite columns. Fire Saf. J. 2021, 121, 103273. [Google Scholar] [CrossRef]
- Du, E.F.; Shu, G.P.; Qin, L.; Lai, B.L.; Zhou, X.L.; Zhou, G.G. Experimental investigation on fire resistance of sandwich composite walls with truss connectors. J. Constr. Steel Res. 2022, 188, 107052. [Google Scholar] [CrossRef]
- Oliveira, R.B.; Moreno, A.L.; Vieira, L.C.M. Intumescent paint as fire protection coating. Rev. IBRACON Estrut. Mater. 2017, 10, 220–231. [Google Scholar] [CrossRef]
- TS EN13501-1; Fire Classification of Construction Products and Building Elements—Part 1: Classification Using Data from Reaction to Fire Tests. Institute of Turkish Standards: Ankara, Türkiye, 2019.
- EN 13381-8:2013; Test Methods for Determining the Contribution to the Fire Resistance of Structural Members—Part 8: Applied Reactive Protection to Steel Members. European Committee for Standardization: Brussels, Belgium, 2013.
- EN 13501-2:2016; Fire Classification of Construction Products and Building Elements: Classification Using Data from Fire Resistance Tests, Excluding Ventilation Services. European Committee for Standardization: Brussels, Belgium, 2016.
- ISONEM Anti-Fire Paint Plus: Technical Data Sheet (TDS). 2025. Available online: https://isonem.ge/wp-content/uploads/2025/04/TDS-EN-ISONEM-ANTI-FIRE-PAINT-PLUS.pdf (accessed on 1 January 2025).
- ISO 2808; Paints and Varnishes—Determination of Film Thickness. ISO: Geneva, Switzerland, 2019.
- ISO 834-1; Fire-Resistance Tests—Elements of Building Construction. ISO: Geneva, Switzerland, 2025.
- EN 1363-1; Fire Resistance Tests—Part 1: General Requirements. European Committee for Standardization: Brussels, Belgium, 2020.
- EN 1991-1-2; Eurocode 1: Actions on Structures—Part 1–2: General Actions on Structures Exposed to Fire. European Committee for Standardization: Brussels, Belgium, 2024.
- TS EN ISO 6892-1; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature (ISO 6892-1:2019). Institute of Turkish Standards(TSE): Ankara, Türkiye, 2020.
- ISO 898-1:2013; Mechanical Properties of Fasteners Made of Carbon Steel and Alloy Steel Part 1: Bolts, Screws and Studs with Specified Property Classes—Coarse Thread and Fine Pitch Thread. ISO: Geneva, Switzerland, 2013.
- Ekşi, H.; Maali, M.; Yaman, Z.; Ağcakoca, E.; Sadid, M.S.; Aydın, A.C. Experimental Investigation of Steel Bolted T-Stub Connections at Different Post-Fire Condition. Arch. Civ. Mech. Eng. 2025. under review. [Google Scholar]
- AISC (American Institute of Steel Construction). ANSI/AISC360-10: Specification for Structural Steel Buildings; A.I.S.C.: Chicago, IL, USA, 2010. [Google Scholar]
- ABAQUS. G Abaqus 6.11; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2011; p. 3. [Google Scholar]
- Chen, B.; Roy, K.; Uzzaman, A.; Lim, J.B. Moment capacity of cold-formed channel beams with edge-stiffened web holes, un-stiffened web holes and plain webs. Thin-Walled Struct. 2020, 157, 107070. [Google Scholar] [CrossRef]
- Schaumann, P.; Tabeling, F.; Weisheim, W. Numerical simulation of the heating behaviour of steel profiles with intumescent coating adjacent to trapezoidal steel sheets in fire. J. Struct. Fire Eng. 2016, 7, 158–167. [Google Scholar] [CrossRef]
- Weisheim, W.; Schaumann, P.; Sander, L.; Zehfuß, J. Numerical model for the fire protection performance and the design of intumescent coatings on structural steel exposed to natural fires. J. Struct. Fire Eng. 2020, 11, 33–50. [Google Scholar] [CrossRef]
- Barata, P.; Ribeiro, J.; Rigueiro, C.; Santiago, A.; Rodrigues, J.P. Assessment of the T-stub joint component at ambient and elevated temperatures. Fire Saf. J. 2014, 70, 1–13. [Google Scholar] [CrossRef]

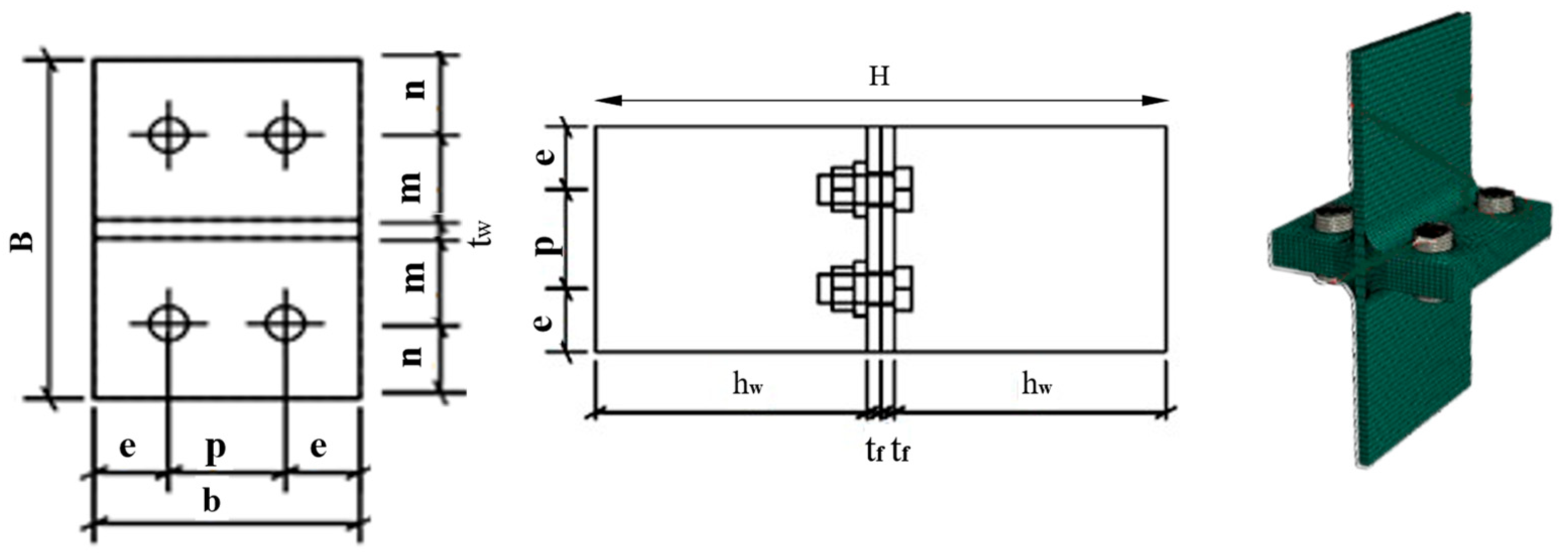







| Group | Paint Thickness (μm) | Specimens | Temperature (°C) | Bolt | tf (mm) | tw (mm) | H (2hw + 2tf) (mm) | B (mm) | n (mm) | m (mm) | b (2e + P) (mm) | e (mm) | p (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IPE 200 | 200 | I200-T300-200 μ | 300 | M12 | 8.5 | 5.6 | 380 | 100 | 22 | 25.2 | 100 | 20 | 60 |
| I200-T450-200 μ | 450 | ||||||||||||
| I200-T600-200 μ | 600 | ||||||||||||
| I200-T900-200 μ | 900 | ||||||||||||
| 400 | I200-T300-400 μ | 300 | 24.5 | 27.55 | |||||||||
| I200-T450-400 μ | 450 | ||||||||||||
| I200-T600-400 μ | 600 | ||||||||||||
| I200-T900-400 μ | 900 | ||||||||||||
| 600 | I200-T300-600 μ | 300 | 26.5 | 30.4 | |||||||||
| I200-T450-600 μ | 450 | ||||||||||||
| I200-T600-600 μ | 600 | ||||||||||||
| I200-T900-600 μ | 900 | ||||||||||||
| IPE 220 | 200 | I220-T300-200 μ | 300 | M12 | 9.2 | 5.9 | 420 | 110 | 22 | 25.2 | 100 | 20 | 60 |
| I220-T450-200 μ | 450 | ||||||||||||
| I220-T600-200 μ | 600 | ||||||||||||
| I220-T900-200 μ | 900 | ||||||||||||
| 400 | I220-T300-400 μ | 300 | 24.5 | 27.55 | |||||||||
| I220-T450-400 μ | 450 | ||||||||||||
| I220-T600-400 μ | 600 | ||||||||||||
| I220-T900-400 μ | 900 | ||||||||||||
| 600 | I220-T300-600 μ | 300 | 26.5 | 30.4 | |||||||||
| I220-T450-600 μ | 450 | ||||||||||||
| I220-T600-600 μ | 600 | ||||||||||||
| I220-T900-600 μ | 900 | ||||||||||||
| IPE 240 | 200 | I240-T300-200 μ | 300 | M12 | 9.8 | 6.2 | 460 | 120 | 22 | 25.2 | 100 | 20 | 60 |
| I240-T450-200 μ | 450 | ||||||||||||
| I240-T600-200 μ | 600 | ||||||||||||
| I240-T900-200 μ | 900 | ||||||||||||
| 400 | I240-T300-400 μ | 300 | 24.5 | 27.55 | |||||||||
| I240-T450-400 μ | 450 | ||||||||||||
| I240-T600-400 μ | 600 | ||||||||||||
| I240-T900-400 μ | 900 | ||||||||||||
| 600 | I240-T300-600 μ | 300 | 26.5 | 30.4 | |||||||||
| I240-T450-600 μ | 450 | ||||||||||||
| I240-T600-600 μ | 600 | ||||||||||||
| I240-T900-600 μ | 900 |
| Surface heat conductivity value | min 0.80 |
| Thermal paint surface resistance (RS) | 0.0495 ± 1.5% |
| Thermal conductivity coefficient (W/mK) | 0.023; λ < 0.060 |
| Impact resistance | No cracking, no breaking |
| Density (25 °C, g/mL) | 1.40 ± 0.10 |
| pH (25 °C) | 7.0–9.0 |
| Viscosity (25 °C, mPas) | 12,500–15,000 |
| Resistance | 5 kOhm: 30–150 mm |
| Resistance tolerance | ± %20 |
| Load resistance | 100 kOhm.min |
| Solids ratio (% by Weight) | 76 ± 2 |
| Water transfer rate (kg/m2.h0.5) | <0.1 Grade W3 |
| Water vapor permeability (m) | 5 ≤ SD ≤ 50 Grade II |
| Bolt (M10-8.8) | IPE 200 Web | IPE 200 Flange | IPE 220 Web | IPE 220 Flange | IPE 240 Web | IPE 240 Flange | |
|---|---|---|---|---|---|---|---|
| E (MPa) | - | 203,214 | 204,314 | 204,444 | 204,215 | 205,116 | 206,301 |
| fy (MPa) | 817.2 | 368 | 367 | 396 | 393 | 401 | 398 |
| fu (MPa) | 902.5 | 533 | 526 | 565 | 553 | 570 | 568 |
| ρy = fy/fu | 0.91 | 0.69 | 0.70 | 0.70 | 0.71 | 0.71 | 0.72 |
| Group | Bolt Load Capacity (kN) | Specimens | Max. Load (kN) | Max.Load / Bolts Load Capacity | Stiffness (kN/mm) | Energy Dissipation (Joule) | |||
|---|---|---|---|---|---|---|---|---|---|
| Initial Stiffness (Ke) | Post-Limit Stiffness (Kp) | Ke/Kp | Kp/Ke | ||||||
| IPE 200 | 135.648 | IPE200-T300 (Ekşi et al. 2025) | 127.97 | 0.94 | 8.57 | 1.66 | 5.16 | 0.19 | 4987.48 |
| IPE200-T450 (Ekşi et al. 2025) | 118.70 | 0.90 | 15.86 | 3.36 | 4.72 | 0.21 | 2863.89 | ||
| IPE200-T600 (Ekşi et al. 2025) | 103.70 | 0.90 | 15.00 | 2.52 | 5.95 | 0.17 | 2815.65 | ||
| IPE200-T900 (Ekşi et al. 2025) | 83.60 | 0.62 | 13.33 | 1.18 | 11.30 | 0.09 | 2603.54 | ||
| IPE200-T300-200 μ | 151.35 | 1.12 | 10.00 | 3.92 | 2.55 | 0.39 | 3441.07 | ||
| IPE200-T450-200 μ | 139.66 | 1.03 | 8.75 | 3.12 | 2.80 | 0.36 | 3003.22 | ||
| IPE200-T600-200 μ | 132.83 | 0.98 | 9.22 | 3.28 | 2.81 | 0.36 | 3498.93 | ||
| IPE200-T900-200 μ | 99.82 | 0.74 | 8.83 | 2.03 | 4.35 | 0.23 | 3158.13 | ||
| IPE200-T300-400 μ | 151.42 | 1.12 | 9.29 | 3.84 | 2.42 | 0.41 | 3533.93 | ||
| IPE200-T450-400 μ | 144.73 | 1.07 | 6.65 | 2.29 | 2.90 | 0.34 | 4106.30 | ||
| IPE200-T600-400 μ | 133.23 | 0.98 | 9.76 | 3.24 | 3.01 | 0.33 | 3283.36 | ||
| IPE200-T900-400 μ | 103.56 | 0.76 | 8.62 | 1.82 | 4.74 | 0.21 | 3210.93 | ||
| IPE200-T300-600 μ | 141.68 | 1.04 | 10.50 | 3.77 | 2.79 | 0.36 | 3741.66 | ||
| IPE200-T450-600 μ | 128.56 | 0.95 | 12.41 | 3.84 | 3.23 | 0.31 | 3360.60 | ||
| IPE200-T600-600 μ | 104.83 | 0.76 | 8.57 | 1.88 | 4.56 | 0.22 | 3138.87 | ||
| IPE200-T900-600 μ | 80.39 | 0.59 | 7.50 | 1.79 | 4.19 | 0.24 | 2201.79 | ||
| IPE 220 | IPE220-T300 (Ekşi et al. 2025) | 146.40 | 1.08 | 10.93 | 1.30 | 8.41 | 0.12 | 4123.50 | |
| IPE220-T450 (Ekşi et al. 2025) | 136.80 | 1.01 | 12.82 | 2.31 | 5.55 | 0.18 | 3482.50 | ||
| IPE220-T600 (Ekşi et al. 2025) | 133.90 | 0.99 | 12.89 | 2.45 | 5.26 | 0.19 | 3230.04 | ||
| IPE220-T900 (Ekşi et al. 2025) | 81.50 | 0.60 | 10.89 | 1.13 | 9.64 | 0.10 | 2417.50 | ||
| IPE220-T300-200 μ | 135.60 | 1.00 | 10.40 | 2.89 | 3.60 | 0.28 | 3780.49 | ||
| IPE220-T450-200 μ | 130.62 | 0.96 | 9.78 | 3.06 | 3.20 | 0.31 | 3250.55 | ||
| IPE220-T600-200 μ | 115.16 | 0.85 | 6.40 | 2.00 | 3.20 | 0.31 | 3273.41 | ||
| IPE220-T900-200 μ | 94.52 | 0.70 | 8.50 | 3.58 | 2.37 | 0.42 | 1900.43 | ||
| IPE220-T300-400 μ | 130.25 | 0.96 | 7.29 | 2.32 | 3.14 | 0.32 | 3598.55 | ||
| IPE220-T450-400 μ | 126.82 | 0.93 | 8.18 | 2.21 | 3.70 | 0.27 | 3727.68 | ||
| IPE220-T600-400 μ | 118.85 | 0.87 | 6.85 | 1.53 | 4.48 | 0.22 | 3618.14 | ||
| IPE220-T900-400 μ | 98.47 | 0.73 | 12.50 | 1.62 | 7.72 | 0.13 | 3065.51 | ||
| IPE220-T300-600 μ | 126.59 | 0.93 | 8.68 | 2.65 | 3.28 | 0.31 | 3357.49 | ||
| IPE220-T450-600 μ | 115.54 | 0.85 | 7.14 | 2.23 | 3.20 | 0.31 | 3445.52 | ||
| IPE220-T600-600 μ | 97.21 | 0.72 | 12.14 | 1.52 | 7.99 | 0.13 | 3067.05 | ||
| IPE220-T900-600 μ | 76.06 | 0.56 | 11.43 | 1.47 | 7.78 | 0.13 | 1979.75 | ||
| IPE 240 | IPE240-T300 (Ekşi et al. 2025) | 153.20 | 1.13 | 12.00 | 2.02 | 5.94 | 0.17 | 4314.70 | |
| IPE240-T450 (Ekşi et al. 2025) | 142.50 | 1.05 | 9.17 | 1.90 | 4.83 | 0.21 | 3405.10 | ||
| IPE240-T600 (Ekşi et al. 2025) | 110.80 | 1.03 | 8.50 | 2.18 | 3.90 | 0.26 | 2978.37 | ||
| IPE240-T900 (Ekşi et al. 2025) | 94.75 | 0.70 | 7.88 | 0.99 | 7.96 | 0.13 | 2505.80 | ||
| IPE240-T300-200 μ | 162.37 | 1.20 | 13.75 | 2.90 | 4.74 | 0.21 | 4375.86 | ||
| IPE240-T450-200 μ | 159.47 | 1.18 | 16.89 | 3.65 | 4.63 | 0.22 | 3989.23 | ||
| IPE240-T600-200 μ | 110.54 | 0.81 | 11.33 | 2.59 | 4.37 | 0.23 | 2156.21 | ||
| IPE240-T900-200 μ | 91.81 | 0.68 | 15.94 | 2.85 | 5.59 | 0.18 | 1877.63 | ||
| IPE240-T300-400 μ | 170.17 | 1.25 | 8.62 | 2.56 | 3.37 | 0.30 | 4746.73 | ||
| IPE240-T450-400 μ | 163.41 | 1.20 | 9.06 | 2.53 | 3.58 | 0.28 | 4361.47 | ||
| IPE240-T600-400 μ | 115.83 | 0.85 | 10.38 | 1.74 | 5.97 | 0.17 | 3551.94 | ||
| IPE240-T900-400 μ | 94.72 | 0.70 | 6.71 | 1.62 | 4.14 | 0.24 | 2798.28 | ||
| IPE240-T300-600 μ | 161.62 | 1.19 | 8.65 | 2.88 | 3.00 | 0.33 | 4727.62 | ||
| IPE240-T450-600 μ | 134.98 | 1.00 | 7.52 | 2.36 | 3.19 | 0.31 | 3758.08 | ||
| IPE240-T600-600 μ | 93.13 | 0.69 | 10.00 | 1.92 | 5.21 | 0.19 | 2780.18 | ||
| IPE240-T900-600 μ | 71.45 | 0.53 | 8.16 | 1.68 | 4.86 | 0.21 | 1963.72 | ||
| Specimens | Δmax (mm) | Δe (mm) | Δp (mm) | Δp/Δe | Δe/ Δmax | Δp/Δmax | Δmax/Δe | Δmax/Δp | |
|---|---|---|---|---|---|---|---|---|---|
| IPE 200 | IPE200-T300-200 μ | 31.93 | 9.5 | 21.87 | 2.30 | 0.30 | 0.68 | 3.36 | 1.46 |
| IPE200-T450-200 μ | 32.04 | 12.8 | 21.66 | 1.69 | 0.40 | 0.68 | 2.50 | 1.48 | |
| IPE200-T600-200 μ | 36.61 | 9.2 | 24.19 | 2.63 | 0.25 | 0.66 | 3.98 | 1.51 | |
| IPE200-T900-200 μ | 41.05 | 6.2 | 29.06 | 4.69 | 0.15 | 0.71 | 6.62 | 1.41 | |
| IPE200-T300-400 μ | 32.44 | 11.2 | 23.55 | 2.10 | 0.35 | 0.73 | 2.90 | 1.38 | |
| IPE200-T450-400 μ | 40.62 | 15.8 | 33.16 | 2.10 | 0.39 | 0.82 | 2.57 | 1.22 | |
| IPE200-T600-400 μ | 32.47 | 8.2 | 24.63 | 3.00 | 0.25 | 0.76 | 3.96 | 1.32 | |
| IPE200-T900-400 μ | 40.8 | 5.8 | 35.16 | 6.06 | 0.14 | 0.86 | 7.03 | 1.16 | |
| IPE200-T300-600 μ | 38.07 | 8 | 23.3 | 2.91 | 0.21 | 0.61 | 4.76 | 1.63 | |
| IPE200-T450-600 μ | 33.78 | 5.8 | 20.54 | 3.54 | 0.17 | 0.61 | 5.82 | 1.64 | |
| IPE200-T600-600 μ | 40.87 | 7 | 29.81 | 4.26 | 0.17 | 0.73 | 5.84 | 1.37 | |
| IPE200-T900-600 μ | 36.84 | 6 | 25.8 | 4.30 | 0.16 | 0.70 | 6.14 | 1.43 | |
| IPE 220 | IPE220-T300-200 μ | 39.08 | 10.05 | 20.97 | 2.09 | 0.26 | 0.54 | 3.89 | 1.86 |
| IPE220-T450-200 μ | 32.84 | 9 | 22.95 | 2.55 | 0.27 | 0.70 | 3.65 | 1.43 | |
| IPE220-T600-200 μ | 39.62 | 12.5 | 30.04 | 2.40 | 0.32 | 0.76 | 3.17 | 1.32 | |
| IPE220-T900-200 μ | 29.19 | 8 | 15.41 | 1.93 | 0.27 | 0.53 | 3.65 | 1.89 | |
| IPE220-T300-400 μ | 38.15 | 14 | 26.04 | 1.86 | 0.37 | 0.68 | 2.73 | 1.47 | |
| IPE220-T450-400 μ | 40.72 | 11 | 27.68 | 2.52 | 0.27 | 0.68 | 3.70 | 1.47 | |
| IPE220-T600-400 μ | 40.77 | 13 | 32.3 | 2.48 | 0.32 | 0.79 | 3.14 | 1.26 | |
| IPE220-T900-400 μ | 39.18 | 4 | 33.94 | 8.49 | 0.10 | 0.87 | 9.80 | 1.15 | |
| IPE220-T300-600 μ | 35.78 | 9.2 | 35.08 | 3.81 | 0.26 | 0.98 | 3.89 | 1.02 | |
| IPE220-T450-600 μ | 40.49 | 11.2 | 27.17 | 2.43 | 0.28 | 0.67 | 3.62 | 1.49 | |
| IPE220-T600-600 μ | 40.43 | 4.2 | 34.57 | 8.23 | 0.10 | 0.86 | 9.63 | 1.17 | |
| IPE220-T900-600 μ | 33.28 | 3.5 | 28 | 8.00 | 0.11 | 0.84 | 9.51 | 1.19 | |
| IPE 240 | IPE240-T300-200 μ | 35.29 | 8 | 26.07 | 3.26 | 0.23 | 0.74 | 4.41 | 1.35 |
| IPE240-T450-200 μ | 34.46 | 6.1 | 21.57 | 3.54 | 0.18 | 0.63 | 5.65 | 1.60 | |
| IPE240-T600-200 μ | 26.61 | 6.4 | 21.06 | 3.29 | 0.24 | 0.79 | 4.16 | 1.26 | |
| IPE240-T900-200 μ | 25.02 | 3.2 | 17.53 | 5.48 | 0.13 | 0.70 | 7.82 | 1.43 | |
| IPE240-T300-400 μ | 40.08 | 14.5 | 32.14 | 2.22 | 0.36 | 0.80 | 2.76 | 1.25 | |
| IPE240-T450-400 μ | 36.76 | 13.8 | 29.01 | 2.10 | 0.38 | 0.79 | 2.66 | 1.27 | |
| IPE240-T600-400 μ | 40.54 | 7.9 | 27.36 | 3.46 | 0.19 | 0.67 | 5.13 | 1.48 | |
| IPE240-T900-400 μ | 40.79 | 8.2 | 32.76 | 4.00 | 0.20 | 0.80 | 4.97 | 1.25 | |
| IPE240-T300-600 μ | 40.04 | 13.3 | 29.46 | 2.22 | 0.33 | 0.74 | 3.01 | 1.36 | |
| IPE240-T450-600 μ | 38.16 | 13.5 | 27.7 | 2.05 | 0.35 | 0.73 | 2.83 | 1.38 | |
| IPE240-T600-600 μ | 36.28 | 5.5 | 25.32 | 4.60 | 0.15 | 0.70 | 6.60 | 1.43 | |
| IPE240-T900-600 μ | 33.39 | 5.15 | 22.68 | 4.40 | 0.15 | 0.68 | 6.48 | 1.47 | |
| Specimen | Max Load (kN) | Energy Dissipation (Joules) | ||||
|---|---|---|---|---|---|---|
| Exp | FEM | Dif (%) | Exp | FEM | Dif (%) | |
| IPE200-T300-200 μ | 151.35 | 147.7 | 2.47 | 3441.07 | 4209.2 | 18.25 |
| IPE200-T450-200 μ | 139.66 | 135.65 | 2.97 | 3003.22 | 3341.8 | 10.1 |
| IPE200-T600-200 μ | 132.83 | 131.36 | 1.12 | 3498.93 | 3458.02 | 1.18 |
| IPE200-T900-200 μ | 99.82 | 90.97 | 9.73 | 3158.13 | 2222.05 | 42.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaman, Z.; Maali, M.; Ağcakoca, E.; Sadid, M.S.; Aydin, A.C.; Ekşi, H. Post-Fire Performance of Bolted Steel T-Joints with Varying Coating Thicknesses: Experimental and Finite Element Analysis. Buildings 2025, 15, 3257. https://doi.org/10.3390/buildings15183257
Yaman Z, Maali M, Ağcakoca E, Sadid MS, Aydin AC, Ekşi H. Post-Fire Performance of Bolted Steel T-Joints with Varying Coating Thicknesses: Experimental and Finite Element Analysis. Buildings. 2025; 15(18):3257. https://doi.org/10.3390/buildings15183257
Chicago/Turabian StyleYaman, Zeynep, Mahyar Maali, Elif Ağcakoca, Mohammad Saber Sadid, Abdulkadir Cüneyt Aydin, and Hüsna Ekşi. 2025. "Post-Fire Performance of Bolted Steel T-Joints with Varying Coating Thicknesses: Experimental and Finite Element Analysis" Buildings 15, no. 18: 3257. https://doi.org/10.3390/buildings15183257
APA StyleYaman, Z., Maali, M., Ağcakoca, E., Sadid, M. S., Aydin, A. C., & Ekşi, H. (2025). Post-Fire Performance of Bolted Steel T-Joints with Varying Coating Thicknesses: Experimental and Finite Element Analysis. Buildings, 15(18), 3257. https://doi.org/10.3390/buildings15183257







