Mechanism of Load Transfer and Deformation Coordination for a Novel Sliding-Type Connection Structure in Bridge Widening: Model Test and Numerical Investigations

Abstract

In lateral-joint-widening projects of multi-span continuous concrete box girder bridges, significant discrepancies in longitudinal shrinkage, creep deformation, and vertical displacement between the existing and newly added bridge sections can lead to stress concentration and subsequent concrete cracking. Notably, such incompatibility often results in pronounced overall lateral bending deformation, which compromises the structural safety and service reliability of the widened bridge. To address these challenges, this study proposes a novel sliding-type transverse connection structure. This innovative connection enables the independent development of longitudinal shrinkage and creep deformation in the new bridge superstructure relative to the old one through a sliding mechanism, thereby effectively mitigating stress concentration and minimizing overall bending deformation caused by differential deformations. To validate the feasibility and elucidate the load transfer mechanism of the proposed structure, both scaled model tests and finite element simulations were conducted. The results indicate that the connection not only effectively coordinates longitudinal deformation differences and accommodates vertical deformation between the flange plates of the new and old bridges, but also ensures efficient transverse load transfer through shear force transmission. The structural behavior is primarily governed by shear stress distribution. These findings demonstrate that the sliding-type transverse connection significantly improves deformation compatibility in bridge widening applications, thereby enhancing the mechanical performance and safety reliability of the overall structure.

1. Introduction

For multi-span concrete continuous box-girder bridges widened using traditional connection methods (such as wet joints or cast-in-place concrete slabs), noticeable transverse deformation often occurs at the bridge ends after several years. This is accompanied by significant shear deformation in the supports beneath the bridge ends, as well as the emergence of other related structural issues [1,2]. For example, as reported in some literature [3], for a specific continuous box-girder bridge, two years after the completion of bridge widening, significant lateral displacement occurred at the beam end, with a measured lateral offset of up to 50 mm. This led to cracking of the seismic blocks, excessive lateral shear deformation of the bridge bearings, and a loss of horizontal shear resistance capability. Additionally, longitudinal cracks were observed at the joints between the new and old sections of the bridge at the beam end.

In the widening of a continuous box-girder bridge, the longitudinal deformation caused by concrete shrinkage and creep in the new bridge is substantial, leading to a significant difference in longitudinal deformation between the new and existing bridges [3]. This difference gives rise to the following two major issues: (1) Transverse Bending Deformation: Longitudinal deformation differences between the new and existing bridges can induce significant transverse bending deformation, especially at the end section of the widened structure. With an increasing span length and number of spans, this transverse deformation increases rapidly, making it increasingly difficult to control. (2) Transverse Tensile Stress Concentration: In addition to the difference in longitudinal deformation, there is also a disparity in foundation settlement deformation between the new and existing bridges. Under the combined influence of these two factors, the connection flange at the bridge end may experience substantial transverse tensile stress. This increases the likelihood of concrete cracking and poses a serious threat to structural safety.

Some scholars have carried out a lot of monitoring and analysis on the bridge widening of concrete girders, and the research results show that the problems mentioned above are common, and the generation mechanism and prevention measures concerning the problems have also been explored. In 1998, Hosseini and Jefferson [4] studied a reinforced concrete, simply supported solid slab bridge which had been widened, and the results showed that the longitudinal bending moment of the connection slab in the mid-span cross-section was twice the longitudinal bending moment produced by loading a 28,000 kg truck there. However, no obvious transverse bending deformation was observed in this particular case. Several scholarly articles have conducted theoretical investigations and on-site monitoring of the widening of numerous long multi-span concrete continuous beam bridges [5,6,7,8]. The findings uniformly point to the significant difference by concrete shrinkage and creep between the new and existing ones, which leads to considerable transverse displacement at the end section of widened structures adopting cast-in-place concrete joints or slabs, with noticeable tensile stress detected at the connection flanges, severely impacting structural security. Researchers have proposed solutions to these problems, such as allowing the new bridge to stand for 3 to 6 months or even longer after pouring [9,10,11], but this would prolong the construction period, increase the time cost, and it would still be difficult to completely avoid structural defects such as lateral bending deformation after several years of connection [1,2,3].

In light of the aforementioned issues, this paper aims to investigate the control and coordination mechanism of longitudinal and transverse deformation differences between the existing and new bridges by proposing a novel sliding-type transverse connection structure. This innovative design seeks to minimize deformation differences and stress concentration, enhance the shear resistance of the structure, and improve the overall performance of the widened bridge. Furthermore, this study aims to offer a new approach and methodology for addressing structural defects in the widening of long multi-span concrete continuous box girders.

2. Segmental Model Test of Sliding-Type Transverse Connection Structure

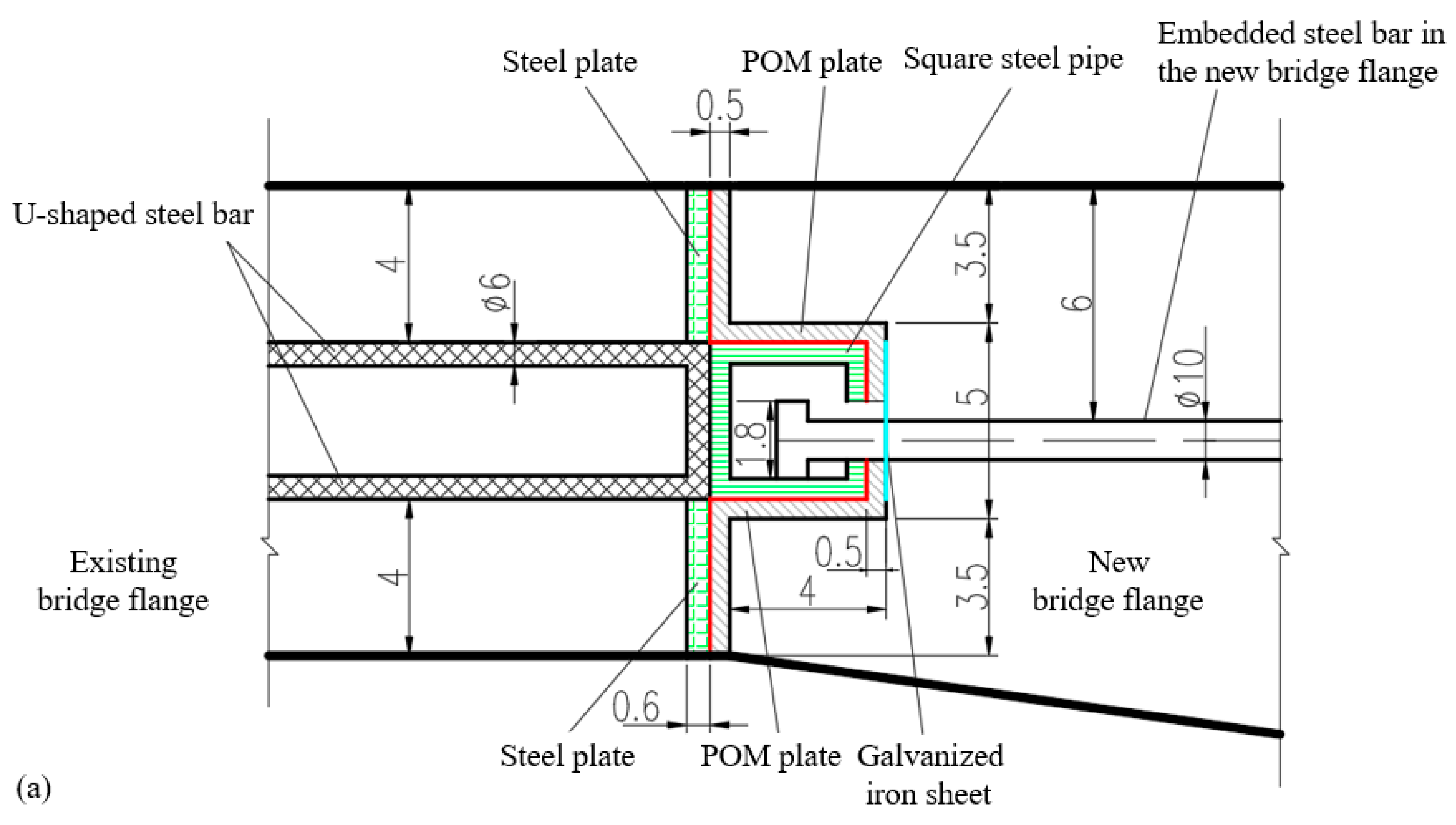
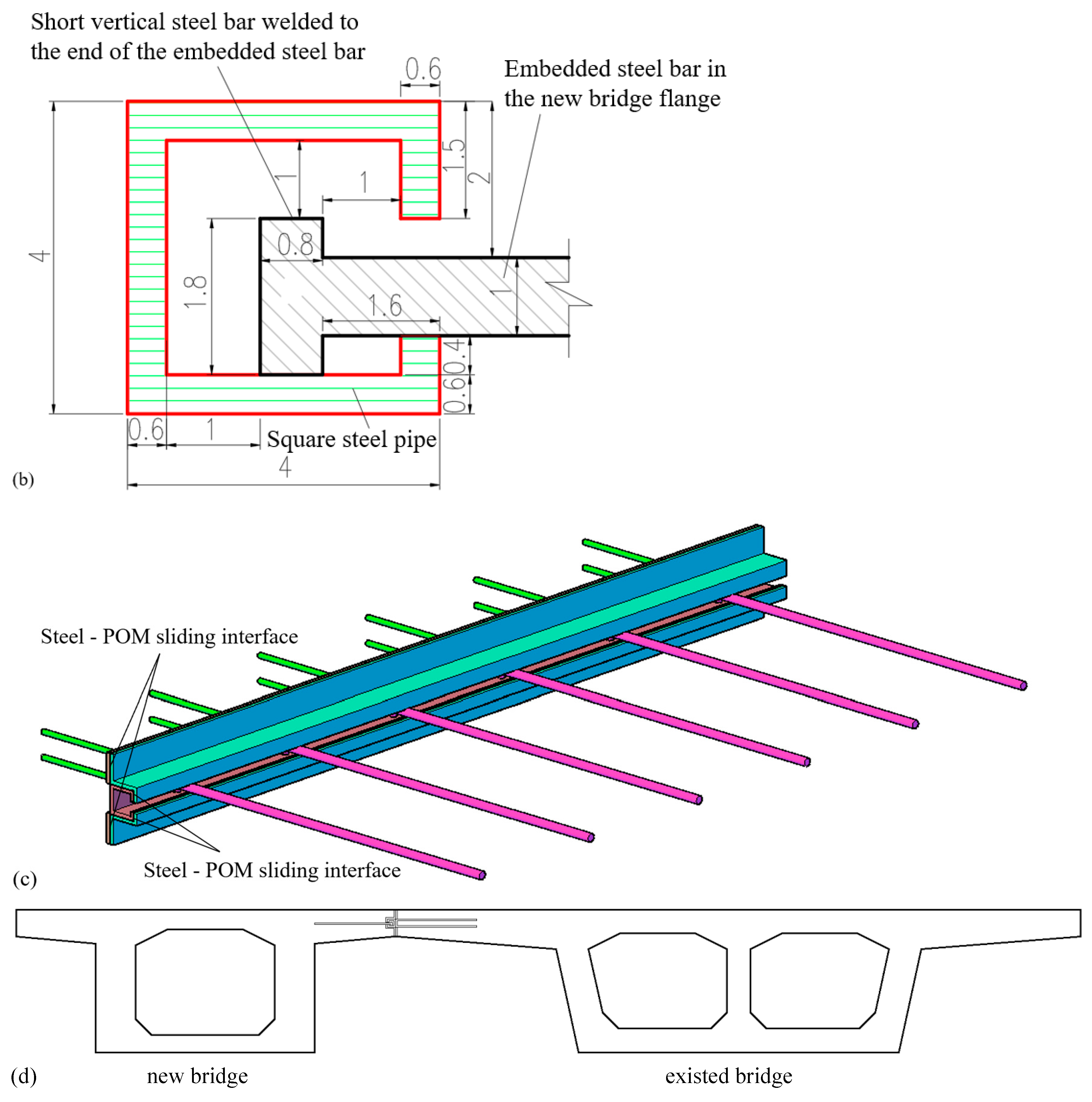
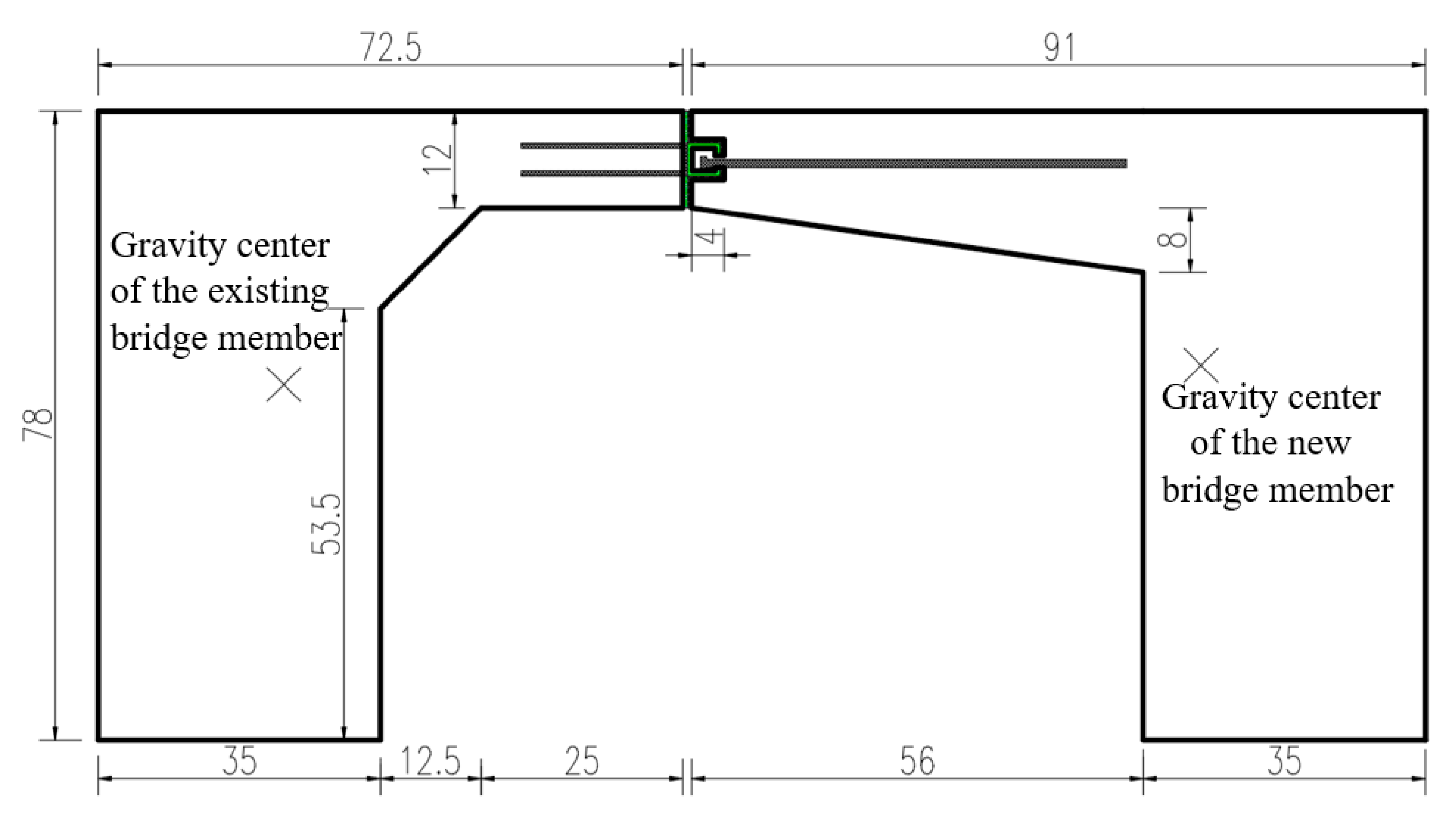
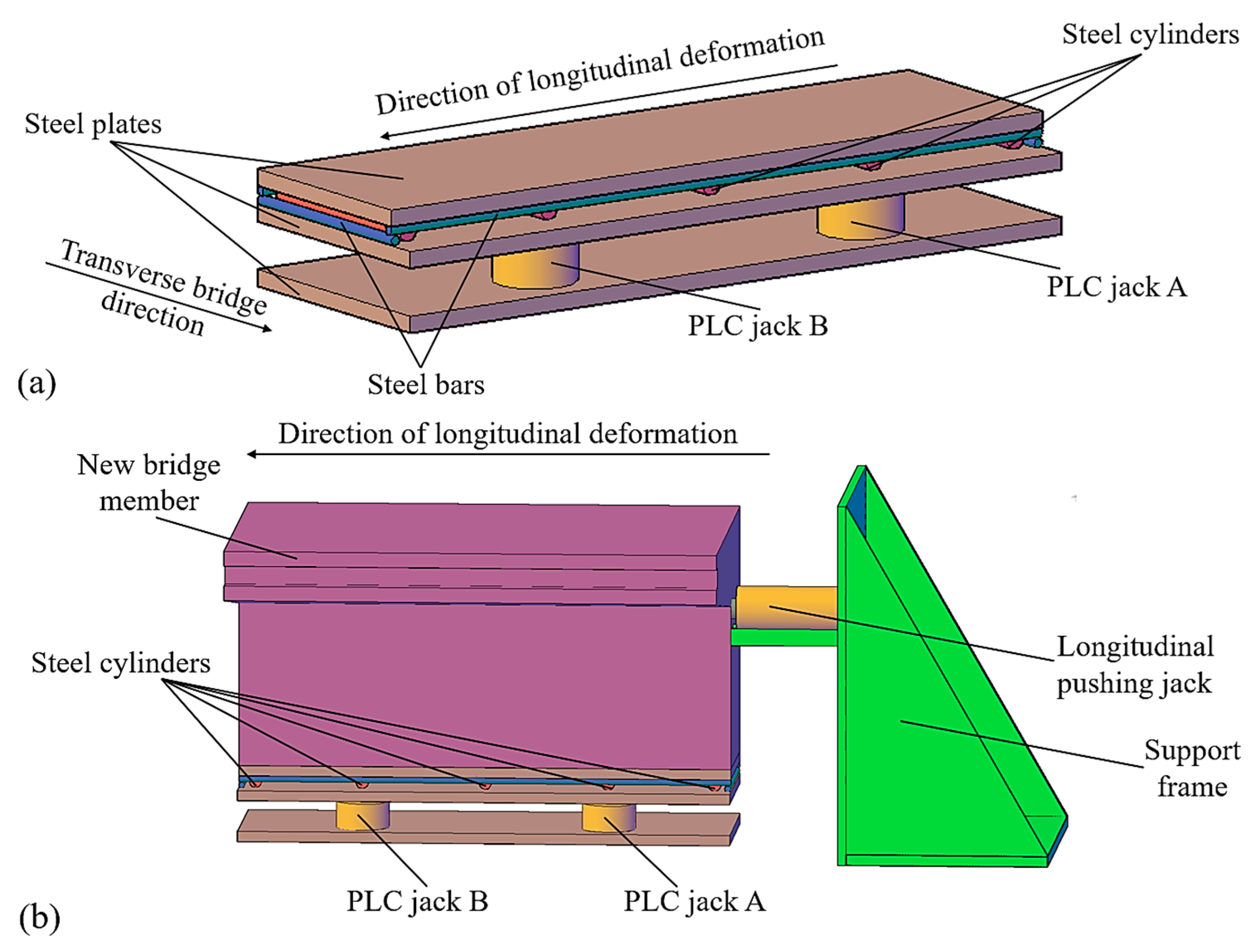
2.1. Overview of the Test Model

To allow the new bridge to undergo free longitudinal deformation under the action of concrete shrinkage and creep, a novel sliding-type transverse connection structure (Figure 1) is proposed for the widening of long multi-span concrete continuous box girders by splicing.

The sliding-type transverse connection structure primarily consists of a square steel pipe, U-shaped steel bars, embedded steel bars, polyoxymethylene (POM) plates, and steel plates. Its operational principle is as follows:

(1)

Primary structural framework: The U-shaped steel bars are embedded transversely into the existing bridge flange, and the square steel pipe is subsequently welded onto these bars to form the main structural framework.

(2)

Transverse connection: A longitudinal slot is machined into the square steel pipe adjacent to the new bridge flange. The embedded steel bars are pre-installed within the new bridge flange, with stub steel bars welded to their end, and then the embedded steel bars are horizontally inserted into the slot of the square steel pipe. Then, after being rotated 90 degrees about their own axis, the stubs become vertically oriented, preventing the embedded steel bars from being pulled out of the square steel pipe slot. This ensures secure transverse connection between the new and existing bridge flanges without risk of separation.

(3)

The first sliding interface: After the embedded steel bars are horizontally inserted into the slot of the square steel pipe, the interface between the embedded steel bars and the square steel pipe is meticulously polished, forming the first longitudinal sliding interface.

(4)

The second sliding interface: POM plates and steel plates are placed between the new and existing bridge flanges, with the POM plates positioned against the new flange and the steel plates against the existing flange. This arrangement forms the second longitudinal sliding interface (as indicated by the red lines in Figure 1a).

Based on the widening of a three-span continuous concrete box girder bridge with variable-height cross-sections, located on the Shanghai–Nanjing Expressway in China and having a total length of approximately 140 m, this paper proposes the use of a sliding-type transverse connection structure for the widening of the aforementioned bridge. This proposal has been studied through both model testing and finite element analysis. Given that the stress state at the end segment of the widened structure is the most complex [12,13,14], this paper selects a segment of the box girder with a specific length as the research object. A segmental model of the sliding-type transverse connection structure is then designed and subjected to model testing. This paper will focus on the following aspects:

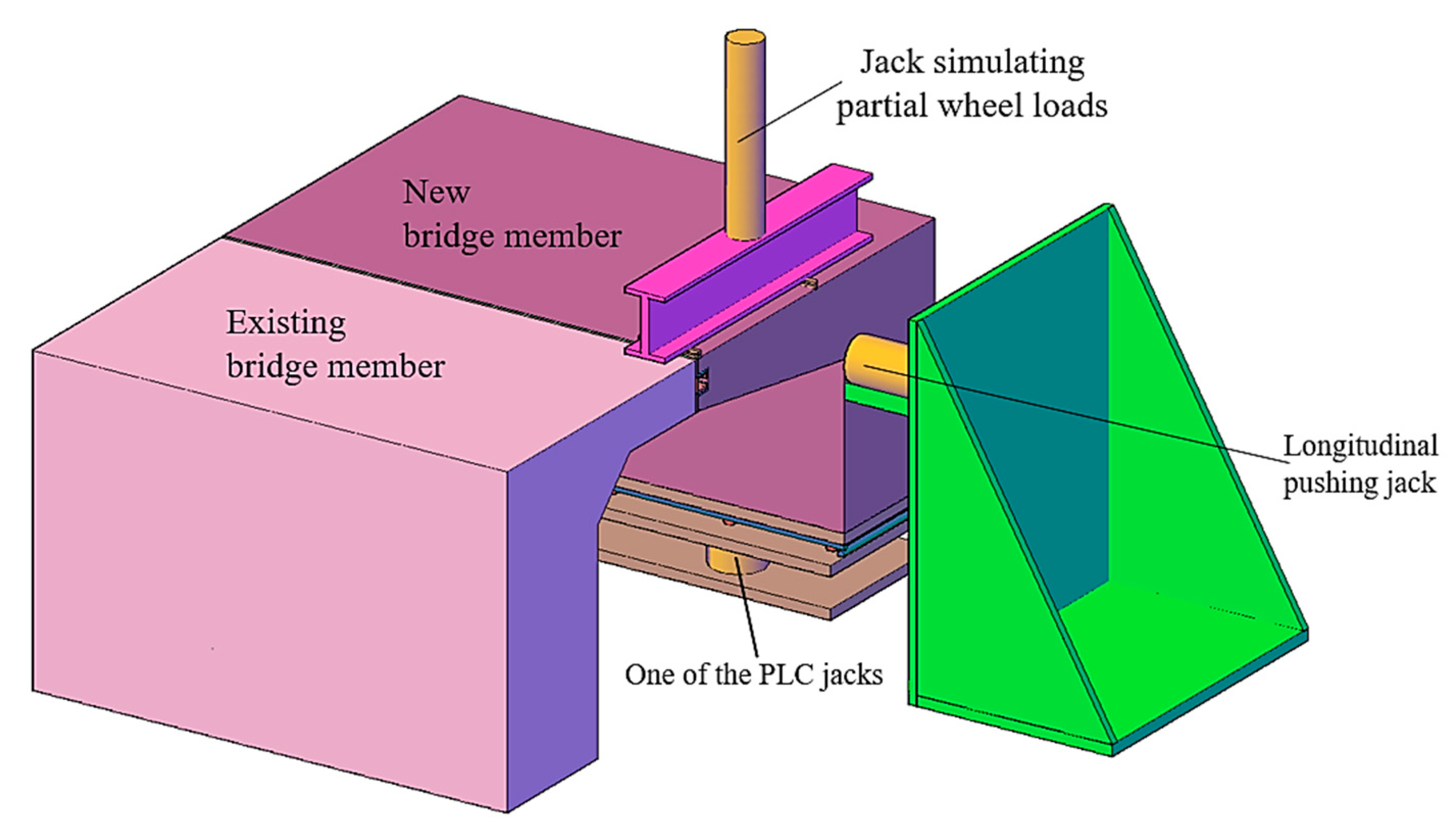
(1)

In-service state of the connection structure. Under the combined effect of partial wheel loads and the differential foundation settlement difference between the new and existing bridges, the focus is on whether the shear stress, tensile stress, deflection, and other structural response indicators of the connection structure comply with the requirements of the design code.

(2)

Longitudinal sliding performance. Under the combined effect of partial wheel loads, differential foundation settlement, and longitudinal deformation differences between new and existing bridges, we carefully observe whether the sliding deformation and the amplitude of stress variation at the sliding interface during the sliding process comply with the requirements of the design code to verify the reliability of the sliding interface performance.

To accurately simulate the local stress characteristics of the transverse joint region in the spliced structure, a 1:2 scale model was adopted. This scaling was primarily based on the principle of structural stress similarity, ensuring that the stress state of the model closely resembled that of the prototype. Accordingly, the applied loads were scaled down by the square of the geometric scale factor. Efforts were also made to maintain material and geometric similarity. Although certain local stress behaviors may be affected by scale effects, the overall structural performance remains representative.

To realistically simulate the boundary conditions of the transversely spliced flanges between the new and existing box girders, the root sections of the flanges are assumed to be fixedly connected to both sides of the box girders. A portal-frame test model was developed to replicate this fixed-end constraint.

The cross-section of the model is shown in Figure 2. The longitudinal dimension of the model is 1.2 m, referring to the maximum effective distribution width of the wheel load acted on the end of the new bridge flange in the “General Specifications for Highway Bridge and Culvert Design (JTG D60-2015)” [15]. Based on the anchorage capacity of a single post-installed steel bar as specified in the Code for Design of Reinforcement of Concrete Structures (GB50367-2013) [16], the embedment lengths of U-shaped steel bars in the existing bridge flange and the embedded steel bars in the new bridge flange are determined.

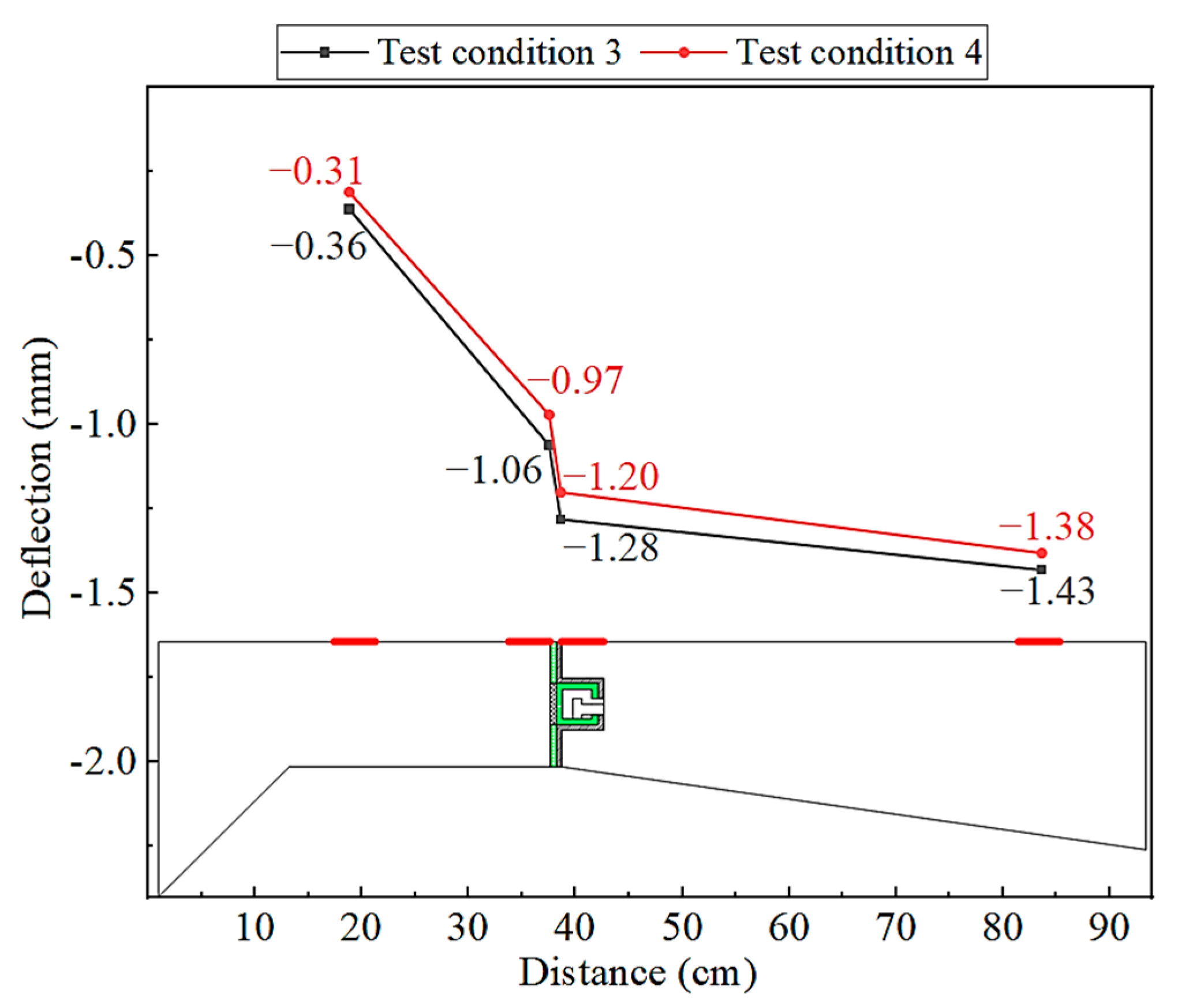
2.2. Test Conditions

A sum of four test conditions were designed in this paper to evaluate the reliability of the mechanical properties and longitudinal sliding effect during the elastic working stage (as shown in

Table 1. Key conditions achieved in the model test.

Elastic Working Stage	Test Conditions (No.)	Wheel Loads on the Bridge Deck (Double-Point Static Load)	Uniform Settlement of New Bridge Member	Non-Uniform Settlement of New Bridge Member		Concrete Shrinkage and Creep of New Bridge Segment
				PLC Jack A	PLC Jack B
Elastic working stage	1	+	1 mm	-	-	-
	2	+	-	1 mm	0 mm	-
	3	+	-	2 mm	1 mm	-
	4	+	-	2 mm	1 mm	+

Note: The symbol + indicates that the corresponding action of this column has occurred at this location; if the action of this column has not been applied, the symbol - is used.

).

2.3. Methods of Test Loading

During the test process, it is assumed that the existing bridge member remains fixed, and the new bridge member is longitudinally displaced by a longitudinal pushing jack, as shown in Figure 3.

Several AISI1045 steel cylinders are arranged longitudinally between the bottom formwork and bottom steel plate under the new bridge member in the test model, facilitating longitudinal sliding of the new bridge member, as shown in Figure 4a. Then, a longitudinal pushing jack applies longitudinal force to the new bridge member, inducing longitudinal displacement of the new bridge member, as shown in Figure 4b.

Two jacks are arranged at the bottom of the new bridge member, as illustrated in Figure 4. The vertical settlement deformation is controlled by the control system (PLC) within an electric oil pump, and displacement sensors are arranged for monitoring, thereby creating a differential settlement difference between the new and existing bridge members. The maximum settlement displacement is set to 2.5 mm, simulating the foundation settlement deformation difference of approximately 5 mm at a scale ratio of 1:2 [2,3].

The double-point static loading method is adopted to simulate partial wheel loads, and the test model is loaded through a load-distribution beam and two loading pads, as shown in Figure 3. According to the “General Code for Design of Highway Bridges and Culverts (JTG D60-2015)” [15], the test selects a rear-axle load of 140 kN as the single-axle wheel load. According to the principle of equal stress and a scale ratio of 1:2, the calculated value of loading in the jack is 70 kN, with each loading point being applied to a load of 35 kN. To test the most unfavorable stress state of the test model, the load-distribution beam is placed at the end of the model, as shown in Figure 3. Since the longitudinal deformation difference at the beam end section is the greatest after the transverse connection of the old and new bridges, it is considered that the beam end section is subjected to the most unfavorable loading condition as previously described. Based on the above reasoning, the transverse loading beam is therefore arranged at the beam end section.

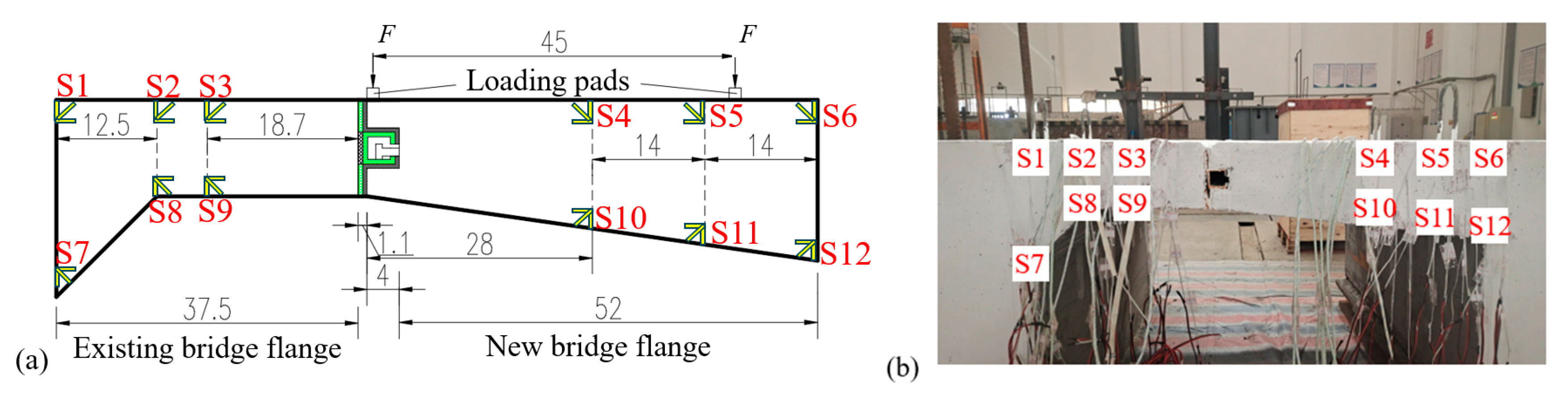
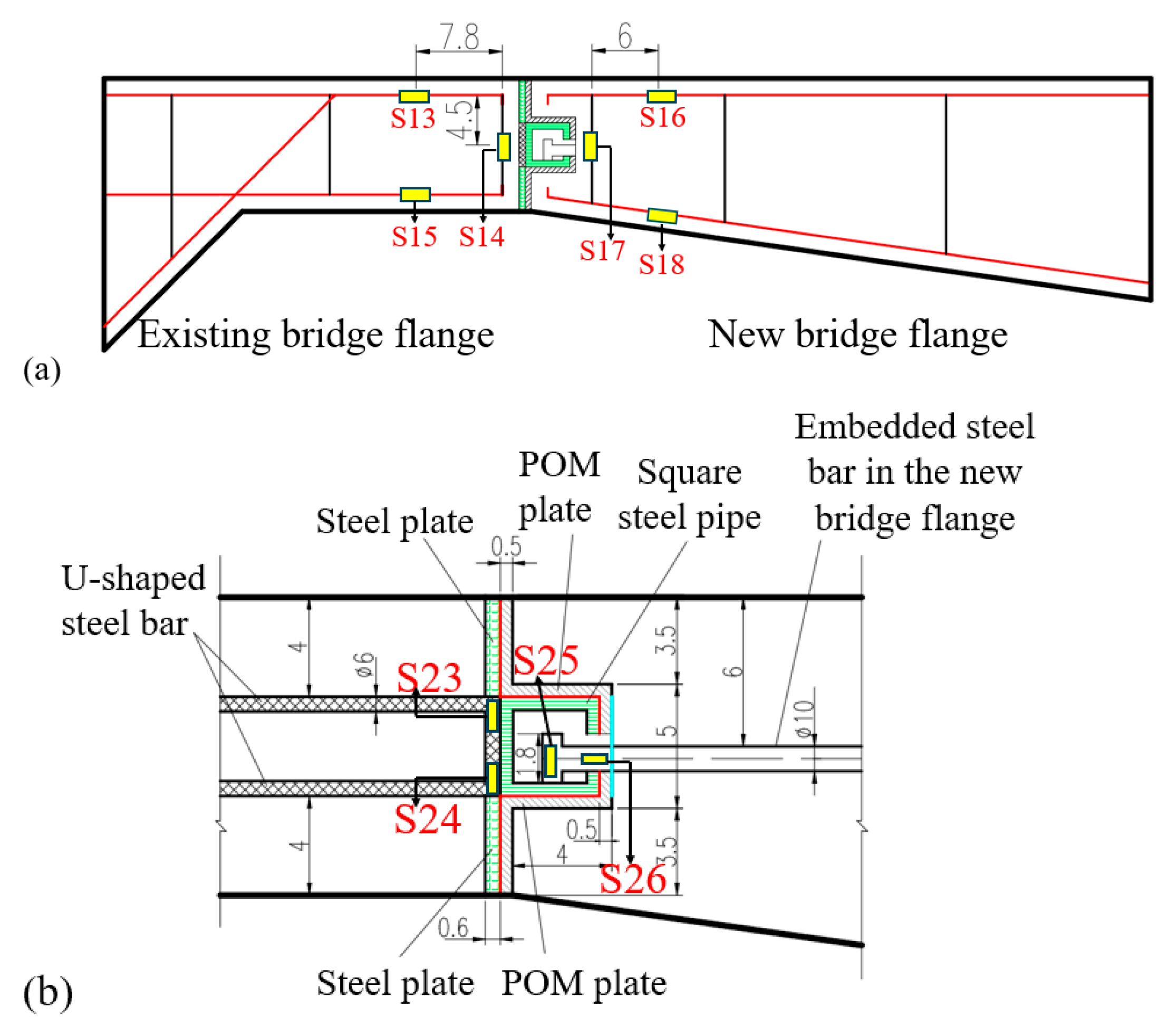
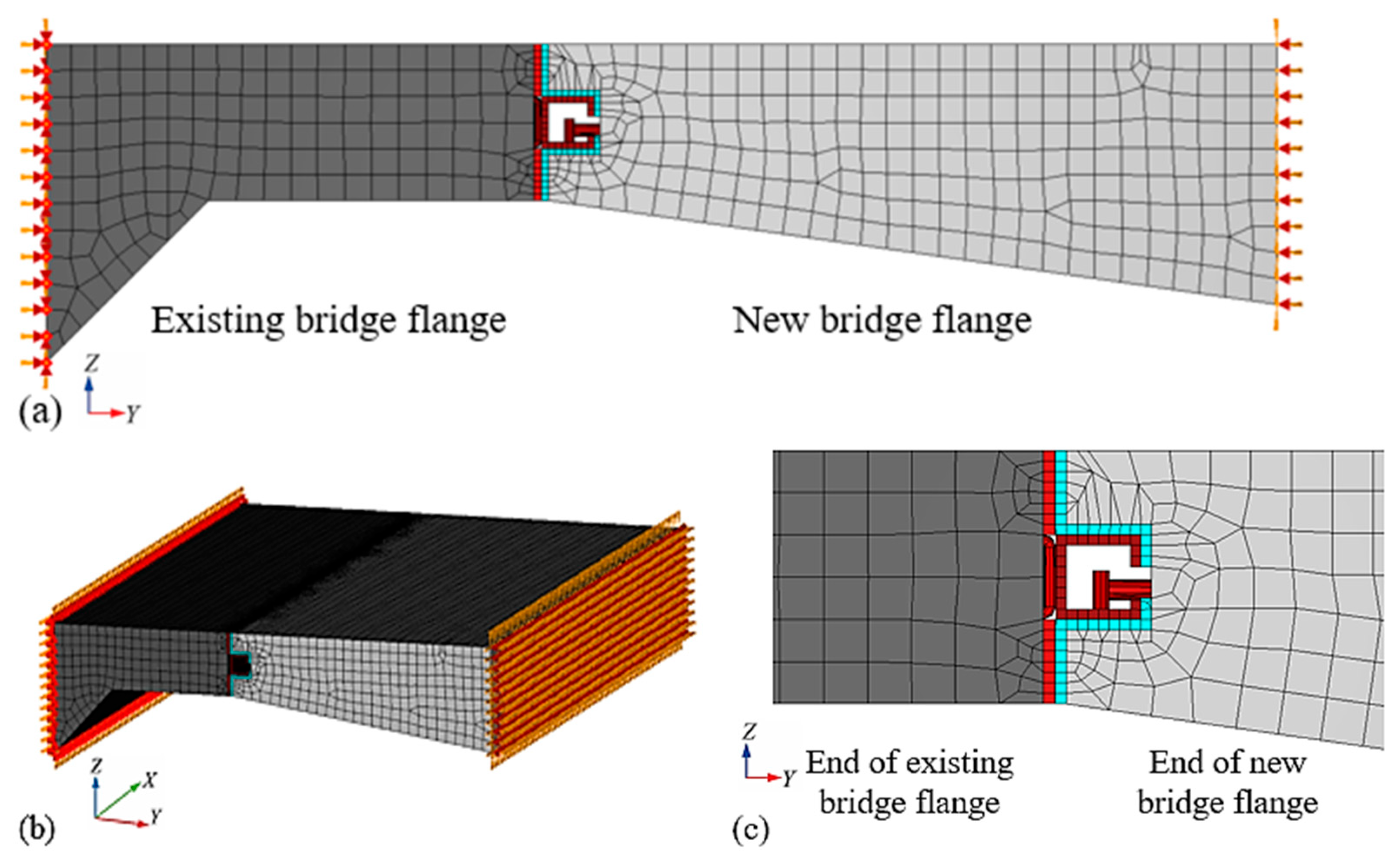
2.4. Arrangement of Stress and Deflection Monitoring Instruments

The measurement points of concrete stress are only arranged on the front side of the model, as shown in Figure 5, with a 45° strain rosette attached at each measurement point. In Figure 5, F represents the single wheel load on the bridge deck, and points S1 to S12 represent the stress measurement points.

Stress measurement points for the steel bars inside the model are distributed on the surfaces. For the square steel pipe, the steel plates, the embedded steel bars, and other components, stress measurement points are also distributed on the surfaces. Strain gauges arranged on the structural steel bars are shown in Figure 6, and strain rosettes arranged on the surfaces of the square steel pipe and steel plates are shown in Figure 7. In Figure 6 and Figure 7, S13 to S26 represent the stress measurement points.

The deflection measurement points as shown in Figure 8 are arranged on the top surface of the test model, where points a and b are arranged on the surface of existing bridge flange, and points c and d are arranged on the surface of new bridge flange. Dial gauges are used to measure the deflection.

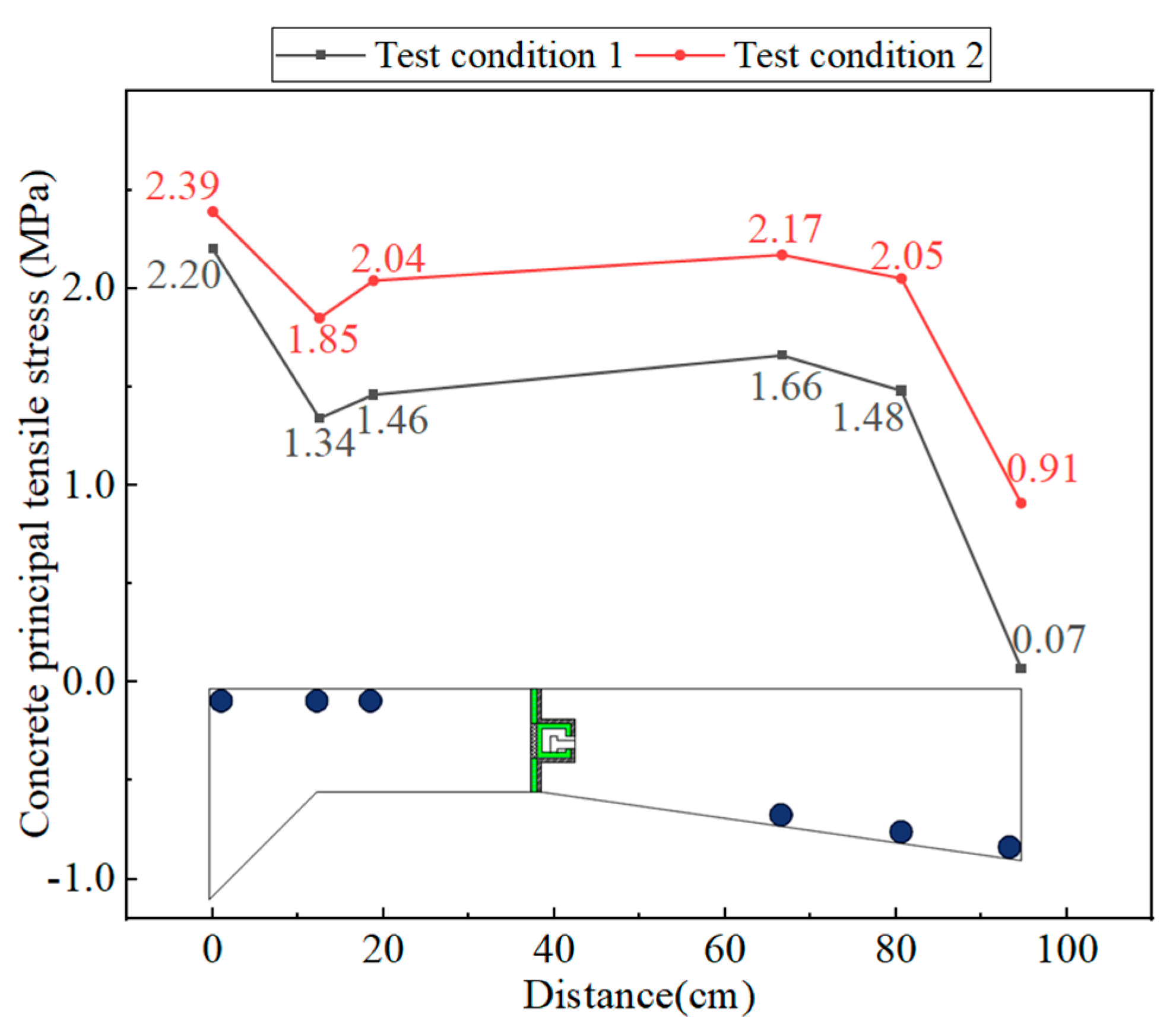
3. In-Service State of the Sliding-Type Transverse Connection Structure

The failure tests under ultimate loading conditions were also completed, and the resulting data will provide important support for structural safety assessments. This paper focuses on the mechanical behavior of the structure in the elastic stage; detailed analyses of the ultimate load capacity will be reported in a forthcoming paper.

Based on the test data from conditions 1 to 3, the safety of an in-service stress state of the connection structure is demonstrated under the combined action of wheel loads on the bridge deck and the foundation settlement of a new bridge.

The deflection distribution patterns of the deflection measurement points under each test condition are shown in Figure 9. The deflection data indicate that the sliding-type transverse connection structure can coordinate the vertical deformation between the new and existing bridge flanges. The deflection difference at the joint indicates that the core component, the square steel pipe, underwent shear deformation, accompanied by the transverse transmission characteristics of vertical shear force.

Figure 10 shows the distribution of concrete principal tensile stress at each stress measurement point. It can be seen from the figure that the maximum concrete principal tensile stress at the root section of the flange is 2.39 MPa, which is close to the standard value of tensile strength for C40 concrete, 2.40 MPa. The sliding-type transverse connection structure does not crack, indicating that the connection flange remains in the elastic working stage, with a sound in-service state.

Take condition 3 as an example; the stress scatter plot is shown in Figure 11. As can be seen from the figure, the stress at most measurement points on the steel bars is small. Only the stress measurement point S23 on the U-shaped steel bar at the loading cross-section, which is near the application point of single wheel load, has the maximum axial tensile stress of 267.78 MPa at the top of the vertical part, but this value is lower than the design value of tensile strength in HRB400.

The longitudinal stress and shear stress generated at the ends of the square steel pipe and steel plates are exceedingly small, which is not listed in detail due to space limitations. Both the square steel pipe and steel plates are in the safe in-service states.

As mentioned above, the test model is in the elastic working state, the sliding-type transverse connection structure does not crack, and the durability of the structure is guaranteed.

4. Verification Analysis of Sliding Performance

Based on condition 3, a longitudinal thrust is applied to the end section of the new bridge member to generate longitudinal displacement, forming a new test condition (condition 4). The longitudinal jacking displacement shall be controlled within 10 mm to ensure the loading safety of the test structure. The comparing of deflection data at all measurement points between conditions 3 and 4 (Figure 12) indicates that the sliding-type transverse connection structure remains in an elastic working state throughout the longitudinal sliding process. The comparison of concrete first principal stress from measurement points at the tensile zone between conditions 3 and 4 is shown in Figure 13. It can be seen from the figure that the deflection or stress state of this connection structure does not change significantly during the two conditions, and the transverse distribution law of the settlement deformation difference in the connection flange does not change either. This indicates that the longitudinal deformation difference does not affect the transverse connection function of the structure.

In conclusion, the sliding-type transverse connection structure can effectively absorb the longitudinal deformation difference by concrete shrinkage and creep between the new and existing bridges, thereby avoiding the adverse mechanical effects resulting from the difference by concrete shrinkage and creep between the new and existing ones in the widened structure, which has good application prospects for bridge connection widening.

5. Analysis of the Transverse Load Transferring Mechanism

To research the transverse load transferring mechanism of the sliding-type transverse connection structure, a finite element model of the segmental test model is established and analyzed by adopting Diana FEA finite element analysis software.

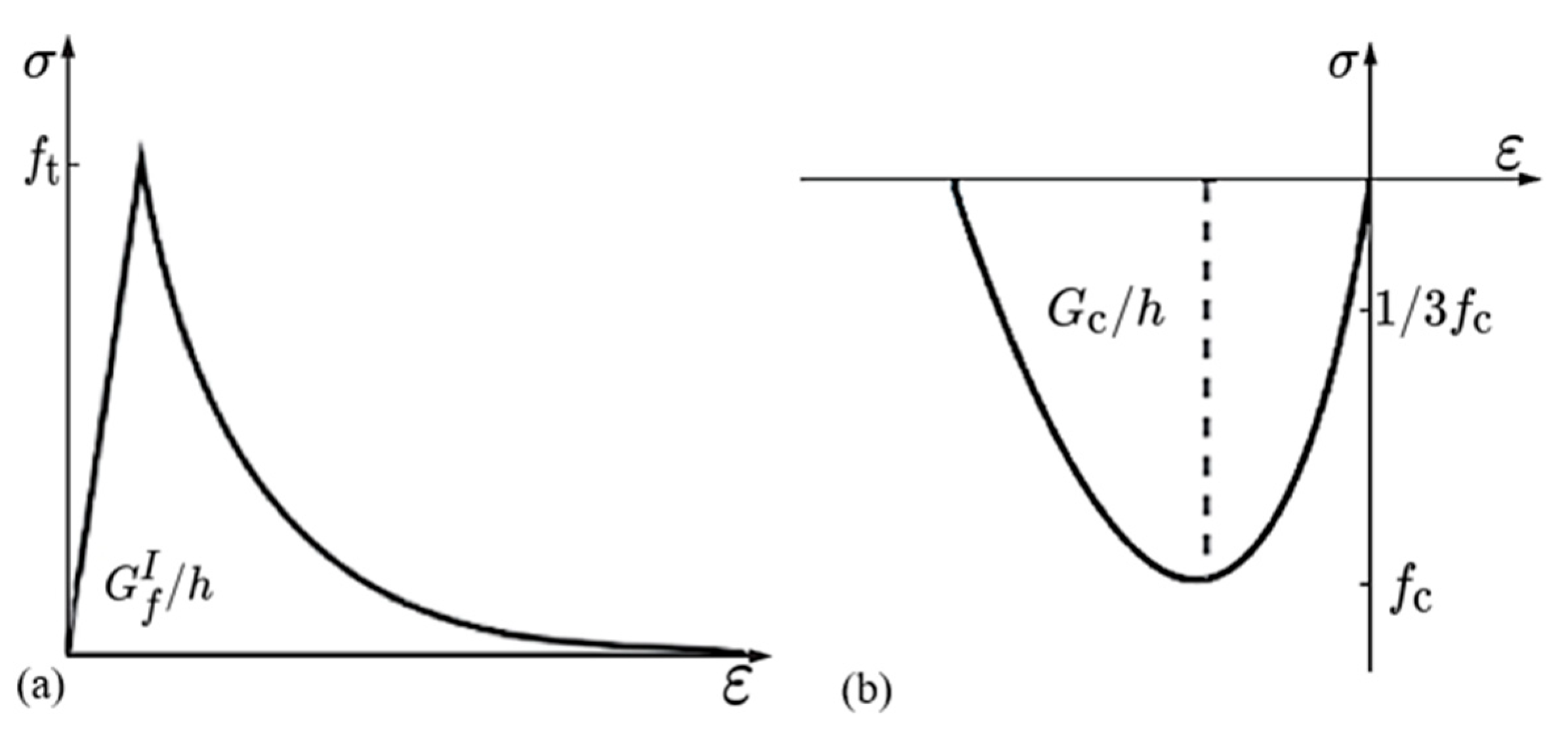
5.1. Material Properties and Constitutive Relationship

According to the “Design Code for Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG 3362-2018)” [17], the material properties are shown in

Table 2. Material properties of concrete, rebar, and AISI1045 steel.

Materials	Modulus of Elasticity (MPa)	Density (kg/m3)	Poisson’s Ratio	Main Mechanical Parameters (MPa)
C40 concrete	3.25 × 104	2.43 × 103	0.2	Tensile strength (design value) $f_t$	1.65
				Compressive strength (design value) $f_c$	18.4
HRB400 rebar	2 × 105	7.85 × 103	0.3	Yield strength (design value of tensile strength)	330
AISI1045 steel	2.06 × 105	7.85 × 103	0.3	Yield strength	355

.

In the finite element model, the Von Mises plasticity model is selected as the constitutive relationship of the reinforcement and AISI1045 steel. The constitutive relationship of concrete in the tensile state adopts the exponential model (as shown in Figure 14a). The constitutive relationship of concrete in the compressive state adopts the parabolic model (as shown in Figure 14b). In the figure, $G_f^I$ is the I-type (open-type) tensile fracture energy, and its calculation formula refers to the relevant literature [18,19]; $G_c$ is the nonlinear compressive fracture energy, and its value is taken according to the relevant literature [20,21]; $f_t$ is the standard value of tensile strength; $f_c$ is the standard value of compressive strength; and h is the thickness index. According to the literature [22,23], the yield tensile strength of the copolymerized formaldehyde material, POM M90, can be taken as 60 MPa, and the tensile modulus of elasticity can be taken as 2760 MPa; the flexural strength is 61 MPa, and the flexural modulus is 2400 MPa. The bond-slip constitutive relationship of anchored rebars in the concrete is set according to the relevant provisions in the “Code for Design of Concrete Structures (2015 Edition) (GB 50010-2010)” [24], and the allowable stress of the welds between U-shaped steel bars and the square steel pipe is 49.5 MPa.

The connection structure mainly adopts hexahedral solid HX24L elements, while a small number of tetrahedral solid TE12L elements and triangular prism solid TP18L elements are adopted for the concrete, steel plates, polyformaldehyde plates, etc., which are at the end of the flanges near the joint. The concrete element mesh size is set to 25 mm. The thickness of the polyformaldehyde plates and steel plates at the connection structure is relatively small, and the corresponding element mesh sizes are set to 5 mm and 6 mm, respectively. Rebar-type elements are adopted for the steel bars inside the concrete, with an element mesh size of 50 mm. Beam-type L13BE elements are adopted for U-shaped steel bars and embedded steel bars, both with an element mesh size of 25 mm.

In the finite element model of Diana FEA [25], discrete interface elements are adopted to simulate the interface performance between U-shaped steel bars and the square steel pipe. Bond-slip interface elements are adopted to simulate the interface performance between U-shaped steel bars or embedded steel bars and the concrete. Nonlinear friction interface elements are adopted to simulate the characteristics of the POM–steel interface. The finite element model contains 154,392 elements.

Figure 15 shows the finite element model and the simulated boundary conditions in which the consolidated walls of the flanges are omitted. The X-axis in the coordinate system is the longitudinal bridge direction of the test model, and the longitudinal push direction is the positive direction. The Y-axis is the transverse bridge direction, and the new bridge member is in the positive Y-axis direction. The Z-axis is the vertical bridge direction, and the positive direction is upward. The boundary conditions of the sliding-type transverse connection structure can be simulated as a fixed constraint set at the root section of the existing bridge flange, restricting all degrees of freedom. For the new bridge flange, a translational constraint is set at its root section, restricting its translational degree of freedom in the transverse direction (Y-axis) and all rotational degrees of freedom.

Under the same test conditions, select key deflection measurement points, and then compare test results with the finite element analysis results to verify the accuracy of the finite element model in simulating the actual deformation for the sliding-type transverse connection structure.

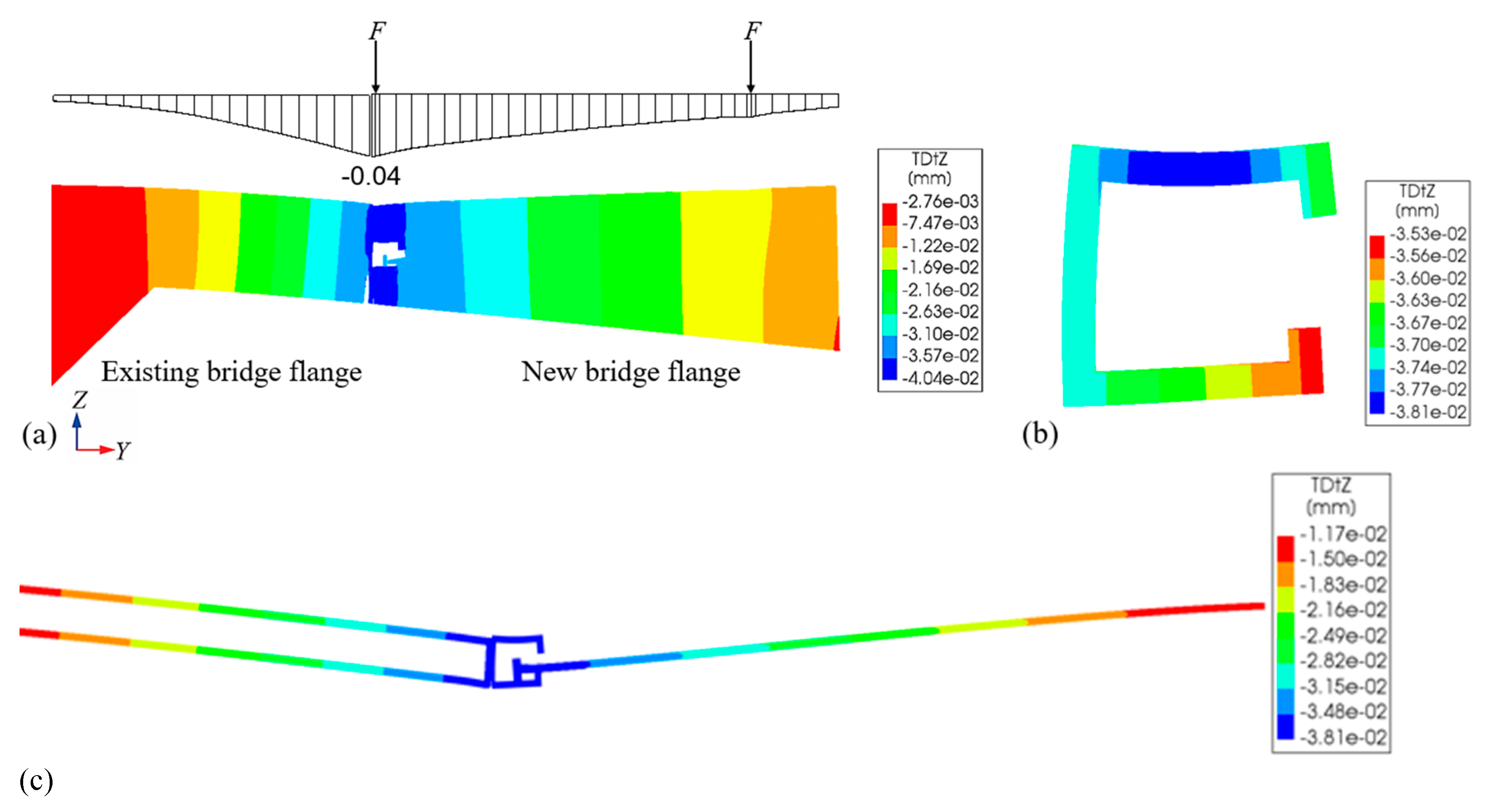
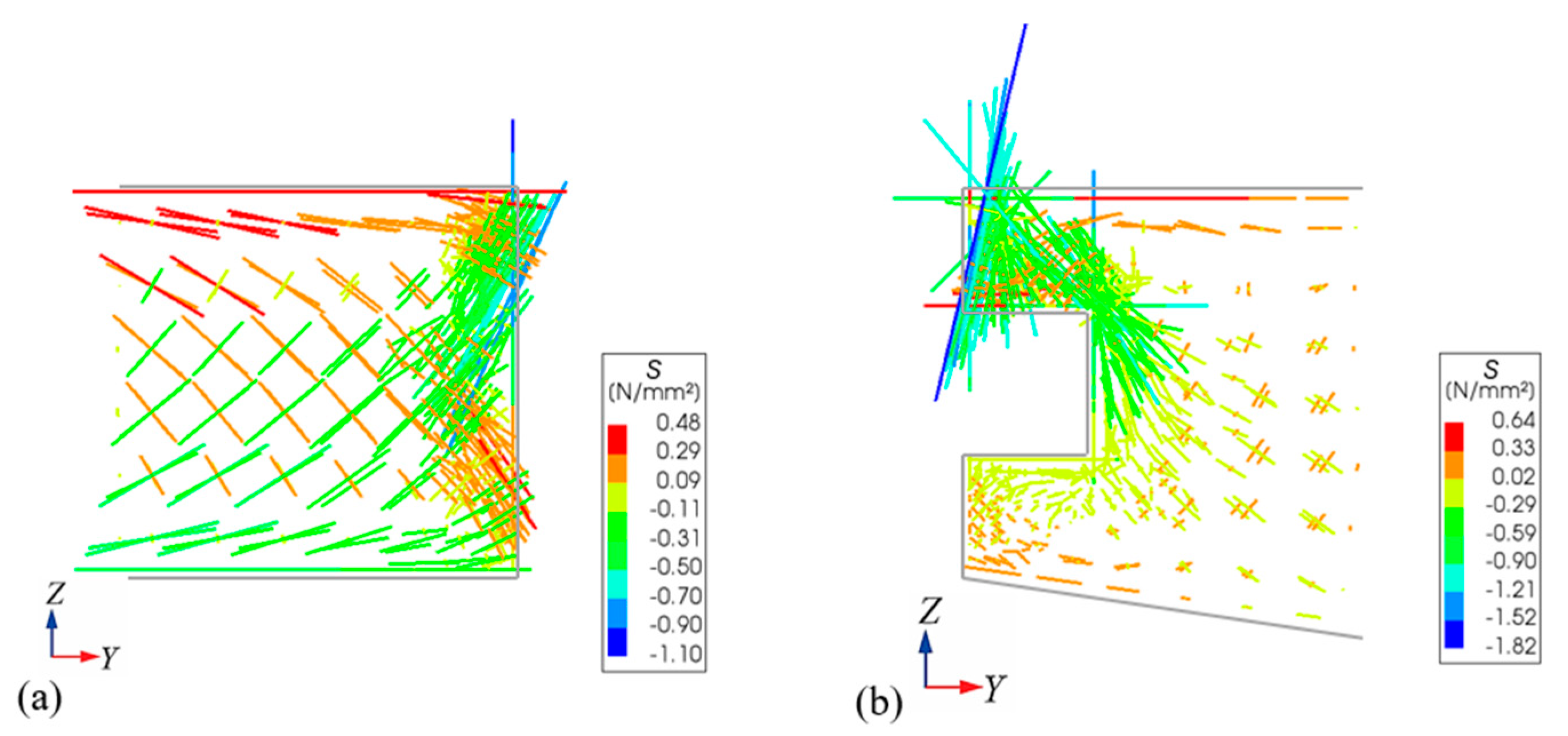
5.2. Elastic Working State

This section focuses on analyzing the working mechanism of the sliding-type transverse connection structure under the action of partial wheel loads when the internal force is transferred from the new bridge flange to the existing bridge flange. This study aims to investigate the vertical deformation behavior of the connection structure and the stress distribution within the key components.

The partial wheel loads are consistent with the ones in the model test. Under the action of partial wheel loads, vertical deformation diagrams of the new and existing bridge flanges at the loading cross-section, as well as the square steel pipe, U-shaped steel bars, and embedded steel bars, are shown in Figure 16. As shown in Figure 16, the wheel loads on the bridge deck were applied on the new bridge flange, causing its end to deflect downward. The deflection of the new bridge flange also causes the square steel pipe to deflect downward. Subsequently, the vertical parts of the U-shaped steel bars welded to the square steel pipe also undergo vertical displacement, causing the existing bridge flange to deflect downward ultimately. This realizes the transverse load transmission and deformation coordination between the new and existing bridge flanges. The vertical deformation curves of the two flanges have different curvatures at the connection structure, indicating that the deformation coordination between the new and existing bridge flanges is achieved by transferring shear force rather than bending moment.

To clearly illustrate the transverse load transmission mechanism, the principal stress trajectory lines of each component in the sliding-type transverse connection structure are analyzed. The principal stress trajectory lines at the ends of the new and existing bridge flanges, as well as the square steel pipe, the U-shaped steel bar, and the embedded steel bar at the cross-section of the wheel load application, are shown in Figure 17. In the figure, S is the principal stress, the warm-colored lines represent the principal tensile stress, and in contrast, the cool-colored lines represent the principal compressive stress. The longer the line, the larger the principal stress at the location, and the extension direction of the line is the direction of the principal stress.

From the principal stress trajectory lines, it can be known that the transverse load transferring mechanism of the sliding-type transverse connection structure under the partial wheel loads is as follows: A single wheel load causes the concrete above the groove of the new bridge flange to experience shear stress and deform downward to squeeze the square steel pipe, resulting in significant principal compressive stress in the concrete above the groove (as shown in Figure 17a,b). The concrete above the groove of the new bridge flange transmits pressure to the upper surface of the square steel pipe, causing the upper limb of the square steel pipe to bend transversely, and at the same time, the vertical part of the square steel pipe experiences significant vertical shear force, resulting in large principal compressive stress in it (as shown in Figure 17c). As the vertical part of the square steel pipe experiences significant downward shear stress, the vertical part of the U-shaped steel bar at the loading cross-section primarily experiences vertical principal stress, and the axial tensile stress decreases gradually from top to bottom until the lower part enters the compressive state (as shown in Figure 17d). There is almost no transverse principal stress in the horizontal part of the U-shaped steel bar, indicating that, after transverse load is transferred to the vertical parts of U-shaped steel bars, the load continues to be transferred to the interior of existing bridge flanges in the form of shear force.

According to the above analysis, it can be known that the path of transverse load transmission from the new bridge flange to the existing bridge flange is as follows: The single wheel load acting on the end of the new bridge flange causes the new bridge flange to deflect downward, and the downward deformation of the square steel pipe is caused by the squeezing of the concrete above the groove of the new bridge flange and the upper limb of the square steel pipe. Then, through the welding relationship between the vertical parts of the square steel pipe and the U-shaped steel bars, the vertical parts of the U-shaped steel bars experience vertical displacement, resulting in the deflection of the existing bridge flange. This achieves transverse load transferring and deformation coordination between the new and existing bridge flanges.

Figure 17d also shows that the embedded steel bars experience transverse principal stress at only one end, near the base of the flange, which is related to the fixed constraint there. This indicates that the embedded steel bars do not participate in the transverse load transmission, which only serve the function of connecting components to limit the width of the connection joint, avoiding separation of new and existing bridge flanges from each other. As shown in the stress distribution contour in Figure 11, the transverse connecting rebars near the joint interface remain at a relatively low stress level under elastic loading conditions, and therefore do not contribute significantly to shear force transfer. With the gradual increase in loading during the test, the structural behavior transitions from elastic to elasto-plastic, leading to crack initiation and a significant increase in shear deformation at the joint interface. Under such conditions, the transverse connecting rebars become progressively engaged, thereby exerting their shear resistance and enhancing the overall shear capacity of the structure.

The transverse load transferring mechanism in the elastic working stage shows that the transverse stress state of the sliding-type transverse connection structure is mainly controlled by shear stress, and the transverse load transmission is realized by transferring shear force. The squeeze deformation between the concrete above the groove and the upper limb of the square steel pipe is closely related to the following: the shear resistance of the concrete above the groove, the thickness of the square steel pipe, and the welding strength between the vertical part of the square steel pipe and the vertical parts of the U-shaped steel bars.

6. Conclusions

(1)

When the novel sliding-type transverse connection structure is employed for the widening of long multi-span concrete continuous box girder bridges, the new bridge is capable of effectively accommodating longitudinal deformations caused by concrete shrinkage and creep. This capability holds even under the combined effects of wheel loads on the bridge deck and differential foundation settlement. Overall, the widened bridge can effectively accommodate the longitudinal deformation difference between the new and existing bridge segments, thereby significantly reducing structural incompatibility and stress concentration at the connection interface.

(2)

This paper proposes a testing method that simultaneously imposes wheel loads on the bridge deck, differential foundation settlement, and longitudinal deformation differences between the new and existing bridge segments onto the transverse connection structure. This approach effectively simulates actual engineering conditions, producing more realistic structural responses and enhancing the overall quality of the research.

(3)

The transverse stress state of the sliding-type transverse connection structure is predominantly governed by shear stress, with the structure primarily relying on the transfer of shear forces to achieve effective transverse load transmission. The squeeze deformation at the interface between the upper limb of the square steel pipe and the overlying concrete together with the shear action between the vertical segments of the square steel pipe and the U-shaped steel bars constitute the two primary mechanisms for transverse load transfer between the new and existing bridge flanges. In addition, the transverse flexural stiffness of the square steel pipe and the shear resistance of the welds connecting it to the U-shaped steel bars contribute to enhanced transverse connection stiffness of the structural system. To ensure effective transverse load transmission between the new and existing bridge flanges, all these factors are critical and require careful consideration during the design phase.

Future Research and Practical Considerations

The experimental results demonstrate the effectiveness of the proposed sliding-type transverse connection in accommodating longitudinal deformations and ensuring transverse load transfer. However, further studies are needed to evaluate its failure mechanisms and load-carrying capacity under extreme conditions. Optimization of the sliding interface geometry is also recommended to enhance structural performance.

Practically, the high construction accuracy required for alignment and welding may increase labor and time on site. Long-term durability under environmental and traffic loads remains a concern, potentially affecting maintenance cost and service life. These factors should be considered in future field applications.