Evaluating Algorithm Efficiency in Large-Scale Dome Truss Optimization Under Frequency Constraints
Abstract
1. Introduction
2. Optimization of Truss Structures
Natural Frequency Constraints
3. Optimization Algorithms
3.1. Full Distance-Based-Adaptive Guided Differential Evolution Algorithm (FDB-AGDE)
3.2. Cheetah Optimizer (CO)
3.2.1. Searching
3.2.2. Sit-and-Wait Strategy
3.2.3. Attack Strategy
3.2.4. Leave the Prey and Go Back Home
3.3. Bonobo Optimizer (BO)
3.3.1. Bonobo Selection Using Fission–Fusion Social Strategy:
3.3.2. Promiscuous and Restrictive Mating Used During the Positive Phase
3.3.3. Consortship and Extra-Group Mating Is Used During the Negative Phase
3.4. Flood Algorithm (FLA)
3.4.1. Regular Movement Phase
3.4.2. Flooding Phase: Increase and Decrease in Basin Water
3.5. Lung Performance Algorithm (LPO)
3.5.1. The Entrance and Exit of Air Into and Out of the Lungs
3.5.2. Carbon Dioxide Separation from the Air and Blood Movement in the Veins
3.5.3. Carbon Dioxide Separation from Blood
4. Numerical Examples
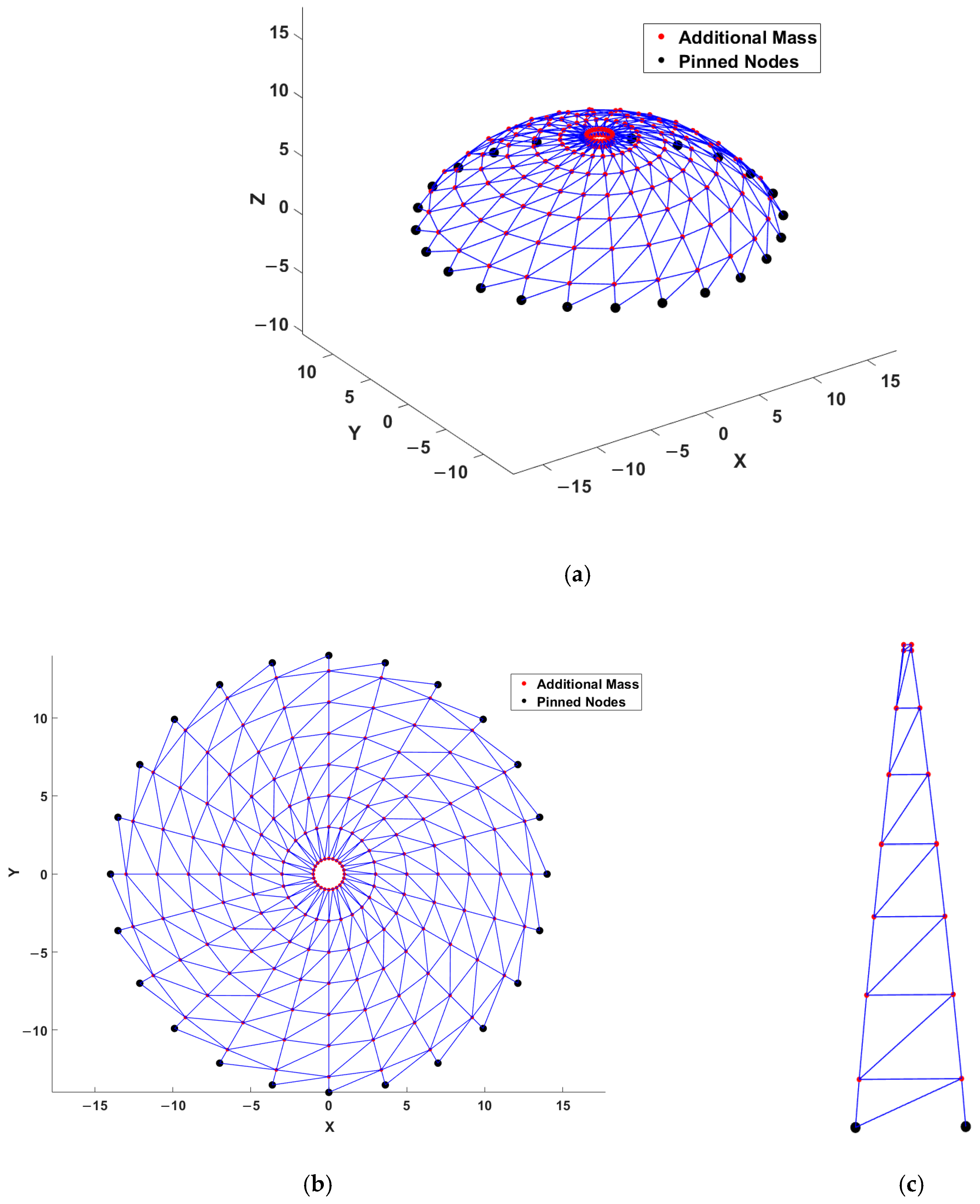
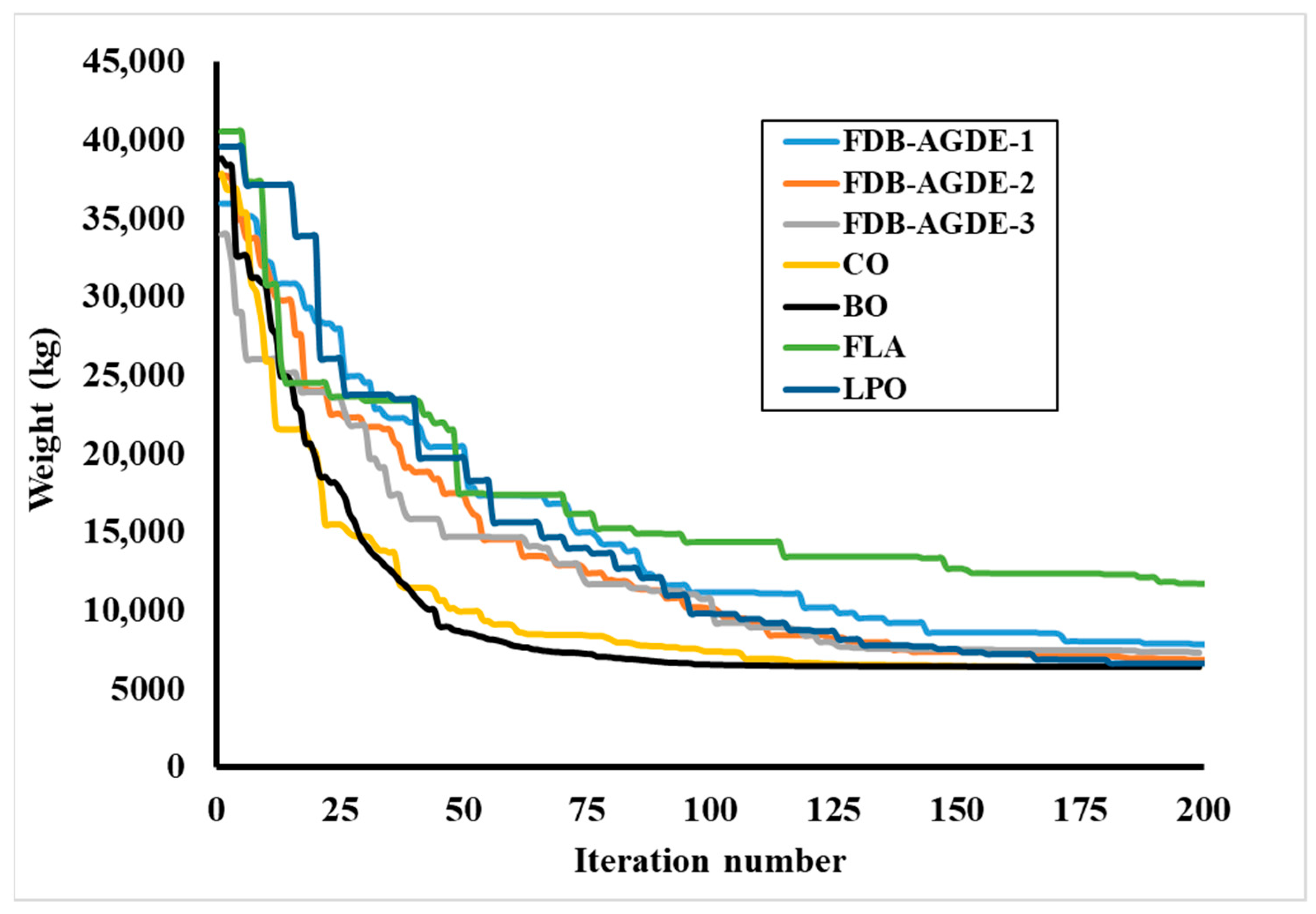
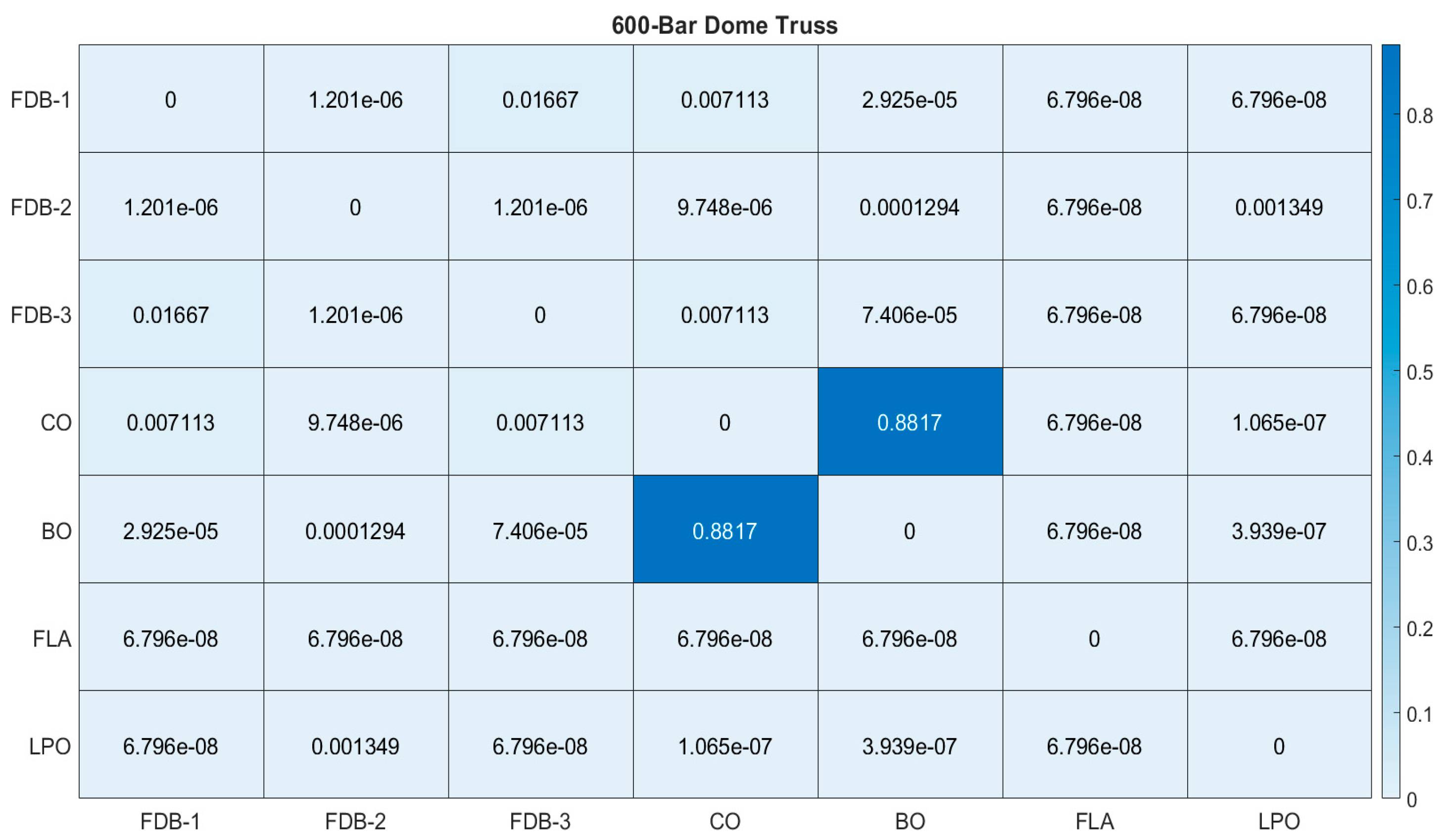
4.1. The 600-Bar Spatial Dome Truss
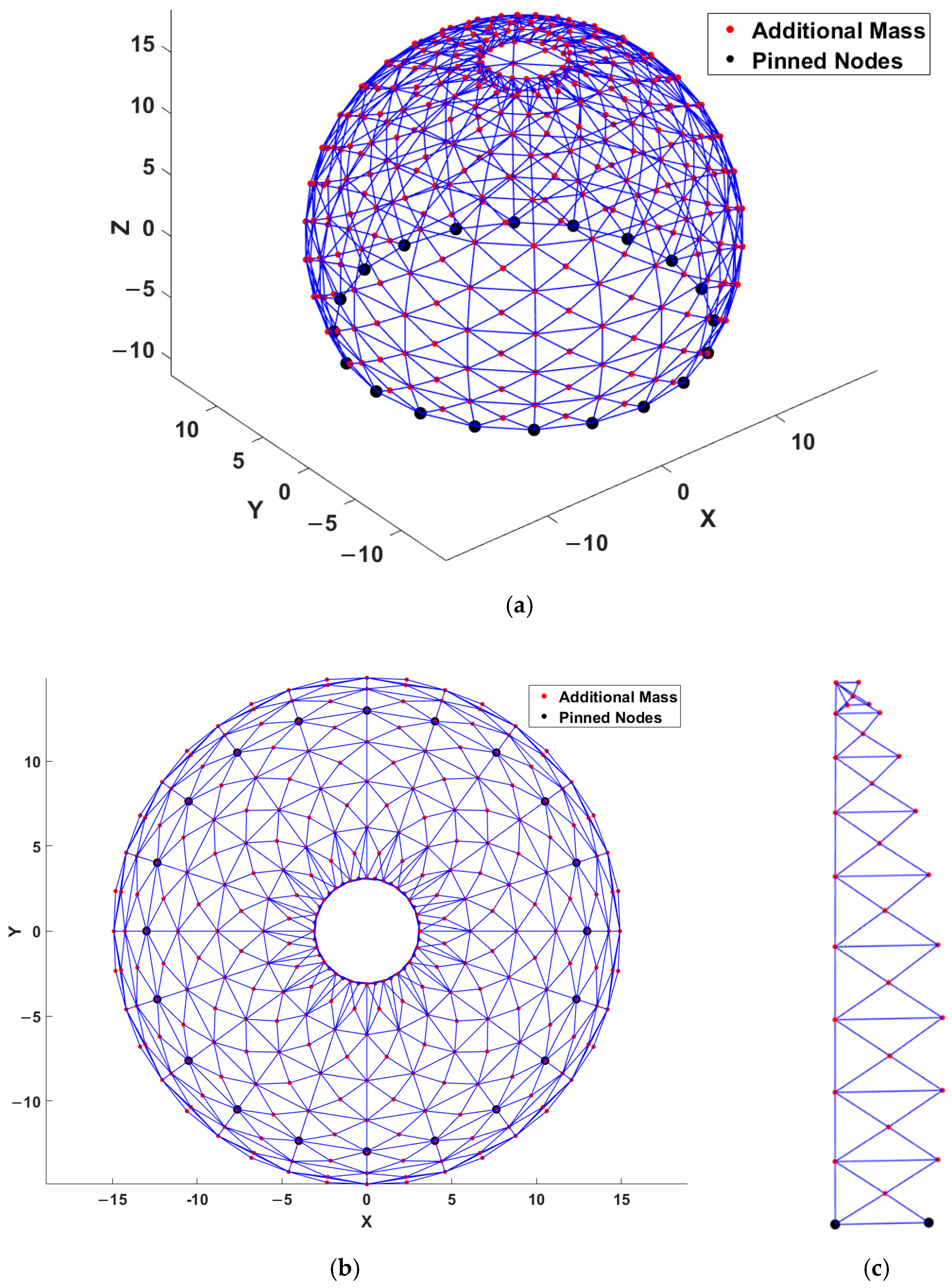
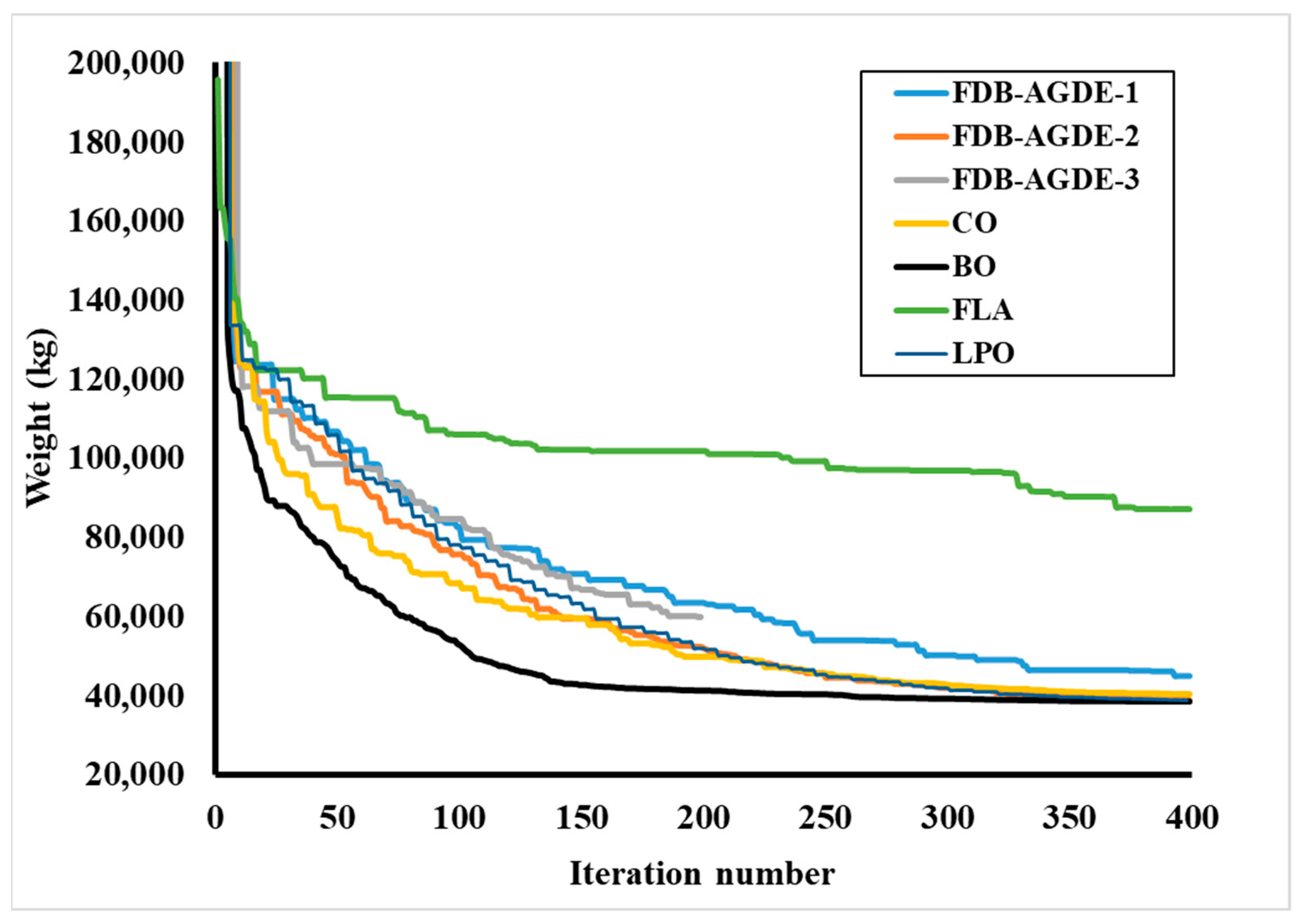
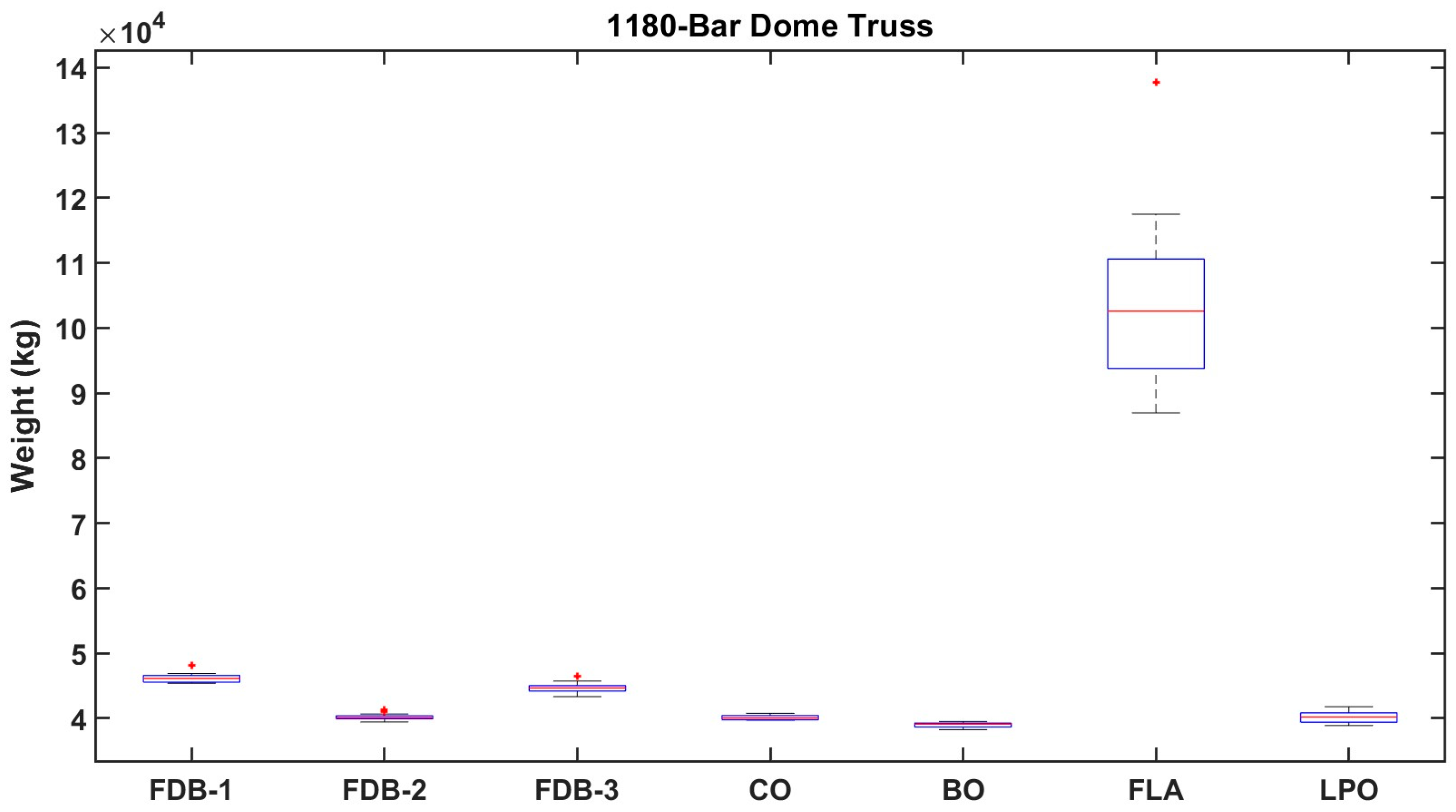
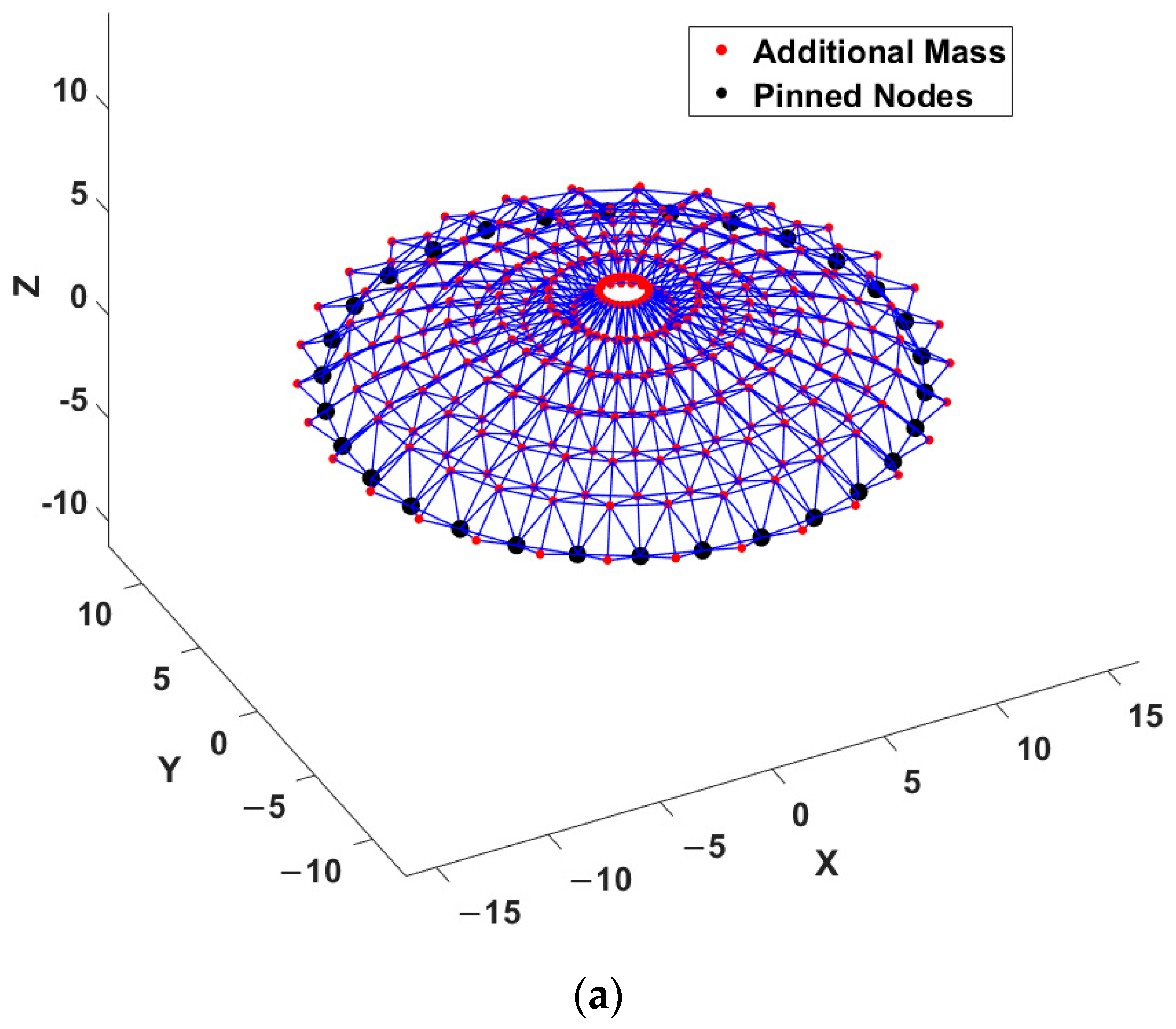
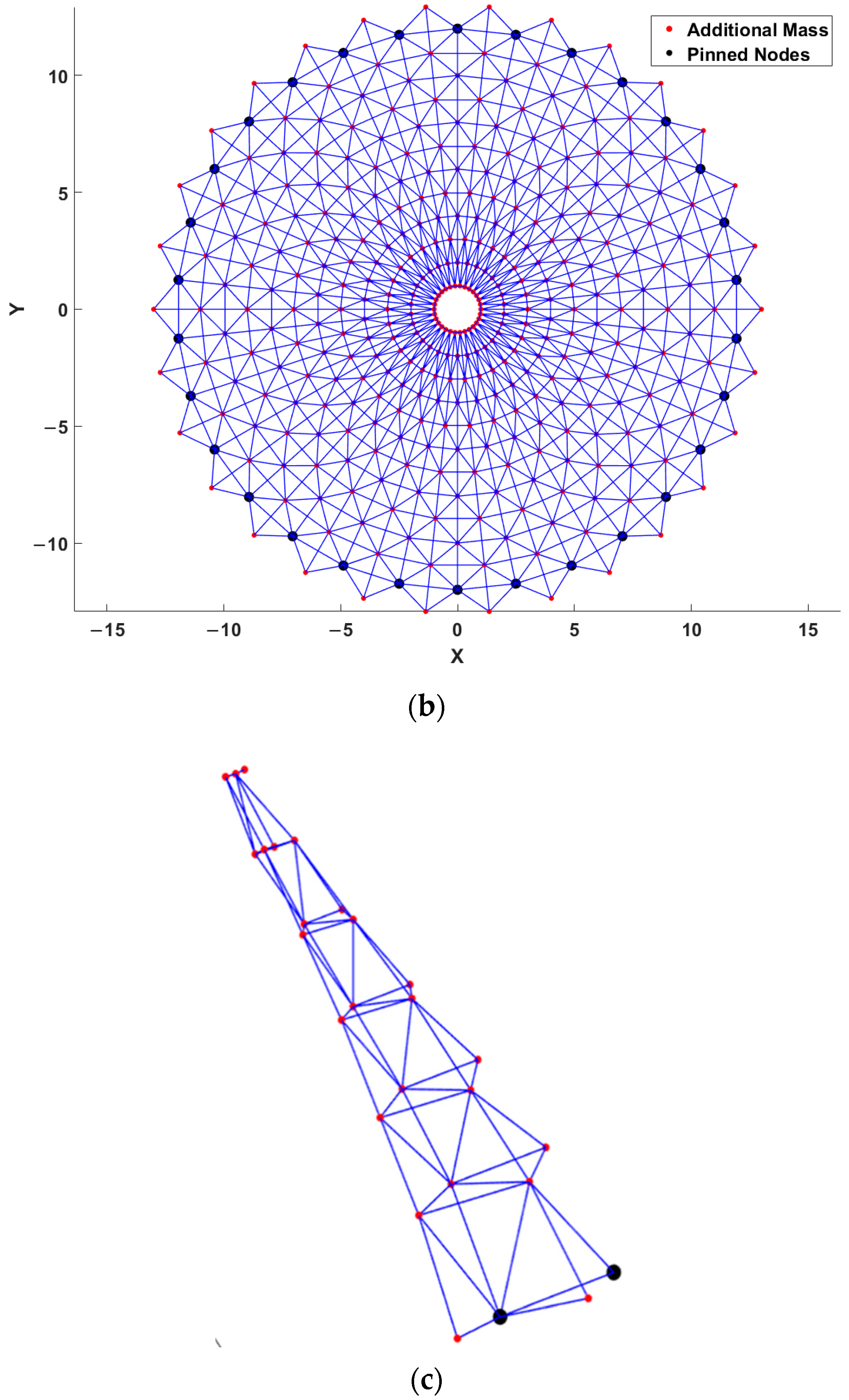
4.2. The 1180-Bar Spatial Dome Truss
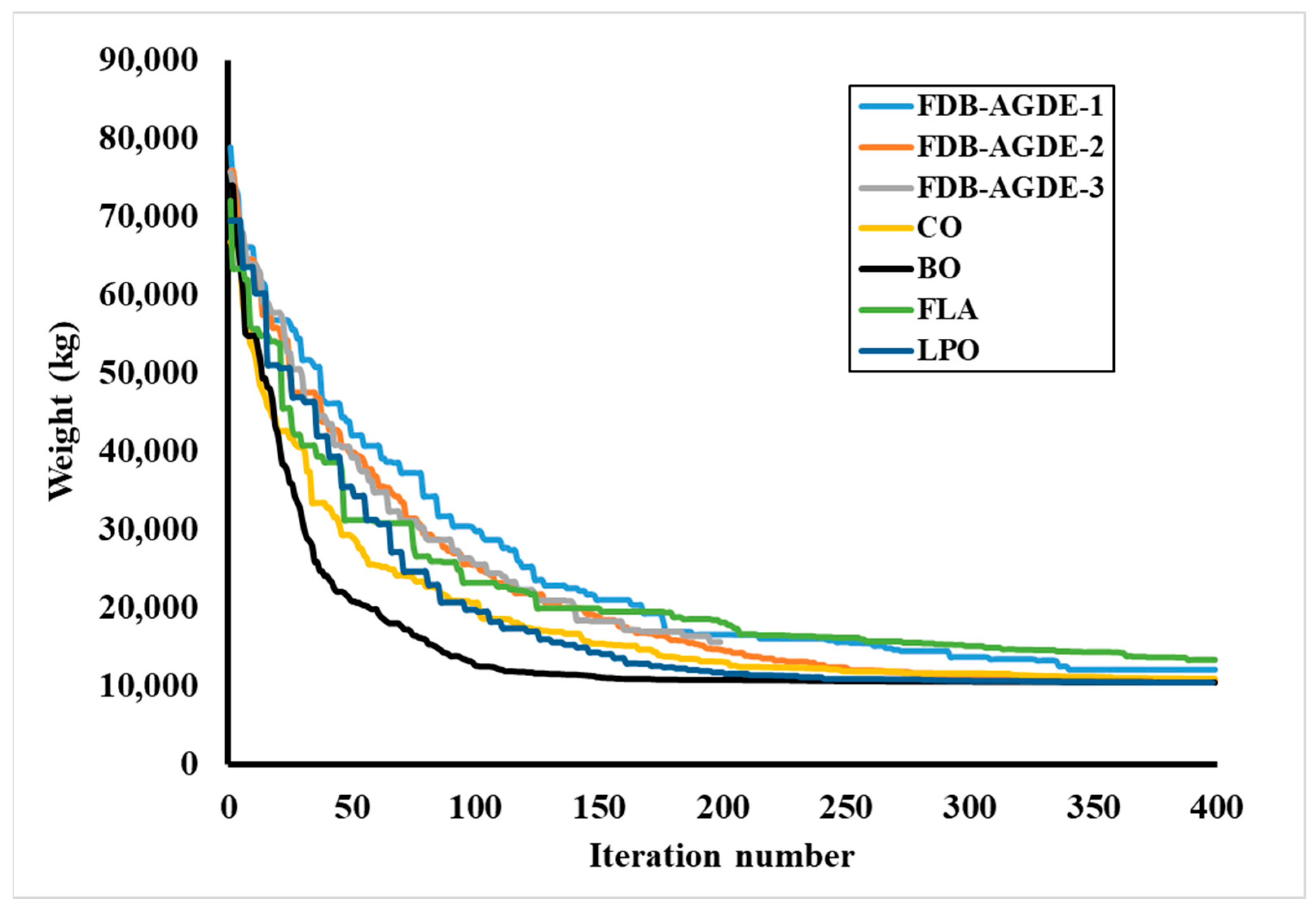
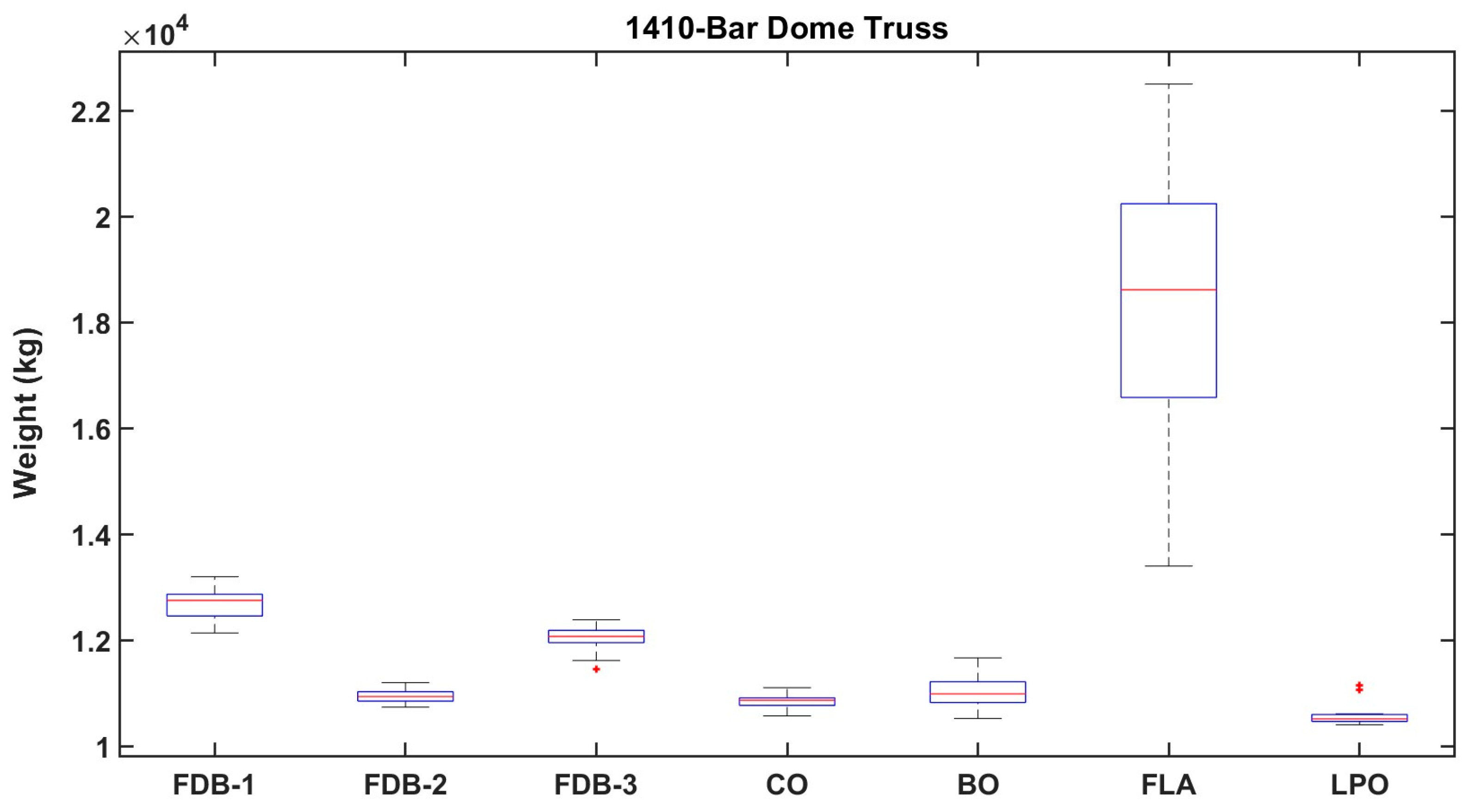
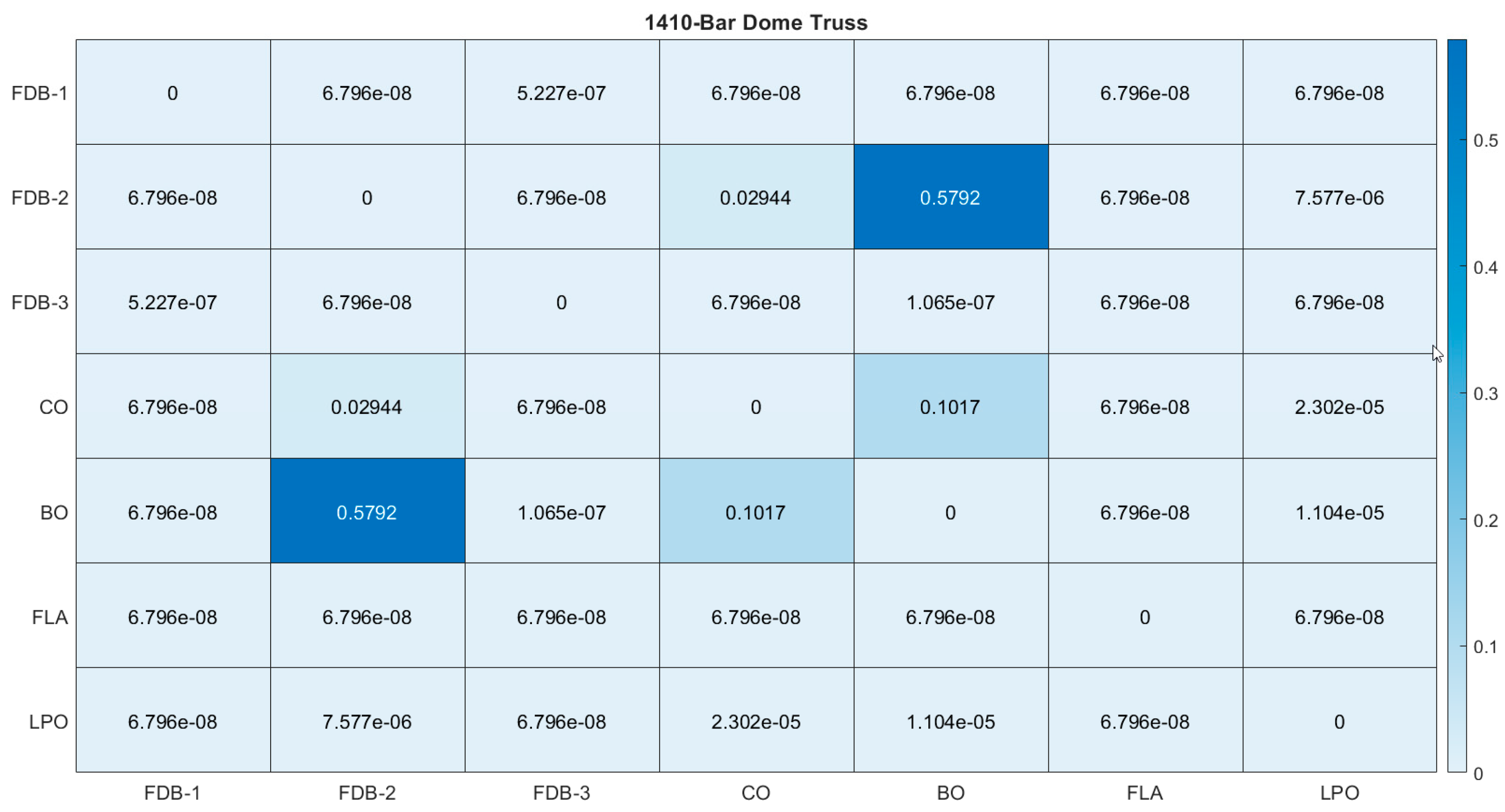
4.3. The 1410-Bar Spatial Dome Truss
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Salajegheh, F.; Salajegheh, E.; Shojaee, S. Optimum Design of Truss Structures with Frequency Constraints by an Enhanced Particle Swarm Optimization Method with Gradient Directions Based on Emigration Philosophy. Eng. Optim. 2023, 55, 434–456. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Shishehgarkhaneh, M.B. Shape and Size Optimization of Truss Structures by Chaos Game Optimization Considering Frequency Constraints. J. Adv. Res. 2022, 41, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Millan-Paramo, C.; Abdalla Filho, J.E. Size and Shape Optimization of Truss Structures with Natural Frequency Constraints Using Modified Simulated Annealing Algorithm. Arab. J. Sci. Eng. 2020, 45, 3511–3525. [Google Scholar] [CrossRef]
- Mortazavi, A. Size and Layout Optimization of Truss Structures with Dynamic Constraints Using the Interactive Fuzzy Search Algorithm. Eng. Optim. 2021, 53, 369–391. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the Performance of Artificial Bee Colony (ABC) Algorithm. Appl. Soft Comput. J. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Venkata Rao, R. Jaya: A Simple and New Optimization Algorithm for Solving Constrained and Unconstrained Optimization Problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: A Novel Method for Constrained Design Optimization Problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithms for Multimodal Optimization. In Stochastic Algorithms: Foundations and Applications; Lecture Notes in Computer Science (Including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer, Berlin/Heidelberg, Germany, 2009; Volume 5792 LNCS. [Google Scholar]
- Akbari, M.A.; Zare, M.; Azizipanah-abarghooee, R.; Mirjalili, S.; Deriche, M. The Cheetah Optimizer: A Nature-Inspired Metaheuristic Algorithm for Large-Scale Optimization Problems. Sci. Rep. 2022, 12, 1–20. [Google Scholar] [CrossRef]
- Das, A.K.; Pratihar, D.K. Bonobo Optimizer (BO): An Intelligent Heuristic with Self-Adjusting Parameters over Continuous Spaces and Its Applications to Engineering Problems. Appl. Intell. 2022, 52, 2942–2974. [Google Scholar] [CrossRef]
- Ghasemi, M.; Golalipour, K.; Zare, M.; Mirjalili, S.; Trojovský, P.; Abualigah, L.; Hemmati, R. Flood Algorithm (FLA): An Efficient Inspired Meta-Heuristic for Engineering Optimization. J. Supercomput. 2024, 80, 22913–23017. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Zahedi, A.; Trojovský, P.; Abualigah, L.; Trojovská, E. Optimization Based on Performance of Lungs in Body: Lungs Performance-Based Optimization (LPO). Comput. Methods Appl. Mech. Eng. 2024, 419, 116582. [Google Scholar] [CrossRef]
- Tang, H.; Huynh, T.N.; Lee, J. A Novel Adaptive 3-Stage Hybrid Teaching-Based Differential Evolution Algorithm for Frequency-Constrained Truss Designs. Structures 2022, 38, 434–456. [Google Scholar] [CrossRef]
- Kaveh, A.; Ilchi Ghazaan, M. Optimal Design of Dome Truss Structures with Dynamic Frequency Constraints. Struct. Multidiscip. Optim. 2016, 53, 605–621. [Google Scholar] [CrossRef]
- Kaveh, A. Optimal Analysis and Design of Large-Scale Domes with Frequency Constraints. In Applications of Metaheuristic Optimization Algorithms in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Dede, T.; Grzywiński, M.; Venkata Rao, R. Jaya: A New Meta-heuristic Algorithm for the Optimization of Braced Dome Structures. In Advanced Engineering Optimization Through Intelligent Techniques; Advances in Intelligent Systems and, Computing; Venkata Rao, R., Taler, J., Eds.; Springer: Singapore, 2020; Volume 949, pp. 13–20. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, H.; Chen, Z.; Cao, H. Frequency-Constrained Truss Optimization Using the Fruit Fly Optimization Algorithm with an Adaptive Vision Search Strategy. Eng. Optim. 2020, 52, 777–797. [Google Scholar] [CrossRef]
- Degertekin, S.O.; Yalcin Bayar, G.; Lamberti, L. Parameter Free Jaya Algorithm for Truss Sizing-Layout Optimization under Natural Frequency Constraints. Comput. Struct. 2021, 245, 106461. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B.; Kamalinejad, M. An Enhanced Forensic-Based Investigation Algorithm and Its Application to Optimal Design of Frequency-Constrained Dome Structures. Comput. Struct. 2021, 256, 106643. [Google Scholar] [CrossRef]
- Kaveh, A.; Amirsoleimani, P.; Dadras Eslamlou, A.; Rahmani, P. Frequency-Constrained Optimization of Large-Scale Dome-Shaped Trusses Using Chaotic Water Strider Algorithm. Structures 2021, 32, 1604–1618. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B.; Hamedani, K.B.; Kamalinejad, M. Improved Arithmetic Optimization Algorithm for Structural Optimization with Frequency Constraints. Int. J. Optim. Civ. Eng. 2021, 11, 663–693. [Google Scholar]
- Dede, T.; Atmaca, B.; Grzywinski, M.; Venkata Rao, R. Optimal Design of Dome Structures with Recently Developed Algorithm: Rao Series. Structures 2022, 42, 65–79. [Google Scholar] [CrossRef]
- Khodadadi, N.; Mirjalili, S. Truss Optimization with Natural Frequency Constraints Using Generalized Normal Distribution Optimization. Appl. Intell. 2022, 52, 10384–10397. [Google Scholar] [CrossRef]
- Kaveh, A.; Biabani Hamedani, K.; Kamalinejad, M. Improved Slime Mould Algorithm with Elitist Strategy and Its Application to Structural Optimization with Natural Frequency Constraints. Comput. Struct. 2022, 264, 106760. [Google Scholar] [CrossRef]
- Öztürk, H.T.; Kahraman, H.T. Meta-Heuristic Search Algorithms in Truss Optimization: Research on Stability and Complexity Analyses. Appl. Soft Comput. 2023, 145, 110573. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B.; Hamedani, B.B. Optimal Design of Large-Scale Dome Truss Structures with Multiple Frequency Constraints Using Success-History Based Adaptive Differential Evolution Algorithm. Period. Polytech. Civ. Eng. 2023, 67, 36–56. [Google Scholar] [CrossRef]
- Moosavian, H.; Mesbahi, P.; Moosavian, N.; Daliri, H. Optimal Design of Truss Structures with Frequency Constraints: A Comparative Study of DE, IDE, LSHADE, and CMAES Algorithms. Eng. Comput. 2023, 39, 1499–1517. [Google Scholar] [CrossRef]
- Goodarzimehr, V.; Talatahari, S.; Shojaee, S.; Gandomi, A.H. Computer-Aided Dynamic Structural Optimization Using an Advanced Swarm Algorithm. Eng. Struct. 2024, 300, 117174. [Google Scholar] [CrossRef]
- Sheng-Xue, H. Truss Optimization with Frequency Constraints Using the Medalist Learning Algorithm. Structures 2023, 55, 1–15. [Google Scholar] [CrossRef]
- Truong, D.-N.; Chou, J.-S. Metaheuristic Algorithm Inspired by Enterprise Development for Global Optimization and Structural Engineering Problems with Frequency Constraints. Eng. Struct. 2024, 318, 118679. [Google Scholar] [CrossRef]
- Goodarzimehr, V.; Topal, U.; Das, A.K.; Vo-Duy, T. SABO Algorithm for Optimum Design of Truss Structures with Multiple Frequency Constraints. Mech. Based Des. Struct. Mach. 2024, 52, 7745–7777. [Google Scholar] [CrossRef]
- Abbasi, M.; Zakian, P. Optimal Design of Truss Domes with Frequency Constraints Using Seven Metaheuristic Algorithms Incorporating a Comprehensive Statistical Assessment. Mech. Adv. Mater. Struct. 2024, 31, 12533–12559. [Google Scholar] [CrossRef]
- Guvenc, U.; Duman, S.; Kahraman, H.T.; Aras, S.; Katı, M. Fitness–Distance Balance Based Adaptive Guided Differential Evolution Algorithm for Security-Constrained Optimal Power Flow Problem Incorporating Renewable Energy Sources. Appl. Soft Comput. 2021, 108, 107421. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Mohamed, A.K. Adaptive Guided Differential Evolution Algorithm with Novel Mutation for Numerical Optimization. Int. J. Mach. Learn. Cybern. 2019, 10, 253–277. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-Distance Balance (FDB): A New Selection Method for Meta-Heuristic Search Algorithms. Knowl.-Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Kaveh, A.; Kamalinejad, M.; Hamedani, K.B.; Arzani, H. Quantum Version of Teaching-Learning-Based Optimization Algorithm for Optimal Design of Cyclic Symmetric Structures Subject to Frequency Constraints. Int. J. Optim. Civ. Eng. 2022, 12, 245–278. [Google Scholar]


| Truss Example | Modulus of Elasticity, E (N/m2) | Material Density, q (kg/m3) | Allowable Cross-Sectional Areas, A (cm2) | Natural Frequency Constraints (Hz) |
|---|---|---|---|---|
| 600-bar dome truss | 2.1 × 1011 | 7800 | 1 ≤ A ≤ 100 | |
| 1180-bar dome truss | 2.1 × 1011 | 7860 | 1 ≤ A ≤ 100 | |
| 1410-bar dome truss | 2.1 × 1011 | 7860 | 1 ≤ A ≤ 100 |
| Algorithms | Specific Parameters |
|---|---|
| FDB-AGDE-1 | - |
| FDB-AGDE-2 | - |
| FDB-AGDE-3 | - |
| BO | pxgm_init = 0.03; scab = 1.25; scsb = 1.3; rcpp = 0.0035; tsgsfactor = 0.05; pp = pd = 0.5 |
| CO | m = 2 |
| FLA | Ne = 5 |
| LPO | Ne = 5 |
| Node Number | x, y, and z Coordinates (m) | Node Number | x, y, and z Coordinates (m) |
|---|---|---|---|
| 1 | 1.0 0.0 7.0 | 6 | 9.0 0.0 5.0 |
| 2 | 1.0 0.0 7.5 | 7 | 11.0 0.0 3.5 |
| 3 | 3.0 0.0 7.25 | 8 | 13.0 0.0 1.5 |
| 4 | 5.0 0.0 6.75 | 9 | 14.0 0.0 7.0 |
| 5 | 7.0 0.0 6.0 |
| Design Variables Ai (cm2) | FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO |
|---|---|---|---|---|---|---|---|
| A1 | 3.023791 | 1.129101 | 1.876414 | 1.629717 | 1.257963 | 6.728939 | 1.246882 |
| A2 | 2.013871 | 1.163617 | 1.904015 | 1.241892 | 1.386239 | 1.231096 | 1.240454 |
| A3 | 5.143588 | 4.281071 | 7.394453 | 4.395661 | 4.314845 | 2.382298 | 4.243337 |
| A4 | 1.262915 | 1.338621 | 3.649760 | 1.490243 | 1.000000 | 1.002197 | 1.243932 |
| A5 | 19.983319 | 17.854018 | 19.913364 | 18.396481 | 18.114738 | 21.181630 | 18.071250 |
| A6 | 30.923535 | 36.261520 | 42.801216 | 35.300747 | 39.270116 | 31.480740 | 38.225070 |
| A7 | 14.672528 | 14.122496 | 11.807665 | 15.161942 | 13.316925 | 13.863900 | 14.108590 |
| A8 | 15.437327 | 16.829486 | 17.129579 | 16.811120 | 16.741512 | 18.784730 | 16.636750 |
| A9 | 12.269978 | 13.446700 | 13.105120 | 12.208512 | 13.171590 | 21.821850 | 13.183480 |
| A10 | 8.866545 | 9.582605 | 9.433643 | 10.005481 | 9.339057 | 8.423471 | 9.449940 |
| A11 | 9.517119 | 9.400067 | 10.370055 | 9.183313 | 10.186414 | 8.751362 | 9.537473 |
| A12 | 9.693147 | 10.015833 | 9.422258 | 9.687101 | 9.961688 | 14.226620 | 9.879310 |
| A13 | 7.452563 | 7.191178 | 6.146992 | 7.224946 | 6.916795 | 8.373427 | 7.297250 |
| A14 | 5.915914 | 5.583175 | 5.544019 | 5.544384 | 5.520614 | 4.685899 | 5.591398 |
| A15 | 6.661043 | 6.997372 | 7.160914 | 6.526607 | 6.532547 | 21.243240 | 7.003780 |
| A16 | 5.212128 | 5.039284 | 4.662089 | 5.471954 | 4.928692 | 4.140340 | 5.257701 |
| A17 | 5.807982 | 3.820944 | 3.574381 | 3.683945 | 3.918022 | 2.571551 | 3.851501 |
| A18 | 7.722593 | 7.667613 | 8.595977 | 7.728200 | 7.654024 | 7.157081 | 7.516086 |
| A19 | 3.882874 | 4.194781 | 4.656853 | 3.843037 | 4.366477 | 5.477364 | 4.088303 |
| A20 | 1.918084 | 2.176175 | 2.107502 | 2.058667 | 2.482042 | 1.377286 | 2.251530 |
| A21 | 4.804600 | 4.982080 | 5.534956 | 4.577454 | 4.841515 | 3.915202 | 4.529711 |
| A22 | 3.043238 | 3.324548 | 2.821205 | 3.311281 | 3.970928 | 2.733476 | 3.628636 |
| A23 | 2.273651 | 1.752116 | 1.905604 | 1.999731 | 1.683172 | 5.349617 | 1.796958 |
| A24 | 6.119064 | 4.977984 | 5.504228 | 5.050156 | 4.890802 | 18.268850 | 4.905784 |
| A25 | 2.084542 | 1.673162 | 1.632660 | 1.572683 | 1.520068 | 3.372308 | 1.598683 |
| Best weight (kg) | 6598.6592 | 6339.9902 | 6507.9279 | 6352.8637 | 6345.9484 | 8260.9300 | 6335.1780 |
| Mean weight (kg) | 6706.9439 | 6400.5998 | 6625.1324 | 6719.0154 | 6563.4734 | 10,368.3000 | 6345.0550 |
| Worst weight (kg) | 6873.6474 | 7728.2814 | 6809.6114 | 7753.3576 | 7831.8871 | 12,274.3600 | 6361.9060 |
| STD (kg) | 72.5950 | 250.9175 | 73.0005 | 600.6546 | 451.1856 | 1221.3330 | 5.6611 |
| CV (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NSA | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 |
| Friedman Rank | 6 | 2 | 5 | 4 | 3 | 7 | 1 |
| Mode | FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO | |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.223125 | 5.010574 | 5.024269 | 5.000221 | 5.000368 | 5.195123 | 5.010798 | |
| 2 | 5.223125 | 5.010574 | 5.024269 | 5.000221 | 5.000368 | 5.195123 | 5.010798 | |
| MATLAB | 3 | 7.019655 | 7.000239 | 7.018063 | 7.000111 | 7.000001 | 7.024405 | 7.000080 |
| 4 | 7.019655 | 7.000618 | 7.018063 | 7.000111 | 7.000010 | 7.024405 | 7.000133 | |
| 5 | 7.022560 | 7.000618 | 7.020028 | 7.000224 | 7.000010 | 7.082534 | 7.000133 | |
| 1 | 5.223125 | 5.010574 | 5.024269 | 5.000221 | 5.000368 | 5.195123 | 5.010798 | |
| 2 | 5.223125 | 5.010574 | 5.024269 | 5.000221 | 5.000368 | 5.195123 | 5.010798 | |
| SAP2000 | 3 | 7.019655 | 7.000239 | 7.018063 | 7.000111 | 7.000001 | 7.024405 | 7.000080 |
| 4 | 7.019655 | 7.000618 | 7.018063 | 7.000111 | 7.000010 | 7.024405 | 7.000133 | |
| 5 | 7.022560 | 7.000618 | 7.020028 | 7.000224 | 7.000010 | 7.082534 | 7.000133 |
| FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO | |
|---|---|---|---|---|---|---|---|
| FDB-AGDE-1 | 1.27973 | 0.81225 | 0.019112 | 0.560244 | 4.225151 | 6.156702 | |
| FDB-AGDE-2 | 1.27973 | 1.014166 | 0.621575 | 0.322801 | 4.43077 | 0.355874 | |
| FDB-AGDE-3 | 0.81225 | 1.014166 | 0.165109 | 0.35634 | 4.30046 | 6.188649 | |
| CO | 0.019112 | 0.621575 | 0.165109 | 0.343111 | 3.791843 | 0.880433 | |
| BO | 0.560244 | 0.322801 | 0.35634 | 0.343111 | 4.190787 | 0.660715 | |
| FLA | 4.225151 | 4.43077 | 4.30046 | 3.791843 | 4.190787 | 4.658568 | |
| LPO | 6.156702 | 0.355874 | 6.188649 | 0.880433 | 0.660715 | 4.658568 |
| Node Number | x, y, and z Coordinates (m) | Node Number | x, y, and z Coordinates (m) |
|---|---|---|---|
| 1 | 3.1181 0.0 14.6723 | 11 | 4.5788 0.7252 14.2657 |
| 2 | 6.1013 0.0 13.7031 | 12 | 7.4077 1.1733 12.9904 |
| 3 | 8.8166 0.0 12.1354 | 13 | 9.9130 1.5701 11.1476 |
| 4 | 11.1476 0.0 10.0365 | 14 | 11.9860 1.8984 8.8165 |
| 5 | 12.9904 0.0 7.5000 | 15 | 13.5344 2.1436 6.1013 |
| 6 | 14.2657 0.0 4.6358 | 16 | 14.4917 2.2953 3.1180 |
| 7 | 14.9179 0.0 1.5676 | 17 | 14.8153 2.3465 0.0 |
| 8 | 14.9179 0.0 −1.5677 | 18 | 14.4917 2.2953 −3.1181 |
| 9 | 14.2656 0.0 −4.6359 | 19 | 13.5343 2.1436 −6.1014 |
| 10 | 12.9903 0.0 −7.5001 | 20 | 3.1181 0.0 13.7031 |
| Design Variables Ai (cm2) | FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO |
|---|---|---|---|---|---|---|---|
| A1 | 7.874257 | 7.406661 | 7.137683 | 7.341092 | 8.033436 | 12.065870 | 7.586136 |
| A2 | 10.063780 | 8.895251 | 11.788799 | 8.344326 | 10.403249 | 18.883870 | 8.903712 |
| A3 | 4.910137 | 4.809313 | 13.614719 | 3.180261 | 2.711354 | 26.737830 | 11.403790 |
| A4 | 14.695244 | 19.069249 | 23.679900 | 16.392227 | 15.006789 | 28.308650 | 15.534610 |
| A5 | 2.909845 | 5.293858 | 6.986300 | 3.345957 | 3.896306 | 12.904980 | 3.764825 |
| A6 | 7.115904 | 7.095440 | 6.228295 | 6.554237 | 5.851600 | 27.076660 | 6.674349 |
| A7 | 6.846220 | 6.836420 | 6.387648 | 6.090645 | 7.289934 | 8.864943 | 7.834553 |
| A8 | 8.800411 | 7.543361 | 9.590688 | 6.208024 | 6.949541 | 13.544940 | 6.571596 |
| A9 | 1.673241 | 3.476135 | 2.475425 | 3.540716 | 1.879956 | 1.092358 | 2.190498 |
| A10 | 14.991772 | 11.881658 | 7.964409 | 11.483886 | 11.311291 | 10.191710 | 11.688330 |
| A11 | 16.363290 | 7.167235 | 11.791246 | 6.178595 | 7.471935 | 29.124340 | 7.865906 |
| A12 | 8.481276 | 5.033267 | 11.763259 | 5.537235 | 6.065526 | 63.762680 | 6.436489 |
| A13 | 6.170349 | 8.099839 | 7.245651 | 8.155172 | 7.101260 | 6.708742 | 7.969050 |
| A14 | 9.015904 | 6.593022 | 11.534725 | 11.377883 | 6.898631 | 6.013308 | 7.292745 |
| A15 | 9.383343 | 10.243248 | 10.153842 | 8.704600 | 9.752487 | 72.305020 | 10.477170 |
| A16 | 5.084130 | 7.726060 | 8.501315 | 6.542469 | 6.545987 | 8.504965 | 5.577529 |
| A17 | 9.901966 | 8.148965 | 6.434932 | 6.812164 | 7.210488 | 16.684040 | 9.067837 |
| A18 | 7.212494 | 9.423108 | 8.026447 | 7.634667 | 8.751584 | 25.917830 | 7.722360 |
| A19 | 14.900105 | 10.738194 | 9.968436 | 12.857575 | 14.054030 | 18.073100 | 13.969100 |
| A20 | 4.471479 | 9.155714 | 11.479431 | 8.200010 | 6.429336 | 20.478890 | 9.843234 |
| A21 | 9.834071 | 8.347413 | 8.419979 | 10.329897 | 10.047452 | 35.691520 | 11.025380 |
| A22 | 12.464360 | 9.200902 | 5.763701 | 9.210465 | 9.070010 | 14.227740 | 9.142028 |
| A23 | 13.279927 | 15.734809 | 20.932816 | 17.566533 | 17.172019 | 19.178010 | 21.280410 |
| A24 | 12.909323 | 9.879389 | 8.879572 | 13.236654 | 10.765740 | 42.416180 | 10.116070 |
| A25 | 19.849410 | 14.450982 | 16.254258 | 9.782828 | 13.643317 | 34.920030 | 12.228450 |
| A26 | 17.116466 | 11.102753 | 6.027643 | 11.314389 | 10.427723 | 19.341960 | 12.398480 |
| A27 | 25.230044 | 26.513425 | 21.529700 | 27.203381 | 22.742262 | 15.162700 | 25.406910 |
| A28 | 11.384612 | 14.169903 | 19.223520 | 16.708121 | 11.949719 | 54.156250 | 13.552570 |
| A29 | 13.256166 | 18.420711 | 19.726730 | 22.512111 | 15.483744 | 36.372350 | 21.023240 |
| A30 | 18.706791 | 14.483310 | 16.383395 | 16.627003 | 16.013196 | 27.273130 | 17.371400 |
| A31 | 42.960011 | 39.078312 | 48.417718 | 35.344354 | 37.503834 | 39.237400 | 33.663920 |
| A32 | 16.490115 | 19.402189 | 25.786561 | 17.694735 | 19.678845 | 38.985940 | 19.147790 |
| A33 | 30.200266 | 24.419041 | 28.723833 | 34.863078 | 29.031532 | 59.195030 | 26.353450 |
| A34 | 26.428994 | 21.441246 | 23.842243 | 20.774481 | 21.351047 | 43.429560 | 20.196950 |
| A35 | 54.489776 | 48.292333 | 59.666863 | 46.117090 | 53.202618 | 79.609570 | 43.312430 |
| A36 | 23.641724 | 22.003935 | 38.880077 | 27.760575 | 27.033619 | 33.187020 | 28.010940 |
| A37 | 29.134567 | 30.744031 | 26.408696 | 37.229955 | 32.893607 | 39.655420 | 34.872710 |
| A38 | 22.696805 | 34.245250 | 48.070078 | 31.976388 | 30.070674 | 39.799000 | 27.073780 |
| A39 | 41.181191 | 47.060922 | 36.881653 | 36.821762 | 35.539288 | 44.507250 | 33.745320 |
| A40 | 5.913338 | 1.988946 | 2.655745 | 2.607668 | 1.000000 | 3.009441 | 1.408517 |
| A41 | 7.547779 | 8.019023 | 8.536639 | 14.904613 | 10.478436 | 11.027630 | 8.988470 |
| A42 | 16.820410 | 7.338677 | 10.579021 | 7.875747 | 5.840658 | 71.282890 | 6.986653 |
| A43 | 7.469341 | 7.646755 | 8.213646 | 6.861987 | 5.949529 | 10.640270 | 7.601176 |
| A44 | 9.131612 | 5.736607 | 7.635684 | 7.361532 | 6.340990 | 55.241720 | 6.781792 |
| A45 | 5.796440 | 9.024426 | 3.739599 | 5.754250 | 6.893456 | 9.912174 | 7.375494 |
| A46 | 6.831707 | 8.653040 | 7.966721 | 5.646005 | 5.600438 | 24.713670 | 6.003010 |
| A47 | 10.743584 | 10.845934 | 7.118326 | 7.563096 | 8.920467 | 23.365030 | 9.659027 |
| A48 | 13.541436 | 9.554500 | 13.673555 | 8.866247 | 5.665204 | 18.299500 | 7.527485 |
| A49 | 11.731393 | 9.547094 | 10.036086 | 12.792507 | 10.709867 | 17.926910 | 11.049190 |
| A50 | 12.890989 | 12.429990 | 14.567269 | 10.181782 | 9.280738 | 23.102630 | 11.502510 |
| A51 | 25.563242 | 13.640546 | 11.930903 | 15.209169 | 13.411523 | 76.953520 | 14.859430 |
| A52 | 10.118511 | 14.698245 | 13.804554 | 13.119193 | 12.723477 | 13.043160 | 14.238340 |
| A53 | 19.802142 | 19.562892 | 16.259706 | 19.478679 | 19.150101 | 43.757370 | 17.925480 |
| A54 | 27.251787 | 18.091759 | 16.667135 | 18.809209 | 21.334890 | 43.904440 | 16.480130 |
| A55 | 39.500083 | 19.882811 | 19.703237 | 21.962420 | 26.309583 | 32.657630 | 28.848710 |
| A56 | 20.852584 | 24.350124 | 30.319425 | 25.522552 | 24.625139 | 26.114530 | 26.045850 |
| A57 | 47.364580 | 32.664712 | 41.999328 | 28.322514 | 34.803636 | 74.924180 | 35.628560 |
| A58 | 40.438513 | 37.172432 | 47.688660 | 35.955349 | 36.755497 | 51.762490 | 37.183100 |
| A59 | 11.901404 | 5.376399 | 5.221828 | 3.649674 | 5.166103 | 13.086730 | 6.384748 |
| Best weight (kg) | 42,941.683 | 38,767.648 | 43,042.693 | 38,963.136 | 38,030.272 | 76,891.100 | 38,610.050 |
| Mean weight (kg) | 46,075.984 | 40070.648 | 44,339.278 | 40,032.339 | 38,863.270 | 10,0367.200 | 39,999.660 |
| Worst weight (kg) | 48,104.622 | 41,353.299 | 46,513.243 | 40,761.896 | 39,511.108 | 137,741.500 | 41,774.340 |
| STD (kg) | 970.924 | 563.950 | 770.571 | 426.182 | 408.772 | 12,928.480 | 815.643 |
| CV (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NSA | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 |
| Friedman Rank | 6 | 3 | 5 | 4 | 1 | 7 | 2 |
| Mode | FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO | |
|---|---|---|---|---|---|---|---|---|
| MATLAB | 1 | 7.009174 | 7.003915 | 7.003153 | 7.001028 | 7.000115 | 7.017611 | 7.003076 |
| 2 | 7.009174 | 7.003915 | 7.003153 | 7.001028 | 7.000115 | 7.017611 | 7.003076 | |
| 3 | 9.043173 | 9.013461 | 9.105209 | 9.004496 | 9.000323 | 9.156227 | 9.047232 | |
| 4 | 9.043173 | 9.013461 | 9.105209 | 9.004496 | 9.000323 | 9.156227 | 9.047232 | |
| 5 | 9.462299 | 9.233525 | 9.200931 | 9.190641 | 9.000420 | 9.551542 | 9.172685 | |
| SAP2000 | 1 | 7.009174 | 7.003915 | 7.003153 | 7.001028 | 7.000115 | 7.017611 | 7.003076 |
| 2 | 7.009174 | 7.003915 | 7.003153 | 7.001028 | 7.000115 | 7.017611 | 7.003076 | |
| 3 | 9.043173 | 9.013461 | 9.105209 | 9.004496 | 9.000323 | 9.156227 | 9.047232 | |
| 4 | 9.043173 | 9.013461 | 9.105209 | 9.004496 | 9.000323 | 9.156227 | 9.047232 | |
| 5 | 9.462299 | 9.233525 | 9.200931 | 9.190641 | 9.000420 | 9.551542 | 9.172685 |
| FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO | |
|---|---|---|---|---|---|---|---|
| FDB-AGDE-1 | 10.41499 | 2.225914 | 11.17907 | 13.43934 | 6.865008 | 8.20034 | |
| FDB-AGDE-2 | 10.41499 | 7.393442 | 0.082439 | 2.867457 | 7.586172 | 0.018019 | |
| FDB-AGDE-3 | 2.225914 | 7.393442 | 7.903801 | 10.01145 | 7.04714 | 5.924849 | |
| CO | 11.17907 | 0.082439 | 7.903801 | 3.191828 | 7.592472 | 0.036963 | |
| BO | 13.43934 | 2.867457 | 10.01145 | 3.191828 | 7.729345 | 1.907356 | |
| FLA | 6.865008 | 7.586172 | 7.04714 | 7.592472 | 7.729345 | 7.576501 | |
| LPO | 8.20034 | 0.018019 | 5.924849 | 0.036963 | 1.907356 | 7.576501 |
| Node Number | x, y, and z Coordinates (m) | Node Number | x, y, and z Coordinates (m) |
|---|---|---|---|
| 1 | 1.0 0.0 4.0 | 8 | 1.989 0.209 3 |
| 2 | 3.0 0.0 3.75 | 9 | 3.978 0.418 2.75 |
| 3 | 5.0 0.0 3.25 | 10 | 5.967 0.627 2.25 |
| 4 | 7.0 0.0 2.75 | 11 | 7.956 0.836 1.75 |
| 5 | 9.0 0.0 2 | 12 | 9.945 1.0453 1 |
| 6 | 11.0 0.0 1.25 | 13 | 11.934 1.2543 −0.5 |
| 7 | 13.0 0.00 0.0 |
| Design Variables Ai (cm2) | FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO |
|---|---|---|---|---|---|---|---|
| A1 | 5.181748 | 3.594279 | 4.128842 | 5.098185 | 3.330343 | 2.679416 | 6.395886 |
| A2 | 1.945098 | 5.373930 | 5.491109 | 4.511558 | 3.795250 | 4.360587 | 4.697734 |
| A3 | 33.630189 | 23.011743 | 21.197120 | 24.711879 | 16.473644 | 3.405862 | 31.194970 |
| A4 | 10.178946 | 8.717958 | 10.186617 | 6.766575 | 9.314022 | 11.670340 | 10.309150 |
| A5 | 3.673742 | 5.951188 | 7.129077 | 5.348120 | 6.629964 | 3.058517 | 6.045048 |
| A6 | 6.059775 | 2.842269 | 3.088278 | 2.392626 | 1.574074 | 4.369000 | 1.608069 |
| A7 | 28.682730 | 18.055471 | 17.468484 | 12.740975 | 31.719067 | 69.743820 | 16.595200 |
| A8 | 11.922395 | 11.440906 | 12.596099 | 7.903293 | 9.916940 | 17.442140 | 9.176643 |
| A9 | 4.514635 | 3.251135 | 6.235259 | 2.959766 | 1.684694 | 8.080519 | 2.562129 |
| A10 | 3.190210 | 3.878719 | 5.020697 | 2.821628 | 2.485740 | 2.276878 | 2.728512 |
| A11 | 8.538754 | 10.711261 | 6.258136 | 10.721724 | 12.235064 | 18.486370 | 6.636622 |
| A12 | 11.455126 | 10.641076 | 10.398511 | 11.869204 | 8.319166 | 10.645770 | 10.014390 |
| A13 | 9.043816 | 2.509710 | 2.689918 | 2.486207 | 2.979454 | 1.028391 | 2.002495 |
| A14 | 5.889539 | 5.267594 | 3.831996 | 4.990523 | 4.475278 | 9.597372 | 5.723452 |
| A15 | 19.981151 | 15.628517 | 9.685841 | 14.253720 | 10.809117 | 19.895660 | 17.743890 |
| A16 | 7.070823 | 8.065009 | 6.107678 | 9.215784 | 8.825649 | 15.175880 | 8.554423 |
| A17 | 4.755079 | 5.327118 | 6.677618 | 3.906221 | 3.512708 | 4.770585 | 4.330146 |
| A18 | 6.747342 | 4.719784 | 6.635954 | 6.187140 | 6.312047 | 11.168100 | 6.739172 |
| A19 | 7.591766 | 5.327164 | 9.054030 | 10.391954 | 13.392728 | 12.466510 | 9.594120 |
| A20 | 10.863922 | 15.010132 | 16.617751 | 15.560866 | 13.383526 | 15.074720 | 13.816910 |
| A21 | 8.763071 | 4.511277 | 3.793691 | 5.317987 | 5.412711 | 8.739791 | 5.802691 |
| A22 | 7.266203 | 7.157492 | 6.952273 | 6.431795 | 8.362446 | 8.053586 | 7.125749 |
| A23 | 6.865031 | 5.736343 | 6.540901 | 2.101887 | 1.000000 | 1.614472 | 1.541427 |
| A24 | 2.809976 | 3.728914 | 7.259128 | 6.379180 | 4.692243 | 6.361013 | 4.646534 |
| A25 | 2.885440 | 3.774084 | 2.658645 | 2.439425 | 2.843081 | 1.703143 | 2.851894 |
| A26 | 4.888448 | 3.582424 | 6.774899 | 5.023449 | 5.540875 | 1.378022 | 5.251167 |
| A27 | 2.749199 | 6.736315 | 3.550336 | 4.951499 | 5.848941 | 4.942347 | 6.898313 |
| A28 | 10.495416 | 11.462157 | 10.544361 | 9.336837 | 11.950240 | 10.126170 | 12.228630 |
| A29 | 4.543833 | 4.397680 | 3.762613 | 4.254605 | 4.076259 | 4.422458 | 3.572397 |
| A30 | 1.563968 | 1.554140 | 4.245685 | 2.773976 | 2.039153 | 7.784655 | 1.545229 |
| A31 | 4.180324 | 2.373279 | 2.844768 | 3.699297 | 1.739721 | 9.756918 | 2.421220 |
| A32 | 7.728548 | 3.410971 | 11.128707 | 5.240978 | 3.058070 | 8.822998 | 3.724947 |
| A33 | 4.087358 | 5.998652 | 5.826317 | 5.734029 | 6.345732 | 2.524770 | 4.162181 |
| A34 | 4.329644 | 3.830342 | 4.498434 | 3.876574 | 3.261677 | 1.836376 | 2.599018 |
| A35 | 7.719226 | 4.005101 | 3.739867 | 2.500021 | 2.769724 | 4.488586 | 2.737338 |
| A36 | 4.611545 | 4.390313 | 1.051559 | 1.565100 | 3.072166 | 2.160384 | 3.413748 |
| A37 | 8.490724 | 6.892918 | 7.236847 | 9.557572 | 5.928834 | 9.411659 | 7.220829 |
| A38 | 6.378797 | 4.884825 | 6.897034 | 4.543275 | 4.352731 | 3.515112 | 5.408577 |
| A39 | 2.360077 | 4.696529 | 4.951945 | 4.204315 | 3.289214 | 7.944206 | 3.544814 |
| A40 | 3.733957 | 1.032798 | 3.203468 | 1.187727 | 1.000000 | 1.211464 | 1.085991 |
| A41 | 8.002200 | 7.661073 | 8.267425 | 7.971756 | 7.438468 | 4.951190 | 6.904313 |
| A42 | 4.764519 | 5.650634 | 5.297260 | 5.537456 | 6.310769 | 3.008724 | 6.314960 |
| A43 | 10.970546 | 5.004071 | 5.104024 | 5.390138 | 5.314027 | 3.478641 | 4.912087 |
| A44 | 1.365050 | 1.381780 | 2.566834 | 1.155712 | 1.036771 | 1.036164 | 1.000000 |
| A45 | 5.098131 | 7.429253 | 7.154799 | 7.956031 | 8.010678 | 11.350250 | 7.727939 |
| A46 | 3.666173 | 4.737608 | 5.180218 | 3.926615 | 5.003753 | 5.912236 | 3.267847 |
| A47 | 8.426747 | 1.666773 | 1.540386 | 1.274095 | 3.052483 | 1.907582 | 1.142857 |
| Best weight (kg) | 12,136.585 | 10,738.563 | 11,450.266 | 10,573.074 | 10,524.036 | 13,400.360 | 10,407.260 |
| Mean weight (kg) | 12,695.509 | 10,946.306 | 12,043.612 | 10,845.924 | 11,021.863 | 18,448.180 | 10,575.910 |
| Worst weight (kg) | 13,198.014 | 11,200.830 | 12,387.130 | 11,105.419 | 11,666.720 | 22,500.480 | 11,157.420 |
| STD (kg) | 287.632 | 139.758 | 230.137 | 135.411 | 313.799 | 2413.004 | 193.226 |
| CV (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NSA | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 |
| Friedman Rank | 6 | 4 | 5 | 2 | 3 | 7 | 1 |
| FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO | |
|---|---|---|---|---|---|---|---|
| MATLAB | 7.004349 | 7.005965 | 7.014940 | 7.001217 | 7.000325 | 7.037261 | 7.002323 |
| 7.004349 | 7.005965 | 7.014940 | 7.001217 | 7.000325 | 7.037261 | 7.002323 | |
| 9.062186 | 9.006729 | 9.008920 | 9.000524 | 9.000150 | 9.279117 | 9.004569 | |
| 9.140402 | 9.014389 | 9.046751 | 9.000524 | 9.000150 | 9.279117 | 9.004569 | |
| 9.140402 | 9.014389 | 9.046751 | 9.001757 | 9.000423 | 9.303549 | 9.017862 | |
| SAP2000 | 7.004349 | 7.005965 | 7.014940 | 7.001217 | 7.000325 | 7.037261 | 7.002323 |
| 7.004349 | 7.005965 | 7.014940 | 7.001217 | 7.000325 | 7.037261 | 7.002323 | |
| 9.062186 | 9.006729 | 9.008920 | 9.000524 | 9.000150 | 9.279117 | 9.004569 | |
| 9.140402 | 9.014389 | 9.046751 | 9.000524 | 9.000150 | 9.279117 | 9.004569 | |
| 9.140402 | 9.014389 | 9.046751 | 9.001757 | 9.000423 | 9.303549 | 9.017862 |
| FDB-AGDE-1 | FDB-AGDE-2 | FDB-AGDE-3 | CO | BO | FLA | LPO | |
|---|---|---|---|---|---|---|---|
| FDB-AGDE-1 | 7.735565 | 2.502715 | 8.227756 | 5.560281 | 3.347824 | 8.650732 | |
| FDB-AGDE-2 | 7.735565 | 5.763521 | 0.729512 | 0.31106 | 4.389342 | 2.196544 | |
| FDB-AGDE-3 | 2.502715 | 5.763521 | 6.343328 | 3.713209 | 3.736632 | 6.907323 | |
| CO | 8.227756 | 0.729512 | 6.343328 | 0.728022 | 4.448531 | 1.618359 | |
| BO | 5.560281 | 0.31106 | 3.713209 | 0.728022 | 4.316072 | 1.711356 | |
| FLA | 3.347824 | 4.389342 | 3.736632 | 4.448531 | 4.316072 | 4.599055 | |
| LPO | 8.650732 | 2.196544 | 6.907323 | 1.618359 | 1.711356 | 4.599055 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ugur, I.B. Evaluating Algorithm Efficiency in Large-Scale Dome Truss Optimization Under Frequency Constraints. Buildings 2025, 15, 3238. https://doi.org/10.3390/buildings15173238
Ugur IB. Evaluating Algorithm Efficiency in Large-Scale Dome Truss Optimization Under Frequency Constraints. Buildings. 2025; 15(17):3238. https://doi.org/10.3390/buildings15173238
Chicago/Turabian StyleUgur, Ibrahim Behram. 2025. "Evaluating Algorithm Efficiency in Large-Scale Dome Truss Optimization Under Frequency Constraints" Buildings 15, no. 17: 3238. https://doi.org/10.3390/buildings15173238
APA StyleUgur, I. B. (2025). Evaluating Algorithm Efficiency in Large-Scale Dome Truss Optimization Under Frequency Constraints. Buildings, 15(17), 3238. https://doi.org/10.3390/buildings15173238






