Assessment of Steel-Framed Subassemblies with Extended Reverse Channel Connections Under Falling Debris Impact

Abstract

Progressive collapse of building structures induced by accidental extreme loads has garnered significant attention. This study aimed to assess the impact resistance of steel-framed subassemblies with extended reverse channel connections under falling debris impact. It also sought to provide technical support for anti-collapse design. Drop-hammer impact tests were conducted to obtain baseline data. A validated finite element model using ANSYS/LS-DYNA was employed for the parametric analyses. The key parameters investigated included the impact location (mid-span vs. beam end), falling height of the impactor, and span-to-depth ratio of steel beams, with a focus on the impact resistance. The results reveal that the impact resistance depends on both the peak load capacity and the deformation capacity. The mid-span impacts exhibited higher resistance at falling heights ≥ 1.0 m due to greater plastic deformation. In contrast, the beam-end impacts performed better when the falling heights were ≤0.5 m. The impact resistance decreased with an increasing falling height. The reduction ratios exceeded the theoretical values due to the post-impact gravitational energy input. Smaller SDRs enhanced the peak resistance under both impact scenarios, with more pronounced effects in the mid-span cases. Catenary action significantly improved the mid-span impact resistance (19.3–66.7%). However, it contributed minimally to the beam-end impact resistance (0.61–1.09%), where shear action dominated. These findings offer critical technical support for optimizing steel structure designs to resist falling debris impact and enhance overall structural robustness.

1. Introduction

Since the beginning of the 21st century, an increasing focus has been placed on the progressive collapse of building structures triggered by accidental extreme loads. After the attacks on the Alfred P. Murrah Federal Building in Oklahoma City in 1995 and the World Trade Center in New York in 2001, scholars around the globe have carried out comprehensive research on the progressive collapse behaviour and resistance capabilities of building structures [1]. Moreover, different countries have formulated relevant codes and specifications to direct the design of building structures to prevent progressive collapse [2,3,4]. Up to now, the majority of research on the progressive collapse resistance of building structures has been carried out under the column-removal scenario [5]. Nevertheless, typical extreme load incidents, like the gas explosion at the Ronan Point apartments in 1968 and the attack on the World Trade Center in 2001, have indicated that column failure may not be the only factor leading to the progressive collapse of structures.

Falling debris impact refers to the phenomenon where a building is damaged by accidental extreme loads, causing the upper structural or non-structural elements to collapse downward and impact the remaining lower structures [6]. After the 9.11 incident, Lu and Jiang [7] and Omika et al. [8] pointed out that the falling debris impact was an important reason for the final collapse of the World Trade Center. In recent years, typical falling debris impact phenomena have also been observed in progressive collapse events of buildings, such as the Hard Rock Hotel in New Orleans (2019) and the Thailand Audit Office Building (2025).

It is crucial to clarify that structural collapse under extreme events arises from a combination of factors rather than a single cause. While the falling debris impact is a critical trigger, its effect interacts with other mechanisms: column failure due to overload, loss of load-carrying capacity in the connections, and progressive degradation of structural stiffness. Historical cases like the World Trade Center collapse have shown that impact-induced debris loads exacerbate the initial damage, but that collapse progression depends on concurrent loss of vertical support and inadequate redundancy. The falling debris impact acts as both an immediate load and a secondary hazard that amplifies the primary failures, accelerating collapse by compromising the remaining structural integrity. Distinguishing its relative role in aggravating existing vulnerabilities helps to create target designs that can mitigate both the initial impacts and subsequent cascading failures.

For framed structures subjected to impact from falling floors, Kaewkulchai et al. [9] conducted a simplification and equivalence. They treated the impactor and the impacted beam as a spring–mass system during the impact process. Based on this, they proposed a failure model. This model was used to analyse the progressive collapse of frame structures under the impact of falling floors. Based on the “Simplified assessment framework for progressive collapse” proposed by Izzuddin et al. [10] and Vlassis et al. [11], Vlassis et al. [12] put forward an energy-based assessment method for building structures subjected to impact from an upper floor. Jawdhari et al. [13] analysed the energy transfer during impact for reinforced concrete flat-plate and steel-framed buildings. The results showed that the impacted floors had little ability to withstand the impacts from the upper floors. Meanwhile, Haas et al. [14] reviewed the analysis methods for debris impact. These methods included conservation of energy, SDOF, and MDOF approaches. They emphasized the validation of these methods and their applications in design. This review helped evaluate structural performance under such dynamic loads. These studies, proceeding from a theoretical perspective, have laid the foundation for evaluating the performance of framed structures against falling debris impact. Further research is needed to enhance understanding of falling debris impact mechanisms and structural robustness.

When steel-framed structures experience progressive collapse due to falling debris impact, the steel beams are likely to be the first components to bear the impact loads. Thus, exploring the mechanical characteristics of steel beam members under impact loads serves as the foundation for enhancing the resistance of building structures to falling debris impacts. So far, numerous experimental and numerical simulation studies have been carried out on the impact behaviour of diverse flexural members, including H-shaped steel beams [15,16], castellated beams [17,18], square-hole castellated beams [19], sandwich beams [20,21], planar tubular trusses [22], and concrete beams [23].

In the occurrence of accidental extreme loads like impact and explosion, the mechanical performance of beam–column connections is of crucial significance for the overall structural resistance. Consequently, it is essential to study the impact-resistant capacity of these connections [24]. To date, a great deal of research has been conducted on the dynamic responses and failure modes of various connection types, such as end-plate connections [25,26], welded unreinforced flange-bolted web connections [27], fin-plate connections [28], welded connections [29], square tubular T-joints [30], and concrete connections [31,32] under impact-loading conditions.

Extensive research has been conducted on steel-framed beams under impact loading. Similarly, various types of beam–column connections under impact loading have also been widely studied. However, none of the above studies have considered the combined performance of steel beams and connections under such dynamic loads. In real-world scenarios of falling debris impacts, the beam members cannot resist the impact load alone. Similarly, the beam–column connections cannot withstand the impact load in isolation either. Instead, the entire structure must work together to resist such loads. The existing studies have explored the impact behaviour of structures under falling debris impact scenarios. Wang et al. [33] conducted numerical analyses on steel beams with fin-plate connections under impact loads. Their findings revealed several key factors. The impact energy, impact location, and material strength significantly affect the dynamic responses. Additionally, reducing the bolt hole distance or fin-plate thickness may lead to premature failure. Wang et al. [6,34] conducted experimental tests on steel frames with five types of connections under various impact locations. The results indicated that the impact resistance relies on two factors: the load-carrying capacity and ductility. Additionally, catenary action was found to enhance energy absorption in ductile connections. Wang et al. [35] studied steel-framed subassemblies with reverse channel connections under falling debris impact. They analysed the effect of span-to-depth ratio via simulations. A simplified approach was proposed to predict the load-carrying capacity. Chen et al. [36] conducted parametric studies on composite beams with various connections. Their findings showed that composite slabs enhance energy absorption. Higher reinforcement ratios were found to benefit the impact resistance of fin-plate connections and reverse channel connections. Wang et al. [37] investigated the residual impact resistance of CFST composite frames. The study focused on the frames after column removal. The results showed that the beam–column connections and composite slabs are the key energy-consuming components. Additionally, over 75% of the resistance comes from the flexural action of the beams. These studies have provided the foundation, but further research on assessment of structures with high-performance beam–column connections against falling debris impact is need.

Considering the importance of beam–column connections in frame structures, ongoing endeavours have been dedicated to discovering the connection types that combine outstanding performance with construction convenience. Wang and Xue [38] put forward a novel beam–column connection, namely the reverse channel connection. They conducted a succession of experimental tests to explore the impact of parameters on the moment–rotation behaviour and failure patterns of this connection. This connection, which exhibits remarkable deformation performance, can be designed as either a rigid or semi-rigid one. It enables easy connections between steel beams and columns of diverse cross-sections, including steel hollow section columns, concrete-filled steel tubular columns, and conventional steel section columns. Wang et al. [6,34,35] investigated steel-framed subassemblies with reverse channel connections under the impact of falling debris. Their research unveiled the effects of engineering parameters on the impact response and formulated a simplified prediction method for assessing the load-bearing capacity.

The process of structures resisting impact loads is essentially a process of absorbing impact energy. Good impact resistance performance does not only depend on the load-carrying capacity of a structure. Instead, it necessitates a comprehensive consideration of the relationship between the structural load-bearing capacity and deformation to elucidate its energy-absorption ability. However, prior studies have focused on the static and dynamic responses and failure modes of reverse channel connections and steel-framed subassemblies. There is still a lack of effective assessments on the impact resistance performance of steel-framed structures with reversed channel connections. To precisely assess the impact resistance of steel-framed subassemblies with extended reverse channel connections, this paper undertakes research based on the fundamental data acquired from drop-hammer impact tests and numerical simulations. It adheres to the structural impact resistance assessment approach proposed by Vlassis et al. [12]. The study explores the impacts of engineering parameters, like the impact positions and the span-to-depth ratio (SDR) of steel beams, on the impact resistance of steel-framed subassemblies with extended reverse channel connections. The findings of this research can offer technical support for steel-framed structures to resist the impact of falling debris.

2. Previous Experimental Tests and Finite Element Modelling

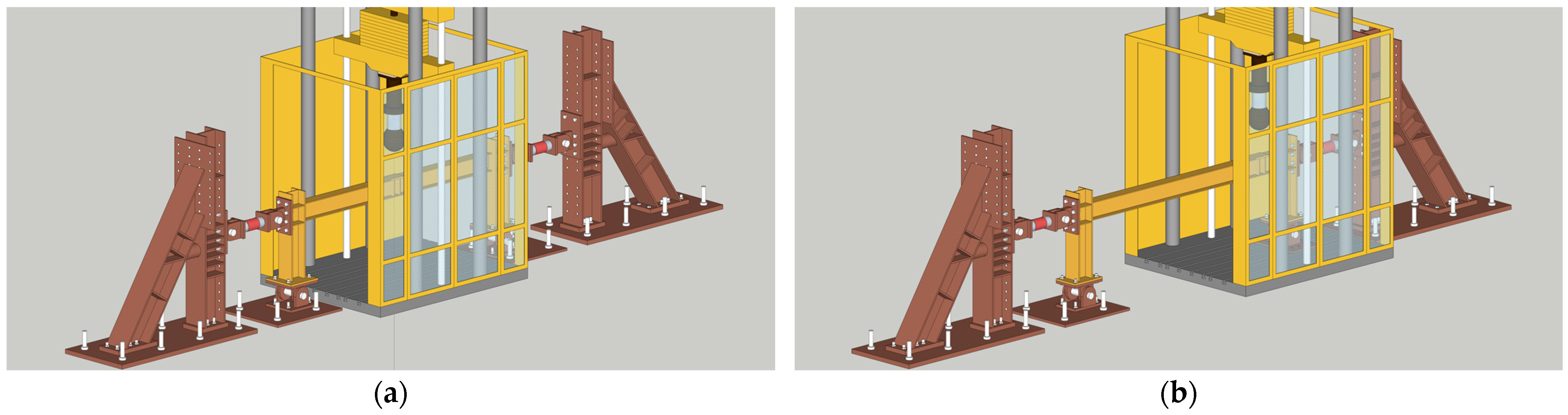
2.1. Drop-Hammer Impact Tests

To investigate the impact response of steel-framed subassemblies under falling debris impact scenarios, a series of drop-hammer impact tests of steel-framed subassemblies with various beam–column connections, including reverse channel connections, have been carried out and reported on elsewhere [6,34]. The drop-hammer impact tests hypothesized that abnormal loads cause the falling debris to impact the steel-framed beams. Considering the unpredictable impact location on the steel beams, two typical load locations, viz., the midspan and beam end, were selected for the drop-hammer impact tests. These impact locations represent the adverse bending condition of a steel beam and the adverse shear condition of a beam–column connection, respectively, as shown in Figure 1.

Horizontal restraints were provided by the steel A-frames on both sides of the specimens, and the column bases were connected to the reaction floor via hinged supports to simulate the constraint effect of undamaged surrounding structural components on the test subassemblies. Due to space limitations of the drop-hammer testing machine, no out-of-plane restraint devices were installed in this test. At the position where the beam would be impacted by the drop hammer, reinforced steel plates were welded to the upper flange, and stiffeners were arranged on the web to restrict potential local deformation and out-of-plane distortion.

All the specimens adopted the same geometric dimensions, including a span of 3120 mm. British Universal Beams [39] UB 203 × 133 × 30 and British Universal Columns [39] UC 203 × 203 × 71 were employed for the sections of steel beams and steel columns, respectively. The extended reverse channel connection consisted of a parallel flange channel (PFC) 150 × 75 × 18 and an 8 mm thick end plate. The PFC and end plate were welded to the column flange and beam end, respectively, and then connected using 10.9-grade M20 bolts. The detailed dimensions of the extended reverse channel connection are shown in Figure 2.

All components of the test specimens were fabricated from British steel [40]. The beams, columns, and parallel flange channels of the specimens were made of S355 steel, while the end plates were made of S275 steel. To determine the mechanical properties of the steel for analysing the mechanical performance of the specimens and conducting the finite element modelling, tensile coupons were taken from the same batch of materials used in the beam flanges, beam webs, column flanges, column webs, channel flanges, channel webs, stiffeners, and end plates. Steel tensile mechanical property tests were carried out. Both the sampling of steel materials and the tensile testing of steel were conducted in accordance with the requirements of British standards [41,42], respectively. The obtained mechanical parameters of the steel at different positions are listed in

Table 1. Mechanical parameters of steel at different positions.

Component	Yield Stress (MPa)	Ultimate Stress (MPa)	Elongation 1
Column flange	375	556	0.29
Column web	412	574	0.29
Beam flange	370	536	0.33
Beam web	386	540	0.32
Channel flange	402	555	0.27
Channel web	406	552	0.33
End plate	311	460	0.36
Stiffener	395	553	0.29

¹ Elongation is based on proportional coupon gauge length of $5.56\sqrt{S_0}$, where S₀ is original cross-sectional area of coupons.

.

2.2. Finite Element Modelling

To perform a parametric analysis of steel-framed assemblies with extended reverse channel connections under falling debris impact, a 3-D finite element model was developed by utilizing ANSYS/LS-DYNA. The bilinear elastoplastic model (MAT 003, Plastic Kinematic Model within LS-DYNA) was utilized to imitate the mechanical characteristics of the steel. The material constitutive parameters were determined based on the mechanical properties of the steel for each component, which are presented in Table 1. Given that the response of steel-framed subassemblies when subjected to an impact load represents a typical dynamic process, the strain rate-dependent Dynamic Increase Factor (DIF) derived from the Cowper–Symonds model was adopted to simulate the strengthening of steel under high-strain-rate conditions, as depicted in Equation (1):

$$\mathrm{DIF}=1+{\left({\displaystyle \frac{\dot{\epsilon }}{C}}\right)}^{{\displaystyle \frac{1}{p}}}$$

(1)

where $\dot{\epsilon }$ is the strain rate and C and p are the Cowper–Symonds parameters, which are set to 6844 s⁻¹ and 3.91, respectively, according to Reference [30].

To model the specimens under impact loading, 3-D finite element models were developed using the 8-node hexahedral element Solid 164. Reduced integration algorithms were employed to enhance the computational efficiency while implementing hourglass control. The mesh size of the finite element model was determined based on the existing research [35]. Specifically, the critical components, such as bolts and end plates, were assigned a mesh size of 5 mm. For the beams and columns away from the impact zone, the mesh size was set to 10 mm in the depth direction, 40 mm in the axial direction, and two elements through the thickness regardless of the actual thickness. The finite element models simplified the experimental setup. Regarding the constraint system, the column bottoms were modelled as ideal pinned supports, and the horizontal restraints were replaced with 3-D spring elements (Link 160). Instead of modelling the entire drop hammer to its actual dimensions, only the head portion was retained, with the material density adjusted to ensure the same mass as the physical hammer used in experiments. The initial velocity applied to the hammer in the model was set equal to the impact velocity measured during testing. During the impact process, numerous contact interactions between different components of the specimen were modelled using Automatic Single-Surface Contact (ASSC) algorithms. This approach automatically detects the potential contact surfaces and applies the appropriate constraints, eliminating the need to manually define numerous contact pairs. The finite element model of the steel-framed subassembly with extended reverse channel connection under the impact loading established using ANSYS/LS-DYNA is illustrated in Figure 3.

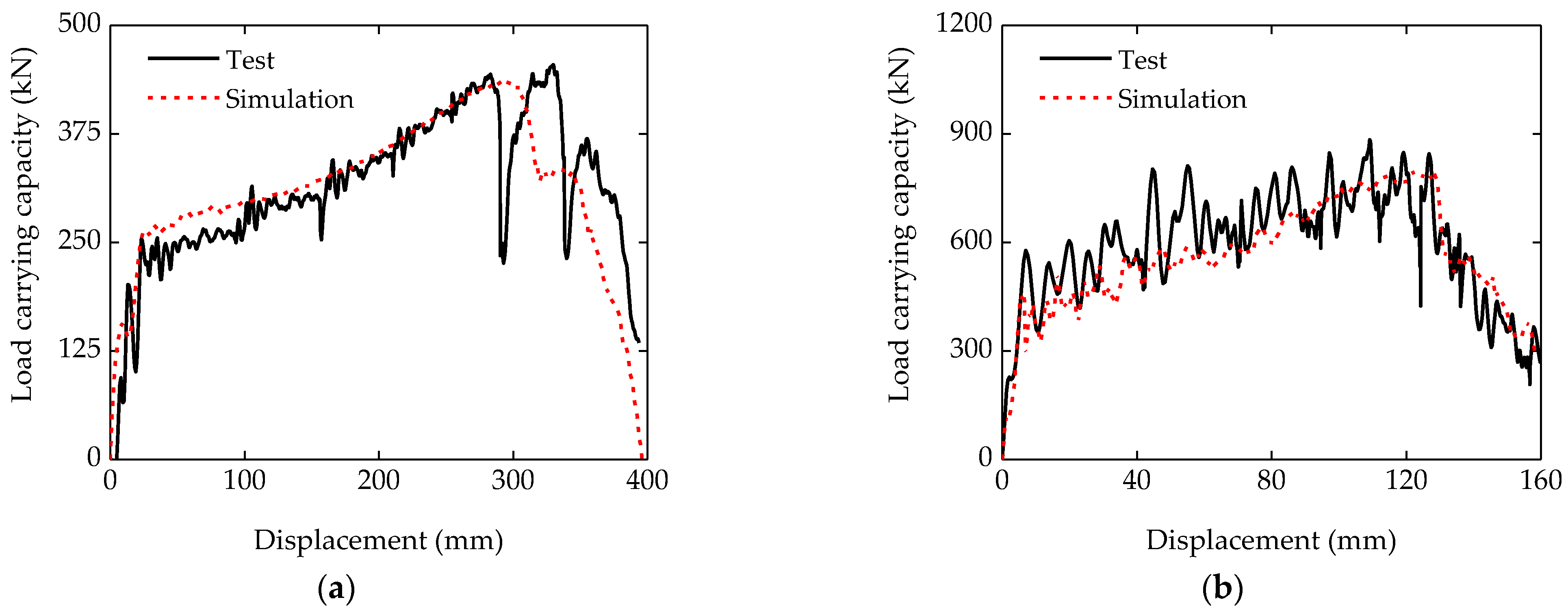
2.3. Validation of Finite Element Models

The drop-hammer impact tests described in Section 2.1 were used to validate the finite element models established with ANSYS/LS-DYNA. Figure 4 presents the comparison of load-carrying capacity versus displacement curves obtained from the drop-hammer impact tests and numerical simulations under the mid-span impact scenario and beam-end impact scenario, respectively. The curves from the simulations are in good agreement with those from the drop-hammer impact tests.

Table 2. Primary results of drop-hammer impact tests and numerical simulations.

Impact Scenario	Peak Load-Carrying Capacity (kN)			Peak Displacement (mm)			Energy Absorption (kJ)
	Test	Sim	S/T	Test	Sim	S/T	Test	Sim	S/T
Mid-span impact	454.5	438.1	0.96	330	293	0.89	121.6	122.9	1.01
Beam-end impact	883.5	797.0	0.90	109	122	1.12	94.9	88.9	0.94

lists the peak load-carrying capacity, peak displacement, and energy absorption under each impact scenario. The three primary parameters were accurately estimated by the finite element models.

It should be noted that compared with the experimental results, the displacement error obtained by the finite element model was relatively large. This discrepancy may have stemmed from two factors: (1) The finite element model was built under ideal conditions, while there were errors in the size and installation position of the test specimens compared to the ideal state. (2) The friction variations between the bolted connections in the experiments were difficult to fully replicate numerically. These factors collectively contributed to the relatively large error, which, however, remained within the acceptable range for engineering analysis.

According to the comparison above, the finite element models can predict the dynamic response of steel-framed subassemblies under falling debris impact scenarios. The modelling approach can also be used to conduct parametric analyses of steel-framed subassemblies subjected to impact loads.

3. Assessment Method of Impact Resistance

Izzuddin et al. [10] proposed a multi-level framework for assessing the progressive collapse of multi-storey buildings under sudden column loss, encompassing the nonlinear static response, simplified dynamic assessment, and ductility evaluation, with the system’s pseudo-static capacity serving as a robustness measure. Its application to steel-framed composite buildings revealed vulnerabilities due to insufficient joint ductility, highlighting inadequacies in the tying force [11]. Building on the above-proposed approach, Vlassis et al. [12] further developed a methodology for floor impact-induced collapse, focusing on the energy transfer, and demonstrated that such structures are highly vulnerable under an impact.

Based on the method proposed by Vlassis et al. [12], the assessment steps for steel-framed subassemblies subjected to falling debris impact are as follows:

1.

Determining the load-carrying capacity–displacement curves:

• The load-carrying capacity–displacement (R-u) curves of steel-framed subassembly under falling debris impact scenarios can be obtained through experimental tests, numerical simulations, or a simplified approach [35].

2.

Modifying the load-carrying capacity–displacement curves:

• After determining the R-u curve of the subassembly, its coordinate axes need to be offset to account for the deformation of the impacted subassemblies caused by their self-gravitational load G after the collision, as shown in Figure 5. Thus, the resulting offset R’-u’ curve will be used in the subsequent impact resistance assessments.

3.

Initializing the impact resistance curve (R’_d-u’_d curve):

• Set R’_d,i = 0, u’_d,i = 0, i = 0, and E_a,i = 0, where parameter i is the step number and E_a is the energy absorbed by the steel-framed subassembly. Determine the displacement increment δ_i from step i to step i+1.

4.

Determine the modified load-carrying capacity R’_i+1 at displacement u’_d,i+1:

• Calculate u’_d,i+1 = u’_d,i + δ_i. Determine R’_i+1 from the modified load-carrying capacity–displacement R’-u’ curve based on u’_d,i+1.

5.

Determine the impact resistance R’_d,i+1 at displacement u’_d,i+1:

• Calculate the energy absorbed by subassembly E_a,i+1, i.e., the area enclosed by the R’-u’ curve and the coordinate axes between u’_d = 0 to u’_d,i+1: E_a,i+1 = E_a,i + (R’_i+1−R’_i)δ_i/2. Determine the current impact resistance R’_d,i+1 = αE_a,i+1/(αu’_d,i+1+h), where α is a parameter depending on the assumed impact load distribution on the subassembly with a value of 1.0, and h is the falling height of drop hammer.

6.

Obtain the entire R’_d-u’_d curve:

• If there are more points in the R’-u’ curve, set i = i + 1 and repeat Steps 3 to 5 until a complete impact resistance curve is obtained.

The impact resistance curve of the steel-framed subassembly obtained through the procedures outlined in Steps 1 to 6 is such that each point on the curve represents the maximum self-weight of an impactor that the subassembly can withstand when undergoing a certain degree of deformation. In the impact-resistant design of framed structures, if the self-weight of components of the upper floors that may collapse is less than the maximum self-weight of an impactor the subassembly can withstand, the subassembly can meet the safety requirements; conversely, the subassembly suffers failure.

4. Impact Resistance Assessment Based on Drop-Hammer Impact Tests

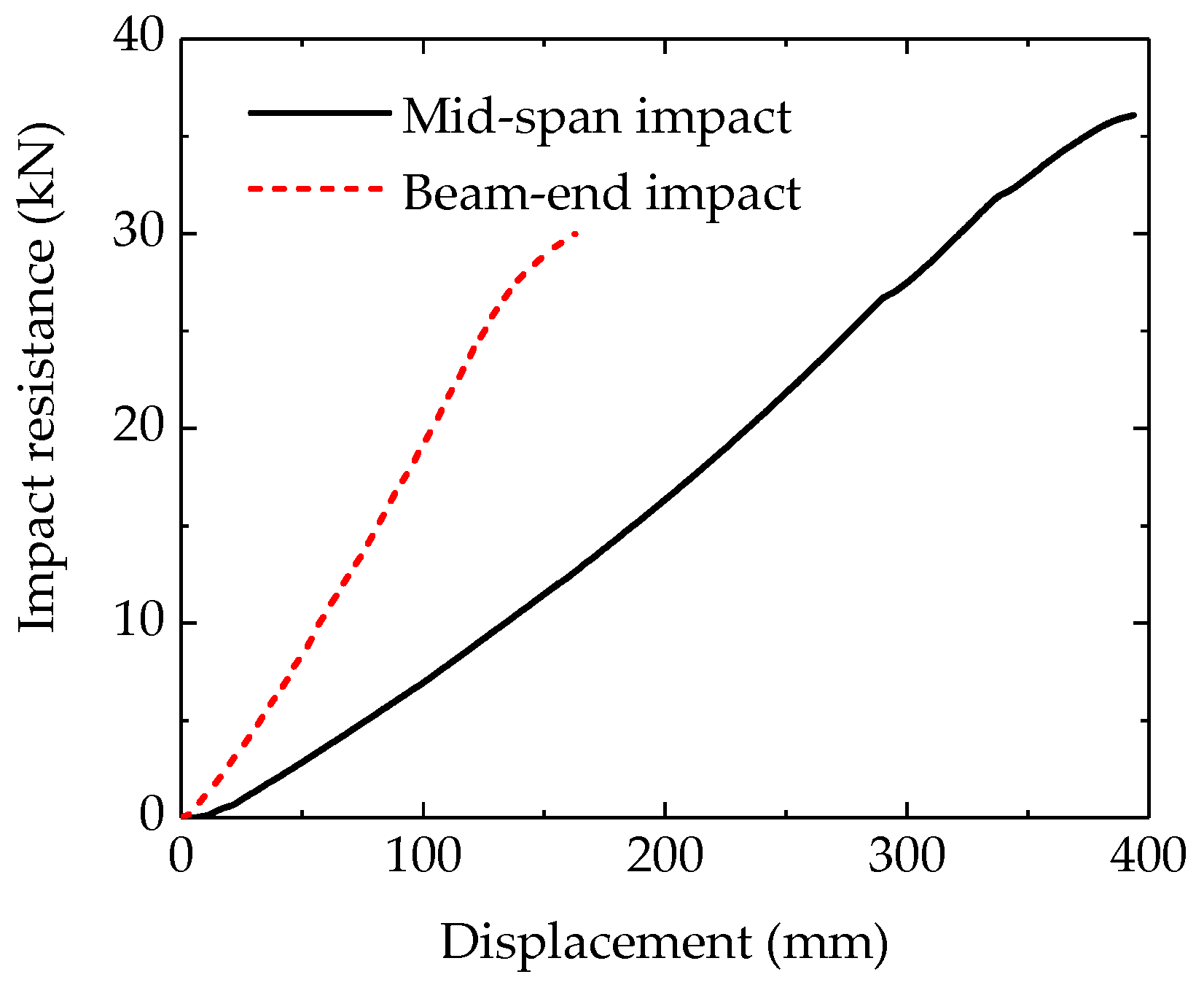
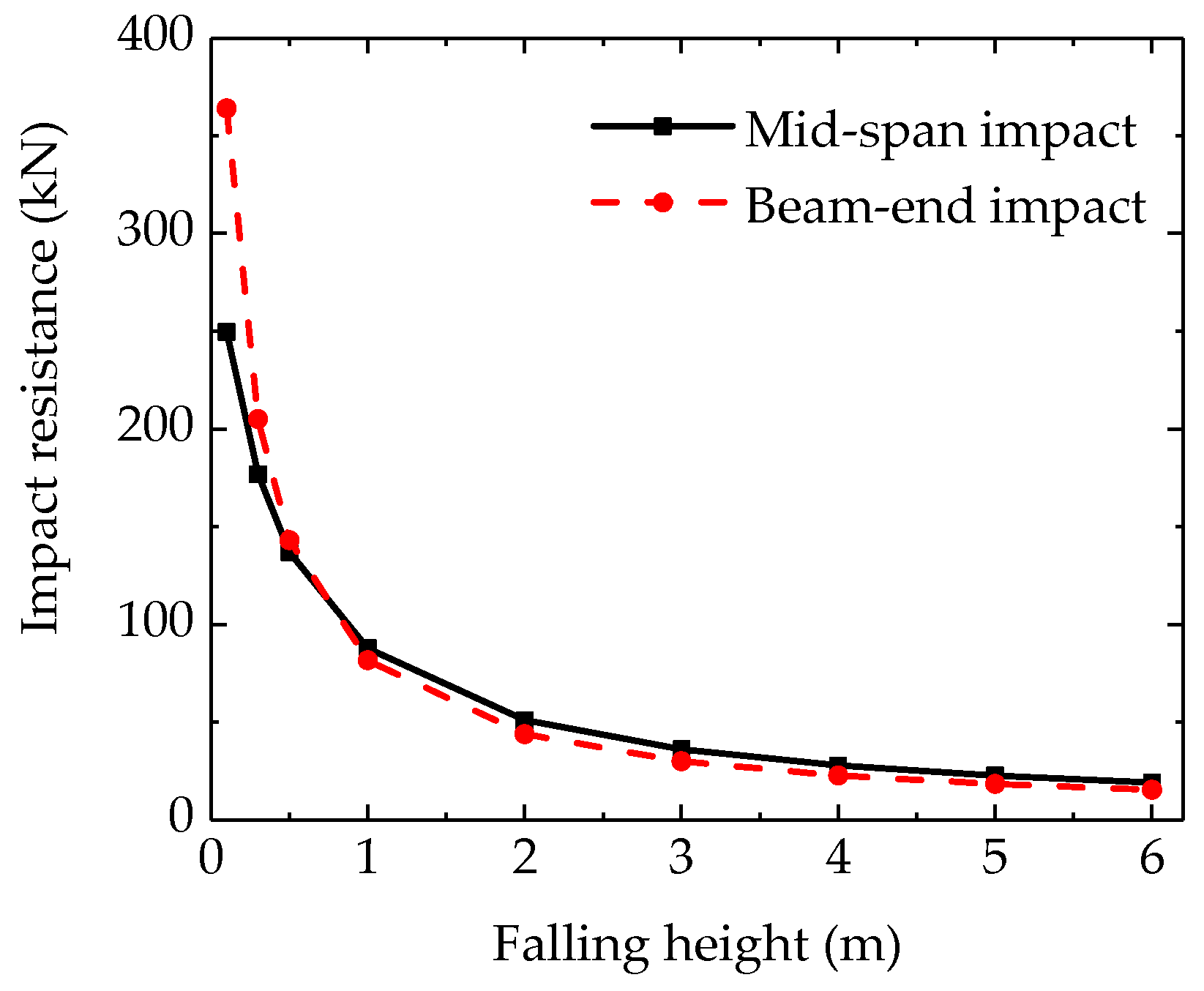
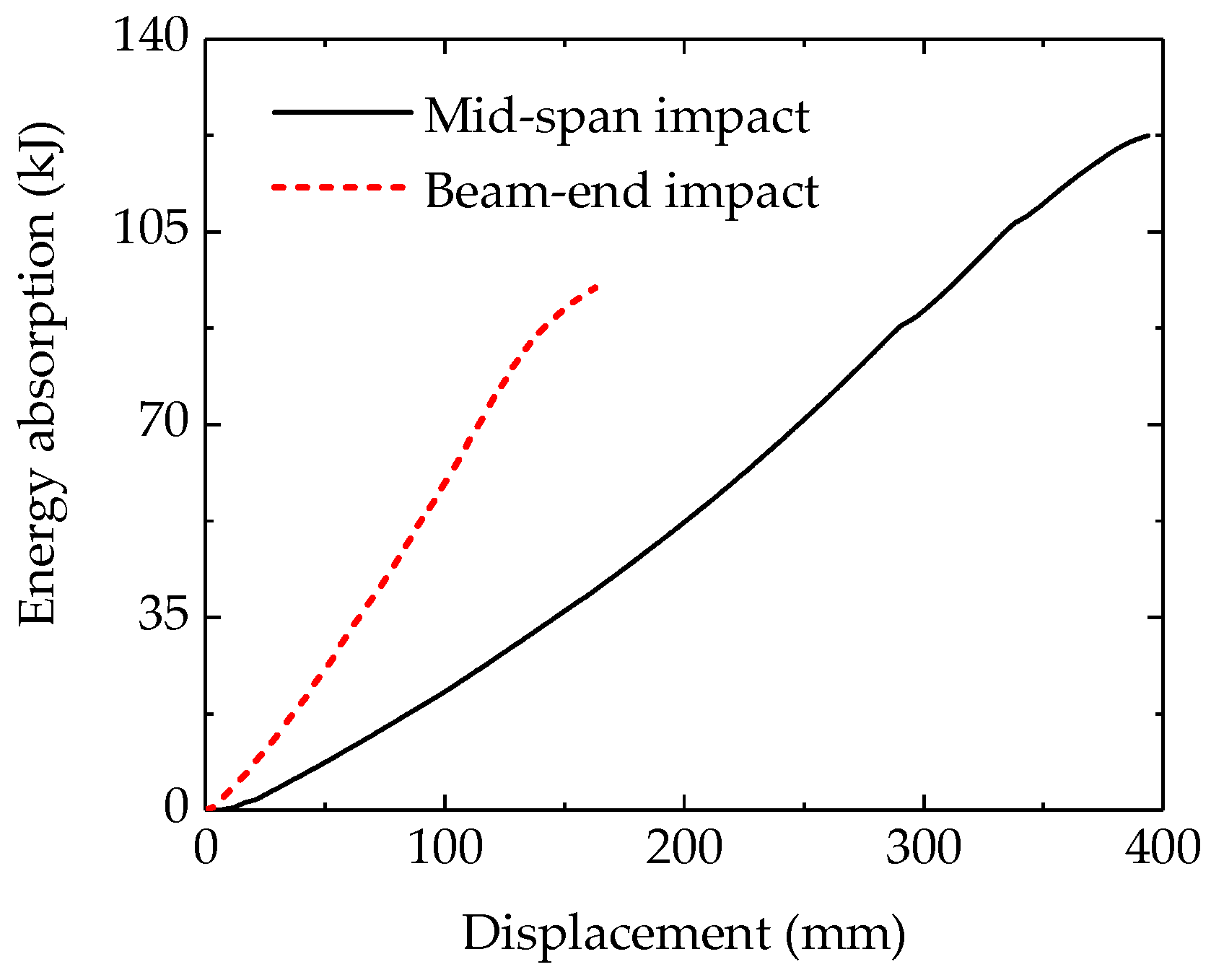
4.1. Effect of Impact Locations

The load-carrying capacity curves of steel-framed subassemblies under falling debris impact scenarios are shown in Figure 4. Since the falling height of the drop hammer was 3 m in the impact tests, the parameter h was set to 3.0 m in Step 5. Based on the assessment method described in Section 3, the impact resistance curves of subassemblies under various impact scenarios were obtained and are shown in Figure 6.

Based on the data in Table 2, the peak load-carrying capacities of the steel-framed subassemblies in the mid-span impact and beam-end impact situations are 454.5 kN and 883.5 kN, respectively. The peak load-bearing capacity of the steel-framed subassembly in the beam-end impact case is 94.4% greater than that in the mid-span impact case. Nevertheless, once the load-bearing capacity curve is transformed into the impact resistance curve, it becomes clear that the impact resistance of the specimens in the mid-span impact situation is 36.1 kN. This value is 20.3% higher compared to the 30.0 kN in the beam-end impact situation. When the hammer’s drop height is 3 m, if the impact takes place at the mid-span position, the steel-framed subassembly will remain intact when the mass of the impactor is less than 3610 kg. On the other hand, if the impact occurs at the beam-end, the maximum mass of the impactor that the steel-framed subassembly can endure is 3000 kg (calculated with a gravitational acceleration of g = 10 m/s²).

Clearly, although the peak load-carrying capacity of the specimen under the beam-end impact scenario is much higher than that under the mid-span impact scenario, its impact resistance is lower than that under the mid-span impact scenario. Since the structure resists impact loads mainly by absorbing the kinetic energy of the impactor through its own large plastic deformation, its impact resistance depends not only on its peak load-carrying capacity but also on its deformation capacity. For the test specimen, under the beam-end impact scenario, due to the constraint effect of the joint near the impact location, the maximum deformation of the specimen is significantly smaller than that under the mid-span impact scenario, ultimately resulting in a lower impact resistance compared to the mid-span impact scenario.

4.2. Effect of Falling Height

In the experiment, the falling height of the hammer is 3 m. To further investigate the influence of the falling height on the impact resistance of the steel-framed subassemblies, the parameter h in Step 5 is set to 0.5 m, 1.0 m, 2.0 m, 4.0 m, 5.0 m, and 6 m, respectively. All these heights are possible falling debris impact heights for actual steel-framed structures. The impact resistance–displacement curves of steel-framed subassemblies under various falling heights of hammer are shown in Figure 7.

Whether under the mid-span impact scenario or the beam-end impact scenario, the variation trend of the steel-framed subassemblies’ impact resistance curves with the drop height of the hammer is consistent: the higher the drop height of the hammer, the lower the impact resistance of the steel-framed subassemblies. This is because, at a specific impact location, the impact kinetic energy that the steel-framed subassemblies can absorb is a fixed value. The kinetic energy is converted from the gravitational potential energy of the impactor during its falling process. Thus, when the impactor falls from a higher position, a smaller mass is sufficient to reach the critical value of the energy absorbed by the steel-framed subassemblies, resulting in a reduction in the impact resistance of the steel-framed subassemblies.

Theoretically, if the energy absorption of a structure is E_a, the failure will occur when the impact energy E_k equals E_a. The impact energy is converted from the gravitational potential energy of the impactor. The critical condition for structural failure can be expressed as Equation (2):

$$E_a=E_k=Gh=mgh$$

(2)

where G is the gravity of the impactor, m is the mass of the impactor, and g is the gravity acceleration.

According to Equation (2), when the falling height of the impactor increases by 100%, the gravity of the impactor required to cause the structure to fail will decrease to 50%.

Under the mid-span impact scenario, when the falling height is increased by 100% (i.e., increased from 0.5 m to 1.0 m, 1.0 m to 2.0 m, 2.0 m to 4.0 m, and 3.0 m to 6.0 m, respectively), the impact resistance of the steel-framed subassemblies decreases from 137.0 kN to 87.8 kN, 87.8 kN to 51.1 kN, 51.1 kN to 27.9 kN, and 36.1 kN to 19.1 kN, respectively. The decreasing ratios are 64.1%, 58.2%, 54.6%, and 52.9%, respectively, rather than the theoretically expected 50.0%. Under the beam-end impact scenario, when the falling height is increased from 0.5 m to 1.0 m, 1.0 m to 2.0 m, 2.0 m to 4.0 m, and 3.0 m to 6.0 m, respectively, the impact resistance of the steel-framed subassemblies decreases from 143.1 kN to 81.6 kN, 81.6 kN to 43.9 kN, 43.9 kN to 22.8 kN, and 30.0 kN to 15.4 kN, respectively. The decreasing ratios are 57.0%, 54.0%, 51.9%, and 51.3%, respectively, which are also higher than the theoretical value of 50.0%.

The found decreasing ratios of the impact resistance of the steel-framed subassemblies with an increase in the falling height are higher than the theoretical values. This phenomenon is related to the process of falling debris impact. When the hammer comes into contact with the steel-framed subassemblies, both the hammer and the steel-framed subassemblies will continue to deform downward. During the deformation process, gravity always exists, continuously converting the gravitational potential energy of the hammer and the steel-framed subassemblies into kinetic energy, which is then absorbed by the deformation of the steel-framed subassemblies until both come to rest. During the impact process, the energy absorbed by the steel-framed subassemblies includes not only the kinetic energy converted from the gravitational potential energy of the hammer before the collision, but also the kinetic energy converted from the gravitational potential energy of the hammer and the steel-framed subassemblies during their continuous downward movement during the deformation process after the collision. Hence, the actual decreasing ratio of the impact resistance of the steel-framed subassembly is higher than the theoretical value.

Figure 8 contrasts the impact resistance of steel-framed subassemblies at different impact positions when subjected to hammers with varying falling heights. When the falling height is 0.5 m or lower, the beam-end impact configuration demonstrates superior impact resistance. Conversely, when the falling height is 1.0 m or higher, the steel-framed subassemblies exhibit better impact resistance in the mid-span impact scenario. This occurrence is associated with the deformation performance and energy absorption ability of the steel-framed subassemblies. The energy absorbed by the steel-framed subassemblies during the impact process consists of two components. One is the kinetic energy transformed from the gravitational potential energy of the hammer during its free-fall phase prior to the collision. The other is the kinetic energy converted from the gravitational potential energy during the continued descent of the hammer and the deformation of the steel-framed subassemblies after the collision. As depicted in Figure 9, the steel-framed subassemblies possess greater deformation capacity in the mid-span impact situation. However, under the beam-end impact scenario, they have a stronger energy absorption capacity when the same displacement occurs before failure.

When the falling height is lower, if the hammer hits the mid-span position of the steel beam, the steel-framed subassemblies need a greater deformation to absorb the kinetic energy after the collision. A larger deformation means that more gravitational potential energy is converted into kinetic energy after the collision. When the hammer hits the two ends of the steel beam, the steel-framed subassemblies need a smaller deformation to absorb the same free-fall kinetic energy of the hammer, which means that less additional kinetic energy is converted from gravitational potential energy after the collision. Therefore, when the falling height is lower, the proportion of the kinetic energy from the free-fall stage of the hammer to the total energy absorbed by the steel-framed subassemblies under the mid-span impact scenario is smaller (for example, when the falling height is 0.3 m, the proportion of the free-fall kinetic energy of the hammer to the total energy absorbed by the steel-framed subassemblies is 43.7% under the mid-span impact scenario and 64.8% under the beam-end impact scenario). That is, a large proportion of the energy absorption capacity needs to resist the gravitational potential energy during its own deformation stage, resulting in a lower impact resistance than that under the beam-end impact scenario.

When the falling height is higher, the proportion of the free-fall kinetic energy of the hammer to the energy absorbed by the steel-framed subassemblies under the mid-span impact condition is still lower than that under the beam-end impact condition. Since the falling height is much larger than the displacements caused by the deformations of the steel-framed subassemblies, most of the total energy absorbed by the steel-framed subassemblies is the kinetic energy from the free-fall stage of the hammer (for example, when the falling height is 5 m, the proportion of the free-fall kinetic energy of the hammer to the total energy absorbed by the steel-framed subassemblies is 92.7% under the mid-span impact condition and 96.8% under the beam-end impact condition). Therefore, the impact resistance of steel-framed subassemblies under different conditions mainly depends on their energy absorption capacity.

In summary, the steel-framed subassemblies had a better impact resistance under the mid-span impact scenario (with a stronger deformation capacity) when resisting impacts from a higher falling height, and had a stronger capacity under the beam-end impact scenario (with a weaker deformation capacity) when resisting large-mass impact loads from a lower falling height.

5. Impact Resistance Assessment Based on Numerical Simulations

In the design of steel-framed beams, the SDR is a crucial design parameter. Its rational value directly influences the load-bearing capacity, stiffness, and cost-effectiveness of steel beams. In real-world engineering, taking into account the load conditions, boundary conditions, construction and transportation limitations, etc., the SDR of steel-framed beams is typically controlled within the range of 8 to 32, as per Reference [35]. To explore the impact of the SDR on the impact resistance of steel-framed subassemblies, the validated finite element model was employed to perform parameter analyses under both mid-span impact and beam-end impact scenarios. During the parametric analyses, the cross-section of the steel beam was kept constant, and the SDR was adjusted by modifying the span of the steel beam in the finite element models. The numerical simulations were designated as SDR-X-Y. Here, X represents the SDR, ranging from 8 to 32, and Y represents the impact locations, specifically the mid-span impact scenario (M) and the beam-end impact scenario (B). For example, SDR-8-M signifies that the specimen with an SDR of 8 was subjected to the mid-span impact scenario.

It is worth noting that the mid-span and beam-end impact scenarios had different SDRs. The numerical simulations indicated that when the SDR was greater than 16 in the beam-end impact scenario, the differences in the energy absorption capacity were relatively small. To display the numerical results more distinctly, in the beam-end impact scenario, the cases with SDRs of 20 and 28 were removed, and the case with an SDR of 10 was included.

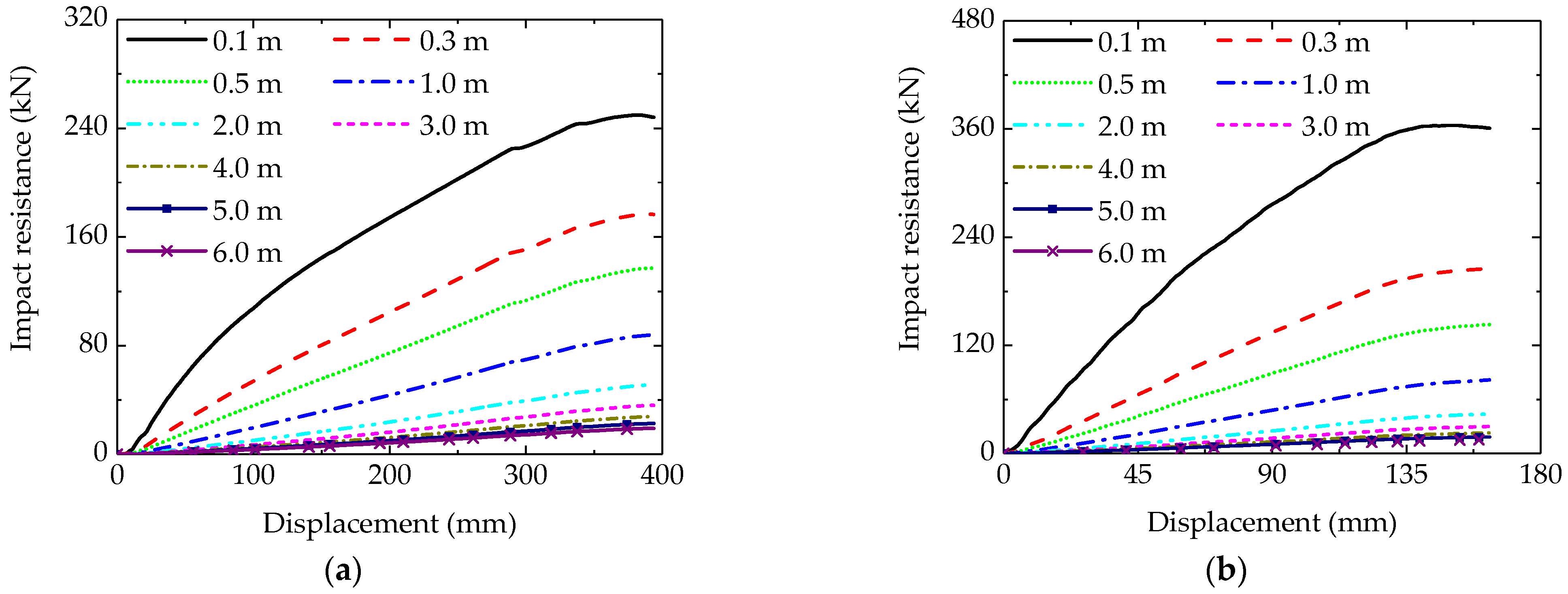
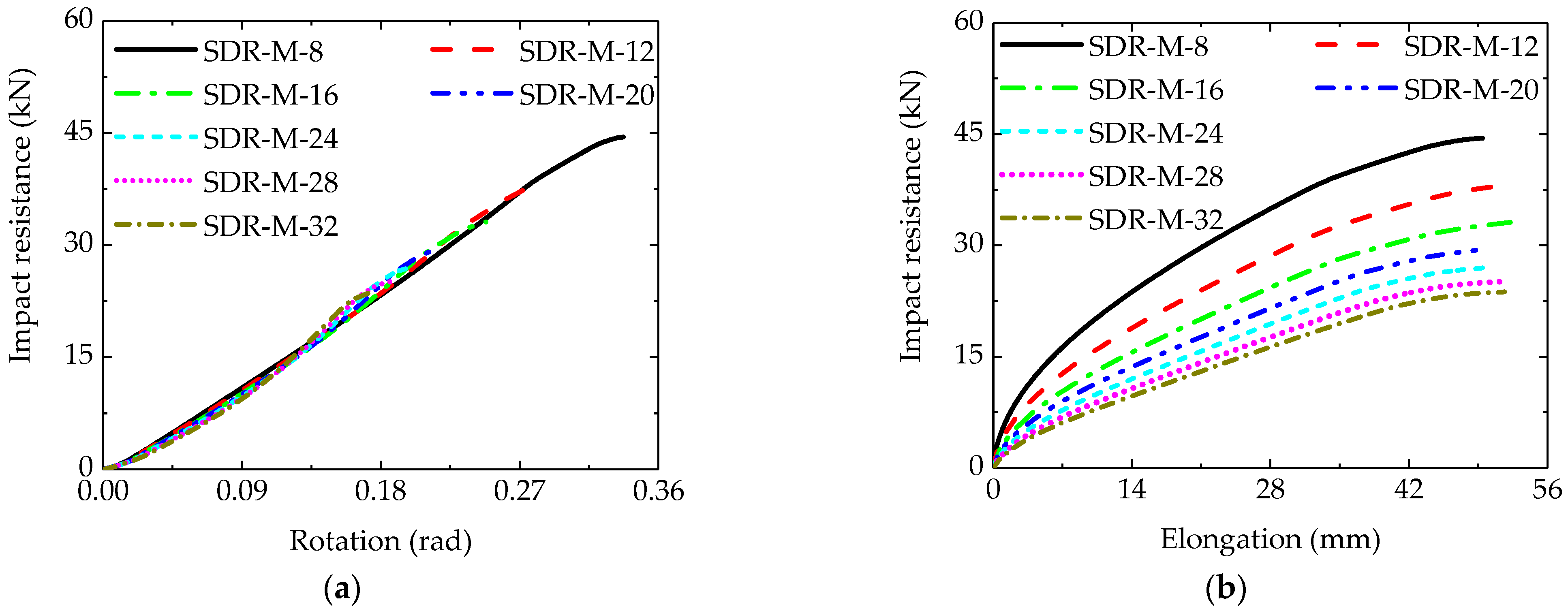
5.1. Effect of SDR on Impact Resistance

Figure 10 shows the effect of the SDR on the impact resistance–displacement curves of steel-framed subassemblies covering both the mid-span impact scenario and the beam-end impact scenario.

Table 3. Effect of SDR on subassemblies under impact load.

Impact Scenario	SDR	Peak Impact Resistance (kN)	Peak Displacement (mm)	Energy Absorption (kJ)
Mid-span impact	8	44.44	290.1	146.2
	12	38.12	364.1	128.2
	16	33.12	419.4	113.2
	20	29.43	454.8	101.7
	24	27.02	501.9	94.62
	28	25.19	550.4	89.43
	32	23.74	587.0	85.15
Beam-end impact	8	30.59	156.7	96.57
	10	29.69	157.1	93.75
	12	29.01	157.2	91.60
	16	28.08	160.0	88.73
	24	28.03	162.6	88.64
	32	27.86	162.6	88.10

summarizes the corresponding peak impact resistance, displacement, and energy absorption.

Under the mid-span impact scenario, significant differences can be observed among the impact resistance–displacement curves with different SDRs, as shown in Figure 10a. The curve for the specimen with a small SDR (e.g., SDR-M-8) shows a steep slope, with the impact resistance increasing rapidly as the displacement increases. This reflects that steel-framed structures can rapidly establish impact resistance during the deformation stage, which is attributed to the greater stiffness of steel beams under a small SDR. However, as the SDR increases (e.g., SDR-M-32), the curve slope becomes gentler and the growth rate of impact resistance decreases. This reflects that beams with a large SDR, due to reduced stiffness, require larger displacements to absorb sufficient impact energy and resist impact loads. Ultimately, the peak impact resistance of steel-framed subassemblies with a small SDR is significantly higher than that of those with a large SDR.

Under the beam-end impact scenario, the curves of steel-framed subassemblies with different SDRs show a high degree of overlap in the initial stage, indicating that the initial response of the subassemblies is less affected by the SDR, as shown in Figure 10b. As the displacement increases, the impact resistance of the steel-framed subassemblies with smaller SDRs increases more rapidly, while the curve growth for those with larger SDRs lags. Eventually, the peak impact resistance of the steel-framed subassemblies with smaller SDRs is slightly higher than that of those with larger SDRs, and the trend of peak impact resistance as affected by the SDR is consistent with that under the mid-span impact scenario.

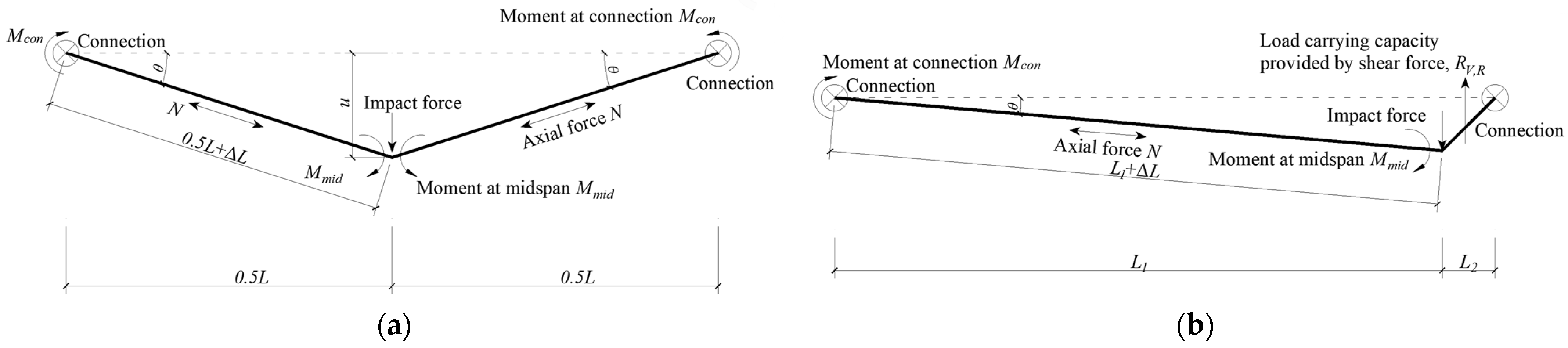
5.2. Impact Load-Resisting Mechanism

The influence of SDR on the impact resistance of steel-framed subassemblies is associated with their load resistance mechanisms. Figure 11 illustrates the impact load resistance mechanisms of steel-framed subassemblies under mid-span and beam-end impact loads, respectively.

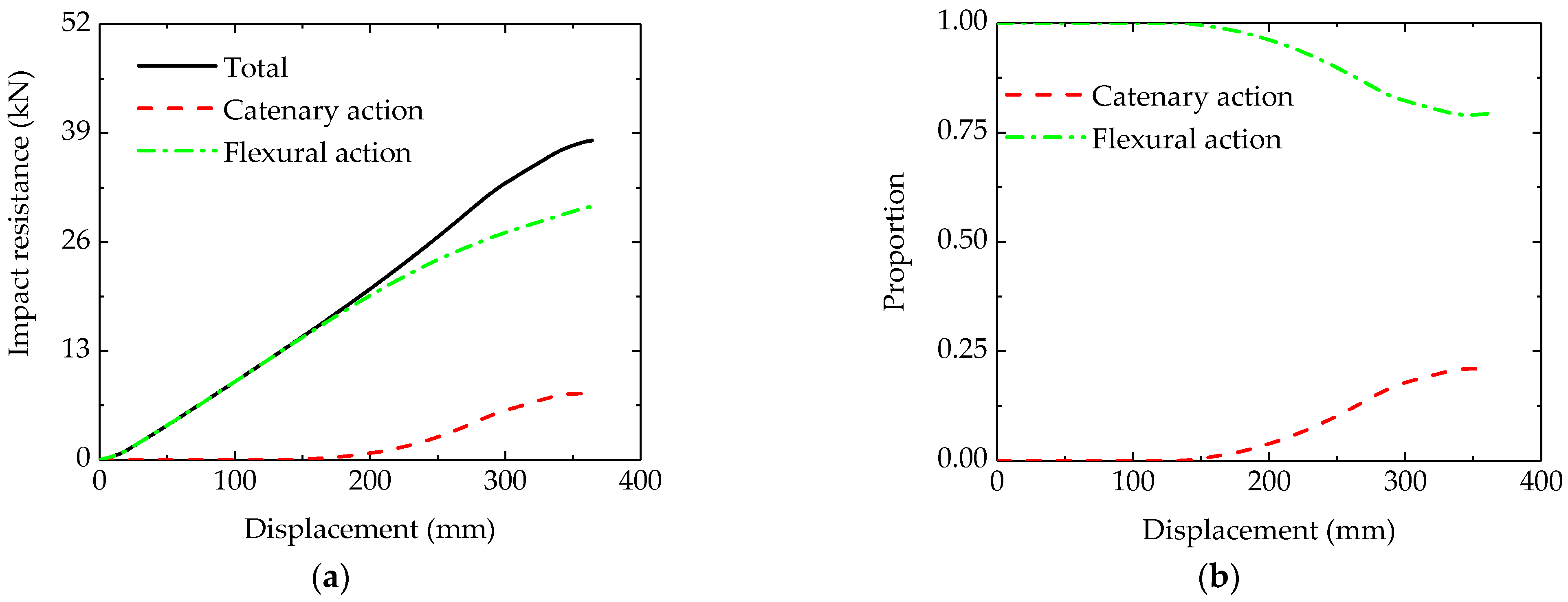
5.2.1. Mid-Span Impact Scenario

Under the mid-span impact scenario, according to the load-resisting mechanism shown in Figure 11a, the load-carrying capacity R can be expressed as follows:

$$R=\underset{\begin{array}{cc}\mathrm{Catenary}& \mathrm{action}\end{array}}{\underbrace{2N\sin \theta }}+\underset{\begin{array}{cc}\mathrm{Flexural}& \mathrm{action}\end{array}}{\underbrace{2{\displaystyle \frac{\left(M_{mid}-M_{con}\right)}{0.5L+\Delta L}}\cos \theta }}$$

(3)

where θ is the rotation of the connection and can be calculated as follows:

$$\theta =\arctan {\displaystyle \frac{u}{0.5L}}$$

(4)

where u is the displacement at the impact location.

Parameter ΔL is the axial elongation and can be calculated as follows:

$$\Delta L=\sqrt{u^2+{(0.5L)}^2}-0.5L$$

(5)

Based on Equations (4) and (5), the impact resistance–displacement curves in Figure 10a can be converted into impact resistance–rotation curves, as shown in Figure 12a, and impact resistance–elongation curves, as shown in Figure 12b. It can be seen in Figure 12a that the impact resistance–rotation curves of steel-framed subassemblies with different SDRs are nearly coincident, indicating that the impact resistance of the subassemblies is the same when the beam–column connections undergo the same rotational deformation. The SDR mainly affects the maximum rotation angle that the subassemblies can reach before failure. Although the maximum displacement of the steel-framed subassemblies increases with an increase in the SDR, the maximum rotation angle of the beam–column connections decreases with an increase in the SDR. For example, the maximum displacement of SDR-M-8 is 290.1 mm, which is only 49.4% of the maximum displacement of 587.0 mm of SDR-M-32. However, the maximum beam–column connection rotation of SDR-M-8 reaches 0.337 rad, which is 1.91 times that of SDR-M-32 (0.176 rad). It can be seen from Figure 12b that the maximum elongation of different SDR cases is basically the same, indicating that the axial elongation is the controlling factor for the failure of the specimens under the mid-span impact scenario. The failure mode reported in Reference [34] also clearly shows the tensile failure pattern of beam–column connections. According to Equations (4) and (5), the relationship between the beam–column connection rotation and the axial elongation can be expressed as Equation (6), which shows that when the axial elongation is a constant value, the beam–column connection rotation is inversely proportional to the span. Since the steel beam cross-sections are identical across all the SDR cases in this study, and the SDRs are adjusted by modifying the span, it can be concluded that the maximum beam–column connection rotation is inversely related to the SDR.

$$\theta =\arctan {\displaystyle \frac{\sqrt{{\left(\Delta L+0.5L\right)}^2-{\left(0.5L\right)}^2}}{0.5L}}={\displaystyle \frac{\Delta L}{0.5L}}+\sqrt{{\displaystyle \frac{2\Delta L}{0.5L}}}$$

(6)

In summary, although steel-framed subassemblies with different SDRs exhibit varying failure rotations, their axial elongations at the ultimate failure of the structures are nearly identical. This phenomenon indicates that the ultimate failure mode of steel-framed subassemblies is consistent, with the core cause attributable to the tensile failure of beam–column connections, i.e., when the axial deformation reaches a critical value, the beam–column connections fail due to the excessive tensile force, which becomes the dominant factor controlling structural failure. Since the impact resistance–rotation curves of steel-framed subassemblies with different SDRs basically coincide, a smaller SDR leads to a larger rotation angle of the structure, and a larger rotation angle means more energy is absorbed through rotational deformation, thereby yielding better impact resistance.

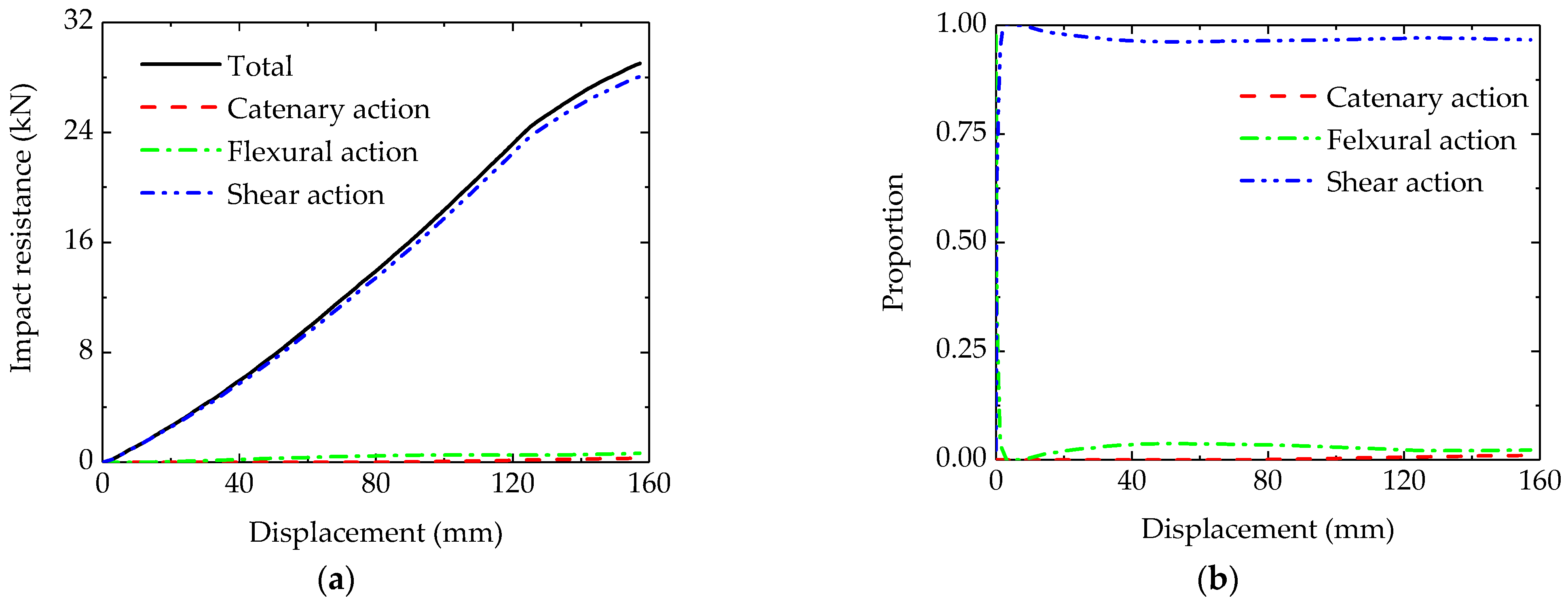
5.2.2. Beam-End Impact Scenario

Figure 11b depicts the impact load-resisting mechanism in the case of beam-end impact scenarios. Regarding the left part of the specimens, the impact load-resisting mechanism during beam-end impact is identical to that during mid-span impact. Here, the load-carrying capacity results from both catenary action and flexural action.

Conversely, the right part of the specimens shows a shear-dominated deformation pattern. Since the lever arm L₂ is nearly zero, the load-carrying capacity provided by the right part, R_V,R, is mainly related to the shearing force. The total load-carrying capacity R in the beam-end impact scenario is represented by Equation (6):

$$R=\underset{\begin{array}{ccccccc}\mathrm{Load}& \mathrm{carrying}& \mathrm{capacity}& \mathrm{provided}& \mathrm{by}& \mathrm{left}& \mathrm{part}\end{array}}{\underbrace{\underset{\begin{array}{cc}\mathrm{Catenary}& \mathrm{action}\end{array}}{\underbrace{N\sin \theta }}+\underset{\begin{array}{cc}\mathrm{Flexural}& \mathrm{action}\end{array}}{\underbrace{{\displaystyle \frac{\left(M_{mid}-M_{con}\right)}{L_1+\Delta L}}\cos \theta }}}}+\underset{\begin{array}{ccccccc}\mathrm{Load}& \mathrm{carrying}& \mathrm{capacity}& \mathrm{provided}& \mathrm{by}& \mathrm{right}& \mathrm{part}\end{array}}{\underbrace{R_{V,R}}}$$

(7)

Based on Equation (7), the impact load-resisting mechanism of the specimens on the left side of the impact location is in line with that of the mid-span impact scenario. Figure 13a presents the impact resistance–displacement curves of the specimens on the left side of the impact location under the beam-end impact scenario. The tendency for the impact resistance provided by the left-hand part to decline as the SDR increases is similar to that in the mid-span impact scenario. When compared with the specimens having the same SDR in the mid-span impact scenario, the impact resistance provided by the specimens on the left side of the impact location under the beam-end impact scenario is substantially decreased. In the beam-end impact scenario, the span length L₁ of the specimens on the left side of the impact location is nearly equal to the full span length, and the maximum displacement also drops significantly. This leads to a marked reduction in the impact resistance provided by the left-hand part, as shown in

Table 4. Comparison of peak impact resistance of the specimens to the left of the impact location under various impact scenarios (unit: kN).

Impact Scenario	SDR
	8	10	12	16	20	24	28	32
Mid-span impact	22.22	20.64 *	19.06	16.56	14.72	13.51	12.60	11.87
Beam-end impact	4.87	3.57	2.79	1.91	1.54 *	1.16	0.99 *	0.82

* The peak impact resistances of SDR-10-M, SDR-20-B, and SDR-28-B are obtained by function fitting for auxiliary comparison use only.

.

Figure 13b shows the impact resistance–displacement curves provided by the specimens to the right of the impact location under the beam-end impact scenario. The lever arm L₂ of the specimens to the right of the impact location is nearly zero. The load-carrying capacity is provided by the shear force rather than flexural action or catenary action. All the specimens with different SDRs ultimately fail due to the shear failure of the right-side beam–column connections, and their maximum displacements are basically the same. Thus, the impact resistance–displacement curves of specimens with different SDRs exhibit a high degree of consistency.

5.3. Effect of Catenary Action on Impact Resistance

In the design of structures that can resist progressive collapse following the column-removal scenario, catenary action is a vital mechanism for boosting a structure’s resistance to progressive collapse. For steel-framed subassemblies affected by falling debris impact, Equations (5) and (7) suggest that catenary action is part of the resistance mechanism of steel-framed subassemblies, regardless of whether it is under a mid-span impact or beam-end impact. Taking the cases with an SDR of 12 as an example, Figure 14 contrasts the total impact resistance of the steel-framed subassemblies with the impact resistance provided by different load-resisting mechanisms, namely catenary action and flexural action, under various impact scenarios.

As shown in Figure 14, under the mid-span impact scenario, when the displacement is less than 136 mm, the impact resistance of the steel-framed subassembly is entirely provided by the flexural action; when the displacement exceeds 136 mm, catenary action begins to act alongside flexural action in resisting the impact load. When the steel-framed subassembly fails, the peak impact resistance with and without considering the catenary action is 38.11 kN and 30.25 kN, respectively. The presence of catenary action increases the peak impact resistance by 26.0%.

As depicted in Figure 15, under the beam-end impact scenario, the impact resistance of the steel-framed subassembly is jointly provided by the flexural action and catenary action on the specimens to the left of the impact location, and by the shear action on the specimens to the right of the impact location. When the steel-framed subassembly starts to deform, the impact resistance is provided by the flexural action on the specimens to the left of the impact location, and by the shear action on the specimens to the right of the impact location. After the displacement reaches 16 mm, catenary action begins to take effect. From the initiation of deformation to final failure of the steel-framed subassembly, the impact resistance is always dominated by the shear action, with the flexural action playing a supplementary role. The peak impact resistance provided by the shear action, flexural action, and catenary action is 28.05 kN, 0.66 kN, and 0.30 kN, respectively. The catenary action makes virtually no contribution to the improvement of impact resistance.

To further clarify the contribution of catenary action to the impact resistance of specimens with different SDRs,

Table 5. Comparison of catenary action on peak impact resistance under various impact scenarios.

Impact Scenario	SDR	Peak Impact Resistance Considering Catenary Action (kN)	Peak Impact Resistance Without Catenary Action (kN)	Peak Impact Resistance Increase Caused by Catenary Action
Mid-span impact	8	44.44	37.26	19.3%
	12	38.11	30.25	26.0%
	16	33.12	24.72	34.0%
	20	29.43	20.67	42.4%
	24	27.02	17.87	51.2%
	28	25.19	15.97	57.7%
	32	23.74	14.24	66.7%
Beam-end impact	8	30.59	30.28	1.02%
	10	29.69	29.37	1.09%
	12	29.01	28.71	1.04%
	16	28.08	27.83	0.90%
	24	28.03	27.81	0.79%
	32	27.86	27.69	0.61%

lists the peak impact resistance considering the catenary action, the peak impact resistance excluding it, and the enhancement effect of the catenary action on the impact resistance of the steel-framed subassemblies for all the parametric analysis cases.

Under the mid-span impact scenario, as the SDR increases, the rotation angle of the steel-framed subassembly at failure decreases, while the axial elongation remains essentially unchanged. Consequently, the flexural action diminishes whereas the catenary action remains roughly constant, leading to an increase in the proportion of catenary action to the total impact resistance with a rising SDR. For the specimens with different SDRs, the enhancement effect of the catenary action on the impact resistance ranges from 19.3% to 66.7%, indicating that the catenary action significantly improves the impact resistance of the steel-framed subassembly under the mid-span impact scenario.

Under the beam-end impact scenario, the failure displacements of steel-framed subassemblies with different SDRs are basically consistent. The axial elongation of the specimen to the left of the impact location decreases with an increase in the SDR, resulting in a corresponding weakening of the catenary action. Due to the small failure displacement of the steel-framed subassembly, the specimens to the left of impact location cannot form an effective catenary mechanism. The enhancement effect of the catenary action on the impact resistance of specimens with different SDRs ranges from 0.61% to 1.09%. Therefore, it can be considered that the catenary action has almost no influence on the impact resistance.

6. Conclusions

This research systematically evaluates the impact resistance of steel-framed subassemblies with extended reverse channel connections under falling debris impact through experimental tests and numerical parametric analyses, leading to the following conclusions:

(1)

Impact Location Effects: Although the beam-end impact scenarios exhibit higher peak load-carrying capacities, the mid-span impact scenarios result in superior impact resistance when the falling height exceeds 1.0 m. This is attributed to the greater plastic deformation and energy absorption capacity of specimens under mid-span impacts, whereas beam-end impacts are constrained by joint stiffness, limiting the deformation.

(2)

Falling Height Effects: The impact resistance decreases with an increasing falling height, with the reduction ratio exceeding the theoretical 50% due to the additional gravitational potential energy conversion during post-impact deformation. For falling heights ≤ 0.5 m, beam-end impacts show better resistance, while mid-span impacts are advantageous for heights ≥ 1.0 m.

(3)

SDR Effects: Under a mid-span impact, smaller SDRs (stiffer beams) lead to steeper impact resistance–displacement curves and a higher peak resistance, while larger SDRs require greater displacements for energy absorption. Under a beam-end impact, the SDR has a weaker influence, with the curves overlapping initially and smaller SDRs showing slightly higher peak resistances.

(4)

Load-Resisting Mechanisms: Flexural action dominates the initial deformation, with catenary action contributing significantly under mid-span impacts (especially for large displacements). Shear action is the primary resistance under beam-end impacts, overshadowing the flexural and catenary effects.

(5)

Design suggestions: In progressive collapse-resistant design, the structural parameters should be considered differentially according to the potential impact locations. For areas prone to mid-span impacts, the SDR of steel beams should be reasonably controlled, with priority given to smaller SDRs to enhance the initial stiffness. Meanwhile, the contribution of catenary action in the large deformation stage can be utilized to improve the impact resistance. For the parts with a higher risk of beam-end impact, emphasis should be placed on strengthening the shear performance of beam–column connections, and the dominance of shear action on the impact resistance dominated should be ensured through optimizing the connection configurations. In addition, the structural scheme needs to be adjusted in combination with the expected falling height of debris. For low-height impact scenarios, focus should be placed on connection stiffness to reduce the additional energy input caused by deformation; for high-height impact scenarios, the potential of deformation-based energy absorption should be fully exerted by improving the structural ductility. Ultimately, the anti-collapse performance of steel-framed structures under different impact conditions can be optimized.

It should be noted that since representative subassemblies rather than full-scale structures were used for testing and simulation, the scale effect may have affected the dynamic response. In addition, the loading was simplified to a vertical impact at a specific location, ignoring the oblique impact or combined loading in actual collapses. Future work can quantify the scale effect by conducting full-scale tests and studying multi-directional and combined loading scenarios to strengthen the practical applications for anti-collapse design.