Blast-Resistant Performance Evaluation of Steel Box Girder of Suspension Bridge
Abstract
1. Introduction
2. FE Models and Validation
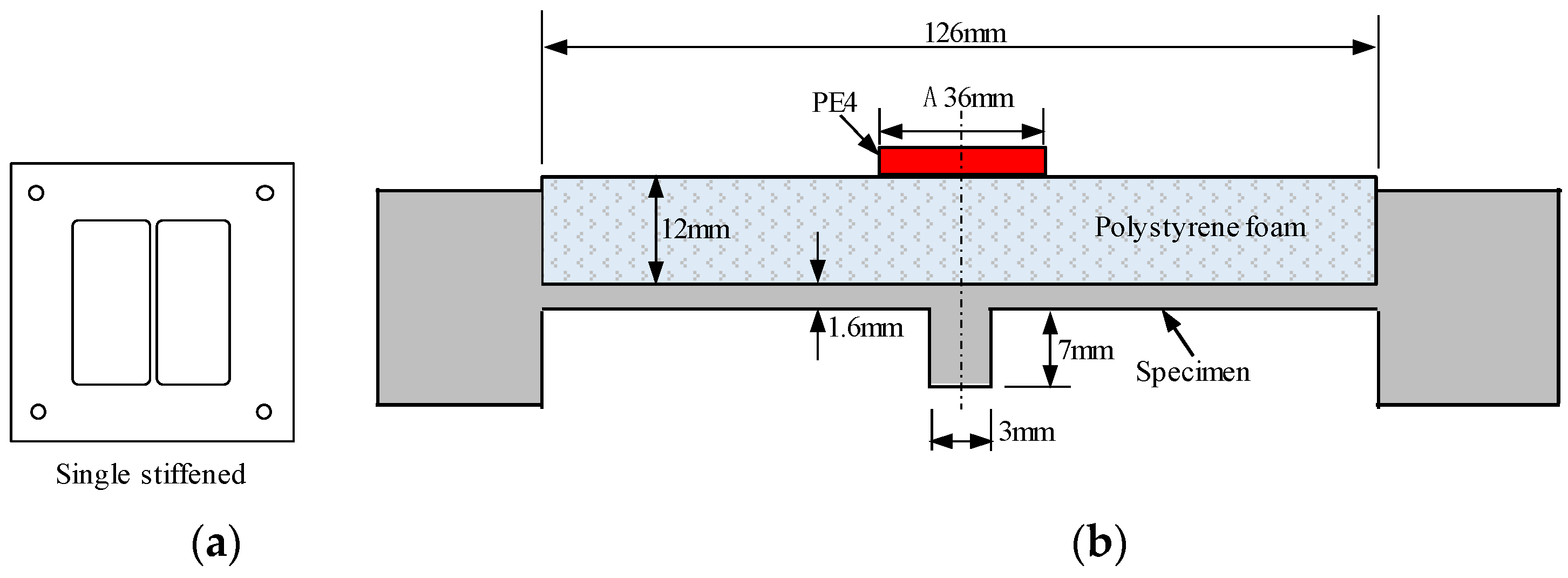
2.1. Test Introduction
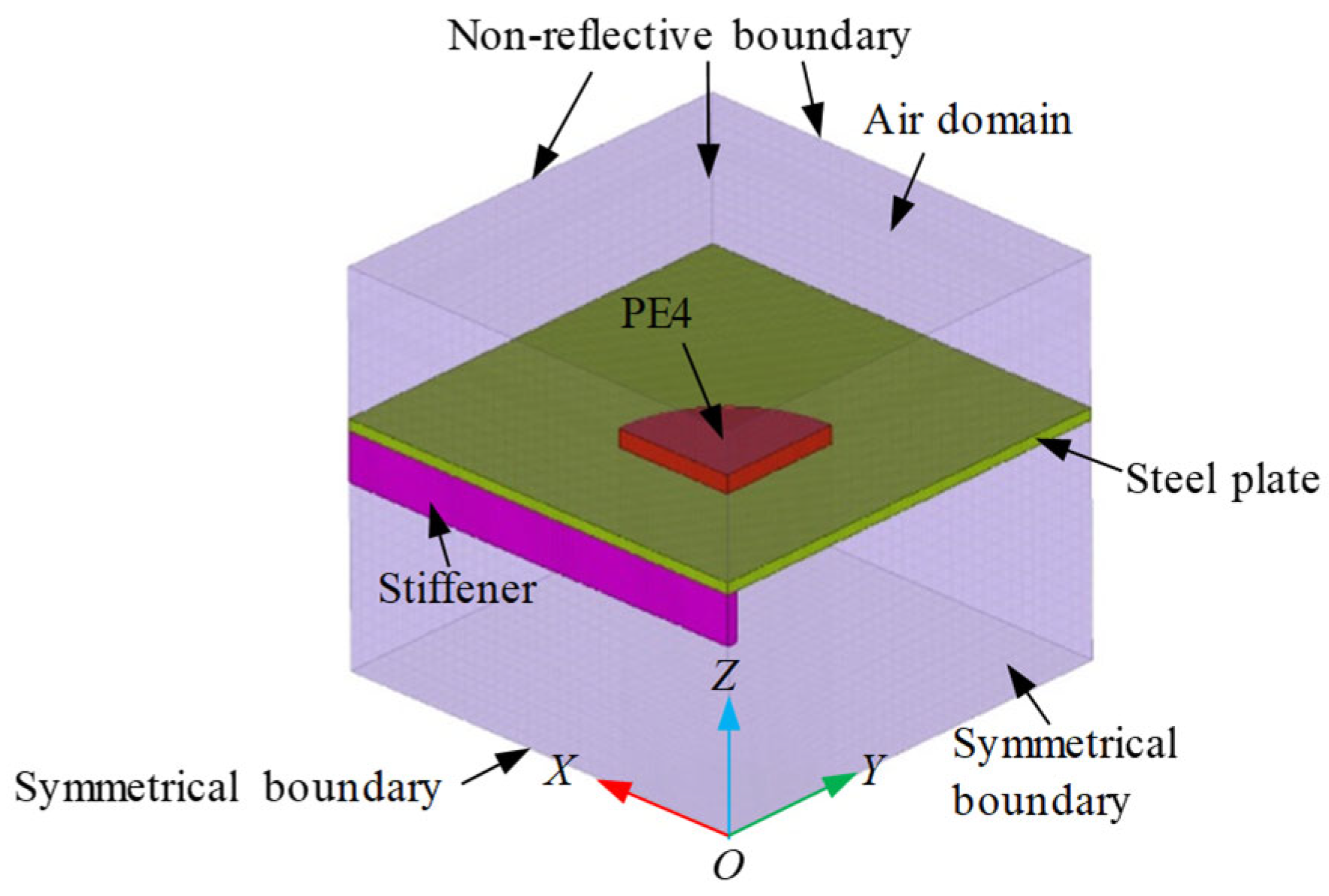
2.2. FE Models
2.2.1. Material Models
2.2.2. Blast Load Application
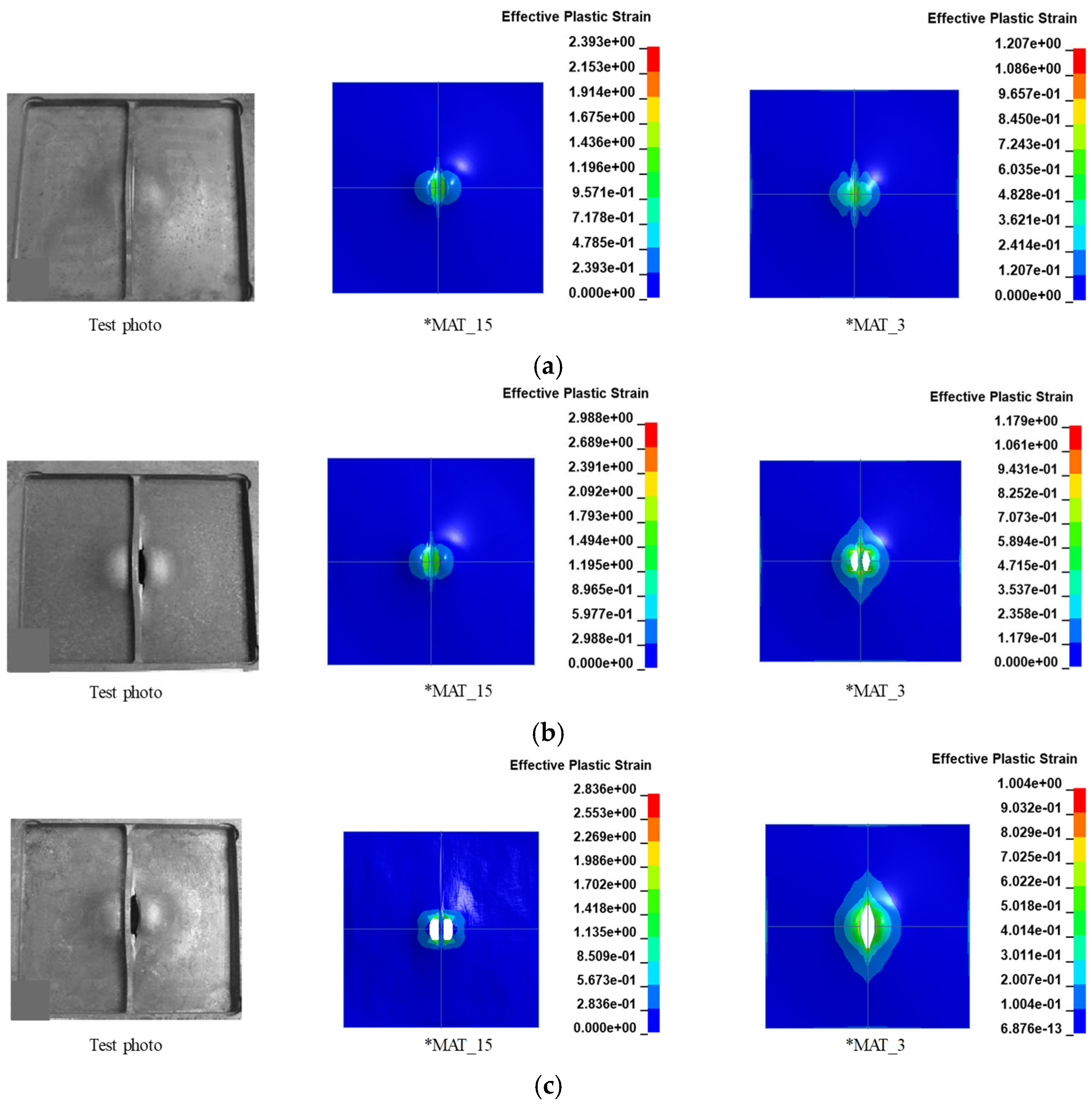
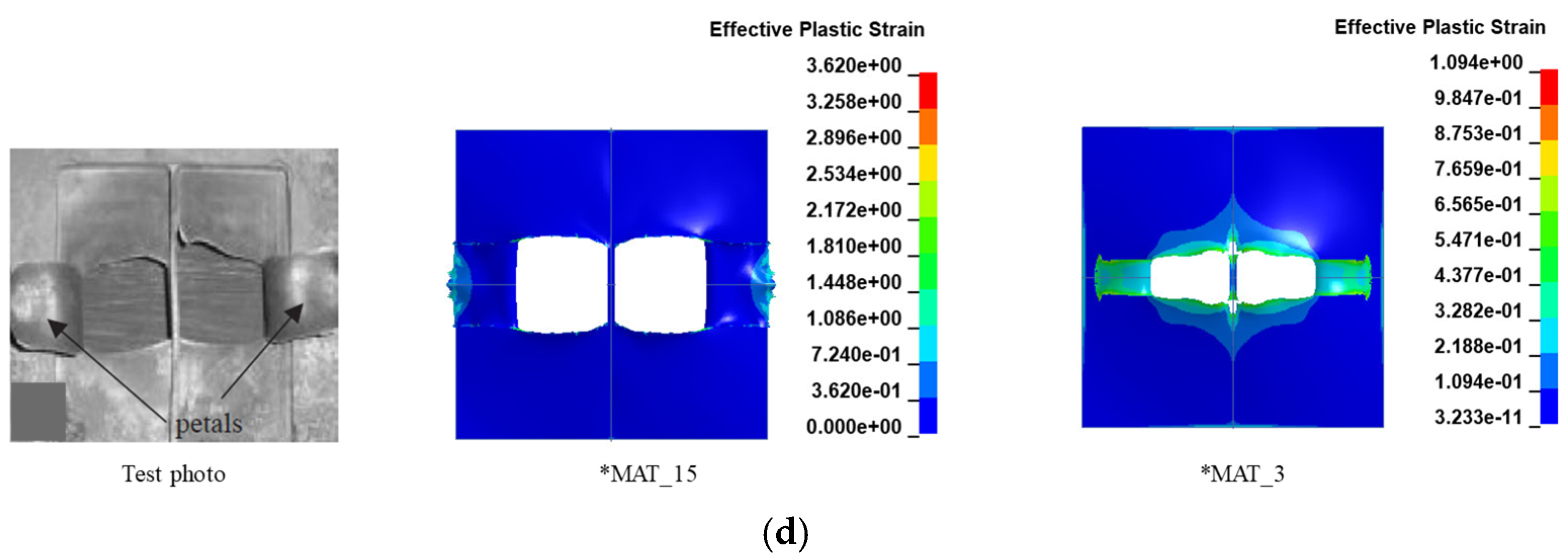
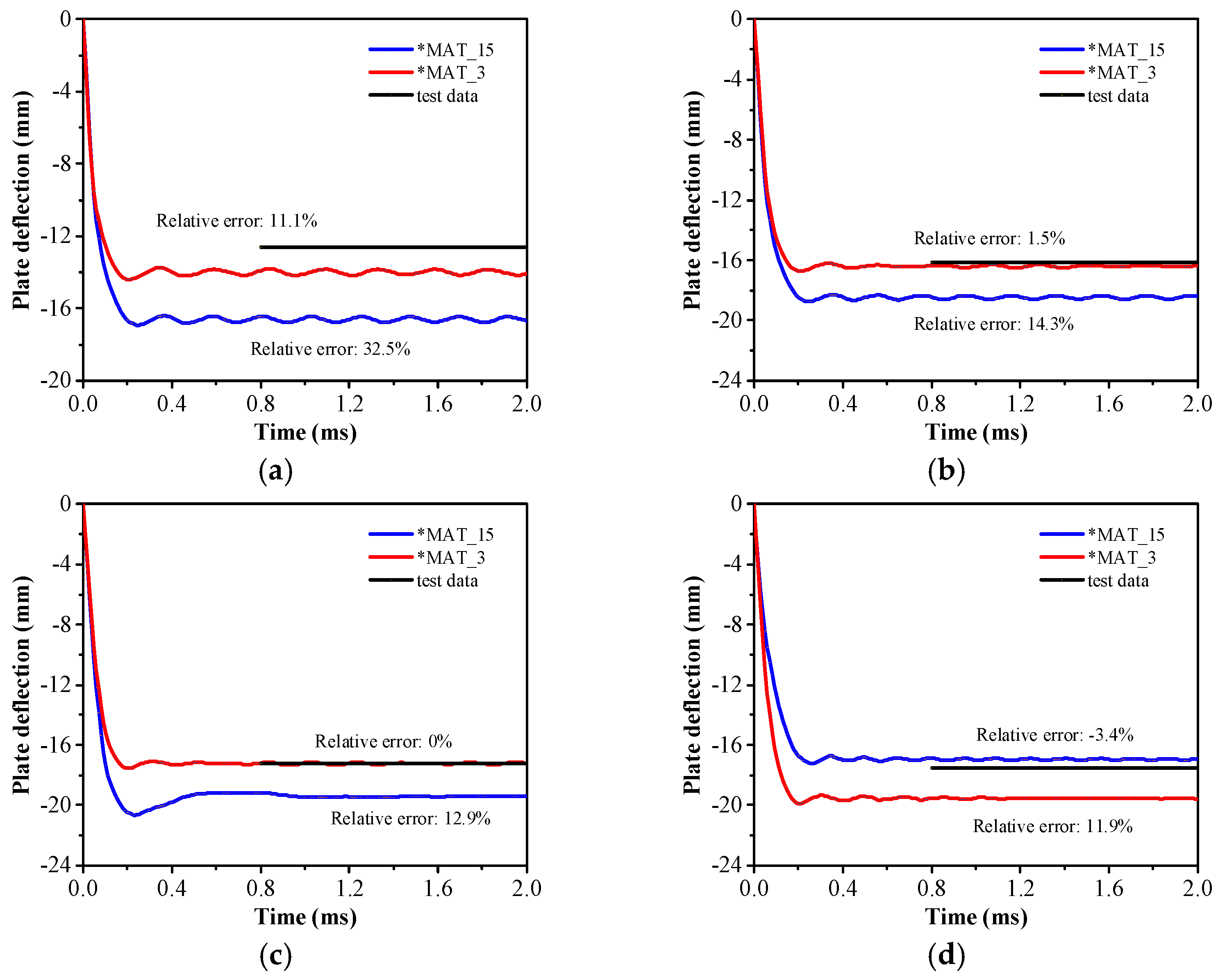
2.3. Comparisons
3. Dynamic Behavior of Orthotropic Steel Bridge Deck Under Above-Deck Explosions
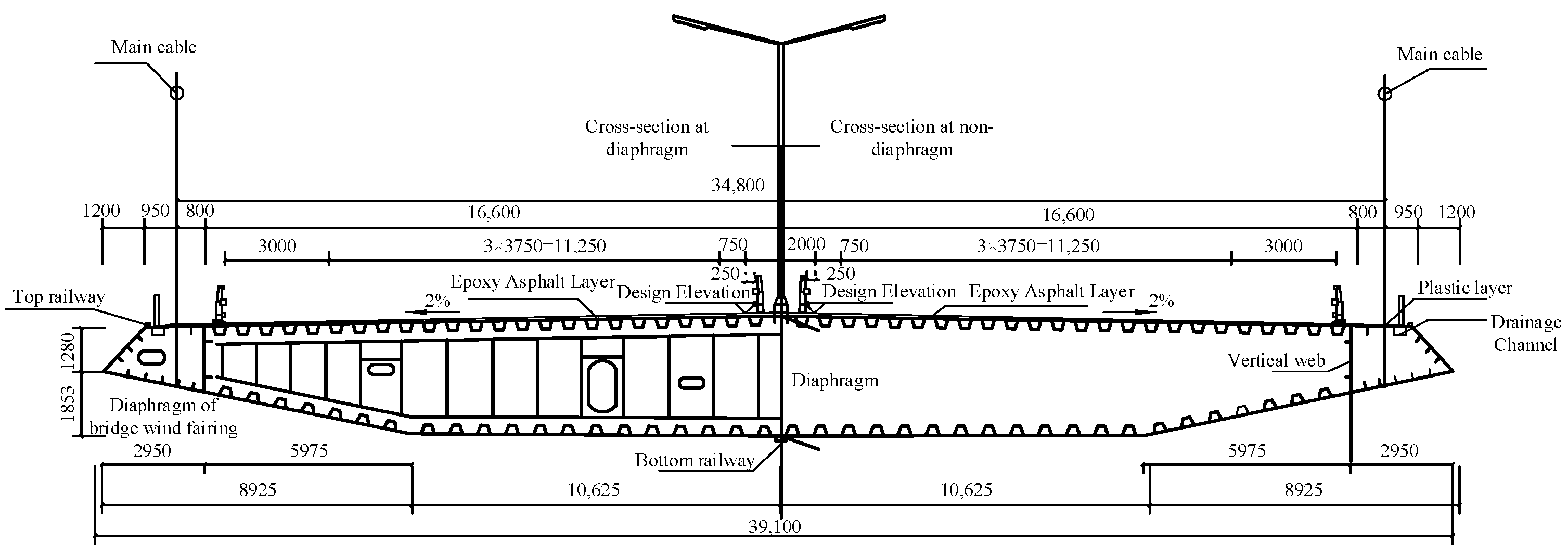
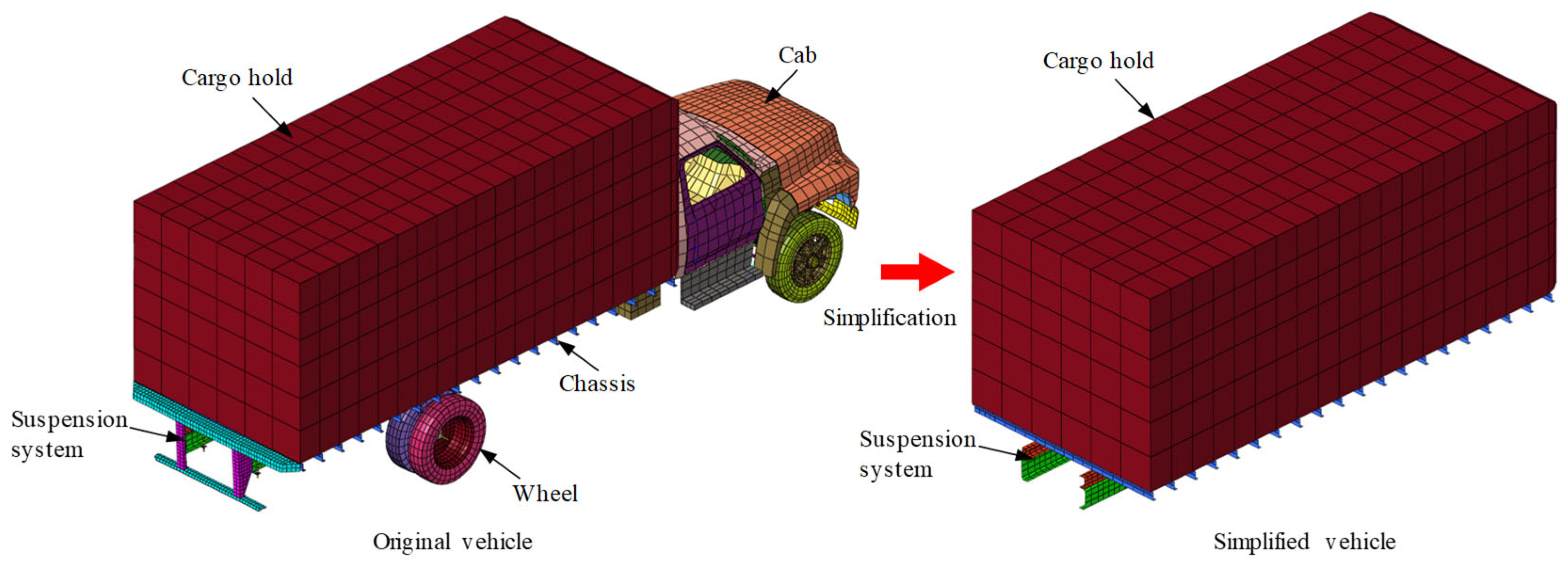
3.1. FE Model of Prototype Bridge Deck
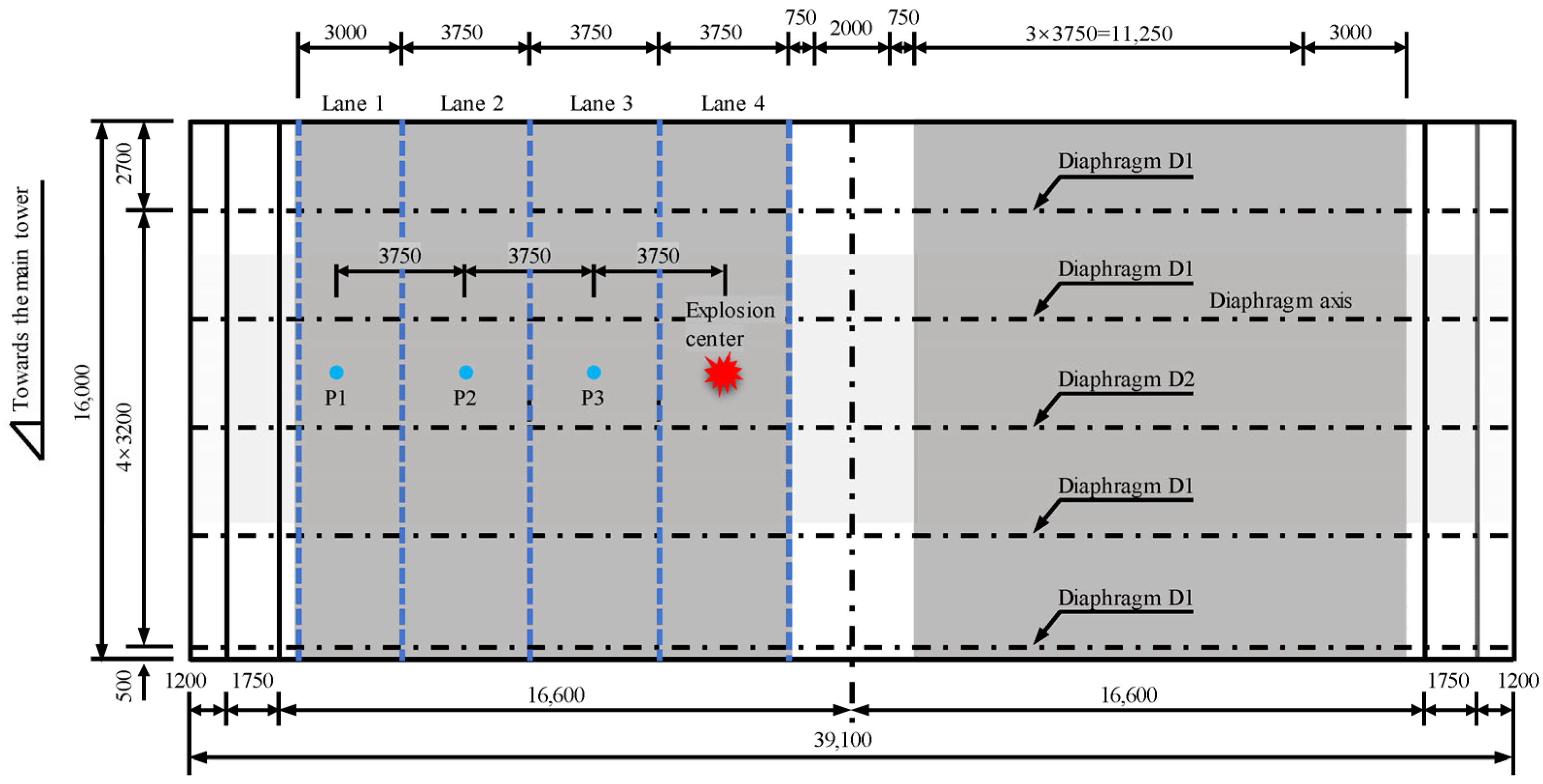
3.2. Explosion Scenarios
3.3. Results and Discussions
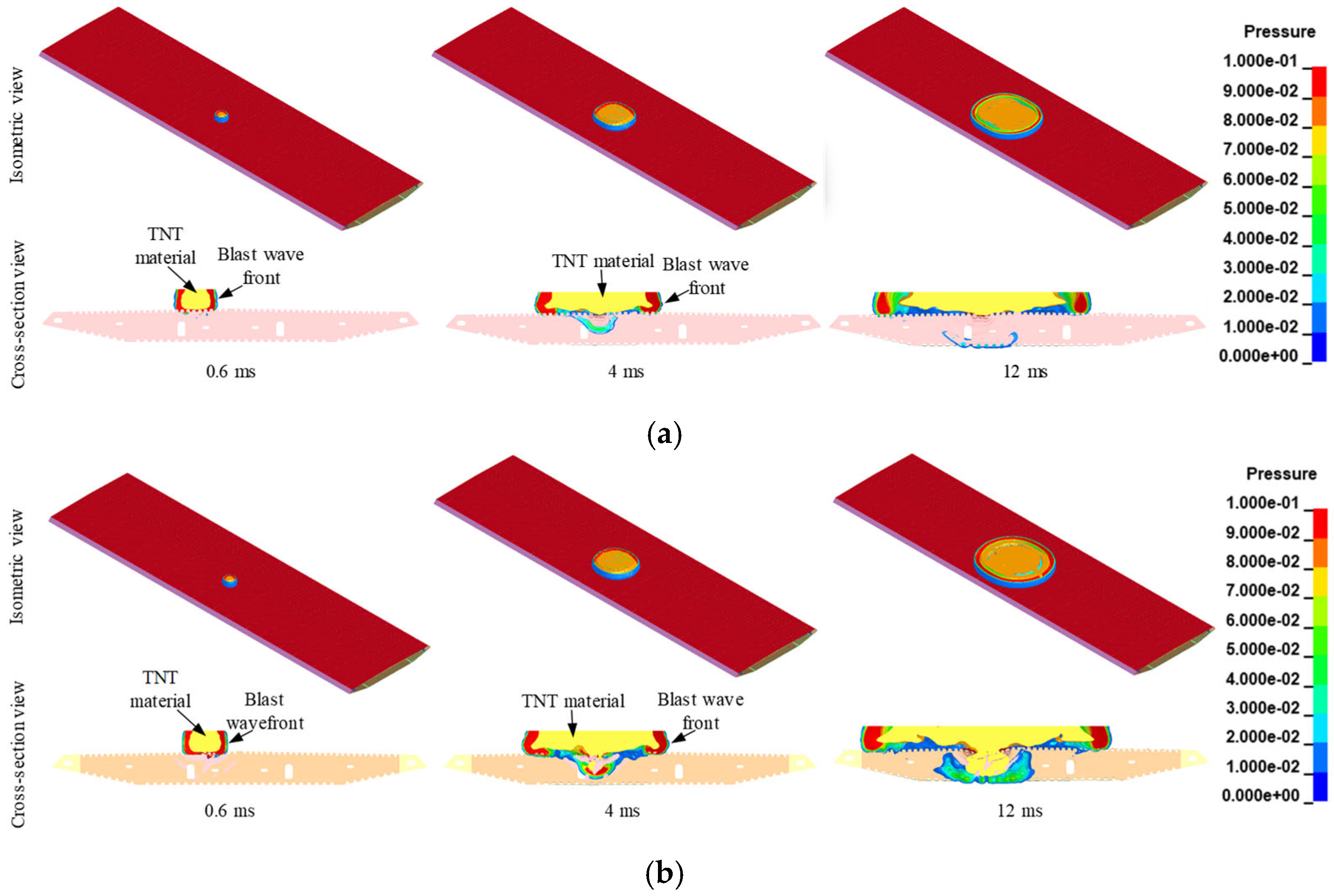
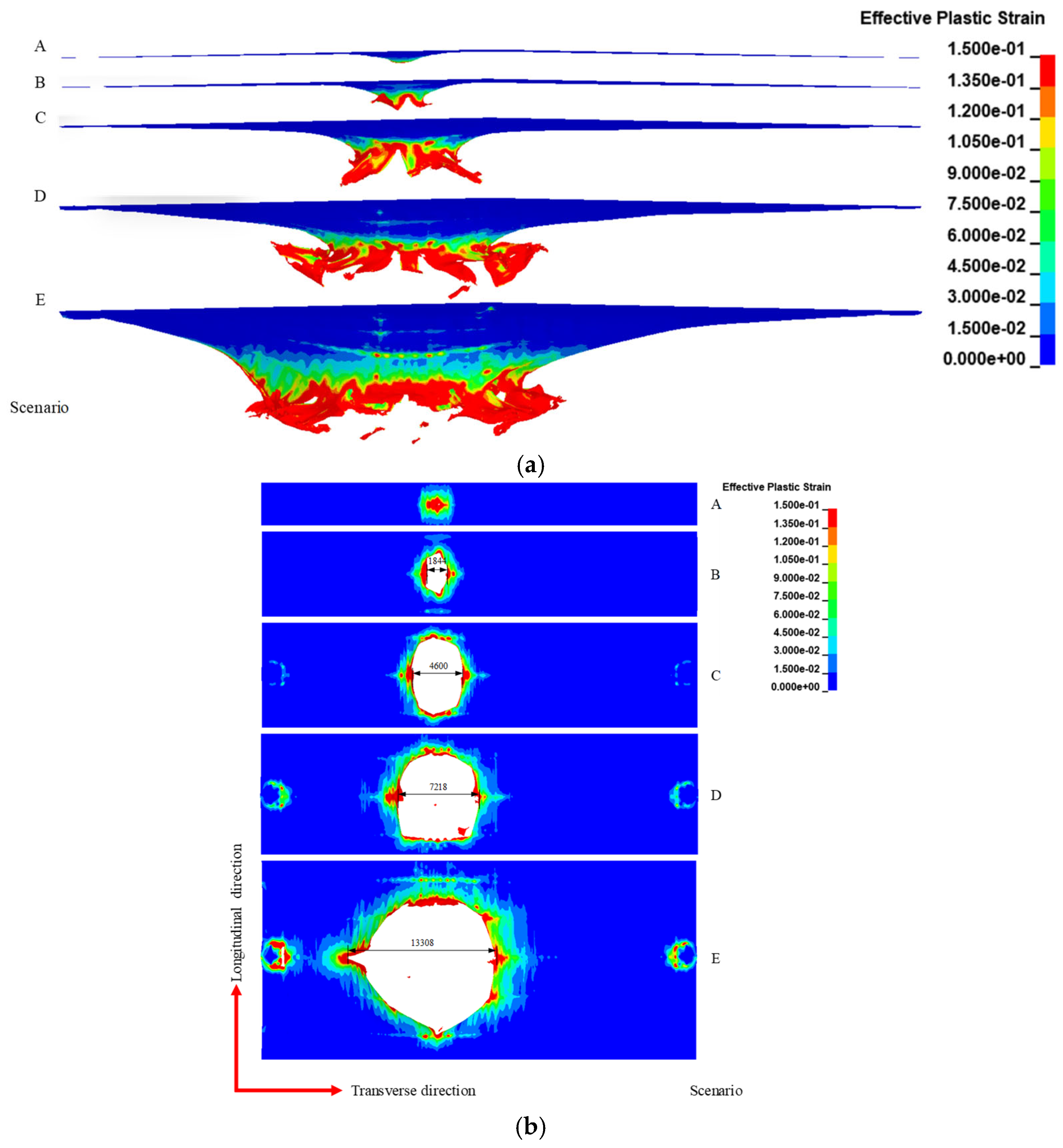
3.3.1. Blast Wave Propagation
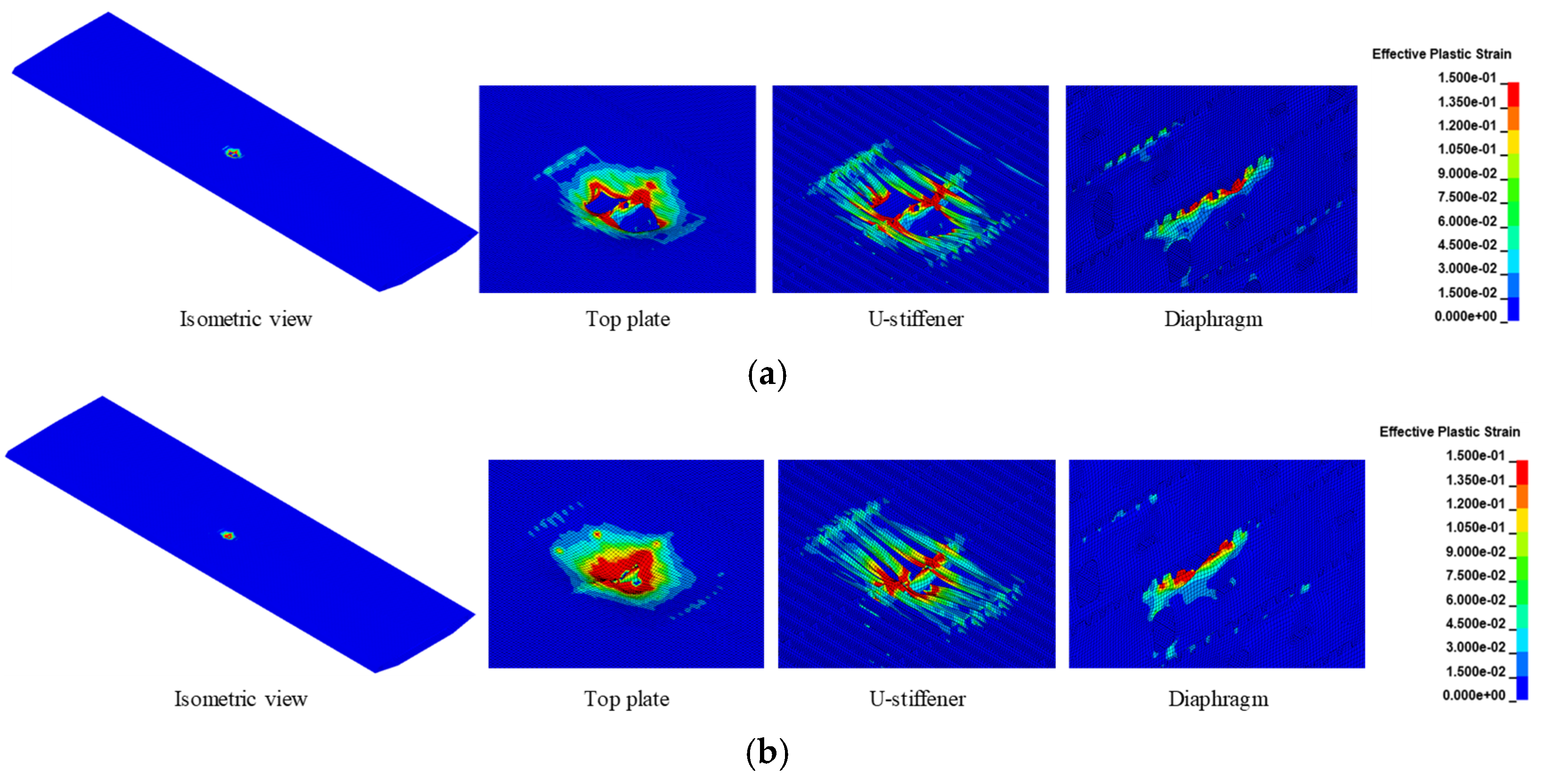
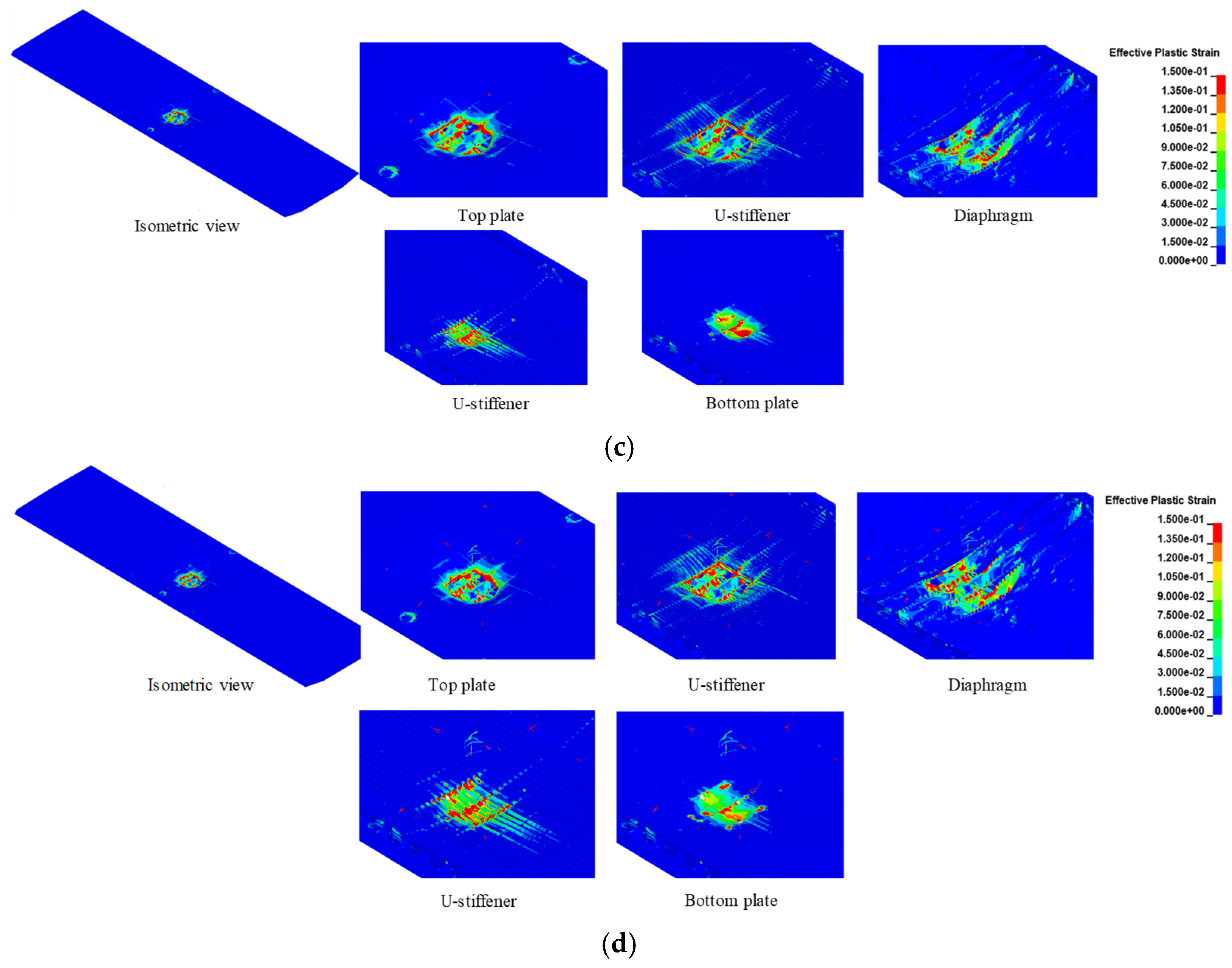
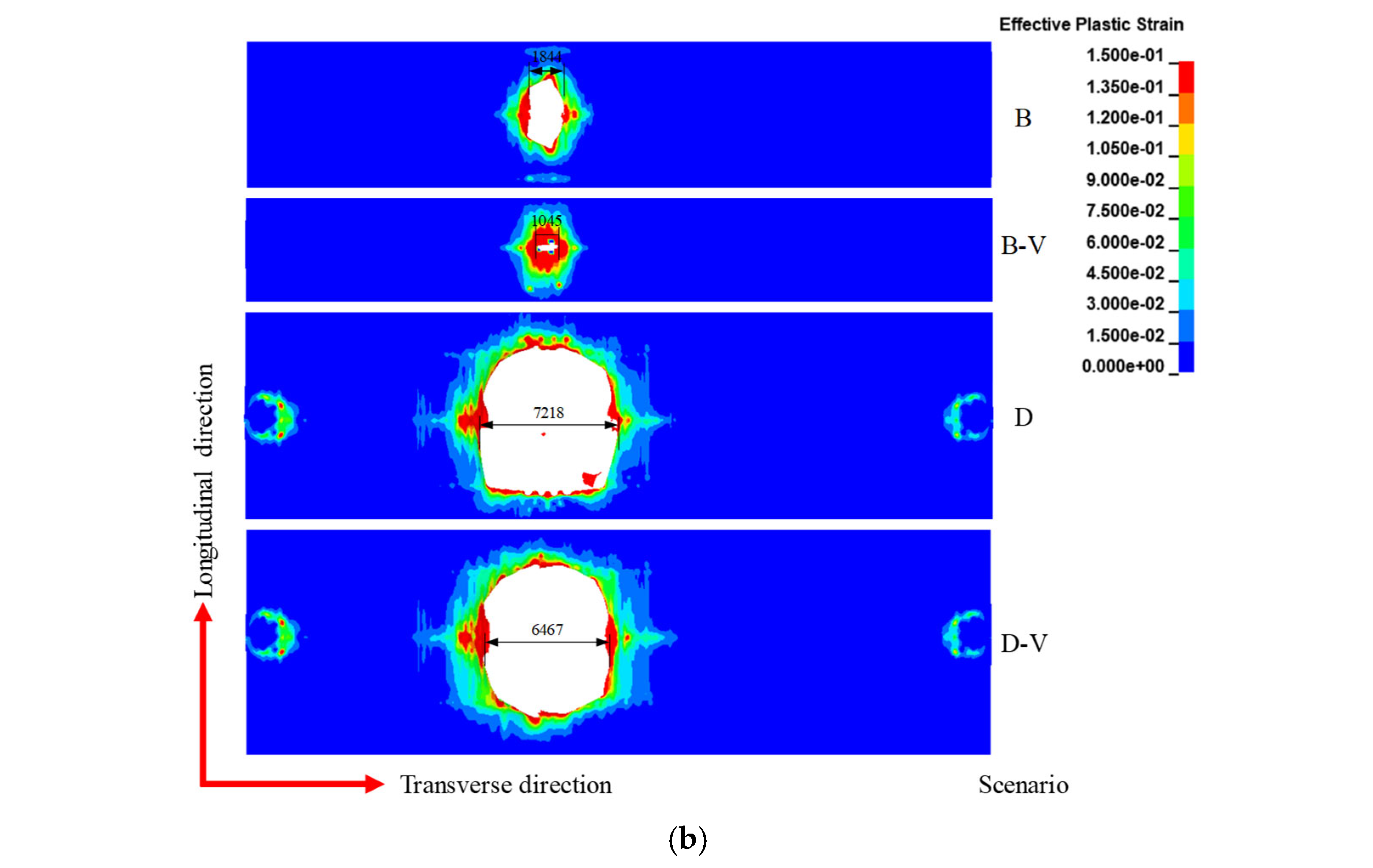
3.3.2. Failure Mode
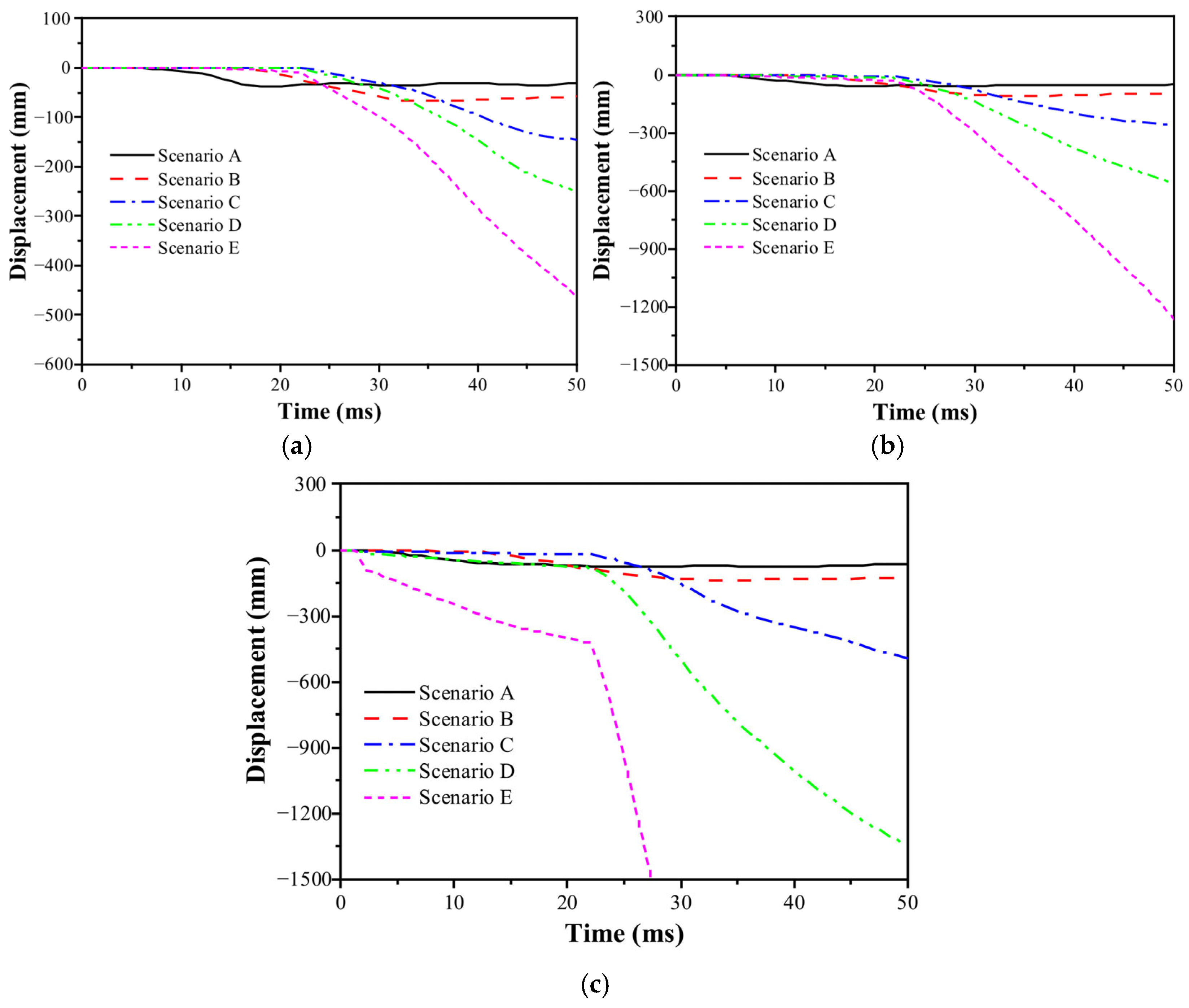
3.3.3. Dynamic Response
3.4. Further Discussion
4. Conclusions
- (1)
- The steel box girder deck primarily exhibits localized damage under blast load. The extent of localized damage correlates with whether the blast wave penetrates the girder interior through openings in the top plate. Specifically, blast waves entering the girder interior cause more severe damage. Typical failure modes of the bridge deck were summarized, including the petal-shaped opening of the top plate, fracture, tearing or rupture of U-stiffeners, plastic deformation, out-of-plane bending, local buckling, and fracture of the diaphragms, and bulging deformation or openings of the bottom plate.
- (2)
- For explosion scenarios with smaller TNT masses, the top plate and U-stiffeners dominate energy dissipation, collectively accounting for over 70% of the total energy absorption by plastic deformation or damage, which aligns with conventional mechanisms observed in prior studies. For explosion scenarios with larger TNT masses, explosion energy is dissipated by plastic deformation and failure of multiple components-the top plate, top U-stiffeners, diaphragms, bottom plate, and bottom U-stiffeners, collectively contributing over 90% of total energy absorption. This shift arises because blast waves in these scenarios directly act on the bottom plate, inducing perforation failure.
- (3)
- For vehicular bomb explosion scenarios with charge mass of 454 kg, the vehicle shell can effectively reduce the damage range of the top plate by about 43.2%, and the displacement response by about 26%. Nevertheless, there is minor mitigation effect of the vehicle shell for explosion scenarios with TNT mass larger than 4536 kg.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Zhang, X.; Liu, R.; Chen, G. Design and mechanical properties of steel-UHPC lightweight composite decks. Adv. Civ. Eng. 2021, 2021, 8508795. [Google Scholar] [CrossRef]
- Worku, Z.; Liu, M.; Wang, X.; Sheng, G. Flexural behavior of orthotropic steel–LUHPC composite bridge decks: Experimental and numerical study. Materials 2025, 18, 2106. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.L.; Wu, H.; Fang, Q.; Xu, J.P. Displacement-based blast-resistant evaluation for simply-supported RC girder bridge under below-deck explosions. Eng. Struct. 2022, 266, 114637. [Google Scholar] [CrossRef]
- Ma, L.L.; Wu, H.; Fang, Q. Damage mode and dynamic response of RC girder bridge under explosions. Eng. Struct. 2021, 243, 112676. [Google Scholar] [CrossRef]
- Remennikov, A.; Ngo, T.; Mohotti, D.; Uy, B.; Netherton, M. Experimental investigation and simplified modeling of response of steel plates subjected to close-in blast loading from spherical liquid explosive charges. Int. J. Impact Eng. 2017, 101, 78–89. [Google Scholar] [CrossRef]
- Remennikov, A.; Mentus, I.; Uy, B. Explosive breaching of walls with contact charges: Theory and applications. Int. J. Prot. Struct. 2005, 6, 629–647. [Google Scholar] [CrossRef]
- Henchie, T.F.; Yuen, S.; Nurick, G.N.; Ranwaha, N.; Balden, V.H. The response of circular plates to repeated uniform blast loads: An experimental and numerical study. Int. J. Impact Eng. 2014, 74, 36–45. [Google Scholar] [CrossRef]
- Yang, M.; Wu, H.B.; Wu, Y.; Xu, K.; Xie, P.; Li, M.Z.; He, Y.H. Experimental study on influence of explosion source explosion on steel plate under different contact conditions. J. Saf. Environ. 2022, 22, 1878–1884. (In Chinese) [Google Scholar]
- Han, L.; Yuan, J.F.; Zhang, Y.L.; Xu, Q.P.; Li, Z.R. Damage Characteristics of Fixed Rectangular Steel Plate under Close-in Explosion. Chin. J. Explos. Propellants 2021, 44, 225–232. (In Chinese) [Google Scholar]
- Yuen, S.C.K.; Nurick, G.N. Experimental and numerical studies on the response of quadrangular stiffened plates. Part I: Subjected to uniform blast load. Int. J. Impact Eng. 2005, 31, 55–83. [Google Scholar] [CrossRef]
- Langdon, G.S.; Yuen, S.C.K.; Nurick, G.N. Experimental and numerical studies on the response of quadrangular stiffened plates. Part II: Localised blast loading. Int. J. Impact Eng. 2005, 31, 85–111. [Google Scholar] [CrossRef]
- Yuen, S.; Nurick, G.N.; Langdon, G.S.; Iyer, Y. Deformation of thin plates subjected to impulsive load: Part III—An update 25 years on. Int. J. Impact Eng. 2017, 107, 108–117. [Google Scholar] [CrossRef]
- Yuen, S.C.K.; Langdon, G.S.; Nurick, G.N.; Pickering, E.G.; Balden, V.H. Response of V-shape plates to localised blast load: Experiments and numerical simulation. Int. J. Impact Eng. 2012, 46, 97–109. [Google Scholar] [CrossRef]
- Gan, L.; Zong, Z.; Lin, J.; Wu, T.; Chen, Z.; Chen, L. Damage mechanism of U shaped ribs stiffened steel flat plates subjected to close in explosion. Thin-Walled Struct. 2022, 179, 109656. [Google Scholar] [CrossRef]
- Gan, L.; Zong, Z.; Lin, J.; Chen, Y.; Xia, M.; Chen, L. Influence of U-shaped stiffeners on the blast-resistance performance of steel plates. J. Constr. Steel Res. 2022, 188, 107046. [Google Scholar] [CrossRef]
- Goe, M.D.; Matsagar, V.A.; Gupta, A.K. Dynamic Response of Stiffened Plates under Air Blast. Int. J. Prot. Struct. 2011, 2, 139–156. [Google Scholar] [CrossRef]
- Razak, N.S.A.; Alias, A.; Mohsan, N.M.; Masjuki, S.A. Numerical investigation of the failure of stiffened steel plates subjected to near-field blast loads. J. Fail. Anal. Prev. 2023, 23, 569–591. [Google Scholar] [CrossRef]
- Gan, L.; Zong, Z.H.; Li, M.H.; Qian, H. Dynamic response and failure mode of U shaped stiffener stiffened steel plate under blast loading. J. Southeast Univ. (Nat. Sci. Ed.) 2020, 50, 207–214. (In Chinese) [Google Scholar]
- Liu, Y.L.; Liu, Y.C.; Geng, S.B.; Wang, W.Y.; Xue, J.Y.; Liu, L. An experimental study on the local damage and influence factors of a steel box girder under explosive shock wave. J. Vib. Shock 2018, 37, 229–236. (In Chinese) [Google Scholar]
- Bai, Z.H. Investigation of Failure Mechanisms of Orthotropic Steel Bridge Decks Undern Terror Blast Loading. Master’s Thesis, National University of Defense Technology, Changsha, China, 2010. (In Chinese). [Google Scholar]
- Jiang, Z.G.; Bai, Z.H.; Yan, B.; Zhu, X.-B. Numerical simulation for response of a steel box girder deck to blast loading. J. Vib. Shock 2012, 31, 77–81. (In Chinese) [Google Scholar]
- Hu, Z.J.; Tang, X.H.; Fang, J.Q. Analysis of Pressure Field and Response for Concrete Bridges Under Close Blast Loading. China J. Highw. Transp. 2014, 27, 141–167. (In Chinese) [Google Scholar]
- Zeng, Z. Study of Pressure Distribution and Damage Effect for Concrete Bridges Subjected to Vehicle-Mounted Blast Loads. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2016. (In Chinese). [Google Scholar]
- FEMA-428; Buildings and Infrastructure Protection Series, Primer to Design Safe School Projects in Case of Terrorist Attacks and School Shootings. Department of Homeland Security, Science and Technology Directorate, Infrastructure Protection and Disaster Management Division: Washington, DC, USA, 2012.
- Livermore Software Technology Corporation. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2022. [Google Scholar]
- Jiangsu Provincial Transportation Planning and Design Institute Co., Ltd.; China Railway Major Bridge Reconnaissance; Design Institute Co., Ltd.; Tongji University Architectural Design and Research Institute. Design of Construction Drawings for the Main Bridge of Taizhou Yangtze River Highway Bridge, Volume II, First Part of the Main Bridge (1)-Stiffening Girder; Jiangsu Provincial Transportation Planning and Design Institute Co., Ltd.: Nanjing, China, 2009. (In Chinese) [Google Scholar]
- Lou, F. Experimental Study on Blast Resistance of Prestressed Concrete Continuous Beams. Master’s Thesis, Southeast University, Nanjing, China, 2018. (In Chinese). [Google Scholar]
- Mohan, P.D.; Marzougui; Kan, C.D.S. Validation of a single unit truck model for roadside hardware impact. Int. J. Veh. Syst. Model. Test. 2007, 2, 1–15. [Google Scholar] [CrossRef]







| Air (*MAT_NULL&*EOS_LINEAR_POLYNOMIAL) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial density | Initial energy E0 | Pressure cutoff | Dynamic viscosity coefficient | C0, C1, C2, C3, C6 | C4, C5 | ||||||||
| 1.29 kg/m3 | 2.5 × 105 J/m3 | 0 | 0 | 0 | 0.4 | ||||||||
| TNT (*MAT_HIGH_EXPLOSIVE_BURN & *EOS_JWL) | |||||||||||||
| Initial density | Detonation velocity D | Burst pressure PCJ | A | B | R1 | R2 | E0 | ||||||
| 1630 kg/m3 | 6930 m/s | 21 GPa | 373.8 GPa | 3.747 GPa | 4.15 | 0.9 | 0.35 | 6 × 109 J/m3 | |||||
| Component | Thickness (mm) |
|---|---|
| Top plate | 16 |
| Bottom plate | 10 |
| Vertical web | 14 |
| Top/bottom U-stiffener | 6 |
| Top/bottom inclined plate of bridge wind fairing | 8 |
| Diaphragm | 10/14 |
| Diaphragm of bridge wind fairing | 10/14 |
| Threat |  (A) (A) |  (B) (B) |  (C) (C) |  (D) (D) |  (E) (E) |
|---|---|---|---|---|---|
| TNT mass (kg) | 227 | 454 | 1814 | 4536 | 13,608 |
| Burst height (m) | 0.76 | 0.83 | 1.02 | 1.20 | 1.51 |
| Scenario | Top Plate | Top U-Stiffener | Wind Fairing Stiffener | Web | Wind Fairing Diaphragm | Diaphragm D1 | Diaphragm D2 | Bottom Plate | Bottom U-Stiffener | Inclined Plate on the Wind Fairing |
|---|---|---|---|---|---|---|---|---|---|---|
| A | Opening with dimensions of about 0.1 m × 0.14 m, region connected to the diaphragm experiences large deformation (36.8%) | 3 U-stiffeners’ edges are torn and undergo significant plastic deformation (32.9%) | Intact (0.3%) | Local plasticity (0.9%) | Intact (0.0%) | Local plasticity (4.9%) | Curved incision fracture (20.0%) | Intact (2.7%) | Intact (1.2%) | Intact (0.3%) |
| B | Petal-shaped opening with dimensions of about 1.8 m × 3.4 m (45.3%) | 3 U-stiffeners fractured and 2 U-stiffeners experienced significant plastic deformation (29.6%) | Intact (0.2%) | Local plasticity (1.5%) | Intact (0.0%) | Local plasticity (5.3%) | Curved incision fracture (20.0%) | Intact (2.5%) | Intact (0.8%) | Intact (0.2%) |
| C | Petal-shaped opening with dimensions of about 4.6 m × 6.5 m (38.1%) | 7 U-stiffeners fractured and 4 U-stiffeners experienced significant plastic deformation (23.7%) | Local plasticity (0.3%) | Local flexure (1.6%) | Intact (0.0%) | 2 diaphragms exhibit significant plastic deformation and another 2 diaphragms exhibit out-of-plane bending (13.8%) | Curved incision fracture, 30% buckling of the diaphragm along the height direction (9.5%) | 9 openings with diameters ranging from 0.3 m to 0.6 m (7.1%) | Local opening (5.6%) | Intact (0.3%) |
| D | Petal-shaped opening with dimensions of about 7.2 m × 7.3 m, plastic deformation near the cable anchorage region (31.5%) | 12 U-stiffeners fractured and 4 U-stiffeners experienced significant plastic deformation (19.7%) | Flexural deformation (0.3%) | Local plasticity (1.7%) | Intact (0.0%) | Arc-shaped incision fracture, large plastic deformation, out-of-plane bending, and 38% buckling of the diaphragm along the height direction (16.0%) | Curved incision fracture, large plastic deformation, out-of-plane bending, and 40% buckling of the diaphragm along the height direction (10.1%) | 9 openings with diameters ranging from 0.3 m to 0.5 m, and 2 bulges (11.3%) | 5 U-stiffeners fractured and 2 U-stiffeners experienced significant plastic deformation (8.9%) | Local plasticity (0.4%) |
| E | Petal-shaped opening with dimensions of about 13.3 m × 10.9 m, tearing near the cable anchorage region (25.6%) | 18 U-stiffeners fractured and 4 U-stiffeners experienced significant plastic deformation (14.8%) | Flexural deformation (0.3%) | Local plasticity (1.6%) | Intact (0.0%) | Curved incision fracture, large plastic deformation, out-of-plane bending, and fracture of 2 diaphragms (15.5%) | Complete fracture of 1 diaphragm, localized plasticity at the ends of 4 diaphragms (6.1%) | Petal-shaped opening with dimensions of 11.8 m × 12.2 m (21.0%) | 15 U-stiffeners fractured (14.6%) | Local plasticity (0.4%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Q.; Wang, Q.; Ma, L. Blast-Resistant Performance Evaluation of Steel Box Girder of Suspension Bridge. Buildings 2025, 15, 3210. https://doi.org/10.3390/buildings15173210
Peng Q, Wang Q, Ma L. Blast-Resistant Performance Evaluation of Steel Box Girder of Suspension Bridge. Buildings. 2025; 15(17):3210. https://doi.org/10.3390/buildings15173210
Chicago/Turabian StylePeng, Qi, Qizhen Wang, and Liangliang Ma. 2025. "Blast-Resistant Performance Evaluation of Steel Box Girder of Suspension Bridge" Buildings 15, no. 17: 3210. https://doi.org/10.3390/buildings15173210
APA StylePeng, Q., Wang, Q., & Ma, L. (2025). Blast-Resistant Performance Evaluation of Steel Box Girder of Suspension Bridge. Buildings, 15(17), 3210. https://doi.org/10.3390/buildings15173210





