Parametric Analysis of a 400-Meter Super-High-Rise Building: Global and Local Structural Behavior
Abstract
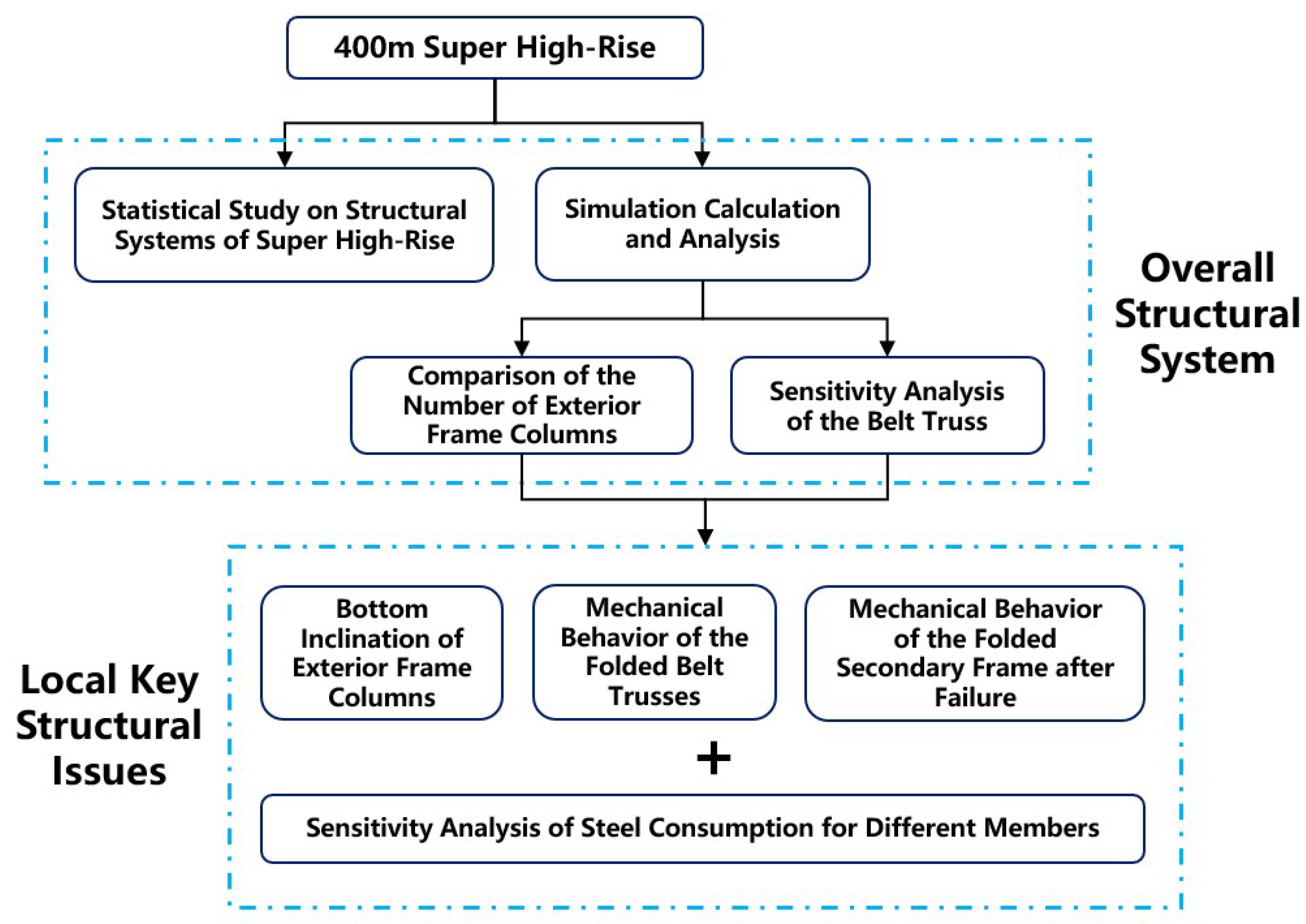
1. Introduction
- (1)
- How to select the lateral force-resisting system of the structure and determine the appropriate number of exterior frame columns.
- (2)
- How to determine the number and position of the belt trusses.
- (3)
- The problems caused by the inward inclination of the bottom columns and their solutions.
- (4)
- The problems brought about by the folded floor outline and their corresponding solutions.
- (5)
- The optimization efficiency of various components?
2. Research Objects and Methods
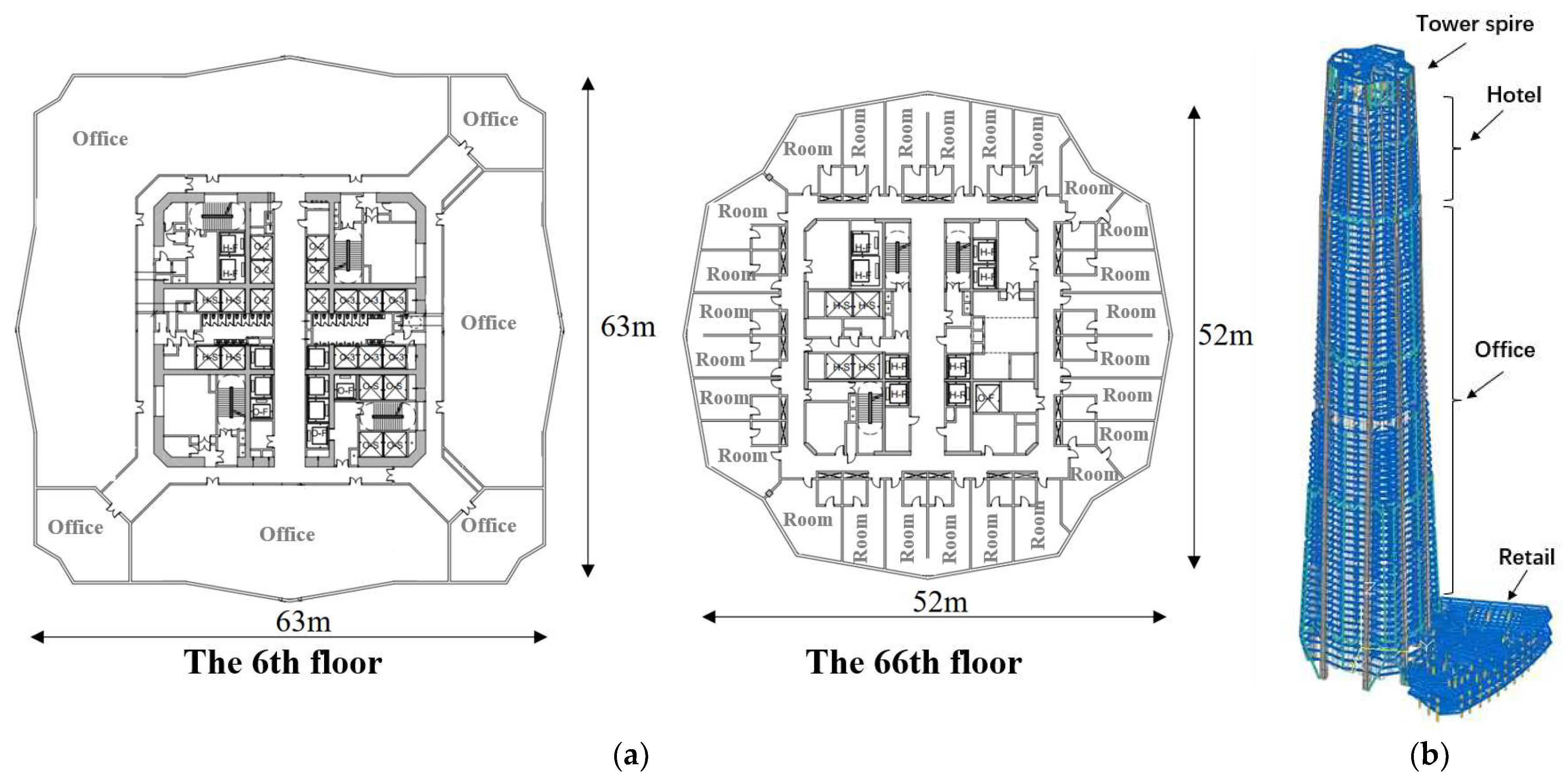
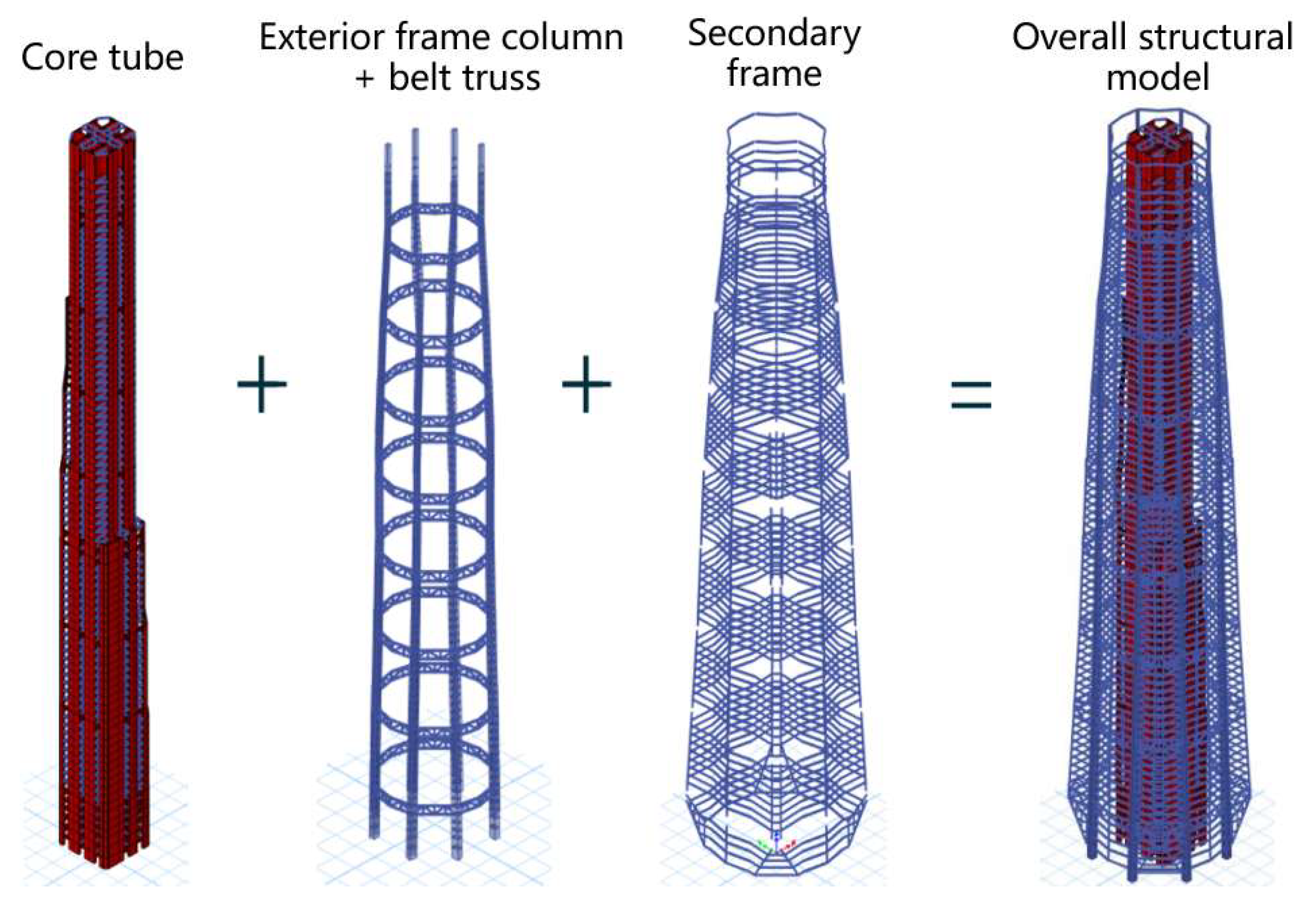
2.1. Project Overview
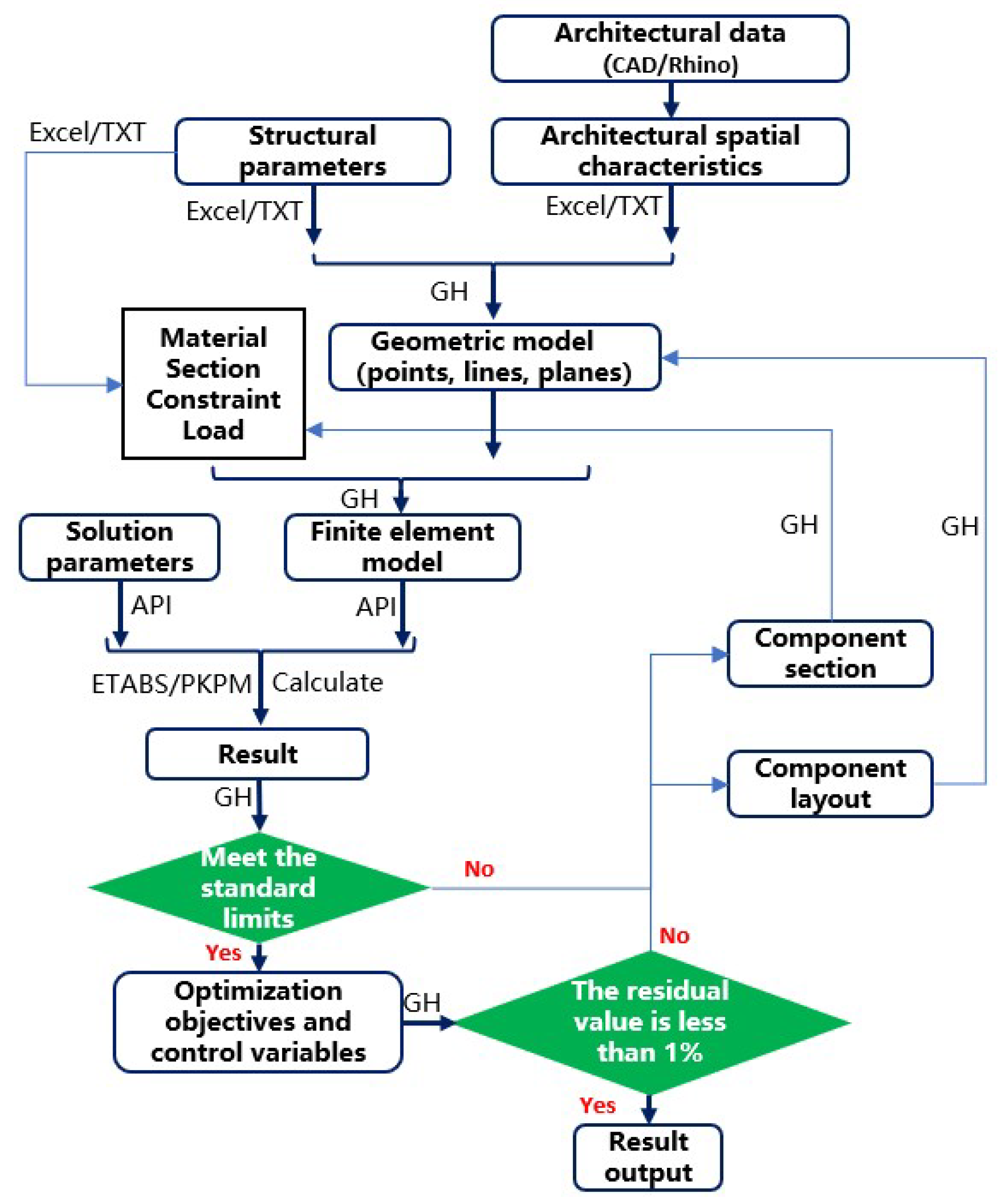
2.2. Research Methods and Approach
3. Research on Structural Lateral Force-Resisting System
3.1. Statistical Study on Structural Systems of Super-High-Rise Buildings
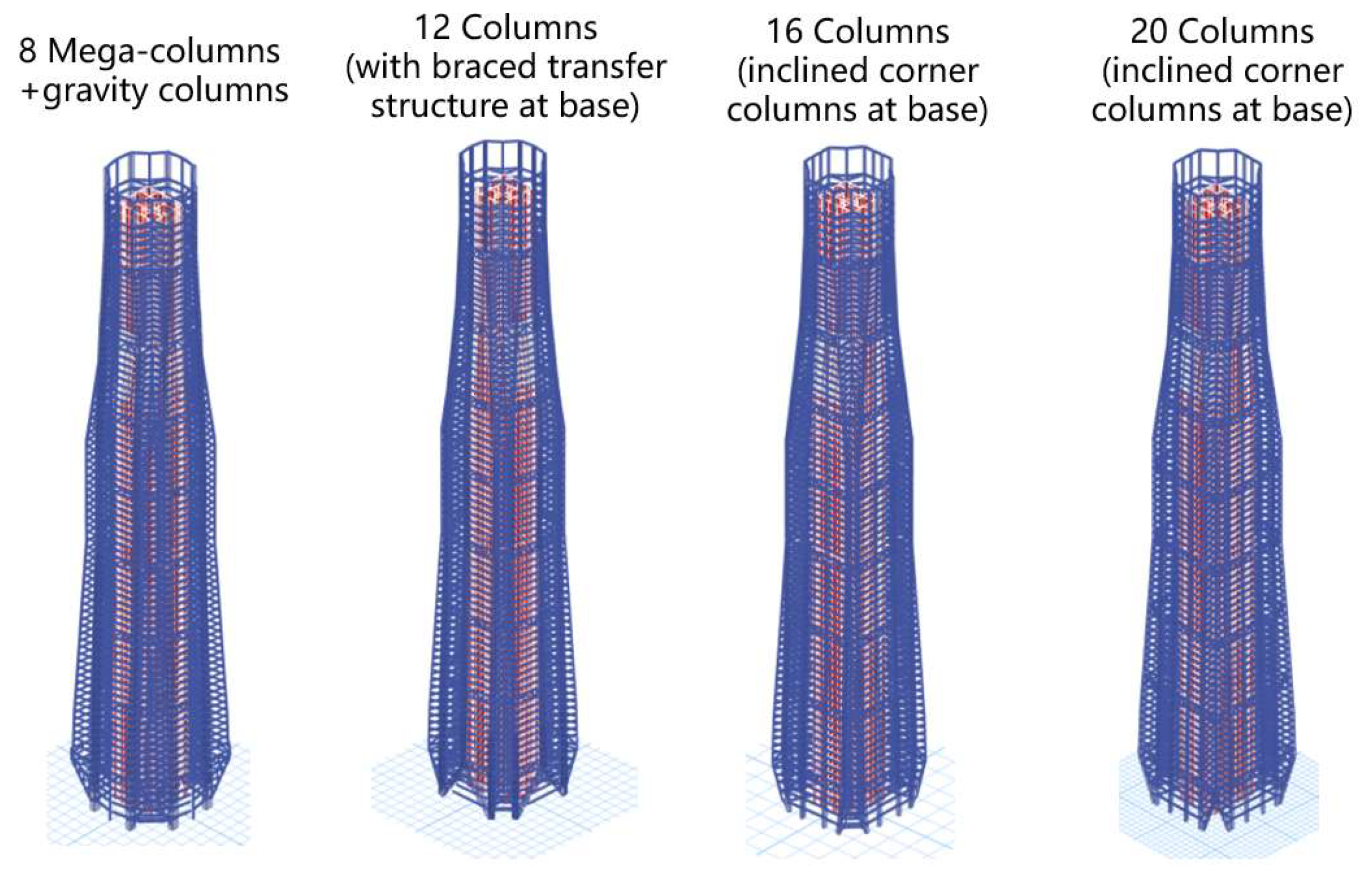
3.2. Comparative Study on the Number of Exterior Frame Columns
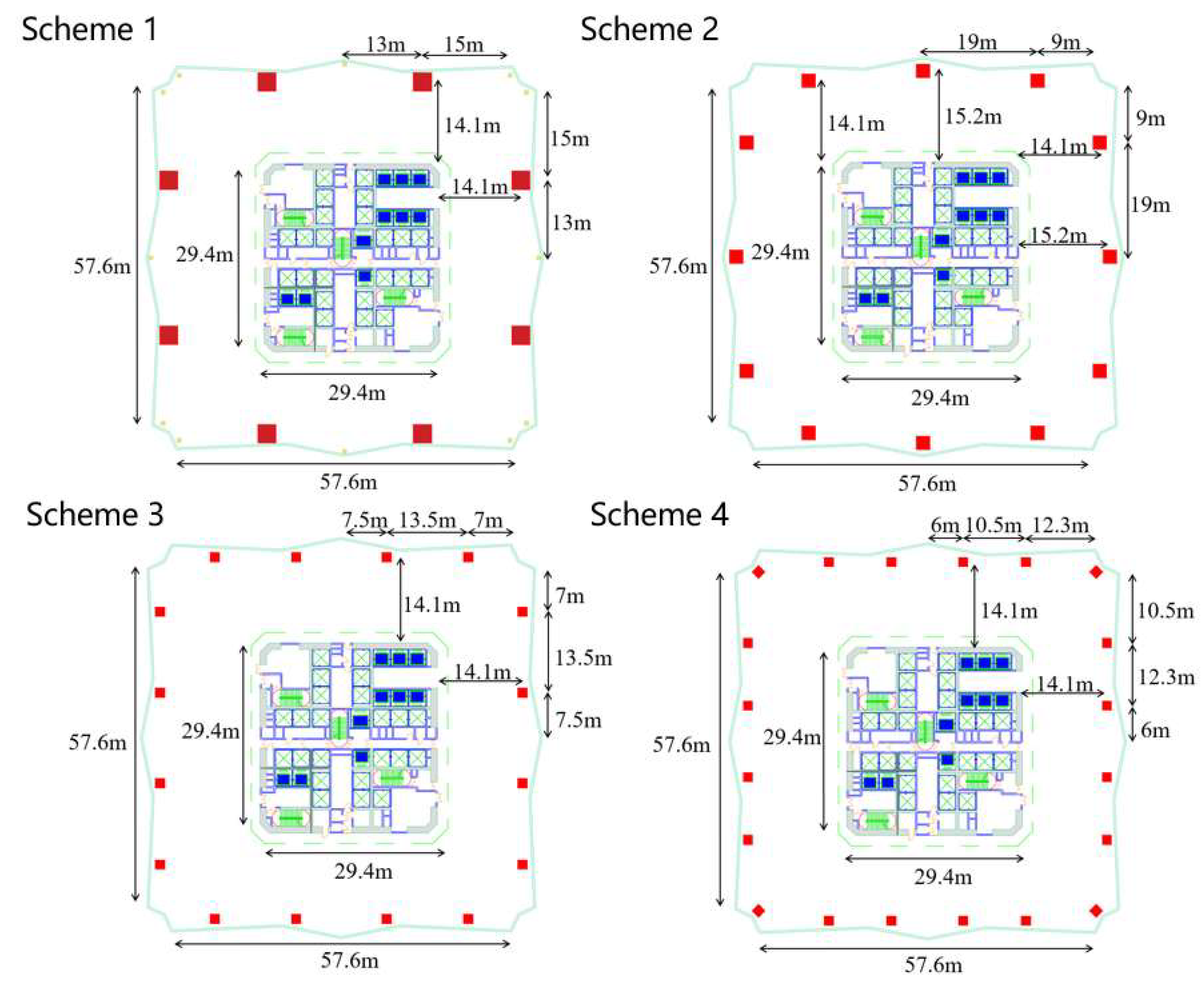
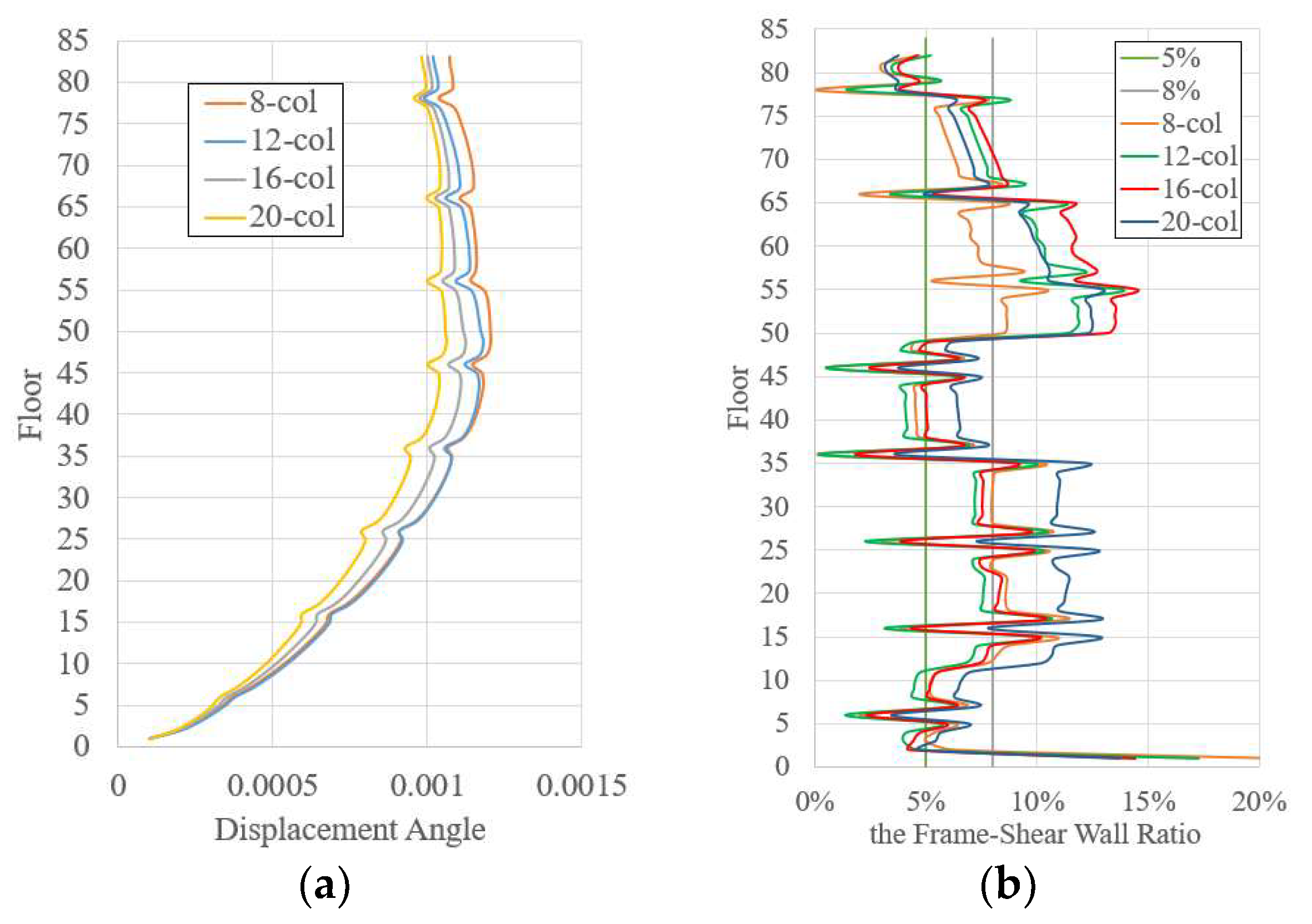
3.2.1. Comparison Scheme
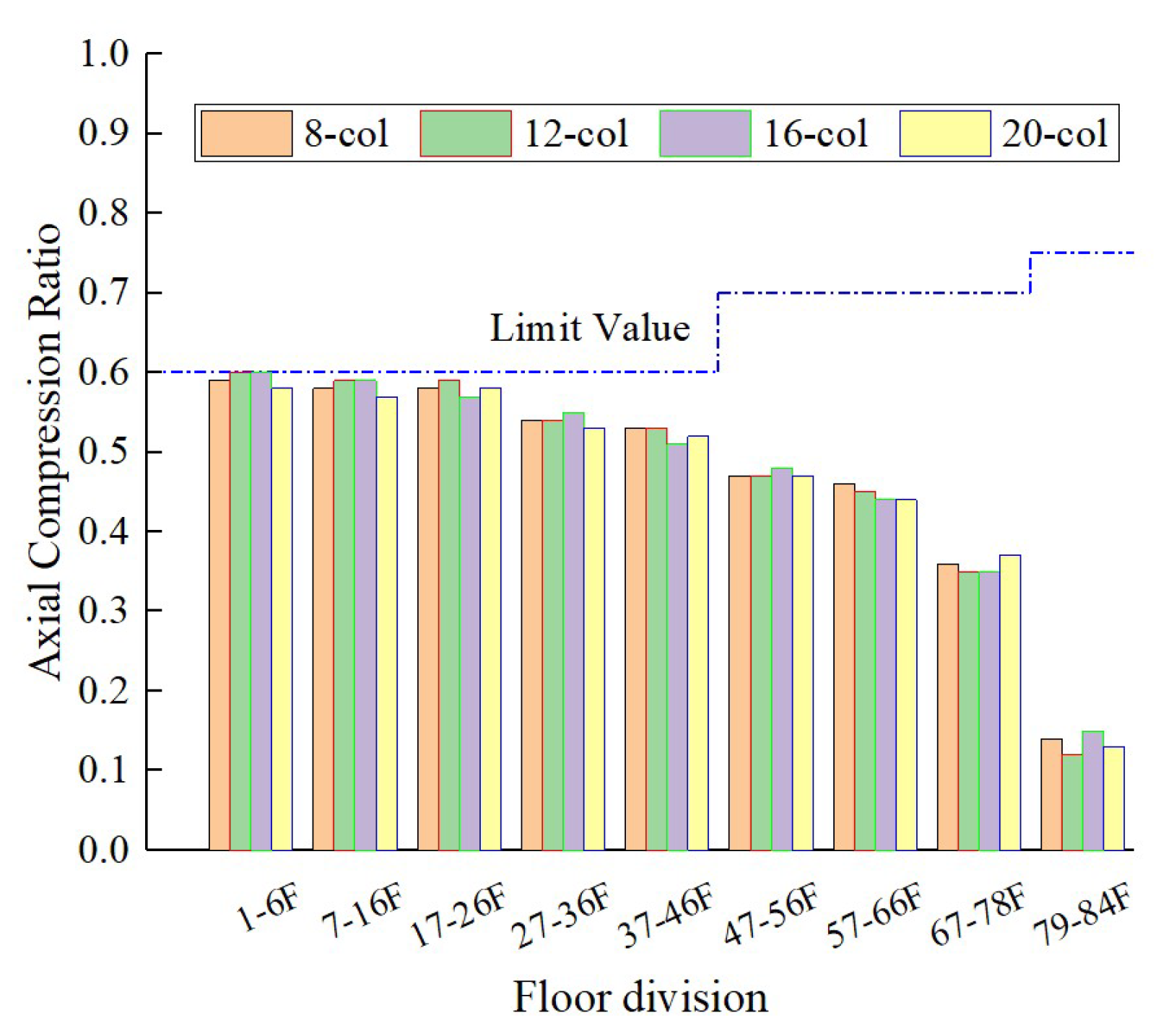
3.2.2. Results
- (1)
- Comparison of structural lateral stiffness
- (2)
- Comparison of seismic forces
- (3)
- Distribution of internal and external shear forces
- (4)
- Comparison of steel consumption
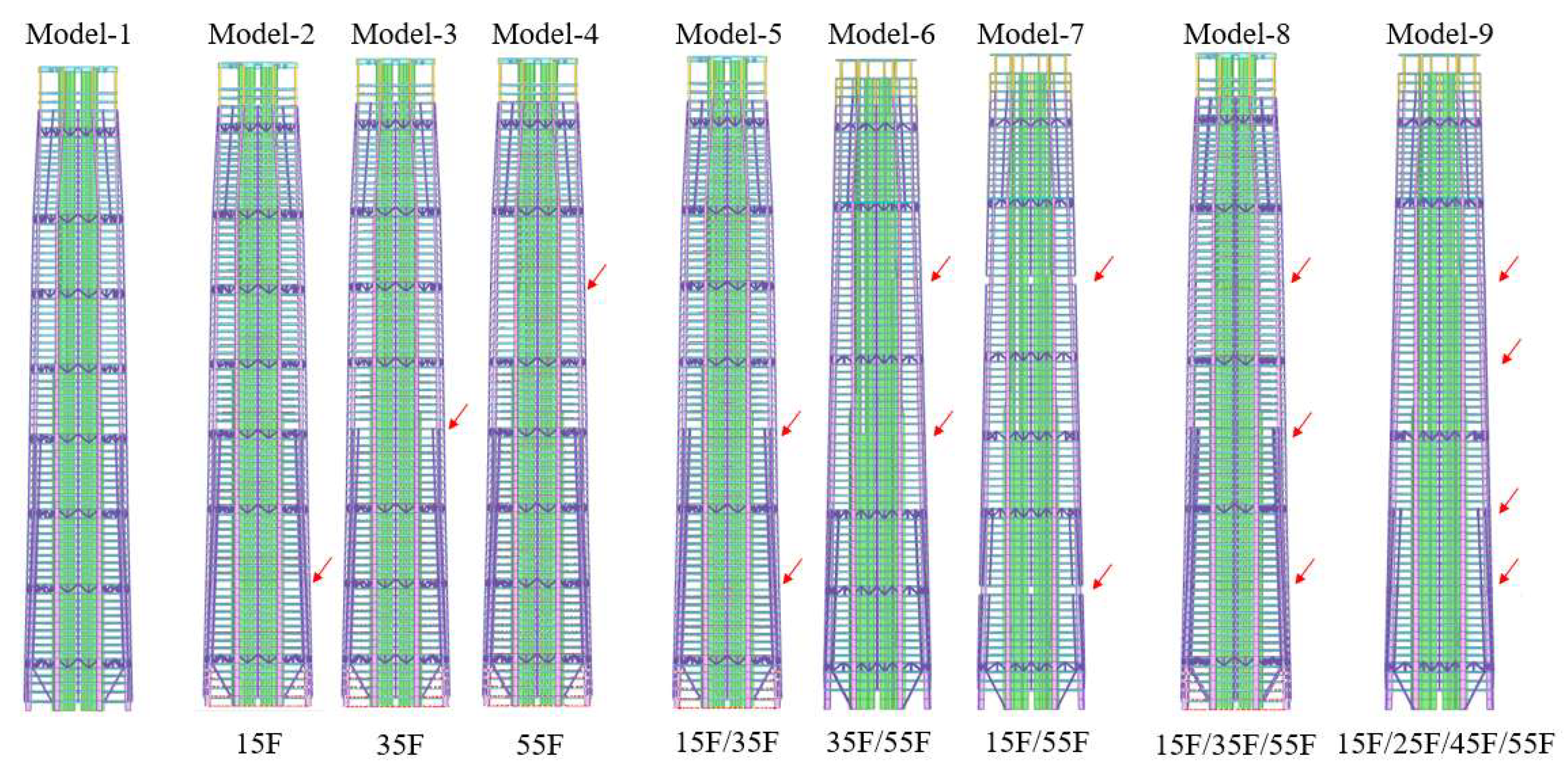
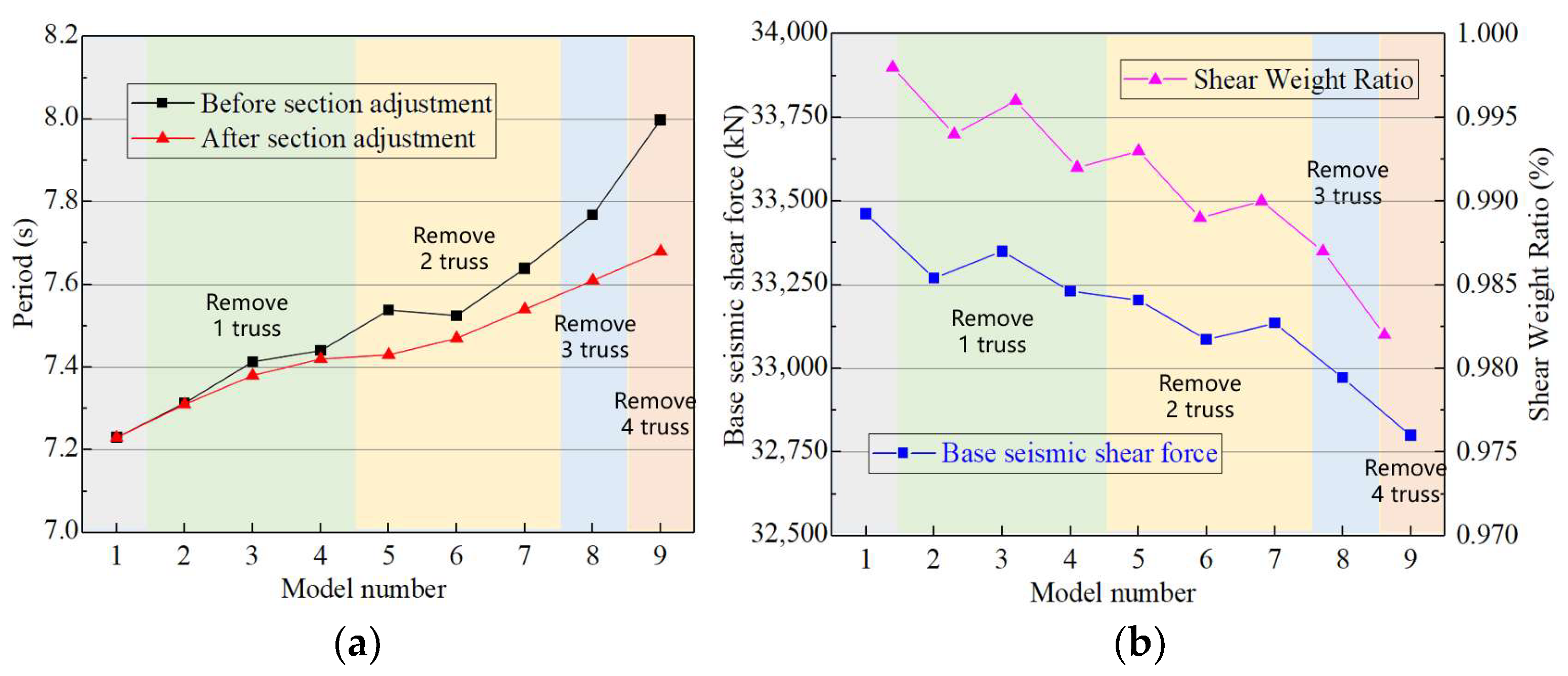
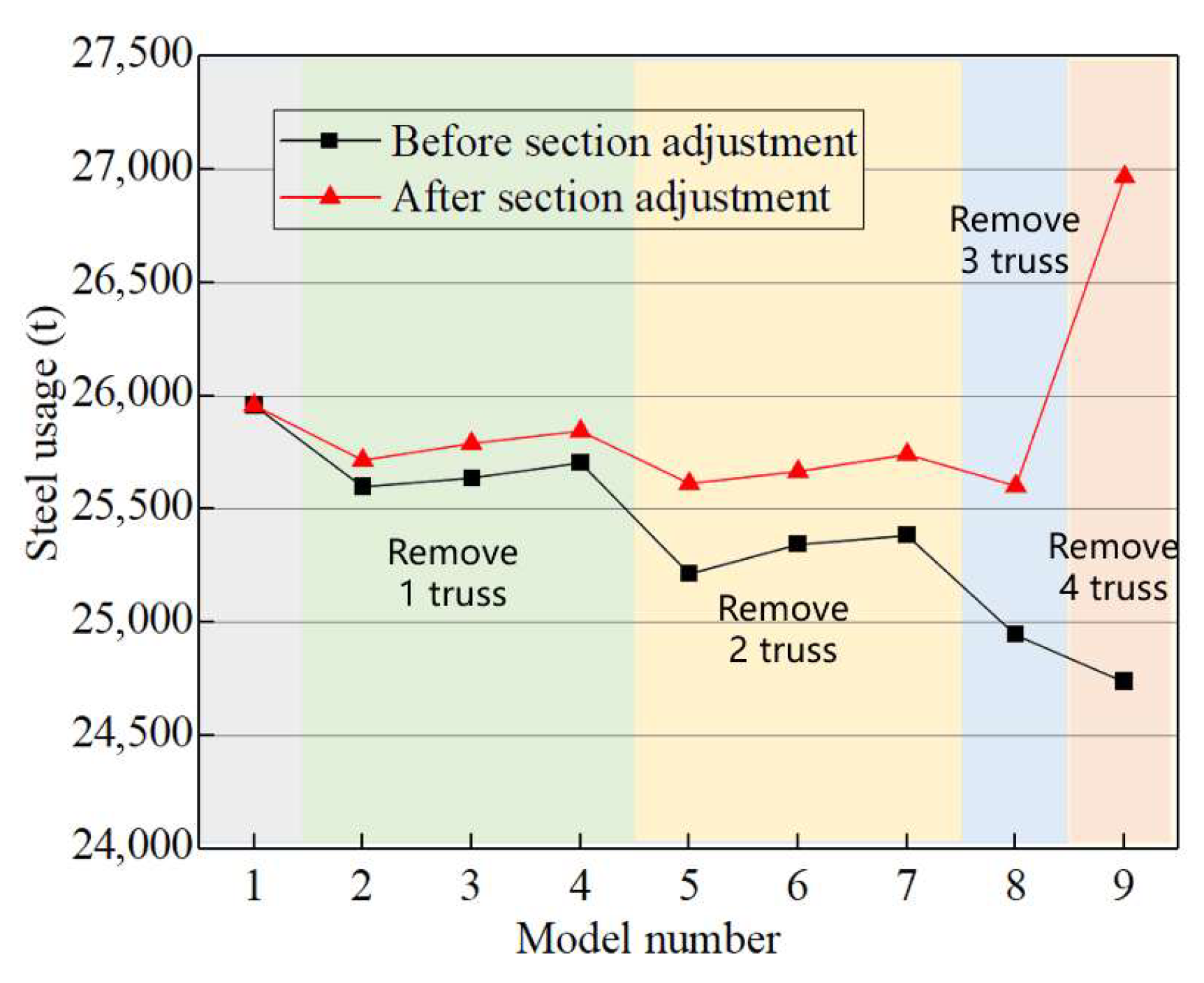
3.3. Sensitivity Analysis of the Number of the Belt Truss
- As the number of removed belt trusses increases, the overall translational stiffness of the structure decreases, and the first-order period becomes longer. Optimizing or strengthening structural members does not change this law, indicating that the impact of adjusting the number of belt trusses on structural stiffness is greater than that of modifying member sizes.
- The contribution of belt trusses located in the high zone to structural stiffness is generally greater than that of those situated in the low zone.
4. Research on Key Local Issues of the Structure
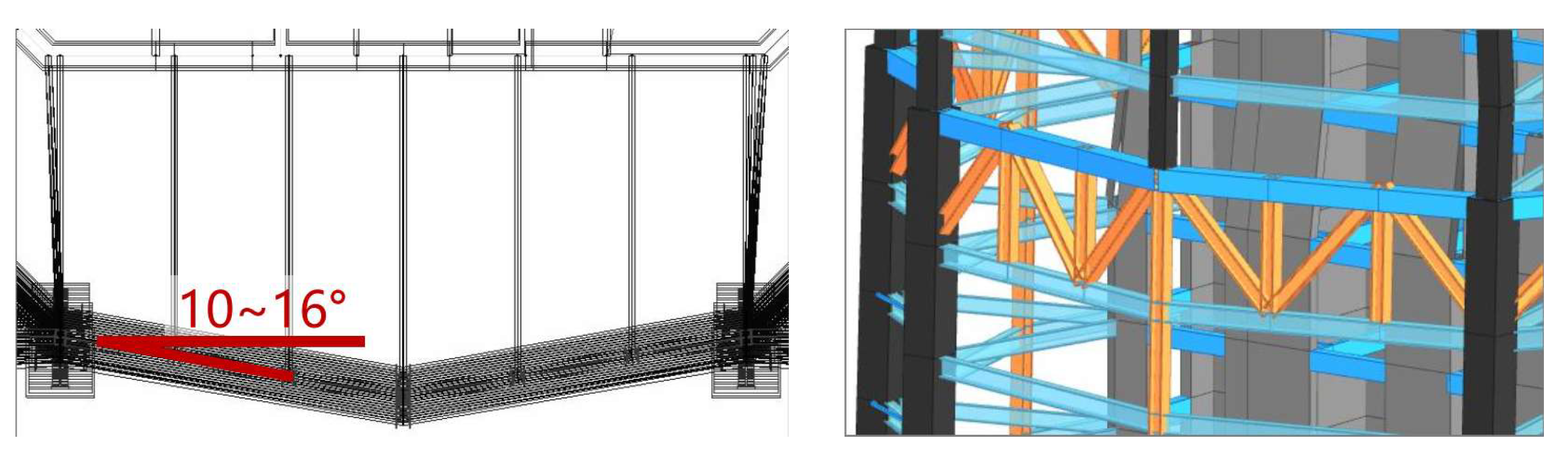
4.1. Study on the Bottom Inclination of Mega-Columns
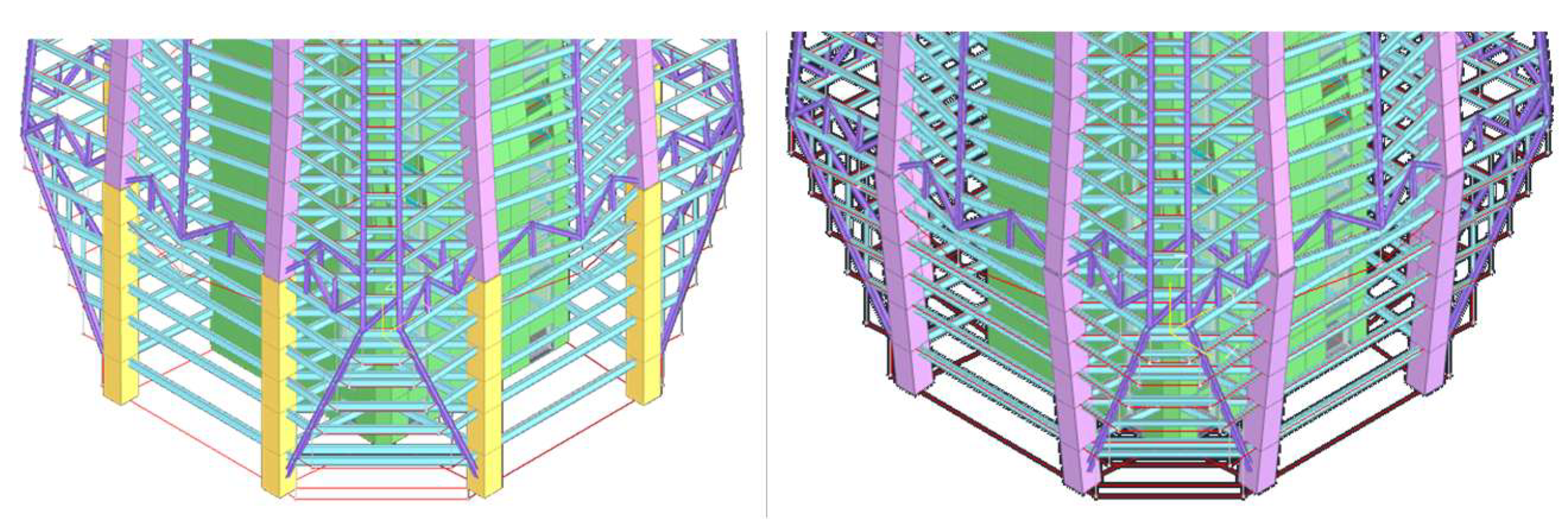
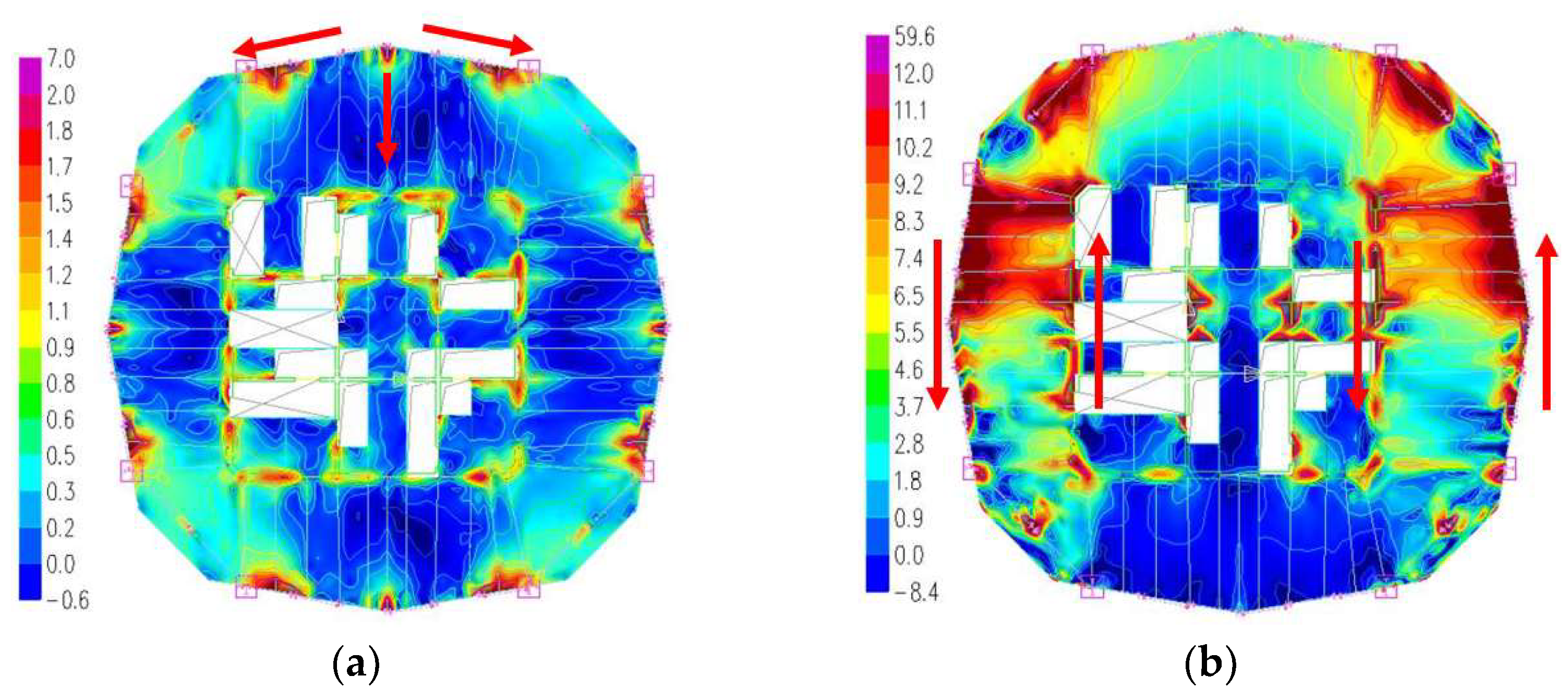
4.2. Mechanical Behavior of the Folded Belt Trusses and Floor Strengthening
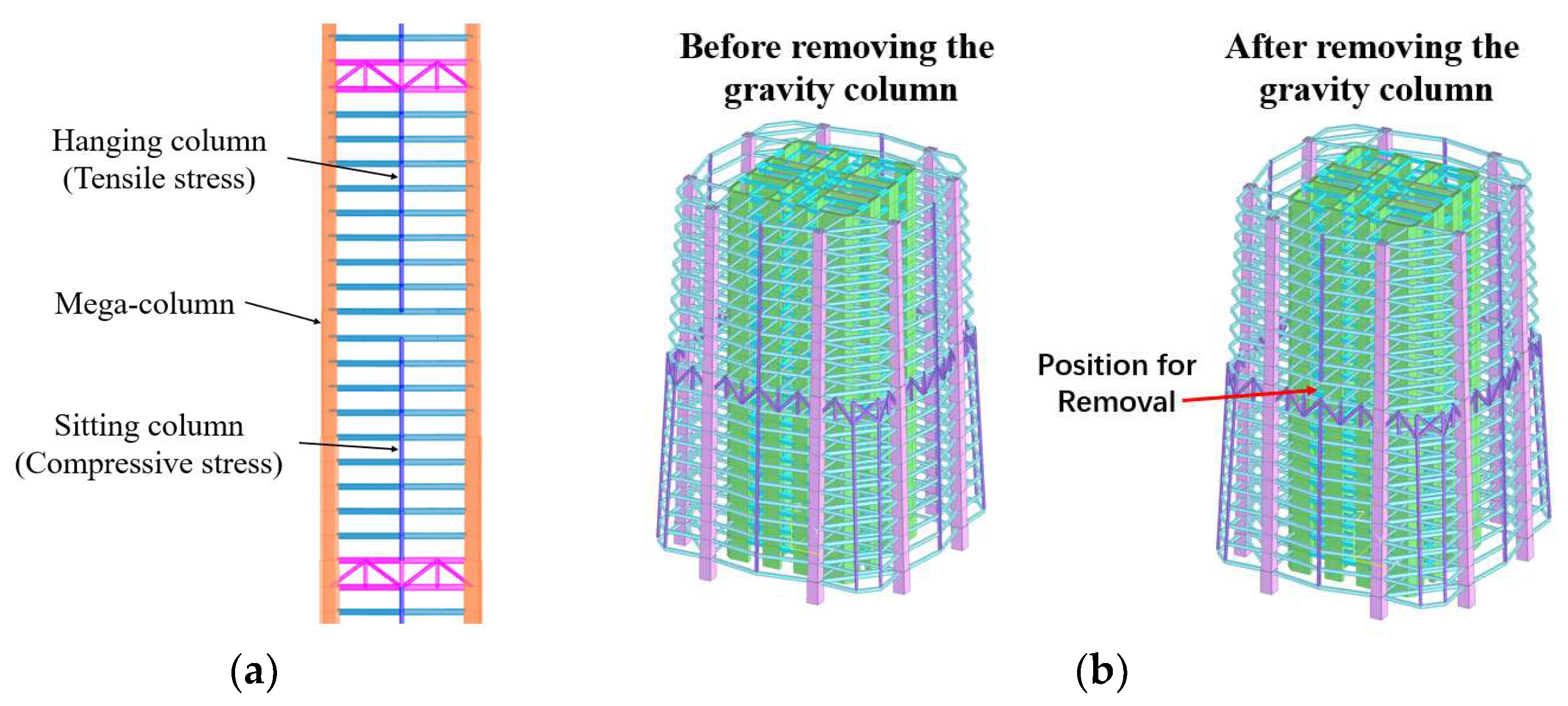
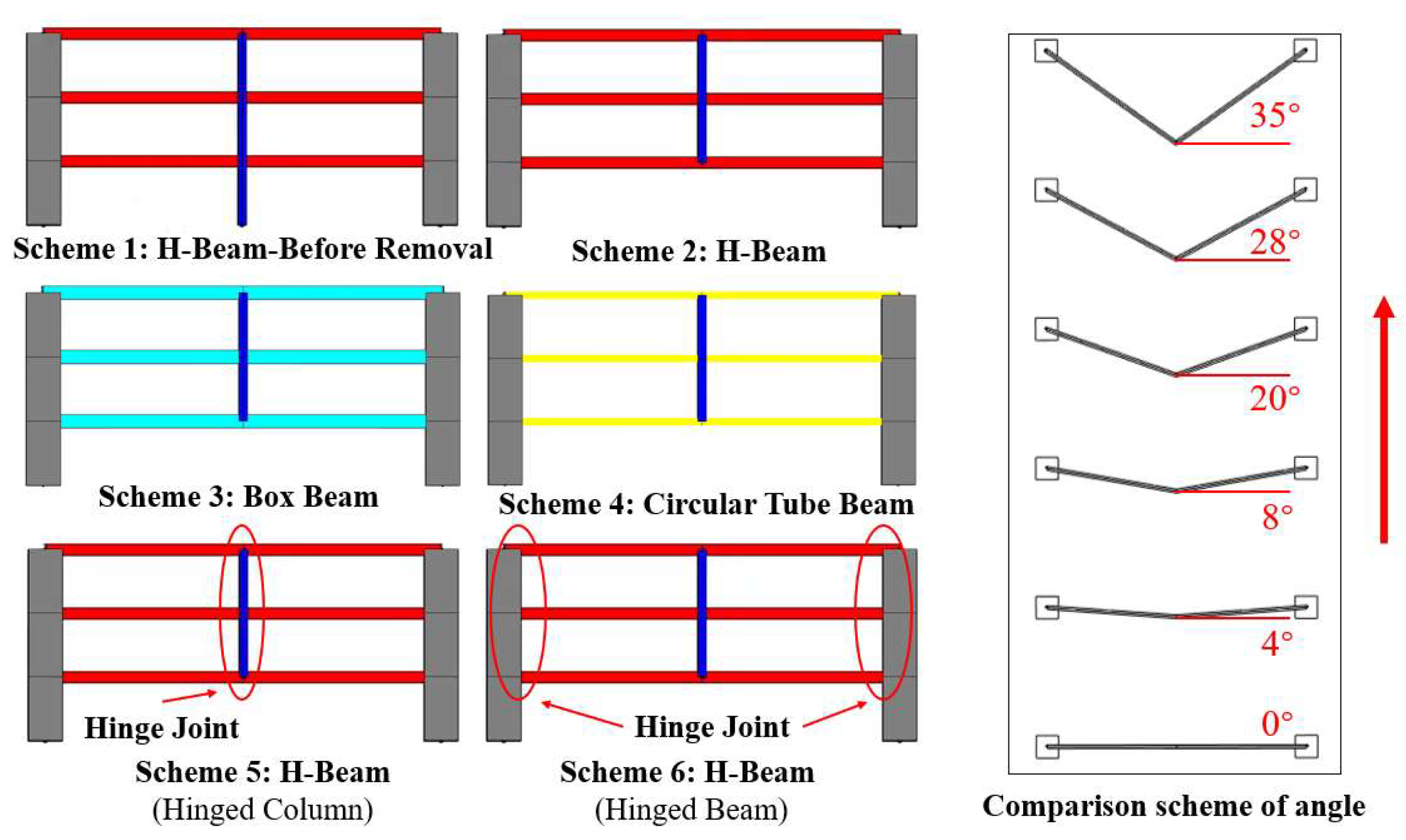
4.3. Mechanical Behavior of the Folded Secondary Frame After the Failure of a Gravity Column
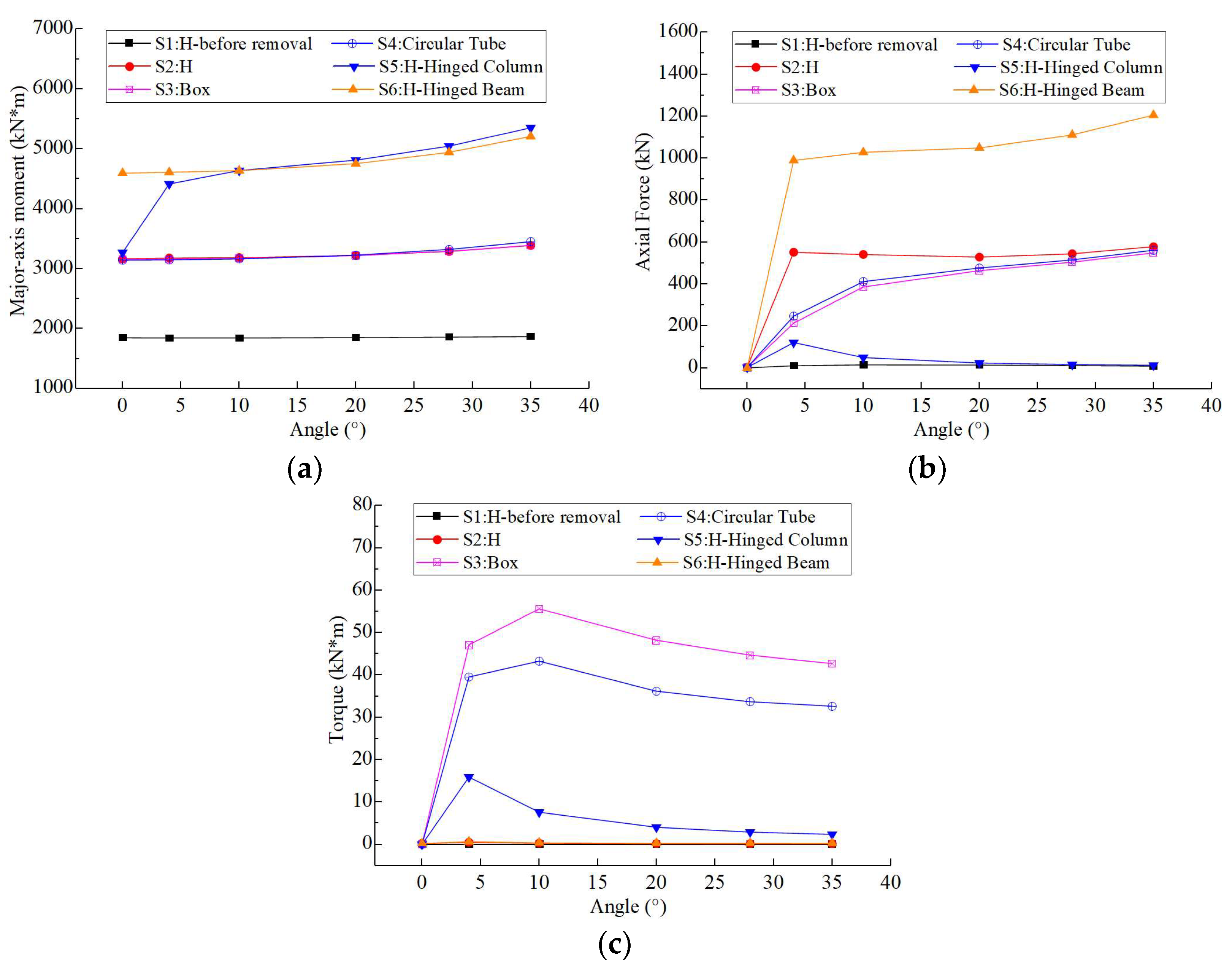
- (1)
- Within the range of 0° to 35° of the angle, for the common cross-sectional types and the above-mentioned constraint conditions, the folded beam mainly bears the strong-axis bending moment and axial force, while the torque and weak-axis bending moment are relatively small and their influences can be ignored.
- (2)
- With the increase in the angle, the strong-axis bending moment and axial force of the folded beam generally show an increasing trend, while the torque first increases and then decreases.
- (3)
- The cross-sectional type has little influence on the bending moment of the folded beam, but has a certain influence on the axial force and torque of the beam. In terms of axial force, the order is H-shaped section > circular tube section ≈ box-shaped section; in terms of torque, the order is box-shaped section > circular tube section, and the torque of the H-shaped section is negligible.
- (4)
- After removing the lower gravity column, the strong-axis bending moment, axial force of the folded beam, and the bending moment of the gravity column will increase significantly, and the vertical deformation will also increase considerably. Once plastic hinges appear at the beam end or the end of the gravity column, the bending moment and vertical deformation will further increase sharply, which may lead to a progressive collapse. Therefore, in the design, it is necessary to ensure that the gravity column or the folded beam has sufficient redundancy to avoid such a situation.
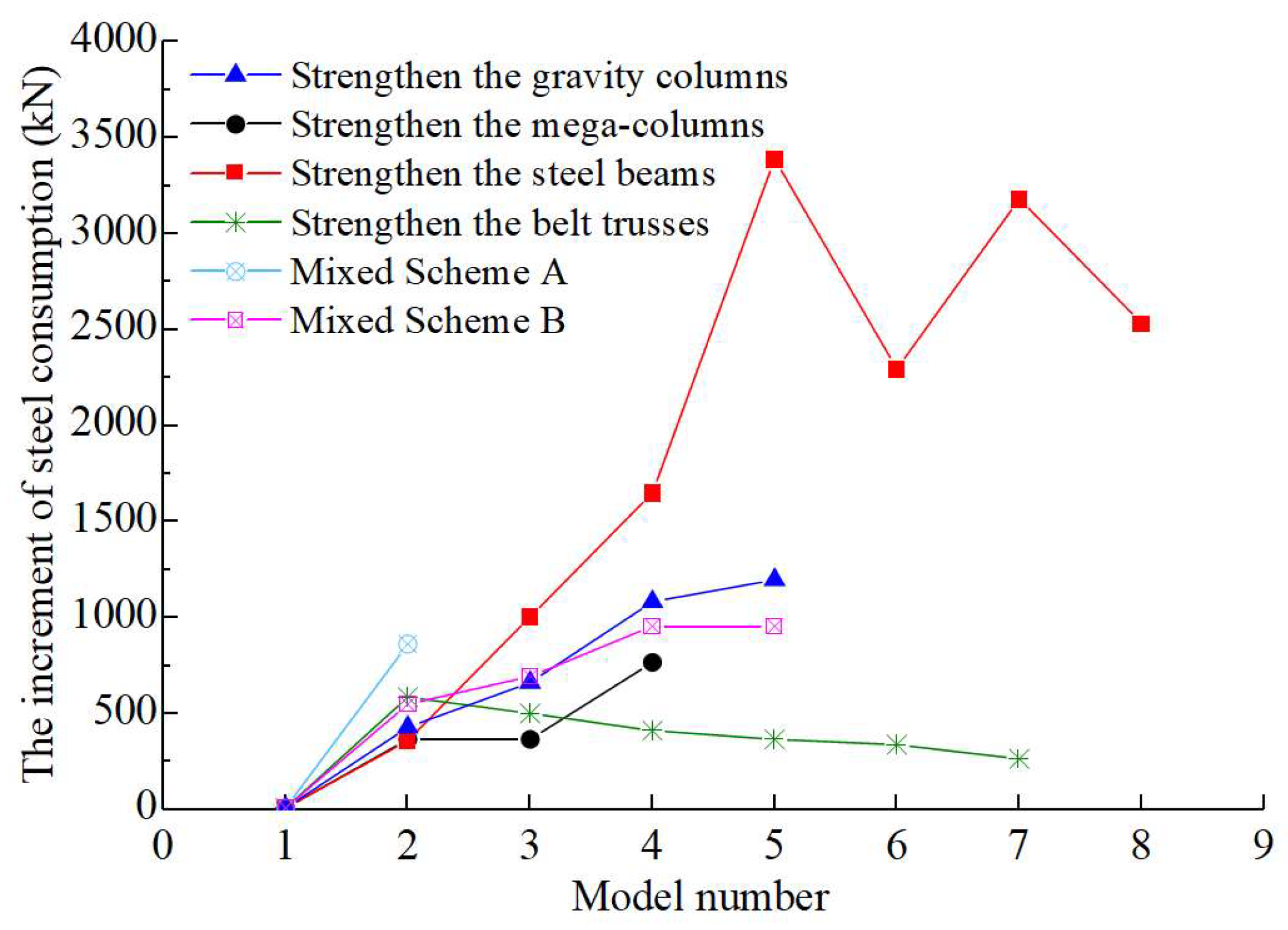
4.4. Sensitivity Analysis of Steel Consumption for Different Members
5. Conclusions
- (1)
- First, through a statistical analysis of the structural systems of super-high-rise building cases with a height of over 300 m, the structural system for this project is initially established. Then, four types of exterior frame column schemes (8, 12, 16, and 20 columns) are calculated and compared. Considering the structural performance, material consumption, and architectural effect comprehensively, the 8-mega-column scheme is ultimately determined.
- (2)
- Starting from the 8 belt trusses, the sensitivity analysis of the belt trusses is carried out using the decreasing method. Finally, the solution corresponding to Model-8 belt trusses (with five belt trusses) is determined as the optimal solution. Regarding the structural stiffness, the high-zone belt trusses usually contribute more than the low-zone belt trusses; for the total steel consumption of the structure, as the number of belt trusses decreases, the steel consumption first decreases and then increases, and the steel consumption is minimized when the spacing between belt trusses is 20 floors.
- (3)
- Using the inwardly inclined column scheme for the bottom mega-columns will significantly increase the axial force of the floor beams compared to the straight column scheme, resulting in an increase in the beam section, greater difficulty in connecting with the core tube, and a more unfavorable situation in terms of seismic resistance. Therefore, the seismic grade of the relevant beams and columns should be raised by one level, the thickness and reinforcement of the floor slabs should be strengthened, and the connection nodes between the beams and the core tube need further analysis and treatment.
- (4)
- Horizontal braces can enhance the integrity of polygonal belt trusses when floor slabs crack and lose their function under rare earthquakes, but their role under vertical loads is limited, and the scheme of horizontal braces directly connected to the core tube is more effective and cost-efficient.
- (5)
- For the secondary frame structure composed of gravity columns and folded beams, after removing a lower gravity column, the internal forces of the beams and the remaining gravity columns increase significantly. Once plastic hinges form, the internal forces and deformations will further increase, so strengthening measures are required in the design to avoid progressive collapse. After removing a lower gravity column, the folded beams are mainly subjected to the strong-axis bending moment and axial force, while the torque and weak-axis bending moment are relatively small and can be ignored. The strong-axis bending moment and axial force of the folded beam will increase with the increasing angle. The section type has little influence on the bending moments of the folded beams: the axial force of the H-shaped section is greater than that of the circular tube and box-shaped sections; the torque of the box-shaped section is larger than that of the circular tube section; and the torque of the H-shaped section can be ignored.
- (6)
- A sensitivity analysis of steel consumption is carried out for different types of structural members. The scheme with the smallest increase in steel consumption is the one that only adjusts the belt truss members, and the scheme with the greatest increase in steel consumption is the one that only adjusts the steel beams. The efficiency of cross-section adjustment in descending order is as follows: belt truss members > mega-column > mixed A > mixed B > gravity column > steel beam.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shepherd, R. Skyscraper: An Architectural Record Book; McGraw-Hill Education: New York, NY, USA, 2002; pp. 10–25. ISBN 978-0071369701. [Google Scholar]
- Zhen, Q.H. The Analysis of Some Key Problems in Structural Design of a High-Rise Building in Guangzhou. Master’s Thesis, South China University of Technology, Guangzhou, China, 2011. [Google Scholar]
- Sarkisian, M.; Mathias, N.J.; Long, E.; Mazeika, A.; Gordon, J.; Chakar, J.-P. Jin Mao Tower’s Influence on China’s New Innovative Tall Buildings. In Proceedings of the 2006 International Seminar of Design and Construction Technologies of Super High-Rise Buildings, Shanghai, China, 15–16 May 2006; pp. 1–6. [Google Scholar]
- CTBUH Council on Tall Buildings and Urban Habitat. Illinois Institute of Technology, S.R. Crown Hall, 3360 South State Street, Chicago, IL, USA. Available online: www.ctbuh.org (accessed on 20 June 2025).
- Gong, J.; Fang, T.; Zuo, J. A Review of Key Technologies Development of Super High-Rise Building Construction in China. Adv. Civ. Eng. 2022, 13, 5438917. [Google Scholar] [CrossRef]
- Al, S. Supertall: How the World’s Tallest Buildings Are Reshaping Our Cities and Our Lives; WW Norton & Company: New York, NY, USA, 2022. [Google Scholar]
- Li, J.; Wang, D.; Geng, J. Relationship Between Super-tall Buildings and the Economic Development. Constr. Technol. 2014, 15, 1–5. [Google Scholar] [CrossRef]
- Ilgın, H.E.; Aslantamer, Ö.N. Comparative Analysis of Space Efficiency in Skyscrapers with Prismatic, Tapered, and Free Forms. Buildings 2024, 14, 3345. [Google Scholar] [CrossRef]
- Lai, H.; Lin, S.; Tang, J. Research on Structural System Compatibility of Super High-rise Building. Build. Struct. 2024, 54, 1–5. [Google Scholar]
- Dong, X.; Wang, Y. Reshaping the city: Does the skyscraper cause the formation of subcenters? Real Estate Econ. 2025, 53, 763–807. [Google Scholar] [CrossRef]
- Li, Y. Research on the Selection of a Super-High-Rise Building Structure. Master’s Thesis, Zhengzhou University, Zhengzhou, China, October 2017. [Google Scholar]
- Fur, L.-S.; Yang, H.T.Y.; Ankireddi, S. Vibration Control of Tall Building under Seismic and Wind Loads. J. Struct. Eng. 1996, 122, 122–126. [Google Scholar] [CrossRef]
- Smith, F.C. The Architecture of Tall Buildings; McGraw-Hill Education: New York, NY, USA, 1991; ISBN 978-0-07-059352-9. [Google Scholar]
- Wang, D.; Zhou, J.; Bao, L. Analysis on the Cost of Structural Construction in Super-Tall Buildings. Build. Struct. 2012, 42, 1–7. [Google Scholar]
- Zhou, J.; Bao, L.; Qian, P. Study on the Economy of Structural Design of Super-Tall Buildings and Relevant Issues. Eng. Mech. 2015, 36, 9–15. [Google Scholar] [CrossRef]
- Qu, J.; Wang, Z.; Du, P. Comparative Study on the Development Trends of High-rise Buildings Above 200 Meters in China, the USA and the UAE. Int. J. High Rise Build. 2021, 10, 63–71. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for the Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- Abed, J.; Rayburg, S.; Rodwell, J.; Neave, M. A Review of the Performance and Benefits of Mass Timber as an Alternative to Concrete and Steel for Improving the Sustainability of Structures. Sustainability 2022, 14, 5570. [Google Scholar] [CrossRef]
- Qu, J.; Zhuang, K.; Zhou, J. Structural and Material Comparison Analysis of Super High-Rise Buildings Above 300 Meters Height. Archit. Tech. 2021, 27, 32–35. [Google Scholar]
- JGJ 138-2016; Code for Design of Composite Structures. China Architecture & Building Press: Beijing, China, 2016.
- Qi, F. Application of Parametric Method Based on Grasshopper in Structure Design. J. Civ. Eng. Inf. Technol. 2018, 10, 105–110. [Google Scholar] [CrossRef]
- Liang, D.; Hou, S.; Wang, X.; Jin, L. Application of Parametric Modeling in Structural Design of a Super High-Rise Building Tower in Ningbo Eastern New Town. Build. Struct. 2018, 48, 30–35. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Q.; Xing, Y.; Kang, Y. Secondary Development and Application of Parametric Modeling and Integrated Analysis Program for Super High Rise Structure Based on GH and SAP2000. Build. Struct. 2021, 51, 212–216. [Google Scholar]
- Li, Y.; Zhou, J. Application of Parametric Technology in Structural Design. Build. Struct. 2022, 52, 142–147. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, J.; Sun, Y.; Wang, H.; Gong, M. Application of Parametric Technology in the Design of Super High-Rise Structures. Build. Struct. 2022, 52, 29–37. [Google Scholar] [CrossRef]
- Sha, X.; Li, H.; Li, Y.; Qiu, H.; Chen, Z. Application of Numerical Intelligence Design of Building Structure Under the Development of Information Technology. Buildings 2024, 6, 128–131. [Google Scholar]
- JGJ 3-2010; Technical Specification for Concrete Structure of Tall Building. China Architecture & Building Press: Beijing, China, 2010.
- Bin, W. Analysis on Structural Selection and Economy of Super High-Rise Building. Urban. Archit. 2021, 18, 88–90. [Google Scholar]
- Yang, W. Study and Optimization on the Structural Scheme Selection of Ultra High-Rise Building. Master’s Thesis, Chang’an University, Xi’an, China, 2013. [Google Scholar]
- Ali, M.M.; Al-Kodmany, K. Structural systems for tall buildings. Encyclopedia 2022, 2, 1260–1286. [Google Scholar] [CrossRef]
- Yu, D.; Lin, H.; Lv, W. Structural scheme selection for Wuhan CTF Finance Centre. Build. Struct. 2017, 47, 6–11. [Google Scholar]
- Xu, P.; Chen, C.; Qiu, S. Study on reasonable range of fundamental natural period of vibration of high-rise buildings. J. Build. Struct. 2024, 45, 16–24. [Google Scholar]
- Wang, D.; Bao, L. Development and prosperity of structural design of super tall buildings in China. Build. Struct. 2019, 49, 11–24. [Google Scholar]
- Zhao, Q. Research on the Design Theory of Support Columns in the Super High-Rise Multi-Column Frame-Core Tube Structure Constructed by the Top-Down Technique. Ph.D. Thesis, Tianjin University, Tianjin, China, 2017. [Google Scholar]
- Xia, H.; Zhang, X.; Li, W.; Chen, C. Design and research on a sparse column frame-corewall office building in high wind pressure area. J. Build. Sci. 2023, 39, 174–182. [Google Scholar]
- Ke, C.; Fan, Y.; Chen, L. Ultra-limit High-rise Structural Design of Building D in Hefei Greenland Center. J. Anhui Jianzhu Univ. 2021, 29, 15–19. [Google Scholar]
- Cao, L. Structure Systems and Optimization Program of Super-High-Rise Buildings. Low Temp. Archit. Technol. 2011, 12, 52–54. [Google Scholar]
- Wu, X.; Peng, Z.; Liu, Y.; Chen, Q.; Xie, J.; Zhang, Q.; Qin, P.; Tu, Y. Structural design of super high-rise project in Chengdu Zhonghai Tianfu New District. Build. Struct. 2024, 54, 1–10. [Google Scholar]
- Gong, Z.; Yang, Y.; Chang, W. Design Research on Mega Columns of CITIC Tower. Ind. Constr. 2022, 52, 80–86. [Google Scholar]
- Wu, G.; Fu, X.; Huang, Y.; Liu, Y.; Zhang, X.; He, Z. Structural design on Shenzhen Bay Headquarters Building of China Resources Group. Build. Struct. 2019, 49, 43–50. [Google Scholar]
- Ilgın, H.E. Space Efficiency in Tapered Super-Tall Towers. Buildings 2023, 13, 2819. [Google Scholar] [CrossRef]
- GB 50010-2010(2015); Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- Chen, C.; Wang, C.; Pan, C. Study on the Frame-Shear Ratio of Frame-Core Tube Structure Based on the Cooperative Work Principle. Build. Sci. 2019, 35, 1–6. [Google Scholar] [CrossRef]
- ASCE/SEI 7-05; Minimum Design Loads for Buildings and Other Structures. ASCE: Reston, VA, USA, 2005.
- IBC 2009; International Building Code. ICC: Country Club Hills, IL, USA, 2009.
- Fu, C.; Zhang, X.; Zhou, L. Frame-Core Wall Structural System and Seismic Shear Distribution Ratio. Build. Struct. 2015, 45, 1–8. [Google Scholar]
- Chen, C.; Wang, C.; Pan, Y.; Xiong, Y.; Pan, C. Research on Frame Shear Adjustment Method of the Frame-Core Tube Structure. Build. Struct. 2021, 51, 8–14. [Google Scholar] [CrossRef]
- Xiao, C.; Li, J.; Sun, C.; Wei, Y.; Li, Y. Discussion on Performance-Based Seismic Design Method of Out-of-Code High-Rise Structures. Build. Struct. 2022, 52, 8–13. [Google Scholar] [CrossRef]
- Huang, G.; Cheng, W.; Zhang, Q.; Xie, Z.; Chen, C.; Xiong, Y.; Chen, H. Design study of half-sitting half-hanging secondary frames in Chengdu Zhonghai Tianfu New Area super high-rise project. Build. Struct. 2025, 55, 29–33. [Google Scholar]

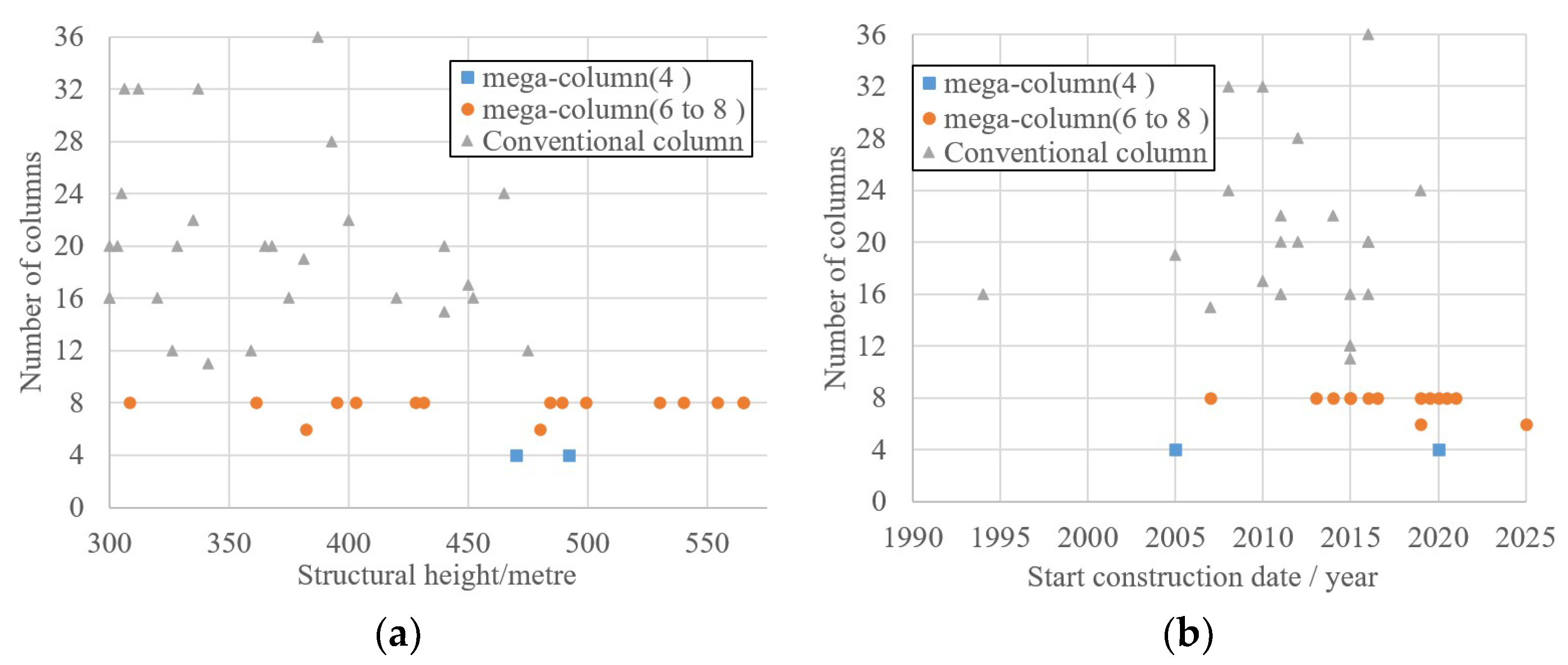



| Column Type | Square | Circle | Triangle | Other |
|---|---|---|---|---|
| 4 mega-columns | 2 | 0 | 0 | 0 |
| 6–8 mega-columns | 14 | 0 | 1 | 1 |
| conventional column (≥12) | 11 | 2 | 3 | 12 |
| Structural Indicator | 8-Col | 12-Col | 16-Col | 20-Col | |
|---|---|---|---|---|---|
| Period/s | T1 | 7.23 | 7.11 | 6.96 | 6.71 |
| T2 | 7.2 | 7.09 | 6.94 | 6.69 | |
| T3 | 4.37 | 4.42 | 4.22 | 4.11 | |
| Period Ratio | ≤0.85 | 0.60 | 0.62 | 0.61 | 0.61 |
| Displacement Angle (Maximum) | earthquake | 1/628 | 1/647 | 1/690 | 1/742 |
| wind | 1/1108 | 1/1137 | 1/1207 | 1/1230 | |
| Frame-Shear Ratio | >0.05 | 83% | 76% | 87% | 97% |
| >0.08 | 37% | 34% | 43% | 54% | |
| Shear Weight Ratio | 1.071% | 1.061% | 1.082% | 1.093% | |
| Seismic shear force/kN | 33,463 | 33,160 | 33,834 | 34,193 | |
| Total weight/t (D + 0.5L) | 328,198 | 329,149 | 315,453 | 311,667 | |
| Column steel consumption/t | 4894 | 5722 | 5587 | 5323 | |
| Total steel consumption/t | 25,959 | 25,628 (−1.3%) | 25,258 (−2.7%) | 24,048 (−7.4%) | |
| Structural Scheme | 8-Col | 12-Col | 16-Col | 20-Col |
|---|---|---|---|---|
| Structural Performance | reasonable | Needs transfer structure at the first floor, low efficiency | reasonable | Needs transfer structure at the first floor, low efficiency |
| Architectural Effect | Transparent, good | Transfer structure at the first floor, poor | relatively poor | Small column spacing, worst effect |
| Construction Complexity | General | General | General | General |
| Material Cost | Relatively high | Moderate | Relatively small | Minimum |
| Comprehensive Evaluation | Optimal | Poor | General | Poor |
| Model Number | Position of Removing the Belt Truss | Period/s (Adjusted) | Seismic Displacement Angle | Frame–Shear Ratio > 0.05 | Steel Consumption/t | ||||
|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | EX | EY | X | Y | |||
| 1 | No | 7.23 | 7.20 | 4.37 | 1/628 | 1/650 | 84% | 83% | 25,959 |
| 2 | 15F | 7.31 | 7.27 | 4.52 | 1/630 | 1/649 | 84% | 85% | 25,716 |
| 3 | 35F | 7.38 | 7.34 | 4.54 | 1/635 | 1/656 | 85% | 84% | 25,791 |
| 4 | 55F | 7.42 | 7.37 | 4.50 | 1/633 | 1/653 | 85% | 87% | 25,845 |
| 5 | 15F/35F | 7.43 | 7.39 | 4.68 | 1/633 | 1/651 | 85% | 87% | 25,613 |
| 6 | 35F/55F | 7.47 | 7.42 | 4.65 | 1/635 | 1/651 | 85% | 87% | 25,667 |
| 7 | 15F/55F | 7.54 | 7.49 | 4.67 | 1/640 | 1/659 | 89% | 87% | 25,742 |
| 8 | 15F/35F/55F | 7.61 | 7.56 | 4.81 | 1/637 | 1/652 | 91% | 89% | 25,602 |
| 9 | 15F/25F/45F/55F | 7.68 | 7.62 | 4.90 | 1/631 | 1/646 | 89% | 88% | 26,968 |
| Load Case | Results | Initial | Scheme 1 | Scheme 2 |
|---|---|---|---|---|
| Dead load | Floor slab stress/MPa | 7.0 | 5.6 | 5.1 |
| Torsional deformation of the belt truss/mm | 5.2 | 3.1 | 3.8 | |
| axial force of the floor beam/kN | 484 | 313 | 365 | |
| axial force of the horizontal bracing/kN | - | 238 | 181 | |
| Weak-axis bending moment of the belt truss chords/kN·m | 315 | 200 | 239 | |
| Rare Earthquake | Floor slab stress/MPa | 59.6 | 51.8 | 50.0 |
| Torsional deformation of the belt truss/mm | 2.3 | 1.4 | 1.9 | |
| axial force of the floor beam/kN | 422 | 228 | 297 | |
| axial force of the horizontal bracing/kN | - | 985 | 2553 | |
| Weak-axis bending moment of the belt truss chords/kN·m | 292 | 166 | 214 |
| Type of Member | Results | Before Removal | After Removal |
|---|---|---|---|
| Folded Exterior Frame Beam | Vertical deformation/mm | 7 | 103 |
| Axial force/kN | 370 | 1210 | |
| Strong-axis moment/kN·m | 2477 | 6494 | |
| Weak-axis moment/kN·m | 0.4 | 13 | |
| Torque/kN·m | 1.0 | 2.6 | |
| Gravity Column | Axial force/kN | 2543 | 26 |
| Strong-axis moment/kN·m | 237 | 1022 | |
| Weak-axis moment/kN·m | 1 | 1.6 | |
| Torque/kN·m | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Hao, W.; Cheng, W.; Wang, J.; Chen, H. Parametric Analysis of a 400-Meter Super-High-Rise Building: Global and Local Structural Behavior. Buildings 2025, 15, 3199. https://doi.org/10.3390/buildings15173199
Chen J, Hao W, Cheng W, Wang J, Chen H. Parametric Analysis of a 400-Meter Super-High-Rise Building: Global and Local Structural Behavior. Buildings. 2025; 15(17):3199. https://doi.org/10.3390/buildings15173199
Chicago/Turabian StyleChen, Jiafeng, Wei Hao, Weihong Cheng, Jie Wang, and Haokai Chen. 2025. "Parametric Analysis of a 400-Meter Super-High-Rise Building: Global and Local Structural Behavior" Buildings 15, no. 17: 3199. https://doi.org/10.3390/buildings15173199
APA StyleChen, J., Hao, W., Cheng, W., Wang, J., & Chen, H. (2025). Parametric Analysis of a 400-Meter Super-High-Rise Building: Global and Local Structural Behavior. Buildings, 15(17), 3199. https://doi.org/10.3390/buildings15173199





