Experimental Study on the Horizontal Bearing Performance of Pile–Soil Composite Foundation Under Coupled Action of Active and Passive Loads

Abstract

The pile–soil composite foundation system, highly acclaimed for its remarkable load-bearing capacity and limited deformation characteristics, has emerged as a fundamental element in geotechnical engineering practices. In the applications of adjacent slope engineering, such composite foundations are influenced by intricate loading scenarios. These scenarios involve both active vertical–horizontal combined load and passive soil-displacement forces generated due to the alteration of soil constraints. In this study, a self-designed movable retaining wall model box was employed. By applying different vertical and horizontal loads and controlling the rotation of the retaining wall around its base, a systematic investigation was conducted on the horizontal bearing mechanisms of single-pile and four-pile composite. The experimental data indicate that for every increment of 15 kPa in the vertical load, the horizontal bearing capacity experiences an average growth of approximately 18.9%, and the extreme value of the bending moment shows an average increase of 19.6. The analysis reveals coupled effects in internal force distribution and deformation patterns within load-bearing pile segments under concurrent active–passive loading conditions, while the embedded sections remain unaffected. Among four-pile composite foundations, the horizontal bearing mechanism of the front-row piles is consistent with that of a single-pile system. However, the maximum bending moments of the front-row and rear-row piles, compared to the single-pile system, have reached 0.68 times and 1.74 times, respectively. Notably, the bending moment of the front-row piles under the translational mode of the retaining wall is approximately 2.9 times that under the rotational mode, posing a potential risk of damage to the retaining structure, and necessary intervention is required. The results of this study provide a scientific basis for the force and deformation mechanism of piles at different positions in the composite foundation near foundation pit engineering, as well as their design for bending and shear resistance.

1. Introduction

With the development of society and economy, as well as the acceleration of urban renewal, urban land resources have become increasingly strained, posing various foundation treatment challenges for high-rise buildings and slope engineering. Pile–soil composite foundations, distinguished by their low settlement, broad applicability, and cost control advantages, have gained widespread implementation in contemporary construction projects. Particularly in adjacent slope engineering, as shown in Figure 1, these composite foundations not only bear vertical loads, horizontal loads, and overturning moments from above structures such as high-rises and secondary fill slope projects, but also face asymmetric lateral constraints from surrounding excavation slopes that alter soil-displacement patterns [1]. The lateral displacement of soil then acts as a passive load on piles, inducing additional bending moments and deformations [2,3,4]. Therefore, systematic research is needed to investigate the horizontal bearing characteristics of pile–soil composite foundations under both active and passive loads, revealing how their coupled effects influence foundation bearing performance.

Significant breakthroughs have been made in academic research on the horizontal bearing capacity of pile foundations. Sam et al. [5,6] and Zheng et al. [7,8] demonstrated through numerical simulation analysis that the application of vertical loads can significantly enhance the horizontal bearing capacity of piles. Zhao et al. [9] and Lu et al. [10] conducted experimental studies on the bearing characteristics of single piles under vertical–horizontal combined loads, finding that the pre-applied vertical loads can reduce soil displacement and bending moment values by compacting the soil around the piles. However, these studies did not quantify the contribution of vertical load changes to the horizontal bearing capacity. Moreover, for composite foundations with separated pile rafts, the cushion layer plays a role in load regulation, and its bearing mechanism differs from that of pile foundations. In recent years, scholars have extensively studied the bearing mechanism of disconnected piled rafts. Under vertical composite loads, the cushion layer not only regulates the load distribution but also controls settlement [11,12,13,14,15,16,17]. Most academic research on composite foundations has focused on vertical loads, but due to factors such as earthquakes, strong winds, and waves, foundation bases may be subjected to significant lateral loads [18,19,20]. Zhu et al. [21], Zheng et al. [22], Ma [23], and Liu et al. [24] conducted horizontal loading tests on composite foundations, revealing that both vertical loads and cushion layer thickness significantly affect the horizontal bearing capacity of composite foundations, with thicker cushion layers effectively reducing pile displacement. Scholars have also used numerical simulation methods to study the horizontal bearing mechanism of pile groups, revealing the group pile effect and the force–deformation mechanism of pile–soil interaction under horizontal loads [25,26,27]. Although numerous studies have provided the bearing mechanism of composite foundations under uniform vertical loads, many complex practical projects may impose non-uniform vertical loads on the composite foundation raft, complicating its bearing mechanism. Zheng et al. [28], Diao et al. [29], Wei et al. [30], and Zhang et al. [31] used numerical simulation to study the bearing characteristics of pile–soil composite foundations under embankment loads, finding that piles at different positions beneath the embankment exhibit differences in stress–deformation patterns and failure modes, providing design basis for piles at different positions under embankment loads. However, the working mechanism of foundation bases under active loads differs from that affected by soil lateral displacement. Li et al. [32] analyzed the influence of load sequences on the lateral soil–pile interaction caused by excavation, but the coordination mechanism of the cushion layer was lacking. Uge and Guo [33,34] proposed that there is an inevitable soil–structure interaction mechanism between existing pile–soil composite foundations and new foundation pits, especially among core components such as retaining walls, raft slabs, piles, cushion layers, and soil. Numerical simulation shows that as the retaining wall rotates into a new static equilibrium state, the load-sharing ratio of the piles continuously increases. Although previous studies have examined the behavior of piles under vertical–horizontal combined loads or soil-displacement effects, relatively few studies have focused on experimentally evaluating the coupled interaction between active structural loads and passive soil-induced displacements in pile–soil composite foundations, as well as the additional load differences caused by different movement types of retaining walls.

Regarding the complex horizontal bearing mechanism of composite foundations adjacent to foundation pit projects in dense urban areas, there is an urgent need to conduct relevant scientific research. This study employs a self-developed indoor testing apparatus to conduct loading tests on single-pile and four-pile composite foundations, and is dedicated to exploring the mechanism of the effect of vertical load variation on the horizontal bearing capacity of single-pile composite foundations, the differences in the horizontal bearing mechanism of composite foundations caused by the movement types of retaining walls, the group pile effect and coupling effect under the combined action of vertical–horizontal loads and passive loads. The aim is to clarify the specific contribution of vertical load increase to enhancing the horizontal bearing capacity, the differences in the horizontal bearing characteristics of front and rear rows of piles under the rotation and translation modes of retaining walls, and further to derive the transmission efficiency coefficient of horizontal loads (moments) during the transition from single-pile to four-pile composite foundations under the effect of group pile action.

2. Experimental Setup

The loading test is designed to simulate the load conditions borne by composite foundations as realistically as possible. Although full-scale field tests can mirror the actual environmental loading scenarios, during the implementation process, they are frequently restricted by uncontrollable external factors. These tests typically feature long durations, high costs, and low reproducibility. Indoor model tests apply analogous principles through the utilization of scaled-down models within the laboratory environment. Despite being constrained by spatial effects, scale reduction, and boundary conditions [35,36], compared to full-scale tests, indoor model tests possess distinct advantages. They include shorter experimental cycles, easier manipulation of key variables, and the capacity to repeatedly acquire data for in-depth theoretical analysis. In this research, multiple loading tests were carried out in a self-developed indoor model box. By rotating the retaining wall to realize the horizontally constrained deformation, the bearing characteristics under soil displacement were accurately modeled. The study further delved into how the combined influence of active loading and the rotational movement of the wall impacts the horizontal bearing performance of composite foundations.

2.1. Experimental Apparatus

2.1.1. Model Box

In this study, with the aim of investigating the elastic deformation of pile–soil during the loading test of the scaled-down model box, the Cauchy similarity principle was utilized. The intention was to ensure the stress equivalence between the model components and the prototype, as well as the consistency of the relative stiffness of the foundation components, thereby ensuring the accuracy of the experiment. A mobile retaining wall model box designed by the Institute of Geotechnical and Underground Engineering of Zhengzhou University was adopted (Figure 2a). The box measures 1.6 m × 1.6 m × 2.5 m (length × width × height). The pile spacing was set to four times the pile diameter. The minimum horizontal distance between the outer box and the pile side was five times the pile diameter, and the distance between the pile tip and the box was also five times the pile diameter. Given this, the influence of the boundary effect can be neglected [37]. A rigid movable retaining wall is positioned 0.8 m from the front frame, with upper and lower screw rods symmetrically arranged 0.2 m above and below its top and bottom edges (Figure 2b). Wall movement is achieved by rotating the screw rods connected to the outer fixed frame. Figure 2 shows a physical diagram of the experimental setup.

To meet stiffness requirements, the front wall is constructed with an 80 mm steel frame, 40 mm wooden panels, and 6 mm internal PVC boards. The rear wall consists of 5 mm steel plates with 10 articulated panels to monitor soil filling at the required height. Plastic film is attached to the inner surfaces of side walls to minimize friction effects. Guide rails are installed at the bottom of movable retaining box units for translational movement. Rollers measuring 650 mm × 330 mm × 60 mm (length × width × height) are placed on loading plates to reduce load deviations caused by horizontal displacement. The model loading system is illustrated in Figure 3.

2.1.2. Model Pile

In existing studies, the selection of pile material is mostly based on the pile length L and the elastic modulus E of the pile as the basic dimensions for similarity calculation. Given that the similarity ratio does not exert an influence on the horizontal stress, and on the premise that the stress remains invariant with the similarity ratio in this paper, the approach adopted herein is to uphold the consistency of the elastic modulus. Specifically, only the pile length is subject to scaling operations. In this study, the prototype pile used in the model test is a rigid C25 concrete pile with a diameter of 500 mm, a pile spacing of 4 D (D was the pile diameter)a length-to-diameter ratio of 20, an elastic modulus of 25 GPa, and an area replacement rate of 0.038. Following the similarity criterion, an aluminum alloy hollow tube with an elastic modulus of 72 GPa is used for fabrication. After calculation, the pile diameter is determined to be 100 mm and the wall thickness is 5 mm. The magnitude of the lateral frictional resistance of the model pile is influenced by the roughness of the pile shaft, the state of soil particles, and the magnitude of lateral stress. The primary physical factor affecting the lateral frictional resistance is the roughness of the model pile shaft. At present, the common methods for increasing the roughness of the model pile shaft mainly involve either adhering test sand or applying a knurling treatment to the pile surface. However, the method of adhering test sand poses challenges in quantitatively analyzing the impact of pile shaft roughness on the lateral frictional resistance. Therefore, in this study, a knurling treatment is applied to the pile surface to precisely control the roughness, as shown in Figure 4a. The shear strength and friction angle at the pile–soil interface can be determined through direct shear tests. The results of these tests are presented in Figure 4. Specifically, the measured friction angle at the pile–soil interface is 27.3° [38].

The strain gauges employed are of the BFH120-5AA-D150 type, with a resistance value of 120 Ω and a sensitivity coefficient of 2.0 ± 1%. The resistance value of the connecting wire is 0.5 Ω. Strain gauges that were symmetrically arranged on the inner surface of the pile body were installed at 200 mm intervals along the pile length to obtain axial response distribution (Figure 5a). The first and last strain gauges were positioned 100 mm from the pile end. During installation, all coaxial strain gauges were vertically aligned, with protective measures implemented to prevent damage or fracture of connectors caused by tension during testing. The cap at the pile top has a 20 mm thickness and features a groove at its top for routing wire through side openings, as shown in Figure 5b.

2.1.3. Test Soil

As a typical sediment in the alluvial plains of rivers around the world, silt demonstrates cross-regional similarities in terms of its grain-size distribution characteristics and sedimentation processes. In addition, silt widely represents various physical states, such as high-bearing capacity and low-bearing capacity, as well as liquefaction-prone and stable states. Therefore, it is applicable to multiple engineering scenarios, including building pile foundations, road subgrades, and foundation pits. The soil used in this model test was selected from sand samples in Zhengzhou city, which had negligible moisture content after undergoing air-drying and sun-drying treatments. In scale tests, when the B/d50 ratio (the ratio of the foundation diameter to characteristic particle size) exceeds 30, soil particle size reduction does not affect test results [39]. For the 100 mm diameter test piles, characteristic particles must be smaller than 2 mm. The soil contains approximately 82% particles larger than 0.075 mm by weight. According to the “Code for Design of Building Foundation” [34], the sand used in this model test is classified as silty sand. The particle gradation distribution of the test soil is shown in Figure 6.

In this study, the landfill was carried out using the method of artificial free-fall layer-by-layer filling. The designed thickness of each layer was 0.3 m. Subsequently, the sand was placed in the model box. After manual compaction and leveling, the density of the sand was measured. The filling of subsequent sand layers continued until the target height was achieved. The average density of the sand was 1640 kg/m³. The maximum and minimum dry densities of the sand were 1765 kg/m³ and 1606 kg/m³, respectively. After the filling was completed, the model foundation was allowed to rest for seven days before loading commenced. This was to ensure the stabilization of both the soil samples and the testing equipment. According to “Geotechnical Test Method Standard” [40], shear tests yielded an internal friction angle of 32.1 and cohesion of 3.4 kPa.

2.2. Load Scheme

Vertical and horizontal loads were applied using hydraulic jacks through step-loading. The loading sequence was first applying vertical loads to the predetermined value, then rotating the retaining wall via screw rods to achieve displacement at the present value, and finally applying horizontal loads up to the horizontal bearing capacity limit. During the step-loading and wall rotation processes, manual pressure replenishment was required for the vertical jacks to maintain a constant vertical load. The test loading device and layout are shown in Figure 7a,b.

2.2.1. Vertical Loading Scheme

According to existing research [41], in order to balance the equilibrium and accuracy of the application of vertical loads, conform to the progressive pattern of soil structural damage, and prevent impact damage, this study employed a multi-stage loading approach. A total of 8–12 load levels were set for the static load tests. In this experiment, a loading rate of 10 kPa per level was utilized to simulate the actual load increments of building floors. During the vertical loading procedure, the settlement of the loading plate is measured and recorded every 30 min. Once the settlement is found to be less than 0.1 mm over a consecutive period of 60 min, it can be deemed that the composite foundation has reached a stable state. At this point, the application of the next-stage vertical load can be carried out. The maximum loading capacity must not be less than twice the design-specified characteristic value of bearing capacity. When settlement reaches 1% of the bearing plate width, the corresponding load value shall serve as the basis for determining bearing capacity.

2.2.2. Wall Rotation Scheme

According to existing research findings [42], when the backfill soil of the retaining wall is sandy, the soil behind the wall reaches the active limit state when the displacement of the retaining wall is 0.2% to 0.3% of its height. Taking into account that the rotational displacement of the retaining wall ranges from 10 to 15 mm and the translational displacement ranges from 6 to 11 mm [43]. To facilitate the subsequent comparison of the differences between the rotational and translational modes, this study sets the displacement distance of both movement modes at 11 mm (55 × 10⁻⁴ rad). To ensure that the effect of the retaining wall movement is quasi-static, the data acquisition system records in real-time the data of the earth pressure cells and displacement transducers for each incremental rotation. Subsequently, data collection is carried out every five minutes. The next rotation of the retaining wall can be initiated only when the displacement variation of the loading plate is less than 0.017 mm within a continuous ten-minute period and the variation in the measured value of the earth pressure sensor is less than 0.5% of the rated deformation of the pressure cell.

2.2.3. Horizontal Loading Scheme

In the process of applying horizontal loads, this research employs a method that uses force as the control benchmark. According to existing research [44], during horizontal loading, data collection on pile shaft stress and displacement must be conducted using a slow maintenance load. The loading process applies a 0.5 KN horizontal load per stage, with horizontal displacement data from the loading plate recorded every 5 min. If the horizontal displacement remains below 0.1 mm for 20 consecutive minutes, it is considered that the composite foundation has reached a stable state, allowing progression to the next loading stage. When the displacement of the loading plate experiences a significant increase, or when the horizontal displacement under the current load is more than twice that of the previous loading stage, the loading process shall be terminated [45]. The horizontal loading value at this moment is defined as the ultimate horizontal bearing capacity of the composite foundation.

3. Results and Discussion

The loading tests were conducted on both single-pile and four-pile composite foundations, with separate loading trials performed under static retaining wall conditions and rotating retaining wall conditions. Specifically, four sets of horizontal loading tests were carried out on the single-pile composite foundation under varying vertical loads, aiming to investigate how changes in vertical load affect the horizontal bearing capacity of the composite foundation. This study provides fundamental insights for evaluating the horizontal bearing capacity of four-pile composite foundations under uneven vertical loading. To achieve differential loading at the top of front and rear piles, eccentric vertical loads were applied to the four-pile loading plate. The test groups are listed in

Table 1. Test Grouping.

Grouping	Cushion Thickness (mm)	Pile Length (mm)	Pile Diameter (mm)	Vertical Load (kPa)	Wall Rotation (mm)
Single Pile	50	2000	100	75	/
Single Pile	50	2000	100	90	/
Single Pile	50	2000	100	105	/
Single Pile	50	2000	100	120	/
Single Pile	50	2000	100	120	1
Single Pile	50	2000	100	120	3
Single Pile	50	2000	100	120	5
Single Pile	50	2000	100	120	7
Single Pile	50	2000	100	120	9
Single Pile	50	2000	100	120	11
Four Piles	50	2000	100	120 (Axial Load)	/
Four Piles	50	2000	100	120 (Axial Load)	11
Four Piles	50	2000	100	120 (Eccentric Load, e = L/10)	/
Four Piles	50	2000	100	120 (Eccentric Load, e = L/10)	11

.

3.1. Load Test of Single-Pile Composite Foundation Under Different Vertical Loads

3.1.1. Vertical Load–Settlement Curve

Figure 8 presents the load–settlement curve of a single-pile composite foundation under vertical loading, along with a comparison with the elastic theory and Terzaghi’s theory. The experimental results exhibit a high degree of consistency with the theoretical predictions. As is evident from the figure, different from the nonlinear load–settlement characteristics of the full-scale composite foundation, the load–settlement curve of the scaled-down model test exhibits linear development. The curve initially shows linear progression, but the settlement of the loading plate accelerates when the load exceeds 40 kPa. According to Code [46], the characteristic value of the composite foundation’s bearing capacity corresponds to a load of 110 kPa when S/B = 0.01 (where S represents the loading plate settlement and B denotes its width). Therefore, the vertical load groups for this test are determined as 75 kPa, 90 kPa, 105 kPa, and 120 kPa.

3.1.2. Pile–Soil Stress Ratio

As depicted in Figure 9b, when comparing the experimental results with the Poulos and Davis model, the trends of both are consistent. That is, the pile–soil stress ratio increases as the vertical load increases. Considering that the thickness of the cushion layer (0.05 m) is relatively thin, the calculation results somewhat exaggerate the dominant effect of the piles, thereby resulting in a pile–soil stress ratio higher than the experimental value. The average normal stress ratio between the pile top and soil increases from 6.2 to 9.49 with progressively applied vertical loads. In the range where the vertical load varies from 0 to 20 kPa, the pile–soil stress ratio exhibits a linear growth trend. When the vertical load exceeds 20 kPa, the stress-ratio curve experiences a sharp increase. Subsequently, as the load continues to increase, the rate of rise in the curve gradually decelerates. In the early stage of loading, the abrupt increase in the stress-ratio curve can be ascribed to the effect of the pile top penetrating into the cushion layer.

3.1.3. Horizontal Load–Displacement Analysis

The retaining wall was kept stationary while vertical and horizontal loads were sequentially applied in stages until the horizontal displacement of the loading plate showed a sharp increase, thereby terminating the loading process. The horizontal displacement changes in both the loading plate and pile top with increasing horizontal loads are illustrated in Figure 10a,b. When vertical loads were 75 kPa, 90 kPa, 105 kPa, and 120 kPa, respectively, the corresponding horizontal bearing capacities were 5.4 kN, 6.5 kN, 7.7 kN, and 9.1 kN. As the horizontal load increased, both the loading plate and pile top exhibited corresponding increases in horizontal displacement, with greater vertical loads correlating to higher horizontal bearing capacities. Under different vertical load conditions, the horizontal displacement of both the loading plate and the pile top followed a linear development from 0 to 3 kN. However, when the horizontal load exceeded 3 kN, the corresponding horizontal displacement decreased with increased vertical load. The increase in vertical load, by compacting the soil around the pile shaft, causes the soil particles to interlock more closely. This increases the shaft friction resistance of the pile, thereby significantly enhancing its capacity to resist horizontal deformation. Based on the existing p-y curve models for sandy soils, the horizontal load–displacement curve at the pile top is presented. A comparison with the experimental results is also included. The error is found to be 12%, indicating a relatively good agreement. The details are presented in the following Figure 10c.

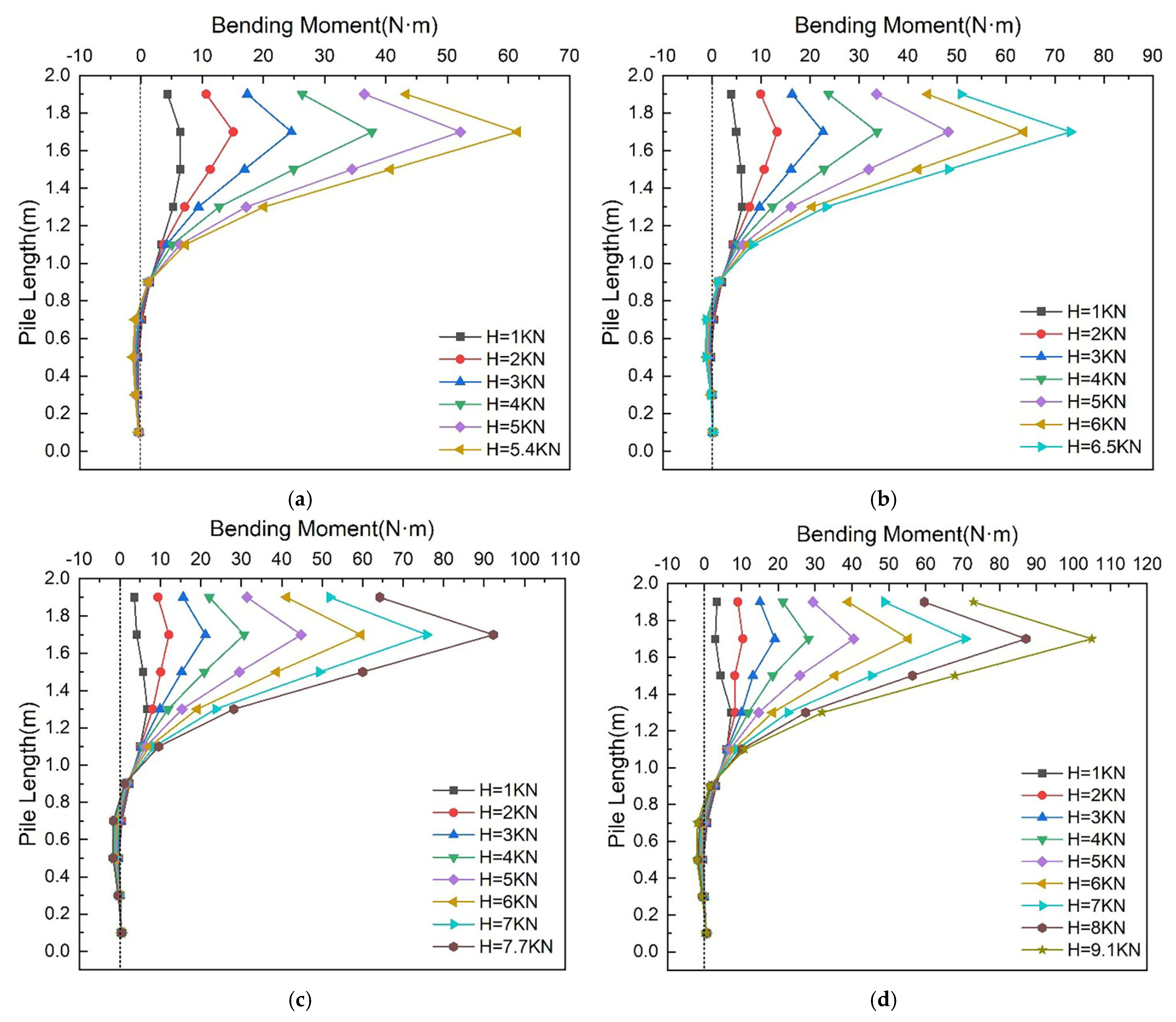
3.1.4. Pile Shaft Internal Force Analysis

The development of bending moments in single-pile composite foundations under varying vertical loads is illustrated in Figure 11. The bending moment distribution curve exhibits a parabolic form, with values initially increasing along the pile shaft then decreasing. The upper part of the pile primarily bears bending moments, reaching a peak at 1.7 m of the pile shaft. As shown in Figure 11, the greater the vertical load, the greater the horizontal bearing capacity of the composite foundation, and the greater the corresponding maximum bending moment of the pile body. The maximum bending moment corresponding to the vertical load of 120 kPa is 107 N·m, which is less than the design value of the prototype pile bending moment of 45.7 kN·m, meeting the design requirements. During the process when the vertical load increases from 75 kPa to 120 kPa, it is observed that the position of the zero-moment point migrates downward from 0.7 m to 0.5 m along the pile body.

Figure 12 shows the shear force diagram of the pile shaft. As the vertical load increased from 75 kPa to 120 kPa, the peak shearing force of the pile shaft rose from 359.4 N to 584.2 N, representing a 47.7% increase, which is less than the design shear force value of 192.4 kN for the prototype pile, meeting the requirements of the design specifications. A linear shear force distribution is observed along the pile top to 1.7 m of the pile shaft, with virtually zero shear force from 0.7 m of the pile shaft to the pile end. The elevated vertical load intensified horizontal load on the pile, which is transmitted deeper into the structure.

3.2. Effect of Retaining Wall Rotation on Horizontal Bearing Capacity of Single-Pile Composite Foundation

3.2.1. Analysis of Loading Plate Settlement Variation

Figure 13 illustrates the variation in settlement in a single-pile composite foundation loading plate under vertical load with the rotation displacement of the retaining wall. When the top of the retaining wall rotates by 11 mm, the settlement on the retaining wall-facing side reaches 20.7 mm, while that on the non-retaining wall side reaches 18.7 mm. Based on the classical retaining wall theories (Coulomb and Rankine), the significant settlement phenomenon at the front of the loading plate can be attributed to the fact that during the rotation of the retaining wall at the base, the significant displacement generated at the top causes the shallow soil mass to fail first. Thereafter, the slip surface gradually extends deeper until the area at the bottom of the wall reaches the limit equilibrium state.

3.2.2. Analysis of Pile Bending Moment Development During Rotating Process of Retaining Wall

Assuming the pile body experiences negative bending moments due to tensile forces away from the retaining wall, Figure 14 illustrates the development of bending moments in the pile during the retaining wall rotation. The maximum absolute value of the bending moment in the experimental data is −222 N·m, whereas the result obtained from the numerical analysis is −239 N·m. The error is 7.7%, which validates the reliability of the experimental data. Unlike horizontal loads that generate positive bending moments, the rotating retaining wall induces negative bending moments in the pile. This occurs because the rotation causes lateral settlement of soil adjacent to the retaining wall, resulting in stress redistribution in the soil ahead of the pile. Meanwhile, the soil behind the pile acts as a passive load, generating negative bending moments. These passive loads primarily affect the area from 0.8 m of the pile shaft to the pile top, with the maximum bending moment occurring at a distance five times the pile diameter from the pile top. In the traditional design of pile reinforcement, it is common practice to arrange the main steel bars at the lower part of the pile foundation to resist positive bending moments. However, when the pile body is subjected to passive loads resulting from lateral soil displacement, the upper part of the pile is under tension, necessitating the additional arrangement of steel bars for negative bending moments. Meanwhile, the area of negative bending moments is often accompanied by concentrated shear forces. Therefore, it is necessary to increase the density of closed stirrups near the inflection point of the pile body (i.e., at a position 0.8 m from the pile top) to enhance the overall structural stability.

3.3. Horizontal Bearing Performance of Single-Pile Composite Foundation Under the Coupling Action of Active and Passive Loads

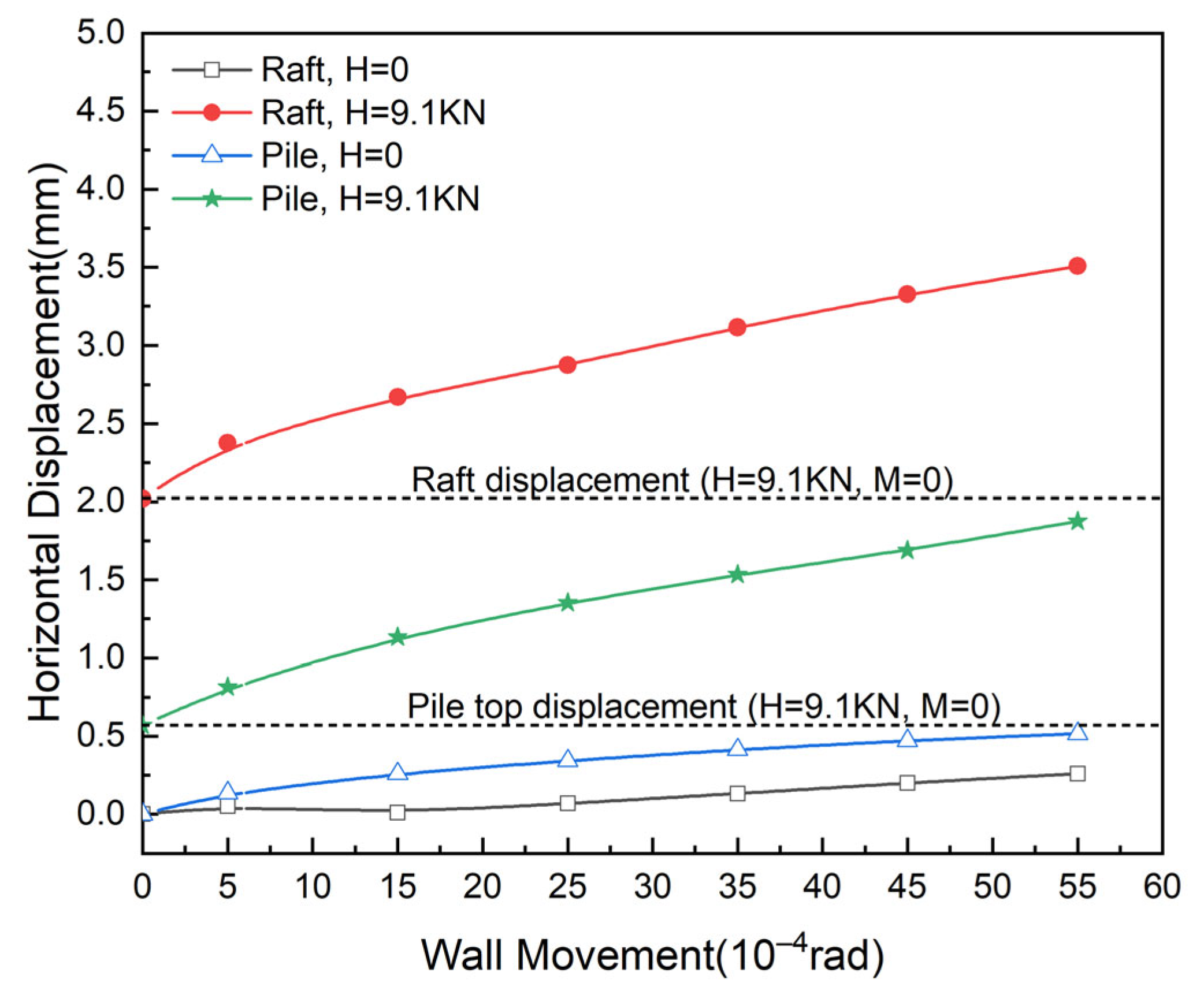
3.3.1. Analysis of Horizontal Displacement Variation Under the Coupling Action of Active and Passive Loads

Figure 15 illustrates the horizontal displacement changes in the loading plate and pile top under coupled active/passive loads. The data show that when only the active load is applied, the displacements reach 2 mm and 0.57, respectively, for both components. Under passive load alone, the displacements increase to 0.26 mm and 0.51 mm, respectively. However, when combined, the loading plate displacement rises from 2 mm to 3.51 mm, which is 1.55 times the superposition value of the active and passive loads. Meanwhile, the pile top displacement increases from 0.57 mm to 1.88 mm, representing 1.74 times the combined value. Under the condition of the combined action of active and passive loads, horizontal loads generate a nonlinear response in piles [47]. This is attributed to the fact that the movement of the soil mass leads to local unloading of the soil in front of the pile. Moreover, the action of the active load further expedites the process of soil stress redistribution. Comparing the results of this experiment, this paper argues that when active and passive loads are coupled, the horizontal displacements of the loading plate and the pile top should not be calculated merely by means of simple linear superposition. Therefore, when taking into account the influence of the nonlinear interaction between piles and soil under such working conditions, during the design process of evaluating the displacement of foundation structures, engineers should not rely merely on conservative traditional calculation methods. On the contrary, they should conduct a comprehensive assessment by integrating theoretical models, numerical analysis tools, and practical experience.

3.3.2. Analysis of Pile Bending Moment Under the Coupling Action of Active and Passive Loads

Figure 16a depicts the evolutionary process of the pile’s bending moment under the combined action of active and passive loads. It is particularly important to note that soil displacement does not influence the ultimate bearing capacity of the composite foundation; however, it can induce additional displacement and bending moment in the pile [48]. When the top of the retaining wall rotates from a stationary state to 11 mm, the peak value of the bending moment gradually transitions from positive to negative. After a rotation of 3 mm, the peak becomes negative, and its location shifts downward from 1.7 m to 1.3 m along the pile. Figure 16b presents the bending moment distributions under the individual actions of active and passive loads, as well as their combined action. The peak bending moment under the active load is 105 N·m, 222.3 N·m under the passive load, and the combined peak reaches −101.2 N·m. The bending moment distribution and its extreme values of the “embedded segment” below the zero-point position of the pile shaft bending moment (0.8 m) coincide with the superposed values obtained when considering active loads and passive loads separately. This indicates that this embedded segment is not significantly influenced by the coupled action of active and passive loads. Under the influence of the coupling effect of active and passive loads, the extreme value of the bending moment reverses and its position shifts downward, causing the failure mode of the pile to transform from shear failure to flexural failure. In light of this, it is essential to increase the reinforcement density in the region of the pile body with relatively weak flexural performance in the middle part.

3.4. Load Test of Four-Pile Composite Foundation

3.4.1. Pile–Soil Stress Ratio Comparison Analysis

The development of pile–soil stress ratios in single-pile and four-pile composite foundations under different loading methods is shown in Figure 17. In light of the interaction effects of group piles, the pile–soil stress ratio of a four-pile composite foundation under axial-loading conditions has increased by 8.4% as compared to that of a single pile. Moreover, influenced by the shielding effect of group piles, the load sharing of the soil in the four-pile foundation has decreased in comparison with that of a single pile. Notably, under eccentric loading (e = L/10), uneven vertical load distribution causes front-row pile P1 (11.5) to have a higher stress ratio than rear-row pile P2 (9.2). This demonstrates that when vertical stress reaches 120 kPa, the pile–soil stress ratio ranking is as follows: front-row piles of eccentrically loaded four-pile composite foundation > front-row piles of axially loaded four-pile composite foundation = back-row piles of axially loaded four-pile composite foundation > single-pile foundation > eccentric loading rear-row piles. This classification provides critical data for evaluating the horizontal bearing capacity of subsequent composite foundations.

3.4.2. Analysis and Comparison of Pile Shaft Bending Moment

Figure 18a,b present the bending moment diagrams of P1 and P2 piles subjected to vertical axial loading. For the front-row piles, the maximum bending moment of 71 N·m emerges at a pile depth of 1.7 m, which is in accordance with the bending moment distribution pattern of single piles. In contrast, the maximum bending moment of the rear-row piles attains 182.3 N·m, approximately 2.5 times the peak value of the front-row piles. This discrepancy stems from the fact that the rear-row piles are the first to endure the horizontal load, along with the “shielding” effect of the front-row piles. The front-row piles compress the soil in front and generate notable reactive forces, thereby resulting in the concentration of bending moments. Meanwhile, the stronger soil confinement acting on the front-row piles may reduce their bending moments. Figure 18c,d illustrate the bending moment distribution under vertical eccentric loading. Different from axial loading, the maximum bending moments of the front-row and rear-row piles are 152.4 N·m and 146.7 N·m, respectively, with a relatively homogeneous distribution. The horizontal ultimate bearing capacities of the composite foundation under axial and eccentric loading are remarkably close, being 28.4 kN and 28 kN, respectively. It is worth noting that the eccentric loading causes the front-row piles to reach a higher bending moment value than axial loading. Integrating the previous analysis of the pile–soil stress ratio, similar to single-pile composite foundations, in the four-pile composite foundation, the extreme values of the bending moments of each pile are proportional to the vertical loads they carry.

Figure 19a presents a comparison of the bending moment distributions of single-pile and four-pile composite foundation piles. Under the condition of a stationary retaining wall, the peak bending moment MP1 of the front-row piles reaches 0.68 times the maximum bending moment Ms of a single pile, while the peak bending moment MP2 of the rear-row piles attains 1.74 times Ms. This suggests that when transitioning from a single-pile foundation to a four-pile foundation, the transfer coefficients of horizontal load (bending moment) for the rear-row and front-row piles are 1.74 and 0.68, respectively. After the rotation of the retaining wall is completed, both the single pile and the front-row piles of the four-pile foundation exhibit similar bending moment patterns. Both show a tendency for the peak bending moment to shift from positive to negative and move downward, approaching −101.2 N·m and −97.6 N·m, respectively. Owing to the passive load induced by the lateral displacement of the soil around the piles, the maximum bending moment of the rear-row piles increases from 182.3 N·m to 219.2 N·m, leading to a more concentrated bending moment. Figure 19b depicts the bending moment diagram of the four-pile composite foundation under eccentric loading. The maximum bending moment of the front-row piles also changes from positive to negative. Due to the relatively large vertical stress they bear, these piles have a larger peak bending moment (−147 N·m). Conversely, the maximum bending moment of the rear-row piles increases to 202.2 N·m, which is lower than the extreme bending moment under axial-loading conditions.

Integrating the foregoing research findings, significant differences exist in the bending moment values of the front-row and rear-row piles before and after the rotation of the retaining wall. Generally speaking, the bending moment values of the rear-row piles are consistently higher than those of the front-row piles, and the positions of the extreme bending moment values remain the same. This suggests that the upper part of the rear-row piles requires corresponding reinforcement measures. Simultaneously, under the influence of the load coupling effect, the front-row piles are more susceptible to bending failure. Therefore, reinforcement measures should also be implemented in the middle section of the pile body.

4. Numerical Simulation Analysis

A numerical model was established using the ABAQUS simulation software, with a 1:1 scale comparison to the laboratory test model (Figure 20). The accuracy of the numerical model was validated through a comparative analysis between its simulation results and experimental data. Through detailed examination of the numerical simulations, this study further investigates the horizontal bearing mechanisms of single-pile and four-pile composite foundations, while conducting comparative analyses on the horizontal bearing performance of a four-pile composite foundation under the retaining wall translation mode.

4.1. Test Verification and Analysis

The grid elements of the numerical model are discretized using eight-node linear brick elements (C3D8R) with simplified integration and hourglass control. The material behaviors of the cushion layer and the soil are characterized by the elastic–perfectly plastic Mohr–Coulomb constitutive model. The material parameters for the simulation tests are set in accordance with those of the model tests, as presented in

Table 2. Material parameters.

Materials	Density (kg/m3)	Elastic Modulus (MPa)	Poisson Ratio	Cohesion (kPa)	Internal Friction Angle (°)
Cushion	1416	30	0.3	3.2	35
Soil	1640	20	0.3	3.4	32.1
Raft	7800	220,000	0.15	/	/
Pile	2500	20,000	0.2	/	/
Retaining Wall	7800	200,000	0.2	/	/

. During the vertical loading process, normal constraints are imposed on the four lateral faces of the loading plate to limit its horizontal displacement. In the stages of retaining wall displacement and horizontal loading, the restrictions on horizontal displacement in the directions of retaining wall rotation and horizontal loading are released. This enables the structure to displace freely under the actions of retaining wall displacement and horizontal loads.

Figure 21 shows the distribution of pile bending moments for single-pile and four-pile composite foundations. It can be seen that the results of the numerical simulation and model test are basically consistent, with RMSE = 13.1%, which verifies the accuracy of the model test results and the rationality of the numerical simulation parameter setting.

4.1.1. Horizontal Load Sharing Between Pile and Soil

The pile–soil composite foundation transfers the upper load to the piles and inter-pile soil through the cushion layer. The soil resistance, side friction of the plate, and bottom friction share the horizontal load acting on the loading plate. The friction between the loading plate and the top of the cushion layer is transmitted to the pile and inter-pile soil through the friction between the cushion layer and inter-pile soil, as well as between the cushion layer and the pile top. As shown in Figure 22a, under the rotational action of the retaining wall, the horizontal load sharing of single-pile and four-pile composite foundation piles under axial loading initially decreases briefly before rising. Specifically, the load sharing of the single-pile composite foundation pile increases from 9.2% (static condition of the retaining wall) to 14.6%, a rise of 5.4 percentage points, while that of the four-pile composite foundation piles increases from 20.7% to 21.7%. Correspondingly, the load sharing of the soil first increases briefly before decreasing. Under eccentric loading, the load-sharing ratio of the four-pile composite foundation piles initially increases from 20.2% to 21.8% before decreasing to 20.3%. The horizontal load borne by the piles remains consistent before and after the rotation of the retaining wall. It can be inferred that during the transition from a single-pile to a four-pile composite foundation, the horizontal load sharing of the piles significantly increases. Moreover, under axial loading, the horizontal load-sharing ratio of the front-row piles in the four-pile composite foundation gradually changes from 9.97% to 10.1% during the rotation of the retaining wall, showing a slight increase before and after the wall rotation. Under eccentric loading, the horizontal load-sharing ratio of the front-row piles decreases from 13.8% to 11.6%, yet remains higher than that under axial loading. This indicates that when the retaining wall is stationary, the greater vertical load under eccentric loading causes the front-row piles to bear more horizontal load compared to the axial-loading condition. However, as the retaining wall rotates, the stress redistribution in the soil surrounding the front-row piles partially offsets the effect of the additional vertical load, thereby balancing the load sharing, as illustrated in Figure 22b.

4.1.2. Horizontal Displacement of Pile Shaft

The displacement curves of single-pile and four-pile composite foundations under varying horizontal loads are shown in Figure 23. It can be observed that the maximum displacement at the pile top of the single-pile composite foundation is 0.56 mm, which is smaller than the displacements at the pile tops of both the front and rear rows in the four-pile composite foundation. Specifically, under axial loading, the displacement at the pile top of the rear-row pile P2 in the four-pile composite foundation is 1.71 mm, greater than the 1.18 mm displacement at the pile top of the front-row pile P1. This is because the rear-row pile is located at the leading edge of the horizontal load and is the first to bear the load, while the front-row pile is “shielded” by the rear-row pile, resulting in more stable soil restraint. Under eccentric loading, the displacements at the pile tops of both the front-row pile P1 and rear-row pile P2 are approximately 1.1 mm, both smaller than those under axial loading. This is attributed to the denser soil in front of the pile, resulting from eccentric loading, which enhances the restraint on the pile. Unlike axial loading, the horizontal displacement of the embedded section of the front-row pile under eccentric loading is smaller. Based on these observations, the ranking of pile top displacements is as follows: single-pile composite foundation < front-row pile of four-pile composite foundation (eccentric-loading) = rear-row pile of four-pile composite foundation (eccentric-loading) < front-row pile of four-pile composite foundation (axial-loading) < rear-row pile of four-pile composite foundation (axial-loading).

Figure 24 illustrates the horizontal displacement of single pile and front-row piles in four-pile composite foundations under horizontal loading during the rotational displacement process of the retaining wall. The figure reveals that the single pile in the composite foundation and the front-row pile P1 in the four-pile composite foundation exhibit similar deformation patterns after the wall rotation. Due to the settlement of soil near the wall side and the thrust from the rear soil, the upper section of the pile gradually transitions from a state of tension deformation to one of compression deformation. The displacement at the pile top of the single-pile composite foundation develops from 1.05 mm to 2.6 mm, while the maximum displacement shifts to 1.5 m along the pile shaft due to compression deformation, reaching 2.7 mm. For the front-row pile in the four-pile composite foundation, the pile top displacement under axial loading increases significantly from 1.18 mm to 5.6 mm, while under eccentric loading, it rises from 0.56 mm to 1.87 mm. Consistent with the deformation of the single pile in the composite foundation, the maximum displacement occurs at a depth of 1.5 m along the pile shaft, measuring 1.89 mm. Based on the analysis of pile–soil stress ratios under various loading conditions, it can be concluded that when the constraint condition of the soil in front of the pile remains consistent. The order of pile top displacement is as follows: single-pile composite foundation < front-row pile in four-pile composite foundation (eccentric-loading) < front-row pile in four-pile composite foundation (axial-loading).

It is noteworthy that, considering 0.3%H as the allowable displacement value of the pile, through calculation, the horizontal displacement safety margins of the piles under the above three working conditions after the rotation of the retaining wall are as follows: 0.57 for single piles, 0.69 for eccentric loading, and 0.07 for axial loading. Evidently, the front-row piles under axial loading require timely intervention to guarantee the stability of the supporting structure.

4.2. Analysis of Horizontal Bearing Performance of Four-Pile Composite Foundation Under Retaining Wall Translational Movement

Both the translational mode and rotational mode of retaining walls induce lateral displacement of foundation soil; their influencing mechanisms differ. When there is no load acting on the back of the retaining wall, with the increase in the translational displacement of the wall, the sliding surface gradually undergoes plastic deformation from the bottom of the wall and the soil surface extending towards the middle of the soil mass [40]. Therefore, it is necessary to conduct analytical research on the horizontal bearing performance of pile-reinforced composite foundations under wall translation, as shown in Figure 25.

4.2.1. Comparative Analysis of Horizontal Displacement at Pile Top

Unlike the rotational mode, when the retaining wall undergoes a translational displacement of 11 mm (55 × 10⁻⁴ rad), the pile top displacements of both the front-row and rear-row piles exceed those under the rotational mode, reaching 8.1 mm and 7.6 mm, respectively. Moreover, the pile top displacement of the front-row pile surpasses that of the rear-row pile after 7 mm of translational movement. This occurs because the translational mode causes the sliding surface to penetrate the pile–soil composite foundation. Both the front-row and rear-row piles above the sliding surface are affected by soil lateral movement, with the rear-row piles and their surrounding soil continuously pushing the front-row piles, resulting in a sustained linear increase in pile top displacement, as shown in Figure 26. In consideration of the safety of the supporting structure, taking 6 mm (0.3 H) as the allowable horizontal displacement, both the front-row and rear-row piles under the translational mode of the retaining wall have exceeded the displacement threshold. Necessary interventions are required to ensure the stability of the supporting structure.

4.2.2. Comparative Analysis of Horizontal Load Sharing

Figure 27a shows the horizontal load sharing between the pile and the soil under two movement modes of the retaining wall. It can be observed that the horizontal load borne by the pile under both modes initially decreases briefly and then continues to increase as the wall moves. After the wall moves by 11 mm (55 × 10⁻⁴ rad), the horizontal load carried by the pile in the translational mode exceeds that in the rotational mode, increasing from 20.7% to 24.4%. This indicates that the pile bears a greater horizontal load in the translational mode. Figure 27b compares the horizontal load sharing of front-row piles under rotational and translational modes as the wall displacement increases. It can be observed that when the distance from the retaining wall remains constant, the horizontal load sharing of front-row piles in the translational mode rises from 10% to 12.4%, which is greater than that in the rotational mode.

4.2.3. Analysis of Pile Bending Moment

Figure 28 depicts the bending moment distribution of the piles under the translational mode. The development of the bending moment in the front-row piles is analogous to that under the rotational mode. The maximum bending moment value is −291 N·m, approximately 2.9 times that under the rotational mode. This is attributable to the fact that the rear-row piles are also directly influenced by the lateral displacement of the soil mass. The lateral displacement continuously propels the soil mass forward, thereby imposing greater compressive stress on the front-row piles. The maximum bending moment of the rear-row piles initially decreases and subsequently increases. In the range from the stationary state to a translational displacement of 5 mm, the maximum bending moment decreases from 191.2 N·m to 121.5 N·m and then rises to 199.4 N·m as the retaining wall continues to move. Through the analysis of the pile bending moments under the two motion modes of the retaining wall, it can be observed that the bending moments of the front-row piles transform from positive to negative in both modes. However, the front-row piles experience a significantly larger bending moment in the translational mode. Simultaneously, the maximum bending moment of the rear-row piles in the translational mode is smaller than that in the rotational mode. This finding establishes a quantitative correlation between the displacement mode of the retaining wall and its bending moment response. The quantified result of 2.9 times the bending moment provides a key basis for design modification in high-risk projects, such as deep foundation pits and landslide-retaining works.

Under the translational mode of the retaining wall, the dramatic increase in bending moment has a cascading impact on the failure modes of the pile foundation. This bending moment amplification effect significantly raises the instability risk of the pile-group system by modifying the internal force distribution within the piles and the response of the foundation soil. The possible exceeding of the bending moment limit can lead to the direct bending failure of the pile foundation. Moreover, when the passive earth pressure surpasses the allowable lateral bearing capacity of the foundation soil, which results in the loss of control of the lateral displacement of the pile body. Therefore, during the construction process, it is necessary to strengthen the intervention in the displacement mode and conduct flexural reinforcement for the front-row piles.

5. Conclusions

In this paper, indoor model tests were carried out to systematically investigate the horizontal bearing performance of single-pile composite foundations under different vertical loads and that of four-pile composite foundations under the coupled action of active and passive loads. Through numerical simulation verification, the bearing mechanism of four-pile composite foundations under the translation mode of the retaining wall was further analyzed and compared. The main conclusions are as follows:

(1)

The horizontal bearing capacity of the pile–soil composite foundation can be enhanced by increasing the vertical load. With every increment of 15 kPa in the vertical load, the horizontal bearing capacity on average experiences an increase of approximately 18.9%. Simultaneously, the bending moment value also rises by 19.6%. Under the same horizontal load, a larger vertical load can reduce the displacement of the loading plate and pile top.

(2)

Under vertical load, the pile–soil stress ratio of the single-pile composite foundation increases from 9.5% to 22.4% during the rotation of the retaining wall, representing a 136% increase. The rotation of the retaining wall induces a negative bending moment in the pile shaft, away from the retaining wall, with the bending moment extremum continuously increasing as the rotation distance grows, reaching its maximum at a depth of 1.5 m in the pile shaft.

(3)

The lateral displacement of the soil induced by the rotation of the retaining wall, acting as a passive load, does not impact the horizontal ultimate bearing capacity of the composite foundation. When the active and passive loads act concurrently, a nonlinear coupling effect will occur in the pile–soil interaction. The horizontal displacement values of the loading plate and the pile top are, respectively, 1.55 times and 1.74 times the linearly superposed displacement values. Similarly, under the influence of the coupling effect, the extreme value of the bending moment in the loaded section of the pile changes from positive to negative, and its position moves downward. Thus, it is necessary to take into account the densification of steel bars in the middle part of the pile body.

(4)

Eccentric loading exerts no notable influence on the horizontal ultimate bearing capacity of the four-pile composite foundation. Taking into account the interaction effects of pile groups, during the transition from a single pile to a four-pile composite foundation, the bending moment values of the front-row and rear-row piles are approximately 0.68 times and 1.74 times that of a single pile, respectively. After the rotation of the retaining wall is completed, the development of the bending moment of the front-row piles tends to be consistent with that of a single pile. The extreme bending moment shifts downward and changes from positive to negative. In light of this, it is necessary to reinforce the upper part of the rear-row piles that bear relatively large bending moments and the middle part of the front-row piles to withstand failures of structures.

(5)

Under the translational mode of the retaining wall, both the displacement value at the pile top and the horizontal load-sharing value are higher than those under the rotational mode. As the translational displacement of the retaining wall increases, the bending moment of the rear-row piles first decreases and then increases. In contrast, the bending moment of the front-row piles increases significantly, reaching approximately 2.9 times that under the rotational mode, which implies a risk of instability and failure. Therefore, corresponding intervention measures must be implemented in accordance with the results of the safety assessment of the foundation structure.

Due to the lack of detailed reports on the test soil samples and the infeasibility of conducting repeated loading tests attributable to the protracted test cycle, there exists scope for enhancing the accuracy of the test data in this study. Moreover, the theoretical calculation methods for evaluating the horizontal load sharing between piles and soil, taking into account the nonlinear coupling effects, have not been established yet. Hence, follow-up research is of great significance. Finally, large-scale field tests should be implemented in the future to delve deeper into the coupling mechanism between displacement and bending moment within complex strata.