Multidimensional Urbanization and Housing Price Changes: Evidence from 35 Large- and Medium-Sized Cities in China

Abstract

To address the issue of spatial mismatch of real estate resources at its source, we incorporate the multidimensional urbanization speeds into the real estate market stock-flow model, simulate the regional real estate resource allocation process from a dynamic perspective, and explore the impact of urbanization on housing prices, as well as the characteristics that a coordinated multidimensional urbanization should possess. Utilizing data on population flow, economic development, and the relative increment of newly built housing units that meet delivery standards from 2008 to 2022 in 35 large- and medium-sized cities in China. We employ the dynamic panel system GMM approach to estimate the direct effect of single-dimensional urbanization on housing prices, and utilize the threshold effect model to examine the comprehensive effect of multidimensional urbanization on housing prices. The findings reveal that population, economic, and spatial urbanization influence housing prices by altering the flow of real estate supply and demand, with their effects being significantly shaped by the scarcity of stock real estate resources. The dynamic coordination of multidimensional urbanization ρ has a significant threshold effect on housing price changes. When Vsu and Vpu reach the optimal match, the real estate market achieves dynamic equilibrium, and housing prices remain relatively stable. This not only underscores the significance of multidimensional urbanization as a driver of urban housing price variations but also provides valuable insights for cities on how to adjust the quantity of new residential construction (or land supply) during the dynamic urbanization process, thereby enhancing the spatial allocation rationality of real estate resources from the source.

1. Introduction

Among the numerous factors influencing the allocation of real estate resources, multidimensional urbanization exerts a complex and subtle impact on regional housing markets. As a dynamic process that encompasses population, economic, and spatial urbanization [1,2,3], multidimensional urbanization affects urban real estate markets from both the supply and demand sides: spatial urbanization, manifested in infrastructure development and real estate construction, reflects changes in supply, whereas population and economic urbanization drive changes in demand [4,5,6,7]. In essence, multidimensional urbanization continuously influences urban housing markets by altering the flow of supply and demand. Moreover, urbanization in China is characterized by a contrast between government-led spatial urbanization and market-driven population and economic urbanization [8,9,10]. These dimensions often lack coherent coordination. Particularly under current land allocation policies that favor industrial use and counteract population concentration trends [11], many cities suffer from serious misalignment among dimensions of urbanization [12,13]. The issue of spatial mismatch among population, land, and housing is particularly acute [14,15,16,17]. Therefore, the degree of coordination in multidimensional urbanization reflects both the structural (long-term) and cyclical (short-term) supply–demand imbalances in different housing markets. Against this backdrop, an in-depth examination of the role of multidimensional urbanization in the housing market is of significant theoretical and practical value in tracing the allocation process of real estate resources and improving their rational distribution at the source.

In 1998, with the abolition of the housing welfare distribution system, China’s real estate industry entered a period of rapid development. By 2014, the supply and demand in China’s real estate market had reached a total balance, but regional imbalance, that is, the problem of regional differentiation in the real estate market was very prominent [18]. Faced with this situation, relevant state departments and governments at all levels have repeatedly emphasized the principle of “one city, one policy” in real estate regulation. On 21 February 2024, the Ministry of Housing and Urban–Rural Development issued the Notice on Improving Housing Development Planning and Annual Planning (Document No. 20 [2024]), calling on local authorities to determine housing demand based on population changes, methodically adjust land supply according to housing demand, and guide the allocation of financial resources to promote a balance between supply and demand in the real estate market. Given the immobility of real estate and the mobility of population and capital, housing markets in specific regions face unique supply–demand dynamics. Therefore, in-depth research on the supply and demand conditions of the real estate market in different regions is the foundation for optimizing real estate regulatory policies.

Numerous researchers have analyzed the causes of regional differentiation in the real estate market [19,20,21,22], among which the most common is the discussion on the regional differentiation of housing prices [23,24]. For example, Han Libin et al. (2018) [25] argue that spatial mismatches in land supply and demand contribute to regional housing price divergence, and Ni Pengfei (2019) [26] finds that spatial mismatches in housing supply and demand are a major factor responsible for the price gap between large and small cities. Although prior studies have recognized differences in supply–demand conditions as a key cause of regional disparities in housing prices and have considered the rationality of the spatial allocation of real estate resources, the authors of the majority of these studies primarily concentrate on outcomes rather than the processes of real estate allocation. They also rarely explore how to improve the rationality of its configuration from the source. Given that the urbanization process and the allocation of urban real estate resources exhibit a certain degree of synchronicity, in this study, we expand the housing supply–demand model within an urbanization framework. Starting from the speed of multidimensional urbanization, we attempt to investigate, from a dynamic perspective, how urbanization leads to changes in housing prices.

Real estate, as a durable consumer good, consists of both existing housing stock and newly constructed units on the supply side. On the demand side, it encompasses both residential and investment needs due to its dual functionality. We first adopt a stock–flow model of the real estate market that incorporates all of these elements and integrates the speeds of multidimensional urbanization to analyze how such urbanizations lead to supply–demand fluctuations in the real estate market. Secondly, we apply a dynamic panel system GMM model to estimate the impact of multidimensional urbanization speeds on changes in housing prices. Lastly, a panel threshold effect model is constructed to examine whether the dynamic characteristics of multidimensional urbanization—determined by the speeds of population, economic, and spatial urbanization—exhibit a threshold effect on housing price changes. The aim is to further elucidate the mechanisms behind housing price fluctuations during urbanization and to offer targeted policy recommendations for promoting the coordinated development of urbanization and the housing market, including strategies for “digesting the existing housing stock and optimizing the new supply.”

The innovations of this study are as follows: (1) Innovative analytical perspective: While the authors of prior studies have identified patterned relationships between urbanization level, development stage, coordination, and housing prices, we adopt a novel dynamic perspective by focusing on the speed of multidimensional urbanization to explore its influence on housing prices. (2) Innovative analysis method: By integrating the speeds of multidimensional urbanization into a stock–flow model of the housing market, we can more accurately quantify the short-term fluctuations in supply and demand induced by urbanization. This approach also sheds light on the underlying processes of regional real estate resource allocation. Additionally, the use of system GMM estimation and threshold effect analysis enables a precise understanding of how different urbanization dimensions drive changes in housing prices. (3) Innovative focus of real estate regulation: Regulatory measures such as purchase and sale restrictions focus on the spatial allocation results of real estate resources and fail to fundamentally solve the problem of its mismatch. Based on the relationship between population, spatial urbanization speeds, and housing price changes when the real estate market achieves partial equilibrium in the process of urbanization, methodically adjusting residential development or land supply facilitates the shift from regulating the spatial allocation results of real estate resources to controlling the process. In addition, examining the connection between multidimensional urbanization speed, coordination, and housing prices not only offers deeper insights into the process of regional real estate resource allocation and the impact of flow markets on stock markets, but also furnishes a relatively novel theoretical foundation for cities to ascertain the number of newly constructed housing units in the new market environment and establish a “supply and demand linked” real estate supply model.

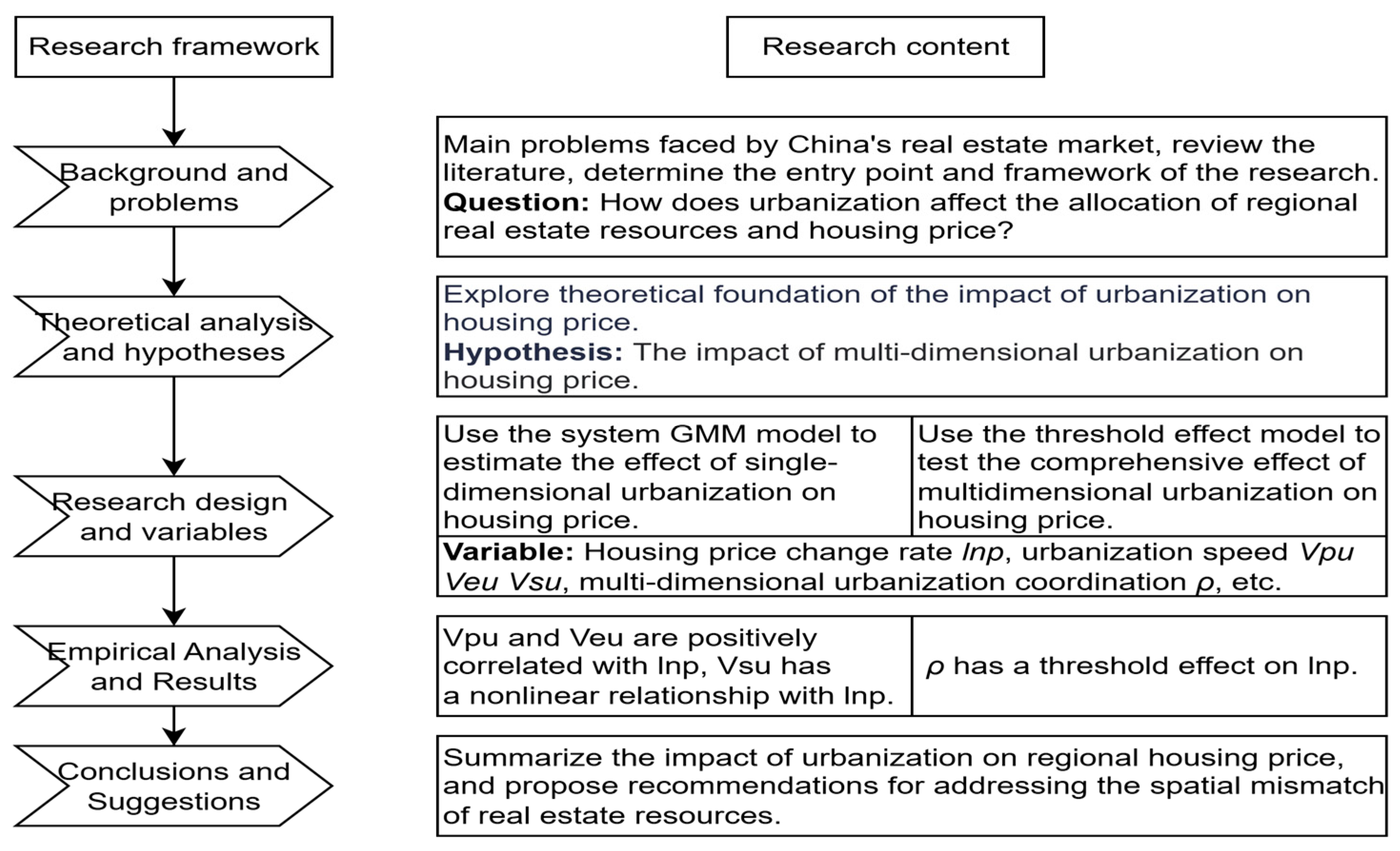
In summary, the objective of this study is to accurately describe the process of regional real estate resource allocation behind multidimensional urbanization to comprehensively depict the impact of multidimensional urbanization on housing prices, and to delve into how to enhance the rationality of spatial allocation of real estate resources from its source. The research framework and main content of this paper are illustrated in Figure 1.

2. Theoretical Analysis and Research Hypotheses

Incorporating all dimensions of urbanization into the real estate market model not only enables a more accurate depiction of the fluctuations in real estate supply and demand driven by multidimensional urbanization, but also facilitates the determination of how each region can enhance the rational allocation of real estate resources based on equilibrium conditions. Hanushek and Quigley (1979) [27] and DiPasquale and Wheaton (1994) [28] both employed stock–flow models to investigate the issue of dynamic equilibrium in the real estate market. This model assumes that housing demand is the product of population size and per capita living area, with investment demand being a linear function of the expected growth rate in housing prices. Accordingly, the demand function of the real estate market in a given location at time t can be expressed as Equation (1):

$$D_t={pp}_{t}la+\theta ∆P_{t+1}^e,$$

(1)

D_t denotes the housing demand in a given locality at time t; pp_t represents the permanent population at time t; la is per capita living area, treated as a constant in this paper; θ is a positive constant representing the adjustment coefficient; Δ$P_{t+1}^e$ = (P_t+1 − P_t)/P_t is the expected growth rate of housing prices, where P_t+1 and P_t are the housing prices at time t + 1 and t, respectively.

The real estate supply S_t consists of the housing stock S_t−1 from the previous period t − 1 and the new supply (flow) ΔS_t in the period t. Accordingly, the supply function of the real estate market in a given region at time t is represented by Equation (2):

$$S_t=S_{t-1}+∆S_t,$$

(2)

To more effectively capture the impact of multidimensional urbanization on housing supply and demand, we incorporate urbanization speeds into the stock–flow model. Although the standard academic definition of urbanization speed is the annual average rate of change in the urbanization level [29,30], we note that real estate residential demand is determined by the total urban population, and population urbanization is closely linked to the emergence of new basic housing needs [31]. We therefore use the rate of change in permanent population to represent the speed of population urbanization (Vpu), which can effectively measure fluctuations in residential demand caused by population change. Thus, we define: Vpu_t = (pp_t − pp_t−1)/pp_t−1. The speed of spatial urbanization (Vsu) refers to the annual growth rate of the floor area of buildings or the area of construction land [32], which intuitively reflects the fluctuation in housing supply. Therefore, we define Vsu_t = ΔS_t/S_t−1. Assuming rational expectations by consumers, we posit that Δ$P_{t+1}^e$ = ΔP_t+1. Furthermore, housing markets are assumed to gradually clear after each period’s stock is formed, and prices adjust based on supply–demand dynamics. Hence, ΔP_t+1 is determined by the supply and demand flows in period t. In order to focus on the spatial allocation of factors such as population, land, and housing during urbanization, the effect of economic urbanization on supply and demand is temporarily excluded (it is analyzed later for robustness testing). We therefore define: ΔP_t+1 = μ${\displaystyle \frac{{Vpu}_t-{Vsu}_t}{1+{Vsu}_t }}$. Here, μ is a positive constant. Accordingly, Equations (1) and (2) can be rewritten as Equations (3) and (4), respectively.

$$D_t={pp}_{t-1}(1+{Vpu}_t)la+\theta \mu {\displaystyle \frac{{Vpu}_t-{Vsu}_t}{1+{Vsu}_t }},$$

(3)

$$S_t=S_{t-1}(1+{Vsu}_t),$$

(4)

Since housing prices adjust after the stock of each period is formed, we substituted S_t−1 = D_t−1, D_t−1 = pp_t−1la + θΔP into Equation (4). We derive the relationship between ΔP_t and Vpu_t, Vsu_t under local market equilibrium, as shown in Equation (5):

$$∆P_t={\displaystyle \frac{{Vpu}_t-{Vsu}_t}{1+{Vsu}_t }}({\displaystyle \frac{{pp}_{t-1}la}{\mu }}+{\displaystyle \frac{\theta }{1+{Vsu}_t }}),$$

(5)

Because pp_t−1la, θ, and μ are all positive, based on the relationships in Equation (5) and the existing literature on the effects of population migration and housing supply on price fluctuations [33,34,35], we propose two hypotheses from a dynamic perspective:

Hypothesis 1.

The speed of population urbanization is positively correlated with changes in housing prices; that is, faster population urbanization leads to housing price increases.

Hypothesis 2.

The speed of spatial urbanization is negatively correlated with changes in housing prices; that is, faster spatial urbanization leads to housing price decreases.

In recent years, changes in urban housing prices in China have shown not only significant spatial disparities but also strong spatial autocorrelation [36]. Factors such as urban economic growth, the scale of the real estate market, land supply, and housing policies have been identified as key drivers of these price changes [37,38]. Notably, these factors correspond to different dimensions of urbanization. To better understand the overall impact of multidimensional urbanization on housing price changes, we draw on the findings of Xie Fuquan et al. 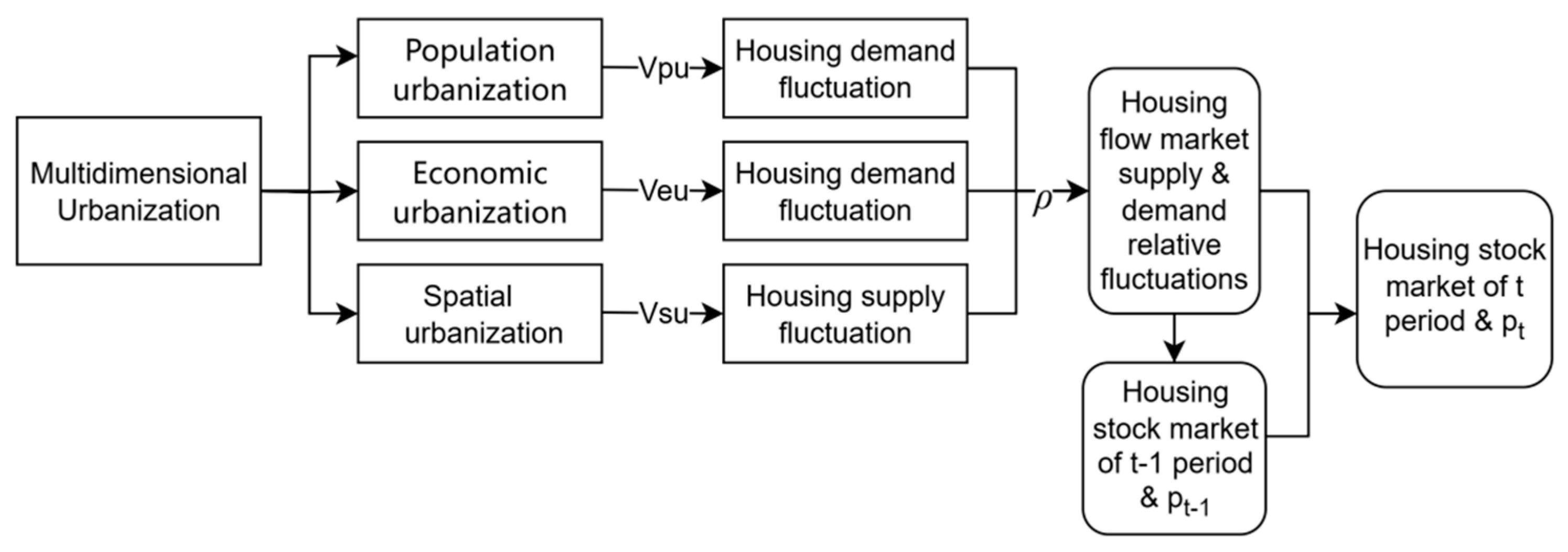(2017) [5], who, in their study of the long-term cointegration and short-term dynamics between urbanization and the real estate market in Shanghai, concluded that improving the coordination of multidimensional urbanization is crucial for promoting the healthy development of the real estate market. The authors of this study additionally explore how the dynamic coordination of multidimensional urbanization affects housing price changes and how such coordination can be improved to ensure harmony between urbanization and the real estate market. To address these questions, we constructed an index to measure the dynamic coordination of multidimensional urbanization: ρ = (Vpu − Vsu)/(1 + Vsu). Based on Equation (5), ρ captures the degree of dynamic coordination in multidimensional urbanization and reflects the presence of an optimal coordination range and the potential threshold that determines whether housing prices rise or fall. Therefore, to investigate the specific influence of multidimensional urbanization’s dynamic coordination on housing price changes, the following hypothesis is proposed:

Hypothesis 3.

The dynamic coordination index ρ of multidimensional urbanization exhibits a threshold effect on changes in housing prices.

The relationships between the relevant concepts presented in this paper and the general research approach are shown in Figure 2.

3. Research Design

3.1. Variable Selection

To visually illustrate the dynamic relationship between multidimensional urbanization and the real estate market, we establish a set of variables that reflect how fluctuations in urbanization processes influence the supply–demand balance in the real estate market, ultimately leading to changes in housing prices. The specific variables and their definitions are presented in

Table 1. Names and meanings of key variables.

Variables	Symbols	Name and Meaning
Dependent Variable	lnPt	Housing price change rate, lnpt = log(Pt)
Instrumental Variables	Pt−1	Average selling price of commercial housing in Phase t − 1
Independent Variables	Vpu	Population urbanization speed, Vpu = (ppt − ppt−1)/ppt−1
	Veu	Economic urbanization speed, Veu = (pcdit − pcdit−1)/pcdit−1
	Vsu	Spatial urbanization speed, VsuH = ΔSH/St−1, VsuL = ΔSL/St−1
Control Variables	Pd	Population density within the jurisdiction (people/km2)
	Gc	Green coverage rate of built-up area (%)
	Lir	Personal housing provident fund loan interest rate (%)
Threshold Variable	ρ	Multidimensional urbanization coordination, ρH = (Vpu − VsuH)/(1 + VsuH), ρL = (Vpu − VsuL)/(1 + VsuL)

Data sources: Compiled by the authors.

.

3.1.1. Dependent Variable

Housing price change rate (lnpit): P_it is calculated based on the average sales price of commercial housing (residential) in city i in year t (yuan/m²), and the natural logarithm is taken to reflect the housing price change rate.

3.1.2. Independent Variables

Population urbanization speed (Vpu), economic urbanization speed (Veu), and spatial urbanization speed (Vsu): Vpu represents changes in housing demand driven by urban population growth. It is measured as the growth rate of permanent population pp(in tens of thousands): (pp_t − pp_t−1)/pp_t−1. Veu reflects the urban economic development status, measured by the growth rate of per capita disposable income (in RMB): (pcdi_t − pcdi_t−1)/pcdi_t−1. Vsu reflects the relative changes in housing market supply. Since new supply can be measured either by the total completed residential floor area in period t (in 10,000 m²), denoted as ΔS_H, or by the land area ΔS_L acquired by real estate development enterprises in period t − 1 (typically reflecting the development cycle of over one year), accordingly, two separate indicators are derived: Vsu_H and Vsu_L based on Vsu_t = ΔS_t/S_t−1.

3.1.3. Instrumental Variable

The housing price in period t − 1 (P_t−1) is not only highly correlated with the endogenous explanatory variable that requires substitution in the model, but it is also uncorrelated with other exogenous variables and random error terms. Furthermore, housing prices in individual cities are typically adjusted based on their levels in the previous period, t − 1. Therefore, P_t−1 is employed as an instrumental variable to analyze the inertia and trajectory of housing price changes across different cities.

3.1.4. Control Variables

Population density (Pd), green coverage rate (Gc), and personal housing provident fund loan interest rate (Lir): Referring to the control variables selected in studies by Antoniucci V. et al. (2016) [39], Zhou J. et al. (2021) [40], and Yu S. et al. (2024) [41] on the impact of urbanization on housing prices, and considering that the average housing prices of each city are influenced not only by supply and demand, but also by regional socioeconomic development and housing regulation policies, we include the following control variables: Population density (Pd, people/km²) within the city’s jurisdiction, green coverage rate of urban built-up areas (Gc, %), and the interest rate on personal housing provident fund loans for terms over five years (Lir, %). These variables can, to some extent, reflect regional heterogeneity and help eliminate city-specific effects to the greatest extent possible.

3.1.5. Threshold Variable

Dynamic coordination of multidimensional urbanization (ρ): Since ρ reflects both the dynamic coordination of multidimensional urbanization and determines the direction and magnitude of housing price changes, it is set as the threshold variable to analyze whether it exhibits a threshold effect on housing price changes. If a significant threshold effect exists, it would indicate that multidimensional urbanization with different characteristics is a crucial factor leading to abrupt changes in housing prices. Given that Vsu is measured both as Vsu_H and Vsu_L, the corresponding ρ indicators are denoted as ρ_H and ρ_L, respectively.

3.2. Model Specification

3.2.1. Dynamic Panel Model

To examine the impact of multidimensional urbanization on housing price changes from a dynamic perspective, we established a dynamic panel model, as shown in Equation (6):

$$ln{P}_{it}={\beta }_{1}ln{P}_{it-1}{+\beta }_2{Vpu}_{it}+{\beta }_3{Veu}_{it}+{\beta }_4{Vsu}_{it}+{\beta }_{5}ln{Pd}_{it}+{\beta }_6{Gc}_{it}+{\beta }_7{Lir}_{it}+{\epsilon }_{it}$$

(6)

In Equation (6), lnp_it denotes the housing price growth rate in city i in year t; P_it−1 is the lagged housing price; Vpu_it, Veu_it, and Vsu_it represent the population, economic, and spatial urbanization speeds in city i in year t, respectively; Pd_it, Gc_it, and Lir_it are the control variables for population density, green coverage rate, and provident fund loan interest rate; β₁–β₇ are parameters to be estimated; and ε_it is the random error term.

3.2.2. Threshold Effect Model

To explore the comprehensive impact of multidimensional urbanization on housing prices, we incorporate the index ρ_it, which describes the dynamic coordination of multidimensional urbanization, into model (6). However, to avoid multicollinearity, the model only examines the effects of ρ_it and Vsu_it on lnp_it. Based on Hansen’s threshold effect model (1953) [42], which identifies threshold points or regions at which the intercept or slope of a model shifts as an explanatory variable reaches a critical value, we constructed a panel threshold effect model, as shown in Equation (7):

$$\begin{gathered} ln{P}_{it}={\beta }_{1}ln{P}_{it-1}+{\beta }_2{Vsu}_{it}({\rho }_{it}\le {\gamma }_1)+{\beta }_3{Vsu}_{it}({\gamma }_1<{\rho }_{it}\le {\gamma }_2)+{\beta }_4{Vsu}_{it}({\gamma }_2 \\ <{\rho }_{it})+{\beta }_{5}ln{Pd}_{it}+{\beta }_6{Gc}_{it}+{\beta }_7{Lir}_{it}+{\epsilon }_{it} \end{gathered}$$

(7)

In Equation (7), ρ_it is the threshold variable, γ₁ and γ₂ are the threshold values, and all other variables are as defined in Model (6). This model enables us to test whether accelerating the process of spatial urbanization—i.e., expanding housing supply—will lead to a structural change in housing price trends when ρ_it reaches threshold values. It also helps identify the dynamic characteristics that coordinated multidimensional urbanization should exhibit based on γ₁ or γ₂.

3.3. Data Sources and Processing

The housing market data used in this study are derived from the China Real Estate Statistical Yearbook (2009–2023). Since this yearbook contains statistics for only 35 large- and medium-sized cities, and these cities present different characteristics in terms of geographical location, natural resources, and economic development, the selection of samples and data has a certain degree of objectivity and representativeness. Data on multidimensional urbanization and control variables are sourced from the China Urban Statistical Yearbook and the China Statistical Yearbook (2009–2023). The variables ρ_it, Vpu_it, Veu_it, and Vsu_it are calculated based on the definitions, formulas, and raw data provided in this paper. To eliminate the influence of the index dimension and heteroscedasticity and to facilitate system GMM estimation, all non-percentage indicators are logarithmically transformed.

3.4. Descriptive Statistics

Descriptive statistics for all variables used in the model are presented in

Table 2. Descriptive statistical results of variables.

Variables	Symbols	Mean	Std. Dev.	Min	Max
Dependent Variable	lnPt	9.096	0.569	7.875	10.98
Instrumental Variables	Pt−1	10,004	7640	2378	58,593
Independent Variables	Vpu	0.024	0.043	−0.120	0.318
	Veu	0.089	0.045	−0.204	0.262
	VsuH	0.049	0.026	0.005	0.165
	VsuL	0.026	0.024	0.001	0.180
Control Variables	Pd	4785	2943	557	15,055
	Gc	40.54	3.953	23.04	49.77
	Lir	3.834	0.640	3.210	4.970
Threshold Variables	ρH	−0.023	0.045	−0.183	0.221
	ρL	−0.001	0.048	−0.162	0.256

Data sources: “China Real Estate Statistical Yearbook”, “China Urban Statistical Yearbook”, and “China Statistical Yearbook” from 2009 to 2023.

. As shown in Table 2, most cities experienced increases in housing prices during most years from 2008 to 2022. Regarding P_t−1, substantial variation is observed across different cities and time periods, with the maximum value exceeding the minimum by more than 24 times. Based on the average values of urbanization speeds, economic urbanization generally outpaces spatial urbanization, which in turn outpaces population urbanization—initially indicating that multidimensional urbanization is uncoordinated in most cities. Notable differences exist between the mean values of Vsu_H and Vsu_L, which is attributable to the fact that they are based on different statistical indicators of new real estate supply—specifically, Vsu_H is measured by the cumulative completed floor area of housing in period t (ΔS_H), while Vsu_L is measured by the land area acquired by real estate development enterprises in period t − 1 (ΔS_L). Given that the floor area ratio during housing development is typically much greater than 1, Vsu_H is significantly larger than Vsu_L. In addition, the descriptive statistics of the control variables and the threshold variable accurately reflect the heterogeneity across cities.

4. System GMM Estimation of the Impact of Multidimensional Urbanization on Housing Price Changes

To address unobserved individual heterogeneity, omitted variable bias, and potential endogeneity, we employed a GMM suitable for dynamic panel data. All data tests and regression analyses described in this section were implemented using Stata 17.0.

4.1. Data Diagnostics

To avoid spurious regression, all variables are subjected to stationarity tests before parameter estimation. To ensure the reliability of the results, the data undergo unit root, cointegration, and endogeneity tests. Since we utilized short panel data in this study, the LLC, Kao, Pedroni, and Hausman tests were employed (see

Table 3. Data verification results.

Types	Method	Statistics	Statistic Value	p Value
Unit root test	LLC	Adjusted T (lnpt)	−7.870	0.00
		Adjusted T (lnpt−1)	−8.606	0.00
		Adjusted T (Vpu)	−15.803	0.00
		Adjusted T (Veu)	−20.282	0.00
		Adjusted T (VsuH)	−1.375	0.04
		Adjusted T (VsuL)	−8.286	0.00
		Adjusted T (lnPd)	−9.392	0.00
		Adjusted T (Gc)	−3.115	0.00
		Adjusted T (Lir)	−1.993	0.02
Cointegration test	Kao	Modified Dickey–Fuller T	−14.073	0.00
		Dickey–Fuller T	−16.195	0.00
		Augmented Dickey–Fuller	−9.870	0.00
	Pedroni	Modified Phillips-Perron T	8.287	0.00
		Augmented Dickey–Fuller T	−8.178	0.00
Endogeneity test	Hausman	Chi2 test value	181.55	0.00

Data sources: as above.

for the results). As shown in Table 3, all p-values associated with the unit root tests are less than 0.05, indicating the absence of unit roots and justifying model estimation. In the cointegration tests, the p-values corresponding to the various T-statistics are all zero, suggesting that the variables are not cointegrated. The Hausman test yields a p-value less than 0.05, indicating the presence of endogeneity among the variables; therefore, a fixed-effects analysis is more appropriate.

4.2. System GMM Estimation for Dynamic Panel Models

It can be observed from the results presented in

Table 4. GMM regression results of the dynamic panel system.

Variables	6-1	6-2	6-3	6-4	6-5	6-6	6-7
	lnPt	lnPt	lnPt	lnPt	lnPt	lnPt	lnPt
lnPt−1	0.882 *** (91.84)	0.883 *** (91.59)	0.630 *** (21.05)	0.629 *** (21.02)	0.627 *** (20.79)	0.612 *** (19.81)	0.684 *** (20.76)
Vpu		0.413 *** (4.15)	0.517 *** (5.76)	0.502 *** (5.52)	0.499 *** (5.49)	0.498 *** (5.47)	0.388 *** (4.12)
Veu			0.288 *** (8.86)	0.282 *** (8.48)	0.284 *** (8.50)	0.280 *** (8.35)	0.134 *** (3.38)
VsuH				−0.282 (−0.94)	−0.268 (−0.89)	−0.290 (−0.96)	0.349 (1.09)
lnPd					0.0127 (0.62)	0.0136 (0.66)	0.0386 (1.82)
Gc						0.0058 * (2.06)	0.0071 * (2.48)
Lir							−0.0610 *** (−7.12)
Constant	1.145 *** (13.13)	1.124 *** (10.71)	0.403 *** (3.57)	0.495 *** (3.32)	0.386 ** (1.68)	0.318 ** (1.37)	1.130 *** (4.30)
Wald-value	8434.73	8391.76	10,561.12	10,574.86	10,581.40	10,578.73	10,200.96
Hansen p	1.000	1.000	1.000	1.000	1.000	1.000	1.000
AR(1) p	0.002	0.002	0.002	0.003	0.003	0.004	0.004
AR(2) p	0.954	0.922	0.874	0.831	0.793	0.757	0.742
Sample size	490	490	490	490	490	490	490

Note: ***, **, and * respectively represent significance at the 1%, 5%, and 10% levels, and the values in parentheses are t-statistics.

that during the process of progressively incorporating instrumental variables, explanatory variables, and control variables (Models 6-1 to 6-7), the Wald value consistently increases. This finding suggests that the explanatory power of the selected variable combination on the dependent variable is steadily improving and that model (6) demonstrates strong explanatory power regarding the relationship between multidimensional urbanization and housing price changes. Based on the regression coefficient and significance of lnp_t−1, it can be inferred that the trend of housing price changes in period t − 1 will be transmitted to period t to a degree of over 60%, and the greater the fluctuation amplitude in period t − 1, the higher the impact on housing prices in period t, and vice versa. This finding implies that housing price changes in various cities exhibit strong inertia. The regression coefficients show that multidimensional urbanization and city-specific effects reduce the influence of P_t−1. The impact of single-dimensional urbanization on real estate prices can be characterized as follows: acceleration in population and economic urbanization significantly increases housing prices, with population urbanization exerting a stronger effect than economic urbanization. This finding supports Hypothesis 1. The regression coefficient of Vsu_H shows that accelerating spatial urbanization may lead to either a decline or an increase in housing prices, thus indicating that Hypothesis 2 cannot precisely capture the impact of supply-side changes in housing prices. This ambiguity warrants further exploration of the impact of multidimensional urbanization on housing prices from multiple perspectives.

There exists an insignificant positive correlation among population density, green coverage rate, and housing prices, which aligns well with expected patterns. As population density rises, the residential demand per unit of land area intensifies, making it more likely to drive up housing prices. Additionally, the enhancement of urban living environments stimulates an increase in real estate demand, subsequently inflating housing prices. Moreover, a 1% increase in the individual housing provident fund loan interest rate is associated with a 6.1% decline in housing prices, and this effect is significant at the 1% level. This finding suggests that stringent housing regulation policies can effectively suppress housing price inflation.

4.3. Heterogeneity Analysis of System GMM Estimation for Dynamic Panel Models

To explore the impact of multidimensional urbanization on housing prices from additional perspectives, we further classify and re-estimate the sample based on temporal and spatial heterogeneity. First, considering that 2014 served as a “watershed” for achieving an overall balance between supply and demand in China’s real estate market [18], and that the real estate market faced a relatively severe liquidity crunch after 2020 [43], we analyze data from two distinct phases—2008–2014 and 2015–2020—based on variations in supply and demand conditions within the real estate stock market. As evident from the regression coefficients presented in

Table 5. Results of the heterogeneity test.

Variables	Different Periods		Different Regions
	Phase 1	Phase 2	Eastern	Central	Western
	lnPt	lnPt	lnPt	lnPt	lnPt
lnPt−1	0.510 *** (8.80)	0.497 *** (8.69)	0.631 *** (13.96)	0.698 *** (8.15)	0.667 *** (10.93)
Vpu	0.741 *** (4.34)	0.064 (0.58)	0.311 (1.72)	0.465 *** (3.94)	0.147 (1.11)
Veu	0.253 *** (3.81)	0.584 *** (6.27)	0.164 ** (2.75)	0.0735 (0.81)	0.183 ** (2.86)
VsuH	0.208 (0.41)	0.128 (0.27)	0.500 (1.09)	−0.0934 (−0.16)	−1.438 *** (−3.41)
lnPd	−0.0308 (−0.82)	0.0199 (0.57)	0.0223 (0.75)	0.0147 (0.65)	0.0309 (1.56)
Gc	0.0085 (1.90)	0.0000 (0.01)	0.0081 (1.40)	0.0014 (0.40)	0.0008 (0.24)
Lir	−0.0124 (−0.64)	2.864 *** (7.47)	−0.0962 *** (−7.56)	−0.0574 *** (−3.31)	0.0012 (0.08)
Constant	1.764 *** (4.13)	−10.97 *** (−6.87)	1.618 *** (3.92)	2.014 *** (5.49)	0.864 * (2.46)
Wald-value	1033.45	1859.33	4682.27	2453.49	3317.86
Sample size	210	245	224	112	154

Note: ***, **, and * respectively represent significance at the 1%, 5%, and 10% levels, and the values in parentheses are t-statistics.

, during the first phase, population urbanization emerged as the primary factor inflating housing prices, with economic urbanization taking second place, while spatial urbanization exhibited an insignificant positive correlation with housing prices. In the second phase, economic urbanization assumed the role of the primary catalyst for housing price increases, with the influence of population and spatial urbanization notably decreasing. Secondly, based on the geographical locations and socio-economic development environments of 35 large- and medium-sized cities, the sample is categorized into three major regions: Eastern, Central, and Western. According to Table 5, there exist notable regional variations in the influence of multidimensional urbanization on housing prices. In the Eastern region, economic urbanization exhibits the strongest impact on inflating housing prices. In the Central region, population urbanization emerges as the primary catalyst for increasing housing prices. In the Western region, while population and economic urbanization have a considerable impact on inflating housing prices, accelerating spatial urbanization results in a steep decline in housing prices.

By examining the characteristics of multidimensional urbanization and the supply–demand dynamics in the real estate stock market across various periods and regions, we have observed that while the effect of accelerating population and economic urbanization on inflating housing prices remains consistent, the extent of their individual impacts has undergone some variations. This finding suggests that, against different historical backdrops, people’s rigid residential needs, upgraded residential demands, and investment demands for real estate have each played a pivotal role in pushing up housing prices. From the stock–flow model’s perspective, accelerating spatial urbanization augments the relative supply of real estate. However, this may result in both a decrease and an increase in housing prices. This discrepancy stems from our oversight of the fact that the housing prices discussed in the text pertain specifically to the average selling prices of newly built commercial residential properties. As a unique commodity characterized by pronounced and ubiquitous individual differences, housing prices are influenced by various factors beyond supply and demand, including construction costs, geographical location, and ancillary qualities of the houses. While spatial urbanization entails the construction of new homes, it also optimizes urban public resources and enhances the urban living environment. Consequently, it is understandable why spatial urbanization may lead to a slight increase in housing prices.

5. Threshold Effect Analysis of Multidimensional Urbanization on Housing Price Changes

Given that, in the preceding text, the comprehensive effects of multidimensional urbanization on housing prices are overlooked and there was a lack of exploration as to why accelerated spatial urbanization can result in both a decline and an increase in housing prices, we employed model (7) to investigate whether the dynamic coordination of multidimensional urbanization ρ exhibits a threshold effect on housing price fluctuations.

5.1. Threshold Effect Testing and Threshold Value Estimation

Through 500 bootstrap resampling tests, it has been established that both ρ_H and ρ_L demonstrate a relatively significant double threshold effect on changes in housing prices, passing the significance test at the 1% level. The test results are outlined in

Table 6. Existence test of threshold effect.

Variable	Model	RSS	MSE	F-Value	p-Value	Critical Value
						10%	5%	1%
ρH	Single threshold	4.84	0.01	9.86	0.18	12.32	15.82	31.28
	Double threshold	4.54	0.01	33.50	0.00	14.86	19.22	26.66
	Triple threshold	4.45	0.01	9.61	0.64	25.87	33.22	66.19
ρL	Single threshold	4.89	0.01	10.83	0.32	16.61	22.05	31.61
	Double threshold	4.22	0.01	82.23	0.00	11.90	13.59	18.68
	Triple threshold	4.13	0.01	10.01	0.53	90.60	108.33	142.86

Note: The p-value and F-value were obtained after 500 self-sampling times through bootstrapping.

, with their respective threshold estimates along with the 95% confidence intervals detailed in

Table 7. Double threshold estimates and 95% confidence intervals.

Threshold Variable	Threshold Value	Estimated Value	95% Confidence Interval
ρH	γ1	0.0037	0.0011	0.0139
	γ2	0.0088	−0.0003	0.0090
ρL	γ1	0.0560	0.0415	0.0575
	γ2	0.0669	0.0592	0.0762

Note: γ and the confidence interval were obtained after 500 self-sampling sessions through bootstrapping.

.

5.2. Estimation Results of the Threshold Effect

As shown in the parameter estimation results in

Table 8. Threshold effect estimation and robustness test results.

Estimation of Threshold Effect Parameters				Robustness Test
Variables	lnPt	Variables	lnPt	Variables	lnPt
lnPt−1	0.771 *** (45.73)	lnPt−1	0.790 *** (48.75)	lnPt−1	0.768 *** (45.68)
VsuH (ρH ≤ γ1)	−0.657 ** (−2.75)	VsuL (ρL ≤ γ1)	−0.211 (−0.88)	VsuH (ρE ≤ γ1)	−0.641 ** (−2.66)
VsuH (γ1 < ρH ≤ γ2)	−4.255 *** (−6.30)	VsuL (γ1 < ρL ≤ γ2)	−16.12 *** (−9.31)	VsuH (γ1 < ρE ≤ γ2)	−3.886 *** (−6.70)
VsuH (γ2 < ρH)	0.198 * (2.32)	VsuL (γ2 < ρL)	1.045 * (2.50)	VsuH (γ2 < ρE)	−0.387 (−0.90)
LnPd	0.0181 (1.36)	lnPd	0.0136 (1.06)	lnPd	0.0278 (2.10)
Gc	0.0023 (1.11)	Gc	0.0010 (0.51)	Gc	0.0028 (1.36)
Lir	−0.0853 *** (−9.02)	Lir	−0.0812 *** (−8.67)	Lir	−0.0829 *** (−7.96)
Constant	2.259 *** (10.99)	Constant	2.133 *** (11.01)	Constant	2.178 *** (10.58)
Sample size	525	Sample size	525	Sample size	525

Note: ***, **, and * respectively represent significance at the 1%, 5%, and 10% levels, and the values in parentheses are t-statistics.

, the effects of instrumental variables and control variables on housing prices remain largely unchanged. The threshold variable ρ_H has the following impact on housing prices: when ρ_H ≤ 0.0037, a 1% increase in Vsu_H leads to a 0.657% decrease in housing prices; when 0.0037 < ρ_H ≤ 0.0088, a 1% increase in Vsu_H results in a 4.255% decrease in housing prices; when ρ_H > 0.0088, a 1% increase in Vsu_H results in a 0.198% increase in housing prices; notably, when ρ_H = 0.088, the impact of Vsu_H on housing prices is zero, and at this point, changes in the relative supply of real estate cause a “V”-shaped reversal in the trend of housing price changes. Since ρ = (Vpu − Vsu)/(1 + Vsu), the underlying reason can be understood as follows: when ρ_H is small, the real estate flow market is in a state of oversupply. At this point, increasing housing supply is akin to “adding insult to injury,” causing housing prices to plummet rapidly; when ρ_H is large, the real estate flow market is in a state of insufficient supply. At this point, increasing housing supply is like “a drought ending with rain,” though it may not immediately cause housing prices to decline, it will weaken the upward trend in housing prices. ρ_L also has a similar impact on housing prices, though the threshold values vary. It is particularly important to note that when 0.056 < ρ_L ≤ 0.0669, a 1% increase in Vsu_L results in a 16.12% decrease in housing prices; when ρ_L = 0.0669, the trend in housing prices also undergoes a “V”-shaped reversal.

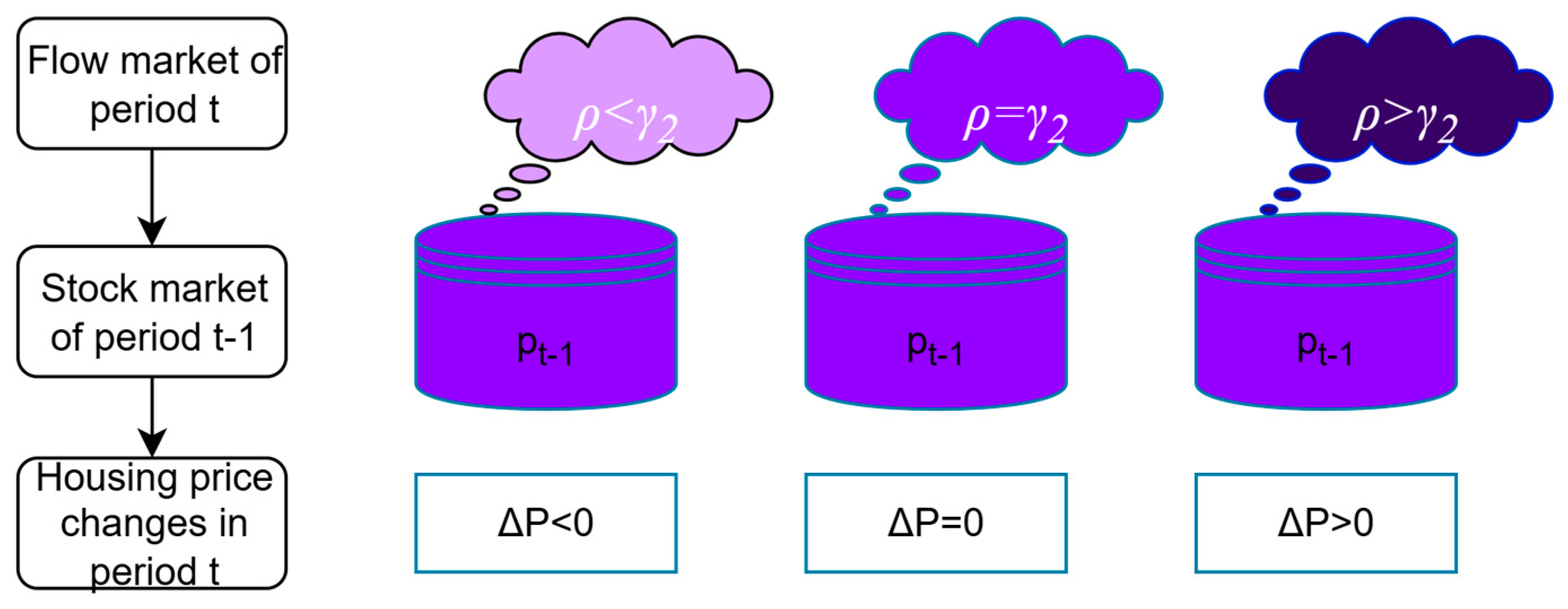
From the above results, it can be seen that the dynamic coordination of multidimensional urbanization has an impact on housing prices, as shown in Figure 3. This finding not only verifies from a dynamic perspective that the supply–demand situation of the real estate market is an important factor affecting the impact of multidimensional urbanization on housing prices, but also reveals the dynamic characteristics that a coordinated multidimensional urbanization should possess. For example, when ρ_H = 0.0088, Vsu_H = 0.991 Vpu + 0.0087. If cities adjust the speed of spatial urbanization according to this relationship, so that the newly added real estate supply can adapt to the changes in housing demand caused by population urbanization, it will help to focus the regulation of the real estate market on the sources of resource allocation such as the quantity of real estate development and land supply area, thus providing a theoretical basis and policy reference for the establishment of a linkage mechanism among the elements of “people, housing, land, and money”.

5.3. Robustness Test

To further ascertain the impact of the supply–demand conditions in the real estate flow market on housing prices, we substitute Veu and Vsu_H into the formula for ρ to derive a new threshold variable, ρ_E, and input ρ_E into model (7) to examine from different perspectives whether multidimensional urbanization dynamic coordination has a threshold effect on housing price changes. The outcomes of 500 bootstrap self-sampling tests reveal that ρ_E passes the significance test for double threshold effects at the 1% level, with threshold values of 0.0697 and 0.0784, and corresponding 95% confidence intervals of [0.0690, 0.0709] and [0.0764, 0.0788], respectively. As indicated by the regression coefficients in Table 8, the effects of P_it−1, Pd_it, Gc_it, and Lir_it on housing prices remain largely unchanged; in comparison, ρ_E has the following impact on housing prices: when the real estate flow market determined by ρ_E is in a state of oversupply, increasing housing supply will lead to a sharp decline in housing prices; when the real estate flow market is in a state of short supply, increasing housing supply will lead to a slight decline in housing prices. This once again demonstrates that multidimensional urbanization dynamic coordination ρ is an important factor determining the direction and magnitude of housing price changes in various cities. Additionally, our analysis of the dynamic heterogeneous effects of ρ on housing price changes reveals that enhancing the dynamic coordination of multidimensional urbanization can foster the sustained, stable, and healthy development of the real estate market.

6. Conclusions and Policy Recommendations

As a multifaceted and dynamic process, urbanization initially impacts the flow of real estate supply and demand across various cities, subsequently influencing the stock market and altering the spatial configuration of real estate resources, ultimately resulting in fluctuations in housing prices. The influence of single-dimensional urbanization on housing prices is contingent upon the relative shifts it induces in real estate supply or demand. If demand is increased, housing prices rise, and the magnitude of the increase is positively correlated with the speed of urbanization; however, it is also influenced by other factors, such as the supply and demand situation in the stock market. If supply is increased, housing prices may either decline or rise, and this uncertainty is related to the characteristics of the house and the social functions of spatial urbanization. The comprehensive effect of multidimensional urbanization on housing prices is influenced by its dynamic coordination. When the degree of coordination is high and the supply–demand gap in the flow market is small, housing prices will be relatively stable; when the degree of coordination is low and the supply–demand gap in the flow market is large, housing prices will undergo drastic changes. In summary, we utilize urbanization speed, urbanization coordination, and other factors to provide a detailed description of the regional real estate resource allocation process behind multidimensional urbanization and its impact on housing prices. Our efforts not only fill the gap in research on the mechanism of action between the real estate flow market and the stock market but also reveal the dynamic characteristics that coordinated multidimensional urbanization should possess, thus providing insights into improving the spatial allocation rationality of real estate resources from the source. Based on these conclusions, we propose the following policy recommendations.

Firstly, pay attention to the supply and demand situation in the real estate stock market. When the stock market is in short supply, accelerating population and economic urbanization are akin to “pouring oil on the fire,” which can lead to a surge in housing prices. Accelerating spatial urbanization can, to some extent, mitigate the upward trend of housing prices. When the stock market is in oversupply, accelerating spatial urbanization is akin to “adding insult to injury,” which can lead to a sharp decline in housing prices. Cities should make reasonable adjustments to the speed of multidimensional urbanization (real estate supply and demand flow) based on a full consideration of the supply and demand situation in the real estate stock market, thereby enhancing the overall rationality of spatial allocation of real estate resources.

Secondly, enhance the dynamic coordination of multidimensional urbanization. The coordination of multidimensional urbanization has a significant threshold effect on housing price changes. When ρ_H reaches 0.0088 and ρ_L reaches 0.0669, the real estate market achieves dynamic equilibrium, and housing prices remain relatively stable. According to the calculation formula of ρ, at this time, Vsu_H = 0.991Vpu + 0.0087, while Vsu_L = 0.937Vpu + 0.0627. Cities should adjust the spatial urbanization speed, the relative supply of newly built housing, based on this relationship, in order to adapt to the changes in housing demand caused by population urbanization and dynamically improve the spatial allocation rationality of real estate resources.

Thirdly, utilize the regulation of the flow of supply and demand on housing prices. There may be certain differences in the supply–demand conditions between the real estate flow market and the stock market, and these differences determine the direction and magnitude of housing price changes in the process of urbanization. Cities can adjust the quantity of newly built housing supply according to their own realities and local conditions. For cities with relatively scarce real estate resources, while increasing the relative supply of housing, they should also activate the stock of existing housing as much as possible. By adopting measures such as renting and selling simultaneously, ensuring the supply of affordable housing [44], and fully tapping the potential of housing supply, cities can effectively solve the housing problems of urban residents and avoid a significant increase in housing prices. For cities with relatively abundant real estate resources, it is necessary to reduce the supply of new housing or land while accelerating population inflow and urban economic development. By reducing supply and increasing demand, cities can avoid a significant decrease in housing prices.

Fourthly, establish a “supply-demand linked” real estate supply model. The speed and coordination of multidimensional urbanization provide a detailed depiction of the process of regional real estate resource allocation behind urbanization. In order to fundamentally address the issue of spatial mismatch of real estate resources, cities should adjust the supply of new housing or land in a timely manner based on changes in housing demand driven by population and economic urbanization, and gradually establish a “supply-demand linked” real estate supply model.

Lastly, enhance the overall utilization efficiency of real estate resources. For existing residential properties, issues such as information asymmetry and high costs in the second-hand housing transaction process can be addressed by establishing high-quality trading platforms and implementing proactive fiscal and tax policies. For newly built housing, we can improve the scientificity of new supply by controlling the scale of supply, enhancing the quality of the houses, and optimizing the product structure. For inventory commercial residential buildings, measures such as centralized acquisition, unified management [45], and resale-to-rent can be taken to accelerate the circulation of housing property rights and enhance the liquidity of real estate enterprises. In summary, by promoting the transformation of the real estate market from “extensive development” to “refined operation”, we can enhance the overall utilization efficiency of real estate resources.